Improved design and analysis of practical minimizers

Abstract

Motivation

Minimizers are methods to sample k-mers from a string, with the guarantee that similar set of k-mers will be chosen on similar strings. It is parameterized by the k-mer length k, a window length w and an order on the k-mers. Minimizers are used in a large number of softwares and pipelines to improve computation efficiency and decrease memory usage. Despite the method’s popularity, many theoretical questions regarding its performance remain open. The core metric for measuring performance of a minimizer is the density, which measures the sparsity of sampled k-mers. The theoretical optimal density for a minimizer is $1/w$, provably not achievable in general. For given k and w, little is known about asymptotically optimal minimizers, that is minimizers with density $O(1/w)$.

Results

We derive a necessary and sufficient condition for existence of asymptotically optimal minimizers. We also provide a randomized algorithm, called the Miniception, to design minimizers with the best theoretical guarantee to date on density in practical scenarios. Constructing and using the Miniception is as easy as constructing and using a random minimizer, which allows the design of efficient minimizers that scale to the values of k and w used in current bioinformatics software programs.

Availability and implementation

Reference implementation of the Miniception and the codes for analysis can be found at https://github.com/kingsford-group/miniception.

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

The minimizer (Roberts et al., 2004a, b; Schleimer et al., 2003), also known as winnowing, is a method to sample positions or k-mers (substrings of length k) from a long string. Given two strings that share long enough exact substrings, the minimizer selects the same k-mers in the identical substrings, making it suitable to quickly estimate how similar two strings are, and to quickly locate shared substrings. The minimizers method is very versatile and is used in various ways in many bioinformatics programs [see the reviews (Marçais et al., 2019; Rowe, 2019) for examples] to reduce the total computation cost or the memory usage.

A minimizer has three parameters: $(w,k,\mathcal{O})$. k is the length of the k-mers of interest while w is the length of the window: a least one k-mer in any window of w consecutive k-mers, or equivalently in any substring of length $w+k-1$, must be selected. Finally, $\mathcal{O}$ is a total order (i.e. a permutation) of all the k-mers, and it determines how the k-mers are selected: in each window the minimizer selects the minimum k-mer according to the order $\mathcal{O}$ (hence the name minimizer), and in case of multiple minimum k-mers, the leftmost one is selected. The main measure of performance for minimizer is the density: the expected number of positions selected divided by the length of the string. In general, minimizers with lower densities are desirable as fewer selected positions imply a further reduction in the run time or memory usage of applications using minimizers, while preserving the guarantee that for similar strings the same k-mers are selected. For given parameters w and k, the choice of the order $\mathcal{O}$ changes the expected density.

For example, a long-read aligner like Minimap2 (Li and Birol, 2018) stores the positions of every selected k-mers of a reference genome, to find exact match anchors for seed-and-extent alignment. The parameters k and w are constrained by the required sensitivity of alignment. Any choice of order $\mathcal{O}$ provides the same guarantees, but an order with a lower density reduces the size of the storage and computation time by lowering the number of anchors to consider.

The density of a minimizer is lower bounded by $1/w$, where exactly one position per window is selected, and upper bounded by 1, where every position is selected. A minimizer with a density of $1/w$ may not exist for every choice of w and k, and how to find an order $\mathcal{O}$ with the smallest possible density for any w and k efficiently is still an open question. We are interested in constructing minimizers with density of $O(1/w)$—that is, within constant factor of optimal density—and avoid minimizers with density of $\Omega (1)$.

Schleimer et al. gave two results about the density of minimizers: under some simplifying assumptions, (i) the expected density obtained by a randomly chosen order on a random input string is $2/(w+1)$ and (ii) the density is lower bounded by $1.5/(w+1)$. Although these estimates are useful in practice, they are dependent on some hidden assumptions and do not represent the behavior of minimizers in all cases.

In previous publications we refined these results in multiple ways by looking at the asymptotic behavior of minimizers, by considering the cases where k is fixed and $w\gg k$ and where w is fixed and $k\gg w$. First, when w is fixed and $k\gg w$, we gave a construction of a minimizers with density of $1/w+O(k{e}^{-\alpha k})$, for some $\alpha >0$ (Marçais et al., 2018). That is, density arbitrarily close to the optimal $1/w$ is achievable for large values of k. The apparent contradiction between this result and Schleimer’s lower bound stems from a hidden assumption: k should not be too large compared to w. Second, we showed that when k is fixed and $w\gg k$, the density of any minimizer is $\Omega (1)$. Hence, a density of $2/(w+1)$, or even $O(1/w)$, as proposed for a random order does not apply for large w and fixed k (Marçais et al., 2018). In other words, this original density estimate relies on a hidden assumption: k should not be too small compared to w.

Examples of minimizers with density <$2/(w+1)$ exist in practice, but these examples are one-off construction for a particular choice of parameters w and k (Marçais et al., 2017). Methods to construct minimizers that have density lower than $\Omega (1)$ and work for any w exist: a density of $O(\sqrt{w}/w)$ is obtained by Marçais et al. and Zheng et al. improves the result to $O(\ln (w)/w)$. But neither of them reaches the desired asymptotically optimal $O(1/w)$ density. This naturally raises the question on whether a minimizer with density $2/(w+1)$ or $O(1/w)$ is possible assuming that both parameters k and w can be arbitrarily large.

This paper has three main contributions. First, in Section 2.2, we prove that as w grows asymptotically, the condition that ${\hspace{0.17em}\text{log}\hspace{0.17em}}_{\sigma }(w)-k=O(1)$ is both a necessary and sufficient condition for the existence of minimizers with density of $O(1/w)$. In other words, to construct asymptotically optimal minimizers, it is sufficient and necessary that the length of the k-mers grows at least as fast as the logarithm of the window size.

Second, in Section 2.3, by slightly strengthening the constraint on k—i.e. $k\ge (3+ϵ){\hspace{0.17em}\text{log}\hspace{0.17em}}_{\sigma }(w)$, for any fixed $ϵ>0$—we show that a random minimizer has expected density of $2/(w+1)+o(1/w)$. This theorem is a direct extension of the result by Schleimer et al. as it removes any hidden assumptions and gives a sufficient condition for the result to hold.

Third, in Section 2.4, we give a construction of minimizers, called the Miniception, with expected density on a random string of $1.67/w+o(1/w)$ when $k\approx w$. This is an example of minimizers with guaranteed density $<2/(w+1)$ that works for infinitely many w and k, not just an ad hoc example working for one or a small number of parameters w and k. This is also the first example of a family of minimizers with guaranteed expected density $<2/(w+1)$ that works when $k\approx w$ instead of the less practical case of $k\gg w$. Moreover, unlike other methods with low density in practice (DeBlasio et al., 2019; Ekim et al., 2020; Orenstein et al., 2016), the Miniception does not require the use of expensive heuristics to precompute and store a large set of k-mers. Selecting k-mers with the Miniception is as efficient as a selecting k-mers with a random minimizer using a hash function, and does not require any additional storage.

2 Materials and Methods

2.1 Preliminary

In this section, we restate several theorems from existing literature that are useful for later sections. Most definitions follow existing literatures (Roberts et al., 2004b; Schleimer et al., 2003). In the following, $\Sigma =\{0,1,\dots ,\sigma -1\}$ is an alphabet (mapped to integers) of size σ and we assume that $\sigma \ge 2$ and is fixed. If $S\in {\Sigma }^{*}$ is a string, we use $\left|S\right|$ to denote the length of S.

Definition 1

(Minimizer and Windows). A ‘minimizer’ is characterized by $(w,k,\mathcal{O})$where w and k are integers and $\mathcal{O}$is a complete order of ${\Sigma }^k$. A ‘window’ is a string of length $(w+k-1)$, consisting of exactly w overlapping k-mers. Given a window as input, the minimizer outputs the location of the smallest k-mer according to $\mathcal{O}$, breaking ties by preferring leftmost k-mer.

When $\mathcal{O}$ is the dictionary order, it is called a lexicographic minimizer. A minimizer created by randomly choosing a permutation of ${\Sigma }^k$ uniformly over all possible permutations is called a random minimizer. (See Fig. 1 for an illustration of these and the following concepts.)

Definition 2

(Density). Given a string $S\in {\Sigma }^{*}$and a minimizer, a position in S is selected if the minimizer picks the k-mer at that position in any window of w consecutive k-mers. The specific density of a minimizer on S is the number of selected positions divided by the total number of k-mers in S. The density of a minimizer is the expected specific density on a sufficiently long random string.

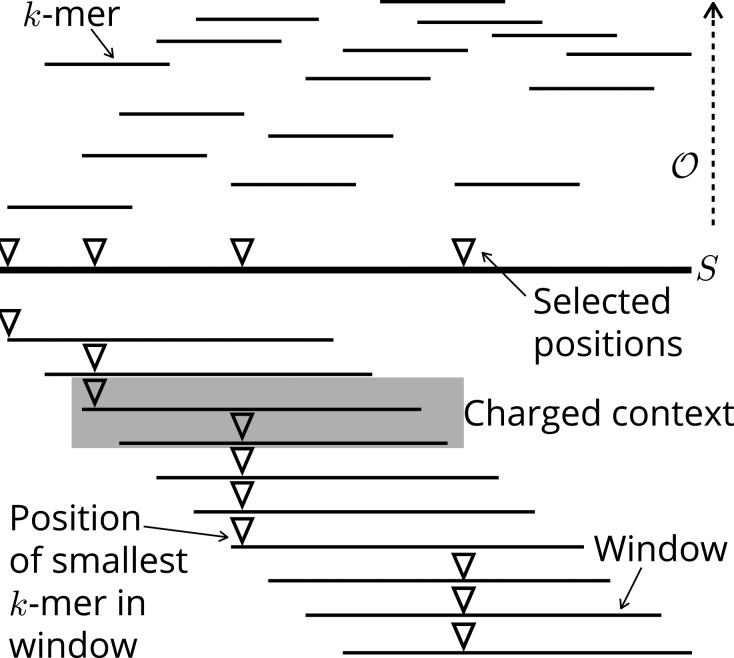
Fig. 1.

The string S is broken into k-mers. In each window (w consecutive k-mers), the position of the lowest (smallest according to $\mathcal{O}$) k-mer is selected. The gray context (two consecutive windows) is an example of a charged window because the first and second windows selected different positions. There are a total of three charged contexts in this example

Note that the density is calculated by expectation over random strings and is independent from S. For the ease of comparison, we will also use the concept of contexts and density factors:

Definition 3

(Contexts and Charged Contexts). A ‘context’ of S is a substring of length $(w+k)$, or equivalently, two overlapping windows. The minimizer is applied to both the first and last windows, and a context is ‘charged’ if different positions are picked.

Definition 4

(Density Factor). The density factor of a minimizer is its density multiplied by $(w+1)$. Intuitively, this is the expected number of selected locations in a random context.

The idea for charged contexts is to attribute picked k-mers to the window that first picked it (it is charged for picking a new k-mer). To determine whether a window is actually picking a new k-mer, it is sufficient to look back exactly one window due to the fact that minimizers pick k-mers in a forward manner, and the context is the union of the two windows necessary to determine whether this happens. This means counting picked k-mers in a string is equivalent to counting charged contexts (in other words, only charged contexts contribute to the density). Consequently, the (non-specific) density of a minimizer equals the probability that a context drawn from uniform distribution over ${\Sigma }^{w+k}$ is a charged one.

We denote by $W={\Sigma }^{w+k-1}$ the set of all possible windows and $C={\Sigma }^{w+k}$ the set of all contexts. The following lemma gives a slightly stronger condition on the positions of selected k-mers in a charged context. A similar lemma was proved by Schleimer et al. (2003) and a proof is given here for clarity.

Lemma 1

(Charged Contexts of Minimizers). For a minimizer, a context is charged if and only if the minimizer picks either the first k-mer of the first window or last k-mer in the last window.

Proof. On one hand, if the minimizer picks either the first or the last k-mer in the context, it cannot be picked in both windows. On the other hand, if the minimizer does not pick either the first or the last k-mer, it will pick the same k-mer in both windows. Assuming otherwise, both picked k-mers are in both window so this means one of them is not minimal, leading to a contradiction. □

A related concept is universal hitting sets (UHS) (Orenstein et al., 2016), which is central to the analysis of minimizers (Ekim et al., 2020; Marçais et al., 2017, 2018).

Definition 5

(Universal Hitting Sets). Assume $U\subseteq {\Sigma }^k$. If U intersects with every w consecutive k-mers (or equivalently, the set of k-mers in every $S\in W_{w,k}$), it is a UHS over k-mers with path length w and relative size $\left|U\right|/{\sigma }^k$.

Lemma 2

(Minimal Decycling Sets) (Mykkeltveit, 1972). Any UHS over k-mers has relative size at least $1/k-o(1/k)$.

2.2 Condition for asymptotically optimal minimizers

In this section, culminating with Theorem 2, we prove that to have asymptotically optimal minimizers (i.e. minimizers with density of $O(1/w)$), the value k (for the k-mers) must be sufficiently large compared to the length w of the windows, and that this condition is necessary and sufficient. To be more precise, we treat k as a function of w, and study the density as w grows to infinity. We show that the lexicographic minimizers are asymptotically optimal provided that k is large enough: ${\hspace{0.17em}\text{log}\hspace{0.17em}}_{\sigma }(w)-k=O(1)$. This result may be surprising as in practice the lexicographic minimizers have high density (Marçais et al., 2017; Roberts et al., 2004a; and see Section 4). One interpretation of Theorem 2 is that asymptotically, all minimizers behave the same regarding density.

2.2.1 Minimizers with exceedingly small k

If k is exceedingly small, in the sense that k does not even grow as fast as the logarithm of w—i.e. ${\hspace{0.17em}\text{log}\hspace{0.17em}}_{\sigma }(w)-k\to \infty$ as w grows—no minimizer will obtain density $O(1/w)$. To see this, for any order $\mathcal{O}$, let y be the smallest of all k-mers. Any context starting with y is charged, and the proportion of such context is ${\sigma }^{-k}$. The density calculated from these contexts only is already $>\Theta (1/w)$, as $w{\sigma }^{-k}={\sigma }^{{\hspace{0.17em}\text{log}\hspace{0.17em}}_{\sigma }(w)-k}\to \infty$.

For this reason, in the following we are only interested in the case where k is large enough. That is, there exists a fixed constant c such that $k\ge {\hspace{0.17em}\text{log}\hspace{0.17em}}_{\sigma }(w)-c$ for all sufficiently large w.

2.2.2 Lexicographic minimizers

We first prove the special case that the lexicographic minimizer achieves $O(1/w)$ density with parameter $k=\lfloor {\hspace{0.17em}\text{log}\hspace{0.17em}}_{\sigma }(w/2)\rfloor -2$. Recall $W={\Sigma }^{k+w-1}$ is the set of all windows, and $C={\Sigma }^{k+w}$ is the set of all contexts. Let $z\in W$ be a window, $f(z):W\to \{0,1,\dots ,w-1\}$ be the minimizer function, and $\mathcal{C}\subset C$ be the set of charged contexts for this minimizer. Let $W^{+}=\{z\in W|f(z)=0\}$, the set of windows where the minimizer picks the first k-mer, and similarly $W^{-}=\{z\in W|f(z)=w-1\}$. By Lemma 1, we know $\left|\mathcal{C}\right|\le \sigma (|W^{+}|+|W^{-}|)$.

We now use the notion $\#$ to denote any non-zero character of Σ, and $0^d$ to denote d consecutive zeroes. Let $A_{*}^{+}$ be the set of windows whose first k-mer is $0^k$, and for $1\le i\le k$, let $A_i^{+}=\{z\in W|z=0^{i-1}\#\cdots ,f(z)=0\}$, that is, the set of windows that starts with exactly i – 1 zeros and have the minimizer function pick the first k-mer. All $A_i^{+}$ and A⁺ are mutually disjoint. Since the minimizer always pick $0^k$ at the start of the window, we have $W^{+}=A_{*}^{+}\cup \underset{i=1}{\overset{k}{\cup }}{A}_i^{+}$.

Lemma 3

For $1\le i\le k,\hspace{0.17em}{A}_i^{+}\subseteq B_i^{+}$, where $B_i^{+}=\{z\in W|z=0^{i-1}\#st,\left|s\right|=w-1,\left|t\right|=k-i,0^i\notin s\}$, that is, the set of windows that starts with $0^{i-1}\#$and does not contain $0^i$in the next w−1 bases.

Proof. We need to show that if a window z starts with $0^{i-1}\#$ and is not in $B_i^{+},\hspace{0.17em}f(z)\ne 0$. As $z\notin B_i^{+}$, there is a stretch of $0^i$ in z before the last k−i characters. This means that there is a k-mer of form $0^i\cdots$ in z, and since the first k-mer is of form $0^{i-1}\#\cdots$, the minimizer will never pick the first k-mer. □

In our previous paper (Zheng et al., 2020), we proved that.

Lemma 4

The probability that a random string of length $\ell$does not contain $0^d$anywhere is at most $3{(1-1/{\sigma }^{d+1})}^{\ell }$.

Setting $\ell =w-1$ and d = i and noting there are ${\sigma }^{k-i}$ choices for t in B_i, we know $\left|B_i^{+}\right|\le 3{\sigma }^{w+k-i}{(1-1/{\sigma }^{i+1})}^{w-1}$ for every i. This is sufficient to prove the following:

Lemma 5

$\left|W^{+}\right|=O({\sigma }^w)$.

Proof. Let $b_i=3{\sigma }^{w+k-i}{(1-1/{\sigma }^{i+1})}^{w-1}$, combined with the fact that $\left|A_{*}^{+}\right|={\sigma }^{w-1}$, we know $\left|W^{+}\right|\le {\sigma }^{w-1}+{\sum }_{i=1}^k{b}_i$. It remains to bound the summation term.

We next prove $b_i>2b_{i-1}$ for $2\le i\le k$:

$$\begin{array}{c}{b}_i/b_{i-1}=\frac{3{\sigma }^{w+k-i}{(1-1/{\sigma }^{i+1})}^{w-1}}{3{\sigma }^{w+k-i+1}{(1-1/{\sigma }^i)}^{w-1}}\\ =\frac{1}{\sigma }{\left(1+\frac{\sigma -1}{{\sigma }^{i+1}-\sigma }\right)}^{w-1}\\ >\frac{1}{\sigma }\left(1+\frac{w-1}{{\sigma }^{i+1}-\sigma }\right)>\frac{w}{{\sigma }^{i+2}}.\end{array}$$

Note that we also use the fact ${(1+x)}^t>1+xt$ and $\sigma -1\ge 1$ in the last line. The right-hand side is minimum when i = k. By our choice of k, ${\sigma }^{k+2}<w/2$, so the term is lower bounded by 2.

This implies ${\sum }_{i=1}^k{b}_i<2b_k$, and since $b_k=O({\sigma }^w)$, we have $\left|W^{+}\right|=O({\sigma }^w)$. □

The bound for $\left|W^{-}\right|$ is computed similarly. It is different from W⁺ as in case of ties for the minimal k-mer, the leftmost one is picked. Hence, we define $W^{‡}$ as the set of windows such that the last k-mer is one of the minimal k-mers in the window. We have $W^{-}\subseteq W^{‡}$, as the last k-mer needs to be the minimal, with no ties, for the minimizer to pick it.

Similarly, we define $A_{*}^{-}$ as the set of windows that ends with $0^k$. For $1\le i\le k$, we define $A_i^{-}=\{z\in W^{‡}|z=s{0}^{i-1}\#t,\left|s\right|=w-1,\left|t\right|=k-i\}$. This is the set of windows whose last k-mer starts with $0^{k-1}\#$ while satisfying the condition for $W^{‡}$. Again, $A_{*}^{-}$ and all $A_i^{-}$ are mutually disjoint, and we have $W^{‡}=A_{*}^{-}\cup {\cup }_{i=1}^k{A}_i^{-}$. There is an analogous lemma for bounding $\left|A_i^{-}\right|$:

Lemma 6

For $1\le i\le k,\hspace{0.17em}{A}_i^{-}\subseteq B_i^{-}$, where $B_i^{-}=\{z\in W|z=s{0}^{i-1}\#t,\left|s\right|=w-1,\left|t\right|=k-i,0^i\notin s\}$.

Proof. We need to show that if a window ends with a k-mer of form $0^{i-1}\#t$ and contains $0^i$ before last k-mer, it is not in $W^{‡}$. In that case the window contains a k-mer of form $0^i\cdots$, which is strictly smaller than the last k-mer of the form $0^{i-1}\#\cdots$, violating the condition of $W^{‡}$. □

Note that $B_i^{+}$ and $B_i^{-}$ have highly similar expressions. In fact, we can simply bound the size of $B_i^{-}$ by b_i (defined in the proof of Lemma 5) using the identical argument. This immediately means that we have the exactly same bound for $\left|W^{‡}\right|$ and $\left|W^{+}\right|$, as $A_{*}^{-}$ also has the same size as $A_{*}^{+}$.

Theorem 1The lexicographic minimizer with $k_0=\lfloor {\hspace{0.17em}\text{log}\hspace{0.17em}}_{\sigma }(w/2)\rfloor -2$has density $O(1/w)$.

Proof. We have $\left|\mathcal{C}\right|\le \sigma (|W^{+}|+|W^{-}|)\le \sigma (|W^{+}|+|W^{‡}|)=O({\sigma }^w)$, and the density is $\left|\mathcal{C}\right|/{\sigma }^{w+k_0}=O({\sigma }^{-k_0})=O(1/w)$. □

Next, we extend this result to show that this bound holds for all k as long as $k>{\hspace{0.17em}\text{log}\hspace{0.17em}}_{\sigma }(w)-c$ for some constant c. As $k_0<{\hspace{0.17em}\text{log}\hspace{0.17em}}_{\sigma }w$, the following lemmas establish our claim for small and large k:

Lemma 7

The lexicographic minimizer with $k=k_0-c$for constant $c\ge 0$has density $O(1/w)$.

Lemma 8

The lexicographic minimizer with $k>k_0$has density $O(1/w)$.

We prove both lemmas in Supplementary Section S1. Combining everything we know, we have the following theorem.

Theorem 2For $k\ge {\hspace{0.17em}\text{log}\hspace{0.17em}}_{\sigma }(w)-c$with constant c, the lexicographic minimizer achieves density of $O(1/w)$. Otherwise, no minimizer can achieve density of $O(1/w)$.

2.3 Density of random minimizers

We now study the density of random minimizers. Random minimizers are of practical and theoretical interest. In practice, implementing a random minimizer is relatively easy using a hash function, and these minimizers usually have lower density than lexicographic minimizers. Consequently, most software programs using minimizers use a random minimizer. The constant hidden in the big-O notation of Theorem 2 may also be too large for practical use, while later in Theorem 3, we guarantee a density of $2/(w+1)+o(1/w)$ with a slightly more strict constraint over k.

Schleimer et al. (2003) estimated the expected density of random minimizers to be $2/(w+1)$ with several assumptions on the string (which do not strictly hold in practice), and our main theorem (Theorem 3) achieves the same result up to $o(1/w)$ with a single explicit hypothesis between w and k. Combined with our previous results on connecting UHS to minimizers, we also provide an efficient randomized algorithm to construct compact UHS with $2+o(1)$ approximation ratio.

2.3.1 Random minimizers

In the estimation of the expected density for random minimizers, there are two sources of randomness: (i) the order $\mathcal{O}$ on the k-mers is selected at random among all the permutations of ${\Sigma }^k$ and (ii) the input string is a very long random string with each character chosen IID. The key tool to this part is the following lemma to control the number of ‘bad cases’ when a window contains two or more identical k-mers. Chikhi et al. (2016) proved a similar statement with slightly different methods.

Lemma 9

For any $ϵ>0$, if $k>(3+ϵ){\hspace{0.17em}\text{log}\hspace{0.17em}}_{\sigma }w$, the probability that a random window of $w k$-mers contains two identical k-mers is $o(1/w)$.

Proof. We start with deriving the probability that two k-mers in fixed locations i and j are identical in a random window. Without loss of generality, we assume i < j. If $j-i\ge k$, the two k-mers do not share bases, so given they are both random k-mers independent of each other, the probability is ${\sigma }^{-k}=1/w^{3+ϵ}=o(1/w^3)$.

Otherwise, the two k-mers intersect. We let $d=j-i$, and m_i to denote ith k-mer of the window. We use x to denote the substring from the start of m_i to the end of m_j with length k + d (or equivalently, the union of m_i and m_j). If m_i = m_j, the nth character of m_i is equal to the nth character of m_j, meaning $x_n=x_{n+d}$ for all $0\le n<k$. This further means that x is a repeating sequence of period d, so x is uniquely determined by its first d characters and there are σ^d possible configurations of x. The probability a random x satisfies m_i = m_j is then ${\sigma }^d/{\sigma }^{k+d}={\sigma }^{-k}=o(1/w^3)$, which is also the probability of m_i = m_j for a random window.

The event that the window contains two identical k-mers is the union of events of form m_i = m_j for i < j, and each of these events happens with probability $o(1/w^3)$. Since there are $\Theta (w^2)$ events, by the union bound, the probability that any of them happens is upper bounded by $o(1/w)$. □

We are now ready to prove the main theorem of this section.

Theorem 3For $k>(3+ϵ){\hspace{0.17em}\text{log}\hspace{0.17em}}_{\sigma }(w+1)$, the expected density of a random minimizer is $2/(w+1)+o(1/w)$.

Proof. Given a context $c\in {\Sigma }^{w+k}$, we use I(c) to denote the event that c has two identical k-mers. As c has $(w+1) k$-mers, by Lemma 9, $P_c(I(c))=o(1/w)$ assuming that c is a random context.

Recall that a random minimizer means the order $\mathcal{O}$ is randomized, and $\mathcal{C}$ is the set of charged contexts. For any context c that does not have duplicate k-mers, we claim $P_{\mathcal{O}}(c\in \mathcal{C})=2/(w+1)$. This is because given all k-mers in c are distinct, under the randomness of $\mathcal{O}$, each k-mer has probability of exactly $1/(w+1)$ to be the minimal. By Lemma 1, $c\in \mathcal{C}$ if and only if the first or the last k-mer is the minimal, and as these two events are mutually exclusive, the probability of either happening is $2/(w+1)$. The expected density of the random minimizer then follows:

$$\begin{array}{c}{P}_{c,\mathcal{O}}(c\in \mathcal{C})=P(I(c))P(c\in \mathcal{C}|I(c))+P(\overline{I\left(c\right)})P(c\in \mathcal{C}|\overline{I(c)})\\ \le P(I(c))+P(c\in \mathcal{C}|\overline{I(c)})\\ =o(1/w)+2/(w+1).\end{array}$$

□

2.3.2 Approximately optimal UHS

One interesting implication of Theorem 3 is on construction and approximation of compact UHS. In our previous paper (Zheng et al., 2020), we proved a connection between UHS and forward schemes. We restate it with minimizers, as follows.

Theorem 4For any minimizer $(w,k,\mathcal{O})$, the set of charged contexts $\mathcal{C}$over a de Bruijn sequence of order w + k is a UHS over $(w+k)$-mers with path length w, and with relative size identical to the density of the minimizer.

This theorem, combined with the density bound derived last section, allows efficient construction of approximately optimal UHS. We say that an algorithm for constructing UHS is efficient if it runs in $\text{poly}(w,k){\sigma }^{w+k}$ time, as the output length of such algorithms is already at least ${\sigma }^{w+k}$.

Theorem 5For sufficiently large k and for arbitrary w, there exists an efficient randomized algorithm to generate a $(2+o(1))$-approximation of a minimum size UHS over k-mers with path length w.

We prove this by discussing the case with k > w and k < w separately, as shown in Supplementary Section S2. This is also the first known efficient algorithm to achieve constant approximation ratio, as previous algorithms (DeBlasio et al., 2019; Ekim et al., 2020; Orenstein et al., 2016) use path cover heuristics with approximation ratio dependent on w and k.

2.4 The Miniception

In this section, we develop a minimizer (or rather, a distribution of minimizers) with expected density strictly below $2/(w+1)+o(1/w)$. The construction works as long as w < xk for some constant x. One other method exists to create minimizers with density below $2/(w+1)$ (Marçais et al., 2018), but it requires $w\ll k$, a much more restrictive condition.

The name ‘Miniception’ is shorthand for ‘Minimizer Inception’, a reference to its construction that uses a smaller minimizer to construct a larger minimizer. In the estimation of the expected density of Miniception minimizers, there are multiple sources of randomness: the choice of orders in the small and in the large minimizers, and the chosen context. The construction and the proof of Miniception use these sources of randomness to ensure its good performance on average.

2.4.1 A tale of two UHS

UHS are connected to minimizers in two ways. The first connection, via the charged context set of a minimizer, is described in Theorem 4. The second and more known connection is via the idea of compatible minimizers. Detailed proof of the following properties are available in Marçais et al. (2017, 2018).

Definition 6

(Compatibility). A minimizer $(w,k,\mathcal{O})$is said to be compatible with a UHS U, if the path length of U is at most w and for any $m\in U,m\prime \notin U,\hspace{0.17em}m<m\prime$under $\mathcal{O}$.

Lemma 10

(Properties of Compatible Minimizers). If a minimizer is compatible with a UHS, (i) any k-mer outside the UHS will never be picked by the minimizer, and (ii) the relative size of the UHS is an upper bound to the density of the minimizer.

Theorem 6Any minimizer $(w,k,\mathcal{O})$is compatible with the set of selected k-mers over a de Bruijn sequence of order w + k.

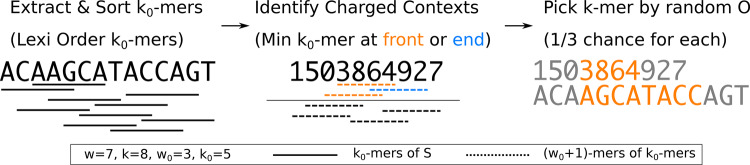
The Miniception is a way of constructing minimizers that uses the UHS in both ways. Assume that we have a minimizer $(w_0,k_0,{\mathcal{O}}_0)$. By Theorem 4, its charged context set ${\mathcal{C}}_0$ is a UHS over $(w_0+k_0)$-mers with path length w₀. According to Definition 6 and Theorem 6, we can construct a minimizer $(w,k,\mathcal{O})$ that is compatible with ${\mathcal{C}}_0$, where $k=w_0+k_0,\hspace{0.17em}w\ge w_0$ and any k-mer in ${\mathcal{C}}_0$ is less than any k-mer outside ${\mathcal{C}}_0$ according to $\mathcal{O}$.

We assume that the smaller minimizer $(w_0,k_0,{\mathcal{O}}_0)$ is a random minimizer and that the larger minimizer $(w,k,\mathcal{O})$ is a random compatible minimizer (meaning the order of k-mers within ${\mathcal{C}}_0$ is random in $\mathcal{O}$). The Miniception is formally defined as follows:

Definition 7

(The Miniception). Given parameters w, k and k₀, set $w_0=k-k_0$. The Miniception is a minimizer with parameters w and k constructed as follows:

• A random minimizer $(w_0,k_0,{\mathcal{O}}_0)$called the ‘seed’ is generated.

• The set of charged contexts ${\mathcal{C}}_0\subset {\Sigma }^k$is calculated from the seed minimizer (note that $k=w_0+k_0$).

• The order $\mathcal{O}$of the resulting minimizer is constructed by generating a random order within ${\mathcal{C}}_0$, and having every other k-mer compare larger than any k-mers in ${\mathcal{C}}_0$.

Note that by Lemma 10, the order within k-mers outside ${\mathcal{C}}_0$ does not matter in constructing $\mathcal{O}$. In the following three sections, we will prove the following theorem:

Theorem 7With $w=w_0+1,\hspace{0.17em}k=w_0+k_0$and $k_0>(3+ϵ){\hspace{0.17em}\text{log}\hspace{0.17em}}_{\sigma }(2w_0+2)$, the expected density of the Miniception is upper bounded by $1.67/w+o(1/w)$.

As $k=w_0+k_0$, for large values of w₀, we can take for example $k_0=4{\hspace{0.17em}\text{log}\hspace{0.17em}}_{\sigma }{w}_0$, meaning $w\approx k$ in these cases. This makes the Miniception the only known construction with guaranteed density $<2/(w+1)+o(1/w)$ and with practical parameters.

Figure 2 provides an example of the Miniception. The Miniception can be implemented efficiently in practice. Assuming that a random order is computed with a hash function in O(k) time for a k-mer, determining the set of picked k-mers in a string S in takes $O(k|S|)$ time. This is as fast as a random minimizer. In particular, there is no need to precompute the set ${\mathcal{C}}_0$. We discuss the implementation in more detail in Supplementary Section S4 and provide a reference implementation in the GitHub repository.

Fig. 2.

An example of running the Miniception in a window. The k₀-mers and $(w_0+1)$-mers are displayed by their order in $\mathcal{O}$ and ${\mathcal{O}}_0$, where the minimal elements appear at the top. We take ${\mathcal{O}}_0$ to be lexicographic order for simplicity, and $\mathcal{O}$ is a random order. The idea of sorting k₀-mers will be important in deriving the theoretical guarantees of the Miniception

2.4.2 The permutation argument

We now focus on the setup outlined in Theorem 7. Our goal is to measure the density of the Miniception, which is equivalent to measuring the expected portion of charged contexts, that is, $P(c\in \mathcal{C})$. There are three sources of randomness here: (i) the randomness of the seed minimizer, (ii) the randomness of the order within ${\mathcal{C}}_0$ (which we will refer to as the randomness of $\mathcal{O}$), and (iii) the randomness of the context.

A context of the Miniception is a $(w+k)=(2w_0+k_0+1)$-mer, which contains $(2w_0+2) k_0$-mers. By our choice of k₀ and Lemma 9, the probability that the context contains two identical k₀-mers is $o(1/w_0)=o(1/w)$ (as $w=w_0+1$). Similar to our reasoning in proving Theorem 3, let I₀ denote the event of duplicate k₀-mers in a Miniception context:

$$\begin{array}{c}P(c\in \mathcal{C})=P(I_0(c))P(c\in \mathcal{C}|I_0(c))+P(\overline{I_0(c)})P(c\in \mathcal{C}|\overline{I_0(c)})\\ \le P(I_0(c))+P(c\in \mathcal{C}|\overline{I_0(c)})\\ =o(1/w)+P(c\in \mathcal{C}|\overline{I_0(c)}).\end{array}$$

We now consider a fixed context that has no duplicate k₀-mers. Recall the way we determine whether a k-mer is in ${\mathcal{C}}_0$: we check whether it is a charged context of the seed minimizer, which involves only comparisons between its constituent k₀-mers. This means that given a context of the Miniception, we can determine whether each of its k-mer is in the UHS ${\mathcal{C}}_0$ only using the order between all k₀-mers. We use $\text{Ord}(c)$ to denote the order of k₀-mers within c according to ${\mathcal{O}}_0$. Conditioned on any c with $\overline{I_0}(c)$, over the randomness of ${\mathcal{O}}_0$, the order of the k₀-mers inside c now follows a random permutation of $(2w_0+2)=2w$, which we denote as $\mathcal{R}(2)$.

Next, we consider fixing both c and ${\mathcal{O}}_0$ (the only randomness is in $\mathcal{O}$) and calculate probability that the context is charged. Note that fixing c and ${\mathcal{O}}_0$ means fixed $\text{Ord}(c)$, and fixed set of k-mers in ${\mathcal{C}}_0$. The order of the k-mers is still random due to randomness in $\mathcal{O}$. For simplicity, if a k-mer is in ${\mathcal{C}}_0$, we call it a UHS k-mer. A boundary UHS k-mer is a UHS k-mer that is either the first or the last k-mer in the context c.

Lemma 11

Assume a fixed context c with no duplicate k₀-mers and a fixed ${\mathcal{O}}_0$. Denote $m_{\text{boundary}}$as the number of boundary UHS k-mers ($m_{\text{boundary}}\in \{0,1,2\}$) and let $m_{\text{total}}$be the number of total UHS k-mers in the context. The probability that the context is charged, over the randomness of $\mathcal{O}$, is $m_{\text{boundary}}/m_{\text{total}}$.

Proof. We first note that $m_{\text{total}}\ge 1$ for any context and any ${\mathcal{O}}_0$, due to ${\mathcal{C}}_0$ being a UHS over k-mers with path length $w_0\le w$, so the expression is always valid. Furthermore, there are also no duplicate k-mers as $k>k_0$. As $\mathcal{O}$ is random, every UHS k-mer in the window has equal probability to be the minimal k-mer. The context is charged if one of the boundary UHS k-mers is chosen in this process, and the probability is $1/m_{\text{total}}$ for each boundary UHS k-mer, so the total probability is $m_{\text{boundary}}/m_{\text{total}}$. □

This proof holds for every c and ${\mathcal{O}}_0$ satisfying $\overline{I_0}$. In this case, both $m_{\text{boundary}}$ and $m_{\text{total}}$ are only dependent on $\text{Ord}(c)$. This means that we can write the probability of charged context conditioned on $\overline{I_0}$ with a single source of randomness, as follows:

$$\begin{array}{c}P(c\in \mathcal{C})\le P_{c,{\mathcal{O}}_0,\mathcal{O}}(c\in \mathcal{C}|\overline{I_0(c)})+o(1/w)\\ ={\mathbb{E}}_{c,{\mathcal{O}}_0}(m_{\text{boundary}}/m_{\text{total}})+o(1/w)\\ ={\mathbb{E}}_{\text{Ord}(c)\sim \mathcal{R}(2)}(m_{\text{boundary}}/m_{\text{total}})+o(1/w).\end{array}$$

Next, we use E₀ to denote the event that the first k-mer in the context is a UHS k-mer, and E₁ to denote the event for the last k-mer. These two events are also only dependent on $\text{Ord}(c)$. We then have $m_{\text{boundary}}=1(E_0)+1(E_1)$. By linearity of expectation, we have the following:

$$\begin{array}{c}P(c\in \mathcal{C})={\mathbb{E}}_{\text{Ord}(c)\sim \mathcal{R}(2)}(m_{\text{boundary}}/m_{\text{total}})+o(1/w)\\ ={\mathbb{E}}_{\text{Ord}(c)\sim \mathcal{R}(2)}((1(E_0)+1(E_1)/m_{\text{total}})+o(1/w)\\ ={\mathbb{E}}_{\text{Ord}(c)\sim \mathcal{R}(2)}(1/m_{\text{total}}|E_0)P(E_0)\\ \hspace{1em}+{\mathbb{E}}_{\text{Ord}(c)\sim \mathcal{R}(2)}(1/m_{\text{total}}|E_1)P(E_1)+o(1/w).\end{array}$$

As the problem is symmetric, it suffices to solve one term. We have $P(E_0)=2/w$, because E₀ is true if and only if the minimal k₀-mer in the first k-mer is either the first or the last one, and there are $w k_0$-mers in a k-mer. The only term left is ${\mathbb{E}}_{\text{Ord}(c)\sim \mathcal{R}(2)}(1/m_{\text{total}}|E_0)$.

In the next two sections, we will upper bound this last term, which in turn bounds $P(c\in \mathcal{C})$. It helps to understand why this argument achieves a bound better than a purely random minimizer, even though the Miniception looks very randomized. The context contains two UHS k-mers on average, because the relative size of ${\mathcal{C}}_0$ is $2/w+o(1/w)$, so it may appear that the expectation term is close to 0.5, which leads to a density bound of $2/w+o(1/w)$, identical to a random minimizer. However, conditioned on E₀, the context provably contains at least one other UHS k-mer, and with strictly positive chance contains two or more other UHS k-mers, which brings the expectation down strictly below 0.5.

2.4.3 Deriving the unconditional distribution

In this section, we bound the quantity ${\mathbb{E}}_{\text{Ord}(c)\sim \mathcal{R}(2)}(1/m_{\text{total}}|E_0)$ by deriving the distribution of $m_{\text{total}}$, where $\text{Ord}(c)$ is sampled from $\mathcal{R}(2)$ conditioned on E₀. We emphasize that at this point the actual k₀-mers are not important and only their order matters. It is beneficial to view the sequence simply as the order $\text{Ord}(c)$. To prepare for the actual bound, we will first derive the distribution of $m_{\text{total}}$ assuming $\text{Ord}(c)\sim \mathcal{R}(2)$ without extra conditions.

We are interested in the asymptotic bound, meaning $w\to \infty$, so we use the following notation. Let $\mathcal{R}(x)$ denote the distribution of random order of xw elements. This is consistent with previous definition of $\mathcal{R}(2)$, as a context contains $2w k_0$-mers. The relative length of a sequence is defined by its number of k₀-mers divided by w. Given a sequence of relative length x, where the order of its constituent k₀-mers follows $\mathcal{R}(x)$, let $P_n(x)$ denote the probability that the sequence contains exactly n UHS k-mers. As a context is a sequence of relative length 2, we are interested in the value of $P_n(x)$ for $x\le 2$.

We derive a recurrence for $P_n(x)$. Fix x, the relative length of the sequence. We iterate over the location of the minimal k₀-mer and let its location be tw where $0\le t\le x$.

There are two kinds of UHS k-mers for this sequence. The first kind contains the minimal k₀-mer of the sequence, and there can be at most two of them: one starting with that k₀-mer and one ending with that k₀-mer. The second kind does not contain the minimal k₀-mer, so it is either to the left of the minimal k₀-mer or to the right of the minimal k₀-mer, in the sense that it does not contain the minimal k₀-mer in full. Precisely, it is from the substring that contains exactly the set of k₀-mers left to the minimal k₀-mer or from the substring that contains exactly the set of k₀-mers right to the minimal k₀-mer: these two substrings have an overlap of $k_0-2$ bases but do not share any k₀-mer, and neither contain the minimal k₀-mer. We refer to these sequences as the left and right substring for conciseness.

This divides the problem of finding n UHS k-mers into two subproblems: finding UHS k-mers left of location tw and finding UHS k-mers right of location tw. If we sample an order from $\mathcal{R}(x)$, conditioned on the minimal k₀-mer on location tw, the order of the k₀-mers left of the minimal k₀-mer follows $\mathcal{R}(t)$, and similarly $\mathcal{R}(x-t)$ for the k₀-mers right of the minimal k₀-mer. As we assume $w\to \infty$, we ignore that two substrings combined have one less k₀-mer. We prove in Supplementary Section S3.6 that this simplification introduces a negligible error. This means that the subproblems have an identical structure to the original problem.

We start with the boundary conditions. For x < 1, corresponding to a sequence with relative length <1, it contains no k-mer so with probability 1 the sequence contains no UHS k-mer. This means that $P_0(x)=1$ and $P_n(x)=0$ for $n\ge 1$. We now derive the value of $P_0(x)$, that is, the probability the sequence contains no UHS k-mer for $1\le x\le 2$. Define the middle region as the set of k₀-mer locations that are at most $w-2 k_0$-mers away from both the first and the last k₀-mer. The sequence contains no UHS k-mer if and only if the minimal k₀-mer falls within the middle region, as only in this case every k-mer contains the minimal k₀-mer but none has it at the boundary. The relative length of the middle region is $2-x$, as we assume $w\to \infty$ (see Fig. 3). As the order of k₀-mers follows $\mathcal{R}(x)$, every k₀-mer has equal probability to be the minimal and it is in the middle region with probability $(2-x)/x=2/x-1$.

Fig. 3.

Setup for derivation of $P_n(x)$ with $n\ge 1$ and $1\le x\le 2$. The text denotes the relative length of the corresponding substrings. If the minimal k₀-mer falls into the middle region (left panel), there are zero UHS k-mers in the sequence. Otherwise (right panel), there is at least one UHS k-mer with possibility for more from the substring

For $1\le x\le 2$, we next derive the recurrence for $P_n(x)$ with $n\ge 1$ (as seen in Fig. 3). We define the middle region in an identical way as in last lemma, whose relative length is again $2-x$. If the minimal k₀-mer is in the middle region, the sequence has exactly zero UHS k-mers. Otherwise, by symmetry we assume that it is to the left of the middle region (that is, at least $w-1 k_0$-mers away from the last k₀-mer in the sequence), with location tw where $0\le t<x-1$. The sequence now always has one UHS k-mer, that is the k-mer starting with the minimal k₀-mer, and all other $(n-1)$ UHS k-mers come from the substring right to the minimal k₀-mer. The substring has relative length x – t, and as argued above, the probability of observing exactly $(n-1)$ UHS k-mers from the substring is $P_{n-1}(x-t)$. Averaging over t, we have the following:

$$P_n(x)=\frac{2}{x}{\int }_0^{x-1}{P}_{n-1}(x-t)\mathrm{d}t,n\ge 1,1\le x\le 2.$$

Given $P_0(x)=2/x-1$, we can solve for the next few P_n for $1\le x\le 2$ as described in Supplementary Section S3.3. Recall our goal is to upper bound ${\mathbb{E}}_{\text{Ord}(c)\sim \mathcal{R}(2)}(1/m_{\text{total}}|E_0)$. For this purpose, $P_n(x)$ is not sufficient as the expectation is conditioned on E₀.

2.4.4 Deriving the conditional distribution

We now define the events $E_0^{+}$ and $E_0^{-}$. $E_0^{+}$ is the event that the first k-mer of the Miniception context is a UHS k-mer, because inside the first k-mer the minimal k₀-mer is at the front. Similarly, $E_0^{-}$ is the event where the first k-mer is a UHS k-mer, because the last k₀-mer in the first k-mer is minimal. These events are mutually exclusive and have equal probability of $1/w$, so $P(E_0^{+}|E_0)=P(E_0^{-}|E_0)=1/2$.

Definition 8

(Restricted Distribution). ${\mathcal{R}}^{+}(x)$for $x\ge 1$is the distribution of random permutations of xw elements, conditioned on the event that the first element is minimum among first w elements. Similarly, ${\mathcal{R}}^{-}(x)$for $x\ge 1$is the distribution of random permutations of xw elements, conditioned on the event that the last element is minimum among first w elements.

We now have the following:

$$\begin{array}{c}{\mathbb{E}}_{\text{Ord}(c)\sim \mathcal{R}(2)}(1/m_{\text{total}}|E_0)\\ =\mathbb{E}(1/m_{\text{total}}|E_0^{+})P(E_0^{+}|E_0)+\mathbb{E}(1/m_{\text{total}}|E_0^{-})P(E_0^{-}|E_0)\\ =({\mathbb{E}}_{\text{Ord}(c)\sim {\mathcal{R}}^{+}(2)}(1/m_{\text{total}})+{\mathbb{E}}_{\text{Ord}(c)\sim {\mathcal{R}}^{-}(2)}(1/m_{\text{total}}))/2.\end{array}$$

Based on this, we define $Q_n^{+}(x)$ to be the probability that a sequence of relative length xw, where the order of k₀-mers inside the sequence follows ${\mathcal{R}}^{+}(x)$, contains exactly n UHS k-mers. Our goal now is to determine $Q_n^{+}(x)$ for $x\le 2$, which also bounds ${\mathbb{E}}_{\text{Ord}(c)\sim {\mathcal{R}}^{+}(2)}(1/m_{\text{total}})$.

The general idea of divide-and-conquer stays the same in deriving a recurrence for $Q_n^{+}(x)$. It is, however, trickier to apply this idea with a conditional distribution. We solve this issue by defining the following:

Definition 9

(Restricted Sampling). With fixed x and w, the restricted sampling process samples a permutation of length xw, then swap the minimum element in the first w element with the first element.

Lemma 12

Denote the distribution generated by the restricted sampling process as ${\mathcal{S}}^{+}(x)$, then ${\mathcal{S}}^{+}(x)={\mathcal{R}}^{+}(x)$.

We prove this in Supplementary Section S3.1. As the distributions are the same, we redefine $Q_n^{+}(x)$ with ${\mathcal{S}}^{+}(x)$. The boundary condition for $Q^{+}(x)$ is $Q_0^{+}(x)=0$ for all x, because the first k-mer is guaranteed to be a UHS k-mer (note that $Q_n^{+}(x)$ is defined only with $x\ge 1$).

For $n\ge 1$ and $x\le 2$, from the process of restricted sampling, we know with probability $1/x$ the minimal k₀-mer in the sequence is the first k₀-mer overall. In this case, the first k-mer is the only UHS k-mer that contains the minimal k₀-mer, and all other UHS k-mers come from the substring without the first k₀-mer whose relative length is still x as we assume $w\to \infty$. We claim the following:

Lemma 13

Given an order of k₀-mers sampled from ${\mathcal{S}}^{+}(x)$, conditioned on the first k₀-mer being overall minimal, the k₀-mer order excluding the first k₀-mer follows the unrestricted distribution $\mathcal{R}(x)$.

This is proved in Supplementary Section S3.1. This lemma means that the probability of observing $(n-1)$ UHS k-mers outside the first k₀-mer is $P_{n-1}(x)$. Otherwise, we use the same argument as before by setting the location of the minimal k₀-mer to be tw, where $1\le t\le x$. Only one UHS k-mer contains the minimal k₀-mer with probability 1 (if x = 2, t = 2 happens with probability 0), and all other UHS k-mers come from the substring to the left of the minimal k₀-mer. By a similar argument, the order of k₀-mers within the left substring follows ${\mathcal{S}}^{+}(t)$. These arguments are also shown in Figure 4. Averaging over t, we have the following recurrence for $Q_n^{+}(x)$, valid for $1<x\le 2$ and $n\ge 1$:

$$Q_n^{+}(x)=\frac{1}{x}\left(P_{n-1}(x)+{\int }_1^x{Q}_{n-1}^{+}(t)\mathrm{d}t\right).$$

Fig. 4.

Setup for derivation of $Q_n^{+}(x)$ with $n\ge 1$ and $1\le x\le 2$. The text denotes the relative length of the corresponding substrings. If the minimal k₀-mer is in the first k-mer, it will be the first k₀-mer overall. In this case, there is one guaranteed UHS k-mer and possibility more in the substring without first k₀-mer. Otherwise, the analysis is similar to the derivation of $P_n(x)$

Replacing ${\mathcal{R}}^{+}(x)$ with ${\mathcal{R}}^{-}(x)$, we can similarly define and derive the recurrence for $Q_n^{-}(x)$ given $1\le x\le 2$. The process is highly symmetric to the previous case for $Q_n^{+}(x)$, and we leave it to Supplementary Section S3.2. Similar to $P_n(x)$, we can derive the analytical solution to these integrals (see Supplementary Section S3.3). By definition of $Q_n^{+}(x)$, we now bound ${\mathbb{E}}_{\text{Ord}(c)\sim {\mathcal{R}}^{+}(2)}(1/m_{\text{total}})$ by truncating the distribution’s tail, as follows (omitting the condition for clarity):

$$\begin{array}{c}\mathbb{E}(1/m_{\text{total}})={\sum }_{i=1}^{\infty }{Q}_i^{+}(2)/i\\ \le {\sum }_{i=1}^n{Q}_i^{+}(2)/i+(1-{\sum }_{i=1}^n{Q}_i^{+}(2))/(n+1).\end{array}$$

We can derive a similar formula for the symmetric term ${\mathbb{E}}_{\text{Ord}(c)\sim {\mathcal{R}}^{-}(2)}(1/m_{\text{total}})$. For both Q⁺ and Q^-, at n = 6 the tail probability $1-{\sum }_{i=1}^n{Q}_i(2)<0.01$, so we bound both terms using n = 6, resulting in the following:

$$\begin{array}{c}{\mathbb{E}}_{\text{Ord}(c)\sim \mathcal{R}(2)}(1/m_{\text{total}}|E_0)\\ =({\mathbb{E}}_{\text{Ord}(c)\sim {\mathcal{R}}^{+}(2)}(1/m_{\text{total}})+{\mathbb{E}}_{\text{Ord}(c)\sim {\mathcal{R}}^{-}(2)}(1/m_{\text{total}}))/2\\ <0.417.\end{array}$$

Finally, we bound the density of the Miniception, now also using the symmetry conditions (omitting the condition $\text{Ord}(c)\sim \mathcal{R}(2)$ for clarity):

$$\begin{array}{c}P(c\in \mathcal{C})=\mathbb{E}(m_{\text{boundary}}/m_{\text{total}})+o(1/w)\\ \le \mathbb{E}(1/m_{\text{total}}|E_0)P(E_0)+\mathbb{E}(1/m_{\text{total}}|E_1)P(E_1)\\ \hspace{1em}+o(1/w)\\ =4\mathbb{E}(1/m_{\text{total}}|E_0)/w+o(1/w)\\ <1.67/w+o(1/w).\end{array}$$

2.4.5 Density bounds beyond x = 2

We can derive the recurrence for $P_n(x),\hspace{0.17em}{Q}_n^{+}(x)$ and $Q_n^{-}(x)$ for x > 2, corresponding to the scenario where $w\approx (x-1)k>k$. By similar techniques, with suitably chosen n, we can upper bound the density of the Miniception from the values of $Q_i^{+}(x)$ and $Q_i^{-}(x)$ with $i\le n$. The resulting bound has form of $D(x)/w+o(1/w)$, where D(x) is the density factor bound. The detailed derivations can be found in Supplementary Section S3.4. We then have the following theorem:

Theorem 8With $x\ge 2,\hspace{0.17em}w=(x-1)(w_0+1),\hspace{0.17em}k=w_0+k_0$and $k_0>(3+ϵ){\hspace{0.17em}\text{log}\hspace{0.17em}}_{\sigma }(x(w_0+1))$, the expected density of the Miniception is upper bounded by $D(x)/w+o(1/w)$.

3 Results

3.1 Asymptotic performance of the Miniception

We use a dynamic programming formulation (Supplementary Section S3.5) to calculate the density factor of the Miniception given $w\approx (x-1)k$, with a large value of k = 2500. As analyzed in Supplementary Section S3.6, this accurately approximates D(x), which in turn approximates the density factor of the Miniception with other values of k up to an asymptotically negligible error. Figure 5 shows estimated D(x) for $2\le x\le 8$.

Fig. 5.

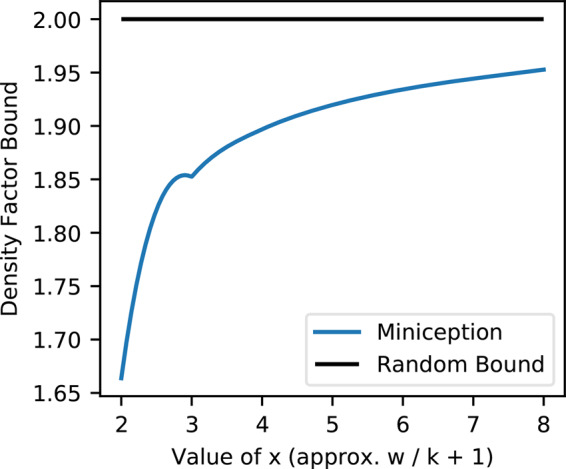
Density factor for the Miniception when $w\approx (x-1)k$ and k = 2500. The random minimizer achieves density factor of constant 2 and is plotted for comparison

Consistent with Section 2.4, $D(2)\approx 1.67$, as x = 2 corresponds to the case $w\approx k$. There is no analytical form for D(x) with x > 2, but this experiment suggests that as x grows, D(x) increases while staying below 2, the density factor of a random minimizer. That is, as w gets increasingly larger than k, the Miniception performance regresses to that of a random minimizer. We conjecture that $D(x)=2-o(1)$ as x grows.

3.2 Designing minimizers with large k

As seen in the implementation of Miniception (Supplementary Section S4), the run time of the Miniception minimizer is the same as a random minimizer. Therefore, it can be used even for large values of k and w. This contrasts to PASHA (Ekim et al., 2020), the most efficient minimizer design algorithm, which only scales up to k = 16.

We implemented the Miniception and calculated its density by sampling 1 000 000 random contexts to estimate the probability of a charged context (which is equivalent to estimating the density as discussed before). The Miniception has a single tunable parameter k₀. It is important to pick an appropriate value of k₀: too small value of k₀ invalidates the assumption that most k₀-mers are unique in a window, and too large value of k₀ increases the value of x. In general, we recommend setting k₀ close to k - w if k is larger than w (which corresponds roughly to x = 2 in our analysis of the Miniception), and a constant multiple of ${\hspace{0.17em}\text{log}\hspace{0.17em}}_{\sigma }w$ if w is larger than k (roughly corresponding to $x=w/k+1$ in our analysis).

We tune this parameter in our experiments by setting $k_0=k-w$ if k is larger than w + 3. If this does not hold, we test the scheme with $3\le k_0\le 7$ and report the best-performing one. We show the results for Miniception against lexicographic and random minimizers in four setups: two with fixed w and two with fixed k (Fig. 6). These parameter ranges encompass values used by bioinformatics software packages.

Fig. 6.

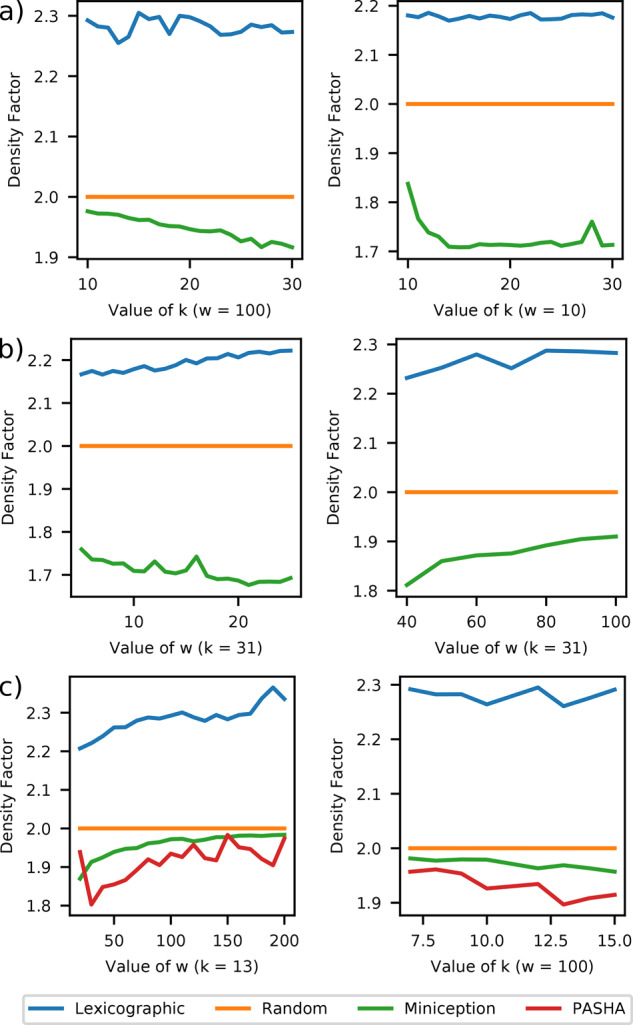
Comparing density of the Miniception against lexicographic, random and PASHA minimizers. Two setups are considered: fixed w and varying k in a), and fixed w and varying k in b) and c). PASHA is computationally limited to $k\le 15$ and is therefore not included in b)

The Miniception consistently performs better than the lexicographic and random minimizers in all tested scenarios. For the setups with fixed w = 10, k is larger than w and the Miniception achieves density factor of $\approx 1.72$ for $k\ge 13$. Given that $1/w=0.1$, our bound on the density factor of $1.67+o(1/w)$ holds relatively well for these experiments. Same conclusion holds for the setup with fixed k = 31 and $5\le w\le 20$.

For w = 100, w is larger than k and we observe the same behavior as in Section 3.1: the performance degrades when k becomes smaller than w. Same conclusion holds for the setup with fixed k = 31 and $40\le w\le 100$. Our theory also correctly predicts this behavior, as the decrease of $x\approx w/k+1$ improves the density bound as seen in Section 2.4.

3.3 Comparison with PASHA

In Figure 6c, we compare the Miniception with PASHA. We downloaded the PASHA-generated UHS from the project website and implemented the compatible minimizers according to Ekim et al. (2020). Our test consists of two parts. For the first part, we fix k = 13 and vary w from 20 to 200. For the second part, we fix w = 100 and vary k from 7 to 15. This setup features some of the largest minimizers designed by PASHA, the state of the art in large minimizer design (we are unable to parse the UHS file for k = 16).

The Miniception still performs better than the random minimizers for these configurations, but PASHA, even though it is a heuristic without a density guarantee, overall holds the edge. We also perform experiments on the hg38 human reference genome sequence, where we observe similar results with a smaller performance edge for PASHA, as shown in Supplementary Section S5.

Although PASHA has lower density than Miniception, it is limited to $k\le 16$. Moreover, computing minimizers with PASHA requires storing in memory a relatively large set of k-mers (5–10 million mers for k = 13). Miniception does not need any to store any set.

4 Discussion

4.1 Limitations and alternatives to minimizers

The $1/w$ bound is not the only density lower bound for minimizers. Specifically, Marçais et al. (2018) proved the following lower bound:

$$\frac{1.5+\frac{1}{2w}+\max (0,\lfloor \frac{k-w}{w}\rfloor )}{w+k}.$$ (1)

As w grows compared to k, this implies that the density factor of the minimizers is lower bounded by a constant up to 1.5. We also observed that performance of minimizers, both the Miniception and the PASHA compatible ones, regresses to that of a random minimizer when w increases. Unfortunately, this is inherent to minimizers. With a fixed k, as the window size w grows, the k-mers become increasingly decoupled from each other and the ordering $\mathcal{O}$ plays less of a role in determining the density.

The minimizers are not the only class of methods to sample k-mers from strings. Local schemes are generalizations of minimizers that are defined by a function $f:{\Sigma }^{w+k-1}\to \{0,1,\dots ,w-1\}$ with no additional constraints. They may not be limited by existing lower bounds ((1) for example), and developing local schemes can lead to better sampling methods with densities closer to $1/w$.

4.2 Perfect schemes and beyond

This work answers positively the long-standing question on the existence of minimizers that are within a constant factor of optimal. Even though the original papers introducing the winnowing and minimizer methods proposed a density of $2/(w+1)$, their analysis only applied to particular choices of k and w. Theorems 2 and 3 give the necessary and sufficient conditions for k and w to be able to achieve $O(1/w)$ density. Theorem 2 also results in the first constant factor approximation algorithm for a minimum size UHS, which improves on our previous result of a $\ln (w)$ factor approximation (Zheng et al., 2020). These theorems also settle the question on existence of asymptotically perfect forward and local schemes.

In general, studies on the asymptotic behavior of minimizers have proven very fruitful to deepen our understanding of the minimizers and of the associated concepts (structure of the de Bruijn graph, decycling sets and UHS). However, there is a sizable gap between the theory and the practice of minimizers.

One example of this gap is the way we prove Theorem 2: the density of the lexicographic minimizers reaches $O(1/w)$ whenever it is possible for any minimizer. This means that the lexicographic minimizers are optimal for asymptotic density. However, in practice, they are usually considered the worst minimizers and are avoided. Another example is the fact that heuristics such as PASHA, while unable to scale as our proposed methods and being computationally extensive, achieves better density in practice (for the set of parameters it is able to run on) with worse theoretical guarantee. Now that we have mostly settled the problem of asymptotical optimality for minimizers, working on bridging the theory and the practice of minimizers is an exciting future direction.

The core metric for minimizers, the density, is measured over assumed randomness of the string. In many applications, especially in bioinformatics, the string is usually not completely random. For example, when working with a read aligner, the minimizers are usually computed on a reference genome, which is known to contain various biases. Moreover, this string may be fixed (e.g. the human genome). In these cases, a minimizer with low density on average may not be the best choice. Instead, a minimizer which selects a sparse set of k-mers specifically on these strings would be preferred. The idea of ‘sequence specific minimizers’ is not new (DeBlasio et al. 2019); however, it is still largely unexplored.

Funding

This work was partially supported in part by the Gordon and Betty Moore Foundation’s Data-Driven Discovery Initiative [GBMF4554 to C.K.]; the US National Science Foundation [CCF-1256087, CCF-1319998]; and the US National Institutes of Health [R01GM122935].

Conflict of Interest: C.K. is a co-founder of Ocean Genomics, Inc. G.M. is a V.P. of software development at Ocean Genomics, Inc.