Periodicity in the Electrochemical Dissolution of Transition Metals

Abstract

Extensive research efforts are currently dedicated to the search for new electrocatalyst materials in which expensive and rare noble metals are replaced with cheaper and more abundant transition metals. Recently, numerous alloys, oxides, and composites with such metals have been identified as highly active electrocatalysts through the use of high‐throughput screening methods with the help of activity descriptors. Up to this point, stability has lacked such descriptors. Hence, we elucidate the role of intrinsic metal/oxide properties on the corrosion behavior of representative 3d, 4d, and 5d transition metals. Electrochemical dissolution of nine transition metals is quantified using online inductively coupled plasma mass spectrometry (ICP‐MS). Based on the obtained dissolution data in alkaline and acidic media, we establish clear periodic correlations between the amount of dissolved metal, the cohesive energy of the metal atoms (E _coh), and the energy of oxygen adsorption on the metal (ΔH _O,ads). Such correlations can support the knowledge‐driven search for more stable electrocatalysts.

In this study, intrinsic metal descriptors based on theoretical considerations are linked to experimentally determined dissolution rates. Clear trends are identified between the dissolution during oxide formation and the metal–metal cohesive energy, as well as between the dissolution during the reduction of an oxide and the metal–oxygen adsorption energy.

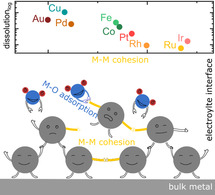
Introduction

With the goal of establishing a fossil‐fuel‐ and nuclear‐power‐free economy based on renewable energy, research and development on electrochemical energy conversion and storage technologies are currently thriving. Nevertheless, while various alternative energy sources like solar, wind, and hydropower are already deployed worldwide, the widespread use of water electrolyzers and fuel cells required to efficiently utilize renewable energy in other sectors, for example, in transportation, is limited. Scarcity and the high price of noble metal‐based electrocatalysts are considered as one of the main factors hindering the development of these technologies. Hence, a significant part of modern electrocatalysis research is devoted to the search for advanced electrocatalysts. ^[1]

In this pursuit, high throughput screening and, to some extent, chance have played an essential role in identifying electrocatalysts with high catalytic activities.[ ^1b , ² ] Stability is another crucial parameter required to ensure the long term operation of fuel cells and electrolyzers. Indeed, even state‐of‐the‐art noble metal electrocatalysts, including Pt and Pt alloys during oxygen reduction reaction (ORR), suffer from severe degradation issues. ^[3] Especially for alloys, preferential leaching of less noble elements and resulting increase in electrochemically active surface area may lead to materials degradation. These issues may also plaque experimental observations potentially causing misinterpretation of experimentally obtained data on activity. ^[4] Similarly, there are correlations between activity and stability of metal oxide‐based oxygen evolution reaction (OER) electrocatalysts. ^[5] Despite the importance of this topic, understanding the mechanisms governing electrocatalysts’ stability, particularly dissolution, is lacking.

With the absence of reliable descriptors to predict the stability of electrocatalysts, one has to rely on thermodynamic data summarized by M. Pourbaix back in 1945. ^[6] This approach allows to assess the stability window of metals by locating the thermodynamically stable solid, aqueous, and gaseous species on E vs. pH diagrams. However, it does not give any insights into the kinetics of dissolution processes. Moreover, both thermodynamics and kinetics of dissolution during a transition between two stable solid phases—the so‐called transient dissolution, for example, during oxidation of a metal to its oxide or reduction of the oxide, are not available in the classical E vs. pH diagrams. To this point, there is little information available as to what the governing factors of electrocatalyst's transient dissolution are. Such insights, however, are of significant importance in evaluating the stability of electrocatalysts during transient operation in fuel cells and electrolyzers.

While the research on electrocatalyst stability struggles from the absence of stability descriptors, significant progress has been achieved in recent years in understanding the parameters governing materials electrocatalytic activity. According to the so‐called Sabatier principle, the adsorption energy of intermediate species controls the rate of a reaction. ^[7] As for now, there is no similar universal principle to estimate materials stability other than available thermodynamic data. ^[6] Indeed, parameters explaining kinetics of metal dissolution are rare. A link to the crystallinity and, therefore, the number of surface defects have been suggested previously.[ ^5c , ⁸ ] However, crystallinity is not an easily quantifiable variable, and even on single crystalline surfaces, inconsistencies in preparation can yield drastically different results. ^[9] For researchers to evaluate stability of a given material under the harsh electrochemical conditions in real applications, it is necessary to find so‐called common descriptors. Such a descriptor is an intrinsic property of electrocatalyst materials that should be easily extractable from theoretical calculations or material scientific experiments and ideally be directly related to the stability.

The discovery of stability descriptors is impossible without reliable experimental data on metal dissolution rates. Hence, the first attempt to rationalize different dissolution behavior of noble metals was made only in 1976, ^[10] soon after Rand and Woods estimated dissolution of five noble metals using the oxidation/reduction charge imbalance, atomic absorption spectroscopy, and spectrophotometry. ^[11] Thus, Vijh and Bélanger suggested that the metal‐metal bond energy, E _M‐M, can be correlated with the estimated dissolution currents of some platinum group metals (PGM). ^[10] Applying several approximations, it was found that the mean dissolution decreases with E _M‐M. Unfortunately, as will be shown below, transition metals dissolution is typically more complex than simple anodic corrosion considered by Rand and Woods. Hence, it is questionable if such data can be used to provide stability trends. In 1994, P. Marcus developed this idea further to describe alloys’ corrosion and passivation behavior. It was suggested that E _M‐M and the affinity of individual metals to adsorb oxygen control the extent of dissolution and passivation. ^[12] Nevertheless, no experimental data on dissolution of electrocatalysis relevant metals and correlation of such data with the suggested descriptors have been presented so far.

Over the last decade, with the invention of electrochemical on‐line inductively coupled plasma mass spectrometry (ICP‐MS), much progress has been made in accumulating experimental data and understanding the potential resolved dissolution processes at PGM electrodes. Thus, unlike half a century ago, a considerable body of experimental data became available. Moreover, it was shown that electrochemical dissolution of noble metals is a complex potential and electrode prehistory dependent process. It occurs during both the oxide formation (anodic dissolution) and oxide reduction (cathodic dissolution). Depending on the metal, either anodic or cathodic dissolution is dominating. Despite this new data and knowledge, parameters governing the dissolution rate and extent are still elusive. Discussions on the mechanism of anodic and cathodic dissolution typically end, stating that surface atoms’ rearrangement causes such transient dissolution. ^[13]

Here, using state‐of‐the‐art on‐line ICP‐MS technique to precisely quantify dissolution rates at identical (important, as available experimental data are scattered) experimental conditions, we correlate transient dissolution for a broad range of transition metals to their common descriptors. Namely, the cohesive energy of metals (E _coh) and the adsorption energy of oxygen (ΔH _O,ads) are considered. ^[14] We show how these two fundamental properties impact both anodic and cathodic dissolution processes at the electrode/electrolyte interface. We observe a trend in both alkaline and acidic electrolytes over a range of 3d, 4d, and 5d metals and discuss the implication of our findings for future catalyst development.

Results and Discussion

Before evaluating dissolution rates of metals during oxidation and reduction processes, we establish a dataset of parameters that can influence dissolution. Figure 1 presents thermodynamic data on A) the first oxide transition (E ⁰),[ ⁶ , ¹⁵ ] B) oxygen adsorption energy at a quarter monolayer coverage (ΔH _O,ads), ^[14b] and C) cohesive energy (E _coh) ^[14a] of each studied metal. Note there is a direct correlation between E _coh and E _M‐M. Similar to most element‐specific descriptors, there are apparent trends to be observed within the periodic table. First, with increased d‐band filling, the first oxidation potential (Figure 1 A) or, in other words, the metal nobility increases. The nobility increases gradually from 3 to 5d‐shells. Like nobility, the affinity to form an oxide (Figure 1 B) increases with increased d‐shell filling but drops slightly with an increased number of d‐shells. The bond strength between metal atoms (Figure 1 C), on the other hand, decreases with increased d‐band filling while increasing again with each additional d‐shell.

Figure 1.

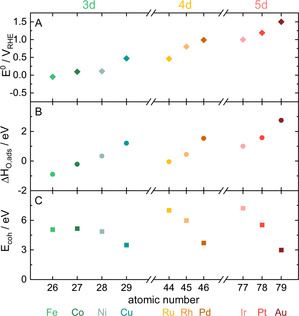
Thermodynamic values for A) E ⁰, B) ΔH _O,ads, and C) E _coh of all investigated metals. This data was extracted from ref. [6, 15] for (A), ref. [14b] for (B), and ref. [14a] for (C). For more information on these descriptors, please refer to the supporting information.

To correlate these thermodynamic data to experimentally determined transient dissolution rates during oxidation and reduction of the metals and their electrochemically formed oxides, we oxidized all metals at a constant overpotential (η=200 mV) to E ⁰. Just before starting the measurements, all electrodes underwent a thorough polishing procedure which is required to minimize the amount of native oxides formed in the air ^[16] (please refer to the experimental part for more information). Equal overpotentials impede consistent oxidative stress in each metal. Therefore, the recorded dissolution appears to be a good measure of stability comparable between metals and directly correlated to a common descriptor. Figure 2 shows the results for nine of the investigated metals in an alkaline electrolyte (while some other transition metals, for example, Mo and Ag were also studied, data are not shown here as the dissolution was very fast and impossible to quantify). Here, all the investigated metals are expected to form the corresponding thermodynamically stable oxides. We also repeated the same experiment for all metals in the acidic environment. However, only data for PGM metals are presented in Figure S1 since none of the investigated 3d metals form a stable oxide in acidic pH. Indeed, the outcome of such an oxidation experiment on 3d metals in acid using ICP‐MS to track the dissolution rate is shown in Figure S2. One can observe an exponential increase of active dissolution with potential. During oxide formation at η=200 mV in alkaline media, all the investigated metals undergo transient dissolution marked by the colored brackets in Figure 2. The extent of transient dissolution increases within each d‐shell.

Figure 2.

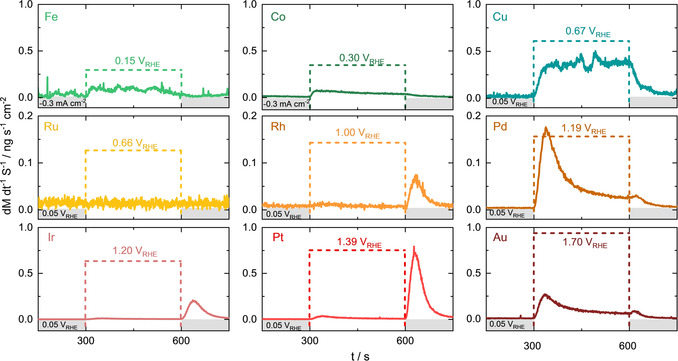
Dissolution rates in an alkaline electrolyte (0.05 M NaOH) for three metals of each transition metal d‐shell. The oxidative potential was applied as shown by the colored brackets from t=300–600 s. A reductive current or potential step was applied to all samples before and after (−0.3 mA cm⁻² for Fe, Co and 0.05 V_RHE for Cu, Ru, Rh, Pd, Ir, Pt, Au).

Only Ni (Figure S3) and Ru do not exhibit a measurable dissolution upon oxidation during these measurements. Ni has previously been reported to show unprecedented dissolution stability during redox reactions in alkaline electrolyte, and it has been hypothesized to be due to the formation of Ni(OH)₂ through a dissolution precipitation mechanism. Here, the oxide is formed through the precipitation of poorly soluble Ni species. ^[17] Since Ru does dissolve transiently during oxide formation, as was shown in our previous works, ^[13b] we investigated the impact of increased overpotentials further. Indeed, as shown in Figure S4, already at η=300 mV some Ru was detected in the electrolyte, while dissolution was increasing with potential. Therefore, the lack of dissolution at 200 mV can be attributed to experimental limitations; ICP‐MS cannot resolve such low dissolution rates (between all studied noble metals, Ru has the highest detection limit). In the following, we use the Ru amount dissolved at η=300 mV.

During the reduction of the oxide layers (Figure 2, t>600 s), the behavior differs more notably. No dissolution is observed for 3d metals. Here, it is important to note the difference in the protocol used for 3d and 4d/5d elements. A constant potential of 0.05 V_RHE was chosen to reduce oxides of 4d and 5d elements, to minimize bubble formation during the hydrogen evolution reaction (HER). This potential results in a significant reductive overpotential of E>300 mV. The same procedure cannot be used for Fe, Ni, and Co as 0.05 V_RHE is similar to their redox potentials. Hence, to reduce these 3d element's oxides, a constant reductive current of −0.3 mA cm⁻² was applied, but the resulting low overpotentials (E<200 mV) might not be enough to reduce the surface entirely. For Rh, Ir, Pt, and Ru in Figure S1 a clear indication of transient dissolution during the reduction is observed. Pd and Au, on the other hand, show only a very slight increase in dissolution rate, which is followed by an immediate decline to the baseline. When quantifying dissolution after this fast reduction event, it can be a combination of anodic dissolution tailing and cathodic dissolution. In any case, this value of cathodic dissolution will be overestimated. On the other hand, literature reports of dissolution during cycling voltammetry typically show transient dissolution for all these PGM associated with oxide reduction.[ ^5a , ^13b ] As a control experiment, we repeated the same 300 s oxidation experiment (see in Figure S5), followed by a linear sweep (2 mV s⁻¹) to 0.05 V_RHE, instead of a step to this potential. Indeed, in this case, all PGMs dissolve upon reduction within a 200 mV overpotential to their thermodynamic M/M_ox couple. Previously, we suggested that such dissolution can be due to anodic processes taking place during the relatively slow reduction of oxide. ^[18] Additional research is required to clarify the discrepancy in Au and Pd dissolution during the reductive potential step vs. sweep.

The online ICP‐MS investigation of nine d‐block metals during oxidation and reduction has revealed similarities in their transient dissolution behavior. To quantify the dissolution's extent, the corresponding dissolution rates were integrated over time, and the resulting dissolution amounts were used to identify dissolution stability descriptors for transient metals. Further, by comparing the dissolution amounts to the descriptors summarized in Figure 1, we establish periodic dissolution dependences shown in Figure 3. In alkaline media, the dependence of transient anodic dissolution spans over all d‐block metals. The same trend is observed in the acidic environment for 4 and 5d metals, while due to severe corrosion (Figure S2), 3d metals are excluded.

Figure 3.

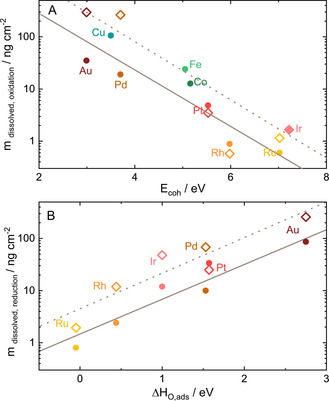
Correlation of the integrated mass of dissolved metals (alkaline, 0.05 M NaOH: solid circles; acidic, 0.1 M H₂SO₄: hollow squares) to their common descriptors gathered from the literature. A) Dissolution during oxidation plotted as a function of E _coh and B) dissolution associated with the reduction from Figure S5, plotted as a function of ΔH _O,ads. The linear fit added as a guide to the eye, visualizes the correlation in both alkaline (solid line) and acidic (dotted line) electrolytes.

Figure 3 A presents an exponential dependence of transient dissolution during oxide formation on E _coh. Here, results from alkaline (solid circles) and acidic (hollow squares) electrolytes show similar trends suggesting that the same intrinsic properties govern the stability of metals in the studied media.

Metals with higher E _coh, like Ru and Ir, tend to dissolve less than that with lower E _coh, like Au and Pd. Another important finding is that transient anodic dissolution at a given overpotential is not governed by the nobility of atoms. In fact, the noblest element, Au, dissolves most. With this, we unambiguously demonstrate that there is indeed a correlation between dissolution and metal‐metal bond energy, suggested by Vijh and Bélanger. ^[10] There are no literature data on descriptors for dissolution taking place during the reduction of oxide. Now we turn our attention to cathodic dissolution.

As shown in Figure 3 B, the transient cathodic dissolution scales exponentially with another descriptor, that is, ΔH _O,ads. The adsorption energy of oxygen was considered by P. Marcus as a parameter governing formation of 3D oxides and, hence, metals passivation. Besides, E _M‐M was proposed to influence the activation barrier of metal‐metal bond breaking. He classified metals with high M‐M bond strength as dissolution blockers due to a high barrier to the formation of 3D oxides from adsorbed oxygen overlayers. Metals with low M‐M bond strength but a high O adsorption energy (ΔH _O,ads) were considered as surface passivation promoters. ^[12] Our data demonstrate that by considering both descriptors we can reveal correlations in both anodic and cathodic dissolution in acidic and alkaline electrolytes. Note, depending on the metal, sulfate anions can adsorb on the surface and influence dissolution. Nevertheless, since the dissolution is initiated by the irreversible oxidation of the metal surface at relatively high coverages of oxygen species, ^[19] such influence should be minimal. Indeed, as was previously shown for Au and Pt, dissolution of these metals in sulfuric and perchloric acid electrolytes is comparable. ^[20]

A schematic representation of possible surface processes during metal oxidation and reduction is given in Figure 4. As the most studied, the Pt(111) surface is considered. Fuchs et al. have recently resolved the Pt atoms’ exact motions for this most stable Pt surface during an oxidation and reduction event. ^[19] The hypothesis is that after monolayer oxidation (transition from Figure 4 A to B), the crystal lattice has to rearrange and incorporate O atoms via a place‐exchange or other mechanism involving oxygen incorporation into the crystal lattice.[ ^3a , ^17b , ²¹ ] The rearrangement during oxidation requires the breaking of M−M bonds (represented by E _coh), which governs the rate of oxide formation (transition from Figure 4 B to C). During place‐exchange, undercoordinated M^δ+ atoms are exposed to the solvent. These atoms can now either undergo incorporation into the oxide layer or be prone to solvation by electrolyte species and dissolve as Mⁿ⁺ (Figure 4 C). Note, since ΔH _O,ads, representing the M‐O interactions, scales inversely with the E _coh (Figure 1), cations of metals with high E _coh should be less prone to solvation. The solvation of a metal cation and its dependence on metal‐electrolyte interaction is relatively poorly investigated in electrochemistry but has been addressed in other research fields. ^[22] Hence, interdisciplinary research initiatives would be beneficial in understanding the effect of cations solvation on the overall dissolution stability of electrocatalysts. As trends are similar for acidic and alkaline electrolytes, however, we anticipate that the role of solvation is not dominating here.

Figure 4.

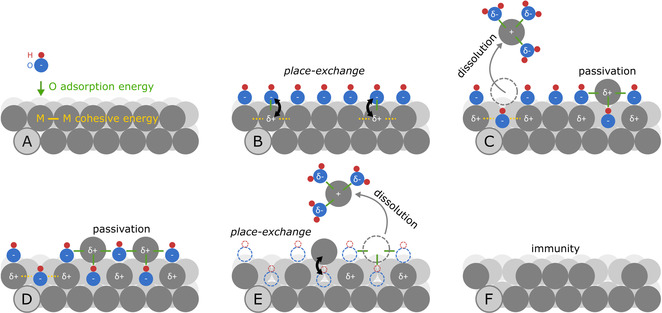
Schematic of surface processes on Pt(111), governing anodic (A–C) and cathodic (D–F) transient dissolution. Pt (gray), O (blue), and H (red).

Through the described mechanism, the dissolution rate is tied to the rate and extent of oxide formation, which both depend on the ease of M−M bond breaking. At low bond strength, breaking of M−M bonds is easier, reflected in a higher rate of oxide formation and high dissolution through a stronger M−O interaction. During oxide layer growth, its passivation effect increases, while both the oxide formation and M−M bond breakage decrease. ^[20] The passivation is reflected in the dissolution rate's slow decay over the applied 300 s of oxidative potential. For example, a combination of high E _coh values and lower ΔH _O,ads in Ir results in very fast passivation during oxidation. Low E _coh and high ΔH _O,ads in Au, on the other hand, result in a substantial dissolution rate even after 5 min of oxidation.

When reducing the oxidic passivation layer (Figure 4 D), a large number of oxygen species leave the surface leading to formation of undercoordinated metal sites. When solvated by the electrolyte, these metal cations can be released from the surface (Figure 4 E). The extent of cathodic dissolution should depend on both the amount of oxide present (influences the number of undercoordinated metal sites) on the electrode and the interaction of metal cations with the solvent. In the first place, the overall dissolved amount during reduction is related to the oxide layer thickness. The latter, however, is difficult to estimate precisely. We have previously suggested that the thickness of native oxides on PGMs is a function of the time PGMs are exposed to air, and it governs the dissolution amount during their reduction. It was shown that cathodic dissolution was increasing with time (see Figure 2 in ref. [16]). Comparing the dissolution amount of different metals at a given time (especially at shorter intervals) and considering the descriptors from Figure 1, we reveal here a clear increase in dissolution with ΔH _O,ads. The rationale behind this is that metals with high ΔH _O,ads form thicker oxides, resulting in higher dissolution. In the current study, however, the oxidation overpotential and time were the same for all metals so that the dissolved amount during reduction is only dependent on the material properties.

Surprisingly, in step experiments (Figure 2 and Figure S6), we find that there is an opposite trend to what was observed for the oxides formed in the air—dissolution decreases with ΔH _O,ads, but only for Ru, Rh, Ir and Pt, while dissolution of Pd and Au is lower than the trend suggests. When the reductive step is replaced with a slow potential sweep, however, (Figure S5 and Figure 3 B) a fairly linear dependence of dissolution vs. ΔH _O,ads is observed for all metals. Obviously, next to the total amount, the rate of oxide reduction plays an important role. Metals with high ΔH _O,ads have higher activation barrier towards oxide reduction. This implies, that when a reductive step is applied, due to sluggish reduction, uncoordinated sites stay longer on the surface and dissolve. For metals with low ΔH _O,ads it is opposite—due to fast oxide reduction (and redeposition of possibly dissolved species), the overall dissolution is low. During slow oxide reduction, however, in sweep experiments, we control the rate of oxide reduction and, hence, dissolution. Here, dissolution is governed by the strengths of M‐M bond—higher dissolution for lower E _coh. Last, after complete reduction, some of the undercoordinated metal sites are incorporated into the metal structure (Figure 4 F).

In our schematic, the ideal case scenario of Pt(111) surface oxidation and reduction at potentials below 1.2 V_RHE, where the undercoordinated Pt atom undergoes place‐exchange in its original position, ^[19] is considered. On other surfaces and at higher overpotentials, the place‐exchange and incorporation can be less reversible. ^[19] Here, the surface mobility of adatoms play a role during both oxidation and reduction. ^[9] Moreover, the oxidation mechanism of other metals can be very different from that observed at Pt single crystals. ^[17b] Unfortunately, none of the metals have been studied in such detail. Hence, while we use this Scheme as a first approach to visualize the trends in metals’ dissolution, it is not complete. Further in situ operando measurements on model single‐crystal surfaces, complemented with advanced theoretical models, are required to fully understand oxidation and dissolution of each of the studied metals.

Thermodynamic values, as well as intrinsic material properties used herein, were mostly calculated for bulk materials. However, electrochemical processes happen at the electrode surface, which is known to show diverging properties than those of the bulk material. The M−M bond strength depends on the coordination number of a metal, which can drastically differ at the surface and defect sites. Nevertheless, we argue that the periodic table's trends, for example, d‐band filling, electronegativity, hydration energy of cations, ionic radii, etc. would govern the properties at the surface in reasonable correlation to bulk materials. Even though absolute values might differ for surface sites and defects, the order in which it changes between elements would be the same as the data presented here. Therefore, we strongly believe that our dissolution data would still scale exponentially also in such optimized calculations.

The described above correlations can be considered a starting point in predicting dissolution stability of electrocatalysts (not only for the investigated metals but also metal alloys), for example, stability descriptors. It has been proposed previously that the introduction of heteroatoms by alloying influences factors such as electrocatalytic activity, the E _coh and the ΔH _O,ads, and therefore the passivation and dissolution properties.[ ^4b , ¹² ] The presented descriptors are extractable from theory even for more complex alloyed systems. We believe that these descriptors extend base metal catalysts and are also valid for alloys, nanoparticulate materials, and possibly even single‐atom catalysts, which rely on the interaction with ligating species in a substrate.[ ^3a , ²³ ] On the other hand, additional considerations are required when the stability is influenced by electrochemical reactions other than surface oxidation/reaction. A representative example is OER, which, depending on the mechanism, can lead to significant surface destabilization and dissolution.[ ^5a , ^5b , ^13b ]

Conclusion

The presented data shows that intrinsic metal properties like M−M and M−O bond energies can be used as descriptors for stability of d‐metals in acidic and alkaline electrolytes. By quantifying the amount of dissolved metal during oxidation and subsequent reduction, we can directly correlate them to thermodynamic values for E _coh and ΔH _O,ads, respectively. We attribute this relationship to the following main processes. During oxidation, the incorporation of oxygen atoms into the crystal lattice leads to the breaking of M−M bonds. If this requires little energy, the tendency of dissolution increases through the formation and dissolution of formed undercoordinated metal sites. During reduction, dissolution depends on the amount of formed oxide (governed by both M−M and M−O interactions) and the rate of oxide reduction (mainly M−O). These descriptors give researchers a clear metric of stability that can be calculated for many materials and help future catalyst development. Moreover, since there is a clear exponential dependence of M−M on M−O, at least for the considered metals, it is likely that either of these descriptors can be considered.

Conflict of interest

The authors declare no conflict of interest.

Supporting information

As a service to our authors and readers, this journal provides supporting information supplied by the authors. Such materials are peer reviewed and may be re‐organized for online delivery, but are not copy‐edited or typeset. Technical support issues arising from supporting information (other than missing files) should be addressed to the authors.

Supplementary

F. D. Speck, A. Zagalskaya, V. Alexandrov, S. Cherevko, Angew. Chem. Int. Ed. 2021, 60, 13343.