Inertial microfluidics in contraction–expansion microchannels: A review

Abstract

Inertial microfluidics has brought enormous changes in the conventional cell/particle detection process and now become the main trend of sample pretreatment with outstanding throughput, low cost, and simple control method. However, inertial microfluidics in a straight microchannel is not enough to provide high efficiency and satisfying performance for cell/particle separation. A contraction–expansion microchannel is a widely used and multifunctional channel pattern involving inertial microfluidics, secondary flow, and the vortex in the chamber. The strengthened inertial microfluidics can help us to focus particles with a shorter channel length and less processing time. Both the vortex in the chamber and the secondary flow in the main channel can trap the target particles or separate particles based on their sizes more precisely. The contraction–expansion microchannels are also capable of combining with a curved, spiral, or serpentine channel to further improve the separation performance. Some recent studies have focused on the viscoelastic fluid that utilizes both elastic forces and inertial forces to separate different size particles precisely with a relatively low flow rate for the vulnerable cells. This article comprehensively reviews various contraction–expansion microchannels with Newtonian and viscoelastic fluids for particle focusing, separation, and microfluid mixing and provides particle manipulation performance data analysis for the contraction–expansion microchannel design.

I. INTRODUCTION

The advent of inertial microfluidics has provided brand new opportunities for point of care testing (POCT) without complex external force fields.^1–3 Through utilizing the hydrodynamic inertial effects of microfluids, particle manipulation functions such as focusing,^4,5 separation,^6,7 and trapping⁸ can be creatively conducted with extremely small sample volume demand, dramatically high efficiency, and reasonably low cost, which makes the inertial microfluidics an ideal candidate for the isolation of rare cells such as circulating tumor cells (CTCs) in whole blood or other target particles/cells.⁹ Inertial microfluidics was first employed in a straight microchannel to focus particles at their equilibrium positions usually between centerline and walls (e.g., two positions near the center of long sidewalls in the rectangle section channel).¹⁰ Not long after that, various other channel patterns such as contraction–expansion channels,¹¹ spiral channels,^12,13 and serpentine channels^14–16 were introduced for particle focusing and separation. The secondary flows in these microchannels contribute to the particle lateral migration and separation based on their sizes more precisely and efficiently.^17,18 Among these microchannels, the contraction–expansion channels have attracted extensive attention because of their versatile functions with diverse forms employed in various applications.

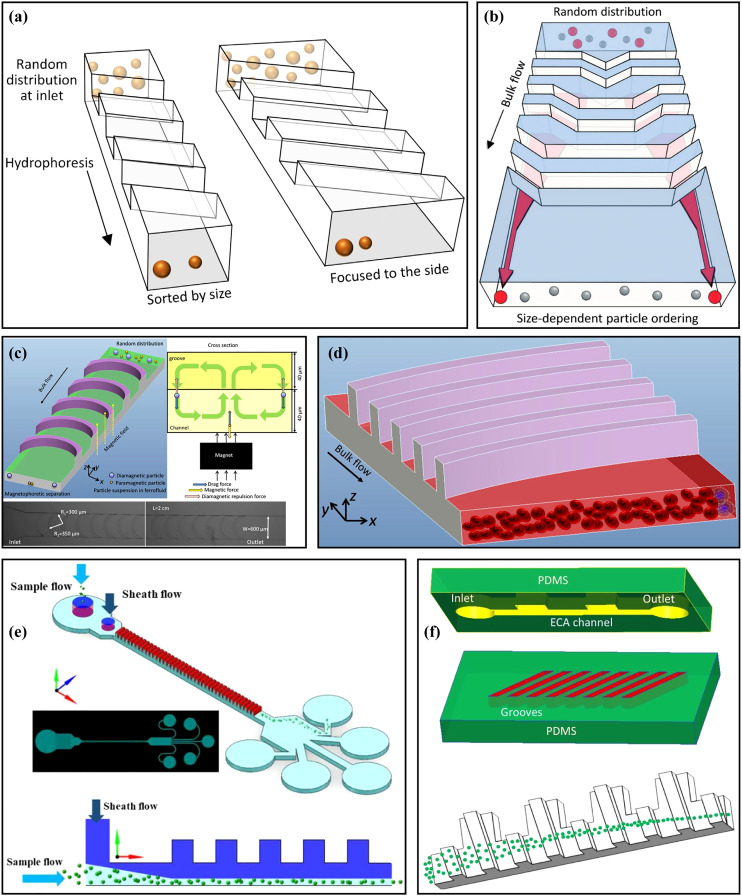
The versatility of the contraction–expansion channel is realized through different chamber sizes and shapes and can be easily paralyzed¹⁹ and double graded²⁰ to multiply the throughput and improve sorting purification. With the appropriate geometric design, the contraction–expansion channel can achieve efficient and relatively precise particle focusing,²¹ sorting,²² isolation, and solution mixing.²³ The vortex in the large size chamber can trap target particles and realize isolation; however, the small chamber can be designed to force the small-sized particles away from the centerline toward the sidewalls and achieve the separation of differently sized particles. Lee et al.²⁴ achieved the separation of breast cancer cells from whole blood with a recovery rate of >99% and a blood cell rejection ratio of 97.4% in a symmetric contraction–expansion channel. Fan et al.²⁵ successfully ordered differently sized particles over a large range of Re from 19.1 to 142.9 in an asymmetric contraction–expansion channel with sharp corners. Not only square or rectangular chambers can be designed as the convex structure, semi-circle,²⁶ triangle,²⁷ and fishbone shape²⁸ chambers but also can be found in contraction–expansion designs. Besides the chamber aside from the main flow channel, various shape chambers can also be placed on the top of the channel. The top convex chamber can be orthogonal, slant, or curved to the main flow channel for different manipulation aims. For example, Song et al.²⁹ designed a robust flow-rate insensitive isolator to isolate large particles to the sidewalls in a straight channel with a series of inclined and gradually changing grooves on the channel top surface.

The contraction–expansion channel can also combine with various microchannel patterns (e.g., curved,³⁰ spiral,^31,32 and serpentine³³ microchannel) to improve the manipulation performance. Moreover, viscoelastic fluid is another candidate buffer solution employed in the contraction–expansion channel to further increase the particle recovery rate, sorting efficiency, and slow down the flow rate to protect vulnerable cells during separation processes.³⁴ The elastic effects on particles are helpful to manipulate particles more precisely and focus on small particles more effectively.³⁵

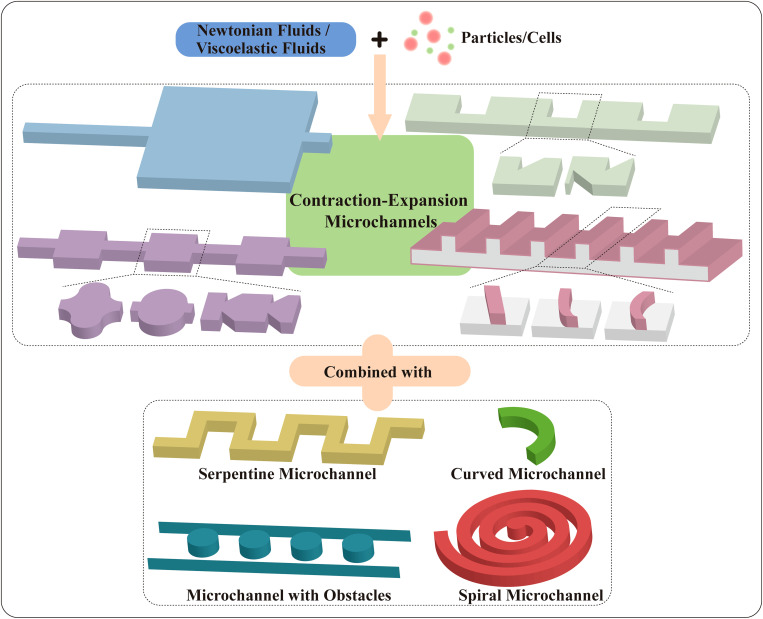
Even though inertial microfluidics has been a hot topic since it was born, inertial microfluidics in the contraction–expansion structure has not been reviewed comprehensively. The diverse functions of contraction–expansion microchannels are worthy of further discussion. The purpose of this review is to provide an overview of various patterns of contraction–expansion microchannels with Newtonian or viscoelastic fluids employed for diverse applications. The basic particle manipulation mechanisms of the existing contraction–expansion microchannels will be introduced in order of channel structure characters that are classified into symmetric and asymmetric channels, and the asymmetric channels also will be divided into contraction–expansion arrays orthogonal or non-orthogonal to the main flow channel. Finally, contraction–expansion channels combined with other channel patterns are reviewed as well (Fig. 1).

FIG. 1.

Contraction–expansion channels in microfluidics.

II. INERTIAL MICROFLUIDICS

As a popular particle manipulation technology, inertial microfluidics utilizes the inertial effects of the microfluids flow for high-throughput particle manipulation with Reynold numbers, Re ( $\mathrm{Re}=\rho \mathrm{U}{\mathrm{D}}_{\mathrm{h}}/{\mu }_{\mathrm{f}}$, where ρ is the fluid density, U is the average flow velocity, D_h is the hydraulic diameter of the microchannel, and μ_f is the dynamic viscosity) ranging from 1 to 100 in a micro-scale channel.³⁶

In the straight channels, particles migrate under the inertial lift force F_L ( ${\mathrm{F}}_L={\mathrm{f}}_L\rho {\mathrm{U}}^2{\mathrm{a}}^4{/\mathrm{D}}_h^2$, where f_L is the dimensionless lift coefficient and a is particle diameter), which is composed of a wall-induced inertial lift force F_LW and a shear-induced inertial lift force F_LS.^37,38 F_LW is induced due to the interaction of the particle and walls and pushes the particles away from the microchannel walls.³⁹ F_LS is induced by the velocity gradient of the Poiseuille flow and drives the particles away from the microchannel centerline.⁴⁰ When the particle migrates to the equilibrium positions between the centerline and walls, the net force of the two opposite inertial lift forces on the particle becomes zero. Equilibrium positions of particles correspond to the geometry of the microchannel cross section. In a cylindrical channel, particles are focused into an annulus with a radius of 0.6r (r is the channel radius).^41,42 While in a square channel, particles migrate to the four equilibrium positions near the centers of the walls.⁴³ In a rectangular channel (AR < 1, AR is the aspect ratio of the channel), particles first migrate toward the two long walls, and then are slowly focused to the two equilibrium positions close to the middle points of the long walls.⁴⁴

In the curved channels, in addition to inertial lift force F_L, particles are also affected by a drag force F_D ( ${\mathrm{F}}_D\propto \rho {\mathrm{U}}^{2}a{D}_h/R$, where R is the channel curvature radius) due to the Dean flow (secondary flow) in the channel cross section.^45,46 The fluid in the horizontal center plane flows to the outer wall due to the influence of centrifugal force and the unbalanced radial pressure gradient, then the fluid at the outer wall flows back along the upper and lower bottom surfaces, thereby generating two vortices in opposite directions.¹ Combined with inertial lift force F_L and drag force F_D, more refined particle manipulation can be achieved, and particles with different sizes and deformability can be separated more precisely.

The microfluidics in contraction–expansion array (CEA) microchannels contains the inertial lift force, vortex flow, Dean flow, and other secondary flows, which make the contraction–expansion microchannels a multifunctional device for particle manipulation. To further elaborate on the various applications of contraction–expansion channels, these channels are classified as symmetric channels and asymmetric channels based on their geometries.

A. Symmetric channels

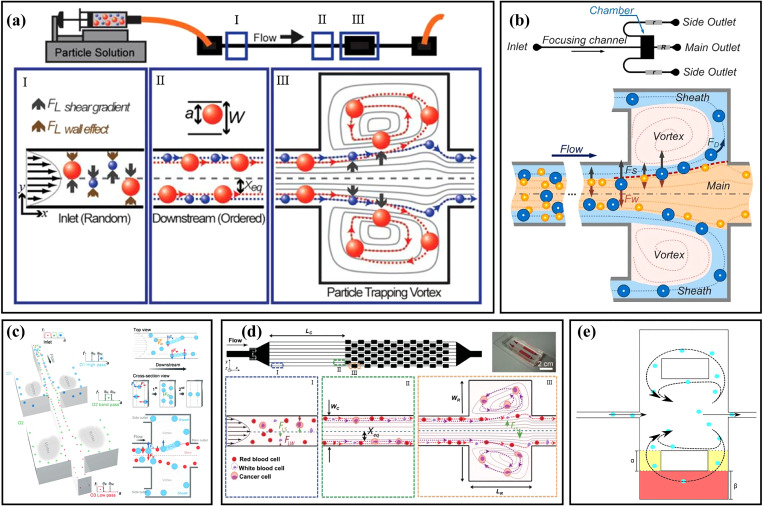
Although the particles can be focused at the two equilibrium positions close to the centers of the long sidewalls in the rectangular straight channels, as mentioned above, it is not easy to realize the size-based sorting of particles in a simple straight channel. To realize the particle sorting, Mach et al.^19,47 demonstrated a high aspect ratio straight microchannel with an expansion–contraction chamber, as shown in Fig. 2(a). In the initial stage, the particles are focused at dynamic equilibrium positions close to the sidewalls by the combined action of F_LW and F_LS in the straight channel. As the focused particles enter the expansion region, particle migration is dominated by F_LS due to the absence of channel walls. Larger particles migrate laterally into the chamber under larger F_LS and recirculate with the vortex, while small particles migrate slowly and cannot enter into the vortex when passing through the expansion region. Utilizing this phenomenon, they achieved the separation of cancer cells from human blood. Zhou et al.⁴⁸ used experimental and numerical simulation methods to study the microchannel with a similar structure. Their results showed that there were the low-velocity and drag dominance for particle recirculating within the channel expansion region, and the formation of particle recirculating orbit in the chamber depended on the particle diameter and flow conditions. Based on the above-mentioned channel structure, Wang et al.⁴⁹ added two side outlets at the corners of the chambers and three resistance devices at the outlets, as shown in Fig. 2(b). By adjusting the resistance ratio between the side outlets and the main outlet, the flow rates of the outlets could be controlled and the microfluidic device performance was optimized so that small particles exited through the main outlet, while large particles exited through the side outlets. Under the optimized experimental conditions (Re = 100, the resistance ratio of 5), the separation and collection of 21 and 18.5 μm particles were achieved, and the purity of the two kinds of particles was 93% and 91%, respectively. What is more, they realized the secondary separation of the ternary mixture by connecting another expansion region to the original channel,⁵⁰ as shown in Fig. 2(c). Through the redesign of the microchannel resistance network, the 21, 18.5, and 15 μm diameter particles were separated in order from large to small, and particle separation efficiencies were 78%, 87%, and 99%, respectively. Subsequently, with the assistance of sheath flow, they successfully realized the continuous separation of rare cells from the diluted human blood, with a separation efficiency of 90% for rare cells and a blood cell removal efficiency of 99.97%.²⁰ Recently, Volpe et al.⁵¹ used computational fluid dynamics based on the lattice Boltzmann method to numerically simulate a microchannel whose channel structure was similar to that in Fig. 2(b) and evaluated the performance of the microchannel for extracting and capturing particles. Based on the results of their simulations and experiments, they developed an optimum inertial microfluidic sorter with multiple microchambers utilizing the femtosecond laser microfabrication.⁵²

FIG. 2.

(a) Schematic diagram of the microchannel with an expansion–contraction chamber and particle migration mechanism. Reproduced with permission from Mach et al., Lab Chip 11, 17 (2011). Copyright 2011 Royal Society of Chemistry. (b) Schematic diagram of the vortex-aided inertial microfluidic with side outlets. Reproduced with permission from Wang et al., Biomicrofluidics 7, 4 (2013). Copyright 2013 AIP Publishing LLC. (c) Schematic diagram of the microfluidic device principle for the secondary separation of ternary mixture. Reproduced with permission from Wang et al., Lab Chip 15, 5 (2015). Copyright 2015 Royal Society of Chemistry. (d) Schematic diagram of the design and principle of the Vortex chip with multiple expansion–contraction chambers placed in series and parallel. Reproduced with permission from Sollier et al., Lab Chip 14, 1 (2014). Copyright 2014 Royal Society of Chemistry. (e) Schematic diagram of lateral channels and connection channels structure in the expansion–contraction chamber. Reproduced with permission from Paiè et al., Microfluid. Nanofluid. 21, 6 (2017). Copyright 2017 Springer Publishing.

To improve the channel throughput of the device for processing large-volume samples, Sollier et al.⁵³ demonstrated a microfluidic device with multiple expansion–contraction chambers arranged in series and parallel as shown in Fig. 2(d). They systematically studied the effects of the channel length, channel aspect ratio, blood dilution, and throughput on particle sorting. The results showed that purity could usually reach 80%–100% by using spiked samples. Subsequently, based on the research of Sollier et al.,⁵³ Dhar et al.⁵⁴ further studied the influence of channel cross-sectional geometry on the efficiency and stability for trapping particles. The results proved that the channel cross-sectional area had an important influence on the threshold size of the captured particles. They further modified the channel and realized the capture of circulating tumor cells (CTCs) with a high purity. At the same time, Che et al.⁵⁵ replaced the original long upstream straight channel with 1000 μm spaced contraction–expansion chambers to improve the particle trapping efficiency. Compared with the original device, the modified channel obtained 1.6 times higher capture efficiency for MCF-7 breast cancer cells. What is more, combining the modified channel structure and deformability cytometry technique, they proposed a system integrated with the vortex trapping and deformability cytometry (VDC) and achieved the seamless capture, release, and measurement of target rare cells.⁵⁶ Paiè et al.⁵⁷ also modified the vortex chip to improve the trapping efficiency of the chip. Lateral channels (yellow) and connection channels (red) were added to the expansion–contraction chamber, as shown in Fig. 2(e). They compared the particle trapping efficiency under different dimensions of lateral channels and connection channels. The results showed that when the widths of the lateral channel and the connection channel were α = 200 μm and β = 200 μm, respectively, the trapping efficiency was increased by 19% while maintaining high throughputs.

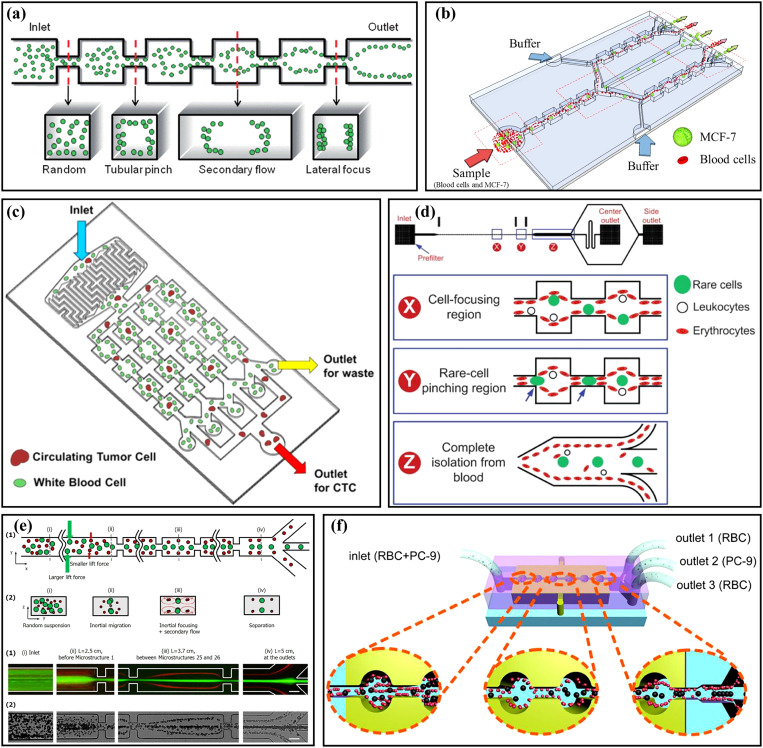
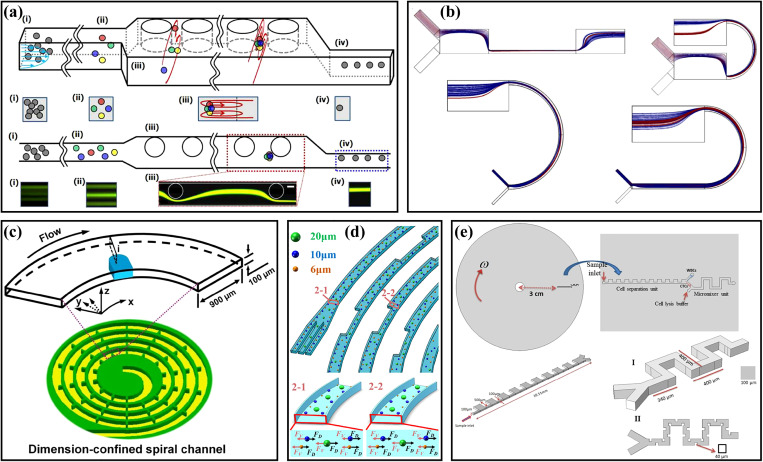
Without particle pre-focusing, particle focusing and sorting could also be achieved by directly using the contraction–expansion channels. In 2008, Jung and co-workers²¹ first proposed a microchannel with expansion–contraction channels in turn and series to achieve particle focusing, as shown in Fig. 3(a). As mentioned above, in a simple square straight channel, particles could be focused at the four equilibrium positions close to the walls. However, with the addition of expansion–contraction channels, the particles could be focused on both sides of the channel under the combined action of inertial lift force and secondary flow. They also studied the focusing of particles of different diameters under the same initial conditions and found that when Re was in the range of 63 ∼ 91, large particles (15 μm) were aligned along the centerline at the channel outlet, while small particles (7 μm) were focused near the sidewalls.⁵⁸ Two years later, they⁵⁹ designed a multi-stage multi-orifice flow fractionation (MS-MOFF) device by connecting two sets of multi-orifice segments at the outlet of the original channel, which improved the recovery rate and purity of large particles (15 μm) to 88.7% and 89.1%, respectively. Based on these studies, they²² applied a MS-MOFF device to cancer cell sorting, and the device channel structure is shown in Fig. 3(b). The sample of mixed MCF-7 cells and blood cells was injected into the inlet. At the first stage, the MCF-7 cells were focused at the channel center and directed to the middle of the channel outlet, while the blood cells and a few unfocused MCF-7 cells were near the two sidewalls and directed to the side channels. At the second stage, the unfocused MCF-7 cells were isolated to the channel center, and the recovery rate of the MCF-7 cells reached 98.9%. At the same time, they⁶⁰ also proposed another microfluidic chip by connecting four multi-orifice flow fractionations (MOFFs) in parallel, as shown in Fig. 3(c). Before the experiment, blood samples from breast cancer patients were pretreated to remove red blood cells, and then CTCs were sorted from white blood cells through using their microfluidic chip.

FIG. 3.

(a) Schematic diagram of particles focusing in the contraction–expansion microchannel. Reproduced with permission from Jung et al., Lab Chip 9, 7 (2009). Copyright 2009 Royal Society of Chemistry. (b) Schematic diagram of the channel structure and particle sorting of MS-MOFF. Reproduced with permission from Moon et al., Biomicrofluidics 7, 014105 (2013). Copyright 2013 AIP Publishing LLC. (c) Schematic diagram of the microfluidic device with a filter and four MOFFs in parallel. Reproduced with permission from Hyun et al., Biosens. Bioelectron. 40, 206 (2013). Copyright 2013 Elsevier. (d) Schematic diagram of rare cells separation from blood in a contraction–expansion microchannel with rare cell pinching regions. Reproduced with permission from Bhagat et al., Lab Chip 11, 11 (2011). Copyright 2011 Royal Society of Chemistry. (e) Schematic diagram of particle sorting in the microchannel with long expansion channels. Reproduced with permission from Wu et al., Lab Chip 16, 3 (2016). Copyright 2016 Royal Society of Chemistry. (f) Schematic diagram of the separation of lung cancer cells (PC-9) from red blood cells (RBCs) in a circular contraction–expansion microchannel. Reproduced with permission from Yao et al., Talanta 196, 546 (2019). Copyright 2019 Elsevier.

The dimension also played an important role in cell collecting. Bhagat et al.⁶¹ designed a contraction–expansion microchannel with a small width (20 and 60 μm for the widths of contraction and expansion regions) to study the separation of rare cells from blood cells. The channel was divided into a cell focusing region and a narrow rare cell pinching region, as shown in Fig. 3(d). The effects of different aspect ratios, hematocrit, and Reynolds numbers on the focusing of RBCs and the impact of pinching region width on CTCs recovery were studied. Under the optimal parameters, the recovery of CTCs was higher than 80%. Later, the same group⁶² studied the enrichment and purification of malaria parasites from the lysed blood by using a high-aspect-ratio contraction–expansion microchannel. The effects of contraction/expansion widths and outlet designs were explored. When the widths were 30/90 μm and the outlet width ratio was 1:1:1, 99.99% depletion of WBCs and 70.9 ± 11.4% collection of malaria parasites were achieved, respectively. Wu et al.⁶³ lengthened the chambers as shown in Fig. 3(e), and the channel could be regarded as a 120 μm width straight channel with 40 pairs of 45 μm width contraction channels with a spacing of 500 μm. They studied the focusing performances of various sized particles (from 4.8 μm to 13 μm) and found that large particles (>9.9 μm) were focused at the channel center while small particles (<6.8 μm) were focused close to the two sidewalls. Then, the device was applied to the separation of RBCs and WBCs, and the separation efficiency and purity were 89.7% and 91.0% for RBCs and 99.8% and 99.6% for WBCs, respectively. Recently, Liu et al.⁶⁴ compared the particle separation of four sets of contraction–expansion microchannels with different structures and shapes. The results showed that the circular channel had the best separation performance, and the efficiency of >95% for the separation of NCI-H1299 cells from RBCs was achieved using this microchannel. In the above studies, the contraction–expansion ratios were all fixed. Our group⁶⁵ compared and studied the migration characteristics of particles in the microchannels with contraction–expansion ratios of 1 and 2 through numerical simulation and experimental verification and found that for the large contraction–expansion ratio channel, a higher flow rate was required to focus particles of different sizes at their respective equilibrium positions (large particles in the channel center, small particles close to the two sidewalls), and small particles were more easily driven away from the channel center. A reasonable increase in the contraction–expansion ratio might help us to achieve the separation of differently sized particles at relatively high throughput. In addition, Yao et al.⁶⁶ used a circular contraction expansion channel [Fig. 3(f)] combined with dielectrophoresis (DEP) to achieve high sorting efficiencies of 90.21% for PC-9 cells and 94.35% for red blood cells, respectively. The structure and performance for particle sorting in symmetric contraction–expansion straight microchannels are summarized in Table I.

TABLE I.

Structures and sorting performances in symmetric contraction–expansion straight microchannels.

Target	Aspect ratio	Geometric size(contraction/expansion width × length × height)	Note	Recovery	Reference
15/7 μm particles	∼1	45 ∼ 50/200 × 100/200 × 50 ∼ 55 μm	Lower purity	75.2%/93.7%	58
15 μm particle	1	40/200 × 100/200 × 40 μm	Two stage MOFF	88.7%	59
MCF-7 cells	1	60/300 × 150/300 × 60 μm	Two stage MOFF	98.9%	22
MCF-7 cells/ MDA-MB-231 cells	1	60/300 × 150/300 × 60 μm	Four MOFF in parallel	93.75%/91.60%	60
CTCs	5	20/60 × 100/100 × 100 μm	With rare cell pinching region	85%	61
Malaria parasites/WBCs	…	30/90 × −/− × − μm	…	70.9 ± 11.4%/99.99%	62
5.5/9.9 μm particles WBCs/RBCs	∼2	45/120 × 45/500 × 21 μm	Long expansion channel	>92%/>98% 89.7%/99.8%	63
CTCs	1	60/300 × 150/300 × 60 μm	…	>80%	67
NCI-H1299 cells	2	100/400 × 200/400 × 50 μm	The shape of the cavity is a circle	>95%	64

Although both types of structures in Figs. 2 and 3 could achieve particle sorting, their sorting mechanisms were not consistent. For the former, the differently sized particles were first focused near the two sidewalls in the straight channel. Then, the large particles were captured by the vortex and remained in the expansion chambers, while the small particles did not enter into the expansion chambers and exited through the outlet. For the latter, due to the secondary flow and contraction and expansion effects, the different size particles had different equilibrium positions. Large particles were focused at the channel center while small particles were close to the two sidewalls, and then the outlet branch channels were used to sort and collect differently sized particles. Since the former needed to form vortices and capture particles in the expansion chambers, it had a larger expansion region, and the channel contraction–expansion ratio was >10, while that of the latter was generally 2–5.

In addition to particle focusing and sorting, symmetric contraction–expansion channels could be employed for other applications. Yun et al.⁶⁸ developed a microfluidic vortex-assisted electroporation system by combining a pre-focusing contraction–expansion channel and electroporation. In their system, MDA-MB-231 cells were captured by the expansion chambers and distributed evenly in the chambers, which facilitated subsequent electroporation. Using their system, the number of transfected cells obtained was threefold higher than that of the conventional device. Xia et al.²³ proposed a micromixer with a contraction–expansion channel and baffles. The effects of different baffle positions and contraction–expansion channel for the micromixer were studied numerically and experimentally, and the mixing efficiencies under different Reynolds numbers were tested. As the entrance width ratio was set to 1:2:1, and the four baffles in the contraction–expansion cavity were arranged in a cross. The mixing efficiency of >94%was achieved at Re > 40. Suwannaphan et al.⁶⁹ studied the damage and loss of cells during the sorting process of the contraction–expansion microchannel and spiral microchannel. The results proved that the cell deformed more significantly in the spiral channel, while the contraction–expansion channel had a higher possibility of damaging the intracellular structures of cells.

B. Asymmetric channels

1. Orthogonal contraction–expansion arrays

The structure of the asymmetric channel is more diversified compared with the structure of the symmetric channel, and the application of the asymmetric channel is more flexible. In 2009, Lee et al.⁷⁰ first reported the three-dimensional hydrodynamic focusing by an asymmetric contraction–expansion microchannel with a single sheath flow, as shown in Fig. 4(a). The expansion chamber was orthogonal to the main flow microchannel. When the fluid entered into the contraction region from the expansion region, the centrifugal effect pushed the sample flow to the sidewall and induced a secondary flow to make the sheath flow envelope the sample flow, achieving three-dimensional focusing of the sample flow on the cross section. The effects of the expansion chamber number, flow rate, and flow ratio of the sample flow to the sheath flow were also systematically studied. Using a similar channel, a laminating mixing was carried out and studied,⁷¹ and the mixing efficiency was improved by adopting the alternately placed expansion–contraction structure on the left and right sidewalls.⁷² At the same time, they applied their system to particle sorting.⁷³ Similar to Fig. 4(a), the mixed particles were injected from the s2 side, and the sheath flow was injected from the s1 side. Small particles (4 μm) were pushed to the s1 sidewall due to the dominance of the Dean flow, while large particles (10 μm) migrated to the s2 sidewall under the dominance of inertial lift force. Then, based on this principle, a series of sorting applications were realized by this group, including the separation of blood plasma from the whole blood with a recovery rate of 62.2%,⁷⁴ and the separation of breast cancer cells from the whole blood with a recovery rate of >99% and a blood cell rejection ratio of 97.4%.²⁴ In addition, they also achieved the separation of MCF-7 breast cancer cells from U937 lymphoma cells with a recovery rate of 97.6% by labeling MCF-7 cells with beads [Fig. 4(b)].⁷⁵ By redesigning the size of the similar contraction–expansion structure and adding multiple outlets, Kim et al.¹¹ achieved the separation of Chlorella vulgaris and Haematococcus pluvialis with the purity of 97.9% and 94.9%, respectively.

FIG. 4.

(a) Schematic diagram of an asymmetry contraction–expansion array microchannel for three-dimensional focusing. Reproduced with permission from Lee et al., Lab Chip 9, 21 (2009). Copyright 2009 Royal Society of Chemistry. (b) Schematic diagram of the separation MCF-7 from U937 cells based on their difference in surface protein by an asymmetry contraction–expansion array microchannel. Reproduced with permission from Shin et al., RSC Adv. 4, 74 (2014). Copyright 2014 Royal Society of Chemistry. (c) Schematic diagram of single-stream focusing of particles in a stepped microchannel. Reproduced with permission from Chungs et al., Small 9, 5 (2013). Copyright 2013 John Wiley and Sons. (d) Comparison of particle focusing in a straight microchannel and an asymmetric contraction–expansion array microchannel with sharp conners at different flow rates. Reproduced with permission from Fan et al., Microfluid. Nanofluid. 17, 4 (2014). Copyright 2014 Springer Publishing.

Combining symmetry and asymmetry contraction–expansion channels, Yang et al.⁷⁶ proposed an interesting microfluidic system for the label-free separation of CTCs. Different from the symmetry contraction–expansion channel introduced in Sec. II A, the symmetry channel employed as the first stage here was to focus all particles into tight streamlines close to the two sidewalls. Then, differently sized particles were sorted in the second stage of asymmetry channels. Chung et al.⁷⁷ proposed an inertial microfluidic platform to achieve single-stream particle focusing, as shown in Fig. 4(c). The combination of the inertial effect and the secondary flow was realized by inserting a series of contraction regions in a low-aspect-ratio straight microchannel. Randomly distributed particles were focused toward two equilibrium positions through the upstream straight channel, and then the focused particles were repositioned under the action of secondary flow induced by the stepped channels. Through a series of stepped channels, the single-stream focusing was achieved with a focusing efficiency of 99.77% and a throughput of ∼36 000 particles/s. On this basis, Li et al.⁷⁸ replaced the original contraction regions with expansion regions to form a novel stepped microchannel to achieve single-line focusing of the ellipsoid-shaped Euglena gracilis (E. gracilis) cells and studied the effects of Re and AR on the focusing and rotation of E. gracilis cells with various aspect ratios and sizes. Fan et al.⁷⁹ designed a CEA microchannel with a series of asymmetrical sharp corners on one side of the channel, as shown in Fig. 4(d). The centrifugal force induced by the sharp corners forced the particles to migrate to the opposite sidewall without sharp corners and the single-stream focusing of 9.94 μm particles over the flow rate range of 300 ∼ 700 μl/min was successfully achieved. Based on this research, they⁸⁰ changed the two sides of the microchannel to the symmetric sharp corner structures and combined a 90° curved channel to study the 3D focusing of the particles. The particles in the curved channel were focused at the center plane by the drag force F_D induced by the Dean flow and then focused at the channel center under the effects of the symmetric sharp corner structures. To solve the problem that the microchannel [Fig. 4(d)] could not focus different size particles in a small bandwidth, they²⁵ redesigned the sharp corner structure and, finally, achieved the single-stream focusing of differently sized particles (7.32, 9.94, and 15.45 μm) over a large range of Re from 19.1 to 142.9.

2. Nonorthogonal contraction–expansion arrays

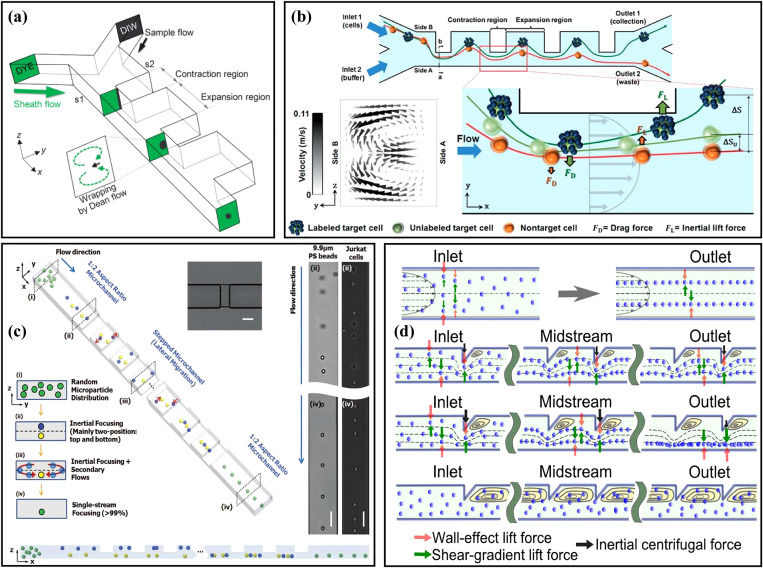
Hydrophoresis is a passive approach for particle manipulation utilizing a pressure gradient induced by the microchannel structure.⁸¹ Song et al.⁸² designed a microchannel with slanted grooves to achieve the size-based hydrophoretic sorting and focusing, as shown in Fig. 5(a). Particles migrated laterally under the effects of the helical streamline and lateral rotational flows generated by the slanted grooves. In their research, the oblique angle of grooves and Re (Re < 10) did not have significant effects on particle sorting. In contrast, the channel width was an important key parameter. However, with further increasing Re to be larger than 10, the inertial lift force might affect the particle sorting performance; hence, they⁸³ also reported a microfluidic technology to modulate the hydrophoretic sorting and focusing by changing Reynolds number instead of the channel width. At low Re, particle sorting was achieved by hydrophoresis to move differently sized particles to their equilibrium positions, while at high Re, the particles migrated to a narrow focusing flow in the channel center under the combined effects of hydrophoresis and inertial forces. Then, the same group⁸⁴ used the hydrophoresis coupled with inertial effect to achieve a robust flow-rate insensitive particle ordering through a microfluidic device with slanted contraction and expansion structures on the sidewalls. Compared with the vertical-wall device without hydrophoresis, the inclined-wall device could realize the stable particle ordering regardless of the Re. This method could be achieved by manual injection, avoiding the need for high-precision and costly pumps. What is more, they²⁹ proposed another microfluidic sorting device [Fig. 5(b)] to overcome the limitation that hydrophoresis separation performance was usually affected by flow rate. There were a series of inclined and gradually changing grooves on the channel top surface. These grooves locally created a rotational flow to guide the large cells to migrate toward both sides of the channel, regardless of the flow rate, while small cells remained randomly distributed under negligible hydrophoresis.

FIG. 5.

(a) Schematic diagram of the microchannels with slanted groove arrays for particle hydrophoresis sorting and focusing. Reproduced with permission from Song et al., J. Chromatogr., A 1302, 191 (2013). Copyright 2013 Elsevier. (b) Schematic diagram of a microchannel with a series of inclined and gradually changing grooves for size-based cell sorting. Reproduced with permission from Song et al., Lab Chip 15, 5 (2015). Copyright 2015 Royal Society of Chemistry. (c) Schematic diagram of a microchannel for separating magnetic and non-magnetic particles through magnetic force and hydrophoresis. Reproduced with permission from Yan et al., Appl. Phys. Lett. 109, 21 (2016). Copyright 2016 AIP Publishing LLC. (d) Schematic diagram of the distribution of Jurkat cells and RBCs at the cross section of the channel after flowing through the microchannel with arc-shaped groove structure. Reproduced with permission from Yan et al., Micromachines 8, 11 (2017). Copyright 2017 Molecular Diversity Preservation International. (e) Schematic diagram of the microchannel for manipulating and focusing small particles with the assistance of sheath flow. Reproduced with permission from Zhao et al., Microfluid. Nanofluid. 23, 1 (2019). Copyright 2019 Springer Publishing. (f) Schematic diagram of the double-layer microchannel consisting of a straight channel with contraction–expansion arrays and slanted grooves. Reproduced with permission from Yan et al., Biomed. Microdevices 20, 2 (2018). Copyright 2018 Springer Publishing.

Slanted groove and other expansion–contraction structures have been systematically studied by Yan's group. They⁸⁵ used a microchannel with crescent-shaped grooves combined with dielectrophoresis to achieve active hydrophoretic focusing of particles. The microfluidic device was fabricated by two-step photolithography⁸⁶ and composed of two corresponding polydimethylsiloxane (PDMS) layers, one with a straight channel and the other with crescent-shaped grooves. The particles were guided to both sidewalls of the channel under the combination of the negative DEP force and the hydrophoretic effect. Based on this principle, improved focusing performance of murine erythroleukemia (MEL) cells at a high throughput of ∼150 ml/min was achieved. Then, they⁸⁷ combined this microchannel structure with magnetophoresis [Fig. 5(c)] to verify the high-throughput, sheath-free separation of magnetic and non-magnetic beads. The magnetic and non-magnetic particles could be respectively focused at the center and both sidewalls of the channel under the magnetic force and hydrophoresis, and this method could be carried out over a wide flow rate range and convenient for manual operation. Later, to realize the flow rate-insensitive passive particle sorting without external forces, the same group redesigned the microchannel structure and changed the shape of the groove to an arc and adopted a straight channel with AR = 0.2. The equilibrium position of the particles depended on their sizes. Large particles were guided by the secondary flow induced by the grooves to the left side of the channel, and balanced near the sidewall under the effect of inertial lift force, while small particles were apt to follow the rotating streamline of the secondary flow due to the weak inertial lift force, and finally focused near the vortex core. Based on this principle, the recovery efficiency and purity of 4.8 μm particles reached ∼80% and >99.9%; meanwhile, the recovery efficiency and purity of 13 μm particles were >99.9% and ∼35%.⁸⁸ Then, Jurkat cells were separated [Fig. 5(d)] from blood cells with the recovery rate of ∼83.4%.⁸⁹ This group⁹⁰ also studied particle sorting in a microchannel with slanted grooves. Large particles (>8 μm) were dominated by hydrophoresis at low Re and inertial lift force at high Re and migrated to the sidewall regardless of the flow rate (20 ∼ 500 μl/min), while small particles (2 μm) remained randomly distributed under negligible hydrophoresis. Based on this design, the extraction of peripheral blood mononuclear cells (PBMCs) from platelets was achieved, and the purity of PBMCs was increased from 0.8% to 10.4%. To effectively manipulate small-sized particles (<8 μm), based on the original microchannel structure, the group⁹¹ added a top sheath flow [Fig. 5(e)] to improve the focusing efficiency of small particles and studied the effects of particle concentration, the flow rate ratio of sheath flow to sample flow, and the number of grooves on particle focusing. Under the total flow rate of 700 μl/min and the flow rate ratio of 6, the extraction purity of plasma up to ∼99% was successfully achieved. To further enhance the particle focusing, they⁹² proposed another double-layer microfluidic device, which consisted of a straight channel with contraction–expansion arrays and slanted grooves, as shown in Fig. 5(f). Particles were focused into a narrower band under the CEA channel flow pattern modulated by the secondary flow induced by the grooves, and the lateral migration of particles could be adjusted by changing the flow rate.

3. Other asymmetric channels

The CEA microchannel could also be combined with obstacles, curved microchannels, and spiral microchannels for particle focusing and sorting. Chung et al.⁹³ designed a three-stage straight microchannel with different structures for particle single-stream focusing. The main body of the microchannel was an expansion rectangular channel with a series of cylindrical obstacles, and its entrance and exit were a square channel (AR = 1.0) and a rectangular channel (AR = 2.0), respectively, as shown in Fig. 6(a). The particles were first focused to four equilibrium positions in the square channel, and then migrated into a narrow band under the effect of the secondary flow induced by the pillars, and finally dominated by the wall-induced inertial lift force in the high aspect ratio channel, achieving the single-stream focusing with a high focusing efficiency of 98.33%. To explore particle separation based on the combination of contraction–expansion channels and curved channels, Shamloo et al.³⁰ studied the influence of the channel aspect ratio and different geometric shape combinations [Fig. 6(b)] on particle separation through numerical simulation methods. The microchannel structure in the upper right corner of Fig. 6(b) could produce the strongest secondary flow, which focused the small particles closer to the sidewall at the outlet, achieving the isolation of small particles from large particles. Separation could be completed within a shorter channel length compared with the straight CEA microchannels. Subsequently, this team⁹⁴ applied the contraction–expansion arrays to the disk centrifugal device to separate MCF-7 cells from L929 cells, and the recovery rate of MCF-7 cells was increased from 76% of passive technology to 85% by combining magnetophoretic techniques.

FIG. 6.

(a) Schematic diagram of a three-stage straight microchannel with different structures for particle single-stream focusing. Reproduced with permission from Chung et al., Lab Chip 13, 15 (2013). Copyright 2013 Royal Society of Chemistry. (b) Schematic diagram of several different geometric shape combinations of curved channels and contraction–expansion channels. Reproduced with permission from Shamloo et al., Aiche J. 65, 11 (2019). Copyright 2019 John Wiley and Sons. (c) Schematic diagram of a spiral microchannel with obstacles. Reproduced with permission from Shen et al., Lab Chip 17, 21 (2017). Copyright 2017 Royal Society of Chemistry. (d) Schematic diagram of a spiral contraction–expansion microchannel for efficient and stable particle separation. Reproduced with permission from Gou et al., Anal. Chem. 92, 2 (2020). Copyright 2020 American Chemical Society. (e) Schematic diagram of a centrifugal microfluidic platform with a unilateral contraction–expansion channel and a serpentine channel with obstacles for cell sorting and lysis. Reproduced with permission from Nasiri et al., Micromachines 11, 7 (2020). Copyright 2020 Molecular Diversity Preservation International.

Expansion–contraction structures are also capable of combining spiral or serpentine microchannel. Shen et al.³¹ added obstacles to the spiral microchannel [see Fig. 6(c)] to realize the fast, high-throughput, and high-efficient particle focusing and sorting. Obstacles could cause a significant acceleration of secondary flow on the cross section, which was beneficial to particle focusing. Based on this design, a series experiments of particle focusing and sorting have been realized, including the focusing of 15.5, 9.9, and 7.3 μm particles with focusing efficiencies of 99.8%, 98.6%, and 90.9%, respectively. The separation of blood plasma from blood cells with a blood plasma recovery rate of 67.6%, and a blood cell rejection efficiency of 99.96% were also achieved. Gou et al.³² proposed a spiral microchannel combined with contraction–expansion structures, as shown in Fig. 6(d), overcoming the shortcoming that the equilibrium position of the particles in the conventional spiral microchannels was not fixed under different channel dimensions and flow rates. What is more, Nasiri et al.³³ designed a centrifugal microfluidic platform integrating cell sorting and mixing, as shown in Fig. 6(e). Their platform was composed of a rotating compact disk, a unilateral contraction–expansion channel, and a serpentine channel with obstacles. The cells were separated in the CEA channel, and then the separated target cells were lysed by being mixed with the cell lysis chemical reagent in the serpentine channel. Through using the numerical methods, the separation efficiency at different angular velocities from 500 to 3000 rpm was simulated. At 2000 rpm, the separation efficiency of CTCs from WBCs was as high as ∼90%, and the mixing quality of the separated CTCs was as high as ∼98%.

The asymmetric contraction–expansion channels provide more options for particle manipulation. Specifically for the particle single-line focusing, the asymmetric contraction–expansion channels have distinct advantages and make up for the shortcomings of inertial symmetric contraction–expansion channels. Among them, the non-orthogonal contraction–expansion arrays can realize particle manipulation over a wide range of Re, which greatly facilitates manual operation. In addition, the asymmetric channels can be more flexibly combined with other microchannels to modify the manipulation more stable, efficient, and sensitive for particles. The structure and performance of various inertial contraction–expansion microfluidics are summarized in Table II.

TABLE II.

Recent advances of inertial contraction–expansion microfluidics.

Structure of contraction–expansion microfluidics	Role of contraction–expansion channels	Targets	Applications	Performance	Reference
Single large symmetrical contraction–expansion chamber	Capture large particles	CTCs	Enrichment of cancer cells from spiked blood samples	Throughput: ∼5 ml/min	19
		MCF-7 cells	Separation of larger cancer cells from the blood cells	Processing rate: 7.5 × 106 cells/s	47
		Rare cells	Selective isolation and trapping of large rare cells	The best performance: concentrations below 102 particles/ml	48
Large symmetrical contraction–expansion chamber with two side outlets	Capture large particles	21 μm particles	Separation of 21 μm particles from human blood	Capture efficiency: 86%	49
		21/18.5/15 μm particles	Secondary separation of ternary mixture	Purity: 89.4% (21 μm) 80.7% (18.5 μm) 95.9% (15 μm)	50
		HuSLCs	Sorting of HuSLCs from RBCs	Sorting efficiency: ∼90% RBCs removal efficiency: ∼99.97%	20
		15 μm beads	Sorting of 15 μm particle from 6 μm ones	Capture efficiency: >80%	52
Multiple large symmetrical contraction–expansion chamber in series and parallel	Capture large particles	MCF-7 cells	High-purity extraction of CTCs from blood samples	Processing time: <7.5 ml sample per 20 min	53
		CTCs	Enrichment and concentration of rare cells.	Capture efficiency: 83% Throughput: 8 ml/min	55
		CTCs	Enrichment and enumeration of CTCs from blood	Enumeration processing time: <1 h	56
		CTCs	Sorting of rare cells from blood	Trapping efficiency: 67% Throughput: 5 ml/min	57
Direct symmetric contraction–expansion array channel	Produce inertial forces (secondary flow) to affect the lateral migration of particles (large particles were focused at the channel center while small particles were close to the two sidewalls)	15 μm/7 μm particles	Size-based separation	Recovery: 75.2% (15 μm) 93.7% (7 μm) Throughput: 1 ∼ 5 × 104 particles/s	58
		15 μm particles	Size-based separation	Recovery: 88.7% Purity: 89.1%	59
		MCF-7 cells	Separation of breast cancer cells from blood cells	Recovery: 98.9% Blood cells removal rate: 93.3%	22
		MCF-7/MDA_MB_231 cells	Separation and collection of breast cancer cells from the whole blood	Recovery: 93.75% (MCF-7) 91.60% (MDA_MB_231)	60
		MCF-7 cells	Enrichment of rare cells from blood	Separation efficiency: ∼80% Throughput: ∼0.4 ml/min	61
		Malaria parasites	Separation and collection of malaria parasites from WBCs	Collection yield: 70.9 ± 11.4% WBCs depletion: 99.99%	62
		WBCs/RBCs	Size-based separation	Purity: 91.0% (WBCs) 99.6% (RBCs) Separation efficiency: 89.7%(WBCs) 99.8% (RBCs) Throughput: 10.8 ml/min	63
		Plasma NCI-H1299 cells	Separation of plasma, RBCs, and NCI-H1299 cancer cells from blood in different shape CEA channels	Separation efficiency: 96.0% (plasma) >95% (NCI-H1299)	64
Unilateral contraction–expansion array channel with a sheath flow	Produce Dean drag force (induced by the secondary flow) combined with inertial lift force to achieve size-based separation (large particles were close to the side of the contraction–expansion wall while small particles were close to the side of the straight wall)	10/4 μm particles	Separation of different-sized particles	Purity: 100% (10 μm) 99%(4 μm) Throughput: 111 particles/s	73
		Plasma	Separation of plasma from RBCs	Separation efficiency: 62% Throughput: 1.2 ml/h	74
		Plasma	Separation of plasma from human whole blood	Separation efficiency: 69.5% Blood cell rejection ratio: 92.6% Throughput: 5.4 × 1011 cells/min	95
		CTCs	Separation of cancer cells from human whole blood	Recovery: 99.1% Blood cell rejection ratio: 88.9% Throughput: 1.1 × 108 cells/min	24
		MCF-7 cells U937 cells	Separation of immune-specifically labeled cells from other cells	Recovery: 97.6% (MCF-7) Rejection ratio: 95% (U937) Purity: 73.8% (U937) Throughput: 8.75 ml/h	75
Unilateral contraction–expansion array channel on the top surface of low aspect ratio channel	Induce fluid helical rotation to promote particle focusing position from the original two (caused by inertial lift force) to a single one	9.9 μm particles	Three-dimensional single-stream particle focusing	Focusing efficiency: 99.77% Throughout: 36 000 particles/s	77
		Euglena gracilis	Three-dimensional single-stream particle focusing	High aspect ratio particles have better focusing performance at higher Re	78
A series of repeated sharp corner structures	Produce inertial forces to affect the lateral migration of particles	9.94 μm particles	Three-dimensional single-stream particle focusing	Throughput: 0.7 ml/min	79
		7.32 μm particles	Three-dimensional single-stream particle focusing	Throughput: 66.7 μl/min (sample flow) 400 μl/min (sheath flow)	80
		7.32 ∼ 15.5 μm particles	Three-dimensional single-stream particle focusing	Single-stream particle focusing over a wide range of Re from 19.1 to 142.9	25
Nonorthogonal groove array structure	Produce hydrophoresis effect and combine with inertial lift force to realize particle manipulation	K562 cells	Size-based cell sorting and focusing.	Optimal width for cell sorting (3 × cell diameter) and focusing (>400 μm)	82
		12.4/15.6 μm particles	Size-based particle sorting and focusing	Particle sorting at Re = 2.4 Particle focusing at Re = 50.8	83
		Blood cells	Particle ordering and liquid-medium recovery from blood cells	Rejection efficiency: 99.3% Throughput: 1.63 × 106 cells/s	84
		G1 cells	Size-based cell sorting	Purity: 90.3% Throughput: 1.2 × 105 cells/s	29
		13/4.8 μm particles	Size-based particle separation and filtration	Recovery: >99.9% (13 μm) ∼80% (4.8 μm) Purity: ∼35% (13 μm) >99.9% (4.8 μm)	88
		Jurkat cells	Separation of Jurkat cells from undiluted blood	Recovery: ∼83.4%	89
		PBMCs/ platelets	Extraction of peripheral blood mononuclear cells (PBMCs) from platelets	Purity: 10.4% (PBMCs) ∼100% (platelets)	90
		Plasma	Manipulation of small-sized particles (<8 μm) with the assistance of sheath flow	Purity: ∼99% Throughput: 0.7 ml/min	91
Combination of slanted groove array and contraction–expansion array	To obtain the enhanced particle focusing	10 μm particles	Three-dimensional single-stream particle focusing	Focusing efficiency: >95% Particle focusing over a wide range of flow rate from 50 to 500 μl/min	92
Others (add obstacles, or combine with other channels)	Make the devices more stable and efficient for particle manipulation	19 μm particles	Three-dimensional single-stream particle focusing by adding a series of cylindrical obstacles	Focusing efficiency: 91.65%	93
		15.5/9.9/7.3 μm particles	The fast, high-throughput and high-efficient particle focusing and sorting by adding obstacles to the spiral microchannel	Focusing efficiency: 99.8% (15.5 μm) 98.6% (9.9 μm) 90.9% (7.3 μm) Recovery: 98.7% (15.5 μm) 97.8% (9.9 μm) 85.8% (7.3 μm) Purity: 97.5% (15.5 μm) 86.1% (9.9 μm) 98.4% (7.3 μm)	31
		MCF-7 cells Hela cells A549 cells	Separation of rare cancer cells from the blood sample by a spiral microchannel combined with CEA	Recovery: 93.5% (MCF-7) 89.5% (HeLa) 88.6% (A549)	32
		CTCs	Separation and cell Lysis of CTCs by a centrifugal microfluidic platform integrating CEA and serpentine channel	Separation efficiency: ∼90% Mixing quality: ∼98%	33

III. ELASTO-INERTIAL MICROFLUIDIC

In addition to inertial microfluidics with Newtonian fluids, elasto-inertial microfluidics have recently received much attention due to the ability of single-line particle focusing in simple channels.^96,97 In viscoelastic fluids, particles are affected by the elastic effect which is characterized by the Weissenberg number Wi⁹⁸(Wi = λγ, where λ is the relaxation time and γ is the average shear rate). When Wi is small, the elastic force F_E on the particle can be expressed as ${\mathrm{F}}_E=\text{-}2{\mathrm{C}}_{eL}{\mathrm{a}}^3\lambda \mathrm{\nabla }{\gamma }^2$,⁹⁹ where C_eL is the dimensionless elastic lift coefficient and η_p is the polymer viscosity. Yang et al.¹⁰⁰ first proposed the concept of elasto-inertial focusing by combining the elastic force with the inertial lift force. With the appropriate elastic number El (El = Wi/Re), the single-line particle focusing in the center of the square channel can be realized.

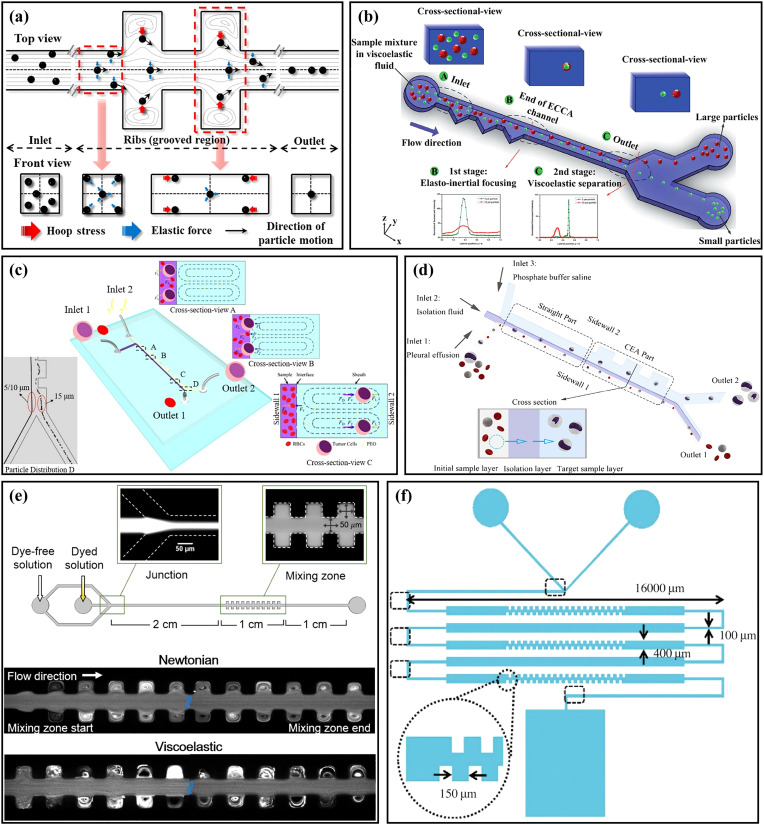
Recently, many scholars have begun to combine viscoelastic fluids with contraction–expansion channels to study particle focusing and sorting. Cha et al.¹⁰¹ utilized a symmetrical CEA channel [Fig. 7(a)] to study the elasto-inertial particle focusing. Through using the hoop stress induced in the CEA structure, single-line particle focusing could be achieved with a high focusing efficiency of >99%. Yuan et al.²⁷ designed a straight microchannel with a unilateral triangular-shaped contraction–expansion structure for single-line particle focusing. In this microchannel, the particles migrated to a single focusing equilibrium position between the channel center and the straight sidewall under the combined effects of inertial lift force, elastic force, and the Dean drag force induced by the expansion–contraction cavity arrays (ECCA). Differently sized particles of 3.2, 4.8, and 13 μm were used for verification of particle focusing, and all of them were focused near the straight sidewall. Based on this principle, they¹⁰² utilized the microchannel for plasma extraction. Blood cells were all focused near the sidewall, and the plasma purity reached as high as 99.99%. With the well-studied phenomenon that small particles have an equilibrium position closer to the channel center than large ones in low-aspect-ratio microchannels of viscoelastic fluids,¹⁰³ the same group¹⁰⁴ proposed a two-stage viscoelastic microfluidic device for particle focusing and sorting, as shown in Fig. 7(b). In the first stage, particles with different sizes were focused near the sidewall in the ECCA channel, and in the second-stage rectangular channel, small particles migrated toward the channel center under the viscoelastic effect, while large ones still stayed near the sidewall. Through using their device, the separation of Jurkat cells and yeast cells was achieved. The recovery rate and purity of Jurkat cells were 99.6% and 24%, respectively. Shi et al.¹⁰⁵ proposed a unilateral CEA microchannel using viscoelastic sheath flow, as shown in Fig. 7(c). The sample flow was injected close to the side of the straight wall, while the sheath flow was injected close to the CEA side to form the Dean flow. By adjusting the viscoelasticity of sheath flow, the interfacial elastic force was controlled to enable the large particles to penetrate the interface while the small ones remained in the sample layer. The large particles entering into the sheath layer were further separated from the small ones under the effects of the elastic force and the drag force induced by the CEA channel. The separation performance of the device was verified by testing differently sized particles and the separation of H1299 cells from blood cells was achieved with a separation efficiency of 98%. On this basis, this group¹⁰⁶ subsequently proposed a microchannel with a sandwich structure, as shown in Fig. 7(d). There were three inlets in the microchannel connecting to the sample layer, isolation layer (viscoelastic fluid), and target sample layer (Newtonian fluid) separately. When the flow rate ratio was 1:1:6, the optimal separation of tumor cells and blood cells was achieved, and the separation efficiency was ∼100% for tumor cells and >90% for blood cells, respectively. What is more, Fan et al.¹⁰⁷ added sheath flow to the aforementioned CEA microchannel with a series of asymmetric sharp corners²⁵ to study the viscoelastic particle separation. The sample flow and sheath flow were viscoelastic fluid and Newtonian fluid, respectively. Based on this design, they successfully achieved the separation of 2 and 10 μm particles at low flow rate ratios (sheath flow/sample flow of 3:1) and low flow rates (<1 μl/min), which was suitable for the separation of vulnerable cells. The performance of various elasto-inertial contraction–expansion microfluidics is summarized in Table III. Compared with the data of inertial microfluidics in Table II, the elasto-inertial contraction–expansion microfluidics tend to run at lower flow rates and are more friendly to the manipulation of small particles.

FIG. 7.

(a) Schematic diagram of the particle focusing principle in a straight microchannel with a symmetrical CEA structure. Reproduced with permission from Cha et al., Rheol. Acta 53, 127 (2014). Copyright 2014 Springer Publishing. (b) Schematic diagram of a two-stage viscoelastic microfluidic device for particle elasto-inertial focusing and viscoelastic separation. Reproduced with permission from Yuan et al., RSC Adv. 7, 6 (2017). Copyright 2017 Royal Society of Chemistry. (c) Schematic diagram of the unilateral CEA microchannel using viscoelastic fluid sheath flow and the principle of size-based particle separation. Reproduced with permission from Shi et al., Analyst 144, 20 (2019). Copyright 2019 Royal Society of Chemistry. (d) Schematic diagram of a sandwich structure microfluidic device with three inlets for label-free and size-based sorting of tumor cells. Reproduced with permission from Shi et al., Anal. Bioanal. Chem. 412, 5513 (2020). Copyright 2020 Springer Publishing. (e) Schematic diagram of the microchannel for elasto-inertial fluid mixing, and the images of Newtonian fluids and viscoelastic fluids after mixing. Reproduced with permission from Hong et al., Appl. Phys. Lett. 108, 1 (2016). Copyright 2016 AIP Publishing LLC. (f) Schematic diagram of a micromixer combining a serpentine channel and a tooth-shaped contraction–expansion structure. Reproduced with permission from Julius et al., Biochip J. 10, 1 (2016). Copyright 2016 Springer Publishing.

TABLE III.

Recent advances of elasto-inertial contraction–expansion microfluidics.

Targets	Applications	Sample flow rate	Performance	Reference
6 μm beads	Three-dimensional single-stream particle focusing	300 μl/h	Focusing efficiency:>99%	101
3.2/4.8/13 μm particles	Three-dimensional single-stream particle focusing	60 μl/min	4.8 μm particles have the best focusing performance	27
Plasma	Plasma extraction in the diluted blood sample	50 μl/min	Plasma purity: 99.93% (the first filtration) 99.99% (the second filtration)	102
Jurkat cells	Separation of Jurkat cells and yeast cells	20 μl/min	Recovery rate: 99.6% Purity: 24% Enrichment ratio: 11.9%	104
H1299 cells	Separation of H1299 cells from the blood cells	500 μl/h	Separation efficiency: 98%	105
NCI-H1299 cells / Blood cells	Separation of tumor cells from the blood cells	10 μl/min	Separation efficiency: 100% (NCI-H1299 cells) >90% (blood cells)	106
2/10 μm particles	Size-based particle separation	∼1 μl/min	Achieving complete particle separation	107

What is more, the viscoelastic fluid has flow instability¹⁰⁸ and can be easily combined with the secondary flow induced by the CEA channel, which is beneficial to the mixing of different microfluids. Hong et al.¹⁰⁹ compared the mixing performance of Newtonian fluid and viscoelastic fluid in a straight microchannel with a symmetrical CEA structure, as shown in Fig. 7(e). When using viscoelastic fluids, chaotic vortices that appeared in the expansion cavities could improve the mixing performance, while there was no chaotic vortex phenomenon in Newtonian fluids, regardless of flow rates. Julius et al.¹¹⁰ proposed a micromixer combining a serpentine channel and a tooth-shaped contraction–expansion structure [Fig. 7(f)] to improve fluid mixing efficiency. The mixing efficiency was verified by mixing experiments of two different dyes, and the lysis of RBCs as the mixing experiment was successfully achieved with this device. In addition, the combination of viscoelastic fluids and contraction–expansion channels can also be used in other research and applications, including the study of flow instability caused by various viscoelastic fluids,^111,112 and the application of fluid viscosity measurement.¹¹³

IV. CONCLUSIONS AND PERSPECTIVES

Inertial microfluidics is increasingly indispensable for high throughput cell detection in a miniaturized flow cytometer, especially the introduction of the secondary flow further improves the efficiency of the manipulation. As an all-rounder, the inertial contraction–expansion microchannel has been one of the most common microchannel structures for particle manipulation. The diverse applications of the contraction–expansion microchannel have been classified based on structural characteristics and comprehensively reviewed in this article. Particle isolation through vortex or sorting in the main flow can be easily realized with appropriate dimension designs. Extremely high throughput and precision can be guaranteed by a parallel design and double-grade structure. Friendliness for manual manipulation of different size particles focusing or sorting over a wide range of Re has been validated through experiments by adding sharp corners or non-orthogonal chambers to the contraction–expansion microchannels. Even better performance can also be obtained by the combination of spiral, serpentine, or other patterns to the contraction–expansion microchannel. With the addition of the elastic force provided by viscoelastic fluid, particle separation with a greatly lower flow rate can be achieved, which is conducive to the manipulation of vulnerable particles.

Although the contraction–expansion microchannels have accomplished so many achievements, the mechanisms and interrelation behind different types of inertial contraction–expansion microfluidics are still unclear and need to be systematically studied further. Numerical simulation is an increasingly ripe method for microfluidics researching with the development of computers, especially the performance improvement of GPU (graphics processing unit), which parallelizes and dramatically accelerates the simulation program. More information on the fluid field evolution and particle migration can be provided through calculation, and all details about the particle position can be illustrated clearly. Computer aided microfluidics learning and microchannel design can provide a strong reference for practical contraction–expansion microchannel structure building for various particle manipulation aims, and the fluid and particle simulation technique needs to be further developed for more efficiency and precisely manipulation results forecast.

With regard to the inertial microfluidic chips, there is a trade-off between particle manipulation efficiency and precision. In order to obtain good integrated performance of a microfluidic channel, a combination of the secondary flow from the contraction–expansion microchannel and elastic force from viscoelastic flow has great prospect in the future. The dean flow in the contraction–expansion microchannel may dramatically reduce the channel length and processing time. The elastic force is more sensitive to the different particle sizes. The combination of contraction–expansion microchannel and the viscoelastic flow may be employed for the future precise and efficient microfluidic chip design.

Even though the contraction–expansion microchannel is a basic pattern for particle manipulation, the versatility of this kind of channel introduced in this review demonstrated the complexity of the mechanics between channel graphic characters and particle migration rules. Researchers may study and design microchannels through advanced numerical simulation methods avoiding the conventional trial-and-error experimental method, and other techniques like viscoelastic fluid and external force fields may improve the distinguishability of contraction–expansion microchannels and expand the applications. We hope the advances of inertial contraction–expansion microchannels introduced in this review will provide comprehensive knowledge of particle manipulation in contraction–expansion microchannels and inspiration for further invention of a highly efficient and precise microfluidic device.

DATA AVAILABILITY

The data that support the findings of this study are available within the article.