The origin of cooperation

Significance

We develop a mathematical theory of how natural selection operates in the presence of interaction between replicating units. Our results show that with interaction, natural selection does more than seek to selfishly maximize fecundity. It also seeks to minimize correlation of fecundity between replicating units. We argue that correlation is a mechanism by which evolution can select for cooperation. This mechanism is distinct from standard biological explanations like kin selection, group selection, and reciprocity, and relies only on natural selection, and without recourse to notions of evolutionary stability.

Abstract

We construct an evolutionary model of a population consisting of two types of interacting individuals that reproduce under random environmental conditions. We show that not only does the evolutionarily dominant behavior maximize the number of offspring of each type, it also minimizes the correlation between the number of offspring of each type, driving it toward −1. We provide several examples that illustrate how correlation can be used to explain the evolution of cooperation.

Cooperation is a key feature of human evolution, and many theories have been developed to explain its existence. These theories typically introduce auxiliary concepts such as inclusive fitness (1, 2), kin selection (3), group selection (4–10), multilevel selection (11), and reciprocal altruism (12). These auxiliary concepts are needed to reconcile the apparent conflict between natural selection—which is assumed to select for selfish offspring-maximizing behavior—and unselfish cooperation. Indeed, inclusive fitness, kin selection, group selection, multilevel selection, and reciprocal altruism are all mechanisms in which cooperation is selfish.

In this article, we develop an alternate theory for the evolution of cooperation. We construct a simple, but general, evolutionary model of a population consisting of two types of interacting individuals that reproduce under stochastic environmental conditions. Without making any additional assumptions about the nature of the individuals or their interactions, we characterize precisely how natural selection operates in this setting. We show that natural selection does more than select for selfish offspring-maximizing behavior. It also selects for behavior that minimizes the correlation of fecundity between individuals. In particular, we show, both theoretically and computationally, that behaviors that decrease correlation (i.e., driving it toward $-1$), cause exponential increases in population size. We argue that correlation is an avenue by which evolution can select for cooperation without any auxiliary assumption that cooperation is selfish.

Our framework also contributes to the mathematical biology literature. Previous theories of evolution and cooperation have their origins in evolutionary game theory (13–15) and depend on the concept of evolutionary stability, rather than natural selection. They are also tailored to specific interactions. Economists, similarly, have used evolutionary models to explain how humans interact with one another, but also only in specific economic settings (16–19). Our results provide a key step toward a general theory of evolution when replicating units interact with one another and affect each other’s reproductive success, assuming nothing more than the principle of natural selection.

Theory

Our starting point is similar to that of Brennan and Lo (20) and Zhang, Brennan, and Lo (21): A population of individuals reproduces asexually and only once in their lifetime, giving rise to offspring that inherit the behaviors of their parent. “Behavior” in this simple context is modeled abstractly as a single parameter $p$ for a Bernoulli trial that yields one of two possible outcomes for the individual’s number of offspring, each of which is a random variable. Deterministic behavior is modeled as $p=0$ or 1, and randomizing behavior is any value of $p\in \left(\mathrm{0,1}\right)$. The evolutionarily dominant behavior is then determined as the $p^{*}\in \left[\mathrm{0,1}\right]$ that maximizes population growth.

In contrast to refs. 20 and 21, we model behavior as a general random variable, not just a Bernoulli trial. More importantly, instead of assuming that every individual in the population has the same distribution of offspring, we allow for two types of individuals with different, but correlated, distributions of offspring, which we argue is necessary and sufficient to capture interaction between individuals.

Model

Assumptions.

We assume the existence of two types of individuals, called $A$ and $B$, that have different distributions of random offspring. In generation $t$, each individual of type $j$ produces a random number of offspring $x_{j,t}$, $j=A,B$. The vector $\left(x_{A,t},x_{B,t}\right)$ has some well-defined, but arbitrary, joint distribution function. The only assumptions we impose on the vectors $\left(x_{A,t},x_{B,t}\right)$ are that, across generations $t$, they are independently and identically distributed (IID) and that all first and second moments of $\left(\log x_{A,t},\log x_{B,t}\right)$ exist and are given by:

$$\begin{array}{ll}\hfill & {\mu }_A\equiv \mathbb{E}\left[\log x_{A,t}\right]\hspace{0.17em},\hspace{1em}{\mu }_B\equiv \mathbb{E}\left[\log x_{B,t}\right]\hspace{0.17em},\hspace{1em}\hfill \\ \hfill & {\sigma }_A^2\equiv Var\left(\log x_{A,t}\right)\hspace{0.17em},\hspace{1em}{\sigma }_B^2\equiv Var\left(\log x_{B,t}\right),\hfill \\ \hfill & \rho \equiv Corr\left(\log x_{A,t},\log x_{B,t}\right).\hfill \end{array}$$ [1]

Because individuals reproduce only once, the total population sizes at generation $T$ of types $A$ and $B$ are given by:

$$P_{A,T}\equiv \prod _{t=1}^T{x}_{A,t}\hspace{0.17em},P_{B,T}\equiv \prod _{t=1}^T{x}_{B,t}.$$ [2]

Note that, because the joint distribution of $\left(x_{A,t},x_{B,t}\right)$ is arbitrary, reproduction of type $A$ and reproduction of type $B$ are generally dependent. This dependence is both the simplest and most general way to capture interactions between reproducing individuals. The generality of this model of interaction can be illustrated with the following example. Denote by $\mathrm{\Omega }$ the set of all possible states of nature for a given generation. In the simplest case, $\mathrm{\Omega }$ might contain just two outcomes representing the possibility of rain or shine, each having probability, say, $\frac{1}{2}$. The randomness of $x_{A,t}$ and $x_{B,t}$ then represents different reproductive possibilities in these two states of nature. Suppose that when it rains, type $A$ individuals become predators of type $B$ individuals, but in the absence of rain, the two types do not interact. Therefore, in the rain state, $x_{A,t}$ is large and $x_{B,t}$ is small (say, three and one), and in the sunshine state, $x_{A,t}$ is small and $x_{B,t}$ is large (say, one and three). Since the probability of rain is assumed to be $\frac{1}{2}$, the joint distribution of the vector of random offspring is:

$$\left(x_{A,t},x_{B,t}\right)=\left\{\begin{array}{cc}\left(\mathrm{3,1}\right)\hspace{1em}\hfill & \text{with probability}\hspace{0.17em}\frac{1}{2}\hfill \\ \left(\mathrm{1,3}\right)\hspace{1em}\hfill & \text{with probability}\hspace{0.17em}\frac{1}{2}\hfill \end{array}\right..$$

Given that the states of nature can include not just rain or shine, but outcomes representing many types of environmental constraints, as well as outcomes representing physiological traits, foraging behavior, predator/prey relations, and so on, this framework can capture a broad spectrum of behaviors and interactions between individuals. But, as we show in the next section, despite the complexity of behaviors that this specification can generate, the characterization of evolutionarily dominant behaviors depends only on the five parameters (${\mu }_A,{\mu }_B,{\sigma }_A^2,{\sigma }_B^2$, and $\rho$) of the joint distribution of $x_{A,t}$ and $x_{B,t}$.

Observe that a change in behaviors (or traits) of individuals of type $A$ and $B$ will induce a change in the random vector $\left(x_{A,t},x_{B,t}\right)$. For example, in our rain/shine example, if type $B$ individuals are able to evade type $A$ individuals in the rain state, then $x_{A,t}$ may be smaller and $x_{B,t}$ may be larger in that state (say, two and two), in which case the joint distribution of $\left(x_{A,t},x_{B,t}\right)$ becomes:

$$\left(x_{A,t},x_{B,t}\right)=\left\{\begin{array}{cc}\left(\mathrm{2,2}\right)\hspace{1em}\hfill & \text{with probability}\hspace{0.17em}\frac{1}{2}\hfill \\ \left(\mathrm{1,3}\right)\hspace{1em}\hfill & \text{with probability}\hspace{0.17em}\frac{1}{2}\hfill \end{array}\right..$$

Therefore, analyzing a particular behavior/trait amounts to analyzing the properties of a particular random vector $\left(x_{A,t},x_{B,t}\right)$.

Results.

We consider a behavior to be evolutionarily optimal if the total population, $P_{A,T}+P_{B,T}$, grows exponentially faster under the behavior than under any other behavior. To see why this is the correct notion of evolutionary optimality that follows from natural selection, suppose types $A$ and $B$ follow a behavior $V_1$. Suppose some subset of individuals of these types (by agreement, chance, or some other mechanism) engages in behavior $V_2$, and suppose that the sum of populations under $V_2$ grows exponentially faster than under $V_1$. After a few generations, the individuals following $V_2$ will exponentially outnumber those following $V_1$, and behavior $V_2$ dominates. This is the principle of natural selection.

Note that this notion of evolutionary optimality is not incompatible with competition between types $A$ and $B$. The evolutionarily optimal behavior may have one type growing faster than another type, in which case one type will dominate the population.

We proceed to characterize the growth rate of $P_{A,T}+P_{B,T}$ in full generality for an arbitrary offspring vector, $\left(x_{A,t},x_{B,t}\right)$. To determine which among feasible behaviors is evolutionarily optimal, one can simply compare the growth rate of $P_{A,T}+P_{B,T}$ under the offspring vectors induced by each of them. The following two theorems show that

$$P_{A,T}+P_{B,T}\approx e^{\alpha T+\beta \sqrt{T}}$$ , [3]

for some scalars $\alpha$ and $\beta$ (proofs for all theorems are provided in SI Appendix).

Theorem 1 (Characterization of $\alpha$). Let the vector $\left(\log x_{A,t},\log x_{B,t}\right)$ be IID across $t$ with finite first and second moments denoted by Eq. 1. Let $P_{A,T}$ and $P_{B,T}$ be defined as in Eq. 2. Then, as $T$ increases without bound, we have:

$$\frac{\log \left(P_{A,T}+P_{B,T}\right)}{T}\hspace{0.17em}\stackrel{\mathrm{a}.\mathrm{s}.}{\to }\hspace{0.17em}max\left({\mu }_A,{\mu }_B\right),$$ [4]

where “$\stackrel{\mathrm{a}.\mathrm{s}.}{\to }$” denotes almost sure convergence.

Theorem 2 (Characterization of $\beta$). Let the vector $\left(\log x_{A,t},\log x_{B,t}\right)$ be IID across $t$ with finite first and second moments denoted by Eq. 1. Let $P_{A,T}$ and $P_{B,T}$ be defined as in Eq. 2. Assume that ${\mu }_A={\mu }_B=\mu$. Then, as $T$ increases without bound, we have:

$$\frac{\log \left(P_{A,T}+P_{B,T}\right)-T\mu }{\sqrt{T}}\hspace{0.17em}\stackrel{d}{\to }\hspace{0.17em}max\left(N_A,N_B\right),$$ [5]

where “$\stackrel{\mathrm{d}}{\to }$” denotes convergence in distribution, $N_A$ and $N_B$ are normally distributed random variables with means zero, variances ${\sigma }_A^2$ and ${\sigma }_B^2$, respectively, and correlation $\rho$.

Theorem 1 confirms that the key parameters in determining the growth rate of the combined population are ${\mu }_A$ and ${\mu }_B$. That is, the traits or behaviors that increase the number of offspring of type $A$ and $B$ individuals separately also increase the growth rate of the total population. To find which traits or behaviors dominate evolutionarily, we can analyze the effects of the traits and behaviors on the fitness of types $A$ and $B$ separately. This is already well known to evolutionary biologists. Theorem 2, though, suggests something additional about evolution. Not only does the number of offspring of each type matter, but the correlation $\rho$ between the reproductive output of these two types also matters. This correlation is determined by the nature of the interaction between the two types.

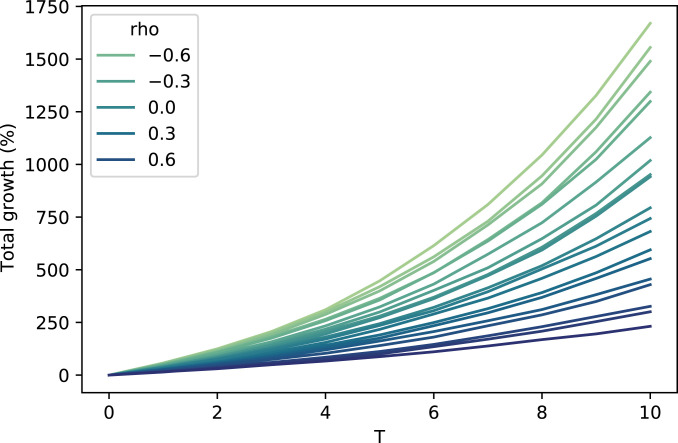
The main thrust of Theorems 1 and 2 is that evolutionarily optimal behaviors are those that maximize $\mu$ and minimize $\rho$. SI Appendix contains additional propositions that formalize this result, but, intuitively, it is clear from Theorem 1 that increasing $\mu$ will increase $\alpha$, thereby increasing the growth rate of the total population. From Theorem 2, increasing $max\left(N_A,N_B\right)$ increases $\beta$, thus also increasing the growth rate. The parameter $\rho$ comes into play because decreasing the correlation between two normal random variables increases their maximum, so decreasing $\rho$ will also increase the exponential growth rate. Fig. 1 provides computational confirmation of this relation.

Fig. 1.

Total population growth vs. time. Values of $\rho$ range from $-0.9$ (lightest) to 0.9 (darkest). The number of offspring for both types follows a lognormal distribution with $\mu =0.1$ and $\sigma =1.0$.

An important caveat to Theorems 1 and 2 is that, because of the IID assumption, they only apply to behaviors that are sustainable over time. For example, one cannot use Theorem 1 to conclude that a purely altruistic behavior on the part of type $A$ that decreases ${\mu }_A$ and increases ${\mu }_B$ is evolutionarily optimal through its increase of $max\left({\mu }_A,{\mu }_B\right)$. This is because such a behavior would lead to type $B$ growing exponentially faster than type $A$; hence, the altruistic type will be exponentially outnumbered, and the behavior is not sustainable.

In general, a behavior is sustainable if ${\mu }_A={\mu }_B$ so that both types are growing at the same rate, or if ${\mu }_A\hspace{0.17em}\ne \hspace{0.17em}{\mu }_B$, but the difference is not due to the nature of the interaction, but, rather, due to better utilization of environmental resources. Naturally, in this article, we are more interested in the case when ${\mu }_A={\mu }_B$ and there can be sustained meaningful interaction.

Although Theorems 1 and 2 show that the effect of $\rho$ on the asymptotic growth rate is second order compared to $\mu$, simulation results show that $\rho$ is often more important than $\mu$ in its effect on growth rates over finite time intervals. For example, Table 1 shows that after 10 generations, decreasing $\rho$ from 0.5 to $-0.5$ has approximately the same effect as increasing $\mu$ by about 0.09. More concretely, going from $\left(\mu =0.05,\rho =0.5\right)$ to $\left(\mu =0.0,\rho =-0.5\right)$ increases the growth rate, despite $\mu$ being lower. (Additional simulation results are reported in SI Appendix.) In the same way that the function $y=\sqrt{x}$ grows faster than $y=x$ for some time before its growth rate becomes sublinear, an offspring vector with better $\rho$ and worse $\mu$ can grow exponentially faster than one with worse $\rho$ and better $\mu$ for many generations before being overtaken.

Table 1.

Simulated population growth rate

$\mu /\rho$	–0.9	–0.8	–0.7	–0.6	–0.5	–0.4	–0.3	–0.2	–0.1	0.0	0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9
0.00	21%	20%	19%	18%	18%	17%	16%	15%	15%	13%	12%	11%	10%	9%	8%	7%	5%	4%	2%
0.01	22%	21%	20%	20%	18%	18%	17%	16%	15%	14%	13%	12%	11%	10%	9%	8%	7%	5%	3%
0.02	23%	22%	21%	21%	20%	19%	18%	17%	16%	16%	15%	14%	12%	12%	10%	8%	8%	6%	5%
0.03	24%	24%	23%	22%	21%	20%	19%	19%	18%	17%	16%	15%	14%	13%	11%	10%	9%	7%	5%
0.04	26%	25%	24%	23%	22%	22%	20%	20%	19%	17%	16%	16%	14%	13%	12%	11%	10%	8%	7%
0.05	26%	26%	25%	24%	23%	23%	22%	21%	19%	19%	18%	17%	16%	15%	13%	12%	11%	9%	7%
0.06	28%	27%	26%	26%	24%	24%	23%	22%	21%	20%	19%	18%	16%	16%	15%	14%	12%	10%	8%
0.07	29%	29%	27%	27%	26%	25%	24%	23%	22%	21%	20%	19%	18%	16%	16%	15%	13%	11%	9%
0.08	31%	30%	29%	28%	27%	26%	25%	25%	24%	23%	21%	20%	19%	18%	17%	15%	14%	13%	11%
0.09	32%	31%	30%	29%	28%	28%	27%	26%	25%	24%	22%	22%	21%	20%	18%	17%	15%	13%	12%
0.10	34%	32%	31%	30%	30%	29%	28%	27%	26%	25%	24%	23%	22%	21%	19%	18%	16%	15%	13%
0.11	34%	33%	33%	32%	31%	30%	29%	29%	27%	26%	25%	24%	23%	22%	19%	19%	18%	16%	14%
0.12	36%	35%	34%	34%	32%	31%	30%	29%	28%	28%	27%	26%	23%	23%	22%	20%	20%	17%	15%
0.13	37%	36%	36%	35%	34%	33%	32%	31%	30%	29%	28%	27%	25%	25%	23%	21%	20%	19%	16%
0.14	39%	38%	37%	36%	35%	34%	33%	32%	31%	30%	29%	28%	27%	25%	25%	23%	21%	19%	17%
0.15	40%	39%	39%	38%	37%	36%	35%	33%	33%	31%	30%	29%	27%	27%	25%	24%	22%	21%	19%
0.16	41%	41%	40%	39%	38%	37%	36%	35%	34%	33%	31%	31%	30%	27%	27%	25%	23%	22%	20%
0.17	43%	42%	41%	40%	39%	39%	37%	37%	36%	34%	33%	32%	31%	29%	28%	26%	25%	23%	21%
0.18	44%	43%	42%	42%	41%	39%	39%	39%	36%	36%	34%	33%	32%	30%	29%	28%	26%	24%	22%
0.19	46%	45%	44%	43%	42%	41%	39%	39%	38%	37%	35%	35%	33%	32%	31%	28%	27%	25%	23%
0.20	47%	46%	45%	45%	44%	42%	42%	40%	39%	38%	37%	36%	35%	33%	32%	30%	29%	26%	26%

The number of offspring for both types follows a lognormal distribution with the stated μ and ρ, and with σ =1.0. Quantities shown represent population growth rate per generation after 10 generations, computed as $e^{\mathbb{E}\left[\log \left(P_{10}/P_0\right)\right]/10}$, where $P_T=P_{A,T}+P_{B,T}$.

There is yet another reason for taking an interest in finite-horizon growth rates besides developing an understanding of short-term behaviors. The next theorem shows that if the proportion of types in the population is rebalanced every $T_0$ generations—which could be expected in the presence of intraspecies interaction—the finite-horizon growth rate for $T_0$ generations becomes the asymptotic growth rate.

Theorem 3. Let $T_0$ be a positive integer. Let the vector $\left(\log x_{A,t},\log x_{B,t}\right)$ be IID across $t$ with finite first and second moments denoted by Eq. 1. Let $P_0>0$, let $P_{A,T}$ and $P_{B,T}$ be defined as

$$\begin{array}{l}\hfill P_{A,n{T}_0+i}\equiv \frac{P_{n{T}_0}}{2}\prod _{t=1}^{n{T}_0+i}{x}_{A,t},\hspace{1em}i=1,\dots ,T_0,\hspace{0.17em}n=0,\dots ,\infty ,\\ \hfill \end{array}$$ [6]

and

$$\begin{array}{l}\hfill P_{B,n{T}_0+i}\equiv \frac{P_{n{T}_0}}{2}\prod _{t=1}^{n{T}_0+i}{x}_{B,t},\hspace{1em}i=1,\dots ,T_0,\hspace{0.17em}n=0,\dots ,\infty ,\\ \hfill \end{array}$$ [7]

and let $P_T$ be defined for multiples of $T_0$ as

$$P_{n{T}_0}=P_{A,n{T}_0}+P_{B,n{T}_0},\hspace{1em}n=1,\dots ,\infty .$$ [8]

Then, as $n$ increases without bound, we have:

$$\frac{\log \left(P_{n{T}_0}\right)}{n{T}_0}\hspace{0.17em}\stackrel{\mathrm{a}.\mathrm{s}.}{\to }\hspace{0.17em}\frac{\mathbb{E}\left[\log \left(P_{T_0}/P_0\right)\right]}{T_0}.$$ [9]

This theorem implies that if the types in Table 1 are rebalanced every 10 generations, then the population under behavior $\left(\mu =0.0,\rho =-0.5\right)$ grows faster asymptotically than under behavior $\left(\mu =0.05,\rho =0.5\right)$.

Although we did not assume group selection as a primitive, the fact that, even asymptotically, $\rho$ can be more important than $\mu$ illustrates when and how group selection can appear to occur. When a particular behavior decreases $\rho$ enough to offset a decrease in $\mu$, it can appear that selection is happening at a level other than that of the individual.

Idiosyncratic Risk.

So far, we have assumed that reproductive risk—as represented by the random variables $\left\{x_{j,t}\right\}$—is purely systematic, meaning that all type-$j$ individuals have an identical number of random offspring $x_{j,t}$ in a given state of the world. Suppose we assume that reproductive risk is, instead, partly idiosyncratic, so that type-$j$ individuals can have different numbers of offspring in a given state of the world. Namely, we allow the number of offspring of a type-$A$ individual $i$ at time $t$ to be the sum of $x_{A,t}$ and ${\overline{x}}_{A,i,t}$, where ${\overline{x}}_{A,i,t}$ are independent across individuals $i$ in the same generation. In this setting, populations of type $A$ and $B$ at time $T$ can be written

$$P_{A,T}\equiv \sum _{i=1}^{P_{A,T-1}}{x}_{A,T}+{\overline{x}}_{A,i,T},$$ [10]

$$P_{B,T}\equiv \sum _{i=1}^{P_{B,T-1}}{x}_{B,T}+{\overline{x}}_{B,i,T}.$$ [11]

The analogue of Theorem 1 for the case with idiosyncratic reproductive risk is:

Theorem 4. Assume the following. For $j=A,B$

• 1.The random variable $x_{j,t}$ is IID across $t$;
• 2.For some $C_l>0$ and $C_u>C_l$, $C_l\le x_{j,t}\le C_u$;
• 3.The random variable ${\overline{x}}_{j,i,t}\ge 0$ is IID across $i$ and $t$;
• 4.The expectations $\mathbb{E}\left[{\overline{x}}_{j,i,t}\right]$ and $\mathbb{E}\left[\log \left(\mathbb{E}\left[{\overline{x}}_{j,i,t}\right]+x_{j,t}\right)\right]$ exist; and
• 5.$\mathbb{E}\left[\log x_{j,t}\right]>0$.

Let $P_{A,T}$ and $P_{B,T}$ be defined as in Eqs. 10 and 11. Then, as $T$ increases without bound, we have:

$$\begin{array}{l}\hfill \frac{\log \left(P_{A,T}+P_{B,T}\right)}{T}\stackrel{\mathrm{a}.\mathrm{s}.}{\to }max\left(\mathbb{E}\left[\log \left(\mathbb{E}\left[{\overline{x}}_{A,i,t}\right]+x_{A,t}\right)\right],\right.\\ \hfill \left.\mathbb{E}\left[\log \left(\mathbb{E}\left[{\overline{x}}_{B,i,t}\right]+x_{B,t}\right)\right]\right).\end{array}$$ [12]

We see that idiosyncratic risk gets averaged out over time. Any idiosyncratic component to the number of offspring of a given type modifies the growth rate identically to adding a constant number of offspring. It is important to keep in mind that, by definition, idiosyncratic risk cannot be correlated, so when we refer to correlation of fecundity throughout the article, we mean correlation due to systematic risk. In SI Appendix, we repeat the simulation in Table 1 for the case with idiosyncratic risk. Adding enough idiosyncratic risk to make the growth rate of $\left(\mu =0.0,\rho =-0.5\right)$ equal to 131% decreases the impact of correlation such that decreasing $\rho$ from 0.5 to $-0.5$ is equivalent to increasing $\mu$ by 0.07 (instead of 0.09, as in Table 1).

Random Matching.

We can also extend the model to use random matching, a more specific mechanism of interaction that allows explicitly for different behaviors to exist in the same environment and for intermixing of individuals with different behaviors. We show that, even in this case, correlation still plays a key role in determining the evolutionarily dominant behavior.

Instead of types $A$ and $B$, suppose that there are types 1 and 2. Each generation, all individuals in the population are randomly paired with each other. If a type 1 is paired with a type 1, the offspring vector of the pair is $\left(x_{A,1,t},x_{B,1,t}\right)$. Otherwise, the offspring vector of the pair is $\left(x_{A,2,t},x_{B,2,t}\right)$. We see that, as suggested by the notation, the random pairings determine which individuals play the role of type $A$ and type $B$ from the original model. The new types 1 and 2 represent different behaviors. When two individuals of type 1 are paired, the behavior $\left(x_{A,1,t},x_{B,1,t}\right)$ occurs, but otherwise, the behavior $\left(x_{A,2,t},x_{B,2,t}\right)$ occurs. We use the variable $q$ to denote the pair that each individual is in. For example, in generation $T$, if individual $i$ of type 1 is matched with type 1 as the first component of the pair, then $q_{1,i,T}=A1$. The population sizes at generation $T$ of types 1 and 2 are defined recursively:

$$\begin{array}{l}\hfill P_{1,T}\equiv \sum _{i=1}^{P_{1,T-1}}{1}_{\left\{q_{1,i,T-1}=A1\right\}}{x}_{A,1,T}+1_{\left\{q_{1,i,T-1}=B1\right\}}{x}_{B,1,T}\\ \hfill +1_{\left\{q_{1,i,T-1}=A2\right\}}{x}_{A,2,T}+1_{\left\{q_{1,i,T-1}=B2\right\}}{x}_{B,2,T},\\ \hfill \end{array}$$ [13]

$$\begin{array}{l}\hfill P_{2,T}\equiv \sum _{i=1}^{P_{2,T-1}}{1}_{\left\{q_{2,i,T-1}=A2\right\}}{x}_{A,2,T}+1_{\left\{q_{2,i,T-1}=B2\right\}}{x}_{B,2,T}.\\ \hfill \end{array}$$ [14]

The next theorem provides a sufficient condition for type 1 individuals to exponentially outnumber type 2 individuals in the limit. We assume a law of large numbers for random matching. As noted by Duffie and Sun (22), such laws of large numbers are nontrivial to prove, but have been assumed without proof by evolutionary biologists dating back to Hardy (23) and Weinberg (24).

Theorem 5. Assume the following:

• 1.For $j=A,B$ and $k=\mathrm{1,2}$, the random variable $x_{j,k,t}$ is IID across $t$.
• 2.For $j=A,B$ and $k=\mathrm{1,2}$, for some $C_l>0$ and $C_u>C_l$, $C_l\le x_{j,k,t}\le C_u$.
• 3.For $k=\mathrm{1,2}$, the expectations $\mathbb{E}\left[\log \left(\frac{1}{2}{x}_{A,k,t}+\frac{1}{2}{x}_{B,k,t}\right)\right]$ exist.
• 4.(Law of large numbers for random matching) As $T\to \infty$, $P_{1,T}\stackrel{\mathrm{a}.\mathrm{s}.}{\to }\infty$, $P_{2,T}\stackrel{\mathrm{a}.\mathrm{s}.}{\to }\infty$, and

$$\frac{{\sum }_{i=1}^{P_{1,T}}{1}_{\left\{q_{1,i,T}=A2\right\}}}{{\sum }_{i=1}^{P_{1,T}}{1}_{\left\{q_{1,i,T}=A2\right\}}+1_{\left\{q_{1,i,T}=B2\right\}}}\stackrel{\mathrm{a}.\mathrm{s}.}{\to }\frac{1}{2}.$$

In words, the proportion of type 1 individuals matched with type 2 in the left side of the pairing converges almost surely to $1/2$.

Let $P_{1,T}$ and $P_{2,T}$ be defined as in Eqs. 13 and 14. Then, if

$$\begin{array}{l}\hfill \mathbb{E}\left[\log \left(\frac{1}{2}{x}_{A,1,t}+\frac{1}{2}{x}_{B,1,t}\right)\right]>\mathbb{E}\left[\log \left(\frac{1}{2}{x}_{A,2,t}+\frac{1}{2}{x}_{B,2,t}\right)\right],\\ \hfill \end{array}$$ [15]

as $T$ increases without bound, we have:

$$\begin{array}{l}\hfill \frac{\log \left(P_{1,T}/P_{2,T}\right)}{T}\stackrel{\mathrm{a}.\mathrm{s}.}{\to }\mathbb{E}\left[\log \left(\frac{1}{2}{x}_{A,1,t}+\frac{1}{2}{x}_{B,1,t}\right)\right]\\ \hfill -\mathbb{E}\left[\log \left(\frac{1}{2}{x}_{A,2,t}+\frac{1}{2}{x}_{B,2,t}\right)\right].\end{array}$$ [16]

The condition Eq. 15 has a close connection to correlation. Decreasing the correlation between $x_{A,k,t}$ and $x_{B,k,t}$ decreases the second-order Taylor approximation of $\mathbb{E}\left[\log \left(\frac{1}{2}{x}_{A,k,t}+\frac{1}{2}{x}_{B,k,t}\right)\right]$. Thus, in general, unless the distributions are highly skewed, if $x_{A,1,t}$ and $x_{B,1,t}$ have the same means, but lower correlation, than $x_{A,2,t}$ and $x_{B,2,t}$, then 1-types will grow exponentially faster than 2-types. In other words, even with random matching, behaviors that result in lower correlation will dominate the population. It is also significant that in the random matching model, correlation is a first-order factor, impacting the coefficient of $T$ in the growth rate and not only $\sqrt{T}$.

Density Dependence.

In this section, we study the effect of correlation on population growth when population growth is density-dependent. We do this by extending the standard biological model of density-dependent population growth—in which population at any point in time is the solution to a system of ordinary differential equations (ODEs)—to the stochastic case so that the population size is a solution to a system of stochastic differential equations (SDEs).

To see more clearly the analogy we make between ODEs and SDEs, we consider first a model of population growth with no density dependence. Given types $A$ and $B$, the standard model is given by:

$$d{P}_{A,t}=r_A{P}_{A,t}\hspace{0.17em}dt,$$ [17]

$$d{P}_{B,t}=r_B{P}_{B,t}\hspace{0.17em}dt.$$ [18]

We add randomness by introducing (possibly correlated) Wiener processes, $W_{A,t}$ and $W_{B,t}$, and converting the standard model to the following SDE:

$$d{P}_{A,t}=r_A{P}_{A,t}\hspace{0.17em}dt+s_A{P}_{A,t}\hspace{0.17em}d{W}_{A,t},$$ [19]

$$d{P}_{B,t}=r_B{P}_{A,t}\hspace{0.17em}dt+s_B{P}_{B,t}\hspace{0.17em}d{W}_{B,t}.$$ [20]

Whereas an equation of the type Eq. 17 implies that for small $\mathrm{\Delta }$,

$$P_{A,t+\mathrm{\Delta }}-P_{A,t}=r_A{P}_{A,t}\mathrm{\Delta },$$

an equation of the type Eq. 19 implies that

$$P_{A,t+\mathrm{\Delta }}-P_{A,t}=r_A{P}_{A,t}\mathrm{\Delta }+s_A{P}_{A,T}\left(W_{A,t+\mathrm{\Delta }}-W_{A,t}\right),$$

where $W_{A,t+\mathrm{\Delta }}-W_{A,t}$ is normally distributed with mean zero and variance $\mathrm{\Delta }$. Eqs. 19 and 20 have closed-form solutions, from which we can derive continuous-time versions of Theorems 1 and 2, namely:

$$\frac{\log \left(P_{A,T}+P_{B,T}\right)}{T}\hspace{0.17em}\stackrel{\mathrm{a}.\mathrm{s}.}{\to }\hspace{0.17em}max\left(r_A-\frac{1}{2}{s}_A^2\hspace{0.17em},\hspace{0.17em}{r}_B-\frac{1}{2}{s}_B^2\right),$$ [21]

and (when $r\equiv r_A=r_B$ and $s\equiv s_A=s_B$)

$$\frac{\log \left(P_{A,T}+P_{B,T}\right)-\left(r-\frac{1}{2}{s}^2\right)}{\sqrt{T}}\hspace{0.17em}\stackrel{\mathrm{d}}{\to }\hspace{0.17em}max\left(N_A,N_B\right),$$ [22]

where $N_A$ and $N_B$ are normally distributed random variables with means zero, variances $s^2$, and the same correlation as the Wiener processes, $W_{A,t}$ and $W_{B,t}$.

Adding density dependence, the standard population-growth model becomes:

$$d{P}_{A,t}=r_A{P}_{A,t}\left(1-\frac{P_{A,t}}{K_A}-\frac{P_{B,t}}{L_A}\right)\hspace{0.17em}dt,$$ [23]

$$d{P}_{B,t}=r_B{P}_{B,t}\left(1-\frac{P_{B,t}}{K_B}-\frac{P_{A,t}}{L_B}\right)\hspace{0.17em}dt,$$ [24]

and the stochastic counterpart is simply:

$$d{P}_{A,t}=r_A{P}_{A,t}\left(1-\frac{P_{A,t}}{K_A}-\frac{P_{B,t}}{L_A}\right)\hspace{0.17em}dt+s_A{P}_{A,t}\hspace{0.17em}d{W}_{A,t},$$ [25]

$$d{P}_{B,t}=r_B{P}_{B,t}\left(1-\frac{P_{B,t}}{K_B}-\frac{P_{A,t}}{L_B}\right)\hspace{0.17em}dt+s_B{P}_{B,t}\hspace{0.17em}d{W}_{B,t}.$$ [26]

The key issue in this setting is how the impact of $\rho$ changes with $K$. (We assume $L$ is fixed to $K$.) Tables 2–4 show the population growth rate after 10 generations for different values of $K$ and $\rho$ when $r=0.5$, $r=0.6$, and $r=0.7$, respectively. As $K$ increases without bound, Tables 2–4 approach continuous-time versions of Table 1 with $\mu =0.0$, $\mu =0.1$, and $\mu =0.2$, respectively.

Table 2.

Simulated density-dependent population growth rate ($r=0.5$)

$K/\rho$	–0.9	–0.7	–0.5	–0.3	–0.1	0.1	0.3	0.5	0.7	0.9
5.0	–5.4%	–6.3%	–7.3%	–8.1%	–9.1%	–9.8%	–11.3%	–12.6%	–13.8%	–15.5%
10.0	–0.0%	–1.1%	–2.2%	–3.0%	–4.4%	–5.6%	–6.6%	–8.3%	–9.4%	–11.3%
20.0	5.0%	3.6%	2.7%	1.4%	–0.1%	–1.2%	–2.6%	–3.7%	–6.1%	–7.9%
40.0	9.2%	8.1%	6.9%	5.4%	3.9%	2.8%	0.9%	–0.8%	–3.2%	–5.6%
80.0	12.4%	11.1%	10.0%	8.5%	7.1%	5.2%	4.1%	1.4%	–0.6%	–3.3%

The number of offspring for both types follows Eqs. 25 and 26 with the stated K and $\rho$, and with $r=0.5$, $s=1.0$, and $L=K$. Quantities shown represent population growth rate per generation after 10 generations, computed as $e^{\mathbb{E}\left[\log \left(P_{10}/P_0\right)\right]/10}$, where $P_T=P_{A,T}+P_{B,T}$.

Table 4.

Simulated density-dependent population growth rate ($r=0.7$)

$K/\rho$	–0.9	–0.7	–0.5	–0.3	–0.1	0.1	0.3	0.5	0.7	0.9
5.0	–1.3%	–1.9%	–2.4%	–2.9%	–3.7%	–4.6%	–5.3%	–6.0%	–7.5%	–9.0%
10.0	5.5%	4.8%	3.9%	3.1%	2.4%	1.8%	0.7%	–0.5%	–2.1%	–3.4%
20.0	12.2%	11.4%	10.4%	9.5%	8.5%	7.5%	6.6%	5.0%	3.5%	1.6%
40.0	19.2%	17.9%	17.1%	16.0%	14.5%	13.3%	11.5%	10.8%	8.6%	5.8%
80.0	25.2%	24.0%	22.7%	21.5%	20.1%	18.4%	16.8%	15.3%	13.1%	10.4%

The number of offspring for both types follows Eqs. 25 and 26 with the stated K and $\rho$, and with $r=0.7$, $s=1.0$, and $L=K$. Quantities shown represent population growth rate per generation after 10 generations, computed as $e^{\mathbb{E}\left[\log \left(P_{10}/P_0\right)\right]/10}$, where $P_T=P_{A,T}+P_{B,T}$ .

Table 3.

Simulated density-dependent population growth rate ($r=0.6$)

$K/\rho$	–0.9	–0.7	–0.5	–0.3	–0.1	0.1	0.3	0.5	0.7	0.9
5.0	–3.1%	–3.9%	–4.5%	–5.4%	–6.0%	–7.0%	–8.0%	–8.9%	–10.4%	–11.7%
10.0	3.1%	2.3%	1.4%	0.4%	–0.5%	–1.7%	–2.7%	–4.2%	–5.4%	–7.5%
20.0	9.2%	8.2%	7.0%	5.9%	4.9%	3.6%	2.4%	0.8%	–1.0%	–2.7%
40.0	15.0%	13.7%	12.4%	11.2%	9.7%	8.1%	6.8%	5.1%	3.1%	0.7%
80.0	19.8%	18.3%	16.6%	15.5%	13.8%	12.4%	10.8%	9.1%	6.9%	4.1%

The number of offspring for both types follows Eqs. 25 and 26 with the stated K and $\rho$, and with $r=0.6$, $s=1.0$, and $L=K$. Quantities shown represent population growth rate per generation after 10 generations, computed as $e^{\mathbb{E}\left[\log \left(P_{10}/P_0\right)\right]/10}$, where $P_T=P_{A,T}+P_{B,T}$ .

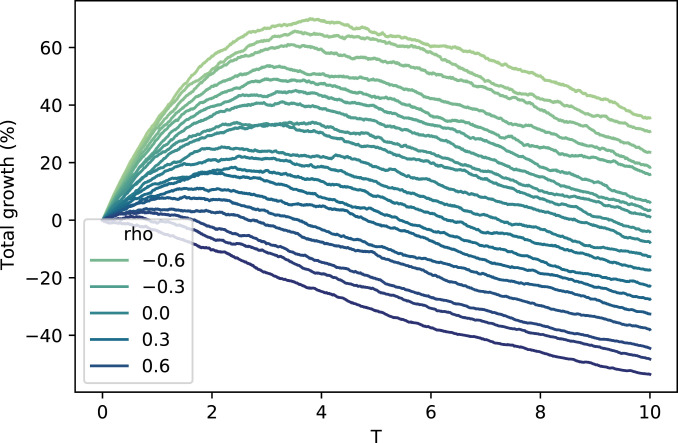
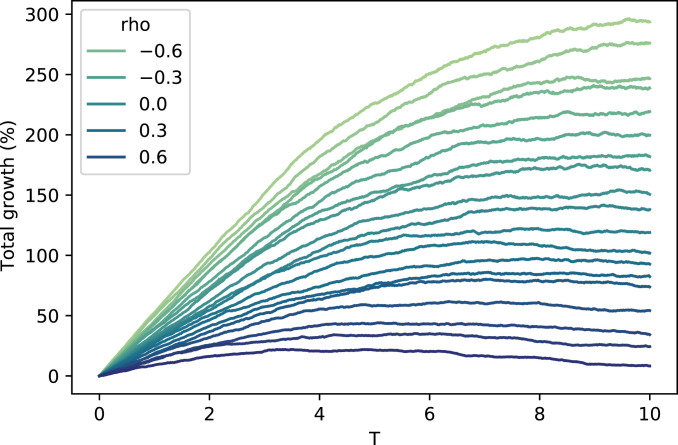
It is apparent that correlation has a significant impact on the growth rate, even with density dependence extreme enough to cause the population decline over time. In an absolute sense, the impact of correlation appears to decrease with density dependence. But in a relative sense, it appears to increase. For example, to achieve the same impact on the growth rate as increasing $r$ from 0.5 to 0.6, $\rho$ must be decreased from 0.5 to $-0.3$ when $K=80$, but only from 0.5 to $-0.1$ when $K=5$. Figs. 2 and 3 show that when density dependence increases, correlation matters more for earlier time horizons and less for later time horizons.

Fig. 2.

Total density-dependent population growth vs. time ($K=10$). Values of $\rho$ range from $-0.9$ (lightest) to 0.9 (darkest). The number of offspring for both types follows Eqs. 25 and 26 with $r=0.6$, $K=10$, $L=10$, and $s=1.0$.

Fig. 3.

Total density-dependent population growth vs. time ($K=40$). Values of $\rho$ range from $-0.9$ (lightest) to 0.9 (darkest). The number of offspring for both types follows Eqs. 25 and 26 with $r=0.6$, $K=40$, $L=40$, and $s=1.0$.

Behavioral Implications

Having shown that evolutionarily optimal behaviors minimize the correlation of fecundity ($\rho$) along with maximizing fecundity ($\mu$), we now give two examples of behaviors that decrease $\rho$. The first behavior, which we call “specialization,” causes good outcomes for the two types to occur in different states. The second behavior, “sacrifice,” decreases fecundity for one type in a given state, while increasing fecundity for the other type in the same state. In SI Appendix, we provide a third and more abstract example, which we call “coordination,” where an uncertain action of one type becomes conditionally certain given the action of the other type. Specialization, sacrifice, and coordination can all be considered forms of cooperation.

Specialization.

Let there be two states of the world, ${\omega }_r$ and ${\omega }_s$, representing rain and shine. Consider the two behaviors in Fig. 4. Behavior 1 implies no specialization because the good outcomes for types $A$ and $B$ both occur in the rain state. Behavior 2 implies specialization because the good outcomes occur in different states. Since $max\left({\mu }_A,{\mu }_B\right)$ is the same under both behaviors, according to Theorems 1 and 2, $\rho$ determines which action is evolutionarily optimal. It is clear that $\rho$ is smaller under Behavior 2; hence, Behavior 2 is evolutionarily optimal. It is worth noting that although Theorems 1 and 2 suggest that a behavior can only be evolutionarily optimal on the basis of $\rho$ if it is not dominated on the basis of $\mu$, the finite-horizon results and Theorem 3 suggest that a behavior can be evolutionarily optimal on the basis of $\rho$, even if it is dominated on the basis of $\mu$. In other words, there exists some $\delta$ sufficiently small such that it could be subtracted from $v$, $w$, $z$, and $y$ in Behavior 2 and still leave Behavior 2 to be evolutionarily optimal.

Fig. 4.

Specialization.

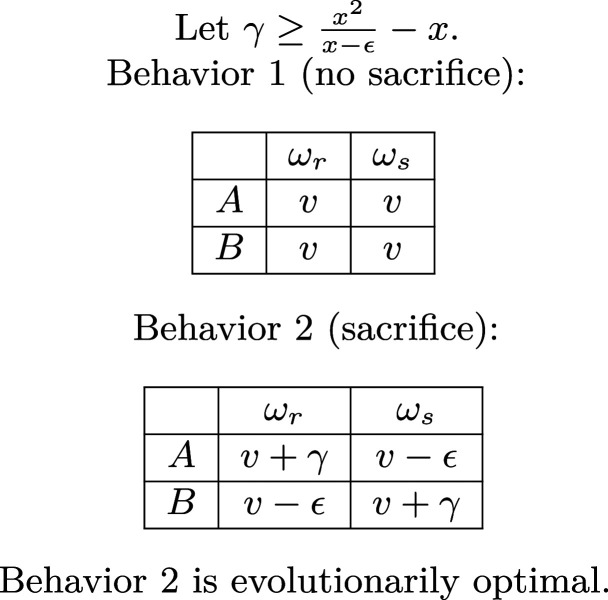
Sacrifice.

We continue with our two states, ${\omega }_r$ and ${\omega }_s$, representing rain and shine, each with probability $\frac{1}{2}$ of occurring. Consider the two behaviors in Fig. 5. Under Behavior 2, type $B$ individuals sacrifice for type $A$ in state ${\omega }_r$, and type $A$ individuals sacrifice for type $B$ individuals in state ${\omega }_s$. On the other hand, under Behavior 1, both types have the same number of offspring in both states.

Fig. 5.

Sacrifice

We claim that sacrifice is the evolutionarily optimal behavior according to Theorems 1 and 2 when $\gamma \ge \frac{v^2}{v-ϵ}-v$. When $\gamma >\frac{v^2}{v-ϵ}-v$, $max\left({\mu }_A,{\mu }_B\right)$ under Behavior 2 is larger than under Behavior 1, which means that Behavior 2 is evolutionarily optimal. However, we are particularly interested in the case $\gamma =\frac{v^2}{v-ϵ}-v$. In this case, neither type benefits from sacrifice, which is to say that ${\mu }_A$ is the same under Behavior 1 and Behavior 2, and ${\mu }_B$ is the same under Behavior 1 and Behavior 2. Yet, simply by inducing negative correlation, Behavior 2 becomes evolutionarily optimal. Moreover, as in the case of specialization, if we expand our definition of evolutionary optimality by considering finite-horizon results and Theorem 3, Behavior 2 can be evolutionarily optimal if $\gamma <\frac{v^2}{v-ϵ}$, in which case ${\mu }_A$ and ${\mu }_B$ would be smaller under Behavior 2 than Behavior 1, and both types would individually be harmed by sacrifice.

Discussion

We propose to resolve the apparent conflict between natural selection and cooperation by showing that natural selection is not necessarily selfish, giving rise to not only behaviors that increase fecundity, but also behaviors that decrease the correlation of fecundity between individuals. We use a simple model of evolutionary dynamics without any strategic interactions, assuming nothing about the knowledge, intelligence, or even sentience of individuals in the population. Our principal result (Theorem 2) shows that in a population with two types of individuals, a decrease in correlation of fecundity between the two types increases the exponential growth rate of the population. This result shows that correlation of fecundity has a second-order effect on the growth rate, as compared to the separate fecundity of each type. However, we also show that correlation has a first-order effect in certain situations, including with periodic rebalancing of type proportions (Theorem 3) or in a random matching setting (Theorem 5). Simulation results also suggest that correlation matters relatively more over finite time horizons and if population growth is density-dependent.

We conclude by discussing some limitations of our work. First, our most general model assumes that offspring vectors are IID over time. As we have mentioned, this means that our model is silent regarding behaviors that cannot be sustained, such as purely altruistic behaviors of one type that result in the other type growing exponentially faster. Second, although our results show that correlation of fecundity can play a significant role in determining growth rates, we have not attempted to quantify how much correlation (or systematic risk in general) exists in real-world settings, and whether this is enough to drive natural selection. Finally, while the framework we have developed implies that the evolution of cooperation can be explained without a separate theory of group selection, the fact that correlation can confer survival benefits shows why it is so tempting to identify groups within a given population. Accordingly, there may still be conceptual benefits from viewing selection as operating at multiple levels, even if not strictly necessary from a purely theoretical perspective. We hope to explore these issues in future research.

Data Availability

All study data are included in the article and/or supporting information.