Summary
Electric-field (E-field) control of magnetic switching provides an energy-efficient means to toggle the magnetic states in spintronic devices. The angular tunneling magnetoresistance (TMR) of an magnetic tunnel junction (MTJ)/PMN-PT magnetoelectronic hybrid indicates that the angle-dependent switching fields of the free layer can decrease significantly subject to the application of an E-field. In particular, the switching field along the major axis is reduced by 59% from 28.0 to 11.5 Oe as the E-field increases from 0 to 6 kV/cm, while the TMR ratio remains intact. The switching boundary angle decreases (increases) for the parallel (antiparallel) to antiparallel (parallel) state switch, resulting in a shrunk switching window size. The non-volatile and reversible 180° magnetization switching is demonstrated by using E-fields with a smaller magnetic field bias as low as 11.5 Oe. The angular magnetic switching originates from competition among the E-field-induced magnetoelastic anisotropy, magnetic shape anisotropy, and Zeeman energy, which is confirmed by micromagnetic simulations.
Subject areas: magnetism, electromagnetic field, devices
Graphical abstract
Highlights
-
•
A magnetoelectronic hybrid device based on MTJ and ferroelectric is demonstrated
-
•
The E-field control of angle-dependent magnetic switching behavior is unveiled
-
•
The E-field-assisted non-volatile 180° magnetization reversal is achieved
-
•
The E-field-induced magnetoelastic and shape anisotropy contributes to switching
Magnetism; Electromagnetic field; Devices
Introduction
Spintronics with the advantages of high information density, fast speed, and low power consumption plays an important role in massive data storage and memory technology, as well as in data communication. The emerging technology of magnetic random access memory (MRAM) has the potential to fulfill the promise of a universal memory scheme (Akerman, 2005; Hu and Nan, 2019). There are multiple means of magnetic switching for MRAM (Akerman, 2005; Jia et al., 2018), including the utilization of Oster fields (Coey 2010), current-induced spin-transfer torque (Železný et al., 2018; Puebla et al., 2020; Mangin et al., 2006; Ralph and Stiles, 2008; Brataas et al., 2012), and spin-orbit torque (SOT) (Cao et al., 2020; Liu et al., 2012; Peng et al., 2020). However, these methods suffer from endurance issues and high energy dissipation (Wang et al., 2012; Buzzi et al., 2013). Other switching schemes have been proposed based on voltage-controlled magnetic anisotropy manipulation (Wang et al., 2012; Zhao et al., 2018a, 2018b), magnetoionics (Bauer et al., 2015; Li et al., 2017a, 2017b; Tan et al., 2019), and magnetoelectric effect (ME) (Li et al., 2014, 2018; Nan et al., 2019; Baldrati et al., 2016; Chen et al., 2019a; Lu et al., 2015). Among these, the magnetoelectric coupling using multiferroic heterostructures is particularly energy-efficient (Spaldin and Ramesh, 2019; Wang et al., 2018a; Ghidini et al., 2019; Manipatruni et al., 2019).
To enable multiferroic magnetoelectric coupling into MRAM, both Pertsev and Nan et al. theoretically studied a type of magnetoelectric heterostructures, in the form of a stack of magnetic tunnel junction/ferroelectric (MTJ/FE) hybrid structure (Guo et al., 2020; Pertsev and Kohlstedt, 2012; Hu et al., 2011). They demonstrated an ultralow writing energy on the order of fJ/bit using strain-mediated magnetoelectric coupling in an MTJ/FE hybrid. Bandyopadhyay et al. (Roy et al., 2011; Mondal et al., 2018) further showed that the switching energy can be down to a scale of ∼ aJ/bit in a single nano-magnet on a piezoelectric (PE) substrate. Recently, Carman et al. (Wang et al., 2018b) conceptualized an MTJ/FE structure which is controlled by SOT and ME effect. You et al. (Su et al., 2019) theoretically predicted high performance in antiferromagnetic tunnel junction enabled hybrid structure where an applied E-field controls the strength of magnetoelastic anisotropy. All these works open the possibility of energy-efficient switching by relying on E-field-induced ME effect.
Experimental progress is also promising on the MTJ/FE structure (Chen et al., 2019b; Zhao et al., 2016). Recently, Li et al. (Li et al., 2014) demonstrated a reversible E-field controlled MTJs on PMN-xPT ferroelectric substrates. Unfortunately, magnetization switching in the magnetic FL is volatile after removing the applied E-field. To overcome this drawback, Zhao et al. (Chen et al., 2019b) patterned an MgO-based MTJ in a round-disk geometry on PMN-xPT substrates and demonstrated a reversible, and non-volatile E-field manipulation for magnetization switching by controlling the E-field-induced non-volatile piezo-strain. However, the FL of the MTJs is easily disturbed from external magnetic fields (H-fields) due to its weak magnetic anisotropy, which could result in poor memory retention (Iwata-Harms et al., 2018). Moreover, the applied E-fields used in these works were in the vicinity of the opposite coercive field of the FE substrates, rendering the hybrid structures inoperable. Wang et al. (Zhao et al., 2016) demonstrated E-field manipulation of MTJs on (001)-Pb(Mg1/3Nb2/3)0.7Ti0.3O3 FE substrates. Two local gating configurations were applied to produce anisotropic strain from the isotropic FE layer in affecting magnetization switching, which in this work is volatile once the E-field is removed. Overall, few experimental works have been available on E-field controlled MTJ/FE hybrids (Li et al., 2014; Chen et al., 2019b, 2019c; Zhao et al., 2016). The integration of spintronic and FE components remains a challenging task (Heron et al., 2014; Yang et al., 2014).
In this work, we focus on a hybrid structure consisting of an MgO-based MTJ built on the (011)-oriented PMN-PT (PT, at. 30%) single crystal substrate serving as the FE component. By applying a vertical E-field, we create an in-plane anisotropic piezo-strain, which affects 180° magnetization reversal in the FL of the MTJ through a strain-mediated magnetoelectric coupling. The magnetic switching is non-volatile upon the release of the E-field. Relying on the measurements of in-plane angular transfer curve (TC) and circle transfer curve (CTC) under E-field and angular H-field, we perform a systematic investigation on a plethora set of parameters including switching field, tunneling magnetoresistance (TMR), switching boundaries, and switching window size.
Results
Device construction
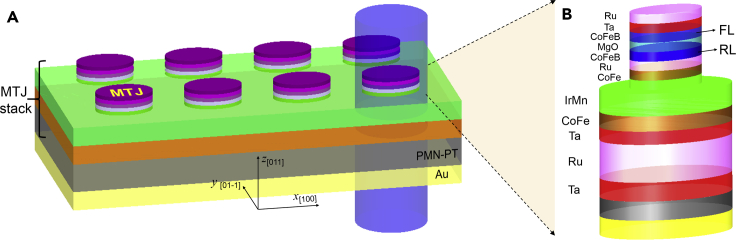
Figure 1A shows a schematic diagram of the MTJ/(011)-PMN-PT magnetoelectronic hybrid. We pattern the MTJ stack into ovals with a size of 30 μm ×100 μm2 with an etching depth down to the IrMn layer. Optical micrographs of the lithography-patterned MTJs on PMN-PT substrates are shown in Figure S1A in the supplemental information. Figure 1B shows the layered sequence of the MTJ stack, including the FL and RL components. The Ta/Ru/Ta/CoFe/IrMn assembly serves as the top electrode, and the Au layer below the PMN-PT serves as the bottom electrode for the applied E-fields, saving the top MTJ ovals from the potential damage as a result of the E-field (Wang et al., 2012; Chen et al., 2019c). The length of the MTJ ovals is along the in-plane [100] direction of the PMN-PT substrate. Detailed information on the FL and RL can be found in the literature (Shen et al., 2006; Parkin et al., 1999; Matsumoto et al., 2007). The fabrication methods of the magnetoelectronic hybrid devices, the associated TMR measurements under E-field and angular H-fields, magnetic hysteresis-loop measurements, and microstructural characterizations can be found in Transparent Methods in the first section of the SI. Taking recent progress on fabrication of free-standing PMN-PT membranes (Kum et al., 2020), we can promisingly build all-thin-film MTJ/PMN-PT hybrid devices instead of the bulk PMN-PT single crystals, which are enabled to be transferred on arbitrary substrates, including Si, to develop practical magnetoelectronic devices and integrate with other microelectronic devices in the future (Zhang et al., 2020; Nagarajan et al., 2003). Additionally, the magnetoelectric coupling and E-field control of magnetic switching can be greatly enhanced in the free-standing MTJs/PMN-PT hybrid devices by being declamped from the single-crystal PMN-PT substrates (Kum et al., 2020).
Figure 1.
Structure of the MTJ/FE PMN-PT magnetoelectronic hybrid devices
(A) Schematic of the MTJs on the (011)-oriented PMN-PT ferroelectric substrate. The IrMn and Au layers serve as the top and bottom electrodes for the applied E-fields across the thickness of the ferroelectric PMN-PT layer.
(B) Cross-sectional view of the oval-shaped MTJs with a layer structure of PMN-PT/Ta (50)/Ru (300)/Ta (50)/CoFe (20)/IrMn (180)/CoFe (30)/Ru (8.5)/CoFeB (30, reference layer, RL)/MgO (20, barrier layer, BL)/CoFeB (30, free layer, FL)/Ta (50)/Ru (100). The numbers refer to thicknesses in angstroms.
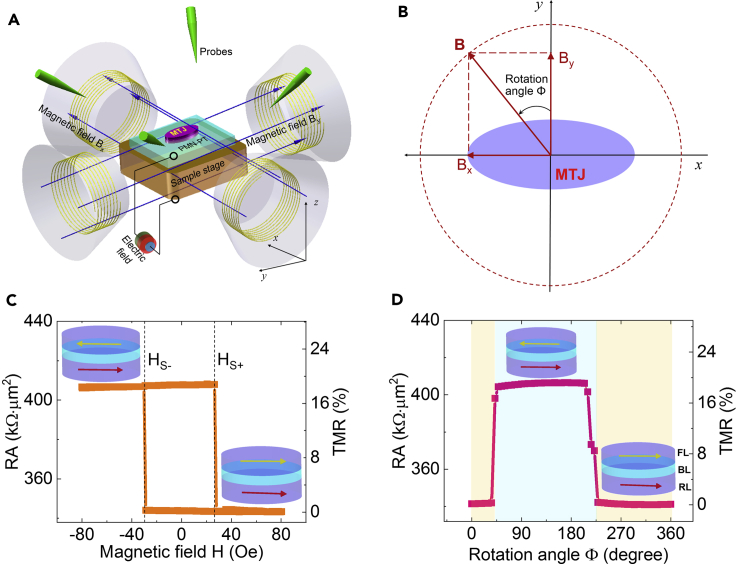
Investigating angular magnetization reversal
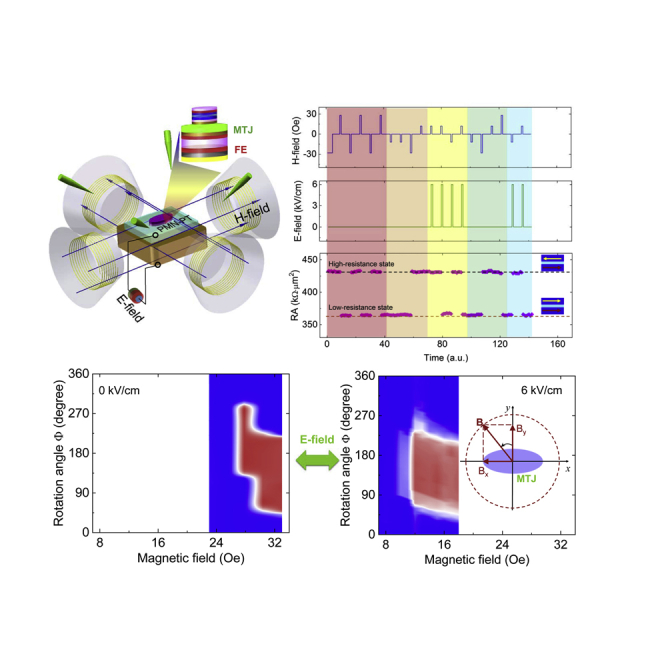
Figure 2A shows a schematic setup to characterize the angular magnetic response of our hybrid. Two pairs of electromagnets were mounted on the probe station to provide two-axis in-plane H-fields, namely, Bx and By, as illustrated in Figure 2B. The angle Φ specifies the in-plane direction of the B field. It is worth mentioning that the I-V curves were generated in advance to ensure the devices sufficiently robust for tests. The MTJs show symmetrical rectification characteristics under bipolar voltages as shown in Figure S1B in the supplemental information. Moreover, the I-V curves indicate two distinct resistance states under H-fields of −80 and +80 Oe, which correspond to the parallel and antiparallel magnetization configurations, respectively. Furthermore, the curves can be theoretically fitted by using a metal/insulator/metal junction model (Simmons, 1963) (see details in Figure S2 in the supplemental information).
Figure 2.
Measurement schemes to evaluate the angular TMR and magnetic switching
(A) Schematic of the four-probe station used for the magnetotransport measurements of the MTJ/PMN-PT magnetoelectric hybrid structure under in situ electric and magnetic fields. The E-fields were applied across the thickness of the PMN-PT. The preserved multilayers after lithography processing served as the top electrode.
(B) The in-plane 2-axis H-field B (Bx, By) generated from a pair of orthogonal electromagnets, as schematically shown in (A). The rotation angle Φ is defined with respect to MTJ's minor axis (+y axis).
(C) Transfer curve for a representative MTJ measured along the major axis (i.e., Φ ∼ 90°), showing the resistance-area product (RA) and the corresponding TMR ratio.
(D) Circle transfer curve for a representative MTJ. The insets in (C) and (D) show the parallel and antiparallel states of the MTJ, corresponding to the low-resistance and high-resistance states, respectively. The error bar of TMR ratio is estimated approximately ±0.5% through making multiple measurements of the magnetoresistance of the MTJs.
Figure 2C displays the TC of one representative device to illustrate magnetization switching through the measured TMR by sweeping the H-fields along a certain in-plane direction. The TMR loop was acquired for an H-field that was set to Φ = 90°. The switching fields (defined as HS) indicate that the critical fields of the FL magnetization switching, which can be estimated from the first derivatives of the TMR loop (Zhao et al., 2016; Anguelouch et al., 2000). In this typical MTJ/(011)-PMN-PT hybrid, the switching fields HS- and HS+ are approximately −29.0 and +28.0 Oe, with an Oster field tolerance of ±1 Oe, indicating a very sharp transition from parallel (0°) to antiparallel (180°) magnetization for the FL, and vice versa. The repeatability of the angular TC loops was checked and illustrated in Figure S3 for the other hybrid devices (see details in the supplemental information). The sharp switching between the stable magnetic states is favored in spintronic devices (Das et al., 2018). In this MTJ/(011)-PMN-PT hybrid, the two distinct magnetic states can be sharply switched from 0° (inset on the bottom right of Figure 2C to 180° [inset of the top left of Figure 2C] and back using a larger H-field than the switching field. The TMR ratio is defined as [RA(B)-RA(+80 Oe)]/RA(+80 Oe))×100%, where B is the scanning H-field strength and RA value is defined as the resistance-area (RA) product. The RAs at −80 and +80 Oe represent the high- and low-resistance states with antiparallel and parallel magnetization alignments, respectively. The TMR ratio is correspondingly shown in the right axis of Figure 2C. It is mentionable that the RA has sample difference, probably owing to the rougher surface of the PMN-PT substrate than that of oxide-Si wafer for fabricating MTJs (Shen et al., 2006).
The CTC measurements were performed to further study the angle-dependent magnetization switching behavior. The RA product was measured by sweeping a constant, in-plane H-field (∼80 Oe) at various applied directions (the scanning range is a circle at 360°), as shown in Figure 2D. The TMR ratio was derived and is shown in the right axis of Figure 2D. The sharp switching behavior is observed based on the direction (i.e., the H-field rotation angle) of the applied H-field. A nearly rectangular window indicates the antiparallel state with a higher RA product, which is shaded in a light blue color. The parallel state with a lower RA product is shown in light yellow. The two distinct high- and low-resistance states represent the antiparallel (180°) and parallel (0°) magnetization alignments, respectively, as illustrated in the inset of Figure 2D. This behavior for our MTJ/(011)-PMN-PT hybrid, which has not been previously observed, is significantly different from the results of MTJs on Si wafers, where the CTCs usually have a sine- or cosine-like profile (Safron et al., 2008). This rectangular shape for the CTC is desired because of its much higher stability for the magnetic states. We attribute this sharper magnetic switching to strain-enhanced coherent spin tunneling through the MgO barrier (Loong et al., 2014), domain wall generation and propagation of the FL in the MgO-based magnetic tunnel junctions (Chanthbouala et al., 2011), which is modulated by the piezo-strain as induced by the FE layer after E-field cycling. The effect of the leakage current from the FE layer on the TMR measurements is also excluded (see more details in Figure S4 in the supplemental information).
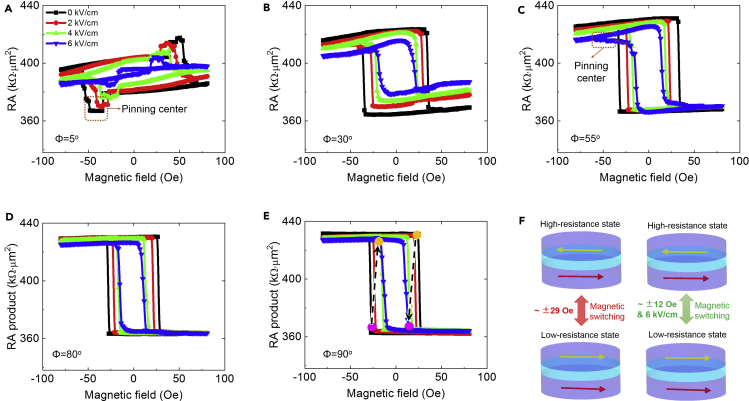
E-field effects on angular switching field and TMR
We have studied the E-field control of the angular switching field by measuring the TCs at various angles (Φ), as shown in Figures 3A–3E. At 0 kV/cm, the shapes of the TCs and associated switching fields depend strongly on the direction of the sweeping H-field. This behavior could be ascribed primarily to magnetic shape anisotropy (Biswas, et al., 2017) and the initial magnetization configuration (Zhao et al., 2018b) of the FL and RL. At Φ = 90°, magnetic switching is sharp and TMR is maximized, confirming the FL's easy axis is along [100] (i.e., x axis) and the hard axis along the [01-1] (i.e., y axis) of the substrate. At 6 kV/cm, Figure 3A shows that the TC becomes gradually varying and are nearly horizontal, indicating that the easy axis of the FL might have rotated from the +x toward the +y direction. Figure 3E shows that the TC along the major axis of FL changes from a square loop to a narrower loop upon an increasing E-field (Zhao et al., 2018b; D'Souza et al., 2016). The easy axis turns into a hard axis, as E-field-induced magnetoelastic anisotropy plays an increasingly important role in the FL (Atulasimha and Bandyopadhyay, 2010; Conte et al., 2018; Pertsev and Kohlstedt, 2010). In addition, Figure 3E shows that TMR value is not sensitive the E-field, but the switching field, from 0 to 6 kV/cm, decreases from 28.0 to 11.5 Oe (see dotted arrows), a 59% reduction. One can expect that a further reduction of the switching field could be achieved by on-going increasing E-fields. However, the zero switching field cannot be realized in the present device configuration. There are two reasons accounting for the lower limit of switching field. On one hand, the lower limit of switching filed directly depends on the competing interaction between the E-field-induced magnetoelastic and magnetic shape anisotropy (Wang et al., 2018b). On the other hand, in the present device configuration, the E-field-induced magnetoelastic anisotropy is naturally 2-fold symmetric owing to the biaxial piezo-strain symmetrically along the long and short axis of the MTJs. In addition to the degenerate bistable magnetic states (0° and 180°) of the free layer, the E-field-induced magnetoelastic anisotropy cannot break the symmetry of the magnetic states (Matsukura et al., 2015). Thus, an external magnetic field has to be needed to ensure the degenerate bistable magnetic states asymmetric, leading to an 180° reversal of the free layer. Therefore, a minimum magnetic field (switching field) is a prerequisite to realize a 180° magnetic switching. Such a large reduction in switching field is highly beneficial to energy-efficient spintronic devices (Liu, et al., 2011; Yang, et al., 2019). The magnetic switching can be achieved by the E-field (∼6 kV/cm) with a relatively small H-field (∼12 Oe) bias, as illustrated in Figure 3F. Such a tunability can be comparable with that (−75% with a 400 V gate voltage) in the PMN-PT (011)/Ta/Ru/IrMn/CoFe/Ru/CoFeB/MgO/CoFeB/Ta/Ru hybrid device with a lateral electric field configuration (Zhang et al., 2020). Additionally, the switching field is increased by approximately +320% upon applying a lateral voltage of 150 V in the PMN-PT (001)/Ta/CoFeB/MgO/CoFeB/Ta hybrid device (Zhao et al., 2016). This increment of switching field may be harmful to design low-power spintronic devices. The differences in the variation of the switching field by E-fields and voltages are closely related to the layer sequence, thickness and magnetic interaction in the MTJs, and strain transfer efficiency from the interface to the free layer [Hu and Nan (2019); Roy et al. (2011)].
Figure 3.
Angular dependence of TCs under E-fields
(A–E) The applied magnetic field was set at rotation angles of (A) Φ = 5°, (B) 30°, (C) 55°, (D) 80°, and (E) 90°. The MTJ was initially set in an antiparallel configuration. In E, the dashed arrows indicate the switching process near the switching field with the assistance of in situ E-fields.
(F) Schematic of the high- and low-resistance states those are reversibly switched: (left panel) solely with an H-field of +29 and −29 Oe (left panel); (right panel) with a smaller H-field of +12 and −12 Oe and under the assistance of an E-field of 6 kV/cm.
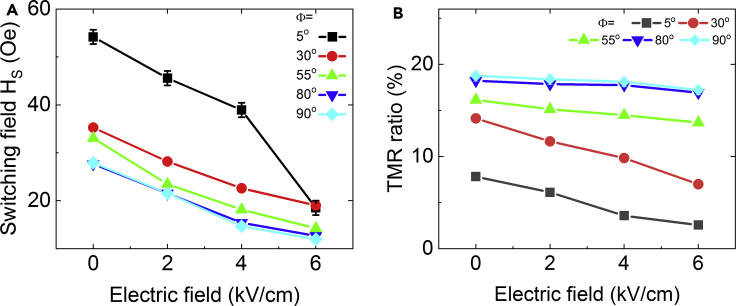
Figure 4A shows the strong effect of E-field on the reduction of magnetic switching field (Hs) at various field angles (Φ). Figure 4B shows that the E-field has a moderate effect on the TMR ratios. At relatively smaller Φ angles, the angular TMR ratio decreases with increasing E-fields. At Φ = 5°, the TMR ratios are ∼7.8% and ∼2.6% at 0 and 6 kV/cm, respectively. However, at Φ = 90°, the TMR ratio remains around 18.2% and is weakly dependent on the E-field. This result occurs for the following two reasons. First, magnetic switching should be mainly coherent and is modulated by the E-fields (Al-Rashid et al., 2016). Hence, the magnetization switching remains very sharp before becoming more gradual at 6 kV/cm. Second, the E-field induced piezo-strain is insufficient to change the TMR ratio because of strain losses across imperfect interfaces, including intrinsic ferroelastic domain structures after polishing treatment, even cracks of the PMN-PT surface after electric-field cycling, a possible additional roughness induced during thin-film deposition, and multi-interfaces of the Ta/Ru/Ta/CoFe/IrMn/CoFe/Ru/CoFeB/MgO/CoFeB layer structures (Hu et al., 2018; Ziss et al., 2017; Liu et al., 2018), but the thickness effect does not weaken strain transfer efficiency to the FL according to finite element simulations (Hu et al. 2014, 2018) (see more details in Figures S5 and S6 in the supplemental information). Thus, a slim, narrow, and gradual TC loop, rather than a slanted loop, is observed, as previously shown in Figure 3, even though the E-field was increased to 6 kV/cm. This conjecture has been experimentally evidenced by Wang and Zhang (Zhao et al., 2016; Chen et al., 2019c), who showed efficient strain transfer and slanted TC loops in thinner MTJ/(001)-PMN-PT hybrids (∼24 nm and ∼27 nm, respectively) along the major axis of the MTJs. Therefore, angular magnetic switching should result from competition among the magnetic shape anisotropy, the E-field-induced magnetoelastic anisotropy, and the external Zeeman energy in the FL (Zhao et al., 2018b; Chen et al., 2016).
Figure 4.
Angle-dependent switching fields and TMR ratios under the influence of an E-field
(A) E-field dependence of switching field at various angles.
(B) E-field dependence of TMR ratio at various angles. It is noted that, at Φ = 90°, the TMR ratio is weakly dependent on E-field.
E-field-assisted angular magnetic switching
CTC measurements were performed to further study the magnetic switching behaviors in the 360° region under the E-fields. This technique can measure the angular TMR in a rotating, constant-magnitude H-field. Unlike TCs, CTCs can provide intuitive information on the 180° magnetization switching boundary from the antiparallel (parallel) to parallel (antiparallel) magnetization configurations, the window size of the parallel and antiparallel states, and even the intermediate state during magnetization reversal under angular H-field sweeping with the aid of the E-fields (Safron et al., 2008). Moreover, CTCs can more accurately determine the true TMR ratio of the MTJ because these curves guarantee that the true parallel and antiparallel magnetic states are reached (Heron et al., 2014).
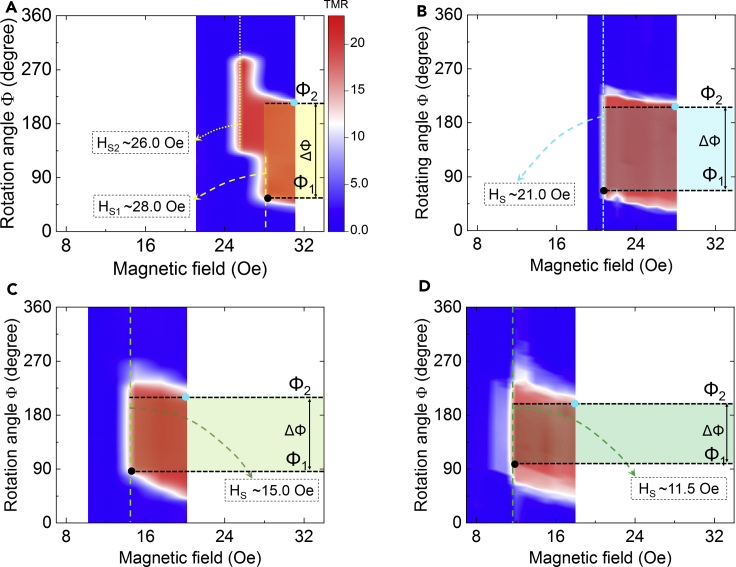
Figure 5 combines CTCs with a series of sweeping H-fields and constructs a CTC mapping diagram. According to the CTC mappings (CTCMs), the switching fields at an E-field of 0 kV/cm have two values, namely, HS1 ∼ 26 Oe and HS2 ∼ 28 Oe, in the higher- and lower-angle regions, as shown in Figure 5A, strongly suggesting that the 180° magnetization switching is angularly dependent. In addition, the two different switching fields confirm the existence of an intermediate state as the angular H-fields are swept over a series of magnitudes. Figures 5B–5D show that the switching field Hs is ∼21.0 Oe at 2 kV/cm, ∼ 15.0 Oe at 4 kV/cm, and ∼11.5 Oe at 6 kV/cm, which is roughly in accordance with the angular TC measurements that were described above. The switching windows are correspondingly shaded in Figures 5A–5D with varying E-fields. The resultant window size ΔΦ decreases under larger E-fields. Moreover, 180° magnetization switching becomes more gradual at the switching boundary angles Φ1 and Φ2 for larger E-fields. The switching boundary angle Φ1 represents the onset of magnetization switching from 0° (parallel configuration) to 180° (antiparallel configuration) under relatively smaller switching fields, as indicated by the black dot. Φ2 indicates the onset of magnetization switching from 180° (antiparallel configuration) back to 0° (parallel configuration) under larger external H-fields (near the saturation magnetic field), as labeled by the cyan dot. The switching boundary angles Φ1 and Φ2 are defined as the TMR ratio over 14.5% (∼80% of the saturated TMR ratio). In particular, the 180° magnetization switching at 6 kV/cm in Figure 5D is gradual, and the TMR ratio is slightly reduced, compared to the values in Figure 5A at 0 kV/cm, which also agrees well with the above TC measurements.
Figure 5.
Magnetic switching behaviors characterized by CTC mappings (CTCMs)
(A−D) show the CTCs with in situ E-fields of (A) 0, (B) 2, (C) 4, and (D) 6 kV/cm, respectively. The H-fields are scanned in a series of constant magnitudes while rotating their directions stepwise (6°/step). The switching boundaries Φ1 and Φ2 are defined as the rotation angle of the H-field where the TMR ratio is greater than ∼14.5% (more than 80% of the full TMR ratio). At these boundaries, the magnetization of the free layer began to switch from the parallel to the antiparallel configuration and vice versa. The resultant switching window size ΔΦ is indicated by rectangular windows with a double arrow line. The switching fields are shown in the dashed square frames.
Except for the switching boundary region, the red and blue contrast in the CTCMs represent the stable antiparallel and parallel magnetization alignments in Figure 5, respectively. The junction resistance in the parallel and antiparallel states over the entire scanning space of the azimuth rotation angle Φ is barely affected by the E-fields, except for the switching boundary area. Additionally, the conductivity of the MgO barrier has not been further modulated by the E-field-induced strain because the junction resistance (resultant TMR ratio) depends exponentially on the thickness of the MgO barrier (Simmons, 1963). A slight modulation in the MgO barrier's thickness and barrier should greatly boost the junction resistance (or TMR ratio), which is not observed here. Naturally, the magnetic states of the FL should be responsible for the TMR response to the E- and H-fields in the hybrid device (see details in Figure S7 in the supplemental information). Therefore, the CTC results again demonstrate that E-field-induced magnetoelastic anisotropy is the primary contributor over the magnetic anisotropy rotation and the relative magnetization orientation of the FL with respect to the RL (Chen et al., 2019b, 2019c).
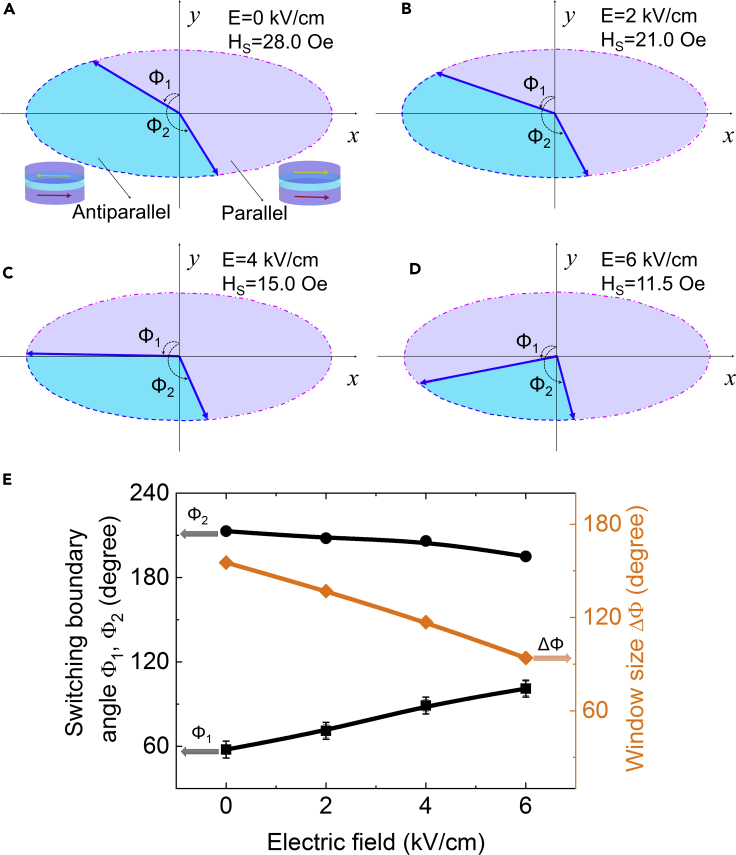
We then project the switching boundary angles Φ1 and Φ2 onto the MTJ surface to visualize the angular dependence of the magnetic switching as controlled by the E-fields, as shown in Figures 6A–6D. The switching boundary angle Φ1 increases as the E-field increases; however, the switching boundary angle Φ2 decreases with the E-field. As summarized in Figure 6E, the boundary angle Φ1 is ∼58° at 0 kV/cm, ∼ 71° at 2 kV/cm, ∼ 89° at 4 kV/cm, and ∼101° at 6 kV/cm, and the boundary angle Φ2 is ∼213° at 0 kV/cm, ∼ 208° at 2 kV/cm, ∼ 206° at 4 kV/cm, and ∼195° at 6 kV/cm. Consequently, the switching window size ΔΦ along the right axis in Figure 6E is derived as ∼ 155° at 0 kV/cm, ∼ 137° at 2 kV/cm, ∼ 117° at 4 kV/cm, and ∼94° at 6 kV/cm, indicating a noticeably shrinking window induced by the E-fields. Previous studies (Zhang et al., 2011) suggest that Φ1 is controlled primarily by the magnetic shape anisotropy with a smaller H-field bias and thus is modulated relatively easily by E-fields because of considerable piezo-strain-induced magnetoelastic anisotropy. Φ2 is determined primarily by the Zeeman energy under larger H-field applications and is synergistically affected by the shape anisotropy energy (Safron et al., 2008). Hence, the effect of E-field-induced magnetoelastic anisotropy on Φ2 is weaker than that on Φ1, which is further evidenced by the slower change in Φ2 than that in Φ1, as shown in Figure 6E. These experimental studies show that the angle-dependent magnetic switching behaviors are the result of a combination of E-field-induced magnetoelastic anisotropy through ME, the magnetic shape anisotropy, and the Zeeman energy by breaking the two-fold symmetric uniaxial anisotropy of the FL in the hybrid (Liu et al., 2011; Chen et al., 2016). Hence, the switching field, switching boundary, switching window size, magnetization alignment, and resultant TMR ratio are modulated significantly by E-fields.
Figure 6.
180° magnetization switching boundary angle and switching window size controlled by E-fields
(A–D) Schematics of the 180° magnetization switching boundary angles Φ1 and Φ2 at (A) 0 kV/cm, (B) 2 kV/cm, (C) 4 kV/cm, and (D) 6 kV/cm, respectively. The switching window size is defined as the difference between the switching boundary angles. The oval-shaped FL of the MTJ is divided into two regions that represent the antiparallel (cyan) and the parallel (light violet) magnetization configurations.
(E) The switching boundary angles and switching window size are functions of the applied E-field. For accuracy, the angle error bar is overestimated to be ±5°.
E-field-assisted 180° magnetization reversal
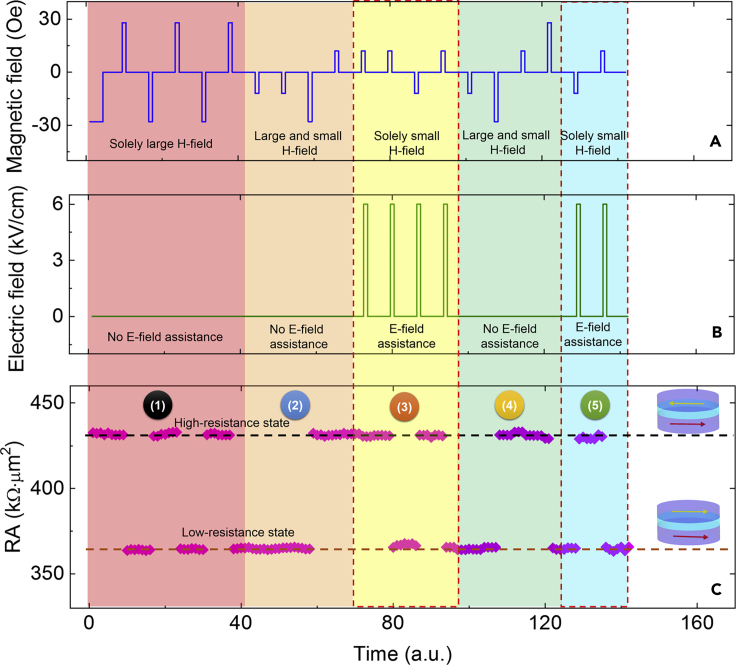
To highlight the role and benefits of E-fields in magnetic switching in the hybrid, we demonstrate that the 180° magnetization reversal is manipulated via the programmable H- and E-fields, as shown in Figures 7A and 7B, respectively. The following five steps for E-field-assisted magnetic switching are marked in different colors in Figure 7C. (1) As previously demonstrated, a relatively large H-field has to be required for magnetic switching when no E-field is applied. The solely large H-field (∼29 Oe, slightly larger than the switching field at 0 kV/cm) along the major direction of the MTJs can switch the parallel and antiparallel states [see the two insets of Figure 7C] back and forth according to the RA values. (2) If a solely smaller H-field (∼12 Oe, slightly larger than the switching field at 6 kV/cm) is applied, 180° magnetization reversal does not occur and successively requires a larger H-field to recover, as shown in Figure 7C. (3) After applying an E-field of ∼6 kV/cm, 180° magnetization switching is reversibly and non-volatilely controlled by a smaller H-field with the assistance of the E-field. (4) To further confirm this result, a solely smaller H-field is again applied and magnetic switching from the parallel to antiparallel states is not triggered. Thus, a larger H-field has to be applied in a similar manner as in step (2) to toggle 180° magnetization reversal. (5) Here, 180° magnetization reversal by a reduced H-field with the assistance of E-fields is verified, similarly to the case in step (3). The corresponding magnetic states stabilize from the magnetic shape anisotropy after removing the external E- and H-fields, in agreement with previous reports (Pertsev and Kohlstedt, 2012; Chen et al., 2019b, 2019c). Therefore, non-volatile and reversible 180° magnetization switching is controlled by a reduced H-field when using applied E-fields.
Figure 7.
Experimental demonstration of the non-volatile and reversible 180° magnetization reversal with the assistance of E-fields
(A) Programmable pulsed H-fields along the major axis of the MTJs. The larger and smaller H-fields are ∼29 Oe and 12 Oe, respectively.
(B) Programmable pulsed E-fields applied across the ferroelectric PMN-PT layer.
(C) Corresponding resistance states of the MTJs under the programmable E- and H-fields, with the insets showing the relative magnetization states.
One of the key advantages of the proposed hybrid is the reduced operating H-field, which benefits both low-power consumption and high-density memory. Another advantage is the simple unipolar E-field sequence, as shown in Figure 7B, which can avoid aging of the ferroelectric layer and is much more easily controlled, compared to cases with asymmetric or symmetric bipolar E-field sweeping in the existing literature (Chen et al., 2019b; Zheng and Zheng, 2016). The piezo-strain under a unipolar E-field is directly related to the polarization and ferroelastic domain switching pathways in the PMN-PT substrates, which are shown in Figures S8–S10 in the supplemental information. A previous report shows that tiny cracks are easily generated on the surface of the PMN-PT layer under a sequence of bipolar E-fields, damaging the ferroelectric layer and its neighboring magnetic layers (Liu et al., 2018). Using unipolar E-fields can enable these layers to be immune to switching fatigue. However, the operating unipolar E-fields are usually not over 6 kV/cm because a larger E-field will also induce cracks in the PMN-PT owing to electrostriction and domain wall propagations, which imprint on the adjacent layers, also leading to failure of the MTJs (Liu, et al., 2018).
Non-volatile and reversible switching mechanism
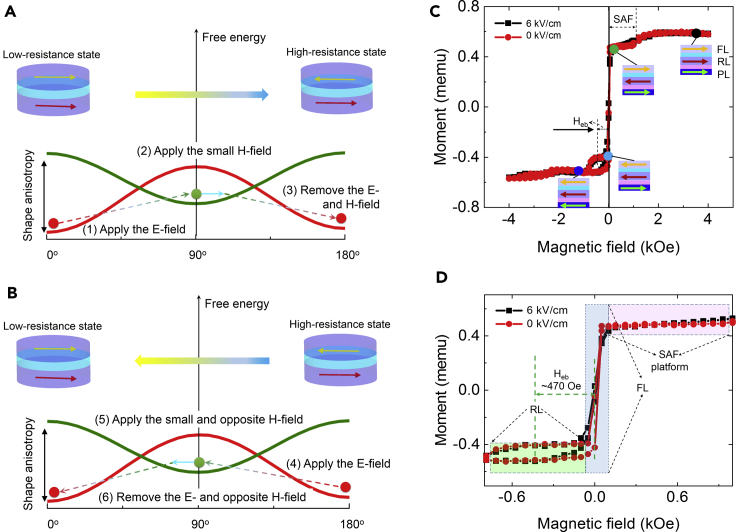
This section illustrates the physical mechanism for non-volatile and reversible 180° magnetization reversal under an E-field and a reduced H-field. Figures 8A and 8B show the evolution of the free-energy profile of the FL under the co-actions of shape anisotropy energy, E-field-induced magnetoelastic anisotropy energy, and external Zeeman energy in the hybrid. The free-energy profile is labeled with a red line and shows the two stable magnetization configurations at 0° (parallel configuration) and 180° (antiparallel configuration) for 0 kV/cm, which correspond to the low- and high-resistance states in the insets of Figures 8A and 8B, respectively. The energy barrier from the parallel to antiparallel states and vice versa is dominated by the magnetic shape anisotropy, as shown vertically by the two-way arrow in Figures 8A and 8B. The FL anisotropy mainly originates from the magnetic shape anisotropy of the FL, where the anisotropy field could be determined from the saturation field of the TC loop as the H-field swept along the minor axis (short axis) of the MTJs, as shown in Figure S11 in the supplemental information. In addition, the effective anisotropy field is estimated to be approximately 100 Oe, which is as similar to the value of ∼120 Oe in the MTJ/(001)-PMN-PT hybrids (Zhao et al., 2016). The corresponding shape anisotropy energy is ∼6000 J/m3. Upon application of the E-fields, the E-field-induced strain on the MTJs can be seen as an effective anisotropy field Heff on the FL and RL because of the magnetoelastic coupling. Hence, Heff could be calculated from the following formula (Liu et al., 2010):
where and are the Young's modulus and Poisson ratio for the CoFeB, respectively, and and are the in-plane strain along the [100] and [01-1] directions of the PMN-PT substrate, respectively. The parameter λ is the saturation magnetostriction of the CoFeB. The detailed calculations for Heff are shown in Figure S12 and Table S1, and the required parameters are shown in Table S2 in the supplemental information. Thus, Heff and the corresponding magnetoelastic anisotropy energy at 6 kV/cm are calculated to be ∼150 Oe and ∼9200 J/m3, respectively. This effective magnetoelastic anisotropy energy is comparable to the shape anisotropy energy, indicating the possibility of achieving an in-plane 90° rotation for the easy-axis of the FL (Li et al., 2014).
Figure 8.
Mechanism of the E-field control of magnetic switching
(A) Schematic of 180° magnetization switching from a low-resistance to high-resistance state from the perspective of the FL free energy. (B) Schematic of 180° magnetization switching back from a high-resistance to low-resistance state from the perspective of the FL free energy. The competition among the E-field-induced magnetoelastic anisotropy energy, the magnetic shape anisotropy energy, and the Zeeman energy is the driving force for the E-field-controlled magnetic switching.
(C) Magnetic hysteresis for the unpatterned MTJs under in-situ E-fields along the major-axis direction.
(D) Magnified moment vs. magnetic field (M-H) hysteresis around the low H-field switching region for the FL and RL with the assistance of the E-fields.
The E-field control of the non-volatile and reversible 180° magnetization reversal can be understood through the following six steps. (1) After applying an E-field of ∼6 kV/cm, the free-energy profile changes, as demonstrated by the green line in Figure 8A. The magnetic anisotropy of the FL with a two-fold symmetry rotates by 90° because of the E-field-induced magnetoelastic anisotropy (Chen et al., 2019b, 2019c; Liu et al., 2010). Hence, the magnetization of the FL is primarily stable along the y axis, as marked by the green solid circle. (2) A small H-field must be applied to break the two-fold symmetry of magnetoelastic anisotropy (Chen et al., 2019c). Hence, a small bias H-field is applied along the -x-axis, which further rotate the magnetization toward the antiparallel configuration (180°), as shown by the small cyan arrow in Figure 8A. (3) Removing the E- and H-fields causes the magnetization of the FL to become energetically stable at the antiparallel state because of the magnetic shape anisotropy in the hybrid (Pertsev and Kohlstedt, 2012; Conte et al., 2018). Thus, 180° magnetization switching from the low-resistance (0°) to high-resistance state (180°) is achieved. Analogously, the magnetization could be switched back from 180° to 0° alignment through the following steps. (4) The E-field is applied when the magnetization is in the antiparallel state; thus, the free-energy profile is changed from the red solid line to the green solid line, as shown in Figure 8B. The effective magnetic anisotropy is rotated by 90° and the magnetization then rotates along the +y axis. (5) A small and opposite H-field, which breaks the two-fold symmetry of the magnetoelastic coupling, further rotates the magnetization toward the parallel configuration, as marked by the small cyan arrow in Figure 8B. (6) Removing the E- and H-fields causes the magnetization of the FL to become energetically stable at the parallel state because of the magnetic shape anisotropy. Therefore, non-volatile and reversible magnetic switching is realized under the programmable sequence of simple unipolar E-fields and reduced bias H-fields.
To further prove the E-field control of the anisotropy rotation in the FL, the magnetic hysteresis loop is measured at the unpatterned MTJ multilayers on the (011)-PMN-PT ferroelectric substrate. As shown in Figure 8C, the magnetic hysteresis loop is measured along the pinning direction under the in-situ E-fields, which is often referred to as the major loop. In the SAF platform, soft magnetic characteristics and an exchange bias field Heb are clearly observed at 0 and 6 kV/cm, indicating the good quality of our samples. These features were previously observed in AlOx- and MgO-based MTJs on ferroelectric PMN-PT substrates (Chen et al., 2019c; Li et al., 2014). The corresponding magnetic states of the FL, RL, and PL are illustrated in the insets of Figure 8C. As shown in the magnified M-H loop of Figure 8D at 0 kV/cm, the easy-axis is indeed along the pinning direction (the [100] direction of the PMN-PT substrate or major axis). Moreover, the applied E-field of 6 kV/cm pushes the magnetization away from the major axis, which is marked in light blue in Figure 8D. The exchange bias field Heb is estimated to be approximately 470 Oe. Additionally, the magnetization switching of the RL is not modulated by the E-field, as shown in the shaded light green in Figure 8D because the SAF structure provides a strong RKKY interaction for the RL (Wang et al., 2018a, 2018b). From the magnetic hysteresis loop along the minor axis (the [01-1] direction of the PMN-PT substrate), the magnetic switching becomes easier after applying an E-field of 6 kV/cm, as shown in Figure S13A in the supplemental information. These experimental results confirm that the magnetic anisotropy is rotated by 90° via the E-field-induced magnetoelastic coupling between the FL and ferroelectric PMN-PT layers, as shown in Figures S13B and S13C in the supplemental information. Accordingly, the E-field-induced Heff can reversibly rotate magnetization toward 180° with the aid of successively opposite and small H-fields (Wang et al., 2018a; Zhao et al., 2016). It is mentionable that the physical limit of E-field-induced 180° magnetization reversal lies in how to break the 2-fold symmetry of the degenerate bistable magnetic states of the FL in MTJs/PMN-PT hybrid structures (Matsukura et al., 2015). Owing to the symmetric configuration of the present device, the E-field-induced magnetic switching without H-field bias is impossible. Therefore, our devices still have room for performance improvement toward full E-field-controlled 180° magnetization switching in the future.
Micromagnetic simulations
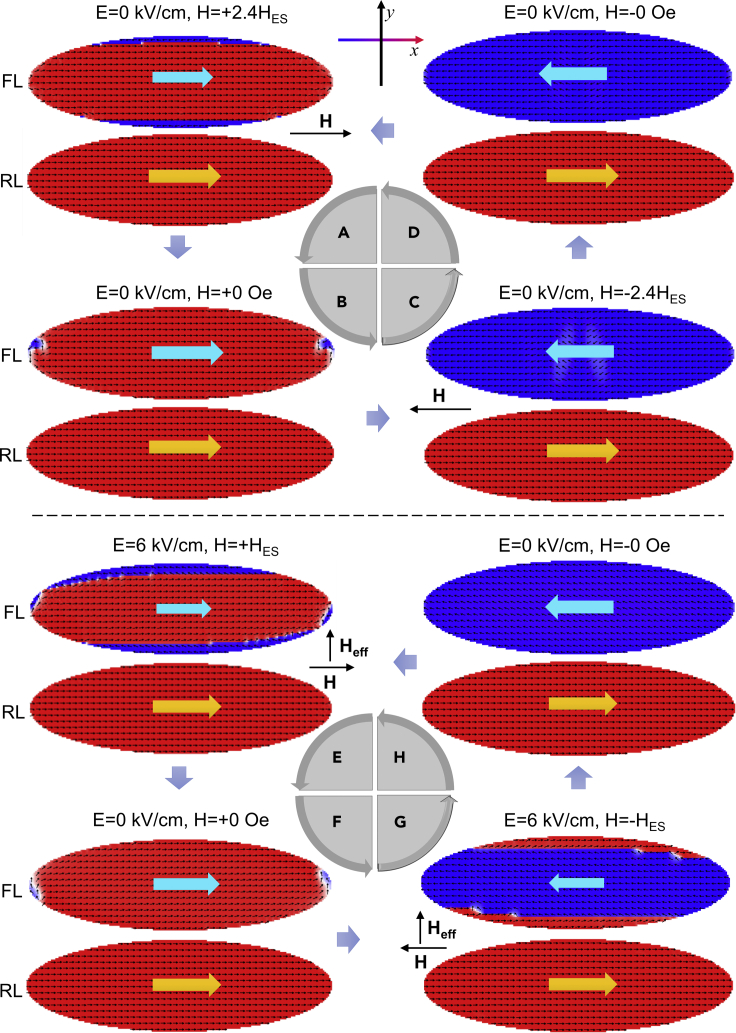
Micromagnetic simulations were performed to further prove the scheme for E-field-assisted, non-volatile, and reversible 180° magnetization switching (Donahue and Porter, 1999). We initialize the FL and RL to the single domain states along the [100] direction (–x-axis in the x-y plane or the major axis of the MTJ) of the PMN-PT substrate. More details on the sample structure and simulated parameters are provided in Figure S14 and Table S2 in the supplemental information.
At 0 kV/cm, the magnetization of the FL is aligned with the parallel state from the intial antiparallel state, which requires a larger H-field of approximately +2.4HES to overcome the shape anisotropy energy without the assistance of E-fields, as mentioned in Sec. 2.3 and 2.6, 2.3 and 2.6. The corresponding simulated moment profile for FL and RL are shown in Figure 9A. The local moments are aligned along the major axis (+x axis) due to application of a larger H-field (∼+2.4HES). This result corresponds to a low-resistance state with the parallel magnetization configuration of the FL and RL, which is indicated by wide cyan and orange arrows, respectively. Here, HES (∼11.5 Oe) is referred to as the aforementioned switching field under an E-field of 6 kV/cm. The magnetization remains stable after removing the H-field owing to the shape magnetic anisotropy, as shown in Figure 9B. Here, H = +0 Oe means that the magnetic field decreases to 0 Oe from a positive direction (+x axis). This simulation further verifies that the magnetic shape anisotropy can stabilize the magnetic state after removing any E- and H-fields. To realize 180° magnetization switching at 0 kV/cm, an opposite and large H-field (∼−2.4 HES) must be applied. The corresponding moment profiles for FL and RL are shown in Figure 9C, which suggest that the magnetization rotated from 0° to 180°. After removing the H-field, the magnetic state remains in the antiparallel configuration (∼−0 Oe), as marked by the wide cyan and orange arrows in Figure 9D. At 6 kV/cm, the magnetic switching only requires a smaller H-field (∼+HES) bias from the initial antiparallel state with the assistance of the E-field-induced Heff, as shown in Figure 9E. After removing the E- and H-fields, the magnetization remains stable in the parallel state, as shown in Figure 9F, indicating non-volatile magnetic switching. To switch from the parallel to antiparallel state, a smaller and opposite H-field (∼–HES) along the major axis (–x direction) is required under 6 kV/cm as shown in Figure 9G, definitely indicating that the magnetization rotation of the FL is facilitated by E-field-induced Heff. After removing the E- and H-fields, the FL magnetization rotates 180° and stabilizes in the antiparallel state because of the magnetic shape anisotropy as shown in Figure 9H. Hence, the E-field-induced magnetoelastic anisotropy dominates over the magnetic shape anisotropy (see details in Figure S15 in the supplemental information) and helps the magnetization overcome the energy barrier to facilitate the 180° reversal of the FL (Hu et al., 2011). Both the aforementioned experimental and simulation results firmly elucidate that the angle-dependent magnetic switching, the TMR modulation and non-volatile and reversible 180° magnetization switching by the E-fields should result from competition among the E-field-induced magnetoelastic anisotropy, the magnetic shape anisotropy, and the unidirectional anisotropy introduced from the external small H-field in the hybrid, facilitating energy-efficient spintronic devices (Yang et al., 2019). The simulated moments of the RL are hardly influenced by due to the strong exchange bias field, which is consistent with the experimental results in Sec. 2.3 and 2.6, 2.3 and 2.6. It is mentionable that the magnetic switching process of the parallel (antiparallel) to antiparallel (parallel) state with the H-field bias is completed through the domain wall formation and propagation under both 0 kV/cm and 6 kV/cm (see Figure S16 in the supplemental information), resulting in a sharp magnetization reversal in the vicinity of the switching fields (Czapkiewicz et al., 2004; Ba et al., 2021). This simulation result is well consistent with our aforementioned experimental observation.
Figure 9.
Micromagnetic simulations of reversible and non-volatile magnetic switching by a reduced H-field with the assistance of E-fields
(A−D) Simulated magnetization profiles of the FL (top) and RL (bottom) under a large H-field H (∼+2.4HES) along the +x direction, after removing the H-field (in the remnant state), under a large and opposite H-field H (∼−2.4HES) along the –x direction, and after removing the opposite H-field (in another remnant state), respectively. The E-field is set to zero (depolarized state) in (A−D).
(E−H) Simulated magnetization profiles of the FL and RL under a relatively small H-field (∼+HES) along the +x direction, after removing the H-field (in the remnant state), under a small and opposite H-field H (∼–HES) along the -x direction, and after removing the small and opposite H-field, respectively. The assisted E-field is set to 6 kV/cm in (E−H). The initial magnetic state is within an antiparallel configuration for both cases. H: the external H-field, Heff: the effective anisotropy field.
Conclusions
In conclusions, we have successfully constructed an MgO-based MTJ/Pb(Mg2/3Nb1/3)0.7Ti0.3O3 (MTJ/PMN-PT) magnetoelectronic hybrid structure, for the investigation of an applied electric field on the angular magnetic switching behavior and TMR. Relying the measurements of TCs and CTCs, we have observed that the switching field is angle-dependent, and can be reduced by as much as 59% along the major axis subjecting to an E-field. The switching boundary for magnetic switching is modulated by E-fields, resulting in a reduced switching window size. In addition, we have used the E-field to achieve reversible and non-volatile 180° magnetization switching experimentally, which is further confirmed by micromagnetic simulations. Overall, the magnetization states of the hybrid are the results of competition among the E-field controlled magnetoelastic anisotropy energy, the magnetic shape anisotropy energy in the MTJ, and the Zeeman energy introduced by the relatively small H-field. Our work provides a promising means to realizing E-field controlled magnetic switching for low energy consuming spintronic devices.
Limitations of the study
In this work, we provide insights on E-field-control of the angle-dependent magnetic switching in the two-dimensional H-fields. The critical switching field is reduced by 59% with the assistance of E-fields and the non-volatile 180° magnetization reversal in the optimized direction is also demonstrated. However, even though the external bias magnetic field is largely decreased, the H-field-free magnetic switching is urgently required for fully electrically controlled spintronic device in future.
STAR★Methods
Key resources table
| REAGENT or RESOURCE | SOURCE | IDENTIFIER |
|---|---|---|
| Chemicals | ||
| Tantalum (Ta) | Angstrom Sciences, Inc. | CAS: 7440-25-7 |
| Cobalt Iron Boron (CoFeB) | Custom-made from Angstrom Sciences, Inc. | https://www.angstromsciences.com/pvd-materials-list |
| Ruthenium (Ru) | Angstrom Sciences, Inc. | CAS: 7440-18-8 |
| Magnesium Oxide (MgO) | Angstrom Sciences, Inc. | CAS: 10043-11-5 |
| Cobalt Iron (CoFe) | Custom-made from Angstrom Sciences, Inc. | https://www.angstromsciences.com/pvd-materials-list |
| Iridium Manganese (IrMn) | Custom-made from Angstrom Sciences, Inc. | https://www.angstromsciences.com/pvd-materials |
| Pb(Mg1/3Nb2/3)0.7Ti0.3O3 (PMN-PT) | HEFEI KEJING MATERIALS TECHNOLOGY CO., LTD | http://www.kjmti.com/product/15466.html |
| Software and algorithms | ||
| OOMMF 1.2 alpha | Donahue and Porter, 1999 | https://math.nist.gov/oommf/ |
| Origin 2020 | Graphing and data analysis software from OriginLab | https://www.originlab.com/ |
| SolidWorks 2014 | 3DEXPERIENCE Company | https://www.solidworks.com/ |
| ANSYS 2020 R1 | ANSYS | https://www.ansys.com/ |
| Instruments | ||
| Keithley 2400, 2410 | Tektronix | https://www.tek.com/keithley |
| Superconducting quantum interference device (SQUID) | Quantum Design | http://www.qd-china.com/zh |
| Ultrahigh-vacuum magnetron sputtering system | Home-built, at Department of Physics, Brown University | https://www.brown.edu/research/labs/xiao/about/text-style-reference |
Resource availability
Lead contact
Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Yuanjun Yang (yangyuanjun@hfut.edu.cn).
Materials availability
This study did not generate new unique reagents.
Data and code availability
The datasets generated during this study are available at Mendeley Data: https://doi.org/10.17632/6kpb9zcn5x.1.
Method details
Fabrication of magnetic multilayers/ferroelectric heterostructures
The MTJ stacks had the following sequence: Ta (50)/Ru (300)/Ta (50)/CoFe (20)/IrMn (180)/CoFe (30)/Ru (8.5)/CoFeB (30)/MgO (20)/CoFeB (30)/Ta (50)/Ru (100) (the numbers represent the nominal thickness in angstroms). The stacks were fabricated on (011)-PMN-PT substrates (5 mm × 5 mm × 0.5 mm) in a custom multi-target high-vacuum magnetron sputtering system with a base pressure of ∼ 2×10−8 Torr). CoFe, CoFeB, and IrMn denote Co70Fe30, Co40Fe40B20, and Ir25Mn75 alloys with their nominal target compositions, respectively. We employed this layered structure which is commonly used in commercial MTJ sensors and MRAMs. In particular, the hard layer below the MgO barrier consisted of an exchange-biased synthetic antiferromagnetic (SAF) pinned layer, which was considered to be a more stable magnetic structure than a simple hard magnet or exchange-biased magnet. All metallic layers were deposited via DC sputtering at a constant Ar pressure of 2.05 mTorr. The tunneling-barrier MgO was deposited through RF-magnetron sputtering in Ar at a pressure of 1.10 mTorr. During deposition, the substrates were rotated at a constant speed to maximize the uniformity of the multilayer structures. An Au layer (100 nm) was deposited on the backside as the bottom electrode.
Lithography and thermal treatments
Oval shaped junctions with lateral sizes of 30 μm × 100 μm were defined on the PMN-PT substrates by using standard photolithography. The major (long) axis is along the [100] axis of the PMN-PT substrate. The samples were etched to the anti-ferromagnetic layer (IrMn) by using physical ion-beam milling. The IrMn and the layers below it serves as the top electrode. We then deposited a 180-nm-thick SiO2 layer to the patterned structure to electrically isolate the top and bottom electrodes of the MTJs. Afterward, the MTJs were thermally annealed at 320°C for 4 h at a pressure of ∼8×10-7 Torr under a magnetic field of 4.5 kOe applied along the major axis of the MTJs. Consequently, both the magnetic easy-axis of the free layer and the pinning direction of the SAF layer were defined along the major axis of the MTJ, a configuration for magnetic memory. The thermal treatment also affects a large TMR ratio through crystallization of the amorphous CoFeB layers on both sides of MgO.
TMR measurements under E- and H-fields
The TMR was measured by using a four-probe technique with in-situ H- and E-fields on a probe station, with a probe voltage of 40 mV across an MTJ. The orthogonal H-fields were generated with two pairs of perpendicular electromagnets. The in-plane two-axis H-field was along the horizontal plane of the MTJ/(011)-PMN-PT structure. A transfer curve (TC) was recorded by sweeping the H-field magnitude at a fixed angle. And a circle transfer curve (CTC) was recorded by rotating an H-field vector at a constant magnitude. The experimental data acquisition rate is about one second per point. An in-situ E-field was applied across the thickness of the PMN-PT substrate by using a high-voltage source (Keithley 2410), where a positive E-field was defined from the top to the bottom electrode. The leakage current was monitored during the angular magnetoresistance measurements. All the measurements were performed at room temperature.
Magnetic hysteresis-loop measurements
The magnetic hysteresis loop with in-situ E-fields was measured by using a Quantum Design® SQUID magnetometer at room temperature.
Microstructural and strain measurements
Reciprocal space mappings (RSMs) of the ferroelectric PMN-PT layer with the in-situ E-fields was performed at the Shanghai Synchrotron Radiation Facilities. Line scans were performed by using high-resolution X-ray diffraction (XRD) with Cu Kα1 (λ=1.5406 Å) radiation (Rigaku SmartLab Film Version). The in-plane piezo-strain that was induced from the E-fields in the ferroelectric PMN-PT layer along the [100] and [01−1] axes was measured by using linear foil strain gauges (Micro-Measurements, USA).
Micromagnetic simulation method
Micromagnetic simulations were performed by using the object-oriented micromagnetic framework (OOMMF) software. An oval-shaped tri-layer structure that consisted of a free layer, a barrier layer, and a reference layer was used based on the shape and size of the MTJ layer structure. An exchange bias field (∼ 470 Oe) was applied in the reference layer based on the magnetic hysteresis-loop measurements. The major axis of the oval-shaped tri-layer structure was along the [100] crystal axis, and the minor axis was along the [01−1] of the ferroelectric PMN-PT substrate. The effective magnetic field (Heff) for the magnetoelectric devices is the sum of the exchange field (Hex), demagnetization field (Hd), and magnetoelastic anisotropy field (Hme), all considered in the micromagnetic simulations.
Finite element method (FEM)
Finite-element-method simulations were performed by using the finite element software ANSYS (Zu et al., 2018). The truncated pyramid was introduced to mimic the imperfect interfaces between the MTJ and PMN-PT single crystal. The 3-dimensional strain distribution and strain transfer efficiency were simulated. The material parameters of the PMN-PT single crystal and Ta buffer layer can be found in previous reports (Hu et al., 2018; Guisbiers et al., 2010), respectively. All materials used were assumed to be linear-elastic.
Acknowledgments
This work was mainly supported by the National Key Research and Development Program of China (2016YFA0300102). This research was in part supported by the National Natural Science Foundation of China (52072102, 11775224), partially funded through the Fundamental Research Funds for the Central Universities (108-4115100092, PA2019GDQT0023) at Hefei University of Technology and also the Open Foundation of the Hefei National Laboratory for Physical Sciences at the Microscale (KF2020002). The work of S.W. and G.X. was supported by Brown University. The authors thank the beamlines BL07W, BL11U and BL12B-α at the National Synchrotron Radiation Laboratory (NSRL) for the micro-device fabrications and characterizations. We also gratefully acknowledge Xingmin Zhang, Yueliang Gu, Tieying Yang, Xiaolong Li, and Xingyu Gao for the X-ray diffraction measurements at beamlines BL14B1 and BL02U2 at the Shanghai Synchrotron Radiation Facilities (SSRF).
Author contributions
Y.Y., C.G., and G.X. conceived the work and designed the entire project. Y.Y., S.W., and G.X. prepared the samples and fabricated the MTJ/PMN-PT magnetoelectric hybrid devices. Y.Y. and Z.L. performed the experiments, analyzed the experimental data, and wrote the paper. W.H., C.W., J.Z., Y.D., H. L., Z.W., and Y.Y. discussed the experimental results and carried out micromagnetic simulations. Y.G. and Y.T. helped fabricate and characterize the micro-devices. C.F. and Y.Z. carried out the magnetic property measurements and date analysis. All authors reviewed, revised, and approved of this manuscript.
Declaration of interests
The authors declare no competing interests.
Published: July 23, 2021
Footnotes
Supplemental information can be found online at https://doi.org/10.1016/j.isci.2021.102734.
Contributor Information
Yuanjun Yang, Email: yangyuanjun@hfut.edu.cn.
Chen Gao, Email: gaochen@ucas.ac.cn.
Gang Xiao, Email: gang_xiao@brown.edu.
Supplemental information
References
- Akerman J. Toward a universal memory. Science. 2005;308:508–510. doi: 10.1126/science.1110549. [DOI] [PubMed] [Google Scholar]
- Al-Rashid M.M., Bandyopadhyay S., Atulasimha J. Dynamic error in strain-induced magnetization reversal of nanomagnets due to incoherent switching and formation of metastable states: a size-dependent study. IEEE Trans. Electron. Devices. 2016;63:3307–3313. [Google Scholar]
- Anguelouch A., Schrag B.D., Xiao G., Lu Y., Trouilloud P.L., Wanner R.A., Gallagher W.J., Parkin S.S.P. Two-dimensional magnetic switching of micron-size films in magnetic tunnel junctions. Appl. Phys. Lett. 2000;76:622. [Google Scholar]
- Atulasimha J., Bandyopadhyay S. Bennett clocking of nanomagnetic logic using multiferroic single-domain nanomagnets. Appl. Phys. Lett. 2010;97:173105. [Google Scholar]
- Ba Y., Zhuang S., Zhang Y., Wang Y., Gao Y., Zhou H., Chen M., Sun W., Liu Q., Chai G. Electric-field control of skyrmions in multiferroic heterostructure via magnetoelectric coupling. Nat. Commun. 2021;12:322. doi: 10.1038/s41467-020-20528-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baldrati L., Rinaldi C., Manuzzi A., Asa M., Aballe L., Foerster M., Bertacco R. Electrical switching of magnetization in the artificial multiferroic CoFeB/BaTiO3. Adv. Electron. Mater. 2016;2:1600085. [Google Scholar]
- Bauer U., Yao L., Tan A.J., Agrawal P., Emori S., Tuller H.L., Dijken S., Beach G.S. Magneto-ionic control of interfacial magnetism. Nat. Mater. 2015;14:174–181. doi: 10.1038/nmat4134. [DOI] [PubMed] [Google Scholar]
- Biswas A.K., Ahmad H., Atulasimha J., Bandyopadhyay S. Experimental demonstration of complete 180° reversal of magnetization in isolated Co nanomagnets on a PMN-PT substrate with voltage generated strain. Nano Lett. 2017;17:3478–3484. doi: 10.1021/acs.nanolett.7b00439. [DOI] [PubMed] [Google Scholar]
- Brataas A., Kent A.D., Ohno H. Current-induced torques in magnetic materials. Nat. Mater. 2012;11:372–381. doi: 10.1038/nmat3311. [DOI] [PubMed] [Google Scholar]
- Buzzi M., Chopdekar R.V., Hockel J.L., Bur A., Wu T., Pilet N., Nolting F., Warnicke P., Carman G.P., Heyderman L.J., Nolting F. Single domain spin manipulation by electric fields in strain coupled artificial multiferroic nanostructures. Phys. Rev. Lett. 2013;111:027204. doi: 10.1103/PhysRevLett.111.027204. [DOI] [PubMed] [Google Scholar]
- Cao Y., Xing G., Lin H., Zhang N., Zheng H., Wang K. Prospect of spin-orbitronic devices and their applications. iScience. 2020;23:101614. doi: 10.1016/j.isci.2020.101614. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chanthbouala A., Matsumoto R., Grollier J., Cros V., Anane A., Fert A., Khvalkovskiy A.V., Zvezdin K.A., Nishimura K., Nagamine Y. Vertical-current-induced domain-wall motion in MgO-based magnetic tunnel junctions with low current densities. Nat. Phys. 2011;7:626–630. [Google Scholar]
- Chen A., Zhao Y., Li P., Zhang X., Peng R., Huang H., Zou L., Zheng X., Zhang S., Miao P. Angular dependence of exchange bias and magnetization reversal controlled by electric-field-induced competing anisotropies. Adv. Mater. 2016;28:363. doi: 10.1002/adma.201503176. [DOI] [PubMed] [Google Scholar]
- Chen A.P., Dai Y., Eshghinejad A., Liu Z., Wang Z., Bowlan J., Knall E., Civale L., Judith L., MacManus-Driscoll Competing interface and bulk effect-driven magnetoelectric coupling in vertically aligned nanocomposites. Adv. Sci. 2019;6:1901000. doi: 10.1002/advs.201901000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen A.T., Wen Y., Fang B., Zhao Y., Zhang Q., Chang Y., Zhao Y. Giant nonvolatile manipulation of magnetoresistance in magnetic tunnel junctions by electric fields via magnetoelectric coupling. Nat. Commun. 2019;10:243. doi: 10.1038/s41467-018-08061-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen A.T., Zhao Y., Wen Y., Pan L., Li P., Zhang X.-X. Full voltage manipulation of the resistance of a magnetic tunnel junction. Sci. Adv. 2019;5:eaay5141. doi: 10.1126/sciadv.aay5141. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Coey J.M. Cambridge university press; 2010. Magnetism and Magnetic Materials. [Google Scholar]
- Conte R.L., Xiao Z., Chen C., Stan C.V., Gorchon J., El-Ghazaly A., Nowakowski M.E., Sohn H., Pattabi A., Scholl A. Influence of nonuniform micron-scale strain distributions on the electrical reorientation of magnetic microstructures in a composite multiferroic heterostructure. Nano Lett. 2018;18:1952–1961. doi: 10.1021/acs.nanolett.7b05342. [DOI] [PubMed] [Google Scholar]
- Czapkiewicz M., Zoladz M., Wisniowski J.P., Rak R., Stobiecki T., Kim C.G., Kim C.O., Takahashi M., Tsunoda Magnetization process and domains in MTJ. M. Phys. Stat. Sol. 2004 [Google Scholar]
- Das S., Avraham L., Telepinsky Y., Mor V., Schultz M., Klein L. Magnetization switching of multi-state magnetic structures with current-induced torques. Sci. Rep. 2018;8:15160. doi: 10.1038/s41598-018-33554-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Donahue M.J., Porter D.G. National Institute of Standards and Technology; 1999. OOMMF User’s Guide, Version 1.0; Interagency Report NISTIR 6376.http://math.nist.gov/oommf [Google Scholar]
- D’Souza N., Fashami M.S., Bandyopadhyay S., Atulasimha J. Experimental clocking of nanomagnets with strain for ultralow power boolean logic. Nano Lett. 2016;16:1069–1075. doi: 10.1021/acs.nanolett.5b04205. [DOI] [PubMed] [Google Scholar]
- Ghidini M., Mansell R., Maccherozzi F., Moya X., Phillips L.C., Yan W., Mathur N.D. Shear-strain-mediated magnetoelectric effects revealed by imaging. Nat. Mater. 2019;18:840. doi: 10.1038/s41563-019-0374-8. [DOI] [PubMed] [Google Scholar]
- Guisbiers G., Herth E., Buchaillot L., Pardoen T. Fracture toughness, hardness, and Young’s modulus of tantalum nanocrystalline films. Appl. Phys. Lett. 2010;97:143115. [Google Scholar]
- Guo R., Lin W., Yan X., Venkatesan T., Chen J. Ferroic tunnel junctions and their application in neuromorphic networks. Appl. Phys. Rev. 2020;7:011304. [Google Scholar]
- Heron J.T., Bosse J.L., He Q., Gao Y., Trassin M., Ye L., Ramesh R. Deterministic switching of ferromagnetism at room temperature using an electric field. Nature. 2014;516:370–373. doi: 10.1038/nature14004. [DOI] [PubMed] [Google Scholar]
- Hu J.M., Nan C.W. Opportunities and challenges for magnetoelectric devices. APL Mater. 2019;7:080905. [Google Scholar]
- Hu J.M., Li Z., Chen L.Q., Nan C.W. High-density magnetoresistive random access memory operating at ultralow voltage at room temperature. Nat. Commun. 2011;2:553. doi: 10.1038/ncomms1564. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hu J.-M., Shu L., Li Z., Gao Y., Shen Y., Lin Y.H., Chen L.Q., Nan C.W. Film size-dependent voltage-modulated magnetism in multiferroic heterostructures. Phil. Trans. R. Soc. A. 2014;372:20120444. doi: 10.1098/rsta.2012.0444. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hu J.-M., Yang T.N., Chen L.Q. Strain-mediated voltage-controlled switching of magnetic skyrmions in nanostructures. NPJ Comput. Mater. 2018;4:62. [Google Scholar]
- Iwata-Harms J.M., Jan G., Liu H., Serrano-Guisan S., Zhu J., Thomas L., Wang P.K. High-temperature thermal stability driven by magnetization dilution in CoFeB free layers for spin-transfer-torque magnetic random-access memory. Sci. Rep. 2018;8:14409. doi: 10.1038/s41598-018-32641-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jia T., Cheng Z., Zhao H., Kimura H. Domain switching in single-phase multiferroics. Appl. Phys. Rev. 2018;5:021102. [Google Scholar]
- Kum H.S., Lee H., Kim S., Lindemann S., Kong W., Qiao K., Chen P., Irwin J., Lee J.H., Xie S. Heterogeneous integration of single-crystalline complex-oxide membranes. Nature. 2020;578:75–81. doi: 10.1038/s41586-020-1939-z. [DOI] [PubMed] [Google Scholar]
- Li P., Chen A., Li D., Zhao Y., Zhang S., Yang L., Han X. Electric field manipulation of magnetization rotation and tunneling magnetoresistance of magnetic tunnel junctions at room temperature. Adv. Mater. 2014;26:4320–4325. doi: 10.1002/adma.201400617. [DOI] [PubMed] [Google Scholar]
- Li H.B., Lu N., Zhang Q., Wang Y., Feng D., Chen T., Yang S., Duan Z., Li Z., Shi Y. Electric-field control of ferromagnetism through oxygen ion gating. Nat. Commun. 2017;8:2156. doi: 10.1038/s41467-017-02359-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li P., Zhao Y., Zhang S., Chen A., Li D., Ma J., Liu Y., Pierce D.T., Unguris J., Piao H. Spatially resolved ferroelectric domain-switching-controlled magnetism in Co40Fe40B20/Pb(Mg1/3Nb2/3)0.7Ti0.3O3 multiferroic heterostructure. ACS Appl. Mater. Interfaces. 2017;9:2642. doi: 10.1021/acsami.6b13620. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li X., Lee A., Razavi S.A., Wu H., Wang K.L. Voltage-controlled magnetoelectric memory and logic devices. MRS Bull. 2018;43:970–977. [Google Scholar]
- Liu M., Obi O., Cai Z., Lou J., Yang G., Ziemer K.S., Sun N.X. Electrical tuning of magnetism in Fe3O4/PZN–PT multiferroic heterostructures derived by reactive magnetron sputtering. J. Appl. Phys. 2010;107:073916. [Google Scholar]
- Liu M., Lou J., Li S., Sun N.X. E-Field control of exchange bias and deterministic magnetization switching in AFM/FM/FE multiferroic heterostructures. Adv. Funct. Mater. 2011;21:2593–2598. [Google Scholar]
- Liu L., Pai C.-F., Li Y., Tseng H.W., Ralph D.C., Buhrman R.A. Spin-torque switching with the giant spin Hall effect of tantalum. Science. 2012;336:555. doi: 10.1126/science.1218197. [DOI] [PubMed] [Google Scholar]
- Liu Z.Q., Liu J.H., Biegalski M.D., Hu J.-M., Shang S.L., Ji Y., Wang J.M., Hsu S.L., Wong A.T., Cordill M.J. Electrically reversible cracks in an intermetallic film controlled by an electric field. Nat. Commun. 2018;9:41. doi: 10.1038/s41467-017-02454-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Loong L.M., Qiu X., Neo Z.P., Deorani P., Wu Y., Bhatia C.S., Saeys M., Yang H. Strain-enhanced tunneling magnetoresistance in MgO magnetic tunnel Junctions. Sci. Rep. 2014;4:6505. doi: 10.1038/srep06505. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lu C., Hu W., Tian Y., Wu T. Multiferroic oxide thin films and heterostructures. Appl. Phys. Rev. 2015;2:021304. [Google Scholar]
- Mangin S., Ravelosona D., Katine J.A., Carey M.J., Terris B.D., Fullerton E.E. Current-induced magnetization reversal in nanopillars with perpendicular anisotropy. Nat. Mater. 2006;2006:210. [Google Scholar]
- Manipatruni S., Nikonov D.E., Lin C.C., Gosavi T.A., Liu H., Prasad B., Young I.A. Scalable energy-efficient magnetoelectric spin–orbit logic. Nature. 2019;565:35–42. doi: 10.1038/s41586-018-0770-2. [DOI] [PubMed] [Google Scholar]
- Matsukura F., Tokura Y., Ohno H. Control of magnetism by electric fields. Nat. Nanotechnl. 2015;10:209. doi: 10.1038/nnano.2015.22. [DOI] [PubMed] [Google Scholar]
- Matsumoto R., Fukushima A., Nagahama T., Suzuki Y., Ando K., Yuasa S. Oscillation of giant tunneling magnetoresistance with respect to tunneling barrier thickness in fully epitaxial Fe/MgO/Fe magnetic tunnel junctions. Appl. Phys. Lett. 2007;90:252506. [Google Scholar]
- Mondal S., Abeed M.A., Dutta K., De A., Sahoo S., Barman A., Bandyopadhyay S. Hybrid magnetodynamical modes in a single magnetostrictive nanomagnet on a piezoelectric substrate arising from magnetoelastic modulation of precessional dynamics. ACS Appl. Mater. Interfaces. 2018;10:43970–43977. doi: 10.1021/acsami.8b19243. [DOI] [PubMed] [Google Scholar]
- Nagarajan V., Roytburd A., Stanishevsky A., Prasertchoung S., Zhao T., Chen L., Melngailis J., Auciello O., Ramesh R. Dynamics of ferroelastic domains in ferroelectric thin films. Nat. Mater. 2003;2:43–47. doi: 10.1038/nmat800. [DOI] [PubMed] [Google Scholar]
- Nan T., Hu J.M., Dai M., Emori S., Wang X., Hu Z., Matyushov A., Chen L.Q., Sun N. A strain-mediated magnetoelectric-spin-torque hybrid structure。. Adv. Funct. Mater. 2019;29:1806371. [Google Scholar]
- Parkin S.S.P., Roche K.P., Samant M.G., Rice P.M., Beyers R.B., Scheuerlein R.E., O’Sullivan E.J., Brown S.L., Bucchigano J., Abraham D.W. Exchange-biased magnetic tunnel junctions and application to nonvolatile magnetic random access memory. J. Appl. Phys. 1999;85:5828. [Google Scholar]
- Peng S., Zhu D., Li W., Wu H., Grutter A.J., Gilbert D.A., Lu J., Xiong D., Cai W., Shafer P. Exchange bias switching in an antiferromagnet/ferromagnet bilayer driven by spin–orbit torque. Nat. Electron. 2020;3:757–764. [Google Scholar]
- Pertsev N., Kohlstedt H. Resistive switching via the converse magnetoelectric effect in ferromagnetic multilayers on ferroelectric substrates. Nanotechnology. 2010;21:475202. doi: 10.1088/0957-4484/21/47/475202. [DOI] [PubMed] [Google Scholar]
- Pertsev N.A., Kohlstedt H. Magnetoresistive memory with ultralow critical current for magnetization switching. Adv. Funct. Mater. 2012;22:4696–4703. [Google Scholar]
- Puebla J., Kim J., Kondou K., Otani Y. Spintronic devices for energy-efficient data storage and energy harvesting. Commun. Mater. 2020;1:24. [Google Scholar]
- Ralph D.C., Stiles M.D. Spin transfer torques. J. Magn. Magn. Mater. 2008;320:1190. [Google Scholar]
- Roy K., Bandyopadhyay S., Atulasimha J. Hybrid spintronics and straintronics: a magnetic technology for ultra low energy computing and signal processing. Appl. Phys. Lett. 2011;99:063108. [Google Scholar]
- Safron N.S., Schrag B.D., Liu X.Y., Shen W.F., Muzumdar D., Carter M.J., Xiao G. Magnetic characterization of magnetic tunnel junction devices using circle transfer curves. J. Appl. Phys. 2008;103:033507. [Google Scholar]
- Shen W., Mazumdar D., Zou X., Liu X., Schrag B.D., Xiao G. Effect of film roughness in MgO-based magnetic tunnel junctions. Appl. Phys. Lett. 2006;88:182508. [Google Scholar]
- Simmons J.G. Generalized formula for the electric tunnel effect between similar electrodes separated by a thin insulating film. J. Appl. Phys. 1963;34:1793. [Google Scholar]
- Spaldin N.A., Ramesh R. Advances in magnetoelectric multiferroics. Nat. Mater. 2019;18:203–212. doi: 10.1038/s41563-018-0275-2. [DOI] [PubMed] [Google Scholar]
- Su Y., Zhang J., Lü J.T., Hong J., You L. Large magnetoresistance in an electric-field-controlled antiferromagnetic tunnel junction. Phys. Rev. Appl. 2019;12:044036. [Google Scholar]
- Tan A.J., Huang M., Avci C.O., Büttner F., Mann M., Hu W., Mazzoli C., Wilkins S., Tuller H.L., Beach G.S. Magneto-ionic control of magnetism using a solid-state proton pump. Nat. Mater. 2019;18:35–41. doi: 10.1038/s41563-018-0211-5. [DOI] [PubMed] [Google Scholar]
- Wang W.G., Li M., Hageman S., Chien C.L. Electric-field-assisted switching in magnetic tunnel junctions. Nat. Mater. 2012;11:64–68. doi: 10.1038/nmat3171. [DOI] [PubMed] [Google Scholar]
- Wang X., Yang Q., Wang L., Zhou Z., Min T., Liu M., Sun N.X. E-field control of the RKKY interaction in FeCoB/Ru/FeCoB/PMN-PT (011) multiferroic heterostructures. Adv. Mater. 2018;30:1803612. doi: 10.1002/adma.201803612. [DOI] [PubMed] [Google Scholar]
- Wang Q., Domann J., Yu G., Barra A., Wang K.L., Carman G.P. Strain-mediated spin-orbit-torque switching for magnetic memory. Phys. Rev. Appl. 2018;10:034052. [Google Scholar]
- Yang S.W., Peng R.C., Jiang T., Liu Y.K., Feng L., Wang J.J., Nan C.W. Non-volatile 180° magnetization reversal by an electric field in multiferroic heterostructures. Adv. Mater. 2014;26:7091–7095. doi: 10.1002/adma.201402774. [DOI] [PubMed] [Google Scholar]
- Yang Q., Zhong T., Tu Z., Zhu L., Wu M., Zeng X.C. Design of single-molecule multiferroics for efficient ultrahigh-density nonvolatile memories. Adv. Sci. 2019;6:1801572. doi: 10.1002/advs.201801572. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Železný J., Wadley P., Olejník K., Hoffmann A., Ohno H. Spin transport and spin torque in antiferromagnetic devices. Nat. Electron. 2018;14:220–228. [Google Scholar]
- Zhang Y.L., Wang C.S., Huang H.B., Lu J.D., Liang R.R., Liu J., Peng R.C., Zhang Q.T., Zhang Q.H., Wang J. Deterministic reversal of single magnetic vortex circulation by an electric field. Sci. Bull. 2020;45:1260–1267. doi: 10.1016/j.scib.2020.04.008. [DOI] [PubMed] [Google Scholar]
- Zhang W., Xiao G., Carter M.J. Two-dimensional field-sensing map and magnetic anisotropy dispersion in magnetic tunnel junction arrays. Phys. Rev. B. 2011;83:144416. [Google Scholar]
- Zhao Z., Jamali M., D'Souza N., Zhang D., Bandyopadhyay S., Atulasimha J., Wang J.P. Giant voltage manipulation of MgO-based magnetic tunnel junctions via localized anisotropic strain: a potential pathway to ultra-energy-efficient memory technology. Appl. Phys. Lett. 2016;109:092403. [Google Scholar]
- Zhao S., Wang L., Zhou Z., Li C., Dong G., Zhang L., Peng B., Min T., Hu Z., Ma J. Ionic liquid gating control of spin reorientation transition and switching of perpendicular magnetic anisotropy. Adv. Mater. 2018;30:1801639. doi: 10.1002/adma.201801639. [DOI] [PubMed] [Google Scholar]
- Zhao W., Huang W., Liu C., Hou C., Chen Z., Yin Y., Li X. Positive and negative magnetoresistances in Co/Cu/Ni spin-valves. ACS Appl. Mater. Interfaces. 2018;10:21390. doi: 10.1021/acsami.8b03761. [DOI] [PubMed] [Google Scholar]
- Zheng M., Zheng R.K. Electric-field-Tunable ferroelastic control of nonvolatile resistivity and ferromagnetic switching in multiferroic La0.67Ca0.33MnO3/[PbMg1/3Nb2/3O3]0.7[PbTiO3]0.3 heterostructures. Phys. Rev. Appl. 2016;5:044002. [Google Scholar]
- Ziss D., Martín-Sánchez J., Lettner T., Halilovic A., Trevisi G., Trotta R., Rastelli A., Stangl J. Comparison of different bonding techniques for efficient strain transfer using piezoelectric actuators. J. Appl. Phys. 2017;121:135303. doi: 10.1063/1.4979859. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zu L., Xu H., Zhang B., Li D., Zi B. Design of filament-wound composite structures with arch-shaped cross sections considering fiber tension simulation. Compos. Struct. 2018;194:119–125. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The datasets generated during this study are available at Mendeley Data: https://doi.org/10.17632/6kpb9zcn5x.1.