Abstract
Accurate, cost-effective, easy-to-use, and point-of-care sensors for protein biomarker levels are important for disease diagnostics. A cost-effective and compact readout approach that has been used for several diagnostic applications is lens-free holographic microscopy, which provides an ultra-large field of view and submicron resolution when it is coupled with pixel superresolution techniques. Despite its potential as a diagnostic technique, lens-free microscopy has not previously been applied to quantitative protein molecule sensing in solution, which can simplify sensing protocols and ultimately enable measurements of binding kinetics in physiological conditions. Here we sense interferon-gamma (an immune system biomarker) and NeutrAvidin molecules in solution by combining lens-free microscopy with a one-step bead-based agglutination assay, enabled by a custom high-speed LED array and automated image processing routines. We call this a quantitative large-area binding (QLAB) sensor. The high-speed light source provides, for the first time, pixel-superresolved imaging of > 104 2-micron beads in solution undergoing Brownian motion, without significant motion blur. The automated image processing routines enable the counting of individual beads and clusters, providing a quantitative sensor readout that depends on both bead and analyte concentrations. Fits to chemical binding theory are provided. For NeutrAvidin, we find a limit of detection (LOD) of < 27 ng/mL (450 pM) and a dynamic range of 2–4 orders of magnitude. For mouse interferon-gamma, the LOD is < 3 ng/mL (200 pM) and the dynamic range is at least 4 orders of magnitude. The QLAB sensor holds promise for point-of-care applications in low-resource communities and where protocol simplicity is important.
Keywords: Protein biomarkers, Lens-free holographic microscopy, Brownian motion, Agglutination assay, Point-of-care, High-speed superresolution
Graphical TOC Entry
Lens-free holographic microscopy (LFHM) computationally reconstructs diffraction patterns of microscopic objects to reconstruct images of those objects.1 Due to the elimination of microscope objectives, LFHM can be cost-effective and field-portable, which makes it particularly suitable for point-of-care or space-constrained agricultural or environmental applications.2–6 LFHM provides better space-bandwidth product (i.e., fine resolution over a larger field of view (FOV)) than conventional lens-based optical instruments.7–9 LFHM resolution can be enhanced when combined with pixel superresolution (PSR),10–13 where holograms from the same sample are acquired at slightly different illumination angles. As this is time-consuming, many applications of LFHM have used dried (static) samples.11,14 Since many clinically-relevant samples are in liquids, the ability to image samples in solution undergoing Brownian motion in LFHM is highly desired as this would enable point-of-care diagnostics on human samples. In one example, Su et al. studied human and horse sperm swimming patterns by tracking the centroid positions of sperms,15 yet the sperms are not necessarily resolved. Fang et al. demonstrated the ability to image 5-μm polystyrene beads and red blood cells with Brownian motion.16 However, it is limited to a small number of objects.
Previously, micro- or nano-scale beads have been used as labels for biosensing applications based on LFHM. The high-throughput and quantitative nature of the tests together with the low-cost hardware of LFHM makes it a potential alternative to widely-used enzyme-linked immunosorbent assays17–20 and lateral flow assays,21 combining some of the advantages of each. Antibody-conjugated plasmonic nanoparticles have been used to identify different types of lymphocyte T-cells, 22 and magnetic beads have been used as labels in a nucleic acid hybridization assay.23 Protein molecules have been previously sensed using beads as labels, however the imaging was done in a dry format, did not provide single-bead resolution, and relied on a surface acoustic wave transducer.24
Another way that beads can be used as sensing elements is in agglutination assays. Traditionally, viruses, bacteria, and abnormal red blood cells have been detected by large scale agglutination of microsphere beads visible to the unaided eye,25,26 or in low-magnification microscopes. 27 However, the result is qualitative, and at low concentrations of the analyte, it can be difficult to identify rare agglutinated bead clusters. Previously, agglutination assays have been performed in microfluidic devices using Mie scattering to assess average bead size, which is a bulk measurement and does not measure individual beads or clusters,28–30 which can limit ultimate sensitivity. In sensing bacteria, the limit of detection was 10 cfu/mL,28,29 while the limit of detection in sensing viral antigens was 1 pg/mL.30 A quantitative and sensitive agglutination assay is possible provided the ability to image and analyze small beads and clusters individually. There is one previous example of combining an agglutination assay with LFHM to detect viruses, 31 however the imaging was performed on an open substrate as the solution was drying, posing limitations for clinical applications. Furthermore, this previous approach used a plasma-treated glass substrate, which causes particles to adhere to the surface, even when in solution.
In this article, we sense proteins in solution using beads undergoing Brownian motion in an enclosed microfluidic device. We present a quantitative large area binding (QLAB) sensor, comprising: (1) a high-speed LFHM capable of imaging and resolving diffusing and binding beads in solution; (2) a microfluidic chip (MC) with a well-defined imaging area and a small solution volume; and (3) automatic image processing routines for counting bead cluster size distributions. The high-speed LFHM has the ability to image > 104 2-μm polystyrene beads simultaneously in liquid undergoing Brownian motion with high signal-to-noise ratio (SNR) over a FOV > 12.5 mm2. These beads are smaller and faster-moving than the 5-μm beads imaged by Fang et al.16 The high throughput of the QLAB sensor enables the detection of rare events, enhances dynamic range, and reduces error bars. In this article, we perform over 100 experiments on different samples using the QLAB sensor. While bead-based assays have been previously used in many other different sensing configurations,32–34 our approach is significantly unique in its ability to image, enumerate, and resolve anywhere from 1 to 104 beads and/or clusters with Brownian motion in solution, enabling us to use a bead-based agglutination assay to sense protein molecules at concentrations as low as 3 ng/ml.
To sense a particular analyte, beads functionalized with corresponding capture agents are incubated with the sample (Figure 1a). In the presence of analytes, two functionalized beads can bind to different binding sites on the same analyte molecule, resulting in agglutination. Here, we demonstrate the sensing of free NeutrAvidin (NA) molecules with biotin (B)-coated beads (Figure 1d) as well as the sensing of of mouse interferon-gamma (IFN-γ) using antibody-coated beads (Figure 1e). Agglutination can be quantified by the bound ratio to infer analyte concentrations, which is defined as the ratio of the number of beads in clusters to the total number of beads in both monomers and clusters. IFN-γ is an immune system response biomarker. As one example, it is one of several cytokines monitored in mouse models of graft versus host disease due to bone marrow transplants as a treatment for leukemia.35
Figure 1:

Quantitative large area binding assay. (a) Incubation of analytes and functionalized beads. (b) Photograph of sample being delivered into a MC. (c) Photograph of a MC sitting on a CMOS sensor. (d) Illustration of binding between two biotin coated beads and a NA molecule. (e) Illustration of binding between two anti-mouse-IFN-γ coated beads and a mouse IFN-γ molecule. (f) Computational imaging-based sensor response for sensing mouse IFN-γ. Bovine serum albumin is used as a negative control. (g) Illustration of monomers and clusters.
Experimental Section
Image sensor platform
The high-speed LFHM is shown in Supporting Figure S1. At its base is a complementary metal-oxide-semiconductor (CMOS) monochromatic image sensor (ON Semiconductor AR1335) with 1.1 μm pixel size and a 4.6 mm × 3.4 mm active area. A MC containing the bead and analyte mixture (Supporting Figure S1c) is placed directly on the image sensor. Although the image sensor cover glass was removed by Pacific X-ray Imaging, the sample to sensor distance is z2 ≈ 700 μm due to oxide on the CMOS chip itself, wires on the image sensor board, and the MC coverslip thickness.
Custom high-speed LED array
Approximately 20 cm above the sample, illumination is provided by a light-emitting diode (LED) array, as shown in Supporting Figure S1b. This LED array was custom-designed and assembled to provide high-speed and high-power illumination for fast image acquisition with PSR. We use 15 LEDs distributed across a 31 mm × 35 mm area, as illustrated in Supporting Figure S1b. An Arduino Leonardo microcontroller communicates with two cascaded 8-bit shift registers (Texas Instruments SNx4HC595) via a serial peripheral interface to turn on the 15 high-power green LEDs (Osram Golden Dragon LT W5SM) in sequence. The LEDs are triggered at the beginning of each image sensor frame to achieve synchronization between the LED exposure and sensor acquisition. A current-limiter circuit is shared among 15 LEDs that are biased at ~1.5 A, delivering ~5 W of power to each LED when turned on. A doublesided aluminum-core printed circuit board is manufactured by Best Technology to house the high-power LEDs. The board previews are shown in Supporting Figure S2 and the schematic for our custom LED array is shown in Supporting Figure S3.
The temporal and spatial coherence necessary for holographic imaging1,2 are provided by a bandpass filter and large pinholes placed on the LEDs (Supporting Figure S1b and d). The bandpass filter (Thorlabs FL532-3) has a central wavelength of 532 nm and a 3 nm bandwidth. The pinholes were hand-punched from black anodized aluminum foil using a 178-μm diameter precision punch (QB-style core pin, Precision Punch and Plastics). The coherence provided by these elements causes the shadows of the objects in the MC to take the form of interference patterns between light scattered from the objects and light passing through transparent regions of the sample, constituting an in-line hologram.
Microfluidic chip
Our MC (Supporting Figure S1c) is assembled from laser-cut polycarbonate (PC) layers and a glass coverslip. The chamber patterns are designed using computer-aided design software. To ensure MCs are clean, PC sheets are laser cut with their protective films and coverslips are first cleaned with 2% RBS 35 detergent (Thermo Fisher Scientific) then rinsed thoroughly with DI water. A diamond-shaped pattern is laser cut from a 125-μm thick PC sheet (Mcmaster-Carr) to define a chamber region with an area slightly larger than the active area of the image sensor. Inlet and outlet ports are laser cut from a 250-μm thick PC sheet to facilitate liquid sample delivery. The 125-μm PC is then sandwiched between the 250-μm PC and a No 1 glass coverslip with UV-curable adhesive (Norland Products 7230B), and cured for two minutes. The central chamber dimensions are 6 mm × 8 mm × 170 μm, where the thickness is due to the PC sheet and the glue. Liquid samples are delivered to the chamber region with a syringe pump over 30 seconds. Figure 1b is a photograph of a MC while the chamber is being filled. After loading, two drops of UV adhesive are placed and cured at both the inlet and outlet to seal the MC.
Motion blur and pixel superresolution experiments
Our custom high-speed high-power LED array enables our QLAB sensor to image samples with Brownian motion. To investigate how Brownian motion limits performance, we image 2-μm carboxylate modified latex beads (Thermo Fisher Scientific C37248, lot 2086308, 5.0% coefficient of variation) dispersed in 1× phosphate buffered saline (PBS) with 0.2% Tween 20 (which we will henceforth refer to as PBST buffer) at a concentration of 0.01% weight/volume (w/v). These beads do not significantly cluster or adhere to the walls of the MC.
The first three system configurations used for measuring the effect of motion blur on PSR are shown in Table 1. For settling times tset < 30 min, beads have not fully sedimented at the bottom of the chamber, and are undergoing three-dimensional motion that is a combination of Brownian motion and sedimentation. For tset ≥ 191 min, the majority of beads have fully sedimented at the bottom of the MC and only exhibit 2D Brownian motion. The same MC was used in all configurations. The reduction of z1 in the third configuration increases image brightness and potentially SNR, but reduces spatial coherence, potentially limiting hologram resolution1.
Table 1:
System configurations for evaluating motion blur. The distance between the light source and sample is z1. The settling time before imaging is tset. The sensor gain is set to unity for all three configurations.
| Config. | z1 (cm) | tset (min) | Motion type | ton (ms) | |||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 20 | 10–25 | 3D | 120 | 45 | 480 | 60 | 240 | 30 |
| 2 | 20 | 191–198 | 2D | 60 | 480 | 45 | 240 | 30 | 120 |
| 3 | 15 | 209–216 | 2D | 30 | 240 | 60 | 120 | 45 | |
The total elapsed time required to collect nLED = 15 frames is
| (1) |
where ton is on-time for each individual LED. A fixed 15 ms buffer is employed between two LEDs to avoid bleeding into the next frame, as illustrated in Figure 2a. Here, 30 ms ≤ ton ≤ 480 ms, corresponding to 0.675 s ≤ ttot ≤ 7.425 s. For configuration 3 in Table 1, no data was collected for ton = 480 ms due to pixel saturation. The process of setting ton and saving 15 holograms can take 1–2 minutes, limited by the time required to save images to the hard drive. To mitigate any systematic bias due to slightly differing sedimentation times, experiments were conducted with the randomly-generated order of ton values shown in Table 1. To evaluate the effect of sensor gain on imaging performance, various combinations of ton and gain values ranging from 1× to 4× were tested.
Figure 2:
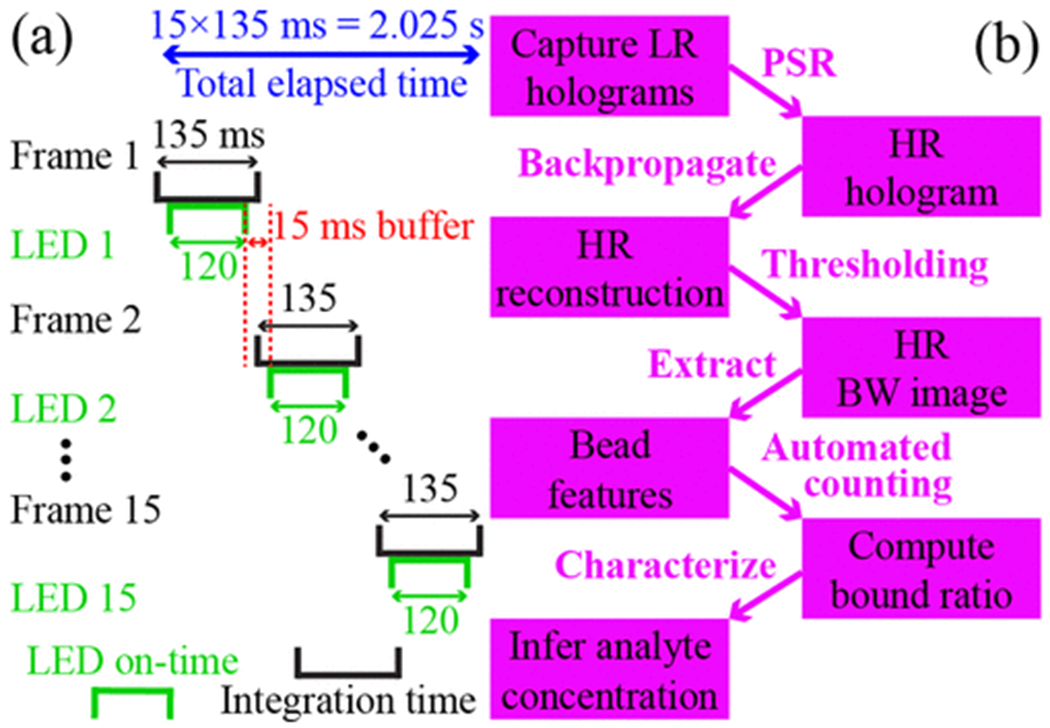
Image acquisition and reconstruction. (a) Illustration of the exposure sequence for an LED on-time of ton = 120 ms. The sensor integration time for each frame is ton + 15 ms of buffer, providing sensor frames per second in this example. (b) Workflow of QLAB sensing from image acquisition, image processing, automated bound ratio calculation, to analyte concentration characterization.
Solutions for NeutrAvidin sensing
Free NA molecules (Thermo Fisher Scientific 31050) are initially dissolved at a concentration of 5 mg/mL in 1× PBS and 10% glycerol, which is recommended by the datasheet to help prevent precipitation and does not interfere with B-binding. Serial dilutions ranging from 1 mg/mL to 1 pg/mL are prepared in the same PBS/glycerol buffer. B-coated beads (Spherotech TFP-2058-5) with 2 μm diameter (10% coefficient of variation) are provided at a stock concentration of 0.1% w/v. Samples are prepared by mixing 2.67 μL of a specific NA dilution with 10 μL of stock bead suspension, 10 μL of 10 × PBS containing 2% Tween 20, and 77.3 μL of Milli-Q ultrapure water to bring the total volume up to 100 μL. This results in solutions with 0.01% B-beads and NA concentrations ranging from 26.7 pg/mL to 267 μg/mL (one concentration per decade) in PBST.
These solutions were used to compare two different incubation protocols: mixing at 1000 RPM at room temperature for 2 hours and mixing at 1000 RPM at room temperature for 17 hours on a vortex mixer (Fisher Scientific).
For experiments involving different bead concentrations, the same procedure as above is used, but with different volumes of stock bead solution and water to maintain a total sample volume of 100 μL. Final bead concentrations of 0.00033%, 0.0033% 0.01% and 0.033% were compared to evaluate QLAB sensor performance using 17 hours of mixing. After mixing, to keep most of the bead concentrations in the MC of the same order of magnitude, the 0.01% and 0.033% samples are diluted in PBST to a bead concentration equal to that of the 0.0033% sample, which results in ~ 104 beads in the FOV. We chose not to dilute all the way down to 0.00033% because that leads to a relatively small number of beads in the imaging chamber. The 0.00033% bead solutions were imaged undiluted.
For experiments testing the repeatability of the sensor, the same procedure is used, but always with a 0.01% final bead concentration, and final NA concentrations ranging from 6 ng/mL to 20 μg/mL at two concentrations per decade. For each concentration, three repeats are performed to study batch-to-batch variations. All mixtures are mixed for 17 hours, then diluted in PBST by a factor of three and loaded into a MC. In addition, one of the 600 ng/mL concentration samples is imaged three times using three different MCs to quantify chip-to-chip variations.
The MCs are filled by first loading a syringe with 30 μL of a mixed solution. A syringe pump is used to deliver ~13 μL into the MC, where ~2 μL of sample is within the imaging volume. All MCs are left to settle for one hour before imaging with the QLAB sensor.
Solutions for mouse IFN-γ sensing
Free mouse IFN-γ molecules (Shenandoah Biotechnology 200-16) and, as a negative control, bovine serum albumin (BSA) molecules (Thermo Fisher Scientific BP1600) are initially dissolved at a concentration of 1 mg/mL in 1× PBS. Serial dilutions ranging from 0.1 mg/mL to 1 pg/mL are prepared in the same buffer. Anti-mouse-IFN-γ coated magnetic beads (Creative Diagnostics WHM-G268) with 2 μm diameter (10% coefficient of variation) are provided at a stock concentration of 2.5% w/v. An intermediate 0.1% w/v bead suspension is prepared in PBST. Samples are prepared by mixing 2.67 μL of a specific dilution of mouse IFN-γ or BSA with 3.33 μL of intermediate bead suspension, 10 μL of 10× PBS containing 2% Tween 20, and 84 μL of Milli-Q ultrapure water to bring the total volume up to 100 μL. This results in solutions with 0.0033% anti-mouse-IFN-γ-beads and mouse IFN-γ or BSA concentrations ranging from 26.7 pg/mL to 26.7 μg/mL (one concentration per decade) in PBST. All samples are mixed for 17 hours. For each MC, coverslip is treated with 0.01% w/v poly-l-lysine solutions (Sigma-Aldrich) for 5 minutes prior to sample delivery. All MCs are left to settle for one hour before imaging.
Computational imaging, reconstruction, and sensing
After loading the MC, the workflow of QLAB sensing is shown in Figure 2b. For ease of job queuing, reconstructions are performed on the High Performance Computing services at the University of Arizona with 28 cores and 192 GB RAM. However, we have also performed the reconstructions on laptop computers. The low-resolution (LR) holograms from the 15 different LEDs are each divided into 5 × 7 partially overlapping patches for computational efficiency and to allow for different computational focusing distances (z2) to account for any slight tilt between the MC and image sensor. A PSR technique optimized for small-target sensing is used to synthesize a high-resolution (HR) hologram for each patch using a parallel computing approach 12,13. A cardinal-neighbor regularization method12,13 with a regularization weight of 200 is used. The reconstructed image is obtained by back-propagating the HR holograms to the sample plane. 1 Twin image artifacts are suppressed to enhance SNR using previously described methods. 3,12,13
The back-propagation distance is chosen by a two-stage autofocusing algorithm. First, a routine based on the Brenner gradient provides a coarse focus for the majority of beads in each patch. The Brenner gradient measures the difference between a pixel and a neighbor that is typically two pixels away36. Here, a distance of eight pixels is used to account for our PSR factor of four.13 For each individual feature found in each reconstructed patch, a fine focus is then found by scanning across a 25-μm z2 range around the coarse focus with 1 μm step size. The fine focus z2 is chosen based on maximum SNR for that feature.
To generate a complete image, the HR reconstructions can be stitched together to obtain a HR image of all beads in the full FOV. Binary thresholding is then applied and all the bead monomers and clusters are extracted by finding connected features. To compute the bound ratio, a custom automated counting routine decides the number of beads in each feature based on its size and eccentricity.
For each sample, the total amount of time for all data processing is approximately one hour. The bulk of this time is in synthesizing PSR holograms and reconstructing many planes in the imaging volume during the auto-focus procedure. We use standard CPU algorithms, as opposed to a parallelized GPU implementation, which has been shown to improve processing speeds by about an order of magnitude.37 After reconstructing an image, the time to automatically find and classify the features and calculate the bound ratio is less than 5 minutes.
Results and Discussion
High-speed pixel superresolution and motion blur
The average peak SNR (APSNR)12,13 of all features in the FOV relative to the background is used to evaluate imaging performance. Because the beads in these motion blur experiments are not functionalized, there is only a small amount of (nonspecific) binding. There are several effects that could limit APSNR: motion blur due to Brownian motion, motion blur due to sedimentation, low light levels due to short integration times or large z1, and limited optical coherence that results in limited resolution.1 The relative contributions of these effects are compared in Figure 3, and some characteristic images are shown in Supporting Figure S4. For ton < 120 ms, performance is limited by low light levels, whereas for ton > 120 ms, performance is limited by motion blur. Images of beads undergoing 3D motion exhibit slightly lower SNR than 2D motion for most values of ton.
Figure 3:
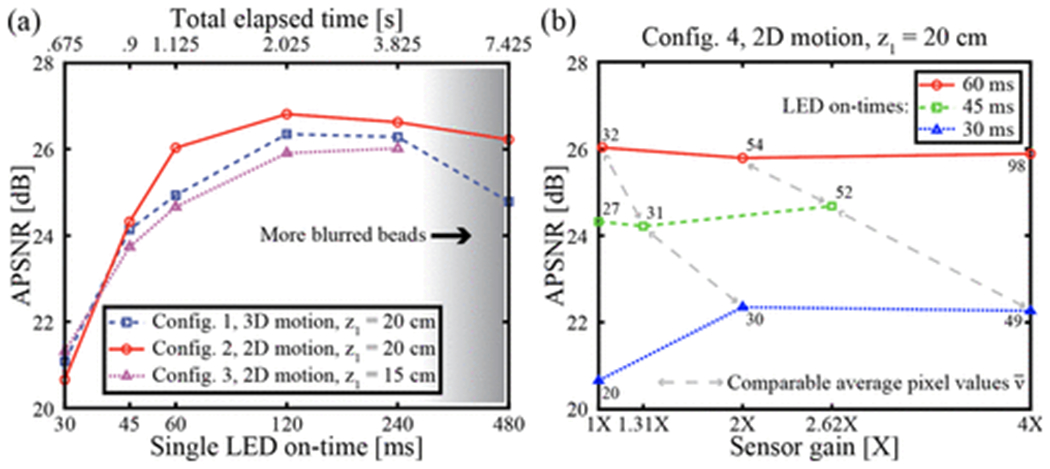
Imaging performance for beads undergoing Brownian motion. (a) Performance for the three system configurations given in Table 1, plotted on a log-log scale. APSNR is limited by brightness for small ton, and by motion blur for large ton. Each point represents one reconstructed image. (b) Imaging performance at different gain levels. Each line connected by gray arrows has comparable average pixel values (brightness). The numbers next to each point are the average pixel values in the image. Each point represents one reconstructed image.
The diffusivity of spherical beads in liquid can be modeled by the Stokes-Einstein equation: 38
| (2) |
where kB is the Boltzmann constant, T = 298 K, μ = 0.89 mPa s is the dynamic viscosity of water, and d =2 μm is the bead diameter. The mean displacement over time ttot is where N is the dimensionality of Brownian motion.39 For a 2-μm bead under a LED on-time of ton = 120 ms (tot = 2.02 s), the mean displacements for 2D and 3D Brownian motion are 1.41 μm and 1.73 μΜ, respectively. These values are close to the bead diameter and explain why motion blur can limit SNR performance for larger tan.
The impact of sedimentation in 3D motion can be predicted using Stokes’ law for bead terminal velocity , where g is the gravity of Earth, = 1055 kg/m3 is the bead density, and = 997 kg/m3 is the water density. For our beads, = 0.14 μm/s, so 12 s are needed for the displacement due to sedimentation to equal that of 3D Brownian motion when = 120 ms. Brownian motion has a more significant effect than sedimentation for all LED on-times tested here.
To investigate whether performance at short ton values could be improved, we explored two methods of increasing image brightness. In the first method, image brightness was increased by reducing z1 (configuration 3 in Table 1), however this resulted in reduced performance, as as shown in Figure 3a. This could perhaps be due to reduced spatial coherence or worse frame shift estimation in the PSR procedure.1
The second method of increasing image brightness we attempted was to increase the gain setting of the image sensor. As shown in Figure 3b, increased gain provided a moderate improvement for the lowest values of ton: 30 ms and 45 ms, however an increased gain could never provide better performance than that of ton = 60 ms at unity gain. For images of comparable brightness achieved by balancing ton with the gain setting, larger gain values always resulted in lower SNR. This is expected as gain amplifies signal and noise together, while longer illuminations amplify SNR. Based on these results, the best imaging system parameters are z1 = 20 cm and ton = 120 ms for both 2D and 3D motion, providing APSNR values of 26–27 dB. These parameters were used for all following results.
Feature identification and classification
Figure 4a shows the full FOV PSR reconstruction for > 104 2-μm B-coated beads. Our microscope offers a FOV > 12.5 mm2 with high SNR and good resolution as shown in the insert of Figure 4a. Binary thresholding is illustrated in Figure 4c and d to extract bead features in the sensor FOV. The feature sizes and eccentricities of 18747 features are shown in Figure 4b, where a clear monomer-cluster boundary is drawn. This sample contains 60 ng/mL of NA and 0.01% 2-μm B-beads in PBST. Features below the monomer-cluster boundary are classified as monomers and features above are classified as clusters. For clusters, their feature sizes are used to infer the number of beads in each cluster, which is used in the automated calculation of bound ratio. In Figure 4b, the coefficient of variation in feature size is 7.8%, which is consistent with the vendor’s 10% coefficient of variation specification. The boundary line was initially drawn by hand, but was then optimized separately for each sample using the built-in Matlab classifier function fitcsvm.
Figure 4:
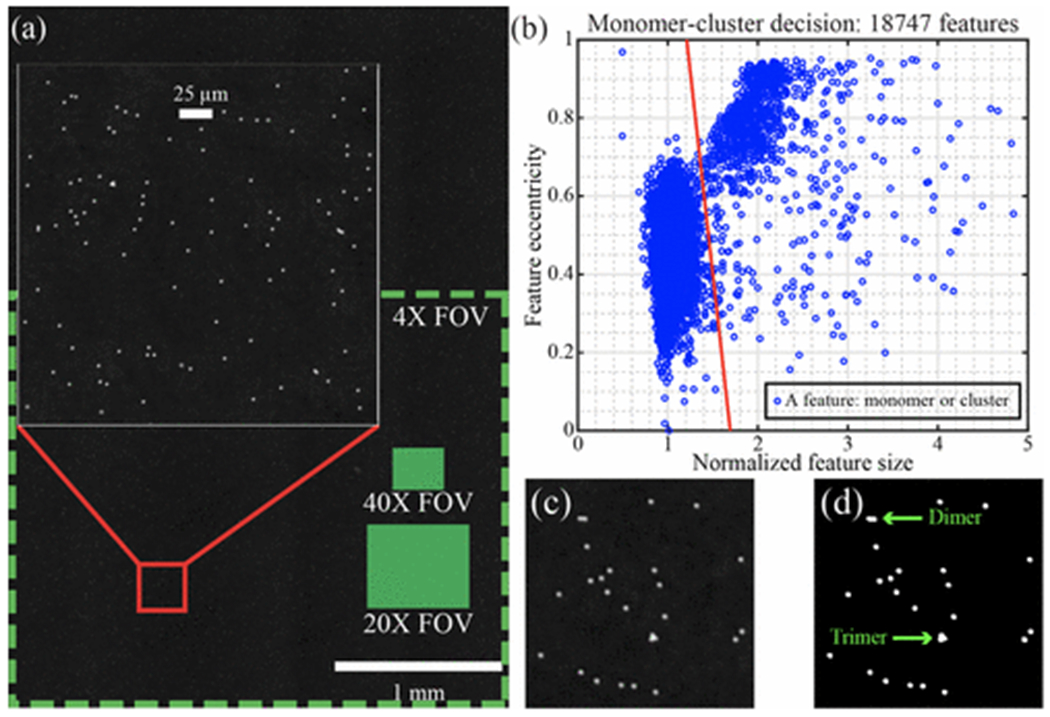
Quantifying agglutination. (a) Full FOV image of 2-μm beads undergoing Brownian motion. The large inset is a zoomed region demonstrating high SNR imaging. Green boxes show the fields of view for typical conventional microscope objectives. (b) Scatter plot of a single sample with 18747 features, exhibiting a clear monomer-cluster boundary (red line). (c) A small reconstructed region before thresholding. (d) The same region after binary thresholding.
A comparison of LFHM to conventional brightfield and darkfield imaging using a 4× microscope objective is provided in Supporting Figure S5. These images show that LFHM imaging performs significantly better than the 4× objective in both resolution and SNR. Additionally, LFHM provides a FOV that is about 1.75 times greater than this conventional microscope and objective (Figure 4a). In our LFHM, the resolution is better than 1 μm,13 making the space-bandwidth product > 1.5 × 107, which is significantly greater than that of the conventional 4× objective with numerical aperture (NA) 0.13 and space-bandwidth product FOV/[ƛ/(2NA)]2 = 1.7 × 106. Conventional microscope images with higher magnifications (40×) and smaller fields of view (0.0753 mm2) were used to validate the monomer / cluster decision threshold.
Incubation protocols and test time
NA binding curves for two incubation protocols are shown in Figure 5a. Mixing for 17 hours leads to more agglutination in NA solutions with concentrations ranging from 1–1000 ng/mL. However, at higher NA concentrations, similar agglutination levels are observed for both 2 hours and 17 hours of mixing. At very high NA concentrations, the bound ratio falls due to NA molecules occupying most of the B sites on beads faster than bead-to-bead binding can occur. The total number of beads observed are plotted in Figure 5b, where the bead concentration is consistent for all NA concentrations under both protocols, with a coefficient of variation of 26% for the 2 hour mixing time and 31% for the 17 hour mixing time. This indicates that the the change in signal shown in Figure 5a is a result of changes in bead agglutination and not a result of different numbers of beads being imaged. In order to maximize agglutination at low concentrations, all remaining results use a 17-hour mixing time.
Figure 5:
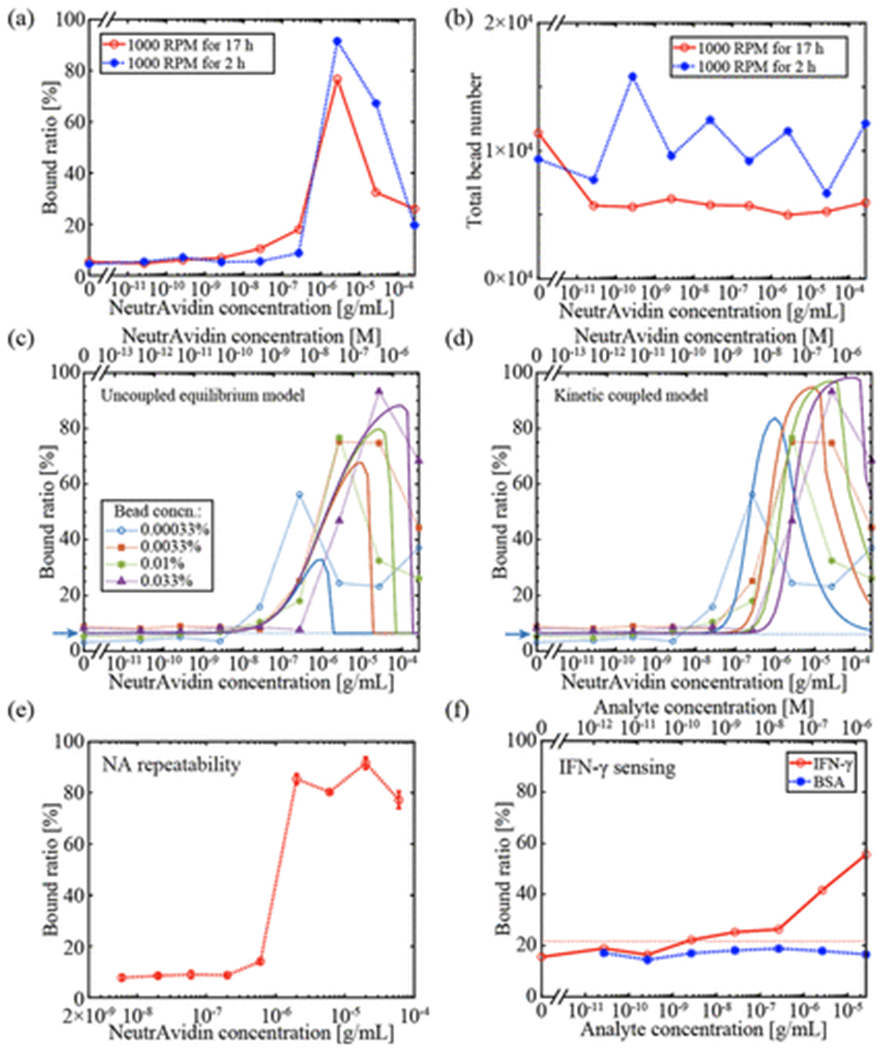
QLAB sensor results. (a) Binding results for two different mixing times. The longer (17 hour) mixing time results in more binding for NA concentrations less than 1 μg. (b) Total numbers of beads observed in the MCs are consistent for all samples for both mixing times. (c), (d) NA binding curves for various bead concentrations. Dotted lines are experimental data and solid lines are fitted based on (c) an uncoupled equilibrium model or (d) a coupled kinetic model. The blue arrow and dashed line represent the LOD threshold for the 0.00033% bead concentration. (e) Batch-to-batch repeatability of the bound ratio at each NA concentration. Each data point corresponds to the mean of three repeats of mixing a particular NA concentration with beads at 0.01% w/v concentration. The error bars are the standard deviations. (f) IFN-γ sensing results with BSA as a negative control. At high concentrations of mouse IFN-γ, the bound ratio exhibits an observable increase while no significant binding above the NSB level is observed for BSA. The red dashed line represents the LOD threshold. Except for panel (e), each point in every panel corresponds to a single image.
For the QLAB sensing experiments performed here, the total time consists of the 17 hours of mixing, 1 hour for sample sedimentation, and ~1 hour for imaging and computational reconstruction. Currently, the assay time is comparable to ELISA. However, the sensor response for 2 hours of mixing in Figure 5a indicates that significantly shorter incubation times may be acceptable for some applications where a higher limit of detection (LOD) is acceptable. Other mixing protocols, such as on-chip mixing methods,40 could be used to significantly reduce incubation time without sacrificing LOD.
NeutrAvidin sensing with biotin coated beads
Binding curves for NA molecules are shown in Figure 5c and d where the experimental data is represented by points connected by dotted lines for four different B-coated bead concentrations. For lower bead concentrations, the binding curves shift towards lower NA concentrations, and in general, lower LODs are found for lower bead concentrations. However, these lower LODs come at the expense of reduced peak bound ratio and reduced dynamic range. The LOD is limited by non-specific binding (NSB), which is present even without any NA molecules. For the 0.00033% bead concentration, we estimate the LOD by assuming all observed binding for the three lowest NA concentration samples (0, 26.7, and 267 pg/mL) is NSB. The LOD threshold is estimated as41 μNSB + 3σNSB = 6.7%, where μNSB = 4.0% is the average NSB in these three samples and σNSB = 0.9% is the standard deviation. The first NA concentration with observed bound ratio exceeding this threshold is 26.7 ng/mL, which has a bound ratio of 15.9%, indicating that the QLAB sensor LOD is below 27 ng/mL for this bead concentration. Note that this is a conservative estimate of the LOD as we have not interpolated between data points and we have based the threshold calculation on some samples with nonzero analyte concentration, which will exhibit slightly more binding than truly blank samples.
The peaks in the sensor response curves mean that there is a two-fold degeneracy in the NA concentration that leads to a particular sensor response. If this degeneracy can be resolved by prior knowledge of the sample, e.g., the maximum clinically-relevant concentration, then the QLAB sensor has a monotonic dynamic range of ~2 orders of magnitude. The full dynamic range of the sensor response is ~4 orders of magnitude, including both the rising and falling regions of the curve. To utilize this full dynamic range, a two-step sensing protocol could be employed where, after an initial binding measurement, the sample is mixed with a known, moderate concentration of analyte to see if this generates more binding. If it does, then the initial measurement corresponds to a point on the rising slope (lower NA) concentration region. Otherwise, the initial measurement corresponds to a high-NA concentration.
To understand the shapes of these curves, we consider two reactions:
| (3) |
| (4) |
where N represents a free NA molecule, B is a biotin group attached to a bead, NB is a NA molecule bound to a biotin group on a bead, M represents a monomer (single bead), and D represents a dimer (two beads bound to each other). Other reactions for larger bead clusters can also be considered, however we find that much of the experimental results can be explained without considering larger clusters.
A particularly simple model that explains some of the experimental results is to treat the two reactions as uncoupled and assume that reaction (4) is much slower than reaction (3) because of the large size of the beads compared to N molecules. In this case, in equilibrium (t → ∞), the concentration of NB is,
| (5) |
where K1 ≈ 1014 M−1 is the biotin-NeutrAvidin association constant,42 CN(∞) is the equilibrium concentration of N, and CB(∞) is the equilibrium concentration of B. Based on the conservation of molecules, CNB(∞) can be solved for in terms of the initial concentrations:
| (6) |
The value of CB(0) is the product of the bead concentration and the avidin binding capacity of the beads, which is provided by the manufacturer as 2.40 × 104 molecules per bead. The total concentration of beads at any time is .
The same general approach can be applied to reaction (4):
| (7) |
We assume an equilibrium constant K2 = αp1, where α is a fitting parameter that accounts for the rate of collisions between beads as well as any activation energy necessary to form a bond, and is a factor representing the probability that the point of collision between two beads involves a free B group on one bead and a NB group on the other bead. In addition to α, this model includes a second fitting parameter for the bound ratio due to NSB, RNSB = 6.38%, which is the mean of the experimental binding ratios for the lowest three concentrations (including the zero concentration) of each of the four bead concentrations, (i.e., the mean of 12 different values). We assume that nonspecifically bound beads do not participate in reaction 4, and thus . In this model, the bound ratio is calculated as .
The least-squares fit of this model in log space to the experimental data is shown in Figure 5c, where α = 1.7 × 103 M−1 with a 95% confidence interval of [4.9 × 102 M−1,5.8 × 103 M−1]. This model accurately captures the progression of local maxima for the different bead concentrations. However, the overall fit is not particularly good (coefficient of determination R2 and adjusted R2 values are both 0.23) and there are two features of the experimental data that are not well explained: the relatively gradual drop in bound ratio for very high NA concentrations and the relative order of the four curves for g/mL.
To explain these features of the experimental data, we fit the results to a kinetic model where the reactions are coupled and we further consider that stable bead-to-bead binding may require multiple bonds between beads, represented by a valency number u. In this case, the relevant reactions are:
| (8) |
| (9) |
The coupled ordinary nonlinear differential equations describing the evolution of the concentrations are:
| (10) |
| (11) |
| (12) |
| (13) |
| (14) |
where is the probability that v available biotin groups and v NB groups are involved in a collision between two beads. Because the B and NB groups are anchored to the beads, we have assumed that the kinetics of reaction (9) are not based on its stoichiometry alone. We use the Matlab function ode45 to numerically solve this system of coupled ODEs over the 17-hour mixing time. Four fitting parameters are used to simultaneously fit all curves to the data: k1f, k2f, k2b, and v. The parameter k1b is directly determined by k1f according to k1b = k1f/K1. The result of this nonlinear least-squares fit is shown in Figure 5d, where the best-fit values with 95% confidence intervals are: k1f = 2.9 × 103 [4.2 × 102, 2.0 × 104] M−1s−1, k2f = 1.2 × 10−12 [1.5 × 10−19, 9.4 × 10−6] M−1s−1, k2b = 5.8 × 10−6 [2.8 × 10−7,1.2 × 10−4] s−1, and v = 2.4 [1.5, 3.4]. The overall fit is better in this kinetic model (R2 = 0.61, adjusted R2 = 0.57) than in the previous uncoupled model. Because this kinetic model treats the two reactions as competitively coupled, it can reproduce the gradual drop in bound ratio for high NA concentrations, where some bead-to-bead binding occurs before all beads are completely coated with NA. The valency factor v > 2 enables the model to reproduce the order of the four curves in the vicinity of CN(0) ≈ 10−7 g/mL, which indicates that multiple bonds may be necessary to keep beads bound. Perhaps in the future, lower valency numbers may be found for less vigorous mixing protocols, although that is expected to increase the assay time. We also note that the NA binding rate constant k1f is a couple orders of magnitude lower than the 105–107 M−1s−1 found in surface binding studies.43 These fitted models explain some of the key features of our data, but the fits are not perfect and we expect that more complex models together with more experimental data may provide further insight in the future.
Repeatability in NeutrAvidin sensing
One measure of repeatability is the total number of beads observed in the chamber in each experiment. Stability in total bead counts reflects the quality of mixing and dilution during sample preparation. Many reasons could lead to variations in total bead count, such as inaccuracy of the pipette, slightly different dilutions prior to observation, and different numbers of beads stuck to the side walls of centrifuge tubes due to tube inconsistency. For the experiments plotted in Figure 5c and d, bead count statistics are given in Table 2. Note that the 0.00033% and 0.0033% samples are imaged without dilution, while the 0.01% samples are diluted three times and 0.033% samples are diluted 10 times before imaging, which is why the total numbers of beads are similar for the three largest bead concentrations. The number of beads observed was ~3× lower than expected for the 0.01% concentration. For each of the four bead concentrations, the number of beads within the field of view varies between 8–31% among repeats (Table 2), indicating moderate repeatability in our bead solution preparation.
Table 2:
Average and standard deviation of the total number of beads observed in the MCs across all NA concentrations. Data corresponds with the experiments plotted in Figure 5c and d, and thus there are 9 data points for each bead concentration. These data indicate the repeatability of the bead sample preparation.
| Bead concentration | Total number of beads |
|---|---|
| 0.00033% | 1607 ± 228 |
| 0.0033% | 19447 ± 1646 |
| 0.01% | 6300 ± 1945 |
| 0.033% | 21011 ± 1765 |
The repeatability in the bound ratio measurements, which is the primary output of our sensor, is quantified in Figure 5e, where three repeats of each NA concentration were performed. The error bars for most of the points are shorter than the points themselves. Across all NA concentrations, the average coefficient of variation among the repeats is 6.5%. For these experiments, the observed bead numbers are shown in Supporting Figure S6, and are also consistent. The full FOV image for a sample containing 2 μ/mL of NA and 0.01% 2-μm B-beads in PBST exhibits a bound ratio of 80.39%, as shown in Supporting Figure S7.
Chip-to-chip variations are shown in Table 3. The variations in both bound ratio and total bead number are significantly smaller than the batch-to-batch variations. This indicates that the bead count variability primarily stems from sample preparation, dilution, and mixing rather than inconsistencies in the sizes of the MCs, or how the MCs are loaded.
Table 3:
Chip-to-chip repeatability. The bound ratios and bead counts for three chips are shown, together with the means and standard deviations for the 3 repeated experiments. The coefficients of variation are 2.4% in bound ratio and 4.8% in bead number. All experiments are for 600 ng/mL NA concentration and 0.01% w/v bead concentration.
| MC | Bound ratio (%) | Total bead number |
|---|---|---|
| 1 | 15.09 | 17781 |
| 2 | 14.68 | 18770 |
| 3 | 15.39 | 19590 |
| 1–3 | 15.05 ± 0.36 | 18714 ± 906 |
Mouse IFN-γ sensing
The sensor responses to various mouse IFN-γ and BSA concentrations are shown in Figure 5f. For these experiments, the observed bead numbers are shown in Supporting Figure S8, and are also consistent for both mouse IFN-γ and BSA. IFN-γ is a dimerized cytokine, so it is expected that two antibodies can bind to a single dimerized molecule. As a protein molecule that is not expected to cause binding, BSA is used as a negative control. When anti-mouse-IFN-γ coated beads are mixed with mouse IFN-γ, bound ratios significantly higher than the NSB level are observed. No significant binding above the NSB level is observed for BSA. The binding capacity for these beads is 8.51 × 104 molecules per bead, as reported by the manufacturer, which is the same order of magnitude as the B-beads used earlier. We estimate the LOD by assuming all observed binding for the three lowest mouse IFN-γ concentration samples (0, 26.7, and 267 pg/mL) is NSB. The LOD threshold is estimated as μNSB + 3σNSB = 22.1%, where μNSB = 17.0% is the average NSB in these three samples and σNSB = 1.7% is the standard deviation. The first mouse IFN-γ concentration with observed bound ratio exceeding this threshold is 2.67 ng/mL, which has a bound ratio of 22.2%, indicating that the QLAB sensor LOD is below 3 ng/mL for this bead concentration. Like the NA LOD discussed above, this is a conservative estimate of the LOD as we have not interpolated between data points and we have based the threshold calculation on some samples with nonzero analyte concentration, which will exhibit slightly more binding than truly blank samples. Including the negative control BSA samples as additional measurements of blank variability results in the same <3 ng/mL LOD value. Note that NSB levels are significantly larger than for the NA sensing results. A possible reason is that these beads are magnetic (our vendor only supplies magnetic anti-mouse-IFN-γ beads). Due to their higher density compared to polystyrene beads and potential for magnetization, magnetic beads tend to agglomerate more. The QLAB sensor exhibits higher bound ratio for higher mouse IFN-γ concentrations, demonstrating a monotonic dynamic range of ≥4 orders of magnitude.
Conclusions
We demonstrate a high-speed lens-free holographic microscope with the ability to image > 104 2-μm beads undergoing Brownian motion in liquid. The QLAB sensor automatically measures the distribution of bead cluster sizes based on the sizes and eccentricities of all features in the images. In the presence of a target analyte, the binding between beads coated with capture agents is quantified in solution. We find a LOD of < 27 ng/mL (450 pM) for NA protein molecules and < 3 ng/mL (200 pM) for mouse INF-γ molecules. These LOD values are below the clinically-relevant levels of a number of different protein disease biomarkers, e.g., prostate-specific antigen,44 or antibodies in nasal secretions,45 which is relevant to COVID-19 testing,46 making the QLAB sensor applicable to current sensing tasks. The LOD is limited by NSB. In the future, alternative mixing, filtration,47 or buffer chemistries could reduce nonspecific binding and improve the LOD. More advanced binding models together with a wider range of experimental data could also help to further elucidate and confirm the chemical binding mechanism we propose here. The dynamic range of the QLAB sensor is 2–4 orders of magnitude, depending on sensing protocol. The ability to sense subtle changes in bead agglutination using simple, cost-effective, and compact hardware makes the QLAB sensor particularly promising for point-of-care protein biomarker diagnostic applications.
Supplementary Material
Acknowledgement
This material is based upon High Performance Computing (HPC) resources supported by the University of Arizona TRIF, UITS, and Research, Innovation, and Impact (RII) and maintained by the UArizona Research Technologies department. The authors are grateful for the financial support of the University of Arizona and the University of Technology and Research Initiative Fund. Colin Potter acknowledges the support of the University of Arizona’s NIH-funded Translational Research in Alzheimer’s Disease and Related Dementias training grant T32AG061897-2.
Footnotes
Supporting information
The supporting information is available free of charge (Xiong_McLeod_SI.pdf).
LFHM platform photograph and schematic; circuit board previews for the high speed LED array; circuit schematic for the high speed LED array; characteristic images of beads undergoing Brownian motion with different levels of motion blur; comparisons between LFHM and conventional microscope images; bead counts for NA batch-to-batch repeatability measurements; full field of view reconstruction; bead counts for IFN-γ measurements (PDF).
References
- (1).McLeod E; Ozcan A Unconventional methods of imaging: computational microscopy and compact implementations. Reports on Progress in Physics 2016, 79, 076001. [DOI] [PubMed] [Google Scholar]
- (2).Tseng D; Mudanyali O; Oztoprak C; Isikman SO; Sencan I; Yaglidere O; Ozcan A Lensfree microscopy on a cellphone. Lab on a Chip 2010, 10, 1787–1792. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (3).McLeod E; Dincer TU; Veli M; Ertas YN; Nguyen C; Luo W; Greenbaum A; Feizi A; Ozcan A High-throughput and label-free single nanoparticle sizing based on time-resolved on-chip microscopy. ACS nano 2015, 9, 3265–3273. [DOI] [PubMed] [Google Scholar]
- (4).McLeod E; Wei Q; Ozcan A Democratization of nanoscale imaging and sensing tools using photonics. Analytical chemistry 2015, 87, 6434–6445. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (5).Kesavan SV; Momey F; Cioni O; David-Watine B; Dubrulle N; Shorte S; Sulpice E; Freida D; Chalmond B; Dinten J-M, et al. High-throughput monitoring of major cell functions by means of lensfree video microscopy. Scientific reports 2014, 4, 5942. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (6).Jin G; Yoo I-H; Pack SP; Yang J-W; Ha U-H; Paek S-H; Seo S Lens-free shadow image based high-throughput continuous cell monitoring technique. Biosensors and Bioelectronics 2012, 38, 126–131. [DOI] [PubMed] [Google Scholar]
- (7).Tian L; Li X; Ramchandran K; Waller L Multiplexed coded illumination for Fourier Ptychography with an LED array microscope. Biomedical optics express 2014, 5, 2376–2389. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (8).Nguyen T; Xue Y; Li Y; Tian L; Nehmetallah G Deep learning approach for Fourier ptychography microscopy. Optics express 2018, 26, 26470–26484. [DOI] [PubMed] [Google Scholar]
- (9).Zheng G; Horstmeyer R; Yang C Wide-field, high-resolution Fourier ptychographic microscopy. Nature photonics 2013, 7, 739–745. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (10).Hardie RC; Barnard KJ; Bognar JG; Armstrong EE; Watson EA High-resolution image reconstruction from a sequence of rotated and translated frames and its application to an infrared imaging system. Optical Engineering 1998, 37. [Google Scholar]
- (11).Bishara W; Su T-W; Coskun AF; Ozcan A Lensfree on-chip microscopy over a wide field-of-view using pixel super-resolution. Optics express 2010, 18, 11181–11191. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (12).Xiong Z; Engle I; Garan J; Melzer JE; McLeod E Optimized computational imaging methods for small-target sensing in lens-free holographic microscopy. Optical Diagnostics and Sensing XVIII: Toward Point-of-Care Diagnostics. 2018; p 105010E. [Google Scholar]
- (13).Xiong Z; Melzer JE; Garan J; McLeod E Optimized sensing of sparse and small targets using lens-free holographic microscopy. Optics express 2018, 26, 25676–25692. [DOI] [PubMed] [Google Scholar]
- (14).Mudanyali O; Bishara W; Ozcan A Lensfree super-resolution holographic microscopy using wetting films on a chip. Optics express 2011, 19, 17378–17389. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (15).Su T-W; Choi I; Feng J; Huang K; McLeod E; Ozcan A Sperm trajectories form chiral ribbons. Scientific reports 2013, 3, 1–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (16).Fang Y; Yu N; Jiang Y Super-Resolution Lensless Imaging of Cells Using Brownian Motion. Applied Sciences 2019, 9, 2080. [Google Scholar]
- (17).Crowther JR The ELISA guidebook; Springer Science & Business Media, 2001; Vol. 149. [Google Scholar]
- (18).Lequin RM Enzyme immunoassay (EIA)/enzyme-linked immunosorbent assay (ELISA). Clinical chemistry 2005, 51, 2415–2418. [DOI] [PubMed] [Google Scholar]
- (19).Rød AMK; Harkestad N; Jellestad FK; Murison R Comparison of commercial ELISA assays for quantification of corticosterone in serum. Scientific reports 2017, 7, 1–5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (20).Wolpaw BJ; Mathews C; Chopra M; Hardie D; Lurie MN; Jennings K Diagnosis and counselling of patients with acute HIV infection in South Africa. Sexually transmitted infections 2011, 87, 71–72. [DOI] [PubMed] [Google Scholar]
- (21).Koczula KM; Gallotta A Lateral flow assays. Essays in biochemistry 2016, 60, 111–120. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (22).Wei Q; McLeod E; Qi H; Wan Z; Sun R; Ozcan A On-chip cytometry using plasmonic nanoparticle enhanced lensfree holography. Scientific reports 2013, 3, 1699. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (23).Colle F; Vercruysse D; Peeters S; Liu C; Stakenborg T; Lagae L; Del-Favero J Lens-free imaging of magnetic particles in DNA assays. Lab on a Chip 2013, 13, 4257–4262. [DOI] [PubMed] [Google Scholar]
- (24).Bourquin Y; Reboud J; Wilson R; Zhang Y; Cooper JM Integrated immunoassay using tuneable surface acoustic waves and lensfree detection. Lab on a chip 2011, 11, 2725–2730. [DOI] [PubMed] [Google Scholar]
- (25).Xu X; Jin M; Yu Z; Li H; Qiu D; Tan Y; Chen H Latex agglutination test for monitoring antibodies to avian influenza virus subtype H5N1. Journal of clinical microbiology 2005, 43, 1953–1955. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (26).Sato Y; Toma H; Kiyuna S; Shiroma Y Gelatin particle indirect agglutination test for mass examination for strongyloidiasis. Transactions of the Royal Society of Tropical Medicine and Hygiene 1991, 85, 515–518. [DOI] [PubMed] [Google Scholar]
- (27).Mrazkova J; Malinovska L; Wimmerova M Microscopy examination of red blood and yeast cell agglutination induced by bacterial lectins. PLoS ONE 2019, 14, e0220318. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (28).You DJ; Geshell KJ; Yoon J-Y Direct and sensitive detection of foodborne pathogens within fresh produce samples using a field-deployable handheld device. Biosensors and Bioelectronics 2011, 28, 399–406. [DOI] [PubMed] [Google Scholar]
- (29).Fronczek CF; You DJ; Yoon J-Y Single-pipetting microfluidic assay device for rapid detection of Salmonella from poultry package. Biosensors and Bioelectronics 2013, 40, 342–349. [DOI] [PubMed] [Google Scholar]
- (30).Heinze BC; Gamboa JR; Kim K; Song J-Y; Yoon J-Y Microfluidic immunosensor with integrated liquid core waveguides for sensitive Mie scattering detection of avian influenza antigens in a real biological matrix. Analytical and Bioanalytical Chemistry 2010, 398, 2693–2700. [DOI] [PubMed] [Google Scholar]
- (31).Wu Y; Ray A; Wei Q; Feizi A; Tong X; Chen E; Luo Y; Ozcan A Deep learning enables high-throughput analysis of particle-aggregation-based biosensors imaged using holography. ACS Photonics 2018, 6, 294–301. [Google Scholar]
- (32).De Jager W; te Velthuis H; Prakken BJ; Kuis W; Rijkers GT Simultaneous detection of 15 human cytokines in a single sample of stimulated peripheral blood mononuclear cells. Clin. Diagn. Lab. Immunol 2003, 10, 133–139. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (33).Cretich M; Daaboul GG; Sola L; Ünlü MS; Chiari M Digital detection of biomarkers assisted by nanoparticles: application to diagnostics. Trends in biotechnology 2015, 33, 343–351. [DOI] [PubMed] [Google Scholar]
- (34).Rissin DM; Kan CW; Campbell TG; Howes SC; Fournier DR; Song L; Piech T; Patel PP; Chang L; Rivnak AJ, et al. Single-molecule enzyme-linked immunosorbent assay detects serum proteins at subfemtomolar concentrations. Nature biotechnology 2010, 28, 595. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (35).Zeng Y; Stokes J; Hahn S; Hoffman E; Katsanis E Activated MHC-mismatched T helper-1 lymphocyte infusion enhances GvL with limited GvHD. Bone marrow transplantation 2014, 49, 1076–1083. [DOI] [PubMed] [Google Scholar]
- (36).Yazdanfar S; Kenny KB; Tasimi K; Corwin AD; Dixon EL; Filkins RJ Simple and robust image-based autofocusing for digital microscopy. Optics express 2008, 16, 8670–8677. [DOI] [PubMed] [Google Scholar]
- (37).Isikman SO; Bishara W; Sikora U; Yaglidere O; Yeah J; Ozcan A Field-portable lensfree tomographic microscope. Lab on a Chip 2011, 11, 2222–2230. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (38).Edward JT Molecular volumes and the Stokes-Einstein equation. Journal of Chemical Education 1970, 47, 261. [Google Scholar]
- (39).Einstein A On the theory of the Brownian movement. Ann. Phys 1906, 19, 371–381. [Google Scholar]
- (40).Ahmed D; Mao X; Juluri BK; Huang TJ A fast microfluidic mixer based on acoustically driven sidewall-trapped microbubbles. Microfluidics and nanofluidics 2009, 7, 727. [Google Scholar]
- (41).Shrivastava A; Gupta VB Methods for the determination of limit of detection and limit of quantitation of the analytical methods. Chronicles of Young Scientists 2011, 2, 21. [Google Scholar]
- (42).Duan X; Li Y; Rajan NK; Routenberg DA; Modis Y; Reed MA Quantification of the affinities and kinetics of protein interactions using silicon nanowire biosensors. Nature nanotechnology 2012, 7, 401. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (43).Delgadillo RF; Mueser TC; Zaleta-Rivera K; Carnes KA; Gonzalez-Valdez J; Parkhurst LJ Detailed characterization of the solution kinetics and thermodynamics of biotin, biocytin and HABA binding to avidin and streptavidin. PloS one 2019, 14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (44).Stamey TA; Yang N; Hay AR; McNeal JE; Freiha FS; Redwine E Prostate-specific antigen as a serum marker for adenocarcinoma of the prostate. New England Journal of Medicine 1987, 317, 909–916. [DOI] [PubMed] [Google Scholar]
- (45).Kirkeby L; Rasmussen TT; Reinholdt J; Kilian M Immunoglobulins in nasal secretions of healthy humans: structural integrity of secretory immunoglobulin A1 (IgA1) and occurrence of neutralizing antibodies to IgA1 proteases of nasal bacteria. Clin. Diagn. Lab. Immunol 2000, 7, 31–39. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (46).Ma H; Zeng W; He H; Zhao D; Yang Y; Jiang D; Zhou P; Qi Y; He W; Zhao C, et al. COVID-19 diagnosis and study of serum SARS-CoV-2 specific IgA, IgM and IgG by chemiluminescence immunoanalysis. medRxiv 2020, [Google Scholar]
- (47).Gossett DR; Weaver WM; Mach AJ; Hur SC; Tse HTK; Lee W; Amini H; Di Carlo D Label-free cell separation and sorting in microfluidic systems. Analytical and bioanalytical chemistry 2010, 397, 3249–3267. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


