Soft-Tissue Imaging in Low-Dose, C-Arm Cone-Beam CT Using Statistical Image Reconstruction

Abstract

C-arm cone-beam CT (CBCT) is an emerging tool for intraoperative imaging, but current embodiments exhibit modest soft-tissue imaging capability and are largely constrained to high-contrast imaging tasks. A major advance in image quality is facilitated by statistical iterative reconstruction techniques. This work adapts a general penalized likelihood (PL) reconstruction approach with variable penalties and regularization to C-arm CBCT and investigates performance in imaging of large (>10 mm), low-contrast (<100 HU) tasks pertinent to soft-tissue surgical guidance. Experiments involved a mobile C-arm for CBCT with phantoms and cadavers presenting soft-tissue structures imaged using 3D filtered backprojection (FBP), quadratic, and non-quadratic PL reconstruction. Polyethylene phantoms with various tissue-equivalent inserts were used to quantity contrast-to-noise / resolution tradeoffs in low-contrast (~40 HU) structures, and the optimal reconstruction parameters were translated to imaging an anthropomorphic head phantom with low-contrasts targets and a cadaveric torso. Statistical reconstruction - especially non-quadratic PL variants - boosted soft-tissue image quality through reduction of noise and artifacts (e.g., a ~2-4 fold increase in contrast-to-noise ratio (CNR) at equivalent spatial resolution). For tasks relating to large, low-contrast tissues, even greater gains were possible using non-quadratic penalties and strong regularization that sacrificed spatial resolution in a manner still consistent with the imaging task. The advances in image quality offered by statistical reconstruction present promise and new challenges for interventional imaging, with high-speed computing facilitating realistic application. Careful investigation of performance relative to specific imaging tasks permits knowledgeable application of such techniques in a manner that overcomes conventional tradeoffs in noise, resolution, and dose and could extend application of CBCT-capable C-arms to soft-tissue interventions in neurosurgery as well as thoracic and abdominal interventions.

I. INTRODUCTION

Mobile C-arms are being increasingly used for 3D cone-beam CT (CBCT) surgical guidance, providing navigation in up-to-date images that properly reflect anatomical change as well as a valuable tool for verification of the surgical product.^1–4 While image quality with traditional reconstruction techniques like filtered backprojection (FBP) is sufficient for visualization of high-contrast, bone structures, soft-tissue imaging remains a major challenge due to inherently low contrast relative to fairly high levels of noise and artifact.⁵ The ability to delineate soft tissues in C-arm CBCT would facilitate broader application of high-precision guidance in surgery of the head (e.g., brain lesions), thorax (e.g., mediastinal masses), and abdomen (e.g., liver and kidney tumors);^6–8 improve patient safety through detection of complications within the operating room, such as intracranial hemorrhage or device malplacement; and provide quality assurance, including verification and quantification of the surgical product.

Specific challenges for C-arm CBCT compared to diagnostic CT include non-circular orbits, limited view angles, large scatter-to-primary ratio, reduced detection efficiency, object truncation, and increased electronic noise. FBP presents a classic and well understood tradeoff between spatial resolution and noise, while a growing arsenal of statistical iterative reconstruction approaches offer the potential for higher image quality. By incorporating a statistical model of the imaging chain in combination with regularization, such approaches can overcome conventional noise-resolution tradeoffs, and they can further incorporate prior images (e.g., preoperative planning ⁹) and improve robustness to artifacts. Such characteristics make them attractive to application in interventional imaging. While significantly more computationally intensive, parallelizable implementations on high-speed computer architecture continues to accelerate statistical reconstruction methods to meet the demands of clinical workflow.¹⁰ This work adapts statistical reconstruction (viz., variants of penalized likelihood, PL, estimation) to C-arm CBCT in the context of soft-tissue surgical guidance, seeking to quantify the limits of soft-tissue visualization and the dependency of soft tissue detectability on imaging dose, object contrast, and object size while stressing fair comparison of noise properties at matched spatial resolution.

II. METHODS

Experimental System.

A prototype mobile C-arm system (modified Siemens PowerMobil) with a flat-panel detector (PaxScan 3030+, Varian) was used for volumetric imaging of the phantoms and cadavers. The system has a (15×15×15) cm³ FOV and maximum angular range of 178°. A typical low-dose acquisition involves 200 projections [768×768 pixels (2×2 mode)] at 100 kVp, 40 mAs (1.6 mGy for a head scan, c.f., ~20-60 mGy for diagnostic CT ¹¹). All images were reconstructed with isotropic (0.6×0.6×0.6) mm³ voxels using a GPU implementation (GTX 580, NVIDIA). A separable footprints forward and backprojector (Fig. 2) provided increased accuracy over the commonly used Siddon or distance-driven methods by geometrically computing the “footprint” of each voxel onto the detector grid.¹² Two phantoms were used to study imaging of low-contrast targets: a 15 cm polyethylene “head” cylinder with tissue-equivalent inserts ranging from high-contrast bone (+640 HU contrast with respect to the polyethylene) to low-contrast adipose (−40 HU contrast). A second phantom involved an anthropomorphic head with spherical low-contrast inserts ranging from 110 HU to −30 HU.

Fig. 2:

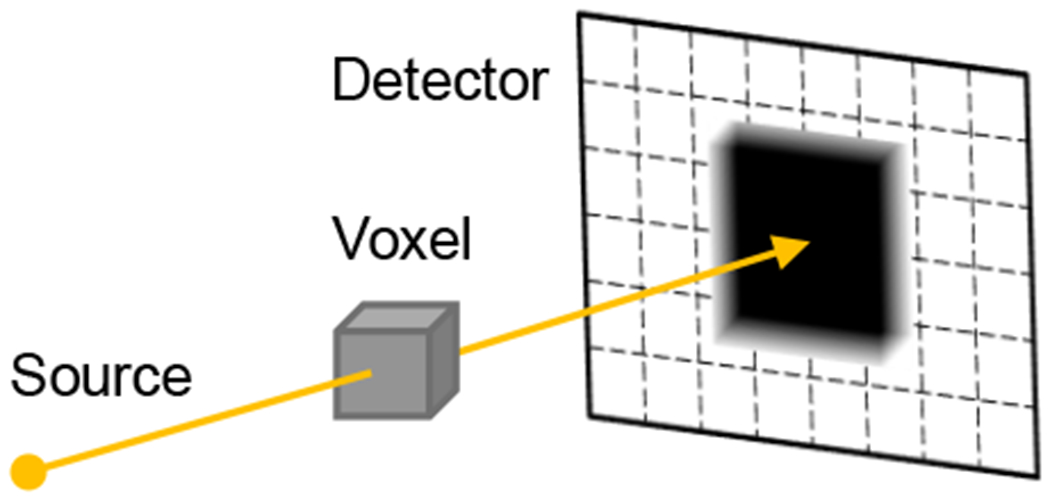
Separable footprints projector. The contribution of each projected voxel onto pixels within the detector can be accurately approximated using separable trapezoidal functions along each detector axis.

Penalized-Likelihood (PL) Estimation.

As shown in Eqs. (1–3), the reconstructed image $\widehat{\mu }$ is solved from measurements y by iterative updates using the parallelizable separable quadratic surrogates (SQS) technique.¹³ The log-likelihood term L maximizes consistency of the reconstructed image with the measurements while simultaneously accounting for the statistics of the measured data. The strength of regularization R(μ) is controlled by the parameter β and depends on the penalty function ψ(x) of neighboring pixel signal differences. While regularization seeks to reduce noise, its behavior depends not only on β, but also the function ψ(x). which can vary from quadratic (PL-Q), to Huber (PL-H), to linear (commonly called total variation, TV ¹⁴) as shown in Fig. 3. The edge-preserving Huber penalty is parameterized by the transition width. δ, below which PL-H applies a quadratic penalty and above which a linear (TV) penalty is applied. Importantly, it is convex, continuous, and differentiable. The parameter δ carries units of the difference in voxel values (attenuation coefficient or Hounsfield Units (HU)).

Fig. 3:

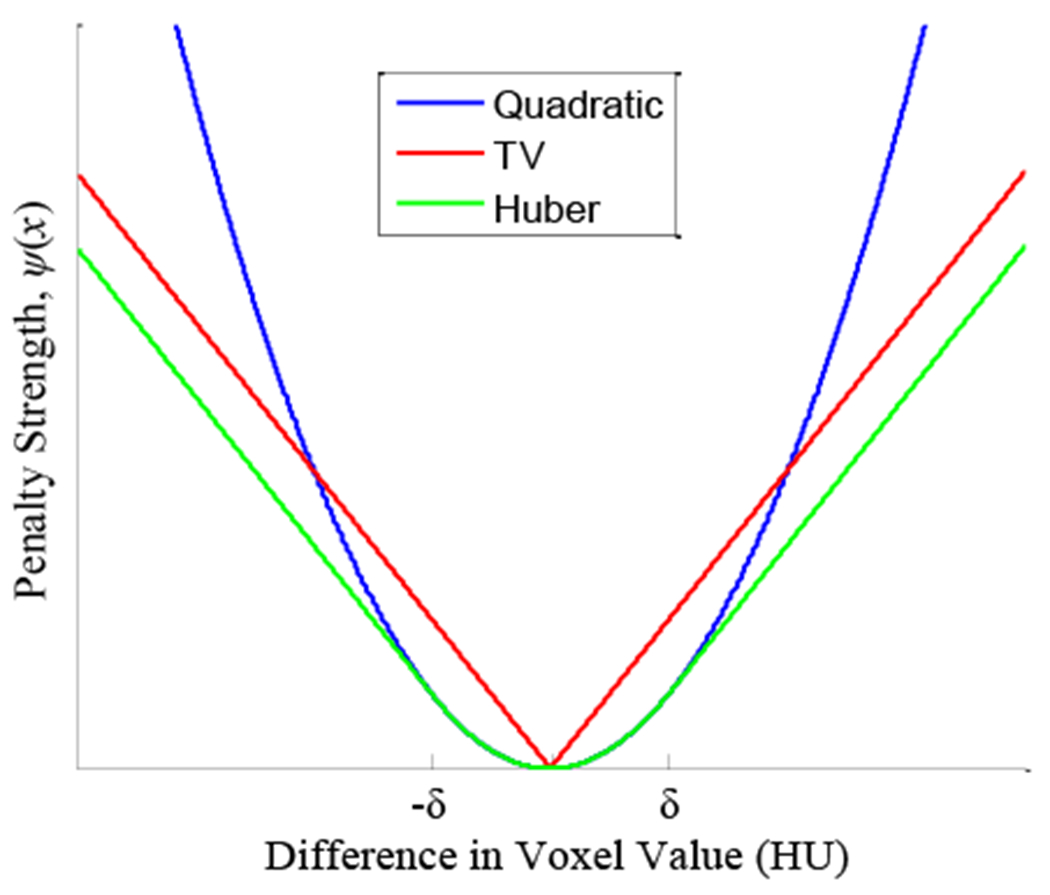
Penalty functions for the quadratic, TV, and Huber variants.

$$\widehat{\mu }=\begin{array}{c}\arg \max \\ \mu \end{array}\log L(\mu ;y)-\beta R(\mu )$$ (1)

$$R(\mu )={\sum }_{i\in I}{\sum }_{j\in N}\psi ({\mu }_i-{\mu }_j)$$ (2)

$${\psi }_Q(x)=\frac{1}{2}{x}^2;{\psi }_H(x)=\{\begin{array}{cc}\frac{1}{2\delta }{x}^2& \left|x\right|\le \delta \\ \left|x\right|-\frac{\delta }{2},& \left|x\right|>\delta \end{array};{\psi }_{TV}(x)=\left|x\right|$$ (3)

Filtered Backprojection.

Fair comparison of imaging performance in FBP and PL requires careful “matching” of spatial resolution or noise - e.g., comparison of contrast-to-noise ratio performed at equivalent spatial resolution, since each approach has parameters allowing free variation (tradeoff) of noise and resolution. Because both FBP and PL can exhibit anisotropic spatial resolution in-plane (x, y) and axially (z), “matching” spatial resolution should be done in a manner that is local (i.e., at a common location in the image over which the image statistics to do not vary) and object-specific (i.e., at a specified level of contrast (difference in voxel values)). Since PL regularization is applied in all directions in a 3D neighborhood of the reconstruction, the apodization “smoothing” kernel in the FBP filtration step should not be limited to a ID filter in the u direction along detector rows (as in typical FBP implementations, where the smoothing filter is only applied in the u direction to mitigate high-frequency noise imparted by the ramp filter). Rather, a 2D apodization kernel should be applied along both the u (row) and v (column) directions (e.g., cosine filter with cutoff frequency f_c in both directions) to provide fair matching of 3D spatial resolution (Fig. 4). This is an important consideration that is often overlooked and is intrinsic to the comparisons of FBP and PL reported below.

Fig. 4:

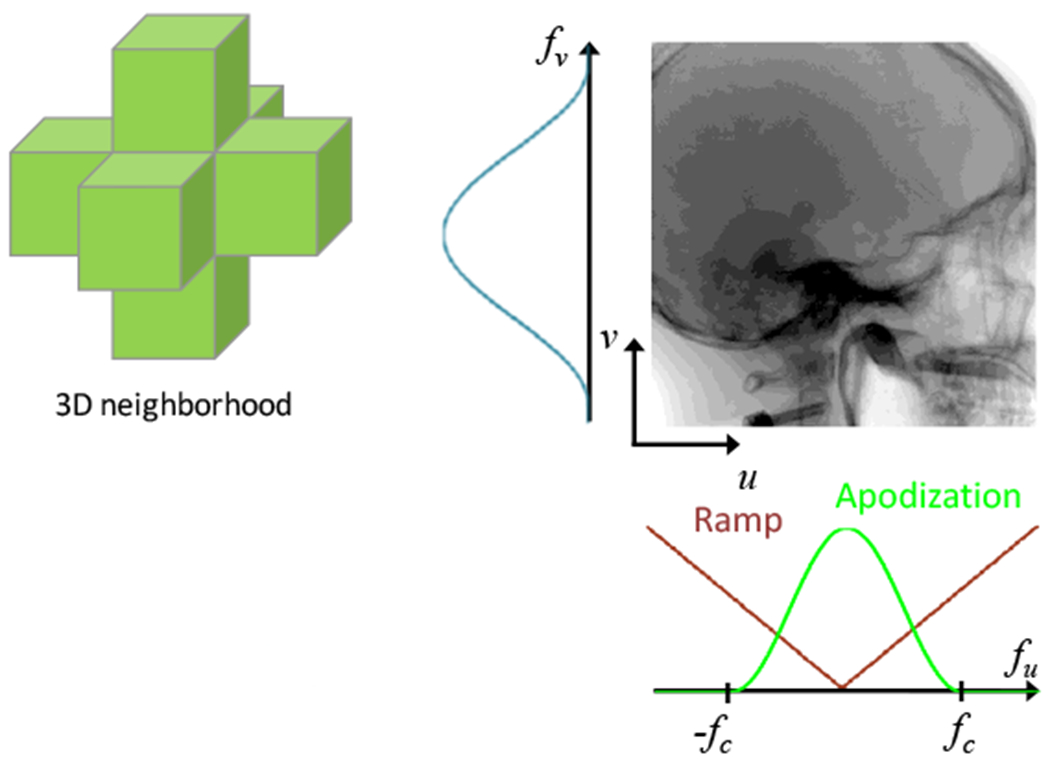
PL penalizes in all three dimensions, so fair comparison to FBP should involve matching the spatial resolution such that the smoothing kernel is also extended in the z-direction of the reconstructed volume.

Analysis of Noise-Resolution Tradeoffs.

Recognizing that contrast-to-noise ratio (CNR) is not a comprehensive image quality metric (viz., describing only the large-area, low-frequency transfer characteristics), it is nonetheless a reasonable starting point for analysis of low-contrast, low-frequency tasks pertinent to soft-tissue visualization. The edge spread function (ESF) of each tissue-equivalent insert was fit to an error function (erf) that provided the insert contrast c and edge width parameterized by σ to provide basic characterization of spatial resolution (Fig. 5). It bears reiteration that comparing the ESFs of FBP and PL is local and object-specific and that resolution “matching” pertains to a specific contrast, object, and location (and does not necessarily apply to the entire image). As the image is smoothed (either by reducing the FBP apodization cutoff frequency f_c or increasing the PL regularization β). the CNR reflects the corresponding reduction in noise. The PL-H variant has an additional dependency on the transition width δ, whose effect is contrast-dependent. Soft-tissue imaging performance (CNR) was analyzed as a function of f_c, β, and δ with comparisons at matched ESF (σ) balanced by qualitative assessment of resulting images by a clinician.

Fig. 5:

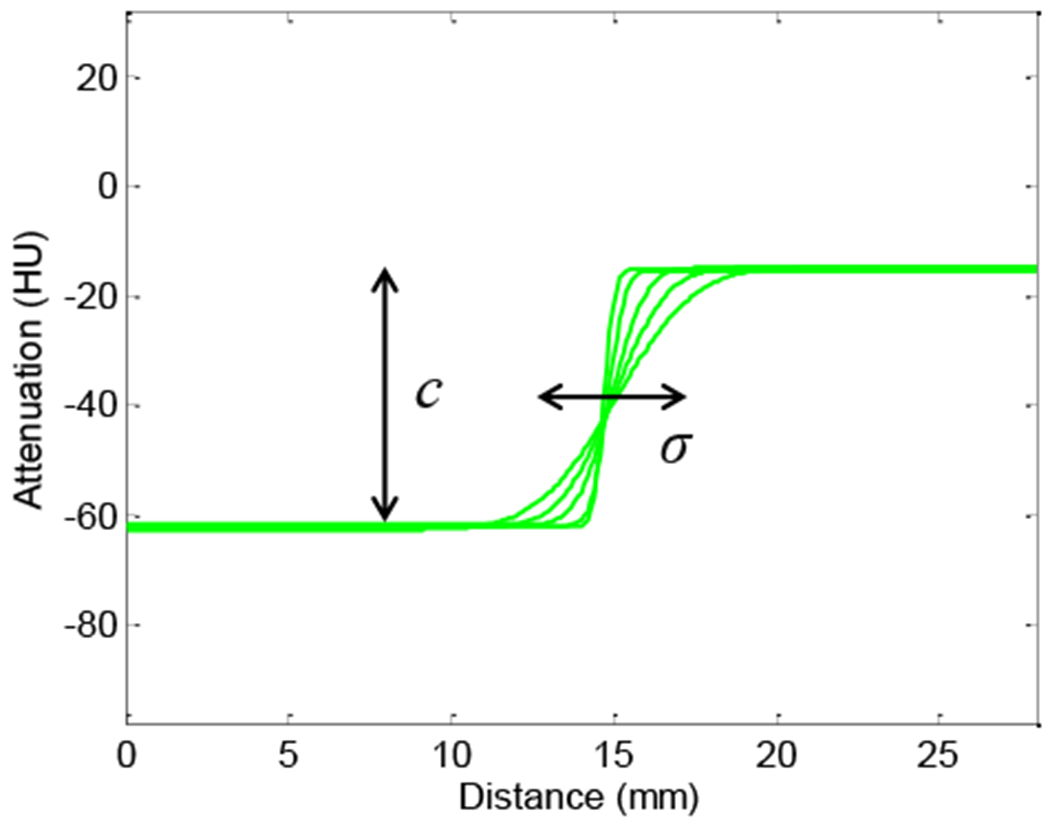
Spatial resolution characterized by an error function fit to the edge spread. Varying the FBP cutoff frequency f_c or PL regularization strength β provides a range in the edge smoothness of the adipose insert, as captured by this family of fits.

III. RESULTS

The CNR as a function of ESF width (Fig. 6) immediately conveys several interesting points among the various reconstruction techniques. First, we observe that spatial resolution is directionally dependent, and the noise is spatially nonstationary, which can be independently predicted using analytic models.¹⁵ The ESF of an insert depends on its contrast and whether it is considered in the radial or tangential direction. For example, in the bone insert, FBP shows higher resolution than PL-Q in the tangential direction, while the converse is true in the radial direction. Subsequent measurements of the ESF width, σ, involve the median width (more robust against outliers than the mean) measured in all directions.

Fig. 6:

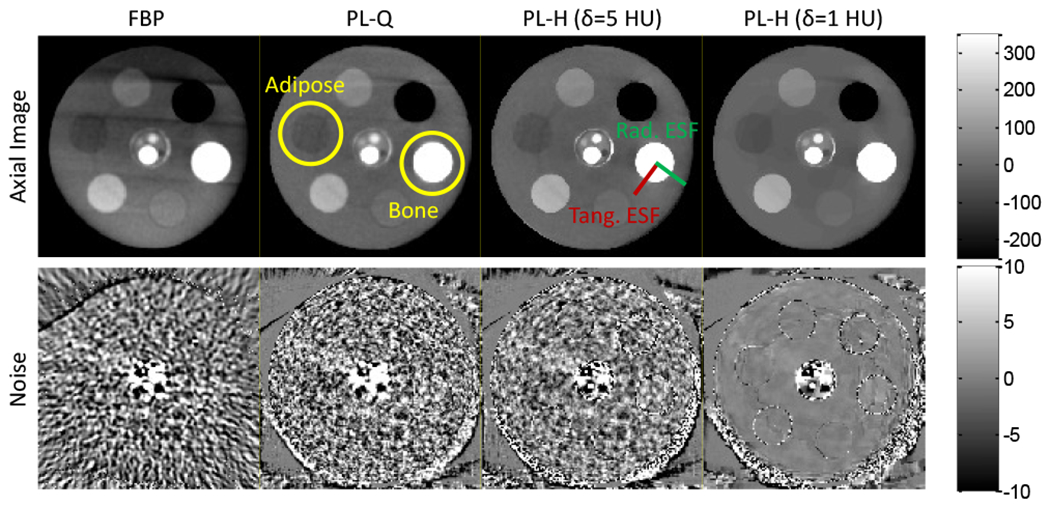
Axial slices of a cylindrical phantom for various reconstruction methods. (Top) Axial images. (Bottom) Noise maps computed from the difference of non-adjacent slices. The low-contrast Adipose insert is marked at the ~9:00 position, while high-contrast Bone is marked at ~3:00. The FBP and PL variants show differences in noise magnitude, correlation, and stationarity. The examples shown have a cutoff frequency (f_c) and regularization (β) such that the adipose ESF is matched at 1.1 mm.

FBP and PL-Q show comparable performance for both high and low contrast, showing - perhaps surprisingly - that quadratic penalties alone give little improvement over the classic noise-resolution tradeoffs of FBP. However, PL-H exhibits sharper edge-preservation for bone while significantly reducing the noise due to the linear region of the penalty preferring sharp, high-contrast edges (bone, +640 HU) and otherwise uniform regions with fluctuations on the order of δ. For low-contrast edges (adipose, −40 HU), however, the linear penalty is only exercised when δ is smaller than the contrast, and even for δ = 5 HU, PL-H is seen to behave similarly to PL-Q. The low-contrast edge is preserved only at δ = 1 HU, at which point the Huber penalty approaches TV.

Based on the quantitative analysis of CNR and ESF in low-contrast inserts in simple phantoms, the resulting parameters were applied to CBCT images of an anthropomorphic head phantom and (with separate parameter sets) to a cadaveric torso. While the optimal parameters in each case are recognized to depend on the object size, dose, and contrast associated with the particular task, the head phantom - for example - was approximately the same size as the CNR phantom, the scan parameters were identical, and the target tissues were roughly the same contrast (−30 HU) and size (12 mm diameter). Figure 8 provides a quantitative and qualitative summary of results for CBCT of the anthropomorphic head. Analysis of CNR versus ESF shows that FBP and PL-Q follow similar, conventional noise-resolution tradeoffs, as does PL-H for the larger value of δ. A steep dependence on δ is observed as PL-H becomes heavily edge-preserving in its noise reduction performance, departing from the classic tradeoff and giving significant gains in CNR at equivalent spatial resolution. The seeming gains in soft-tissue image quality must be balanced relative to the clinical acceptability of the images, which exhibit the characteristic “patchy” texture of TV for small δ. The steep dependence on δ in this regime requires a careful, quantitative guide to parameter selection, with results in Fig. 8 presenting an initial map of task-dependent CNR-ESF tradeoffs that help navigate the complex parameter space presented by these reconstruction methods. A qualitative comparison of the reconstruction techniques is shown in Fig. 9 for a cadaver torso, with future work required to more quantitatively assess the low-contrast imaging performance of PL in regions outside of the head such as the torso.

Fig. 8:

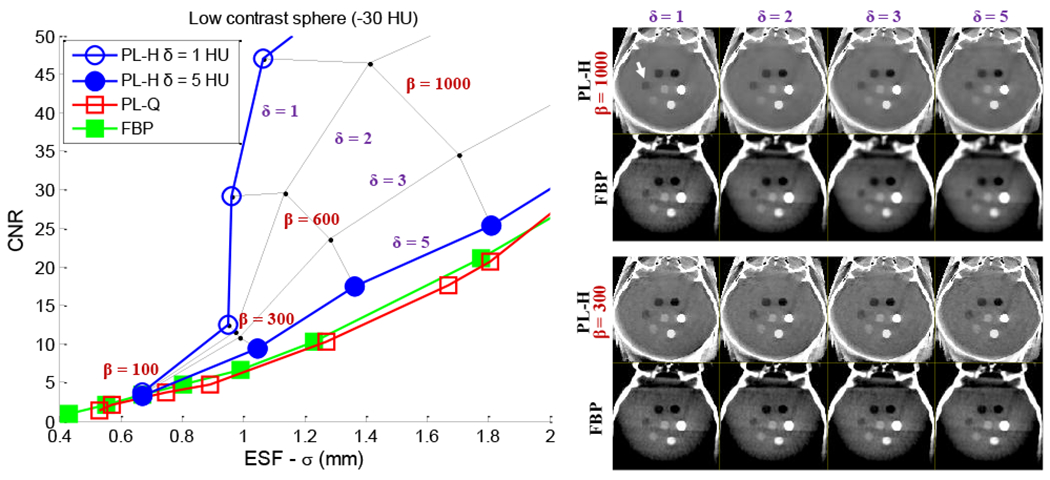
Analysis of noise-resolution tradeoffs among various reconstruction methods in C-arm CBCT of the head. (Left) CNR versus ESF width. PL-H, δ = 5 HU behaves approximately like the quadratic penalty for the low contrast (−30 HU) sphere, while PL-H, δ = 1 HU is TV-like. The CNR benefit of PL-H is greatest at lower spatial resolution, but the increase in CNR is steep. Several intermediate points are plotted to show the rapid gain in CNR at low δ. (Right) Axial images of the head phantom. Each PL-H image is paired with an FBP image below at matched spatial resolution (for the low-contrast sphere).

Fig. 9:

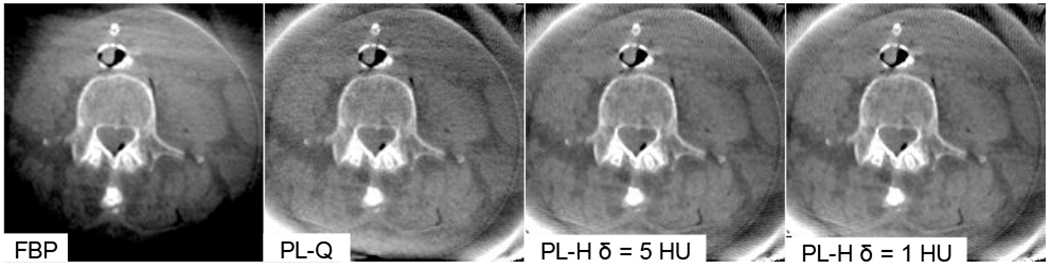
C-arm CBCT of a cadaver torso in the region of paraspinal muscles. Intra-operative soft tissue imaging in larger regions of the body (e.g., thorax or abdomen) poses further challenges, such as scatter, lateral truncation, and electronic noise.

IV. DISCUSSION AND CONCLUSIONS

Application of statistical iterative reconstruction methods - like the PL variants summarized above - hold considerable promise for low-dose, soft-tissue imaging capability in C-arm CBCT and raise new challenges in quantifiably assessing and validating imaging performance, especially in fair comparison of noise and spatial resolution characteristics. The parameters intrinsic to such algorithms (e.g., β and δ) impart tradeoffs in noise and spatial resolution that in some cases have little or no gain over conventional FBP, and in other cases depart rapidly with significant gain in CNR achieved via edge-preserving noise reduction. The optimal choice of parameters is task-dependent, and the analysis detailed herein begins to construct an understanding and framework by which such parameters may be knowledgeably selected with respect to the task. Future work includes applying quantitative noise-resolution tradeoff analysis to determine low dose limits of soft-tissue imaging for intracranial neurosurgery applications as well as soft-tissue imaging for spine and abdominal surgery. Incorporation of more advanced modeling of the imaging physics and statistics (e.g., scatter, polyenergetic spectrum, detector correlations, and electronic noise) into statistical reconstruction is anticipated to yield further improvement in image quality and low-dose imaging capabilities beyond conventional limits of soft-tissue visualization.

Fig. 1:

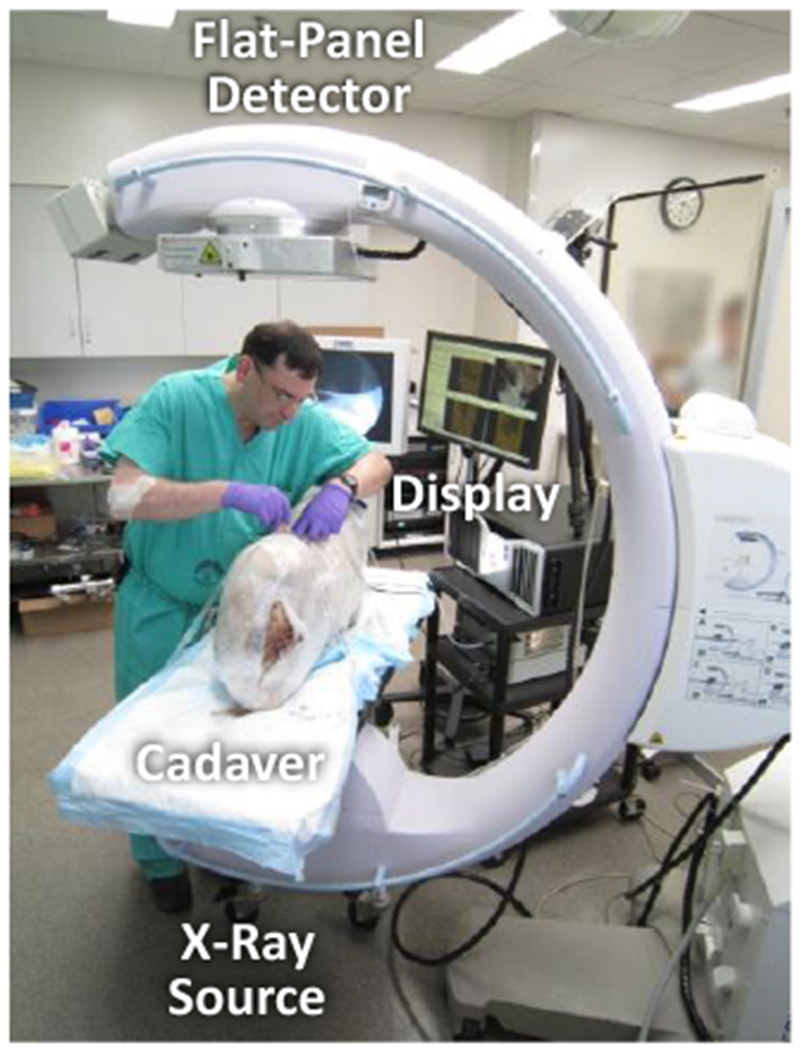
A prototype mobile C-arm CBCT imaging system assists the surgeon during a cadaver procedure.

Fig. 7:

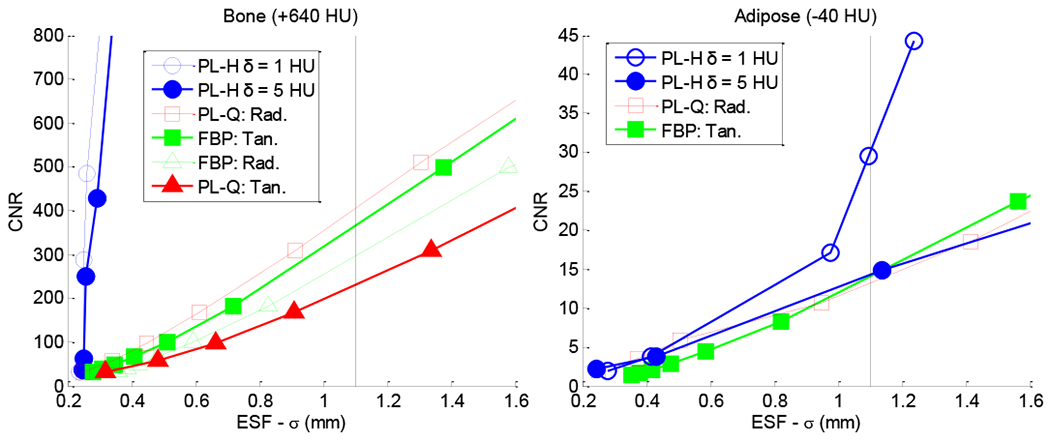
Analysis of the noise-resolution tradeoff in various reconstruction methods. Each plot shows CNR in a given insert as a function of ESF width (σ). A vertical line therefore compares noise at matched spatial resolution. (Left) Directional-dependence in spatial resolution. (Right) CNR in adipose versus ESF, showing the Huber penalty with δ = 1 HU to depart from classic noise-resolution tradeoffs as it approaches a TV-like penalty.