Bayesian Joint Modeling of Multiple Brain Functional Networks

Abstract

Investigating the similarity and changes in brain networks under different mental conditions has become increasingly important in neuroscience research. A standard separate estimation strategy fails to pool information across networks and hence has reduced estimation accuracy and power to detect between-network differences. Motivated by a fMRI Stroop task experiment that involves multiple related tasks, we develop an integrative Bayesian approach for jointly modeling multiple brain networks that provides a systematic inferential framework for network comparisons. The proposed approach explicitly models shared and differential patterns via flexible Dirichlet process-based priors on edge probabilities. Conditional on edges, the connection strengths are modeled via Bayesian spike and slab prior on the precision matrix off-diagonals. Numerical simulations illustrate that the proposed approach has increased power to detect true differential edges while providing adequate control on false positives and achieves greater network estimation accuracy compared to existing methods. The Stroop task data analysis reveals greater connectivity differences between task and fixation that are concentrated in brain regions previously identified as differentially activated in Stroop task, and more nuanced connectivity differences between exertion and relaxed task. In contrast, penalized modeling approaches involving computationally burdensome permutation tests reveal negligible network differences between conditions that seem biologically implausible.

1. Introduction

The Stroop task (Stroop, 1935) is one of the most reliable psychometric tests (MacLeod, 1991) that is widely used as an index of attention and executive control. It has been extensively employed to investigate the neural underpinnings of mental effort that is defined as the deployment of mental resources in a demanding task that needs to be willfully maintained. Stroop task experiments have been successfully adopted in neuroimaging studies targeting child development (Levinson et al., 2018) and aging (Duchek et al., 2013), addictive behavior (Wang et al., 2018), psychiatric conditions (Woodward et al., 2016), and several other areas. Neuroimaging studies have shown differential activation in several brain regions related to the Stroop task (Gruber et al., 2002; Shan et al., 2018). However, there are limited advances for understanding the neural circuitry changes related to differences in the capacity to exert mental effort (Levinson et al., 2018). Existing connectivity studies have focused on independent component analysis or ICA (Wang et al., 2018), seed region based correlation analysis (Levinson et al., 2018), and pairwise correlation analysis (Peterson et al., 1999). While useful, ICA based studies do not provide edge-level interpretations necessary for graph theoretic insights, whereas seed region-based analysis are subjective and do not use whole brain information. Moreover, pairwise correlations fail to account for spurious effects of third party nodes (Smith et al., 2011) that may lead to misleading connectivity findings. In addition, none of existing methods investigated connectivity differences related to varying mental effort in Stroop task, although recent evidence point to significant brain activation differences when the task is performed by voluntarily engaging a maximum or a minimum of mental effort (Khachouf et al., 2017).

In one of the first such efforts to our knowledge, we investigate how the brain network reorganizes under different cognitive conditions corresponding to passive fixation and task performance, as well as between effortful and relaxed task performance, under a Stroop task experiment. The scientific hypothesis based on previous studies is that considerable neurobiological and connectivity differences should be present between the different cognitive conditions. The investigation of brain network differences may be performed on a single subject or, as in our case, at a group level which is expected to average out subject-specific idiosyncrasies (Kim et al., 2015). Under a graph-theoretic approach, edges featuring differential strengths correspond to brain connections that are more activated or suppressed during one experimental condition as compared to others. On the other hand, connections shared across networks may represent an intrinsic functional network architecture which is common across experimental conditions (Fox et al., 2007). However, separate estimation of multiple networks may not have enough power to accurately detect shared and differential features between networks due to the inherent noise in fMRI data. Separate network estimation may also be inadequate in terms of comparing multiple networks (a central question of interest in our applications), due to a lack of systematic inferential tools to test significant connectivity differences between experimental conditions. The above factors could potentially result in a loss of biological interpretability, as illustrated via our Stroop task data analysis. These critical issues can be potentially resolved via a joint learning approach for multiple networks that pools information across experimental conditions to learn shared and differential features. Such an approach is motivated by the success of recent data fusion methods for multiple datasets in literature (Lahat et al., 2015).

There has been a limited development of approaches for the joint estimation of multiple networks. Penalized approaches for the joint estimation of multiple Gaussian graphical models (GGM) (Guo et al., 2011; Danaher et al., 2014; Zhu et al., 2014) typically smooth over the strength of connections across networks to enforce shared edges, which is a useful modeling assumption but may not be supported in practical brain network applications. Further, they often require a careful choice of more than one tuning parameter that results in an increase in computational burden, and they do not provide measures of uncertainty which are often desirable in characterizing heterogeneity in group level analyses. With the exception of a recent penalized neighborhood selection approach by Belilovsky et al. (2016), few penalized methods have been vetted for the joint estimation of multiple brain networks. Unfortunately, the approach by Belilovsky et al. (2016) cannot be used to obtain positive definite precision matrices that are necessary for quantification of edge strengths via partial correlations. Moreover, a major difficulty under penalized approaches arises when comparing multiple networks, since the estimated network differences may be artifacts resulting from estimation errors under point estimates (Kim et al., 2015). Penalized methods for comparing networks rely on permutation tests that are computationally burdensome and hence not scalable, or they construct null distributions to conduct hypothesis testing (Higgins et al., 2019) that may be restrictive when the associated assumptions are not satisfied. Hence, penalized approaches may not be adequate for inferring network differences between multiple experimental conditions, which is a central objective in this article.

Several Bayesian approaches, including spike and slab methods (Yu and Dauwels, 2016; Peterson et al., 2015), and continuous shrinkage methods (Carvalho et al., 2010; Polson and Scott, 2010; Piironen et al., 2017; Li et al., 2017) have been proposed for individual precision matrix estimation. Though Bayesian approaches have proven extremely useful in estimating brain networks (Mumford and Ramsey, 2014), few attempts have been made to develop Bayesian methods for the joint estimation of multiple networks. Some existing Bayesian methods for joint network estimation include the approach by Yajima et al. (2012), who focused on multiple directed acyclic graphs, and the Bayesian Markov random field approach by Peterson et al. (2015) for estimating multiple protein-protein interaction networks. The former cannot be used to obtain undirected brain networks which is the focus of this article, while the latter is only applicable to examples involving a small number of nodes and can not be scaled up to whole brain network analysis considered in this study. There is also some recent work on jointly estimating multiple temporally dependent networks (Qiu et al., 2016; Lin et al., 2017), but these approaches cannot be directly generalized for the integrative analysis of multiple brain networks across different experimental conditions. The above discussion suggests a clear need for developing flexible and scalable Bayesian approaches for joint estimation of multiple brain networks which pool information across experimental conditions to provide more accurate estimation and inferences. An appealing feature of Bayesian joint modeling approaches is that they provide a rigorous inferential framework for comparing networks at multiple scales using Markov chain Monte Carlo (MCMC) samples, which precludes the need for computationally involved permutation tests or constructing test statistics based on heuristic null distributions. While a separate Bayesian estimation for multiple networks also enables one to test for network differences using MCMC samples, it is unable to pool information across experimental conditions and can not account for dependencies across multiple related networks.

In this article, we develop a Bayesian GGM approach for jointly estimating multiple networks. This approach models the probability of a connection as a parametric function of a baseline component shared across networks and differential components unique to each network. The shared and differential effects are modeled under a Dirichlet process (DP) mixture of Gaussians prior (Müller et al., 1996), and the edge probabilities are estimated by pooling information across experimental conditions, thereby resulting in the joint estimation of multiple networks. An exploratory analysis of the Stroop task data, which involved deriving the subject-specific network for each of the 45 subjects under the task and rest conditions using the graphical lasso (Friedman et al., 2008), and then estimating the group level probability for each edge by combining the edge sets across all subjects, followed by a K-means algorithm on the edge probabilities, revealed clearly defined and well separated clusters for these probabilities. This provides a strong motivation for a DP mixture approach to cluster the edge probabilities under BJNL. The role of the edge probabilities is twofold - they characterize uncertainty in network estimation and allows one to pool information across networks. The connection strengths are encapsulated via network specific precision matrices, which are modeled separately for each network under a spike and slab Bayesian graphical lasso prior conditional on the above edge probabilities. Adopting a joint modeling approach that involves a combination of a parametric link function with flexible DP priors on the shared and differential components within the edge probabilities results in an interpretable and flexible approach. It also enables more accurate estimation of edge strengths and provides improved network comparisons (greater power to detect true differential connections while ensuring adequate control for false positives), as demonstrated via extensive numerical experiments. Another important advantage in using the DP prior on the components is the robustness to the specification of the parametric link function, as evident from simulation results. The approach, denoted as Bayesian Joint Network Learning (BJNL), is implemented via a fully Gibbs posterior computation scheme.

Our BJNL analysis of the Stroop task data confirmed the hypothesis that brain connections as well as global and local topological characteristics of the brain network are considerably different when subjects are actively engaged in the task as compared with the rest condition, which is not surprising given the difference in the cognitive requirements of the two conditions. The connectivity differences between task and passive fixation also aligned with the theory of global workspace (Gießing et al., 2013), which confirms the biological interpretability of the BJNL findings. Subtler network differences were observed between effortful and relaxed task conditions that is somewhat expected, since these conditions differ only in the mental attitude voluntarily applied to the performance of the same task. The BJNL connectivity differences were concentrated in brain regions previously shown to be differentially activated by a varying degree of willfully applied mental effort (Khachouf et al., 2017), which supports the plausibility of BJNL findings and provides important evidence supporting the scientific hypothesis of connectivity differences formed under the different cognitive conditions. In addition to the BJNL analysis, we also performed a comparative analysis using penalized approaches such as the graphical lasso and the joint graphical lasso (JGL) (Danaher et al., 2014). The analysis under the penalized approaches revealed negligible network differences between effortful and relaxed task performance, and very limited network differences between task and passive fixation, which did not always involve brain regions implicated in previous activation studies (Khachouf et al., 2017). Hence these findings appeared to be inconsistent with our scientific hypothesis.

In addition to the advantage in terms of biological interpretability of findings, the BJNL analysis of Stroop task data also provides another major advantage over penalized methods for joint modeling in terms of computation time. Unlike BJNL that provided a robust inferential framework for comparing networks via MCMC samples, network comparisons under penalized approaches involved computationally burdensome permutation tests. In fact, the permutation tests under JGL using a full tuning parameter search procedure requires an hour to run per permutation (compared to an overall run time of a few hours for BJNL), which makes the approach impractical in terms of comparing brain networks. Due to this prohibitive computational burden, tuning parameters for JGL were chosen in an iterative manner across permutations, which reduced the computation time to around 27 hours but also potentially resulted in sub-optimal performance in brain network analysis. The computation efficiency of BJNL represents an important practical advantage in terms of comparing multiple whole brain networks, compared to other methods for joint estimation of multiple networks that may be hindered by computational bottlenecks.

2. Methodology

2.1. Description of the fMRI data set

Forty-five volunteers participated in the study. All subjects were right handed with an average age of 21.9 (SD = 2.2) years. MRI scanning was performed at the N.O.C.S.A.E Hospital in Baggiovara (MO), Italy, using a 3T Philips Achieva scanner. For each subject, the imaging session consisted of the collection of 6 echo-planar imaging (EPI) runs (112 volumes each, TR=2.5s, 25 axial slice, 3 × 3 × 3 mm voxels) and a T1-weighted high-resolution volume (180 sagittal slices, 1mm isotropic voxels) for anatomical reference. While in the scanner, subjects performed a 4-color version of the Stroop task with a button-press response modality (Gianaros et al., 2005). In this task, subjects are presented with a color word displayed in colored fonts in the center of a computer screen and are asked to press a button on a response device corresponding to the font color of the stimulus. There are two types of trials: congruent trials, where the font color matches the text (e.g., the word ‘RED’ in red fonts), and incongruent trials, where the font color does not match the text (e.g., the word ‘RED’ in green fonts). The ‘Stroop effect’ refers to a significant slowing of response times to the incongruent trials compared to the congruent ones (Stroop, 1935). Figure 1 illustrates the Stroop task experiment.

Fig. 1.

An illustration of the Stroop task involving task blocks of congruent and incongruent trials, indicated by purple bars and yellow bars respectively, and fixation blocks denoted by a centrally fixated cross. The purple and yellow bars are expanded into two boxes, and the correct button presses are indicated with a rectangle within each box. Subjects were instructed to perform odd-numbered runs “with maximum exertion” (EXR condition) and even-numbered runs “as relaxed as possible” (RLX condition).

Stimuli were presented in (task) blocks of 30s containing 6 congruent and 6 incongruent trials appearing in a pseudo-random order with a 2.5s inter-trial interval. Each task block was alternated with 25s-blocks of passive fixation on a centrally presented cross. Six fMRI runs were collected for each subject, with each run consisting of 4 blocks of task and 5 blocks of passive fixation appearing in ABABABABA order (A=passive fixation, B=task). Crucially, subjects were instructed to perform odd-numbered runs “with maximum exertion” (EXR condition) and even-numbered runs “as relaxed as possible” (RLX condition). This scheme was reversed for a subset of volunteers to check for potential order effects. A major aim of the study was to compare the brain connectivity under REST (passive fixation) and the two TASK conditions (RLX and EXR) (Khachouf et al., 2017).

2.2. Bayesian modeling of multiple networks

We develop a novel Bayesian approach for jointly estimating multiple group-level brain functional networks from multi-subject fMRI data. For each subject, the data are demeaned and pre-whitened across time points, where the pre-whitened fMRI observations are considered statistically independent. The pre-whitened fMRI data over p nodes or regions of interest (ROI) for the i-th subject and gth experimental condition at time point t is denoted by y_it (g) = (y_it1(g), … , y_itp(g)), i = 1, … , n, t = 1, … , T_ig, g = 1, … , G. Our goal is to jointly estimate multiple networks denoted by G₁, … , G_G using Gaussian graphical models characterized by sparse inverse covariance matrices. The graph G_g is defined by the vertex set V= {1, … , p} containing p nodes and the edge set E_g containing all edges/connections in the graph G_g, g = 1, … , G.

The pre-whitened fMRI measurements for g-th experimental condition are modeled as y_it(g) ~ N_p(0, ${\text{Ω}}_g^{-1}$), i =1, …, n, t =1, …,T_ig, g =1, …, G, where

$$\pi \left({\Omega }_g\right)=C_g^{-1}\prod _{k=1}^{p}E\left({\omega }_{g,kk};\frac{\alpha }{2}\right)\left\{\prod _{k<l}{w}_{g,kl}N\left({\omega }_{g,kl};0,{\tau }_{g,kl}^{-1}\right)+\left(1-w_{g,kl}\right)DE\left({\omega }_{g,kl};{\lambda }_0\right)\right\}I\left({\Omega }_g\in M^{+}\right),$$ (1)

where π(·) denotes the prior distribution, ω_g,kl and w_g,kl denote the strength and probability of the functional connection between nodes k and l for network G_g respectively, M⁺ denotes the space of all positive definite matrices, I(·) denotes the indicator function, C_g is the intractable normalizing constant for the prior on the precision matrix, N_p (·;0,Σ) denotes a p-variate Gaussian distribution with mean 0 and covariance Σ, and E(α) and DE(λ) denote the exponential and double exponential distributions with scale parameters α⁻¹ and λ⁻¹ respectively. Small values of the scale parameters τ_g,kl ~ π (τ_g,kl) and ${\lambda }_0^{-1}$ in equation (3) result in a spike and slab prior (George and McCulloch, 1993) on the precision off-diagonals, so that Ω_g ~π(Ω_g) is denoted as the spike and slab Bayesian graphical lasso. The spike and slab prior shrinks the values corresponding to absent edges toward zero and encourages values away from zero for important connections. The slab component is modeled under a Gaussian distribution having thick tails under small values of the precision parameter, while the spike component is modeled under a double exponential distribution having a sharp spike at zero under a large value of λ₀. It is straightforward to show that C_g < ∞ so that the prior in model (1) is proper using the results in Wang et al. (2012).

Pooling Information Across Experimental Conditions:

Information is pooled across experimental conditions to estimate the edge weights w_g,kl, k ≠ l, k, l =1, …, p, leading to joint estimation of multiple networks. Note that by pooling information to model the edge probabilities instead of the edge strengths, we are able to jointly model multiple brain networks without constraining the edge strengths in separate networks to be similar. The prior weights represent the unknown probabilities of having functional connections, and are modeled via a parametric link function comprising unknown shared and differential effects as described below

$$w_{g,kl}=h\left({\eta }_{0,kl},{\eta }_{g,kl}\right),{\eta }_{0,kl}\sim f_0,{\eta }_{g,kl}\sim f_g,f_0\sim DP\left(M{P}_0\right),f_g\sim DP\left(M{P}_0\right),$$ (2)

for k ≠l, k, l = 1, …, p, g = 1, …, G, where h(·) is the parametric link function relating the probability for edge (k, l) in network G_g to the network specific differential effect (η_g,kl) and common effect (η_0,kl) across all networks, and DP (MP₀) denotes a Dirichlet process mixture prior defined by the precision parameter M and base measure $P_0\equiv N\left(0,{\sigma }_{\eta }^2\right)$. The Dirichlet process mixture prior induces a flexible class of distributions on the edge probabilities and also results in clusters of edges having the same prior inclusion probabilities, enforcing parsimony in the number of model parameters. The number of clusters and the cluster sizes are unknown and controlled via the precision parameter M (Antoniak, 1974).

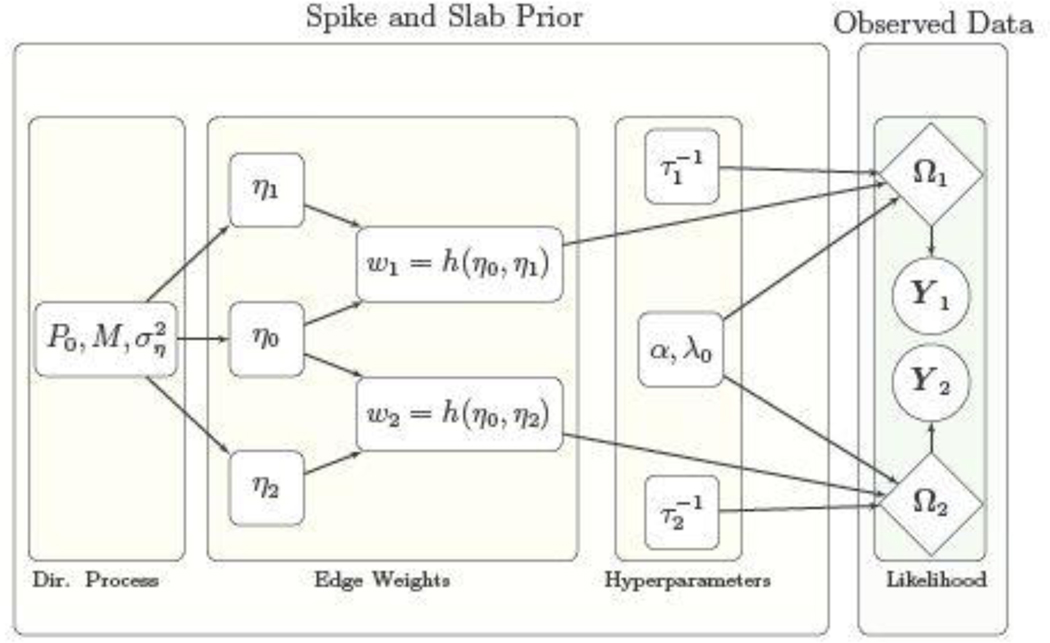
Under specification (2), the baseline effect η_0,kl represent the shared feature for edge (k, l) which is estimated by pooling information across experimental conditions, resulting in the joint estimation of multiple networks. The baseline effect controls the overall probability of having an edge across all networks, while the differential effects contribute to the network specific variations which are estimated using the information from individual experimental conditions. For example, large differences between η_g,kl and η_g′,kl, g ≠ g′ potentially imply a differential status for edge (k, l) between G_g and G_g′. On the other hand when η_g,kl = η_g′,kl , g ≠ g′, the model specifies equal probability for edge (k, l) in networks G_g and G_g′. For ease in interpretability we choose a logistic form link in (2) as h(η_0,kl, η_g,kl) = exp{η_0,kl + η_g,kl}/[1 + exp {η_0,kl + η_g,kl}], g= 1, …, G, so that η_g,kl + η_0,kl can be interpreted as the log odds of having the edge (k, l) in the network G_g , and the log odds ratio of having edge (k, l) in the brain network G_g versus G_g′ can be expressed as η_g′,kl − η_g,kl (g ≠ g′). A schematic representation of the proposed model is illustrated in Figure 2.

Fig. 2.

Directed graph illustrating the relationships between the model parameters for the case of two experimental conditions represented by fMRI data matrices Y₁ and Y₂. Rectangular nodes correspond to parameters which are updated or tuned, diamond-shaped nodes correspond to parameters involved in the likelihood, and the circular nodes correspond to the observed data.

Note that the parameters η_0,kl, η_g,kl, in (2) are not identifiable since h(η_0,kl, η_g,kl) = h(η_0,kl +c, η_g,kl −c) for any real constant c. However, the functionals of interest such as the log odds (η_0,kl + η_g,kl), the log-odds ratio (η_g,kl − η_g′,kl), and the edge probabilities themselves are clearly identifiable, which is adequate for our purposes. The proposed specification (2) is purposely overcomplete, which is an issue routinely arising in Bayesian models. By “overcomplete,” we mean that we include G + 1 parameters in the weights model when G parameters would suffice. Such overcompleteness allows us to pool information in a systematic manner, and ensures computational efficiency and interpretability in terms of shared and differential group effects and is designed to avoid any problems in identifiability of functionals of interest - refer, for example, to Ghosh and Dunson (2009).

Our treatment of the edge weights is motivated by existing literature on modeling binary or ordered categorical responses using mixture distributions (Kottas et al., 2005; Jara et al., 2007; Gill and Casella, 2009; Canale and Dunson, 2011). Specifically we are able to achieve both the interpretability discussed above and a high degree of flexibility while also reducing the sensitivity to the link function and enabling straightforward posterior computation. A similar approach was taken by Durante et al. (2017) who modeled structural connections in a population of networks via a mixture of Bernoulli distributions, although they did not focus on joint estimation of multiple networks.

3. Posterior Computation

We design a block Gibbs sampler in order to fit the proposed model (1). The sampler enables data adaptive shrinkage by introducing latent scale parameters to sample the precision matrix off-diagonals corresponding to the spike component under a scale mixture representation of Gaussians while defining conjugate priors on the precision parameters in the slab component. Define edge inclusion indicators as δ_g,kl =1 if edge (k, l) is included in G_g , and δ_g,kl = 0 otherwise, where P(δ_g,kl = 1) = w_g,kl . The augmented likelihood for equation (1) can be written as

$$\begin{array}{l}\pi \left({\Omega }_g\mid {\lambda }_0,{\tau }_g,{\tau }_g^{\ast }\right)=C_{\tau ,g}^{-1}1\left({\Omega }_g\in M^{+}\right)\prod _{l=1}^{p}Exp\left({\omega }_{g,ll};\alpha /2\right)\times \prod _{l=1}^p\prod _{k<l}{w}_{g,kl}^{{\delta }_{g,kl}}{\left(1-w_{g,kl}\right)}^{1-{\delta }_{g,k}}\\ \times \prod _{l=1}^p\prod _{k<l}{\left[N\left({\omega }_{g,kl};0,{\tau }_{g,kl}^{-1}\right)\right]}^{{\delta }_{gk}}{\left[\int N\left({\omega }_{g,kl};0,{\tau }_{g,kl}^{-1}\right)Exp\left({\tau }_{g,kl};\frac{{\lambda }_0^2}{2}\right)d{\tau }_{g,kl}\right]}^{1-{\delta }_{g,kl}},\text{ with }\\ \pi \left({\tau }_g,{\tau }_g^{\ast }\right)\propto C_{\tau ,g}\left(\prod _p^{l=1}\prod _{k<l}Ga\left({\tau }_{g,kl};a_{\tau },b_{\tau }\right)\times Exp\left({\tau }_{g,kl}^{\ast };{\lambda }_0^2/2\right)\right),\end{array}$$ (3)

where τ_g ={τ_g,kl, k ≠ l, k, l =1, …, p}, ${\tau }_g^{\ast }=\left\{{\tau }_{g,kl}^{\ast },k\ne l,k,l=1,\dots ,p\right\}$, Ga(·;a_τ,b_τ) corresponds to a Gamma distribution with mean a_τ/b_τ, and C_τ,g is the intractable normalizing constant which cancels out in the expression for π(Ω_g , λ₀, τ_g, ${\tau }_g^{\ast }$) to yield a marginal prior π(Ω_g, λ₀, τ_g) as in (1) after integrating out ${\tau }_g^{\ast }$. In our implementation we pre-specify λ₀ =100 to ensure a sharp spike at zero leading to strong shrinkage for precision off-diagonals corresponding to absent edges. On the other hand, we choose a_τ and b_τ such that a_τ/b_τ is small, enabling adaptive thick tails for the Gamma prior on the latent scale parameters corresponding to the slab component.

We choose a logistic link function in (2) for our purposes, although more general link functions can also be used. For implementing a fully Gibbs sampler, we rely on an approximation to the logistic function using a probit link, which employs a data augmentation scheme as in O’brien and Dunson (2004). In particular,

$$\frac{e^{{\mu }^{\ast }}}{\left(1+e^{l^{\ast }}\right)}\approx {\int }_0^{\infty }t\left(u;{\mu }^{\ast },\frac{{\pi }^2(\varphi -2)}{3\varphi }\right)du={\int }_0^{\infty }N\left(u;{\mu }^{\ast },\frac{{\pi }^2(\varphi -2)}{3\varphi }{\sigma }_{\varphi }^2\right)\pi \left({\sigma }_{\varphi }^2;\frac{\varphi }{2},\frac{\varphi }{2}\right)du,$$

where t(·) denotes a t-distribution, $\pi \left({\sigma }_{\varphi }^2\right)$ corresponds to a inverse Gamma distribution, ϕ= 7.3, and u is the Gaussian latent variable used for data augmentation. This approximation results in sampling from a posterior that is approximately equal to the posterior under specification (1)-(2) using a logistic link function. Although such an approximation is used, we note that the resulting posterior computation is fully Gibbs since all MCMC samples are drawn from exact posterior distributions. Alternatively, one could adapt the Polya-gamma data augmentation in Polson et al. (2013) for Bayesian logistic regression. However, the approximation in O’brien and Dunson (2004) works reasonably well in a wide variety of numerical studies in our experience. Moreover, the stick-breaking representation (Sethuraman, 1994) is used for the Dirichlet process mixture prior in (2), which facilitates posterior computation and can be written as

$${\eta }_{g,kl}\sim f_g,f_g=\sum _{h=1}^{\infty }{v}_{g,h}{\delta }_{{\eta }_{g,h}},{\eta }_{g,h}^{\ast }\sim N\left(0,{\sigma }_{\eta }^2\right),v_{g,h}=\left(v_{g,h}\prod _{l<h}\left[1-v_{g,l}\right]\right),v_{g,h}\sim Beta(1,M),g=0,\dots ,G,$$ (4)

where Beta(·) denotes a Beta distribution. The slice sampling technique (Walker, 2007) is used to sample the atoms from the infinite mixture in (2), which significantly expedites computation. See Section 1 of the Supplementary Materials for posterior computation details.

Edge Detection:

The important network edges (and hence the network structure) can be estimated by either including edges with high marginal inclusion probabilities or those with non-negligible absolute values for the precision off-diagonals, lying above a chosen threshold. We propose a strategy to choose such thresholds in a manner which controls the false discovery rate (FDR). Denoting ζ_g,kl as the marginal posterior exclusion probability for edge (k, l) in network G_g , one can compute the FDR as in Peterson et al. (2015) as

$$FDR=\frac{\sum _{g=1}^G\sum _{k<l}{\zeta }_{g,kl}1\left({\zeta }_{g,kl}<\kappa \right)}{\sum _{g=1}^G\sum _{k<l}1\left({\zeta }_{g,kl}<\kappa \right)},\text{ or }FDR=\frac{\sum _{g=1}^G\sum _{k<l}{\zeta }_{g,kl}1\left(\left|{\widehat{\omega }}_{g,kl}\right|>{\kappa }^{\ast }\right)}{\sum _{g=1}^G\sum _{k<l}1\left(\left|{\widehat{\omega }}_{g,kl}\right|>{\kappa }^{\ast }\right)},$$ (5)

depending on whether the edges are included based on posterior inclusion probabilities or edge strengths. Clearly the FDR increases with κ/κ*, and one can choose a suitable threshold to control the FDR. In our numerical experiments we found that choosing the edges based on whether the absolute precision off-diagonals were greater than 0.1 results in overall good numerical performance and FDR values which are less than 0.03 across a wide spectrum of scenarios. Hence we recommend this as a default threshold under our approach, and we note that the corresponding threshold for posterior probability for edge selection can be obtained as one which yields similar FDR as computed using (5).

Inferring Network Differences:

In addition to network estimation, the proposed BJNL provides a natural framework for testing network differences between experimental conditions at multiple scales. In particular, for our Stroop task data analysis, we use MCMC samples under BJNL to obtain the posterior distribution for differences in edge level partial correlations as well as global and local network metrics. At the edge-level, T-tests of the Fisher Z-transformed partial correlation differences for all MCMC samples (after burn-in) were used to infer differences in edge strengths across networks. Similarly, the differences in the graph metrics across conditions were computed at each MCMC iteration, and the central tendency and dispersion of their distributions were statistically assessed by T-tests and Kolmogorov-Smirnov (KS) tests. The p-values of these tests were used to assess significance after controlling for false discoveries (Benjamini and Hochberg, 1995).

4. Numerical Studies

4.1. Simulation Setup

We conducted a series of simulations to compare group level network estimation between BJNL and competing methods. These approaches include the graphical horseshoe estimator (HS) (Carvalho et al., 2010; Li et al., 2017) which extends the horseshoe prior in regression settings to graphical model estimation, and the graphical lasso approach (GL) (Friedman et al., 2008) which imposes L₁ penalty on the off-diagonals to impose sparsity, as well as the Joint Graphical Lasso (JGL) (Danaher et al., 2014) which uses a fused lasso penalty to pool information across graphs while encouraging sparsity via a L₁ penalty. While both the HS and GL approaches estimate individual networks separately, the JGL approach is designed to jointly estimate multiple networks. The HS was implemented using Matlab codes provided on the author’s website. The JGL and the graphical lasso were implemented using the JGL and glasso packages in R, respectively. Our method was implemented in Matlab, version 8.3.0.532 (R2014a), and a GUI implementing the method has been submitted as a Supplemental Material.

The data for the simulation study was generated under a Gaussian graphical model for n=60 subjects with T=300 time points each and for dimensions p = 40, 100. Each subject had data corresponding to two experimental conditions having networks with shared and differential patterns. We considered three different network structures: (a) Erdos-Renyi networks which randomly generate edges with equal probabilities, (b) small-world networks generated under the Watts-Strogatz model (Watts and Strogatz, 1998), and (c) scale-free networks generated using the preferential attachment model (Barabási and Albert, 1999) resulting in a hub network. For each type of network, we obtained an adjacency matrix corresponding to the first experimental condition, and then flipped a proportion of the edges in this adjacency matrix to obtain the second network, adding edges where there were no edges and removing an equal number of edges. The proportion of flipped edges was set to 25%(low), 50%(medium), and 75%(high), which correspond to varying levels of discordance between the experimental conditions.

After generating the networks, the corresponding precision matrices were constructed as follows. For each edge, we generated the corresponding off-diagonal element from a Uniform(−1,1) distribution and fixed the diagonal elements to be one and the off-diagonals corresponding to absent edges as zero. In order to ensure that the resulting precision matrices were positive definite, we subtracted the minimum of the eigenvalues from each diagonal element of the generated precision matrix. To enable a group level comparison for each scenario, all subjects had the same network across all time points within each experimental condition and the same precision matrices for each network.

Tuning:

We used BJNL with 1000 burn-in iterations and 5000 MCMC iterations. We specified the tuning parameters as follows. We chose λ₀ =100 and τ_g,kl ~ Ga(a_τ,b_τ) with a_τ = 0.1 and b_τ = 1 in prior specification (3) to enforce a sharp spike at zero and thick tails for the slab component. The stick breaking weights in the mixture distribution in (4) were modeled as ν_g,h ~ Be(1,M) , where M ~ Ga(a_m, b_m), and we choose a_m =1, b_m =1, to encourage a small number of edge clusters for a parsimonious representation. We could increase a_m to encourage a larger number of clusters. However, we have observed that varying a_m has a limited effect on the final estimated network, as demonstrated through simulations in Section 2 of the Supplementary Materials. Our experience in extensive numerical studies suggests that the performance of the approach is not overly sensitive to the choice of λ₀ as long as it is large enough (> 100); however, extremely large values of λ₀ can result in numerical instability. Moreover, performance is fairly robust to the choice of the hyperparameters in the prior for the precision parameter of the slab component in (3), as long as the ratio a_τ/b_τ <1. For the joint graphical lasso that depends on two tuning parameters (a lasso penalty and a fused lasso penalty), we searched a 30×30 grid over [0.01, 0.1] for both parameters to find the best combination using a AIC criteria as recommended in Danaher et. al (2014). The graphical lasso was run independently for each network over a grid of regularization parameter values, and the optimal graph was selected for each network using a BIC criteria as described in Yuan and Lin (2007).

Performance metrics:

We assessed the performance of the three algorithms in terms of the ability to estimate the individual networks, as measured by the area under the receiver operating characteristic (ROC) curve (AUC), the accuracy in estimating the strength of connections, as measured by the L₁ error in estimating the precision matrix (L₁ error), the power to detect true differential edges as measured via sensitivity (TPR) and control over false positives for differential edges which is computed as 1-specificity (FPR). For all the metrics, we performed pairwise comparisons using Wilcoxon signed rank tests in order to assess whether one approach performed significantly better than the others. For edge detection, point estimates for the penalized networks were obtained by choosing the threshold for the absolute off-diagonal elements as 0.005, while for BJNL we computed thresholds controlling for false discoveries as described in Section 3.

4.2. Simulation Results

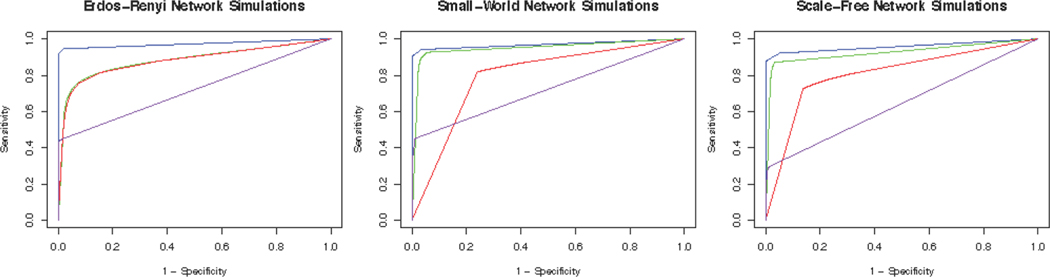
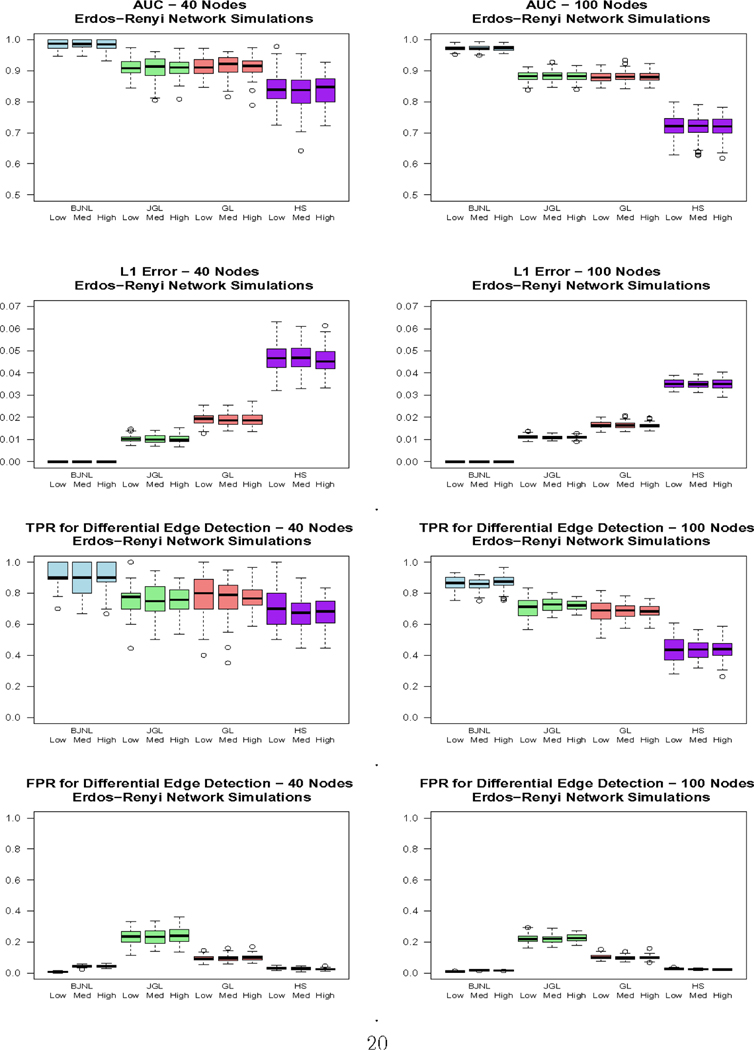
Figure 3 displays the ROC curves for the 100 node simulations, Figure 4 displays box plots of the reported metrics for the Erdos-Renyi case, and Table 1 reports results for the 100 node simulations. The box plots for the other networks and the results for the 40 node case are reported in the Supplementary Materials due to space constraints. The results across the three network types are relatively consistent. First, we note that the degree of dissimilarity between the networks does not appear to have a major effect on the relative performance of the algorithms, although we conjecture that the differences could be more pronounced for smaller sample sizes. For all settings involving Erdos-Renyi graphs, the proposed BJNL approach outperformed the HS, JGL, and GL uniformly across all metrics under the Wilcoxon signed rank test. Notably, the proposed approach simultaneously achieved a significantly higher TPR and a significantly lower FPR for differential edges, indicating that it was both better able to detect significant differences and less likely to incorrectly classify an edge as differential. These, and the additional box plots in the Supplementary Materials, suggest a greater power to detect true differential edges with an adequate control over false positives across all network types, under the BJNL. Further, an increased improvement of the TPR over competing approaches and relative stability of the FPR for differential edges for p = 100 versus p = 40 indicates a clear advantage of the proposed joint estimation approach for increasing dimensions. For the small-world and scale-free networks, the BJNL also had significantly improved AUC, TPR, and L₁ error metrics, and a comparable or lower FPR, compared to all other considered approaches.

Fig. 3.

ROC curves for edge detection for the 100 node simulations. The blue, green, red, and purple solid lines correspond to BJNL, JGL, GL, and HS respectively.

Fig. 4.

Box plots of the AUC, L₁ Error, and TPR/FPR for differential edge detection for the Erdos-Renyi simulations for Bayesian Joint Network Learning (BJNL), the Joint Graphical Lasso (JGL), Graphical Lasso (GL) and the Graphical Horseshoe Estimator (HS). Within each approach, the box plots are organized as: low difference, medium difference, and high difference in edges between experimental conditions, in that order.

Table 1.

100 node simulation results comparing Bayesian Joint Network Learning (BJNL), the Joint Graphical Lasso (JGL), Graphical Lasso (GL) and the Graphical Horseshoe Estimator (HS). Text in bold indicates a method was better than all other competing methods as assessed through Wilcoxon signed rank tests at α= 0.05.

	AUC				L1 Error × 100
	BJNL	JGL	GL	HS	BJNL	JGL	GL	HS
Erdos-Renyi
low	0.97 (0.01)	0.88 (0.02)	0.88 (0.02)	0.72 (0.03)	0.11 (0.01)	1.11 (0.09)	1.66 (0.13)	3.51 (0.19)
med	0.97 (0.01)	0.88 (0.02)	0.88 (0.02)	0.72 (0.04)	0.11 (0.01)	1.09 (0.09)	1.65 (0.14)	3.50 (0.20)
high	0.97 (0.01)	0.88 (0.02)	0.88 (0.02)	0.73 (0.03)	0.11 (0.01)	1.09 (0.07)	1.62 (0.11)	3.50 (0.23)
Small World
low	0.97 (0.01)	0.95 (0.01)	0.79 (0.01)	0.72 (0.04)	0.25 (0.01)	0.75 (0.12)	2.06 (0.08)	4.70 (0.15)
med	0.97 (0.01)	0.95 (0.01)	0.80 (0.01)	0.72 (0.03)	0.24 (0.01)	0.77 (0.13)	2.07 (0.08)	4.65 (0.14)
high	0.97 (0.01)	0.95 (0.01)	0.79 (0.01)	0.73 (0.03)	0.24 (0.01)	0.78 (0.13)	2.06 (0.08)	4.65 (0.14)
Scale Free
low	0.96 (0.01)	0.93 (0.01)	0.81 (0.01)	0.64 (0.03)	0.20 (0.01)	1.01 (0.20)	2.23 (0.10)	5.30 (0.23)
med	0.96 (0.01)	0.92 (0.01)	0.81 (0.01)	0.64 (0.03)	0.19 (0.01)	1.02 (0.21)	2.24 (0.90)	5.26 (0.24)
	AUC				L1 Error × 100
high	0.96 (0.01)	0.92 (0.01)	0.81 (0.01)	0.64 (0.03)	0.19 (0.01)	1.00 (0.21)	2.20 (0.08)	5.23 (0.23)
	TPR				FPR
	BJNL	JGL	GL	HS	BJNL	JGL	GL	HS
Erdos- Renyi
low	0.87 (0.05)	0.71 (0.07)	0.68 (0.07)	0.43 (0.08)	0.01 (0.001)	0.22 (0.03)	0.10 (0.02)	0.03(0.00)
med	0.88 (0.04)	0.73 (0.04)	0.69 (0.05)	0.44 (0.06)	0.01 (0.001)	0.22 (0.03)	0.10 (0.01)	0.03(0.00)
high	0.88 (0.02)	0.72 (0.03)	0.69 (0.04)	0.44 (0.06)	0.01 (0.001)	0.23 (0.02)	0.10 (0.02)	0.02 (0.00)
Small World
low	0.86 (0.04)	0.47 (0.07)	0.66 (0.06)	0.44 (0.07)	0.02 (0.002)	0.02 (0.00)	0.36 (0.01)	0.06 (0.01)
med	.86 (0.04)	0.49 (0.04)	0.67 (0.04)	0.46 (0.05)	0.02 (0.002)	0.02 (0.00)	0.36 (0.01)	0.05 (0.01)
high	0.86 (0.02)	0.48 (0.04)	0.67 (0.03)	0.46 (0.05)	0.01 (0.002)	0.02 (0.00)	0.36 (0.01)	0.05 (0.01)
Scale Free
low	0.87 (0.05)	0.39 (0.06)	0.63 (0.07)	0.25 (0.06)	0.02 (0.002)	0.02 (0.00)	0.24 (0.03)	0.04 (0.01)
med	0.87 (0.03)	0.41 (0.05)	0.63 (0.04)	0.26 (0.05)	0.02 (0.002)	0.02 (0.00)	0.24 (0.02)	0.04 (0.01)
high	0.87 (0.03)	0.42 (0.04)	0.64 (0.04)	0.27 (0.05)	0.01 (0.002)	0.02 (0.00)	0.25 (0.02)	0.04 (0.01)

On the other hand, the significantly higher L₁ error under the JGL potentially points to the perils of smoothing over edge strengths across networks under penalized approaches. In particular, assigning similar magnitudes for precision matrix off-diagonals for shared edges may adversely affect the identification of differential edges, as well as the estimation of varying edge strengths for common edges across networks. Moreover while HS has low FPR, it consistently exhibits the lowest AUC and TPR and the highest L₁ error for p = 100 across all scenarios, which is concerning. On the other hand, the GL had the highest FPR for both the small-world and scale-free network simulations, but has a reasonable TPR. These results under HS and GL illustrate the difficulties resulting from the separate estimation of individual networks which may result in exceedingly low power to detect true positives (as with HS), or an inflated number of false positives (as with GL).

To examine the sensitivity of the proposed approach with respect to the chosen link function, we performed additional simulation studies by fitting the proposed model to the 100 node data generated as above, but under a probit link. The results in Table 2 illustrate non-significant differences in the performance metrics for network estimation across the logit and the probit links, which illustrate the robustness of the proposed approach resulting from the specification of the DP prior on the shared and differential components in (2).

Table 2.

Comparison of the 100 node simulation results using the probit link function to the simulation results using the logit link function.

Erdos Renyi				Small World			Scale Free
	AUC	TPR	FPR	AUC	TPR	FPR	AUC	TPR	FPR
Probit	0.97	0.88	0.01	0.96	0.86	0.02	0.97	0.87	0.02
Logit	0.97	0.88	0.01	0.97	0.87	0.02	0.96	0.86	0.02

5. Stroop task analysis

5.1. Description of Analysis

We applied the proposed BJNL to the fMRI Stroop task study to investigate similarities and differences in the brain network under the two experimental conditions and passive fixation (REST). The first analysis was aimed at comparing the mental states of task performance (TASK) and passive fixation (REST), with the hypothesis that the brain networks exhibit major differences between these two grossly different conditions. The TASK data consisted of the subject-wise concatenation of the prewhitened fMRI time courses acquired during the exertion (EXR) and relaxed (RLX) task blocks, while the REST data consisted of the subject-wise concatenation of the prewhitened fMRI time courses acquired during the passive fixation blocks. The second analysis aimed to detect finer differences in connectivity between the mental states of EXR and RLX task performance. The study hypothesized that the mental states should be similar between the two task conditions with some fine network differences. In this case, the subject-wise prewhitened fMRI time courses were concatenated for the EXR blocks and also separately for the RLX blocks for analysis.

We performed a brain network analysis based on region of interest (ROI) level data, adopting the 90 node Automated Anatomical Labeling (AAL) cortical parcellation scheme described in Tzourio-Mazoyer et al. (2002). For each ROI, we estimated the representative BOLD time series by performing a singular value decomposition on the time series of the voxels within the ROI and extracting the first principal time series. This resulted in 90 time courses of fMRI measurements, one for each ROI, which were then demeaned. We classified each ROI into one of nine functional modules as defined in Smith et al. (2009). We performed standard pre-processing including slice-timing correction, warping to standard Talairach space, blurring, demeaning, and pre-whitening. The fMRI time series was prewhitened using an ARMA(1,1) model, as is common in imaging toolboxes such as AFNI (Cox, 1996). Further details are provided in Section 5 of the Supplementary Materials. The proposed BJNL was run using the same tuning parameters as in the simulations. Dickey-Fuller tests of stationarity were performed to assess convergence of the MCMC sampler (see Section 7 of the Supplementary Materials). We also examined the widths of the credible intervals in Section 8 of the Supplementary Materials, where Figure 7 of the Supplementary Materials demonstrates that the credible intervals for absent-edges are much narrower than the credible intervals for present-edges. Finally, we performed chi-squared goodness of fit tests under BJNL (see Section 9 of the Supplementary Materials).

Graph metrics:

We analyzed the brain’s connectivity structure during the different mental states in terms of four graph metrics: global efficiency, local efficiency, clustering coefficient, and characteristic path length. Efficiency and characteristic path length measure how effectively information in transmitted between nodes, while clustering coefficient measures the interconnectedness of the network -see Section 6 in the Supplementary Materials for a full description. All metrics were calculated using the Matlab Brain Connectivity Toolbox (Rubinov and Sporns, 2010). In addition, we also examined differences in local graph metrics across experimental conditions corresponding to several brain regions (see Tables 2-3 in the Supplementary Materials) that were found to be differentially activated in a previous study using the same Stroop task experiment (Khachouf et al., 2017). Although distinct from earlier activation analysis, potential connectivity differences in these previously identified brain regions will bolster earlier activation based discoveries and also help illustrate the biological interpretability of the connectivity analysis.

5.2. Results

TASK vs REST Conditions:

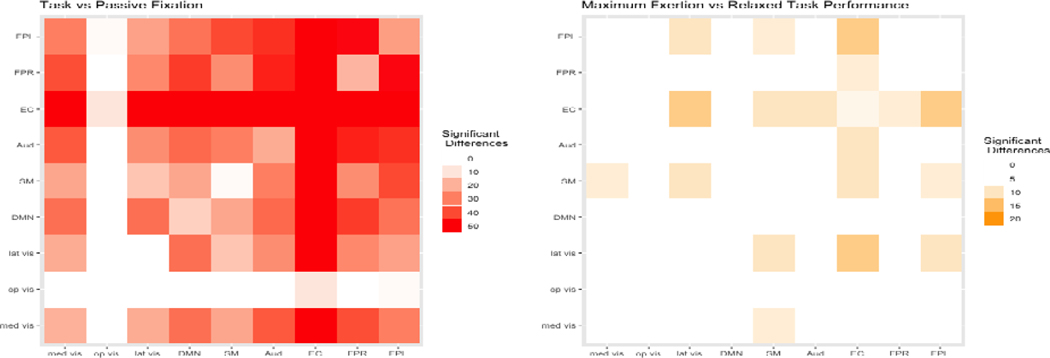
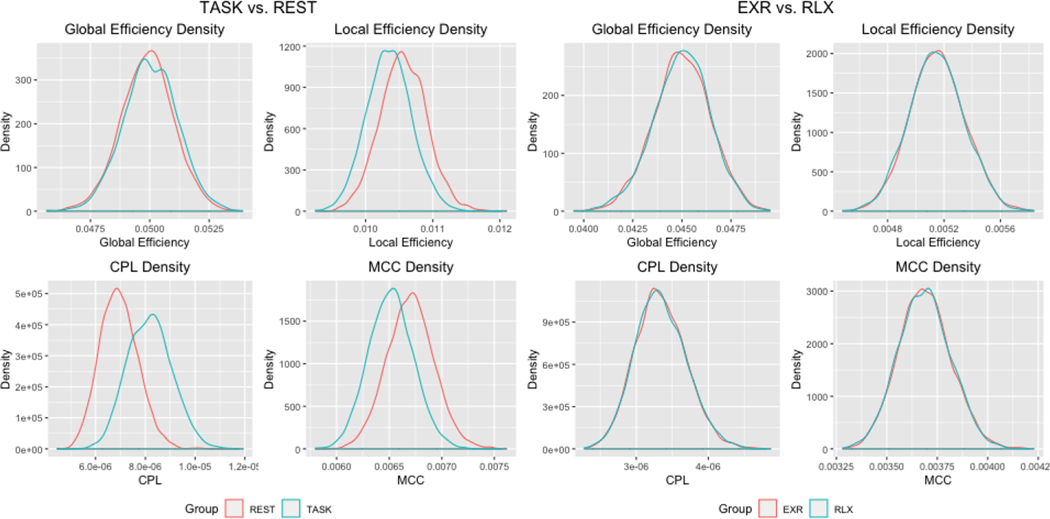
The analysis produced a large contingent of edges with significantly different edge strengths in the two mental states - Figure 6 displays a heatmap of the significant edge counts by functional module. Our analysis revealed 1550 significantly different edges (under T-tests) that provide evidence supporting the study hypothesis that there are major differences in the brain networks due to the manifest phenomenological and procedural dissimilarity of task performance and rest. Moreover, our examination revealed significant differences in the mean (under T-tests) and the posterior distributions (under KS tests) for all network metrics between the two conditions (Figure 5). Additional examination of local network differences between task and fixation conditions corresponding to 20 pre-specified regions revealed larger clustering coefficients for REST in all implicated regions, and larger local efficiencies for REST in 18 of the 20 regions (see the Supplementary Materials Table 2 for the brain regions and p-values).

Fig. 6.

Heatmaps of the number of differential edges between conditions. The heatmap on the left corresponds to the analysis of task vs. passive fixation, and the heatmap on the right corresponds to the analysis of maximum exertion (EXR) vs. relaxed task performance (RLX).

Fig. 5.

Estimated densities of graph metrics for the analysis of task vs. passive fixation and maximum exertion (EXR) vs. relaxed (RLX) task performance.

EXR vs. RLX conditions of task performance:

Compared with the relatively large network differences between TASK and REST, the network structures corresponding to the EXR and RLX task conditions exhibited more nuanced differences. Our analysis revealed 226 significantly different edges between the EXR and RLX conditions - see Figure 6 for a heatmap of the significant edge counts by functional module. None of the graph metrics were significantly different between the EXR and RLX conditions, implying that the network differences did not manifest at a global level (Figure 5). However, more localized changes were discovered in the pre-selected regions that were previously shown to be differentially activated between EXR versus RLX (Khachouf et al., 2017). Significant differences were found in terms of mean local efficiency in the right inferior occipital node and the left caudate. Similarly, significant differences were found in mean and distribution for the clustering coefficient for the right inferior occipital node. Several borderline network differences were also identified - see Table 3 in the Supplementary Materials for reported p-values.

Interpretation of Findings:

Our BJNL analysis identified strong connectivity differences between Stroop task performance and passive fixation in terms of significantly higher efficiency and clustering, and lower characteristic path length for REST as well as stronger positive connections involving frontoparietal circuits, EC, DMN, sensorimotor, and visual cortices in the TASK condition compared to REST. Our findings also aligned with the widely used theory of global workspace where more difficult tasks are associated with increased connection distance, as well as reduced clustering (GeiBerg et. al, 2013). More localized associations were also discovered in all regions identified as differentially activated in previous studies (Khachouf et al., 2017), which highlights the biological interpretability of our connectivity findings. Our analysis provides exciting new insights into the connectivity differences between passive fixation and the task-related network that requires a rearrangement of connections in order to perform the task.

On the other hand, fewer connectivity differences were discovered between EXR and RLX task performance, as expected due to the only difference between conditions being the level of voluntary effort invested in the task. While no global topological differences between the EXR and RLX conditions were discovered, the BJNL analysis did reveal some fine differences in the functional modules including the EC and FPL that are involved in high level cognitive function, as well as some limited localized connectivity differences in 23 pre-specified brain regions that previously showed major activation differences in (Khachouf et al., 2017). In general compared to TASK versus REST, the RLX task performance condition featured significantly more negative connections between regions compared to EXR, and there were fewer connectivity differences between nodes within the EC. Compared to a much larger number of connectivity differences in EC and other functional modules in TASK versus REST, the limited connectivity differences between EXR and RLX implies a restricted rearrangement of the network between EXR and RLX.

Comparison with penalized approaches:

We are also interested in comparing the network differences under BJNL with those obtained under penalized methods. Hence we performed an illustrative analysis for the Stroop task data using the GL and JGL approaches that involved permutation testing to infer significant network differences between experimental conditions. A permuted sample for two experimental conditions was generated by randomly switching the labels across conditions multiple times. Then, the networks corresponding to these permuted samples were computed using JGL and GL. Subsequently, the network differences corresponding to distinct experimental conditions were computed. The above process was repeated 10,000 times, and the permutation distributions for between-network differences were constructed to compute p-values to test for significant differences.

Note that it was computationally infeasible to use AIC to select the tuning parameters for JGL for all 10,000 permutations since the run time for the best tuning parameter search over a grid took one hour per permutation. Hence, the starting values for the tuning parameters for JGL were selected as those values used for the JGL analysis for the original data without permutation. The tuning parameters were then adaptively searched on a permutation-by-permutation basis until the resulting edge density was within 20% of the edge density for the network corresponding to the original samples. While the process was required to make testing under the JGL computationally feasible, it could potentially result in misleading results under JGL due to possible mis-specification of network densities.

The analysis revealed that only one of the resulting edges for the EXR versus RLX network comparisons was significant under the GL, whereas only 62 edges were significant for the JGL. Similarly, for the analysis of TASK versus REST, the JGL identified 476 edges with differential strengths and 3873 common edges (versus 1550 differential edges and 1565 common edges under BJNL). In this case, GL was able to identify 51 edges with differential strengths, and 552 common edges. We believe that the low number of differential edges between EXR versus RLX conditions under the penalized approaches is unrealistic, and that more differences are to be expected between TASK and REST since it involves significant differences in brain activation across the brain (Khachouf et al., 2017). Further, only 5 of the 20 pre-specified brain regions which were shown to be differentially activated had significant network differences between TASK and REST under the penalized approaches (see Supplementary Materials Table 1). These results suggests the proposed BNJL method has much better statistical power to detect differences in brain networks under different cognitive states compared to penalized approaches for modeling networks.

6. Discussion

In this paper we introduced a novel Bayesian approach to joint estimation of multiple group level brain networks that pools information across networks to estimate shared and differential patterns in brain functional networks formed under different cognitive conditions. The proposed BJNL approach naturally enables a systematic inferential framework for comparing networks, which is a central question of interest in many connectome studies including our Stroop task application where the focus is to investigate connectivity differences between passive fixation and relaxed and exertion modes of Stroop task. Our analysis of Stroop task data revealed important dissimilarities between the task and rest conditions, but more subdued differences between the two task conditions, which aligns with the scientific hypotheses of the study. Moreover the connectivity differences were found to be concentrated in brain regions shown to be differentially activated for Stroop task in previous studies, which signifies that the connectivity differences are biological interpretability. In contrast, a separate estimation of networks using penalized approaches identified negligible or limited connectivity differences between varying modes of mental effort that seem biologically implausible. In addition, the joint estimation of multiple networks under a penalized approach is not naturally conducive for comparing networks and hence one had to use computationally prohibitive permutation tests that tend to give sub-optimal results in terms of network accuracy and inferring between-network differences.

In this paper, we demonstrated BJNL for estimating networks using fMRI data because they are the most prevalent type of functional images. However, our method can also be generalized to data from other imaging modalities in a straightforward manner. One advantage of our proposed approach for clustering the edge weights is that it allows for unsupervised estimation of the number of clusters. This means that in generalizing the method to other modalities, we do not have to laboriously tune the clustering parameters to each individual problem. Going beyond multiple experimental conditions, our approach can also be used to jointly model networks across multiple cohorts, such as healthy individuals, subjects with mild cognitive disorder, and those with Alzheimer’s disease (Kundu et al., 2019). Future work should investigate the scalability of BJNL to larger numbers of conditions while taking into account the dynamic nature of the brain networks over time.