Predicting hydrogen storage in MOFs via machine learning

Alauddin Ahmed; Donald J Siegel

doi:10.1016/j.patter.2021.100291

. 2021 Jun 24;2(7):100291. doi: 10.1016/j.patter.2021.100291

Predicting hydrogen storage in MOFs via machine learning

Alauddin Ahmed ¹, Donald J Siegel ^1,^2,^3,^4,^5,^∗

PMCID: PMC8276024 PMID: 34286305

Summary

The H₂ capacities of a diverse set of 918,734 metal-organic frameworks (MOFs) sourced from 19 databases is predicted via machine learning (ML). Using only 7 structural features as input, ML identifies 8,282 MOFs with the potential to exceed the capacities of state-of-the-art materials. The identified MOFs are predominantly hypothetical compounds having low densities (<0.31 g cm⁻³) in combination with high surface areas (>5,300 m² g⁻¹), void fractions (∼0.90), and pore volumes (>3.3 cm³ g⁻¹). The relative importance of the input features are characterized, and dependencies on the ML algorithm and training set size are quantified. The most important features for predicting H₂ uptake are pore volume (for gravimetric capacity) and void fraction (for volumetric capacity). The ML models are available on the web, allowing for rapid and accurate predictions of the hydrogen capacities of MOFs from limited structural data; the simplest models require only a single crystallographic feature.

Keywords: energy storage, fuel cells, metal-organic frameworks, hydrogen storage, machine learning, materials discovery, chemistry, materials science

Graphical abstract

Highlights

•
Accurate and general ML models for predicting H₂ storage in MOFs are developed
•
The models require minimal input data that are easily derived from the MOF structure
•
High-capacity MOFs are identified, and capacity-structure connections are revealed
•
The web models (https://sorbent-ml.hymarc.org) can predict the performance of new MOFs

The bigger picture

The efficient storage of hydrogen fuel remains a barrier to the adoption of fuel cell vehicles. Although many storage technologies have been proposed, adsorptive storage in metal-organic frameworks (MOFs) holds promise due to the low operating pressures, fast kinetics, reversibility, and high gravimetric densities typical of MOFs. Nevertheless, the volumetric storage densities of known MOFs are generally low; hence, new MOFs with improved volumetric performance are desired. Identifying optimal MOFs remains a challenge, however, because relatively few MOFs have been characterized experimentally, and the building-block structure of MOFs suggests that the number of possible materials is limitless. To accelerate the discovery process, this study develops machine learning models that predict the hydrogen capacity of MOFs. The models identify promising materials, clarify structure-property relations, and can be used—on the web or through an API—to predict the performance of new MOFs.

The adoption of hydrogen as a low-carbon fuel has been slowed by the low energy density of H₂ gas. Hydrogen adsorption in MOFs presents a pathway for storing hydrogen at the densities desired for mobile applications, such as fuel cell vehicles. Nevertheless, identifying a suitable MOF remains a challenge because the number of MOFs is essentially limitless. To accelerate the discovery of high-capacity hydrogen adsorbents, machine learning models are developed to predict hydrogen uptake across a diverse set of MOFs.

Introduction

Hydrogen (H₂) is considered to be a future automotive fuel.1, 2, 3, 4, 5, 6 This potential reflects its high specific energy compared with competing fuels, such as natural gas and gasoline, and the ability of H₂ to be produced renewably and consumed without CO₂ emissions.²^,⁷ Nevertheless, the adoption of hydrogen in mobile applications, such as fuel cell (FC) vehicles has been limited by its low volumetric energy density.²^,⁶^,⁷ Consequently, the design of low-cost H₂ storage systems that overcome these volumetric limitations has been the focus of recent research.⁴^,8, 9, 10, 11, 12 At present, FC vehicles employ storage systems based on gaseous H₂ compressed to pressures up to 700 bar.¹³ This approach is costly and can incur limitations in driving range.⁷^,¹¹^,¹³^,¹⁴

Storage based on adsorption in porous hosts is an alternative to high-pressure compression.¹⁵ Due to their high gravimetric densities, fast kinetics, and reversibility, metal-organic frameworks (MOFs) have emerged as one of the most promising classes of hydrogen sorbents.²^,⁷ MOFs are crystalline materials formed by the self-assembly of inorganic metal clusters and organic linkers.16, 17, 18, 19, 20, 21, 22 By virtue of their building-block structure and the large number of potential components, the number of MOFs is potentially limitless.21, 22, 23, 24, 25 Further modifications to MOF chemistry can be achieved by introducing functional groups, substituting different metals, and by mixing metals and/or linkers.26, 27, 28

Despite these many possibilities, a relatively small fraction of MOFs have been synthesized.²⁹^,³⁰ While the crystal structures of these “real” MOFs are available in the Cambridge Structural Database (CSD),²⁹^,³⁰ many exhibit disorder, missing atoms, or have negligible porosity; consequently, these materials are not immediately amenable to assessment via computational modeling.²⁹^,31, 32, 33, 34, 35

One way to bypass these complications is through computational design. To date, nearly a million “hypothetical” MOFs have been reported,¹^,36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46 and it is reasonable to expect that many more materials will be proposed.47, 48, 49, 50, 51 High-throughput screening using Grand Canonical Monte Carlo (GCMC)52, 53, 54, 55, 56 has been successful in identifying promising candidates with superior gas storage capacities on sub-sets of these catalogs.³⁶^,³⁸^,³⁹^,⁴⁶^,⁵⁰^,57, 58, 59, 60 Nevertheless, given the large number of possibilities, a systematic search across all of these materials is challenging even with high-throughput techniques.¹^,⁶¹ Furthermore, differences in the implementation (i.e., use of different temperature/pressure conditions or interatomic potentials) can complicate comparisons between screening studies. Thus, more efficient and consistent screening approaches are desirable for predicting the gas storage properties of MOFs in existing and future databases.

Machine learning (ML) could provide a path forward.62, 63, 64, 65 For ML to be helpful, access to high-quality training data is essential. Unfortunately, training on experimental H₂ storage data in MOFs is non-trivial¹^,²^,⁶^,66, 67, 68: experimental uptake data are generally restricted to a relatively small number of MOFs, and can depend sensitively upon the experimental conditions and the purity of the sample.²^,⁶⁷^,⁶⁹ Employing a dataset based on a consistent set of computational predictions may be a better choice.⁶²^,⁶³

Earlier work has demonstrated that accurate isotherms for H₂ uptake in MOFs can be predicted using the pseudo-Feynman-Hibbs potential (to describe H₂) combined with general interatomic potentials to describe the MOF.¹^,²^,⁶^,⁶⁸ This approach was used to screen a database of 5,309 real MOFs, from which IRMOF-20 was identified and experimentally demonstrated to have a favorable balance of high gravimetric and volumetric H₂ density.² In a follow-on study, a larger database of 495,305 MOFs was compiled from several publicly available databases (see Table S1 for details).¹^,²⁹^,³¹^,³³^,36, 37, 38, 39, 40^,⁴⁵ Following a pre-screen based on crystallographic properties and empirical correlations, the H₂ capacities of a subset of 43,777 MOFs were evaluated using GCMC. Three additional MOFs—SNU-70, UMCM-9, and PCN-610/NU-100—were identified and shown experimentally to out-perform the leading MOF candidate, IRMOF-20.¹

The database of MOF properties⁷⁰ generated in these previous studies presents an opportunity to develop ML models that can predict H₂ uptake across even larger MOF datasets.¹^,⁷⁰ Table 1 summarizes previous ML studies of H₂ storage in MOFs. (Reports employing ML for other adsorbates, such as CH₄,⁷¹^,⁷² CO₂,⁷³^,⁷⁴ and N₂⁷³^,⁷⁴ are summarized in Table S2.) To the best of our knowledge, ML was first used to predict H₂ uptake in compounds from the Nanoporous Materials Genome.⁷⁵ A neural network (NN)⁷⁶ was used to predict usable capacities on a test set of ∼1,000 compounds, including MOFs.⁶¹ In the same year, Borboudakis et al.⁶³ predicated H₂ capacities in 100 MOFs using 92 binary features related to a MOF's linker, metal cluster, and functional group(s). Ridge linear regression (RR)76, 77, 78 and support vector machine (SVM)⁷⁶^,⁷⁹ algorithms were used to predict gravimetric capacity. Later, Bucior et al⁸⁰ predicted the H₂ capacities of 54,776 MOFs extracted from the CSD using multilinear regression (MLR).⁷⁶ The models were trained using the energetics of H₂-MOF interactions and the usable volumetric capacities predicted by GCMC. More recently, ML was used to predict H₂ storage capacities in 105 hypothetical MOFs constructed from 17 different topologies, 4 distinct metal clusters, and 5 unique organic linkers.⁴³ NN⁷⁶ models employing 11 features were trained to predict total volumetric uptake at various temperatures and pressures.⁴³

Table 1.

Summary of recent studies that use machine learning to predict H₂ adsorption in MOFs

Study	ML features	ML method	Properties predicted	Accuracy
Anderson et al.⁴³	epsilon, temperature, pressure, ρ_crys, vf, vsa, mpd, lcd, alchemical catecholate site density, unit cell volume	neural network⁷⁶	total volumetric H₂ for pressures 0.1, 1, 5, 35, 65, and 100 bar at 77, 160, and 295 K	AUE = 0.75–2.93 g-H₂ L⁻¹
Bucior et al.⁸⁰	energetics of MOF-guest interactions	multilinear regression with LASSO⁷⁶	deliverable H₂ storage capacity between 2 and 100 bar at 77 K	R² = 0.96; AUE = 1.4–3.4 g-H₂ L⁻¹; RMSE = 3.1–4.4 g-H₂ L⁻¹
Borboudakis et al.⁶³	92 binary features based on linker, metal cluster, and 12 functional groups	ridge linear regression and support vector machine with polynomial/Gaussian kernel76, 77, 78	total H₂ storage capacity at 1 bar and 77 K	AUE = 0.47 (ridge regression), 0.50 (SVM) g-H₂ g⁻¹-MOF
Thornton et al.⁶¹	adsorption energy, ρ_crys, vf, gsa, vsa, lcd	neural network⁷⁶	net H₂ capacity for pressure swing between 1 and 100 bar at 77 and 298 K	R² = 0.88; RMSE = 3.6 g-H₂ L⁻¹

Open in a new tab

ρ_crys, vf, vsa, mpd, lcd represent single-crystal density, void fraction, volumetric surface area, maximum pore diameter, and largest cavity diameter, respectively. R², AUE, and RMSE represent the coefficient of determination, average unsigned error, and root-mean-square error, respectively.

Expanding upon these previous reports, this study applies ML to explore a large database of 918,734 known and proposed MOFs. The database was assembled from a diverse collection of publicly available MOF repositories,¹^,²⁹^,³¹^,³³^,³⁴^,36, 37, 38, 39, 40, 41, 42, 43, 44, 45^,⁸¹^,⁸² and allows for a wide-ranging and consistent assessment of H₂ uptake in MOFs.

Here, the extremely randomized trees (ERT)⁷⁶^,⁸³ algorithm was identified as the most accurate ML model for predicting H₂ uptake. A training set comprising 24,674 MOFs was sufficient to enable accurate predictions of usable capacities across 820,039 unseen compounds.⁷⁰ These predictions were made using a small set of seven crystallographic features as input: single-crystal density, pore volume, gravimetric and volumetric surface area, void fraction, largest cavity diameter, and pore limiting diameter. Importantly, ML identified 8,282 MOFs—8,187 appropriate for pressure swing (PS) operation and 95 for temperature-PS (TPS) use—with the potential to exceed both the gravimetric and volumetric capacities of state-of-the-art materials. These compounds are comprised predominantly of hypothetical MOFs, and exhibit low densities (<0.31 g cm⁻³) in combination with high surface areas (>5,300 m² g⁻¹), void fractions (∼0.90), and pore volumes (>3.3 cm³ g⁻¹). In addition to identifying high-capacity MOFs, the relative importance of the input features is quantified; dependencies on the ML algorithm and training set size and are also assessed. The most important features for predicting H₂ uptake are pore volume (for gravimetric capacity) and void fraction (for volumetric capacity). A simplified model using only two input features is demonstrated to predict capacities with high accuracy—within 0.2 wt % and 1.4 g-H₂ L⁻¹ of more expensive Monte Carlo calculations. The ML models are available for use via the web,⁸⁴ allowing for rapid and accurate predictions of hydrogen capacities with only a small amount of structural data required as input.

Methods

MOF database

A database of crystal structures for 918,734 MOFs was created by combining 19 existing databases.¹^,²⁹^,³¹^,³³^,³⁴^,36, 37, 38, 39, 40, 41, 42, 43, 44, 45^,⁸¹^,⁸² Table 2 summarizes the source databases and the number of MOFs contained in each. Out of these 19 databases, only the UM,³¹ CSD,²⁹^,³⁰ and CoRE³³^,³⁴ databases contain data on MOFs that have been previously synthesized. (MOFs listed in these datasets are referred to as “real” MOFs.) The remaining databases contain data for proposed, or “hypothetical”, MOFs. The seven crystallographic properties for all MOFs in the database were calculated using the zeo++ code²⁵^,⁴⁷ with a probe radius of 1.86 Å. These data are available at the HyMARC data hub.⁷⁰ Additional details can be found in our previous work.¹ These properties include: single-crystal density (d), pore volume (pv), gravimetric surface area (gsa), volumetric surface area (vsa), void fraction (vf), largest cavity diameter (lcd), and pore limiting diameter (pld).

Table 2.

MOF datasets employed in this study

Source	Database identity	No. of MOFs
Goldsmith et al.,³¹ Chung et al.,³³ Moghadam et al.,²⁹ Groom et al.³⁰	real MOFs: UM³¹+CoRE³³+CSD²⁹^,³⁰	15,235
Chung et al.³⁴	CoRE 2019³⁴	14,142
Moghadam et al.,²⁹ Groom et al.³⁰	^aCSD 2017 additional²⁹^,³⁰	48,696
Martin et al.³⁸	mail-order³⁸	112
Bao et al.⁴⁶	in silico deliverable⁴⁶	2,816
Bao et al.³⁹	in silico surface³⁹	8,885
Witman et al.⁴⁰	MOF-74 analogs⁴⁰	61
Colón et al.⁵⁹	ToBaCCo⁵⁹	13,512
Gomez-Gualdron et al.⁴⁵	Zr-MOFs⁴⁵	204
Wilmer et al.³⁶	Northwestern³⁶	137,000
Aghaji et al.,³⁷ Boyd et al.⁸⁵^,⁸⁶	^bUniv. of Ottawa³⁷^,⁸⁵^,⁸⁶	317,462
Lan et al.⁸¹	BJT MOFs⁸¹	303,793
Chung et al.⁴¹^,⁸⁷	^cR-WLLFHS⁴¹^,⁸⁷	51,163
Li et al.⁸²	MTV⁸²	11,555
Anderson et al.⁴²	CSM-2018-I⁴²	117
Anderson et al.⁴³	CSM-2018-II⁴³	32
Anderson et al.⁴⁴	CSM-2019-I⁴⁴	99
Ahmed et al.¹	in-house¹	18
	total	918,734

Open in a new tab

A subset of the CSD 2017 MOF dataset²⁹^,³⁰ whose crystallographic properties were found to exhibit extremely low values (e.g., GSA ~0) in a previous study.

A recent version of this database is available publicly;⁸⁵^,⁸⁶ however, this study employs an earlier version³⁷ that was shared privately.

A curated subset of the Northwestern³⁶ database.

A previous study examined a subset of the present database, wherein the hydrogen uptake in 495,305 MOFs was estimated using the Chahine rule.¹^,²^,⁷⁰ Subsequently, usable uptake in a portion of this subset comprising 43,777 MOFs predicted to be promising based on the Chahine rule was evaluated using GCMC. This GCMC-evaluated dataset contained a mix of real and hypothetical MOFs: 15,235 real MOFs were sourced from the UM,³¹ CoRE,³³ and CSD,²⁹^,³⁰ and 28,542 hypothetical MOFs were extracted from the mail-order,³⁸ in silico deliverable,⁴⁶ in silico surface,³⁹ MOF-74 analogs,⁴⁰ ToBaCCo,⁵⁹ Zr-MOFs,⁴⁵ Northwestern,³⁶ University of Ottawa,³⁷^,⁸⁵^,⁸⁶ and in-house¹ hypothetical MOF databases (see Ahmed et al.¹ or Table S1 for details).¹^,²⁹^,³¹^,³³^,36, 37, 38, 39, 40 Hydrogen uptake isotherms for two operating conditions were predicted: for an isothermal PS at T = 77 K between 5 and 100 bar, and for a combined TPS between 77 K/100 bar (filled state) and 160 K/5 bar (empty state). UG and UV capacities were then calculated based on the isotherm data.

In addition to the 43,777 MOFs examined in Ahmed et al.,¹ in this study GCMC isotherms were evaluated for an additional 54,918 MOFs (see Ahmed et al.¹ and Table S1 for further details). These additional MOFs were selected at random from the 495,305-entry HyMARC database and therefore represent a more diverse sampling of the MOF property space. To this dataset, 423,429 additional compounds were added from 7 additional datasets: BJT (Beijing, Jiangsu, Tianjin) MOFs,⁸¹ R-WLLFHS,⁴¹^,⁸⁷ MTV,⁸² CSM-2018-I,⁴² CSM-2018-II,⁴³ and CSM-2019-I,⁴⁴ and selected MOFs from the CSD 2017 dataset.²⁹^,³⁰ Subsequently, the capacities of the MOFs from these additional datasets were predicted by the ML models without retraining (i.e., no MOFs from these datasets were used for training or testing, and none of their isotherms were evaluated in advance with GCMC). In total, the dataset employed in this study contains H₂ uptake data for 98,695 MOFs⁷⁰ and crystallographic property data for 918,734 MOFs.

The present dataset includes approximately 74,000 MOFs having open metal sites (OMS), comprising roughly 8% of the total dataset. As the interatomic potential used in our GCMC calculations is not tuned to capture the unique aspects of the H₂-OMS interaction, it is possible that the calculated capacities for this class of MOFs will be less accurate. Figure S1 and Table S3 compare experiments and the present GCMC calculations of H₂ capacities across a benchmark set of OMS MOFs discussed by García-Holley et al.⁸⁸ and in our previous work.¹ These data show that GCMC calculations using the pseudo-Feynman-Hibbs potential are in good agreement with experimental data for these OMS MOFs. The good agreement between theory and experiments is a consequence of the low temperature operating conditions used in our study, combined with the relatively low density of OMS in these MOFs.

ML models

The No Free Lunch Theorem⁸⁹ implies that the optimal choice of ML algorithm is problem specific. The differing performance of the algorithms summarized in Tables 1 and S2 is consistent with this notion. Identifying the best algorithm for a given dataset requires comparing multiple ML methods, each with optimized hyperparameters. Unfortunately, few comparisons of ML methods for gas adsorption exist; although dozens of ML algorithms are available,76, 77, 78, 79^,⁸³^,90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100, 101, 102, 103, 104 only RR,76, 77, 78 MLR,⁷⁶ SVM,⁷⁶^,⁷⁹ and NN⁷⁶ have been examined for predicting H₂ storage.⁴³^,⁶¹^,⁶³^,⁸⁰^,¹⁰³ This study casts a wider net by comparatively assessing 14 ML algorithms (Table 3).76, 77, 78, 79^,⁸³^,90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100, 101, 102, 103, 104

Table 3.

Machine learning regression algorithms employed in this work

Machine learning algorithm	Abbreviation
Extremely randomized trees⁷⁶^,⁸³^,¹⁰³^,¹⁰⁴	ERT
Boosted decision trees⁷⁶^,⁹²^,102, 103, 104	BDT
Bagging with decision trees⁷⁶^,⁹⁰,⁹³^,¹⁰³^,¹⁰⁴	B/DT
Random forest⁷⁶^,⁹⁰^,⁹⁴^,¹⁰³^,¹⁰⁴	RF
Bagging with random forest⁷⁶^,⁹³^,⁹⁴^,¹⁰³^,¹⁰⁴	B/RF
Gradient boosting⁷⁶^,⁹²^,⁹⁵^,102, 103, 104	GB
Decision trees⁷⁶^,⁹⁰^,¹⁰³,¹⁰⁴	DT
Nu-support vector machine with radial basis function (RBF) kernel⁷⁶^,⁷⁹^,⁹⁰^,⁹⁶^,⁹⁸^,¹⁰³,¹⁰⁴	Nu-SVM/RBF-K
Support vector machine RBF kernel⁷⁶^,⁷⁹^,⁹⁰^,⁹⁷^,⁹⁸^,¹⁰³,¹⁰⁴	SVM/RBF-K
Support vector machine with linear kernel⁷⁶^,⁷⁹^,⁹⁶^,⁹⁹^,¹⁰³,¹⁰⁴	SVM/L-K
Linear regression76, 77, 78^,⁹⁹^,¹⁰⁰^,¹⁰³,¹⁰⁴	LR
Ridge regression76, 77, 78^,⁹⁹^,¹⁰⁰^,¹⁰³,¹⁰⁴	RR
K-nearest neighbors⁷⁶^,⁹⁰^,¹⁰¹^,¹⁰³,¹⁰⁴	K-NN
AdaBoost⁷⁶^,⁹²^,102, 103, 104	AB

Open in a new tab

The crystallographic properties of MOFs are known to correlate with H₂ capacities.²^,³¹^,⁸⁸^,105, 106, 107, 108 The ML models developed here exploit these correlations by adopting only crystallographic properties as input features. Moreover, the number of features was restricted to a small set comprising seven properties: d, pv, gsa, vsa, vf, lcd, and pld. These are the same properties employed in our previous work.¹^,²^,⁴⁷^,¹⁰⁹ Figure S2 shows the distribution of crystallographic properties for the training, test, and unseen datasets. Also, Table S4 summarizes five descriptive (minimum, maximum, mean, median, and percent of 0's) and two distribution statistics (skew and kurtosis) of all crystallographic features for the training, test, and unseen datasets. (The details regarding these statistics and the definitions of skew and kurtosis can be found in Table S4.) The maxima and minima of the features in the training set establish the validity ranges of the ML models developed here.

The goal of the ML models is to predict four output properties: UG and UV for each of PS and TPS operating conditions. This was accomplished by developing separate ML models for each of the four targeted capacities. Figure S3 illustrates the overall work flow.

The existing dataset of 98,695 MOFs (for which both crystallographic and capacity data are available)⁷⁰ was initially split into training and test sets of 74,201 and 24,674 MOFs, respectively, after shuffling the entire dataset.¹⁰⁴ ML algorithms⁹⁰^,⁹³^,⁹⁴^,¹⁰⁴ (Table 3) were implemented using the Scikit-learn library.¹⁰⁴ Both scaled and unscaled features were used in training ML models. Ten-fold cross-validation was used to optimize the hyperparameters of each model. The performance of the ML algorithms was assessed by comparing the predicted H₂ capacities with the capacity predicted by GCMC for the MOFs in the test set. The metrics used for the performance assessment of ML models were the R², AUE, RMSE, MAE, and $τ$ . Additional details regarding these calculations can be found in supplemental note S2 of the supplemental information.

Dataset size

An obstacle to wider adoption of ML in materials science is the availability of sufficient quantities of high-quality training data.¹¹⁰^,¹¹¹ Unfortunately, it is not yet clear how much data are needed to construct a useful ML model for a given system. Fernandez et al.⁷² found that a reasonable balance between accuracy (R² ∼ 0.85–0.93) and computational expense for predicting methane storage in MOFs was achieved for a training set containing data on 10,000 MOFs with 3 features. In contrast, Fanourgakis et al.¹¹² showed that a much smaller training set of ∼1,000 MOFs was sufficient to predict methane uptake when using six crystallographic features and four fictitious features. The different training set sizes required in these previous studies arise from the differing numbers and types of features used.

This study explores this issue further by systematically examining the effect of training set size, and the training set to test set ratio, on ML accuracy. For each of the four targeted capacity outputs, 100 independent ML models were developed by varying the size of the training set between 100 and 74,000 MOFs (see Table S5 for a list of the training set sizes). The four best-performing ERT ML algorithms identified earlier were used with 10-fold cross-validation. The resulting models were assessed using a common test set of 24,674 MOFs.

Feature importance/selection

The well-known Chahine rule proposes a linear correlation between gravimetric surface area and excess gravimetric H₂ capacity in adsorbents.¹¹³^,¹¹⁴ Nevertheless, the Chahine rule overpredicts H₂ capacities for MOFs with high surface areas,¹¹⁴ and has not been extended to predict usable capacities.¹^,²^,⁶ Hence, a model for predicting H₂ uptake that is more general than the Chahine rule, yet requires limited input data, would be very helpful. In principle, ML could be used to generate such a predictive model if the features that are the most important for predicting H₂ uptake could be identified. Along these lines, Pardakhti et al. reported improved accuracy in predicting CH₄ adsorption when using a combination of (7) crystallographic and (19) chemical features.⁷¹ Recently, Moosavi et al. explored feature importance in predicting the synthesis of MOFs.¹¹⁵

This study determines the minimum number and optimal combination of crystallographic features necessary to achieve a specified accuracy in predicting H₂ uptake. The relative importance of the input features was assessed for all possible univariate and multivariate feature combinations using ERT ML models. The number of multivariate feature combinations, M, is given by: $M (n_{t o t}, n_{s u b}) = \frac{n_{t o t}!}{n_{s u b}! (n_{t o t} - n_{s u b})!}$ , where n_tot = 7 is the total number of available features, and 1 ≤ n_sub ≤ 7 is the number of features used as input to a given ML model. A total of 127 feature combinations are possible. ML models were developed for each of these feature combinations for each of the 4 output capacities, resulting in a total of 508 distinct ML models. All models were trained using a dataset of 74,021 MOFs and tested on a common set of 24,674 MOFs. Ten-fold cross-validation was used for tuning and validating the models using only the training set. Univariate feature importance was further assessed using (1) Pearson's correlation coefficient (r),116, 117, 118 (2), Breiman and Friedman's tree-based algorithm as implemented in Scikit-learn,⁹⁰^,¹⁰⁴ and (3) the permutation importance method as implemented in rfpimp package.¹¹⁹ Additional details regarding these methods can be found in Figure S7.

Results

Evaluating ML algorithms

Tables S6–S9 illustrate the effect of several feature scaling methods on the performance of the ML algorithms examined here. Only the SVM family of models (SVM/L-K, SVM/RBF-K, and Nu-SVM/RBF-K)⁷⁶^,⁹⁰^,⁹⁶^,⁹⁸^,⁹⁹^,¹⁰⁴ were impacted by the choice of scaling method.

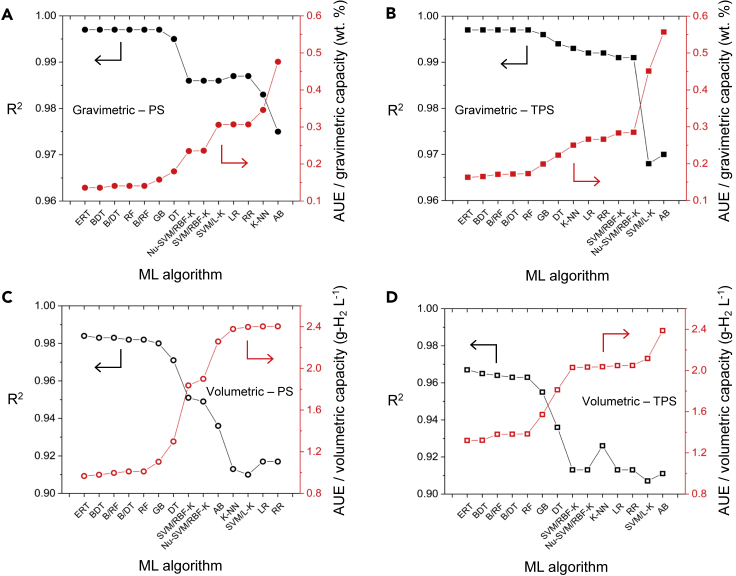
Figure 1 compares the accuracy of the ML algorithms for predicting hydrogen uptake in MOFs. Coefficient of determination (R²) and average unsigned error (AUE) were used as performance metrics. SVM variants were trained using min-max feature scaling; unscaled features were used in training the remaining models. The performance of the algorithms as measured by four additional metrics—root-mean-square error (RMSE), explained variance (EV), median absolute error (MAE), and Kendall rank correlation coefficient ( $τ$ )—is reported in Tables S6–S9.

Comparison of ML algorithms for predicting hydrogen uptake in MOFs

(A and C) Left and (B and D) right panels report performance for PS and TPS conditions, respectively. (A and B) Top and (C and D) bottom panels report performance for usable gravimetric and volumetric capacities, respectively. The abbreviations for the ML methods are defined in Table 3.

Overall, these data indicate that the tree-based ensemble methods are superior to the other methods examined. In particular, the ERT⁷⁶^,⁸³^,¹⁰⁴ algorithm exhibited the best performance overall. Boosted decision trees,⁷⁶^,90, 91, 92^,¹⁰²^,¹⁰⁴ random forest,⁷⁶^,⁹⁴^,¹⁰⁴ and Bagging algorithm variants⁷⁶^,⁹³^,¹⁰⁴^,¹²⁰^,¹²¹ (with tree-based base estimators) are nearly as accurate. The R² values for ERT predictions exceed 0.997 for gravimetric capacities, which are equivalent to errors of ∼0.14 wt %. Volumetrically, the accuracy of the ERT algorithm is slightly worse than its gravimetric performance: R² = 0.967–0.984, equivalent to errors of ∼1.1 g-H₂ L⁻¹ on average. In general, the worst-performing algorithms were linear regression, ridge regression, and SVM with linear kernel. For these algorithms R² varies between 0.913 and 0.992 depending on the conditions (i.e., gravimetric/volumetric and PS/TPS). As expected, the linear nature of these algorithms fails to fully capture the nonlinear dependence of output capacities on the multiple input features.

Figure 1 also shows that all the algorithms tested yield more accurate predictions of usable gravimetric (UG) capacities compared with those for usable volumetric (UV) capacities. Likewise, all algorithms more accurately predict usable capacities under PS conditions than under TPS conditions. This reflects the fact that the functional relationships between output capacities (UG/UV) and input features under PS and TPS conditions are likely different, as was observed in previously reported structure(feature)-property(capacity) relationships.¹^,⁶^,¹²² Table 4 summarizes the performance of the ERT algorithm in further detail. A comparison of Tables 1 and 4 indicates that the accuracy of the present ML models surpass previously reported models for H₂ uptake. Furthermore, the present models also appear to be an improvement over earlier models that aim to predict the adsorption capacities of MOFs for any gas species, Table S2. This improved performance can be attributed to the exploration and optimization of multiple ML algorithms, use of an appropriate feature set, and the relatively large size of the present training set.

Table 4.

Performance of the extremely randomized trees ML algorithm in predicting UG and UV H₂ capacities of MOFs under PS and TPS conditions

H₂ capacity type	R²	AUE (capacity units)	RMSE (capacity units)	Kendall τ	MAE (capacity units)
UG at PS (wt %)	0.997	0.14	0.18	0.961	0.10
UV at PS (g-H₂ L⁻¹)	0.984	0.97	1.40	0.922	0.69
UG at TPS (wt %)	0.997	0.16	0.23	0.966	0.10
UV at TPS (g-H₂ L⁻¹)	0.967	1.32	1.92	0.819	0.91

Open in a new tab

R², AUE, RSME, and MAE represent the coefficient of determination, average unsigned error, root-mean-squared error, and median absolute error, respectively.

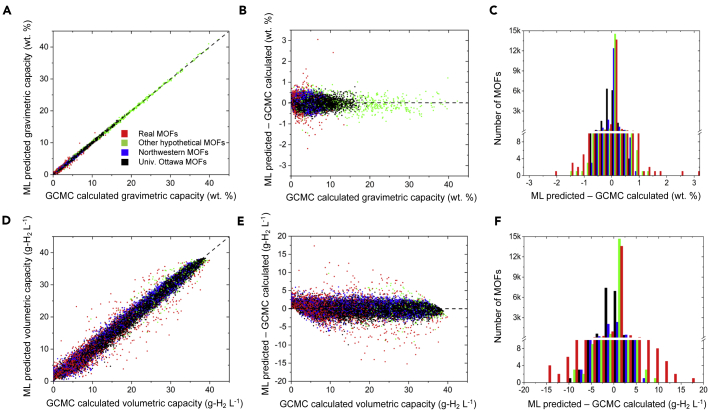
Figure 2 illustrates the degree of agreement between ERT ML predictions and GCMC calculations of usable H₂ capacities under PS conditions as a function of MOF source database (Figure S4 shows similar data for TPS conditions; see also Table 4). As mentioned above, the present ML models more accurately predict UG capacities than UV capacities. The largest differences between ML and GCMC capacities (Figures 2C, 2F, S4C, and S4F) primarily occur for the real MOF dataset. In principle, these differences may arise either from ML overfitting or from inaccurate GCMC predictions caused by non-ideal/incomplete MOF crystal structure data (i.e., missing atoms, disorder, etc.), as mentioned in previous studies.¹^,³²^,³⁵^,123, 124, 125 ERT algorithms are fairly robust against overfitting.⁸³ To examine the possibility for overfitting, test set errors were compared with training set errors, as shown in Figure S5 and Table 4. These data suggest that the outliers are not a consequence of over fitting; hence, inaccuracies in the crystal structure data are proposed as the most likely source of this disagreement.¹^,³²^,³⁵^,123, 124, 125

Performance of the ERT algorithm with respect to GCMC calculations for predicting usable H₂ capacities in MOFs

Data were collected at 77 K for a pressure swing (PS) between 100 and 5 bar on a test set of 24,674 MOFs. Different colors represent different categories of MOFs. (A–C) Top and (D–F) bottom panels illustrate performance for usable gravimetric and volumetric capacities, respectively. (A and D) Agreement between ML and GCMC predictions. (B and E) Difference between ML and GCMC as a function of GCMC capacity. (C and F) Distribution of differences in predictions between ML and GCMC.

Effect of training set size

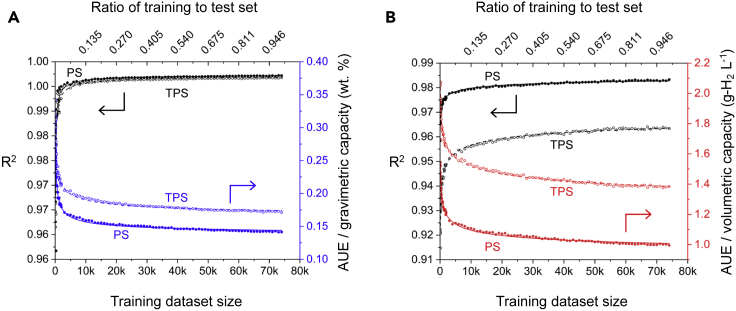
Figure 3 illustrates the impact of training set size on the accuracy of the ERT ML models, as quantified using R² and AUE (Table S5 summarizes the dataset sizes used in these plots). For training sets containing more than 5,000 MOFs, R² and AUE vary slowly and in a monotonic fashion, with AUE decreasing and R² increasing. The accuracy of the models is more sensitive to the size of the training set for smaller training sets containing roughly 5,000 or fewer MOFs. Figure S6 highlights the variation in performance for these smaller training sets.

ML performance versus training set size

Performance of ERT ML models for predicting usable (A) gravimetric and (B) volumetric H₂ capacity as a function of training set size and the ratio of training to test set size. One hundred different training sets, ranging in size between 100 and 74,021 MOFs were examined. A common set of 24,674 MOFs was used for testing. Performance is quantified using R² (left axis, black) and the AUE (right axis, blue and red for UG and UV, respectively). Lines represent a power law fit to the data.

The trends AUE as a function of training set size can be fit to a power law expression of the form AUE(m) = αm^β + γ, wherem represents the size of the training set and β is the power law exponent. Fitting this model to the data shown in Figure 3 reveals that the AUE for UG converges faster with training set size (β = −0.37 and −0.43) than it does for UV (β = −0.16 and −0.23). A full tabulation of the power law parameters is given in Table S10. Based on these power law expressions, one can determine the necessary size of the training set to achieve a desired level of accuracy. For example, assuming PS operation, to achieve an AUE of approximately 0.25 wt % and 1.5 g-H₂ L⁻¹ requires training set sizes (for UG and UV) of less than 300 MOFs randomly selected from the diverse datasets used here.

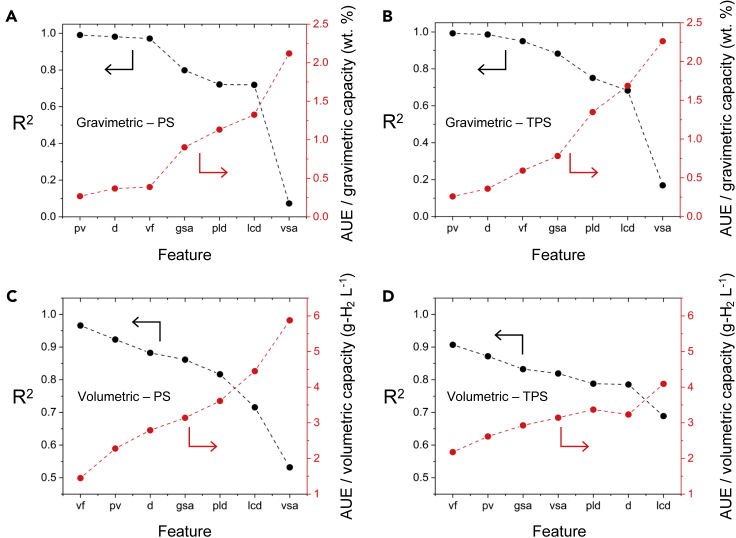
Univariate feature importance

Figure 4 illustrates the relative importance of the seven crystallographic features in predicting usable hydrogen uptake in MOFs. Feature importance was determined by developing ERT models for each single feature individually. Additional details for these models are provided in the supplemental information. Based on these models, it is evident that pore volume (pv) and void fraction (vf) are the dominant features in predicting H₂ capacity; these two properties appear as the first- or second-most important single features regardless of operating condition or capacity type. The importance of these features can be rationalized by two factors. First, based on the empirical Chahine rule, the pore volume of an MOF correlates with its excess uptake.¹¹³ Second, pore volume and void fraction are related (since pv = vf d⁻¹)—MOFs with larger pv have larger vf, and vice versa.¹

Conversely, the largest cavity diameter (lcd) and volumetric surface area (vsa) are the single features whose ML models yield the lowest accuracy. The relative importance of the individual features for predicting UG capacities is: pv > d > vf > gsa > pld > lcd > vsa. This ordering is the same for PS and TPS conditions. In contrast, the importance ordering for UV capacities differs based on the operating condition. Nevertheless, vf and pv remain the two most important single features for both UV conditions, in that order (Figure 4).

Despite their limited input, the single-feature ML models illustrated in Figure 4 achieve high accuracy. For example, any of the three independent models for UG-PS based only on pv, d, or vf can predict capacities with R² > 0.95 and with AUE of less than 0.5 wt %. The accuracy and simplicity of the univariate ML models suggest that they can be used to quickly screen new MOFs for their utility in hydrogen storage. To that end, optimized single-feature ML models for the four categories of usable capacities considered here have been made available for use on the web with an interactive web form or with a python API.⁸⁴ Furthermore, the ML models can be downloaded via figshare.¹²⁶ These models take as input either pv (for UG predictions) or vf (for UV predictions) of a given MOF. These input data can be quickly calculated from a MOF's crystal structure using modern structure analysis codes.²⁵^,⁴⁷^,127, 128, 129, 130 As shown in Figure 4, these models can predict UG with an average error of less than 0.4 wt %, and UV with errors less than 2.2 g-H₂ L⁻¹.

Figure S7 compares the single-feature importance assessments based on ERT ML models (as reported in Figure 4) with three popular methods for determining feature importance: Pearson's correlation coefficient (r),116, 117, 118 Breiman and Friedman's tree-based algorithm as implemented in Scikit-learn,⁹⁰^,¹⁰⁴ and the permutation importance method as implemented in the rfpimp package.¹¹⁹ It is clear that the feature importance methods do not reproduce in detail the rank ordering of feature importance that is suggested by our ERT ML models. Nevertheless, good agreement is evident more broadly. For example, in the case of UG (Figures S7A and S7C), the three feature importance methods suggest that in aggregate pv is the most important feature, while vsa is the least, in agreement with the ERT models (Figures 4A and 4B). Similarly, for UV, the importance methods suggest that vf and lcd are among the most and least important features, respectively. This is the same trend found in the univariate ERT models (Figures 4C and 4D).

Multivariate feature importance

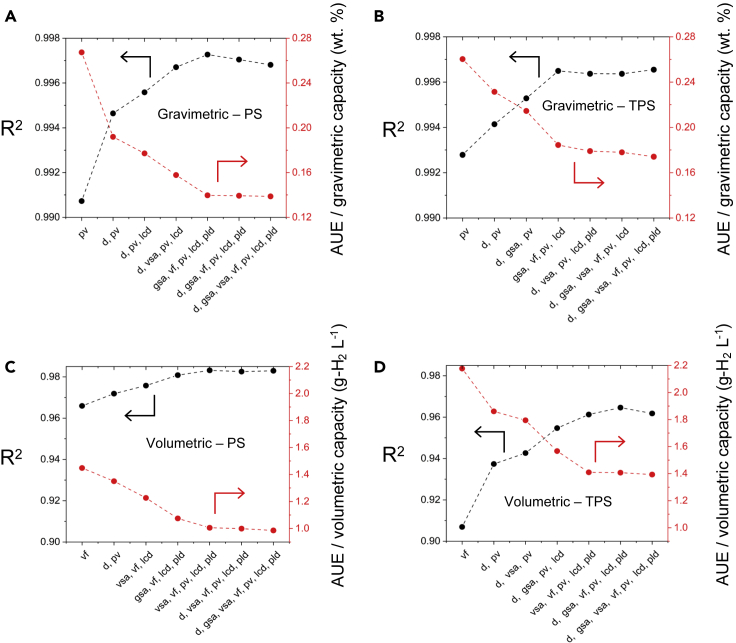
Figure 5 illustrates how the accuracy of the ML models varies with the number and combination of features. Assuming 7 features, 2⁷ – 1 = 127 possible combinations exist. For a given number of features, Figure 5 plots the combination of features resulting in the highest accuracy model. (The supplementary file [Table S11] summarizes the performance for all 508 possible feature combinations and capacity/operating condition types.) As expected, Figure 5 shows that ML accuracy generally increases as the number of input features increases. As previously discussed, when limited to a single feature, vf yields the best accuracy for predicting UV, while pv is the best choice for UG. When the feature set is extended to 2 features, the combination of d and pv is the optimal choice among the $(\begin{array}{l} 7 \\ 2 \end{array}) = 21$ possible pairs regardless of the capacity (UG versus UV) or operating condition (PS versus TPS). For larger numbers of features, the optimal feature combination depends upon the operating condition and the capacity type. Based on the AUE, whose value tends to plateau as more features are added, highly accurate ML models can be generated using only 5 input features (Table 5). These data lend further support to the notion that the accuracy of a given ML model depends on both the number and identity of the input features. As a slightly more accurate alternative to the univariate web models described above, a subset of the present multivariate ML models that use 4, 5, and 7 input features are also available on the web using an interactive web form and via a python API.⁸⁴ The ML models can also be downloaded via figshare.¹²⁶

Table 5.

Optimal combinations of features for predicting UG and UV H₂ storage capacities at PS and TPS conditions

Condition	Feature combination	No. of features	R²	AUE	RMSE	Kendall τ
UG at PS	gsa, vf, pv, lcd, pld	5	0.997	0.14 wt %	0.19 wt %	0.959
UG at TPS	d, vsa, pv, lcd, pld	5	0.996	0.18 wt %	0.25 wt %	0.959
UV at PS	vsa, vf, pv, lcd, pld	5	0.983	1.01 g-H₂ L⁻¹	1.45 g-H₂ L⁻¹	0.920
UV at TPS	vsa, vf, pv, lcd, pld	5	0.961	1.41 g-H₂ L⁻¹	2.10 g-H₂ L⁻¹	0.814

Open in a new tab

H₂ uptake in unseen MOFs

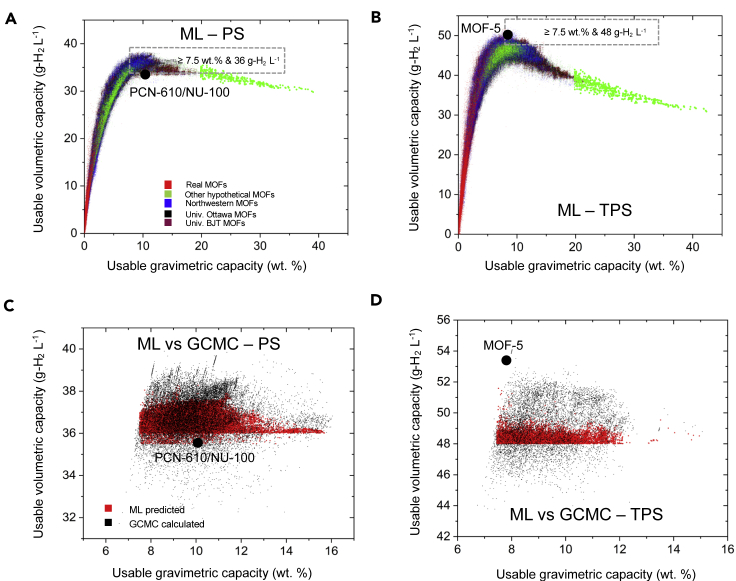
Figure 6 illustrates the H₂ storage capacities of 820,039 MOFs as predicted by the 7-feature ERT ML models developed here. (This dataset is publicly accessible via HyMARC data hub.⁷⁰) These MOFs are referred to as “unseen”, in that they have not been included in the training or test sets used to develop the models. Figures 6A and 6B show UV capacities as functions of UG capacities under PS and TPS conditions, respectively. Both plots exhibit a rapid increase in UV at low values of UG, and reach a maximum in UV at UG values of approximately 9 wt %. Beyond the maximum, UV decreases relatively slowly with increasing UG. These trends are consistent with our earlier findings derived from GCMC calculations on smaller datasets.¹^,²^,⁶

ML predictions of H₂ capacities for 820,093 unseen MOFs

Predicted capacities for (A) PS and (B) temperature + PS operation. Colors indicate the originating database for a given MOF. (C and D) Validation of ML-predicted capacities for the highest-capacity MOFs identified by ML; shown in the rectangular regions in (C and D) using GCMC simulations. For comparison, the capacities of PCN-610/NU-100 (PS: 10.1 wt %, 35.5 g-H₂ L⁻¹) and MOF-5 (TPS: 7.8 wt %, 51.9 g -H₂ L⁻¹) are shown.¹

In the case of PS operation, the maximum UV across the MOFs in the dataset is 37.4 g-H₂ L⁻¹; for TPS operation the maximum UV is 48.5 g-H₂ L⁻¹. In the case of UG, the maximum value predicted is 39 wt % for PS operation and 42 wt % for TPS. These values can be placed in context by comparing against the Department of Environment hydrogen storage targets, which stipulate system-level hydrogen densities of 5.5 wt % and 40 g-H₂ L⁻¹ by 2025 and 6.5 wt %/50 g-H₂ L⁻¹ longer-term (“Ultimate target”).⁶ Given that the tank and balance-of-plant for the storage system have non-zero mass and volume, the MOFs examined here cannot meet the Ultimate target for UV, regardless of operating condition.¹² More optimism exists, however, for meeting the gravimetric targets given the high UG exhibited by these systems on a MOF-only basis. Of course, an additional challenge is to identify MOFs that excel both gravimetrically and volumetrically.¹^,²^,⁶^,³¹^,¹³¹

It is also helpful to compare the performance predictions in Figures 6A and 6B with that of state-of-the-art materials. In the case of PS operation, our previous study demonstrated that PCN-610 (NU-100) exhibits a hydrogen capacity of 10.1 wt % and 35.5 g-H₂ L⁻¹,¹ which, to our knowledge, is the best combination of gravimetric and volumetric capacities reported for any MOF under these conditions. The data in Figure 6A reveal that 16,345 MOFs can, in principle, exceed this capacity on both a UG and UV basis. In the case of TPS operation (Figure 6B), MOF-5 remains the benchmark, which a measured capacity of 7.8 wt % and 51.9 g-H₂ L⁻¹.² Figure 6D shows that only 21 MOFs out-perform MOF-5 under these conditions.

Regarding the accuracy of the present ML predictions, Table 4 shows that the AUE of these models are on the order of 0.15 wt % and 1.3 g-H₂ L⁻¹. Although these errors are small, a more rigorous validation of the ML can be achieved with GCMC calculations. Thus, GCMC calculations were performed on a subset of MOFs that ML predicted to exhibit high UV and UG capacities. These MOFs fall within the rectangular regions shown in Figures 6A and 6B, and exhibit capacities that meet or exceed 36 g-H₂ L⁻¹ and 7.5 wt % for PS conditions and 48 g-H₂ L⁻¹ and 7.5 wt % under TPS conditions. In total, 21,700 compounds were re-examined with GCMC based on their ML-predicted PS capacities, and another 7,901 were re-examined for TPS.

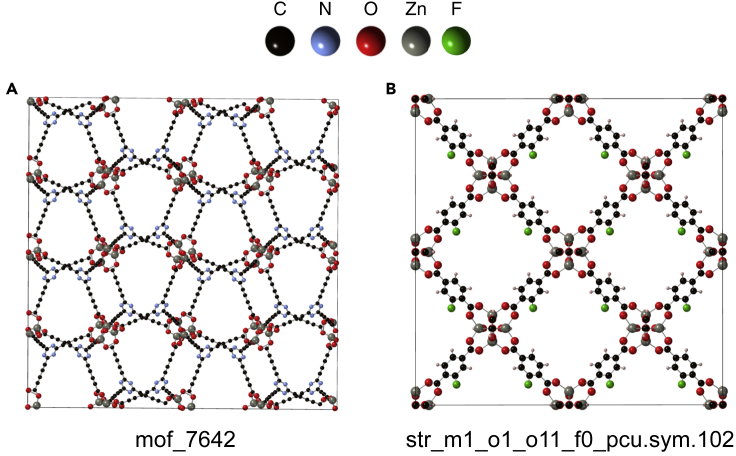
Figure 6C compares ML and GCMC predictions for usable capacities for 21,700 high-capacity MOFs under PS conditions. The strong overlap in the two datasets further highlights the accuracy of the ML models. A total of 8,187 MOFs were predicted by GCMC to out-perform PCN-610/NU-100 under these conditions. A summary of the 10 highest-capacity MOFs, sorted based on their GCMC capacities, is provided in Table 6 (a more extensive listing is provided in Table S12). The highest-capacity MOFs are all hypothetical compounds: five originate from the ToBaCCo database,⁵⁹ two are from the University of Ottawa database,³⁷ and the remainder are from the Northwestern³⁶ database. These MOFs all exhibit high surface areas (average = 5,746, range = 4,346–7,835 m² g⁻¹) and large void fractions of 0.89, on average. The range of these property values are consistent with those reported in an earlier study,¹^,¹³²^,¹³³ and suggest that maximizing the surface area is an important design guideline for PS operation. The highest-capacity MOF, mof_7642,⁵⁹ is predicted to exhibit capacities of 11.1 wt % and 40.5 g-H₂ L⁻¹, surpassing that of PCN-610/NU-100, the record-holder under PS conditions. The crystal structure of mof_7642 is shown in Figure 7A.

Table 6.

Highest-capacity MOFs, as identified by ML and verified with GCMC, under pressure swing and temperature + pressure swing conditions

Name	Source	Density (g cm⁻³)	Grav. surface area (m² g⁻¹)	Vol. surface area (m² cm⁻³)	Void fraction	Pore volume (cm³ g⁻¹)	Largest cavity diameter (Å)	Pore limiting diameter (Å)	Usable grav. capacity (wt %)		Usable vol. capacity (g-H₂ L⁻¹)
Name	Source	Density (g cm⁻³)	Grav. surface area (m² g⁻¹)	Vol. surface area (m² cm⁻³)	Void fraction	Pore volume (cm³ g⁻¹)	Largest cavity diameter (Å)	Pore limiting diameter (Å)	GCMC	ML	GCMC	ML
Pressure swing
mof_7642	ToBaCCo	0.30	5,561	1,695	0.89	2.93	12.8	11.8	11.1	10.3	40.5	37.4
mof_7690	ToBaCCo	0.30	5,715	1,706	0.89	2.98	12.8	12.0	11.3	10.4	40.3	37.3
mof_7594	ToBaCCo	0.40	5,070	2,031	0.86	2.15	11.2	9.7	8.6	7.9	39.9	37.0
mof_7210	ToBaCCo	0.29	5,936	1,730	0.89	3.04	13.4	11.7	11.4	10.5	39.8	37.1
mof_7738	ToBaCCo	0.25	6,054	1,502	0.90	3.64	14.5	13.5	13.0	12.0	39.7	37.0
hypotheticalMOF_5045702_i_1_j_24_k_20_m_2	NW	0.31	5,926	1,820	0.88	2.87	16.0	11.0	10.9	10.1	39.7	37.2
str_m3_o19_o19_f0_nbo.sym.1.out	UO	0.31	5,073	1,583	0.90	2.88	17.7	12.9	10.8	10.1	39.7	37.1
hypotheticalMOF_5037315_i_1_j_20_k_12_m_1	NW	0.31	5,818	1,787	0.88	2.86	16.0	11.0	10.9	10.0	39.7	37.0
hypotheticalMOF_5037467_i_1_j_20_k_12_m_8	NW	0.31	5,860	1,800	0.88	2.85	16.0	11.0	10.9	10.0	39.7	37.0
str_m3_o5_o20_f0_nbo.sym.1.out	UO	0.39	4,772	1,882	0.87	2.22	14.1	9.6	8.7	8.1	39.7	37.2

Temperature + pressure swing
str_m1_o1_o11_f0_pcu.sym.102.out	UO	0.45	4,352	1,974	0.84	1.84	12.9	10.1	10.4	9.7	53.1	48.1
str_m1_o1_o11_f0_pcu.sym.117.out	UO	0.47	4,162	1,977	0.83	1.74	12.8	9.9	9.9	9.0	52.8	48.0
str_m1_o1_o11_f0_pcu.sym.121.out	UO	0.47	4,263	2,006	0.83	1.76	12.1	10.2	10.0	9.4	52.7	48.1
str_m1_o1_o11_f0_pcu.sym.13.out	UO	0.46	4,326	2,005	0.83	1.79	12.7	9.9	10.1	9.3	52.6	48.0
str_m1_o1_o11_f0_pcu.sym.159.out	UO	0.58	3,703	2,138	0.80	1.38	10.4	8.6	8.3	7.6	52.6	48.5
str_m1_o1_o11_f0_pcu.sym.200.out	UO	0.45	4,359	1,978	0.84	1.84	12.9	10.1	10.3	9.6	52.6	48.1
str_m1_o1_o11_f0_pcu.sym.212.out	UO	0.60	3,417	2,035	0.83	1.39	12.0	10.1	8.1	7.5	52.5	48.1
str_m1_o1_o11_f0_pcu.sym.51.out	UO	0.46	4,330	2,007	0.83	1.79	11.9	9.9	10.1	9.3	52.5	48.1
str_m1_o1_o11_f0_pcu.sym.71.out	UO	0.45	4,436	1,980	0.84	1.87	13.0	10.9	10.4	9.7	52.5	48.1
str_m1_o1_o11_f0_pcu.sym.89.out	UO	0.58	3,507	2,043	0.83	1.42	12.4	9.8	8.2	7.7	52.5	48.1

Open in a new tab

Here, NW and UO refer to the Northwestern³⁶ and University of Ottawa databases.³⁷ Grav., gravimetric; Vol., volumetric.

Crystal structures of high-capacity MOFs

Highest-capacity MOFs under (A) PS and (B) temperature + PS conditions. These MOFs originate from the ToBaCCo⁵⁹ and University of Ottawa³⁷ databases, respectively.

A search in the CCDC¹³⁴ was performed to identify MOFs that have been synthesized that are similar to the high-capacity compounds identified here. The existence of similar MOFs may suggest synthetic procedures that could be adapted to the present systems. The top 5 MOFs under PS conditions contain relatively long tritopic linkers. In the case of mof_7642, this search identified the interpenetrated MOF RANCEQ¹³⁵ as having a similar index of 0.82. Interpenetration is fairly common in MOFs (such as mof_7642) with longer linkers, and is generally undesirable for achieving high uptake. Nevertheless, several examples of successful synthesis of MOFs with long, multi-topic linkers that do not undergo interpenetration, have been reported. These include MOF-180 and MOF-200,¹³⁶ the PCN-6X series,¹³⁷ and NOTT-112.¹³⁸ The next four PS candidates in Table 6 exhibit pillared Zn paddlewheel clusters with long ditopic linkers. Karagiaridi et al.¹³⁹ demonstrated the feasibility of synthesizing pillared paddlewheel MOFs with long linkers; the SALEM-X series are examples.¹³⁹ Finally, str_m3_o5_o20_f0_nbo.sym.1.out is based on a Zn paddlewheel cluster and a ditopic linker. HOFSUS (CSD Refcode) is an example of such a MOF.¹⁴⁰

Figure 6D provides a similar comparison between ML predictions and GCMC calculations for MOFs expected to exhibit high capacities under TPS conditions. Under these conditions, only 95 MOFs were predicted by GCMC to out-perform MOF-5. A summary of the 10 highest-capacity MOFs, sorted by their GCMC capacities, is provided in Table 6 (see Table S13 for a more extensive tabulation). As found for PS operation, all of the top performing candidates are hypothetical compounds. One difference with the PS case is that all of these MOFs originate from the University of Ottawa database.³⁷ Furthermore, none of the highest-capacity MOFs identified for PS operation appear as top candidates for TPS. Comparing the highest-capacity MOFs for both operating conditions, it can be seen that the high-capacity TPS MOFs systematically exhibit lower surface areas (average = 4,073 m² g⁻¹), smaller void fractions (average = 0.83), and higher densities. Hence, the categories of MOFs that maximize uptake under PS and TPS conditions exhibit distinct properties. These differences suggest that maximizing the surface area—which, as discussed above, is desirable for maximizing PS capacity—is not advantageous for TPS operation. This behavior can be explained by trends in total capacities,⁶ which the TPS capacities reported here approximate. More specifically, it is known that total volumetric capacities are maximized for intermediate values of the surface area; for larger surface areas the volumetric capacity decreases.

Returning to the list of promising MOFs for TPS operation, Table 6 reports that the highest-capacity MOF, str_m1_o1_o11_f0_pcu.sym.102.out, has a GCMC-predicted capacity of 10.4 wt % and 53.1 g-H₂ L⁻¹. This capacity surpasses that of MOF-5, which, to our knowledge, holds the capacity record under these conditions. The crystal structure of this MOF is shown in Figure 7B.

The top 10 MOFs under TPS conditions contain the same Zn metal cluster and terephthalic acid linkers, where the linkers have been modified with varying functional groups. The slight differences in the capacities of these MOFs can be traced to differences in the functional groups. A similarity search based on str_m1_o1_o11_f0_pcu.sym.117.out identified 40 similar MOFs. Approximately 30 of these (for example, HIFTOG, MIBQAR, UNIGEE, VUSJUP, and ZELROZ) contain Zn metal clusters and linkers based on variants of terephthalic acid.

Figures S8 and S9 and Table S14 quantify the differences between ML and GCMC predictions on the subset of high-capacity MOFs shown in Figures 6C and 6D. For PS operation, the AUE of ML relative to GCMC is 0.24 wt % and 0.66 g-H₂ L⁻¹, while for TPS the AUE is 0.24 wt % and 1.28 g-H₂ L⁻¹. Both sets of errors are comparable with the errors reported in Table 4 for the original test set of MOFs. Figures S8C and S8F and S9(c,f) plot the frequency distribution of the differences between GCMC and ML. These distribution plots suggest that the largest differences occur for predictions involving real MOFs and for hypothetical MOFs extracted from databases other than those from Northwestern,³⁶ University of Ottawa,³⁷ and BJT.⁸¹ (These MOFs are referred to as “other hypothetical MOFs” in Figure 6). These MOFs, along with the real compounds, exhibit higher structural diversity than those contained in the other databases. For example, the diversity of the topologies used in the ToBaCCo⁵⁹ and Zr-MOFs⁴⁵ databases and in the linkers used in MTV-MOF⁸² database are larger than what is found in the databases from Northwestern,³⁶ University of Ottawa,³⁷ and BJT.⁸¹

Discussion

Limitations of this study

As described previously, some of the high-capacity MOFs identified here may prove difficult to synthesize. Although this limitation applies primarily to the hypothetical MOFs, in some cases real MOFs are also known to undergo framework collapse during activation, which would reduce capacity.¹^,² Nevertheless, future improvements to synthesis techniques may overcome these limitations—what is difficult to make today may be possible in the future. Secondly, our models do not distinguish between realistic MOFs having non-defective crystal structures and those for which the structures are defective/unrealistic. Unrealistic structures can result from incomplete or imperfect virtual solvent removal and the presence of partial occupancies or symmetry disorder in the crystal structure.³¹ Consequently, a defective/unrealistic MOF could be erroneously predicted to be a promising candidate. Follow-up calculations using GCMC and visual inspection of the crystal structure are recommended for all promising candidates identified by ML. Finally, the ML models developed here are non-interpretable, “black-box” models. Although these models are demonstrated to be highly accurate, additional effort is required to assess the relative importance of their input data. (The approach demonstrated here for evaluating feature importance involved the development of multiple models with varying numbers and combinations of features.) Alternatively, interpretable white-box ML models could be developed to provide more insight into feature importance. However, our experience suggests that white-box models generate less accurate predictions.

Concluding remarks

The H₂ storage capacities of nearly a million MOFs have been predicted via ML. The predictions span a diverse collection of MOFs sourced from 19 databases and reveal performance under two operating conditions: PS and temperature + PS. More than a dozen ML algorithms were benchmarked, with the ERT method found to be the most accurate. The resulting ML models are accessible on the web at the HyMARC data hub.⁸⁴ These models allow for accurate, rapid screening of the hydrogen storage properties of new MOFs using minimal structural data as input; only a single feature is needed for the simplest models.

The accuracy of the ML models was characterized as a function of training set size and the number/combination of input features. Regarding the dependence on the training set, the accuracy of the models can be well described using a simple power law function of the training set size. The dependence on the number and combination of input features was determined by evaluating 508 independent ML models generated from all possible combinations of the seven features. The most important features for predicting H₂ uptake are pore volume (for gravimetric capacity) and void fraction (for volumetric capacity).

Using these models, 8,282 MOFs are identified that have the potential to exceed the capacities of state-of-the-art materials under usable conditions. The identified MOFs are predominantly hypothetical compounds, which (for PS operation) exhibit low densities (<0.31 g cm⁻³) in combination with high surface areas (>5,300 m² g⁻¹), void fractions (∼0.90), and pore volumes (>3.3 cm³ g⁻¹). These MOFs are suggested as targets for experimental synthesis.

Experimental procedures

Resource availability

Lead contact

Prof. Donald Siegel, djsiege@umich.edu.

Materials availability

This study did not generate new reagents.

Data and code availability

•
Original data have been deposited to HyMARC Data Hub: https://datahub.hymarc.org/dataset/computational-prediction-of-hydrogen-storage-capacities-in-mofs
•
Interactive ML models: https://sorbent-ml.hymarc.org/
•
Python API: https://sorbent-ml.hymarc.org/
•
Downloadable ML models and instructions: https://doi.org/10.6084/m9.figshare.14173520.v1

Acknowledgments

Financial support was provided by the U.S. Department of Energy, Office of Energy Efficiency and Renewable Energy, grant no. DE-EE0007046. Computing resources were provided by the NSF via grant 1531752 MRI: Acquisition of Conflux, A Novel Platform for Data-Driven Computational Physics (Tech. Monitor: Ed Walker). The authors acknowledge Jesse Adams, Dr. Zeric Hulvey, Ms. Courtney Pailing, Mr. Nick Wunder, Ms. Nalinrat Guba, and Dr. Caleb Phillips for facilitating web hosting of the ML models and the development of an application programmers interface. A.A. acknowledges Profs. Randall Snurr and Tom Woo for providing access to their MOF databases; Dr. Maciej Haranczyk for use of the Zeo++ code and the mail-order MOF database; and Prof. Adam J. Matzger, Dr. Antek G. Wong-Foy, Dr. Saona Seth, Dr. Yiyang Liu, Dr. Suresh Kuthuru, and M. Veensra for helpful discussions.

Author contributions

A.A. conducted the computational components of the project. Both authors contributed to the drafting of the paper and to the project idea.

Declaration of interests

The authors declare no competing interests.

Published: June 24, 2021

Footnotes

Supplemental information can be found online at https://doi.org/10.1016/j.patter.2021.100291.

Supplemental information

Document S1. Supplemental experimental procedures, Figures S1–S8, Tables S1–S10 and S12–S14

mmc1.pdf^{(29.4MB, pdf)}

Table S11. Machine learning models based on feature combinations

mmc2.xlsx^{(41.9KB, xlsx)}

Document S2. Article plus supplemental information

mmc3.pdf^{(32.8MB, pdf)}

References

1.Ahmed A., Seth S., Purewal J., Wong-Foy A.G., Veenstra M., Matzger A.J., Siegel D.J. Exceptional hydrogen storage achieved by screening nearly half a million metal-organic frameworks. Nat. Commun. 2019;10:1568. doi: 10.1038/s41467-019-09365-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
2.Ahmed A., Liu Y., Purewal J., Tran L.D., Veenstra M., Wong-Foy A., Matzger A., Siegel D. Balancing gravimetric and volumetric hydrogen density in MOFs. Energy Environ. Sci. 2017;10:2459–2471. [Google Scholar]
3.Wong-Foy A.G., Matzger A.J., Yaghi O.M. Exceptional H2 saturation uptake in microporous metal-organic frameworks. J. Am. Chem. Soc. 2006;128:3494–3495. doi: 10.1021/ja058213h. [DOI] [PubMed] [Google Scholar]
4.Satyapal S., Petrovic J., Read C., Thomas G., Ordaz G. The U.S. Department of Energy’s National Hydrogen Storage Project: progress towards meeting hydrogen-powered vehicle requirements. Catal. Today. 2007;120:246–256. [Google Scholar]
5.Greene D.L., Duleep G. Worldwide Status of Hydrogen Fuel Cell Vehicle Technology and Prospects for Commercialization. U.S. Department of Energy. 2013 https://www.hydrogen.energy.gov/pdfs/progress13/xi_1_greene_2013.pdf [Google Scholar]
6.Allendorf M.D., Hulvey Z., Gennett T., Ahmed A., Autrey T., Camp J., Seon Cho E., Furukawa H., Haranczyk M., Head-Gordon M. An assessment of strategies for the development of solid-state adsorbents for vehicular hydrogen storage. Energy Environ. Sci. 2018;11:2784–2812. [Google Scholar]
7.Yang J., Sudik A., Wolverton C., Siegel D.J. High capacity hydrogen storage materials: attributes for automotive applications and techniques for materials discovery. Chem. Soc. Rev. 2010;39:656–675. doi: 10.1039/b802882f. [DOI] [PubMed] [Google Scholar]
8.Long J.R. . U.S. Department of Energy, Hydrogen and Fuel Cells Program 2015 Annual Merit Review Proceedings: Project ST103. 2015. Hydrogen Storage in Metal-Organic Frameworkshttps://www.hydrogen.energy.gov/pdfs/review15/st103_long_2015_o.pdf [Google Scholar]
9.U.S. Department of Energy. (n.d.) DOE Technical Targets for Onboard Hydrogen Storage for Light-Duty Vehicles, https://energy.gov/eere/fuelcells/doe-technical-targets-onboard-hydrogen-storage-light-duty-vehicles.
10.Astiaso Garcia D., Barbanera F., Cumo F., Di Matteo U., Nastasi B. Expert opinion analysis on renewable hydrogen storage systems potential in Europe. Energies. 2016;9:963. [Google Scholar]
11.Riis T., Sandrock G., Ulleberg Ø., Vie P.J.S. Hydrogen Production and Storage: R&D Priorities and Gaps. International Energy Agency); 2006. Hydrogen storage R&D: priorities and gaps; pp. 19–33. [Google Scholar]
12.Purewal J., Veenstra M., Tamburello D., Ahmed A., Matzger A.J., Wong-Foy A.G., Seth S., Liu Y., Siegel D.J. Estimation of system-level hydrogen storage for metal-organic frameworks with high volumetric storage density. Int. J. Hydrogen Energy. 2019;44:15135–15145. [Google Scholar]
13.Manoharan Y., Hosseini S.E., Butler B., Alzhahrani H., Senior B.T.F., Ashuri T., Krohn J. Hydrogen fuel cell vehicles; current status and future prospect. Appl. Sci. 2019;9:2296. [Google Scholar]
14.Makridis S.S. Hydrogen storage and compression. In: Carriveau R., Ting D.S.-K., editors. Methane and Hydrogen for Energy Storage. The Institution of Engineering and Technology); 2016. pp. 1–28. [Google Scholar]
15.Veenstra, M., Purewal, J., Xu, C., Yang, J., Blaser, R., Sudik, A., Siegel, D., Ming, Y., Liu, D., Hang, C., et al. (2015). Ford/BASF-SE/UM Activities in Support of the Hydrogen Storage Engineering Center of Excellence. U.S. Department of Energy, Office of Scientific and Technical Information, 10.2172/1296578.
16.Öhrström L. Let’s talk about MOFs—topology and terminology of metal-organic frameworks and why we need them. Crystals. 2015;5:154–162. [Google Scholar]
17.Fischer R.A., Schwedler I. Terminologie von Metall-organischen Gerüstverbindungen und Koordinationspolymeren (IUPAC-Empfehlungen 2013) Angew. Chem. Int. Ed. 2014;126:7209–7214. [Google Scholar]
18.Batten S.R., Champness N.R., Chen X.-M., Garcia-Martinez J., Kitagawa S., Öhrström L., O’Keeffe M., Paik Suh M., Reedijk J. Terminology of metal-organic frameworks and coordination polymers (IUPAC Recommendations 2013) Pure Appl. Chem. 2013;85:1715–1724. [Google Scholar]
19.Thommes M., Kaneko K., Neimark A.V., Olivier J.P., Rodriguez-Reinoso F., Rouquerol J., Sing K.S.W. Physisorption of gases, with special reference to the evaluation of surface area and pore size distribution (IUPAC Technical Report) Pure Appl. Chem. 2015;87:1051–1069. [Google Scholar]
20.Batten S.R., Champness N.R., Chen X.-M., Garcia-Martinez J., Kitagawa S., Öhrström L., O’Keeffe M., Suh M.P., Reedijk J. Coordination polymers, metal-organic frameworks and the need for terminology guidelines. CrystEngComm. 2012;14:3001. [Google Scholar]
21.O’Keeffe M. Nets, tiles, and metal-organic frameworks. APL Mater. 2014;2:124106. [Google Scholar]
22.Tranchemontagne D.J., Mendoza-Cortés J.L., O’Keeffe M., Yaghi O.M. Secondary building units, nets and bonding in the chemistry of metal-organic frameworks. Chem. Soc. Rev. 2009;38:1257. doi: 10.1039/b817735j. [DOI] [PubMed] [Google Scholar]
23.Reymond J.-L. The chemical space project. Acc. Chem. Res. 2015;48:722–730. doi: 10.1021/ar500432k. [DOI] [PubMed] [Google Scholar]
24.Kontijevskis A. Mapping of drug-like chemical universe with reduced complexity molecular frameworks. J. Chem. Inf. Model. 2017;57:680–699. doi: 10.1021/acs.jcim.7b00006. [DOI] [PubMed] [Google Scholar]
25.Martin R.L., Smit B., Haranczyk M. Addressing challenges of identifying geometrically diverse sets of crystalline porous materials. J. Chem. Inf. Model. 2012;52:308–318. doi: 10.1021/ci200386x. [DOI] [PubMed] [Google Scholar]
26.Sun D., Sun F., Deng X., Li Z. Mixed-metal strategy on metal-organic frameworks (MOFs) for functionalities expansion: Co substitution induces aerobic oxidation of cyclohexene over inactive Ni-MOF-74. Inorg. Chem. 2015;54:8639–8643. doi: 10.1021/acs.inorgchem.5b01278. [DOI] [PubMed] [Google Scholar]
27.Deng H., Doonan C.J., Furukawa H., Ferreira R.B., Towne J., Knobler C.B., Wang B., Yaghi O.M. Multiple functional groups of varying ratios in metal-organic frameworks. Science. 2010;327:846–850. doi: 10.1126/science.1181761. [DOI] [PubMed] [Google Scholar]
28.Park J., Kim H., Han S.S., Jung Y. Tuning metal-organic frameworks with open-metal sites and its origin for enhancing CO2 affinity by metal substitution. J. Phys. Chem. Lett. 2012;3:826–829. doi: 10.1021/jz300047n. [DOI] [PubMed] [Google Scholar]
29.Moghadam P.Z., Li A., Wiggin S.B., Tao A., Maloney A.G.P., Wood P.A., Ward S.C., Fairen-Jimenez D. Development of a Cambridge structural database subset: a collection of metal-organic frameworks for past, present, and future. Chem. Mater. 2017;29:2618–2625. [Google Scholar]
30.Groom C.R., Bruno I.J., Lightfoot M.P., Ward S.C. The Cambridge Structural Database. Acta Crystallogr. Sect. B Struct. Sci. Cryst. Eng. Mater. 2016;72:171–179. doi: 10.1107/S2052520616003954. [DOI] [PMC free article] [PubMed] [Google Scholar]
31.Goldsmith J., Wong-Foy A.G., Cafarella M.J., Siegel D.J. Theoretical limits of hydrogen storage in metal–organic frameworks: opportunities and trade-offs. Chem. Mater. 2013;25:3373–3382. [Google Scholar]
32.Altintas C., Avci G., Daglar H., Nemati Vesali Azar A., Erucar I., Velioglu S., Keskin S. An extensive comparative analysis of two MOF databases: high-throughput screening of computation-ready MOFs for CH4 and H2 adsorption. J. Mater. Chem. A. 2019;7:9593–9608. [Google Scholar]
33.Chung Y.G., Camp J., Haranczyk M., Sikora B.J., Bury W., Krungleviciute V., Yildirim T., Farha O.K., Sholl D.S., Snurr R.Q. Computation-ready, experimental metal-organic frameworks: a tool to enable high-throughput screening of nanoporous crystals. Chem. Mater. 2014;26:6185–6192. [Google Scholar]
34.Chung Y.G., Haldoupis E., Bucior B.J., Haranczyk M., Lee S., Zhang H., Vogiatzis K.D., Milisavljevic M., Ling S., Camp J.S. Advances, updates, and analytics for the computation-ready, experimental metal-organic framework database: CoRE MOF 2019. J. Chem. Eng. Data. 2019;64:5985–5998. [Google Scholar]
35.Chen T., Manz T.A. Identifying misbonded atoms in the 2019 CoRE Metal-Organic Framework Database. RSC Adv. 2020;10:26944–26951. doi: 10.1039/d0ra02498h. [DOI] [PMC free article] [PubMed] [Google Scholar]
36.Wilmer C.E., Leaf M., Lee C.Y., Farha O.K., Hauser B.G., Hupp J.T., Snurr R.Q. Large-scale screening of hypothetical metal-organic frameworks. Nat. Chem. 2011;4:83–89. doi: 10.1038/nchem.1192. [DOI] [PubMed] [Google Scholar]
37.Aghaji M.Z., Fernandez M., Boyd P.G., Daff T.D., Woo T.K. Quantitative Structure-Property Relationship Models for Recognizing Metal Organic Frameworks (MOFs) with High CO2 Working Capacity and CO2/CH4 Selectivity for Methane Purification. Eur. J. Inorg. Chem. 2016;2016:4505–4511. [Google Scholar]
38.Martin R.L., Lin L.C., Jariwala K., Smit B., Haranczyk M. Mail-order metal-organic frameworks (MOFs): designing isoreticular MOF-5 analogues comprising commercially available organic molecules. J. Phys. Chem. C. 2013;117:12159–12167. [Google Scholar]
39.Bao Y., Martin R.L., Haranczyk M., Deem M.W. In silico prediction of MOFs with high deliverable capacity or internal surface area. Phys. Chem. Chem. Phys. 2015;17:11962–11973. doi: 10.1039/c5cp00002e. [DOI] [PubMed] [Google Scholar]
40.Witman M., Ling S., Anderson S., Tong L., Stylianou K.C., Slater B., Smit B., Haranczyk M. In silico design and screening of hypothetical MOF-74 analogs and their experimental synthesis. Chem. Sci. 2016;7:6263–6272. doi: 10.1039/c6sc01477a. [DOI] [PMC free article] [PubMed] [Google Scholar]
41.Chung Y.G., Gómez-gualdrón D.A., Li P., Leperi K.T., Deria P., Zhang H., Vermeulen N.A., Stoddart J.F., You F., Hupp J.T. In Silico Discovery of Metal-Organic Frameworks for Precombustion CO2 Capture Using a Genetic Algorithm. Sci. Adv. 2016;2:e1600909. doi: 10.1126/sciadv.1600909. [DOI] [PMC free article] [PubMed] [Google Scholar]
42.Anderson R., Rodgers J., Argueta E., Biong A., Go D.A. Role of pore chemistry and topology in the CO2 capture capabilities of MOFs: from molecular simulation to machine learning. Chem. Mater. 2018;30:11. [Google Scholar]
43.Anderson G., Schweitzer B., Anderson R., Gómez-Gualdrón D.A. Attainable volumetric targets for adsorption-based hydrogen storage in porous crystals: molecular simulation and machine learning. J. Phys. Chem. C. 2019;123:120–130. [Google Scholar]
44.Anderson R., Gómez-Gualdrón D.A. Increasing topological diversity during computational “synthesis” of porous crystals: how and why. CrystEngComm. 2019;21:1653–1665. [Google Scholar]
45.Gomez-Gualdron D.A., Gutov O.V., Krungleviciute V., Borah B., Mondloch J.E., Hupp J.T., Yildirim T., Farha O.K., Snurr R.Q. Computational design of metal-organic frameworks based on stable zirconium building units for storage and delivery of methane. Chem. Mater. 2014;26:5632–5639. [Google Scholar]
46.Bao Y., Martin R.L., Simon C.M., Haranczyk M., Smit B., Deem M.W. In silico discovery of high deliverable capacity metal-organic frameworks. J. Phys. Chem. C. 2015;119:186–195. [Google Scholar]
47.Willems T.F., Rycroft C.H., Kazi M., Meza J.C., Haranczyk M. Algorithms and tools for high-throughput geometry-based analysis of crystalline porous materials. Microporous Mesoporous Mater. 2012;149:134–141. [Google Scholar]
48.Addicoat M.A., Coupry D.E., Heine T. AuToGraFS: automatic topological generator for framework structures. J. Phys. Chem. A. 2014;118:9607–9614. doi: 10.1021/jp507643v. [DOI] [PubMed] [Google Scholar]
49.Boyd P.G., Woo T.K. A generalized method for constructing hypothetical nanoporous materials of any net topology from graph theory. CrystEngComm. 2016;18:3777–3792. [Google Scholar]
50.Gómez-Gualdrón D.A., Colón Y.J., Zhang X., Wang T.C., Chen Y.-S., Hupp J.T., Yildirim T., Farha O.K., Zhang J., Snurr R.Q. Evaluating topologically diverse metal-organic frameworks for cryo-adsorbed hydrogen storage. Energy Environ. Sci. 2016;9:3279–3289. [Google Scholar]
51.Yao Z., Sánchez-Lengeling B., Bobbitt N.S., Bucior B.J., Kumar S.G.H., Collins S.P., Burns T., Woo T.K., Farha O., Snurr R.Q. Inverse design of nanoporous crystalline reticular materials with deep generative models. Nat. Mach. Intell. 2021;3:76–86. [Google Scholar]
52.Sadus R.J. Elsevier; 1999. Molecular Simulation of Fluids: Theory, Algorithms, and Object-Orientation. [Google Scholar]
53.Allen M.P., Tildesley D.J. Oxford University Press; 1989. Computer Simulation of Liquids. [Google Scholar]
54.Frenkel D., Smit B. 2nd ed. Academic Press, Inc.; 2001. Understanding Molecular Simulation: From Algorithms to Applications. [Google Scholar]
55.Hill T.L. Dover Publications; 1986. An Introduction to Statistical Thermodynamics. [Google Scholar]
56.Dubbeldam D., Torres-Knoop A., Walton K.S. Molecular simulation on the inner workings of Monte Carlo codes. Mol. Simul. 2013;39:14–15. [Google Scholar]
57.Fernandez M., Boyd P.G., Daff T.D., Aghaji M.Z., Woo T.K. Rapid and accurate machine learning recognition of high performing metal organic frameworks for CO2 capture. J. Phys. Chem. Lett. 2014;5:3056–3060. doi: 10.1021/jz501331m. [DOI] [PubMed] [Google Scholar]
58.Martin R.L., Simon C.M., Smit B., Haranczyk M. In silico design of porous polymer networks: high-throughput screening for methane storage materials. J. Am. Chem. Soc. 2014;136:5006–5022. doi: 10.1021/ja4123939. [DOI] [PubMed] [Google Scholar]
59.Colón Y.J., Gómez-Gualdrón D.A., Snurr R.Q. Topologically guided, automated construction of metal-organic frameworks and their evaluation for energy-related applications. Cryst. Growth Des. 2017;17:5801–5810. [Google Scholar]
60.Boyd P.G., Moosavi S.M., Witman M., Smit B. Force-field prediction of materials properties in metal-organic frameworks. J. Phys. Chem. Lett. 2017;8:357–363. doi: 10.1021/acs.jpclett.6b02532. [DOI] [PMC free article] [PubMed] [Google Scholar]
61.Thornton A.W., Simon C.M., Kim J., Kwon O., Deeg K.S., Konstas K., Pas S.J., Hill M.R., Winkler D.A., Haranczyk M. Materials genome in action: identifying the performance limits of physical hydrogen storage. Chem. Mater. 2017;29:2844–2854. doi: 10.1021/acs.chemmater.6b04933. [DOI] [PMC free article] [PubMed] [Google Scholar]
62.Bobbitt N.S., Snurr R.Q. Molecular Simulation Molecular Modelling and Machine Learning for High-Throughput Screening of Metal-Organic Frameworks for Hydrogen Storage Molecular Modelling and Machine Learning for High-Throughput Screening of Metal-Organic Frameworks for Hydrogen Storage. Mol. Simul. 2019;45:1069–1081. [Google Scholar]
63.Borboudakis G., Stergiannakos T., Frysali M., Klontzas E., Tsamardinos I., Froudakis G.E. Chemically intuited, large-scale screening of MOFs by machine learning techniques. NPJ Comput. Mater. 2017;3 doi: 10.1038/s41524-017-0045-8. [DOI] [Google Scholar]
64.Broom D.P., Webb C.J., Hurst K.E., Parilla P.A., Gennett T., Brown C.M., Zacharia R., Tylianakis E., Klontzas E., Froudakis G.E. Outlook and challenges for hydrogen storage in nanoporous materials. Appl. Phys. A. 2016;122:151. [Google Scholar]
65.Butler K.T., Davies D.W., Cartwright H., Isayev O., Walsh A. Machine learning for molecular and materials science. Nature. 2018;559:547–555. doi: 10.1038/s41586-018-0337-2. [DOI] [PubMed] [Google Scholar]
66.Wahiduzzaman M., Walther C.F.J., Heine T. Hydrogen adsorption in metal-organic frameworks: the role of nuclear quantum effects. J. Chem. Phys. 2014;141:064708. doi: 10.1063/1.4892670. [DOI] [PubMed] [Google Scholar]
67.Durette D., Bénard P., Zacharia R., Chahine R. Investigation of the hydrogen adsorbed density inside the pores of MOF-5 from path integral grand canonical Monte Carlo at supercritical and subcritical temperature. Sci. Bull. 2016;61:594–600. [Google Scholar]
68.Fischer M., Hoffmann F., Fröba M. Preferred hydrogen adsorption sites in various MOFs—a comparative computational study. ChemPhysChem. 2009;10:2647–2657. doi: 10.1002/cphc.200900459. [DOI] [PubMed] [Google Scholar]
69.Furukawa H., Miller M.A., Yaghi O.M. Independent verification of the saturation hydrogen uptake in MOF-177 and establishment of a benchmark for hydrogen adsorption in metal-organic frameworks. J. Mater. Chem. 2007;17:3197. [Google Scholar]
70.Ahmed A., Siegel D.J. 2019. HyMARC Datahub.https://datahub.hymarc.org/dataset/computational-prediction-of-hydrogen-storage-capacities-in-mofs [Google Scholar]
71.Pardakhti M., Moharreri E., Wanik D., Suib S.L., Srivastava R. Machine learning using combined structural and chemical descriptors for prediction of methane adsorption performance of metal organic frameworks (MOFs) ACS Comb. Sci. 2017;19:640–645. doi: 10.1021/acscombsci.7b00056. [DOI] [PubMed] [Google Scholar]
72.Fernandez M., Woo T.K., Wilmer C.E., Snurr R.Q. Large-scale quantitative structure-property relationship (QSPR) analysis of methane storage in metal-organic frameworks. J. Phys. Chem. C. 2013;117:7681–7689. [Google Scholar]
73.Fernandez M., Trefiak N.R., Woo T.K. Atomic property weighted radial distribution functions descriptors of metal-organic frameworks for the prediction of gas uptake capacity. J. Phys. Chem. C. 2013;117:14095–14105. [Google Scholar]
74.Fernandez M., Barnard A.S. Geometrical properties can predict CO2 and N2 adsorption performance of metal-organic frameworks (MOFs) at low pressure. ACS Comb. Sci. 2016;18:243–252. doi: 10.1021/acscombsci.5b00188. [DOI] [PubMed] [Google Scholar]
75.Nanoporous Materials Genome Center http://www.chem.umn.edu/nmgc/
76.Hastie T., Tibshirani R., Friedman J. Springer; 2009. The Elements of Statistical Learning. [Google Scholar]
77.Dorugade A.V., Kashid D.N. Alternative Method for Choosing Ridge Parameter for Regression. Appl. Math. Sci. 2010;4:447–456. [Google Scholar]
78.Van Wieringen W.N. Lecture Notes on Ridge Regression. arXiv. 2020 https://arxiv.org/abs/1509.09169 1509.09169. [Google Scholar]
79.Smola A.J., Smola A.J., Schölkopf B. A tutorial on support vector regression. Stat. Comput. 2004;14:199–222. [Google Scholar]
80.Bucior B.J., Bobbitt N.S., Islamoglu T., Goswami S., Gopalan A., Yildirim T., Farha O.K., Bagheri N., Snurr R.Q. Energy-based descriptors to rapidly predict hydrogen storage in metal-organic frameworks. Mol. Syst. Des. Eng. 2019;4:162–174. doi: 10.1039/c8me00050f. [DOI] [Google Scholar]
81.Lan Y., Yan T., Tong M., Zhong C. Large-scale computational assembly of ionic liquid/MOF composites: synergistic effect in the wire-tube conformation for efficient CO2/CH4 separation. J. Mater. Chem. A. 2019;7:12556–12564. [Google Scholar]
82.Li S., Chung Y.G., Simon C.M., Snurr R.Q. High-throughput computational screening of multivariate metal-organic frameworks (MTV-MOFs) for CO2 capture. J. Phys. Chem. Lett. 2017;8:19. doi: 10.1021/acs.jpclett.7b02700. [DOI] [PubMed] [Google Scholar]
83.Geurts P., Ernst D., Wehenkel L. Extremely randomized trees. Mach. Learn. 2006;63:3–42. [Google Scholar]
84.Ahmed A., Siegel D.J. HyMARC Sorbent Machine Learning Model: Predicting the Hydrogen Storage Capacity of Metal-Organic Frameworks via Machine Learning. https://sorbent-ml.hymarc.org/
85.Boyd P.G., Chidambaram A., García-Díez E., Ireland C.P., Daff T.D., Bounds R., Gładysiak A., Schouwink P., Moosavi S.M., Maroto-Valer M.M. Data-driven design of metal-organic frameworks for wet flue gas CO2 capture. Nature. 2019;576:253–256. doi: 10.1038/s41586-019-1798-7. [DOI] [PubMed] [Google Scholar]
86.Boyd P.G., Chidambaram A., García-Díez E., Ireland C.P., Daff T.D., Bounds R., Gładysiak A., Schouwink P., Moosavi S.M., Maroto-Valer M.M. Data-driven design of metal-organic frameworks for wet flue gas CO2 capture, Materials Cloud Archive 2018.0016/v3 (2019) Nature. 2019;576:253–256. doi: 10.24435/materialscloud:2018.0016/v3. [DOI] [PubMed] [Google Scholar]
87.Snurr R.Q. 2016. Reduced-mHOF-database.https://github.com/snurr-group/Reduced-hMOF-database [Google Scholar]
88.García-Holley P., Schweitzer B., Islamoglu T., Liu Y., Lin L., Rodriguez S., Weston M.H., Hupp J.T., Gómez-Gualdrón D.A., Yildirim T. Benchmark study of hydrogen storage in metal-organic frameworks under temperature and pressure swing conditions. ACS Energy Lett. 2018:748–754. [Google Scholar]
89.Wolpert D.H., Macready W.G. No free lunch theorems for optimization. IEEE Trans. Evol. Comput. 1997;1 doi: 10.1109/4235.585893. [DOI] [Google Scholar]
90.Breiman L., Friedman J.H., Olshen R.A., Stone C.J. Routledge; 2017. Classification and Regression Trees. [Google Scholar]
91.Freund Y., Schapire R.E. A decision-theoretic generalization of on-line learning and an application to boosting. J. Comput. Syst. Sci. 1997;55:119–139. [Google Scholar]
92.Drucker H. ICML ’97 Proc. Fourteenth Int. Conf. Mach. Learn. 1997. Improving regressors using boosting techniques; pp. 107–115.https://dl.acm.org/doi/10.5555/645526.657132 [Google Scholar]
93.Breiman L. Bagging predictors. Mach. Learn. 1996;24:123–140. [Google Scholar]
94.Breiman L. Random forests. Mach. Learn. 2001;45:5–32. [Google Scholar]
95.Friedman J. Greedy function approximation: a gradient boosting machine. Ann. Stat. 2001;29:1189–1232. [Google Scholar]
96.Chang C.-C., Lin C.-J. LIBSVM: A Library for Support Vector Machines. ACM Transactions on Intelligent Systems and Technology. 2001;2:1–27. [Google Scholar]
97.Platt J.C., Platt J.C. Advances in Large Margin Classifiers. MIT Press; 1999. Probabilistic outputs for support vector machines and comparisons to regularized likelihood methods; pp. 61–74. [Google Scholar]
98.Buhmann M.D. Cambridge University Press; 2002. Radial Basis Functions: Theory and Implementations. [Google Scholar]
99.Fan R.-E., Chang K.-W., Hsieh C.-J., Wang X.-R., Lin C.-J. LIBLINEAR: A Library for Large Linear Classification. J. Mach. Learn. Res. 2008;9:1871–1874. [Google Scholar]
100.Rifkin R.M., Lippert R.A. Notes on Regularized Least Squares. MIT. 2007 http://128.30.100.62:8080/media/fb/ps/MIT-CSAIL-TR-2007-025.pdf [Google Scholar]
101.Altman N.S. An introduction to kernel and nearest-neighbor nonparametric regression. Am. Stat. 1992;46:175–185. [Google Scholar]
102.Freund Y., Schapire R.E. A short introduction to boosting. J. Jpn. Soc. Artif. Intell. 1999;14:771–780. [Google Scholar]
103.Fernández-Delgado M., Sirsat M.S., Cernadas E., Alawadi S., Barro S., Febrero-Bande M. An extensive experimental survey of regression methods. Neural Networks. 2019;111:11–34. doi: 10.1016/j.neunet.2018.12.010. [DOI] [PubMed] [Google Scholar]
104.Pedregosa F., Varoquaux G., Gramfort A., Michel V., Thirion B., Grisel O., Blondel M., Prettenhofer P., Weiss R., Dubourg V. Scikit-learn: machine learning in Python. J. Mach. Learn. Res. 2011;12:2825–2830. [Google Scholar]
105.Richard M.-A., Bénard P., Chahine R. Gas adsorption process in activated carbon over a wide temperature range above the critical point. Part 1: modified Dubinin-Astakhov model. Adsorption. 2009;15:43–51. [Google Scholar]
106.Gomez-Gualdron D.A., Wang T.C., García-Holley P., Sawelewa R.M., Argueta E., Snurr R.Q., Hupp J.T., Yildirim T., Farha O.K. Understanding volumetric and gravimetric hydrogen adsorption trade-off in metal-organic frameworks. ACS Appl. Mater. Interfaces. 2017;9:33419–33428. doi: 10.1021/acsami.7b01190. [DOI] [PubMed] [Google Scholar]
107.Düren T., Bae Y.-S., Snurr R.Q. Using molecular simulation to characterise metal-organic frameworks for adsorption applications. Chem. Soc. Rev. 2009;38:1237. doi: 10.1039/b803498m. [DOI] [PubMed] [Google Scholar]
108.Allendorf M.D., Bauer C.A., Bhakta R.K., Houk R.J.T. Luminescent metal-organic frameworks. Chem. Soc. Rev. 2009;38:1330. doi: 10.1039/b802352m. [DOI] [PubMed] [Google Scholar]
109.Gómez-Gualdrón D.A., Moghadam P.Z., Hupp J.T., Farha O.K., Snurr R.Q. Application of consistency criteria to calculate BET areas of micro- and mesoporous metal-organic frameworks. J. Am. Chem. Soc. 2016;138:215–224. doi: 10.1021/jacs.5b10266. [DOI] [PubMed] [Google Scholar]
110.Himanen L., Geurts A., Foster A.S., Rinke P. Data-driven materials science: status, challenges, and perspectives. Adv. Sci. 2019:1900808. doi: 10.1002/advs.201900808. [DOI] [PMC free article] [PubMed] [Google Scholar]
111.Wei J., Chu X., Sun X., Xu K., Deng H., Chen J., Wei Z., Lei M. Machine learning in materials science. InfoMat. 2019;1:338–358. [Google Scholar]
112.Fanourgakis G.S., Gkagkas K., Tylianakis E., Klontzas E., Froudakis G. A robust machine learning algorithm for the prediction of methane adsorption in nanoporous materials. J. Phys. Chem. A. 2019 doi: 10.1021/acs.jpca.9b03290. acs.jpca.9b03290. [DOI] [PubMed] [Google Scholar]
113.Panella B., Hirscher M., Roth S. Hydrogen adsorption in different carbon nanostructures. Carbon N. Y. 2005;43:2209–2214. [Google Scholar]
114.Balderas-Xicohténcatl R., Schlichtenmayer M., Hirscher M. Volumetric Hydrogen Storage Capacity in Metal–Organic Frameworks. Energy Technol. 2017;6 578–582. [Google Scholar]
115.Moosavi S.M., Chidambaram A., Talirz L., Haranczyk M., Stylianou K.C., Smit B. Capturing chemical intuition in synthesis of metal-organic frameworks. Nat. Commun. 2019;10:539. doi: 10.1038/s41467-019-08483-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
116.Zwillinger D., Kokoska S. CRC Press; 2000. Standard Probability and Statistics Tables and Formulae. [Google Scholar]
117.Oliphant T.E. Python for scientific computing. Comput. Sci. Eng. 2007;9:10–20. [Google Scholar]
118.Millman K.J., Aivazis M. Python for scientists and engineers. Comput. Sci. Eng. 2011;13:9–12. [Google Scholar]
119.Parrt T., Turgutlu K. Rfpimp 1.3.4. https://github.com/parrt/random-forest-importances
120.Frank E., Hall M.A., Witten I.H. 2016. The WEKA Workbench.https://www.cs.waikato.ac.nz/ml/weka/Witten_et_al_2016_appendix.pdf [Google Scholar]
121.Kuhn M., Johnson K. Applied predictive modeling. Springer; 2013. [Google Scholar]
122.Witman M., Ling S., Grant D.M., Walker G.S., Agarwal S., Stavila V., Allendorf M.D. Extracting an empirical intermetallic hydride design principle from limited data via interpretable machine learning. J. Phys. Chem. Lett. 2020;11:40–47. doi: 10.1021/acs.jpclett.9b02971. [DOI] [PubMed] [Google Scholar]
123.Sturluson A., Huynh M.T., Kaija A.R., Laird C., Yoon S., Hou F., Feng Z., Wilmer C.E., Colón Y.J., Chung Y.G. The role of molecular modelling and simulation in the discovery and deployment of metal-organic frameworks for gas storage and separation. Mol. Simul. 2019;45:1082–1121. doi: 10.1080/08927022.2019.1648809. [DOI] [PMC free article] [PubMed] [Google Scholar]
124.Barthel S., Alexandrov E.V., Proserpio D.M., Smit B. Distinguishing Metal-Organic Frameworks. Cryst. Growth Des. 2018;18:1738–1747. doi: 10.1021/acs.cgd.7b01663. [DOI] [PMC free article] [PubMed] [Google Scholar]
125.Chen T., Manz T.A. A collection of forcefield precursors for metal-organic frameworks. RSC Adv. 2019;9:36492–36507. doi: 10.1039/c9ra07327b. [DOI] [PMC free article] [PubMed] [Google Scholar]
126.Ahmed A., Siegel D.J. Machine learning models for predicting hydrogen storage in metal-organic frameworks. Figshare. 2021 doi: 10.6084/m9.figshare.14173520.v1. [DOI] [Google Scholar]
127.Pinheiro M., Martin R.L., Rycroft C.H., Jones A., Iglesia E., Haranczyk M. Characterization and comparison of pore landscapes in crystalline porous materials. J. Mol. Graph. Model. 2013;44:208–219. doi: 10.1016/j.jmgm.2013.05.007. [DOI] [PubMed] [Google Scholar]
128.Pinheiro M., Martin R.L., Rycroft C.H., Haranczyk M. High accuracy geometric analysis of crystalline porous materials. CrystEngComm. 2013;15:7531–7538. [Google Scholar]
129.Ongari D., Boyd P.G., Barthel S., Witman M., Haranczyk M., Smit B. Accurate Characterization of the Pore Volume in Microporous Crystalline Materials. Langmuir. 2017;33:14529–14538. doi: 10.1021/acs.langmuir.7b01682. [DOI] [PMC free article] [PubMed] [Google Scholar]
130.Sarkisov L., Bueno-Perez R., Sutharson M., Fairen-jimenez D. Material Informatics with PoreBlazer v4.0 and CSD MOF Database. Chem. Mater. 2020;32:9849–9867. [Google Scholar]
131.Chen Z., Li P., Anderson R., Wang X., Zhang X., Robison L., Redfern L.R., Moribe S., Islamoglu T., Gómez-Gualdrón D.A. Balancing volumetric and gravimetric uptake in highly porous materials for clean energy. Science. 2020;368:297–303. doi: 10.1126/science.aaz8881. [DOI] [PubMed] [Google Scholar]
132.Camp J.S., Stavila V., Allendorf M.D., Prendergast D., Haranczyk M. Critical Factors in Computational Characterization of Hydrogen Storage in Metal-Organic Frameworks Critical Factors in Computational Characterization of Hydrogen Storage in Metal-Organic Frameworks. J. Phys. Chem. C. 2018;122:18957–18967. [Google Scholar]
133.Churchard A.J., Banach E., Borgschulte A., Caputo R., Chen J.C., Clary D., Fijalkowski K.J., Geerlings H., Genova R.V., Grochala W. A multifaceted approach to hydrogen storage. Phys. Chem. Chem. Phys. 2011;13:16955–16972. doi: 10.1039/c1cp22312g. [DOI] [PubMed] [Google Scholar]
134.MacRae C.F., Sovago I., Cottrell S.J., Galek P.T.A., McCabe P., Pidcock E., Platings M., Shields G.P., Stevens J.S., Towler M. Mercury 4.0: from visualization to analysis, design and prediction. J. Appl. Crystallogr. 2020;53:226–235. doi: 10.1107/S1600576719014092. [DOI] [PMC free article] [PubMed] [Google Scholar]
135.Manos M.J., Markoulides M.S., Malliakas C.D., Papaefstathiou G.S., Chronakis N., Kanatzidis M.G., Trikalitis P.N., Tasiopoulos A.J. A highly porous interpenetrated metal-organic framework from the use of a novel nanosized organic linker. Inorg. Chem. 2011;50:11297–11299. doi: 10.1021/ic201919q. [DOI] [PubMed] [Google Scholar]
136.Furukawa H., Ko N., Go Y.B., Aratani N., Choi S.B., Choi E., Yazaydin A.Ö., Snurr R.Q., O’Keeffe M., Kim J. Ultrahigh porosity in metal-organic frameworks. Science. 2010;329:424–428. doi: 10.1126/science.1192160. [DOI] [PubMed] [Google Scholar]
137.Yuan D., Zhao D., Sun D., Zhou H.-C. An isoreticular series of metal-organic frameworks with dendritic hexacarboxylate ligands and exceptionally high gas-uptake capacity. Angew. Chem. Int. Ed. 2010;49:5357–5361. doi: 10.1002/anie.201001009. [DOI] [PubMed] [Google Scholar]
138.Yan Y., Telepeni I., Yang S., Lin X., Kockelmann W., Dailly A., Blake A.J., Lewis W., Walker G.S., Allan D.R. Metal-organic polyhedral frameworks: high H2 adsorption capacities and neutron powder diffraction studies. J. Am. Chem. Soc. 2010;132:4092–4094. doi: 10.1021/ja1001407. [DOI] [PubMed] [Google Scholar]
139.Karagiaridi O., Bury W., Tylianakis E., Sarjeant A.A., Hupp J.T., Farha O.K. Opening metal-organic frameworks. Vol. 2: inserting longer pillars into pillared-paddlewheel structures through solvent-assisted linker exchange. Chem. Mater. 2013;25:3499–3503. [Google Scholar]
140.Zheng X., Huang Y., Duan J., Wang C., Wen L., Zhao J., Li D. A microporous Zn(II)-MOF with open metal sites: structure and selective adsorption properties. Dalt. Trans. 2014;43:8311–8317. doi: 10.1039/c4dt00307a. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Document S1. Supplemental experimental procedures, Figures S1–S8, Tables S1–S10 and S12–S14

mmc1.pdf^{(29.4MB, pdf)}

Table S11. Machine learning models based on feature combinations

mmc2.xlsx^{(41.9KB, xlsx)}

Document S2. Article plus supplemental information

mmc3.pdf^{(32.8MB, pdf)}

Data Availability Statement

•
Original data have been deposited to HyMARC Data Hub: https://datahub.hymarc.org/dataset/computational-prediction-of-hydrogen-storage-capacities-in-mofs
•
Interactive ML models: https://sorbent-ml.hymarc.org/
•
Python API: https://sorbent-ml.hymarc.org/
•
Downloadable ML models and instructions: https://doi.org/10.6084/m9.figshare.14173520.v1

[bib1] 1.Ahmed A., Seth S., Purewal J., Wong-Foy A.G., Veenstra M., Matzger A.J., Siegel D.J. Exceptional hydrogen storage achieved by screening nearly half a million metal-organic frameworks. Nat. Commun. 2019;10:1568. doi: 10.1038/s41467-019-09365-w. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib2] 2.Ahmed A., Liu Y., Purewal J., Tran L.D., Veenstra M., Wong-Foy A., Matzger A., Siegel D. Balancing gravimetric and volumetric hydrogen density in MOFs. Energy Environ. Sci. 2017;10:2459–2471. [Google Scholar]

[bib3] 3.Wong-Foy A.G., Matzger A.J., Yaghi O.M. Exceptional H2 saturation uptake in microporous metal-organic frameworks. J. Am. Chem. Soc. 2006;128:3494–3495. doi: 10.1021/ja058213h. [DOI] [PubMed] [Google Scholar]

[bib4] 4.Satyapal S., Petrovic J., Read C., Thomas G., Ordaz G. The U.S. Department of Energy’s National Hydrogen Storage Project: progress towards meeting hydrogen-powered vehicle requirements. Catal. Today. 2007;120:246–256. [Google Scholar]

[bib5] 5.Greene D.L., Duleep G. Worldwide Status of Hydrogen Fuel Cell Vehicle Technology and Prospects for Commercialization. U.S. Department of Energy. 2013 https://www.hydrogen.energy.gov/pdfs/progress13/xi_1_greene_2013.pdf [Google Scholar]

[bib6] 6.Allendorf M.D., Hulvey Z., Gennett T., Ahmed A., Autrey T., Camp J., Seon Cho E., Furukawa H., Haranczyk M., Head-Gordon M. An assessment of strategies for the development of solid-state adsorbents for vehicular hydrogen storage. Energy Environ. Sci. 2018;11:2784–2812. [Google Scholar]

[bib7] 7.Yang J., Sudik A., Wolverton C., Siegel D.J. High capacity hydrogen storage materials: attributes for automotive applications and techniques for materials discovery. Chem. Soc. Rev. 2010;39:656–675. doi: 10.1039/b802882f. [DOI] [PubMed] [Google Scholar]

[bib8] 8.Long J.R. . U.S. Department of Energy, Hydrogen and Fuel Cells Program 2015 Annual Merit Review Proceedings: Project ST103. 2015. Hydrogen Storage in Metal-Organic Frameworkshttps://www.hydrogen.energy.gov/pdfs/review15/st103_long_2015_o.pdf [Google Scholar]

[bib9] 9.U.S. Department of Energy. (n.d.) DOE Technical Targets for Onboard Hydrogen Storage for Light-Duty Vehicles, https://energy.gov/eere/fuelcells/doe-technical-targets-onboard-hydrogen-storage-light-duty-vehicles.

[bib10] 10.Astiaso Garcia D., Barbanera F., Cumo F., Di Matteo U., Nastasi B. Expert opinion analysis on renewable hydrogen storage systems potential in Europe. Energies. 2016;9:963. [Google Scholar]

[bib11] 11.Riis T., Sandrock G., Ulleberg Ø., Vie P.J.S. Hydrogen Production and Storage: R&D Priorities and Gaps. International Energy Agency); 2006. Hydrogen storage R&D: priorities and gaps; pp. 19–33. [Google Scholar]

[bib12] 12.Purewal J., Veenstra M., Tamburello D., Ahmed A., Matzger A.J., Wong-Foy A.G., Seth S., Liu Y., Siegel D.J. Estimation of system-level hydrogen storage for metal-organic frameworks with high volumetric storage density. Int. J. Hydrogen Energy. 2019;44:15135–15145. [Google Scholar]

[bib13] 13.Manoharan Y., Hosseini S.E., Butler B., Alzhahrani H., Senior B.T.F., Ashuri T., Krohn J. Hydrogen fuel cell vehicles; current status and future prospect. Appl. Sci. 2019;9:2296. [Google Scholar]

[bib14] 14.Makridis S.S. Hydrogen storage and compression. In: Carriveau R., Ting D.S.-K., editors. Methane and Hydrogen for Energy Storage. The Institution of Engineering and Technology); 2016. pp. 1–28. [Google Scholar]

[bib15] 15.Veenstra, M., Purewal, J., Xu, C., Yang, J., Blaser, R., Sudik, A., Siegel, D., Ming, Y., Liu, D., Hang, C., et al. (2015). Ford/BASF-SE/UM Activities in Support of the Hydrogen Storage Engineering Center of Excellence. U.S. Department of Energy, Office of Scientific and Technical Information, 10.2172/1296578.

[bib16] 16.Öhrström L. Let’s talk about MOFs—topology and terminology of metal-organic frameworks and why we need them. Crystals. 2015;5:154–162. [Google Scholar]

[bib17] 17.Fischer R.A., Schwedler I. Terminologie von Metall-organischen Gerüstverbindungen und Koordinationspolymeren (IUPAC-Empfehlungen 2013) Angew. Chem. Int. Ed. 2014;126:7209–7214. [Google Scholar]

[bib18] 18.Batten S.R., Champness N.R., Chen X.-M., Garcia-Martinez J., Kitagawa S., Öhrström L., O’Keeffe M., Paik Suh M., Reedijk J. Terminology of metal-organic frameworks and coordination polymers (IUPAC Recommendations 2013) Pure Appl. Chem. 2013;85:1715–1724. [Google Scholar]

[bib19] 19.Thommes M., Kaneko K., Neimark A.V., Olivier J.P., Rodriguez-Reinoso F., Rouquerol J., Sing K.S.W. Physisorption of gases, with special reference to the evaluation of surface area and pore size distribution (IUPAC Technical Report) Pure Appl. Chem. 2015;87:1051–1069. [Google Scholar]

[bib20] 20.Batten S.R., Champness N.R., Chen X.-M., Garcia-Martinez J., Kitagawa S., Öhrström L., O’Keeffe M., Suh M.P., Reedijk J. Coordination polymers, metal-organic frameworks and the need for terminology guidelines. CrystEngComm. 2012;14:3001. [Google Scholar]

[bib21] 21.O’Keeffe M. Nets, tiles, and metal-organic frameworks. APL Mater. 2014;2:124106. [Google Scholar]

[bib22] 22.Tranchemontagne D.J., Mendoza-Cortés J.L., O’Keeffe M., Yaghi O.M. Secondary building units, nets and bonding in the chemistry of metal-organic frameworks. Chem. Soc. Rev. 2009;38:1257. doi: 10.1039/b817735j. [DOI] [PubMed] [Google Scholar]

[bib23] 23.Reymond J.-L. The chemical space project. Acc. Chem. Res. 2015;48:722–730. doi: 10.1021/ar500432k. [DOI] [PubMed] [Google Scholar]

[bib24] 24.Kontijevskis A. Mapping of drug-like chemical universe with reduced complexity molecular frameworks. J. Chem. Inf. Model. 2017;57:680–699. doi: 10.1021/acs.jcim.7b00006. [DOI] [PubMed] [Google Scholar]

[bib25] 25.Martin R.L., Smit B., Haranczyk M. Addressing challenges of identifying geometrically diverse sets of crystalline porous materials. J. Chem. Inf. Model. 2012;52:308–318. doi: 10.1021/ci200386x. [DOI] [PubMed] [Google Scholar]

[bib26] 26.Sun D., Sun F., Deng X., Li Z. Mixed-metal strategy on metal-organic frameworks (MOFs) for functionalities expansion: Co substitution induces aerobic oxidation of cyclohexene over inactive Ni-MOF-74. Inorg. Chem. 2015;54:8639–8643. doi: 10.1021/acs.inorgchem.5b01278. [DOI] [PubMed] [Google Scholar]

[bib27] 27.Deng H., Doonan C.J., Furukawa H., Ferreira R.B., Towne J., Knobler C.B., Wang B., Yaghi O.M. Multiple functional groups of varying ratios in metal-organic frameworks. Science. 2010;327:846–850. doi: 10.1126/science.1181761. [DOI] [PubMed] [Google Scholar]

[bib28] 28.Park J., Kim H., Han S.S., Jung Y. Tuning metal-organic frameworks with open-metal sites and its origin for enhancing CO2 affinity by metal substitution. J. Phys. Chem. Lett. 2012;3:826–829. doi: 10.1021/jz300047n. [DOI] [PubMed] [Google Scholar]

[bib29] 29.Moghadam P.Z., Li A., Wiggin S.B., Tao A., Maloney A.G.P., Wood P.A., Ward S.C., Fairen-Jimenez D. Development of a Cambridge structural database subset: a collection of metal-organic frameworks for past, present, and future. Chem. Mater. 2017;29:2618–2625. [Google Scholar]

[bib30] 30.Groom C.R., Bruno I.J., Lightfoot M.P., Ward S.C. The Cambridge Structural Database. Acta Crystallogr. Sect. B Struct. Sci. Cryst. Eng. Mater. 2016;72:171–179. doi: 10.1107/S2052520616003954. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib31] 31.Goldsmith J., Wong-Foy A.G., Cafarella M.J., Siegel D.J. Theoretical limits of hydrogen storage in metal–organic frameworks: opportunities and trade-offs. Chem. Mater. 2013;25:3373–3382. [Google Scholar]

[bib32] 32.Altintas C., Avci G., Daglar H., Nemati Vesali Azar A., Erucar I., Velioglu S., Keskin S. An extensive comparative analysis of two MOF databases: high-throughput screening of computation-ready MOFs for CH4 and H2 adsorption. J. Mater. Chem. A. 2019;7:9593–9608. [Google Scholar]

[bib33] 33.Chung Y.G., Camp J., Haranczyk M., Sikora B.J., Bury W., Krungleviciute V., Yildirim T., Farha O.K., Sholl D.S., Snurr R.Q. Computation-ready, experimental metal-organic frameworks: a tool to enable high-throughput screening of nanoporous crystals. Chem. Mater. 2014;26:6185–6192. [Google Scholar]

[bib34] 34.Chung Y.G., Haldoupis E., Bucior B.J., Haranczyk M., Lee S., Zhang H., Vogiatzis K.D., Milisavljevic M., Ling S., Camp J.S. Advances, updates, and analytics for the computation-ready, experimental metal-organic framework database: CoRE MOF 2019. J. Chem. Eng. Data. 2019;64:5985–5998. [Google Scholar]

[bib35] 35.Chen T., Manz T.A. Identifying misbonded atoms in the 2019 CoRE Metal-Organic Framework Database. RSC Adv. 2020;10:26944–26951. doi: 10.1039/d0ra02498h. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib36] 36.Wilmer C.E., Leaf M., Lee C.Y., Farha O.K., Hauser B.G., Hupp J.T., Snurr R.Q. Large-scale screening of hypothetical metal-organic frameworks. Nat. Chem. 2011;4:83–89. doi: 10.1038/nchem.1192. [DOI] [PubMed] [Google Scholar]

[bib37] 37.Aghaji M.Z., Fernandez M., Boyd P.G., Daff T.D., Woo T.K. Quantitative Structure-Property Relationship Models for Recognizing Metal Organic Frameworks (MOFs) with High CO2 Working Capacity and CO2/CH4 Selectivity for Methane Purification. Eur. J. Inorg. Chem. 2016;2016:4505–4511. [Google Scholar]

[bib38] 38.Martin R.L., Lin L.C., Jariwala K., Smit B., Haranczyk M. Mail-order metal-organic frameworks (MOFs): designing isoreticular MOF-5 analogues comprising commercially available organic molecules. J. Phys. Chem. C. 2013;117:12159–12167. [Google Scholar]

[bib39] 39.Bao Y., Martin R.L., Haranczyk M., Deem M.W. In silico prediction of MOFs with high deliverable capacity or internal surface area. Phys. Chem. Chem. Phys. 2015;17:11962–11973. doi: 10.1039/c5cp00002e. [DOI] [PubMed] [Google Scholar]

[bib40] 40.Witman M., Ling S., Anderson S., Tong L., Stylianou K.C., Slater B., Smit B., Haranczyk M. In silico design and screening of hypothetical MOF-74 analogs and their experimental synthesis. Chem. Sci. 2016;7:6263–6272. doi: 10.1039/c6sc01477a. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib41] 41.Chung Y.G., Gómez-gualdrón D.A., Li P., Leperi K.T., Deria P., Zhang H., Vermeulen N.A., Stoddart J.F., You F., Hupp J.T. In Silico Discovery of Metal-Organic Frameworks for Precombustion CO2 Capture Using a Genetic Algorithm. Sci. Adv. 2016;2:e1600909. doi: 10.1126/sciadv.1600909. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib42] 42.Anderson R., Rodgers J., Argueta E., Biong A., Go D.A. Role of pore chemistry and topology in the CO2 capture capabilities of MOFs: from molecular simulation to machine learning. Chem. Mater. 2018;30:11. [Google Scholar]

[bib43] 43.Anderson G., Schweitzer B., Anderson R., Gómez-Gualdrón D.A. Attainable volumetric targets for adsorption-based hydrogen storage in porous crystals: molecular simulation and machine learning. J. Phys. Chem. C. 2019;123:120–130. [Google Scholar]

[bib44] 44.Anderson R., Gómez-Gualdrón D.A. Increasing topological diversity during computational “synthesis” of porous crystals: how and why. CrystEngComm. 2019;21:1653–1665. [Google Scholar]

[bib45] 45.Gomez-Gualdron D.A., Gutov O.V., Krungleviciute V., Borah B., Mondloch J.E., Hupp J.T., Yildirim T., Farha O.K., Snurr R.Q. Computational design of metal-organic frameworks based on stable zirconium building units for storage and delivery of methane. Chem. Mater. 2014;26:5632–5639. [Google Scholar]

[bib46] 46.Bao Y., Martin R.L., Simon C.M., Haranczyk M., Smit B., Deem M.W. In silico discovery of high deliverable capacity metal-organic frameworks. J. Phys. Chem. C. 2015;119:186–195. [Google Scholar]

[bib47] 47.Willems T.F., Rycroft C.H., Kazi M., Meza J.C., Haranczyk M. Algorithms and tools for high-throughput geometry-based analysis of crystalline porous materials. Microporous Mesoporous Mater. 2012;149:134–141. [Google Scholar]

[bib48] 48.Addicoat M.A., Coupry D.E., Heine T. AuToGraFS: automatic topological generator for framework structures. J. Phys. Chem. A. 2014;118:9607–9614. doi: 10.1021/jp507643v. [DOI] [PubMed] [Google Scholar]

[bib49] 49.Boyd P.G., Woo T.K. A generalized method for constructing hypothetical nanoporous materials of any net topology from graph theory. CrystEngComm. 2016;18:3777–3792. [Google Scholar]

[bib50] 50.Gómez-Gualdrón D.A., Colón Y.J., Zhang X., Wang T.C., Chen Y.-S., Hupp J.T., Yildirim T., Farha O.K., Zhang J., Snurr R.Q. Evaluating topologically diverse metal-organic frameworks for cryo-adsorbed hydrogen storage. Energy Environ. Sci. 2016;9:3279–3289. [Google Scholar]

[bib51] 51.Yao Z., Sánchez-Lengeling B., Bobbitt N.S., Bucior B.J., Kumar S.G.H., Collins S.P., Burns T., Woo T.K., Farha O., Snurr R.Q. Inverse design of nanoporous crystalline reticular materials with deep generative models. Nat. Mach. Intell. 2021;3:76–86. [Google Scholar]

[bib52] 52.Sadus R.J. Elsevier; 1999. Molecular Simulation of Fluids: Theory, Algorithms, and Object-Orientation. [Google Scholar]

[bib53] 53.Allen M.P., Tildesley D.J. Oxford University Press; 1989. Computer Simulation of Liquids. [Google Scholar]

[bib54] 54.Frenkel D., Smit B. 2nd ed. Academic Press, Inc.; 2001. Understanding Molecular Simulation: From Algorithms to Applications. [Google Scholar]

[bib55] 55.Hill T.L. Dover Publications; 1986. An Introduction to Statistical Thermodynamics. [Google Scholar]

[bib56] 56.Dubbeldam D., Torres-Knoop A., Walton K.S. Molecular simulation on the inner workings of Monte Carlo codes. Mol. Simul. 2013;39:14–15. [Google Scholar]

[bib57] 57.Fernandez M., Boyd P.G., Daff T.D., Aghaji M.Z., Woo T.K. Rapid and accurate machine learning recognition of high performing metal organic frameworks for CO2 capture. J. Phys. Chem. Lett. 2014;5:3056–3060. doi: 10.1021/jz501331m. [DOI] [PubMed] [Google Scholar]

[bib58] 58.Martin R.L., Simon C.M., Smit B., Haranczyk M. In silico design of porous polymer networks: high-throughput screening for methane storage materials. J. Am. Chem. Soc. 2014;136:5006–5022. doi: 10.1021/ja4123939. [DOI] [PubMed] [Google Scholar]

[bib59] 59.Colón Y.J., Gómez-Gualdrón D.A., Snurr R.Q. Topologically guided, automated construction of metal-organic frameworks and their evaluation for energy-related applications. Cryst. Growth Des. 2017;17:5801–5810. [Google Scholar]

[bib60] 60.Boyd P.G., Moosavi S.M., Witman M., Smit B. Force-field prediction of materials properties in metal-organic frameworks. J. Phys. Chem. Lett. 2017;8:357–363. doi: 10.1021/acs.jpclett.6b02532. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib61] 61.Thornton A.W., Simon C.M., Kim J., Kwon O., Deeg K.S., Konstas K., Pas S.J., Hill M.R., Winkler D.A., Haranczyk M. Materials genome in action: identifying the performance limits of physical hydrogen storage. Chem. Mater. 2017;29:2844–2854. doi: 10.1021/acs.chemmater.6b04933. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib62] 62.Bobbitt N.S., Snurr R.Q. Molecular Simulation Molecular Modelling and Machine Learning for High-Throughput Screening of Metal-Organic Frameworks for Hydrogen Storage Molecular Modelling and Machine Learning for High-Throughput Screening of Metal-Organic Frameworks for Hydrogen Storage. Mol. Simul. 2019;45:1069–1081. [Google Scholar]

[bib63] 63.Borboudakis G., Stergiannakos T., Frysali M., Klontzas E., Tsamardinos I., Froudakis G.E. Chemically intuited, large-scale screening of MOFs by machine learning techniques. NPJ Comput. Mater. 2017;3 doi: 10.1038/s41524-017-0045-8. [DOI] [Google Scholar]

[bib64] 64.Broom D.P., Webb C.J., Hurst K.E., Parilla P.A., Gennett T., Brown C.M., Zacharia R., Tylianakis E., Klontzas E., Froudakis G.E. Outlook and challenges for hydrogen storage in nanoporous materials. Appl. Phys. A. 2016;122:151. [Google Scholar]

[bib65] 65.Butler K.T., Davies D.W., Cartwright H., Isayev O., Walsh A. Machine learning for molecular and materials science. Nature. 2018;559:547–555. doi: 10.1038/s41586-018-0337-2. [DOI] [PubMed] [Google Scholar]

[bib66] 66.Wahiduzzaman M., Walther C.F.J., Heine T. Hydrogen adsorption in metal-organic frameworks: the role of nuclear quantum effects. J. Chem. Phys. 2014;141:064708. doi: 10.1063/1.4892670. [DOI] [PubMed] [Google Scholar]

[bib67] 67.Durette D., Bénard P., Zacharia R., Chahine R. Investigation of the hydrogen adsorbed density inside the pores of MOF-5 from path integral grand canonical Monte Carlo at supercritical and subcritical temperature. Sci. Bull. 2016;61:594–600. [Google Scholar]

[bib68] 68.Fischer M., Hoffmann F., Fröba M. Preferred hydrogen adsorption sites in various MOFs—a comparative computational study. ChemPhysChem. 2009;10:2647–2657. doi: 10.1002/cphc.200900459. [DOI] [PubMed] [Google Scholar]

[bib69] 69.Furukawa H., Miller M.A., Yaghi O.M. Independent verification of the saturation hydrogen uptake in MOF-177 and establishment of a benchmark for hydrogen adsorption in metal-organic frameworks. J. Mater. Chem. 2007;17:3197. [Google Scholar]

[bib70] 70.Ahmed A., Siegel D.J. 2019. HyMARC Datahub.https://datahub.hymarc.org/dataset/computational-prediction-of-hydrogen-storage-capacities-in-mofs [Google Scholar]

[bib71] 71.Pardakhti M., Moharreri E., Wanik D., Suib S.L., Srivastava R. Machine learning using combined structural and chemical descriptors for prediction of methane adsorption performance of metal organic frameworks (MOFs) ACS Comb. Sci. 2017;19:640–645. doi: 10.1021/acscombsci.7b00056. [DOI] [PubMed] [Google Scholar]

[bib72] 72.Fernandez M., Woo T.K., Wilmer C.E., Snurr R.Q. Large-scale quantitative structure-property relationship (QSPR) analysis of methane storage in metal-organic frameworks. J. Phys. Chem. C. 2013;117:7681–7689. [Google Scholar]

[bib73] 73.Fernandez M., Trefiak N.R., Woo T.K. Atomic property weighted radial distribution functions descriptors of metal-organic frameworks for the prediction of gas uptake capacity. J. Phys. Chem. C. 2013;117:14095–14105. [Google Scholar]

[bib74] 74.Fernandez M., Barnard A.S. Geometrical properties can predict CO2 and N2 adsorption performance of metal-organic frameworks (MOFs) at low pressure. ACS Comb. Sci. 2016;18:243–252. doi: 10.1021/acscombsci.5b00188. [DOI] [PubMed] [Google Scholar]

[bib75] 75.Nanoporous Materials Genome Center http://www.chem.umn.edu/nmgc/

[bib76] 76.Hastie T., Tibshirani R., Friedman J. Springer; 2009. The Elements of Statistical Learning. [Google Scholar]

[bib77] 77.Dorugade A.V., Kashid D.N. Alternative Method for Choosing Ridge Parameter for Regression. Appl. Math. Sci. 2010;4:447–456. [Google Scholar]

[bib78] 78.Van Wieringen W.N. Lecture Notes on Ridge Regression. arXiv. 2020 https://arxiv.org/abs/1509.09169 1509.09169. [Google Scholar]

[bib79] 79.Smola A.J., Smola A.J., Schölkopf B. A tutorial on support vector regression. Stat. Comput. 2004;14:199–222. [Google Scholar]

[bib80] 80.Bucior B.J., Bobbitt N.S., Islamoglu T., Goswami S., Gopalan A., Yildirim T., Farha O.K., Bagheri N., Snurr R.Q. Energy-based descriptors to rapidly predict hydrogen storage in metal-organic frameworks. Mol. Syst. Des. Eng. 2019;4:162–174. doi: 10.1039/c8me00050f. [DOI] [Google Scholar]

[bib81] 81.Lan Y., Yan T., Tong M., Zhong C. Large-scale computational assembly of ionic liquid/MOF composites: synergistic effect in the wire-tube conformation for efficient CO2/CH4 separation. J. Mater. Chem. A. 2019;7:12556–12564. [Google Scholar]

[bib82] 82.Li S., Chung Y.G., Simon C.M., Snurr R.Q. High-throughput computational screening of multivariate metal-organic frameworks (MTV-MOFs) for CO2 capture. J. Phys. Chem. Lett. 2017;8:19. doi: 10.1021/acs.jpclett.7b02700. [DOI] [PubMed] [Google Scholar]

[bib83] 83.Geurts P., Ernst D., Wehenkel L. Extremely randomized trees. Mach. Learn. 2006;63:3–42. [Google Scholar]

[bib84] 84.Ahmed A., Siegel D.J. HyMARC Sorbent Machine Learning Model: Predicting the Hydrogen Storage Capacity of Metal-Organic Frameworks via Machine Learning. https://sorbent-ml.hymarc.org/

[bib85] 85.Boyd P.G., Chidambaram A., García-Díez E., Ireland C.P., Daff T.D., Bounds R., Gładysiak A., Schouwink P., Moosavi S.M., Maroto-Valer M.M. Data-driven design of metal-organic frameworks for wet flue gas CO2 capture. Nature. 2019;576:253–256. doi: 10.1038/s41586-019-1798-7. [DOI] [PubMed] [Google Scholar]

[bib86] 86.Boyd P.G., Chidambaram A., García-Díez E., Ireland C.P., Daff T.D., Bounds R., Gładysiak A., Schouwink P., Moosavi S.M., Maroto-Valer M.M. Data-driven design of metal-organic frameworks for wet flue gas CO2 capture, Materials Cloud Archive 2018.0016/v3 (2019) Nature. 2019;576:253–256. doi: 10.24435/materialscloud:2018.0016/v3. [DOI] [PubMed] [Google Scholar]

[bib87] 87.Snurr R.Q. 2016. Reduced-mHOF-database.https://github.com/snurr-group/Reduced-hMOF-database [Google Scholar]

[bib88] 88.García-Holley P., Schweitzer B., Islamoglu T., Liu Y., Lin L., Rodriguez S., Weston M.H., Hupp J.T., Gómez-Gualdrón D.A., Yildirim T. Benchmark study of hydrogen storage in metal-organic frameworks under temperature and pressure swing conditions. ACS Energy Lett. 2018:748–754. [Google Scholar]

[bib89] 89.Wolpert D.H., Macready W.G. No free lunch theorems for optimization. IEEE Trans. Evol. Comput. 1997;1 doi: 10.1109/4235.585893. [DOI] [Google Scholar]

[bib90] 90.Breiman L., Friedman J.H., Olshen R.A., Stone C.J. Routledge; 2017. Classification and Regression Trees. [Google Scholar]

[bib91] 91.Freund Y., Schapire R.E. A decision-theoretic generalization of on-line learning and an application to boosting. J. Comput. Syst. Sci. 1997;55:119–139. [Google Scholar]

[bib92] 92.Drucker H. ICML ’97 Proc. Fourteenth Int. Conf. Mach. Learn. 1997. Improving regressors using boosting techniques; pp. 107–115.https://dl.acm.org/doi/10.5555/645526.657132 [Google Scholar]

[bib93] 93.Breiman L. Bagging predictors. Mach. Learn. 1996;24:123–140. [Google Scholar]

[bib94] 94.Breiman L. Random forests. Mach. Learn. 2001;45:5–32. [Google Scholar]

[bib95] 95.Friedman J. Greedy function approximation: a gradient boosting machine. Ann. Stat. 2001;29:1189–1232. [Google Scholar]

[bib96] 96.Chang C.-C., Lin C.-J. LIBSVM: A Library for Support Vector Machines. ACM Transactions on Intelligent Systems and Technology. 2001;2:1–27. [Google Scholar]

[bib97] 97.Platt J.C., Platt J.C. Advances in Large Margin Classifiers. MIT Press; 1999. Probabilistic outputs for support vector machines and comparisons to regularized likelihood methods; pp. 61–74. [Google Scholar]

[bib98] 98.Buhmann M.D. Cambridge University Press; 2002. Radial Basis Functions: Theory and Implementations. [Google Scholar]

[bib99] 99.Fan R.-E., Chang K.-W., Hsieh C.-J., Wang X.-R., Lin C.-J. LIBLINEAR: A Library for Large Linear Classification. J. Mach. Learn. Res. 2008;9:1871–1874. [Google Scholar]

[bib100] 100.Rifkin R.M., Lippert R.A. Notes on Regularized Least Squares. MIT. 2007 http://128.30.100.62:8080/media/fb/ps/MIT-CSAIL-TR-2007-025.pdf [Google Scholar]

[bib101] 101.Altman N.S. An introduction to kernel and nearest-neighbor nonparametric regression. Am. Stat. 1992;46:175–185. [Google Scholar]

[bib102] 102.Freund Y., Schapire R.E. A short introduction to boosting. J. Jpn. Soc. Artif. Intell. 1999;14:771–780. [Google Scholar]

[bib103] 103.Fernández-Delgado M., Sirsat M.S., Cernadas E., Alawadi S., Barro S., Febrero-Bande M. An extensive experimental survey of regression methods. Neural Networks. 2019;111:11–34. doi: 10.1016/j.neunet.2018.12.010. [DOI] [PubMed] [Google Scholar]

[bib104] 104.Pedregosa F., Varoquaux G., Gramfort A., Michel V., Thirion B., Grisel O., Blondel M., Prettenhofer P., Weiss R., Dubourg V. Scikit-learn: machine learning in Python. J. Mach. Learn. Res. 2011;12:2825–2830. [Google Scholar]

[bib105] 105.Richard M.-A., Bénard P., Chahine R. Gas adsorption process in activated carbon over a wide temperature range above the critical point. Part 1: modified Dubinin-Astakhov model. Adsorption. 2009;15:43–51. [Google Scholar]

[bib106] 106.Gomez-Gualdron D.A., Wang T.C., García-Holley P., Sawelewa R.M., Argueta E., Snurr R.Q., Hupp J.T., Yildirim T., Farha O.K. Understanding volumetric and gravimetric hydrogen adsorption trade-off in metal-organic frameworks. ACS Appl. Mater. Interfaces. 2017;9:33419–33428. doi: 10.1021/acsami.7b01190. [DOI] [PubMed] [Google Scholar]

[bib107] 107.Düren T., Bae Y.-S., Snurr R.Q. Using molecular simulation to characterise metal-organic frameworks for adsorption applications. Chem. Soc. Rev. 2009;38:1237. doi: 10.1039/b803498m. [DOI] [PubMed] [Google Scholar]

[bib108] 108.Allendorf M.D., Bauer C.A., Bhakta R.K., Houk R.J.T. Luminescent metal-organic frameworks. Chem. Soc. Rev. 2009;38:1330. doi: 10.1039/b802352m. [DOI] [PubMed] [Google Scholar]

[bib109] 109.Gómez-Gualdrón D.A., Moghadam P.Z., Hupp J.T., Farha O.K., Snurr R.Q. Application of consistency criteria to calculate BET areas of micro- and mesoporous metal-organic frameworks. J. Am. Chem. Soc. 2016;138:215–224. doi: 10.1021/jacs.5b10266. [DOI] [PubMed] [Google Scholar]

[bib110] 110.Himanen L., Geurts A., Foster A.S., Rinke P. Data-driven materials science: status, challenges, and perspectives. Adv. Sci. 2019:1900808. doi: 10.1002/advs.201900808. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib111] 111.Wei J., Chu X., Sun X., Xu K., Deng H., Chen J., Wei Z., Lei M. Machine learning in materials science. InfoMat. 2019;1:338–358. [Google Scholar]

[bib112] 112.Fanourgakis G.S., Gkagkas K., Tylianakis E., Klontzas E., Froudakis G. A robust machine learning algorithm for the prediction of methane adsorption in nanoporous materials. J. Phys. Chem. A. 2019 doi: 10.1021/acs.jpca.9b03290. acs.jpca.9b03290. [DOI] [PubMed] [Google Scholar]

[bib113] 113.Panella B., Hirscher M., Roth S. Hydrogen adsorption in different carbon nanostructures. Carbon N. Y. 2005;43:2209–2214. [Google Scholar]

[bib114] 114.Balderas-Xicohténcatl R., Schlichtenmayer M., Hirscher M. Volumetric Hydrogen Storage Capacity in Metal–Organic Frameworks. Energy Technol. 2017;6 578–582. [Google Scholar]

[bib115] 115.Moosavi S.M., Chidambaram A., Talirz L., Haranczyk M., Stylianou K.C., Smit B. Capturing chemical intuition in synthesis of metal-organic frameworks. Nat. Commun. 2019;10:539. doi: 10.1038/s41467-019-08483-9. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib116] 116.Zwillinger D., Kokoska S. CRC Press; 2000. Standard Probability and Statistics Tables and Formulae. [Google Scholar]

[bib117] 117.Oliphant T.E. Python for scientific computing. Comput. Sci. Eng. 2007;9:10–20. [Google Scholar]

[bib118] 118.Millman K.J., Aivazis M. Python for scientists and engineers. Comput. Sci. Eng. 2011;13:9–12. [Google Scholar]

[bib119] 119.Parrt T., Turgutlu K. Rfpimp 1.3.4. https://github.com/parrt/random-forest-importances

[bib120] 120.Frank E., Hall M.A., Witten I.H. 2016. The WEKA Workbench.https://www.cs.waikato.ac.nz/ml/weka/Witten_et_al_2016_appendix.pdf [Google Scholar]

[bib121] 121.Kuhn M., Johnson K. Applied predictive modeling. Springer; 2013. [Google Scholar]

[bib122] 122.Witman M., Ling S., Grant D.M., Walker G.S., Agarwal S., Stavila V., Allendorf M.D. Extracting an empirical intermetallic hydride design principle from limited data via interpretable machine learning. J. Phys. Chem. Lett. 2020;11:40–47. doi: 10.1021/acs.jpclett.9b02971. [DOI] [PubMed] [Google Scholar]

[bib123] 123.Sturluson A., Huynh M.T., Kaija A.R., Laird C., Yoon S., Hou F., Feng Z., Wilmer C.E., Colón Y.J., Chung Y.G. The role of molecular modelling and simulation in the discovery and deployment of metal-organic frameworks for gas storage and separation. Mol. Simul. 2019;45:1082–1121. doi: 10.1080/08927022.2019.1648809. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib124] 124.Barthel S., Alexandrov E.V., Proserpio D.M., Smit B. Distinguishing Metal-Organic Frameworks. Cryst. Growth Des. 2018;18:1738–1747. doi: 10.1021/acs.cgd.7b01663. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib125] 125.Chen T., Manz T.A. A collection of forcefield precursors for metal-organic frameworks. RSC Adv. 2019;9:36492–36507. doi: 10.1039/c9ra07327b. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib126] 126.Ahmed A., Siegel D.J. Machine learning models for predicting hydrogen storage in metal-organic frameworks. Figshare. 2021 doi: 10.6084/m9.figshare.14173520.v1. [DOI] [Google Scholar]

[bib127] 127.Pinheiro M., Martin R.L., Rycroft C.H., Jones A., Iglesia E., Haranczyk M. Characterization and comparison of pore landscapes in crystalline porous materials. J. Mol. Graph. Model. 2013;44:208–219. doi: 10.1016/j.jmgm.2013.05.007. [DOI] [PubMed] [Google Scholar]

[bib128] 128.Pinheiro M., Martin R.L., Rycroft C.H., Haranczyk M. High accuracy geometric analysis of crystalline porous materials. CrystEngComm. 2013;15:7531–7538. [Google Scholar]

[bib129] 129.Ongari D., Boyd P.G., Barthel S., Witman M., Haranczyk M., Smit B. Accurate Characterization of the Pore Volume in Microporous Crystalline Materials. Langmuir. 2017;33:14529–14538. doi: 10.1021/acs.langmuir.7b01682. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib130] 130.Sarkisov L., Bueno-Perez R., Sutharson M., Fairen-jimenez D. Material Informatics with PoreBlazer v4.0 and CSD MOF Database. Chem. Mater. 2020;32:9849–9867. [Google Scholar]

[bib131] 131.Chen Z., Li P., Anderson R., Wang X., Zhang X., Robison L., Redfern L.R., Moribe S., Islamoglu T., Gómez-Gualdrón D.A. Balancing volumetric and gravimetric uptake in highly porous materials for clean energy. Science. 2020;368:297–303. doi: 10.1126/science.aaz8881. [DOI] [PubMed] [Google Scholar]

[bib132] 132.Camp J.S., Stavila V., Allendorf M.D., Prendergast D., Haranczyk M. Critical Factors in Computational Characterization of Hydrogen Storage in Metal-Organic Frameworks Critical Factors in Computational Characterization of Hydrogen Storage in Metal-Organic Frameworks. J. Phys. Chem. C. 2018;122:18957–18967. [Google Scholar]

[bib133] 133.Churchard A.J., Banach E., Borgschulte A., Caputo R., Chen J.C., Clary D., Fijalkowski K.J., Geerlings H., Genova R.V., Grochala W. A multifaceted approach to hydrogen storage. Phys. Chem. Chem. Phys. 2011;13:16955–16972. doi: 10.1039/c1cp22312g. [DOI] [PubMed] [Google Scholar]

[bib134] 134.MacRae C.F., Sovago I., Cottrell S.J., Galek P.T.A., McCabe P., Pidcock E., Platings M., Shields G.P., Stevens J.S., Towler M. Mercury 4.0: from visualization to analysis, design and prediction. J. Appl. Crystallogr. 2020;53:226–235. doi: 10.1107/S1600576719014092. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib135] 135.Manos M.J., Markoulides M.S., Malliakas C.D., Papaefstathiou G.S., Chronakis N., Kanatzidis M.G., Trikalitis P.N., Tasiopoulos A.J. A highly porous interpenetrated metal-organic framework from the use of a novel nanosized organic linker. Inorg. Chem. 2011;50:11297–11299. doi: 10.1021/ic201919q. [DOI] [PubMed] [Google Scholar]

[bib136] 136.Furukawa H., Ko N., Go Y.B., Aratani N., Choi S.B., Choi E., Yazaydin A.Ö., Snurr R.Q., O’Keeffe M., Kim J. Ultrahigh porosity in metal-organic frameworks. Science. 2010;329:424–428. doi: 10.1126/science.1192160. [DOI] [PubMed] [Google Scholar]

[bib137] 137.Yuan D., Zhao D., Sun D., Zhou H.-C. An isoreticular series of metal-organic frameworks with dendritic hexacarboxylate ligands and exceptionally high gas-uptake capacity. Angew. Chem. Int. Ed. 2010;49:5357–5361. doi: 10.1002/anie.201001009. [DOI] [PubMed] [Google Scholar]

[bib138] 138.Yan Y., Telepeni I., Yang S., Lin X., Kockelmann W., Dailly A., Blake A.J., Lewis W., Walker G.S., Allan D.R. Metal-organic polyhedral frameworks: high H2 adsorption capacities and neutron powder diffraction studies. J. Am. Chem. Soc. 2010;132:4092–4094. doi: 10.1021/ja1001407. [DOI] [PubMed] [Google Scholar]

[bib139] 139.Karagiaridi O., Bury W., Tylianakis E., Sarjeant A.A., Hupp J.T., Farha O.K. Opening metal-organic frameworks. Vol. 2: inserting longer pillars into pillared-paddlewheel structures through solvent-assisted linker exchange. Chem. Mater. 2013;25:3499–3503. [Google Scholar]

[bib140] 140.Zheng X., Huang Y., Duan J., Wang C., Wen L., Zhao J., Li D. A microporous Zn(II)-MOF with open metal sites: structure and selective adsorption properties. Dalt. Trans. 2014;43:8311–8317. doi: 10.1039/c4dt00307a. [DOI] [PubMed] [Google Scholar]

PERMALINK

Predicting hydrogen storage in MOFs via machine learning

Alauddin Ahmed

Donald J Siegel

Summary

Graphical abstract

Highlights

The bigger picture

Introduction

Table 1.

Methods

MOF database

Table 2.

ML models

Table 3.

Dataset size

Feature importance/selection

Results

Evaluating ML algorithms

Figure 1.

Table 4.

Figure 2.

Effect of training set size

Figure 3.

Univariate feature importance

Figure 4.

Multivariate feature importance

Figure 5.

Table 5.

H2 uptake in unseen MOFs

Figure 6.

Table 6.

Figure 7.

Discussion

Limitations of this study

Concluding remarks

Experimental procedures

Resource availability

Lead contact

Materials availability

Data and code availability

Acknowledgments

Author contributions

Declaration of interests

Footnotes

Supplemental information

References

Associated Data

Supplementary Materials

Data Availability Statement

ACTIONS

PERMALINK

RESOURCES

Similar articles

Cited by other articles

Links to NCBI Databases

H₂ uptake in unseen MOFs