A causal inference framework for cancer cluster investigations using publicly available data

Summary.

Often, a community becomes alarmed when high rates of cancer are noticed, and residents suspect that the cancer cases could be caused by a known source of hazard. In response, the US Centers for Disease Control and Prevention recommend that departments of health perform a standardized incidence ratio (SIR) analysis to determine whether the observed cancer incidence is higher than expected. This approach has several limitations that are well documented in the existing literature. In this paper we propose a novel causal inference framework for cancer cluster investigations, rooted in the potential outcomes framework. Assuming that a source of hazard representing a potential cause of increased cancer rates in the community is identified a priori, we focus our approach on a causal inference estimand which we call the causal SIR (cSIR). The cSIR is a ratio defined as the expected cancer incidence in the exposed population divided by the expected cancer incidence for the same population under the (counterfactual) scenario of no exposure. To estimate the cSIR we need to overcome two main challenges: 1) identify unexposed populations that are as similar as possible to the exposed one to inform estimation of the expected cancer incidence under the counterfactual scenario of no exposure, and 2) publicly available data on cancer incidence for these unexposed populations are often available at a much higher level of spatial aggregation (e.g. county) than what is desired (e.g. census block group). We overcome the first challenge by relying on matching. We overcome the second challenge by building a Bayesian hierarchical model that borrows information from other sources to impute cancer incidence at the desired level of spatial aggregation. In simulations, our statistical approach was shown to provide dramatically improved results, i.e., less bias and better coverage, than the current approach to SIR analyses. We apply our proposed approach to investigate whether trichloroethylene vapor exposure has caused increased cancer incidence in Endicott, New York.

1. Introduction

Across the United States, citizens routinely recognize higher than expected rates of cancer in their community and request that the local health department conduct an investigation, with hopes of identifying a common cause. According to a review by Goodman et al. (2012), at least 2,876 cancer cluster investigations were conducted by health departments in the US between 1990 and 2011, most of which were initiated in response to alarm in the community.

1.1. Cancer cluster investigation protocol

The US Centers for Disease Control and Prevention (CDC) have provided a protocol to guide health departments in responding to requests for cancer cluster investigations (Centers for Disease Control and Prevention, 2013). The first challenge in this process is that the definition of a cancer cluster is notoriously vague and contested. The CDC defines a cancer cluster as “a greater than expected number of cancer cases that occurs within a group of people in a geographic area over a defined period of time” (Centers for Disease Control and Prevention, 2013). They recommend that cancer cluster investigations proceed by first performing a standardized incidence ratio (SIR) analysis to determine whether the cancer incidence experienced by the community represents a statistically significant elevation compared to what would be expected. The SIR is estimated as the ratio of the observed cancer incidence to the expected incidence based on background rates, and uncertainties and p-values are computed (Sahai and Khurshid, 1993) to determine whether the SIR significantly exceeds the null value of 1.

If statistical significance is found, then the event constitutes a cancer cluster by their definition. Only if a cancer cluster is confirmed does the CDC recommend that health departments proceed to seek possible environmental causes. If the statistical evidence for a cancer cluster is strong and an epidemiological study to test for relationships between environmental factors and the cancer cases is deemed “warranted” and “feasible”, then the CDC suggests conducting such a study.

Although widely used, the protocol for cancer cluster analyses described above has been criticized on practical grounds, with objectors pointing to the fact that such analyses rarely lead to definitive identification of the cause(s) of the cluster (Goodman et al., 2012, 2014). With no conclusion about the cause(s) of a cluster, simply the identification of one provides no guidance for the concerned public in removing the cause or preventing future cases.

The most prominent statistical limitation is the silent multiple comparisons problem (SMCP), also known as the Texas Sharpshooter problem (Bender et al., 1995), which arises due to the use of observed cancer location data to inform the development of the statistical hypothesis. Fundamental statistical principles dictate that, occasionally, the locations of cancer diagnoses will cluster together in space and time due to chance alone, i.e. not due to any common cause. Thus, we would expect, due only to chance, to occasionally encounter what appears to be an unusual excess of cancer cases within a small area. If we first evaluate the spatial distribution of the cancer cases and draw a boundary around a small area that appears to have a high cancer incidence, and then ask if that area is experiencing a higher cancer incidence than expected, we inflate the probability of finding a false positive. Standard multiple comparisons adjustment procedures are not equipped to handle the complexities of this setting. Another limitation of the current SIR analysis approach is the failure to sufficiently adjust for covariates that could explain differences in incidence rates.

There have been attempts to address the SMCP, including the introduction of Bayesian methodology (Coory et al., 2009) in which uncertainty arising from the multiple comparisons problem can be accounted for through the prior distribution. However, the presence of alternative approaches has failed to produce changes in the way cancer cluster analyses are carried out. In order to completely avoid the multiple comparison problem, it has also been suggested that cancer clusters investigations should abandon statistical analyses entirely (Coory and Jordan, 2013).

1.2. Causal inference approach to SIR analyses

We take the position that statistical analyses can provide important insights to cancer cluster investigations; however, both the protocol and the statistical procedures must be modified in order to produce useful and reliable inference. In this paper, we propose a number of changes to the cancer cluster investigation protocol in order to situate it within a causal inference framework. The most notable procedural change required is that a suspected cause of increased cancer incidence in the community, i.e. a putative source of hazard, must be identified prior to any statistical analyses. The CDC’s current approach is statistically backwards in that it tests for elevated cancer risk in a community prior to identifying potential sources of hazard that could be responsible for such elevation. Because no specific source(s) of exposure are postulated prior to analysis, the geographic region, time period, and disease types used to formulate the statistical hypothesis are at best defined arbitrarily, or at worst defined based on observed distributions of cancer outcomes, leading to the SMCP. By identifying putative source(s) of hazard a priori, we can investigate questions regarding the causal effect of exposure on cancer incidence, and the statistical hypotheses can be formed around the exposed population and time period, thus avoiding the pitfalls of the current approach.

Existing literature provides several approaches for testing for relationships between cancer risk and a known point source of contamination, with the work of Diggle et al. (1997) and Wakefield and Morris (2001) being some of the most cited. These approaches use small areal units near the point source as the units of analysis and parametrically model the relationship between the units’ distance from the point source and cancer risk, with adjustment for covariates. While the a priori identification of a point source relieves concerns about the SMCP, we must assume that the form of the parametric models relied upon are known and correctly specified in order to interpret the results from these models as causal. In practice, such assumptions are generally not realistic.

In this paper, we propose the use of a causal inference approach rooted in the potential outcomes framework (Rubin, 1974) to evaluate the strength of evidence that a given exposure caused increased cancer incidence in the exposed population and time period. We focus our efforts on a causal estimand which we call the causal standardized incidence ratio (cSIR). The cSIR is the following ratio: the expected cancer incidence in the exposed population divided by the expected cancer incidence in the same population under the counterfactual scenario of no exposure. In practice, our units of analysis will be areal units overlapping the exposed area rather than individuals in the exposed area, and thus the exposed population referenced in the cSIR definition is in fact the population of exposed areal units (and to avoid the ecological fallacy, inference should always be restricted to the level of areal units used in the analysis). Estimating causal effects with observational data requires rigorous approaches for eliminating confounding bias, and we explain our approach in the following section.

1.3. Case study and approach to cSIR estimation

To clarify our approach to cSIR estimation, we now introduce the cancer cluster investigation that will be used as a case study in this paper. However, the proposed approach applies to cancer cluster investigations more broadly. Endicott, New York (NY) was the home of the first IBM manufacturing complex. A spill of thousands of gallons of a mixture of chemicals by IBM in 1979 has plagued the town for decades. According to the NY State Department of Environmental Conservation (DEC) (2018), trichloroethylene (TCE), a metal degreaser and a known carcinogen, was the spilled contaminant that migrated the furthest outside the IBM plant and into the surrounding community, carried via groundwater. In 2002, an investigation mandated by the DEC discovered that TCE that had migrated into the soil in residential areas was evaporating and the resultant vapors entering indoor air in homes at dangerous levels, a process known as vapor intrusion. How long prior to 2002 the community had been exposed to TCE vapor intrusion remains unknown. TCE exposure is known to cause kidney cancer, but evidence in human studies has also suggested associations with lymphomas and childhood leukemia and liver, biliary tract, bladder, esophageal, prostate, cervical, and breast cancers (Environmental Protection Agency, 2011).

In 2006, the NY State Department of Health (DOH) conducted an investigation of cancer rates in Endicott between 1980–2000 using a SIR analysis. They found rates of kidney and testicular cancer were significantly higher than background rates (New York State Department of Health, 2006). To our knowledge, no follow up investigation has been conducted to determine whether residential exposure to the TCE vapors, detected in 2002, after the end date of the DOH study, has led to increased cancer rates in the community. We wish to estimate the cSIR for kidney/renal pelvis cancer and for bladder cancer in the TCE-exposed population of Endicott in order to investigate whether TCE exposure caused increased incidence of these cancers in Endicott during 2005–2009.

To estimate the cSIRs, we need information about what the incidence of these cancers in the TCE-exposed portion of Endicott would have been both with and without the TCE exposure. The observed cancer incidence in Endicott provides information about the former, since exposure to TCE was the observed scenario. To learn about what the cancer incidence might have been in the counterfactual scenario of no exposure, we obtain cancer data from unexposed populations that are similar to the exposed population in Endicott in terms of potential confounders of the effect of TCE exposure on cancer. To identify these populations, we will rely on causal matching.

Matching is one of the most well established causal inference approaches for eliminating confounding in observational data (Rubin, 1973; Rubin and Thomas, 2000; Abadie and Imbens, 2006; Ho et al., 2007; Stuart, 2010; Abadie and Imbens, 2011; Iacus et al., 2011). Matching is nonparametric and requires fewer assumptions than parametric models, thus increasing the plausibility that results are causal. For each exposed unit in the data, matching methods identify a fixed number (M) of “matched control” units that are not exposed to the hazard but are as similar as possible to the exposed unit in terms of observed confounders. In the matched data, the distributions of confounders are similar in the exposed and unexposed groups, as under randomization. Matching is known as a “design phase method”, because it aims to remove confounding without invoking outcome data. Procedures applied subsequently using the outcomes to estimate causal effects are known as “analysis phase methods”. Matching was first applied to SIR analyses by Dominici et al. (2007).

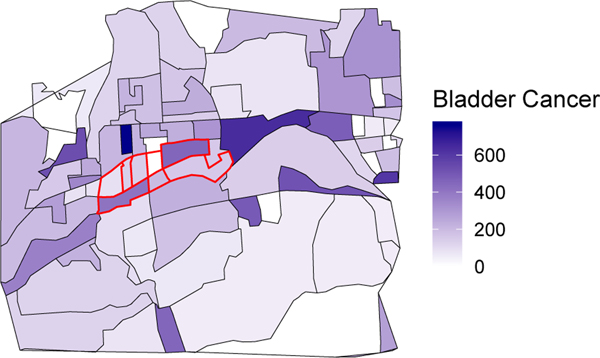
We partition the exposed area (Endicott) into exposed sub-units (census block groups; CBGs), and these will be our units of analysis. For each of the exposed sub-units we assume that cancer incidences are known (in many cases, the exact locations of diagnoses will be reported by the concerned community) and that confounder data are publicly available. Figure 1 provides a map of the bladder cancer incidence by CBG in the exposed Endicott area (red lines) and the surrounding area. Our goal is to identify matched controls for the sub-units within the exposed area.

Fig. 1.

Bladder cancer incidence rate per 100,000 population 2005–2009 by census block group for the TCE-exposed area of Endicott (red borders) and surrounding area.

We perform this spatial partitioning for two reasons. First, matching on confounders for the sub-units (e.g. CBGs) is more likely to eliminate confounding bias than matching on confounders for the whole exposed area, as levels of the confounders may vary widely within the exposed area. Second, partitioning provides a larger sample of exposed units, allowing for the application of classic statistical models to the data.

Nation-wide confounder data (e.g., socioeconomic and demographic variables) at the CBG level are publicly released by the US Census Bureau. For many types of environmental hazard, relevant geocoded contaminant and toxic chemical use information is available from the Environmental Protection Agency (EPA) (see Section 4 for more information). Therefore we assume that exposure and confounder data are both available for all CBGs and similar small administrative units nation-wide. Obtaining small area cancer incidence data, on the other hand, is challenging.

Cancer registries in most states collect detailed data on nearly all patients at the time of diagnosis, including age, sex, address, and diagnosis codes. While improvements are being made in accessibility, privacy concerns mean that, even when aggregated over small geographic areas, these data may be inaccessible to researchers or the request and approval process may take many months, delaying time-sensitive work. The high degree of aggregation in most publicly available cancer incidence data often renders it too coarse to perform the desired analyses. To make our methods as accessible as possible, they will rely solely on publicly available cancer incidence data.

The most commonly used publicly available cancer incidence data are collected and published by the Surveillance, Epidemiology, and End Results (SEER) Program of the US National Cancer Institute (National Cancer Institute Surveillance, Epidemiology, and End Results Program, 2018). Today, SEER compiles cancer diagnosis records from 18 state and city cancer registries, each contributing data dating back to 2000 or prior. Each record in the SEER data provides demographic and diagnosis information, as well as the year and the county of residence at the time of diagnosis. Thus, the lowest available level of spatial aggregation for these data is the county level.

To our knowledge, only two states have made small area cancer data publicly available. Illinois provides zip code level cancer incidence data for 11 anatomic site groupings (Illinois State Cancer Registry, 2017); however kidney and bladder cancer incidences are combined with all other urinary tract cancers. NY provides CBG level cancer incidences for 23 different anatomic sites, including kidney and bladder (separately), over the period 2005–2009 (Boscoe et al., 2016). We refer to the set of regions from which we have either SEER data or relevant small area cancer incidence data as SEER+. For our Endicott case study, SEER+ includes all SEER-participating regions and all of NY state.

After partitioning the exposed area of Endicott into CBGs, we identify matched control CBGs within SEER+. In the matched dataset, we are faced with the challenge of having cancer incidence data for (some or all of) the matched controls at the county level while our analysis is carried out at the smaller CBG level. This problem is referred to as spatial over-aggregation. Spatial data misalignment and the modifiable areal unit problem have received a good deal of attention in other contexts (Openshaw, 1984; Cressie, 1996; Gotway and Young, 2002), but to our knowledge previous literature has not addressed the spatial over-aggregation of cancer incidence data. In this paper we construct a Bayesian model to be applied to the matched data that resolves the spatial over-aggregation and estimates the cSIR. This model jointly (1) imputes the cancer incidence in matched control CBGs by borrowing information from the publicly available small area NY cancer incidence data and (2) fits a log-linear model to the cancer incidences in the matched data, utilizing the imputed incidences for the matched controls, to estimate the cSIR.

In Section 2, we formally define the cSIR and lay out our proposed estimation procedure. In Section 3, we use simulations to compare our methods to the existing SIR analysis methods used in cancer cluster investigations. In Section 4, we describe the analysis and results of the Endicott case study. Finally, we discuss our findings and conclude in Section 5.

2. Methods

2.1. The potential outcomes framework and notation

The population of interest in this context is the population exposed to the source of hazard within the concerned community under scrutiny. Without loss of generality, we assume that, as in our case study, the exposed region is partitioned into its component CBGs. In defining the cSIR and its identifying assumptions and formalizing the statistical models, CBGs are the units of analysis.

We now define notation that will be used to develop the estimand and methods. Causal inference methods are often situated within the potential outcomes framework, as defined by Rubin (1974), which we will now adapt to the cancer cluster analysis setting. We let subscript h = 1, …, H index the CBGs of the exposed region. Let Y_h be a random variable representing the observed cancer incidence in CBG h during the time period of interest, h = 1, …, H. We let T_h denote an indicator of exposure status, with T_h = 1 for all h = 1, …, H because each CBG in this set was exposed to source of hazard. Let X_h be a vector of observed confounder values for CBG h. Then the potential outcomes are Y_h(T = 1), the cancer incidence that would have been observed in CBG h under exposure to the source of hazard, and Y_h(T = 0), the cancer incidence that would have been observed in CBG h under no exposure.

The fundamental problem of causal inference is that, at most, only one of the two potential outcomes can ever be observed for a given unit, either its outcome under exposure or its outcome under no exposure. In this case, within the population of interest, we only observe outcomes under exposure to the source of hazard. The unobserved potential outcome is called the counterfactual. As in nearly all causal inference analyses, we invoke the stable unit treatment value assumption (SUTVA) in order to ensure the existence of the potential outcomes (Rubin, 1980). SUTVA requires that 1) the exposure be well-defined, i.e. that there is only a single “version” of exposure, and 2) that the exposure status of a given unit does not affect the outcome of other units. We note that both components of SUTVA may be strong assumptions in this context. The first could be violated if there are different degrees of exposure within the exposed units. The second could be violated if the cancer cases in one unit are caused by exposures its residents received while in a different unit (e.g., at work). See Section 5 for further consideration of the appropriateness of SUTVA in the cancer cluster setting.

2.2. The causal SIR and identifying assumptions

Using the potential outcomes, we now define the cSIR as:

$$cSIR=\frac{E[Y(T=1)\mid T=1]}{E[Y(T=0)\mid T=1]}$$

Again, we only wish to estimate the cSIR for the exposed population in the community under study. The cSIR is a ratio analogue to the average treatment effect on the treated, which is a commonly used causal inference estimand. As with the classic SIR analysis, we are interested in evaluating the strength of evidence that cSIR ≠ 1, with cSIR = 1 equivalent to E [Y (T = 1)|T = 1] = E [Y (T = 0)|T = 1], i.e., no causal effect of exposure in the exposed population (as we discuss in Section 1.2, in practice this is the population of exposed CBGs).

Now, drawing on additional data from populations unexposed to the same type of hazard as the population under study, the cSIR can be estimated under the following identification assumptions. These assumptions are nearly identical to those needed to estimate the average treatment effect on the treated– ignorability and causal consistency. First, cSIR identification relies on the assumption of no unobserved confounding, stated mathematically as T ⫫ Y (T = 0)|X. Moreover, we must assume positivity, stated mathematically as P(T = 1|X) < 1. The assumption of positivity requires that every unit in the exposed area could feasibly have been unexposed. Together, the assumptions of no unobserved confounding and positivity are known as ignorability. Finally, the causal consistency assumption states that Y = Y (T = 1)×T +Y (T = 0)×(1−T), i.e. the observed outcome is equal to the potential outcome under the observed exposure level.

By applying these assumptions, we can show that

$$E\left[Y\left(T=1\right)|T=1\right]=E_{\mathit{X}}\left[E\right[Y|T=1,\mathit{X}]]$$

and that

$$E\left[Y\left(T=0\right)|T=1\right]=E_{\mathit{X}}\left[E\right[Y|T=0,\mathit{X}]]$$

so that both the numerator and denominator of the cSIR are identifiable from the observed data. Proofs are provided in the Section 1 of the Supplemental Materials.

The assumption of no unobserved confounding is untestable, and its plausibility must be assessed based on subject matter knowledge. The plausibility of the positivity assumption can often be evaluated by determining whether suitable unexposed matches can be found for each exposed unit. If unexposed units exist that are otherwise similar to an exposed unit, then this provides evidence that the exposed unit could feasibly have been unexposed.

2.3. Estimation of the cSIR: design phase

To estimate the cSIR, matching is used in the design phase to remove confounding, followed by a Bayesian estimation procedure in the analysis stage to appropriately account for all sources of uncertainty. We begin by describing the design phase of our approach below.

The goal of our matching procedure is to obtain a set of unexposed CBGs with confounder distributions as similar as possible to those of the exposed CBGs. We recommend utilizing the matching procedure that provides the best covariate balance between the exposed and unexposed regions, i.e. the smallest standardized differences in means (Stuart, 2010). Moreover, because small area cancer incidence rates are often unstable, we suggest applying ratio matching, i.e., multiple matched controls for each exposed unit, to obtain as much information as possible about the expected cancer incidence under no exposure.

2.4. Estimation of the cSIR: analysis phase

After matching, if the cancer incidence data for both exposed and matched control CBGs are available at the CBG level (in our case they are not, cancer incidence data for the matched control CBGs are over-aggregated at the county level), a loglinear modeling approach can be used to estimate the cSIR. For clarity, we first describe the model that would be applied in this simplified setting. The model should be fit using data from both the exposed CBGs and the matched control CBGs and should include both exposure status and confounder variables as predictors. If matching procedures are entirely successful at removing all differences in confounder distributions between the exposed and unexposed, then adjustment for the confounders in the analysis phase is not needed. However, in practice, matching may not remove these differences entirely, thus adjustment for the confounders in analysis phase modeling is recommended (Ho et al., 2007). While analysis phase adjustment for confounders could lead to modest increases in variance, these concerns are likely to be outweighed by the need for bias reduction in observational data settings.

Let i (i = 1, …, N) index the matched dataset. The loglinear model has the form

$$\text{log}\left(E\left[Y_i\right]\right)={\alpha }_0+T_i{\alpha }_1+\mathit{X}{\prime }_i{\mathit{\alpha }}_2+\text{log}\left(P_i\right)$$

where P_i is the population size in CBG i, and log(P_i) is an offset term used to account for potential differences in population size across the CBGs. If the cancer incidence data are collected over different time periods for some of the matched control CBGs, the offset could represent persontime. Because the sample size for this model, N, will generally be small, a Bayesian approach to model fitting may provide more stable estimates than frequentist models. The cSIR estimate is exp(ˆα₁), and uncertainties and confidence regions follow accordingly.

We now introduce our approach to estimate the cSIR when the cancer incidence data for some or all of the matched control CBGs are over-aggregated to the county level, as described in Section 1.3. We propose a two-stage Bayesian model that (1) predicts cancer incidence in the matched control CBGs and (2) using these predictions and the observed incidence data from the exposed CBGs, fits the loglinear model described above to estimate the cSIR.

2.4.1. Stage 1: prediction model

The goal of the prediction model is to use the publicly available NY CBG cancer incidence data to model relationships between CBG incidence and community characteristics and to apply that model to predict cancer incidences in the matched control CBGs, taking into account the additional information provided by the observed SEER county level cancer incidences. In order to account for the observed county level cancer incidences, our model must incorporate the constraint that the CBG predicted incidences within a given county should sum to the observed county incidence. Finally, because this model is fit only to NY data but is employed for prediction of CBG cancer incidences in other states, we must make an additional assumption that the results of this model are transportable, or equivalently, that the model has external validity (Singleton et al., 2014).

Subscript j = 1, …, J is used to index the set of all NY CBGs. Let Z_j denote the vector of predictors to be included in the prediction stage for CBG j. The variables in Z should include all the confounders in X, but may include additional variables that are predictive of cancer incidence but are not believed to be confounders. We assume Y_j ∼ Poisson(λ_j) and log(λ_j) = Z_jβ+log(P_j), where P_j is the population size (or person-time, if needed). We denote by ψ(j) the set of indices for all CBGs in the same county as CBG j, and Y _ψ(j) the vector of all CBGs in the same county as CBG j. Then, it is a well-known property of independent Poisson random variables that

$$\left({\mathit{Y}}_{\psi (j)}\mid \sum _{l\in \psi (j)}{Y}_l=K_j\right)\sim \text{Multinomial}\left(K_j,{\mathit{\pi }}_{\psi (j)}\right)$$

with K_j the observed cancer incidence in the county containing CBG j (K_j is the same for all CBGs from the same county) and π_ψ(j) a vector whose elements are the proportions of the K_j cancer cases that fall into each of the county’s CBGs. Thus, in order to have our model account for the constraint that CBG incidence predictions should sum to their county’s observed incidence, we will develop the model around a multinomial likelihood. For each Y_j we have corresponding multinomial distribution parameters K_j and π_j, where π_j is the proportion of the cancer incidence in its encompassing county that falls into CBG j. Note that, by the same distributional result given above,

$${\pi }_j=\frac{{\lambda }_j}{{\sum }_{l\in \psi (j)}{\lambda }_l}$$

and this property dictates the form of the prediction model.

The prediction model is a loglinear model that includes a non-traditional offset that imposes the constraint that the estimated multinomial proportions must sum to one. It follows from the properties laid out above that the π_j should have the following relationship to the predictors:

$$\log \left({\pi }_j\right)={\mathit{Z}}_j^{\prime }\beta +\log \left(P_j\right)-\log \left(\sum _{l\in \psi (j)}{e}^{{\mathit{Z}}_l^{\prime }\beta }{P}_l\right)$$

where the final term is an offset which imposes the constraint. Note that this implies that

$${\pi }_j=\frac{e^{{\mathit{Z}}_j^{\prime }\beta }{P}_j}{{\sum }_{l\in \psi (j)}{e}^{{\mathit{Z}}_l^{\prime }\beta P_l}}$$

so that the CBG proportions within a county sum to one, as desired. This results in the following data likelihood:

$$L(\beta \mid \mathit{Y},\mathit{Z})=\prod _{j=1}^J{\left(K_j!\right)}^{1/\parallel \psi (j)\parallel }\frac{{\left(e^{{\mathit{Z}}_j^{\prime }\beta }{P}_j\right)}^{Y_j}}{Y_j!{\left({\sum }_{l\in \psi (j)}{e}^{{\mathit{Z}}_l^{\prime }\beta }{P}_l\right)}^{Y_j}}$$

where ∥ψ(j)∥ denotes the cardinality of ψ(j). For more details on the likelihood derivation, see Section 5 of the Supplemental Materials. Using a Bayesian approach, we can fit this model to the NY CBG cancer incidence data through the use of a simple Metropolis sampler. The resulting posterior summaries of β speak to the associations between a CBG’s features and the proportion of the cancer incidence of its larger county that it accounts for.

For any CBG in the SEER states, where Z_j and K_j are observed, we can obtain posterior predictive samples of its cancer incidence from the corresponding multinomial distribution. We note that we only need posterior predictive samples from the matched control CBGs in order to do cSIR estimation. However, because the model relies on normalization of the CBG proportions within counties, in order to obtain the multinomial posterior predictive samples for any CBG we must utilize the predictor data from all the other CBGs in its encompassing county, as well as the observed SEER incidence for the county. For a given matched control CBG, we denote the posterior predictive samples of its cancer incidence as {Y⁽¹⁾, …, Y^(B)}, where B is the number of samples, and these get passed into the estimation stage of the model.

This model is a straightforward extension of a log-linear model; yet, we are not aware of other papers that use this type of model to predict small area disease counts in areas where only larger-area counts are observed. However, the motivation for this model is similar to that of benchmarking approaches in the survey sampling literature. From survey data, investigators often produce modeled estimates of small area features (for which direct survey estimates would be unstable) but rely on direct estimates of the same features for larger areas. Without model constraints, these two sets of estimates may be incompatible. Benchmarking (Datta et al., 2011; Bell et al., 2012; Molina et al., 2014) is used to constrain the model-based small area estimates within a given larger area so that they agree with the direct estimate for the larger area. In contrast, here we are building a model to predict disease counts in small areas where no data are observed, by utilizing information on risk factors in the small areas and larger-area observed counts.

2.4.2. Stage 2: estimation model

Using the observed incidences in the exposed CBGs and the posterior predictive samples of the incidence in the matched control CBGs, we estimate the cSIR in the second stage of the model. As at the beginning of Section 2.4, we employ a Bayesian loglinear model, now integrating in the sampled outcomes for the controls at each iteration of the sampler. By including the full distribution of predicted cancer incidences in the estimation stage, rather than a single summarized predicted value, our cSIR estimate will capture the additional variability generated by the use of predicted cancer incidences for the matched controls.

Now utilizing only the matched data, let

$${\tilde{Y}}_i^{(b)}=\{\begin{array}{cc}{Y}_i,& \text{if }{T}_i=1\\ Y_i^{(b)},& \text{if }{T}_i=0\end{array}$$

i = 1, …, N. Then in each iteration of the Metropolis sampler for the estimation model, we plug in a different ${\tilde{Y}}_i^{(b)}$ sample, i.e. for b = 1, … B we collect a posterior sample of {α₀, α₁, α₂} from

$$\log \left(E\left[{\tilde{Y}}_i^{(b)}\right]\right)={\alpha }_0+T_i{\alpha }_1+{\mathit{X}}_i^{\prime }{\mathit{\alpha }}_2+\log \left(P_i\right).$$

The cSIR and its uncertainties can be estimated as described above.

As presented here, both stages of the model rely on the Poisson distribution. The appropriateness of this assumption should be assessed in the real data. Moreover, cancer incidence prediction models based on publicly available data have not yet been validated and the results and model fit should be evaluated on a case-by-case basis. We provide model fit information and study predictive accuracy for the kidney and bladder cancer models used here (see the Supplemental Materials), but broader validation of these models is an important topic for future work.

3. Simulations

In this section, simulations are conducted to compare the CDC’s SIR analysis to our proposed method. Our intent is to demonstrate how the use of matched controls and Bayesian estimation methods, under the assumptions laid out above, leads to stable and unbiased estimation of the effect of an exposure on cancer incidence. All simulations are carried out in R statistical software (R Core Team, 2018), and code is available at https://github.com/rachelnethery/causalSIR.

3.1. Simulation structure

The simulations are constructed using real confounder data from the SEER states to ensure that the simulated data reflect the complexity of real data. For each CBG in the SEER areas, we obtain the following variables (in parentheses, the names used hereafter): percent of the population age 65+ (P65+), percent of the population male (PMale), percent of the population white (PWhite), percent of the adult population unemployed (Unemploy), average commute time (Commute), median household income (Income), dollars spent on smoking products as a portion of per capita income (MoneySmoke), and percent of total dollars spent on food that was spent on food outside the home (MoneyFood). All variables come from ESRI Business Analyst (ESRI, 2018).

Let X denote a matrix of these confounders for each CBG in the SEER states, P denote a vector of the population in each CBG, T denote the vector of exposure indicators for each CBG, and Y denote the vector of cancer incidences for each CBG. We generate T and Y from the models

$$\text{logit}(P(\mathit{T}=1))={\gamma }_0+\mathit{X}{\gamma }_1$$

$$\log (E[\mathit{Y}])={\alpha }_0+\mathit{T}{\alpha }_1+\mathit{X}{\mathit{\alpha }}_2+\log (\mathit{P})$$

using different specifications of the parameter values to obtain different simulated conditions. Through these specifications, we produce the following four simulation structures:

1. no exposure effect (T ↛ Y) and no confounding (X ↛ T, X ↛ Y)

2. no exposure effect (T ↛ Y) and confounding (X → T, X → Y)

3. exposure effect (T → Y) and no confounding (X ↛ T, X → Y)

4. exposure effect (T → Y) and confounding (X → T, X → Y)

See Section 2 of the Supplemental Materials for the parameter values used to construct each simulation. Within each of the simulation scenarios, we generate 5,000 datasets, with T ∼ Bernoulli(P(T = 1|X)) held fixed across simulations but a different Y ∼ Poisson(E [Y |X, T]) simulated in each. Ten exposed CBGs (T = 1) are randomly selected to represent the exposed population of interest, and these are also fixed across simulations.

3.2. Methods compared

We analyze the simulated data using three different methods: CDC’s recommended SIR analysis (abbreviated as CDC), a variant of the CDC’s method that employs Poisson regression modeling (abbreviated as PR), and our proposed cSIR analysis (abbreviated as cSIR). We formalize the CDC’s SIR analysis here. Let D represent the observed cancer incidence in the concerned community during the relevant time period. An expected number of cancer cases E is computed for the community based on the incidence in a background population. Then, the SIR is estimated as$\widehat{S}=\frac{D}{E}$. Using the assumption that D ∼ Poisson(S × E), where S is the true relative risk, confidence intervals are computed by invoking the relationship between the Poisson and Chi-Square distributions (Sahai and Khurshid, 1993).

Note that our proposed method and the CDC’s protocol for SIR estimation differ in their approach to identifying the population and time period under study. Our method investigates the population/time period exposed to a pre-specified source of hazard. The CDC protocol studies the population/time period in which high cancer incidence is reported. In practice, these populations/time periods would likely differ, but in our simulations we study the same one with each method for comparability (i.e., the ten exposed CBGs selected as described above).

The CDC method is implemented by using the simulated cancer incidences from all the SEER CBGs outside the community of interest to compute the expected incidence (i.e., background rate). The PR variant of the CDC’s method does make some effort at adjustment for confounding–a frequentist Poisson regression model is fitted to the data from all the CBGs, using the confounding variables as covariates, but estimating the SIR as the exponentiated parameter estimate corresponding to an indicator of inclusion in the community of interest, rather than the true exposure indicator. Finally, we implement cSIR, assuming appropriate spatial aggregation of the cancer incidence data. We identify matched controls for each exposed CBG using 20:1 mahalanobis distance nearest neighbor ratio matching, then fit the Bayesian loglinear model.

3.3. Simulation results

The main results of the simulations are given in Table 1, which provides for each method the bias in the point estimate, the coverage rate of the true SIR for 95% confidence/credible intervals, and the width of the 95% confidence/credible intervals. For simulations 3 and 4, Table 1 shows results with the true SIR=1.5. We performed additional simulations with other strengths of exposure effect (true SIR ranging from 1.1–2), and those results are consistent with the ones shown here and are provided in Section 2 of the Supplemental Materials. In the Supplemental Materials, we also study the power of each method to detect non-null exposure effects, an important consideration given that the number of CBGs containing the exposed population is generally small (i.e., ten or fewer).

Table 1.

Simulation results comparing the proposed cSIR method with the standard cancer cluster SIR estimation method (CDC) and a similar Poisson regression approach (PR). Shown are the bias in the point estimate, the coverage rate of the true SIR for 95% confidence/credible intervals (Coverage), and the width of the 95% confidence/credible intervals (CI Width).

	True SIR	Method	Bias	Coverage	CI Width
Simulation 1	1	CDC	−0.00	0.96	0.70
		PR	0.20	0.99	4.81
		cSIR	−0.02	0.94	0.66
Simulation 2	1	CDC	0.55	0.13	0.79
		PR	−0.27	0.99	5.86
		cSIR	−0.00	0.95	0.50
Simulation 3	1.5	CDC	−0.54	0.09	0.58
		PR	1.23	1.00	49.08
		cSIR	−0.05	0.94	0.87
Simulation 4	1.5	CDC	0.51	0.26	0.83
		PR	3.76	0.99	112.96
		CSIR	−0.01	0.94	0.62

In all the simulations, cSIR gives results with small and stable bias close to 0. The other two methods estimate the SIR with bias often exceeding 0.5. Because the true SIR is 1 or 1.5 in these simulations, this magnitude of bias is large. The poor performance of PR, even in the simplest settings with no exposure effect and no confounding, seems to be attributable to instability in the model due to the small number of exposed units in the data.

cSIR’s 95% confidence interval has a stable approximately 95% coverage rate of the true SIR across all simulations. Due to high bias, CDC often gives low coverage of the true SIR, in some cases lower than 50%. PR, on the other hand, is unstable as discussed above, and this instability leads to extraordinarily wide confidence intervals and, therefore, highly conservative coverage rates.

In summary, the simulations demonstrate that our approach provides more reliable and stable results than existing alternative cancer cluster investigation procedures. We note that the structure of these simulations is favorable to CDC’s method because we have assumed that the CDC’s method is studying the true exposed population and time period, when in fact the CDC’s protocol does not consider exposures when structuring the SIR analysis and therefore would be unlikely to analyze the appropriate population. Moreover, our simulation structure is also favorable to the Poisson regression method, as all the associations in the simulations are linear. In the presence of non-linear relationships, we expect even greater gains in our method compared to others, because matching automatically resolves even non-linear confounding effects. Yet, even in these conditions favorable to CDC and PR, the improvements offered by our proposed approach are clear.

4. An investigation of kidney and bladder cancer incidence in Endicott, NY

We define the boundaries of the exposed area in Endicott based on the work of previous NY state investigations, which determined the boundaries of the area affected by TCE vapor intrusion (New York State Department of Health, 2006). We use in our analysis all CBGs fully or partially overlapping the exposed area. This leads to eight exposed CBGs, as shown in Figure 1. We rely on the NY data to obtain cancer incidences for the CBGs in Endicott, and some CBGs are merged in the NY data to protect privacy. Two of the Endicott CBGs are merged so that we can only obtain their combined incidence. Thus, we treat these two CBGs as one in our analysis, leading to seven exposed CBGs in Endicott.

TCE vapor exposure is only known to have affected Endicott in/after 2002, it is unclear when it began affecting the community; therefore, the appropriate time period to study is not obvious. Such uncertainties are likely to plague any cancer cluster investigation. The time period under study here, 2005–2009, was chosen primarily based on cancer data availability. Because urinary tract cancer latency periods are relatively short compared to other cancers (Yuan et al., 2010), any effects of TCE vapor exposure from the early 2000s or prior may already be detectable during this time period.

4.1. Data

We use the SEER+ cancer incidence data described in Section 1.3 for the years 2005–2009. In the US, a common set of codes provided in the third edition of the International Classification of Diseases for Oncology (ICD-O-3) is used across health care providers to systematically classify cancer types (World Health Organization, 2000). ICD-O-3 codes are recorded for all cancers in both SEER and the NY cancer data, and we use these codes to define the cancer types under investigation. For kidney/renal pelvis cancer incidence, we use all diagnoses during 2005–2009 with ICD-O-3 codes C649 and C659, and for bladder cancer incidence we use ICD-O-3 codes C670-C679. We obtained potential TCE exposure information for SEER+ areas from the EPA’s publicly available Toxics Release Inventory (TRI) data (Environmental Protection Agency, 2018b) and Superfund site data (Environmental Protection Agency, 2018a). The use of over 650 toxic chemicals, including TCE, is tracked by the EPA. Businesses manufacturing or using more than a specified threshold amount of any of these chemicals (and meeting certain other criteria) are required to submit yearly release reports to the EPA. Current and historic information about the location of these businesses, as well as the chemical types and amounts used by each, is provided to the public via the TRI data. The geocoded locations of all the Superfund hazardous waste sites, many of which have been contaminated by TCE, are also available through the EPA.

We employed the TRI and Superfund site location data to create a binary indicator of potential TCE exposure, around or before the time of Endicott’s TCE vapor exposure, for each CBG in SEER+. We classify a CBG as potentially exposed to TCE if (a) a facility using TCE in or before 2000 or a Superfund site is/was located within its boundaries or (b) a facility using TCE in or before 2000 or a Superfund site is/was located within 2 miles of its centroid. We allow a CBG to serve as a potential matched control for the Endicott CBGs if it is classified as having no potential for exposure to TCE.

Finally, for each CBG in SEER+, we have collected data from ESRI Business Analyst (ESRI, 2018) on the following potential confounders of the association between TCE exposure and cancer incidence (many overlap with those used to construct simulations): percent of the population age 65+ (P65+), percent of the population male (PMale), percent of the population white (PWhite), rural indicator (Rural), percent of the adult population unemployed (Unemploy), average commute time (Commute), median household income (Income), total dollars spent on smoking products as a portion of per capita income (MoneySmoke), percent of total dollars spent on food that was spent on food outside the home (MoneyFood), percent of the population that reports exercising at least 2 times per week (Exercise), and percent of the population working in the agriculture, mining, construction, or manufacturing industries (Industry). A similar dataset could be constructed from US Census or American Community Survey data, if exclusively public data sources are desired. Because confounders should precede exposure, these confounder data come from the year 2000, just prior to the time that TCE vapor exposure was detected in Endicott.

4.2. CBG cancer incidence prediction and cSIR estimation

R code for the analysis is available at https://github.com/rachelnethery/causalSIR. Our first step in estimating the cSIR is to identify M matched control CBGs from SEER+ for each of the Endicott CBGs. We test different approaches to matching in search of a method that provides a reasonable compromise between our desire for (1) good confounder balance across exposure groups and (2) a substantial number of controls to stabilize the estimation. Some of these approaches involve the propensity score, the probability of exposure conditional on observed confounders, e_i = P(T_i = 1|X_i). The distributions of the observed confounders in the exposed and unexposed groups are identical conditional on e_i, making it a convenient one-dimensional measure that can be matched on to eliminate confounding (Rosenbaum and Rubin, 1983; Austin, 2011). In practice, the propensity score is unknown and must be estimated. We apply both 3:1 and 5:1 nearest neighbor matching to our data and for each ratio, 3 different distance metrics are tested: mahalanobis distance, distance in propensity scores estimated via logistic regression with linear terms, and distance in propensity scores estimated via logistic regression with splines (a generalized additive model). The logistic regressions have the form logit$\left(P\left(T_i=1\right)\right)={\gamma }_0+{\mathit{X}}_i^{{\ast }^{\prime }}{\gamma }_1$, where ${\mathit{X}}_i^{\ast }$ is the usual vector of confounders in the linear version and a vector of penalized spline bases for each confounder in the generalized additive model. We focus on lower matching ratios here than in the simulations because large ratios like 20:1 do not provide the desired balance in these data.

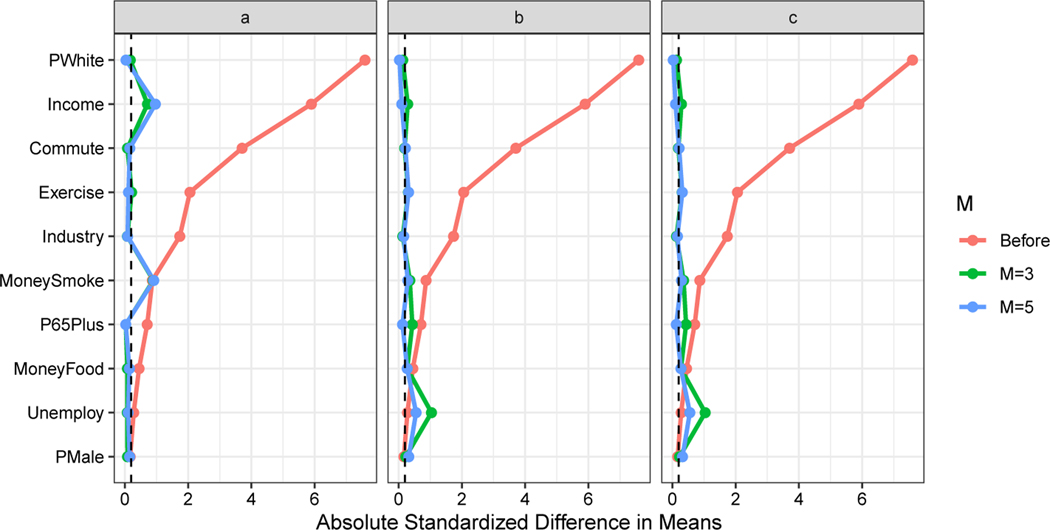
Figure 2 shows the balance of each confounder before matching and after application of each of these matching methods (Rural, a binary variable, is not shown in the figure but is matched on exactly). The matching procedures dramatically improve the balance in most confounders. The different methods provide comparable results, and, for our analysis, we choose to use the matched data from the 5:1 matching on propensity scores estimated via linear model. Although the standardized differences in means after matching are not all less than the commonly recommended (but arbitrary) threshold of 0.2 (Linden and Samuels, 2013), we are not concerned about these minor deviations from perfect balance, because we are also adjusting for the confounders in the analysis phase modeling. Note that 5:1 matching produces a matched dataset with N = 42, i.e., seven exposed CBGs and 35 unexposed CBGs.

Fig. 2.

Balance before matching and after 3:1 and 5:1 ratio matching on (a) the mahalanobis distance, (b) propensity scores estimated via linear model, and (c) propensity scores estimated via generalized additive model. Covariates are considered well-balanced if the absolute standardized difference in means is less than 0.2 (marked by the dashed line).

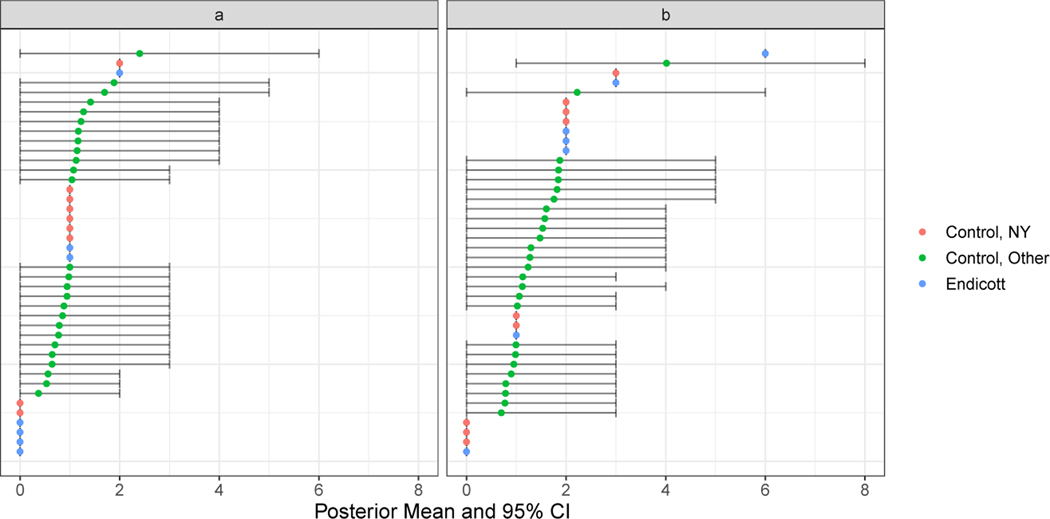
Due to the spatial over-aggregation of the SEER data, the next step in the analysis is to apply the joint Bayesian model to predict the CBG kidney cancer and bladder cancer incidence for the matched controls outside NY (note that we utilize observed incidences for matched control CBGs within NY) and fit the loglinear model for cSIR estimation. We fit the prediction models using the CBG cancer incidence data from NY and the confounder variables described above as predictors. We exclude all the CBGs in the same county as Endicott from the prediction model, because residents of nearby unexposed CBGs may be likely to work in the TCE-exposed areas (and thereby receive exposure). We also hold out data from six other NY counties to serve as a test set to evaluate the model’s out-of-sample predictive performance. In Section 3 of the Supplemental Materials, we provide the details of the model fitting, e.g. prior distribution choices and convergence checks, and the resulting point estimates and uncertainties, and we also study the in- and out-of-sample predictive performance of the models and compare them with a competing ad-hoc prediction method. We find that our models generally perform favorably to the competitor and produce reasonably accurate out-of-sample predictions. We use these models to collect posterior predictive samples of the kidney and bladder cancer incidence for the non-NY matched control CBGs. Figure 3 shows the posterior means and 95% credible intervals for the predicted incidences in the non-NY matched controls and the observed incidences in the Endicott CBGs and NY matched controls.

Fig. 3.

Predicted (a) kidney cancer incidence and (b) bladder cancer incidence and 95% credible intervals for matched control CBGs outside NY and observed incidences for Endicott CBGs and matched controls within NY.

In the cSIR estimation models, all confounders are included besides Rural, because all CBGs in the matched dataset are non-rural. Details of the model fitting and results are provided in Section 4 of the Supplemental Materials, along with the descriptions and results of two sensitivity analyses. The cSIR estimate and 95% credible interval for kidney cancer are 0.75 (0.30, 1.50). Using the other 5 matching methods/ratios considered above, the kidney cancer cSIR estimates range from 0.61 to 0.87. None are statistically significant. We also applied the CDC’s SIR analysis as described in Section 3.2 to estimate the SIR for kidney cancer in the TCE-exposed area of Endicott, using all of NY state as the background population to compute the expected kidney cancer incidence. The resulting SIR and 95% confidence interval are 0.63 (0.17, 1.61).

For bladder cancer, the cSIR and 95% credible interval are 1.57 (0.89, 2.68). The estimates produced by the other 5 matching methods/ratios range from 1.24 to 1.54, with none statistically significant. Using the CDC’s method, the bladder cancer SIR estimate and 95% confidence interval are 1.63 (0.93, 2.65).

If we are willing to make the assumptions of SUTVA, ignorability, and causal consistency described in Section 2.2, then our results have a causal interpretation. The assumption of no unobserved confounding could be violated in this analysis. As in most studies, we do not have information about potentially important confounders such as diet, accessibility of health care, and exposure to other sources of pollution/contamination. To interpret our results as causal, we must assume that these factors are not confounders of the TCE exposure-kidney/bladder cancer relationship.

5. Discussion

In this paper, we have introduced a causal inference framework for cancer cluster analyses, which relies on a priori identification of sources of hazard that could cause increased cancer incidence. By constructing statistical analyses around exposure hypotheses rather than observed cancer outcomes, the SMCP associated with the traditional approach to cancer cluster investigations is resolved so that statistically valid results are possible. Moreover, this approach allows us to directly ask and answer the question of interest– whether exposure to a specific hazard caused increased cancer incidence in a community.

We focus our analysis on a causal inference estimand, the causal SIR, and provide identifying assumptions. We propose a two-stage Bayesian model that resolves the problem of spatial over-aggregation in cancer incidence data. This model, applied to a matched dataset, allows the cSIR to be estimated from publicly available data. In simulations, our statistical approach was shown to provide dramatically improved results, i.e., less bias and better coverage, than the current approach to SIR analyses. Finally, we demonstrated the use of our method by applying it to investigate whether TCE vapor exposure, resulting from a chemical spill dating back the the 1970s, caused increased kidney or bladder cancer incidence in Endicott, NY during 2005–2009. Our method did not produce any statistically significant cSIR estimates. We note that the cSIRs estimated here should be interpreted as effects in the exposed CBGs, and due to the modifiable areal unit problem, results could change under different choices of areal units.

A direct comparison of our approach here and existing methods for testing for relationships between a point source and cancer risk, such as those of Diggle et al. (1997) and Wakefield and Morris (2001), is warranted. We first note that the previous literature on this topic does not take a causal inference approach, thus our work is the first to formally pursue a causal estimand and lay out causal identifying assumptions in this context. As noted in Section 1.2, one advantage of our methods compared to existing ones is that they provide flexible confounding adjustment and therefore strong parametric modeling assumptions are not required to achieve a causal interpretation. Another advantage is that our approach allows for cancer data from control areas to be spatially over-aggregated and can therefore be implemented using publicly available data. On the other hand, the approaches of Diggle et al. (1997) and Wakefield and Morris (2001) allow for the relationship between cancer risk and the point source to be modeled as a function of the distance between each unit and the point source. This may provide more information than our method, which dichotomizes exposure, in settings where exposure decreases monotonically as distance from a point source increases. However, in settings with diffuse contamination or when exposure does not decrease monotonically as distance from a point source grows, our approach may be more likely to detect relationships.

A possible concern about our proposed approach is related to the appropriateness of the SUTVA assumptions in this setting. One requirement of SUTVA is that there is only one “version” of exposure. In many investigations, some CBGs in the exposed area will be more highly exposed than others, leading to multiple different versions of exposure. Another requirement of SUTVA, referred to as “no interference”, is that the treatment status of one unit cannot affect the outcome of another unit. This assumption also may be dubious in many cancer cluster analyses, because within the exposed community, some people may live in one exposed CBG and work in another exposed CBG. Chronic exposure in one’s workplace may be just as likely to cause cancer as exposure in the home; therefore, the exposure status of the workplace CBG may impact the cancer incidence in the CBG of residence. This would be a violation of SUTVA. In such a setting, our method can still be used to evaluate associations between exposure and cancer incidence, but the results may not be causal. Recently developed methods to handle multiple exposure classes (VanderWeele and Hernan, 2013; Yang et al., 2016; Lopez et al., 2017) and interference (Barkley et al., 2017; Papadogeorgou et al., 2017) could be integrated into the causal SIR framework in future work.

While our method provides an improvement over existing methods for cancer cluster investigation, it has numerous limitations. First, although it avoids the SMCP and provides rigorous adjustment for confounding, other complicated issues that affect all cancer cluster investigations such as population migration are not directly addressed by this method. If substantial population migration has occurred in the community under study between the time of exposure and the time that cancer outcomes are investigated, then the results from this method may not be reliable and should not be interpreted as causal. Second, we rely heavily on the assumption that the results of our cancer incidence prediction models, fit on data from NY, are transportable to the SEER-covered areas. While we study the models’ predictive performance in the Supplemental Materials, broader validation is needed and, ideally, more small area cancer incidence data will soon be made public and can be used to build increasingly accurate prediction models. Moreover, our prediction model relies on a Poisson likelihood and should be extended to handle zero-inflation (for rare cancer types) and extra-Poisson variation (Ghosh et al., 2006; Özmen and Demirhan, 2010; Liu and Powers, 2012). More work is also needed to adapt this framework to the setting in which multiple exposures affecting a community may have synergistic effects on cancer incidence. In some contexts, small sample size of the matched data and a potentially large number of confounders may mean that causal methods for p > N need to be integrated into this approach.

Likely the most challenging aspects of applying these methods in real cancer cluster investigations will be (1) determining the population and time period exposed to a given source and (2) collecting reliable data. With regards to the former, we remark that the exposure hypotheses on which analyses are based do not have to be perfect nor unanimously agreed upon. First, multiple different potential exposures can be considered and analyzed (separately), i.e., a single exposure for investigation need not be settled on from the beginning. Moreover, while some research should be done regarding the area, time period, and cancer types reasonably associated with a given exposure, these determinations need not be set in stone in order to proceed with statistical analyses. Different reasonable specifications of population, time period, and cancer types could be tested and the results multiple comparisons adjusted accordingly, using standard multiple comparisons corrections like Bonferroni (Dunn, 1961).

Obtaining reliable data to carry out these analyses is a less forgiving endeavor. While a good deal of confounder data is readily available from the census, cancer incidence and exposure data are more limited. As described here, a few states are beginning to take the lead in public release of small area cancer incidence data. If this movement spreads, it stands to deliver huge improvements to the efficiency and reliability of cancer cluster investigations. Exposure data may be difficult to obtain for certain types of hazard, and its reliability is often dubious. For instance, the TRI data only represent businesses using large amounts of certain chemicals, and businesses self-report usage to the TRI database. Moreover, the TRI data do not capture events like spills of chemicals that may put communities at highest risk. In order to carry out cancer cluster investigations with maximal rigor, more work is needed both to collect better data and to make the data more easily accessible.