Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2021 Apr 28;125(17):9556–9563. doi: 10.1021/acs.jpcc.1c02327

Atomic Undercoordination in Ag Islands on Ru(0001) Grown via Size-Selected Cluster Deposition: An Experimental and Theoretical High-Resolution Core-Level Photoemission Study

Luca Sbuelz †, Federico Loi †, Monica Pozzo ‡, Luca Bignardi †, Eugenio Nicolini §, Paolo Lacovig §, Ezequiel Tosi §, Silvano Lizzit §, Aras Kartouzian ∥, Ueli Heiz ∥, Dario Alfé †,⊥, Alessandro Baraldi †,§,*
PMCID: PMC8279646  PMID: 34276855

Abstract

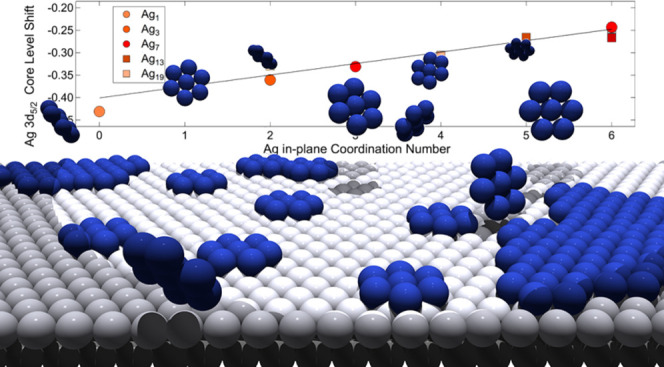
graphic file with name jp1c02327_0008.jpg

The possibility of depositing precisely mass-selected Ag clusters (Ag1, Ag3, and Ag7) on Ru(0001) was instrumental in determining the importance of the in-plane coordination number (CN) and allowed us to establish a linear dependence of the Ag 3d5/2 core-level shift on CN. The fast cluster surface diffusion at room temperature, caused by the low interaction between silver and ruthenium, leads to the formation of islands with a low degree of ordering, as evidenced by the high density of low-coordinated atomic configurations, in particular CN = 4 and 5. On the contrary, islands formed upon Ag7 deposition show a higher density of atoms with CN = 6, thus indicating the formation of islands with a close-packed atomic arrangement. This combined experimental and theoretical approach, when applied to clusters of different elements, offers the perspective to reveal nonequivalent local configurations in two-dimensional (2D) materials grown using different building blocks, with potential implications in understanding electronic and reactivity properties at the atomic level.

Introduction

The atomic coordination number (CN) plays a crucial role in determining physical and chemical properties in condensed matter. The importance of this quantity is well recognized in the field of heterogeneous catalysis.1 It is well-established that the chemical properties for several systems are determined by the presence of a large population of atoms sitting at defect sites, edges, corners, and nanofacets in catalytic active nanoparticles.2,3 The importance of these local configurations was revealed both in noble4,5 and transition metal6,7 nanoparticles, for which it has been demonstrated that a high concentration of low-coordination atomic sites results in increased chemical reactivity. An example of this phenomenon is the promotion of the O2 molecular adsorption and dissociation,4 the hydrocarbon dehydrogenation,8 and the chemical conversion of N-heterocyclic carbene molecules.9 Besides nanoparticles, the presence of these specific configurations is known to contribute to the chemical reactivity of solid surfaces as well. According to the Hammer–Nørskov model,10,11 the main reason for the high adsorption energies and for the energy barrier reduction for molecular dissociation on transition metal surfaces can be explained in terms of the d-band center shift on undercoordinated atoms. This is true also in the case of the bimetallic surfaces and interfaces and for near-surface alloy catalysts.12 For these systems, the different structural and morphological properties of the surface, which determine the presence of undercoordinated atoms, are driven by the interplay between atom–atom and atom–substrate interactions. The same quantities are used in conjunction with diffusion properties, to determine growth, nucleation, and aggregation processes,13 which in turn define the presence of undercoordinated atomic species in the adlayer structure.

The possibility of discriminating nonequivalent atoms of the same species sitting on solid surfaces in different local environments, and in particular with different CNs, is a well-known characteristic of high-resolution core-level spectroscopy (HR-CLS).14 This experimental approach has been employed to distinguish top-layer atoms that have a number of broken bonds with respect to the bulk ones,15−18 atoms at step edges,19 strained stepped surfaces,20 adatoms/ad-dimers in homo-21,22 and heteroatomic surfaces,23 for atomic nanowires,24 edge atoms in two-dimensional (2D) materials,25 and for nanoclusters grown on graphene.26 In the case of single-layer metal islands supported on different metallic substrates, the ability to distinguish atoms with different CNs depends on the surface density of these local configurations, which in turn depends on the extension of the islands and the degree of surface order. In fact, the greater the latter, the lower the density of the undercoordinated atoms sitting on the periphery of the islands or which are incorporated into disordered islands, where the in-plane coordination is not equal to an ideal close-packed configuration.

When species A is deposited, for example, on an fcc(111) or hcp(0001) surface of metal B, the possible in-plane CN ranges from CNA = 0 (single monomer) to CNA = 6 (complete monolayer), while CNB, which is the coordination number with the substrate, is CNB = 3 for threefold adsorption sites and CNB = 1 for atop sites (for both monomers and atoms of a complete single layer). Atomic undercoordination modifies the core level from its value of an isolated atom because of the presence of neighboring atoms (tight-binding theory); on the other hand, the atoms are fully coordinated when we consider atoms belonging to the second and lower layers at solid–vacuum interfaces.

In this experimental and theoretical investigation, we employ HR-CLS to study the coordination effects on single-layer Ag islands prepared by depositing size-selected clusters of Ag1 (monomers), Ag3 (trimers), and Ag7 (heptamers) on Ru(0001). Clusters of this size, used as building blocks for the formation of two-dimensional islands, allow us to exploit their different individual structures to create configurations with a different density of undercoordinated atoms in a two-dimensional Ag layer. However, silver has a peculiar valence band electronic structure, which makes the distinction of the effects of reduced surface coordination arduous to reveal using HR-CLS.15 In addition to that, the detection of the local atomic configuration with a small CN is complicated by the process of cluster surface diffusion. Therefore, one expects that when Ag clusters are deposited on Ru(0001), they will diffuse and join other clusters to form small islands, which then can act as centers of nucleation for larger structures or can further diffuse on the surface. The latter process will depend on substrate temperature and island critical size for the diffusion process which, thanks to the immiscibility of Ag in Ru,27 takes place likely with simple hopping events among nearest neighbor sites.

Methods

Experimental Methods

The measurements were performed in an ultrahigh vacuum (UHV) chamber at the SuperESCA beamline of the Elettra synchrotron radiation facility in Trieste, Italy. The photoemission spectra were collected by means of a Phoibos 150 mm mean radius hemispherical electron energy analyzer from SPECS, equipped with an in-house developed delay line detector. The overall experimental energy resolution (which accounts for both the electron energy analyzer and the X-ray monochromator) was always kept within 70 meV in all measurements, as determined by probing the width of the Fermi level of an Ag polycrystal.

The Ru(0001) single crystal was mounted on a sample manipulator with 4 degrees of freedom. The sample was heated by electron bombardment from hot tungsten filaments mounted behind it. The temperature of the sample was monitored by means of two K–type thermocouples directly spot-welded on the back of the specimen. The Ru(0001) surface was cleaned by repeated cycles of Ar+ sputtering and flash annealing to 1500 K, followed by annealing in O2 and in H2 gas.28,29 The surface long-range order and cleanliness were checked by low-energy electron diffraction, which exhibited a sharp (1 × 1) pattern with low background intensity, and by X-ray photoelectron spectroscopy (XPS). During cluster deposition and photoemission measurements, the background pressure was always kept below 1.5 × 10–10 mbar, with just the He pressure rising up to 10–8 mbar, as monitored with a mass spectrometer.

The Ag clusters were deposited on Ru(0001) at room temperature using ENAC (Exact Number of Atoms in each Cluster), a size-selected nanocluster source based on laser ablation/supersonic aggregation, which was developed and built at the Nanoscale Materials Laboratory of Elettra Sincrotrone Trieste. The working principles on which ENAC relies follow the design of a similar size-selected cluster source developed at the Technical University of Munich,30 which has been successfully used in the past years to perform experiments involving Ag clusters.31−34 ENAC has been developed to produce size-selected nanoclusters in UHV conditions and its design was optimized to connect it to the experimental station of the SuperESCA beamline, to perform in situ characterization of the clusters using synchrotron radiation. ENAC is composed of five vacuum chambers equipped with a differential pumping system and a set of ion optics to transport the nanoclusters and perform the mass selection. In the first stage, ablation of a metal target takes place using a pulsed (120 Hz) Nd-YAG laser operating at 532 nm. The target is constantly kept in motion to avoid its perforation. The ablation process produces a metallic plasma that is transported by a He gas pulse into a thermalization chamber, where it undergoes a supersonic adiabatic expansion. In the second and third stages, the charged nanoclusters are guided through a 500 mm home-built radiofrequency octupole set to transport nanoclusters with masses from 10 to 16 000 amu. The positively charged nanoclusters are then separated from negatively charged and neutral ones using an electrostatic quadrupole bender. The size selection occurs in the fourth stage of the cluster source using a quadrupole mass spectrometer (QMS) that can provide high mass resolution up to a single amu in a wide range from 1 to 16 000 amu. After the QMS, the size-selected nanoclusters are further transported through the fifth stage using a second radiofrequency octupole and then focused with an Einzel lens on the sample located in the SuperESCA preparation UHV chamber. The number of clusters reaching the Ru(0001) surface can be monitored by reading the current on the sample itself. Soft landing conditions35 were achieved by controlling the kinetic energy of the ionized cluster, which was kept below 1 eV/atom. A mass spectrum performed with ENAC is presented in the Supporting Information for Ag clusters made of a number of atoms from 1 to 46.

The XPS spectra were acquired by tuning the photon energy to have a photoelectron kinetic energy of about 100 eV to enhance surface sensitivity. For each spectrum, the photoemission intensity was normalized to the photon flux and the binding energy (BE) scale was aligned to the Fermi level of the Ru substrate. Doniach–Šunjić line profiles have been used to fit each spectral component, convoluted with a Gaussian distribution, which accounts for the experimental, phonon, and inhomogeneous broadening.36

Theoretical Methods

The calculations have been performed using density functional theory (DFT) as implemented in the VASP code.37 The atomic structure of the studied systems was fully relaxed until the largest residual force was less than 0.02 eV/Å. We employed the projector augmented wave (PAW) method38 to account for the core electrons, using PBE potentials,39 with 8 and 11 electrons in the valence band for Ru and Ag, respectively. Single-particle orbitals were expanded in plane waves using a kinetic energy cutoff of 400 eV and the relaxations were performed using a 3 × 3 × 1 uniform grid to k-points to sample the Brillouin zone.

The Ru(0001) surface was modeled with a slab geometry, using a (5 × 5) supercell with four layers, of which the bottom two were kept frozen at the bulk interatomic distances. The vacuum distance between the two surfaces of the periodically repeated slabs was at least 13 Å for the clean and Ag cluster-covered surface. Core-level binding energies have been estimated within the final state approximation. Diffusion barriers were estimated with the climbing-image Nudged Elastic Band method.40

Results and Discussion

The first step of the experiment was the measurement of the 3d5/2 core-level spectrum of a Ag(111) single crystal, to establish the most accurate way to measure the core electron binding energy (BE) of bulk atoms. This served as a reference for comparing the experimental and theoretical results and will be used to convert theoretically calculated BE shifts into absolute BE values. As anticipated, the measurement of the surface core-level shift (SCLS is the shift between the core level of the surface atoms with respect to the bulk ones) in silver is a very challenging task. Andersen et al.15 have found that the surface component of the 3d5/2 spectrum of clean Ag(111) is indeed difficult to discern from the bulk component, presenting an SCLS that was estimated to be ca. 100 meV toward lower BEs. Such a small value is caused by final state effects, namely, by the core–hole screening properties of the 5s valence band electrons and by the reduced electron density of states at the Fermi energy of noble metals with respect to transition metals, where SCLSs are typically much larger.

Figure 1a shows the Ag 3d5/2 spectrum of the clean Ag(111) surface measured with a photon energy of 470 eV, together with the spectral decomposition. The unusual asymmetric spectral lineshape toward lower BEs, which cannot be justified by electron–hole pair excitation or energy losses, as it would result in the build-up of a tail at higher BEs, clearly reveals the presence of a multicomponent structure The spectrum can be properly fitted with two components at 368.20 and 368.05 eV, corresponding to bulk (Agbulk) and first-layer (Agsurface) components. The values for the lineshape parameters Γ (Lorentzian), G (Gaussian), and α (asymmetry) resulting from the fit were 340 meV, 70 meV, and 0 for both bulk and surface components, respectively. The latter value confirms a low density of states at the Fermi level, as expected for a noble metal. This peak assignment is based on the fact that the 3d5/2 spectrum measured at high photon energy (650 eV) shows a reduced spectral weight at lower binding energies. This can be interpreted based on the increased mean free path of photoelectrons at higher kinetic energies. This assignment is confirmed by DFT calculations of the SCLS, which was estimated to be of −146 ± 20 meV with respect to the bulk component, in very good agreement with our experimental outcomes.

Figure 1.

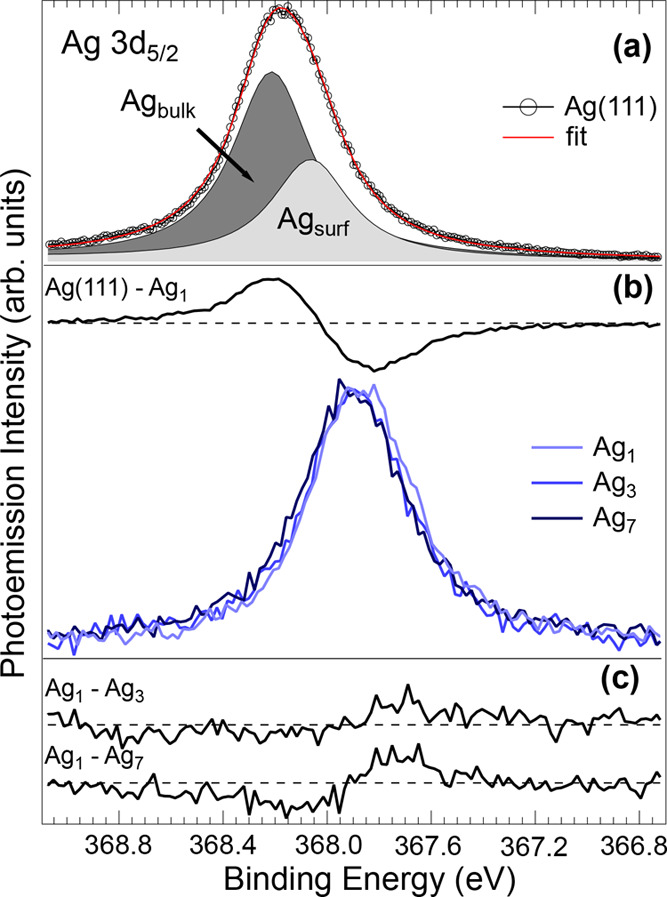
Figure 1

Open in a new tab

(a) Ag 3d5/2 core-level spectra from the Ag(111) surface recorded at a photon energy of 470 eV and T = 300 K. The spectral components obtained by the fit originate from bulk (Agbulk) and first-layer (Agsurf) atoms. (b) Ag 3d5/2 core-level spectra measured after deposition of Ag1 (0.0051 ML), Ag3 (0.0067 ML), and Ag7 (0.0073 ML) clusters on Ru(0001) and the difference spectrum Ag(111)–Ag1, divided by 4. (c) Ag 3d5/2 difference spectra Ag1–Ag3 and Ag1–Ag7.

The high-resolution Ag 3d5/2 spectra measured upon deposition of Ag1, Ag3, and Ag7 clusters on the Ru(0001) surface are reported in Figure 1b together with the difference spectrum Ag(111)–Ag1, divided by 4. The total Ag coverages for the three depositions were 5.1 × 10–3 ML (Ag1), 6.7 × 10–3 ML (Ag3), and 7.3 × 10–3 ML (Ag7), where 1 ML (monolayer) is equal to 1.38 × 1015 atoms/cm2. Such very small surface coverages were dictated by the idea of preventing cluster collisions, merging already upon deposition, and hindering the island nucleation process. The main results from this experiment were (i) an overall core-level shift toward lower BEs with respect to the bulk Agbulk component, which amounts to about −400 meV and (ii) a shift between the spectra that inversely decreases with the size of the deposited clusters. Even if the spectral differences are not large, it is possible to appreciate the shift of the spectral maximum, given the good signal-to-noise ratio (considering the extremely small Ag coverage). The difference spectra, plotted in Figure 1c, show the shift of the spectral intensity toward higher BEs as the cluster sizes increase.

To obtain a thorough understanding of the experimentally prepared system, we resorted to DFT calculations, initially investigating the structure and preferred adsorption sites for the three different types of clusters. It should be emphasized that the monodisperse clusters produced by ENAC and guided to the surface sample are positively charged. For these reasons, we considered the starting cluster geometry to be the minimum energy configuration structure that Ag1+, Ag3+, and Ag7+ adopt in the gas phase (GP). In agreement with previous theoretical calculations,41 we found that the preferred configuration for Ag3+ is an equilateral triangle, while for Ag7+, it corresponds to a planar hexagonal wheel with an atom in the center. The configurations studied on the Ru(0001) are shown in Figure 2. The deposition of the clusters is performed in soft landing conditions, thus strongly reducing the possible breakup of the Ag–Ag bonds that the cluster could experience upon impacting the surface.

Figure 2.

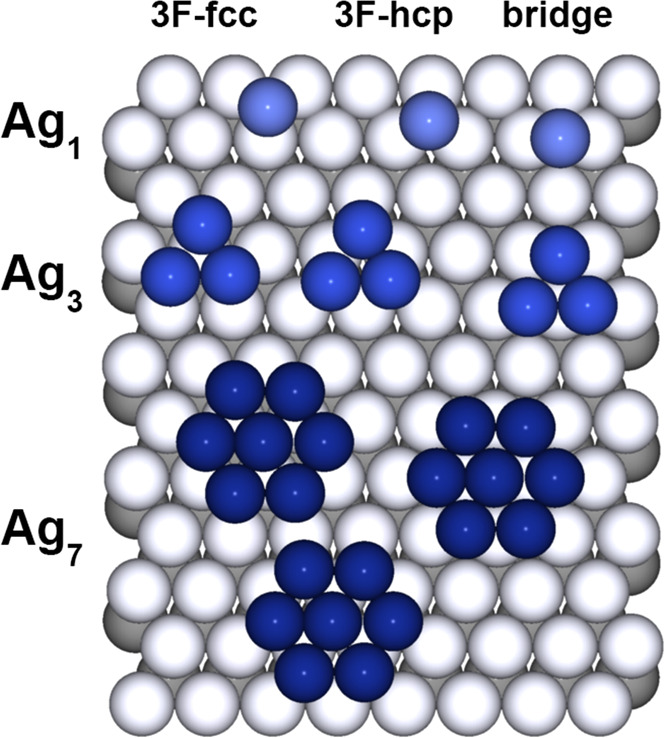
Figure 2

Open in a new tab

Different adsorption configurations of Ag1, Ag3, and Ag7 clusters tested in the DFT calculations.

We tested the energetics for adsorption in 3-fold fcc, 3-fold hcp, bridge, and on-top sites. The test on the latter site has been performed only for Ag1 since it appeared to be markedly the least favorite configuration. Monomers, trimers, and heptamers in fcc and hcp sites resulted in equally stable adsorption configurations (within the numerical errors) and are only slightly preferred (by about 50 meV) than the bridge configuration (see Table 1). The results, which for single adatoms turn out to be in very good agreement with previous DFT calculations,42 show that the adsorption energy/atoms ratio increases with the local density of Ag atoms, i.e., by spanning from monomers to heptamers. This fact indicates an attractive Ag–Ag interaction and can explain the tendency of Ag to form on Ru(0001) small compact islands at low coverage and temperature.

Table 1. Adsorption Energies (in eV) for the Different Combinations of Clusters and Adsorption Sites Investigated in the DFT Calcualtions.

cluster fcc hcp bridge top
Ag1 2.483 2.483 2.424 2.076
Ag3 2.57 2.566 2.519  
Ag7 2.647 2.646 2.602  
Open in a new tab

Similar adsorption energies for the two nonequivalent 3-fold adsorption sites are due to the very large covalent radius of Ag atoms (1.53 Å) and indicate therefore a negligible influence of the second layer Ru atoms.

The role of the Ru substrate is reduced when increasing the cluster size and the local density of Ag atoms. This is also confirmed by the heights of Ag atoms with respect to the Ru first layer, which for the most stable adsorption configurations (fcc and hcp sites) goes from 2.78 Å for Ag1 (a value that is in excellent agreement with previous findings42) to 2.84 Å (Ag7), as shown in Figure 3. This suggests that the Ag–Ag interatomic interactions become larger when increasing the Ag island size.

Figure 3.

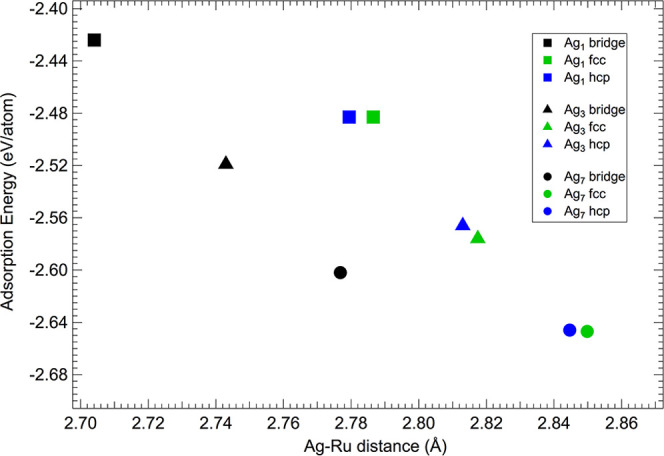
Figure 3

Open in a new tab

Adsorption energy per Ag atom as a function of average Ag–Ru distance for Ag1, Ag3, and Ag7 clusters on Ru(0001).

A further significant aspect of this analysis is the understanding of the dependence of the Ag–Ag bond length on the number of atoms in the islands, thus addressing the issue of induced strain in the Ag bonds.43 In figure 4, we report the calculated bond length for Ag clusters composed of different numbers of atoms and adsorbed in different sites on the Ru(0001) surface. The distance reported in the figure was obtained by calculating the average distance from the nearest neighbors for each atom in the clusters. We report as well the values calculated for Ag3 and Ag7 in the gas phase (GP) as a reference. We can observe that there is no significant dependence of the bond length on the in-plane CN. In the gas phase, we observe a shrinking of ca. 7% of the bond length for the Ag3 cluster, while the contraction is smaller for Ag7 (ca. 4%). On the other hand, we observe an expansion of the bond length when the clusters are adsorbed on the surface, with a dependence on both the size of the cluster and the adsorption site. This strain ranges from ca. 3% for Ag7 on bridge adsorption sites to about 1% for Ag7 on 3-fold adsorption sites, with adsorption on the fcc and hcp configurations being almost equivalent.

Figure 4.

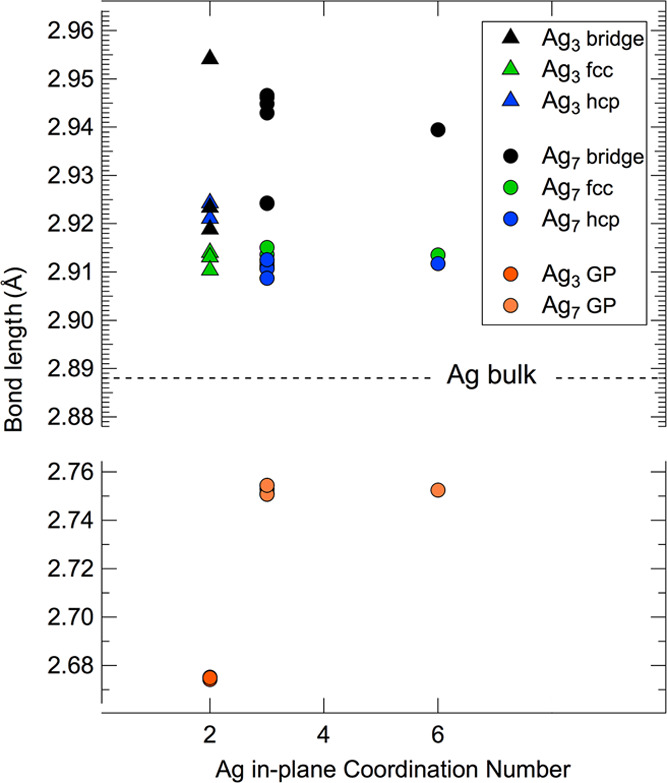
Figure 4

Open in a new tab

Calculated bond length for Ag3 and Ag7 clusters both in the gas phase (GP) and for different adsorption configurations on the Ru(0001) surface. The value for Ag in the bulk is reported for reference.

The difference induced by the in-plane CN can be appreciated by observing the trend of the calculated 3d5/2 core-level shifts in the various Ag structures with different coordination numbers, as reported in Figure 5. To increase the data set and to probe the changes in 3d5/2 core electron binding energies caused by different CNs, we also investigated the effects caused by increasing island sizes, simulating structures with Ag atoms in a hexagonal close-packed arrangement, as for the Ag7 case, but forming larger clusters/islands. We expect that all types of clusters, in particular monomers because of a diffusion energy of only 59 meV we found using NEB (in agreement with the value reported in ref (42)), will indeed diffuse on the Ru(0001) surface and start forming islands with different sizes. If this would be the case, the density of undercoordinated atoms would be lower than in the situation with clusters randomly distributed on the surface. The two configurations used to model this conjecture (shown in the Supporting Information) are composed of Ag atoms with CN ranging from 6 to 2. Ag dimers (CN = 1) have not been considered in this calculation and thus are absent in Figure 5.

Figure 5.

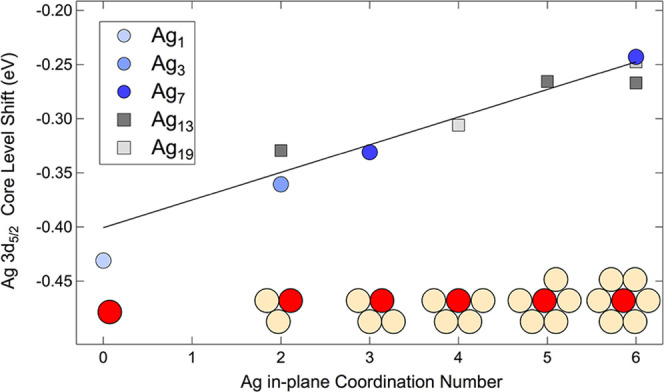
Figure 5

Open in a new tab

Calculated Ag 3d5/2 core electron binding energy shifts dependence on the in-plane coordination number (CN) for different local configurations. The values are reported with respect to the binding energy of bulk atoms.

Figure 5 shows a remarkable, and up to now never detected, linear dependence of the core-level shift in a bimetallic surface composition with the overall in-plane coordination, with a proportionality coefficient between the shift and the number of Ag nearest neighbors of 25 ± 5 meV per bond. The very small shift predicted by the theoretical calculations further proves that measuring the structure-related properties of undercoordinated Ag clusters/islands on a transition metal surface is extremely challenging. When we compare the changes in core levels of undercoordinated configurations (but in this case, for three-dimensional (3D) systems) obtained upon formation of Rh adatoms and ad-dimers on (111) and (100) rhodium surfaces,21 a value of 130 meV per bond (3d5/2 core level) is larger by a factor of 5 with respect the one obtained for our system. A large difference has also been obtained in the case of undercoordinated Pt atoms when measuring the Pt 4f7/2 core-level shift for which a value of 120 meV per bond was found.22

The calculated CN-dependent core electron binding energy shift was used to fit the Ag 3d5/2 spectra measured after deposition of Ag1, Ag3, and Ag7 on Ru(0001), as shown in Figure 6, using a method already applied in the case of the analysis of the C 1s spectrum of a graphene layer on Re(0001)44 and Ru(0001).45 Each spectrum has been fitted using seven components spaced by 25 ± 5 meV, each corresponding to a different CN ranging from CN = 0 (monomer) to CN = 6 (Ag monolayer). It was possible to obtain the absolute BE of each component combining the experimental and theoretical work performed considering a Ag(111) single crystal. The relative CL shifts were calculated using as a reference the theoretical BE of atoms in the bulk of a Ag(111) single crystal previously simulated; subsequently, this value has been aligned to the experimentally measured one, as extrapolated from the Ag 3d5/2 core-level spectrum reported in Figure 1a. Given this assumption, the core electron binding energy shifts can be considered as the experimental values, and the absolute BE of the components associated to each CN can easily be obtained by applying a shift to this value. The Γ and α parameters were kept fixed to the bulk values, while G was calculated to be equal to 0.20, 0.19, and 0.23 eV, respectively, for the Ag1, Ag3, and Ag7 depositions.

Figure 6.

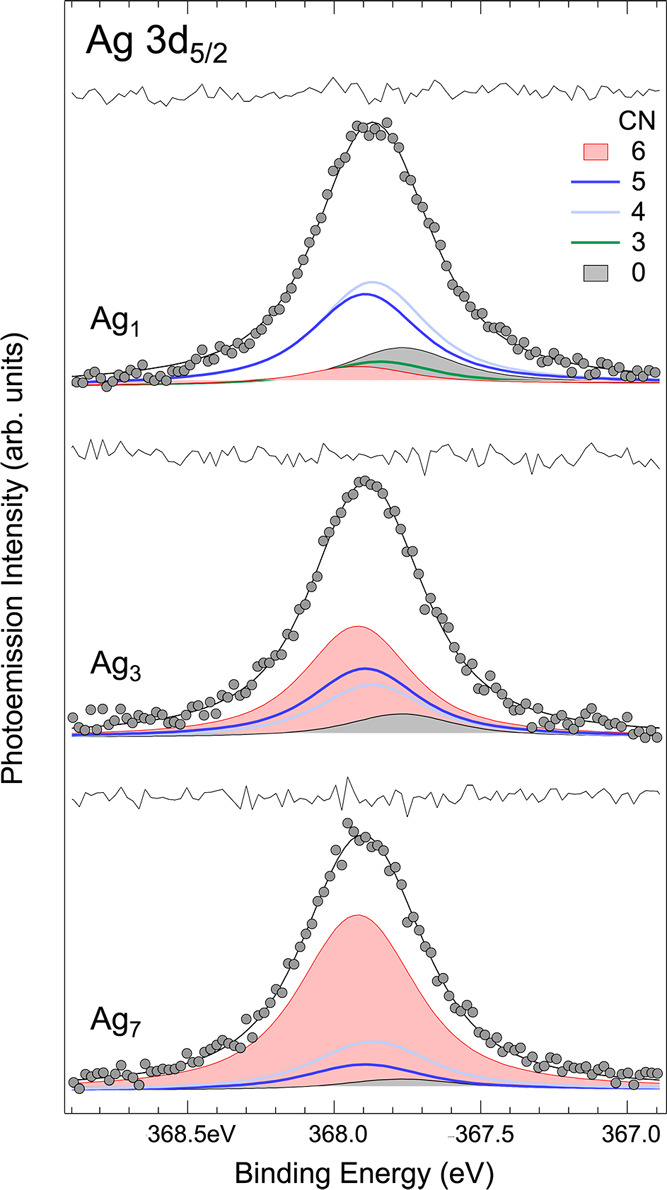
Figure 6

Open in a new tab

Ag 3d5/2 core-level spectra from Ag1, Ag3, and Ag7 clusters deposited on Ru(0001). Spectra are collected using a photon energy of 470 eV. Each spectrum is fitted using seven components separated by 25 meV, according to the DFT results.

The modification in the spectral weight previously discussed is confirmed by the data analysis, showing that after the deposition of the Ag7 clusters, most of the atoms are in CN = 6. This clearly suggests that Ag7 is very mobile even at T = 300 K and quite large islands are present on the surface after deposition. Since the populations of CN = 5 and 4 atoms are very low, the islands formed are expected to have a high degree of order, thus suggesting that Ag7 is a good building block to form a hexagonal close-packed atomic arrangement. Consequently, if we ideally think of Ag7 as flat and unbreakable clusters, it is possible to form a 2D Ag layer by simply aligning the clusters along the <120> direction, forming monolayer islands having atoms in the inner part with CN = 6 and atoms at the edges with CN = 4 and 3. While the population of 5 and 4 species is very small, the component related to CN = 3 cannot be detected within our error bar. The good mobility of Ag7, which is known to be related to decreased cluster mobility (see for example Re clusters on Ru(0001)46), could be related to the large lattice mismatch between the Ag7 cluster and Ru, with the average distance between the atoms of the first (2.91 Å) being 7.4% larger than the lattice parameter of Ru (2.71 Å), which is known to reduce the overall Ag–Ru affinity and hence increase the Ag cluster mobility. A further indication of the weak interaction of Ag7 with the substrate is that such configuration is characterized by the highest height of Ag atoms with respect to the Ru first layer, as previously discussed in Figure 3. The presence of a small component related to Ag1 indicates that a limited part of Ag7 clusters dissociates upon impacting the surface forming monomers, which remain on the surface as isolated atoms. Even if the cluster energy increases with size, we cannot exclude the activation of an Ostwald ripening process where the Ag atoms at the edges of the clusters detach from Ag7 and migrate on the surface. This is indeed the process found in the case of monodisperse Pd19 clusters deposited on Rh(111).47 However, contrary to our system, the Pd–Pd binding energy is considerably lower than the binding energy of the cluster to the substrate. The spectrum measured after deposition of Ag3 clusters shows a reduced population of atoms with CN = 6 with a corresponding increase of atoms with few in-plane nearest neighbors, thus supporting the idea that even for these clusters, the formation of 2D Ag island with the high density of defects is dominant.

Surprisingly, the Ag 3d5/2 spectrum for the Ag1 deposition indicates that there is a very small number of atoms in a close-packed arrangement. To explain this unforeseen result, we can take into account that the deposition took place at a substrate temperature (300 K) much lower than the value used to achieve a well ordered Ag adlayer structure on Ru(0001), which is between 69048 and 790 K.49 Despite the fact that the deposition temperature we used was high enough to make the Ag atoms highly mobile on this surface, it could not be sufficient to promote the formation of a full close-packed atomic arrangement, producing instead a lot of local defects (CN = 5 and 4). For a similar system, i.e., Au on Ru(0001),50 the room temperature deposition resulted in the formation of a dendritic structure caused by kinetic limitations, which was found to be thermodynamically unstable.51 According to the Witten and Sander aggregation model,52 this effect can be due to the lower mobility of adatoms on the periphery of the noble metal islands. The presence of a disordered layer upon Ag1 deposition is also supported by the large density of Ag atoms with CN = 5, with this value being incompatible with the formation of high-symmetry and low-energy Ag islands with quasihexagonal symmetry, which are energetically favorite. In this case, besides the number of Ag atoms with CN = 6 in the inner part of the island, we would expect to have atoms with CN = 3 and 4 but not 5, independent of the island size (see the Supporting Information).

Besides the growth mode, we cannot ignore the role played by surface steps, which have been found to be the preferential attachment site in the case of the growth of Ag on Ru(0001) at room temperature.53 For a very similar system, although at much larger coverage with respect to the ones used in our work, i.e., deposition of 0.1 ML of Ag on Re(0001) at room temperature,54 atoms bind exclusively at step edges where they form irregularly shaped small atomic aggregates. In particular, it was found that adatoms do not wet step edges and are responsible for an irregular and fairly porous shape of individual Ag aggregates, with large “cavities” caused by a totally unidirectional growth. Since the electronic structure of Re is quite comparable to Ru, we can imagine a similar behavior in our systems, which would result in relevant populations of Ag atoms with CNs lower than 6.

Even if the motion of the island for several systems is related to the island size (diffusion coefficient scales as the inverse radius of the island55), especially in the case of Ag, there are examples in which the atomic island motion can take place also for extremely large islands. This can occur also by means of a collective diffusion mechanism involving each atom in the island, as in the case of relatively small homoepitaxial islands on fcc(111) transition metals. The atomistic mechanism could be different depending on the island size, ranging from a gliding process (N < 20), in which all of the atoms of the small island move simultaneously, to a kink dislocation motion (N > 100), for which an atomic row of atoms moves simultaneously from fcc to hcp three-fold sites.56

Conclusions

In summary, by means of HR-CLS, we have investigated the local configurations of Ag atoms with a low CN obtained upon deposition of mass-selected Ag clusters on Ru(0001). We have found that the Ag 3d5/2 core-level shift shows a linear dependence on the in-plane CN. The very small core-level shift/bond and the large mobility of Ag clusters on the Ru surface are two intrinsic limitations, which hindered the possibility to distinguish clearly the spectral features originating by each nonequivalent atom in the cluster. On the other hand, our approach is potentially a starting point paving the way to the investigation of the properties of 2D materials grown using adsorbed clusters, which are expected to present, according to the different structures, a number of nonequivalent local configurations related to different CNs. We believe that this methodology could be the key to a deeper understanding of the factors driving the electronic and reactivity properties of undercoordinated atoms in 2D materials.

Acknowledgments

A.B. acknowledges funding from the University of Trieste through the METAMAT project. L.B. acknowledges funding from the University of Trieste through the D55 Microgrants funding initiative. M.P. and D.A. are supported by the Natural Environment Research Council Grant No. NE/R000425/1. DFT calculations were performed on Monsoon2 system, a collaborative facility supplied under the Joint Weather and Climate Research Programme, a strategic partnership between the U.K. Met Office and the Natural Environment Research Council.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jpcc.1c02327.

  • Mass spectrum of Ag+ clusters produced by the ENAC source and simulations with large Ag islands; mass spectrum obtained transporting and depositing on a Ru(0001) surface Ag cluster within the mass range of about 100–5000 amu; models used to perform the simulation with larger islands composed of (a) 13 and (b) 19 Ag atoms; and models and related histograms of the percentage of atoms for each CN in Ag islands with a hexagonal close-packed arrangement made of (a) 19, (b) 37, and (c) 61 Ag atoms (PDF)

The authors declare no competing financial interest.

Supplementary Material

jp1c02327_si_001.pdf (2.2MB, pdf)

References

  1. Liu L.; Corma A. Metal Catalysts for Heterogeneous Catalysis: From Single Atoms to Nanoclusters and Nanoparticles. Chem. Rev. 2018, 118, 4981–5079. 10.1021/acs.chemrev.7b00776. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Sun C. Q. Dominance of broken bonds and nonbonding electrons at the nanoscale. Nanoscale 2010, 2, 1930–1961. 10.1039/c0nr00245c. [DOI] [PubMed] [Google Scholar]
  3. Sun C. Q.Electron and Phonon Spectrometrics; Springer: Singapore, 2020. [Google Scholar]
  4. Hughes M. D.; Xu Y.-J.; Jenkins P.; McMorn P.; Landon P.; Enache D. I.; Carley A. F.; Attard G. A.; Hutchings G. J.; King F.; et al. Tunable gold catalysts for selective hydrocarbon oxidation under mild conditions. Nature 2005, 437, 1132–1135. 10.1038/nature04190. [DOI] [PubMed] [Google Scholar]
  5. Fujita T.; Guan P.; McKenna K.; Lang X.; Hirata A.; Zhang L.; Tokunaga T.; Arai S.; Yamamoto Y.; Tanaka N.; et al. Atomic origins of the high catalytic activity of nanoporous gold. Nat. Mater. 2012, 11, 775–80. 10.1038/nmat3391. [DOI] [PubMed] [Google Scholar]
  6. Valden M.; Lai X.; Goodman D. W. Onset of Catalytic Activity of Gold Clusters on Titania with the Appearance of Nonmetallic Properties. Science 1998, 281, 1647–1650. 10.1126/science.281.5383.1647. [DOI] [PubMed] [Google Scholar]
  7. Tian N.; Zhou Z.-Y.; Sun S.-G.; Ding Y.; Wang Z. L. Synthesis of Tetrahexahedral Platinum Nanocrystals with High-Index Facets and High Electro-Oxidation Activity. Science 2007, 316, 732–735. 10.1126/science.1140484. [DOI] [PubMed] [Google Scholar]
  8. Vajda S.; Pellin M. J.; Greeley J. P.; Marshall C. L.; Curtiss L. A.; Ballentine G. A.; Elam J. W.; Catillon-Mucherie S.; Redfern P. C.; Mehmood F.; et al. Subnanometre platinum clusters as highly active and selective catalysts for the oxidative dehydrogenation of propane. Nat. Mater. 2009, 8, 213–216. 10.1038/nmat2384. [DOI] [PubMed] [Google Scholar]
  9. Wu C.-Y.; Wolf W. J.; Levartovsky Y.; Bechtel H. A.; Martin M. C.; Toste F. D.; Gross E. High-spatial-resolution mapping of catalytic reactions on single particles. Nature 2017, 541, 511–515. 10.1038/nature20795. [DOI] [PubMed] [Google Scholar]
  10. Hammer B.; Nørskov J.. Impact of Surface Science on Catalysis. In Advances in Catalysis; Academic Press, 2000; Vol. 45, pp 71–129. [Google Scholar]
  11. Nørskov J.; Bligaard T.; Logadottir A.; Bahn S.; Hansen L.; Bollinger M.; Bengaard H.; Hammer B.; Sljivancanin Z.; Mavrikakis M.; et al. Universality in Heterogeneous Catalysis. J. Catal. 2002, 209, 275–278. 10.1006/jcat.2002.3615. [DOI] [Google Scholar]
  12. Greeley J.; Nørskov J. K.; Mavrikakis M. Electronic structure and catalysis on metal surfaces. Annu. Rev. Phys. Chem. 2002, 53, 319–348. 10.1146/annurev.physchem.53.100301.131630. [DOI] [PubMed] [Google Scholar]
  13. Brune H. Microscopic view of epitaxial metal growth: nucleation and aggregation. Surf. Sci. Rep. 1998, 31, 125–229. 10.1016/S0167-5729(97)00015-0. [DOI] [Google Scholar]
  14. Liu X.; Zhang X.; Bo M.; Li L.; Tian H.; Nie Y.; Sun Y.; Xu S.; Wang Y.; Zheng W.; et al. Coordination-Resolved Electron Spectrometrics. Chem. Rev. 2015, 115, 6746–6810. 10.1021/cr500651m. [DOI] [PubMed] [Google Scholar]
  15. Andersen J. N.; Hennig D.; Lundgren E.; Methfessel M.; Nyholm R.; Scheffler M. Surface core-level shifts of some 4d-metal single-crystal surfaces: Experiments and ab initio calculations. Phys. Rev. B 1994, 50, 17525–17533. 10.1103/PhysRevB.50.17525. [DOI] [PubMed] [Google Scholar]
  16. Lizzit S.; Pohl K.; Baraldi A.; Comelli G.; Fritzsche V.; Plummer E. W.; Stumpf R.; Hofmann P. Physics of the Be(10 1̅0) Surface Core Level Spectrum. Phys. Rev. Lett. 1998, 81, 3271–3274. 10.1103/PhysRevLett.81.3271. [DOI] [Google Scholar]
  17. Baraldi A. Structure and chemical reactivity of transition metal surfaces as probed by synchrotron radiation core level photoelectron spectroscopy. J. Phys.: Condens. Matter 2008, 20, 093001 10.1088/0953-8984/20/9/093001. [DOI] [Google Scholar]
  18. Baraldi A.; Lizzit S.; Comelli G.; Paolucci G. Oxygen adsorption and ordering on Ru(10 1̅0). Phys. Rev. B 2001, 63, 115410 10.1103/PhysRevB.63.115410. [DOI] [Google Scholar]
  19. Gustafson J.; Borg M.; Mikkelsen A.; Gorovikov S.; Lundgren E.; Andersen J. N. Identification of Step Atoms by High Resolution Core Level Spectroscopy. Phys. Rev. Lett. 2003, 91, 056102 10.1103/PhysRevLett.91.056102. [DOI] [PubMed] [Google Scholar]
  20. Walter A. L.; Schiller F.; Corso M.; Merte L. R.; Bertram F.; Lobo-Checa J.; Shipilin M.; Gustafson J.; Lundgren E.; Brión-Ríos A. X.; et al. X-ray Photoemission Analysis of Clean and Carbon Monoxide-Chemisorbed Platinum(111) Stepped Surfaces using a Curved Crystal. Nat. Commun. 2015, 6, 8903 10.1038/ncomms9903. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Baraldi A.; Bianchettin L.; Vesselli E.; de Gironcoli S.; Lizzit S.; Petaccia L.; Zampieri G.; Comelli G.; Rosei R. Highly under-coordinated atoms at Rh surfaces: interplay of strain and coordination effects on core level shift. New J. Phys. 2007, 9, 143. 10.1088/1367-2630/9/5/143. [DOI] [Google Scholar]
  22. Bianchettin L.; Baraldi A.; de Gironcoli S.; Vesselli E.; Lizzit S.; Petaccia L.; Comelli G.; Rosei R. Core level shifts of undercoordinated Pt atoms. J. Chem. Phys. 2008, 128, 114706 10.1063/1.2841468. [DOI] [PubMed] [Google Scholar]
  23. Baraldi A.; Bianchettin L.; de Gironcoli S.; Vesselli E.; Lizzit S.; Petaccia L.; Comelli G.; Rosei R. Enhanced Chemical Reactivity of Under-Coordinated Atoms at Pt-Rh Bimetallic Surfaces: A Spectroscopic Characterization. J. Phys. Chem. C 2011, 115, 3378–3384. 10.1021/jp110329w. [DOI] [Google Scholar]
  24. Schoiswohl J.; Mittendorfer F.; Surnev S.; Ramsey M. G.; Andersen J. N.; Netzer F. P. Chemical Reactivity of Ni-Rh Nanowires. Phys. Rev. Lett. 2006, 97, 126102 10.1103/PhysRevLett.97.126102. [DOI] [PubMed] [Google Scholar]
  25. Bruix A.; Füchtbauer H. G.; Tuxen A. K.; Walton A. S.; Andersen M.; Porsgaard S.; Besenbacher F.; Hammer B.; Lauritsen J. V. In Situ Detection of Active Edge Sites in Single-Layer MoS2 Catalysts. ACS Nano 2015, 9, 9322–9330. 10.1021/acsnano.5b03199. [DOI] [PubMed] [Google Scholar]
  26. Cavallin A.; Pozzo M.; Africh C.; Baraldi A.; Vesselli E.; Dri C.; Comelli G.; Larciprete R.; Lacovig P.; Lizzit S.; et al. Local Electronic Structure and Density of Edge and Facet Atoms at Rh Nanoclusters Self-Assembled on a Graphene Template. ACS Nano 2012, 6, 3034–3043. 10.1021/nn300651s. [DOI] [PubMed] [Google Scholar]
  27. Ruban A. V.; Skriver H. L.; Nørskov J. K. Surface segregation energies in transition-metal alloys. Phys. Rev. B 1999, 59, 15990–16000. 10.1103/PhysRevB.59.15990. [DOI] [Google Scholar]
  28. Lizzit S.; Baraldi A.; Groso A.; Reuter K.; Ganduglia-Pirovano M. V.; Stampfl C.; Scheffler M.; Stichler M.; Keller C.; Wurth W.; et al. Surface core-level shifts of clean and oxygen-covered Ru(0001). Phys. Rev. B 2001, 63, 205419 10.1103/PhysRevB.63.205419. [DOI] [Google Scholar]
  29. Ulstrup S.; Lacovig P.; Orlando F.; Lizzit D.; Bignardi L.; Dalmiglio M.; Bianchi M.; Mazzola F.; Baraldi A.; Larciprete R.; et al. Photoemission investigation of oxygen intercalated epitaxial graphene on Ru(0001). Surf. Sci. 2018, 678, 57–64. 10.1016/j.susc.2018.03.017. [DOI] [Google Scholar]
  30. Heiz U.; Vanolli F.; Trento L.; Schneider W.-D. Chemical reactivity of size-selected supported clusters: An experimental setup. Rev. Sci. Instrum. 1997, 68, 1986–1994. 10.1063/1.1148113. [DOI] [Google Scholar]
  31. Lünskens T.; Heister P.; Thämer M.; Walenta C. A.; Kartouzian A.; Heiz U. Plasmons in supported size-selected silver nanoclusters. Phys. Chem. Chem. Phys. 2015, 17, 17541–17544. 10.1039/C5CP01582K. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Thämer M.; Kartouzian A.; Heister P.; Lünskens T.; Gerlach S.; Heiz U. Small supported plasmonic silver clusters. Small 2014, 10, 2340–2344. 10.1002/smll.201303158. [DOI] [PubMed] [Google Scholar]
  33. Lünskens T.; Walenta C. A.; Heister P.; Kartouzian A.; Heiz U. Surface oxidation of supported, size-selected silver clusters. J. Cluster Sci. 2017, 28, 3185–3192. 10.1007/s10876-017-1285-y. [DOI] [Google Scholar]
  34. Lünskens T.; von Weber A.; Jakob M.; Lelaidier T.; Kartouzian A.; Heiz U. Effect of thiol-ligands on the optical response of supported silver clusters. J. Phys. Chem. C 2017, 121, 9331–9336. 10.1021/acs.jpcc.7b00827. [DOI] [Google Scholar]
  35. Binns C. Nanoclusters deposited on surfaces. Surf. Sci. Rep. 2001, 44, 1–49. 10.1016/S0167-5729(01)00015-2. [DOI] [Google Scholar]
  36. Doniach S.; Šunjić M. Many-electron singularity in X-ray photoemission and X-ray line spectra from metals. J. Phys. C: Solid State Phys. 1970, 3, 285–291. 10.1088/0022-3719/3/2/010. [DOI] [Google Scholar]
  37. Kresse G.; Furthmüller J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. 10.1103/PhysRevB.54.11169. [DOI] [PubMed] [Google Scholar]
  38. Blöchl P. E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. 10.1103/PhysRevB.50.17953. [DOI] [PubMed] [Google Scholar]
  39. Perdew J. P.; Burke K.; Ernzerhof M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. 10.1103/PhysRevLett.77.3865. [DOI] [PubMed] [Google Scholar]
  40. Henkelman G.; Uberuaga B. P.; Jónsson H. A climbing image nudged elastic band method for finding saddle points and minimum energy paths. J. Chem. Phys. 2000, 113, 9901–9904. 10.1063/1.1329672. [DOI] [Google Scholar]
  41. Gamboa G. U.; Reber A. C.; Khanna S. N. Electronic subshell splitting controls the atomic structure of charged and neutral silver clusters. New J. Chem. 2013, 37, 3928–3935. 10.1039/c3nj01075a. [DOI] [Google Scholar]
  42. Lu Y.; Sun Q.; Jia Y.; He P. Adsorption and diffusion of adatoms on Ru(0001): A first-principles study. Surf. Sci. 2008, 602, 2502–2507. 10.1016/j.susc.2008.05.043. [DOI] [Google Scholar]
  43. Sun C. Q.; Wang Y.; Nie Y.; Sun Y.; Pan J.; Pan L.; Sun Z. Adatoms-Induced Local Bond Contraction, Quantum Trap Depression, and Charge Polarization at Pt and Rh Surfaces. J. Phys. Chem. C 2009, 113, 21889–21894. 10.1021/jp908220a. [DOI] [Google Scholar]
  44. Miniussi E.; Pozzo M.; Baraldi A.; Vesselli E.; Zhan R. R.; Comelli G.; Menteş T. O.; Niño M. A.; Locatelli A.; Lizzit S.; et al. Thermal Stability of Corrugated Epitaxial Graphene Grown on Re(0001). Phys. Rev. Lett. 2011, 106, 216101 10.1103/PhysRevLett.106.216101. [DOI] [PubMed] [Google Scholar]
  45. Alfè D.; Pozzo M.; Miniussi E.; Günther S.; Lacovig P.; Lizzit S.; Larciprete R.; Burgos B. S.; Menteş T. O.; Locatelli A.; et al. Fine tuning of graphene-metal adhesion by surface alloying. Sci. Rep. 2013, 3, 2430 10.1038/srep02430. [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Liu F.; Hu W.; Deng H.; Luo W.; Xiao S.; Yang J. Self-diffusion dynamic behavior of atomic clusters on Re(0001) surface. Appl. Surf. Sci. 2009, 255, 8883–8889. 10.1016/j.apsusc.2009.06.078. [DOI] [Google Scholar]
  47. Fukamori Y.; König M.; Yoon B.; Wang B.; Esch F.; Heiz U.; Landman U. Fundamental Insight into the Substrate-Dependent Ripening of Monodisperse Clusters. ChemCatChem 2013, 5, 3330–3341. 10.1002/cctc.201300250. [DOI] [Google Scholar]
  48. Zajonz H.; Gibbs D.; Baddorf A. P.; Zehner D. M. Nanoscale strain distribution at the Ag/Ru(0001) interface. Phys. Rev. B 2003, 67, 155417 10.1103/PhysRevB.67.155417. [DOI] [Google Scholar]
  49. Ling W.; Hamilton J.; Thürmer K.; Thayer G.; de la Figuera J.; Hwang R.; Carter C.; Bartelt N.; McCarty K. Herringbone and triangular patterns of dislocations in Ag, Au, and AgAu alloy films on Ru(0001). Surf. Sci. 2006, 600, 1735–1757. 10.1016/j.susc.2006.01.055. [DOI] [Google Scholar]
  50. Pötschke G.; Schröder J.; Günther C.; Hwang R.; Behm R. A STM investigation of the nucleation and growth of thin Cu and Au films on Ru(0001). Surf. Sci. 1991, 251–252, 592–596. 10.1016/0039-6028(91)91061-2. [DOI] [Google Scholar]
  51. Metal Clusters at Surfaces: Structure, Quantum Properties, Physical Chemistry; Meiwes-Broer K.-H., Ed.; Springer Berlin Heidelberg: Berlin, Heidelberg, 2000. [Google Scholar]
  52. Witten T. A.; Sander L. M. Diffusion-Limited Aggregation, a Kinetic Critical Phenomenon. Phys. Rev. Lett. 1981, 47, 1400–1403. 10.1103/PhysRevLett.47.1400. [DOI] [Google Scholar]
  53. Mascaraque A.; Menteş T. O.; McCarty K. F.; Marco J. F.; Schmid A. K.; Locatelli A.; de la Figuera J. Valence band circular dichroism in non-magnetic Ag/Ru(0001) at normal emission. J. Phys.: Condens. Matter 2011, 23, 305006 10.1088/0953-8984/23/30/305006. [DOI] [PubMed] [Google Scholar]
  54. Parschau M.; Schlatterbeck D.; Christmann K. Nucleation and growth of silver films on a rhenium (0001) surface: a combined STM and LEED study. Surf. Sci. 1997, 376, 133–150. 10.1016/S0039-6028(96)01303-9. [DOI] [Google Scholar]
  55. Wen J. M.; Chang S. L.; Burnett J. W.; Evans J. W.; Thiel P. A. Diffusion of Large Two-Dimensional Ag Clusters on Ag(100). Phys. Rev. Lett. 1994, 73, 2591–2594. 10.1103/PhysRevLett.73.2591. [DOI] [PubMed] [Google Scholar]
  56. Jensen P. Growth of nanostructures by cluster deposition: Experiments and simple models. Rev. Mod. Phys. 1999, 71, 1695–1735. 10.1103/RevModPhys.71.1695. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

jp1c02327_si_001.pdf (2.2MB, pdf)

Articles from The Journal of Physical Chemistry. C, Nanomaterials and Interfaces are provided here courtesy of American Chemical Society

RESOURCES