Abstract
Background: Policy-makers have attempted to mitigate the spread of covid-19 with national and local non-pharmaceutical interventions. Moreover, evidence suggests that some areas are more exposed than others to contagion risk due to heterogeneous local characteristics. We study whether Italy’s regional policies, introduced on 4th November 2020, have effectively tackled the local infection risk arising from such heterogeneity.
Methods: Italy consists of 19 regions (and 2 autonomous provinces), further divided into 107 provinces. We collect 35 province-specific pre-covid variables related to demographics, geography, economic activity, and mobility. First, we test whether their within-region variation explains the covid-19 incidence during the Italian second wave. Using a LASSO algorithm, we isolate variables with high explanatory power. Then, we test if their explanatory power disappears after the introduction of the regional-level policies.
Findings: The within-region variation of seven pre-covid characteristics is statistically significant (F-test p-value ) and explains 19% of the province-level variation of covid-19 incidence, on top of region-specific factors, before regional policies were introduced. Its explanatory power declines to 7% after the introduction of regional policies, but is still significant (p-value ), even in regions placed under stricter policies (p-value ).
Interpretation: Even within the same region, Italy’s provinces differ in exposure to covid-19 infection risk due to local characteristics. Regional policies did not eliminate these differences, but may have dampened them. Our evidence can be relevant for policy-makers who need to design non-pharmaceutical interventions. It also provides a methodological suggestion for researchers who attempt to estimate their causal effects.
Funding: None.
Keywords: COVID-19, non-pharmaceutical interventions, italy, regional policies, local risk factors
1. Introduction
Since fall 2020, several European countries have introduced local non-pharmaceutical interventions (henceforth, NPIs) instead of the national lockdowns that have characterised the first wave of restriction policies in spring 2020. While some countries and local authorities have targeted single municipalities (i.e., the U.K. with Manchester or the U.S. with the Chicago mayor’s city-wide lockdown), other countries, such as Italy, designed regional policies.1 Several studies have exploited these differences in local restrictions to try to calculate their efficacy [1], [2], [3], [4], [5].
Research in context.
Evidence before this study
To restrain the spread of covid-19, many countries have introduced national and local non-pharmaceutical interventions. Evidence suggests that only harsh and centralised policies seem effective enough to keep the spread of covid-19 under control in certain countries. However, several studies find that geographical, demographic, and social local factors are correlated (or causally connected) with the local spread of covid-19. Have Italy’s regional policies, introduced on 4th November 2020, effectively tackled the infection risk arising from such local factors? We look for studies related to these facts by using keywords such as “covid-19”, “covid-19 policies,“ and “covid-19 non-pharmaceutical interventions”. We look for evidence circa possible covid-19 geographic, environmental or socio-economic factors by adding to “covid-19” keywords such as “risk factors”, “spread, and “infection risk”.
Added value of this study
Italy has 19 regions (and 2 autonomous provinces), further divided into 107 provinces. In November 2020, Italy has adopted non-pharmaceutical interventions (NPIs) at regional level. We provide robust statistical evidence that province-specific pre-determined (i.e., pre-covid) socio-economic and geographical characteristics have a sizeable explanatory power for local covid-19 incidence in Italy, even within the same region. We also find that these characteristics’ importance persists after the introduction of Italy’s regional policies on 4th November 2020. Hence, the introduction of regional-level policies did not entirely cancel these differences in systematic local risk. However, we find suggestive evidence that they have been partially effective at dampening their relevance. Due to Italy’s specific institutional framework and policy design, we can back our claims with a parsimonious but statistically valid model, focusing on within-region variations of covid-19 incidence after 1st September 2020 (the “second wave”). Our findings point out a potential concern regarding conventional estimates of the efficacy of NPIs obtained by exploiting their spatial variation, but without taking into account local factors.
Implications of all the available evidence
Several risk factors seem to contribute to the spread of covid-19. NPIs have tackled them with various degrees of efficacy, with some policies being more effective than others. We provide evidence that heterogeneous socio-economic characteristics can help explaining the different levels of covid-19 incidence of geographically close areas in Italy, and that the importance of those local characteristics persisted, at least partially, after regional policies were implemented. In this sense, our results provide an additional argument supporting NPIs targeted to local risk factors. The significant role of pre-determined characteristics in explaining the covid-19 incidence, before and after introducing regional measures in Italy, suggests that those policies have been, at best, imperfect at equally tackling covid-19 infection risk at the local level. Additionally, this works highlight the importance of accounting for spatial heterogeneity when identifying the causal effects of policies on infection risk. For example, this can be achieved by employing statistical methods that can explicitly control local characteristics (such as epidemiological models, randomised control trials, or propensity score matching) or partial them out (such as interrupted time series or regression discontinuity).
Alt-text: Unlabelled box
However, regions can be large, and even neighboring areas can have highly heterogeneous characteristics. For example, a large region such as Lombardia, in Northern Italy, extends over 23863 squared kilometers and contains both rural areas and dense urban centers with crowded public transports (with population density ranging from 56 people per km, in the Sondrio province, to 2072, in the Milano province) or areas with different economic structures that might imply different shares of jobs that can be carried out from home. Some of these heterogeneous local characteristics may be important determinants of covid-19 infection risk. If this is the case, narrowly-defined neighboring geographies could have experienced different infection incidence levels attributable - at least in part - to those characteristics.
In this paper, we investigate two questions. First, can the covid-19 incidence heterogeneity across Italian provinces, during the second wave in fall 2020, be explained by province-specific pre-determined (i.e., pre-covid) characteristics, in addition to region-specific ones? These characteristics vary between provinces because: (i) on average they are different from one region to another (henceforth, between-region variation); and (ii) they differ between provinces within the same region (henceforth, within-region variation). If the between-region variation of these factors is the only systematic determinant of the observed incidence, regional policies might be the right tool to tackle local infections uniformly. Instead, if the within-region variation of those characteristics is important, a second question arises: are regional policies, which impose uniform restrictions over heterogeneous local areas, sufficient to target local risk equally? Potentially, regional policies could successfully address the province-level incidence heterogeneity because their effectiveness is also a function of province-specific characteristics. If the pre-determined province characteristics contribute to explain the covid-19 incidence both before and after the introduction of the regional policies, then we argue that such policies were imperfectly-designed to target local risk. We focus on the second wave (in fall 2020) because during the first wave (in spring 2020) Italy adopted almost exclusively country-wide policies.
We address these questions by looking at provincial (NUTS-3) data for Italy. Italy represents the ideal candidate to study this phenomenon for several reasons. First, as already mentioned, Italy implemented consistent regional-level measures starting from 4th November 2020 until late January 2021. Second, the regional restriction measures were decided with an objective national algorithm, with little to no discretionary political interventions after it was set up. Third, these measures were almost entirely uniform within regions. Finally, all healthcare policies, including test-and-trace programs and priorities, are managed within regional powers. These characteristics create an ideal environment to study within-region differences in covid-19 incidence without worrying about confounders such as divergent testing policies across regions.
The study of factors associated with covid-19 infections can be relevant for both policy-makers and researchers. Investigating the existence of local risk factors, potentially not addressed by regional policies, can be viewed as a contributing argument for/against local interventions in the context of the quite complex and not yet fully-settled debate about the right NPIs policy design. Moreover, the relevance of local factors might suggest that studies that try to identify the effectiveness of non-pharmaceutical interventions based on spatial variations could achieve biased estimates unless correct statistical tools that control for local factor heterogeneity are employed. Our results inform researchers of whether this can be an empirically relevant concern.
2. Methods
In this section we describe the variable of interest, the set of explanatory variables, and then the statistical strategy adopted.
2.1. Data
2.1.1. Covid-19 incidence
Our variable of interest is the incidence of covid-19 for each of the 107 Italian provinces during the second wave, computed as the average number of weekly positive covid-19 cases officially reported by the Minister of Health[6], for the period 1st September 2020 - 23rd December 2020, per 100 thousand people.2 We focus on the second wave since the first wave did not develop uniformly across Italian regions, hitting harder and earlier the Northern regions than the Southern ones. Moreover, the first and second wave differ for the geographical level of NPIs: they were mainly national during the former, and differentiated across regions during the latter. We consider covid1-19 cases until 23rd December 2020 because, after that date, different nation-wide restrictions came temporarily into place. Nevertheless, we will show that our results hold under several time-windows that define the epidemic wave.
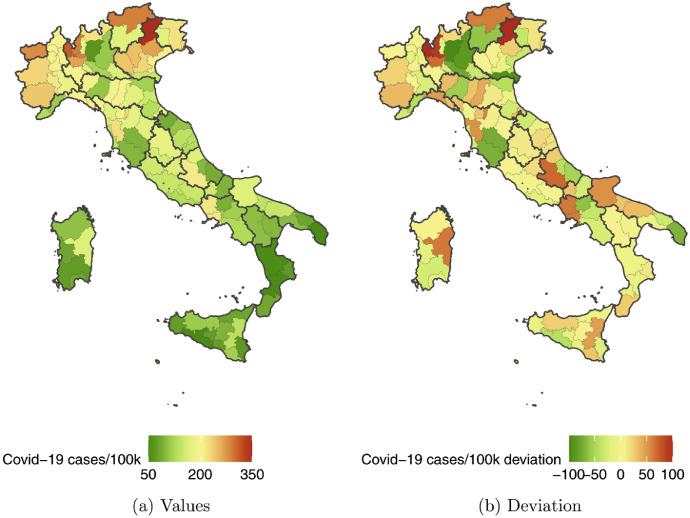
Figure 1 a displays our benchmark measure of incidence. The highest incidence occurred in the province of Belluno, in the Veneto region, with a weekly average of 3514 cases per 100 thousand people. The lowest incidence occurred in Lecce, in the Puglia region, with 444 cases. The average incidence is 1583 cases, with a standard deviation of 6459. This sizeable standard deviation captures two features. First, the majority of cases occurred in the North. Second, the significant heterogeneity across provinces within the same region.
Fig. 1.
Weekly Cases per 100k people: Second Wave
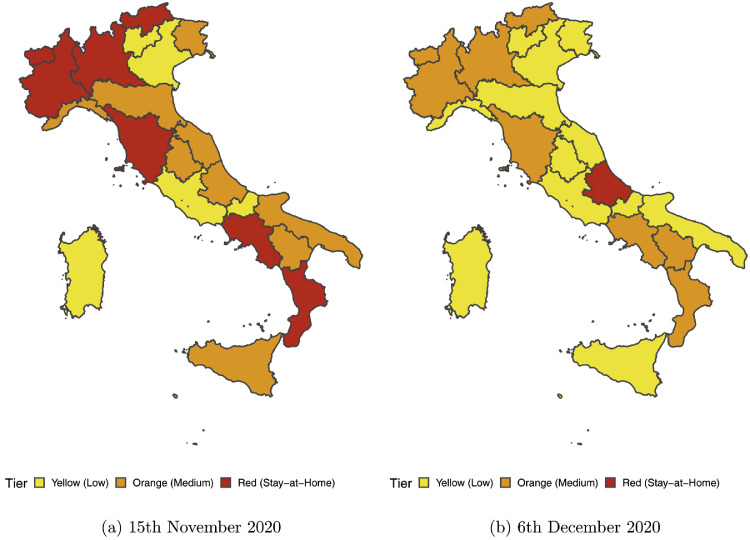
The large differences across regions have led to the implementation of differentiated regional policies. Through an algorithm taking into account estimates of the effective reproduction number, , and hospital loads, among many other parameters, each region was placed under a different regime of restrictions [7]. Figure 2 shows the region-specific restriction policy in place on 15th November 2020 and on 6th December: yellow regions had very mild restrictions, while red regions were under a moderate stay-at-home order. The color of each region was decided by the national government through objective criteria and updated regularly according to the average regional evolution of the epidemic [8], [9], [10].
Fig. 2.
Regional colour-coded restrictions. Note: Yellow: limited opening times of accommodation sector (bars, restaurants) but seated lunch allowed, restricted cross-region mobility. Orange: accommodation sector closed for in-person service, restricted cross-city mobility, night curfew, children aged 13-19 in remote learning. Red: all non-essential services closed but for delivery, gatherings and all non-essential trips from home illegal, children aged 11-19 in remote learning. All tiers include restrictions to: sport facilities, museums, nightclubs, theatres, cinemas closed and public transport at 50% capacity.
However, the regional policies do not fully reflect the differences in incidence across provinces. In Figure 1b we display the deviation of covid-19 incidence, in each province, from their regional mean. By construction, this measure eliminates all the differences across provinces due to regional effects. Notice that a large part of the province heterogeneity is still present after eliminating regional means (mean , SD ).
2.1.2. Explanatory variables
We construct a dataset of explanatory variables at the province level. We select variables that, according to the literature, may affect the spread of the covid-19 virus. These regard demographics [11], socio-economic factors [12], [13], [14], [15], [16], commuting [17], [18], [19], [20] and pollution/health [21], [22], [23]. All the variables are pre-determined with respect to the occurrence of the covid-19 pandemic. This is important because pre-determined variables capture relationships that existed before the pandemic and that could determine a higher (ceteris paribus) risk of infection, but may have been addressed by non-pharmaceutical interventions or by changes in the social behavior of the population.
In Appendix Appendix A we describe in more details the variables and their sources. The dataset of explanatory variables is composed of 35 variables.
2.2. Statistical methods
2.2.1. Objective 1: are province-specific variables important?
Can the covid-19 incidence heterogeneity across space be explained by province-specific pre-determined characteristics, in addition to region-specific ones? This question is important because if region-specific characteristics are the only systematic determinants of the observed incidence, with all the residual being due to random noise, then regional policies might be the right tool to reduce exposure to the infection uniformly.
Let us clarify further the goal of our analysis. We define the province-specific component as important if we can find variables that 1) provide a statistically significant explanatory power of the covid-19 incidence and such that 2) the size of this explanatory power is non-negligible.
Test 1 To formally answer the question, we consider two models. Model 1 is a restricted one and regresses the province level covid-19 incidence in the second wave on region-specific unmodelled characteristics:
| (1) |
Here denotes per-capita covid-19 incidence in province that belongs to region , is a set of dummy variables for each region, are the coefficients associated with each region, capturing any region-specific effect, and are random disturbances. Intuitively, Model 1 restricts all the systematic variation of covid incidence across provinces to be attributable to the between-region variation, captured by the region-specific parameters . Notice that we do not need to be explicit about the source of these regional differences: they could be driven by different regional policies, different territorial or demographic characteristics, or any other different features. Our goal is, in fact, to investigate whether there are province-level characteristics that are important to explain the covid-19 incidence and whose effects are not fully explained by differences in regional means.
Model 2 is a richer one which includes, in addition to region-specific unmodelled characteristics, also other explanatory variables. Specifically, Model 2 is:
| (2) |
Here, represent a set of explanatory variables for each province in region , is the associated set of coefficients, and are random disturbances. Notice that since region-specific effects are also present in Model 2, all the additional information captured by the explanatory variables reflects only the within-region variation across provinces of that variable. The information that Sicily’s average temperature is higher than in Piemonte is not included in the explanatory variable because the regional dummies will soak up all regional differences.
Since Model 1 is nested in Model 2, we can formally test whether the within-region variation contained in the explanatory variable is important in explaining Italy’s incidence by running an F-test. The null hypothesis is: . If the null hypothesis is not rejected, Model 1 and Model 2 are statistically equivalent. In that case, we cannot reject that the between-region differences are the sole determinants of observed covid-19 incidence in Italy.
Remark Correlation Vs Causality —
We make no claims about the causality of our model. In fact, we only need to address the significance of the differences in explained-variance across models to answer our research questions. For this reason, our OLS approach - which captures correlations only - is sufficient to address the problem as we do not seek to achieve causal identification.
Remark Interpretation of the models —
Because the models incorporate region-specific fixed-effects, our estimation results are not affected by factors that may cause differences in the average incidence of positive cases across regions (i.e., number of tests per capita or differences in average levels of factors of risk). However, one might wonder whether our results are driven by few regions with larger within-region variance across provinces. We can show that all the findings are highly robust to a standardisation of the within-region variance, i.e., by normalizing to 1 the variance of the number of positive cases across provinces within a region. Therefore, the results reported below are not due to a disproportionate role of a subset of few regions for the overall within-region variance.3
Model Selection Since we have a relatively large set of potential explanatory variables compared to the number of observations, the first step of the analysis involves a shrinking procedure, which helps condense the relevant information present in the 35 covariates into a smaller subset.
To reduce the number of explanatory variables to a subset important to explain the heterogeneity in province covid-19 incidence, we follow a three-step procedure:
-
1.
We perform a LASSO regression analysis, a shrinkage and selection method that penalizes the regression coefficients’ absolute size. This method is well suited for our purpose because some of our variables are highly correlated, and LASSO penalizes overfitting due to correlated variables strongly;
-
2.
We perform a k-fold validation procedure with to select the optimal shrinkage parameter by randomly splitting the sample. We repeat this step 100 times and select the model which achieves the highest adjusted ;
-
3.
To further minimize overfitting, we select the subset of the chosen covariates that maximizes the adjusted of the model.
In summary, our method has the following advantages: (i) it is objective and rigorous; and (ii) it strongly penalizes overfitting and selecting highly correlated covariates. Notice that our refinement procedure makes it more difficult to reject the F-test mentioned above, making a rejection result more robust.
2.2.2. Objective 2: Are regional-policy sufficient?
Next, we investigate whether the correlation found in the previous set of models disappears after the introduction of regional policies on November 4th, 2020. In principle, this is possible because even regionally homogeneous policies could affect different provinces at different intensities.
Test For this purpose, we construct the following models.
| (3) |
| (4) |
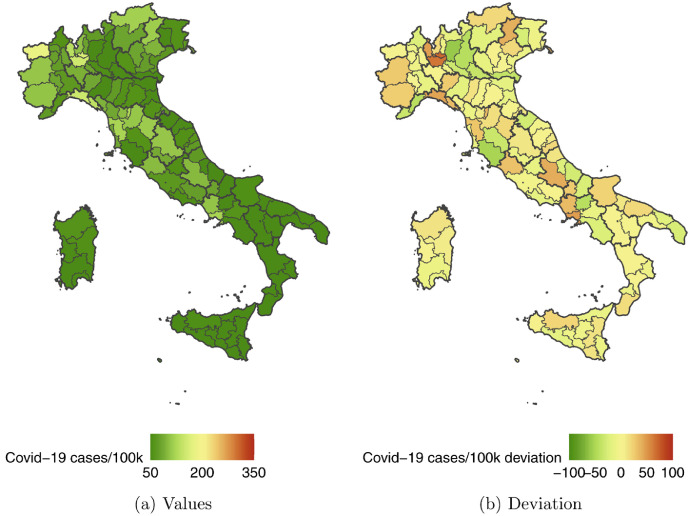
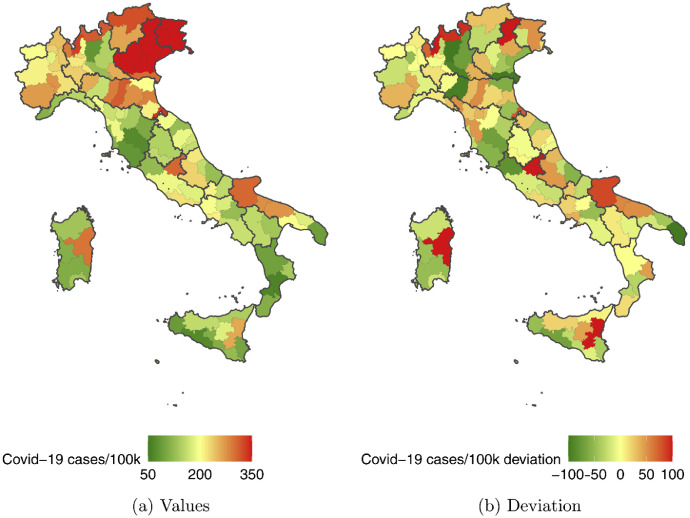
Here, denotes the covid incidence in province in the region after the regional policies were introduced,4 while collects the covariates selected by the shrinkage method explained above. See Fig. 3, Fig. 4 for the map.
Fig. 3.
Weekly Cases per 100k people: Pre-Policy, 1/09/2020 - 3/11/2020
Fig. 4.
Weekly Cases per 100k people: Post-Policy, 25/11/2020 - 23/12/2020
Since Model 3 is nested in Model 4, we can formally test through an F-test whether the within-region variation contained in the explanatory variable is important to explain the distribution of covid-19 cases even after regional policies were introduced. The null hypothesis is: . In both models, we could include a measure of province-level covid incidence pre-policy, denoted , to capture pre-policy trends.
Remark Underlying assumption —
As shown in the result section below, for the relevance of our approach it is not needed to require that the covariates can be directly affected by policies. Those covariates implicitly hint at possible contagion mechanisms. If policies are effective, those mechanisms will be reduced to the point that the province-specific, pre-pandemic distribution of the covariates does not correlate anymore with province-level incidence. Here, there is an important underlying assumption to mention. We assume that a fully effective policy is capable of completely eliminating that correlation. But only a valid counterfactual, in which a feasible fully-effective policy has been implemented, could highlight if that is the case. However, such a control group does not exist. Nevertheless, some of our results below, namely the sensitivity analysis controlling for different policies tiers, suggest that our assumption that policy could affect the link between covariates and covid is reasonable.
2.2.3. Sensitivity Analysis
We conduct a number of robustness checks.
Robust Inference for Models 2 and 4 Since we pre-select the covariates through a LASSO algorithm, traditional inference and critical values of the F-tests may not be valid from a statistical point of view. In Appendix Appendix D we show how our results are robust to an inference procedure that takes into account the covariates’ selection mechanism through LASSO before we perform the OLS. Simulating data under the null hypothesis, we show that our results are at the extremes of an empirical distribution of F-tests and R2-adjusted statistics built from random data.
In Appendix Appendix E we discuss the role of the post-LASSO refinement in the selection of the covariates, and show that this is not essential for our results, but can help to reduce overfitting and the number of selected covariates.
Alternative specifications For further robustness checks where we drop possibly problematic observations and check the role of the covariates over longer time periods, see Table 5 and Table 6, in Appendix C.2 e, ,Ta,
3. Results
Objective 1
Table 1illustrates the results. Column (1) displays estimates for Model (1).5 Column (2) displays estimates for Model (2), in which the covariates are selected with the shrinkage method mentioned above. Three remarks summarize the results. First, we run a formal F-test to determine whether the within-region variation of these pre-determined variables is important in explaining province-level covid-19 incidence. The null hypothesis of the equivalence of Model 2 to Model 1 is rejected at a very low significance level (F-test p-value ). Second, we find that the seven selected province-specific variables explain a considerable share of the overall variance of covid-19 incidence in Italy, as shown by the increase of the from 058 to 077. Hence, the within-region explanatory power of the selected covariates is also quantitatively important. Finally, while we do not claim causality, the selected variables have coefficients with intuitive signs: higher temperatures, a larger share of agricultural employment, and covid-19 incidence during the first wave correlate with lower covid incidence.6 On the other hand, a larger share of families with five components or more, employment in the services sector, the temporal concentration in the use of public transport, and higher income, which we interpret as a proxy of high economic activity, predict an higher covid-19 incidence. In Column (3-4), we repeat the same analysis when considering incidence data up to November 3rd, 2020, the day before regional restriction policies were introduced. The results are all preserved.
Table 1.
OLS estimates
| All Second Wave |
1st Sept. - 3rd Nov. |
|||
|---|---|---|---|---|
| (1) | (2) | (3) | (4) | |
| Regional FE | Baseline | FE | Baseline | |
| Temperature | -13.12*** | -4.945** | ||
| (0.003) | (0.012) | |||
| Income per Capita | 3.468*** | 2.608*** | ||
| (0.000) | (0.000) | |||
| Agriculture Share Population | -0.555 | -0.275 | ||
| (0.107) | (0.185) | |||
| Services Share Population | 0.423** | 0.262** | ||
| (0.021) | (0.014) | |||
| Share families 5+ components | 14.53*** | 6.671*** | ||
| (0.000) | (0.004) | |||
| Cases First Wave | -0.466** | -0.222*** | ||
| (0.011) | (0.003) | |||
| Public Transport Trips Concentration | 16.15*** | 10.41*** | ||
| (0.000) | (0.000) | |||
| Observations | 104 | 104 | 104 | 104 |
| .58 | .768 | .51 | .727 | |
| .491 | .693 | .406 | .639 | |
| Region FE | Yes | Yes | Yes | Yes |
| - | =(1) | - | = (3) | |
| F-Test | - | 9.1 *** | - | 9 *** |
| Critical value (1% sign.) | - | 2.9 | 2.9 | |
Note: Significance levels: * = 010; ** = 005; *** = 001. All specifications use Conley Spatial Standard Errors with a cutoff of 150km. P-values of coefficients in parenthesis. All regressions are controlled for region fixed effects. Therefore, the coefficient on each variable can be interpreted as contributing to increasing (decreasing) Covid-19 cases per capita beyond (below) the regional mean. Specification (1) shows how mean regional differences explain 58% of the variance (49% adjusted for DOF). In specifications 2, we introduce other province-level characteristics and test whether all coefficients are jointly significant to explain more within-region variance in the dependent variable than simple fixed effects (, the test statistic and critical value at 001 significance level reported at the end of the table). Specifications 3 and 4 perform the same exercise but for the pre-regional policy period only (1/09/2020 - 3/11/2020).
Objective 2
Table 2 reports the results. Column (1) and Column (2) presents the estimates for Model 3 and Model 4, respectively, without the regressor . As reported in Column (2), the covariates explain a large share of the residual variation (), similarly to the results provided in Table 1. Hence, we can conclude that local pre-determined characteristics help explain the diffusion of covid-19, both before and after the introduction of regional policies. Column (3) and Column (4) display the estimates for Model 3 and Model 4, respectively, with the regressor . We find that the incidence of cases pre-policies explains a large share of the total variation of incidence post-policy. Intuitively, we should not expect that introducing regional policies alters the course of the epidemic immediately. Nevertheless, Column (4) shows that the same pre-determined variables, in the post-policy period, explain an additional 4.8% of the covid variation on top of their role pre-policy and are still statistically significant (pvalue). In Columns (5)-(8), we repeat the same exercise by defining the post-policy period from 25 November to 23 December 2020. We drop the first 21 days to allow for delays in virus incubation when evaluating the post-policy scenario. We find that our results are robust. Additionally, we find that after the regional policies were introduced, the FE model explains a larger share of the covid-19 incidence variance (73% against 51%).
Table 2.
Effect of Regional Policies
| 4th Nov. - 23rd Dec. |
25th Nov. - 23rd Dec. |
|||||||
|---|---|---|---|---|---|---|---|---|
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | |
| FE post-4nov | Post 4nov | FE post-4nov | Post 4nov | FE post-25nov | Post 25nov | FE post-25nov | Post 25nov | |
| Temperature | -23.48*** | -14.19*** | -20.23*** | -16.33*** | ||||
| (0.003) | (0.003) | (0.003) | (0.001) | |||||
| Income per Capita | 4.518*** | -0.379 | 1.302 | -0.754 | ||||
| (0.003) | (0.850) | (0.423) | (0.660) | |||||
| Agriculture Share Population | -0.907 | -0.390 | -0.523 | -0.306 | ||||
| (0.107) | (0.322) | (0.248) | (0.474) | |||||
| Services Share Population | 0.623** | 0.132 | 0.472* | 0.266 | ||||
| (0.045) | (0.595) | (0.096) | (0.354) | |||||
| Share families 5+ components | 24.46*** | 11.94* | 19.24*** | 13.98** | ||||
| (0.001) | (0.053) | (0.001) | (0.036) | |||||
| Cases First Wave | -0.774** | -0.358 | -0.287 | -0.112 | ||||
| (0.029) | (0.194) | (0.255) | (0.668) | |||||
| Public Transport Trips Concentration | 23.29*** | 3.738 | 8.124 | -0.0847 | ||||
| (0.000) | (0.623) | (0.320) | (0.994) | |||||
| Covid Incidence 1/09/20 - 3/11/20 | 2.176*** | 1.878*** | 1.038*** | 0.788** | ||||
| (0.000) | (0.000) | (0.000) | (0.037) | |||||
| Observations | 104 | 104 | 104 | 104 | 104 | 104 | 104 | 104 |
| .618 | .771 | .828 | .858 | .732 | .804 | .786 | .821 | |
| .537 | .697 | .789 | .810 | .676 | .741 | .737 | .761 | |
| Region FE | Yes | Yes | Yes | Yes | Yes | Yes | Yes | Yes |
| - | = (1) | - | = (3) | - | = (5) | - | = (7) | |
| F-Test | - | 7.5 *** | - | 2.3 *** | - | 4.101 *** | - | 2.2 *** |
| Critical value (1% sign.) | 2.9 | 2.9 | 2.9 | 2.9 | ||||
Note: Significance levels: * = 010; ** = 005; *** = 001. All specifications use Conley Spatial Standard Errors with cutoff 150km. P-values of coefficients in parenthesis. P-values of coefficients in parenthesis. All regressions are controlled for region fixed effects. Due to this, the coefficient on each variable can be interpreted as its contribution in increasing (reducing) Covid-19 cases per capita beyond (below) the regional mean. Column 1 reports the regional fixed effect model for the post-regional policy period. Column 2 shows that adding pre-determined covariates helps explaining the within-province variation in covid-19 incidence (F test statistics are reported at the end of the table). This means that regional policies do not seem to have completely cancelled the effect of these covariates on covid-19 infection risk. Column 3 reports a FE model plus a control for pre-policy covid-19 incidence, that was shown in Table 1 to be highly dependent on the covariates we employ. Column 4 shows that after adding this control, the additional effect of the province-level characteristics is small, but we still reject the F-test of non-joint significance. Columns 5-8 perform the same estimations using data starting 21 days after the introduction of provincial policies (25/11/2020 - 23/12/2020).
3.1. Other results: different restriction tiers
In Table 2 we have shown that after the policy was introduced, the province pre-determined characteristics were still able to explain the observed covid-19 incidence. However, different regions were placed under different tiers of restrictions. Were the higher tier policies able to cancel the explanatory power of the pre-determined characteristics? To answer this question, we modify our model as:
| (5) |
where is the share of days between November 4th and November 25th that region has been in the color tier of type (yellow, orange, or red). The role of the covariates on incidence is then assumed to depend on the restrictions’ intensity potentially. Then, we jointly test for each covariate the following null hypothesis: . If this null hypothesis is rejected, we can conclude that the covariates did not lose all their explanatory power in regions under tier , even after November 25th (three weeks after the policies were introduced).
Table 3 reports the results. Columns (1)-(2) supports the result already obtained in Table 1: considering the degree of intensity of future policies, prevalently yellow or red, does not alter the result that pre-determined characteristics predict local covid-19 incidence in the pre-policy period. Columns (3)-(4) report the results for the post-policy period, regarding the share of days in the yellow and red regime, respectively. While we reject (F-test p-value) the null hypothesis that a whole month in the yellow tier cancels the role of pre-determined characteristics at significance level less than 1%, we can reject the null hypothesis for the red tier only at the level (F-test p-value). Overall, we find no evidence that low-tier regional policies were sufficient to comprehensively tackle the covid-19 infection risk connected to the province’s pre-determined characteristics. However, our results show lower confidence regarding the possibility that the most stringent restrictions were insufficient to reduce to zero the role of local heterogeneity in pre-determined factors, as we find a p-value above .
Table 3.
Effect of Regional Policies by tier
| 1st Sept. - 3rd Nov. |
25th Nov. - 23rd Dec. |
|||
|---|---|---|---|---|
| (1) | (2) | (3) | (4) | |
| Yellow Tier | Red Tier | Yellow Tier | Red Tier | |
| Observations | 104 | 104 | 104 | 104 |
| 0773 | 0755 | 0833 | 0833 | |
| 0676 | 0650 | 0762 | 0761 | |
| Region FE | Yes | Yes | Yes | Yes |
| Model | ||||
| F-Test | 25 ** | 67 *** | 39 *** | 20 * |
| Critical value (1% sign.) | 29 | 29 | 29 | 29 |
Note: Significance levels: * = 010; ** = 005; *** = 001. All models are based on Equation 5.
Importantly, these results point to how the assumption that fully effective policies could reduce to (statistically) zero the correlation between covariates and the covid-19 incidence seems reasonable. In fact, for regions in the strongest restriction tier (but yet far from being as restrictive as the Italian stay-at-home order of the first wave in spring 2020), we cannot anymore reject the null at a 5% confidence level.
4. Discussion
The reported evidence suggests that Italy’s regional policies were not “local enough” to fully tackle local covid-19 risk differences. We support this claim with robust and rigorous statistical analysis. We identify seven province-specific covariates that are relevant to explain the cross-section pre-policy covid-19 infections. They capture 19% of the total variance in the pre-policy period on top of regional-specific effects. We test that their explanatory power and significance also survive when considering the period in which regional policies were in place. We support these findings with several sensitivity checks. Overall, we have found that local factors can explain covid-19 incidence both before and after implementing regional-level (but countrywide-coordinated) policies in Italy, meaning that those policies were not sufficient to eliminate the link between variation in certain pre-determined province-specific factors and the spread of covid-19.
Before discussing the relevance of our findings, let us describe some limitations of our approach. First, while our approach is built to test whether regional policies were fully effective in eliminating province-specific contagion factor, it is not suitable to test whether those policies have been only partially effective and why. Second, our tests rely on the assumptions that the policies, if fully effective, can eliminate the correlation between incidence and province-specific factors. Testing the validity of that assumption requires the existence of a valid counterfactual, in which a feasible, fully effective policy has been implemented; however, such a control group does not exist. Nevertheless, the lower significance level found for the effect of province-specific factors in regions that spent more time in the highest tier of restrictions suggests that our assumption may be reasonable. Finally, different approaches that take into account the time-series properties of covid-19 incidence could be used. However, the limited data available, the complex data generating process behind the spatial and temporal evolution of the pandemic, and the staggered implementation of different tiers of restrictions, make the modelling a complex task. However, under the previously stated assumptions, this does not make our approach any less valid.
Beside the limitations described above, our results are important for policy-makers and have implications for public health. They provide a rationale for implementing more targeted policies that take into account the heterogeneous nature of sources of risk across geographies and their relevance. Nevertheless, our analysis does not conclude that NPIs should necessarily follow administrative borders, such as province or city ones, but it simply suggests that policy interventions should be designed to address - when feasible - local sources of risk. This is particularly relevant because stronger NPIs are likely to be associated with local or neighbouring areas’ economic activity disruption;[27], [28] therefore, policy-makers may be interested in better targeting areas at high contagion risk due to local factors, while, at the same time, in relaxing restrictions in areas with lower infection risk.
As a practical example of how our work could be relevant for policy-makers, consider the case of the Italian national algorithm, which determines the minimum tier of NPIs applied in each region according to a data-driven approach. The variables entering in the algorithm are regional averages of indicators such as , new outbreaks, ICU occupancy rate. This means that sub-regional areas at lower risk - due to local factors - with respect to the regional mean7 cannot be subject to milder restrictions, which could instead benefit the economic outlook or social activities. This degree of flexibility could be quite desirable.
The choice of what is the appropriate administrative unit for NPI policies is particularly challenging, and even more so in a country like Italy where political responsibility and public health policies are shared between national, regional, and municipality authorities. This issue did not make it straightforward to plan, implement and evaluate local-level control policies. For example, see Odone et al. [29] as an example of how local policies have had different epidemiological outcomes during the early phases of the outbreak in Lombardia and Veneto. While NPIs adopted in Italy were mainly at the national level during the first wave (after 8th March 2020), policies were more targeted at the regional level in the second wave during Fall 2020. Only very recently, starting mid-February 2021, Italian policy-makers have adopted a more localized targeting approach. These developments seem to show the policy-makers’ intention to adopt a more localised approach. By showing the relevance of local risk factors that were not addressed by regional policies, our study provides a further justification and possible guidance for implementing highly localised NPIs.
Finally, our results have relevant and general methodological implications for researchers. Our results suggest that local factors are relevant with both mild and harsher policies in place. As a consequence, it is paramount that when attempting to identify the causal effects of policies on infection risk, researchers employ statistical methods that can explicitly control for local characteristics (such as epidemiological models, randomised control trials, or propensity score matching) or that can partial them out (such as interrupted time series or regression discontinuity). If not, the estimated effects of policies on infection risk will be contaminated by the existence of local risk factors.
While our finding regarding the inability of regional policies to target localised risk might have national relevance, extrapolating them to different countries is not straightforward due to differences in the definitions of administrative boundaries and levels, their public health role and the different COVID-19 containment policies adopted. While Italy represents the ideal candidate to study this phenomenon because of its institutional setting, our study does not generalise the findings, nor the methodology, to other countries. Nevertheless, it seems reasonable to expect that local factors can contribute to the spread of covid-19 in a no-policy setting.
Contributions of the Authors
All authors contributed equally.
Funding
The authors received no funding for this study.
Ethics committee approval
No ethical issue requiring the approval of the ethical committee of the authors’ institutions has arisen during the data collection or research phase.
Data Sharing
All source and final data, and the final dataset data dictionary, will be made publicly available online, with publication and no end date, at https://doi.org/10.17632/6d2cxvx5h3.1 and the authors’ personal websites. Data will be available indefinitely at the provided link.
Declaration of Competing Interest
The authors have no conflict of interest of any sort.
Footnotes
In Italy, there are 19 regions and 107 provinces, two of which (Trento and Bolzano) have an autonomous status and, de-facto, can be considered as regions for public-health and administrative purposes.
The number of cases is the only official statistics reported at the province level.
All these additional results are available upon request.
See Appendix B.2 for the map.
We remove Aosta, Trento, and Bolzano as they map one-to-one with their autonomous region.
The negative relationship between first and second wave incidence has already been investigated in Carletti and Pancrazi [24], Perico et al. [25], and Perico et al. [26].
See Bergamo during the second wave, which had an extremely low incidence, both in absolute terms and relative to the regional mean. This could be due to a lower epidemiological risk derived from the high incidence during the first wave (as reported in Perico et al. [25]), a variable which also enters our estimates.[26]
In the bootstrap exercise we resample 1000 times the residual obtained after estimating Model 1 to recreate 1000 dependent variables that have the same systematic component as the one estimated from the data but a different realization of the random component. We then repeat all the steps of our methodology (Lasso selection, and refinement) to each newly obtained dependent variables.
Contributor Information
Gabriele Guaitoli, Email: g.guaitoli@warwick.ac.uk.
Roberto Pancrazi, Email: R.Pancrazi@warwick.ac.uk.
Appendix A. Data Description and sources
In this appendix we describe in more detail the variables and their sources. Table 4 provides summary statistics. The first subset of explanatory variables relates to demographic characteristics. They include population density in each province, average age, the average size of families, the share of students, the share of secondary school acquisition among 19+ years old residents, the share of postgraduate degree acquisition, the share of families with only one component, and the share of families with five or more components. The Italian national statistical agency ISTAT provides these measures either in 2019 or in 2011, the last year of the full Census. We also create a variable that weighs the number of students with the percent of remote-teaching conducted in each province on 15th November 2020 [8]. The second subset of explanatory variables relates to economic characteristics. They include average income per capita (source: Eurostat, 2017), the share of employed workers in the population, share of the agricultural sector, the share of the industrial sector, the share of the service sector, and share of retail and accommodation activities (source: all ISTAT 2019). We also create a variable that weighs the share of retail and accommodation with the percent of businesses that remained open in each province (Ministry of Health) during fall 2020. The third subset of explanatory variables relates to commuting activities. We build two measures based on on the total commuting by public transport with trips longer than 15 minutes for i) work, and ii) study reasons. Using the detail of the hour at which commuters leave home and by what transportation mean, we build a measure of iii) concentration of long (>15 minutes) trips on public transport, weighted by the covid concentration in the province of destination. Finally, we build four measures of exposure through outgoing (OUT) or incoming (IN) commuters to covid. The variables are calculates as
| (6) |
Where is any other province different from , is the covid incidence per capita in province and is the flow from either to if or from to if . In practice, these variables are the average of neighbours’ covid incidence, weighted by the commuting flows. These aim to capture whether commuting is a relevant predictor of local covid incidence as a function of whether local commuters work in provinces with high incidence (OUT) or local workers come from provinces with high incidence (IN). We build four variables of this kind: iv) commuting covid IN, v) commuting covid OUT, vi) commuting covid IN (using public transport flows only), and vii) commuting covid OUT (using public transport flows only). The original commuting data are from ISTAT, 2011 Census; we use the official cases in the whole second wave (1/09/2020-23/12/2020) to construct covid exposure. The fourth subset of variables relates to the health and public health system. They include mortality rate for cancer in the period 2012-2016, the mortality rate for heart attack in the period 2012-2016, increased life expectancy in the period 2002-2017, asthma incidence, measured as pro-capita consumption of medicine for asthma and Chronic Obstructive Pulmonary Disease (COPD), diabetes incidence, measured as pro-capita consumption of medicine for diabetes, hypertension incidence, measured as pro-capita consumption of medicine for hypertension, the average number of general practitioner doctor per capita, average number of hospital beds per capita. These data are retrieved from the Health index survey from il Sole 24 ore. The fifth subset of variables includes a geographical characteristic: the temperature registered in the period 2007-2016. (source: ISTAT). Finally, we include a measure of covid-19 incidence pre-September 2020, which captures the first wave’s strength across provinces. Hence, the dataset of explanatory variables is composed of 35 variable.
Table 4.
Data
| Source | Year | Average | StdDev | Min | Max | |
|---|---|---|---|---|---|---|
| Demographic: | ||||||
| -Density | ISTAT | 2019 | 2669 | 3800 | 36 (Nuoro) | 2574 (Napoli) |
| -Age | ISTAT | 2019 | 4585 | 162 | 4167 (Napoli) | 4920 (Savona) |
| -Age index, percent | ISTAT | 2019 | 195 | 352 | 1215 (Napoli) | 2758 (Biella) |
| -Mortality rate | ISTAT | 2019 | 113 | 141 | 84 (Bolzano) | 147 (Alessandria) |
| -Family size | ISTAT | 2011 | 229 | 014 | 128 (Trieste) | 345 (Napoli) |
| -Students, percent pop | ISTAT | 2019 | 135 | 116 | 112 (Oristano) | 165 (Napoli) |
| -Students in class, percent pop | ISTAT | 2019 | 76 | 32 | 38 (Napoli) | 165 (Ferrara) |
| -Share of secondary degree acquisition, percent 19+ | ISTAT | 2011 | 39.6 | 3.9 | 32.5 (Oristano) | 54.2 (Roma) |
| -Share of postgraduate degree acquisition, percent pop | ISTAT | 2011 | 171 | 047 | 059 (Trapani) | 332 (Roma) |
| -Share Families 1 component | ISTAT | 2011 | 3107 | 419 | 2011 (Barletta) | 4318 (Firenze) |
| -Share Families 5+ components | ISTAT | 2011 | 572 | 195 | 246 (Trieste) | 1247 (Napoli) |
| Economics: | ||||||
| -Income per capita, PPP, 10k euro | EUROSTAT | 2017 | 396 | 393 | 3295 (Oristano) | 5422 (Roma) |
| -Employment, percent pop | ISTAT | 2019 | 389 | 63 | 257 (Crotone) | 477 (Bolzano) |
| -Agriculture Share Population | ISTAT | 2019 | 194 | 147 | 005 (Prato) | 875 (Ragusa) |
| -Industry Share Population | ISTAT | 2019 | 1050 | 450 | 335 (Vibo V) | 1962 (Belluno) |
| -Service Share Population | ISTAT | 2019 | 2650 | 441 | 1728 (Caltanissetta) | 3784 (Roma) |
| -Retail and Accommodation | ISTAT | 2019 | 819 | 149 | 506 (Caserta) | 1317 (Grosseto) |
| -Retail and Accommodation, open | ISTAT | 2019 | 530 | 438 | 0 (Bergamo) | 1317 (Grosseto) |
| Commuting: | ||||||
| -Work with public transport | ISTAT | 2011 | 175 | 146 | 015 (Nuoro) | 869 (Milano) |
| -Study with public transport | ISTAT | 2011 | 347 | 078 | 123 (Sud Sardegna) | 509 (Teramo) |
| -Concentration | ISTAT | 2011 | 097 | 122 | 001 (Nuoro) | 606 (Monza) |
| -Commuting covid IN | ISTAT | 2011 | 024 | 020 | 001 (Palermo) | 101 (Gorizia) |
| -Commuting covid OUT | ISTAT | 2011 | 024 | 019 | 001 (Trapani) | 085 (Vercelli) |
| -Commuting covid IN, public | ISTAT | 2011 | 005 | 006 | 0003 (Trapani) | 034 (Trieste) |
| -Commuting covid OUT, public | ISTAT | 2011 | 005 | 004 | 0004 (Palermo) | 033 (Gorizia) |
| Health: | ||||||
| -Heart attack deaths per 1000 people | ISTAT | 2019 | 220 | 042 | 128 (Sassari) | 345 (Ferrara) |
| -Cancer deaths per 1000 people | ISTAT | 2018 | 150 | 23 | 103 (Sassari) | 2018 (Alessandria) |
| -Increased life expectancy 2002-2017, years | ISTAT | 2019 | 263 | 059 | 120 (Fermo) | 460 (Gorizia) |
| -Asthma and COPD | Il Sole 24 Ore | 2019 | 642 | 109 | 431 (Sud Sardegna) | 965 (Benevento) |
| -Diabetes | ISTAT | 2018 | 4136 | 722 | 2330 (Bolzano) | 6327 (Agrigento) |
| -Hypertension | Il Sole 24 Ore | 2019 | 14501 | 1452 | 9453 (Sud Sardegna) | 18640 (Ferrara) |
| -GPs per 1000 people | ISTAT | 2019 | 093 | 016 | 052 (Nuoro) | 138 (Rovigo) |
| -Hospital beds per per 1000 people | ISTAT | 2017 | 341 | 088 | 155 (Sud Sardegna) | 652 (Isernia) |
| Geograpichs: | ||||||
| -Temperature 2007-2016 | ISTAT | 2016 | 1535 | 176 | 1143 (Belluno) | 1957 (Messina) |
| -First wave Covid incidence | Min. Salute | 2020 | 2446 | 2331 | 180 (Sud Sardegna) | 1154 (Cremona) |
Note: The health data from il Sole 24 ore can be retrevied here: https://lab24.ilsole24ore.com/indice-della-salute/indexT.php
In addition to these, we collect data on the covid-19 incidence between 1/09/2020-3/11/2020, 4/11/2020-23/12/2020, 25/11/2020-23/12/2020, 1/09/2020-26/01/2021, and 26/02/2020-26/01/2020. We do not include these variables in the LASSO selection procedure, as we use them as dependent variables.
Appendix B. Pre- and Post-Policy incidence
B1. Pre-Policy incidence
B2. Post-Policy incidence
Appendix C. Robustness tables
C1. OLS estimates - Red and Yellow Tiers
Table 5.
Yellow and Red Tiers OLS Results
| 1st Sept. - 3rd Nov. |
25th Nov. - 23rd Dec. |
|||||||
|---|---|---|---|---|---|---|---|---|
| (1) | (2) | (3) | (4) | |||||
| Yellow Tier | Red Tier | Yellow Tier | Red Tier | |||||
| Temperature | -2.122 | (0.422) | -5.438** | (0.015) | -5.021 | (0.483) | -24.31*** | (0.000) |
| Income per Capita | 2.675*** | (0.004) | 1.852* | (0.066) | -2.041 | (0.407) | 4.130 | (0.115) |
| Agriculture Share Population | 0.0956 | (0.671) | -0.423** | (0.037) | -0.00667 | (0.991) | -0.737 | (0.161) |
| Services Share Population | 0.433*** | (0.008) | 0.229** | (0.038) | 0.679 | (0.120) | 0.516* | (0.073) |
| Share families 5+ components | 5.983* | (0.083) | 7.699*** | (0.004) | 15.89* | (0.089) | 19.61*** | (0.004) |
| Cases First Wave | -0.406*** | (0.002) | -0.0683 | (0.615) | -0.804** | (0.022) | -0.0195 | (0.956) |
| Public Transport Trips Concentration | 9.804*** | (0.002) | 9.746* | (0.069) | 3.772 | (0.652) | 27.15* | (0.053) |
| Share Yellow Tier Temperature | -2.690 | (0.570) | -36.58*** | (0.006) | ||||
| Share Yellow Tier Income per Capita | -2.058 | (0.300) | 9.936* | (0.067) | ||||
| Share Yellow Tier Agriculture Share Population | -0.903** | (0.027) | -0.334 | (0.758) | ||||
| Share Yellow Tier Services Share Population | -0.326 | (0.185) | -0.172 | (0.795) | ||||
| Share Yellow Tier Share families 5+ components | 1.784 | (0.757) | 8.391 | (0.592) | ||||
| Share Yellow Tier Cases First Wave | 0.521** | (0.033) | 0.862 | (0.189) | ||||
| Share Yellow Tier Public Transport Trips Concentration | -3.307 | (0.702) | 34.29 | (0.147) | ||||
| Share Red Tier Temperature | 9.394 | (0.105) | 33.05** | (0.030) | ||||
| Share Red Tier Income per Capita | 0.0316 | (0.984) | -8.684** | (0.039) | ||||
| Share Red Tier Agriculture Share Population | 0.847* | (0.066) | 2.153* | (0.074) | ||||
| Share Red Tier Services Share Population | 0.150 | (0.608) | 0.153 | (0.841) | ||||
| Share Red Tier Share families 5+ components | -5.801 | (0.438) | -11.24 | (0.565) | ||||
| Share Red Tier Cases First Wave | -0.413** | (0.043) | -1.170** | (0.029) | ||||
| Share Red Tier Public Transport Trips Concentration | 1.063 | (0.871) | -23.69 | (0.168) | ||||
| Observations | 104 | 104 | 104 | 104 | ||||
| .773 | .755 | .833 | .833 | |||||
| .676 | .65 | .762 | .761 | |||||
| Region FE | Yes | Yes | Yes | Yes | ||||
| =(FE model) | See note | =(FE model) | See note | |||||
| F-Test | 2.5 ** | 6.7 *** | 3.9 *** | 2.0 * | ||||
| Critical value (1% sign.) | 2.9 | 2.9 | 2.9 | 2.9 | ||||
Note: Significance levels: * = 0.10; ** = 0.05; *** = 0.01.. In the interaction terms, ”Y” stand for ”Yellow Tier” and ”R” for ”Red Tier”. Number is parenthesis report the p-value of the t-test. All models are based on Equation 5. Specifications (1) and (3) test the model with null hypothesis . Specifications (2) and (4) test the model against the null hypothesis .
C2. Robustness Checks
Table 6.
Robustness checks
| 25th Nov. - 23rd Dec. |
4th Nov. - 26th Jan. | 26th Feb. 2020 - 26th Jan. 2021 | ||
|---|---|---|---|---|
| (1) | (2) | (3) | (4) | |
| No Sardegna | No SAR, CAM, SIC | Extended | All waves | |
| Temperature | -17.88** | -20.11** | -10.34** | -1.261** |
| (0.010) | (0.050) | (0.011) | (0.010) | |
| Income per Capita | 1.129 | 1.017 | 2.077*** | 0.680*** |
| (0.510) | (0.551) | (0.000) | (0.000) | |
| Agriculture Share Population | -0.566 | -0.339 | -0.473* | -0.0638 |
| (0.220) | (0.592) | (0.062) | (0.244) | |
| Services Share Population | 0.506* | 0.550* | 0.372* | 0.0715*** |
| (0.073) | (0.066) | (0.053) | (0.007) | |
| Share families 5+ components | 17.61*** | 22.39*** | 13.71*** | 1.827*** |
| (0.002) | (0.001) | (0.001) | (0.002) | |
| Cases First Wave | -0.273 | -0.288 | -0.402*** | 0.200*** |
| (0.288) | (0.309) | (0.007) | (0.000) | |
| Public Transport Trips Concentration | 9.004 | 7.785 | 11.19*** | 2.719*** |
| (0.302) | (0.349) | (0.001) | (0.000) | |
| Observations | 99 | 85 | 104 | 104 |
| .807 | .815 | .784 | .914 | |
| .744 | .75 | .715 | .886 | |
| Region FE | Yes | Yes | Yes | Yes |
| =(FE model) | =(FE model) | =(FE model) | =(FE model) | |
| F-Test | 3.5 | 3.2 *** | 7.1*** | 18.3 *** |
| Critical value (1% sign.) | 2.9 | 2.9 | 2.9 | 2.9 |
Note: Significance levels: * = 0.10; ** = 0.05; *** = 0.01. All specifications use Conley Spatial Standard Errors with a cutoff of 150km. P-values of coefficients in parenthesis. . All regressions are controlled for region fixed effects. Therefore, the coefficient on each variable can be interpreted as contributing to increasing (decreasing) Covid-19 cases per capita beyond (below) the regional mean. Specification (1) removers Sardegna due to its isolated status. Specification (2) removes also Campania and Sicilia, as they introduced some limited city-wide red tiers before the regional policies. Specification (3) extends the sample to 26th January 2021. Specification (4) considers the whole pandemic period.
Appendix D. Robust Inference and Model Selection
The reader may be worried that the model selection through LASSO may change the inference approach that one should take in assessing the significance of the results. That is: can we really reject the null hypothesis that there are local-level effects in the pre-policy period, since we have selected the regressors in order to maximize R2 adjusted?
The worry here is that under small sample, the pre-selection over a large number of regressors may lead to overfitting and the selection of covariates uncorrelated to the dependent variable in the true data generating process, but correlated in the data due to small sample bias.
In this section, we show that simulating synthetic data allows us to produce an empirical distribution of post-selection OLS F-statistics under the null hypothesis. Using this distribution, we can build confidence intervals and rejection regions that account for the model selection algorithm. In particular, we generate 1000 draws of sets of 38 normally iid distributed regressors (random iid data, henceforth). We subtract regionals means in order to be centered within region. Then, we apply to each of them our model selection procedure and store the F-test p-value of the subsequent OLS regression (we take as reference specification 4, Table 1), assigning a value of one when no variable is selected ( 15% of the cases). Then, we check the 5th percentile of the distribution of p-values so obtained, which represents the critical value representing the OLS F-test p-value such that less than 5% of draws under the null hypothesis of no correlation between covariates and dependent variable sit at lower p-values. Finally, we compare this critical value with the p-value obtained in the real data. We repeat this exercise by drawing 1000 sets of 38 jointly normally distributed regressors, with covariance matrix replicating the one of our true dataset (random correlated data, henceforth). This allows to account for the preference of LASSO of selecting predictors with low correlation, selecting less variables than in the case of uncorrelated sets of regressors.
Our results are confirmed by this empirical, stricter rejection criteria, built to account jointly for the selection and post-selection steps. Table 7 shows how only 0.1% of the simulations in the iid data and 0% of the simulations in the correlated data have an F-test pvalue smaller than the one built using the real data. This is true whether we apply (right column) or do not apply (left column) the refinement process to maximize R2-adjusted after the LASSO. This means that the post-selection OLS p-value of the true data is much smaller than the one of most random data, with 99.9% of all simulations achieving a larger p-value. This means that our results are indeed significant at the 5% level and thus unlikely to be produced by covariates uncorrelated to the dependent variable.
Table 7.
Random Generated Samples and Statistical significance, with and without refinement. Share of simulations
| p-value(Fstat) p-value(Fstat Data) | ||
|---|---|---|
| Without refinement | With refinement | |
| Random iid data | 0.1% | 0.1% |
| Random correlated data | 0.0% | 0.0% |
Note: this table displays the share of simulations (out of 1000), in percent, for which the p-value of the F-statistics (null hypothesis: , in model 2) is less than the one found in the data. The first row displays the results when the regressors are assumed to be iid. The second row displays the results when the regressors are assumed to have the same covariance matrix as the regressors in the data. The first column presents the results without the refinement, while the second column presents the results with the refinement.
In Table 8 we show similar results for the R2 adjusted: it is highly unlikely for randomly generated covariates to generate an amount of R2-adjusted similar to the one of the true data.
Table 8.
Random Generated Samples and Explanatory power, with and without refinement: Additional Adjusted
| Without Refinement | With Refinement | ||||||
| All Samples | Significant Samples | All Samples | Significant Samples | ||||
| Random iid data | |||||||
| Average | 0.09 | 0.20 | 0.10 | 0.22 | |||
| 95% conf Interval | [ 0.0 - 0.21] | [0.16-0.25] | [0.0-0.22] | [0.18-0.26] | |||
| Frequency: | 0.3 % | 6.0% | 0.9% | 14% | |||
| Random correlated data | |||||||
| Average | 0.07 | 0.18 | 0.08 | 0.21 | |||
| 95% conf Interval | [ 0.0 - 0.18] | [0.13-0.22] | [0.0-0.21] | [0.17-0.26] | |||
| Frequency: | 0.0% | 0.0% | 0.5% | 6.0% | |||
Note: this table displays the additional Adjusted of model 2 with respect to model 1 in the 1000 simulations. This statistic captures the additional explanatory power of the selected regressors in addition to the regional fixed effects. The top-panel displays the results when the regressors are assumed to be iid. The second panel displays the results when the regressors are assumed to have the same covariance matrix as the regressors in the data. The left panel presents the results without the refinement, while the right panel presents the results with the refinement. The first column presents the statistics for all the simulations (1000), while the second column presents the statistics for the 5% simulations with the lowest p-value of the F-statistics. The first line displays the average additional Adjusted , across the simulations. The second line displays its 95 percent confidence interval. The third line displays the share of simulations, in percent, for which the Adjusted with the synthetic data is larger than the one found in the data (equal to 0.2449 without the refinement and equal to 0.2524 with the refinement).
Appendix E. Post-LASSO Refinement Procedure
In this section, we discuss the role of the refinement to the LASSO selection discussed in the main text. The refinement works as follows: take all covariates selected by the LASSO procedure. Then, start iterating over the variables with the lowest p-value, perform an OLS regression and: (1) keep the variable if R2-adjusted does not increase, or (2) discard the variables if R2-adjusted increases. Under option (2), repeat the procedure until you find that R2-adjusted does not increase any further.
We have discussed in Appendix Appendix D how this has little impact on the inference procedure and on the explained adjusted of the selected model. In Table 9 we present further evidence of how the variable selection in random data and in a bootstrap exercise is affected by this refinement.8 The refinement reduces the number of selected variables by 1.3 out of an average of 9.7 (when we use 38 random, uncorrelated regressors to simulate our procedure under the null hypothesis), and shrinks by 6 the upper bound of the 95% confidence interval of the distribution. When we simulate the procedure using correlated regressors with the same covariance matrix as the true data, the refinement shrinks the number of selected variables by 2 out of 8.2, and shrinks the upper bound of the confidence interval by 7 out of 29. Finally, when we bootstrap the error terms of the dependent variable, we find that the refinement shrinks the average selected covariates (from the true data) by 5.1 variables.
Table 9.
Regressor Selection: with and without refinement
| Without Refinement | With Refinement | ||
|---|---|---|---|
| Random iid data | |||
| Frequency 0 variables selected | 13.9% | 13.9% | |
| Average Selected | 9.7 | 8.4 | |
| 95% conf Interval | [ 0 - 27] | [0-21] | |
| Random correlated data | |||
| Frequency 0 variables selected | 15.2% | 15.2% | |
| Average Selected | 8.2 | 6.2 | |
| 95% conf Interval | [ 0 - 29] | [0-22] | |
| Bootstrap | |||
| Frequency 0 variables selected | 0.0% | 0.0% | |
| Average Selected | 21.4 | 16.3 | |
| 95% conf Interval | [ 11 - 33] | [9-25] | |
Note: this table displays the share of simulations in which the selection procedure select zero regressors in percent, (first line); the average number of regressors selected (second line), and its 95% confidence interval (third line) obtained by using the Lasso procedure without (first column) and with (second column) our proposed refinement. The top and central panels display the results for the randomly generated data (iid and correlated, respectively). The bottom panel displays the results for the bootstrapping exercise.
Supplementary material
Supplementary material associated with this article can be found, in the online version, at 10.1016/j.lanepe.2021.100169
Appendix F. Supplementary materials
Supplementary Raw Research Data. This is open data under the CC BY license http://creativecommons.org/licenses/by/4.0/
Supplementary Raw Research Data. This is open data under the CC BY license http://creativecommons.org/licenses/by/4.0/
Supplementary Raw Research Data. This is open data under the CC BY license http://creativecommons.org/licenses/by/4.0/
References
- 1.Davies N.G., Barnard R.C., Jarvis C.I., Russell T.W., Semple M.G., Jit M. Association of tiered restrictions and a second lockdown with covid-19 deaths and hospital admissions in england: a modelling study. The Lancet Infectious Diseases. 2020 doi: 10.1016/S1473-3099(20)30984-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Li Y., Campbell H., Kulkarni D., Harpur A., Nundy M., Wang X. The temporal association of introducing and lifting non-pharmaceutical interventions with the time-varying reproduction number (r) of sars-cov-2: a modelling study across 131 countries. The Lancet Infectious Diseases. 2021;21(2):193–202. doi: 10.1016/S1473-3099(20)30785-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Davies N.G., Kucharski A.J., Eggo R.M., Gimma A., Edmunds W.J., Jombart T. Effects of non-pharmaceutical interventions on covid-19 cases, deaths, and demand for hospital services in the uk: a modelling study. The Lancet Public Health. 2020;5(7):e375–e385. doi: 10.1016/S2468-2667(20)30133-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Brauner J.M., Mindermann S., Sharma M., Johnston D., Salvatier J., Gavenčiak T. Inferring the effectiveness of government interventions against covid-19. Science. 2020 doi: 10.1126/science.abd9338. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Haug N., Geyrhofer L., Londei A., Dervic E., Desvars-Larrive A., Loreto V. Ranking the effectiveness of worldwide covid-19 government interventions. Nature human behaviour. 2020;4(12):1303–1312. doi: 10.1038/s41562-020-01009-0. [DOI] [PubMed] [Google Scholar]
- 6.Protezione Civile. Dati covid-19 italia. 2021. Data retrieved from GitHub, https://github.com/pcm-dpc/COVID-19.
- 7.Consiglio dei Ministri Decreto del presidente del consiglio dei ministri 3 novembre 2020. Gazzetta Ufficiale. 2020;(275) [Google Scholar]
- 8.Ministero della Salute Ordinanza del ministero della salute del 13 novembre 2020. Gazzetta Ufficiale. 2020;(284) [Google Scholar]
- 9.Ministero della Salute Ordinanza del ministero della salute del 24 novembre 2020. Gazzetta Ufficiale. 2020;(292) [Google Scholar]
- 10.Ministero della Salute Ordinanza del ministero della salute del 5 dicembre 2020. Gazzetta Ufficiale. 2020;(303) [Google Scholar]
- 11.Li F., Li Y.-Y., Liu M.-J., Fang L.-Q., Dean N.E., Wong G.W. Household transmission of sars-cov-2 and risk factors for susceptibility and infectivity in wuhan: a retrospective observational study. The Lancet Infectious Diseases. 2021 doi: 10.1016/S1473-3099(20)30981-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Borjas G.J. Tech. Rep. National Bureau of Economic Research; 2020. Demographic determinants of testing incidence and covid-19 infections in new york city neighborhoods. [Google Scholar]
- 13.Khalatbari-Soltani S., Cumming R.C., Delpierre C., Kelly-Irving M. Importance of collecting data on socioeconomic determinants from the early stage of the covid-19 outbreak onwards. J Epidemiol Community Health. 2020;74(8):620–623. doi: 10.1136/jech-2020-214297. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Sá F.. Socioeconomic determinants of covid-19 infections and mortality: evidence from england and wales 2020.
- 15.Awang H., Yaacob E.L., Syed Aluawi S.N., Mahmood M.F., Hamzah F.H., Wahab A. A case–control study of determinants for covid-19 infection based on contact tracing in dungun district, terengganu state of malaysia. Infectious Diseases. 2020:1–4. doi: 10.1080/23744235.2020.1857829. [DOI] [PubMed] [Google Scholar]
- 16.Hamidi S., Hamidi I. Subway ridership, crowding, or population density: Determinants of covid-19 infection rates in new york city. American Journal of Preventive Medicine. 2021 doi: 10.1016/j.amepre.2020.11.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Badr H.S., Du H., Marshall M., Dong E., Squire M.M., Gardner L.M. Association between mobility patterns and covid-19 transmission in the usa: a mathematical modelling study. The Lancet Infectious Diseases. 2020;20(11):1247–1254. doi: 10.1016/S1473-3099(20)30553-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Chang S., Pierson E., Koh P.W., Gerardin J., Redbird B., Grusky D. Mobility network models of covid-19 explain inequities and inform reopening. Nature. 2020:1–6. doi: 10.1038/s41586-020-2923-3. [DOI] [PubMed] [Google Scholar]
- 19.Seto C., Khademi A., Graif C., Honavar V.G. Commuting network spillovers and covid-19 deaths across us counties. arXiv preprint arXiv:201001101. 2020 [Google Scholar]
- 20.Vinceti M., Filippini T., Rothman K.J., Ferrari F., Goffi A., Maffeis G. Lockdown timing and efficacy in controlling covid-19 using mobile phone tracking. EClinicalMedicine. 2020;25:100457. doi: 10.1016/j.eclinm.2020.100457. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Guarnieri M., Balmes J.R. Outdoor air pollution and asthma. The Lancet. 2014;383(9928):1581–1592. doi: 10.1016/S0140-6736(14)60617-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Fattorini D., Regoli F. Role of the chronic air pollution levels in the covid-19 outbreak risk in italy. Environmental Pollution. 2020;264:114732. doi: 10.1016/j.envpol.2020.114732. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Travaglio M., Yu Y., Popovic R., Selley L., Leal N.S., Martins L.M. Links between air pollution and covid-19 in england. Environmental Pollution. 2020;268:115859. doi: 10.1016/j.envpol.2020.115859. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Carletti M., Pancrazi R. Geographic negative correlation of estimated incidence between first and second waves of coronavirus disease 2019 (covid-19) in italy. Mathematics. 2021;9(2):133. [Google Scholar]
- 25.Perico L., Tomasoni S., Peracchi T., Perna A., Pezzotta A., Remuzzi G. Covid-19 and lombardy: Testing the impact of the first wave of the pandemic. EBioMedicine. 2020;61:103069. doi: 10.1016/j.ebiom.2020.103069. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Perico N., Fagiuoli S., Di Marco F., Laghi A., Cosentini R., Rizzi M. Bergamo and covid-19: How the dark can turn to light. Frontiers in Medicine. 2021;8:141. doi: 10.3389/fmed.2021.609440. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Bognanni M., Hanley D., Kolliner D., Mitman K. Tech. Rep. IZA Discussion Papers; 2020. Economics and epidemics: Evidence from an estimated spatial econ-sir model. [Google Scholar]
- 28.Guaitoli G., Tochev T. Tech. Rep. Covid Economics n.69; 2021. Do localised lockdowns cause labour market externalities? [Google Scholar]
- 29.Odone A., Delmonte D., Scognamiglio T., Signorelli C. Covid-19 deaths in lombardy, italy: data in context. The Lancet Public Health. 2020;5(6):e310. doi: 10.1016/S2468-2667(20)30099-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary Raw Research Data. This is open data under the CC BY license http://creativecommons.org/licenses/by/4.0/
Supplementary Raw Research Data. This is open data under the CC BY license http://creativecommons.org/licenses/by/4.0/
Supplementary Raw Research Data. This is open data under the CC BY license http://creativecommons.org/licenses/by/4.0/