Neural-ODE for pharmacokinetics modeling and its advantage to alternative machine learning models in predicting new dosing regimens

Summary

Forecasting pharmacokinetics (PK) for individual patients is a fundamental problem in clinical pharmacology. One key challenge is that PK models constructed using data from one dosing regimen must predict PK data for different dosing regimen(s). We propose a deep learning approach based on neural ordinary differential equations (neural-ODE) and tested its generalizability against a variety of alternative models. Specifically, we used the PK data from two different treatment regimens of trastuzumab emtansine. The models performed similarly when the training and the test sets come from the same dosing regimen. However, for predicting a new treatment regimen, the neural-ODE model showed substantially better performance. To date, neural-ODE is the most accurate PK model in predicting untested treatment regimens. This study represents the first time neural-ODE has been applied to PK modeling and the results suggest it is a widely applicable algorithm with the potential to impact future studies.

Graphical abstract

Highlights

• •We describe the first application of neural-ODE to pharmacokinetics modeling
• •The model is accurate and predicts well across dosing regimens
• •The model generalizes well compared to alternate machine and deep learning models

Pharmacological parameters; Bioinformatics; Pharmacoinformatics; Machine learning

Introduction

Determining the optimal dosing regimen for individual patients requires the construction of pharmacokinetics (PK) forecasting models that can extrapolate PK data for treatment regimens differing from those used for model training sets (Sheiner et al., 1979) https://paperpile.com/c/QQNeAs/SoRKv. The population approach to modeling clinical PK data is now well-established after decades of methodological and application development, and it is the current standard for PK modeling in clinical settings (Ette and Williams, 2004). For this methodology, PK data from all patients within a population are described simultaneously using a nonlinear mixed effects (NLME) model (Bonate, 2011; Mold and Upton, 2013; Owen and Fiedler-Kelly, 2014). The resulting population-PK (pop-PK) models have found a wide set of applications within drug development (Aarons, 1991), ranging from determining the right dosage and dosing schedule (Darwich et al., 2017) to therapeutic drug monitoring (McEneny-King et al., 2016). Despite the maturity of the pop-PK modeling, several opportunities exist to further increase the impact of PK forecasting models on drug development and individualized treatment. The construction of a final pop-PK model following an exhaustive covariate search can be time consuming and labor intensive, which limits its “real-time” impact on the increasingly fast paced drug development space. In addition, the ability to individualize patient dosage and the timing thereof in a treatment context (McEneny-King et al., 2020) depends on the capability of models to accurately forecast PK profiles based on sparsely observed, early PK data. As PK models are increasingly critical for supporting dose and regimen decisions, such models should ideally have the ability to predict PK profiles for different untested doses and regimens.

Recent advancements in machine learning (ML) and deesp learning (DL) for healthcare applications (Ngiam and Khor, 2019) have led to a significant interest in applying these approaches to drug development and regulation (Liu et al., 2020). For example, support vector machines and artificial neural networks (ANNs) have been used to predict remifentanil concentrations in healthy populations (Poynton et al., 2009). Additionally, Tang et al. (Tang et al., 2017) has compared the performance for predicting the PK using multiple learning regression, ANN, regression tree, multivariate adaptive regression splines, boosted regression trees, SVM, random forest, Lasso and Bayesian additive regression trees. Furthermore, Liu et al. has used a long short-term memory (LSTM) network to analyze the simulated PK/PD data of a hypothetical drug (Liu et al., 2021).

Emergent neural network-based approaches may enable development of new methodologies for real-time, accurate prediction of PK profiles through direct generation of ordinary differential equation (ODE) models from irregularly observed time series data (Chen et al., 2018; Rubanova et al., 2019; Sun et al., 2020; Kelly et al., 2020). The development of such methodologies may overcome the hurdles associated with the application of PK modeling to support drug development, including increasing the throughput and accuracy of predictions.

In this work, we present the first use of neural-ODE for the automated construction of PK models directly from clinical data. We also compared the proposed approach with alternative ML/DL methodologies and traditional NLME modeling. We applied three ML/DL approaches for clinical PK prediction: a novel variant of neural-ODE, LSTM neural network (Bianchi et al., 2017), and lightGBM (Ke et al., 2017). LSTM is a base learner that was designed specifically for time course prediction tasks (Hochreiter and Schmidhuber, 1997). LightGBM is a popular tree-based algorithm. Like most other traditional base learners, it takes in features whose orders and relationships are considered unimportant; but the number of features for every example must be of the same dimension.

It is an open question whether ML approaches can generalize PK predictions beyond training data despite a general appreciation that the form of equations that underlie existing PK models and the associated model parameters of biological relevance (such as the volume of distribution, clearance rates, and so on) (Ette and Williams, 2004; Bonate, 2011; Mold and Upton, 2013; Owen and Fiedler-Kelly, 2014) enable a reasonable extrapolation (within limits) to untested dosages and dosing regimens. Therefore, we focus on the comparison of ML/DL approaches in their ability to learn from PK data generated from one dosing regimen, to predict an unseen regimen.

This study utilized clinical PK data from trastuzumab emtansine (T-DM1), a conjugated monoclonal antibody drug that has been approved for the treatment of patients with human epidermal growth factor receptor 2 (HER2) positive breast cancers (Boyraz et al., 2013). The PK of various analytes (the T-DM1 conjugate, total trastuzumab, and the payload DM1) following infusions with T-DM1 are well-characterized and described by a linear pop-PK model (Lu et al., 2014). T-DM1 has a narrow therapeutic window, and the appropriate dose and schedule were identified after exposure-response analysis, as well as thrombocytopenia modeling (Chen et al., 2017; Bender 2016; Bender et al., 2020). Two dosing regimens have been tested clinically: once every 3-week (Q3W, various doses, with the majority at the approved dosage of 3.6 mg/kg), as well as once weekly (Q1W, various doses) (Lu et al., 2014). We first tested the models' performance independent of treatment schedule by randomly selecting data based on patient ID. We then trained and evaluated each model across the two regimens: that is, using data from patients on a Q3W dosing regimen only and compared their ability to predict analyte PK concentrations in patients who were treated on a Q1W dosing regimen, and vice versa. The results reveal key advantages for neural-ODE over the other models when it comes to predicting PK for untested dosing regimens.

Results

Data used to predict PK with first cycle observations

The models we developed for this study use first cycle PK observation (of T-DM1 conjugate) to predict subsequent PK concentration values. In a classical population-PK problem, patients are treated with a drug, and the changes of the concentration of the drug inside the body are affected by a variety of factors, such as age, gender, weight, and biomarkers. These factors can in turn inform PK response predictions. Because the drug is administered repeatedly, the first cycle data can also inform predictions of patient response in subsequent cycles.

We discarded patient data with only one cycle of dosing evaluation (39 individuals, all on Q3W dosing schedules). The following features are included in the models (Figure 1): TFDS, the time in hours between each dose; TIME, the time in hours since the start of the treatment; AMT, the dosing amount in milligrams; CYCL, the current dosing cycle number. Additionally, the first cycle of the observation, PK_cycle1 is also available as predictive features for the models. Using the information above, we sought to predict the PK dynamics after the first cycle, i.e., after 168 hr for the Q1W data and after 504 hr for the Q3W data.

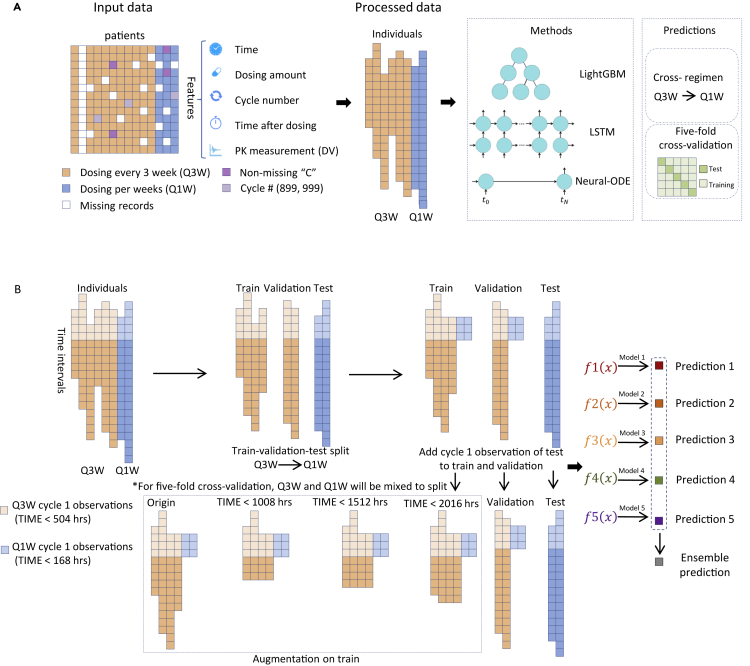
Figure 1.

Data preprocessing

(A) T-DM1 trials consist of patients treated every three weeks (Q3W) and patients treated every week (Q1W). Input data includes time since initial treatment starting point, dosing amount, treatment cycle number, time since the last dosing, and first cycle PK measurements. Patient data that have been marked with non-missing values in the “C” columns have been removed from the analysis. The training target is the PK measurements in later cycles. Three methods were tested in this work: lightGBM, LSTM and neural-ODE. Models were evaluated either in a cross-regimen approach, or using five-fold cross-validation.

(B) In cross-regimen validation of LSTM and neural-ODE, data from individuals treated by Q3W are split into the training set and validation set, in which the latter is used to call back the best epoch of the former. Data from individuals treated Q1W is used as the test set to evaluate the performance. In five-fold cross-validation, Q1W and Q3W are mixed to produce the train, validation and test set. Augmentation was applied to the training set by truncating the observation time at different lengths. We repeated the split of train-validation set five times using different random seeds, and trained five models. The final prediction is the average of the five models.

We used data from a total of 675 patients, which contained a total of 16,472 records of T-DM1 dosing and PK measurements (observations below the minimum quantifiable concentration have been omitted from the analysis (Lu et al., 2014)). The data included two distinct dosing schedules: dosing every week (Q1W, 28 individuals, 2,086 records in total) and dosing every three weeks (Q3W, 647 individuals, 14,385 records in total). The two subsets differ in their dosing schedules, and the Q1W data has a greater number of measurement points per patient, a greater number of dosing cycles, smaller doses, and measurements were collected over a longer time period (See Table 1 and Figure S1 for an overview of the data.). These differences allowed us to examine how well the models extrapolate data when trained on one type of schedule and tested on a different type of schedule. The number of measurement points per patient ranges from 2 to 270, with an average of 24.40 (median = 20). For Q1W, the number of measurement points per patient ranges from 8 to 270, with an average of 74.5 (median = 51.5). For Q3W, the number of measurement points per patient ranges from 2 to 99 with an average of 22.23 (median = 20). The number of dosing cycles ranges from 1 to 39, with an average of 9.1 (median = 8). For Q1W, the number of dosing cycles ranges from 1 to 32, with an average of 9.89 (median = 7). For Q3W, the number of dosing cycles ranges from 1 to 39, with an average of 9.06 (median = 8). Doses range from 19.0 mg to 510.0 mg, with an average of 237.1 mg (median = 234.0 mg, Figure S1). For Q1W, the dose ranges from 81.6 mg to 212.0 mg, with an average of 139.3 mg (median = 144.2 mg); the dose for Q3W ranges from 19.0 mg to 510.0 mg, with an average of 248.4 mg (median = 241.2 mg). Patient data was collected over a time period ranging from 1.75 to 19,487.00 hr, with an average, per patient measurement period of 4,301.81 hr (median = 3528.42). Patients with only the first cycle of data were discarded. The treatment duration for Q1W patients ranged from 239.25 to 17,043.02 with an average total treatment duration of 5,122.62 hr (median = 3195.15), while the treatment duration for Q3W patients ranged from 1.75 to 19,487.00 hr with an average total treatment duration of 4,266.28 hr (median = 3528.50).

Table 1.

Demographic summary of the data.

	Total	Whole population	Q1W	Q3W
		675	28	647
Race	American Indian or Alaska Native	6	NA	6
	Asian	73	NA	73
	Black	49	NA	49
	Hispanic	22	3	19
	Native Hawaiian or Pacific Islander	2	NA	2
	White	523	25	498
Region	Asia	58	NA	58
	Europe	147	NA	147
	Other	66	NA	66
	United States	404	28	376
Sex	Female	671	28	643
	Male	4	NA	4
Age	Max	84	75	84
	Mean	52.90	52.86	52.90
	Median	53	53	53
	Min	27	28	27
Height	Max	188	177.80	188
	Mean	161.98	163.22	161.93
	Median	162.60	163.50	162.60
	Min	128.28	146	128.28
Weight	Max	137.40	135	137.40
	Mean	70.51	73.91	70.37
	Median	68	69.55	67.95
	Min	37.72	47.20	37.72

LightGBM, LSTM, neural-ODE, and NLME model construction

We designed a variety of machine learning models and their corresponding feature engineering methods that were potentially capable of predicting prospective PK dynamics and patient PK response. We selected lightGBM (Ke et al., 2017) (Figure 2A), LSTM (Figure 2B), and neural-ODE. Below, we will describe the feature engineering and model construction methods that we used to build PK problems into the above base learners.

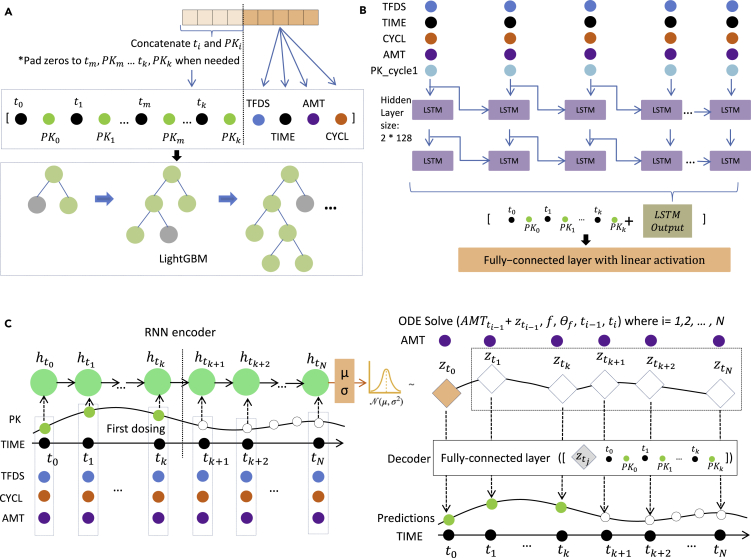
Figure 2.

Feature preprocessing in (A) lightGBM, (B) LSTM, and (C) neural-ODE models

(A) To generate a specific training example, or a test data point, we incorporate first cycle time and PK information as well as the current data point TFDS, ATM, TIME, CYCL information as feature data.

(B) In the LSTM model, TFDS, TIME, CYCL, AMT and PK cycle 1 observation padded with zero are input as five channels in the model.

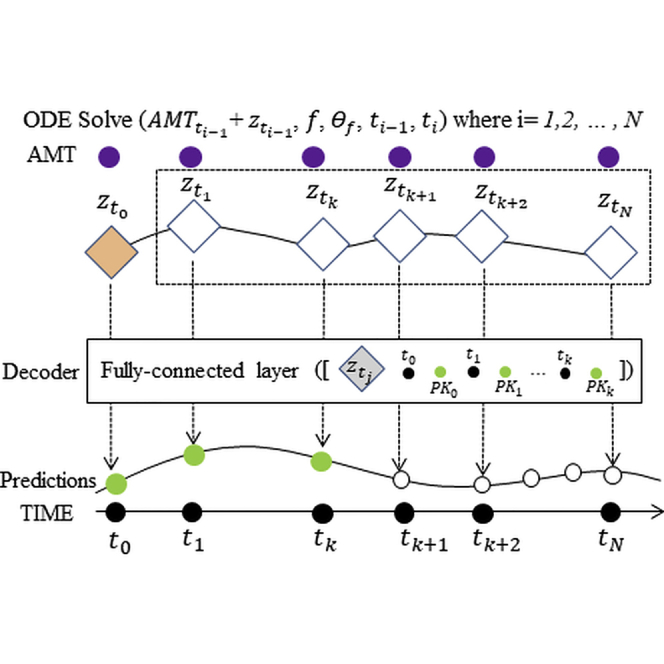
(C) Neural-ODE shares similarly with LSTM in the encoder part that TFDS, TIME, CYCL, AMT and PK cycle 1 observation are used as the input in the encoder part. Then ODE solvers are used to incorporate dosing information into the time sequence before the decoder generates the predictions.

The base features we used for the lightGBM models are TFDS, TIME, AMT, and CYCL at the current time point. Additionally, we flattened the time and the PK observations of the first dosing. Thus, for Q1W, any observations of TIME <168 are included; and for Q3W, any observations of TIME <504 are included. We iterated TIME and PK values from the first time point to the last time point during the first cycle, and padded the vector to 20 elements long with zeros: TIME_t1, PK_t1, TIME_t2, PK_t2, TIME_t3, PK_t3, …,. Next, for the current time point that we wish to predict, we have an additional set of TFDS, TIME, AMT, and CYCL values. Concatenating the 20-element-long vector and these four values resulted in 24 features as the input of lightGBM.

The input features for the LSTM model included TFDS, TIME, CYCL, AMT, and PK_cycle1, a feature copied from the PK observations, and the values with TIME ≥ 504 or 168 were replaced to 0. Time points where AMT was not present (i.e. non-dosing times) were filled with 0. The data were then fed into a 2-layer LSTM architecture with 128 hidden units on each layer. Outputs of the LSTM layers were concatenated with the 20-long flattened first dosing features consisting of the PK observations and TIME as described in the lightGBM version. They were then fed into a fully connected layer with a linear activation to generate the predictions. We masked out the time points without PK observation (i.e., dosing times without PK records) in model training.

We used the same data preprocessing for neural-ODE and LSTM models. The general structure of the neural-ODE model consists of a recurrent neural network (RNN) encoder (GRU unit), an ODE solver, and a decoder. The encoder encodes an initial status for the ODE solver; the ODE solver solves the system over time intervals between doses; and the decoder generates the predictions from the output of the ODE solver and the first dosing observations. In the encoding step, a GRU layer with 128 hidden units scans through the whole time series (5 channel input, TFDS, TIME, CYCL, AMT, and PK_cycle1, as in LSTM model) reversely (i.e., from the end to the start) following the neural-ODE official sample codes (Chen, 2018). It encodes the information to a length-12 array. These numbers can be changed without affecting the results.

Following the concept of the variational autoencoder, the 12-element array in the ODE solver output defines the mean and standard deviation of the latent state distributions, where we sample the latent variables $z_{t_0}$ of the same size as the initial status for the ODE solver. Specifically, 6 elements of the 12-element arrays are used to estimate the mean values and the other 6 were used to estimate the variance. $z_{t_0}$(of dimension 6) is drawn from the Gaussian distribution derived from this mean and standard deviation. Starting from $z_{t_0}$, the ODE solver functions integrate the dosing information and the time interval. Specifically, for each time point t_i under consideration, we first add the dosing amount to the $z_{t_{i-1}}$, if there is a dosing event at t_i-1. Then, both $z_{t_{i-1}}$ and the time interval from the previous time point t_i-t_i-1 are fed into the ODE solver function, which is a four layer fully connected network, each layer with 16 hidden dimensions. The output of the ODE function is the $z_{t_i}$, which is then circulated back to the next time point. From the above steps, we generate a series of $z_t$, which are fed into a decoder, containing one fully connected layer of 32 hidden units, and outputs a series of predictions, corresponding to the each $z_t$’s.

As described above, the models of LSTM and neural-ODE share similar structure in terms of the five channels, TFDS, TIME, CYCL, AMT and PK_cycle1, as well as input of the first dosing PK observations and time in either the decoder part or the last layer of LSTM network. Neural-ODE also contains an RNN layer as the encoder. The main difference between the neural-ODE and LSTM models is the ODE solver in the former that addresses uneven time sampling of the data. Neural-ODE also explicitly incorporates dosing data into the model, unlike other machine learning algorithms presented in this study. As we discuss below these properties contribute to the robust performance of neural-ODE when tested across treatment regimens.

Neural-ODE, lightGBM, and NLME perform similarly when the training data and testing data come from the same treatment regimens, but neural-ODE outperforms other algorithms when generalizing to new dosing regimens

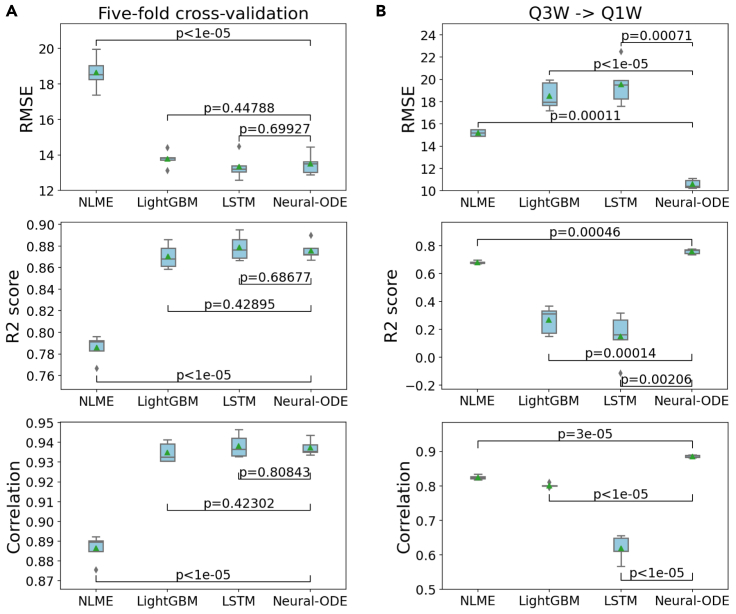
We first examined algorithms' performance at traditional PK prediction by randomly partitioning the data into training set and testing set regardless of their treatment schedule. We partitioned the data by patient IDs and carried out five-fold cross-validation to evaluate the algorithm performance. Overall, we found very similar results using different machine learning algorithms (Figure 3A). For neural-ODE, we obtained an average root mean squared error (RMSE) of 13.50, an R2 score of 0.88, and a Pearson's correlation of 0.94. For lightGBM, we obtained an RMSE of 13.78, an R2 score of 0.87, and a Pearson's correlation of 0.93. For LSTM, we obtained an RMSE of 13.34, an R2 score of 0.88, and a Pearson's correlation of 0.94. For NLME, we obtained an RMSE of 18.64, an R2 score of 0.79, and a Pearson's correlation of 0.89. None of the differences are statistically different (n = 10,000) except for the RMSE, R2 score and Pearson's correlation of the NLME model based on the bootstrap hypothesis test (Table S2).

Figure 3.

Performance comparison of NLME, lightGBM, LSTM and neural-ODE models

(A) Performance in five-fold cross-validation.

(B) Performance using Q3W as the training data and Q1W as the test data. The box plots with center lines indicate the 25th, 50th and 75th percentiles of 5-fold cross-validation results, with the mean values shown as green triangles and the minimum and maximum values indicated by the whiskers. The outliers in the box plots are shown as diamonds. The p-values shown correspond to comparisons between performance metrics obtained using the various algorithms.

We then compared the performance by separating the data into training and testing according to treatment schemes in order to study the models' ability to generalize to new treatment regimens. As discussed above, the T-DM1 data set contains two treatment schedules: Q1W (28 individuals) and Q3W (647 individuals). We used Q3W as the training set and the Q1W as the test set. In this cross-regimen validation scheme, we observed that neural-ODE demonstrated substantial advantage in making meaningful predictions. For neural-ODE, we obtained an average root mean squared error (RMSE) of 10.61, an R2 score of 0.76, and a Pearson's correlation of 0.89. For lightGBM, we obtained an RMSE of 18.50, an R2 score of 0.27, and a Pearson's correlation of 0.80. For LSTM, we obtained an RMSE of 19.56, an R2 score of 0.15, and a Pearson's correlation of 0.62. For NLME, we obtained an RMSE of 15.21, an R2 score of 0.68, and a Pearson's correlation of 0.83. Thus, across all evaluations, neural-ODE performed the top (Figure 3B). Applying the bootstrap hypothesis test, the p values comparing other algorithms and Neural-ODE are all statistically significant (p < 0.05, n = 10,000) (Table S2).

Neural-ODE generates continuous PK profiles and produces correct patterns in artificially simulated experiments

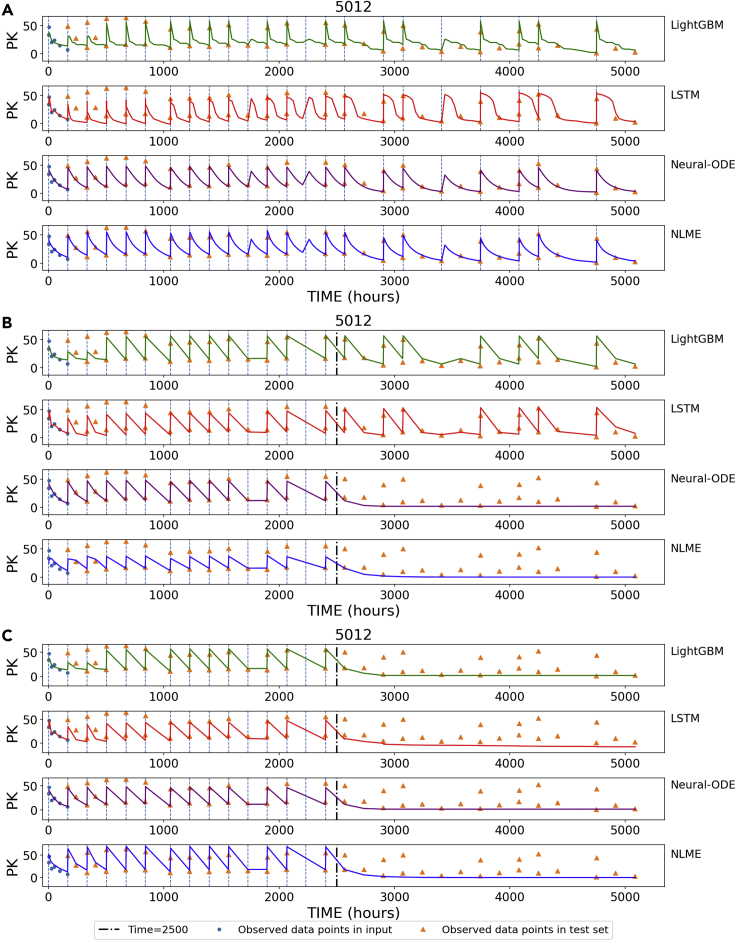
We applied the models to the test set and visualized the predictions. Compared to lightGBM and LSTM, with neural-ODE we observed smoother prediction values after each dosing (Figures 4 and S2–S4), likely because the time variable for neural-ODE is input as a continuous value directly to the decoder. This is an important characteristic that is expected for real-world PK observations.

Figure 4.

Visualization of time course predictions

The vertical lines denote dosing events.

(A) Visualization of interpolated prediction points for patient #5012.

(B) We artificially stopped dosing after 2500 hr for patient #5012 and used the trained models to predict PK values.

(C) We artificially stopped both dosing and TIME after 2500 hr for patient #5012 and used the trained models to predict PK values.

We also simulated a hypothetical situation, where dosing was stopped in the middle of the treatment course. In this case, we expect PK to fall to zero after dosing stops. However, both LSTM and lightGBM models continue to make positive value predictions of PK, which likely results from the model remembering the pattern of training patients (Figure 4B). Conversely, neural-ODE is able to detect and reflect the stop of the treatment and correctly predicts zero after dosing stops. This desirable behavior of neural-ODE likely comes from the direct incorporation of dosing into the model. When stopping dosing and TIME all together, LSTM and lightGBM show the expected behavior (Figure 4C), suggesting that both models are learning from TIME rather than explicit dosing information.

Discussion

Modeling population-PK data is a primary goal of clinical pharmacology. PK modeling enables the selection of a dosage and dosing regimen that balances efficacy with safety and the extrapolation of PK data to different patient populations. However, predicting analyte concentration changes in an untested dosing regimen using models trained on a separate dosing regimen remains the major challenge of PK modeling. We developed and compared three types of machine learning models that had potential for addressing this challenge. We found that the neural-ODE model demonstrated excellent generalizability to new treatment schemes and performed substantially better (evaluated using predictive performance metrics) than both alternative machine learning models, as well as NLME — a commonly used methodology in the pharmacometrics field.

In the clinical pharmacology field, drug dosing and PK measurements in patients are rarely performed at regular intervals, making it essential to consider the sampling variability in this problem. The advantage of the neural-ODE model may come from its ability to deal with unevenly sampled data points. The alternative deep learning models such as LSTM tend to assume even sampling. Neural-ODE directly incorporates dosing and timing data into the model at the decoder stage, which also likely contributes to the stable performance when adopting a model trained on one treatment regimen to a different treatment regimen.

The current work only considers PK predictions related to dosage and dosing regimen. However, neural-ODE has the potential for impact in several underdeveloped methodological areas and applications. For example, the development of ML/DL models for applications such as cross-species prediction and in vitro-in vivo extrapolation (IVIVE), as well as the evaluation of the relative merits of various model formulations is an important area that remains to be further explored. ML could be applied to physiologically based pharmacokinetic (PBPK) modeling (Jones and Rowland-Yeo, 2013; Reddy et al., 2005; Zhao et al., 2011), which is currently used to project the clinical dose for First-In-Human studies. In contrast to “classical” PK models, PBPK models are parametrized using known physiology and enable IVIVE. Amongst the many uses of PBPK models is cross-species prediction, whereby data generated from preclinical species is used to predict human PK using a learn-confirm-refine paradigm (Jones and Rowland-Yeo, 2013). Clinical PK extrapolation to different patient populations also remains unaddressed. This includes PK extrapolations from adults to children using allometric scaling or PBPK modeling (Maharaj and Edginton, 2014; Mahmood, 2014; Yellepeddi et al., 2019; Wu and Peters, 2019), or from healthy volunteers to patients with organ impairment (Heimbach et al., 2020). Another limitation is that deep learning suffers from overfitting when the sample size is small. In initial phases of clinical trials, we may only have around 100 individuals. Methods that leverage the pre-training of neural-ODE on historical drugs can potentially overcome this barrier. Given the ever-increasing accumulation of PK data across molecule types and in patient populations, we expect there to be ample future opportunities for applying ML/DL techniques in a wide range of clinical research settings.

Limitations of the study

This work is based on the PK data collected from patients treated with a conjugated monoclonal antibody drug. The effectiveness of the proposed methodology to predict PK data for small molecule drugs remains to be further evaluated.

STAR★Methods

Key resources table

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Software and algorithms
Torchdiffeq	Chen et al., 2018	https://github.com/rtqichen/torchdiffeq
Lightgbm	Ke et al., 2017	https://github.com/microsoft/LightGBM
Nlmixr	Fidler et al., 2019	https://nlmixrdevelopment.github.io/nlmixr/
Neural-ODE for PK modeling	This paper	https://zenodo.org/badge/latestdoi/377988539

Resource availability

Lead contact

Further information should be directed to James Lu (email: lu.james@gene.com)

Materials availability

This study did not generate new unique reagents.

Data and code availability

The clinical data used in this study is not made available due to reasons of patient privacy, but is available upon reasonable request from the authors with the approval of Genentech. All original code is available in this paper's supplemental information. It has also been deposited at Github and is publicly available as of the date of publication. DOIs are listed in the key resources table. Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.

Methods details

Data summary

The PK data includes 9934 serum concentration values of T-DM1 conjugate from 671 patients with HER2+ breast cancer from the TDM3569g, TDM4258g, TDM4370g, TDM4374g and TDM4450g clinical trials (Table 1). In all studies, T-DM1 was administered via intravenous injection. TDM3569g was a Phase 1, dose-escalation study in patients with HER2-positive MBC that had progressed on prior trastuzumab therapy, where patients were treated with either 0.3-4.8 mg/kg Q3W (once every 3 weeks) or with 1.2-2.9 mg/kg Q1W (once every week) of T-DM1. In all the other studies, patients were treated with 3.6 mg/kg Q3W of T-DM1, either as a monotherapy or in combination with other therapeutic agents. The full details of the study design is described in the Supplementary Material 1 of (Lu et al., 2014). Note that the majority of the patients were treated with the Q3W dosing regimen, with the exception of 28 of the patients in TDM3569g who were treated with Q1W. See (Lu et al., 2014) for further details regarding the patient population, PK sampling, and bioanalysis as well as results of pop-PK modeling of the data.

LightGBM model training parameters

The lightGBM model is trained as a regression problem, with boosting_type = gbdt, learning_rate = 0.005, num_leaves = 30, num_trees = 1000. We used early stopping with a 50 rounds cutoff of non-improvement and RMSE as the metric to call back best models. These parameters were selected through grid search and minor changes of the parameters do not substantially alter performance.

LSTM model training parameters

The LSTM architecture starts with two LSTM layers. The first one with an input length of 5 and output length of 128. The second one with an input length of 128 and output length of 128. Both activation functions are Tanh. The 128-length vector is connected to the 20-length vector which is the first cycle TIME and PK. Then the 148-length vector is fed into the decoder with two fully connected layers. The first fully connected layer has an output length of 128 with ReLU activation, and the second fully connected layer has an output length of 1 with linear activation, generating the prediction values.

In training the LSTM model, we used a batch size = 1 due to different length of the input time course data, initial learning rate = 0.00005 with Adam optimizer (Dash et al., 2019) and L2 regularization = 0.1, RMSE loss. We used normal distribution N(0, 0.1) for weight initialization. The Bias initialization value is 0. We trained for a total of 30 epochs. These parameters were selected through grid search. We implemented the model with Pytorch.

Neural-ODE model training parameters

The encoder part of the Neural-ODE structure has an input length of 5 and an output length of 128, with activation function Tanh. Then it is connected to two fully connected layers. The first fully connected layer has an input length of 128, and an output length of 128, and an activation function of ReLU. The second fully connected layer has an input length of 128 and output length of 12, with linear activation. The ODE function part of the Neural-ODE structure has four fully connected layers, with an input length of 6 (sampled from the 12). Each of the middle fully connected layers has an output length of 128. The last fully connected layer has an output length of 6. This 6-length vector is concatenated to the TIME and PK values in the first cycle (a 20-length vector). The decoder part of the Neural-ODE has two fully connected layers with an input length of 26. The first fully connected layer has an output length of 32. The second fully connected layer has an output length of 1, which is the prediction value.

In training the Neural-ODE model, we used a batch size = 1 due to different length of the input time course data, initial learning rate = 0.00005 with Adam optimizer and L2 regularization = 0.1, RMSE loss, ODE solver tolerance = 0.0001. We trained for a total of 30 epochs. We used normal distribution N(0, 0.001) for weight initialization. The Bias initialization value is 0. The ODE function bias initialization value is 0.5. These parameters were selected through grid search. We implemented the model with Pytorch and torchdiffeq (Chen et al., 2018).

Augmentation

Deep learning is prone to overfitting, and we applied augmentation to prevent overfitting. We applied timewise truncation to increase the number of training examples. For each training example, in addition to the original example, we also truncated the examples at 1008 hr, 1512 hr, and 2016 hr and generated and added a set of new examples to the training examples.

Nonlinear mixed effects modeling (NLME)

We applied NLME modeling (Fidler et al., 2019). We implemented a two-compartment model with first-order absorption and first-order elimination (Strauss and Bourne, 1995), and initialized the parameters (Lu et al., 2014). This system can be described by the following first-order differential equations:

$$\frac{d{X}_0}{dt}=-k_a\ast X_0$$

$$\frac{d{X}_1}{dt}=k_a\ast X_0-\left(\frac{CL+Q}{V_2}\right)\ast X_1+\frac{Q}{V_3}\ast X_2$$

$$\frac{d{X}_2}{dt}=\frac{Q}{V_2}\ast X_1-\frac{Q}{V_3}\ast X_2$$

where the X₀, X₁, and X₂ are the drug amounts in the dosed compartment, the central compartment and the peripheral compartment. The initial values of X₁ and X₂ are both 0. The parameters include: k_a the absorption rate constant; CL the elimination clearance rate; the Q is the distribution clearance rate; and the V₂, V₃ represent the central volume and peripheral volumes of distribution, respectively.

The initial values and the bounds for the parameters are listed in Table S1. The final values and the bounds for the parameters of all NLME models are listed in Tables S3–S12. Visual predictive checks for the cross-regimen NLME models are presented in Figures S5–S9. The five models in cross-regimen analysis are generated with different random seeds during the EM inference.

Evaluation metrics

We used R2 score, and Pearson correlation in this study. Correlation gives an intuitive estimation of the concordance between the predictions and ground truth, while R2 also takes into account whether the overall scale of the predictions is correct.

The initial values and the bounds for the parameters are listed in Table S1. The final values and the bounds for the parameters of all NLME models are listed in Tables S3–S12. Visual predictive checks for the cross-regimen NLME models are presented in Figures S5–S9. The five models in cross-regimen analysis are generated with different random seeds during the EM inference.

Quantification and statistical analysis

To test the significance of the performance between two models, we used the bootstrap hypothesis test with the following steps:

• 1.Select two models M1 and M2, and evaluate the performances ${\mathit{x}}_{\mathit{M}1},{\mathit{x}}_{\mathit{M}2}$for each fold based on the predictions from these two models. The length of this example we denote it as N.
• 2.Calculate the absolute difference between the averages of ${\mathit{x}}_{\mathit{M}1},{\mathit{x}}_{\mathit{M}2}$: $t=\left|\overline{{\mathit{x}}_{\mathit{M}1}}-\overline{{\mathit{x}}_{\mathit{M}2}}\right|$
• 3.Draw B samples of size 2N with replacement from the concatenation of ${\mathit{x}}_{\mathit{M}1},{\mathit{x}}_{\mathit{M}2}$. Regard the first N values as the performances of M1 ($x_{M1}^b$), and the remaining as the performances of M2 ($x_{M2}^b$) in each sample.
• 4.Calculate the absolute difference between the averages of $x_{M1}^b,x_{M2}^b$: $t^b=\left|\overline{x_{M1}^b}-\overline{x_{M2}^b}\right|$
• 5.The p value comes from the numbers of $t^b\ge t$ in the B samples: $p-value=\#\{t^b\ge t\}/B$

Published: July 23, 2021