Observing the subglacial hydrology network and its dynamics with a dense seismic array

Significance

Our understanding of when, where, and under which conditions subglacial water flow favors or impedes glacier flow remains uncertain mainly because of sparse field observations. This strongly limits our capability to assess the susceptibility of glaciers and ice sheets to a future increase in meltwater input due to climate warming. Here, we overcome classic observational difficulties by establishing an innovative seismic-based approach. From dense seismic array observations, we retrieve with unprecedented detail the two-dimensional map of a subglacial hydrology network. We observe its day-to-day evolution from a cavity-like system that favors glacier flow to a channel-like system that impedes glacier flow. Our method is easily adaptable and readily applicable to other settings than alpine glaciers such as Greenland or Antarctica.

Abstract

Subglacial water flow strongly modulates glacier basal motion, which itself strongly influences the contributions of glaciers and ice sheets to sea level rise. However, our understanding of when and where subglacial water flow enhances or impedes glacier flow is limited due to the paucity of direct observations of subglacial drainage characteristics. Here, we demonstrate that dense seismic array observations combined with an innovative systematic seismic source location technique allows the retrieval of a two-dimensional map of a subglacial drainage system, as well as its day-to-day temporal evolution. We observe with unprecedented detail when and where subglacial water flows through a cavity-like system that enhances glacier flow versus when and where water mainly flows through a channel-like system that impedes glacier flow. Most importantly, we are able to identify regions of high hydraulic connectivity within and across the cavity and channel systems, which have been identified as having a major impact on the long-term glacier response to climate warming. Applying a similar seismic monitoring strategy in other glacier settings, including for ice sheets, may help to diagnose the susceptibility of their dynamics to increased meltwater input due to climate warming.

Meltwater produced at the surface of a glacier is mostly routed to its bed through crevasses and moulins and flows toward its terminus through the subglacial drainage system (1). In this system, water pressure regulates the ice–bed mechanical coupling, which determines the glacier sliding speed, and therefore has major effects on the stability of glaciers and ice sheets (2, 3) and their contributions to sea level rise (4–6). Subglacial water pressure shows complex dependency on the subglacial route that the water follows and in particular on whether the water flows through a distributed and inefficient system (7) (e.g., cavity-dominated for hard bed glaciers) or a localized and efficient system (8) (channel-dominated). A cavity-dominated drainage system is expected to be associated with high water pressure, which, by reducing ice–bed mechanical coupling, promotes high glacier sliding speeds (7, 9). On the contrary, the development of a channel-dominated drainage system is expected to be associated with a, comparatively, lower water pressure, which promotes lower glacier sliding speeds (8, 10–12). Where cavities are hydraulically well connected to channels they drain into the efficient drainage system, which tends to lower the overall basal water pressure (13). In addition, recent observations (13) suggested that hydraulically isolated areas of the bed with very low permeability (14) regulate glacier basal traction during winter (15) and over multiannual timescales (16). The spatial persistence of high water pressure at the glacier bed (17) thus depends on the subglacial drainage system configuration and the hydraulic connectivity across the cavities and from the cavities to the channels. However, current observations of subglacial drainage systems are rather point scale (17, 18) (e.g., via ice drilling) or spatially integrated (19, 20) (e.g., via dye-tracing experiments or hydrochemical analysis), such that they provide only partial representations of the heterogeneous nature of the subglacial drainage system(s). It thus remains uncertain where and when isolated cavities, connected cavities, and/or channels operate and therefore under what conditions (e.g., water supply rate, glacier geometry) meltwater supply to the glacial bed enhances or limits glacier flow.

Recent studies have indicated that turbulent subglacial water flow generates detectable seismic noise (21) given flow velocities of the order of a meter per second (22) that can be used to retrieve the physical properties of subglacial channels (e.g., water pressure, conduit size) (22, 23) as well as to estimate their location in space (24, 25). Previous studies that have attempted to spatially track water flow have documented their azimuthal distribution but not their epicentral coordinates (24–26). Location of epicentral coordinates of simultaneously active and spatially spread noise sources indeed represents a major seismological challenge (27), since it requires observations of the wave-field all around the targeted sources with high enough resolution to deal with its strong incoherency (28, 29). Here, we demonstrate that well-resolved maps of subglacial drainage systems can be retrieved using particularly dense seismic arrays and by adapting the matched-field processing (MFP) technique (28) to the particularity of dealing with spatially spread sources.

Seismic Monitoring and Source Location Strategy

We use the 1-mo seismic record from 98 three-component sensors that was acquired at the surface of glacier d’Argentière (French Alps; Fig. 1) during the onset of the 2018 melt season (refer to Materials and Methods and ref. 30 for detailed description of the experiment and ref. 23 for a broader glaciological context). At this location, subglacial water flow strongly influences glacier dynamics (31) and generates continuous seismic noise that is most pronounced in the (3- to 7-) Hz frequency range (23), in which seismic wavelengths are on the order of (200- to 500-) m (32). Our seismic array covers an area of 400 × 600 m² with a 40- to 50-m sensor spacing and an aperture (i.e., largest distance between stations; Fig. 1) of ca. 720 m. Such configuration allows subwavelength sampling while covering all azimuthal directions around the targeted sources, which are two necessary conditions for retrieving epicentral coordinates through application of MFP (28, 29) (Materials and Methods). MFP consists of recursively matching the predicted and observed phase delays (Materials and Methods) and has been extensively applied to locate spatially well-separated sources, such as those generated by hydrothermal activity (33), oil and gas injection (34), icequakes (32), or englacial moulins (32). However, it has been little applied to locate spatially distributed noise sources (34, 35). We adapt this technique to provide such particularity through a systematic analysis of the phase coherence over 1-s-long time windows. Within each window, we apply an efficient gradient-based minimization algorithm that allows us to locate up to 29 simultaneously active sources (Materials and Methods). We obtain each source location from maximizing the correlation between the observed and the modeled phase delays. We refer to this maximum correlation as the MFP output, which ranges from 0 to 1. An MFP output close to 1 indicates global phase coherence, as expected for a dominant and punctual source (36), while a low MFP output indicates several local phase coherences, as expected for multiple sources simultaneously acting over the area. We note that we only keep the sources that are located within 400 m of the center of our array and are associated with realistic physical properties (i.e., wave velocities, source depth; Fig. 2 B and C). This yields more than a million seismic sources per day (Fig. 2A).

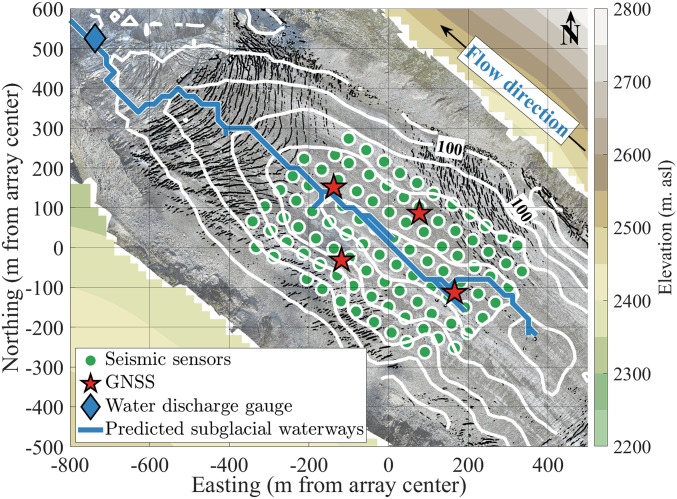
Fig. 1.

Monitoring set-up of Glacier d’Argentière. Aerial view of the Glacier d’Argentière field site (France, Mont Blanc mountain range) and location of the instruments used in this study. The seismic network (green dots) is composed of 98 seismic stations with Fairfield Nodal Z-Land 3 components, which are indicated according to their positions at the beginning of the survey period. Surface displacement was measured through four global navigation satellite system (GNSS) stations that functioned during the study period (red stars). Subglacial water discharge (blue star) was measured through direct access to the glacier base from excavated tunnels. White contour lines show 50-m–spaced ice thickness contours, as obtained from combined radar measurements and surface elevations. The blue line shows the subglacial waterways as predicted from hydraulic potential calculations (Materials and Methods). The glacier flows toward the northwest (Top Left). Aerial view provided by Bruno Jourdain.

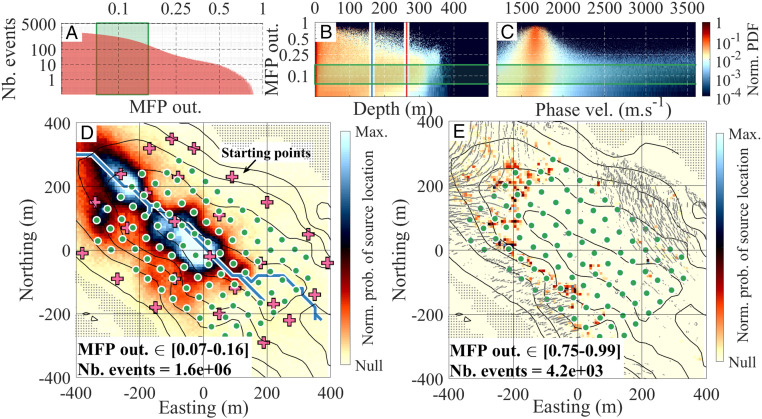
Fig. 2.

Statistics and two-dimensional representation of the MFP output for the 5 ± 2 Hz frequency range. (A) Distribution of the average number of events located per day after applying the selection as a function of the MFP output. Green shaded area shows the [0.07 to 0.16] MFP output range for which the spatial distribution of the sources was investigated. (B) Normalized probability distribution of the MFP output as a function of source depth relative to the surface. The vertical red line shows the maximum ice thickness; the blue line shows the median ice thickness. The green shaded areas show the [0.07 to 0.16] MFP output range. (C) Normalized probability distribution of the MFP output as a function of the phase velocity. Note that the color scales are logarithmic, and the distribution is normalized per MFP output band of 0.01. The green shaded areas show the [0.07 to 0.16] MFP output range. (D and E) Two-dimensional representation of the normalized probability of the source location obtained with 8 × 8 m² pixels grid for the study area for the two MFP output ranges [0.07 to 0.16] (D) and [0.75 to 0.99] (E). Contour lines show 50-m–spaced ice thickness contours, as shown in Fig. 1. The gray shading shows ice-free areas. The green dots show the seismic array. The blue line in D shows the subglacial waterways as predicted from the hydraulic potential calculation, as shown in Fig. 1. The black dots in E show crevasse locations, as shown in Fig. 1. The pink crosses in D show the locations of the 29 starting points used in the location algorithm.

Retrieving the Geometry of the Subglacial System

In Fig. 2 D and E, we show the normalized spatial distribution probability of the source location obtained over the study period for high and low MFP output ranges, as indicated in Fig. 2A. We observe that events associated with high (i.e., global) phase coherence (MFP output, >0.8) are mainly located at the glacier surface (Fig. 2B) where crevasses are observed (Fig. 2E), and are associated with phase velocities that are typical of surface waves (37) (ca. 1,580 m · s⁻¹; Fig. 2C). This is consistent with these events corresponding to crevasse-induced icequakes (Fig. 1). On the contrary, sources associated with low (i.e., local) phase coherence (MFP output, [0.05 to 0.3]) are preferentially located at depth near the ice–bed interface (Fig. 2B). The associated phase velocities (Fig. 2C) vary by up to ca. 3,600 m · s⁻¹, which is consistent with body waves being generated additionally to surface waves and thus with sources that occur at depth (38). The spatial distribution of these sources show two elongated regions located along the glacier centerline (one at maximum ice thickness and one 50 m further down-glacier) where hydraulic potential calculations allow materializing the likely location of subglacial channel(s) (Fig. 2D; Materials and Methods). All of these concomitant features lead us to interpret these observed seismic sources as a depiction of the geometry of the subglacial drainage system. The characteristic width of the observed spots (ca. 50 m, Fig. 2D) is much greater than might be expected for a single subglacial channel [on the order of meter to few meters (8)], which could result from the location resolution being limited by the seismic wavelength investigated (expected to be 1/6 to 1/2 times the ca. 300-m wavelength; Materials and Methods) or from the presence of multiple channels. The absence of clear source locations in the up-glacier part of the array (Fig. 3) might be caused by reduced or less turbulent subglacial water flow there, compared to the down-glacier part, where over-deepening of the glacier bed might favor unstable and more turbulent water flow (39).

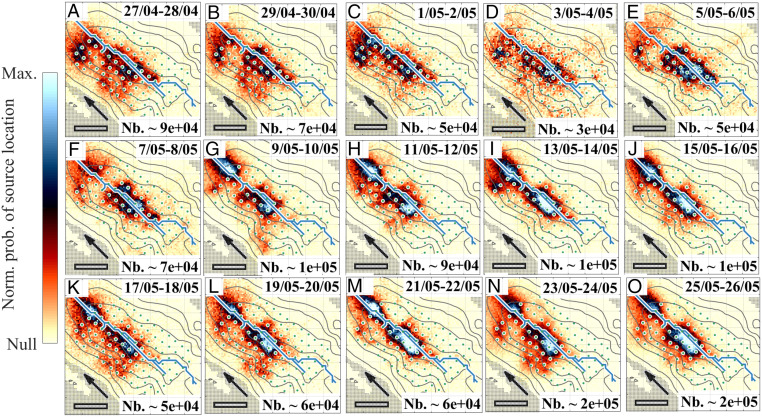
Fig. 3.

(A–O) Two-dimensional maps of subglacial water flow source location obtained from MFP. Temporal evolution of the spatial patterns of the source location densities obtained for the 5 ± 2 Hz frequency range and the [0.07 to 0.16] MFP output range. All of the maps are averaged over 2-d time windows, with the associated number of the sources located shown in the bottom right corner (Nb.). The color scale ranges are normalized for each time window using maximum probability. Contour lines show the 50-m–spaced ice thickness contours, as shown in Fig. 1. The gray shading shows ice-free areas. (Scale bars [Bottom Left], 200 m.) The blue lines show the subglacial waterways, as predicted from the hydraulic potential calculation and as shown in Fig. 1. The black arrows show glacier and subglacial water flow directions. Panel (O) is the characteristic pattern used in Fig. 4 for calculation of the coefficient of determination.

Observing the Switch from a Cavity-like to a Channel-like Drainage System

We further investigate whether with our observational technique we can retrieve the different components of a subglacial drainage system by evaluating temporal changes in the source location maps together with the subglacial flow parameters that characterize average water drainage efficiency and water pressure conditions at the glacier bed (22, 23) (Materials and Methods). We calculate source location maps averaged over 2-d time windows (Fig. 3) and use the combined seismic signal amplitude and water discharge measurements to invert for spatially integrated changes in the hydraulic pressure gradient and hydraulic radius of the subglacial drainage system (Fig. 4) (22, 23). All maps are obtained from sources yielding a similar phase coherence (i.e., associated with MFP output within the same narrow [0.07 to 0.16] range) such that they are retrieved with a similar accuracy (Materials and Methods).

Fig. 4.

Temporal evolution of the subglacial hydraulic properties, seismic observations, and glacier flow. (A) The Left axis shows the relative hydraulic properties, as averaged over the 98 sensors. Hydraulic pressure gradient with ±1 median absolute deviation (MAD), as the shaded envelope (green), and hydraulic radius with ±1 MAD, as the shaded envelope (purple). Both values are expressed as relative to April 26. The Right axis shows temporal evolution of the spatialized seismic observations using the determination coefficient R² of the source location pattern shown in Fig. 3O (red). The closer this coefficient is to 1, the more the drainage system is observed to be channelized. (B) Subglacial water discharge (blue line) with shaded blue area under the curve added for ease of reading. Median surface velocity over the four on-ice GNSS stations (red line) with the minimum/maximum shaded envelope.

We observe that sources are spatially more distributed at the beginning of the period (until ca. May 10; Fig. 3) than when averaging source locations over the whole period (Fig. 2D). At this time, the hydraulic pressure gradient (Fig. 4A, green line) varies significantly with the discharge (from 0.1 m³ · s⁻¹ to 2 m³ · s⁻¹; Fig. 4B, blue line) and the hydraulic radius remains constant (Fig. 4A, purple line), which indicates low drainage efficiency (23). This time period is also associated with marked glacier surface acceleration (velocity increases by up to ca. 50%) due to enhanced basal sliding (31) as a result of the subglacial water pressurization (7). These concomitant observations provide strong support that with our source location analysis, we can observe water flow in a cavity-like system, which promotes high basal water pressure. This has not been suggested in previous cryoseismic studies (21–23, 25) on the premise that fast and turbulent water flow speeds [as meters per second⁻¹; i.e., seismically detectable (22)] only occur in channels. However, this is consistent with borehole field observations (17, 40) and with theoretical studies that have envisioned channel-like flow in connections between cavities (referred to as orifices) (9).

While progressing through time (from ca. May 10), the subglacial water flow localizes into a narrower zone (Fig. 3). This transition toward a channel-like system is well revealed by the significant increase in the two-dimensional coefficient of determination R² (Fig. 4A) calculated between the spatial pattern observed for May 25 to 26 (Fig. 3O) and each of the patterns shown in Fig. 3. Concomitantly and in contrast to the first part of the period, we observe a doubling of the hydraulic radius with a reduced and almost unvarying hydraulic pressure gradient, which indicates that the increasing drainage efficiency lowers the basal water pressure. Such an increase in drainage efficiency is consistent with the increase in water discharge not resulting in glacier acceleration but rather in slight deceleration (41). Our seismic analysis therefore provides independent observational support for the hypothesis that the development of an efficient and channel-like system reduces the basal water pressure and favors slower glacier flow.

Implications for the Monitoring of Hydraulic Connectivity within and across Subglacial Drainage Systems

The presence of seismically detectable turbulent water flow within the cavity-like drainage system suggests that this system is, at least in certain places, associated with high hydraulic connectivity. The absence of seismic sources over many areas of the glacier bed indicates that these, comparatively, have lower hydraulic connectivity and could correspond to hydraulically isolated portions of the bed with higher potential for water storage (13, 14). This shows not only that our seismic analysis can determine when and where the transition from a cavity-dominated to a channel-dominated system occurs but also that it can identify locations with high hydraulic connectivity within the cavities and from the cavities to the channels. This implies that we can discriminate, in space and through time, areas of the glacier bed that are efficiently connected to channels and thus drained when they develop, versus areas where water is stored and is thought to regulate the basal traction over multiyear timescales (14, 16). Yielding such observations in other settings like Greenland has the potential for identifying locations where ice dynamics are expected to be particularly sensitive to the foreseen increase in melt water input rates due to climate warming (3).

Perspectives and Limitations

A successful application of our methodology to other glacier systems like Ice-Sheet outlet glaciers relies on the capability to conduct subwavelength sampling over representative areas (Materials and Methods), ranging from about 1 × 1 km² [e.g., Russel Glacier’s tongue (42)] up to about 10 × 10 km² [e.g., central trunk of Pine Island Glacier (43)]. These scaling constraints can be fulfilled through deploying ca. 100 up to ca. 10,000 sensors in these areas, which we foresee as achievable in the near future given the recent ease of dense seismic array installations in remote areas (44, 45). The increasing use of distributed acoustic sensing using fiber optics deployment (46, 47) could also facilitate such large-scale seismic investigations at a limited cost.

Although the present seismic approach yields unprecedented insights on subglacial hydrology dynamics from the local (Fig. 3) and up to the glacier (Fig. 4) scales, a quantitative interpretation of physical properties at local (e.g., meters) scale will likely still strongly benefit from combination with complementary in situ observations. Such a combination will guide the strategy for conducting local (e.g., via ice-drilling) or spatially integrated (e.g., via dye-tracing experiments or hydrochemical analysis) measurements in targeted and representative places identified from the seismic observations. Such complementary measurements in those targeted places will also help enhance the level of quantitative interpretation of seismic observations through giving more quantitative constraints on the behavior of key physical variables (pressure, flow speed, and connectivity) in each identified subglacial hydrology system. This integrated strategy will allow to better extrapolate physical constraints from the local up to the glacier-wide scale, which will ultimately facilitate the assimilation of seismic observations in subglacial hydrology–ice dynamics–coupled models, which otherwise remain poorly constrained across scales (48).

Conclusion

In this study, we provide well-resolved spatial observations of a localized efficient channel-like system geometry and of the extent of a distributed inefficient cavity-like system. We show that with an adapted systematic seismic investigation of low-spatial phase coherences, we can locate multiple seismic noise sources induced by subglacial water flow that act at the same time. This location procedure is feasible from very low water discharge (∼0.1 m³ · s⁻¹) to peak melt season water discharge. Thus, we can simultaneously observe cavity- and channel-dominated systems through time and space and evaluate the hydraulic connectivity within and across these systems along with their changes through time. Our geophysical approach is also exportable to other glaciers in remote areas, from mountain glaciers to ice caps, especially with the current easing of dense seismic arrays (44) and distributed acoustic sensing (46, 47) deployments. Our innovative way of investigating subglacial drainage systems will allow the glaciological community to diagnose the susceptibility of ice sheets (14, 16) and mountain glaciers (17, 48) to increased meltwater input due to climate warming and/or extreme melt and rainfall events. Our approach will also be particularly appropriate to study processes that generate similar spatially spread seismic noise in other environments, such as for lava flows on volcanoes (49), tremors in fault zones (50), and sediment transport in rivers (51).

Materials and Methods

Dense Seismic Array Survey.

All of the stations have a 500-Hz sampling rate and a low cutoff frequency of 4.5 Hz. The nodes were installed at a depth of 30 cm into the 4-m-thick snow cover and had to be reinstalled on May 11 due to snow melt, which occurred at a rate of 5 cm · day⁻¹. We refer the reader to ref. 30 for the detailed description of the experiment.

Complementary Measurements.

Concomitant with our seismic survey, we use continuous records of subglacial water discharge, which was measured in excavated subglacial tunnels maintained by the hydroelectric power company Emosson SA at ca. 600 m downstream of the center of the node array (at 2,173 m above sea level). We also installed four global navigation satellite system (GNSS) stations at the corners of the seismic array to measure glacial surface velocity, which was on the order of 0.1 m · day⁻¹ at this time of the year and for this part of the glacier (31). One week prior to the seismic deployment, we conducted a ground penetrating radar campaign over the study area with a 5-MHz signal to improve the previous estimates of the bed topography reported by ref. 52. Also, in September 2018, we conducted an aerial survey to derive a digital elevation model of the glacier surface using stereophotogrammetry. Combining these two digital elevation models, we calculated the ice thickness distribution over the study area, as shown in Fig. 1. The ice thickness reached up to 270 m at the center of the seismic array, with a well-marked talweg (i.e., valley-shaped bed) aligned in the glacier flow direction and a progressive diminution of the ice thickness down-glacier both within the area covered by our array and from the location of our array toward the glacier terminus. The reader should refer to ref. 30 for the detailed description of the complementary data associated with this seismic experiment.

MFP.

MFP consists of providing a probabilistic estimate of the epicentral coordinate of dominant source (28) from evaluation of the phase coherence of the seismic signal over an array of sensors. The method consists of recursively matching the phase delays of a model-based synthetic wave-field (i.e., the “trial source”) with the phase delays observed between the sensors over the array. A condition for this method to be applicable is that spatially coherent phase information can be extracted between nearby sensors (28), which requires interstation spacing of less than one-half of the investigated wavelength. We satisfy this condition with our 40- to 50-m interstation spacing for a 200- to 500-m investigated wavelength.

We first compute the discrete Fourier transform of a given data vector $d\left(t\right)$ recorded by the 98 sensors over a frequency ω to obtain the complex data vector $d\left(\text{ω}\right)$ and to calculate the corresponding cross-spectral density matrix as

$$K\left(\text{ω}\right)=d\left(\text{ω}\right)d^H\left(\text{ω}\right),$$

where $H$ is the Hermitian transpose. The cross-spectral density matrix captures the relative spatial phase difference between the sensors. We then define a set of values to be explored for trial sources. In this study, we set four degrees of freedom for the MFP processing, with a depth, range, and phase velocity grid (X, Y, Z, and C). An important condition for retrieving source epicentral coordinate (i.e., X, Y, and Z) and not only source back azimuth is to have a source-to-array distance not greater than two to three times the array aperture (i.e., largest distance between stations) (29). We satisfy this condition with a ca. 750-m array aperture for a c. 270-m source-to-station distance (23) [i.e., maximum glacier thickness (53)]. For each element $a$ of these four dimensions of the grid, we model the Green’s function replica vector $d\left(\text{ω},\text{a}\right)$ under the hypothesis of a homogenous medium as

$$d\left(\text{ω},\text{a}\right)=\exp \left(\raisebox{1ex}{$\hspace{0.17em}i{\text{ωr}}_a$}\!\left/ \!\raisebox{-1ex}{$c$}\right.\right),$$

where $c$ is the medium velocity and $r_a$ is the distance between each receiver and the trial source position $a$.

To match the observed cross-spectral density matrix with the replica vector, we calculate the Bartlett processor as

$$B_{Bartlett}\left(\text{ω},\text{a}\right)={\displaystyle \sum }_{\text{ω}}\left|d{\left(\text{ω},\text{a}\right)}^{H}K\left(\text{ω}\right)d\left(\text{ω},\text{a}\right)\right|.$$

This operation is equivalent to cross-correlation between the observed wave-field phase and the modeled one. We refer to the $B_{Bartlett}\left(\text{ω}\right)$ values as the MFP output. The MFP output is calculated at specific frequencies and ranges from 0 to 1. The closer to 1 the MFP output is, the more the modeled phase matches the observations. Sources that generate a signal resulting in similar phase coherence (i.e., MFP output value) are expected to be localized with a similar accuracy (28).

We perform source location over 1-s-long signal segments of the vertical component only. We filter the signal within the (3- to 7-) Hz frequency range that is the most sensitive to subglacial water flow induced seismic noise (21, 23–25) and coherently apply the MFP for each 0.4 Hz within this range. To maximize the efficiency of our algorithm and minimize the computational costs, we use a gradient-based minimization algorithm [i.e., Nelder–Mead optimization (54)] to converge to the best match between the trial and the observed phase delays rather than exhaustive grid-search exploration. The convergence criterion is reached when the variance of the values obtained over the last five iterations of the optimization is <1 × 10⁻², with a maximum of 3,000 iterations. Our 29 different starting points used for optimization are located 250 m below the glacier surface, and they uniformly cover an area of 800 × 800 m² centered on the array (Fig. 2D). We set the initial velocity to 1,800 m · s⁻¹. The 29 point locations found per signal segment (1 s) after convergence are all located in the same place if clear global convergence exists (i.e., high MFP output) or at up to 29 different locations if up to 29 local minima exist (i.e., low MFP output). The MFP output value can also be understood as an indicator of the number of receivers over which the signal is coherent (e.g., a value of 0.1 indicates a source that generates a signal coherent over 10% of the array). We found that this approach is comparable to using subarrays of variable sizes to perform the MFP over different areas of the glaciers. Further details on the methods and related physics can be found in ref. 55.

MFP Output Statistics.

We narrow the MFP output selection by keeping only the following: (1) the location that yields realistic phase velocities ([1,200 to 3,600] m · s⁻¹) and (2) the localizations at ±400 m from the array center and ≤400 m below the glacier surface. The number of located sources after this selection (Fig. 2A) decreases as the MFP output increases, with >5,000 daily sources associated with MFP output <0.05 and <1 daily source associated with MFP output >0.75. Fig. 2 B and C shows the distribution of the source properties (vertical position), and Fig. 2 E and F shows the spatial probability of the source location over the complete study period for two MFP output bands of ([0.07 to 0.16] and [0.75 to 0.99]). These locations correspond to real and detectable seismic events, since MFP output is much higher than expected for random noise (refer to ref. 30, Fig. 9). This two-dimensional representation is obtained by summing the total number of sources in each 8 × 8 m² cell of an 800 × 800 m² (x, y) grid centered on our seismic array.

It is important to note that at low MFP output (e.g., [0.07 to 0.16]), only a few sensors distinguish the source. This leads to a shorter aperture of the effective seismic array, which limits depth resolution. The trend to higher probability of the source location at depth is however observed here for tens of thousands of sources. The 2-d averaging is long enough to gather sufficient statistics, while it is also short enough to correctly investigate the temporal evolution with high enough spatial accuracy (Fig. 3).

Source Location Precision.

When compared to the crevasse field at our study location (Fig. 1), we observe that our MFP analysis yields source locations with MFP output >0.75, a precision in range down to 10 m (Fig. 2) for an average wavelength λ of ca. 300 m at 5 Hz (37). While the expected Rayleigh limit gives maximum resolution of λ/4 (ca. 75 m at 5 Hz) in the far-field domains (27), laboratory experiments (56) suggest that the seismic signal bears information of spatial structures down to λ/8 (ca. 32 m at 5 Hz) in the near-field of sources. Our unique instrumental set-up combined with our systematic analysis of phase coherence allow us to overcome the Rayleigh far-field limitations and obtain two-dimensional maps of source locations with resolution in the range of ca. 10 m for high MFP outputs. For lower MFP outputs, we expect lower resolution due to the smaller aperture of the array that is sensitive to local phase coherence. We acknowledge that the width of the area shown in Fig. 2D might not represent the true width of a single subglacial channel, which is expected to be of the order of one to few meters at this location (23). The observed width of ca. 50 m could be due to the uncertainty for the source location or to the presence of multiple channels.

Hydraulic Potential Calculation.

We calculate the hydraulic potential $\mathrm{\Phi }$ following ref. 1, as

$$\mathrm{\Phi }={\rho }_{w}g{z}_b+K\left[{\rho }_{i}g\left(z_s-z_b\right)\right],$$

where $g$ is the acceleration due to gravity (9.81 m · s⁻²), ${\rho }_w$ is the density of water (1,000 kg · m⁻³), ${\rho }_i$ is the density of ice (917 kg · m⁻³), $z_b$ and $z_s$ are the elevation of the glacier bed and surface (m), respectively, and $K$ is the ratio of water pressure to ice overburden pressure (i.e., a uniform flotation fraction). A value of $K$ near 0 represents a condition where basal water pressure is negligible in comparison to ice overburden pressure, and a value near 1 represents a condition in which basal water pressure is high enough to significantly counterbalance ice overburden pressure. Here, we use a flotation fraction of 0.5, which is likely to represent a case in which the subglacial drainage system has developed enough to efficiently drain the bed (1, 57) and therefore reduce subglacial basal water pressure. We consider this flotation fraction to best represent the subglacial water pressure condition in our location at the end of our study period when we observe a decreasing glacier velocity while water discharge still increases (Fig. 4A). We then calculate the water flow directions based on the hydraulic potential gradients by following the path that minimizes the gradient with a minimum upstream area of 150 m² for the waterway, to initiate the use of TopoToolBox, developed by ref. 58. We show in SI Appendix, Fig. S1 that different values of flotation fraction ($K=[0.1,0.5,0.9]$) result in a similar predicted waterway pattern. The expected localization of subglacial water flow thus does not depend much on the flotation fraction, likely as a result of the V-shape of the Argentière glacier being particularly pronounced.

Inverting Hydraulic Properties Using Water Discharge and Seismic Power Measurements.

We use the theoretical framework of ref. 22 to invert for the hydraulic properties of subglacial turbulent water flow using simultaneous measurements of subglacial water discharge and seismic power. The seismic power $P$ is calculated at each sensor using the vertical component of ground motion within [3 to 7] Hz and the Welch method over 4-s time windows with 50% overlap, as reported in ref. 23. The physical framework relates the changes in the measured seismic power P and discharge Q to changes in channel hydraulic radius R and hydraulic pressure gradient S. The basis of these relations is that turbulence within water flow generates frictional forces that act on the boundaries of the channels (i.e., ice, glacier bed) and create ground motion. This approach has been recently shown to be applicable over our study area (23). The hydraulic radius R is defined as the ratio of the cross-sectional area of the channel flow to its wetted perimeter. The hydraulic pressure gradient S is a function of both the rate of change of water pressure and the bed slope in the flow direction. In the case of constant bed slope and channel geometry, increasing S means closed and pressurizing channel flow. Both variables are defined for subglacial conduits in which turbulent water flow dominates. We calculate median values of R and S using the median seismic power P over the 98 sensors and the water discharge Q, as follows:

$$S=S_{ref}{\left(\frac{P}{P_{ref}}\right)}^{24/41}{\left(\frac{Q}{Q_{ef}}\right)}^{-30/41}$$

$$R=R_{ref}{\left(\frac{\text{P}}{P_{ref}}\right)}^{-9/82}{\left(\frac{Q}{Q_{ef}}\right)}^{-33/82},$$

where the subset ref is the reference state, which is April 26 in this study. In the main text, when referring to the temporal evolution of R and S, we therefore refer to their relative changes with respect to this reference period. We evaluate P over the (3- to 7-) Hz frequency band, as it has been shown by ref. 23 to be the best suited in area for studying turbulent water flow. The reader is referred to refs. 22, 23 for more details.

We stress that the inversions of hydraulic properties depend on the average seismic amplitude, with very little dependency on the spatial variations. Therefore, our inversions are to be considered independent of the source location, even if they both arise from the seismic signals. This also implies that our inversions represent averaged hydraulic conditions of the drainage system.

State of Knowledge on the Main Features of Channels and Cavities.

Cavities form in the downstream lee of bedrock bumps, due to ice sliding over the bed, and they close through ice creep. Cavities can be filled with water, which reduces the apparent rugosity of the glacier bed and weakens the ice–bed mechanical coupling (39). For soft-bed glaciers, inefficient drainage systems also include unconsolidated layers of low permeability (59). Weakly connected cavities can have permeability that are lower by ca. 9 orders of magnitude than that of connected cavities (14). For a similar hydraulic gradient to that of connected cavities, turbulent water flow within a weakly connected system therefore requires much higher flow velocities.

Subglacial channels can be of the R-type (8) when melted into the ice by turbulent dissipation of heat or of the N-type (60) when dug into the basal sediments by the flowing water or etched into bedrock by carbonate dissolution (61). Both types close through ice creep. When developing and reaching steady state, a subglacial channel tends to have lower water pressure than cavities, which therefore drains the connected cavity system.

Data Availability

The time series of physical quantities measured at Argentière glacier over the 2017 and 2018 melt season are publically accessible at https://zenodo.org/record/3701520 (62). All of the data associated with the dense array experiment are publically accessible at https://zenodo.org/record/3971815 (63). The spatial maps of source locations, glacier geometries, and hydraulic potentials as well as the code used to processed these data are publically accessible at https://zenodo.org/record/4024660 (64). Part of the dataset of the seismic signals acquired during RESOLVE-Argentière is publically accessible at https://doi.org/10.1785/0220200280 (36) in link with ref. 30. Contact U.N. at ugo.nanni0158@gmail.com or ugo.nanni@univ-grenoble-alpes.fr for questions related to the above-described datasets and codes.