Abstract
Phase synchronization has been an effective measurement of functional connectivity, detecting similar dynamics over time among distinct brain regions. However, traditional phase synchronization-based functional connectivity indices have been proved to have some drawbacks. For example, the phase locking value (PLV) index is sensitive to volume conduction, while the phase lag index (PLI) and the weighted phase lag index (wPLI) are easily affected by noise perturbations. In addition, thresholds need to be applied to these indices to obtain the binary adjacency matrix that determines the connections. However, the selection of the thresholds is generally arbitrary. To address these issues, in this paper we propose a novel index of functional connectivity, named the phase lag based on the Wilcoxon signed-rank test (PLWT). Specifically, it characterizes the functional connectivity based on the phase lag with a weighting procedure to reduce the influence of volume conduction and noise. Besides, it automatically identifies the important connections without relying on thresholds, by taking advantage of the framework of the Wilcoxon signed-rank test. The performance of the proposed PLWT index is evaluated on simulated electroencephalograph (EEG) datasets, as well as on two resting-state EEG datasets. The experimental results on the simulated EEG data show that the PLWT index is robust to volume conduction and noise. Furthermore, the brain functional networks derived by PLWT on the real EEG data exhibit a reasonable scale-free characteristic and high test–retest (TRT) reliability of graph measures. We believe that the proposed PLWT index provides a useful and reliable tool to identify the underlying neural interactions, while effectively diminishing the influence of volume conduction and noise.
Keywords: Phase synchronization, Volume conduction, Wilcoxon signed-rank test, Graph measures, Scale-free characteristic, Test–retest reliability
Introduction
The concept that the human brain is a complex network of interacting brain regions has been generally accepted. The interactions (i.e., temporal correlations) between the spatially remote brain regions are characterized as functional connectivity (Biswal et al. 1997). The functional connectivity has become an important tool to investigate the mechanisms of brain cognitive functions (Zhang et al. 2015a, b; Tafreshi et al. 2019). Therefore, constructing an effective and accurate index to measure the functional connectivity is a critical prerequisite for understanding the brain functions. Electroencephalography (EEG) and magnetoencephalography (MEG) have been two popular brain imaging techniques to study the neural activities and brain cognitive functions due to their high temporal resolution (Mora-Sánchez et al. 2019; Daneshi et al. 2019). For EEG and MEG signals, phase synchronization has been widely used to measure the functional connectivity between neuronal groups. Several phase synchronization-based indices of functional connectivity have been proposed, such as the phase locking value (PLV) (Lachaux et al. 1999), the phase lag index (PLI) (Stam et al. 2007), and the weighted phase lag index (wPLI) (Vinck et al. 2011; Ortiz et al. 2012).
Two major problems have been considered as obstacles for the effective measurement of phase synchronization, which are volume conduction and noise perturbation. Volume conduction, defined as the conductive characteristic of the brain, soft tissues and skull, usually leads to spatial similarity of EEG signals (Nunez and Williamson 1996; Daffertshofer and Stam 2007). As revealed by previous studies, PLV suffers from volume conduction, resulting in spurious functional connectivity for spatially adjacent electrodes with zero phase differences. In contrast, PLI alleviates the problem by excluding the zero phase differences from the calculation (Stam et al. 2007). However, the measured EEG signals are typically a mixture of signals-of-interest and noise. Even in the absence of volume conduction, noise could result in spurious changes in functional connectivity (Bastos and Schoffelen 2016). Some adjustments to PLI have been made to improve the resistance against noise, such as wPLI (Vinck et al. 2011), by reducing the influence of small phase differences that are sensitive to noise. Nevertheless, wPLI is prone to the influence of outliers and tends to overestimate the functional connectivity when the phase differences are small (see the Related work section). Besides, not only the phase information but also the amplitude are needed for the calculation of wPLI.
More importantly, all the above indices produce values between zero and one to quantify the phase synchronization. Most of these values are typically not exact zeros or ones due to the existence of noise. Therefore, additional steps are generally needed to determine whether two signals have a connection or not. A desirable solution is to construct a binary adjacency matrix to pinpoint the connections among sensors. For such purpose, a convenient technique is to apply a threshold to the association matrix which contains the continuous phase synchronization values. By maintaining relatively large values, the threshold is expected to reveal the most important neural interactions. However, it is not straightforward to determine a generally accepted threshold. Moreover, one single threshold may not be appropriate to be applied to different pairs of sensors. An alternative method to determine the binary connections is to use the framework of the permutation test (Lachaux et al. 1999; Stam et al. 2007). Nevertheless, this procedure needs to be performed repeatedly on randomly permutated surrogate data and thus is computationally extensive. Besides, the number of repetitions affects the test result.
To address these issues, in this paper, we propose a novel index of functional connectivity, named the phase lag based on the Wilcoxon signed-rank test (PLWT). A preliminary version of this paper has been published in Wu et al. (2017). Briefly, the proposed PLWT index has the following features. Firstly, to eliminate the spurious non-zero functional connectivity caused by volume conduction, PLWT adopts the phase lag which excludes the zero phase differences rather than the phase locking. Secondly, to reduce the sensitivity to noise, PLWT employs a unique weighting procedure so that the small phase differences are given lower weights in the calculation. In particular, the phase differences are weighted according to their ranks of magnitudes, which also alleviates the overestimation of functional connectivity caused by outliers. Thirdly, PLWT uses the Wilcoxon signed-rank test to determine the statistical significance of each functional connection. Therefore, the important functional connections are automatically selected according to their statistical significances rather than by an arbitrary threshold. Taken together, the proposed PLWT index is expected to accurately identify the relevant functional connections based on the phase lag without applying a threshold, while reducing the influence of volume conduction and noise.
The performance of the proposed PLWT index is evaluated from the following perspectives in the experiment and compared with PLV, PLI and wPLI. Firstly, their robustness to volume conduction and noise is evaluated on simulated EEG datasets. Secondly, the brain functional networks derived by these indices on a resting-state EEG dataset are investigated in terms of the scale-free characteristic. Thirdly, the test–retest (TRT) reliability of each functional connectivity index is analyzed in terms of graph measures computed based on another resting-state EEG dataset.
The rest of the paper is organized as follows. Section 2 briefly introduces the phase synchronization-based functional connectivity indices that are closely related to the proposed PLWT index, specifically the PLV, PLI and wPLI methods. Section 3 elaborates the definition and algorithm of PLWT and describes the other methods and tools used in the experiment, as well as the simulated and real resting-state EEG datasets. Section 4 presents the experimental results, Sect. 5 further discusses these results and Sect. 6 concludes the paper.
Related work
The classic PLV index, proposed by Lachaux et al. (1999), believes that the phase-locking reflects neural interactions. It directly measures the frequency-specific synchronization by using only the phase quantities without the amplitude component. Suppose that is a sequence of instantaneous phase differences between the time series recorded from two channels at different time points, where denotes the phase difference at time point t and N is the sampling points of the time series. The PLV between two channels is mathematically formulated as
| 1 |
where * and compute the mean and absolute value respectively. In other words, PLV projects these instantaneous phase differences at different time points onto the unit circle in the complex plane and then computes the absolute value of the average phase difference over time. PLV is equal to one when the phase differences at different time points are constant; it tends to be zero when the phase differences are randomly distributed on the unit circle. However, PLV is vulnerable to volume conduction, as it would derive spurious non-zero values when the phase differences are centered around due to the common sources.
To circumvent the effect of volume conduction, Stam et al. (2007) have proposed the PLI to measure the phase synchronization, given by
| 2 |
where is the sign function. PLI only uses the imaginary part of , i.e. , thus disregarding the phase differences that are generally caused by volume conduction. For PLI, the phase synchronization is measured by the asymmetry of the distribution of the phase differences around zero. PLI equals to one if there is a consistent lag of phases between the two signals, while it tends to be zero if the distribution of phase differences is symmetric around . In other words, the more consistent the phase lags are, the more asymmetric the distribution of the phase differences will be. Although PLI outperforms PLV in terms of volume conduction, it is still sensitive to noise for that a small perturbation of phases would change the signs of the phase differences that have small magnitudes, thus changing the PLI value.
To diminish the sensitivity to noise, wPLI has been proposed (Vinck et al. 2011). The wPLI value between two time series is given by
| 3 |
where L1 and L2 are the corresponding amplitudes of the two time series respectively. The wPLI weights the phase differences according to their magnitudes and amplitudes, so as to weaken the contribution of the small phase differences that are sensitive to noise. Nevertheless, it still suffers from some limitations. Firstly, wPLI may overestimate the functional connectivity, especially in the case of small phase differences (near O mod π). Such small phase differences could be yielded by volume conduction with noise and result in a small value of the denominator of Eq. (3). For example, if the values of are zeros and is non-zero, the wPLI value would be one. Secondly, wPLI is sensitive to outliers as large phase differences play a dominant role in wPLI. It may happen that one large phase difference caused by an outlier at a time point offsets all the relatively small but consistent phase differences. Consequently, the value of wPLI would roughly be zero, and the true phase lag would not be revealed appropriately. Thirdly, wPLI is also entangled with the amplitude information of the time series.
Methods and materials
Desired properties of an index based on phase synchronization
An ideal index of functional connectivity is expected to discover the intrinsic neural interactions from noisy signals while resisting the influence of volume conduction. By integrating the advantages of the existing indices mentioned above, we present the following requirements for an ideal index based on phase synchronization. Firstly, the phase information of signals is used exclusively, as suggested in PLV. Secondly, the phase lag, rather than the phase locking, is considered, as suggested in PLI. Thirdly, the role of small phase differences is attenuated, as suggested in wPLI. Finally, an explicit conclusion of whether two time series are connected or not is reached.
Procedure for calculating the PLWT index of functional connectivity
Targeting the four requirements, we propose the novel index by resorting to statistical tools, specifically, the Wilcoxon signed-rank test (Wilcoxon 1945; Taheri and Hesamian 2013). Briefly, the Wilcoxon signed-rank test is a non-parametric test that compares two matched samples based on their ranks. The fundamental idea behind the Wilcoxon signed-rank test could be elegantly adopted to determine the statistical significance of the functional connectivity, thus identifying the binary functional connections. In other words, it could be used to test the asymmetry of the distribution of the phase differences between two time series. Driven by this, we propose the PLWT index which meets all the above requirements for identifying the functional connectivity.
Specifically, for each pair of channels, the procedure of calculating the proposed PLWT index is described as follows:
Null hypothesis : The distribution of the phase differences is symmetric around zero.
Alternative hypothesis : The distribution of the phase differences is not symmetric around zero.
Sort the non-zero items in in an ascending order of their values while leaving out zero values. If stands in the -th position of the reordered series, the rank of is denoted by . The rank of ties is computed by averaging the ranks they span.
-
Compute two statistics
4 5 Let
Let be the number of non-zero values of . For n < 25, given a significance level α, the statistic T is compared to the corresponding critical value in the look-up table of the Wilcoxon signed-rank test. If , is rejected, indicating that the distribution of the phase differences is significantly asymmetric.
-
As the sample size increases, the sampling distribution tends to be a normal distribution. Thus for n > 25, a statistic can be calculated as
where and . The statistic is compared to the approximate critical value of the Gaussian distribution Similarly, if , we reject .where and . The statistic is compared to the approximate critical value of the Gaussian distribution Similarly, if , we reject .6 -
Therefore, PLWT is calculated as
7 In other words, if is rejected, we conclude that there is a connection between the two channels and assign the PLWT value as 1; otherwise, the PLWT value is 0. In addition, the weighted association (functional connectivity) between the two channels (if is rejected) can be calculated by
8 To sum up, PLWT identifies the functional connectivity by measuring the asymmetry of the distribution of phase differences between two time series. To reduce volume conduction, PLWT is defined on the phase lag, which excludes phase differences. Besides, to improve the robustness to noise, the influence of the small phase differences is weakened by assigning them with smaller weights in PLWT. More importantly, the sensitivity to outliers is also alleviated for PLWT as the ranks of the phase differences rather than their magnitudes are adopted as weights. Furthermore, the solid statistical framework of the Wilcoxon signed-rank test is utilized to straightforward determine the existence of intrinsic neural interactions, thus deriving the binary-valued functional connectivity.
Kuramoto model
In this paper, we adopt the model of coupled limit-cycle oscillators proposed by Kuramoto (1975) to generate simulated EEG signals for evaluating the indices. A more detailed description of the Kuramoto model can be found in the overview (Strogatz 2000). Briefly, the Kuramoto model describes the phase transition of coupled limit-cycle oscillators. The long-term dynamic of each oscillator is given by the following equation:
| 9 |
where and denote the phase and the natural frequency of the -th oscillator respectively, and is the coupling strength. The frequency is distributed according to a certain density , which is generally assumed as a special case of Cauchy density:
| 10 |
where is the mean frequency and is the half width at the half maximum (HWHM).
The synchronization level of the oscillators can be described by an order parameter (Strogatz 2000):
| 11 |
It assumes that the oscillators run around the unit circle in the complex plane. If all the oscillators move together like a giant oscillator, then , indicating a high level of synchronization. And if the oscillators are scattered around the circle, then which means that the act of the system has no coherency.
There is a phase transition from desynchronization to partial synchronization at the critical point of the coupling strength, denoted as . Specifically, when the coupling strength , the system behaves incoherently where each oscillator runs at its natural frequency. As exceeds , some of the oscillators start to spontaneously synchronize. The relationship between the synchronization level and the coupling strength can be described as follows:
| 12 |
Under the premise that follows the Cauchy distribution, is only determined by , given by
| 13 |
Graph measures
In this paper, we mainly investigate the brain functional networks derived by different functional connectivity indices in terms of four graph measures, including degree, clustering coefficient, characteristic path length, and small-world-index (SWI) (Rubinov and Sporns 2010; Bullmore and Bassett 2011). The calculation of these graph measures in this paper is implemented by using the brain connectivity toolbox (Rubinov and Sporns 2010).
For the proposed PLWT index, no specific threshold is needed to obtain the binary graph for analyzing the graph measures since it automatically derives a binary adjacency matrix. By contrast, the proportional thresholding scheme (Erdős and Rényi 1964) is employed for PLV, PLI and wPLI, with the proportion (i.e., connectivity density ) defined as
| 14 |
where represents the number of nodes (or electrodes).
The degree of node , denoted by , is defined as
| 15 |
where is an element in the binary graph, indicating the connection between node and node . If there is a connection between node and , then ; otherwise . Simply put, counts the number of edges connecting node with other nodes. A higher degree indicates a better-connected node.
The probability distribution of the degrees over all nodes, is called degree distribution, which reflects the fraction of nodes with a degree of . It is defined as
| 16 |
where is the number of nodes with a degree of . Previous studies have proved that the best form of degree distribution for a brain functional network to fit is the distribution following an exponentially truncated power law, as brain functional networks are thought to have scale-free characteristic (Barabási and Albert 1999; Bandettini and Bullmore 2010; Lee et al. 2010).
Clustering coefficient is a measure of segregation of a network, which reflects the degree to which the nodes tend to cluster together. The clustering coefficient of node is calculated as
| 17 |
where is the number of edges connecting the neighbors of node , and denotes the number of all the possible edges connecting these neighbors. The mean clustering coefficient over all nodes is defined as .
Characteristic path length is defined as the average shortest path length between all pairs of nodes in the network, representing a measure of functional integration. It is formulated as
| 18 |
where is the shortest path length between node and node ; if the nodes are not connected, and gives the average shortest path length between node and the other nodes.
The SWI is defined as
| 19 |
where and are the average clustering coefficient and the characteristic path length of the equivalent random network respectively.
Test–retest reliability
Test–retest (TRT) reliability evaluates the consistency of repeated measurements of the same objects. In other words, a high TRT reliability requires both high inter-subject variability and low intra-subject variability, thus implying high stability of the measurements over time. A high TRT reliability is a desirable feature for functional connectivity estimates and graph measures (Braun et al. 2012; Hardmeier et al. 2014; Zuo and Xing 2014). The TRT reliability can be quantified by using the intra-class-correlation coefficient (ICC) (Shrout and Fleiss 1979). Given two repeated measurements of m subjects, ICC is computed by
| 20 |
where and are the measurements of subject calculated on the two repeated trials, represents the merging mean value, and is the pooled standard deviation. The TRT reliability is considered to be excellent if , good if , fair if , and poor if (Deuker et al. 2009).
EEG datasets
Simulated EEG datasets
To compare the influence of volume conduction and noise on different functional connectivity indices, simulated EEG data is generated by utilizing the well-studied Kuramoto model with 64 oscillators . Specifically, we set the mean frequency and the HWHM width in Eq. (10) to 10 Hz (alpha band) and 1 respectively, thus the critical value of coupling strength is 2 according to Eq. (13). Then we range the coupling strength in the Kuramoto model [Eq. (9)] from 0 to 8 with a step size of 0.5. For each oscillator, a time series of phases including 7501 time points is derived by the Kuramoto model with a sampling frequency of 500 Hz. The initial 5000 time points of each oscillator are discarded due to the transients, resulting in a data matrix of size . This process is repeated 10 times for each condition. Assume that is a constant amplitude for all the oscillators, the state of oscillator at time can be described as . In this way, 10 trials of simulated EEG signals with 64 oscillators are produced based on the time series of phases for each value of , where the oscillators can be viewed as EEG channels.
To simulate volume conduction, three levels of overlap are produced for these simulated EEG signals following the procedures used by Stam et al. (2007). Specifically, the voltage of channel at time , , is related to the states of channel and its neighbors, given by
| 21 |
where decides the degree of overlap. In the experiment, we set as 0, 4 and 8, and thus the corresponding number of common sources (CS), i.e., 2i0, is 0, 8, and 16 respectively. Therefore, simulated EEG datasets with different values of the coupling strength K and different levels of overlap (CS) are generated.
Resting-state EEG datasets
Apart from the simulated EEG data, two real resting-state EEG datasets are employed in this experiment to study the brain functional networks derived by different functional connectivity indices, in terms of the scale-free characteristic and the TRT reliability respectively. The dataset used for studying the scale-free characteristic, denoted as dataset 1, was collected at the Research Center for Learning Science of Southeast University in China from 24 adolescent subjects (Zhang et al. 2015a, b). All the subjects were right-handedness and without medical, neurological, psychiatric illness or history of brain injury or surgery, with the age ranging from 15 to 18 years (mean ± SD: 16.3 ± 0.6). The EEG data were recorded from 60 channels by using the Neuroscan international 10–20 system (Homan et al. 1987) with a sampling rate of 1000 Hz. All the subjects kept their eyes closed and stayed awake during the data acquisition process. Two reference electrodes were placed on the bilateral mastoids of the subjects. Artifacts caused by ocular and muscle movements and electrocardiogram noises were removed by using the artifact rejection procedure and independent component analysis (ICA) (Zhang et al. 2015b). After preprocessing, each subject has 18–25 trials and there are 581 trials in total, where each trial lasts for 9500 ms.
The second dataset, denoted as dataset 2, is used to evaluate the TRT reliability of the functional connectivity and graph measures. It is publicly available in the NITRC-open discussion forum (https://www.nitrc.org/). It contains the resting-state EEG dataset of 10 subjects, with the apparent artifacts cleaned. Each subject has 154 ~ 202 trials and each trial lasts for 4 s. During the data collection, the subjects were instructed to keep their eyes closed and to rest. The EEG signals were recorded from 19 channels by the Neuroscan international 10–20 system with a sampling rate of 256 Hz. In the calculation of ICC (Eq. (20)), for each subject we took the first 300 s (75 trials) as epoch 1 and the last 300 s (75 trials) as epoch 2, which were used as the two repeated measurements.
Results
Results on simulated datasets
Influence of volume conduction
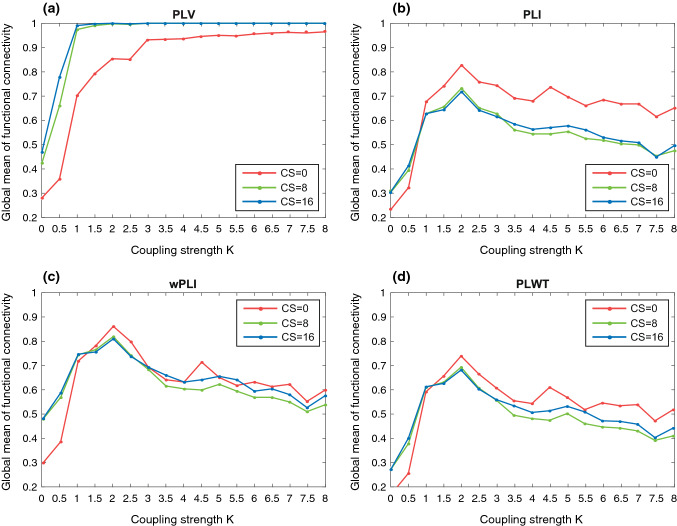
Firstly, the impact of volume conduction is evaluated based on the simulated EEG datasets with three different levels of overlap (CS = 0, 8, 16) for these four indices, i.e., PLV, PLI, wPLI and PLWT. Note that in this experiment, the weighted functional connectivity is computed for PLWT. Specifically, the connections (i.e., the ones) in the binary adjacency matrix detected by PLWT according to Eq. (7) are replaced by their corresponding weighted values calculated by Eq. (8). Figure 1 shows the global mean of functional connectivity that is averaged over all the channels and all the 10 trials for each index as a function of coupling strengths. Roughly, all the indices peak when K reaches the critical point and stay relatively stable when . However, they exhibit significant differences in the responses to volume conduction. Specifically, the value of PLV evidently increases when CS increases from 0 to 8 and 16 and approaches nearly 1 after . Such a high value of functional connectivity indicates that PLV is strongly effected by volume conduction. By contrast, the other three indices effectively suppress the furiously high functional connectivity caused by volume conduction, revealed by the relatively lower global mean values derived at . In particular, for wPLI and PLWT, the global means of functional connectivity show only slight differences across different values of CS. No significant difference is found between different CS values for both wPLI and PLWT (, t-tests). Furthermore, the PLWT index achieves an overall more conservative value of functional connectivity than all the other indices. These results suggest that the PLWT index is more robust to different levels of volume conduction than the other indices and effectively reduces the influence of the connections with spuriously high values.
Fig. 1.
Global mean of functional connectivity derived by PLV, PLI, wPLI and PLWT as a function of the coupling strength K under different degrees of overlapping (CS = 0, 8, 16). The results were derived for a PLV, b PLI, c wPLI and d PLWT. The global mean of functional connectivity of each index was computed by averaging over all the channels and all the trials (Wu et al. 2017)
Sensitivity to noise perturbation
Secondly, the influence of noise is tested based on the simulated EEG dataset with . Specifically, we add white Gaussian noise with the signal-to-noise ratio (SNR) of 20 dB to the simulated EEG signals and then calculate the global mean of functional connectivity for PLV, PLI, wPLI and PLWT separately. The results are displayed in Fig. 2. Overall, all the indices tend to show right displacements with lower values of functional connectivity derived when the noise is added. This is because that the noise prevents some relevant functional connections to be identified. Among these indices, PLV is hardly biased by the perturbation after , as it achieves a high value of functional connectivity due to its overestimation of the synchronization among oscillators. PLI is heavily affected by the noise, which achieves a significantly lower value of functional connectivity after This is rooted in the definition of PLI (Eq. (2)) that small disturbances can easily change the value of PLI. By contrast, PLWT and wPLI are less sensitive to the noise than PLI by obtaining a smaller discrepancy in the functional connectivity derived with and without noise after . It indicates that by weakening the influence of small phase differences, wPLI and PLWT effectively increase their robustness to noise.
Fig. 2.
Global mean of functional connectivity derived by PLV, PLI, wPLI and PLWT as a function of the coupling strength K with white Gaussian noise (SNR = 20 dB) added under CS = 0. The results were derived for a PLV, b PLI, c wPLI and d PLWT. The global mean of functional connectivity of each index was computed by averaging over all the channels and all the trials
Selection of significance level
Finally, we investigate how the selection of the significance level for PLWT would change the derived functional connectivity, by using five different values of , i.e., and 0.0001. Figure 3 shows the global mean of functional connectivity as a function of the coupling strength K under these significance levels. The blue bars at the bottom of the figure represent the standard deviation (SD) over these significance levels. As can be seen, the functional connectivity derived by PLWT is highly consistent across different values of in terms of the global means, indicated by the small SD values. It suggests that the commonly-accepted significance level is adequate for PLWT to stably determine the robust and valid connections on the simulated EEG dataset.
Fig. 3.

Global mean of functional connectivity derived by PLWT as a function of the coupling strength K under different significance levels (α = 0.0001, 0.001, 0.005, 0.01, 0.05). The global mean of functional connectivity was computed by averaging over all the channels and all the trials for each condition. The standard deviation (SD) was computed over different significance levels for each K value, represented by the blue bars at the bottom of the figure
Results on resting-state EEG datasets
Scale-free characteristic of brain functional networks
The analysis of degree distribution is conducted on the real resting-state EEG dataset 1 within four frequency bands (i.e., theta, alpha, beta, gamma). To compute the degree distributions of the derived functional networks, binary graphs are obtained for PLV, PLI and wPLI by adopting the proportional thresholding scheme to the brain functional networks. The connection density p is set to 0.14, which is a generally accepted value for 60 EEG channels according to Eq. (14). For PLWT, the binary adjacency matrices are derived by Eq. (7) automatically, where the significance level is set to 0.05. The degree distributions of the functional networks derived by these indices are plotted in Fig. 4. As can be seen, the degree distributions of all the indices follow the power-law distribution, implying the scale-free characteristic of the brain functional networks. However, the degree distributions of PLI-based indices (i.e. PLI, wPLI and PLWT) are significantly different from that of PLV.
Fig. 4.
Degree distribution (P(d)) of the brain functional networks derived by PLV, PLI, wPLI and PLWT in different frequency bands. The results were derived on the resting-state EEG dataset 1 in (a) theta band, b alpha band, c beta band and d gamma band
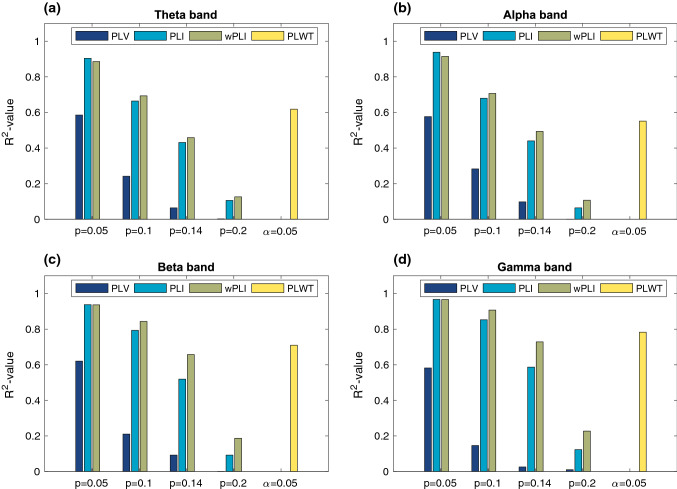
To further quantitatively compare PLWT with the other indices in terms of the degree distribution, we employ the coefficient of determination R2 to measure the goodness of fit for each index. That is, a higher R2 value indicates the derived degree distribution better fits the power-law distribution. For a more comprehensive analysis, the goodness of fit is initially tested over four different thresholds for PLV, PLI and wPLI with the connection density and 0.05 and with for PLWT, as shown in Fig. 5. Overall, the R2 value of PLWT is higher than those of PLV, PLI and wPLI when in all the four frequency bands, indicating that the functional networks derived by PLWT exhibit an evident scale-free characteristic. Among PLV, PLI and wPLI, PLV achieves a significantly lower R2-value than the other two indices in all the frequency bands. Besides, the R2-values of the three indices decrease as the networks become denser, which drop below 0.3 when across all the four frequency bands.
Fig. 5.
Goodness of fit (R2-value) between the degree distributions derived by PLV, PLI, wPLI and PLWT and the power-law distribution under different thresholds in four frequency bands. The results were derived on the dataset 1 in (a) theta band, b alpha band, c beta band and d gamma band. The threshold (connection density p) varied in 0.05, 0.1, 0.14 and 0.2 for PLV, PLI and wPLI and the significance level α was set to 0.05 for PLWT
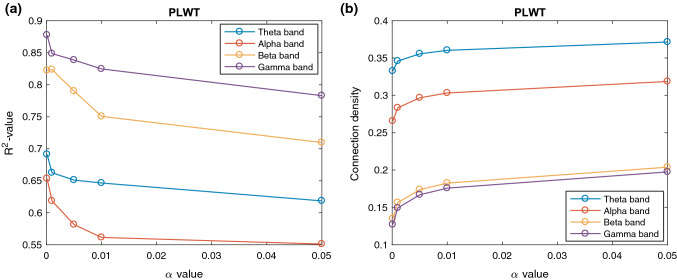
Moreover, the goodness of fit for PLWT is further analyzed under five different significance levels, i.e., and 0.0001. Results of the R2-values and the corresponding connection density of the networks derived under these values of are displayed in Fig. 6a and b respectively. As can be seen, the R2-value of PLWT increases for all the frequency bands as decreases from 0.05 to 0.0001. In the meantime, the corresponding network connection density decreases slightly for each frequency band. The higher R2-values of PLWT further show that the PLWT index exhibits substantially better scale-free characteristics of the derived networks than the other indices, even in the lower frequency bands where the network connection density is relatively high (p ranging from 0.25 to 0.37).
Fig. 6.
Goodness of fit (R2-value) and the connection density of the networks derived by PLWT under different significance level (α = 0.0001, 0.001, 0.005, 0.01, 0.05) in four frequency bands (theta, alpha, beta and gamma bands). a Goodness of fit (R2-value) between the degree distribution and the power-law distribution of PLWT, b connection density of PLWT-derived networks
Test–retest reliability of functional connectivity and graph measures
The TRT reliability is evaluated on two epochs from the real resting-state EEG dataset 2 by using the ICC. Specifically, for each subject, a trial-averaged association matrix is derived over all the 75 trials within each epoch, resulting in two repeated measurements. Four indices are included in the analysis, which are the global mean of functional connectivity, characteristic path length, clustering coefficient and SWI. For PLV, PLI and wPLI, these graph measures are computed on the binary graphs with . For PLWT, we conduct the analysis under a more rigorous significance level, i.e., α = 0.01. The ICC, as a relative measure of reliability, is likely to be biased by large between-subject variance or by few outliers (Weir 2005). To gain a better insight of the ICC values, firstly we show the distribution of the test and retest values of the global mean of functional connectivity over all subjects for each index in each frequency band in Fig. 7. As can be seen, PLI, wPLI and PLWT derive similar distributions of functional connectivity. The between-subject variance is relatively larger in the alpha-1 and alpha-2 bands than in the theta and beta bands. By contrast, the between-subject variance is lower for PLV in all the frequency bands. Then, we provide the absolute within-subject difference between the two epochs (mean ± SD) for the global mean of functional connectivity in Table 1. It shows that the difference of the functional connectivity computed on the two epochs is on average relatively small for all the methods. Next, we estimate the 95% confidence interval for each ICC value by using a bootstrapping procedure with replacements and 1000 repetitions (Hardmeier et al. 2014). The ICC values, as well as the corresponding confidence intervals, of the global mean of functional connectivity are displayed in Table 2. It shows that the TRT reliability of PLWT in terms of functional connectivity achieves an excellent level in the alpha-1, alpha-2 and beta bands (ICC > 0.9) and a good level in the theta band (ICC > 0.7). However, in the theta band PLV achieves a significantly better performance than the other indices.
Fig. 7.
Distribution of the global mean of functional connectivity over all subjects derived by PLV, PLI, wPLI and PLWT in four frequency bands (theta, alpha-1, alpha-2 and beta bands). The results were derived for a PLV, b PLI, c wPLI and d PLWT. The global mean of functional connectivity was computed over all channels and all trials within each epoch of the dataset 2 in each frequency band for each subject separately. The figure was created by using the boxplot function in matlab, where the symbol ‘+’ indicates the outliers and the red mark inside each box represents the median
Table 1.
Within-subject difference between two epochs (mean ± SD) of the global mean of functional connectivity for PLV, PLI, wPLI and PLWT
| Theta | Alpha-1 | Alpha-2 | Beta | |
|---|---|---|---|---|
| PLV | 0.0051 ± 0.0149 | 0.0302 ± 0.0339 | 0.0094 ± 0.0307 | 0.0198 ± 0.0161 |
| PLI | 0.0030 ± 0.0076 | 0.0237 ± 0.0470 | 0.0006 ± 0.0363 | 0.0025 ± 0.0055 |
| wPLI | 0.0110 ± 0.0206 | 0.0137 ± 0.0164 | 0.0129 ± 0.0475 | 0.0001 ± 0.0135 |
| PLWT | 0.0114 ± 0.0185 | 0.0349 ± 0.0467 | 0.0485 ± 0.0460 | 0.0058 ± 0.0094 |
Table 2.
ICC values of the global mean of functional connectivity for PLV, PLI, wPLI and PLWT with 95% confidence intervals in different frequency bands
| Theta | Alpha-1 | Alpha-2 | Beta | |||||
|---|---|---|---|---|---|---|---|---|
| ICC | 95% CI | ICC | 95% CI | ICC | 95% CI | ICC | 95% CI | |
| PLV | 0.9322 | 0.7524–0.9827 | 0.7908 | 0.3603–0.9436 | 0.7578 | 0.2863–0.9338 | 0.9117 | 0.6864–0.9773 |
| PLI | 0.6776 | 0.1276–0.9089 | 0.9203 | 0.7138–0.9796 | 0.9486 | 0.8080–0.9870 | 0.9508 | 0.8155–0.9875 |
| wPLI | 0.4434 | 0–0.8252 | 0.9093 | 0.6789–0.9767 | 0.9565 | 0.8356–0.9890 | 0.9272 | 0.8078–0.9814 |
| PLWT | 0.7060 | 0.1807–0.9179 | 0.9212 | 0.7164–0.9798 | 0.9486 | 0.8078–0.9870 | 0.9501 | 0.8132–0.9874 |
95% CI represents the confidence interval with α = 0.05
The ICC values in terms of the characteristic path length, clustering coefficient and SWI are displayed in Tables 3, 4, 5 respectively. Similar to the results of functional connectivity, on the whole, the PLWT index achieves a good to excellent TRT reliability in all the graph measures across the four frequency bands. It substantially outperforms PLI and wPLI in the theta band and is on a par with the two indices in the other frequency bands. PLV achieves better performance in the theta band than the other indices but achieves lower ICC values especially in the alpha-1 and alpha-2 bands.
Table 3.
ICC values of characteristic path length for PLV, PLI, wPLI and PLWT with 95% confidence intervals in different frequency bands
| Theta | Alpha-1 | Alpha-2 | Beta | |||||
|---|---|---|---|---|---|---|---|---|
| ICC | 95% CI | ICC | 95% CI | ICC | 95% CI | ICC | 95% CI | |
| PLV | 0.9380 | 0.7717–0.9842 | 0.5590 | 0–0.8687 | 0.8116 | 0.4097–0.9496 | 0.9188 | 0.7089–0.9792 |
| PLI | 0.5706 | 0–0.8728 | 0.9258 | 0.7313–0.9810 | 0.9633 | 0.8602–0.9908 | 0.9416 | 0.7840–0.9852 |
| wPLI | 0.4650 | 0–0.8337 | 0.8972 | 0.6419–0.9734 | 0.9630 | 0.8588–0.9907 | 0.9043 | 0.6635–0.9754 |
| PLWT | 0.6107 | 0.0136–0.8867 | 0.9225 | 0.7207–0.9802 | 0.9477 | 0.8047–0.9867 | 0.8584 | 0.5304–0.9628 |
95% CI represents the confidence interval with α = 0.05
Table 4.
ICC values of clustering coefficient for PLV, PLI, wPLI and PLWT with 95% confidence intervals in different frequency bands
| Theta | Alpha-1 | Alpha-2 | Beta | |||||
|---|---|---|---|---|---|---|---|---|
| ICC | 95% CI | ICC | 95% CI | ICC | 95% CI | ICC | 95% CI | |
| PLV | 0.8694 | 0.5609–0.9659 | 0.5610 | 0–0.8694 | 0.6182 | 0.0257–0.8893 | 0.8336 | 0.4649–0.9559 |
| PLI | 0.7065 | 0.1817–0.9181 | 0.8678 | 0.5564–0.9654 | 0.8443 | 0.4926–0.9589 | 0.9226 | 0.7209–0.9802 |
| wPLI | 0.5455 | 0–0.8639 | 0.8483 | 0.5034–0.9601 | 0.7291 | 0.2264–0.9251 | 0.8807 | 0.5932–0.9690 |
| PLWT | 0.8717 | 0.5675–0.9665 | 0.8894 | 0.6186–0.9713 | 0.8705 | 0.5641–0.9662 | 0.9023 | 0.6574–0.9748 |
95% CI represents the confidence interval with α = 0.05
Table 5.
ICC values of SWI for PLV, PLI, wPLI and PLWT with 95% confidence intervals in different frequency bands
| Theta | Alpha-1 | Alpha-2 | Beta | |||||
|---|---|---|---|---|---|---|---|---|
| ICC | 95% CI | ICC | 95% CI | ICC | 95% CI | ICC | 95% CI | |
| PLV | 0.8846 | 0.6045–0.9700 | 0.5493 | 0–0.8652 | 0.5998 | 0–0.8830 | 0.8795 | 0.5896–0.9686 |
| PLI | 0.5458 | 0–0.8640 | 0.6645 | 0.1040–0.9046 | 0.6002 | 0–0.8831 | 0.8108 | 0.4079–0.9494 |
| wPLI | 0.4897 | 0–0.8432 | 0.6498 | 0.0784–0.8998 | 0.6304 | 0.0456–0.8934 | 0.5055 | 0–0.8491 |
| PLWT | 0.8511 | 0.5106–0.9608 | 0.9127 | 0.6896–0.9776 | 0.9284 | 0.7398–0.9817 | 0.9104 | 0.6823–0.9770 |
95% CI represents the confidence interval with α = 0.05
Discussion
In this paper, we propose the phase lag-based PLWT index to measure functional connectivity under the framework of the Wilcoxon signed-rank test. The PLWT index aims to give an accurate and robust estimation of functional connectivity by using only the phase information. Furthermore, it is able to automatically derive the binary adjacency matrix of a functional network by selecting the most relevant connections with the help of the Wilcoxon signed-rank test, avoiding applying an arbitrary threshold. More importantly, the fundamental idea behind the PLWT index is quite straightforward. That is, PLWT employs the Wilcoxon signed-rank test framework to test the asymmetry of the distribution of the phase differences, where the statistic is designed based on the ranks of the phase differences. In this way, the statistical significance of such asymmetry is determined for each pair of channels and then used to identify the underlying neural interactions, i.e., the functional connections.
Compared to PLV, PLI and wPLI, the proposed PLWT is expected to inherit the advantages of these indices while developing its own favorable features. Firstly, PLWT takes advantages of the phase lag, which effectively reduces the volume conduction effect by discarding the 0 mod π phase differences. Secondly, the sensitivity to noise is alleviated for PLWT by assigning the small phases differences with smaller weights. Thirdly, the weights are determined by the ranks of these phase differences rather than their magnitudes or amplitudes, which reduces the influence of outliers and overestimation. Fourthly, PLWT uniquely adopts the Wilcoxon signed-rank test, which provides solid statistical evidence to identify the significant functional connections without applying a threshold. Extensive experiments have been conducted to comprehensively evaluate the performance of PLWT, PLV, PLI and wPLI.
Results on the simulated EEG datasets in Figs. 1 and 2 show that PLWT evidently outperforms PLV and PLI in terms of the resistance against volume conduction and noise, with its performance comparable to that of wPLI. This superior performance of PLWT benefits from the adoption of the phase lag and its weighting procedure of the phase differences. Moreover, PLWT alleviates the problem of overestimating the functional connectivity for that it is less sensitive to outliers by using the ranks of these phase differences as weights. Following the previous studies (Gross et al. 2001; Haufe and Ewald 2019), we have analyzed the sensitivity of these indices to noise on simulated EEG data with the white Gaussian noise added in the experiment. It provides a convenient and straightforward way to test their performance. However, for a better evaluation, other factors such as the SNR level and the types of noise should also be considered and studied on more realistic EEG data. Therefore, we would like to point out that the experiment could be further conducted in more realistic scenarios and by varying the SNR level and including non-Gaussian signals.
Results in Figs. 4, 5, 6 derived on the resting-state EEG data indicate that the brain functional networks constructed by PLWT exhibit an evident scale-free characteristic. It achieves the best goodness of fit between its degree distribution and the power-law distribution among the four indices. Scale-free characteristic has been considered as an important feature of brain networks, as implied by the degree distribution following an exponentially truncated power-law (Bullmore and Sporns 2009). Previous studies have consistently reported the observations of scale-free property in brain networks on fMRI (Eguiluz et al. 2003; Van den Heuvel 2008), MEG (Bassett et al. 2006) and EEG data (Stam and de Bruin 2010). Our results here further validate the effectiveness and soundness of the PLWT index in characterizing the functional connectivity and functional networks.
Results in Tables 2, 3, 5 demonstrate another favorable feature of PLWT, where the overall TRT reliability reaches a good to excellent level for the functional connectivity and the three graph measures. It indicates that the PLWT index is able to remain stable over time. Besides, Fig. 7 shows that the PLWT index is sensitive to inter-subject variability, especially in the alpha band. This could be beneficial for studying individual differences in brain functional networks. One thing to be noted is that we only analyzed the ICC of graph measures with a network size of 19 (i.e., number of nodes) on the EEG data of 10 subjects in this experiment. Previous studies have found that the values of graph measures significantly depend on the network size (Zalesky et al. 2010; Joudaki et al. 2012). Besides, it is believed that sample size has an effect on the power of ICC (Shoukri et al. 2004). Though 10 subjects can provide a power value of 0.8 to achieve the ICC value of at least 0.7, more comprehensive analysis with higher power could be conducted by using datasets of larger sample sizes under different network sizes.
A unique feature of PLWT is that it naturally derives sparse functional connectivity (as shown in Fig. 6 revealed by the connection density), as it has a procedure of selecting significant connections by using the Wilcoxon signed-rank test. Previous studies have explored the sparsity nature in neural activities (Quiroga et al. 2008) and in brain functional networks (Bullmore and Sporns 2012), which provides biological foundations for the sparsity in functional connectivity. On the one hand, such sparseness can reduce the computational burden of the subsequent analysis and improve the interpretability of the derived functional connectivity. On the other hand, this would potentially in theory increase the risk of producing unconnected nodes. This might change the network size, which could cause problems when comparing across networks. However, this could be addressed by selecting a suitable significance level to adjust the network connection density for specific datasets and research aims. In our experiments, no unconnected node was produced with ranging from 0.0001 to 0.05. Besides, we found that the commonly-accepted significance level provides enough power to effectively and stably determine the functional connections, as revealed by Figs. 3 and 6.
Besides, the PLWT index benefits from the Wilcoxon signed-rank test so that it can automatically identify the important connections without applying an arbitrary threshold. However, performing the hypothesis tests would increase the computational burden of PLWT, especially on large datasets. To facilitate the application of PLWT to the real-time analysis of EEG data, techniques such as using lower-level programming languages (e.g. C++) and adopting parallel computing tools could be employed to increase its computational efficiency (García-Prieto et al. 2017).
Moreover, the PLWT index is only studied within specific frequency bands in this paper. Some studies have shown that cross-frequency analysis of functional connectivity provides new insights into the brain functions (Buiza et al. 2018; Yu et al. 2020). Future works could be conducted by applying the PLWT index to cross-frequency analyses. In addition, the PLWT index, as well as the other indices studied in this paper, only computes the pairwise associations between nodes. Other indices that use multivariate or non-linear methods to depict the functional connectivity could be developed to further benefit the study of M/EEG signals (Jalili 2015; Imperatori et al. 2019).
Conclusion
As a novel functional connectivity index, the proposed PLWT index depicts the underlying functional connections that are robust to volume conduction and noise based on the phase lag with a weighting procedure. More importantly, it automatically generates a binary adjacency matrix given a specific significance level under the framework of the Wilcoxon signed-rank test, so that it preserves the most important connections without manually applying a threshold. The experimental results on the simulated datasets show that PLWT is capable of identifying robust connections, which show good resistance to volume conduction as well as to noise perturbation. Besides, on the resting-state EEG datasets, the PLWT-derived brain functional networks exhibit great scale-free characteristics across different frequency bands, further validating the efficacy of PLWT. In addition, both the global mean of functional connectivity and the graph measures extracted from the PLWT-based networks achieve a TRT reliability of a good to excellent level, demonstrating the stability of PLWT as a functional connectivity index. In conclusion, PLWT provides a useful index to reveal the underlying functional connectivity effectively and reliably.
Acknowledgements
This work was supported in part by the National Natural Science Foundation of China under Grant 61773114 and the Key Research and Development Plan (Industry Foresight and Common Key Technology) of Jiangsu Province under Grant BE2017007-1.
Author contributions
XL, YW, and MW incorporated the algorithm and wrote the manuscritpt. YG and ZY collected the data and revised the manuscript. HW and ZL conceived and designed the study. HF reviewed the manuscript. All authors read and approved the manuscript.
Compliance with Ethical Standards
Conflict of interest
The authors declare that they have no conflict of interest.
Ethical approval
All the procedures performed in the studies involving human participants were in accordance with the ethical standards of the institutional and/or national research committee as well as with the 1964 Helsinki declaration and its later amendments, or comparable ethical standards.
Informed consent
Informed consent was obtained from all the individual participants included in the study.
Footnotes
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Xuan Li, Yunqiao Wu, Mengting Wei these authors contributed equally to this work.
Contributor Information
Haixian Wang, Email: hxwang@seu.edu.cn.
Zhanli Li, Email: lizl@xust.edu.cn.
References
- Bandettini PA, Bullmore E. Endogenous oscillations and networks in functional magnetic resonance imaging. Hum Brain Mapp. 2010;29(7):737–739. doi: 10.1002/hbm.20607. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barabási AL, Albert R. Emergence of scaling in random networks. Science. 1999;286:509–512. doi: 10.1126/science.286.5439.509. [DOI] [PubMed] [Google Scholar]
- Bassett DS, Meyer-Lindenberg A, Achard S, Duke T, Bullmore E. Adaptive reconfiguration of fractal small-world human brain functional networks. Proc Natl Acad Sci. 2006;103(51):19518–19523. doi: 10.1073/pnas.0606005103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bastos AM, Schoffelen JM. A tutorial review of functional connectivity analysis methods and their interpretational pitfalls. Front Syst Neurosci. 2016;9:175. doi: 10.3389/fnsys.2015.00175. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Biswal BB, Van KJ, Hyde JS. Simultaneous assessment of flow and BOLD signals in resting-state functional connectivity maps. NMR Biomed. 1997;10(4–5):165–170. doi: 10.1002/(SICI)1099-1492(199706/08)10:4/5<165::AID-NBM454>3.0.CO;2-7. [DOI] [PubMed] [Google Scholar]
- Braun U, Plichta MM, Esslinger C, Sauer C, Haddad L, Grimm O, Mier D, Mohnke S, Heinz A, Erk S, Walter H. Test–retest reliability of resting-state connectivity network characteristics using fMRI and graph theoretical measures. Neuroimage. 2012;59(2):1404–1412. doi: 10.1016/j.neuroimage.2011.08.044. [DOI] [PubMed] [Google Scholar]
- Buiza E, Rodríguez-Martínez EI, Barriga-Paulino CI, Arjona A, Gomez CM. Developmental trends of theta–beta interelectrode power correlation during resting state in normal children. Cogn Neurodyn. 2018;12(3):255–269. doi: 10.1007/s11571-018-9476-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bullmore ET, Bassett DS. Brain graphs: graphical models of the human brain connectome. Annu Rev Clin Psychol. 2011;7(1):113–140. doi: 10.1146/annurev-clinpsy-040510-143934. [DOI] [PubMed] [Google Scholar]
- Bullmore E, Sporns O. Complex brain networks: graph theoretical analysis of structural and functional systems. Nat Neurosci. 2009;10(3):186–198. doi: 10.1038/nrn2575. [DOI] [PubMed] [Google Scholar]
- Bullmore E, Sporns O. The economy of brain network organization. Nat Neurosci. 2012;13(5):336–349. doi: 10.1038/nrn3214. [DOI] [PubMed] [Google Scholar]
- Daffertshofer A, Stam CJ (2007) Influences of volume conduction on phase distributions. In: International congress series, pp 209–212
- Daneshi A, Azarnoush H, Towhidkhah F, Bernardin D, Faubert J. Brain activity during time to contact estimation: an EEG study. Cogn Neurodyn. 2019;14:155–168. doi: 10.1007/s11571-019-09563-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deuker L, Bullmore ET, Smith M, Christensen S, Nathan PJ, Rockstroh B, Bassett DS. Reproducibility of graph metrics of human brain functional networks. Neuroimage. 2009;47(4):1460–1468. doi: 10.1016/j.neuroimage.2009.05.035. [DOI] [PubMed] [Google Scholar]
- Eguiluz VM, Cecchi G, Chialvo DR, Baliki M, Apkarian AV. Scale-free structure of brain functional networks. Phys Rev Lett. 2003;94(2):018102. doi: 10.1103/PhysRevLett.94.018102. [DOI] [PubMed] [Google Scholar]
- Erdős P, Rényi A. On the strength of connectedness of a random graph. Acta Math Hung. 1964;12(1–2):261–267. doi: 10.1007/BF02066689. [DOI] [Google Scholar]
- García-Prieto J, Bajo R, Pereda E. Efficient computation of functional brain networks: towards real-time functional connectivity. Front Neuroinform. 2017;11:8. doi: 10.3389/fninf.2017.00008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gross J, Kujala J, Hämäläinen M, Timmermann L, Schnitzler A, Salmelin R. Dynamic imaging of coherent sources: studying neural interactions in the human brain. Proc Natl Acad Sci. 2001;98(2):694–699. doi: 10.1073/pnas.98.2.694. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hardmeier M, Hatz F, Bousleiman H, Schindler C, Stam CJ, Fuhr P. Reproducibility of functional connectivity and graph measures based on the phase lag index (PLI) and weighted phase lag index (wPLI) derived from high resolution EEG. PLoS ONE. 2014;9(10):e108648. doi: 10.1371/journal.pone.0108648. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haufe S, Ewald A. A simulation framework for benchmarking EEG-based brain connectivity estimation methodologies. Brain Topogr. 2019;32(4):625–642. doi: 10.1007/s10548-016-0498-y. [DOI] [PubMed] [Google Scholar]
- Homan RW, Herman J, Purdy P. Cerebral location of international 10–20 system electrode placement. Electroencephalogr Clin Neurophysiol. 1987;66(4):376–382. doi: 10.1016/0013-4694(87)90206-9. [DOI] [PubMed] [Google Scholar]
- Imperatori LS, Betta M, Cecchetti L, Canales-Johnson A, Ricciardi E, Siclari F, Pietrini P, Chennu S, Bernardi G. EEG functional connectivity metrics wPLI and wSMI account for distinct types of brain functional interactions. Sci Rep. 2019;9(1):1–15. doi: 10.1038/s41598-019-45289-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jalili M. Multivariate synchronization analysis of brain electroencephalography signals: a review of two methods. Cogn Comput. 2015;7(1):3–10. doi: 10.1007/s12559-013-9213-4. [DOI] [Google Scholar]
- Joudaki A, Salehi N, Jalili M, Knyazeva MG. EEG-based functional brain networks: does the network size matter? PLoS ONE. 2012;7(4):e35673. doi: 10.1371/journal.pone.0035673. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kuramoto Y (1975) Self-entrainment of a population of coupled non-linear oscillators. In: International symposium on mathematical problems in theoretical physics, pp 420–422
- Lachaux J, Rodriguez E, Martinerie J, Varela FJ. Measuring phase synchrony in brain signals. Hum Brain Mapp. 1999;8(4):194–208. doi: 10.1002/(SICI)1097-0193(1999)8:4<194::AID-HBM4>3.0.CO;2-C. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee UC, Oh GJ, Kim S, Noh G, Choi B, Mashour GA. Brain networks maintain a scale-free organization across consciousness, anesthesia, and recovery: evidence for adaptive reconfiguration. Anesthesiology. 2010;113(5):1081–1091. doi: 10.1097/ALN.0b013e3181f229b5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mora-Sánchez A, Dreyfus G, Vialatte FB. Scale-free behaviour and metastable brain-state switching driven by human cognition, an empirical approach. Cogn Neurodyn. 2019;13(5):437–452. doi: 10.1007/s11571-019-09533-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nunez PL, Williamson SJ. Neocortical dynamics and human EEG rhythms. Phys Today. 1996;49(4):177–178. doi: 10.1063/1.2807585. [DOI] [Google Scholar]
- Ortiz E, Stingl K, Münssinger J, Braun C, Preissl H, Belardinelli P. Weighted phase lag index and graph analysis: preliminary investigation of functional connectivity during resting state in children. Comput Math Methods Med. 2012;1:186353. doi: 10.1155/2012/186353. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Quiroga RQ, Kreiman G, Koch C, Fried I. Sparse but not “grandmother-cell” coding in the medial temporal lobe. Trends Cogn Sci. 2008;12(3):87–91. doi: 10.1016/j.tics.2007.12.003. [DOI] [PubMed] [Google Scholar]
- Rubinov M, Sporns O. Complex network measures of brain connectivity: uses and interpretations. Neuroimage. 2010;52(3):1059–1069. doi: 10.1016/j.neuroimage.2009.10.003. [DOI] [PubMed] [Google Scholar]
- Shoukri MM, Asyali MH, Donner A. Sample size requirements for the design of reliability study: review and new results. Stat Methods Med Res. 2004;13(4):251–271. doi: 10.1191/0962280204sm365ra. [DOI] [Google Scholar]
- Shrout PE, Fleiss JL. Intraclass correlations: uses in assessing rater reliability. Psychol Bull. 1979;86(2):420–428. doi: 10.1037/0033-2909.86.2.420. [DOI] [PubMed] [Google Scholar]
- Stam CJ, de Bruin EA. Scale-free dynamics of global functional connectivity in the human brain. Hum Brain Mapp. 2010;22(2):97–109. doi: 10.1002/hbm.20016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stam CJ, Nolte G, Daffertshofer A. Phase lag index: assessment of functional connectivity from multichannel EEG and MEG with diminished bias from common sources. Hum Brain Mapp. 2007;28(11):1178–1193. doi: 10.1002/hbm.20346. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Strogatz SH. From Kuramoto to Crawford: exploring the onset of synchronization in populations of coupled oscillators. Physica D. 2000;143(1–4):1–20. doi: 10.1016/S0167-2789(00)00094-4. [DOI] [Google Scholar]
- Tafreshi TF, Daliri MR, Ghodousi M. Functional and effective connectivity based features of EEG signals for object recognition. Cogn Neurodyn. 2019;13(6):555–566. doi: 10.1007/s11571-019-09556-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taheri SM, Hesamian G. A generalization of the Wilcoxon signed-rank test and its applications. Stat Pap. 2013;54(2):457–470. doi: 10.1007/s00362-012-0443-4. [DOI] [Google Scholar]
- Van den Heuvel MP, Stam CJ, Boersma M, Hulshoff Pol HE. Small-world and scale-free organization of voxel-based resting-state functional connectivity in the human brain. Neuroimage. 2008;43:528–539. doi: 10.1016/j.neuroimage.2008.08.010. [DOI] [PubMed] [Google Scholar]
- Vinck M, Oostenveld R, Van Wingerden MV, Battaglia F, Pennartz CM. An improved index of phase-synchronization for electrophysiological data in the presence of volume-conduction, noise and sample-size bias. Neuroimage. 2011;55(4):1548–1565. doi: 10.1016/j.neuroimage.2011.01.055. [DOI] [PubMed] [Google Scholar]
- Weir JP. Quantifying test-retest reliability using the intraclass correlation coefficient and the SEM. J Strength Cond Res. 2005;19(1):231–240. doi: 10.1519/15184.1. [DOI] [PubMed] [Google Scholar]
- Wilcoxon F. Individual comparisons by ranking methods. Biom Bull. 1945;1:80–83. doi: 10.2307/3001968. [DOI] [Google Scholar]
- Wu Y, Gan JQ, Wang H (2017) Identifying intrinsic phase lag in EEG signals from the perspective of Wilcoxon signed-rank test. In: International conference on neural information processing (ICONIP), pp 709–717
- Yu H, Zhu L, Cai L, Wang J, Liu C, Shi N, Liu J. Variation of functional brain connectivity in epileptic seizures: an EEG analysis with cross-frequency phase synchronization. Cogn Neurodyn. 2020;14(1):35–49. doi: 10.1007/s11571-019-09551-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zalesky A, Fornito A, Harding IH, Cocchi L, Yücel M, Pantelis C, Bullmore ET. Whole-brain anatomical networks: does the choice of nodes matter? Neuroimage. 2010;50(3):970–983. doi: 10.1016/j.neuroimage.2009.12.027. [DOI] [PubMed] [Google Scholar]
- Zhang L, Gan JQ, Wang H. Mathematically gifted adolescents mobilize enhanced workspace configuration of theta cortical network during deductive reasoning. Neuroscience. 2015;289:334–348. doi: 10.1016/j.neuroscience.2014.12.072. [DOI] [PubMed] [Google Scholar]
- Zhang L, Gan JQ, Wang H. Localization of neural efficiency of the mathematically gifted brain through a feature subset selection method. Cogn Neurodyn. 2015;9(5):495–508. doi: 10.1007/s11571-015-9345-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zuo XN, Xing XX. Test-retest reliabilities of resting-state fMRI measurements in human brain functional connectomics: a systems neuroscience perspective. Neurosci Biobehav Rev. 2014;45:100–118. doi: 10.1016/j.neubiorev.2014.05.009. [DOI] [PubMed] [Google Scholar]