Abstract
Geometry and topology are fundamental concepts, which underlie a wide range of fascinating physical phenomena such as topological states of matter and topological defects. In quantum mechanics, the geometry of quantum states is fully captured by the quantum geometric tensor. Using a qubit formed by an NV center in diamond, we perform the first experimental measurement of the complete quantum geometric tensor. Our approach builds on a strong connection between coherent Rabi oscillations upon parametric modulations and the quantum geometry of the underlying states. We then apply our method to a system of two interacting qubits, by exploiting the coupling between the NV center spin and a neighboring 13C nuclear spin. Our results establish coherent dynamical responses as a versatile probe for quantum geometry, and they pave the way for the detection of novel topological phenomena in solid state.
Keywords: quantum geometry, topological physics, quantum measurement, quantum control, quantum information
INTRODUCTION
The quantum geometric tensor (QGT) constitutes a central and ubiquitous concept in quantum mechanics, by providing a geometric structure to the Hilbert space [1–5]. The imaginary part of this tensor corresponds to the well-known Berry curvature [6,7], which acts as an effective ‘electromagnetic’ tensor in parameter space. This geometric quantity, which is formally associated with the parallel transport of wave functions [8], is responsible for striking observable phenomena such as the geometric phase [8], the anomalous Hall effect [9] and topological states of matter [10]. In contrast, the real part of the QGT constitutes the Fubini-Study metric [2,3,5], which defines a notion of distance (a Riemannian metric) in parameter space through the overlap of wavefunctions. This ‘quantum metric’, which is intimately related to quantum fluctuations and dissipative responses of the system [2,5,11,12], has been shown to play an important role in various contexts, including quantum phase transitions [13], open quantum systems [14], orbital magnetism [15,16], localization in insulators [11], semiclassical dynamics [17,18], excitonic Lamb-shifts in transition-metal dichalcogenides [19], superfluidity in flat bands [20] and topological matter [21,22]. In the context of quantum information, the quantum metric is equivalent to the quantum Fisher information, which is a witness for multipartite entanglement [23].
Various manifestations of the QGT have been observed in experiments, using very different physical platforms and probes. On the one hand, the local Berry curvature has been detected in ultracold atomic gases [24–26], coupled optical fibers [27], and solids [28,29]. On the other hand, a first manifestation of the quantum metric—the so-called Wannier-spread functional of Bloch bands [30]—was recently measured in cold atoms [31], based on the proposal [32]; see [12,33–35] for other proposals to detect quantum geometry. Nevertheless, direct and systematic measurement of the complete QGT has never been performed.
Here, we report on the first experimental measurement of the complete QGT, using a qubit formed by an NV center spin in diamond. Following the proposal of [32], we exploit the relation between the QGT and the response of quantum systems upon parametric modulations to map out the full Fubini-Study metric as well as the local Berry curvature of the underlying quantum states. We then apply our method to a system of two interacting qubits, obtained by coupling the NV center spin to a nearby 13C nuclear spin. Our results not only enforce the deep connections between out-of-equilibrium dynamics and quantum geometry [36–44], but also reveal a universal tool for detection of geometric and topological properties in quantum systems.
DETECTING THE QGT THROUGH RABI OSCILLATION
We start by considering the Hamiltonian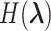 
of a generic discrete quantum system, which depends on a set of dimensionless parameters 
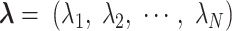, where 
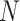is the dimension of parameter space. For a single qubit, the relevant parameter space corresponds to the two-dimensional Bloch sphere. Defining the eigenstates and eigenvalues of this generic Hamiltonian, 
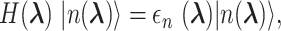a geometric structure emerges upon projecting the dynamics onto a single (non-degenerate) band 
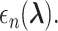The resulting quantum geometry is captured by the QGT, which is defined as [7]
 |
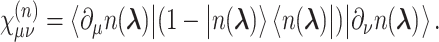(1) |
For simplicity, hereafter we denote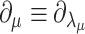 
. The real part 
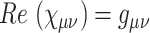is the Fubini-Study metric, which introduces a notion of distance in parameter space, while the imaginary part 
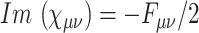is related to the Berry curvature
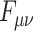responsible for the Berry phase. It is useful to express the QGT in the form
 |
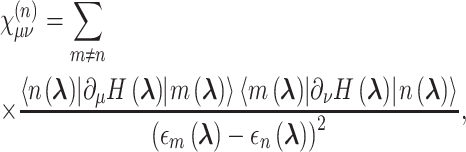(2) |
so as to highlight the relation between this geometric quantity and the coupling matrix elements connecting the eigenstates 
and 
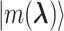upon a parametric modulation [32],
 |
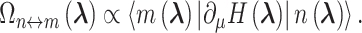(3) |
EXPERIMENTAL SETUP
In our experiment, we first perform a full quantum-geometric measurement using a two-level system, as described by the general Hamiltonian
 |
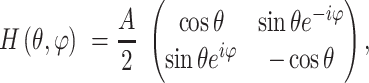(4) |
where the angles 
form the relevant parameter space (the Bloch sphere). Considering the low-energy dressed state, the components of the QGT read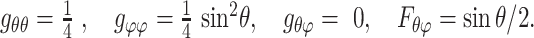 
These components fully characterize the underlying quantum geometry: the quantum metric 
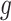corresponds to the natural metric of a sphere 
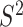, embedded in 
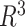with fixed radius 
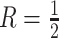, while the Berry curvature 
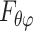corresponds to the ‘magnetic’ field of a fictitious Dirac monopole located at the center of that sphere [22].
The experimental setup is sketched in Fig. 1D. The two-level system in Eq. (4) is obtained from a single nitrogen-vacancy (NV) center in an electronic grade diamond. We apply a magnetic field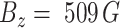 
along the NV axis to lift the degeneracy of the states 
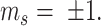A two-level system is supported by the spin sublevels 
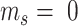and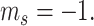 
We first prepare the system in the eigenstate of the Hamiltonian 
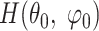, i.e. 
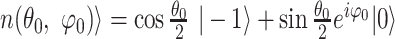. This is achieved by first applying a 532 nm green laser pulse to initialize the NV center spin in the 
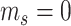state. A subsequent microwave pulse 
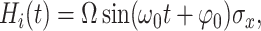applied over a duration 
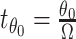, rotates the NV center spin around the axis 
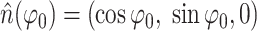by an angle 
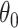. The initial state preparation is verified by a spin-locking type experiment, which confirms that the NV spin is prepared in the eigenstate of 
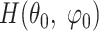[see supplementary data].
Figure 1.
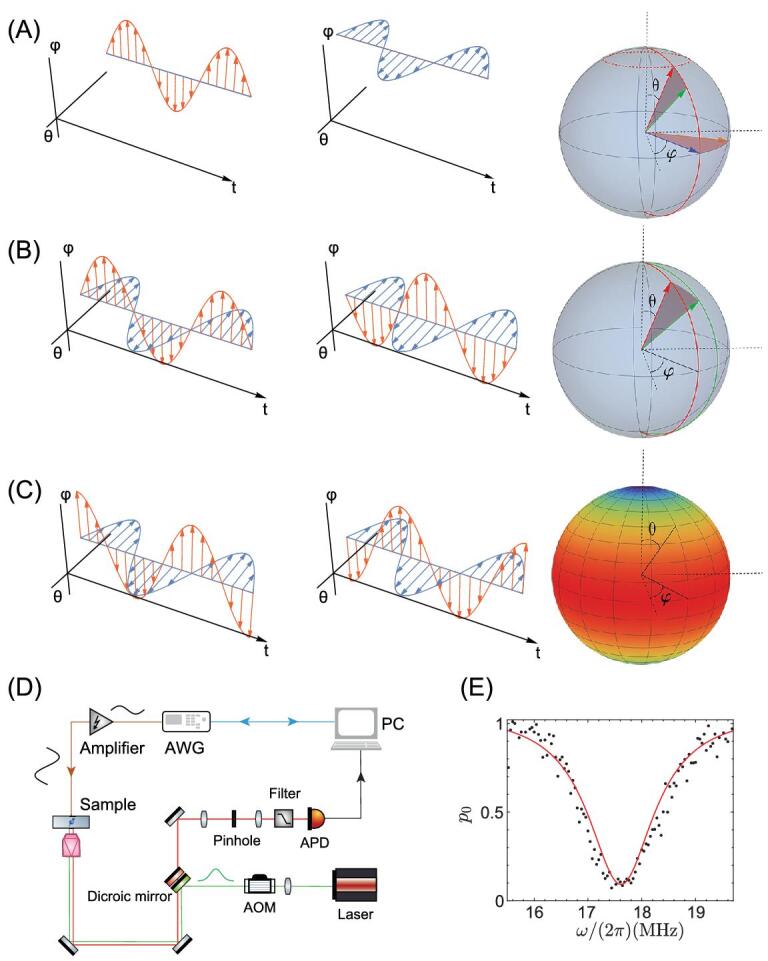
Probing quantum geometry through coherent responses on parametric modulations. (A–C) show different types of parametric modulations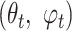 
, including (A, B) linear parametric modulation 
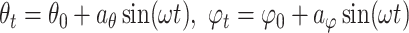for measurement of the diagonal [off-diagonal] element of the Fubini-Study metric with 
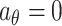or 
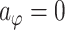(A) [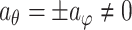
(B)]; (C) elliptical parametric modulation for the measurement of the local Berry curvature (as indicated by color map) with 
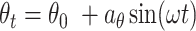and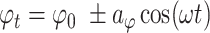 
. (D) Experimental setup used for the quantum-geometric measurement, based on an NV center spin in diamond. A green laser pulse polarizes the NV center spin into the 
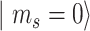state. The engineered microwave created from an arbitrary waveform generator (Tektronix AWG 70002A, 16GS/s) is amplified before being delivered to the sample and coherently drives the NV center spin. The NV center spin state is detected by an APD via spin-dependent fluorescence. (E) An example of parametric-modulation resonance measurement. The probability that the NV center spin remains in the initial eigenstate at time 
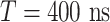as a function of the modulation frequency, for a linear parametric modulation 
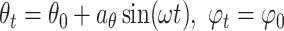with 
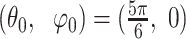and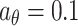 
.
The precise control over the AWG allows us to engineer the microwave driving field with accurate amplitude and phase modulation. This leads to implementation of the generic two-level system
 |
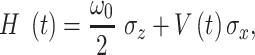(5) |
where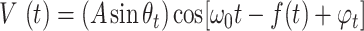
. In the experiment, we calibrate the driving amplitude in the Hamiltonian [Eq. (5)] with the output power of the AWG by measuring the Rabi frequency of the NV center spin [see supplementary data]. The amplitude modulation 
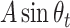and the phase modulation 
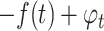are synthesized by waveform programming in the AWG. The additional phase control function has the form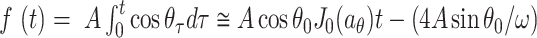 
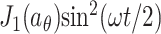, where 
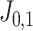are the zeroth and first order Bessel functions of the first kind, respectively [see supplementary data]. Taking the limit
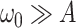, such an engineered microwave driving field allows us to realize the effective Hamiltonian in Eq. (4) with the designed parametric modulation [see supplementary data]:
 |
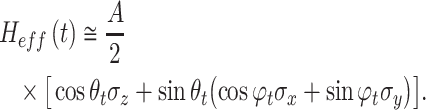(6) |
The parametric modulation drives a coherent transition between the eigenstates of 
, which is detected by rotating the NV center spin around the axis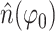 
by an angle 
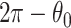. This rotation maps the eigenstates of 
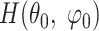back to the NV center spin state 
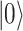and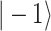 
, which is then measured by spin-dependent fluorescence.
EXPERIMENTAL RESULTS
In the experiment, we implement two types of modulations [32]: (a) a ‘linear’ modulation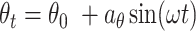 
, 
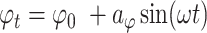; (b) an ‘elliptical’ modulation 
, 
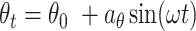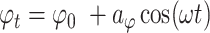; see Fig. 1A–C. Setting 
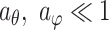, the time-dependent Hamiltonian can be expressed as
 |
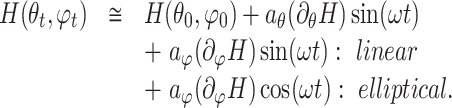(7) |
After preparing the NV center spin in the eigenstate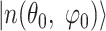 
of the Hamiltonian 
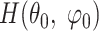, we apply the engineered microwave driving field with parametric modulation [see Eq. (5)] and fix the time duration 
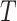. We sweep the parametric modulation frequency 
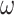, and measure the probability 
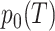that the NV spin remains in the initial eigenstate 
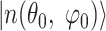. In Fig. 1E, we show an example of such a parametric-modulation resonance measurement; see supplementary data for the experimental data using other types of modulations. The results indicate that a coherent transition between the eigenstates becomes resonant when 
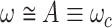. We then measure the resonant coherent oscillation upon parametric modulation with 
=
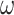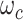, as shown in Fig. 2A–C. The observed Rabi frequencies under resonant parametric modulations, which reveal the information about the coupling matrix elements connecting the eigenstates [see Eq. (3)] upon parametric modulation, are shown in Fig. 2D–F. The experimental results allow us to determine the quantum geometry of the prepared dressed states precisely.
Figure 2.
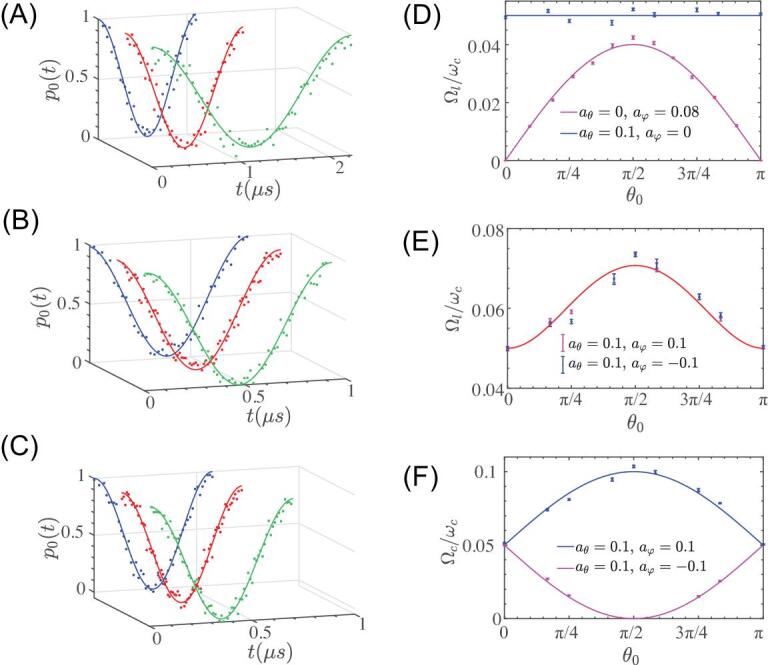
Coherent transitions induced by parametric modulations. (A, B) Resonant oscillation under a linear parametric modulation with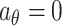 
, 
(A) and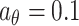 
, 
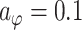(B). (C) Resonant oscillation under an elliptical parametric modulation with 
, 
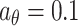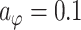. The other experimental parameters are: (A) 
(
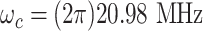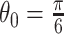, green), 
(
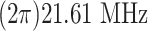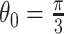, red),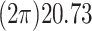 
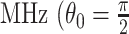, blue); (B) 
(
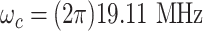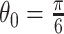, green), 
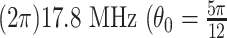, red), 
(
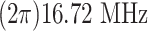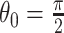, blue); (C) 
(
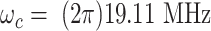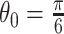, green),
(
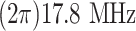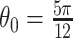, red), 
(
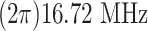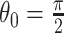, blue). (D–F) Rabi frequency of resonant coherent transitions upon parametric modulations (in the unit of resonant frequency
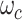), as a function of the parameter 
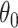, for linear (D, E) and elliptical (F) parametric modulations. The curves show theoretical predictions. In (A–F), we set the parameter 
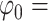0.
As a central result, we show in Fig. 3 the experimental extraction of the full QGT, based on Rabi-oscillation measurements. This provides a first demonstration that coherent responses upon parametric modulations can be used as a powerful tool to access the complete geometry of a discrete quantum system. We point out that the present quantum-geometry measurement is based on coherent dynamic responses upon periodic driving, and in this sense, it does not rely on any adiabaticity constraints (i.e. small modulation velocity [36,37]). It should be noted, however, that this method uses small modulation amplitudes, and hence small Rabi frequencies, which require systems exhibiting long coherence times. The agreement between the experiment results and the theoretical predictions can be improved by increasing the measurement time, which allows for better determination of the oscillation frequency. Furthermore, in contrast with the excitation-rate measurement of [31,32,41], the QGT is extracted from Rabi oscillations [39], where the initial state is recovered after each Rabi period; in principle, this allows for detection of geometry and topology through a non-destructive measurement.
Figure 3.
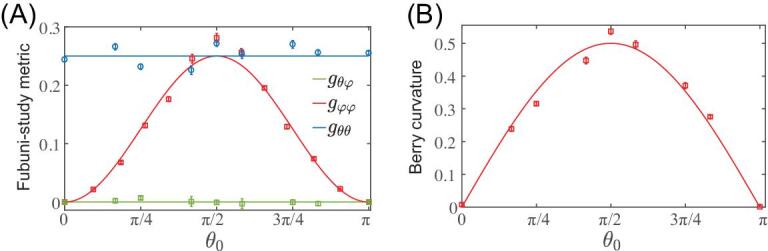
Extraction of the complete quantum geometric tensor. (A) The measured Fubini-Study metric, compared with the theoretical predictions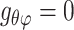 
(green curve), 
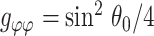(red curve) and 
(blue curve). (B) The measured local Berry curvature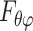 
is compared with the theoretical prediction 
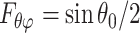. The experimental parameters are the same as in Fig. 2.
Besides, our quantum-geometry measurement can also be used to characterize the topology of the underlying system. For this analysis, we extend the Hamiltonian to the form
 |
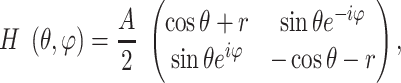(8) |
where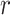 
is a tunable parameter. As for Eq. (4), the geometry of the Hamiltonian in Eq. (8) is that of a fictitious monopole located close to a sphere 
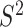, whose position in parametric space depends on the additional parameter 
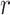. The topology of the system then relies on whether this fictitious monopole is located inside the sphere or not, as captured by the Chern number 
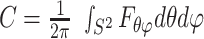[13]. Figure 4 shows the Berry curvature measurement in two distinct topological phases. In the non-trivial regime, the Chern number can equally be determined from the metric
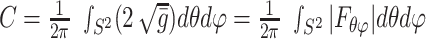, where 
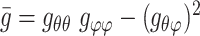is the determinant of the QGT [22]. Altogether, these results indicate that topology can indeed be finely analyzed based on our geometric-detection scheme.
Figure 4.
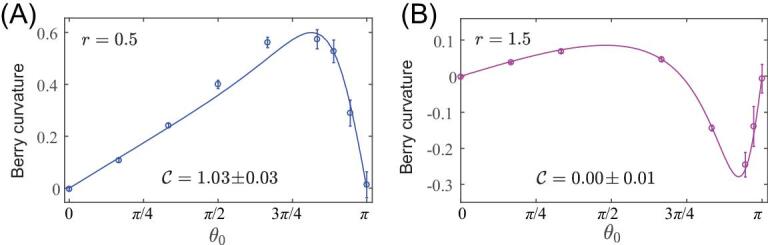
Berry curvature measurement across the topological transition. (A, B) show the measured local Berry curvature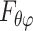 
for the Hamiltonian in Eq. (8), which describes a Dirac monopole located inside (A, 
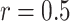) and outside (B, 
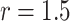) the Bloch sphere. The curves represent the corresponding theoretical values. The Chern number extracted from the data is indicated in both panels.
APPLICATION TO INTERACTING QUBITS
As a second application, we further extend our experiment to extract the QGT of an interacting two-qubit system. The interacting two-qubit system is formed by an NV center electron spin coupled to a 13C nuclear spin located in the vicinity of the NV center. We determine the strength of the corresponding spin-spin interactions using a pulsed optically detected magnetic resonance experiment; we obtain the interaction parameters: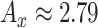 
MHz and 
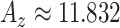MHz [see Eq. (9) below]. By engineering microwave driving fields with designed frequency and phase, we obtain the following effective Hamiltonian
 |
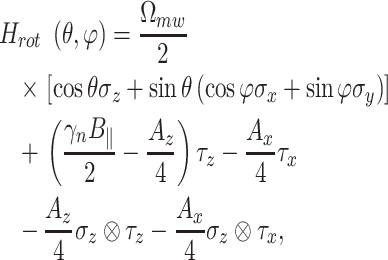(9) |
where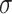 
and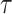 
are Pauli operators associated with the first and second qubits, respectively. Henceforth, we denote the eigenstates of the Hamiltonian in Eq. (9) as 
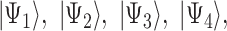according to their ordered eigenenergies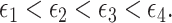 
The competition between the local term (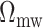
) and the spin-spin interaction in the Hamiltonian Eq. (9) leads to a rich topological phase diagram. In the regime 
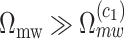, where
 |
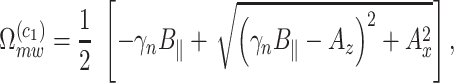(10) |
the spin-spin interaction becomes less significant and we thus recover the topological properties of the two-level system, for which the Chern number is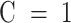 
in the eigenstate 
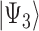(see the measurements described in the previous section); note that the other eigenstates exhibit similar behaviors. The spin-spin interaction eventually dominates upon decreasing the value of the local parameter; below the critical value, 
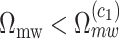, the Chern number of the eigenstate changes from 
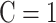to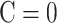 
, which can be seen as a drastic effect of the spin-spin interaction. This vanishing of the Chern number in the strongly interacting regime is clearly captured by our QGT measurement, as reported in Fig. 5. These results demonstrate the measurement of both the Fubini-Study metric and the Berry curvature deep in the interacting regime, and show excellent agreement with theoretical predictions [see supplementary data].
Figure 5.
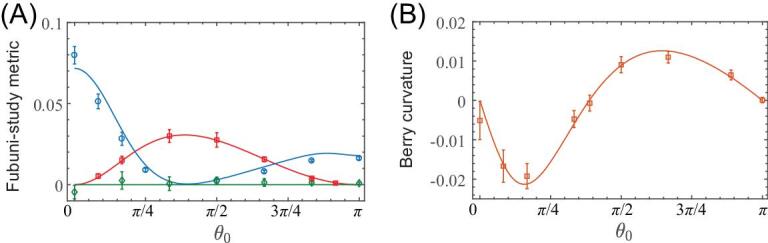
Quantum geometry of an interacting two-qubit system. (A) The measured Fubini-Study metric, compared with the theoretical predictions: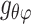 
(green curve), 
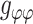(red curve) and 
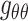(blue curve). (B) The measured local Berry curvature 
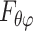is compared with the theoretical prediction (curve). The amplitude of the driving field [see Eq. (9)] is 
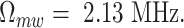The Chern number estimated from the integral of the Berry curvature is 
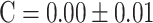, which is in agreement with the prediction (
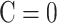) in this strongly interacting regime.
As previously noted, the QGT contains information regarding the entanglement properties of interacting systems, through the concept of quantum Fisher information [23]. As an interesting perspective, our detection method could be applied to more complex interacting systems in view of revealing their quantum fluctuations and entanglement properties.
CONCLUSION
To summarize, we have experimentally demonstrated a powerful connection between the quantum geometric tensor and the coherent dynamic response of a quantum system upon a parametric drive. Based on this fundamental relation, we first extracted the complete QGT, including all the components of the Fubini-Study metric and those of the local Berry curvature, by driving Rabi oscillations in a single qubit. These measurements clearly revealed the topological (monopole-type) structure associated with this simple setting. We point out that this method is readily applicable to observe other intriguing topological defects, such as tensor monopoles defined in 4D parameter spaces [22]. Furthermore, we have applied this detection method to an interacting two-qubit system, which suggests potential applications to many-body quantum systems with geometric features [12,32,45]. Altogether, our results demonstrate that coherent dynamic responses can serve as a powerful tool to access the geometric and topological properties of quantum systems and open a way to explore the fundamental role of the QGT in various scenarios, ranging from many-body systems to open quantum systems.
Note added
Materials and methods are available as supplementary material. Two other experimental measurements of the QGT were reported after the completion of our work [46], in polaritons [47] and superconducting qubits [48].
Supplementary Material
Acknowledgements
We thank G. Palumbo, M. Di Liberto, P. Zoller and Y. Liu for helpful discussions.
FUNDING
This work was supported by the National Natural Science Foundation of China (11574103, 11690030, 11690032, 11874024). M.B.P. is supported by the EU projects HYPERDIAMOND and AsteriQs, the BMBF project NanoSpin and DiaPol and the ERC Synergy grant BioQ. F.J. is supported by DFG (FOR 1493, SPP 1923), VW Stiftung, BMBF, ERC, EU (AsteriQs), BW Stiftung, Ministry of Science and Arts, Center for Integrated Quantum Science and Technology (IQST). T.O. is supported by JSPS KAKENHI (JP18H05857), RIKEN Incentive Research Project, and the Interdisciplinary Theoretical and Mathematical Sciences Program (iTHEMS) at RIKEN. N.G. is supported by the ERC Starting Grant TopoCold and the Fonds De La Recherche Scientifique (FRS-FNRS) (Belgium).
REFERENCES
- 1. Kibble TWB. Geometrization of quantum mechanics. Commun Math Phys 1979; 65: 189–201. [Google Scholar]
- 2. Provost J, Vallee G. Riemannian structure on manifolds of quantum states. Commun Math Phys 1980; 76: 289–301. [Google Scholar]
- 3. Anandan J, Aharonov Y. Geometry of quantum evolution. Phys Rev Lett 1990; 65: 1697–700. [DOI] [PubMed] [Google Scholar]
- 4. Brody DC, Hughston LP. Geometric quantum mechanics. J Geom Phys 2001; 38: 19–53. [Google Scholar]
- 5. Kolodrubetz M, Sels D, Mehta Pet al. Geometry and non-adiabatic response in quantum and classical systems. Phys Rep 2017; 697: 1–87. [Google Scholar]
- 6. Simon B. Holonomy, the quantum adiabatic theorem, and Berry's phase. Phys Rev Lett 1983; 51: 2167–70. [Google Scholar]
- 7. Berry MV. Quantal phase factors accompanying adiabatic changes. Proc R Soc London Ser A 1984; 392: 45–57. [Google Scholar]
- 8. Bohm A, Mostafazadeh A, Koizumi Het al. The Geometric Phase in Quantum Systems: Foundations, Mathematical Concepts, and Applications in Molecular and Condensed Matter Physics. New York: Springer-Verlag Berlin Heidelberg, 2003. [Google Scholar]
- 9. Nagaosa N, Sinova J, Onoda Set al. Anomalous Hall effect. Rev Mod Phys 2010; 82: 1539–92. [Google Scholar]
- 10. Hasan MZ, Kane CL. Colloquium: topological insulators. Rev Mod Phys 2010; 82: 3045–67. [Google Scholar]
- 11. Souza I, Wilkens T, Martin RM. Polarization and localization in insulators: generating function approach. Phys Rev B 2000; 62: 1666–83. [Google Scholar]
- 12. Ozawa T, Goldman N. Probing localization and quantum geometry by spectroscopy. Phys Rev Res 2019; 1: 032019(R). [Google Scholar]
- 13. Zanardi P, Giorda P, Cozzini M. Information-theoretic differential geometry of quantum phase transitions. Phys Rev Lett 2007; 99: 100603. [DOI] [PubMed] [Google Scholar]
- 14. Albert VV, Bradlyn B, Fraas Met al. Geometry and response of Lindbladians. Phys Rev X 2016; 6: 041031. [Google Scholar]
- 15. Gao Y, Yang SA, Niu Q. Geometrical effects in orbital magnetic susceptibility. Phys Rev B 2015; 91: 214405. [Google Scholar]
- 16. Piéchon F, Raoux A, Fuchs J-Net al. Geometric orbital susceptibility: quantum metric without Berry curvature. Phys Rev B 2016; 94: 134423. [Google Scholar]
- 17. Bleu O, Malpuech G, Gao Yet al. Effective theory of nonadiabatic quantum evolution based on the quantum geometric tensor. Phys Rev Lett 2018; 121: 020401. [DOI] [PubMed] [Google Scholar]
- 18. Lapa MF, Hughes TL. Semiclassical wave packet dynamics in nonuniform electric fields. Phys Rev B 2019; 99: 121111(R). [Google Scholar]
- 19. Srivastava A, Imamoğlu A. Signatures of Bloch-band geometry on excitons: nonhydrogenic spectra in transition-metal Dichalcogenides. Phys Rev Lett 2015; 115: 166802. [DOI] [PubMed] [Google Scholar]
- 20. Julku A, Peotta S, Vanhala TIet al. Geometric origin of superfluidity in the Lieb-Lattice flat band. Phys Rev Lett 2016; 117: 045303. [DOI] [PubMed] [Google Scholar]
- 21. Roy R. Band geometry of fractional topological insulators. Phys Rev B 2014; 90: 165139. [Google Scholar]
- 22. Palumbo G, Goldman N. Revealing tensor monopoles through quantum-metric measurements. Phys Rev Lett 2018; 121: 170401. [DOI] [PubMed] [Google Scholar]
- 23. Hauke P, HeyI M, Tagliacozzo Let al. Measuring multipartite entanglement through dynamic susceptibilities. Nat Phys 2016; 12: 778–82. [Google Scholar]
- 24. Li T, Duca L, Reitter Met al. Bloch state tomography using Wilson lines. Science 2016; 352: 1094–7. [DOI] [PubMed] [Google Scholar]
- 25. Duca L, Li T, Reitter Met al. An Aharonov-Bohm interferometer for determining Bloch band topology. Science 2015; 347: 288–92. [DOI] [PubMed] [Google Scholar]
- 26. Fläschner N, Rem BS, Tarnowski Met al. Experimental reconstruction of the Berry curvature in a Floquet Bloch band. Science 2016; 352: 1091–4. [DOI] [PubMed] [Google Scholar]
- 27. Wimmer M, Price HM, Carusotto Iet al. Experimental measurement of the Berry curvature from anomalous transport. Nat Phys 2017; 13: 545–50. [Google Scholar]
- 28. Banks HB, Wu Q, Valovcin DCet al. Dynamical Birefringence: electron-hole recollisions as probes of Berry curvature. Phys Rev X 2017; 7: 041042. [Google Scholar]
- 29. Luu TT, Wörner HJ. Measurement of the Berry curvature of solids using high-harmonic spectroscopy. Nat Commun 2018; 9: 916. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. Marzari N, Vanderbilt D. Maximally localized generalized Wannier functions for composite energy bands. Phys Rev B 1997; 56: 12847–65. [Google Scholar]
- 31. Asteria L, Tran DT, Ozawa Tet al. Measuring quantized circular dichroism in ultracold topological matter. Nat Phys 2019; 15: 449–54. [Google Scholar]
- 32. Ozawa T, Goldman N. Extracting the quantum metric tensor through periodic driving. Phys Rev B 2018; 97: 201117(R). [Google Scholar]
- 33. Neupert T, Chamon C, Mudry C. Measuring the quantum geometry of Bloch bands with current noise. Phys Rev B 2013; 87: 245103. [Google Scholar]
- 34. Kolodrubetz M, Gritsev V, Polkovnikov A. Classifying and measuring geometry of a quantum ground state manifold. Phys Rev B 2013; 88: 064304. [Google Scholar]
- 35. Bleu O, Solnyshkov DD, Malpuech G. Measuring the quantum geometric tensor in two-dimensional photonic and exciton-polariton systems. Phys Rev B 2018; 97: 195422. [Google Scholar]
- 36. Roushan P, Neill C, Chen Yet al. Observation of topological transitions in interacting quantum circuits. Nature 2014; 515: 241–4. [DOI] [PubMed] [Google Scholar]
- 37. Gritsev V, Polkovnikov A. Dynamical quantum Hall effect in the parameter space. Proc Natl Acad Sci USA 2012; 109: 6457–62. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38. Schroer MD, Kolodrubetz MH, Kindel WFet al. Measuring a topological transition in an artificial spin-1/2 system. Phys Rev Lett 2014; 113: 050402. [DOI] [PubMed] [Google Scholar]
- 39. Tran DT, Cooper NR, Goldman N. Quantized Rabi oscillations and circular dichroism in quantum Hall systems. Phys Rev A 2018; 97: 061602(R). [Google Scholar]
- 40. de Juan F, Grushin AG, Morimoto Tet al. Quantized circular photogalvanic effect in Weyl semimetals. Nat Commun 2017; 8: 15995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41. Tran DT, Dauphin A, Grushin AGet al. Probing topology by ‘heating’: quantized circular dichroism in ultracold atoms. Sci Adv 2017; 3: e1701207. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42. Wang C, Zhang P, Chen Xet al. Scheme to measure the topological number of a Chern insulator from quench dynamics. Phys Rev Lett 2017; 118: 185701. [DOI] [PubMed] [Google Scholar]
- 43. Fläschner N, Vogel D, Tarnowski Met al. Observation of dynamical vortices after quenches in a system with topology. Nat Phys 2018; 14: 265–8. [Google Scholar]
- 44. Tarnowski M, Ünal FN, Fläschner Net al. Measuring topology from dynamics by obtaining the Chern number from a linking number. Nat Commun 2019; 10: 1728. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45. Repellin C, Goldman N. Detecting fractional Chern insulators through circular dichroism. Phys Rev Lett 2019; 122: 166801. [DOI] [PubMed] [Google Scholar]
- 46. Yu M, Yang P, Gong Met al. Experimental measurement of the complete quantum geometry of a solid-state spin system. arXiv: 1811.12840. [Google Scholar]
- 47. Gianfrate A, Bleu O, Dominici Let al. Measurement of the quantum geometric tensor and of the anomalous Hall drift. Nature 2020; 578: 381–5. [DOI] [PubMed] [Google Scholar]
- 48. Tan X, Zhang D-W, Yang Zet al. Experimental measurement of the quantum metric tensor and related topological phase transition with a superconducting qubit. Phys Rev Lett 2019; 122: 210401. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.