A hybrid collocation-perturbation approach for PDEs with random domains

Abstract

Consider a linear elliptic PDE defined over a stochastic stochastic geometry a function of N random variables. In many application, quantify the uncertainty propagated to a Quantity of Interest (QoI) is an important problem. The random domain is split into large and small variations contributions. The large variations are approximated by applying a sparse grid stochastic collocation method. The small variations are approximated with a stochastic collocation-perturbation method and added as a correction term to the large variation sparse grid component. Convergence rates for the variance of the QoI are derived and compared to those obtained in numerical experiments. Our approach significantly reduces the dimensionality of the stochastic problem making it suitable for large dimensional problems. The computational cost of the correction term increases at most quadratically with respect to the number of dimensions of the small variations. Moreover, for the case that the small and large variations are independent the cost increases linearly.

1. Introduction

The problem of design under the uncertainty of the underlying domain can be encountered in many real life applications. For example, in semiconductor fabrication the underlying geometry becomes increasingly uncertain as the physical scales are reduced [33]. This uncertainty is propagated to an important Quantity of Interest (QoI), such as the capacitance of the semiconductor circuit. If the variance of the capacitance is high this could lead to low yields during the manufacturing process. Quantifying the uncertainty in a given QoI, such as the capacitance, is of important so as to be able to maximize yields. This will have a direct impact in reducing the costly and time-consuming design cycle. Other examples included graphene nano-sheet fabrication [21]. In this paper we focus on the problem of how to efficiently compute the statistics of the QoI given uncertainty in the underlying geometry.

Uncertainty Quantification (UQ) methods applied to Partial Differential Equations (PDEs) with random geometries can be mostly divided into collocation and perturbation approaches. For large deviations of the geometry the collocation method [6,8,14,32] is well suited. In addition, in [6,18] the authors derive error estimates of the solution with respect to the number of stochastic variables in the geometry description. However, this approach is only effective for medium size stochastic problems. In contrast, the perturbation approaches introduced in [20,33,17,9,13,11,12] are very efficient for high dimension, but with small perturbations of the domain. More recently, new approaches based on multi-level Monte Carlo have been developed [28] that is well suited for low regularity of the solution. Furthermore, the domain mapping approach has been extended to elliptic problems with random domains in [19].

We develop a hybrid collocation-perturbation method that is well suited for a combination of large and small variations. The main idea is to meld both approaches such that the accuracy versus dimension of the problem is significantly accelerated.

We represent the domain in terms of a series of random variables and then remap the corresponding PDE to a deterministic domain with random coefficients. The random geometry is split into small and large deviations. A collocation sparse grid method is used to approximate the contribution to the QoI from the first large deviations N_L terms of the stochastic domain expansion. Conversely, the contribution of the small deviations (the tail) are cheaply computed with a collocation and perturbation method. This contribution is called the variance correction.

For the collocation method we apply an isotropic sparse grid. This is to simplify the presentation in this work. However, we are free to use any collocation method such as anisotropic sparse grids [26], quasi-optimal [25] or dimension adaptive [15,23,22] to increase the efficiency of the collocation computation. The results in this paper show that the variance correction significantly reduces the overall dimensionality of the stochastic problem while the computational cost of the correction term increases at most quadratically with respect to the number of dimensions of the small variations.

A rigorous convergence analysis of the statistics of the QoI in terms of the number of collocation knots and the perturbation approximation of the tail is derived. Analytic estimates show that the error of the QoI for the hybrid collocation-perturbation method (or the hybrid perturbation method for short) decays quadratically with respect to the of sum of the coefficients of the expansion of the tail. This is in contrast to the linear decay of the error estimates derived in [6] for the pure stochastic collocation approach. Furthermore, numerical experiments show a faster convergence rate than the stochastic collocation approach. Moreover, the variance correction is computed at a fraction of the cost of the low dimensional large variations.

In Section 2 mathematical background material is introduced. In Section 3 the stochastic domain problem is introduced. We assume that there exist a bijective map such that the elliptic PDE with a stochastic domain is remapped to deterministic reference domain with a random diffusion matrix. The random boundary is assumed to be parameterized by N random variables. In section 4 the hybrid collocation-perturbation approach is derived. This approach reduces to computing mean and variance correction terms that quantifies the perturbation contribution from the tail of the random domain expansion. In Section 5 we show that analytic extension in ${\mathbb{C}}^{N_L}$ exists for the variance correction term. In Section 6 mean and variance error estimates are derived in terms of the finite element, sparse grid and perturbation approximations. In section 7 complexity and tolerance analysis is derived. In section 8 we test our approach on numerical examples that are consistent with theoretically derived convergence rates.

2. Background

In this section we introduce the general notation and mathematical background that will be used in this paper. Let (Ω, $\mathcal{F}$, $\mathbb{P}$) be a complete probability space, where Ω is the set of outcomes, $\mathcal{F}$ is a sigma algebra of events and $\mathbb{P}$ is a probability measure. Define $L_{\mathbb{P}}^q(\Omega )$, $q\in \mathbb{N}$, as the following Banach spaces:

$$\begin{gathered} L_{\mathbb{P}}^q(\Omega )≔\{v\mid {\int }_{\Omega }\mid v(\omega ){\mid }^q\mathrm{d}\mathbb{P}(\omega )<\infty \}\text{and} \\ {L}_{\mathbb{P}}^{\infty }(\Omega )≔\{v\mid \mathbb{P}-\underset{\omega \in \Omega }{\text{ess sup}}\mid v(\omega )\mid <\infty \}, \end{gathered}$$

where $v:\Omega \to \mathbb{R}$ is a measurable random variable.

Consider the random variables Y₁, … , Y_N measurable in (Ω, $\mathcal{F}$, $\mathbb{P}$). Form the N valued random vector Y := [Y₁, … , Y_N], Y : Ω → Γ, and let $\Gamma ≔{\Gamma }_1\times \cdots \times {\Gamma }_N\subset {\mathbb{R}}^N$. Without loss of generality denote Γ_n := [−1, 1] as the image of Y_n for n = 1, … , N and let $\mathcal{B}(\Gamma )$ be the Borel σ− algebra.

For all $A\in \mathcal{B}(\Gamma )$ consider the induced measure ${\mu }_{\mathbf{Y}}≔\mathbb{P}({\mathbf{Y}}^{-1}(A))$. Suppose that μ_Y is absolutely continuous with respect to the Lebesgue measure defined on Γ. From the Radon–Nikodym theorem [4] we conclude that there exists a density function ρ(y) : Γ → [0, +∞) such that for any event $A\in \mathcal{B}(\Gamma )$ we have that $\mathbb{P}(\mathbf{Y}\in A)≔\mathbb{P}({\mathbf{Y}}^{-1}(A))={\int }_A\rho (\mathbf{y})d\mathbf{y}$. For any measurable function $\mathbf{Y}\in [L_{\mathbb{P}}^1(\Gamma ){]}^N$ define the expected value as $\mathbb{E}[\mathbf{Y}]={\int }_{\Gamma }\mathbf{y}\rho (\mathbf{y})\mathrm{d}\mathbf{y}$. Finally, the following Banach spaces will be useful for the stochastic collocation sparse grid error estimates. For $q\in \mathbb{N}$ let

$$\begin{gathered} L_{\rho }^q(\Gamma )≔\left\{v\mid {\int }_{\Omega }\mid v(\mathbf{y}){\mid }^q\rho (\mathbf{y})\mathrm{d}\mathbf{y}<\infty \right\}\text{and} \\ {L}_{\rho }^{\infty }(\Gamma )≔\left\{v\mid \rho (\mathbf{y})\mathrm{d}\mathbf{y}-\rho -\underset{\mathbf{y}\in \Gamma }{\text{ess sup}}\mid v(\mathbf{y})\mid <\infty \right\}. \end{gathered}$$

We discuss in the next section an approach of approximating a function with sufficient regularity by multivariate polynomials and sparse grid interpolation.

2.1. Sparse Grids

Our goal is to find a compact an accurate approximation of a multivariate function $\tilde{f}:\Gamma \to V$ with sufficient regularity. It is assumed that $\tilde{f}\in C^0(\Gamma ;V)$ where

$$C^0(\Gamma ;V)≔\{v:\Gamma \to V\text{is continuous on}\Gamma {\text{and max}}_{\mathbf{y}\in \Gamma }\Vert v(\mathbf{y}){\Vert }_V<\infty \}$$

and V is a Banach space. Consider the univariate Lagrange interpolant along the n^th dimension of Γ

$${\mathcal{I}}_n^{m(i)}:C^0({\Gamma }_n)\to {\mathcal{P}}_{m(i)-1}({\Gamma }_n),$$

where i ⩾ 1 denotes the level of approximation and m(i) the number of collocation knots used to build the interpolation at level i such that m(0) = 0, m(1) = 1 and m(i) < m(i + 1) for i ⩾ 1. Furthermore let ${\mathcal{I}}_n^{m(0)}=0$. The space ${\mathcal{P}}_{m(i)-1}({\Gamma }_n)$ is the set of polynomials of degree at most m(i) − 1.

We can construct an interpolant by taking tensor products of ${\mathcal{I}}_n^{m(i)}$ along each dimension for n = 1, … , N. However, the number of collocation knots explodes exponentially with respect to the number of dimensions, thus limiting feasibility to small dimensions. Alternately, consider the difference operator along the n^th dimension

$${\Delta }_n^{m(i)}≔{\mathcal{I}}_n^{m(i)}-{\mathcal{I}}_n^{m(i-1)}.$$

The sparse grid approximation of $\tilde{f}\in C^0(\Gamma )$ is defined as

$${\mathcal{S}}_w^{m,g}[\tilde{f}]=\sum _{\mathbf{i}\in {\mathbb{N}}_{+}^N:g(\mathbf{i})⩽w}\underset{n=1}{\overset{N}{\otimes }}{\Delta }_n^{m(i_n)}(\tilde{f}),$$ (1)

where w ⩾ 0, $w\in {\mathbb{N}}_{+}({\mathbb{N}}_{+}≔\mathbb{N}\cup \{0\})$, is the approximation level, $\mathbf{i}=(i_1,\dots ,i_N)\in {\mathbb{N}}_{+}^N$, and $g:{\mathbb{N}}_{+}^N\to \mathbb{N}$ is strictly increasing in each argument. The sparse grid can also we re-written as

$${\mathcal{S}}_w^{m,g}[\tilde{f}]=\sum _{\mathbf{i}\in {\mathbb{N}}_{+}^N:g(\mathbf{i})⩽w}c(\mathbf{i})\underset{n=1}{\overset{N}{\otimes }}{\mathcal{I}}_n^{m(i_n)}(\tilde{f}),\text{with}c(\mathbf{i})=\sum _{\begin{array}{c}\hfill \mathbf{j}\in \{0,1{\}}^N:\hfill \\ \hfill g(\mathbf{i}+\mathbf{j})⩽w\hfill \end{array}}(-1{)}^{\mid \mathbf{j}\mid }.$$ (2)

From the previous expression, we see that the sparse grid approximation is obtained as a linear combination of full tensor product interpolations. However, the constraint g(i) ⩽ w in (2) restricts the growth of tensor grids of high degree.

Consider the multi-indexed vector m(i) = (m(i₁), … , m(i_N)) and the associated polynomial polynomial set

$${\Lambda }^{m,g}(w)=\{\mathbf{p}\in {\mathbb{N}}^N,g({\mathbf{m}}^{-1}(\mathbf{p}+1))⩽w\}.$$

Let ${\mathbb{P}}_{{\Lambda }^{m,g}(w)}(\Gamma )$ be the multivariate polynomial space

$${\mathbb{P}}_{{\Lambda }^{m,g}(w)}(\Gamma )=span\left\{\prod _{n=1}^N{y}_n^{p_n},\text{with}\mathbf{p}\in {\Lambda }^{m,g}(w)\right\}.$$

It can shown that ${\mathcal{S}}_w^{m,g}[\tilde{\mathit{f}}]\in {\mathbb{P}}_{{\Lambda }^{m,g}(w)}(\Gamma )$ (see e.g. [2]). One of the most popular choices for m and g is given by the Smolyak (SM) formulas (see [29,3,2])

$$m(i)=\{\begin{array}{cc}1,\hfill & \text{for}i=1\hfill \\ 2^{i-1}+1,\hfill & \text{for}i>1\hfill \end{array}\phantom{\}}\text{and}g(\mathbf{i})=\sum _{n=1}^N(i_n-1),$$

in conjunction with Clenshaw-Curtis (CC) abscissas interpolation points. This choice gives rise to sequence of nested one dimensional interpolation formulas. The number of interpolation knots of the Smolyak sparse grid grows significantly slower than Tensor Product (TP) (see [2]) and Total Degree (TD) grids. Other popular choices include Hyperbolic Cross (HC) sparse grids.

It can also be shown that the TD, SM and HC anisotropic sparse approximation formulas can be readily constructed with improved convergence rates (see [26]). Moreover, in [10], the authors show convergence of anisotropic sparse grid approximations with infinite dimensions (N → ∞). In [25] the authors show the construction of quasi-optimal grids have been shown to have exponential convergence.

As pointed out in the introduction, we have the option of using any collocation method such as anisotropic [26], quasi-optimal [25] or dimension adaptive [15,23,22] sparse grids to increase the efficiency of the collocation computation. The important result in this paper is that the overall dimensionality of the stochastic problem is significantly reduced with the addition of the perturbation component.

3. Problem setup and formulation

Let $\mathcal{D}(\omega )\subset {\mathbb{R}}^d$, $d\in \mathbb{N}$, be an open bounded domain with Lipschitz boundary $\partial \mathcal{D}(\omega )$ that is shape dependent on the stochastic parameter ω ∈ Ω

Suppose there exist a reference domain $U\subset {\mathbb{R}}^d$, which is open and bounded with Lipschitz boundary ∂U. In addition assume that almost surely in Ω there exist a bijective map $F(\omega ):\overline{U}\to \overline{\mathcal{D}(\omega )}$. The map η ↦ x, $\overline{U}\to \overline{\mathcal{D}(\omega )}$, is written as

$$\eta \mapsto \mathbf{x}=F(\eta ,\omega ),$$

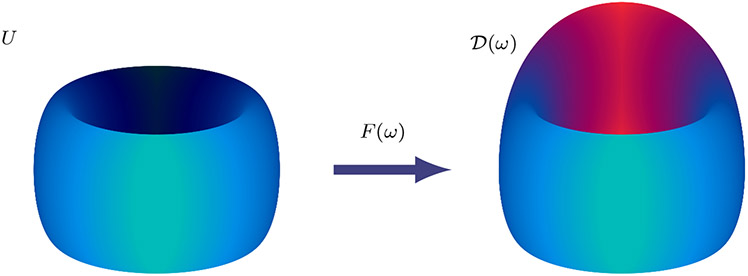
where η are the coordinates for the reference domain U and x are the coordinates for ${\mathbb{R}}^d$ . See the cartoon example in Figure 1. Denote by J(ω) as the Jacobian of F(ω) and suppose that F satisfies the following assumption.

Fig. 1.

Example of reference domain deformation through the bijective map F(ω) for some realization ω ∈ Ω. The image is created Tikz code [30].

Assumption 1 Given a bijective map $F(\omega ):\overline{U}\to \overline{\mathcal{D}(\omega )}$ there exist constants ${\mathbb{F}}_{min}$ and ${\mathbb{F}}_{max}$ such that

$$0<{\mathbb{F}}_{min}⩽{\sigma }_{min}(\mathbf{J}(\omega ))and{\sigma }_{max}(\mathbf{J}(\omega ))⩽{\mathbb{F}}_{max}<\infty$$

almost everywhere in U and almost surely in Ω. We have denoted by σ_min(J(ω)) (and σ_max(J(ω))) the minimum (respectively maximum) singular value of the Jacobian J(ω). In Figure 1 a cartoon example of the deformation of the reference domain U is shown.

By applying the chain rule on Sobolev spaces [1] for any $v\in H^1(\mathcal{D}(\omega ))$ we have that ∇_v = J^-T∇(v ∘ F), where J^-T := (J⁻¹)^T, i.e. the transpose of matrix J⁻¹, and v ∘ F ∈ H¹(U). Therefore we can prove the following result.

Lemma 1 Under Assumptions 1 it is immediate to prove the following results:

1. $L^2(\mathcal{D}(\omega ))$ and L²(U) are isomorphic almost surely.

2. $H^1(\mathcal{D}(\omega ))$ and H¹(U) are isomorphic almost surely.

Proof For i) and ii) see [6] or [18].

Let $\mathcal{G}≔{\cup }_{\omega \in \Omega }\mathcal{D}(\omega )\subset {\mathbb{R}}^d$, i.e. the region in ${\mathbb{R}}^d$ defined by the union of all the perturbations of the stochastic domain. Consider the functions $a:\mathcal{G}\to \mathbb{R}$, and $f:\mathcal{G}\to \mathbb{R}$ that are defined over the region of all the stochastic perturbations of the domain $\mathcal{D}(\omega )$ in ${\mathbb{R}}^d$. Similarly, let $\mathcal{U}≔{\cup }_{\omega \in \Omega }\partial \mathcal{D}(\omega )\subset {\mathbb{R}}^d$ be region formed by the union of all the stochastic perturbations of the boundary. For ω ∈ Ω a.s. let $g\in H^{1∕2}(\mathcal{D}(\omega ))$ be defined as the trace of a deterministic function $\nu \in H^1(\mathcal{G})$.

Consider the following boundary value problem: Given $f(\mathbf{x},\omega ),a(\mathbf{x},\omega ):\mathcal{D}(\omega )\to {\mathbb{R}}^d$ and $g(\mathbf{x},\omega ):\partial \mathcal{D}(\omega )\to {\mathbb{R}}^d$ find $u(\mathbf{x},\omega ):\mathcal{D}(\omega )\to {\mathbb{R}}^d$ such that almost surely

$$\begin{gathered} -\nabla \cdot (a(\mathbf{x},\omega )\nabla u(\mathbf{x},\omega ))=f(\mathbf{x},\omega ),\mathbf{x}\in \mathcal{D}(\omega ) \\ u=g\text{on}\partial \mathcal{D}(\omega ). \end{gathered}$$ (3)

We now make the following assumption:

Assumption 2 Let $a_{max}≔{\text{ess sup}}_{\mathbf{x}\in \mathcal{D}(\omega ),\omega \in \Omega }a(\mathbf{x},\omega )$ and

$$a_{min}≔\underset{\mathbf{x}\in \mathcal{D}(\omega ),\omega \in \Omega }{\text{ess}\text{inf}}a(\mathbf{x},\omega ).$$

Assume that the constants a_min and a_max satisfy the following inequality: 0 < a_min ⩽ a_max < ∞.

Recall that $\mathcal{D}(\omega )$ is open and bounded with Lipschitz boundary $\partial \mathcal{D}(\omega )$. By applying a change of variables the weak form of (3) can be formulated on the reference domain (see [6] for details) as:

Problem 1 Given that (f ∘ F)(η, ω) ∈ L²(U) find $\widehat{u}(\eta ,\omega )\in H_0^1(U)$ s.t.

$$B(\omega ;\widehat{u},v)=\tilde{l}(\omega ;v),\forall v\in H_0^1(U)$$ (4)

almost surely, where $\tilde{l}(\omega ;v)≔{\int }_U(f\circ F)(\eta ,\omega )\mid \mathbf{J}(\eta ,\omega )\mid v-L(\widehat{\nu }(\eta ,\omega ),v)$, $\widehat{g}≔g\circ F$, $\widehat{\nu }≔\nu \circ F$, for any w, $s\in H_0^1(U)$

$$\begin{gathered} B(\omega ;s,w)≔{\int }_U(a\circ F)(\eta ,\omega )\nabla s^T{\mathbf{C}}^{-1}(\eta ,\omega )\nabla w\mid \mathbf{J}(\eta ,\omega )\mid , \\ L(\widehat{\nu }(\eta ,\omega ),v)≔{\int }_U(a\circ F)(\eta ,\omega )(\nabla (\widehat{\nu }(\eta ,\omega ){)}^T{\mathbf{C}}^{-1}(\eta ,\omega )\mid \mathbf{J}(\eta ,\omega )\mid \nabla v, \end{gathered}$$

C(η, ω) := J(ω)^TJ(ω), and $\widehat{\nu }(\eta ,\omega ){\mid }_{\partial U}=\widehat{g}(\eta ,\omega )$. This homogeneous boundary value problem can be remapped to $\mathcal{D}(\omega )$ as $\tilde{u}(\mathbf{x},\omega )≔(\widehat{u}\circ F^{-1})(\mathbf{x},\omega )$, thus we can rewrite $\widehat{u}(\eta ,\omega )=(\tilde{u}\circ F)(\eta ,\omega )$. The solution $u(\mathbf{x},\omega )\in H^1(\mathcal{D}(\omega ))$ for the Dirichlet boundary value problem is obtained as $u(\mathbf{x},\omega )=\tilde{u}(\mathbf{x},\omega )+(\widehat{\nu }\circ F^{-1})(\mathbf{x},\omega )$.

The solution of (4) is numerically computed with a semi-discrete approximation. Suppose that we have a set of regular triangulations ${\mathcal{T}}_h$ with maximum mesh spacing parameter h > 0. Furthermore, let $H_h(U)\subset H_0^1(U)$ be the space of continuous piecewise polynomial defined on ${\mathcal{T}}_h$ with N_h cardinality. Let ${\widehat{u}}_h:\Gamma \to H_h(U)$ be the semi-discrete approximation of the solution of Problem (4) that satisfies the following problem: Find ${\widehat{u}}_h\in H_h(U)$ such that

$$\begin{gathered} {\int }_U[\nabla {\widehat{u}}_h(\cdot ,\mathbf{y}){]}^T\mathbf{G}(\mathbf{y})\nabla v_h\mathrm{d}\eta ={\int }_U(f\circ F)(\cdot ,\mathbf{y})v_h\mid \mathbf{J}(\mathbf{y})\mid \mathrm{d}\eta \\ -L(\widehat{\nu },v_h) \end{gathered}$$ (5)

for all v_h ∈ H_h(U) and for a.s. y ∈ Γ. Note that G(y) := (a ∘ F(y))∣J(y)∣J(y)⁻¹J(y)^−T and $Q_h(\mathbf{y})≔Q({\tilde{u}}_h\circ F)=Q({\widehat{u}}_h(\mathbf{y}))$.

3.1. Quantity of Interest

For many practical problems the QoI is not necessarily the solution of the elliptic PDE, but instead a bounded linear functional $Q:L^2(U)\to \mathbb{R}$ of the solution. For example, this could be the average of the solution on a specific region of the domain, i.e.

$$Q(\widehat{u})≔{\int }_{\overline{U}}q(\eta )\widehat{u}(\eta ,\omega )\mathrm{d}\eta$$ (6)

with q ∈ L²(U) over the region $\tilde{U}\subset U$. It is assumed that there exists δ > 0 such that $dist(\tilde{U},\partial U)>\delta$.

In the next section, the perturbation approximation is derived for Q(u) and not directly from the solution u. It is thus necessary to introduce the influence function $\phi :H_0^1(U)\to \mathbb{R}$, which can be easily computed by the following adjoint problem:

Problem 2 Find $\phi \in H_0^1(U)$ such that for all $v\in H_0^1(U)$

$$B(\omega ;v,\phi )=Q(v)$$ (7)

a.s. in Ω. After computing the influence function φ, the QoI can be computed as $Q(\widehat{u})=B(\widehat{u},\phi )$.

Remark 1 We can pick a particular operator T such that $\widehat{\nu }=T(\widehat{g})$ and vanishes in the region defined by $\tilde{U}$. Thus we have that $Q(\widehat{\nu })=0$ and $Q(\widehat{u}+\widehat{\nu })=Q(\widehat{u})$.

3.2. Domain parameterization

To simplify the analysis of the elliptic PDE with a random domain from equation (3) we remapped the solution onto a fix deterministic reference domain. This approach has also been applied in [6,14,18,17]. This approach is reminiscent of Karhunen-Loève (KL) expansions of random fields (see [18]).

Suppose that b₁, … , b_N are a collection of vector valued Sobolev functions where each of the entries of ${\mathbf{b}}_n:U\to {\mathbb{R}}^d$ for n = 1, … , N belong in the space W^1,∞(U). We further make the following assumptions.

Assumption 3 Assume that F(η, ω) has the finite noise model

$$F(\eta ,\omega )≔\eta +\sum _{n=1}^N\sqrt{{\mu }_n}{\mathbf{b}}_n(\eta )Y_n(\omega ).$$

Assumption 4

1. ∥∥b_n∥_l^∞∥_L^∞(U) = 1 for n =1, … N.

2. ∞ > μ₁ ⩾ ⋯ ⩾ μ_N ⩾ 0.

The stochastic domain perturbation is now split as

$$F(\eta ,\omega )\to F_L(\eta ,\omega )+F_S(\eta ,\omega ),$$

where we denote F_L(η, ω) as the large deviations and F_S(η, ω) as the small deviations modes with the following parameterization:

$$F_L(\eta ,\omega )≔\sum _{n=1}^{N_L}\sqrt{{\mu }_{L,n}}{\mathbf{b}}_{L,n}(\eta )Y_n(\omega )\&F_S(\eta ,\omega )≔\sum _{n=1}^{N_S}\sqrt{{\mu }_{S,n}}{\mathbf{b}}_{S,n}(\eta )Y_{n+N_L}(\omega ),$$

where N_L + N_S = N. Furthermore, for n = 1, … , N_L let μ_L,n := μ_n, b_L,n(η) := b_n(η), and for n = 1, … , N_S let μ_S,n := μ_n+NL and b_S,n(η) := b_n+NL (η).

Denote y_L := [y₁, … ,y_NL], ${\Gamma }_L≔{\prod }_{n=1}^{N_L}{\Gamma }_n$, and $\rho ({\mathbf{y}}_L):{\Gamma }_L\to {\mathbb{R}}_{+}$ as the joint probability density of y_L. Similarly denote y_S := [y_NL+1, … , y_N], ${\Gamma }_S≔{\prod }_{n=N_L+1}^N{\Gamma }_n$, and $\rho ({\mathbf{y}}_S):{\Gamma }_S\to {\mathbb{R}}_{+}$ as the joint probability density of y_S. From the stochastic model the Jacobian J is written as

$$\mathbf{J}(\eta ,\omega )=I+\sum _{n=1}^N\sqrt{{\mu }_n}{\mathbf{B}}_n(\eta )Y_n(\omega )$$ (8)

where for n = 1, … N, B_n(η) is the Jacobian of b_n(η).

4. Perturbation approach

In this section a perturbation method is presented to approximate Q(y) with respect to the domain perturbation. In Section 4.1, the perturbation approach is applied with respect to the tail field F_S(η, ω). A stochastic collocation approach is then used to approximate the contribution with respect to F_L(η, ω). We follow a similar approach as in [20] by using shape calculus. To this end we introduce the following definition.

Definition 1 Let ψ be a regular function of the parameters $\mathbf{y}\in W\subset {\mathbb{R}}^N$, the Gâteaux derivative (shape derivative) evaluated at y on the space of perturbations $W\subset {\mathbb{R}}^N$ is defined as

$$<D_{\mathbf{y}}\psi (\mathbf{y}),\delta \mathbf{y}>=\underset{s\to 0^{+}}{\text{lim}}\frac{\psi (\mathbf{y}+s\delta \mathbf{y})-\psi (\mathbf{y})}{s},\forall \delta \mathbf{y}\in W.$$

Similarly, the second order derivative $D_{\mathbf{y}}^2$ (shape Hessian) as a bilinear form on W is defined as

$$D_{\mathbf{y}}^2\psi (\mathbf{y})(\delta {\mathbf{y}}_1,\delta {\mathbf{y}}_2)=\underset{s\to 0^{+}}{\text{lim}}<\frac{D_{\mathbf{y}}\psi (\mathbf{y}+s\delta {\mathbf{y}}_2)-D_{\mathbf{y}}\psi (\mathbf{y})}{s},\delta {\mathbf{y}}_1>,\forall \delta {\mathbf{y}}_2,\delta {\mathbf{y}}_1\in W.$$

Suppose that Q is a regular function with respect to the parameters y, then for all y = y₀ + δy ∈ W the following expansion holds:

$$Q(\mathbf{y})=Q({\mathbf{y}}_0)+<D_{\mathbf{y}}Q({\mathbf{y}}_0),\delta \mathbf{y}>+\frac{1}{2}{D}_{\mathbf{y}}^{2}Q(\mathbf{y}+\theta \delta \mathbf{y})(\delta \mathbf{y},\delta \mathbf{y})$$ (9)

for some θ ∈ (0, 1). Thus we have a procedure to approximate the QoI Q(y) with respect to the first order term and bound the error with the second order term. To explicitly formulate the first and second order terms we make the following assumption:

Assumption 5 For all v, $w\in H_0^1(U)$, let $\mathcal{G}(\mathbf{y};v,w)≔\nabla v^T\mathbf{G}(y)\nabla w$, where G(y) := (a ∘ F)(η, y)J⁻¹(y)J^−T(y)∣J(y)∣, we have that for all y ∈ W

1. ${\nabla }_{\mathbf{y}}\mathcal{G}(\mathbf{y})\in [L^1(U){]}^N$

2. For n = 1, … , N there exists a uniformly bounded constant ${\mathcal{C}}_{\mathcal{G}}(\mathbf{y})>0$ on W s.t.

   $${\int }_U\partial y_n\mathcal{G}(\mathbf{y};v,w)⩽{\mathcal{C}}_{\mathcal{G}}(\mathbf{y})\Vert v{\Vert }_{H_0^1(U)}\Vert w{\Vert }_{H_0^1(U)}.$$

3. Furthermore, for all y ∈ W we assume that ∇_y(f ∘ F)(y), ${\nabla }_{\mathbf{y}}\widehat{\nu }(\mathbf{y})\in [L^1(U){]}^N$.

Remark 2 Although we have that (i) and (ii) are assumptions for now, under Assumptions 1 - 4, $a(\eta ,\omega )\in W^{1,\infty }({\mathbb{R}}^d)$, and Lemma 9 in Section 6 it can be shown that Assumption 5(i) and (ii) are true for all y ∈ Γ.

Definition 2 For all v, $w\in H_0^1(U)$, and y ∈ W let

$$<D_{\mathbf{y}}B(\mathbf{y};v,w),\delta \mathbf{y}>≔\underset{s\to 0^{+}}{\text{lim}}\frac{1}{s}[B(\mathbf{y}+s\delta \mathbf{y};v,w)-B(\mathbf{y};v,w)]\forall \delta \mathbf{y}\in \Gamma .$$

Remark 3 Under Assumption 5 for any v, $w\in H_0^1(U)$ we have that for all y ∈ W

$$<D_{\mathbf{y}}B(\mathbf{y};v,w),\delta \mathbf{y}>={\int }_U{\nabla }_{\mathbf{y}}\mathcal{G}(\mathbf{y};v,w)\cdot \delta \mathbf{y}=\sum _{n=1}^N{\int }_U(\nabla v^T\partial y_n\mathbf{G}(\mathbf{y})\nabla w)\delta y_n$$

where G(y) := (a ∘ F)(η, y)J⁻¹(y)J^−T(y)∣J(y)∣. Furthermore, under Assumption 5 we have that

$$<D_{\mathbf{y}}(f\circ F)(\cdot ,\mathbf{y}),\delta \mathbf{y}>={\int }_U{\nabla }_{\mathbf{y}}(f\circ F)(\cdot ,\mathbf{y})\cdot \delta \mathbf{y}.$$

We can introduce as well the derivative for any function (v ∘ F)(η, y) ∈ L²(U) with respect to y: For all y ∈ W we have that

$$D_{\mathbf{y}}(v\circ F)(\eta ,\mathbf{y})(\delta \mathbf{y}):=\underset{s\to o^{+}}{\text{lim}}\frac{1}{s}[(v\circ F)(\eta ,\mathbf{y}+s\delta \mathbf{y})-(v\circ F)(\eta ,\mathbf{y})].$$

Lemma 2 Suppose that Assumptions 1 to 5 are satisfied. Then for any y, δy ∈ W and for all $v\in H_0^1(U)$ we have that

$$\begin{gathered} B(\mathbf{y};D_{\mathbf{y}}(\tilde{u}\circ F)(\eta ,\mathbf{y})(\delta \mathbf{y}),v)=\sum _{n=1}^N\delta y_n({\int }_U-(\nabla (\tilde{u}\circ F)(\cdot ,\mathbf{y}){)}^T{\partial }_{y_n}\mathbf{G}(\mathbf{y})\nabla v\phantom{)} \\ +{\partial }_{y_n}(f\circ F)(\cdot ,\mathbf{y})\mid \mathbf{J}(\mathbf{y})\mid v+(f\circ F)(\cdot ,\mathbf{y}){\partial }_{y_n}\mid \mathbf{J}(\mathbf{y})\mid v \\ \phantom{(}-(\nabla \widehat{\nu }{)}^T{\partial }_{y_n}\mathbf{G}(\mathbf{y})\nabla v-({\partial }_{y_n}\nabla \widehat{\nu }(\mathbf{y}){)}^T\mathbf{G}(\mathbf{y})\nabla v). \end{gathered}$$

Proof

$$\begin{gathered} B(\mathbf{y};D_{\mathbf{y}}(\tilde{u}\circ F)(\cdot ,\mathbf{y})(\delta \mathbf{y}),v)=\underset{s\to 0^{+}}{\text{lim}}\frac{1}{s}{\int }_U(\nabla (\tilde{u}\circ F)(\cdot ,\mathbf{y}+s\delta \mathbf{y}{)}^T \\ -\nabla (\tilde{u}\circ F)(\cdot ,\mathbf{y}{)}^T)\mathbf{G}(\mathbf{y})\nabla v \\ =\underset{s\to 0^{+}}{\text{lim}}\frac{1}{s}{\int }_U(\tilde{u}\circ F)(\cdot ,\mathbf{y}+s\delta \mathbf{y}{)}^T\mathbf{G}(\mathbf{y})\nabla v \\ -\nabla (\tilde{u}\circ F)(\cdot ,\mathbf{y}+s\delta \mathbf{y}{)}^T\mathbf{G}(\mathbf{y}+s\delta \mathbf{y})\nabla v \\ +\underset{s\to 0^{+}}{\text{lim}}\frac{1}{s}{\int }_U\nabla (\tilde{u}\circ F)(\cdot ,\mathbf{y}+s\delta \mathbf{y}{)}^T\mathbf{G}(\mathbf{y}+s\delta \mathbf{y})\nabla v-\nabla (\tilde{u}\circ F)(\cdot ,\mathbf{y}{)}^T\mathbf{G}(\mathbf{y})\nabla v \\ =-\sum _{n=1}^N{\int }_U(\nabla (\tilde{u}\circ F)(\cdot ,\mathbf{y}){)}^T{\partial }_{y_n}\mathbf{G}(\mathbf{y})\delta y_n\nabla v \\ +\underset{s\to 0^{+}}{\text{lim}}\frac{1}{s}\left(\tilde{l}(\mathbf{y}+s\delta \mathbf{y};v)-\tilde{l}(\mathbf{y};v)\right) \end{gathered}$$

then

$$\begin{gathered} B(\mathbf{y};D_{\mathbf{y}}(\tilde{u}\circ F)(\cdot ,\mathbf{y})(\delta \mathbf{y}),v)=\sum _{n=1}^N{\int }_U-\nabla (\tilde{u}\circ F)(\cdot ,\mathbf{y}{)}^T{\partial }_{y_n}\mathbf{G}(\mathbf{y})\delta y_n\nabla v \\ +{\int }_U{\partial }_{y_n}(f\circ F)(\cdot ,\mathbf{y})\delta y_n\mid \mathbf{J}(\mathbf{y})\mid v+{\int }_U(f\circ F)(\cdot ,\mathbf{y}){\partial }_{y_n}\mid \mathbf{J}(\mathbf{y})\mid \delta y_{n}v \\ -\underset{s\to 0^{+}}{\text{lim}}\frac{1}{s}{\int }_U(\nabla \widehat{\nu }(\mathbf{y}+s\delta \mathbf{y}){)}^T\mathbf{G}(\mathbf{y}+s\delta \mathbf{y})\nabla v-(\nabla \widehat{\nu }(\mathbf{y}){)}^T\mathbf{G}(\mathbf{y})\nabla v) \end{gathered}$$

The result follows. □

Lemma 3 Suppose that Assumptions 1 to 5 are satisfied. Then for any y, δy ∈ W and for all $v\in H_0^1(U)$ we have that

$$B(\mathbf{y};v,D_{\mathbf{y}}\phi (\mathbf{y})(\delta \mathbf{y}))=\sum _{n=1}^N{\int }_U-(\nabla v{)}^T{\partial }_{y_n}\mathbf{G}(\mathbf{y})\delta y_n\nabla \phi (\mathbf{y}).$$

Proof We follow the same procedure as in Lemma 2. □

A consequence of Lemma 2 and Lemma 3 is that $D_{\mathbf{y}}(\tilde{u}\circ F)(\cdot ,\mathbf{y})(\delta \mathbf{y})$ and D_yφ(y)(δy) belong in $H_0^1(U)$ for any y ∈ W and δy ∈ W.

Lemma 4 Under the same assumptions as Lemma 3 we have that

$$\begin{gathered} \underset{s\to 0^{+}}{\text{lim}}\frac{Q(\mathbf{y}+s\delta \mathbf{y})-Q(\mathbf{y})}{s}=\sum _{n=1}^N\delta y_n{\int }_U(-(\nabla (\tilde{u}\circ F)(\cdot ,\mathbf{y}){)}^T{\partial }_{y_n}\mathbf{G}(\mathbf{y})\nabla \phi (\mathbf{y})\phantom{)} \\ +{\partial }_{y_n}(f\circ F)(\cdot ,\mathbf{y})\mid \mathbf{J}(\mathbf{y})\mid \phi (\mathbf{y})-(\nabla {\partial }_{y_n}\widehat{\nu }(\mathbf{y}){)}^T\mathbf{G}(\mathbf{y})\nabla \phi (\mathbf{y}) \\ \phantom{(}-(\nabla \widehat{\nu }(\mathbf{y}){)}^T{\partial }_{y_n}\mathbf{G}(\mathbf{y})\nabla \phi (\mathbf{y})+(f\circ F)(\cdot ,\mathbf{y}){\partial }_{y_n}\mid \mathbf{J}(\mathbf{y})\mid \phi (\mathbf{y})). \end{gathered}$$ (10)

where the influence function φ(y) satisfies equation (7).

Proof

$$\begin{gathered} \underset{s\to 0^{+}}{\text{lim}}\frac{Q(\mathbf{y}+s\delta \mathbf{y})-Q(\mathbf{y})}{s} \\ =\underset{s\to 0^{+}}{\text{lim}}{\int }_U\frac{1}{s}(\nabla (\tilde{u}\circ F)(\cdot ,\mathbf{y}+s\delta \mathbf{y}){)}^T\mathbf{G}(\mathbf{y}+s\delta \mathbf{y})\nabla \phi (\mathbf{y}+s\delta \mathbf{y}) \\ -(\nabla (\tilde{u}\circ F)(\cdot ,\mathbf{y}){)}^T\mathbf{G}(\mathbf{y})\nabla \phi (\mathbf{y})) \\ =\sum _{n=1}^N\delta y_n{\int }_U(\nabla (\tilde{u}\circ F)(\cdot ,\mathbf{y}){)}^T{\partial }_{y_n}\mathbf{G}(\mathbf{y})\nabla \phi (\mathbf{y}) \\ +{\int }_U(\nabla D_{\mathbf{y}}(\tilde{u}\circ F)(\cdot ,\mathbf{y}){)}^T(\delta \mathbf{y})\mathbf{G}(\mathbf{y})\nabla \phi (\mathbf{y}) \\ +(\nabla (\tilde{u}\circ F)(\cdot ,\mathbf{y}){)}^T\mathbf{G}(\mathbf{y})\nabla D_{\mathbf{y}}\phi (\mathbf{y})(\delta \mathbf{y}). \end{gathered}$$

From Lemma 2 with v = φ(y) and Lemma 3 with $v=(\tilde{u}\circ F)(\cdot ,\mathbf{y})$ we obtain the result. □

Lemma 5 Suppose that Assumptions 1 to 5 are satisfied. Then for any y, δy ∈ W and for all $v\in H_0^1(U)$ we have that

$$\begin{gathered} D_{\mathbf{y}}^{2}Q(\mathbf{y})(\delta \mathbf{y},\delta \mathbf{y})=-\sum _{n,m=1}^N\delta y_n\delta y_m({\int }_U(\nabla (\tilde{u}\circ F)(\cdot ,\mathbf{y}){)}^T({\partial }_{y_m}{\partial }_{y_n}\mathbf{G}(\mathbf{y}))\nabla \phi (\mathbf{y})\phantom{)} \\ +(\nabla {\partial }_{y_m}{\partial }_{y_n}\widehat{\nu }(\mathbf{y}){)}^T\mathbf{G}(\mathbf{y})\nabla \phi (\mathbf{y})+(\nabla {\partial }_{y_n}\widehat{\nu }(\mathbf{y}){)}^T{\partial }_{y_m}\mathbf{G}(\mathbf{y})\nabla \phi (\mathbf{y}) \\ +(\nabla {\partial }_{y_m}\widehat{\nu }(\mathbf{y}){)}^T{\partial }_{y_n}\mathbf{G}(\mathbf{y})\nabla \phi (\mathbf{y})+(\nabla \widehat{\nu }(\mathbf{y}){)}^T{\partial }_{y_m}{\partial }_{y_n}\mathbf{G}(\mathbf{y})\nabla \phi (\mathbf{y}) \\ -{\partial }_{y_m}{\partial }_{y_n}(f\circ F)(\cdot ,\mathbf{y})\mid \mathbf{J}(\mathbf{y})\mid \phi (\mathbf{y})-{\partial }_{y_n}(f\circ F)(\cdot ,\mathbf{y}){\partial }_{y_m}\mid \mathbf{J}(\mathbf{y})\mid \phi (\mathbf{y}) \\ -\phantom{(}{\partial }_{y_m}(f\circ F)(\cdot ,\mathbf{y}){\partial }_{y_n}\mid \mathbf{J}(\mathbf{y})\mid \phi (\mathbf{y})-(f\circ F)(\cdot ,\mathbf{y}){\partial }_{y_m}{\partial }_{y_n}\mid \mathbf{J}(\mathbf{y})\mid \phi (\mathbf{y})) \\ -\sum _{n=1}^N\delta y_n({\int }_U(\nabla D_{\mathbf{y}}(\tilde{u}\circ F)(\cdot ,\mathbf{y}){)}^T(\delta \mathbf{y})({\partial }_{y_n}\mathbf{G}(\mathbf{y}))\nabla \phi (\mathbf{y})\phantom{)} \\ +(\nabla (\tilde{u}\circ F)(\cdot ,\mathbf{y}){)}^T({\partial }_{y_n}\mathbf{G}(\mathbf{y}))\nabla D_{\mathbf{y}}\phi (\mathbf{y})(\delta \mathbf{y})+(\nabla {\partial }_{y_n}\widehat{\nu }(\mathbf{y}){)}^T\mathbf{G}(\mathbf{y})\nabla D_{\mathbf{y}}\phi (\mathbf{y})(\delta \mathbf{y}) \\ +(\nabla \widehat{\nu }(\mathbf{y}){)}^T{\partial }_{y_n}\mathbf{G}(\mathbf{y})\nabla D_{\mathbf{y}}\phi (\mathbf{y})(\delta \mathbf{y})-{\partial }_{y_n}(f\circ F)(\cdot ,\mathbf{y})\mid \mathbf{J}(\mathbf{y})\mid D_{\mathbf{y}}\phi (\mathbf{y})(\delta \mathbf{y}) \\ -\phantom{(}(f\circ F)(\cdot ,\mathbf{y}){\partial }_{y_n}\mid \mathbf{J}(\mathbf{y})\mid D_{\mathbf{y}}\phi (\mathbf{y})(\delta (\mathbf{y})). \end{gathered}$$

Proof Let $E(\mathbf{y},\delta \mathbf{y})≔{\text{lim}}_{s\to 0^{+}}\frac{Q(\mathbf{y}+s\delta \mathbf{y})-Q(\mathbf{y})}{s}$ (see Lemma 4). Taking the first variation of equation of E(y) we have that

$$\begin{gathered} \underset{s\to 0^{+}}{\text{lim}}\frac{E(\mathbf{y}+s\delta \mathbf{y},\delta \mathbf{y})-E(\mathbf{y},\delta \mathbf{y})}{s}=\sum _{n=1}^N\delta y_n\underset{s\to 0^{+}}{\text{lim}}\frac{1}{s}[{\int }_U(-(\nabla \tilde{u}(\mathbf{y}+s\delta \mathbf{y}{)}^T\phantom{)}\phantom{]} \\ {\partial }_{y_n}\mathbf{G}(\mathbf{y}+s\delta \mathbf{y})\nabla \phi (\mathbf{y}+s\delta \mathbf{y})+{\partial }_{y_n}(f\circ F)(\cdot ,\mathbf{y}+s\delta \mathbf{y})\mid \mathbf{J}(\mathbf{y}+s\delta \mathbf{y})\mid \phi (\mathbf{y}+s\delta \mathbf{y}) \\ -(\nabla {\partial }_{y_n}\widehat{\nu }(\mathbf{y}+s\delta \mathbf{y}){)}^T\mathbf{G}(\mathbf{y}+s\delta \mathbf{y})\nabla \phi (\mathbf{y}+s\delta \mathbf{y}) \\ -(\nabla \widehat{\nu }(\mathbf{y}+s\delta \mathbf{y}){)}^T{\partial }_{y_n}\mathbf{G}(\mathbf{y}+s\delta \mathbf{y})\nabla \phi (\mathbf{y}+s\delta \mathbf{y}) \\ +\phantom{(}(f\circ F)(\cdot ,\mathbf{y}+s\delta \mathbf{y}){\partial }_{y_n}\mid \mathbf{J}(\mathbf{y}+s\delta \mathbf{y})\mid \phi (\mathbf{y}+s\delta \mathbf{y})) \\ -{\int }_U(-(\nabla (\tilde{u}\circ F)(\cdot ,\mathbf{y}){)}^T{\partial }_{y_n}\mathbf{G}(\mathbf{y})\nabla \phi (\mathbf{y})+{\partial }_{y_n}(f\circ F)(\cdot ,\mathbf{y})\mid \mathbf{J}(\mathbf{y})\mid \phi (\mathbf{y})\phantom{)} \\ -(\nabla {\partial }_{y_n}\widehat{\nu }(\mathbf{y}){)}^T\mathbf{G}(\mathbf{y})\nabla \phi (\mathbf{y}) \\ -\phantom{[}\phantom{(}(\nabla \widehat{\nu }(\mathbf{y}){)}^T{\partial }_{y_n}\mathbf{G}(\mathbf{y})\nabla \phi (\mathbf{y})+(f\circ F)(\cdot ,\mathbf{y}){\partial }_{y_n}\mid \mathbf{J}(\mathbf{y})\mid \phi (\mathbf{y}))]. \end{gathered}$$

Following the same approach as in Lemma 3) and 4) we obtain the result. □

4.1. Hybrid collocation-perturbation approach

We now consider a linear approximation of the QoI Q(y) with respect to y ∈ Γ. For any y = y₀ + δy, y₀ ∈ Γ, y ∈ Γ, the linear approximation has the form

$$Q({\mathbf{y}}_0)+<D_{\mathbf{y}}Q({\mathbf{y}}_0),\delta \mathbf{y}>$$

where δy = y − y₀ ∈ Γ. Recall that Γ = Γ_L × Γ_S and make the following definitions and assumptions

1. y := [y_L, y_S], δy := [δy_L, δy_S], and ${\mathbf{y}}_0≔[{\mathbf{y}}_0^L,{\mathbf{y}}_0^S]$.

2. ${\mathbf{y}}_0^L$ takes values on Γ_L and δy_L := 0 ∈ Γ_L.

3. ${\mathbf{y}}_0^S≔0\in {\Gamma }_S$ and δy_S = y_S takes values on Γ_S.

We can now construct a linear approximation of the QoI with respect to the allowable perturbation set Γ. Consider the following linear approximation of Q(y_L, y_S)

$$\widehat{Q}({\mathbf{y}}_L,{\mathbf{y}}_S)≔Q({\mathbf{y}}_L,{\mathbf{y}}_0^S)+\tilde{Q}({\mathbf{y}}_L,{\mathbf{y}}_0^S,\delta {\mathbf{y}}_S),$$ (11)

and from Lemma 4 we have that

$$\tilde{Q}({\mathbf{y}}_L,{\mathbf{y}}_0^S,\delta {\mathbf{y}}_S)≔<D_{\mathbf{y}}Q({\mathbf{y}}_L,{\mathbf{y}}_0^S),\delta {\mathbf{y}}_0^S>=\sum _{n=1}^{N_S}\delta y_n^S{\int }_U{\alpha }_n(\eta ,{\mathbf{y}}_L,{\mathbf{y}}_0^S)\mathrm{d}\eta ,$$

where

$$\begin{gathered} {\alpha }_n(\eta ,{\mathbf{y}}_L,{\mathbf{y}}_0^S)≔-(\nabla (\tilde{u}\circ F)(\eta ,{\mathbf{y}}_L,{\mathbf{y}}_0^S){)}^T{\partial }_{y_n^S}\mathbf{G}({\mathbf{y}}_L,{\mathbf{y}}_0^S)\nabla \phi ({\mathbf{y}}_L) \\ +{\partial }_{y_n^S}(f\circ F)(\eta ,{\mathbf{y}}_L,{\mathbf{y}}_0^S)\mid \mathbf{J}({\mathbf{y}}_L,{\mathbf{y}}_0^S)\mid \phi ({\mathbf{y}}_L,{\mathbf{y}}_0^S) \\ -(\nabla {\partial }_{y_n^S}\widehat{\nu }({\mathbf{y}}_L,{\mathbf{y}}_0^S){)}^T\mathbf{G}({\mathbf{y}}_L,{\mathbf{y}}_0^S)\nabla \phi ({\mathbf{y}}_L,{\mathbf{y}}_0^S) \\ -(\nabla \widehat{\nu }({\mathbf{y}}_L,{\mathbf{y}}_0^S){)}^T{\partial }_{y_n^S}\mathbf{G}({\mathbf{y}}_L,{\mathbf{y}}_0^S)\nabla \phi ({\mathbf{y}}_L,{\mathbf{y}}_0^S) \\ +(f\circ F)(\eta ,{\mathbf{y}}_L,{\mathbf{y}}_0^S){\partial }_{y_n^S}\mid \mathbf{J}({\mathbf{y}}_L,{\mathbf{y}}_0^S)\mid \phi ({\mathbf{y}}_L,{\mathbf{y}}_0^S). \end{gathered}$$

This linear approximation only shows the explicit dependence on the variable y_S without the decay of the coefficients ${\mu }_n^S$ for n = 1, … , N_S. However, to obtain directly capture the effect of the coefficients let ${\tilde{y}}_n≔{\mu }_n^{1∕2}{y}_n$ for n = 1, … , N and $\delta {\tilde{y}}_n={\mu }_n^{1∕2}\delta y_n$. It is not hard to see that $<D_{\mathbf{y}}Q({\mathbf{y}}_L,{\mathbf{y}}_0^S)$, $\delta {\mathbf{y}}_0^S>$ can be reformulated with respect to the variables $\tilde{\mathbf{y}}≔[{\tilde{y}}_1,\dots ,{\tilde{y}}_N]$ and $\delta \tilde{\mathbf{y}}≔[\delta {\tilde{y}}_1,\dots ,\delta {\tilde{y}}_N]$ by applying Lemma 4 as

$$<D_{\mathbf{y}}Q({\mathbf{y}}_L,{\mathbf{y}}_0^S),\delta {\mathbf{y}}_0^S>=\sum _{n=1}^{N_S}\sqrt{{\mu }_{S,n}}\delta y_n^S{\int }_U{\tilde{\alpha }}_n(\eta ,{\mathbf{y}}_L,{\mathbf{y}}_0^S)\mathrm{d}\eta$$ (12)

where

$$\begin{gathered} {\tilde{\alpha }}_n(\eta ,{\mathbf{y}}_L,{\mathbf{y}}_0^S)≔-(\nabla (\tilde{u}\circ F)(\eta ,{\mathbf{y}}_L,{\mathbf{y}}_0^S){)}^T{\partial }_{{\tilde{y}}_n^S}\mathbf{G}({\mathbf{y}}_L,{\mathbf{y}}_0^S)\nabla \phi ({\mathbf{y}}_L,{\mathbf{y}}_0^S) \\ +{\partial }_{{\tilde{y}}_n^S}(f\circ F)(\eta ,{\mathbf{y}}_L,{\mathbf{y}}_0^S)\mid \mathbf{J}({\mathbf{y}}_L,{\mathbf{y}}_0^S)\mid \phi ({\mathbf{y}}_L,{\mathbf{y}}_0^S) \\ -(\nabla {\partial }_{{\tilde{y}}_n^S}\widehat{\nu }({\mathbf{y}}_L,{\mathbf{y}}_0^S){)}^T\mathbf{G}({\mathbf{y}}_L,{\mathbf{y}}_0^S)\nabla \phi ({\mathbf{y}}_L,{\mathbf{y}}_0^S) \\ -(\nabla \widehat{\nu }({\mathbf{y}}_L,{\mathbf{y}}_0^S){)}^T{\partial }_{{\tilde{y}}_n^S}\mathbf{G}({\mathbf{y}}_L.{\mathbf{y}}_0^S)\nabla \phi ({\mathbf{y}}_L,{\mathbf{y}}_0^S) \\ +(f\circ F)(\eta ,{\mathbf{y}}_L,{\mathbf{y}}_0^S){\partial }_{{\tilde{y}}_n^S}\mid \mathbf{J}({\mathbf{y}}_L,{\mathbf{y}}_0^S)\mid \phi ({\mathbf{y}}_L,{\mathbf{y}}_0^S) \end{gathered}$$

This will allow an explicit dependence of the mean and variance error in terms of the coefficients μ_S,n, n = 1, … , N_S, as show in in Section 6.

The mean of $\widehat{Q}({\mathbf{y}}_L,{\mathbf{y}}_S)$ can be obtained as

$$\mathbb{E}[\widehat{Q}({\mathbf{y}}_L,{\mathbf{y}}_S)]=\mathbb{E}[Q({\mathbf{y}}_L,{\mathbf{y}}_0^S)]+\mathbb{E}[\tilde{Q}({\mathbf{y}}_L,{\mathbf{y}}_0^S,\delta {\mathbf{y}}_S)].$$

From Fubini’s theorem we have

$$\mathbb{E}[Q({\mathbf{y}}_L,{\mathbf{y}}_0^S)]={\int }_{{\Gamma }_L}Q({\mathbf{y}}_L,0){\rho }_L({\mathbf{y}}_L)\mathrm{d}{\mathbf{y}}_L.$$ (13)

and from equation (12)

$$\mathbb{E}[\tilde{Q}({\mathbf{y}}_L,{\mathbf{y}}_0^S,\delta {\mathbf{y}}_S)]=\sum _{n=1}^{N_S}\sqrt{{\mu }_{S,n}}{\int }_{{\Gamma }_L}{\int }_{[-1,1]}{y}_n^S{\gamma }_n({\mathbf{y}}_L,0)\rho ({\mathbf{y}}_L,y_n^S)\mathrm{d}{\mathbf{y}}_L\mathrm{d}{y}_n^S,$$ (14)

where ${\gamma }_n({\mathbf{y}}_L,0)≔{\int }_U{\tilde{\alpha }}_n(\eta ,{\mathbf{y}}_L,0)\mathrm{d}\eta$, ρ(y_L) is the marginal distribution of ρ(y) with respect to the variables y_L and similarly for $\rho ({\mathbf{y}}_L,y_n^S)(n=1,\dots ,N_S)$. The term $\mathbb{E}[\tilde{Q}({\mathbf{y}}_L,{\mathbf{y}}_0^S,\delta {\mathbf{y}}_S)]$ is referred as the mean correction. The variance of $\widehat{Q}({\mathbf{y}}_L,{\mathbf{y}}_S)$ can be computed as

$$\begin{gathered} \text{var}[\widehat{Q}({\mathbf{y}}_L,{\mathbf{y}}_S)]=\mathbb{E}[\widehat{Q}({\mathbf{y}}_L,{\mathbf{y}}_S{)}^2]-\mathbb{E}[\widehat{Q}({\mathbf{y}}_L,{\mathbf{y}}_S{)}^2]=\text{var}[Q({\mathbf{y}}_L,{\mathbf{y}}_0^S)] \\ \underset{(I)}{\underbrace{+\mathbb{E}[\tilde{Q}({\mathbf{y}}_L,{\mathbf{y}}_0^S,\delta {\mathbf{y}}_S{)}^2]+2\mathbb{E}[Q({\mathbf{y}}_L,{\mathbf{y}}_0^S)\tilde{Q}({\mathbf{y}}_L,{\mathbf{y}}_0^S,\delta {\mathbf{y}}_S)]}} \\ \underset{(I)}{\underbrace{-\mathbb{E}[\tilde{Q}({\mathbf{y}}_L,{\mathbf{y}}_0^S,\delta {\mathbf{y}}_S){]}^2-2\mathbb{E}[Q({\mathbf{y}}_L,{\mathbf{y}}_0^S)]\mathbb{E}[\tilde{Q}({\mathbf{y}}_L,{\mathbf{y}}_0^S,\delta {\mathbf{y}}_S)]}}. \end{gathered}$$

The term (I) is referred as the variance correction of $\text{var}[Q({\mathbf{y}}_L,{\mathbf{y}}_0^S)]$. From Fubini’s theorem and equation (12) we have that

$$\begin{gathered} \mathbb{E}[\tilde{Q}({\mathbf{y}}_L,{\mathbf{y}}_0^S,\delta {\mathbf{y}}_S{)}^2]=\sum _{k=1}^{N_S}\sum _{n=1}^{N_S}{\int }_{{\Gamma }_L}{\int }_{[-1,1]}{\int }_{[-1,1]}\sqrt{{\mu }_{S,k}}\sqrt{{\mu }_{S,n}}{y}_k^S{y}_n^S \\ {\gamma }_k({\mathbf{y}}_L,{\mathbf{y}}_0^S){\gamma }_n({\mathbf{y}}_L,{\mathbf{y}}_0^S)\rho ({\mathbf{y}}_L,y_k^S,y_n^S)\mathrm{d}{\mathbf{y}}_{L}d{y}_k^{S}d{y}_n^S, \end{gathered}$$ (15)

and $\mathbb{E}[Q({\mathbf{y}}_L,{\mathbf{y}}_0^S)\tilde{Q}({\mathbf{y}}_L,{\mathbf{y}}_0^S,\delta {\mathbf{y}}_S)]$ is equal to

$$\sum _{k=1}^{N_S}{\int }_{{\Gamma }_L}{\int }_{[-1,1]}Q({\mathbf{y}}_L,0){\gamma }_k({\mathbf{y}}_L,0)y_k^S\rho ({\mathbf{y}}_L,y_k^S)d{\mathbf{y}}_{L}d{y}_k^S.$$ (16)

Note that the mean $\mathbb{E}[Q({\mathbf{y}}_L,{\mathbf{y}}_0^S)]$ and variance $\text{var}[Q({\mathbf{y}}_L,{\mathbf{y}}_0^S)]$ depend only on the large variation variables y_L. If the region of analyticity of the QoI with respect to the stochastic variables y_L is sufficiently large, it is reasonable to approximate $Q({\mathbf{y}}_L,{\mathbf{y}}_0^S)$ with a Smolyak sparse grid ${\mathcal{S}}_w^{m,g}[Q({\mathbf{y}}_L,{\mathbf{y}}_0^S)]$, with respect to the variable y_L (see [6] for details). Thus in equations (13) - (16) $Q({\mathbf{y}}_L,{\mathbf{y}}_0^S)$ is replaced with the the sparse grid approximation ${\mathcal{S}}_w^{m,g}[Q({\mathbf{y}}_L,{\mathbf{y}}_0^S)]$ and for n = 1, … , N_S γ_n(y_L, 0) is replaced with ${\mathcal{S}}_w^{m,g}[{\gamma }_n({\mathbf{y}}_L,0)]$.

Remark 4 For the special case that for n = 1, … , N and m = 1, … , N $\mathbb{E}[Y_n(\omega )Y_m(\omega )]=\delta [n-m]$, ρ(y) = ρ(y_L)ρ(y_S), for all y_L ∈ Γ_L and y_S ∈ Γ_S (i.e. independence assumption of the joint probability distribution ρ(y_L, y_S)), the mean and variance corrections are simplified. Applying Fubini’s theorem and from equation 13 the mean of $\widehat{Q}({\mathbf{y}}_L,{\mathbf{y}}_S)$ now becomes

$$\begin{gathered} \mathbb{E}[\widehat{Q}({\mathbf{y}}_L,{\mathbf{y}}_S)]=\mathbb{E}[Q({\mathbf{y}}_L,{\mathbf{y}}_0^S)]+\underset{=0}{\underbrace{\mathbb{E}[\tilde{Q}({\mathbf{y}}_L,{\mathbf{y}}_0^S,\delta {\mathbf{y}}_S)]}}=\mathbb{E}[Q({\mathbf{y}}_L,{\mathbf{y}}_0^S)] \\ ={\int }_{{\Gamma }_L}Q({\mathbf{y}}_L,0){\rho }_L({\mathbf{y}}_L)\mathrm{d}{\mathbf{y}}_L, \end{gathered}$$

i.e. there is no contribution from the small variations. Applying a similar argument we have that

$$\begin{gathered} \text{var}[\widehat{Q}({\mathbf{y}}_L,{\mathbf{y}}_S)]=\mathbb{E}[\widehat{Q}({\mathbf{y}}_L,{\mathbf{y}}_S{)}^2]-\mathbb{E}[\widehat{Q}({\mathbf{y}}_L,{\mathbf{y}}_S){]}^2=\text{var}[Q({\mathbf{y}}_L,{\mathbf{y}}_0^S)] \\ +\mathbb{E}[\tilde{Q}({\mathbf{y}}_L,{\mathbf{y}}_0^S,\delta {\mathbf{y}}_S{)}^2]+\underset{=0}{\underbrace{2\mathbb{E}[Q({\mathbf{y}}_L,{\mathbf{y}}_0^S)\tilde{Q}({\mathbf{y}}_L,{\mathbf{y}}_0^S,\delta {\mathbf{y}}_S)]}} \\ \underset{=0}{\underbrace{-\mathbb{E}[\tilde{Q}({\mathbf{y}}_L,{\mathbf{y}}_0^S,\delta {\mathbf{y}}_S){]}^2}}-2\underset{=0}{\underbrace{\mathbb{E}[Q({\mathbf{y}}_L,{\mathbf{y}}_0^S)]\mathbb{E}[\tilde{Q}({\mathbf{y}}_L,{\mathbf{y}}_0^S,\delta {\mathbf{y}}_S)]}} \\ =\text{var}[Q({\mathbf{y}}_L,{\mathbf{y}}_0^S)]+\underset{\text{Variance correction}}{\underbrace{\sum _{n=1}^{N_S}{\mu }_n^S{\int }_U{\alpha }_n(x,{\mathbf{y}}_L,{\mathbf{y}}_0^S)\mathrm{d}x{\int }_U{\alpha }_n(y,{\mathbf{y}}_L,{\mathbf{y}}_0^S)\mathrm{d}y}}. \end{gathered}$$

Notice that for this case the variance correction consists of N_S terms, thus the computational cost will depend linearly with respect to N_S.

5. Analytic correction

In this section we show that the mean and variance corrections are analytic in a well defined region in ${\mathbb{C}}^{N_L}$ with respect to the variables y_L ∈ Γ_L. The size of the region of analyticity will directly correlated with the convergence rate of a Smolyak sparse grid. To this end, let us establish the following definition: For any $0<\beta <\tilde{\delta }$, for some constant $\tilde{\delta }>0$, define the following region in ${\mathbb{C}}^{N_L}$,

$$\begin{gathered} {\Theta }_{\beta ,N_L}≔\{\mathbf{z}\in {\mathbb{C}}^{N_L};\mathbf{z}=\mathbf{y}+\mathbf{w},\mathbf{y}\in [-1,1{]}^{N_L}, \\ \phantom{\{}\sum _{l=1}^{N_L}\underset{\eta \in U}{\text{sup}}\Vert {\mathbf{B}}_l(\eta ){\Vert }_2\sqrt{{\mu }_l}\mid w_l\mid ⩽\beta \}\}. \end{gathered}$$ (17)

Observe that the size of the region Θ_β,NL is mostly controlled by the decay of the coefficients μ_l and the size of ∥B_l(η)∥₂. Thus the faster the coefficient μ_l decays the larger the region Θ_β,NL will be.

Furthermore, rewrite J(η, y_L) as J(y_L) = I+R(y_L), with $\mathbf{R}({\mathbf{y}}_L)≔{\sum }_{n=1}^{N_L}\sqrt{{\mu }_n}{\mathbf{B}}_n(\eta )y_n$. We now state the first analyticity theorem for the solution $(\tilde{u}\circ F)({\mathbf{y}}_L)$ with respect to the random variables y_L ∈ Γ_L.

To simplify the analyticity proof the following assumptions are made.

Assumption 6

1. (a ∘ F)(η, ω) is only a function of η ∈ U and independent of ω ∈ Ω.

2. $(\widehat{\nu }\circ F)(\eta ,\omega )$ is only a function of η ∈ U and independent of ω ∈ Ω.

3. $f:\mathcal{G}\to \mathbb{R}$ can be analytically extended in ${\mathbb{C}}^d$. Furthermore assume that the analytic extension Re(f ∘ F)(η, z), Im(f ∘ F)(η, z) ∈ L²(U).

4. There exists $0<\tilde{\delta }<1$ such that ${\sum }_{n=1}^N\Vert \mathbf{B}(\eta ){\Vert }_2\sqrt{{\mu }_n}⩽1-\tilde{\delta }$, for all η ∈ U.

Remark 5 Note that Assumption 6 (i) is not necessarily hard and Theorem 1, 2 and the error analysis in Section 6 can be easily adapted for a less restrictive hypothesis (See Assumptions 7 and Lemma 2 in [7]). None-the-less, this assumption is still practical for layered materials such as semi-conductor design. For such problems $(\widehat{\nu }\circ F)(\eta ,\omega )$ can be non-constant along the non-stochastic directions.

Remark 6 Under Assumption 6 (iv) we have that $\text{Re}\text{det}(\mathbf{J}(\mathbf{z}))⩾{\tilde{\delta }}^d\alpha$ for all z ∈ Θ_β,NL, where $\alpha =2-\text{exp}\left(\frac{d\beta }{\delta -\beta }\right)>0$. This implies the real part of Redet(J(z)) for all z ∈ Θ_β,NL will never have a sign change.

The following theorem, can be proven with a slight modification of Theorem 7 in [7] to take into account Assumption 6 (ii) and the mapping model of equation (8)

Theorem 1 Let $0<\tilde{\delta }<1$ then the solution $(\tilde{u}\circ F)(\eta ,{\mathbf{y}}_L):{\Gamma }_L\to H_0^1(U)$ of Problem 1 can be extended holomorphically on Θ_β,NL if

$$\beta <min\left\{\tilde{\delta }\frac{\log (2-\gamma )}{d+\log (2-\gamma )},\sqrt{1+{\tilde{\delta }}^2∕2}-1\right\},$$

where $\gamma ≔\frac{2{\tilde{\delta }}^2+(2-\tilde{\delta }{)}^d}{{\tilde{\delta }}^d+(2-\tilde{\delta }{)}^d}$.

Remark 7 By following a similar argument, the influence function φ(y) can be extended holomorphically in Θ_β,NL if

$$\beta <min\left\{\tilde{\delta }\frac{\log (2-\gamma )}{d+\log (2-\gamma )},\sqrt{1+{\tilde{\delta }}^2∕2}-1\right\}.$$

Remark 8 To prove the following theorem will be using the following matrix calculus identity [5]: Suppose that the matrix $\mathbf{A}\in {\mathbb{R}}^{n,n}$ is a function of a the real variable α then

$$\frac{\partial {\mathbf{A}}^{-1}}{\partial \alpha }=-{\mathbf{A}}^{-1}\frac{\partial \mathbf{A}}{\partial \alpha }{\mathbf{A}}^{-1}.$$

We are now ready to show that the linear approximation $\widehat{Q}({\mathbf{y}}_L,{\mathbf{y}}_S)$ can be analytically extended on Θ_β,NL. Note that it is sufficient to show that ${\int }_U{\tilde{\alpha }}_n(\eta ,{\mathbf{y}}_L,0)$ can be analytically extended on Θ_β,NL.

Theorem 2 Let $0<\tilde{\delta }<1$, if $\beta <min\{\tilde{\delta }\frac{\log (2-\gamma )}{d+\log (2-\gamma )}$, $\sqrt{1+{\tilde{\delta }}^2∕2}-1\}$ then there exists an extension of ${\int }_U{\tilde{\alpha }}_n(\eta ,{\mathbf{y}}_L,0)$, for n = 1, … , N_S, which is holomorphic in Θ_β,NL.

Proof Consider the extension of y_L → z_L, where ${\mathbf{z}}_L\in {\mathbb{C}}^{N_L}$. First, we have that

$${\int }_U(\nabla (\tilde{u}\circ F)({\mathbf{y}}_L,{\mathbf{y}}_S){)}^T{\partial }_{{\tilde{y}}_n^S}\mathbf{G}({\mathbf{y}}_L,{\mathbf{y}}_S)\nabla \phi ({\mathbf{y}}_L,{\mathbf{y}}_S)$$ (18)

for n = 1, … , N_S can be extended on Θ_β,NL. Note the for the sake of reducing notation clutter we dropped the dependence of the variable η ∈ U and it is understood from context unless clarification is needed.

We now show that each entry of the matrix ${\partial }_{{\tilde{y}}_n^S}\mathbf{G}({\mathbf{z}}_L,{\mathbf{y}}_S)$ is holomorphic on Θ_β,NL for all y ∈ Γ_S. First, we have that

$$\begin{gathered} {\partial }_{{\tilde{y}}_n^S}\mathbf{G}({\mathbf{z}}_L,{\mathbf{y}}_S)=({\partial }_{{\tilde{y}}_n^S}(a\circ F)({\mathbf{z}}_L,{\mathbf{y}}_S)){\mathbf{C}}^{-1}({\mathbf{z}}_L,{\mathbf{y}}_S)\mid \mathbf{J}({\mathbf{z}}_L,{\mathbf{y}}_S)\mid \\ +(a\circ F)({\mathbf{z}}_L,{\mathbf{y}}_S)({\mathbf{C}}^{-1}({\mathbf{z}}_L,{\mathbf{y}}_S){\partial }_{{\tilde{y}}_n^S}\mid \mathbf{J}({\mathbf{z}}_L,{\mathbf{y}}_S)\mid \phantom{)} \\ \phantom{(}+\mid \mathbf{J}({\mathbf{z}}_L,{\mathbf{y}}_S)\mid {\partial }_{{\tilde{y}}_n^S}{\mathbf{C}}^{-1}({\mathbf{z}}_L,{\mathbf{y}}_S)). \end{gathered}$$

From Assumption 6 (a ∘ F)(·, z_L) and ${\partial }_{{\tilde{y}}_n^S}(a\circ F)(\cdot ,{\mathbf{z}}_L,{\mathbf{y}}_S)=0$ are holomorphic on Θ_β,NL for all y_S ∈ Γ_S. From Remark 8 we have that

$${\partial }_{{\tilde{y}}_n^S}{\mathbf{C}}^{-1}({\mathbf{z}}_L,{\mathbf{y}}_S)=-{\mathbf{C}}^{-1}({\mathbf{z}}_L,{\mathbf{y}}_S)\left({\partial }_{{\tilde{y}}_n^S}\mathbf{C}({\mathbf{z}}_L,{\mathbf{y}}_S)\right){\mathbf{C}}^{-1}({\mathbf{z}}_L,{\mathbf{y}}_S).$$

Since $\beta <\tilde{\delta }$ the series

$${\mathbf{J}}^{-1}({\mathbf{z}}_L,{\mathbf{y}}_S)=(I+\mathbf{R}({\mathbf{z}}_L,{\mathbf{y}}_S){)}^{-1}=I+\sum _{k=1}^{\infty }\mathbf{R}({\mathbf{z}}_L,{\mathbf{y}}_S{)}^k$$

is convergent for all z_L ∈ Θ_β and for all y_S ∈ Γ_S. It follows that each entry of ∂F(z_L, y)⁻¹ and therefore C(z_L, y)⁻¹ is holomorphic for all z_L ∈ Θ_β,NL and for all y_S ∈ Γ_S. We have that ∣J(z_L, y_S)∣ and ${\partial }_{{\tilde{y}}_l^S}C({\mathbf{z}}_L,{\mathbf{y}}_S)$ are functions of a finite polynomial therefore they are holomorphic for all z_L ∈ Θ_β,NL and y_S ∈ Γ_S.

From Jacobi’s formula we have that for all z_L ∈ Θ_β,NL, y_S ∈ Γ_S and l = 1, … , N_S

$$\begin{gathered} {\partial }_{{\tilde{y}}_n^S}\mid \mathbf{J}({\mathbf{z}}_L,{\mathbf{y}}_S)\mid =tr(Adj(\mathbf{J}({\mathbf{z}}_L,{\mathbf{y}}_S)){\partial }_{{\tilde{y}}_n^S}\mathbf{J}({\mathbf{z}}_L,{\mathbf{y}}_S)) \\ =\mid \mathbf{J}({\mathbf{z}}_L,{\mathbf{y}}_S)\mid tr(\mathbf{J}({\mathbf{z}}_L,{\mathbf{y}}_S{)}^{-1}{\mathbf{B}}_n^S(\eta )). \end{gathered}$$

It follows that for all z_L ∈ Θ_β,NL and y_S ∈ Γ_S we have that ${\partial }_{{\tilde{y}}_n^S}\mathbf{G}({\mathbf{z}}_L,{\mathbf{y}}_S)$ are holomorphic for n = 1, … N_L.

We shall now prove the main result. First, extend y_L along the n^th dimension as y_n → z_n, $z_n\in \mathbb{C}$ and let ${\tilde{\mathbf{z}}}_n=[z_1,\dots ,z_{n-1},z_{n+1},\dots ,z_{N_L}]$. From Theorem 1 we have that $(\tilde{u}\circ F)({\mathbf{z}}_L,{\mathbf{y}}_S)$ and φ(z_L, y_S) are holomorphic for z_L ∈ Θ_β,NL and y_S ∈ Γ_S if

$$\beta <min\{\tilde{\delta }\frac{\log (2-\gamma )}{d+\log (2-\gamma )},\sqrt{1+{\tilde{\delta }}^2∕2}-1\}.$$

Thus from Theorem 1.9.1 in [16] the series

$$(\tilde{u}\circ F)({\mathbf{z}}_L,{\mathbf{y}}_S)=\sum _{l=0}^{\infty }{\tilde{u}}_l({\tilde{\mathbf{z}}}_n,{\mathbf{y}}_S)z_n^l\text{and}\phi ({\mathbf{z}}_L,{\mathbf{y}}_S)=\sum _{l=0}^{\infty }{\overline{\phi }}_l({\tilde{\mathbf{z}}}_n,{\mathbf{y}}_S)z_n^l,$$

are absolutely convergent in $H_0^1(U)$ for all $z\in \mathbb{C}$, where ${\tilde{u}}_l({\tilde{\mathbf{z}}}_n,{\mathbf{y}}_S)$, ${\tilde{\phi }}_l({\tilde{\mathbf{z}}}_n,{\mathbf{y}}_S)\in H_0^1(U)$ for l = 0, … , ∞. Furthermore,

$$\begin{gathered} \Vert \nabla (\tilde{u}\circ F)({\mathbf{z}}_L,{\mathbf{y}}_S){\Vert }_{L^2(U)}⩽\sum _{l=0}^{\infty }\Vert \nabla {\tilde{u}}_l({\tilde{\mathbf{z}}}_n,{\mathbf{y}}_S){\Vert }_{L^2(U)}\mid z_n{\mid }^l \\ ⩽\sum _{l=0}^{\infty }\Vert {\tilde{u}}_l({\tilde{\mathbf{z}}}_n,{\mathbf{y}}_S){\Vert }_{H_0^1(U)}\mid z_n{\mid }^l \end{gathered}$$

i.e. $\nabla (\tilde{u}\circ F)({\mathbf{z}}_L,{\mathbf{y}}_S)$ is holomorphic on Θ_β,NL along the n^th dimension. A similar argument is made for ∇φ(z_L, y_S).

Since the matrix ${\partial }_{{\tilde{y}}_n^S}\mathbf{G}({\mathbf{z}}_L,{\mathbf{y}}_S)$ is holomorphic for all z_L ∈ Θ_β,NL and y_S ∈ Γ_S then we can rewrite the (i, j) entry as ${\sum }_{k=0}^{\infty }{g}_k^{i,j}({\tilde{\mathbf{z}}}_n,{\mathbf{y}}_S)z_n^k$ where $g_k^{i,j}({\tilde{\mathbf{z}}}_n,{\mathbf{y}}_S)\in L^{\infty }(U)$. For each i, j = 1, … , d consider the map

$$\begin{gathered} T_{i,j}≔{\int }_U{\partial }_{{\tilde{y}}_n^S}\mathbf{G}({\mathbf{z}}_L,{\mathbf{y}}_S)(i,j){\partial }_{x_i}\tilde{u}({\mathbf{z}}_L,{\mathbf{y}}_S){\partial }_{x_j}\phi ({\mathbf{z}}_L,{\mathbf{y}}_S) \\ =\sum _{k,l,p=0}^{\infty }{z}_n^{k+l+p}{\int }_U{g}_k^{i,j}({\tilde{\mathbf{z}}}_n,{\mathbf{y}}_S){\partial }_{x_i}{\tilde{u}}_l({\tilde{\mathbf{z}}}_n,{\mathbf{y}}_S){\partial }_{x_j}{\tilde{\phi }}_p({\tilde{\mathbf{z}}}_n,{\mathbf{y}}_S). \end{gathered}$$

For i, j = 1, … , d, for all z_L ∈ Θ_β,NL and y_S ∈ Γ_S

$$\begin{gathered} \mid T_{i,j}\mid ⩽\sum _{k,l,p=0}^{\infty }\mid z_n{\mid }^{k+l+p}{\int }_U\mid g_k^{i,j}({\mathbf{z}}_L,{\mathbf{y}}_S){\partial }_{x_i}{\tilde{u}}_l({\tilde{\mathbf{z}}}_n,{\mathbf{y}}_S){\partial }_{x_j}{\phi }_p({\tilde{\mathbf{z}}}_n,{\mathbf{y}}_S)\mid \\ (\text{From Cauchy Schwartz it follows that}) \\ ⩽\sum _{k,l,p=0}^{\infty }\mid z_n{\mid }^{k+l+p}\Vert g_k^{i,j}({\tilde{\mathbf{z}}}_n,{\mathbf{y}}_S){\Vert }_{L^{\infty }(U)}\Vert {\partial }_{x_i}{\tilde{u}}_l({\tilde{\mathbf{z}}}_n,{\mathbf{y}}_S){\Vert }_{L^2(U)} \\ \Vert {\partial }_{x_j}{\phi }_p({\tilde{\mathbf{z}}}_n,{\mathbf{y}}_S){\Vert }_{L^2(U)} \\ ⩽\sum _{k,l,p=0}^{\infty }\mid z_n{\mid }^{k+l+p}\Vert g_k^{i,j}({\tilde{\mathbf{z}}}_n,{\mathbf{y}}_S){\Vert }_{L^{\infty }(U)}\Vert {\tilde{u}}_l({\tilde{\mathbf{z}}}_n,{\mathbf{y}}_S){\Vert }_{H_0^1(U)} \\ \Vert {\phi }_p({\tilde{\mathbf{z}}}_n,{\mathbf{y}}_S){\Vert }_{H_0^1(U)}<\infty . \end{gathered}$$

Thus equation (18) can be analytically extended on Θ_β,NL along the n^th dimensions for all y_S ∈ Γ_S. Equation (18) can now be analytically extended on the entire domain Θ_β,NL. Repeat the analytic extension of (18) for n = 1, … , N_L. Hartog’s Theorem implies that (18) is continuous in Θ_β,NL. Osgood’s Lemma them implies that (18) is holomorphic on Θ_β,NL. Following a similar argument as for (18) we can analytically extended the rest of the terms of α_n(y_L, y_S) on Θ_β,NL for n = 1, … , N_S. □

6. Error analysis

In this section we analyze the perturbation error between the exact QoI Q(y_L, y_S) and the sparse grid hybrid perturbation approximation ${\mathcal{S}}_w^{m,g}[{\widehat{Q}}_h({\mathbf{y}}_L,{\mathbf{y}}_S)]$. With a slight abuse of notation by ${\mathcal{S}}_w^{m,g}[{\widehat{Q}}_h({\mathbf{y}}_L,{\mathbf{y}}_S)]$ we mean the two sparse grids approximations:

$${\mathcal{S}}_w^{m,g}[{\widehat{Q}}_h({\mathbf{y}}_L,{\mathbf{y}}_S)]≔{\mathcal{S}}_w^{m,g}[Q_h({\mathbf{y}}_L,0)]+\sum _{n=1}^{N_S}\sqrt{{\mu }_{S,n}}{y}_n^S{\mathcal{S}}_w^{m,g}[{\int }_U{\tilde{\alpha }}_{n,h}(\eta ,{\mathbf{y}}_L,0)],$$

where α_n,h(·, y_L, 0), for n = 1, … , N_S, and Q_h(y_L, y_S) are the finite element approximations of α_n(·, y_L, 0) and Q(y_L, y_S) respectively. It is easy to show that $\text{var}(Q({\mathbf{y}}_L,{\mathbf{y}}_S))-\text{var}({\mathcal{S}}_w^{m,g}[{\widehat{Q}}_h({\mathbf{y}}_L,{\mathbf{y}}_S)])$ is equal to

$$\underset{(I)}{\underbrace{\mathbb{E}[Q^2({\mathbf{y}}_L,{\mathbf{y}}_S)-{\mathcal{S}}_w^{m,g}[{\widehat{Q}}_h({\mathbf{y}}_L,{\mathbf{y}}_S){]}^2]}}-\underset{(II)}{\underbrace{(\mathbb{E}[Q({\mathbf{y}}_L,{\mathbf{y}}_S){]}^2-\mathbb{E}[{\mathcal{S}}_w^{m,g}[{\widehat{Q}}_h({\mathbf{y}}_L,{\mathbf{y}}_S){]}^2])}}.$$

(I) Applying Jensen’s inequality we have that

$$\begin{gathered} \mid \mathbb{E}[Q^2(\mathbf{y})-{\mathcal{S}}_w^{m,g}[{\widehat{Q}}_h(\mathbf{y}){]}^2]\mid ⩽\Vert Q(\mathbf{y})+{\mathcal{S}}_w^{m,g}[{\widehat{Q}}_h(\mathbf{y})]{\Vert }_{L_{\rho }^{\infty }(\Gamma )}(\Vert Q(\mathbf{y})-\widehat{Q}(\mathbf{y}){\Vert }_{L_{\rho }^2(\Gamma )} \\ +\Vert \widehat{Q}(\mathbf{y})-{\widehat{Q}}_h(\mathbf{y}){\Vert }_{L_{\rho }^1(\Gamma )}+\Vert {\widehat{Q}}_h(\mathbf{y})-{\mathcal{S}}_w^{m,g}[{\widehat{Q}}_h(\mathbf{y})]]{\Vert }_{L_{\rho }^2(\Gamma )}). \end{gathered}$$ (19)

(II) Similarly, we have that

$$\begin{gathered} \mid \mathbb{E}[Q({\mathbf{y}}_L,{\mathbf{y}}_S){]}^2-\mathbb{E}[{\mathcal{S}}_w^{m,g}[{\widehat{Q}}_h({\mathbf{y}}_L,{\mathbf{y}}_S)]{]}^2\mid ⩽\Vert Q(\mathbf{y})+{\mathcal{S}}_w^{m,g}{\widehat{Q}}_h(\mathbf{y}){\Vert }_{L_{\rho }^1(\Gamma )} \\ \Vert Q(\mathbf{y})-{\mathcal{S}}_w^{m,g}{\widehat{Q}}_h({\mathbf{y}}_L){\Vert }_{L_{\rho }^1(\Gamma )} \\ ⩽\Vert Q(\mathbf{y})+{\mathcal{S}}_w^{m,g}{\widehat{Q}}_h(\mathbf{y}){\Vert }_{L_{\rho }^1(\Gamma )}(\Vert Q(\mathbf{y})-\widehat{Q}(\mathbf{y}){\Vert }_{L_{\rho }^1(\Gamma )}+\Vert \widehat{Q}(\mathbf{y})-{\widehat{Q}}_h(\mathbf{y}){\Vert }_{L_{\rho }^1(\Gamma )} \\ +\Vert {\widehat{Q}}_h(\mathbf{y})-{\mathcal{S}}_w^{m,g}{\widehat{Q}}_h(\mathbf{y}){\Vert }_{L_{\rho }^1(\Gamma )}) \end{gathered}$$

Applying Jensen inequality

$$\begin{gathered} \mid \mathbb{E}[Q({\mathbf{y}}_L,{\mathbf{y}}_S){]}^2-\mathbb{E}[{\mathcal{S}}_w^{m,g}[{\widehat{Q}}_h({\mathbf{y}}_L,{\mathbf{y}}_S)]{]}^2\mid ⩽\Vert Q(\mathbf{y})+{\mathcal{S}}_w^{m,g}{\widehat{Q}}_h(\mathbf{y}){\Vert }_{L_{\rho }^2(\Gamma )} \\ (\Vert Q(\mathbf{y})-\widehat{Q}(\mathbf{y}){\Vert }_{L_{\rho }^2(\Gamma )}+\Vert \widehat{Q}(\mathbf{y})-{\widehat{Q}}_h(\mathbf{y}){\Vert }_{L_{\rho }^1(\Gamma )}+\Vert {\widehat{Q}}_h(\mathbf{y})-{\mathcal{S}}_w^{m,g}{\widehat{Q}}_h(\mathbf{y}){\Vert }_{L_{\rho }^2(\Gamma )}). \end{gathered}$$ (20)

Combining equations (19) and (20) we have that

$$\begin{gathered} \mid \text{var}(Q(\mathbf{y}))-\text{var}({\mathcal{S}}_w^{m,g}[{\widehat{Q}}_h(\mathbf{y})])\mid ⩽C_P\underset{\text{Perturbation}}{\underbrace{\Vert Q(\mathbf{y})-\widehat{Q}(\mathbf{y}){\Vert }_{L_{\rho }^2(\Gamma )}}} \\ +C_{PFE}\underset{\text{Finite Element}}{\underbrace{\Vert \widehat{Q}(\mathbf{y})-{\widehat{Q}}_h(\mathbf{y}){\Vert }_{L_{\rho }^1(\Gamma )}}}+C_{PSG}\underset{\text{Sparse Grid}}{\underbrace{\Vert {\widehat{Q}}_h(\mathbf{y})-{\mathcal{S}}_w^{m,g}[{\widehat{Q}}_h(\mathbf{y})]{\Vert }_{L_{\rho }^2(\Gamma )}}}. \end{gathered}$$

Similarly we have that the mean error satisfies the following bound:

$$\begin{gathered} \mid \mathbb{E}[Q({\mathbf{y}}_L,{\mathbf{y}}_S)-{\mathcal{S}}_w^{m,g}[{\widehat{Q}}_h({\mathbf{y}}_L,{\mathbf{y}}_S)]\mid ⩽\underset{\text{Perturbation (I)}}{\underbrace{\Vert Q(\mathbf{y})-\widehat{Q}(\mathbf{y}){\Vert }_{L_{\rho }^2(\Gamma )}}} \\ +\underset{\text{Finite Element (II)}}{\underbrace{\Vert \widehat{Q}(\mathbf{y})-{\widehat{Q}}_h(\mathbf{y}){\Vert }_{L_{\rho }^1(\Gamma )}}}+\underset{\text{Sparse Grid (III)}}{\underbrace{\Vert {\widehat{Q}}_h(\mathbf{y})-{\mathcal{S}}_w^{m,g}[{\widehat{Q}}_h(\mathbf{y})]{\Vert }_{L_{\rho }^2(\Gamma )}}}. \end{gathered}$$

Remark 9 For the case that probability distributions ρ(y_L) and ρ(y_S) are independent then the mean correction is exactly zero, thus the mean error would be bounded by the following terms

$$\begin{gathered} \mid \mathbb{E}[Q({\mathbf{y}}_L,{\mathbf{y}}_S)]-\mathbb{E}[{\mathcal{S}}_w^{m,g}[Q_h({\mathbf{y}}_L)]]\mid ⩽C_T\underset{\text{Truncation}}{\underbrace{\Vert Q({\mathbf{y}}_L,{\mathbf{y}}_S)-Q({\mathbf{y}}_L){\Vert }_{L_{\rho }^2(\Gamma )}}} \\ +C_{FE}\underset{\text{Finite Element}}{\underbrace{\Vert Q({\mathbf{y}}_L)-Q_h({\mathbf{y}}_L){\Vert }_{L_{\rho }^1({\Gamma }_L)}}}+C_{SG}\underset{\text{Sparse Grid}}{\underbrace{\Vert Q_h({\mathbf{y}}_L)-{\mathcal{S}}_w^{m,g}[Q_h({\mathbf{y}}_L)]{\Vert }_{L_{\rho }^2({\Gamma }_L)}}} \end{gathered}$$

for some positive constants C_T, C_FE and C_SG. We refer the reader to Section 5 in [6] for the definition of the constants and the bounds of these errors.

6.1. Perturbation error

In this section we analyze perturbation approximation error

$$\Vert Q({\mathbf{y}}_L,{\mathbf{y}}_S)-\widehat{Q}({\mathbf{y}}_L,{\mathbf{y}}_S){\Vert }_{L_{\rho }^2(\Gamma )}=\Vert \mathcal{R}({\tilde{\mathbf{y}}}_L,\delta {\tilde{\mathbf{y}}}_S){\Vert }_{L_{\rho }^2(\Gamma )}$$ (21)

where the remainder is equal to

$$\mathcal{R}({\tilde{\mathbf{y}}}_L,\delta {\tilde{\mathbf{y}}}_S)≔\frac{1}{2}{D}_{{\tilde{\mathbf{y}}}_S}^{2}Q({\tilde{\mathbf{y}}}_L+\theta \delta {\tilde{\mathbf{y}}}_S)(\delta {\tilde{\mathbf{y}}}_S,\delta {\tilde{\mathbf{y}}}_S)$$

for some θ ∈ (0, 1). Since the perturbation approach involves two derivatives, to obtain a bounded error estimate the following assumptions are made:

Assumption 7 Assume that $f\in H^2(\mathcal{G})$. Furthermore, assume that $F:U\to \mathcal{D}(\omega )$ is also 2-smooth almost surely.

From this assumption the following lemma can be proven.

Lemma 6

$H^2(\mathcal{D}(\omega ))$ and H²(U) are isomorphic almost surely.

Proof See Theorem 3.35 in [1]. □

Remark 10 Note that the previous Sobolev norm equivalence will depend on the parameter ω ∈ Ω. The constant depends on the transformation F and the determinant of the Jacobian ∣J∣. See the proof of Theorem 3.35 in [1] for more details.

To estimate the perturbation error the next step is to bound bound the remainder. To this end the following series of lemmas are useful.

Lemma 7 For all n = 1, … , N_S and for all y ∈ Γ

$$\underset{x\in U}{\text{sup}}{\sigma }_{max}\left({\partial }_{{\tilde{y}}_n^S}{\mathbf{J}}^{-1}(\mathbf{y})\right)⩽\underset{x\in U}{\text{sup}}\Vert {\mathbf{B}}_{S,n}(\eta ){\Vert }_2{\mathbb{F}}_{min}^{-2}.$$

Proof From Remark 8 we have that

$${\partial }_{{\tilde{y}}_n^S}{\mathbf{J}}^{-1}(\mathbf{y})=-\partial F^{-1}(\mathbf{y})\left({\partial }_{{\tilde{y}}_n^S}\mathbf{J}(\mathbf{y})\right){\mathbf{J}}^{-1}(\mathbf{y})$$

and thus

$${\sigma }_{max}\left({\partial }_{{\tilde{y}}_n^S}\partial F(\mathbf{y})\right)⩽{\sigma }_{max}({\mathbf{B}}_{S,n}(\eta )){\mathbb{F}}_{min}^{-2}.$$

From Assumption 1 the result follows. □

Lemma 8 For all y ∈ Γ

$$\underset{x\in U}{\text{sup}}\mid {\partial }_{{\tilde{y}}_n^S}\mid \mathbf{J}(\mathbf{y})\Vert ⩽\underset{x\in U}{\text{sup}}{\mathbb{F}}_{max}^d{\mathbb{F}}_{min}^{-1}\Vert {\mathbf{B}}_{S,n}(\eta ){\Vert }_{2}d$$

Proof Using Jacobi’s formula we have that for all y ∈ Γ

$$\begin{gathered} {\partial }_{{\tilde{y}}_n^S}\mid \mathbf{J}(\mathbf{y})\mid =tr(Adj(\mathbf{J}(\mathbf{y})){\partial }_{{\tilde{y}}_n^S}\mathbf{J}(\mathbf{y})) \\ =\mid \mathbf{J}(\mathbf{y})\sum _{i=1}^d{\lambda }_i(\mathbf{J}(\mathbf{y}{)}^{-1}{\mathbf{B}}_{S,n}(\eta ))) \end{gathered}$$

□

Lemma 9 For all n, m = 1, … , N_S and for all y ∈ Γ

$$\underset{x\in U}{\text{sup}}{\sigma }_{max}\left({\partial }_{{\tilde{y}}_n^S}{\partial }_{{\tilde{y}}_m^S}{\mathbf{J}}^{-1}(\mathbf{y})\right)⩽\underset{x\in U}{\text{sup}}2{\mathbb{F}}_{min}^{-3}\Vert {\mathbf{B}}_{S,n}(\eta ){\Vert }_2\Vert {\mathbf{B}}_{S,m}(\eta ){\Vert }_2.$$

Proof From Remark 8 we have that

$$\begin{gathered} {\partial }_{{\tilde{y}}_n^S}{\partial }_{{\tilde{y}}_m^S}{\mathbf{J}}^{-1}(\mathbf{y})={\mathbf{J}}^{-1}(\mathbf{y})[\left({\partial }_{{\tilde{y}}_m^S}\mathbf{J}(\mathbf{y})\right){\mathbf{J}}^{-1}(\mathbf{y})\left({\partial }_{{\tilde{y}}_n^S}\mathbf{J}(\mathbf{y})\right)\phantom{]} \\ -\phantom{[}{\partial }_{{\tilde{y}}_n^S}{\partial }_{{\tilde{y}}_m^S}\mathbf{J}(\mathbf{y})+\left({\partial }_{{\tilde{y}}_n^S}\partial F(\mathbf{y})\right){\mathbf{J}}^{-1}(\mathbf{y})\left({\partial }_{{\tilde{y}}_m^S}\mathbf{J}(\mathbf{y})\right)] \\ {\mathbf{J}}^{-1}(\mathbf{y}) \end{gathered}$$

Taking the triangular and multiplicative inequality, and following the same approach as Lemma 7 we obtain the desired result. □

Lemma 10 For n, m = 1, … , N_S for all y ∈ Γ

$$\underset{x\in U}{\text{sup}}\mid {\partial }_{{\tilde{y}}_m^S}{\partial }_{{\tilde{y}}_n^S}\mid \mathbf{J}(\mathbf{y})\Vert ⩽\underset{x\in U}{\text{sup}}d(d+1){\mathbb{F}}_{max}^d{\mathbb{F}}_{min}^{-2}\Vert {\mathbf{B}}_{S,n}(\eta ){\Vert }_2\Vert {\mathbf{B}}_{S,m}(\eta ){\Vert }_2.$$

Proof Using Jacobi’s formula we have

$$\begin{gathered} {\partial }_{{\tilde{y}}_m^S}{\partial }_{{\tilde{y}}_n^S}\mid \mathbf{J}(\mathbf{y})\mid ={\partial }_{{\tilde{y}}_m^S}(\mid \mathbf{J}(\mathbf{y})\mid tr(\mathbf{J}(\mathbf{y}{)}^{-1}{\mathbf{B}}_{S,n}(\eta ))) \\ ={\partial }_{{\tilde{y}}_m^S}\mid \mathbf{J}(\mathbf{y})\mid tr(\mathbf{J}(\mathbf{y}{)}^{-1}{\mathbf{B}}_{S,n}(\eta )) \\ +\mid \mathbf{J}(\mathbf{y})\mid tr({\partial }_{{\tilde{y}}_m^S}\mathbf{J}(\mathbf{y}{)}^{-1}{\mathbf{B}}_{S,n}(\eta )) \\ =\mid \mathbf{J}(\mathbf{y})\mid tr(\mathbf{J}(\mathbf{y}{)}^{-1}{\mathbf{B}}_{S,m}(\eta ))tr(\mathbf{J}({\mathbf{y}}^{-1}{\mathbf{B}}_{S,n}(\eta )) \\ -\mid \mathbf{J}(\mathbf{y})\mid tr(\mathbf{J}(\mathbf{y}{)}^{-1}{\mathbf{B}}_{S,m}(\eta )\mathbf{J}(\mathbf{y}{)}^{-1}{\mathbf{B}}_{S,n}(\eta )). \end{gathered}$$

The result follows. □

Lemma 11 For all v, $w\in H_0^1(U)$ and y ∈ Γ we have that

$$\begin{gathered} \mid {\int }_U(a\circ F)(\cdot ,{\mathbf{y}}_L,0)(\nabla v{)}^T{\partial }_{{\tilde{y}}_n^S}\tilde{\mathbf{G}}(\mathbf{y})\nabla w\mid ⩽\Vert v{\Vert }_{H_0^1(U)}\Vert w{\Vert }_{H_0^1(U)}{a}_{max} \\ \mathcal{B}(d,{\mathbb{F}}_{min},{\mathbb{F}}_{max},{\mathbf{B}}_{S,n}). \end{gathered}$$

where $\tilde{G}(\mathbf{y})=\mathbf{J}(\mathbf{y}{)}^{-1}\mathbf{J}(\mathbf{y}{)}^T\mid \partial F(\mathbf{y})\mid$ for all y ∈ Γ and

$$\mathcal{B}(d,{\mathbb{F}}_{min},{\mathbb{F}}_{max},{\mathbf{B}}_{S,n})≔\underset{x\in U}{\text{sup}}(d+2){\mathbb{F}}_{max}^d{\mathbb{F}}_{min}^{-3}\Vert {\mathbf{B}}_{S,n}(\eta ){\Vert }_2.$$

Proof First we expand the partial derivative of $\tilde{\mathbf{G}}(\mathbf{y})$ with respect to ${\tilde{y}}_n^S$:

$$\begin{gathered} {\partial }_{{\tilde{y}}_n^S}\tilde{G}(\mathbf{y})={\partial }_{{\tilde{y}}_n^S}{\mathbf{J}}^{-T}(\mathbf{y}){\mathbf{J}}^{-1}(\mathbf{y})\mid \partial F(\mathbf{y})\mid +{\mathbf{J}}^{-T}(\mathbf{y}){\partial }_{{\tilde{y}}_n^S}\partial F^{-1}(\mathbf{y})\mid \mathbf{J}(\mathbf{y})\mid \\ +{\mathbf{J}}^{-T}(\mathbf{y}){\mathbf{J}}^{-1}(\mathbf{y}){\partial }_{{\tilde{y}}_n^S}\mid \mathbf{J}(\mathbf{y})\mid , \end{gathered}$$

From Lemmas 7, 8 and the triangular inequality we have that

$$\underset{x\in U,\mathbf{y}\in \Gamma }{\text{sup}}{\sigma }_{max}\left({\partial }_{y_n^S}\tilde{G}(\mathbf{y})\right)⩽(d+2){\mathbb{F}}_{max}^d{\mathbb{F}}_{min}^{-3}\Vert {\mathbf{B}}_{S,n}(\eta ){\Vert }_2.$$

□

Lemma 12 For all v, $w\in H_0^1(U)$ and y ∈ Γ we have that

$$\mid {\int }_U(a\circ F)(\cdot ,{\mathbf{y}}_L)(\nabla w{)}^T{\partial }_{{\tilde{y}}_n^S}{\partial }_{{\tilde{y}}_m^S}\tilde{G}(\mathbf{y})\nabla v\mid$$

is less or equal to

$$\Vert v{\Vert }_{H_0^1(U)}\Vert w{\Vert }_{H_0^1(U)}{a}_{max}2(d+3){\mathbb{F}}_{max}^{-4}{\mathbb{F}}_{min}^d\Vert {\mathbf{B}}_{S,n}(\eta ){\Vert }_2\Vert {\mathbf{B}}_{S,m}(\eta ){\Vert }_2.$$

Proof From Remark 8 we have that

$$\begin{gathered} {\partial }_{{\tilde{y}}_m^S}{\partial }_{{\tilde{y}}_n^S}\tilde{G}(\mathbf{y})={\partial }_{{\tilde{y}}_m^S}{\partial }_{{\tilde{y}}_n^S}{\mathbf{J}}^{-T}(\mathbf{y}){\mathbf{J}}^{-1}(\mathbf{y})\mid \partial F(\mathbf{y})\mid \\ +{\partial }_{{\tilde{y}}_n^S}{\mathbf{J}}^{-T}(\mathbf{y}){\partial }_{{\tilde{y}}_m^S}\partial F^{-1}(\mathbf{y})\mid \mathbf{J}(\mathbf{y})\mid \\ +{\partial }_{{\tilde{y}}_n^S}{\mathbf{J}}^{-T}(\mathbf{y}){\mathbf{J}}^{-1}(\mathbf{y}){\partial }_{{\tilde{y}}_m^S}\mid \mathbf{J}(\mathbf{y})\mid \\ +{\partial }_{{\tilde{y}}_m^S}{\mathbf{J}}^{-T}(\mathbf{y}){\partial }_{{\tilde{y}}_n^S}\partial F^{-1}(\mathbf{y})\mid \mathbf{J}(\mathbf{y})\mid \\ +{\mathbf{J}}^{-T}(\mathbf{y}){\partial }_{{\tilde{y}}_m^S}{\partial }_{{\tilde{y}}_n^S}{\mathbf{J}}^{-1}(\mathbf{y})\mid \partial F(\mathbf{y})\mid \\ +{\mathbf{J}}^{-T}(\mathbf{y}){\partial }_{{\tilde{y}}_n^S}{\mathbf{J}}^{-1}(\mathbf{y}){\partial }_{{\tilde{y}}_m^S}\mid \mathbf{J}(\mathbf{y})\mid \\ +{\partial }_{{\tilde{y}}_m^S}{\mathbf{J}}^{-T}(\mathbf{y})\partial F^{-1}(\mathbf{y}){\partial }_{{\tilde{y}}_n^S}\mid \mathbf{J}(\mathbf{y})\mid \\ +{\mathbf{J}}^{-1}(\mathbf{y}){\partial }_{{\tilde{y}}_m^S}{\mathbf{J}}^{-1}(\mathbf{y}){\partial }_{{\tilde{y}}_n^S}\mid \partial F(\mathbf{y})\mid \\ +{\mathbf{J}}^{-T}(\mathbf{y}){\mathbf{J}}^{-1}(\mathbf{y}){\partial }_{{\tilde{y}}_m^S}{\partial }_{{\tilde{y}}_n^S}\mid \mathbf{J}(\mathbf{y})\mid . \end{gathered}$$

From Lemmas 7 - 10, and the triangular inequality we have that for all y ∈ Γ

$$\Vert {\partial }_{{\tilde{y}}_m^S}{\partial }_{{\tilde{y}}_n^S}\tilde{G}(\mathbf{y}){\Vert }_2⩽\underset{x\in U}{\text{sup}}(7+3d+2{\mathbb{F}}_{min}^{-1}{\mathbb{F}}_{max}^{-d}){\mathbb{F}}_{min}^{-4}{\mathbb{F}}_{max}^d\Vert {\mathbf{B}}_{S,n}(\eta ){\Vert }_2\Vert {\mathbf{B}}_{S,m}(\eta ){\Vert }_2$$

□

The next step is to bound $\Vert \nabla D_{{\tilde{\mathbf{y}}}_S}(\tilde{u}\circ F)(\eta ,{\mathbf{y}}_L,0)(\delta {\mathbf{y}}_S){\Vert }_{L^2(U)}$ and $\Vert \nabla D_{{\tilde{\mathbf{y}}}_S}\phi ({\mathbf{y}}_L,0)(\delta {\mathbf{y}}_S){\Vert }_{L^2(U)}$.

Lemma 13 For all y_L ∈ Γ_L and δy_S ∈ Γ we have that:

(a)

$$\begin{gathered} \Vert \nabla D_{{\tilde{\mathbf{y}}}_S}(\tilde{u}\circ F)(\cdot ,{\mathbf{y}}_L,0)(\delta {\mathbf{y}}_S){\Vert }_{L^2(U)}⩽\frac{{\sum }_{n=1}^{N_S}\sqrt{{\mu }_{S,n}}}{a_{min}{\mathbb{F}}_{min}^d{\mathbb{F}}_{max}^{-2}} \\ \underset{x\in U}{\text{sup}}((\Vert (\tilde{u}\circ F)(\cdot ,{\mathbf{y}}_L,0){\Vert }_{H_0^1(U)}+\Vert \widehat{\nu }{\Vert }_{H^1(U)})a_{max}(d+2){\mathbb{F}}_{max}^d{\mathbb{F}}_{min}^{-3}\Vert {\mathbf{B}}_{S,n}(\eta ){\Vert }_2\phantom{)} \\ +C{d}^{\frac{1}{2}}{\mathbb{F}}_{max}^d{C}_P(U)\Vert f{\Vert }_{H^1(\mathcal{G})}+d{C}_P(U){\mathbb{F}}_{max}^d{\mathbb{F}}_{min}^{-(d+1)}\Vert f{\Vert }_{L^2(\mathcal{G})}\Vert {\mathbf{B}}_{S,n}(\eta ){\Vert }_2). \end{gathered}$$

where C is a uniformly bounded constant.

(b)

$$\begin{gathered} \Vert \nabla D_{{\tilde{\mathbf{y}}}_S}\phi ({\mathbf{y}}_L,0)(\delta {\mathbf{y}}_S){\Vert }_{L^2(U)} \\ ⩽\frac{{\text{sup}}_{\eta \in U}{\sum }_{n=1}^{N_S}\sqrt{{\mu }_{S,n}}\Vert \phi ({\mathbf{y}}_L,0){\Vert }_{H_0^1(U)}{a}_{max}(d+2)\Vert {\mathbf{B}}_{S,n}{\Vert }_2}{a_{min}{\mathbb{F}}_{min}^{(d+3)}{\mathbb{F}}_{max}^{-(d+2)}}. \end{gathered}$$

Proof (a) For any $v\in H_0^1(U)$ and for all y_L ∈ Γ_L. and δy_S ∈ Γ from Lemma 2

$$\begin{gathered} a_{min}{\mathbb{F}}_{min}^d{\mathbb{F}}_{max}^{-2}\Vert \nabla D_{\tilde{\mathbf{y}}}\tilde{u}(\cdot ,{\mathbf{y}}_L,0)(\delta {\mathbf{y}}_S){\Vert }_{L^2(U)}\Vert \nabla v{\Vert }_{L^2(U)} \\ ⩽\sum _{n=1}^{N_S}\delta {\tilde{y}}_n^S\mid {\int }_U-\nabla (\tilde{u}\circ F)(\cdot ,{\mathbf{y}}_L,0{)}^T{\partial }_{{\tilde{y}}_n^S}\mathbf{G}({\mathbf{y}}_L,0)\nabla v\phantom{\mid } \\ +({\partial }_{{\tilde{y}}_n^S}(f\circ F)(\cdot ,{\mathbf{y}}_L,0))\mid \mathbf{J}({\mathbf{y}}_L,0)\mid v+(f\circ F)(\cdot ,{\mathbf{y}}_L,0){\partial }_{{\tilde{y}}_n^S}\mid \mathbf{J}({\mathbf{y}}_L,0)\mid v \\ -\phantom{\mid }(\nabla \widehat{\nu }{)}^T{\partial }_{{\tilde{y}}_n^S}\mathbf{G}({\mathbf{y}}_L,0)\nabla v\mid . \end{gathered}$$

With the choice of $v=D_{{\tilde{\mathbf{y}}}_S}(\tilde{u}\circ F)(\cdot ,{\mathbf{y}}_L,0)(\delta {\mathbf{y}}_S)$ and from Lemma 11

$$\begin{gathered} \Vert \nabla D_{{\tilde{\mathbf{y}}}_S}(\tilde{u}\circ F)(\cdot ,{\mathbf{y}}_L,0)(\delta {\mathbf{y}}_S){\Vert }_{L^2(U)}⩽\frac{1}{a_{min}{\mathbb{F}}_{min}^d{\mathbb{F}}_{max}^{-2}\Vert \nabla v{\Vert }_{L^2(U)}}(\phantom{)} \\ \sum _{n=1}^{N_S}\delta y_n^S\mid {\int }_U-(\nabla (\tilde{u}\circ F)(\cdot ,{\mathbf{y}}_L,0){)}^T{\partial }_{{\tilde{y}}_n^S}\mathbf{G}({\mathbf{y}}_L,0)\nabla v\phantom{\mid } \\ +{\partial }_{{\tilde{y}}_n^S}(f\circ F)(\cdot ,{\mathbf{y}}_L,0)\mid \mathbf{J}({\mathbf{y}}_L,0)\mid v+(f\circ F)(\cdot ,{\mathbf{y}}_L,0){\partial }_{{\tilde{y}}_n^S}\mid \mathbf{J}({\mathbf{y}}_L,0)\mid v \\ -\phantom{(}\phantom{\mid }(\nabla \widehat{\nu }{)}^T{\partial }_{{\tilde{y}}_n^S}\mathbf{G}({\mathbf{y}}_L,0)\nabla v\mid ). \end{gathered}$$

Now,

$$\begin{gathered} \mid {\int }_U{\partial }_{{\tilde{y}}_n^S}(f\circ F)(\cdot ,{\mathbf{y}}_L,0)\mid \mathbf{J}({\mathbf{y}}_L,0)\mid v\mid ⩽{\mathbb{F}}_{max}^d{\int }_U\mid {\partial }_{{\tilde{y}}_n^S}(f\circ F)(\cdot ,{\mathbf{y}}_L,0)v\mid \\ ⩽{\mathbb{F}}_{max}^d{C}_P(U)\Vert \nabla v{\Vert }_{L^2(U)}\Vert \sum _{k=1}^d{\partial }_{F_k}f{\partial }_{{\overline{y}}_n}{F}_k{\Vert }_{L^2(U)} \\ ⩽{\mathbb{F}}_{max}^d{C}_P(U)\Vert \nabla v{\Vert }_{L^2(U)}\Vert {\mathbf{b}}_n(\eta ){\Vert }_{[L^{\infty }(U){]}^d}\Vert \nabla f\cdot 1{\Vert }_{L^2(U)} \\ (\text{Applying Lemma 1 ii), where}C>0\text{is a constant}.) \\ ⩽d^{\frac{1}{2}}C{\mathbb{F}}_{max}^d{C}_P(U)\Vert \nabla v{\Vert }_{L^2(U)}\Vert f{\Vert }_{H^1(\mathcal{G})}. \end{gathered}$$

Finally, from Lemma 8 the result follows.

(b) Apply Lemma 3 with $v=D_{{\tilde{\mathbf{y}}}_S}\phi ({\mathbf{y}}_L,0)(\delta {\mathbf{y}}_S)$ and Lemma 11. □

Lemma 14 For all y ∈ Γ and n, m = 1, … , N we have that

$$\Vert \partial {\tilde{y}}_n^S(f\circ F)(\cdot ,\mathbf{y}){\Vert }_{L^2(U)}⩽d^{\frac{1}{2}}{\mathbb{F}}_{min}^{-1}\Vert f{\Vert }_{H^1(\mathcal{G})}.$$

$$\Vert \partial {\tilde{y}}_n^S\partial {\tilde{y}}_m^S(f\circ F)(\cdot ,\mathbf{y}){\Vert }_{L^2(U)}⩽{\mathbb{F}}_{min}^{-d}\Vert f{\Vert }_{H^2(\mathcal{G})}.$$

Proof (a) Follow the proof in Lemma 13. (b) By applying the chain rule for

Sobolev spaces and Lemma 6 we obtain that for all y ∈ Γ

$$\begin{gathered} \Vert \partial {\tilde{y}}_n^S\partial {\tilde{y}}_m^S(f\circ F)(\cdot ,\mathbf{y}){\Vert }_{L^2(U)}=\Vert \sum _{i=1}^d\sum _{j=1}^d{\partial }_{F_i}{\partial }_{F_j}f{\partial }_{y_m^S}{F}_i{\partial }_{y_n^S}{F}_j{\Vert }_{L^2(U)} \\ ⩽d^2{\Vert \sum _{i=1}^d\sum _{j=1}^d{\partial }_{F_i}{\partial }_{F_j}f\Vert }_{L^2(U)}⩽C{d}^2{\Vert \sum _{i=1}^d\sum _{j=1}^d{\partial }_{F_i}{\partial }_{F_j}f\Vert }_{\mathcal{D}(\omega )}⩽C{d}^2\Vert f{\Vert }_{H^2(\mathcal{G})}. \end{gathered}$$

for some constant C > 0. This completes the proof. □

From Lemmas 4 - 5 and 7 - 14 we have that for all y_L ∈ Γ_L and for all δy_S ∈ Γ_S

$$\mid D_{{\tilde{\mathbf{y}}}_S}^{2}Q(\mathbf{y})(\delta {\mathbf{y}}_S,\delta {\mathbf{y}}_S)\mid ⩽\sum _{n,m=1}^{N_S}\mid \delta {\tilde{y}}_n^S\mid \mid \delta {\tilde{y}}_m^S\mid \underset{\mathbf{y}\in \Gamma ,x\in U}{\text{sup}}{G}_{n,m},$$

where

$$\begin{gathered} G_{n,m}(C,C_P(U),a_{max},a_{min},{\mathbb{F}}_{max},{\mathbb{F}}_{min},d,\Vert \widehat{v}{\Vert }_{[L^{\infty }(U){]}^d},\Vert \widehat{\nu }{\Vert }_{H^1(U)},\Vert f{\Vert }_{H^2(\mathcal{G})}, \\ \Vert (\tilde{u}\circ F)({\mathbf{y}}_L,0){\Vert }_{H^1(U)},\Vert \phi ({\mathbf{y}}_L,0){\Vert }_{H^1(U)},\Vert {\mathbf{B}}_{S,n}{\Vert }_2,\Vert {\mathbf{B}}_{S,m}{\Vert }_2,{\mu }_{S,1},\dots ,{\mu }_{S,N_S}) \end{gathered}$$

is a bounded constant that depends on the indicated parameters. We have now proven the following result.

Theorem 3 Let $(\tilde{u}\circ F)({\mathbf{y}}_L,0)$ be the solution to the bilinear Problem 1 that satisfies Assumptions 1-7 then for all y_L ∈ Γ_L and y_S ∈ Γ_S

$$\Vert Q({\mathbf{y}}_L,{\mathbf{y}}_S)-\widehat{Q}({\mathbf{y}}_L,{\mathbf{y}}_S){\Vert }_{L_{\rho }^2(\Gamma )}⩽\frac{1}{2}\sum _{n,m=1}^{N_S}\sqrt{{\mu }_{S,n}}\sqrt{{\mu }_{S,m}}{G}_{n,m}⩽\mathbb{G}(\sum _{k=1}^{N_S}\sqrt{{\mu }_{S,k}}{)}^2,$$

where $\mathbb{G}≔\frac{1}{2}{\text{max}}_{n,m}{\text{sup}}_{\mathbf{y}\in \Gamma ,\eta \in U}{G}_{n,m}$.

6.2. Finite element error

The finite element convergence rate for the solution $(\tilde{u}\circ F)$ and influence function φ are directly dependent on the regularity of these functions, the polynomial order $H_h(U)\subset H_0^1(U)$ of the finite element space and the mesh size h). By applying the triangular inequality

$$\begin{gathered} \Vert \widehat{Q}({\mathbf{y}}_L,{\mathbf{y}}_S)-{\widehat{Q}}_h({\mathbf{y}}_L,{\mathbf{y}}_S){\Vert }_{L_{\rho }^1(\Gamma )}⩽\Vert Q({\mathbf{y}}_L,0)-Q_h({\mathbf{y}}_L,0){\Vert }_{L_{\rho }^1({\Gamma }_L)} \\ +\sum _{n=1}^{N_S}\sqrt{{\mu }_{S,n}}\Vert {\int }_U{\tilde{\alpha }}_n(x,{\mathbf{y}}_L,0)-{\tilde{\alpha }}_{i,h}(x,{\mathbf{y}}_L,0){\Vert }_{L_{\rho }^2({\Gamma }_L)}. \end{gathered}$$

Following a duality argument we obtain

$$\Vert Q({\mathbf{y}}_L,0)-Q_h({\mathbf{y}}_L,0){\Vert }_{L_{\rho }^1({\Gamma }_L)}⩽a_{max}{\mathbb{F}}_{max}^d{\mathbb{F}}_{min}^{-2}{C}_{{\Gamma }_L}(r)D_{{\Gamma }_L}(r)h^{2r}.$$

for some constant $r\in \mathbb{N}$, C_ΓL (r) := ʃ_ΓL C(r, u(y_L, 0))ρ(y_L)dy and D_ΓL (r) := ʃ_ΓL C(r, φ(y_L, 0)) ρ(y_L)dy.

The constant r is function of i) the regularity properties of the influence function and the solution ($\tilde{u}\circ F$)(·, y_L, 0) ii) the polynomial degree of the finite element basis.

It follows that

$$\Vert \widehat{Q}({\mathbf{y}}_L,0)-{\widehat{Q}}_h({\mathbf{y}}_L,0){\Vert }_{L_{\rho }^2(\Gamma )}⩽{\mathbb{S}}_0{h}^{2r}+h^r\sum _{n=1}^{N_S}{\mathbb{S}}_n\sqrt{{\mu }_{S,n}}$$ (22)

where ${\mathbb{S}}_0≔a_{max}$, ${\mathbb{F}}_{max}^d{\mathbb{F}}_{min}^{-2}{C}_{{\Gamma }_L}(r)D_{{\Gamma }_L}(r)$ and

$$\begin{gathered} {\mathbb{S}}_n(a_{max},{\mathbb{F}}_{max},{\mathbb{F}}_{min},d,\Vert \widehat{v}{\Vert }_{[L^{\infty }(U){]}^d},C_{{\Gamma }_L}(r),D_{{\Gamma }_L}(r),\Vert f{\Vert }_{L^2(\mathcal{G})} \\ \Vert \widehat{\nu }({\mathbf{y}}_L,0){\Vert }_{H^1(U)},\Vert {\mathbf{B}}_{S,n}{\Vert }_2) \end{gathered}$$

are bounded constants for n = 1, … , N_S.

6.3. Sparse grid error

For the sake of simplicity only convergence rates for the isotropic Smolyak sparse grid are shown. This analysis can be extended to the anisotropic case without much difficulty.

$$\begin{gathered} \Vert {\widehat{Q}}_h({\mathbf{y}}_L,{\mathbf{y}}_S)-{\mathcal{S}}_w^{m,g}{\widehat{Q}}_h({\mathbf{y}}_L,{\mathbf{y}}_S){\Vert }_{L_{\rho }^2(\Gamma )}⩽a_{max}{\mathbb{F}}_{max}^d{\mathbb{F}}_{min}^{-2}\Vert e_0{\Vert }_{L_{\rho }^2({\Gamma }_L;H_0^1(U))} \\ +\sum _{n=1}^{N_S}\sqrt{{\mu }_{S,n}}\Vert e_n{\Vert }_{L_{\rho }^2({\Gamma }_L)}, \end{gathered}$$

where $e_0≔{\widehat{u}}_h(\cdot ,{\mathbf{y}}_L,0)-{\mathcal{S}}_w^{m,g}{\widehat{u}}_h(\cdot ,{\mathbf{y}}_L,0)]$ and

$$e_n≔{\int }_U{\tilde{\alpha }}_{n,h}(\cdot ,{\mathbf{y}}_L,0)-{\mathcal{S}}_w^{m,g}[{\int }_U{\tilde{\alpha }}_{n,h}(\cdot ,{\mathbf{y}}_L,0)]$$

for n = 1, … , N_S, and

$$L_{\rho }^q({\Gamma }_L;V)≔\{v:{\Gamma }_L\times U\to V\text{is strongly measurable},{\int }_{\Gamma }\Vert v{\Vert }_V^q\rho (\mathbf{y})d\mathbf{y}<\infty \}.$$

for any Banach space V defined on U.

It can be shown that $\Vert e_0{\Vert }_{L_{\rho }^2({\Gamma }_L;H_0^1(U))}$ (and $\Vert e_n{\Vert }_{L_{\rho }^2({\Gamma }_L)}$ for n = 1, … , N_S) have a algebraic or sub-exponential convergence rate as a function of the number of collocation knots η (see [26,27]). necessary condition is that the semi-discrete solution ${\tilde{u}}_{0,h}(\mathbf{z})≔{\widehat{u}}_h(\cdot ,{\mathbf{y}}_L,0)$ and ${\tilde{u}}_{n,h}(\mathbf{z})≔{\int }_U{\widehat{\alpha }}_{k,n}(\cdot ,{\mathbf{y}}_L,0)$, n = 1, … , N_S admit an analytic extension in the same region Θ_β,NL. This is a reasonable assumption to make.

Consider the polyellipse in ${\mathcal{E}}_{{\sigma }_1,\dots ,{\sigma }_{N_L}}≔{\Pi }_{n=1}^{N_L}{\mathcal{E}}_{n,{\sigma }_n}\subset {\mathbb{C}}^{N_L}$ where

$$\begin{gathered} {\mathcal{E}}_{n,{\sigma }_n}≔\{z\in \mathbb{C};{\sigma }_n>0;{\sigma }_n⩾{\kappa }_n⩾0;\text{Re}(z)=\frac{e^{{\kappa }_n}+e^{-{\kappa }_n}}{2}cos(\theta )\phantom{\}}, \\ \phantom{\{}\text{Im}(z)=\frac{e^{{\kappa }_n}-e^{-{\kappa }_n}}{2}sin(\theta ),\theta \in [0,2\pi )\}, \end{gathered}$$

and let

$${\Sigma }_n≔\left\{z_n\in \mathbb{C};y_n=y+w_n,y\in [-1,1],\mid w_n\mid ⩽{\tau }_n≔\frac{\beta }{1-\tilde{\delta }}\right\}$$

for n = 1, … , N_L. For the sparse grid error estimates to be valid the solution ${\tilde{u}}_h(\cdot ,{\mathbf{y}}_L,0)$ and ${\int }_U{\tilde{\alpha }}_{n,h}(\cdot ,{\mathbf{y}}_L,0)$, n = 1, … , N_S, have to admit an extension on the polyellipse ${\mathcal{E}}_{{\sigma }_1,\dots ,{\sigma }_{N_L}}$. The coefficients σ_n, for n = 1, … , N control the overall decay $\widehat{\sigma }$ of the sparse grid error estimate. Since we restrict our attention to isotropic sparse grids the decay will be dictated by the smallest σ_n i.e. $\widehat{\sigma }\equiv {\text{min}}_{n=1,\dots ,N_L}{\sigma }_n$.

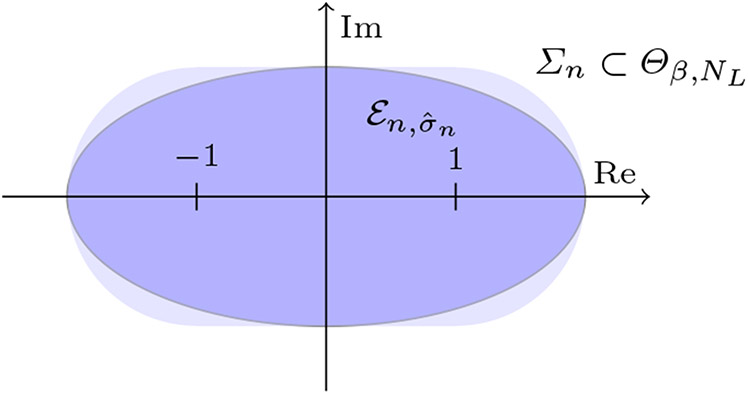
The next step is to find a suitable embedding of ${\mathcal{E}}_{{\sigma }_1,\dots ,{\sigma }_{N_L}}$ in Θ_β,NL. Thus we need to pick the largest σ_n n = 1, … , N_L such that ${\mathcal{E}}_{{\sigma }_1,\dots ,{\sigma }_{N_L}}\subset {\Theta }_{\beta ,N_L}$. This is achieved by forming the set Σ := Σ₁ × ⋯ × Σ_NL and letting ${\sigma }_1={\sigma }_2=\cdots ={\sigma }_{N_L}=\widehat{\sigma }=\log (\sqrt{{\tau }_{N_L}^2+1}+{\tau }_{N_L})>0$ as shown in Figure 2.

Fig. 2.

Embedding of ${\mathcal{E}}_{n,{\widehat{\sigma }}_n}$ in Σ_n ⊂ Θ_β,NL.

We now have almost everything we need to state the sparse grid error estimates. However, in [27] to simplify the estimate it is assumed that if $v\in C^0(\Gamma ;H_0^1(U))$ then the term M(v) (see page 2322) is equal to one. We reintroduce the term M(v) and note that it can be bounded by max_z∈Θβ,NL $\Vert v(\mathbf{z}){\Vert }_{H_0^1(U)}$ and update the sparse grids error estimate. To this end let $\tilde{M}≔\max \{{\max }_{n=1}^{N_L}{\max }_{\mathbf{z}\in {\Theta }_{N_L,\beta }}\Vert {\tilde{u}}_{n,h}(\mathbf{z}){\Vert }_{H_0^1(U)}$, ${\max }_{\mathbf{z}\in {\Theta }_{N_L,\beta }}\mid {\tilde{u}}_{n,h}(\mathbf{z})\mid \}$.

Remark 11 In [6] Corollary 8 a bound for $\Vert (\tilde{u}\circ F)(\cdot ,\mathbf{z}){\Vert }_{H_0^1(U)}$, z ∈ Θ_β,NL, can be obtained by applying the Poincaré inequality. Following a similar argument a bound for $\Vert \phi (\cdot ,\mathbf{z}){\Vert }_{H_0^1(U)}$ for all z ∈ Θ_β,NL. Thus bounds for $\Vert {\tilde{u}}_{n,h}(\mathbf{z}){\Vert }_{H_0^1(U)}$ for n = 0, … , N_L and for all z ∈ Θ_β,NL can be obtained.

Modifying Theorem 3.11 in [27] it can be shown that given a sufficiently large η (w > N_L/log 2) a Smolyak sparse grid with a nested Clenshaw Curtis abscissas we obtain the following estimate

$$\Vert e_0{\Vert }_{L_{\rho }^2({\Gamma }_L;H_0^1(U))}⩽\mathcal{Q}(\sigma ,{\delta }^{\ast }(\sigma ),N_L,\tilde{M}){\eta }^{{\mu }_3(\sigma ,{\delta }^{\ast },N_L)}\text{exp}\left(-\frac{N_L\sigma }{2^{1∕N_L}}{\eta }^{{\mu }_2(N_L)}\right)$$ (23)

and

$$\Vert e_n{\Vert }_{L_{\rho }^2({\Gamma }_L)}⩽\mathcal{Q}(\sigma ,{\delta }^{\ast }(\sigma ),N_L,\tilde{M}){\eta }^{{\mu }_3(\sigma ,{\delta }^{\ast },N_L)}\text{exp}\left(-\frac{N_L\sigma }{2^{1∕N_L}}{\eta }^{{\mu }_2(N_L)}\right)$$ (24)

for n = 1, … , N_S, where $\sigma =\widehat{\sigma }∕2$, ${\delta }^{\ast }(\sigma )≔(e\log (2)-1)∕{\tilde{C}}_2(\sigma )$,

$$\mathcal{Q}(\sigma ,{\delta }^{\ast }(\sigma ),N_L,\tilde{M})≔\frac{C_1(\sigma ,{\delta }^{\ast }(\sigma ),\tilde{M})}{\text{exp}(\sigma {\delta }^{\ast }(\sigma ){\tilde{C}}_2(\sigma ))}\frac{\text{max}\{1,C_1(\sigma ,{\delta }^{\ast }(\sigma ),\tilde{M}){\}}^{N_L}}{\mid 1-C_1(\sigma ,{\delta }^{\ast }(\sigma ),\tilde{M})\mid },$$

${\mu }_2(N_L)=\frac{log(2)}{N_L(1+log(2N_L))}$ and ${\mu }_3(\sigma ,{\delta }^{\ast }(\sigma ),N_s)=\frac{\sigma {\delta }^{\ast }(\sigma ){\tilde{C}}_2(\sigma )}{1+\log (2N_L)}$. Furthermore, $C(\sigma )=\frac{4}{e^{2\sigma }-1}$,

$$\begin{gathered} {\tilde{C}}_2(\sigma )=1+\frac{1}{\log 2}\sqrt{\frac{\pi }{2\sigma }},{\delta }^{\ast }(\sigma )=\frac{e\log (2)-1}{{\tilde{C}}_2(\sigma )}, \\ {C}_1(\sigma ,\delta ,\tilde{M})=\frac{4\tilde{M}C(\sigma )a(\delta ,\sigma )}{e\delta \sigma }, \end{gathered}$$

and

$$a(\delta ,\sigma )≔\text{exp}\left(\delta \sigma \left\{\frac{1}{\sigma {\log }^2(2)}+\frac{1}{\log (2)\sqrt{2\sigma }}+2\left(1+\frac{1}{\log (2)}\sqrt{\frac{\pi }{2\sigma }}\right)\right\}\right).$$

7. Complexity analysis

We now perform an accuracy vs the total work analysis. The objective is to derived total work W as a function of a tolerance TOL > 0, such that $\mid var[Q({\mathbf{y}}_L,{\mathbf{y}}_S)]-var[{\mathcal{S}}_w^{m,g}[{\widehat{Q}}_h({\mathbf{y}}_L,{\mathbf{y}}_S)]]\mid ⩽TOL$ and $\mid \mathbb{E}[Q({\mathbf{y}}_L,{\mathbf{y}}_S)]-\mathbb{E}[{\mathcal{S}}_w^{m,g}[Q_h({\mathbf{y}}_L,{\mathbf{y}}_S)]]\mid ⩽TOL$. We restrict our attention to the isotropic sparse grid with Clenshaw-Curtis abscissas. For each realization of the semi-discrete approximation u_h, it is assumed that it requires $\mathcal{O}(N_h^q)$ work to compute, where N_h is the cardinality of the finite element space $H_h(U)\subset H_0^1(U)$, and the constant q is a function of the regularity of u_h and the efficiency of the solver. The cost for solving the approximation of the influence function φ_h ∈ H_h(U) is also assumed to be $\mathcal{O}(N_h^q)$. Thus for any y_L ∈ Γ_L, the cost for computing Q_h(y_L, 0) := B(y_L, 0; u_h(y_L, 0),φ_h(y_L, 0)) is bounded by $\mathcal{O}(N_h{d}^2+N_h^q)$. Similarly, for any y_L ∈ Γ_L the cost for evaluating ${\int }_U{\tilde{\alpha }}_{n,h}(\cdot ,{\mathbf{y}}_L,0)$ is $\mathcal{O}(N_h{d}^2+N_h^q)$.

Remark 12 To compute the expectation integrals for the mean and variance correction a Gauss quadrature scheme can be used coupled with an auxiliary probability distribution $\widehat{\rho }(\mathbf{y})$ such that

$$\widehat{\rho }(\mathbf{y})={\Pi }_{n=1}^N{\rho }_n(y_n)\text{and}\rho ∕\widehat{\rho }<C<\infty .$$

for some C > 0 (See [6] for details). However, for the sake of simplifying the analysis it is assumed that quadrature is exact and of cost $\mathcal{O}(1)$.

Let η₀(N_L, m, g, w, Θ_β,NL) be the number of the sparse grid knots for constructing ${\mathcal{S}}_w^{m,g}[{\tilde{\alpha }}_{n,h}(\cdot ,{\mathbf{y}}_L,0)]$ and η_n(N_L, m, g, w, Θ_β,NL) for constructing ${\mathcal{S}}_w^{m,g}[{\tilde{\alpha }}_{n,h}(\cdot ,{\mathbf{y}}_L,0)]$, for n = 1, … , N_S. The cost for computing $\mathbb{E}[{\mathcal{S}}_w^{m,g}[Q_h({\mathbf{y}}_L,0)]]$ is $\mathcal{O}((N_h{d}^2+N_h^q){\eta }_0)$ and the cost for computing ${\sum }_{n=1}^{N_S}\sqrt{{\mu }_{S,n}}\mathbb{E}[y_n^S{\mathcal{S}}_w^{m,g}[{\int }_U{\tilde{\alpha }}_n(\cdot ,{\mathbf{y}}_L,0)]]$ is bounded by $\mathcal{O}((N_h{d}^2+N_h^q)N_S\eta )$, where

$$\eta ≔\underset{n=0,\dots ,N_S}{\max }{\eta }_n.$$

The total cost for computing the mean correction is bounded by

$$W_{Total}^{mean}(TOL)=\mathcal{O}((N_h(TOL)d^2+N_h^q(TOL))N_S(TOL)\eta (TOL)).$$ (25)

Following a similar argument the cost for computing the variance correction is bounded by

$$W_{Total}^{var}(TOL)=\mathcal{O}((N_h(TOL)d^2+N_h^q(TOL))N_S^2(TOL)\eta (TOL)).$$ (26)

We now obtain the estimates for N_h(TOL), N_S(TOL) and η(TOL) for the Perturbation, Finite Element and Sparse Grids respectively:

1. Perturbation: From the perturbation estimate derived in Section 6.1 we seek $\Vert Q({\mathbf{y}}_L,{\mathbf{y}}_S)-\widehat{Q}({\mathbf{y}}_L,{\mathbf{y}}_S){\Vert }_{L_{\rho }^2(\Gamma )}⩽\frac{TOL}{3C_P}$ with respect to the decay of the coefficients $\sqrt{{\mu }_{S,n}}$, n = 1, … N_S. First, make the assumption that $B_T≔{\sum }_{n=1}^{N_S}\sqrt{{\mu }_{S,n}}⩽C_D{N}_L^{-l}$ for some uniformly bounded C_D > 0 and l > 0. It follows that $\Vert Q({\mathbf{y}}_L,{\mathbf{y}}_S)-\widehat{Q}({\mathbf{y}}_L,{\mathbf{y}}_S){\Vert }_{L_{\rho }^2(\Gamma )}⩽\frac{TOL}{3C_P}$ if

   $$B_T^2\mathbb{G}⩽C_D^2{N}_L^{-2l}\mathbb{G}⩽\frac{TOL}{3C_P}.$$
   Finally, we have that

   $$N_S(TOL)⩾{\left(\frac{TOL}{3C_P{C}_D^2\mathbb{G}}\right)}^{-1∕(2l)}.$$
2. Finite Element: From Section 6.2 if

   $${\mathbb{S}}_0{h}^{2r}+B_T{\mathbb{T}}_0{h}^r⩽\frac{TOL}{3C_{PFE}},$$
   ${\mathbb{T}}_0≔{\max }_{n=1}^{N_S}{\mathbb{S}}_n$, then $\Vert \widehat{Q}({\mathbf{y}}_L,0)-{\widehat{Q}}_h({\mathbf{y}}_L,0){\Vert }_{L_{\rho }^2(\Gamma ;H_0^1(U))}⩽\frac{TOL}{3C_{PFE}}$. Solving the quadratic inequality we obtain that

   $$h(TOL)⩽{\left(-\frac{B_T{\mathbb{T}}_0}{2{\mathbb{S}}_0}+{\left({\left(\frac{B_T{\mathbb{T}}_0}{4{\mathbb{S}}_0}\right)}^2+\frac{4TOL}{12{\mathbb{S}}_0{C}_{PFE}}\right)}^{1∕2}\right)}^{1∕r}$$
   Assuming that N_h grows as $\mathcal{O}(h^{-d})$ then

   $$N_h(TOL)⩾D_3{\left(-\frac{B_T{\mathbb{T}}_0}{2{\mathbb{S}}_0}+{\left({\left(\frac{B_T{\mathbb{T}}_0}{4{\mathbb{S}}_0}\right)}^2+\frac{4TOL}{12{\mathbb{S}}_0{C}_{FE}}\right)}^{1∕2}\right)}^{-d∕r}$$

   for some constant D₃ > 0.

3. Sparse Grid: We seek $\Vert {\widehat{Q}}_h({\mathbf{y}}_L,0)-{\mathcal{S}}_w^{m,g}{\widehat{Q}}_h({\mathbf{y}}_L,0){\Vert }_{L_{\rho }^2(\Gamma )}⩽\frac{TOL}{3C_{PSG}}$. This is satisfied if $\Vert e_0{\Vert }_{L_{\rho }^2({\Gamma }_L;H_0^1(U))}⩽\frac{TOL}{6a_{max}{\mathbb{F}}_{max}^d{\mathbb{F}}_{min}^{-2}{C}_{PSG}}$ and

   $$\Vert e_n{\Vert }_{L_{\rho }^2({\Gamma }_L)}⩽\frac{TOL}{6B_T{C}_{PSG}}$$
   for n = 1, … , N_S. Now, following a similar approach as in [27] let ${\delta }^{\ast }=(e\log (2)-1)∕{\tilde{C}}_2(\sigma )$. Thus $\Vert {\widehat{Q}}_h(\mathbf{y})-{\mathcal{S}}_w^{m,g}{\widehat{Q}}_h(\mathbf{y}){\Vert }_{L_{\rho }^2(\Gamma )}⩽\frac{TOL}{3C_{PSG}}$ if

   $${\eta }_0(TOL)⩾{\left(\frac{6a_{max}{\mathbb{F}}_{max}^d{\mathbb{F}}_{min}^{-2}{C}_{PSG}{C}_S{\mathbb{F}}^{N_L}\text{exp}(\sigma (\beta ))}{TOL}\right)}^{\frac{1+\log (2N_L)}{\sigma }}$$
   for a sufficiently large N_L, where $C_{\mathbb{F}}≔\frac{C_1(\sigma ,{\delta }^{\ast },\tilde{M})}{\mid 1-C_1(\sigma ,{\delta }^{\ast },\tilde{M})\mid }$, and $\mathbb{F}≔\max \{1,C_1(\sigma ,{\delta }^{\ast },\tilde{M})\}$. Similarly, for a sufficiently large N_L we have that

   $${\eta }_n(TOL)⩾C{\left(\frac{6B_T{C}_{PSG}{C}_{\mathbb{F}}{\mathbb{F}}^{N_L}\text{exp}(\sigma (\beta ))}{TOL}\right)}^{\frac{1+\log (2N_L)}{\sigma }}$$

   for n = 1, … , N_S.

Combining (a), (b) and (c) into equations (25) and (26) we obtain the total work $W_{Total}^{mean}(TOL)$ and $W_{Total}^{var}(TOL)$ as a function of a given user error tolerance TOL.

8. Numerical results

In this section the hybrid collocation-perturbation method is tested on an elliptic PDE with a stochastic deformation of the unit square domain i.e. U = (0, 1) × (0, 1). The deformation map $F:U\to \mathcal{D}(\omega )$ is given by

$$\begin{gathered} F({\eta }_1,{\eta }_2,\omega )=({\eta }_1,({\eta }_2-0.5)(e({\eta }_1,\omega ))+0.5)if{\eta }_2>0.5 \\ F({\eta }_1,{\eta }_2,\omega )=({\eta }_1,{\eta }_2)if0⩽{\eta }_2⩽0.5. \end{gathered}$$

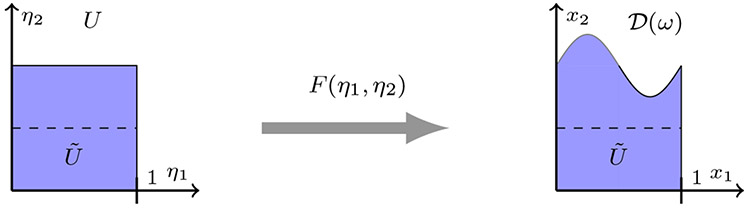
According to this map only the upper half of the square is deformed but the lower half is left unchanged. The cartoon example of the deformation on the unit square U is shown in Figure 3.

Fig. 3.

Stochastic deformation of unit square U according to the rule given by $F:U\to \mathcal{D}(\omega )$. The region $\tilde{U}$ is not deformed and given by (0, 1) × (0, 0.5).

The Dirichlet boundary conditions are set according to the following rule:

$$u({\eta }_1,{\eta }_2,\omega ){\mid }_{\partial \mathcal{D}(\omega )}=\{\begin{array}{c}\vartheta ({\eta }_1)\text{upper border}\hfill \\ 0\text{otherwise}\hfill \end{array}\phantom{\}}$$

where $\vartheta ({\eta }_1)≔\text{exp}(\frac{-1}{1-4({\eta }_1-0.5{)}^2})$. Note that the boundary condition on the upper border does not change even after the stochastic perturbation.

For the stochastic model e(η₁, w) we use a variant of the Karhunen Loève expansion of an exponential oscillating kernel that are encountered in optical problems [24]. This model is given by

$$\begin{gathered} e_L(\omega ,{\eta }_1)≔1+c{Y}_1(\omega ){\left(\frac{\sqrt{\pi }L}{2}\right)}^{1∕2}+c{\sum }_{n=2}^{N_L}\sqrt{{\mu }_n}{\phi }_n({\eta }_1)Y_n(\omega ); \\ {e}_S(\omega ,{\eta }_1)≔c{\sum }_{n=1}^{N_S}\sqrt{{\mu }_n+N_L}{\phi }_n({\eta }_1)Y_n(\omega ) \end{gathered}$$

with decay $\sqrt{{\mu }_n}≔\frac{(\sqrt{\pi }L{)}^{1∕2}}{n^k}$, $n\in \mathbb{N}$, $k\in {\mathbb{R}}^{+}$ and

$${\phi }_n({\eta }_1)≔\frac{sin\left(\frac{n\pi {\eta }_1}{2L_p}\right)-cos\left(\frac{n\pi {\eta }_1}{2L_p}\right)+cosh({\eta }_1)+sinh({\eta }_1)}{n}.$$

It is assumed that $\{Y_n{\}}_{n=1}^N$ are independent uniform distributed in ($-\sqrt{3}$, $\sqrt{3}$), thus $\mathbb{E}[Y_n]=0$, $\mathbb{E}[Y_n{Y}_m]=\delta [n-m]$ for n, m = 1 … N where δ[·] is the Kronecker delta function.

It can be shown that for n > 1 we have that

$$B_n=\left[\begin{array}{cc}\hfill 0\hfill & \hfill 0\hfill \\ \hfill c({\eta }_2-0.5){\partial }_{{\eta }_1}{\phi }_n({\eta }_1)\hfill & \hfill 0\hfill \end{array}\right].$$

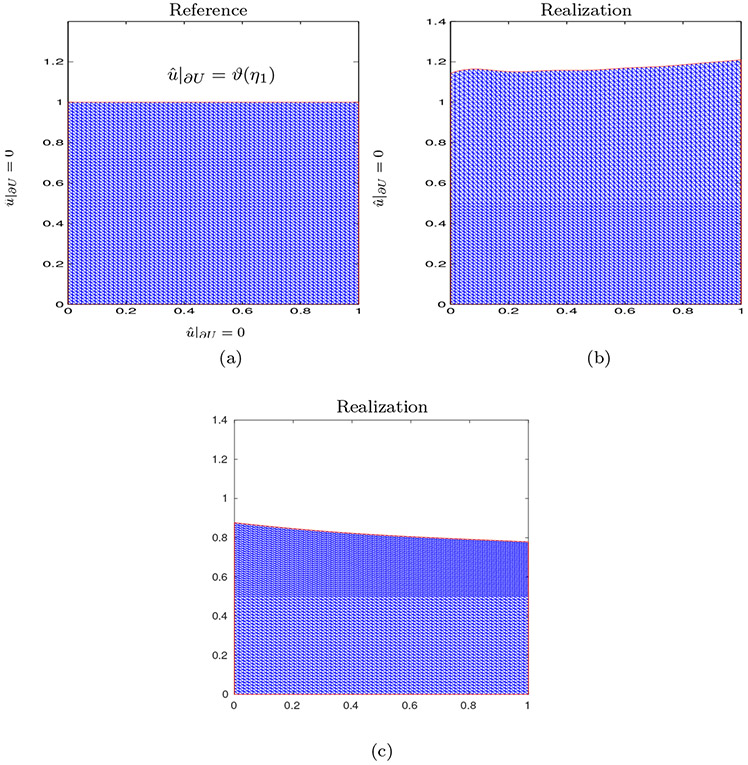
Thus for all $l\in \mathbb{N}$ we have that sup_x∈^U σ_max(B_l(η₁)) < C for some constant C. Thus for k = 1 we obtain linear decay on the gradient of the deformation. In Figure 4 (a) a mesh example of the reference domain is shown with Dirichlet boundary conditions. In Figure 4 (b) and (c) two realizations $\mathcal{D}(\omega )$ of the reference domain U from the deformation model F(η₁, η₂, ω) are shown also. These realizations correspond to the 15 dimensional example (N = 15) with k = 3, c = 1/15 and L = 1/2.

Fig. 4.

Random deformation of a reference square domain U. (a) U reference domain with Dirichlet boundary conditions. (b) Realization of the deformed reference square U. (c) Second realization of the deformed reference square U.

The QoI is defined on the bottom half of the reference domain ($\tilde{U}$), which is not deformed, as

$$Q(\widehat{u})≔{\int }_{(0,1)}{\int }_{(0,1∕2)}\vartheta ({\eta }_1)\vartheta (2{\eta }_2)\widehat{u}({\eta }_1,{\eta }_2,\omega )d{\eta }_{1}d{\eta }_2.$$

In addition, we have the following:

1. a(x) = 1 for all x ∈ U, L = 1/2, L_P = 1, N = 15.

2. The domain is discretized with a 2049 × 2049 triangular or 4097 × 4097 mesh.

3. $\mathbb{E}[Q_h]$, $\mathbb{E}[Q_h^2]$, and ${\sum }_{n=1}^{N_S}{\mu }_{S,n}$ $\mathbb{E}[{\int }_U{\tilde{\alpha }}_{n,h}{]}^2$ are computed with the Clenshaw-Curtis isotropic sparse grid from the Sparse Grids Matlab Kit [31,2].

4. The reference solutions var[Q_h(u_ref)] and $\mathbb{E}[Q_h(u_{ref})]$ for N =15 dimensions are computed with a dimension adaptive sparse grid from the Sparse Grid Toolbox V5.1 [15,23,22]). The choice of abscissas is set to Chebyshev-Gauss-Lobatto.

5. The QoI is normalized by dividing by Q(U) i.e. the QoI of solution $\widehat{u}$ on the reference domain U

6. The reference computed mean value is 1.054 and variance is 0.1122 (0.3349 std) for c = 1/15 and cubic decay (k = 3). This shows a significant aleatory deformation of the solution with respect to the random domain $\mathcal{D}(\omega )$.

Remark 13 The correction variance term is computed on the fixed reference domain U as described by Problem 1 instead of the perturbed domain. The pure collocation approach (without the variance correction) and reference solution are also computed on U. Numerical experiments confirm that computing the pure collocation approach on U, as described by Problem 1, or the perturbed domain $\mathcal{D}(\omega )$ lead to the same answer up to the finite element error. This is consistent with the theory.

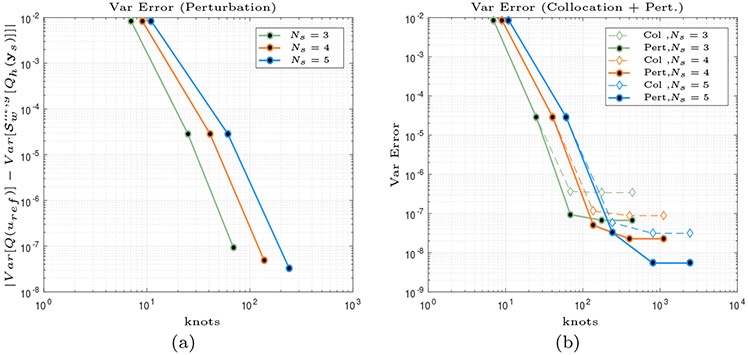
For the first numerical example we assume that we have cubic decay of the deformation i.e. the gradient terms $\sqrt{{\mu }_n}{\text{sup}}_{x\in U}\Vert B_n(x)\Vert$ decay as n⁻³. The domain is formed from a 2049 × 2049 triangular mesh. The reference domain is computed with 30,000 knots (dimension adaptive sparse grid). In Figure 5(a) we show the results for the hybrid collocation-perturbation method for c = 1/15, k = 3 (cubic decay), N_L = 2, 3, 4 dimensions and compare them to the reference solution. For the collocation method the level of accuracy is set up to w = 5. For the variance correction we increase the level until w = 3 is reached since the there is no benefit to increasing w further as the sparse grid error is smaller than the perturbation error. The observed computational cost for computing the variance correction is about 10% of the collocation method.

Fig. 5.

Hybrid Collocation-Perturbation results with k = 3 (cubic decay) and c = 1/15. (a) Variance error for the hybrid collocation-perturbation method as a function of the number of collocation samples with a isotropic sparse grid and Clenshaw Curtis abscissas. The maximum level is set to w = 3. (b) Comparison between the pure collocation (Col) and the hybrid collocation-perturbation (Pert) approaches. As we observe the error decays significantly with the addition of the variance correction. However, the graphs saturate once the perturbation/truncation error is reached. Note that the number of knots of the sparse grid are computed up to w = 5 for the pure collocation method. For the variance correction the sparse grid level is set to w = 3 since at this point the error is smaller than the perturbation error and there is no benefit to increasing w. The sparse grid knots needed for the variance correction are almost negligible compared to the pure collocation.

In Figure 5(b) we compare the results between the pure collocation [6] and hybrid collocation-perturbation method. Notice the hybrid collocation-perturbation shows a marked improvement in accuracy over the pure collocation approach.

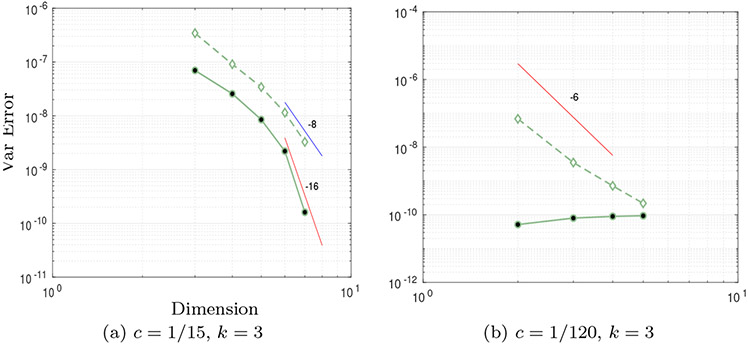
In Figure 6 the variance error decay plots for k = 3 (cubic decay) with (a) c = 1/15 and (b) c = 1/120 are shown for the collocation (dashed line) and hybrid methods (solid line). The reference solutions are computed with a dimension adaptive sparse grid with 20,000 knots for (a) and (b). The mesh size is set to 4097 × 4097 for (a) and 2049 × 2049 for (b). The collocation and hybrid estimates are computed with an isotropic sparse grid with Clenshaw-Curtis abscissas.

Fig. 6.

Variance error comparison of truncation and hybrid collocation-perturbation method as a function of the number of dimensions and different decay rates. (a) Variance error for the pure collocation (dashed line) and hybrid collocation-perturbation (solid line) methods for c = 1/15 and k = 3. (b) Variance error ratio between the collocation and hybrid methods for c = 1/120 (i.e. small perturbation) and k = 3. Note that the finite element error is reached at N_S = 2, saturates the overall accuracy.

It is observed that the error for the hybrid collocation-perturbation method decays faster compared to the pure collocation method. Moreover, as the dimensions are increased the accuracy gain of the perturbation method accelerates significantly (c.f. Figure 6(a). The accuracy improves from around $\frac{1}{N_L^8}$ to about $\frac{1}{N_L^{16}}$. Note that the computational cost for both the hybrid and collocation methods are relatively equal. This method shows a significant reduction in computational cost for the same accuracy, making it suitable for large dimensional problems.

In Figure 6 (b) the perturbation of geometry is significantly reduced (c = 1/120). Due to the small perturbation, the perturbation approximation is significantly higher and the error of the variance decreases substantially for N_s = 2. This is expected since perturbation methods work well under small variations of the geometry. Notice that for N_S = 2, 3, … accuracy of the hybrid method appears not to improve, however the limiting factor at this point is due to the finite element error.

9. Conclusions

In this paper we propose a new hybrid collocation perturbation scheme to computing the statistics of the QoI with respect to random domain deformations that are split into large and small deviations. The large deviations are approximated with a stochastic collocation scheme. In contrast, the small deviations components of the QoI are approximated with a perturbation approach. A rigorous convergence analysis of the hybrid approach is developed.

It is shown that for a linear elliptic partial differential equation with a random domain the variance correction term can be analytically extended to a well defined region Θ_β,NL embedded in ${\mathbb{C}}^{N_L}$ with respect to the random variables. This analysis leads to a provable sub exponential convergence rate of the QoI computed with an isotropic Clenshaw-Curtis sparse grid. The size of the region Θ_β,NL and therefore the rate of convergence of an isotropic sparse grid is a function of the gradient decay of the random deformation.

Error estimates and numerical experiments show that the error decays the square of the polynomial order with respect to the number of dimensions. This shows a marked reduction in effective dimensionality of the problem. Moreover, in practice, the variance correction term can be computed at a fraction of the cost of the low dimensional large variation component.

The hybrid approach is essentially a dimensionality reduction technique. We demonstrate both theoretically and numerically that the variance error with respect to the collocation dimensions N_L decays quadratically faster than the pure stochastic collocation approach. Thus, the hybrid method is compatible with other stochastic collocations approaches such as anisotropic sparse grids [26]. This makes this method well suited for a large number of stochastic variables.