Automatic 3D Monte-Carlo-based secondary dose calculation for online verification of 1.5 T magnetic resonance imaging guided radiotherapy

Highlights

• •First implementation of an independent 3D-secondary dose calculation (3D-SDC).
• •Validation of the 3D-SDC solution using patient plans and experimental plan QA.
• •Online SDC of central targets is feasible with a median calculation time of 1:23 min.
• •Peripheral targets with small beam numbers need alternative validation strategies.

Abstract

Background and purpose

Hybrid magnetic resonance linear accelerator (MR-Linac) systems represent a novel technology for online adaptive radiotherapy. 3D secondary dose calculation (SDC) of online adapted plans is required to assure patient safety. Currently, no 3D-SDC solution is available for 1.5T MR-Linac systems. Therefore, the aim of this project was to develop and validate a method for online automatic 3D-SDC for adaptive MR-Linac treatments.

Materials and methods

An accelerator head model was designed for an 1.5T MR-Linac system, neglecting the magnetic field. The use of this model for online 3D-SDC of MR-Linac plans was validated in a three-step process: (1) comparison to measured beam data, (2) investigation of performance and limitations in a planning phantom and (3) clinical validation using n = 100 patient plans from different tumor entities, comparing the developed 3D-SDC with experimental plan QA.

Results

The developed model showed median gamma passing rates compared to MR-Linac base data of 84.7%, 100% and 99.1% for crossplane, inplane and depth-dose-profiles, respectively. Comparison of 3D-SDC and full dose calculation in a planning phantom revealed that with $⩾$5 beams gamma passing rates $>$95% can be achieved for central target locations. With a median calculation time of 1:23 min, 3D-SDC of online adapted clinical MR-Linac plans demonstrated a median gamma passing rate of 98.9% compared to full dose calculation, whereas experimental plan QA reached 99.5%.

Conclusion

Here, we describe the first technical 3D-SDC solution for online adaptive MR-guided radiotherapy. For clinical situations with peripheral targets and a small number of beams additional verification appears necessary. Further improvement may include 3D-SDC with consideration of the magnetic field.

1. Introduction

Hybrid systems combining a linear accelerator (Linac) and a magnetic resonance imaging (MRI) device (MR-Linac) for online adaptive radiotherapy (RT) are a promising new technology, which has recently been introduced clinically for a broad spectrum of tumor entities [1], [2], [3], [4]. Currently, two different technical realizations of MR-Linac systems with magnetic field strengths of 0.35 and 1.5 T are clinically available [5], [6], [7]. The main advantage of online adaptive MR-guided RT (MRgRT) is the high soft tissue contrast yielded by the MRI and the possibility of real-time RT plan adaptation on the MRI of the day [8], [9]. Such online adaptive MRgRT potentially allows the use of smaller margins and therefore better organ at risk sparing and tumor control in the future [10].

Online MR-guided adaptive RT implies the generation of a new treatment plan for each treatment fraction. Consequently, quality assurance (QA) of such online adapted treatment plans cannot be carried out using time-consuming experimental validation in phantoms which is classically used for conventional RT plan QA [11], [12]. Using simulated dose distributions for an independent secondary dose calculation (SDC) was proposed as an alternative to experimental plan QA [13], [14]. The SDC concept checks the integrity and accuracy of the simulated dose distribution by dose re-calculation using an independent calculation method. In an online setting where the RT plan has to be validated while the patient is on the treatment couch, experimental plan validation can only be done prior to the first treatment fraction [15], [16] but not during daily online adaptation. To bridge this gap and ensure patient safety in MRgRT, a fast solution for real-time evaluation of the dose distribution is required. First implementations for MRI-Linac subsystems used a point dose comparison for a check of monitor units [17], [18]. However, such point dose comparison only gives a rough dose estimation based on radiological depth but does not consider missing segments, patient or leaf positioning errors. An identified main risk of online adaptive workflows is an incorrect assignment of electron densities [19], which can, due to high variability of plans, not be checked comprehensively by monitorunit checks and simplified calculation algorithms. Therefore, an automatic 3D-SDC, identifying dose contributions in off-isocenter positions is needed.

Recently Li et al. [20] quantified differences in dose distribution for utilization of a commercial collapsed cone dose engine in an offline comparison of treatment plans. Whereas, for a fast SDC, accelerating options of the Monte Carlo (MC) code are available for the 0.35 T MR-linac system [18], [22],magnetic field effects can only be simulated in full MC codes [21] on the 1.5 T MR-linac system. The potential of accelerated dose predictions, based on deep learning approaches [23], must still be investigated as they are dependent on training data and do not mechanistically correspond to particle interactions.

The underlying assumption of this study was, that magnetic field effects on dose profiles are most dominant in the penumbra region and that for plans with multiple beams these effects might cancel out, as for opposing beams also the Lorentz force has the opposite direction. Consequently, high dose contributions on multiple beam IMRT should be largely independent of the magnetic field.

Therefore, the hypothesis was that an independently created accelerator head model for 1.5 T MR-Linac systems neglecting the influence of the magnetic field (B = 0 T) allows fast SDC for online verification of MR-Linac plans and provides a similar level of accuracy compared to experimental plan QA at the MR-Linac.

2. Material and methods

An accelerator head model was developed for a 1.5 T MR-Linac, implemented for fast SDC in an online MRgRT setting and the clinical performance evaluated. The MR-Linac head model was validated in a three-step process: (1) comparison to measured beam data, (2) investigation of performance and limitations in a simplified planning phantom and (3) clinical validation using n = 100 patient plans by comparing the differences between SDC and full TPS dose calculation results to those between experimental offline plan QA and the TPS.

2.1. Independent MR-Linac accelerator head model for B = 0 T

The beam data of a 1.5 T MR-Linac (Unity, Elekta AB, Stockholm, Sweden) was collected with a MR-compatible prototype water tank (Beamscan-MR, PTW Freiburg, Germany). Profiles in in- (IP) and cross-plane (CP) direction, percentage depth dose (PDD) curves and output factors (OF) were measured using a microdiamond detector (60019, PTW Freiburg, Germany) for field sizes up to 16 $\times$ 16 cm² and a Semiflex 3D (31021, PTW Freiburg, Germany) for fields from 16 $\times$ 16 to 40 $\times$ 22 cm². Fields were measured with gantry angle 0°at isocenter level with a source-to-isocenter distance (SID) of 143.5 cm. Due to the limited dimensions of the water tank in the bore, for this gantry angle PDDs could only be measured up to a depth of 10 cm. To consider PDDs up to a depth of 30 cm, additional square fields from 2 $\times$ 2 to 16 $\times$ 16 cm² were measured for gantry 270°with a SSD of 113.2 cm. For gantry 0°and 270°, profiles and OFs were assessed in water depths of 10 cm. This corresponds to a respective source-to-detector distances of 143.5 cm and 123.2 cm, and therefore unequal fields size at point of measurement. Profiles were normalized to the mean of the three highest scoring dose values. Profiles measured with the Semiflex 3D were shifted based on a registration from microdiamond to Semiflex to account for the lateral shift of the effective point of measurement induced by the magnetic field and were deconvolved using the BEAMSCAN software (PTW Freiburg, Version 4.3) [24]. Normalization of the PDD was done in 10 cm depth after fitting a 4th order polynomial function to the measured data starting 1 cm after the dose maximum [21]. A detailed list of measured items is shown in Table 1.

Table 1.

2D gamma passing rates, comparing the experimental data in the crossplane (CP), inplane (IP) and percentage depth dose (PDD) curves to the calculated dose distribution of the SDC and TPS for various field sizes.

Gantry angle [°]	Field size CP [cm]	Field size IP[cm]	2D gamma passing rate (Measurement vs. SDC) [%]			2D gamma passing rate (Measurement vs.TPS) [%]
			CP	IP	PDD	CP	IP	PDD
0	2	2	64.0	100.0	58.6	100.0	100.0	100.0
0	3	3	68.3	100.0	95.8	100.0	100.0	100.0
0	5	5	85.3	100.0	98.9	99.7	100.0	100.0
0	10	10	85.2	100.0	99.7	100.0	100.0	100.0
0	15	15	93.4	100.0	99.1	99.7	100.0	100.0
0	22	22	84.1	100.0	99.1	99.4	100.0	100.0
0	40	22	52.3	94.4	98.5	99.2	100.0	100.0
270	2	2	73.9	100.0	100.0	100.0	100.0	100.0
270	3	3	76.7	100.0	100.0	100.0	100.0	100.0
270	5	5	86.0	99.2	100.0	100.0	100.0	100.0
270	10	10	92.4	100.0	99.6	100.0	100.0	100.0
270	16	16	91.1	100.0	98.9	100.0	100.0	100.0
Median			84.7	100.0	99.1	100.0	100.0	100.0

A MC head model, neglecting the influence of the magnetic field (B = 0 T), was created in the research TPS Hyperion [25] for the 1.5 T MR-Linac based on measured PDDs, OFs, and profiles. Hyperion simulates dose distributions based on a XVMC [26], whereas the commercial TPS (Monaco 5.40.01, Elekta, Stockholm, Sweden) uses the GPUMCD algorithm [27], thus ensuring independent calculations. Dose distributions for the water phantom were simulated in Hyperion for all measured fields for both gantry orientations with a MC-variance of 0.1% using a grid size of 3 $\times$ 3 $\times$ 3 mm³ for comparison with the measurements. In addition, the experimental data was compared to the dose distribution simulated by the TPS, taking into account the magnetic field effect [28]. The simulations in the TPS were performed with a statistical uncertainty of 0.5% per calculation and a grid size of 3 $\times$ 3 $\times$ 3 mm³.

All data points were interpolated to the minimal measurement grid of 0.1 mm and compared as reference with the dose distribution using a global 2D gamma criterion [29] of 2 mm/2% in Matlab R2019a (Mathworks Inc., Natick, MA, USA). All data points from −60% to + 60% of the evaluated field size were analyzed.

2.2. Planning phantom

Magnetic field effects on the dose distributions of single beams are expected to be dominant in the penumbra of crossline profiles and, due to the electron-return-effect (ERE) [30], at air-tissue interfaces. Therefore, an in silico phantom study was performed to investigate the influence of the magnetic field on 3D dose distributions, depending on the number of beams and proximity to air-tissue interfaces. In this phantom experiment, two planning scenarios were designed. In scenario A, the plan isocenter was positioned in the center of a cylindrical homogeneous water phantom (r = 13 cm). In scenario B, the isocenter was placed 6 cm below the surface of a half cylindrical homogeneous phantom (r = 19 cm), simulating a target volume near the skin surface. For both scenarios nine different MR-Linac plans were generated, with one to nine equidistant 10x 10 cm² open fields with 200 MU in the TPS (B = 1.5 T) and compared to the dose distributions obtained from the SDC (B = 0 T).

For both scenarios dose distributions of the TPS were compared to the SDC using an interpolated 1 $\times$ 1 $\times$ 1 mm³ grid, a 2 mm/2% gamma criterion and a threshold dose of 40%$D_{\mathit{max}}$, implemented in python 2.7.

2.3. Clinical validation of MR-Linac SDC and comparison with experimental plan QA

A total of 100 plans from 57 patients which had been irradiated in the context of a phase 2 feasibility trial (NCT04172753) at the MR-Linac system between January and November 2019 were retrospectively included into this analysis. The trial was approved by the institutional review board (IRB 659/2017BO1). Plans corresponded to six different treatment sites. For each MR-Linac plan, dose distributions calculated by the TPS including magnetic field effects were compared to dose distributions for those plans generated with SDC. A detailed list of patient data is shown in Table 2.

Table 2.

Entity specific analysis of the evaluated plans. Values are given in median (Interquartile range) for the measurement, fast online criterion (FOC) and precision offline criterion (POC).

Tumor entity	Liver	Prostate	Abdominal	Rectum	Breast	Head & Neck	Total
Number of patients	12	11	8	11	11	4	57
Number of plans	21	24	13	14	18	10	100
Number of Segments	58 (57–60)	32 (21–36)	46 (31–50)	36 (26–36)	23 (20–25	48 (42–54)	35 (25–56)
Calculation time [min] Voxel: 3$\times$3$\times$3 mm3	01:38 (01:05–01:45)	01:07 (0:56–01:19)	01:32 (0:50–01:42)	02:16 (01:52–02:21)	00:57 (0:50–01:03)	01:55 (01:32–02:38)	01:23 (00:58–01:47)
Calculation time [min] Voxel: 1 $\times$ 1 $\times$ 1 mm3	07:49 (04:53–08:20)	07:03 (06:13–07:52)	08:11 (04:21–09:40)	16:08 (15:11–17:30)	06:12 (05:51–06:53)	11:26 (09:01–12:33)	07:47 (06:08–09:50)
Measurement gamma passing rate [%](3 mm/3 %)	99.7 (99.3–100)	99.6 (99.3–99.9)	100 (99.6–100)	96.5 (94.7–97.6)	99.5 (99.1–99.7)	98.4 (96.7–99.8)	99.5 (98.1–100)
FOC gamma passing rate [%](6 mm/3 %)	99.2 (98.8–99.4)	99.4 (99.1–99.7)	99.5 (99.0–99.9)	98.9 (98.7–99.1)	92.7 (90.8–96.2)	94.3 (88.2–96.4)	98.9 (97.0–99.5)
Wilcoxon signed-rank test Measurement vs. FOC	0.31	0.51	0.15	$<$0.001	$<$0.001	0.01	0.005
POC gamma passing rate [%](3 mm/3 %)	99.7 (99.1–99.9)	99.4 (98.9–99.6)	99.2 (98.2–99.5)	98.1 (97.6–98.2)	85.3 (82.2–89.5)	89.4 (88.4–93.8)	98.2 (94.1–99.5)
Wilcoxon signed-rank test Measurement vs. POC	0.71	0.21	0.005	$<$0.001	$<$0.001	0.004	$<$0.001

Experimental plan QA was performed for all 100 plans following our institutional QA protocol [15] with a static hexagonal phantom (Octavius, PTW Freiburg, Germany), using an ion chamber array (1500MR, PTW Freiburg, Germany). Briefly, for the plan QA, beam angle specific measurements were performed, and a weighted average of the different setups was further analyzed. Evaluation of the measurement data was done using a local gamma criterion of 3 mm/3%, excluding doses below 30% of the maximum dose.

For all patient plans included into this analysis, the performance of the proposed SDC approach was assessed in a clinical setting. The dose distribution generated by the TPS during online adaptive MR-guided RT (1% statistical uncertainty per calculation, 3 $\times$ 3 $\times$ 3 mm³ grid) was transferred to the SDC, an isocenter shift was applied based on the registration between the reference planning CT and the daily MR, followed by an immediate recalculation of the plan using the simplified MR-Linac beam model (MC-variance: 5% per control point, 3 $\times$ 3 $\times$ 3 mm³ grid). Calculation time was measured from the plan submission to the finalization of the SDC and gamma analysis.

Gamma analyses were calculated on a voxel grid of 3 $\times$ 3 $\times$ 3 mm³ and evaluated with a cut-off threshold of 40%. Due to the calculation speed requirements during the online workflow on MR-Linac systems, gamma analysis was performed on a non-interpolated voxel grid resulting in a gamma criterion of 6 mm/3% (fast online criterion, FOC). This criterion was chosen to allow evaluation of all neighboring voxels with the greatest diagonal distance being 5.2 mm. To evaluate the accuracy of the FOC, additional gamma analysis was performed using a precision offline criterion (POC) which was recalculated after treatment on an interpolated voxel grid of 1 $\times$ 1 $\times$ 1 mm³ with a gamma criterion of 3 mm/3%. Processing of the DICOM files, voxel interpolation and global gamma analysis were performed in Python V 2.7.

2.4. Statistical analyses

Statistical analyses to assess differences between experimental plan QA results and SDC were evaluated using a Wilcoxon signed-rank test implemented in Matlab (Version R2019a).

3. Results

3.1. Independent MR-Linac accelerator head model for B = 0 T

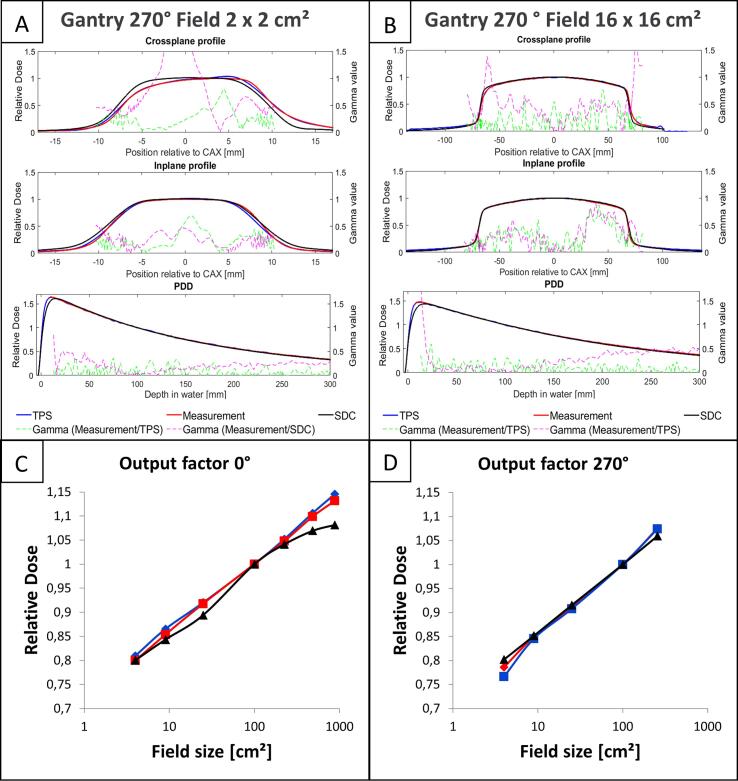
The comparison of measured MR-Linac beam data and the simplified accelerator head model for B = 0 T showed median (range) 2D gamma passing rates of 84.7% (52.3–93.4%), 100.0% (94.4–100%), and 99.1% (58.6–100%) for CP and IP profiles as well as PDDs (cf. Table 1). PDD, as well as profiles simulated with the SDC and the TPS for the largest 16 $\times$ 16 cm² and smallest 2 $\times$ 2 cm² measured field sizes from 270°are depicted in Fig. 1(A-B). The mean relative deviation in OFs between the measurement and the SDC was −1.4%. A maximum deviation was observed for the largest field with −6.4% (cf. Fig. 1C-D). A detailed analysis is shown in the Supplementary material 1.

Fig. 1.

Comparison of the developed simplified in-house head model (black, B = 0 T), the TPS Monaco (blue, B = 1.5 T) and the measurement (red, B = 1.5 T). Dashed magenta lines depict the gamma values comparing measured data with the in-house head model. Green lines represent gamma values comparing measurement and treatment planing system (TPS). Profiles are evaluated at a depth of 10 cm and an SSD of 113.2 cm. Therefore, the shown profiles do not correspond to their field size definition at isocenter. (A) shows the smallest evaluated field size of 2 $\times$ 2 cm², (B) the largest field of 16 $\times$ 16 cm², comparing the profiles relative to the central axis (CAX) and the percentage depth dose (PDD) (C), (D) depict the comparison of the output factors at gantry angles of 0°and 270°, respectively. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

3.2. Planning phantom

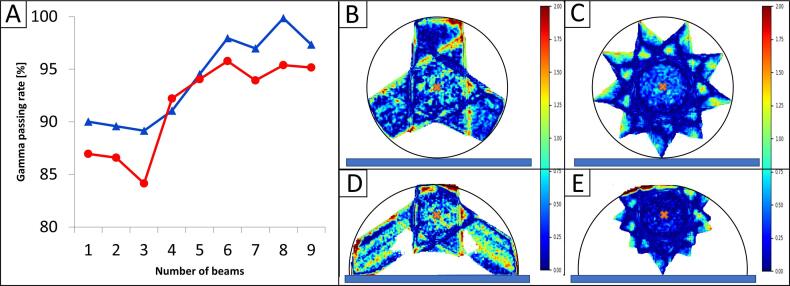
The gamma passing rate for the cylindrical phantom with a central target varied between 89.2% and 99.9% for three and eight beams, respectively whereas for the half cylindrical phantom with the target close to the surface the gamma passing rates varied between 84.2% and 95.8%.

Overall, plans using more than five beams yielded pass rates of approximately 95%. Detailed results of the comparison for both planning scenarios are shown in Fig. 2.

Fig. 2.

Resulting gamma passing rate as a function of the number of beams for planning scenario A (Blue) and scenario B (Red). In B and C the gamma map is shown for the cylindrical phantom, in D-E for the half cylindrical phantom for 3 and 9 beams, respectively. Depicted in black is the external phantom outline. Depicted in blue is the couch position and the corresponding isocenter position is marked in orange. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

3.3. Clinical validation of MR-Linac SDC and comparison with experimental plan QA

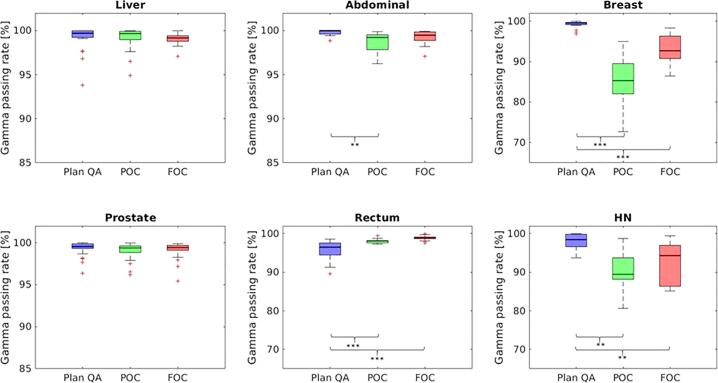
Overall, the measured plan QA data showed a median (IQR) gamma agreement with the simulated dose distributions by the SDC of 98.9 (97.0–99.5)% (p = 0.005) and 98.2 (94.1–99.5)% (p$<$0.001) for the FOC and POC, respectively, whereas the median (IQR) experimental gamma agreement with the TPS was 99.5 (98.1–100)%. However, the gamma analysis of the SDC showed a distinct entity specific variation: For liver, prostate, abdomen and rectum cancer MR-Linac SDC using the FOC resulted in median gamma passing rates with respect to measured data of 99.2% (p = ns), 99.4% (p = ns), 99.5% (p = ns) and 98.9% (p$<$0.001), respectively. For breast cancer the TPS dose agreed with the SDC with a passing rate of only 92.7% (FOC, p$<$0.001), whereas the measurement corresponded to 99.5%. HN plans resulted in 98.4% agreement of measurement with TPS simulation, whereas SDC using the FOC demonstrated a gamma passing rate of 94.3% (p = 0.01). An overview of SDC and experimental results is provided in Fig. 3. A detailed entity specific analysis is presented in Table 2,and an exemplary SDC analysis are presented in the Supplementary Fig. S1. The median calculation time for the FOC over all entities was 01:23 min.

Fig. 3.

Boxplots showing the experimental plan verification (Plan QA) in blue, the precision offline criterion (POC) in green and the fast online criterion (FOC) in red. The y-axis depicts the gamma passing rate in % (*p $<$ 0.05, **p $<$ 0.01, ***p $<$ 0.001). (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

4. Discussion

A simplified MC head model for a 1.5 T MR-linac system neglecting the effects of the magnetic field (B = 0 T) was developed, replicating the experimental data, and implemented as a SDC for online adaptive MRgRT. In the online workflow the developed system was able to verify the dose distribution of the TPS based on a 3D gamma analysis, with a median calculation time of 01:23 min. The analysis showed a good median agreement over all plans between the TPS and the SDC (98.9%) as well as the plan QA measurement (99.5%). In the entity specific analysis, the SDC showed results with accuracies comparable to experimental plan QA for liver, prostate and abdominal cancers, whereas the measured data in breast, HN and rectal cancer was significantly different (p$<$0.01) compared to the SDC.

The proposed approach was successfully implemented in the clinical MR-Linac online workflow. Consequently, the validation of the TPS dose distributions during online MRgRT was shown to be feasible in a clinical setting. The general acceptance criterion for SDC results in the online workflow was a gamma passing rate greater than 95%. For dose distributions that were strongly influenced by the magnetic field, an alternative validation strategy was implemented: Reference plans with gamma passing lower than 95% were experimentally verified. During online validation similar pass rates as for the SDC of the reference plan were accepted if the failed points were clearly located at air-tissue interfaces, which are particularly susceptible to magnetic field effects.

Neglecting the magnetic field effect in the MC dose calculations resulted in differences in the dose distribution between the measured data and the simulated dose distribution. Whereas the IP profiles and the fall-off region of the PDD showed good agreement with the measurement, the dose build-up region as well as the CP profiles presented with magnetic field specific differences. The magnetic field causes a steeper dose build-up in the first 15 mm below the tissue surface and an asymmetrical CP profile, of which the relative influence depends on the evaluated field size [30]. As a consequence, the developed beam model showed best agreement for medium sized fields, due to the high relative magnetic field influence for small fields and, for the biggest fields in the CP profiles, dose overestimation of the model on the field edges were observed. The OF for very large field sizes could not be further improved without loss of quality for smaller fields. Due to a limited impact of segment areas $>$70 cm² [31] in a modulated IMRT, this prioritization of middle-sized fields was chosen. The limited agreement of very small field sizes, which is restricted by the recommended IMRT-parameter on minimal segment size of 4 cm² must be further investigated. The model generation on experimental beam data is transferable to other MC-based calculation systems and not limited to the in-house system Hyperion. The phantom planning study showed that the observed differences were most dominant for targets close to air-tissue interfaces, as well as for plans with a low number of beams. With an increasing number of beams the influence of the magnetic field decreased. However, for regions close to the surface, the magnetic field has a bigger impact due to ERE and electron stream effect (ESE) [32], [33].

In an online workflow, the time delay between plan calculation and application can induce anatomical uncertainties, resulting in differences between dose simulation and application [34], [35]. Therefore, the calculation and evaluation criteria are optimized with respect to speed. This results in the evaluation of a gamma criterion of 6 mm and 3% on the original voxel grid without interpolation between dose points.

The differences for breast cancer are most likely due to the magnetic field effect for a limited number of beams and proximity to air tissue interfaces, as confirmed by our phantom experiments. Also for HN cases, air-tissue interfaces seem to be the reason for the lower observed agreement between SDC and measured plan data. For the rectal cancer cases the SDC showed better agreement to the TPS than the measured data. This is due to limitations reported for experimental MR-Linac QA of plans with large off-axis target volumes [15].

The SDC concept implemented in this study only checks the online adapted dose distribution whereas errors may also occur during dose delivery. Therefore a subsequent offline log file analysis may be added to the proposed SDC workflow to compare the planned dose distribution with the applied dose [35]. Additionally, the calculation of a 3D dose cube may allow an anatomical contour-based evaluation of differences in DVH-parameter [36].

In conclusion, this study showed that 3D-SDC of online adapted MRgRT plans using a simplified MC head model of an 1.5T MR-Linac system, neglecting the magnetic field effects is feasible in a clinical online workflow. The proposed technical 3D-SDC solution is able to accurately estimate the dose distribution for plans with more than five beams and centrally located target volumes. For clinical situations with peripheral targets and a small number of beams additional verification appears necessary. Consequently, for central tumors the fast SDC provides a similar accuracy compared to experimental plan QA. As a next step further improvement may include the consideration of the magnetic field for high precision 3D-SDC.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A. Supplementary data

The following are the Supplementary data to this article: