Abstract
In recent years, there has been significant criticism of functional magnetic resonance imaging (fMRI) studies with small sample sizes. The argument is that such studies have low statistical power, as well as reduced likelihood for statistically significant results to be true effects. The prevalence of these studies has led to a situation where a large number of published results are not replicable and likely false. Despite this growing body of evidence, small sample fMRI studies continue to be regularly performed; likely due to the high cost of scanning. In this report we investigate the use of a moderated t-statistic for performing group-level fMRI analysis to help alleviate problems related to small sample sizes. The proposed approach, implemented in the popular R-package LIMMA (linear models for microarray data), has found wide usage in the genomics literature for dealing with similar issues. Utilizing task-based fMRI data from the Human Connectome Project (HCP), we compare the performance of the moderated t-statistic with the standard t-statistic, as well as the pseudo t-statistic commonly used in non-parametric fMRI analysis. We find that the moderated t-test significantly outperforms both alternative approaches for studies with sample sizes less than 40 subjects. Further, we find that the results were consistent both when using voxel-based and cluster-based thresholding. We also introduce an R-package, LIMMI (linear models for medical images), that provides a quick and convenient way to apply the method to fMRI data.
Keywords: Moderated t-test, fMRI, Group analysis, LIMMA, LIMMI
1. Introduction
In the past decade, there has been a great deal of discussion regarding how studies with small sample sizes undermine the reliability of neuroscience research (Button et al., 2013; Munafò et al., 2014). The argument is that small-sample studies both have low statistical power to detect true effects and a reduced likelihood for statistically significant results to be true effects. Despite this growing body of evidence, most functional magnetic resonance imaging (fMRI) studies continue to be small, with the majority consisting of less than 30 subjects (Poldrack et al., 2017).1 This is problematic, as a large number of published results are likely not replicable and perhaps even false. As the prohibitive costs of performing an fMRI study make it difficult for many labs to conduct larger studies, it makes sense to evaluate whether there exist analytic techniques that can help mitigate some of the problems associated with small sample sizes. Here we propose one such technique in the context of the analysis of multi-subject task fMRI.
Most task-based group fMRI analyses are concerned with determining whether there exists a significant population-wide ‘activation’ in a comparison between two or more conditions. This is typically assessed by testing the average value of a contrast of parameter estimates (COPEs) against zero in a general linear model (GLM) analysis. Standard group analyses typically involve fitting two separate models. A first-level GLM analysis is performed on each subject’s data, providing within-subject COPEs (e.g., activity magnitude estimates for [visual stimulation vs. rest]). A second-level analysis provides population inference on whether COPEs are significantly different from zero and assesses the effects of second-level predictors (e.g., group status, behavioral performance) (Lindquist et al., 2012). Researchers typically perform this analysis using an un-weighted, ordinary least squares (OLS) analysis (Mumford and Nichols, 2009). This is generally equivalent to performing a t-test across subjects at each voxel of the brain.
This approach can be problematic in the small sample setting as errors in estimation of the voxel-wise variance may lead to noisy t-statistic images, which in turn can lead to decreased power to detect effects (Nichols and Holmes, 2002). In the context of non-parametric testing, Nichols and Holmes (2002) addressed this issue by proposing the use of a pseudo t-statistic formed by smoothing the variance across adjacent voxels prior to computing the t-statistic. They explicitly mention that since there is no closed form solution to the distribution of the statistic, it can only be used in a non-parametric analysis. In the genomics literature, where similar sample size issues are common, a moderated t-statistic has been utilized to address the same issue. This approach, implemented in the popular R-package LIMMA (linear models for microarray data) (Ritchie et al., 2015; Smyth, 2005), has been accepted as the standard method for the assessment of differential expression in microarray data. The LIMMA package is available on Bioconductor (Gentleman et al., 2004), which is a collaborative project for the creation of software for computational biology and bioinformatics. The key idea is to construct a t-statistic that has a similar interpretation as the standard t-statistic, but with standard errors moderated using empirical Bayes methods (Efron and Morris, 1975; James and Stein, 1961). This is equivalent to shrinkage of the estimated sample variances towards a pooled estimate, resulting in stable inference even when the sample size is small. Importantly, this moderated t-statistic is shown to follow a t-distribution with augmented degrees of freedom, allowing for straightforward inference.
To evaluate the performance of the method in the context of multi-subject task fMRI data, and to contrast it with the pseudo t-test and the standard t-test, we utilize data from the 500-subject release from the NIH-sponsored Human Connectome Project (HCP) (Van Essen et al., 2013). In particular, we focus our attention on data collected during four experimental tasks: emotion, gambling, motor, and working memory. We treat the complete collection of subjects as our population of interest, and perform single-subject analysis on each subject in the population. To evaluate the properties of the different methods in small sample fMRI studies, we draw multiple samples from the population of sizes ranging from 10 to 100. This allows us to mimic the sample sizes typically used in studies performed by individual labs, and compare the different analytic approaches. In addition, to establish the empirical error control of the methods we are evaluating, we created null data by applying the processing pipeline from the working memory study to resting-state fMRI data in an analogous manner as described in Eklund et al. (2016). Finally, we evaluate the performance of the methods using both voxel-based and cluster-based thresholding.
This report is organized as follows. Section 2 provides an overview of the standard t-statistic, the pseudo t-statistic, and two variants of the moderated t-statistic, followed by a discussion of the data set that will be analyzed and the manner in which the methods will be compared. In addition, we introduce an R-package, LIMMI (linear models for medical images), that provides a quick and convenient way to apply the moderated t-statistic to fMRI data. Section 3 shows the results of the comparison between the methods. The paper concludes with a discussion in Section 4.
2. Methods
2.1. Models
Multi-subject fMRI data is hierarchical in nature, with lower-level observations nested within higher levels (for example, subjects nested within groups). Taking the multi-level nature of the data into consideration can provide the means to generate population level statistics. This is typically done using a two-level hierarchical model (Lindquist et al., 2012). In the first level, we analyze within-subject effects for each participant in the study. In the second level, we perform analyses across subjects or between groups. Researchers can do this either in stages or combined into a single integrated model. Here we focus on the former approach. We discuss a number of different techniques for performing second-level analysis in this manner, including the standard t-statistic (i.e., the OLS approach), the pseudo t-statistic used in non-parametric analysis, and two variants of the moderated t-statistic.
2.1.1. OLS approach
The most popular group analysis is the one sample t-test on differences between two conditions (e.g., Task A–Task B) at each voxel. This analysis, referred to as the ordinary least-squares (OLS) approach (also known as the summary statistics or “random effects” approach in the fMRI literature), tests whether the difference is non-zero on average for the sampled population and provides a starting point for our discussion on population inference.
To illustrate group analysis using the OLS approach (e.g., Holmes and Friston (1998); Mumford and Nichols (2009)), let us denote the COPE for subject i ∈ {1, …, n} and voxel v ∈ {1, …, V} by . For each fixed voxel, we assume that are drawn from the same population distribution . To test the null hypothesis that βv = 0 one can compute the t statistic:
| (1) |
where and , which follows a t-distribution with n − 1 degrees of freedom. This result can be used to compute a p-value and assess significance at every voxel of the brain.
2.1.2. Pseudo t-statistic
The t-statistic described in Eq. (1) can be problematic in the small sample setting, as noisy estimates of the variance term can inflate its values. This, in turn, can lead to an increase in the number of false positives. Nichols and Holmes (2002) offered a non-parametric improvement for the t-statistic, which they refer to as the pseudo t-statistic, that pools the variance estimate at each voxel with those of its neighbors. This is performed by spatially smoothing the variance estimates, and thereby stabilizing its variability. Using the notation from the previous section, the pseudo t-statistic can be formulated as follows:
| (2) |
where the is the smoothed estimates of the standard deviation. A variety of smoothing techniques can potentially be applied here. Here we use a 4 mm FWHM spherical Gaussian smoothing kernel to smooth the variance images.
It should be noted that the pseudo t-statistic was proposed in the context of non-parametric testing. A shortcoming of the approach that there is no closed form solution to the distribution of the statistic that can be used to compute p-values and assess significance. This limits its use to non-parametric group analysis where a closed form solution is not needed, as one instead creates a permutation distribution to test the null. If one does not want to use a non-parametric approach, there is no straightforward way of using the pseudo t-statistic.
To create a permutation distribution to test the null hypothesis of no effect we proceed as follows. For each of 1000 permutations each participant’s data is randomly ‘sign-flipped’ (i.e., multiplied by either 1 or −1). For each permutation, the pseudo t-statistic is calculated at each voxel and its maximum value across the brain recorded. This allows for the derivation of the permutation distribution of the maximal voxel-wise pseudo t-statistic over the entire brain. This distribution is used to test significance for the participant’s actual data. Importantly, this approach provides control over the family-wise error rate (FWER).
2.1.3. Moderated t-statistic
In the genomics literature, issues related to small sample sizes are similarly common. In this setting, a moderated t-statistic has been proposed to improve inference. Here the estimated sample variances are shrunk towards a pooled estimate, which results in stable inference even when the sample size is small. This approach, implemented in the R-package LIMMA (Smyth, 2005), has found wide usage for the assessment of differential expression in microarray data. Though the approach shares some similarity with the pseudo t-statistic, in that the estimated sample variances are stabilized by borrowing strength across voxels, the manner in which this is done for the moderated t-statistic allows one to specify a parametric form for the null distribution.
We begin by providing the technical details for the use of the moderated t-statistic in the context of fMRI data. Let be the COPE for subject i ∈ {1, …, n} and voxel v ∈ {1, …, V}. As before we assume that are drawn from the same population distribution . The distributional assumptions for and the sample variance for voxel v can be summarized as follows:
| (3) |
and
| (4) |
where represents a chi-square distribution with dv = n − 1 degrees of freedom.
Rather than smoothing over neighbouring voxels as in the pseudo t-statistic, here one uses an empirical Bayes approach. A scaled inverse chi-square prior is assigned to , i.e.
| (5) |
where the hyperparameters d0 and represent the prior degrees of freedom and location of the distribution, respectively. In a fully Bayesian approach one would choose these parameters. Here we instead take an empirical Bayes approach and estimate these parameters from the data. This approach provides consistent, closed form estimators of the hyperparameters d0 and s0 using information from other voxels.
We summarize the approach described by Smyth (2004) in the following. The marginal distribution of can be shown to follow a scaled F-distribution with degrees of freedom d0 and dv, i.e., . The distribution of is distributed as a constant plus Fisher’s z distribution (Johnson and Kotz, 1970), which is roughly normal with the first two moments expressed as follows:
| (6) |
| (7) |
where ψ(·) and ψ′(·) are the digamma and trigamma functions, respectively.
Let ev be the adjusted logarithm of sample variance of voxel v,
| (8) |
It has expected value,
| (9) |
and variance
| (10) |
The method of moment estimator for d0 can be obtained by solving
| (11) |
for d0 using Newton’s method. can subsequently be estimated by
| (12) |
Under this model, the posterior mean of given is expressed as follows:
| (13) |
Importantly, the term s0 is estimated using information from other voxels in the analysis. Hence, is the weighted average of the estimated variance from voxel v with the estimated variance obtained using information from the other voxels. Using this estimate allows us to construct the moderated t-statistic,
| (14) |
Under the null hypothesis H0 : βv = 0, the moderated t-statistic can be shown to follow a t-distribution with degrees of freedom dv + d0. Here the added degrees of freedom compared to the standard t-statistic reflects the extra information borrowed from the other voxels.
2.1.4. Locally moderated t-statistic
As described above, the moderated t-statistic borrows strength from voxels across the whole brain. However, we also recognize the sample variance is shrunk towards the pooled variance , which would be misspecified when the variance varies across brain voxels. The performance is expected to improve when applied to a local neighborhood, or alternately a functional parcellation of the brain. Inspired by the pseudo t-statistics approach where the variance estimates are smoothed over a local neighborhood, we also apply the moderated t-statistic in a search-light manner, where we only allow strength to be borrowed from voxels in a neighborhood Nv = {v′ | ∥xv – xv′∥ ≤ r}. The posterior mean of given shown in Eq. (13) is now estimated based on voxels within a neighborhood Nv. We refer to this option as locally moderated t-statistic to differentiate it from the version that uses whole-brain data.
The locally moderated t-statistic allows the estimates of hyperparameters of the prior distribution (5) to vary across voxels. The hyperparameters are denoted by d0v and , where the subscript v indicates the voxel, and are estimated with respect to the local neighborhood. The estimator of d0v can be derived by solving
| (15) |
where |·| is the cardinality, . The estimator of is
| (16) |
We recommend that the size of the neighborhood should be chosen to be relatively large. Estimators of d0v and obtained using small neighborhoods will suffer from the lack of efficiency and precision of the moment estimator. This, in turn, will lead to an excess of false positive rate, as shown in the results.
2.1.5. Cluster-based inference
Statistical maps can be thresholded using either a voxel-based or cluster-based approach. In this section we illustrate how the standard and moderated t-statistics can be used in the context of nonparametric cluster-based inference. In particular, we focus on the cluster-extent (Friston et al., 1996; 1994) and threshold-free cluster enhancement (TFCE) approaches (Smith and Nichols, 2009). Both approaches first compute a voxel-based statistic across the brain (in our application using either the standard or moderated t-statistic) to create a statistical map. The two approaches differ in how they utilize this map. The cluster extent approach thresholds the resulting statistical map using a cluster-defining threshold (p = 0.001 in our application). The thresholded image consists of clusters of contiguous voxels, the size of which are used to compute cluster-extent statistics. The TFCE statistic instead uses the un-thresholded statistical map, and is defined at a given voxel v as follows:
| (17) |
Here hv is the statistic value at voxel v, h is a cluster-forming threshold, and e(h) is the cluster extent at voxel v with cluster-forming threshold h. It is standard practice to set h0 = 0, E = 0.5 and H = 2 (Smith and Nichols, 2009).
For both approaches, we use a nonparametric procedure to create a permutation distribution under the null hypothesis of no effect. We use a similar procedure outlined in Nichols and Holmes (2002) and Noble et al. (2020). For a given permutation, each subject’s data is randomly ‘sign-flipped’. Using the sign-flipped data, voxel-based statistical maps are calculated using both the standard t-statistic and the moderated t-statistic, and the maximum cluster extent and maximum TFCE statistics are computed. This procedure is repeated for 1000 permutations, and the recorded statistics are used to form the null distribution and determine a threshold that allows for nonparametric cluster-based inference with appropriate FWER control.
Note that when performing cluster-based inference we do not evaluate the local moderated t-statistic due to the substantial computational burden involved. On a computation node with 40 cores, it takes about 10 h to complete a computation of 1000 permutations with the locally moderated t-statistics on the neighborhood sized r = 5. This makes it im-practical to use in practice, and we therefore do not consider it further in this context.
2.2. Data sets
The Human Connectome Project 500 subject release (HCP 500) consists of both structural and functional data from approximately 500 subjects. While the functional data include both resting state (rfMRI) and task-related (tfMRI) images of multiple tasks, in this report we focus on the tfMRI GLM contrast images provided by the HCP. All data were acquired on a Siemens Skyra 3T scanner at Washington University in St. Louis. For each task, two runs were acquired, one with a right-to-left and the other with a left-to-right phase encoding. Whole-brain EPI acquisitions were acquired with a 32 channel head coil with TR = 720 ms, TE = 33.1 ms, flip angle = 52 deg, BW = 2290 Hz/Px, in-plane FOV = 208 × 180 mm, 72 slices, 2.0 mm isotropic voxels, with a multi-band acceleration factor of 8. For a complete description of the data acquisition procedure see Van Essen et al. (2012).
Data was preprocessed according to the HCP ‘fMRIVolume’ pipeline (Glasser et al., 2013), which includes gradient unwarping, motion correction, fieldmap-based EPI distortion correction, brain-boundary-based registration of EPI to structural T1-weighted scan, non-linear registration into MNI152 space, grand-mean intensity normalization, and spatial smoothing using a Gaussian kernel with a FWHM of 4 mm.
Data analysis was performed using a general linear model (GLM). For each task, predictors (described below for each task) were convolved with a canonical hemodynamic response function to generate regressors. To compensate for slice-timing differences and variability in the HRF delay across regions, temporal derivatives were included and treated as variable of no interest. Both the data and the design matrix were temporally filtered with a linear high-pass filter (cutoff 200 s). Finally, the time series was pre-whitened to correct for autocorrelation in the fMRI data.
The primary datasets used in this paper are described in greater detail in Barch et al. (2013). Below follows a brief description. In addition, we created a fake dataset to evaluate the empirical false positive rate based on applying the working memory design matrix to resting-state data from the same subjects.
2.2.1. Working memory
Participants (n = 494) completed a version of the N-back task used to assess working memory. Within each run, four different stimuli types (faces, places, tools and body parts) are presented in separate blocks. Half of the blocks use a 2-back task and the other half a 0-back task. A short 2.5 s cue indicates the task type at the start of the block. Each of the two runs contains 8 blocks of 10 trials (2 s stimulus presentation, 500 ms ITI) and 4 fixation blocks (15 s each). Each block contains 2 targets, and 2–3 non-target lures. Eight predictors were included in the design matrix, one for each stimulus type in each of the N-back conditions. Each covered the period from the onset of the cue to the offset of the final trial. A linear COPE comparing 2-back vs. 0-back was used for further analysis.
2.2.2. Motor
Participants (n = 492) were presented with visual cues that ask them to tap their left or right fingers, squeeze their left or right toes, or move their tongue. Each block corresponds to one of the five movements and lasted 12 s, and is preceded by a 3 s cue. In each of the two runs, there are 13 blocks, with 2 tongue movements, 2 of each hand movement, 2 of each foot movement, and three 15 s fixation blocks. Five predictors were included in the design matrix for each movement, each covering the duration of the 10 movements trials (12 s), and the cue was modeled separately. A linear COPE comparing finger-tapping vs. baseline was used for further analysis.
2.2.3. Emotion processing
Participants (n = 483) were presented with blocks of trials that either asked them to decide which of two faces shown at the bottom of the screen matched the face at the top, or which of two shapes presented at the bottom matched the shape at the top. The faces had either angry or fearful expressions. Trials are presented in blocks of 6 trials (2 s stimulus presentation, 1 s ITI) of the same task (face or shape). Each block was preceded by a 3 s task cue (‘shape’ or ‘face’). Each of the two runs includes 3 face blocks and 3 shape blocks. Two different predictors were included in the design matrix, one corresponding to emotional faces and the other to the shape control condition. Each predictor covered a 21 s duration composed of a cue and six trials. A linear COPE comparing emotional faces vs. control was used for further analysis.
2.2.4. Gambling
Participants (n = 492) were asked to guess the number on a mystery card in order to either win or lose money. They are told that the number ranged from 1 to 9, and to guess whether the number on the mystery card number is greater or less than 5 by pressing one of two buttons. Feedback is the number on the card and either a green up arrow with $1 for reward trials; a red down arrow with $0.50 for loss trials; or the number 5 and a gray double headed arrow for neutral trials. The task is presented in blocks of 8 trials with mostly reward (6 reward trials |interleaved with either 1 neutral and 1 loss trial, 2 neutral trials, or 2 loss trials) or mostly loss (6 loss trials interleaved with either 1 neutral and 1 reward trial, 2 neutral trials, or 2 reward trials). In each of the two runs, there are 2 mostly reward and 2 mostly loss blocks, interleaved with 4 fixation blocks (15 s each). Two predictors were included in the design matrix to model mostly reward and mostly punishment or loss blocks, each covering the duration of 8 trials (28 s). A linear COPE comparing reward vs. punishment for gambling was used for further analysis.
2.2.5. Fake ‘working memory’
To establish the empirical error control of the methods we are evaluating, we also created null data in a manner similar to that described in Eklund et al. (2016). For each participant (n = 465) we re-ran the first level GLM analysis using the design matrix from the working memory task (see Section 2.2.1 for details) applied to the same subjects resting-state fMRI data (truncated to have the same length as the working memory data). As in Section 2.2.1 the linear COPE corresponding to the comparison “2-back vs. 0-back” was used for further analysis. However, in this case we don’t anticipate significant activation as the data and model are not linked.
2.3. Model evaluation
Throughout we assume that the population of interest consists of the full collection of roughly 500 subjects. For each task this allows us to compute population effect sizes at each voxel, based on all of the subjects in the population. This provides us with a benchmark that can subsequently be used for direct comparison with results obtained using data from a smaller subset of the population.
It is important to note that the t-statistic is sample size dependent, and relates to the presence of an effect (i.e., statistical significance), not its magnitude. Effect size, by contrast, is a unit-free description of the strength of an effect, independent of sample size (Chen et al., 2016; Reddan et al., 2017). It describes a findings practical significance, which in turn helps determine its clinical impact. This distinction is important because small effects can reach statistical significance given a large enough sample, even if they are unlikely to be of practical importance or replicable across diverse samples. There are multiple ways to compute effect size. Here we use a variant of Cohen’s d that can be computed at voxel v as the mean COPE (across subjects) divided by the standard deviation. Using our notation the effect size can be computed as follows:
| (18) |
Using these values, we group voxels into four different effect size categories (Geuter et al., 2018). Voxels are≤ placed in the ‘low’ group if 0.2 ≤ |θv| < 0.5, the ‘medium’ group if 0.5 ≤ |θv| < 0.8, and the ‘high’ group if 0.8 ≤ |θv|. These groupings are based on guidelines from Cohen (1988). All remaining voxels are placed in a ‘no effect’ group.
In the continuation, we consider the population-level results as our ‘gold standard’, and use these results as a stand in for the ground truth effect size at different voxels for the various tasks. To evaluate the reproducibility of small sample fMRI studies, we draw K = 100 different samples from the population at each of the following sample sizes: N = 10, 20, 40, 60, 80 and 100. This allows us to mimic the typical sample sizes used in studies performed by individual labs. Note that throughout we are sampling without replacement to enable an appropriate comparison with the non-parametric pseudo t-statistic. For each sample we perform a group analysis using the standard t-test, the pseudo t-test, the moderated t-statistic, and the locally moderated t-statistic. A series of different thresholds are applied to the resulting t-maps to assess significance: a voxel-wise threshold of p < 0.001 uncorrected; a voxel-based FWER corrected threshold at the p < 0.05 level; and two cluster-based FWER corrected thresholds at the p < 0.05 level. For the standard t-test, the moderated t-statistic, and the locally moderated t-statistic voxel-based FWER corrected p-values were obtained with a Bonferroni correction for the number of voxels. For the pseudo t-statistic, voxel-based FWER corrected p-values were calculated as the proportion of the max statistic null distribution that were as large or larger than the given statistic value. For the standard t-test and the moderated t-statistic, cluster-based FWER corrected p-values were obtained using both the cluster extent and TFCE approaches.
When computing the locally moderated t-statistic we use neighborhoods with radius r = 1, 3, 5, 7, 9. We begin by evaluating the false positive rate, power, and empirical FWER for each radius in order to determine which value to use in our analysis. For each sample size and method we study how a voxels effect size corresponds to its likelihood to be deemed active. Using the population effect size groups defined above, we measured the proportion of voxels that were deemed significant, as well as the proportion of voxels in each group that were active in more than 80% of samples. This allowed us to assess the false negative rate (under the assumption that voxels with this effect size should be deemed active) associated with each sample size and effect size, as well as the power to detect activation of a certain effect size. Further, using the ‘fake data’ described in Section 2.2.5 we evaluated the empirical false positive rate for each of the sample sizes and methods. Similar to Eklund et al. (2012, 2016), the FWER were estimated by determining the proportion of the K = 100 samples with any significant group activation. Under the assumption that the estimated FWER follows a binomial distribution, approximate 95% confidence intervals can be computed. This is given by , and for a FWER of e = 0.05 this corresponds to (0.73% 9.26%).
2.4. Implementation in R
We implemented both the moderated and locally moderated t-statistic in the R (R Core Team, 2019) software environment. The LIMMI R-package provides a set of functions for running linear models for medical images, adapting the framework of LIMMA to NIfTI images. The package has been developed so that users will have a quick and convenient way to apply the moderated t-statistic to fMRI data. Similar to the LIMMA package, there are specific functions for performing linear fitting and empirical Bayes fitting on both a global and local scale. Our package also allows users to compute in parallel by simply specifying the number of computing threads. It is freely available at https://github.com/muschellij2/limmi. Sample code is provided in the Appendix. Note installation of the LIMMI package from Github requires the package SummarizedExperiment, which is available on Bioconductor (Gentleman et al., 2004).
3. Results
Table 1 shows the number of voxels in each effect-size category for each task. The equivalent percentages are listed in parentheses. There is a clear discrepancy between tasks with regards to the proportion of voxels in each group. In the working memory, emotion, and gambling tasks, the majority of voxels (over 90%) have medium or lower effect sizes (|θv| < 0.8), whereas the motor task has a larger number of voxels (roughly 25%) with large effect sizes. Interestingly, for the gambling task less than 1% of all voxels are in the medium and large effect size groups.
Table 1.
The number of voxels in each effect-size group for each task. The percentages are listed in parentheses.
| Effect-size groups | |||||
|---|---|---|---|---|---|
| No effect | Small | Medium | Large | ||
| Tasks | WM | 77690 (49.05%) | 57655 (36.4%) | 19421 (12.26%) | 3613 (2.28%) |
| Motor | 35079 (22.15%) | 46217 (29.18%) | 37435 (23.64%) | 39648 (25.03%) | |
| Emotion | 75106 (47.42%) | 52498 (33.15%) | 17638 (11.14%) | 13137 (8.29%) | |
| Gambling | 129057 (81.49%) | 28504 (18%) | 775 (0.49%) | 43 (0.03%) | |
We begin by evaluating the optimal neighborhood size to use for the pseudo t-statistic and locally moderated t-statistic. Supplementary Figures S1 and S2 show results obtained using the locally moderated t-statistics approach with different neighborhoods and an uncorrected p-value thresholding at 0.001. The neighborhood size of r = 1 achieved the best performance in terms of false positive rate and power. Similar conclusions can be drawn from Supplementary Figures S1 and S2, which show equivalent results obtained using voxel-based FWER-correction at the 0.05 level. However, even though the smaller neighborhoods appear to outperform the larger ones, results shown in Supplementary Figure S5 indicate that the FWER control for small neighborhoods exceeds the nominal 5%, whereas the inference made using locally moderated t-tests with larger neighborhoods were conservative but controlled at the 5% level. Together, these results suggest using a neighborhood of r = 5, which we use as the default when presenting results below.
The top panel of Fig. 1 shows the estimated false negative rates for each task when using voxel-based FWER correction. The rate is higher when estimated with smaller samples across each task and effect size category. We note that the vast majority of voxels are not significant with N = 10 under FWER correction in each of the effect size groups across tasks. The locally moderated t-statistic approach yields the least number of false negative rates in all effect size categories except for the emotion processing task with N = 20, where the moderated t-statistic performs slightly better. The non-parametric pseudo t-statistic approach performed better than the standard t-statistic for small sample sizes (N = 20), but not for larger sample sizes.
Fig. 1.
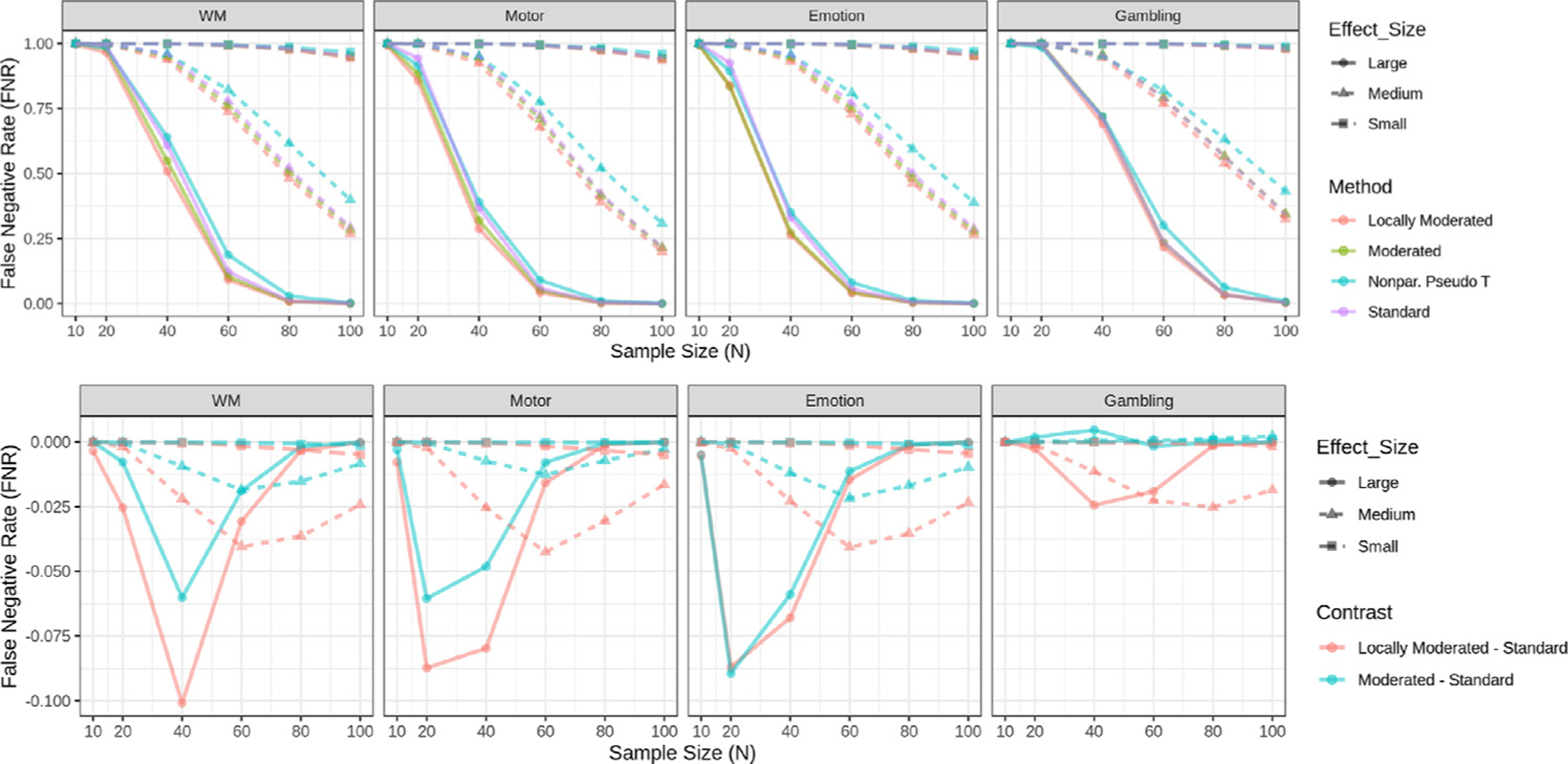
False negative rates for each task using voxel-based FWER-correction at the 0.05 level. (Top) Rates are shown for four different methods: standard t statistics, moderated t-statistics, locally moderated t-statistics with r = 5, and non-parametric pseudo t-statistics. Rates are stratified according to effect size group. (Bottom) The difference in false negative rate between moderated/locally moderated t-statistics and the standard t-statistic is shown for each task and effect size group. The results highlight the differences in results for small sample sizes. The results illustrate that locally moderated t-statistics performs significantly better than the other methods for small sample sizes. Note if two lines overlap their colors are mixed.
To aid in the visualization of differences between methods, the bottom panel of Fig. 1 highlights the differences in the estimated false negative rates between the moderated and standard t-statistics. Here the false negative rates for the standard t-statistic is subtracted from that of the moderated and locally moderated t-statistic. Thus, negative values indicate improved performance using the moderated approaches, and values close to zero indicate minimal difference. The locally moderated t-statistic significantly outperformed the standard t-statistic in all tasks and effect size categories, while the moderated t-statistic also generally performed better than the standard t-statistic, with the exception of the gambling task at N = 40. However, note that this task has an unusually small amount of voxels in the large effect size group. In certain situations, the difference between methods is substantial. For example, the false negative rate obtained using the locally moderated approach is roughly 15% less than the standard t-statistic approach for several of the tasks in the large effect size group for sample sizes between 20 and 40. In addition, the locally moderated t-statistic consistently outperforms the standard moderated t-statistic.
The top panel of Fig. 2 shows the proportion of voxels that are deemed significant with voxel-based FWER correction in at least 80% of samples, in other words, achieved 80% empirical power. We find that the vast majority of voxels are not consistently significant for N = 10 in each of the effect size groups across tasks, and hence the differences between methods are by default negligible. For larger sample sizes, the moderated and locally moderated t-statistic approach tend to outperform both the standard t-statistic and the pseudo t-statistic.
Fig. 2.
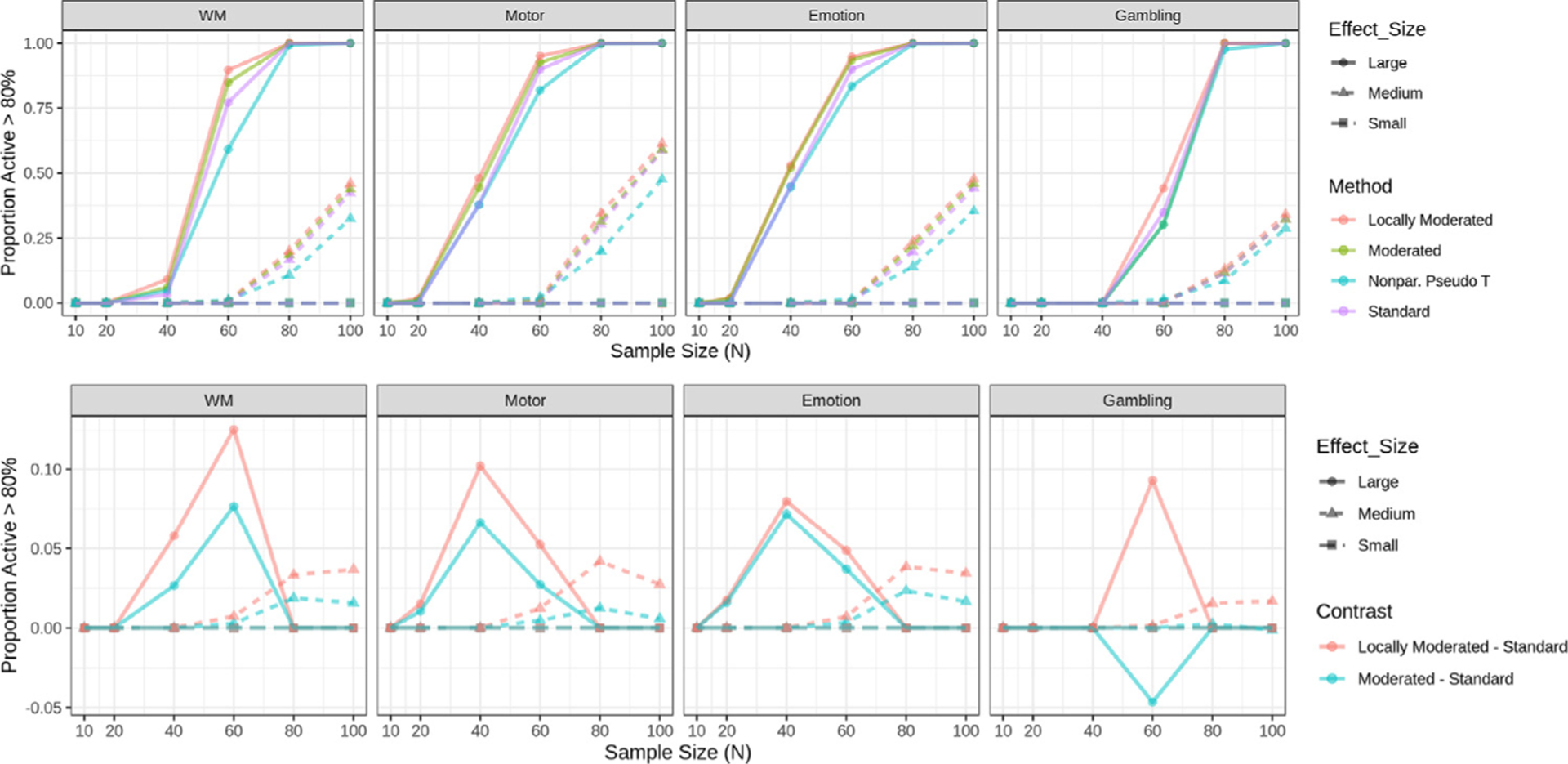
Proportion of active voxels in each task using voxel-based FWER-correction at the 0.05 level. (Top) Proportions are shown for four different methods: standard t-statistics, moderated t-statistics, locally moderated t-statistics with r = 5, and non-parametric pseudo t-statistics. Proportions are stratified according to effect size group. (Bottom) The difference in proportions between moderated/locally moderated t-statistics and the standard t-statistic is shown for each task and effect size group. The results show the proportion is always larger for locally moderated t-statistics, particularly for small sample sizes. Note if two lines overlap their colors are mixed.
The bottom panel of Fig. 2 highlights the differences in the estimated proportion of voxels that are deemed significant between the moderated methods and the standard t-statistic. Here the proportion for the standard t-statistic is subtracted from that of the moderated t-statistic and locally moderated t-statistic. Thus, positive values indicate improved performance by the moderated methods, and values close to zero minimal difference. Once again, the difference can be substantial. For example, for the motor task and large effect sizes locally moderated t-statistic outperforms the standard t-statistic by roughly 15% when N = 60. However, in rare cases, for example, the gambling task and large effect size group at N = 60, the moderated t-statistic approach is outperformed by the standard t-statistic (with the caveat that this task has an small amount of voxels with large effect sizes). In addition, the locally moderated t-statistic consistently outperforms the standard moderated t-statistic.
Fig. 3 shows a comparison of the empirical FWER estimated using the fake ‘working memory’ data. The standard t-test, moderated and locally moderated t-tests are valid at the nominal 5% level. The non-parametric pseudo t-statistic approach consistently has larger FWER than the other three parametric approaches, and exceeds the 5% level at large sample sizes (though still within the 95% confidence interval). This indicates that the moderated t-test approach helps address problems with power rather than lack of control for type-1 errors.
Fig. 3.
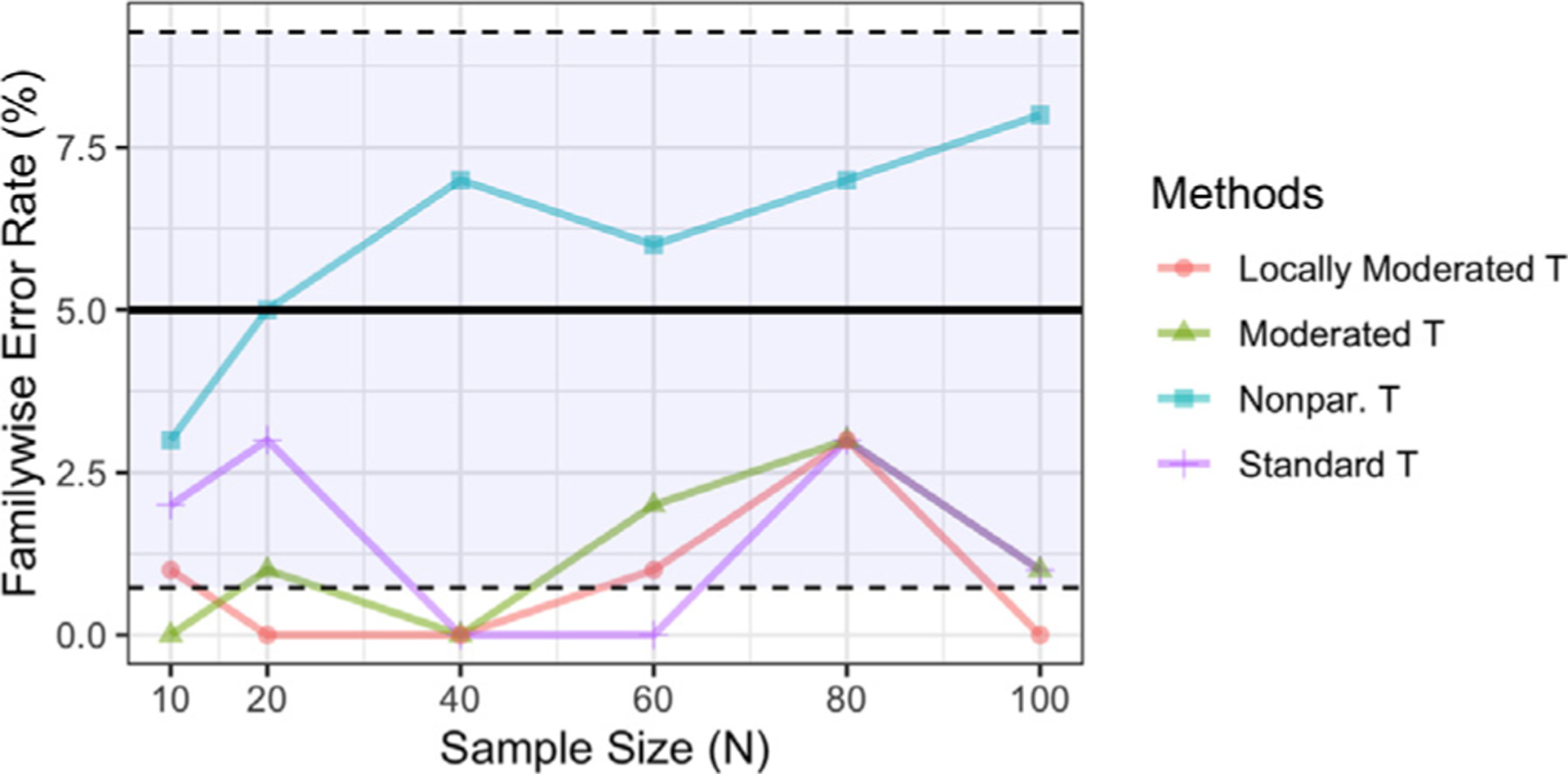
The empirical family-wise error rate control for each method estimated using the fake ‘working memory’ data. The FWER is controlled at the 5% level using voxel-based methods, indicated by the solid black horizonal line. Inference based on the standard t-statistic, moderated t-statistic, and locally moderated t-statistic with r = 5 are valid but conservative, whereas the non-parametric pseudo t-statistic increased FWER at large sample size. Note if two lines overlap their colors are mixed.
Figs. 4 –6 show equivalent results as described above when using cluster-based thresholding instead of voxel-based thresholding. Here we evaluate the cluster extent approach using either the standard or moderated t-statistic to create the initial voxel-based statistic map, and the TFCE approach using either the standard or moderated t-statistic. In contrast to voxel-based inference, cluster-based inference shows lower false negative rate and higher proportion of active voxels across the board for all tasks, effect size groups, and sample sizes. In addition, the TFCE approach consistently outperforms the cluster extent approach. This result is consistent with those found in Noble et al. (2020).
Fig. 4.
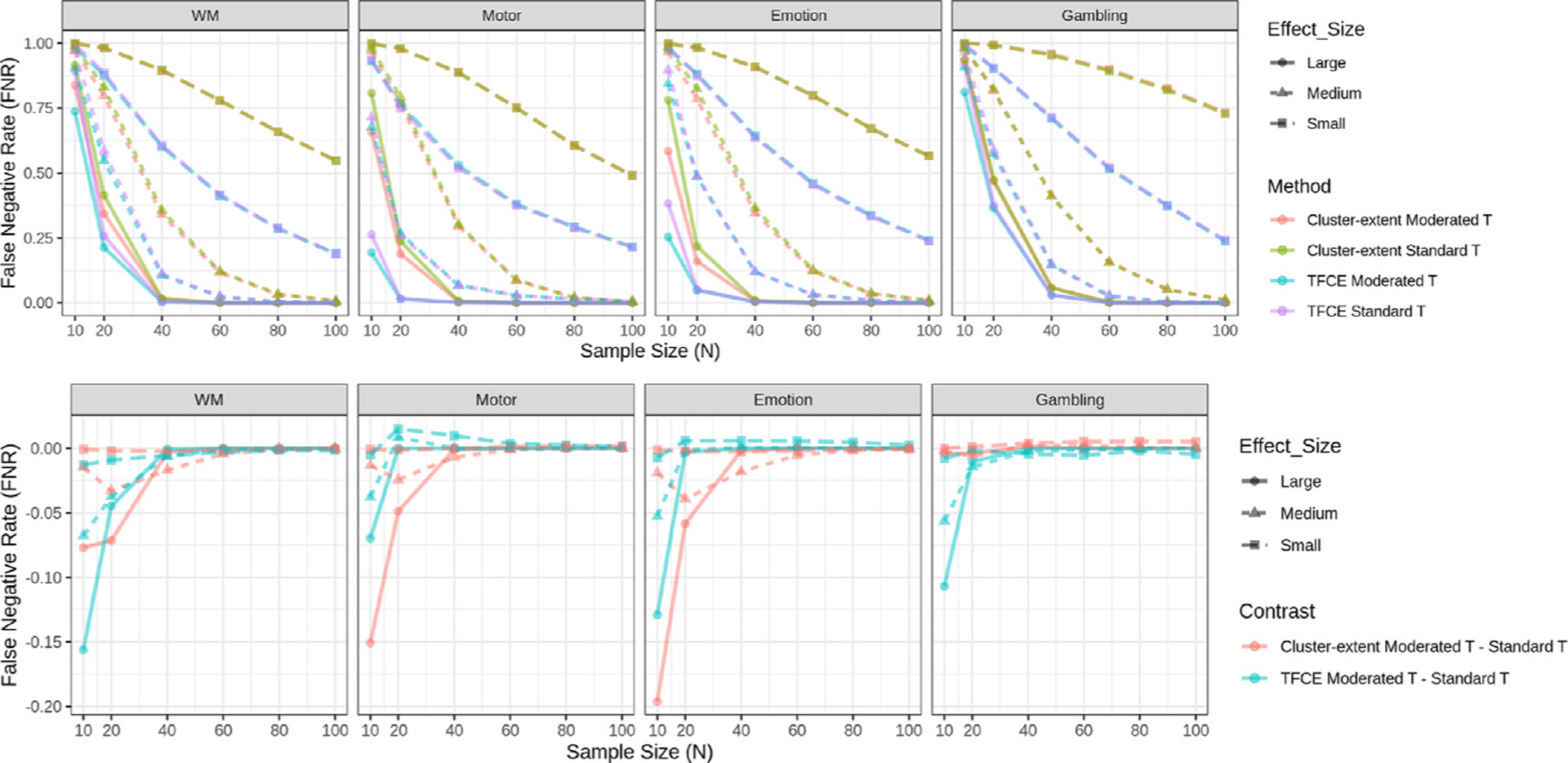
False negative rates for each task using cluster-based FWER-correction at the 0.05 level. We contrast two approaches, cluster extent with a cluster-defining threshold of p = 0.001 and TFCE. Further, standard and moderated t-statistics are combined with each of the cluster-wise methods giving rise to four combinations. (Top) Rates are shown for the four different combinations of methods. Rates are stratified according to effect size group. (Bottom) The difference in false negative rate between cluster extent/TFCE using the moderated t-statistic and cluster extent/TFCE using the standard t-statistic is shown for each task and effect size group. The results illustrate that moderated t-statistics improves the performance of cluster-based methods compared to when using standard t-statistics for small sample sizes, especially in the large effect-size group. Note if two lines overlap their colors are mixed.
Fig. 6.
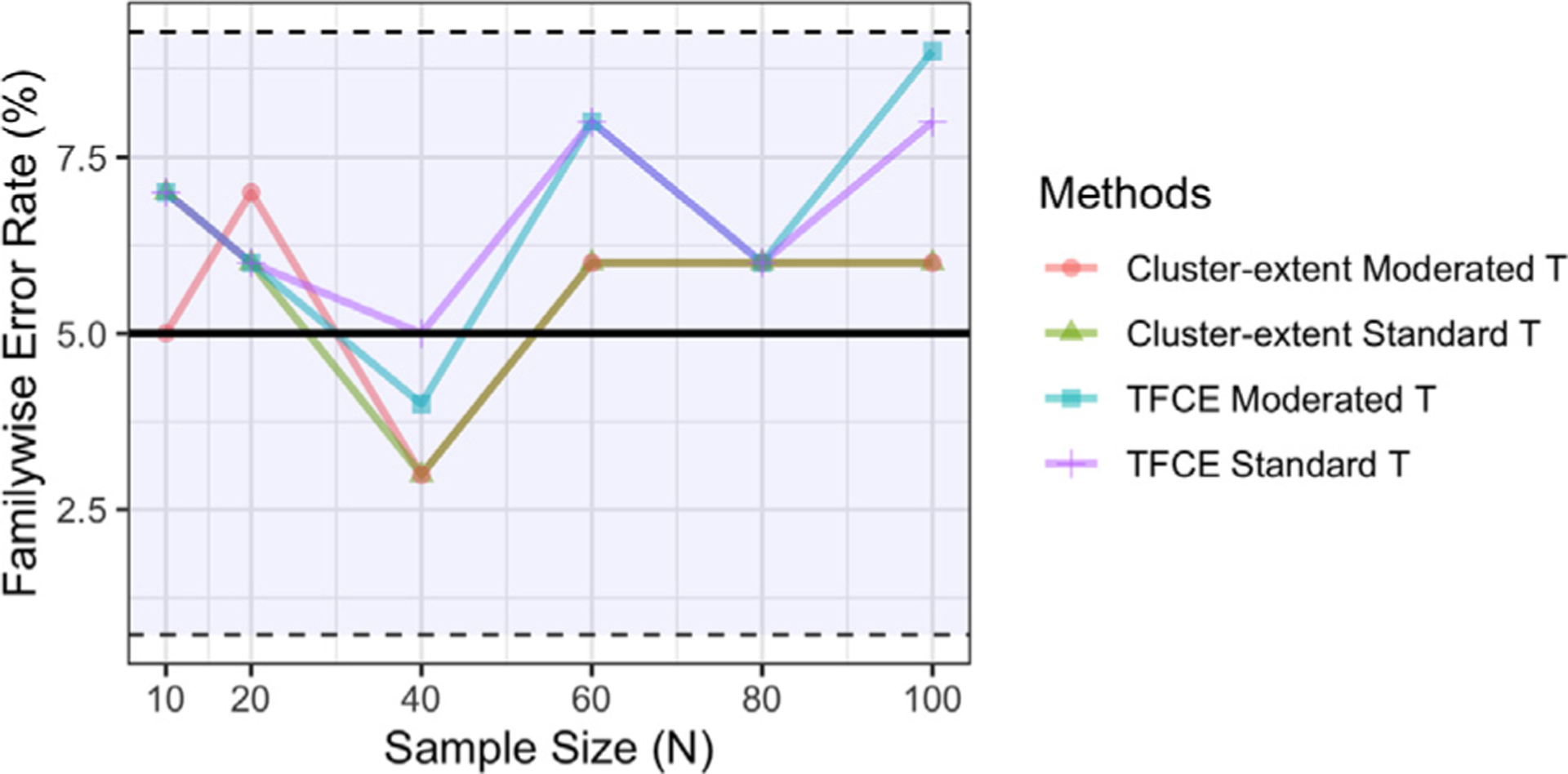
The empirical family-wise error rate control for each method estimated using the fake ‘working memory’ data. The FWER is controlled at the 5% level using cluster-based methods, indicated by the solid black horizontal line. The 95% confidence intervals are included as reference. Note if two lines overlap their colors are mixed.
Figure 4 shows the estimated false negative rates for each task when using cluster-based FWER correction. As expected, the rate is higher when estimated with smaller samples across each task and effect size category. The bottom panel highlights the difference in the estimated false negative rates between cluster extent (TFCE) using the moderated t-statistic and cluster extent (TFCE) using the standard t-statistic. In general, we find that combining cluster extent (TFCE) with the moderated t-statistic performs better than when combining it with the standard t-statistic. This is particularly true in the large effect-size group for small sample sizes (N < 40). For medium and small effect size groups the difference between methods is more negligible, with slight improvements using the moderated t-statistic when N = 10 for several tasks.
Fig. 5 shows the proportion of voxels that are deemed significant with cluster-based FWER correction in at least 80% of samples. The bottom panel highlights the difference in proportion between cluster extent (TFCE) using the moderated t-statistic and cluster extent (TFCE) using the standard t-statistic. In general, combining cluster-based procedures with the moderated t-statistic performs better compared to when using the standard t-statistic. For the large effect size group this improvement is particularly strong for small sample sizes (N < 40). For the medium effect size group improvement is smaller and more apparent at moderate sample sizes (N = 60). We find that for the working memory and gambling tasks, the vast majority of voxels are not consistently significant for N = 10 in each of the effect size groups across tasks, and hence the difference between methods are by default negligible.
Fig. 5.
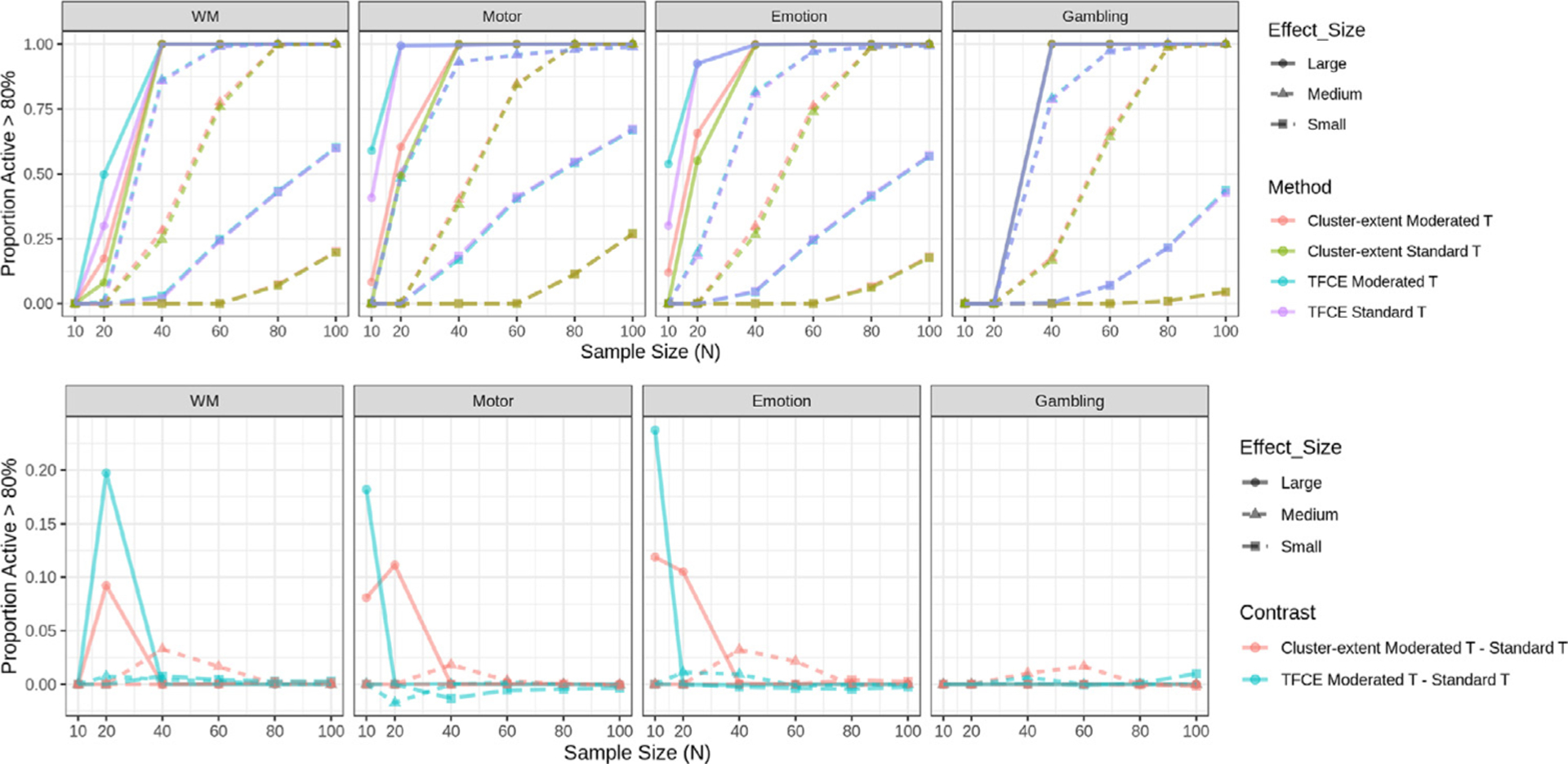
Proportion of active voxels in each task using cluster-based FWER-correction methods. We contrast two approaches, cluster extent with a cluster-defining threshold of p = 0.001 and TFCE. Further, standard and moderated t-statistics are combined with each of the cluster-wise methods giving rise to four combinations. (Top) Proportions are shown for the four different combinations of methods. Proportions are stratified according to effect size group. (Bottom) The difference in proportions between cluster extent/TFCE using the moderated t-statistic and cluster extent/TFCE using the standard t-statistic for each task and effect size group. The results show the proportion is larger when using the moderated t-statistic, particularly for small sample sizes in the large effect-size group. Note if two lines overlap their colors are mixed.
Fig. 6 shows a comparison of the empirical FWER estimated using the fake ‘working memory’ data. While all rates are within the 95% confidence interval, it should be noted that they are consistently higher than those observed for their voxel-based equivalents.
Finally for completeness, Figures S6 and S7 show similar results when thresholding at p < 0.001 uncorrected. Here the results point to a greater difference between the moderated and standard t-statistics at small sample size (i.e., N = 10) for the large effect size group. This is no doubt due to the increased number of significant results obtained in this setting.
4. Discussion
When working with data from studies with small sample sizes, directly using the standard t-statistic can be problematic, as difficulties obtaining an accurate estimate of the variance can lead to noisy t-statistic images and decreased power to detect effects (Nichols and Holmes, 2002). An early solution to this problem, proposed by Nichols and Holmes (2002), is the so-called pseudo t-statistic that spatially smooths the sample variances across voxels, thereby stabilizing their variability. However, the approach lacks a closed-form distribution to access significance and can therefore only be applied in non-parametric analysis.
In this paper we have introduced a moderated t-statistic to the neuroimaging community that has previously found wide usage in the genomics literature for dealing with problems related to small sample sizes. It was popularized through its inclusion in the R-package LIMMA (Ritchie et al., 2015), which is commonly used to analyze gene expression data arising from microarray or RNA-seq technologies. Here we investigated its performance using task-based fMRI data from the Human Connectome Project. Our results show that the moderated t-statistic outperforms both the standard t-statistic and the pseudo t-statistic in terms of both false negative rate and power for small sample sizes.
While both the moderated t-statistic and the pseudo t-statistic stabilize estimates by borrowing strength from neighboring voxels, they do this in different ways. While the pseudo t-statistic uses standard spatial smoothing, the moderated t-statistic uses empirical Bayes (or shrinkage) methods to borrow strength from other voxels to obtain a less noisy estimate of the sample variance. Importantly, in contrast to the pseudo t-statistic, under the null hypothesis, the moderated t-statistic can be shown to follow a t-distribution with augmented degrees of freedom, facilitating its use in a broader context than the pseudo t-statistic.
While empirical Bayes methods have found usage in the neuroimaging community (Chen et al., 2015; Mejia et al., 2015; Shou et al., 2014), the only paper we are aware of that has performed shrinkage on variance components is Su et al. (2008). A major difference between that work and ours, is that they do not shrink voxels within spatial neighborhoods, instead opting to shrink over all voxels in the brain. This highlights an important point when using either the moderated or pseudo t-statistics, namely determining the appropriate neighborhood size to use when borrowing strength. Our findings show (see Supplementary Figure S5) that the size of the neighborhood should be chosen to be relatively large. This is due to difficulties in estimating the hyperparameters for small neighborhoods, which leads to an increased false positive rate.
When performing multi-subject analysis using fMRI data it is common to use a two-level model where the first level deals with individual subjects and the second level deals with groups of subjects. The two-level model can be combined into a mixed-effects model, or alternatively be evaluated using a two-stage group analysis (Mumford and Nichols, 2009) where first level COPEs are modeled at the second level using an un-weighted, ordinary least squares (OLS) approach. While we note that the state-of-the-art solutions for group analysis in fMRI are based on mixed-effects models (see, for example, Chen et al., 2013; Lindquist et al., 2012; Woolrich et al., 2004), the focus of this paper is on second-level analysis within a two-stage group analysis as this is the approach most practitioners use. That said, we note that mixed-effects implementations exist for popular fMRI software packages, and these methods can improve estimation accuracy and increase power in some cases, particularly with dramatically unbalanced designs and/or heterogeneous variances across subjects (Mumford and Nichols, 2009).
We evaluated the performance of the moderated t-statistic both in the context of using voxel-based and cluster-based thresholding. In general, for each task and sample size, cluster-based thresholding had lower false negative rates and a higher proportion of active voxels compared to voxel-based thresholding. In particular, it is interesting to note that when using voxel-wise thresholding roughly 10–50% of large effect size voxels have 80% power with a relatively moderate sample size (n = 40). In contrast, the same power is attained for the large effect size voxels with a small sample size (n = 20). In addition, results were improved when using TFCE relative to cluster extent, which is consistent with findings in Smith and Nichols (2009) and Noble et al. (2020). Finally, central to you goals of this paper, we showed that using the moderated t-statistic instead of the standard t-statistic provided further improvement for the large effect size group at small sample sizes and for the medium effect size group at moderate sample sizes.
To facilitate easy application of our proposed approach to neuroimaging data, we provide an implementation in the R software language (R Core Team, 2019). Our package provides a set of functions for running linear models on NIfTI images. Thus, it provides an extension of the LIMMA package to medical images, providing users with a way to apply the moderated t-statistic to fMRI data.
While the presented approach has been proven to be useful in the small sample setting, we maintain that, if possible, researchers should ideally perform studies with larger sample sizes. However, we are cognizant that due to costs and resources this is often not a feasible solution. Thus, if one is faced with analyzing data from a study with small sample size (i.e., less than 40 subjects) then the use of the moderated t-statistic is an attractive option.
Supplementary Material
Acknowledgments
Data were provided by the Human Connectome Project, WU-Minn Consortium (Principal Investigators: David Van Essen and Kamil Ugurbil; 1U54MH091657) funded by the 16 NIH Institutes and Centers that support the NIH Blueprint for Neuroscience Research; and by the Mc-Donnell Center for Systems Neuroscience at Washington University. This research was supported in part by NIH grants R01EB016061 and R01EB026549 from the National Institute of Biomedical Imaging and Bioengineering and R01 MH116026 from the National Institute of Mental Health.
Footnotes
The median estimated sample size for a group fMRI study in 2015 was 28.5.
Supplementary material
Supplementary material associated with this article can be found, in the online version, at 10.1016/j.neuroimage.2021.118141
References
- Barch DM, Burgess GC, Harms MP, Petersen SE, Schlaggar BL, Corbetta M, Glasser MF, Curtiss S, Dixit S, Feldt C, et al. , 2013. Function in the human connectome: task-fMRI and individual differences in behavior. NeuroImage 80, 169–189. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Button KS, Ioannidis JP, Mokrysz C, Nosek BA, Flint J, Robinson ES, Munafò MR, 2013. Power failure: why small sample size undermines the reliability of neuroscience. Nat. Rev. Neurosci 14 (5), 365–376. [DOI] [PubMed] [Google Scholar]
- Chen G, Saad ZS, Britton JC, Pine DS, Cox RW, 2013. Linear mixed-effects modeling approach to fMRI group analysis. NeuroImage 73, 176–190. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen G, Taylor PA, Cox RW, 2016. Is the statistic value all we should care about in neuroimaging? bioRxiv http://biorxiv.org/content/early/2016/07/15/064212.full.pdf, http://biorxiv.org/content/early/2016/07/15/064212.10.1101/064212 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen S, Kang J, Wang G, 2015. An empirical Bayes normalization method for connectivity metrics in resting state fMRI. Front. Neurosc 9, 316. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cohen J, 1988. Statistical Power Analysis of the Behavioral Sciences. Lawrence Earlbaum Associates doi: 10.1234/12345678. [DOI] [Google Scholar]
- Efron B, Morris C, 1975. Data analysis using stein’s estimator and its generalizations. J. Am. Stat. Assoc 70 (350), 311–319. [Google Scholar]
- Eklund A, Andersson M, Josephson C, Johannesson M, Knutsson H, 2012. Does parametric fMRI analysis with SPM yield valid results? An empirical study of 1484 rest datasets. NeuroImage 61 (3), 565–578. doi: 10.1016/j.neuroimage.2012.03.093. https://www.sciencedirect.com/science/article/pii/S1053811912003825. [DOI] [PubMed] [Google Scholar]
- Eklund A, Nichols TE, Knutsson H, 2016. Cluster failure: why fMRI inferences for spatial extent have inflated false-positive rates. Proc. Natl. Acad. Sci 113 (28), 7900–7905. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Friston K, Holmes A, Poline J-B, Price C, Frith C, 1996. Detecting activations in pet and fMRI: levels of inference and power. NeuroImage 4 (3), 223–235. doi: 10.1006/nimg.1996.0074. https://www.sciencedirect.com/science/article/pii/S1053811996900749. [DOI] [PubMed] [Google Scholar]
- Friston KJ, Worsley KJ, Frackowiak RSJ, Mazziotta JC, Evans AC, 1994. Assessing the significance of focal activations using their spatial extent. Hum. Brain Mapp 1 (3), 210–220. doi: 10.1002/hbm.460010306. https://onlinelibrary.wiley.com/doi/pdf/10.1002/hbm.460010306. [DOI] [PubMed] [Google Scholar]
- Gentleman RC, Carey VJ, Bates DM, Bolstad B, Dettling M, Dudoit S, Ellis B, Gautier L, Ge Y, Gentry J, et al. , 2004. Bioconductor: open software development for computational biology and bioinformatics. Genome Biol 5 (10), R80. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Geuter S, Qi G, Welsh RC, Wager TD, Lindquist M, 2018. Effect size and power in fMRI group analysis. bioRxiv, 1–23295048. 10.1101/295048 [DOI] [Google Scholar]
- Glasser MF, Sotiropoulos SN, Wilson JA, Coalson TS, Fischl B, Andersson JL, Xu J, Jbabdi S, Webster M, Polimeni JR, et al. , 2013. The minimal preprocessing pipelines for the human connectome project. NeuroImage 80, 105–124. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holmes A, Friston K, 1998. Generalisability, random effects and population inference. NeuroImage 7, S754. [Google Scholar]
- James W, Stein C, 1961. Estimation with quadratic loss. In: Proceedings of the Fourth Berkeley Symposium on Mathematical Statistics and Probability, 1, pp. 361–379. [Google Scholar]
- Johnson NL, Kotz S, 1970. Distributions in Statistics: Continuous Univariate Distributions, 2. Wiley, New York, NY. [Google Scholar]
- Lindquist MA, Spicer J, Asllani I, Wager TD, 2012. Estimating and testing variance components in a multi-level GLM. NeuroImage 59 (1), 490–501. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mejia AF, Nebel MB, Shou H, Crainiceanu CM, Pekar JJ, Mostofsky S, Caffo B, Lindquist MA, 2015. Improving reliability of subject-level resting-state fMRI parcellation with shrinkage estimators. NeuroImage 112, 14–29. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mumford JA, Nichols T, 2009. Simple group fMRI modeling and inference. NeuroImage 47 (4), 1469–1475. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Munafò M, Noble S, Browne WJ, Brunner D, Button K, Ferreira J, Holmans P, Langbehn D, Lewis G, Lindquist M, et al. , 2014. Scientific rigor and the art of motorcycle maintenance. Nat. Biotechnol 32 (9), 871–873. [DOI] [PubMed] [Google Scholar]
- Nichols TE, Holmes AP, 2002. Nonparametric permutation tests for functional neuroimaging: a primer with examples. Hum. Brain Mapp 15 (1), 1–25. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Noble S, Scheinost D, Constable RT, 2020. Cluster failure or power failure? Evaluating sensitivity in cluster-level inference. NeuroImage 209, 116468. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Poldrack RA, Baker CI, Durnez J, Gorgolewski KJ, Matthews PM, Munafò MR, Nichols TE, Poline J-B, Vul E, Yarkoni T, 2017. Scanning the horizon: towards transparent and reproducible neuroimaging research. Nat. Rev. Neurosci 18 (2), 115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- R Core Team, 2019. R: A Language and Environment for Statistical Computing R Foundation for Statistical Computing, Vienna, Austria. https://www.R-project.org/. [Google Scholar]
- Reddan MC, Lindquist MA, Wager TD, 2017. Effect size estimation in neuroimaging. JAMA Psychiatry 74 (3), 207–208. [DOI] [PubMed] [Google Scholar]
- Ritchie ME, Phipson B, Wu D, Hu Y, Law CW, Shi W, Smyth GK, 2015. LIMMA powers differential expression analyses for RNA-sequencing and microarray studies. Nucleic Acids Res 43 (7), e47. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shou H, Eloyan A, Nebel MB, Mejia A, Pekar JJ, Mostofsky S, Caffo B, Lindquist MA, Crainiceanu CM, 2014. Shrinkage prediction of seed-voxel brain connectivity using resting state fMRI. NeuroImage 102, 938–944. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith SM, Nichols TE, 2009. Threshold-free cluster enhancement: addressing problems of smoothing, threshold dependence and localisation in cluster inference. NeuroImage 44 (1), 83–98. [DOI] [PubMed] [Google Scholar]
- Smyth GK, 2005. Limma: linear models for microarray data. In: Gentleman R, Carey VJ, Huber W, Irizarry RA, Dudoit S (Eds.). Bioinformatics and Computational Biology Solutions Using R and Bioconductor. Statistics for Biology and Health Springer, New York, NY. doi: 10.1007/0-387-29362-0_23. [DOI] [Google Scholar]
- Smyth GK, 2004. Linear models and empirical Bayes methods for assessing differential expression in microarray experiments. Stat. Appl. Genet. Mol. Biol 3 (1), 1–25. doi: 10.2202/1544-6115.1027. [DOI] [PubMed] [Google Scholar]
- Su S. c., Caffo B, Garrett-Mayer E, Bassett SS, 2008. Modified test statistics by inter-voxel variance shrinkage with an application to fMRI. Biostatistics 10 (2), 219–227. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Essen DC, Smith SM, Barch DM, Behrens TE, Yacoub E, Ugurbil K, Consortium W-MH, et al. , 2013. The WU-minn human connectome project: an overview. NeuroImage 80, 62–79. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Essen DC, Ugurbil K, Auerbach E, Barch D, Behrens T, Bucholz R, Chang A, Chen L, Corbetta M, Curtiss SW, et al. , 2012. The human connectome project: a data acquisition perspective. NeuroImage 62 (4), 2222–2231. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Woolrich MW, Behrens TE, Beckmann CF, Jenkinson M, Smith SM, 2004. Multi-level linear modelling for fMRI group analysis using Bayesian inference. NeuroImage 21 (4), 1732–1747. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


