Perturbing the energy landscape for improved packing during computational protein design

Abstract

The FastDesign protocol in the molecular modeling program Rosetta iterates between sequence optimization and structure refinement to stabilize de novo designed protein structures and complexes. FastDesign has been used previously to design novel protein folds and assemblies with important applications in research and medicine. To promote sampling of alternative conformations and sequences, FastDesign includes stages where the energy landscape is smoothened by reducing repulsive forces. Here, we discover that this process disfavors larger amino acids in the protein core because the protein compresses in the early stages of refinement. By testing alternative ramping strategies for the repulsive weight, we arrive at a scheme that produces lower energy designs with more native-like sequence composition in the protein core. We further validate the protocol by designing and experimentally characterizing over 4000 proteins and show that the new protocol produces higher stability proteins.

1 ∣. INTRODUCTION

Protein design software can be used to stabilize proteins, create novel protein structures and complexes, and introduce new functional sites into proteins.¹ Most protein design programs use rotamer-based side chain optimization to identify amino acid sequences that will stabilize the desired protein structure or complex.² In these simulations, the side chains are modeled using a set of commonly observed discrete conformations, referred to as rotamers, and the protein backbone is often held fixed while the sequence is optimized.³ As a consequence of these approximations, amino acid combinations that could be favorable with small adjustments to side chain and backbone positioning can be missed. The protein design field has been aware of these limitations for many years and a variety of strategies have been developed to increase sampling of alternative sequences and structures.^4-12 Common solutions include reducing repulsive forces to implicitly account for small structural changes that may relieve clashes, allowing small localized changes to the protein backbone during sequence optimization, and iterating between sequence design and larger-scale structure refinement.

In the molecular modeling program Rosetta, the FastDesign protocol uses a combination of reduced repulsive weights and sequence design iterated with structure refinement to facilitate the sampling of lower energy sequences and structures. FastDesign has been used to create novel protein tertiary structures, large macromolecular assemblies, and functional proteins with important applications in medicine and research.^13-16 FastDesign is derived from FastRelax, Rosetta's default protocol for perturbing protein models to sample lower-energy conformations.¹⁷ The FastRelax protocol iterates between fixed backbone side chain optimization (with rotamers) and gradient-based energy minimization of side chain and backbone torsion angles. Side chain optimization is performed using Monte Carlo sampling, in which each Monte Carlo move involves replacing a side chain rotamer at a random sequence position with a different rotamer.¹⁸ The change is accepted or rejected based on the calculated change in the energy of the protein and the Metropolis Criterion. The only difference between FastRelax and FastDesign is that rotamer substitutions during FastDesign are allowed to change the identity of an amino acid. Each round of rotamer optimization involves hundreds of thousands of rotamer substitutions. Following side chain optimization, the gradient of the energy function is used to simultaneously adjust backbone and side chain angles throughout the protein in order to further lower the energy of the protein. In general, the same energy function is used for the side chain sampling and the structure refinement.

FastRelax alternates between side chain optimization and gradient-based minimization four times (Figure 1). Empirical testing has established that ramping the repulsive forces from low to full strength over the four rounds (starting with a weight that is 2% of the final weight) encourages sampling of alternate conformations and after the final round with a full repulsive weight produces models with appropriately spaced atoms. The FastRelax protocol was parameterized for use in structure prediction. During structure prediction, the amino acid sequence is held fixed and the goal is to rapidly identify conformations that lower the energy of the protein.

FIGURE 1.

Amino acid distribution of native proteins and protein interfaces designed with legacy FastDesign

Until recently, the default FastDesign protocol in Rosetta used the same repulsive weight ramping scheme as FastRelax. The hypothesis was that the reduced repulsive weight in the early stages of design would allow larger amino acids to be placed with suboptimal packing, and then optimized in later rounds of structure refinement and sequence design. However, we demonstrate here that the protocol does not perform as expected. Instead, the protein collapses during the initial round of gradient-based minimization, which precludes the design of larger amino acids when the repulsive weight is increased. The result is that proteins are designed with an abundance of small amino acids, notably alanines, in their cores. To achieve native-like packing of protein cores we show that it is useful to lower the repulsive weight in the early rounds of design, but that the repulsive weight should be increased before performing structure refinement to prevent the protein from collapsing. We demonstrate that the reparameterized FastDesign protocol produces models with lower Rosetta energies and that these proteins are more stable when experimentally characterized.

2 ∣. METHODS

2.1 ∣. Rosetta energy function

The Rosetta energy function is a weighted sum of independent terms and has been described in detail previously.¹⁹ Critical components include an implicit solvation model, orientation dependent hydrogen bonding terms, short-range electrostatics, torsional energies and a modified 12-6 Lennard-Jones potential (LJ) that is used to model steric repulsion and attractive dispersion forces. The LJ potential is split into a repulsive component (“fa_rep”) and an attractive component (“fa_atr”). Each component receive its own independent weight in the Rosetta energy function. The division between “attractive” and “repulsive” is constructed so that changing the weights on the terms (fa_atr or fa_rep) does not change the minimum-energy distance between two atoms. In this study, and in the FastDesign protocol, changes are made to the weight on the fa_rep term. The fa_rep term uses different functional forms depending on the distance between the two atoms that are being evaluated. Near the minimum-energy distance (σ_i,j) fa_rep is based on the 12-6 LJ potential while at shorter distances the 12-6 potential is replaced with a linear term to avoid exceptionally high energies that can disrupt sampling protocols:

$$E_{\mathsf{fa}\_\mathsf{rep}}=\sum _{i,j}\phantom{\{}\left\{\begin{array}{cc}{m}_{i,j}{d}_{i,j}+b_{i,j}\hfill & d_{i,j}\le 0.6{\sigma }_{i,j}\hfill \\ {\epsilon }_{i,j}\left[{\left(\frac{{\sigma }_{i,j}}{d_{i,j}}\right)}^{12}-2{\left(\frac{{\sigma }_{i,j}}{d_{i,j}}\right)}^6+1\right]\hfill & 0.6{\sigma }_{i,j}<d_{i,j}\le {\sigma }_{i,j}\hfill \\ 0\hfill & {\sigma }_{i,j}<d_{i,j}\hfill \end{array}\phantom{\}}\right\}.$$

The fa_rep energy for a molecule is the sum of the repulsive energies between pairs of atoms (i, j) and depends on the distances between atoms (d_i,j), the minimum-energy distance between two atoms (σ_i,j), and the well depth (ε_i,j). The parameters for the linear potential used at short distances, m_i,j and b_i,j are constructed to avoid derivative discontinuities at the transition point, 0.6σ_i,j. The atomic radii and well depths used in Rosetta were parameterized using a variety of benchmarks including reproducing small molecule liquid-phase data.²⁰

The fa_atr term is also based on the 12-6 LJ potential but is modified to work in conjunction with fa_rep and is truncated at longer distances with a cubic polynomial function, f_poly(d_i,j), for computational efficiency.

$$E_{\mathsf{fa}\_\mathsf{atr}}=\sum _{i,j}\phantom{\{}\left\{\begin{array}{cc}-{\epsilon }_{i,j}\hfill & d_{i,j}\le {\sigma }_{i,\mathsf{j}}\hfill \\ {\epsilon }_{i,j}\left[{\left(\frac{{\sigma }_{i,j}}{d_{i,j}}\right)}^{12}-2{\left(\frac{{\sigma }_{i,j}}{d_{i,j}}\right)}^6\right]\hfill & {\sigma }_{i,j}<d_{i,j}\le 4.5\mathrm{Å}\hfill \\ f_{p\mathsf{oly}}(d_{i,j})\hfill & 4.5\mathrm{Å}<d_{i,j}\le 6.0\mathrm{Å}\hfill \\ 0\hfill & 6.0\mathrm{Å}<d_{i,j}\hfill \end{array}\phantom{\}}\right\}.$$

In the Rosetta energy functions, ref2015 and beta_nov16, the weight on E_{fa_atr} is 1.0 and the weight on E_{fa_rep} is 0.55. All of the weighting of the repulsive term discussed in this study refers to multiplying 0.55 by an additional factor between 0 and 1. Figure S6 shows plots of E_{fa_atr} and E_{fa_rep} using the standard ref2015 weights as well as what the function looks like when E_{fa_rep} is down weighted as it is in the early stages of FastDesign.

2.2 ∣. Protein structure sets

We assembled a variety of sets of protein models, each either “RC” for relaxed crystal (see below) or “Decoy” for computer-generated models. RC Monomer is a set of relaxed (see below) crystal structures of protein monomers between 80 and 120 residues in length and with resolutions better than 1.5 Å. RC Interface is a set of relaxed crystal structures of interfaces dimeric crystal structures downloaded from the PDBbind database with these filters: resolution must be better than 2.3 Å, the structures could not have more than two proteins chains and no ligand at the interface apart from HOH, SO4, CL, NA, MSE, and/or GOL.²¹ Decoy Interface structures were generated by using SEWING's AppendAssemblyMover^13,22 to design de novo 4-helical bundles that are designed to bind to the active form of the G protein, Gq alpha (see sewing_append_assembly.xml and accompanying flags in the Supporting Information). Decoy Monomer #1 was generated by running Rosetta's Abinitio demo without the final relax step. Decoy Monomer #2 structures come from a previous experiment¹⁷ in which Abinitio backbones were filtered based on downstream success with full-atom design. The goal of this set is to show that designs that previously performed well under legacy FastDesign do not get worse with our new variants. The Decoy Monomer #3 set was created by stripping the non-generated binding partners from the Decoy Interface set, leaving only the protein chain designed by SEWING. Each set contains between 40 and 60 structures.

2.3 ∣. FastDesign benchmarks

We had three different cases for the monomer sets: relax (fixed sequence), design (Rosetta was allowed to change the sequence of the protein), and core design (Rosetta was only allowed to change amino acid identities at core positions). The interface sets also had three cases: relax (fixed sequence), one-sided design (fixed sequence for one binding partner, the other binding partner could change sequence) and two-sided design (both chains can change sequences). We only ran protein sets that were logical for each case. For example, we did not run relax protocols on SEWING designs because there is no native amino acid identity for a SEWING-made structure.

2.4 ∣. Relaxing crystal structures

Each crystal structure was relaxed by running FastRelax 10 times and choosing the output structure with the lowest Rosetta energy. For this purpose, FastRelax is run with coordinate constraints (artificial energy bias that penalizes the protein's backbone for deviating from the starting position).

2.5 ∣. Reference energy fitting

For each repulsive weight, we ran optE_parallel (a Rosetta application) on 48 structures previously used for score function fitting.²³ This application performs fixed-backbone rotamer substitution, allowing all residue positions to change amino acids. This process is repeated many times, each time modifying the amino acids' reference energies in an attempt to optimize a weighted combination of sequence recovery (identity) and the cross entropy (Kullback-Leibler divergence) between the wild-type sequence profile seen over all 48 proteins against the sequence profile over all 48 models that Rosetta produces. optE_parallel was run three times for each repulsive weight and the outcome with the best score was used for PolarDesign2019.

2.6 ∣. De novo design of mini-proteins

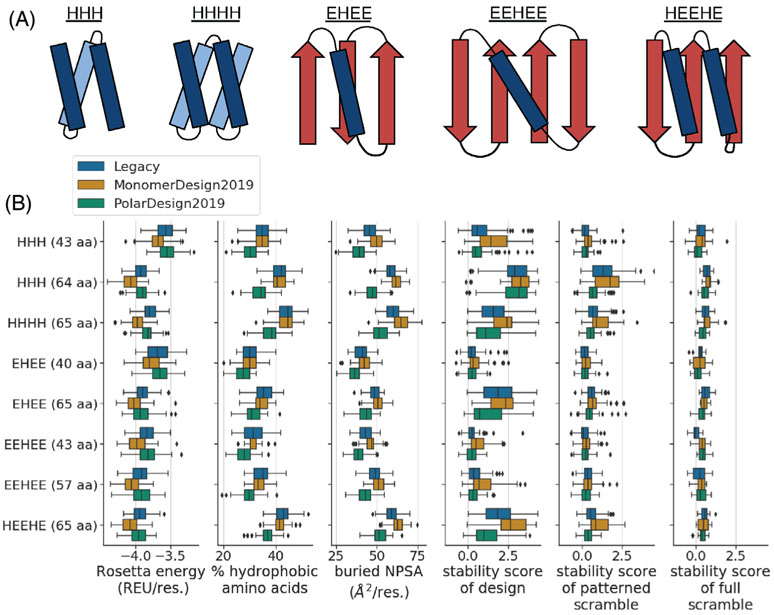
Our design protocol involved two basic steps: (a) generating three-dimensional mini-protein backbones and (b) designing amino-acid sequences onto those backbones. We designed eight pools of mini-proteins, where each pool had a unique topology (defined by the number and ordering of helices and strands) and length (Figure 5).

FIGURE 5.

Comparison of de novo mini-protein designs made using different FastDesign protocols. A, We designed eight structurally unique groups of proteins, where each group had a unique length and topology (see the y axis of the plots in panel B). These groups span five different topologies. This panel shows example diagrams of each topology, with helices in blue, strands in red, and titles indicating the order of helices (H) and strands (E) in primary sequence. B, The box plots compare designs as a function of structural group (y axis) and FastDesign protocol (hue of box). The x axis of each plot quantifies a different property of the designs. The first three box plots quantify computed biophysical properties including: the Rosetta energy of a design (normalized by protein length; REU: Rosetta Energy Units), the percent of amino acids in a design that are hydrophobic, and the amount of buried non-polar surface area (NPSA) in a design (normalized by protein length). The last three box plots show stability scores from the high throughput experiment, with the first plot showing data for designs and the other two showing data for scrambled controls. In all box plots, the box shows the quartiles of the distribution, the whiskers show the range of points that are within 1.5 times the interquartile range beyond the highest and lowest quartiles, and diamonds show outlier points outside of this range. We only show data for designs and controls with high-quality data from the high-throughput stability assay (Figures S2A and S7)

For seven of the eight pools, we performed step (a) using a “blueprint”-based approach.^24,25 A blueprint encodes several aspects of the desired protein structure, including: the length, secondary structure at each position, and pairings or register shifts between secondary structures. For each of the seven pools, we used a single blueprint to generated thousands of protein backbones. Each of these blueprints, and the code for backbone generation, are given in Supporting Information. Three of the blueprints were from Rocklin et al²⁶ (HHH 43aa, EHEE 40aa, EEHEE 43aa) and four are newly generated by us (EEHEE 57aa, HHH 64aa, EHEE 65aa, HEEHE 65aa). After generating pools of backbones, we then removed ones with low designability. We assessed designability using two main metrics, both of which are computed by Rosetta filters in the code used for backbone generation. The first metric, computed by the “percent_core_SCN” filter, quantifies the percent of residues in the protein's core layer, as determined using the side-chain neighbors criteria from Rocklin et al. To select for backbones with large cores, we discarded all backbones with filter values greater than the following topology-specific cutoffs: HHH 43 aa: −0.25; HHH 64 aa: −0.2; EHEE 40 aa: −0.2; EEHEE 43 aa: −0.2; EHEE 65 aa: −0.175; EEHEE 57 aa: −0.2; HEEHE 65 aa: −0.2. The second metric, computed by the “ss1” filter, quantifies the fraction of residues in the design that match the secondary structure specified in the blueprint. To select for backbones that closely matched the blueprint, we discarded all backbones with filter values less than the following topology-specific cutoffs: HHH 43 aa: 0.9; HHH 64 aa: 0.95; EHEE 40 aa: 0.91; EEHEE 43 aa: 0.94; EHEE 65 aa: 0.91; EEHEE 57 aa: 0.975; HEEHE 65 aa: 0.9. Finally, we applied a few topology-specific filters: For the EEHEE 57 aa topology, to help ensure proper sheet formation, we removed backbones that lacked a backbone-backbone hydrogen bond between sites 7 and 53. For the HEEHE 65 aa topology, to help promote structural compactness, we removed backbones where the distance between the C-alpha atoms of residues 3 and 30 was greater than 10 Å. After these filtering steps, for each of the seven pools, we randomly selected 100 backbones for downstream protein design.

For one of the eight pools of designs (the four-helix bundles, denoted HHHH in Figure 5), we performed step (a) by stitching together fragments of helices and loops using a method that is similar to the SEWING protocol.¹³ As input for this approach, we extracted libraries of helical fragments and loop-containing fragments from a set of ~12 000 de novo mini-protein designs determined to be stable using the high-throughput stability assay described below (designs included ones from Rocklin et al, as well as unpublished designs). Specifically, we curated a library of helical fragments that were all 18 amino acids in length, and a separate library of loop-containing fragments that were all 8 to 11 amino acids in length and included exactly three helical residues at each terminus. To further curate these libraries, we removed fragments that lacked close structural matches in the PDB. Specifically, for each 9 amino-acid window in each fragment, we determined if those amino acids aligned with a Cα RMSD of 0.4 Å or lower to at least one member of a library of 9 amino-acid fragments curated from the PDB. We then pruned our library of fragments to only include ones with PDB matches across all 9 amino-acid windows in the fragment. Next, we clustered the remaining fragments by structural similarity, where members of a cluster were alignable with a Cα RMSD of ~0.5 Å or lower, and chose one representative from each cluster with at least one member, resulting in final fragment libraries with 9 helices and 274 loops. PDB files of each fragment in these libraries are in Supporting Information.

Next, we assembled fragments into single-chain three-dimensional backbones that formed four-helix bundles and were 65 amino acids in length. We did so using a piecewise assembly process. Starting from an N-terminal helical fragment, we searched for compatible loop-containing fragments that could be stitched onto the C-terminus of the helix. We continued to grow the chain by assembling helical and loop-containing fragments in alternating order until we generated structures with four helices connected by three loops. At each assembly step, we considered two fragments to be compatible if the terminal two residues of the loop-containing fragment could be aligned to a consecutive pair of residues anywhere along the helical fragment with an RMSD of 0.3 Å or less, as computed over the N, Cα, and C backbone atoms of residues immediately adjacent to the overlapping residues being stitched together. We repeated this process many times using a random, combinatorial algorithm to generate hundreds of thousands of structurally diverse backbones.

Next, we curated the resulting four-helix-bundle backbones using two steps. First, we selected for compact backbones by removing ones that had a radius of gyration greater than 10.5 Å. Second, we selected for designable backbones based on a metric that quantifies the potential of pairs of sites to favorably interact with each other. To do so, we used a database of residue-pair interactions observed in structures from the PDB, as created in Fallas, et al.²⁷ We considered all interactions involving either alanine, phenylalanine, isoleucine, leucine, or valine at one site in the pair, and either phenylalanine, isoleucine, leucine, or valine at the other site in the pair. As in Fallas, et al, we then binned these interactions based on rigid-body transforms between amino-acid pairs, computed using the backbone N, Cα, and C atoms, with bin sizes of 0.5 Å for translational movements and 1° angular movements. We then used this database to evaluate the designability of each of our backbone from above. Specifically, for each pair of residues in a given backbone, we determined if the rigid-body transform between them fell into a bin that also had at least one “matching” residue-pair from the PDB-derived database. We discarded all backbones that had less than 110 residue pairs with “matches” summed over all residue-pairs in the backbone. After the above filtering steps, we randomly selected 100 backbones for downstream design of four-helix bundles.

After generating the eight pools of backbones from above (800 backbones total; 100 per pool), we then used Rosetta to design amino-acid sequences onto each backbone. We conducted this step independently for each combination of energy function and FastDesign protocol that we tested, using the exact same 800 backbones as input each time, so as to enable head-to-head comparisons. Supporting Information contains the code that we used for this step. The first three box plots of Figure 5C report various biophysical metrics that we computed for each protein design. To compute the Rosetta energy of a design, we first minimized the energy of the designed structure using FastRelax as implemented in the code in Supporting Information, and then computed the energy of the minimized structure. To compute the percent of hydrophobic amino-acids in each sequence, we computed the joint frequency of the amino acids: A, F, I, L, M, V, W, and Y. To compute the amount of buried NPSA in each structure, we used the BuriedSurfaceArea filter in Rosetta, as described in more detail in Supporting Information.

2.7 ∣. High-throughput experimental quantification of protein stability

We experimentally measured protein stability using the same method as Rocklin et al²⁶ with the following modifications. We conducted the experiments at the University of Washington BIOFAB (http://www.uwbiofab.org/). Oligonucleotides encoding the library of proteins to be tested were ordered from Agilent (oligonucleotides sequences are in Supporting Information). This library included the protein designs generated above, “scrambled” controls for each design, and 338 proteins from Rocklin et al, enabling us to assess experimental reproducibility with this previous study (the sequences of these 338 proteins are in Supporting Information). The proteins in this library varied in length from 40 to 65 amino acids. Before ordering oligonucleotides, we equalized the length of each protein by adding repeats of glycine-glycine-serine to the C-terminal end of the protein until its total length reached 65 amino acids. This, in turn, equalized the length of the oligonucleotides encoding each protein, helping to avoid length-dependent biases during downstream PCR and sequencing steps. The oligonucleotides were amplified by qPCR as previously described, but cloned into a modified version of the pETcon-3 yeast display vector (Rocklin et al, based on Addgene plasmid # 41522; http://n2t.net/addgene:41522; RRID:Addgene_41 522) which has been selected for increased resistance to trypsin and chymotrypsin. The sequence of the evolved plasmid is in Supporting Information and the plasmid is available upon request.

After transforming the plasmid library into yeast, we performed yeast-display proteolysis as previously described independently for both trypsin and chymotrypsin. For growth and induction of yeast cells, we used Standard Dropout (SDO -His -Trp -Ura) media. We purchased trypsin from Sigma-Aldrich (catalog # T4799) and stored it at a stock concentration of 13 mg/mL (546 μM) in PBS at −80°C. We purchased chymotrypsin from Sigma-Aldrich (catalog # C4129) and stored it at a stock concentration of 1 mg/mL (40 μM) in TBS +100 mM CaCl2 at −80° C.

For the six selection steps with trypsin, we used final concentrations of: 0.49, 1.4, 4.2, 13, 37, and 112 μM. For the six selection steps with chymotrypsin, we used final concentrations of: 0.06, 0.18, 0.55, 1.66, 4.97, and 14.92 μM. For each of these steps, we treated cells at an OD of 5.0. After protease treatment, we washed cells and labeled them with anti-myc-FITC as in Rocklin et al. In parallel, for each protease-treatment step, we ran internal controls to benchmark protease activity. As a FITC-positive control, we used a clonal EBY100 strain expressing a stabilized designed protein (AMA1-best, a gift of Gabriel Rocklin) and treated with either no protease (undigested), 8.3 μM trypsin, or 0.55 μM chymotrypsin. As a FITC-negative (fully digested) control, we used EBY100 transformed with an empty vector that expresses Aga2 without a myc tag and treated with Anti-myc-FITC. We then washed and labeled each control, as above.

After labeling cells, we used a SH800S Cell Sorter to separate FITC-labeled cells from dark cells for all of the above samples and controls, using FITC-labeled cells as input for deep-sequencing as described below. We placed the sorting gate so that 0.1% to 0.5% of the cells from the FITC-negative control passed the gate. Analysis of the controls with the AMA1-best controls allowed us to benchmark protease activity. To do so, we estimated the fractional digestion of each control using the maximum value of a kernel density estimate of the log-transformed FITC fluorescence distributions. We calculated the amount of digestion as: (partially_digested - fully_digested)/(undigested - fully_digested). For 8.3 μM trypsin, the fraction digested was between 0.21 and 0.24. For 0.55 μM chymotrypsin, the fraction digested was between 0.06 and 0.08.

Following these selection steps, the protocol uses deep sequencing to quantify the abundance of each protein design at each step. We prepared the libraries for sequencing as previously described.²⁶ We did so using an Illumina NextSeq550 using a 300-cycle midoutput kit configured for paired-end 150 base-pair reads. The raw sequencing data is available on the Sequence Read Archive under BioProject ID PRJNA607543. Supporting Information gives the SRA accession numbers for each sample. Next, the raw experimental data is used to infer stability values for each protein design. We did so using a computational pipeline adapted from Rocklin et al and available at the GitHub repository: https://github.com/Haddox/prot_stab_analysis_pipeline. A Jupyter notebook that runs this pipeline is available in Supporting Information. As in Rocklin et al, we independently inferred stability scores trypsin and chymotrypsin. Figure S5A shows that stability scores were correlated between the two proteases, showing that our measurements were largely reproducible. The stability scores in Figure 5 report the minimum score between the two proteases. Figure S5C shows that stability scores from our experiment were also correlated with stability scores from Rocklin et al for the 338 sequences common to both experiments, demonstrating reproducibility between our studies.

2.8 ∣. Alternate score function fitting

We aimed to test the durability of the new FastDesign methods by using them with a novel score function. We took the individual score terms from beta_nov16 (the score function used to design the proteins measured in Figure 5), and refit the term weights using the exact method laid out in Park, et al.²⁰ The results of this new score function can be seen in Figures S2 and S4.

3 ∣. RESULTS AND DISCUSSION

3.1 ∣. Characterization of the legacy FastDesign protocol

We first noticed that the FastDesign protocol in Rosetta was biased towards placing smaller amino acids in the protein core when purposely attempting to overpack a previously designed four-helix bundle protein (“DRNN”)²⁸ in order to test if increasing the volume of the hydrophobic core would promote cold denaturation. With the goal of favoring larger amino acids in the protein core, we lowered the weight on the repulsive term in the Rosetta energy function during the last round of sequence optimization of FastDesign. The repulsive weights were left at their default values (ie, reduced) for the earlier rounds of sequence optimization and minimization in FastDesign (Table 1). Lowering the weight on the repulsive term in the Rosetta energy function lowers the penalty for bringing atoms closer than their van der Waals radii, but does not change the most preferred interaction distance between two atoms (see Methods, Section 2). Surprisingly, we found that even with the repulsive weight lowered to 50% of its standard value for the last round of design, we were not observing a significant increase in the size of amino acids placed in the protein core. This result led us to examine what was happening during the early rounds of FastDesign.

TABLE 1.

The repulsive ramping scheme used by legacy FastDesign and our new parameterized set of weights, MonomerDesign2019

Round	1a	1b	2a	2b	3a	3b	4a	4b
Legacy	0.02	0.02	0.25	0.25	0.55	0.55	1.00	1.00
MonomerDesign2019	0.06	0.09	0.28	0.32	0.57	0.63	1.00	1.00

Note: Side chain optimization steps (ie, “Packing”) are labeled with an “a,” minimization steps (gradient-based minimization of backbone and side chain torsion angles) are labeled with a “b.” Each step is annotated with the relative repulsive weight for that round, where a value of 1.0 is equal to the weight used for the default Rosetta score function (ref2015).²⁰

The first stage of legacy FastDesign involves sequence design with a repulsive weight set to 2% of its final value followed by minimization with the same repulsive weight. As was expected, after the first stage of sequence design the core of DRNN was populated with larger amino acids (Table 2). Since the protein core was overpacked at this stage we thought that the subsequent minimization step would adjust the backbone to make room for the larger amino acids. Instead, the protein collapsed by a small but significant amount. Residues on neighboring helices came closer to each other and the radius of gyration for the protein went from 14.4 to 14.0 Å. The repulsive weight was so low during minimization that any penalties accrued from bringing atoms closer than their van der Waals distances was compensated for by a large gain in attractive forces between atoms that are not immediately adjacent to each other.

TABLE 2.

Properties of the protein DRNN while progressing through the steps of legacy FastDesign

FastDesign step	Relative radius of gyration (%)	DRNN core-residue sequence
Native	100	L V I V W I V M V L I M V L
After round 1	97.2	L I W L F L W L L L W W W W
After round 2	96.7	A A L V M V M I V A A A A L
After round 3	96.5	A A L V M V M I V A A A A L
After round 4	97.2	A A L V M V M I V I A A A L

Note: Steps are labeled in concurrence with Table 1. Radius of gyration is reported relative to the native state. Amino acid identities are reported for core (buried) residues of DRNN.

The second stage of legacy FastDesign involves another round of sequence design followed by gradient-based minimization but with a higher repulsive weight than the first round (25%). Since DRNN had collapsed during the first stage, the sequence design in the second stage populated the core residues with an abundance of small amino acids, especially alanine, to avoid clashes. The minimization step further optimized contacts but maintained a collapsed structure to keep the smaller amino acids adjacent to each other. The third and fourth stages of FastDesign further refined the sequence and backbone but did not significantly change the character of the amino acids in the protein core. The final sequences were enriched in alanines in the core.

Surprised by our results with DRNN we sought to test FastDesign on a larger set of proteins. As a benchmark set, we chose 52 smaller proteins (80-120 residues) with crystal structures with resolutions lower than 1.5 Å (a list of the proteins is provided in Supporting Information). We ran FastDesign to redesign each protein's core 10 times and examined the sequences and structures of the design models.

To gauge the compactness of the models we measured the radius of gyration ratio (“RG ratio”), which divides the radius of gyration of the designed protein by that of the input structure. A value less than one means that the designed protein is more compact that the native structure. We measured an average value of 0.97 ± 0.004 for the redesigns.

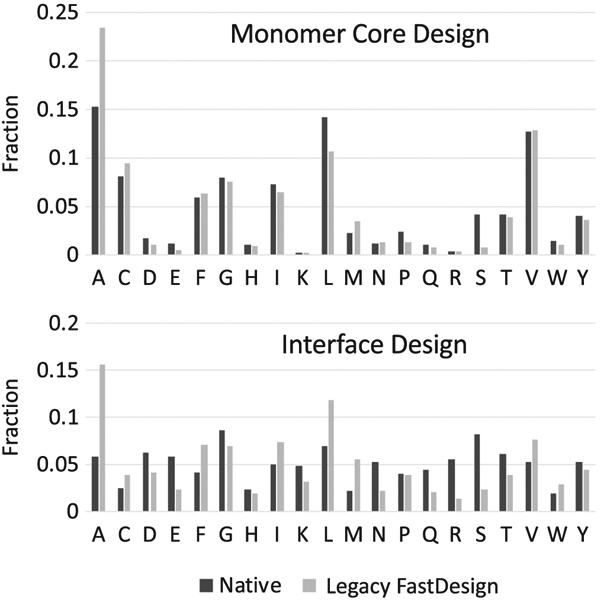
We additionally measured the percentage of core residues that were designed to be alanine. Rosetta defines a residue as “core” if its C-alpha atom is within 10 Å of 18 or more C-alpha atoms from other residues. In the native input structures 15.3% of the core residues were alanine while in the models output by FastDesign 23.4% of the core residues were alanine. Figure 1 compares the amino acid distributions of the native protein cores and the protein cores after being designed by FastDesign. While the smaller cysteine was also overrepresented (disulfides were not allowed), isoleucine, leucine, tyrosine and tryptophan were underrepresented in the design sequences. These results confirmed that the behavior that we observed with DRNN was a general problem with the FastDesign protocol. As illustrated in Figure 2A, the very low repulsion weight during the first stage of gradient based minimization induces the protein to collapse by a small amount, which leads to the placement of an abundance of alanines in the subsequent design steps.

FIGURE 2.

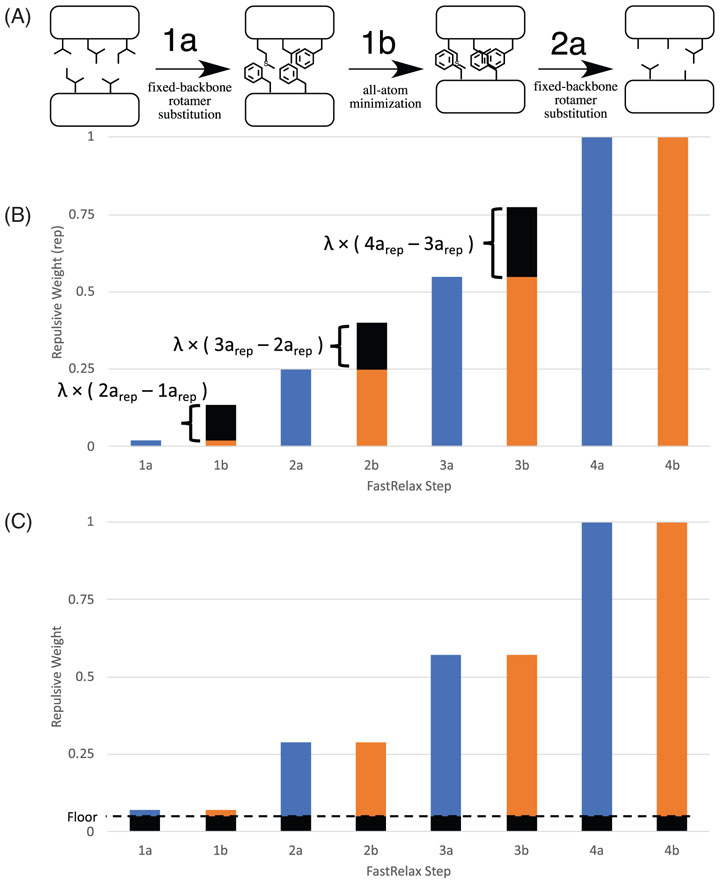
Adjusting the repulsive weighting scheme used by FastDesign. During FastDesign iterative rounds of rotamer-based sequence optimization (1a, 2a, 3a, 4a) and gradient-based minimization of backbone and side chain torsion angles (1b, 2b, 3b, 4b) are used to identify low energy sequences and structures. To promote sampling of alternative sequences and structures the weight on the repulsive term in the Rosetta energy function is ramped up with each subsequent stage. A, Despite placing large amino acids in the core during the first design step (stage 1a), legacy FastDesign is biased towards placing small amino acids in the protein core during later stages of design because the protein collapses during the first minimization step, which occurs with a very low repulsive weight (stage 1b). B and C, To reduce FastDesign's bias for small amino acids, the weights on the repulsive term in the Rosetta energy function were adjusted by sampling two hyperparameters: lambda and floor. The lambda parameter (panel B) adjusts the repulsive weight of the minimization steps (1b, 2b, …) so that the repulsive weight is higher than the previous packing step, but less than the next packing step. The original (ie, legacy) repulsive weights for each stage are shown in blue (packing) and orange (minimization) and shown in black is the increase in repulsive weight provided by the lambda term. Panel C illustrates the effect of the floor parameter which adds a similar amount to the repulsive weight of each stage (shown in black)

We also tested if legacy FastDesign is predisposed to design smaller amino acids when redesigning naturally occurring protein-protein interfaces. The FastDesign protocol was run on 27 naturally occurring protein complexes allowing mutations to be introduced on both sides of the interface. During the minimization step of FastDesign the relative position of the two protein chains was allowed to change in addition to the backbone and side chain torsion angles within the two proteins. The results were even more skewed than what we observed for designing protein monomers (Figure 1). The fraction of residues that were designed to be alanine increased from 5% to 15% and valines and leucines were also overrepresented. Similar to what we observed with designing monomers, the RG of the complexes decreased during the first step of FastDesign (a RG ratio of 0.95) and never returned to their starting values. In the interface design benchmarks it is also notable that legacy FastDesign when used with the default Rosetta energy function designs fewer polar amino acids than are observed at naturally occurring interfaces.

3.2 ∣. Reparameterizing FastDesign

Based on our benchmarking studies with native proteins and protein interfaces we speculated that the FastDesign protocol could be improved by reparameterizing the repulsive weights used in the earlier stages of the protocol. As extensive work has been done recently to optimize the standard energy function in Rosetta,^19,20 we did not explore changing the energy function used for the final round of design and minimization. This allowed us to use the Rosetta energies of the final design models to compare the quality of different ramping schemes. More effective sampling of sequence and conformational space should lead to lower energy designs.

FastDesign consists of four rounds in which each round involves rotamer-based sequence design followed by gradient-based minimization of backbone torsion angles. Within a round of legacy FastDesign, the same repulsive weight is used for the sequence design and the minimization stages (Table 1). In reparameterizing the repulsive weights we sought to test two types of perturbations to the existing parameters: (a) uniformly raising the repulsive weights of both the design and minimization stages in the early rounds of FastDesign and (b) increasing the repulsive weight of each minimization stage relative to the preceding design stage to specifically disfavor the collapse of the backbone during the minimization stage. To accomplish these goals we constructed two parameters, floor and λ, that can be used to systematically to vary the repulsive weights used during FastDesign. The floor parameter can vary from 0 to 1 and pads each FastDesign step with an increase to the repulsive weight (Figure 2B). The λ dimension can also vary from 0 to 1 and only applies to the minimization steps of FastDesign. λ interpolates the repulsive weights between the neighboring packing steps, such that a larger value of λ results in a weight more similar to the subsequent packing step (Figure 2C).

Equations (1) and (2) describe how the repulsive weights of various rounds are changed by these new parameters. For these equations, i denotes a round of FastDesign and is limited to the first three rounds; the fourth and final round of FastDesign always uses a repulsive weight of 1.0. f_pack(i) denotes the original (legacy) repulsive weight for the rotamer substitution portion of round i, g_pack(i) denotes the new repulsive weight for the rotamer substitution portion of round i, and g_min(i) denotes the new repulsive weight for the minimization portion of round i.

$$g_{pack}(i)=floor+(1-floor)f_{pack}(i),$$ (1)

$$g_{min}(i)=(1-\lambda )g_{pack}(i)+\lambda g_{pack}(i+1).$$ (2)

We constructed the repulsive weight for a particular stage of minimization (g_min(i)) to be dependent on the repulsive weight of g_pack(i) and g_pack(i + 1) so that it would it would be constrained to be between these two values and the repulsive weight would always increase with each subsequent stage of FastDesign.

We performed a grid search of these two dimensions on 10 different design scenarios, each explained in more detail in the “Protein Sets” subsection of methods. We aimed to maximize diversity in the design cases in order to represent the wide variety of applications that FastRelax and FastDesign can be applied to. For modeling protein monomers, we performed three types of tests: structure refinement with a fixed amino acid sequence, design simulations where all of the residues were allowed to mutate, and design runs where only the core residues could mutate. These tests were performed on both native crystal structures and computer-generated models. For modeling protein complexes, we also performed three types of tests: two-sided interface design (mutations were permitted on both chains), one-sided interface design (mutations were restricted to one chain), and structure refinement of the complex with a fixed sequence.

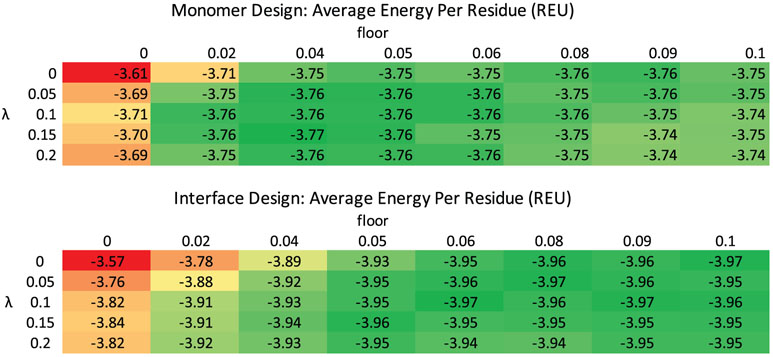
FastDesign ran on each case 10 times for each structure (only five times each for interfaces). Each design scenario and parameter sweep produced a heatmap of Rosetta energies, examples of which are shown in Figure 3. We identified the set of parameters that generated the lowest energy models for each case and used that information to construct four relax scripts that cover all cases: InterfaceDesign2019 (floor = 0.06, λ = 0.10), InterfaceRelax2019 (floor = 0.05, λ = 0.05), MonomerDesign2019 (floor = 0.04, λ = 0.15), and MonomerRelax2019 (floor = 0.02, λ = 0.15), as shown in Table SI1. All cases benefited by introducing a non-zero floor or λ independently, but a mixture of a non-zero floor and a non-zero λ gave the best results. In general, for all of the test sets, once floor and/or lambda were increased above 0.02 and 0.05 respectively, energies remained fairly similar and favorable for alternative parameter sets. From these results it is evident that the key change to the repulsive parameters was the increase in the repulsive weight for the first minimization step (“1b”) from 0.02 in legacy FastDesign to >0.08 in the reparametrized data sets. As evidenced by more native-like RG ratios (see next paragraph) in the redesigns, the greater than 4-fold increase in repulsion weight during the first minimization step is reducing chain collapse and allowing the design of models with lower energies.

FIGURE 3.

Adjusting the repulsive weighting scheme produces lower energy design models. Average Rosetta energies per residue (Rosetta Energy Units, more negative is favorable) for FastDesign runs performed with different values assigned to the hyperparameters floor and lambda. The top table is from the RC monomer design benchmark set and the bottom table is from the RC two-sided interface design benchmark. Results for the legacy FastDesign protocol (floor = 0, lambda = 0) are shown in the top left portion of the table. The individual cells are colored such that the least favorable values for each table are red and the most favorable values are green

The results for all design scenarios are summarized in Table 3. The Rosetta energies improved for all cases when using the new FastDesign protocols compared to legacy FastDesign. Relax cases resulted in a 2% improvement in Rosetta energy per residue, design cases resulted in a 6% improvement, and partial design cases (one-sided interface design and monomer core redesign) resulted in an 8% improvement. These are large improvements considering that hundreds of thousands of independent design simulations are frequently performed with Rosetta when designing proteins de novo in order to identify models that are a few percentages lower in energy than what could be achieved with fewer trajectories. RG ratios became closer to 1.0 in 6 of the 10 cases and unchanged in three of the remaining cases. “Decoy Monomer Design” was the only case in which the RG ratio of the MonomerDesign2019 result was further from 1.0 than that of the legacy FastDesign result. The computer-generated backbones used for that test set are not necessarily optimal, and therefore it is reasonable that they may need to shrink to form well packed proteins. In fact, all of the test cases that use native crystal structures as the starting point (and thus have physically realizable backbone configurations) had improved RG ratios with the new protocol compared to the old legacy protocol.

TABLE 3.

Results of running new protocols on our diverse collection of design cases. In the “relax” simulations the sequence is not varied

		Energy per residue (REU)		Radius-of-gyration ratio		Percent alanine at designable positions
Set	Case	Old	New	Old	New	Native	Old	New
RC monomer	Design (core positions)	−2.81 ± 0.05	−2.96 ± 0.06	0.97 ± 0.06	1.00 ± 0.06	14.7%	28.4%	13.9%
RC monomer	Design	−3.61 ± 0.05	−3.77 ± 0.05	0.96 ± 0.06	0.99 ± 0.06	6.6%	16.2%	5.6%
RC monomer	Relax	−2.78 ± 0.06	−2.85 ± 0.07	0.99 ± 0.06	0.99 ± 0.07
Decoy monomer #1	Relax	−2.70 ± 0.03	−2.73 ± 0.03	0.98 ± 0.002	0.98 ± 0.002
Decoy monomer #2	Relax	−2.39 ± 0.03	−2.43 ± 0.04	0.99 ± 0.001	1.00 ± 0.001
Decoy monomer #3	Design	−3.55 ± 0.01	−3.63 ± 0.02	1.00 ± 0.007	1.04 ± 0.007		13.1%	6.1%
RC interface	TWO-SIDED DESIGN	−3.57 ± 0.05	−3.97 ± 0.05	0.98 ± 0.001	0.99 ± 0.001	5.5%	17.6%	7.3%
RC interface	One-sided design	−3.25 ± 0.06	−3.57 ± 0.06	0.99 ± 0.001	1.00 ± 0.001	5.8%	20.4%	7.3%
RC interface	Relax (interface positions)	−3.06 ± 0.06	−3.15 ± 0.05	0.99 ± 0.001	1.00 ± 0.001
Decoy interface	One-sided design	−3.35 ± 0.005	−3.68 ± 0.005	0.99 ± 0.0003	0.99 ± 0.0002		18.8%	6.6%

Note: “RC” and “Decoy” refer to relaxed crystal structures and computer-generated backbones respectively. For each case, we show the scores with the legacy (Old) protocol and the MonomerDesign2019/InterfaceDesign2019 (New) protocols. For design cases we include the percent of residues at designable positions that end up being alanine. For interface cases, we only analyzed residues at the interface of the two chains for all three metrics. Note, the native alanine percentage is omitted for computationally-generated backbones because they have no native sequence identity.

Another dramatic improvement observed for the new FastDesign protocol is the more native-like placement of alanines at buried positions. When redesigning the core of native proteins legacy FastDesign places alanine at 28% of the residues while the new protocol reduces this to 14%, which is very similar to the 15% observed for native proteins. With one-sided interface design, the fraction of alanines was reduced from 20% to 7% (6% native).

3.3 ∣. Ramping reference weights

Although finding models with lower Rosetta energies, the new FastDesign schemes still did not closely match naturally occurring frequencies for some of the amino acids (Figure S1). Alanine levels came closer to native-like levels, but large hydrophobic amino acids became over-sampled and polar/charged amino acids were under-sampled.

The amino acid frequencies generated by Rosetta's design protocols depend on a set of reference values that are assigned to the 20 amino acids as part of the standard full atom energy function. Each amino acid type has its own unique reference value that is correlated with the average energy of that amino acid when placed in a favorable environment. If the reference value is raised for a particular amino acid, then that amino acid will be placed less frequently in design simulations. The reference values for the default energy function in Rosetta were parameterized by performing fixed backbone design simulations on a set of naturally occurring protein crystal structures and setting the weights so that native-like amino acid frequencies were observed. During legacy FastDesign as well as the FastDesign schemes described above (MonomerDesign2019 etc…), the reference values remain at their default values throughout all the design stages. We hypothesized that to achieve more native-like amino acid distributions from a FastDesign simulation it may be important to have reference values customized for each stage of FastDesign. As the repulsive weight is varied, it will change what constitutes a favorable energy for the different amino acids. To test the hypothesis, we fit custom reference values for each stage of FastDesign (see Methods, Section 2). As predicted, this approach generates amino acid distributions that more closely match native-like proteins and contain a higher fraction of polar amino acids than is observed when the stage-specific reference values are not used (Figure S1). We refer to this variant of FastDesign as PolarDesign2019 because it introduces a higher percentage of polar amino acids than MonomerDesign2019.

Figure 4 compares the Rosetta energies of designs created by PolarDesign2019 and MonomerDesign2019 with designs created with legacy FastDesign. PolarDesign2019 averages −0.41 REU/residue better than the legacy FastDesign in the case of two-sided interface design, while InterfaceDesign2019 averages −0.42 REU/residue of improvement. Both methods achieve comparable Rosetta energies.

FIGURE 4.

Comparison of new FastDesign protocols with Legacy FastDesign for three design cases. Each point shows the average Rosetta score (normalized by residue count) that results from running FastDesign on a different protein. The black diagonal line represents an equal score for the new protocol and legacy protocol. Points below the line represent protein structures that score better with the new protocol than the legacy protocol

3.4 ∣. The new FastDesign protocol improves Rosetta's ability to design stable de novo mini-proteins

Above, we describe how the new FastDesign protocols increase Rosetta's ability to recover native sequences during design and produces models calculated to have more favorable energies. Next, we sought to test these protocols by designing and experimentally characterizing de novo designed proteins. A recently developed high-throughput method makes it possible to quantify the stability of thousands of mini-protein designs (40-65 amino acids) in a single experiment.²⁶ In this assay, a design's stability is measured as a function of its ability to withstand cleavage by proteases. Specifically, a library of designs is displayed on the surface of yeast, with each cell expressing many copies of a single design. Next, cells are treated with a protease for a short time to cleave susceptible designs, where unfolded designs are expected to be more susceptible than stably folded ones. Cells with uncleaved designs are then enriched using flow cytometry, and deep sequencing of libraries before and after selection is used to quantify how much each design was enriched or depleted upon selection. This process is repeated multiple times with increasing protease concentrations, and the resulting data are used to estimate the protease resistance of each design, quantified as an EC50 value. Some sequences are inherently more resistant to proteases than others. To account for this, a model from Rocklin et al is used to predict what a design's EC50 value would be if the protein were in the unfolded state.²⁶ Ultimately, a design's “stability score” is computed as its experimentally observed EC50 value divided by the predicted EC50 value of the designed sequence in the unfolded state. In this study, we report stability scores in log10 space, such that positive values indicate that the design's observed EC50 value is higher than predicted for the unfolded sequence. Using this approach, we compared the legacy FastDesign protocol and two of the new protocols (MonomerDesign2019 and PolarDesign2019) in their ability to design stable de novo mini-proteins, experimentally testing hundreds of designs per protocol.

Our design approach involved two main steps. First, we generated three-dimensional protein backbones lacking amino-acid sequences. Specifically, we generated a total of 800 backbones that were evenly distributed among eight structural groups, each with a defined topology and length (Figure 5). These groups were highly diverse, spanning five topologies and, for some topologies, multiple lengths. Second, we used FastDesign to design amino-acid sequences onto each of the 800 backbones. We conducted this second step independently for each FastDesign protocol, using the exact same 800 backbones as input each time so as to enable a head-to-head comparison between protocols.

Based on our findings from redesigning native proteins, we expected the new protocols to give rise to de novo designs with lower, more favorable Rosetta energies. Figure 5B shows that designs made with MonomerDesign2019 do in fact have much lower energies than ones made with the legacy protocol (see the left-most box plot). Interestingly, designs made with PolarDesign2019 tend to have worse energies than ones made with MonomerDesign2019, indicating that the reference-energy-ramping technique hinders Rosetta from discovering low-energy designs in this particular design task.

The differences in Rosetta energies suggest large biophysical differences between designs. Above, when re-designing native proteins, we observed that the new protocols introduced fewer alanines during design, resulting in better packing. Following this trend, MonomerDesign2019 also introduced fewer alanines in the de novo design task (Figure S3). Figure 5B shows that the percentage of hydrophobic amino acids in designed sequences is similar between MonomerDesign2019 and the legacy protocol (see the second box plot from the left), suggesting that the decrease in the number of alanines is coupled with an increase in the number of bulkier hydrophobic amino acids. As might be expected from this trend, designs made with MonomerDesign2019 tend to have higher levels of buried non-polar surface area (NPSA) compared with designs made using the legacy protocol (see the third box plot from the left). As we restricted hydrophobic amino acids from being designed on the surface of proteins, this result suggests that MonomerDesign2019 produces designs with larger hydrophobic cores. There are also large biophysical differences between designs made with MonomerDesign2019 compared to PolarDesign2019. For instance, Figure 5B shows that designs made using PolarDesign2019 have a much lower percentage of hydrophobic amino acids, coupled with lower levels of buried NPSA. Overall, each FastDesign protocol produced biophysically unique pools of designs.

Next, we wondered whether these biophysical differences corresponded with differences in folding stability. To address this question, we experimentally measured the stability of the designs using the high-throughput stability assay from Rocklin et al.²⁶ Figure 5B shows the results of this experiment (see the fourth boxplot from the left). Most of the designs have positive stability scores, indicating that they are predicted to be more protease-resistant than if they were unfolded. However, there is also a large amount of variation in stability scores both within and between design groups. For instance, in some groups (eg, EHEE 40 aa; EEHEE 43 aa, EEHEE 57aa), almost all designs have low stability scores near zero. In these cases, Rosetta largely failed to produce stable designs, reflecting the challenging nature of designing stable mini-proteins with these topologies. Indeed, designs from these topologies also had low success rates in Rocklin et al.²⁶ In contrast, Rosetta was more successful at designing stable proteins in the other structural groups, in which many designs reached stability scores of >1.0, and some even reached values of >2.0, indicating that the observed EC50 values are >10 or >100 times higher, respectively, than predicted for corresponding unfolded sequences. Across all structural groups, the proteins designed with MonomerDesign2019 were more stable than ones designed with the other two protocols, suggesting that MonomerDesign2019 is the most effective design protocol in this context.

In the same experiment, we also measured the stability of two kinds of control sequences. First, for each design, we created a new protein sequence by shuffling the designed sequence while preserving the hydrophobic and hydrophilic patterning across all sites, as well as the positioning of glycines and prolines. Second, for a subset of designs, we created a second control sequence by fully shuffling the designed sequence without any patterning constraints. We refer to these controls as “patterned scrambles” and “full scrambles,” respectively. Figure 5B shows the distribution of stability scores for the controls (see the two right-most box plots), and Figure S6 shows the data for designs and controls plotted side-by-side to aid with the comparison. As expected, most controls have low stability scores near zero. In structural groups where Rosetta largely failed to design stable proteins, the stability scores of controls are largely similar to the stability scores of designs, indicating that any observed stability likely arises merely from sequence composition and patterning. However, in structural groups where Rosetta was more successful at design, the controls tend to be much less stable than designs (see the right-most box plot), confirming that the stability of these designs does not just arise merely from sequence composition and patterning, but from the designed sequence-structure relationship.

Interestingly, some of the controls, particularly the patterned scrambles, had stability scores greater than zero. Although it may seem unexpected for a scrambled sequence to be stable, there are multiple reasons why this might arise. First, as described above, the patterned scrambles still retain certain patterns from the designed amino-acid sequence. It is not surprising that fixing glycine and proline at turn residues and placing hydrophobic amino acids at core positions results in proteins with low stability some percentage of the time. Indeed, some scrambled controls from Rocklin et al also had positive stability values, and in a classic study with helical bundles Hecht and co-workers demonstrated that binary patterning (ie, nonpolars in, polars out) without explicit consideration of packing is sufficient to create folded proteins in some scenarios.²⁹ In line with this idea, fully scrambled sequences tend to have low stability scores near zero in all structural groups examined, suggesting that the higher stability of certain groups of patterned scrambles is tied to their patterning. Second, the apparent stability of some scrambles could also arise from experimental artifacts, including experimental noise or inaccuracies in the model used to predict the stability of sequences in their unfolded state. However, these experimental artifacts seem unlikely to account for the large stability differences between designs and scrambles, since they would be expected to affect both groups equally.

Within some structural groups, patterned scrambles from one design protocol have systematically higher stability values than controls from the other protocols. In these cases, the stability of patterned scrambles varied between design protocols in a way that correlated with design stability. This raises the question of whether the differences between design protocols are merely due to sequence composition and patterning. However, the between-protocol stability differences for controls is often less than the differences for designs, indicating that the former cannot completely account for the latter. In addition, we designed and tested a second set of designs where this problem is less of a concern. We made the designs in Figure 5B with the current Rosetta energy function. However, we also made another set of designs using a variant of this energy function with reference energies that were fit using a different protocol (see Methods, Section 2). Designs made using this second energy function had differences in amino-acid composition relative to designs in Figure 5B. Figure S2C shows the results of testing these designs in the high-throughput stability assay. Once again, designs made using MonomerDesign2019 tend to be more stable than designs made using the other two protocols. This time, however, fewer controls reached high stability values, further suggesting that differences between protocols cannot be explained by sequence composition and patterning alone.

Why do proteins made with MonomerDesign2019 tend to be more stable than proteins made with the other design protocols? The same study that established the high-throughput assay from above used it to measure the stability of thousands of de novo mini-protein designs.²⁶ They then searched for correlates of design stability among dozens of biophysical features. One of the strongest correlates of stability was buried NPSA: proteins with more of this feature tended to be more stable. In our study, this same feature strongly correlates with stability differences between design protocols: a comparison of the box plots quantifying design stability and buried NPSA in Figure 5B shows a striking pattern, where between-protocol differences in buried NPSA are often closely mirrored in design stability. This pattern suggests that the success of MonomerDesign2019 in this design task is largely rooted in its ability to produce proteins with larger hydrophobic cores. It also suggests that the lower success rate of PolarDesign2019 is rooted in its tendency to incorporate more polar amino acids into designs.

Thus, it appears that PolarDesign2019's increased preference for polar amino acids, which boosts its performance in re-designing native proteins, actually decreases its performance in designing stable de novo mini-proteins. This conflicting pattern points to an interesting difference between our two design benchmarks. Native proteins are typically much larger than mini-proteins, are not usually optimized for stability, and evolve under a complex mixture of selective pressures. It makes sense, therefore, that a protocol optimized for designing native-like sequences might not be optimal for designing stable mini-protein sequences. Thus, not only have we improved FastDesign's performance across two different design benchmarks, but we have also identified strengths and weaknesses in our two new protocols, which should help guide the field in deciding which one to use to meet their own particular design objectives.

Finally, it is notable that Rosetta energy is also predictive of between-protocol differences in mini-protein stability. In this task, MonomerDesign2019 consistently produced designs with more favorable energies across all structural groups, allowing proteins to reach lower points in their computationally modeled energy landscapes. Before experimentally measuring the actual stability of designs, it was unclear whether these computational predictions would be correct, as current macromolecular forcefields still have many inaccuracies. However, these predictions were largely in agreement with our experimental measurements, helping to validate the accuracy of Rosetta's energy function and that MonomerDesign2019 is able to design proteins with more favorable energies. A caveat of these results is that the high-throughput assay involves measuring a protein's stability as a function of its susceptibility to proteases when displayed on the surface of yeast, where factors other than folding stability (eg, oligomerization propensity) might also affect protease susceptibility.

4 ∣. CONCLUSION

Efficient sampling of protein conformational and sequence space is challenging because small perturbations to either the structure or sequence can lead to large spikes in energy. In our study we confirm that sampling can be enhanced by dampening repulsive energies in the early stages of refinement, but also demonstrate that the specific pattern of repulsive weight ramping can have large effects on the types of amino acids that are favored in the protein core and the energies of the final design models. In particular, we found that using very low repulsive weights during the first stage of structure refinement can induce the protein model to collapse by a small amount, which favors the placement of smaller amino acids during subsequent rounds of rotamer-based sequence design. By testing a large set of alternate repulsive weight ramping protocols, we identified schemes that produce design models with lower calculated energies and a more native-like distribution of alanines in protein cores and at protein interfaces.

We also demonstrated that using amino acid reference values customized for the early stages of the FastDesign protocol (ie, when the repulsive weight is reduced) changes amino acid usage in the final design models. This is despite the fact that the same energy function and amino acid reference values are used for the final sequence optimization stage in all the FastDesign design protocols that we computationally benchmarked. This result highlights that favoring a particular amino acid sequence in the early stages of FastDesign can lock that sequence in, as the subsequent structure refinement steps adjust the backbone to be favorable for that sequence. We experimentally tested proteins designed with custom reference values for each stage of FastDesign (PolarDesign2019) and proteins designed with just the standard Rosetta reference values used at each stage of FastDesign (MonomerDesign2019). The sequences designed with MonomerDesign2019 were, in general, more hydrophobic and, consistent with previous findings, these proteins were more stable as judged by resistance to proteases. However, many of the PolarDesign2019 sequences also folded and these proteins had a more native-like distribution of amino acids. It is not straightforward to label one of the protocols as being better as different projects in protein design can have different goals. In some cases, it may be important to maximize solubility while in other cases protein thermostability may be paramount.