Convolutional Neural Network Analysis of Two-Dimensional Hyperfine Sublevel Correlation Electron Paramagnetic Resonance Spectra

Abstract

A machine learning approach is presented for analyzing complex two-dimensional hyperfine sublevel correlation electron paramagnetic resonance (HYSCORE EPR) spectra with the proficiency of an expert spectroscopist. The computer vision algorithm requires no training on experimental data; rather, all of the spin physics required to interpret the spectra are learned from simulations alone. This approach is therefore applicable even when insufficient experimental data exist to train the algorithm. The neural network is demonstrated to be capable of utilizing the full information content of two-dimensional ¹⁴N HYSCORE spectra to predict the magnetic coupling parameters and their underlying probability distributions that were previously inaccessible. The predicted hyperfine (a, T) and ¹⁴N quadrupole (K, η) coupling constants deviate from the previous manual analyses of the experimental spectra on average by 0.11 MHz, 0.09 MHz, 0.19 MHz, and 0.09, respectively.

Graphical Abstract

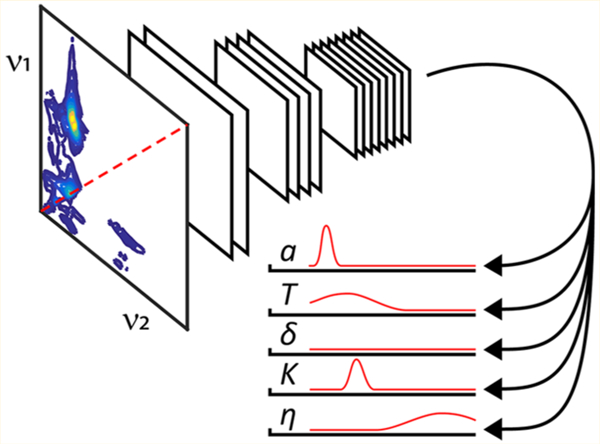
Recent advances in machine learning provide computers with an unprecedented visual capacity to match or even outperform humans in tasks ranging from everyday image recognition^1–3 to disease diagnosis,^4,5 yet only in a handful of cases have these types of neural network architectures been applied to problems in spectroscopy. Central to these computer vision algorithms is the convolutional neural network (CNN), which has allowed automated assignment of Raman spectra even in the presence of significant baseline distortion artifacts⁶ and has demonstrated a high performance level for automatic spectral assignments in multidimensional nuclear magnetic resonance (NMR) spectra.^7,8 In this Letter, we describe a general purpose CNN architecture for extracting parameters of interest directly from two-dimensional (2D) spectra. The spectrum and experimental settings are the input to the algorithm, and the predictions and their associated confidence intervals are returned as output. As a case study, this neural network’s capabilities are demonstrated for the pulsed electron paramagnetic resonance (EPR) experiment HYSCORE (Hyperfine Sublevel Correlation), with the pulse sequence shown in Figure 1.⁹ Specifically, HYSCORE is used to differentiate all the connectivities of the hyperfine levels and the coupling parameters between electron spins (S = 1/2) and their surrounding nuclear spin environments. For spin I = 1/2 nuclei such as ¹H, ¹³C, and ¹⁵N, the hyperfine coupling with the electron spin gives rise to simple cross-ridge lineshapes in HYSCORE spectra of powder samples that allow for the magnetic coupling parameters to be extracted by simple least-squares fitting.^10,11 For ¹⁴N nuclei (I = 1) considered in this work, the situation is complicated by the nonequivalent splitting of the nuclear levels into the m_I = −1, 0, and 1 spin states because of the quadrupolar interaction. The HYSCORE spectrum for even a single ¹⁴N spin is generally a multiline pattern with up to nine cross-peak pairs, and the cross-ridge intensities are a complicated function of the relative hyperfine and nuclear quadrupole couplings and the experimental parameters with which the measurement was performed.¹² Spectral artifacts from τ-suppression¹¹ and the appearance of diagonal peaks from incomplete inversion by the π-pulse can further contribute to complicating the spectral analysis.¹³ These challenges make 2D ¹⁴N HYSCORE an appealing case study for using machine learning to extract information convolved with these spectral artifacts.

Figure 1.

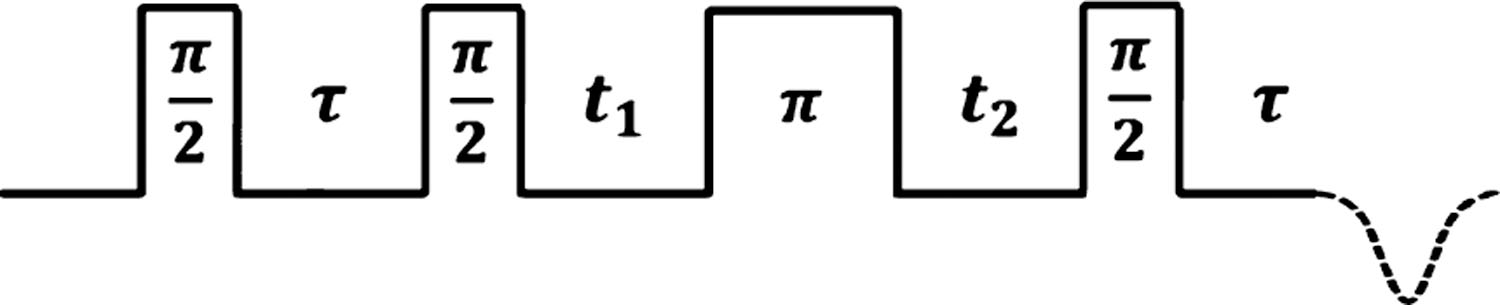
HYSCORE pulse sequence investigated in this work. The delay between the first and second π/2-pulses is held at a fixed value τ. The intensity of the inverted echo (dashed) is acquired as a function of t₁ and t₂, resulting in a 2D time-domain pattern correlating the change in nuclear resonant frequencies as the electron spin is flipped between its +1/2 and −1/2 spin states. All spectra were acquired with a 4-step phase cycle.¹⁴

However, an inherent problem with HYSCORE, as for most multidimensional spectroscopies in magnetic resonance, is a paucity of experimental data available to train the neural network. Here we present a simple, yet novel solution where a CNN is trained on simulations in order to teach it to analyze experimental spectra. A similar strategy of training a neural network on simulations was successfully implemented recently to process double electron–electron resonance data.¹⁵ The result described here is a neural network that solves the inverse problem of extracting magnetic coupling parameters from a HYSCORE spectrum, revealing the full probability distributions of these parameters for the first time.

Hyperfine and Nuclear Quadrupole Couplings.

The goal of analyzing an ¹⁴N HYSCORE spectrum is the determination of the hyperfine and nuclear quadrupole tensors, which provide a quantum mechanical description of the couplings between the nitrogen spin and its nearby electron spin. The principal components of the hyperfine tensor (A_XX, A_YY, and A_ZZ) can be represented in spherical form as a − T(1 + δ), a − T(1 − δ), and a + 2T, respectively, where a is the isotropic constant, T the anisotropic constant, and δ the unitless rhombicity factor that varies between 0 and 1. The tensor for the nuclear quadrupole interaction is traceless, and therefore, its principal components (Q_XX, Q_YY, and Q_ZZ) can be represented with only two values, the quadrupole coupling constant K = e²Qq/h and the unitless asymmetry parameter η = (Q_XX − Q_YY)/Q_ZZ.^13,16

Under most circumstances, currently available analytical expressions allow only for a and K²(3 + η²) to be directly estimated from ¹⁴N spectra (valid only when the hyperfine anisotropy is weak, i.e. T ≈ 0).^16,17 In the special case of the cancellation condition, where the nuclear Larmor frequency (ν_14N) exactly matches the hyperfine interaction (|ν_14N − |a|/2| ≈ 0), direct determinations of K and η may also be possible.^16,17 In order to determine the remaining parameters, ¹⁴N HYSCORE simulations are performed by optimizing a vast parameter space of unknown variables. These simulations are often a tedious trial-and-error task prone to operator bias.

Machine Learning Algorithm.

A CNN architecture was designed and trained on EasySpin v5.2.13²⁰ simulations to extract a, T, δ, K, and η directly from the raw X-band (∼9 GHz) HYSCORE time-domain patterns (Figure 2). For spectra with multiple nitrogen couplings, the cross-peaks were manually separated such that HYSCORE spectra corresponding to a single ¹⁴N served as input to the neural network. The machine learning algorithm’s performance was validated on our previously analyzed experimental HYSCORE spectra^21–25 that exhibit well-resolved ¹⁴N couplings. The outputs of the CNN are unnormalized probability distributions for each parameter, where the amplitudes of the distributions indicate the neural network’s confidence in making its predictions (a flat baseline of zeros indicates no confidence in making a prediction). The CNN outputs are compared with the literature values in Figure 3. The chemical structures of the spin systems considered in this work are shown in Figure 4. Full details on the machine learning architectural design and training are provided in the Supporting Information.

Figure 2.

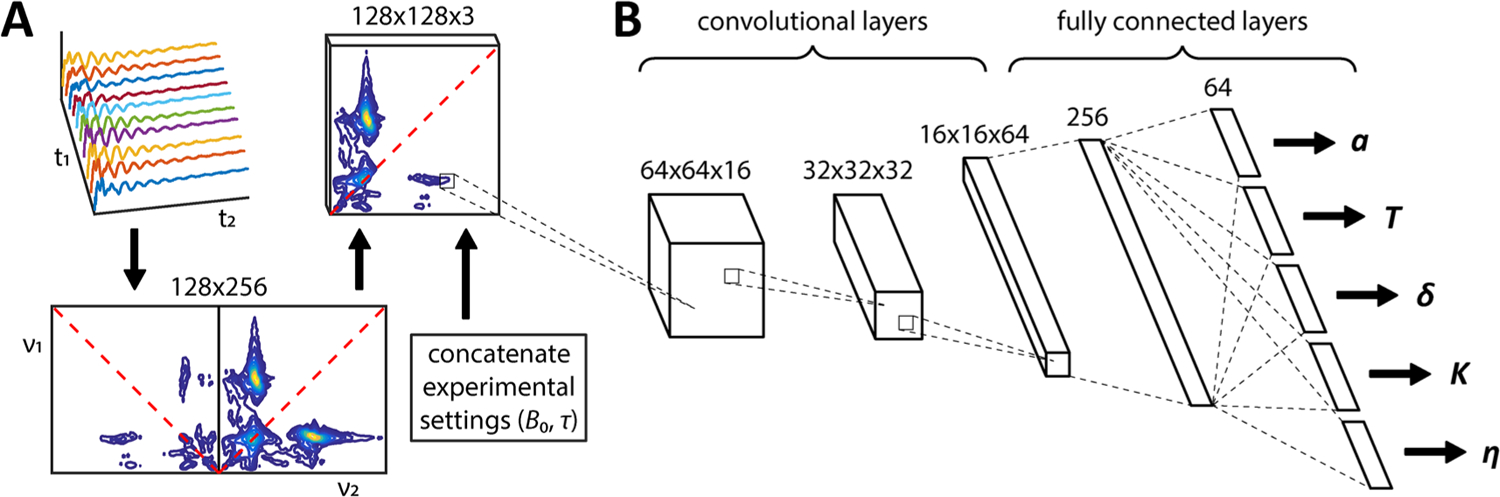
Machine learning architecture for predicting the ¹⁴N hyperfine and nuclear quadrupole coupling constants directly from the raw HYSCORE data. (A) Spectral preprocessing involves 2D Fourier transformation of the time-domain data, followed by averaging and rearranging of the nearly symmetrical triangular halves into a compact square matrix representation. The experimental settings (in this case the magnetic field B₀ and pulse delay time τ) are then concatenated onto the back of the HYSCORE spectrum. (B) Preprocessed HYSCORE spectra are passed through 3 convolutional layers with 16, 32, and 64 channels (kernel size = 3 × 3, stride = 2), and the output is flattened along the image dimensions. After passage through one fully connected layer of size 256, the network branches into 5 parallel fully connected layers each of size 64 for predicting the values of a, T, δ, K, and η. ReLU¹⁸ activations are applied to all layer outputs except for the five final classification layers, where the SoftPlus¹⁹ activation ln(1 + e^x) is used instead. The full details of the spectral preprocessing, CNN architectural design, and network training are provided in the Supporting Information.

Figure 3.

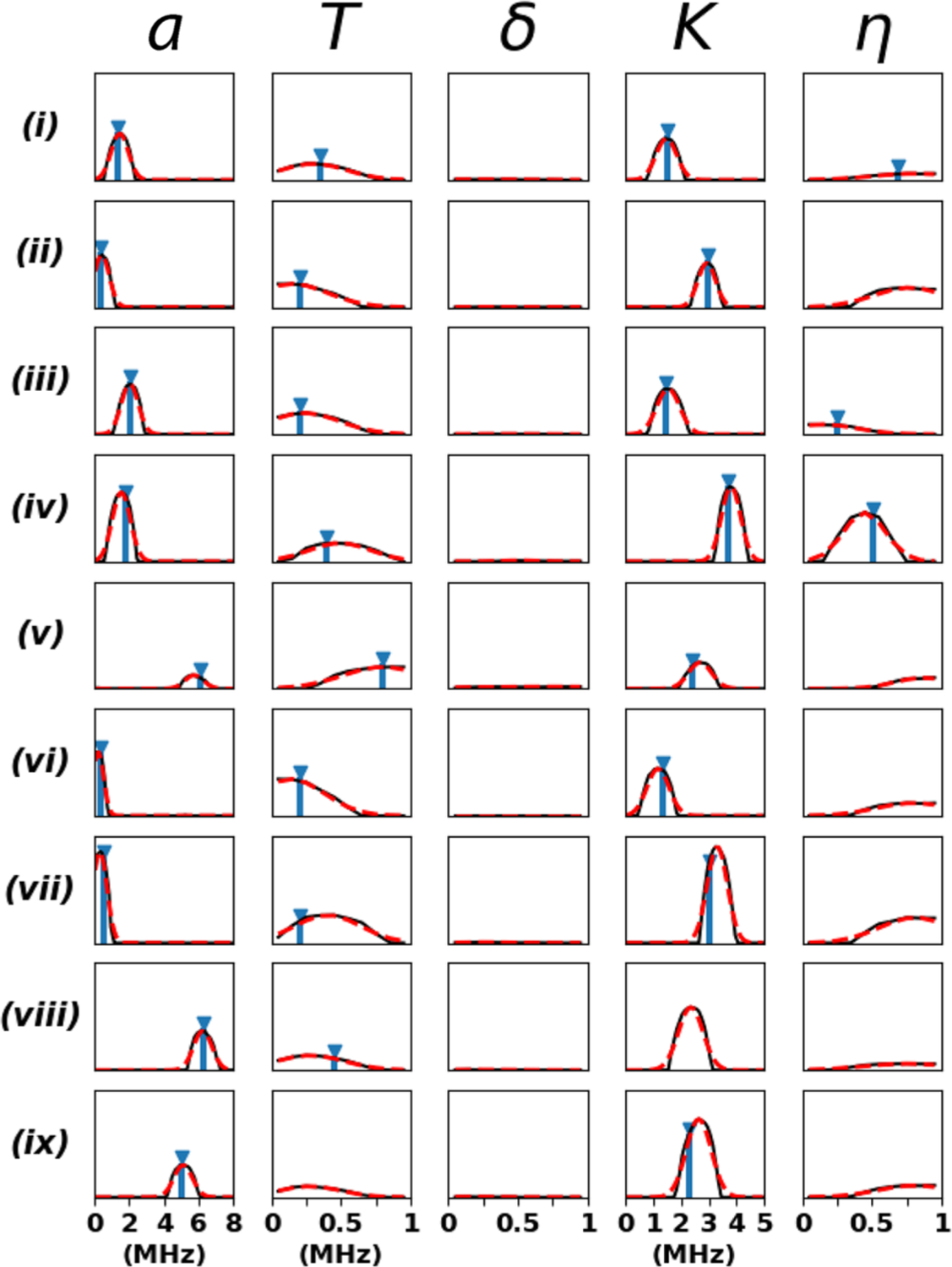
Comparison of the CNN probability distributions for a, T, δ, K, and η (black) with the previously reported literature values (blue) where available: (i) SQ_B RC (L-H190-N_δ) – semiquinone (SQ) in the Q_B ubiquinone binding site of the reaction center from Rhodobacter sphaeroides interacting with N_δ of residue L-H190;²¹ (ii) SQ_B RC (L-G225-N_p) – same as previous for N_p of L-G225;²¹ (iii) SQ_H cyt aa₃ (H70-N_ε) – SQ in the Q_H high-affinity menaquinone binding site of the R70H mutant of cytochrome aa₃-600 menaquinol oxidase from Bacillus subtilis interacting with N_ε of residue H70;²² (iv) SQ_H cyt bo₃ (R71-N_ε) – semiquinone in the Q_H high-affinity ubiquinone binding site of the cytochrome bo₃ ubiquinol oxidase from Escherichia coli interacting with N_ε of residue R71;²³ (v) [2Fe-2S] rat mitoNEET (H87-N_δ) – reduced [2Fe-2S](Cys)₃(His)₁ cluster in rat mitoNEET interacting with N_δ of residue H87;²⁴ (vi) [2Fe-2S] rat mitoNEET (H87-N_ε) – same as previous for N_ε of residue H87;²⁴ [2Fe-2S] rat mitoNEET (N_p) – same as previous for N_p in the cluster environment;²⁴ (viii) VO²⁺ (Imidazole) – VO²⁺ ion interaction with coordinating imidazole ligand nitrogens;²⁵ and (ix) VO²⁺ (Histidine-N_α)₂ – VO²⁺ ion interaction with coordinating N_αH₂ of histidine ligands.²⁵ The final predictions and their standard deviation errors are determined by a Gaussian fit to the probability distributions (dashed red). It took ∼3 s for the machine learning algorithm to process the time-domain patterns and generate this figure on a desktop equipped with an Intel Core i5–4570 processor (3.2 GHz) and 16 GB of RAM.

Figure 4.

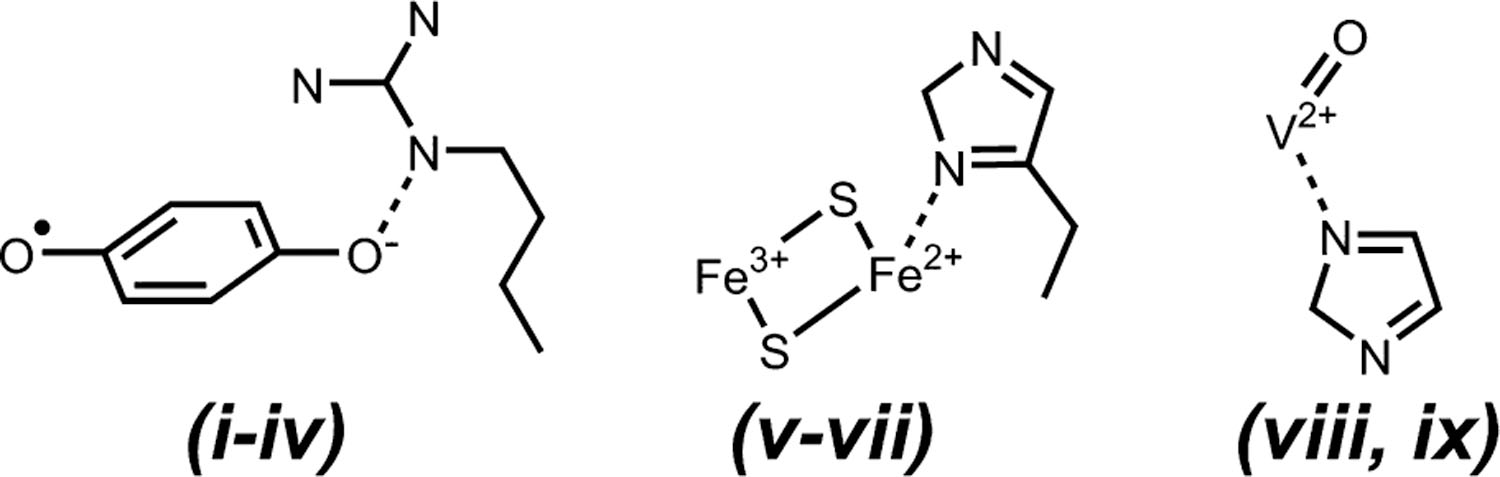
Chemical structures of the three major electron spin systems studied in this work (each shown in complex with an example of one of the ¹⁴N ligands from this Letter): (left) semiquinone hydrogen bonded to N_ε of arginine, (middle) reduced [2Fe-2S] cluster in coordination with histidine, and (right) VO²⁺ ion coordinated to an imidazole. The spin systems in Figure 3 belonging to each class are listed at the bottom.

The predictions and their associated errors were determined by fitting a Gaussian to the CNN output probability distributions (Table S1 in the Supporting Information). The machine learning algorithm in Figure 3 utilizes the HYSCORE spectra along with the experimental settings B₀ and τ to predict a and K to within an average deviation of 0.10 and 0.17 MHz from the manually assigned values, respectively. These errors approach the spectral frequency resolution of 0.1 MHz used in the HYSCORE preprocessing and analysis. Remarkably, the neural network also provides quantitative estimates for the hyperfine anisotropy T, for which no algorithm exists to directly extract this parameter from the spectrum. While T is best estimated from an analysis of ¹⁵N HYSCORE spectra because they lack contributions from the nuclear quadrupole coupling (all of the literature values of T in Table S1 are based on analyses of ¹⁵N-enriched samples), the machine learning algorithm is apparently able to extract this information directly from the natural abundance ¹⁴N spectrum. The error in the prediction for T is on average 0.08 MHz with respect to the manually assigned values. The nuclear quadrupole asymmetry parameter, η, can be determined only in certain cases, but this is understandable as the single-quantum transitions necessary to quantify this parameter appear in HYSCORE spectra only when the cancellation condition is satisfied.^12,16,17 For the spin systems sufficiently near the cancellation condition (SQ_B RC L-H190-N_δ, SQ_H cyt aa₃ H70-N_ε, and SQ_H cyt bo₃ R71-N_ε),^21–23 an average prediction error for η of 0.10 with respect to manual analysis is obtained. We note SQ_B RC L-H190-N_δ satisfies the cancellation condition poorly at X-band, and S-band measurements were required for an accurate determination of η.²¹ Despite this, the machine learning algorithm presented here is able to provide a reasonable estimate of η even without the low-frequency measurements. Finally, the CNN is not able to predict the hyperfine rhombicity parameter, δ. This is consistent with the previous inability to determine δ accurately for these spin systems because of insufficient spectral resolution. The failure of the machine learning algorithm to extract δ suggests the information required for specifying this parameter simply does not exist in these ¹⁴N HYSCORE spectra.

Comparison of neural network models trained with and without various combinations of B₀ and τ shows that only B₀ provides a small but significant improvement to the fit (Table 1). This suggests this neural network is able to infer the magnetic field (within the range of 300–400 mT used in the training set) directly from the spectrum alone. Indeed, when this CNN is repurposed to extract B₀ from the spectrum instead of a, T, δ, K, and η, it does so with an average deviation of 20 mT from the experimental truth value. Therefore, the magnetic field of the spectrum is, to some degree of accuracy, encoded into the pattern of peaks and cross-ridges. Additional performance benchmarks of the neural network as a function of various simulations parameters are provided in the Supporting Information: prediction accuracy does not show any dependence on magnetic field (Figure S3) or τ-value (Figure S4) within the intervals the neural network was trained, performance degrades as the spectrum becomes dominated by diagonal peak intensity (Figure S5), and the machine learning algorithm exhibits robust performance for signal-to-noise ratios above ∼4 (Figure S6).

Table 1.

Comparison of CNN Model Prediction Errors^a

model	Δa (MHz)	ΔT (MHz)	ΔK (MHz)	Δη
HYnetb	0.13 (±0.02)	0.09 (±0.04)	0.26 (±0.04)	0.14 (±0.04)
HYnet-B0c	0.12 (±0.01)	0.08 (±0.01)	0.19 (±0.01)	0.11 (±0.02)
HYnet-τd	0.13 (±0.03)	0.09 (±0.01)	0.25 (±0.08)	0.11 (±0.01)
HYnet-B0τe	0.11 (±0.03)	0.09 (±0.01)	0.19 (±0.02)	0.09 (±0.01)

^aPrediction error is calculated as the absolute difference between the CNN output and the literature values. For each model, the prediction error was averaged over five training runs with the standard deviation in parentheses.

^bCNN model not given any information on the experimental settings at which the HYSCORE spectrum was measured.

^cOnly the magnetic field of the experiment (B₀) is provided to the model.

^dOnly the τ-value of the experiment is provided to the model.

^eBoth B₀ and the τ-value are provided to the model.

Here we describe a CNN architecture capable of utilizing and interpreting the full information content of 2D EPR data and apply this approach for the first time to the analysis of ¹⁴N HYSCORE spectroscopy. The algorithm is trained only on spectral simulations and is robust to variations in diagonal peak intensity, noise, τ-suppression, and variations in t₁ and t₂ step size. However, the training set includes only narrow-line radicals with a maximum g-tensor span of 0.1 and no resolvable splittings in the EPR spectrum. As such, the CNN exhibits instability for cases of complex EPR spectra, such as the VO²⁺ spin system (strong hyperfine interactions with the I = 7/2 vanadium, Figure S7) and to a lesser degree the rat mitoNEET spin system (g-tensor span of 0.11 with small splittings in the EPR spectrum, Figure S8). Accounting for these complex patterns in the EPR spectrum is outside the scope of the present work and is currently not supported in the EasySpin simulation package.²⁰ However, the SPINACH package can model these features and may help generalize the neural network to handle arbitrary EPR spectral patterns.²⁶ An additional limitation of the current approach is that it can only analyze spectra corresponding to a single ¹⁴N nucleus, and therefore, manual intervention is required for analyzing multinuclear spectra. The solution to this problem will likely involve semantic image segmentation, unsupervised clustering, or a combination of the two for automatically separating the spectrum into its different components before being fed into the neural network. Despite the limitations of the present algorithm, it can provide a useful starting point for setting up HYSCORE simulations bounded by confidence intervals that are bias free (Figure S9). The code is provided as an open source package and is available online to download (https://griffingroup.mit.edu/EPR_Spectroscopy).

Thus, the approach outlined here proposes an alternative paradigm to the typical trial-and-error simulation process for interpreting multidimensional spectra. Machine learning has demonstrated the incredible ability to extract the magnetic coupling parameters of interest directly from the multidimensional spectra by treating it as an image classification problem. In the case of HYSCORE spectroscopy, the CNN derives an entirely new algorithm for estimating the hyperfine anisotropy parameter T directly from the spectrum. Importantly, the neural network extracts the full underlying probability distributions of each parameter for the first time, allowing for error estimates free from bias. Future efforts will be applied toward adapting these neural network architectures to the three- and four-dimensional spectra often encountered in NMR, where automation of structure calculations directly from the raw spectra may eventually become a reality.