Deactivation blocks proton pathways in the mitochondrial complex I

Significance

The electron transport chain of mitochondria is initiated by the respiratory complex I that converts chemical energy into a proton motive force to power synthesis of adenosine triphosphate. On a chemical level, complex I catalyzes elementary electron and proton transfer processes that couple across large molecular distances of >300 Å. However, under low oxygen concentrations, the respiratory chain operates in reverse mode and produces harmful reactive oxygen species. To avoid cell damage, the mitochondrial complex I transitions into a deactive state that inhibits turnover by molecular principles that remain elusive. By combining large-scale molecular simulations with cryo-electron microscopy data, we show here that complex I deactivation blocks the communication between proton pumping and redox modules by conformational and hydration changes.

Abstract

Cellular respiration is powered by membrane-bound redox enzymes that convert chemical energy into an electrochemical proton gradient and drive the energy metabolism. By combining large-scale classical and quantum mechanical simulations with cryo-electron microscopy data, we resolve here molecular details of conformational changes linked to proton pumping in the mammalian complex I. Our data suggest that complex I deactivation blocks water-mediated proton transfer between a membrane-bound quinone site and proton-pumping modules, decoupling the energy-transduction machinery. We identify a putative gating region at the interface between membrane domain subunits ND1 and ND3/ND4L/ND6 that modulates the proton transfer by conformational changes in transmembrane helices and bulky residues. The region is perturbed by mutations linked to human mitochondrial disorders and is suggested to also undergo conformational changes during catalysis of simpler complex I variants that lack the “active”-to-“deactive” transition. Our findings suggest that conformational changes in transmembrane helices modulate the proton transfer dynamics by wetting/dewetting transitions and provide important functional insight into the mammalian respiratory complex I.

In mitochondrial cellular respiration, the membrane-bound enzyme complexes I, III, and IV convert chemical energy into a flux of electrons toward dioxygen (1–6). The free energy of the process is transduced by pumping protons across the inner mitochondrial membrane (IMM), powering oxidative phosphorylation and active transport (7, 8). The electron transport process is initiated by the respiratory complex I (NADH:ubiquinone oxidoreductase), a 45-subunit modular enzyme machinery that shuttles electrons from nicotinamide adenine dinucleotide (NADH) to ubiquinone (Q₁₀) and transduces the free energy by pumping protons across the IMM, generating a proton motive force (pmf) (1, 4–6) (Fig. 1). This proton-coupled electron transfer reaction is fully reversible, and complex I can also operate in reverse electron transfer (RET) mode, powering ubiquinol oxidization by consumption of the pmf. Such RET modes become prevalent under hypoxic or anoxic conditions that may result, e.g., from stroke or tissue damage (9), during which the electrons leak from complex I to molecular oxygen and result in the formation of reactive oxygen species (ROS) with physiologically harmful consequences (9–11). To regulate this potentially dangerous operation mode, the mammalian complex I can transition into a “deactive” (D) state with low Q₁₀-turnover activity (12, 13). Although some structural changes involved in the “active”-to-“deactive” (A/D) transition were recently resolved (14–16), the molecular details of how this transition regulates enzyme turnover and its relevance during in vivo conditions still remain puzzling. Moreover, it is also debated whether conformational changes linked to this transition are involved in the native catalytic cycle of all members of the complex I superfamily or whether this transition is specific for the mitochondrial enzyme (12, 13, 17).

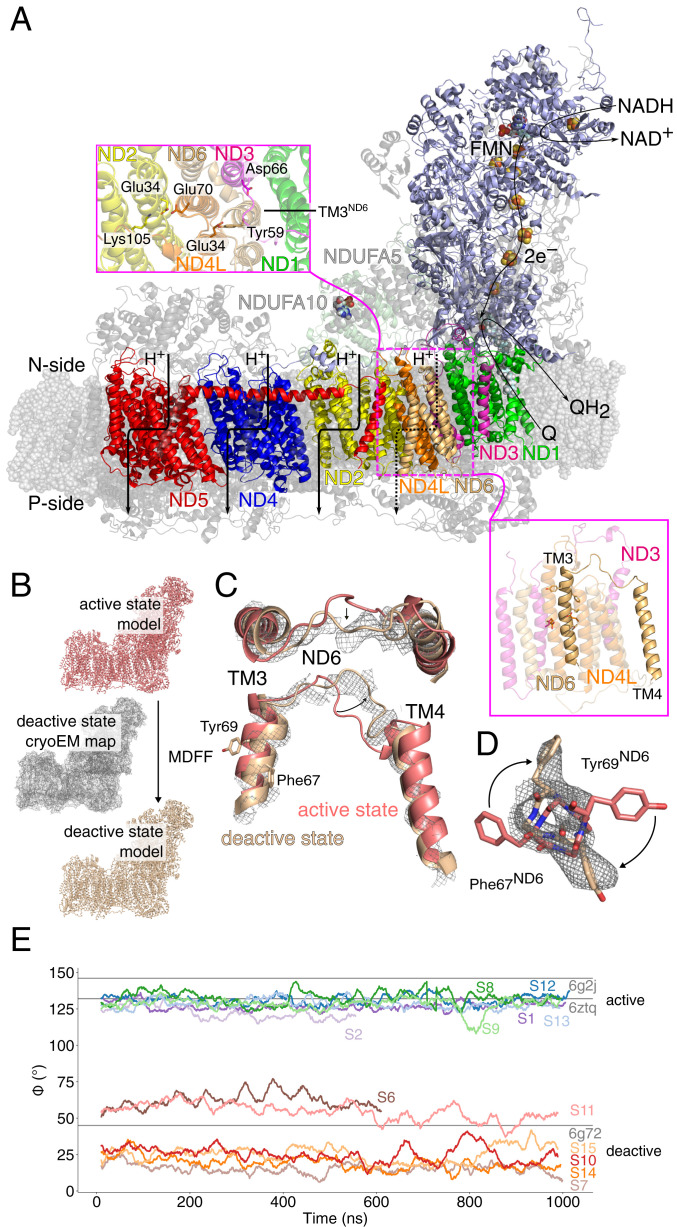
Fig. 1.

Structure and function of the mammalian complex I. (A) Electron transfer from NADH reduces quinone (Q) to quinol (QH₂) and triggers proton pumping across the membrane domain. (Inset) Closeup of the ND1/ND3/ND4L/ND6 interface involved in the "active" to "deactive" transition. TM3^ND6, which has been linked to conformational changes in the A/D transitions, is marked. (B) An intact atomic model of the deactive state was constructed using MDFF based on the cryoEM structure of the “active” state and the density map of the “deactive” state. (C and D) Conformational changes during the A (in pink)/D (in brown) transition during the MDFF simulations at the TM3^ND6 region, with the D state density map shown. Refer to SI Appendix, Figs. S2, S3, and S12 for other conformational changes. (E) The dihedral angle, ϕ, for ND6 residues Leu51(Cβ)-Leu51(Cα)-Phe67(Cα)-Phe67(Cβ) during MD simulations in the “active” and “deactive” states in comparison to refined cryoEM models.

The recently resolved cryo-electron microscopy (cryoEM) structures of the “deactive” mammalian complex I at around 4-Å resolution highlighted conformational changes around several subunits close to the interface between the hydrophilic and membrane domains of complex I. Particularly interesting are the conformational changes around the membrane domain subunits ND4L, ND3, and ND6 (ND for NADH Dehydrogenase) that form a bundle of 11 transmembrane (TM) helices, connected by long loop regions (14–16). Notably, it was observed that TM3 of ND6 transitions from a fully α-helical form in the “active” state to a π-bulge around residues 60 to 65 during the deactivation process (14–16). Although the exact relevance of these conformational transitions remains debated, it is notable that several point mutations in the vicinity of these regions have been linked to mitochondrial disease (11), supporting their possible functional relevance. Structural changes during complex I deactivation, inferred from the lack of density in the cryoEM maps (14–16), were also suggested to take place in several loop regions of the membrane domain, near the Q₁₀ binding site tunnel, and around the supernumerary subunits NDUFA5/NDUFA10 (16, 18). However, the functional consequences of these structural changes and their coupling to the biological activity still remain unclear.

To probe how structural changes linked to deactivation could affect the protonation and quinone dynamics of the mammalian complex I, we combine here atomistic molecular dynamics (MD) simulations and hybrid quantum/classical (QM/MM) free energy calculations with cryoEM data (16, 19). Our combined findings suggest that conformational changes around the ND1/ND3/ND4L/ND6 interface and conserved loop regions could block the coupling between proton pumping- and redox-modules upon complex I deactivation. The explored molecular principles are of general importance for elucidating energy transduction mechanisms in the mammalian respiratory complex I and possibly other bioenergetic enzyme complexes, but also for understanding the development of mitochondrial diseases.

Results

Conformational Dynamics Modulate Water-Mediated Proton Transfer Reactions.

To probe the dynamics of the mammalian complex I, we embedded the 45-subunit “active” state of mouse complex I (19) in a mitochondrial inner lipid membrane-model with POPC/POPE/cardiolipin (2:2:1), solvated the model with water molecules and 150 mM NaCl, and simulated the ca. 1 million atom system in total for around 8.5 μs using atomistic MD simulations. A quinone or quinol molecule was modeled in the primary binding site near the N2 iron–sulfur center (20) or in a membrane-bound binding site located near the Q-tunnel kink region at ND1 that was recently predicted based on simulations and validated experimentally (19, 21). Simulations were also performed with the Q-cavity left in an empty (apo) state (refer to SI Appendix, Fig. S1 and Table S1 for simulation setups and Table S2 for modeled protonation states). To obtain molecular insight into the “deactive” state, we constructed an intact atomistic model of this form by targeting the “active” state model toward the experimental cryoEM “deactive” density (EMD: 4356) (16) using an MD flexible fitting (MDFF) approach, followed by unrestrained MD simulation for a total simulation time of ca. 6 μs (Fig. 1B). In the targeted MDFF simulations, the cryoEM density acts as an external biasing potential that guides the dynamics of the residues, whereas for unresolved regions, the dynamics is directed only by the biomolecular force field (22). This modeling approach is likely to provide a more balanced description of the “deactive” state and a better comparison to our “active” state simulations, as the former state could not be experimentally resolved at the same atomic level of detail as the “active” state. The obtained “deactive” model, created from our “active” state simulation setup, resembles the previously refined 3.9-Å structure of the former [Protein Data Bank (PDB) ID: 6G72] (16) for the experimentally resolved regions but contains more atomic detail for unresolved parts (Fig. 1 C and D and SI Appendix, Figs. S2, S3, and S12, Materials and Methods). The global dynamics observed in the MD simulations resemble the dynamics inferred from the local resolution of the cryoEM map (SI Appendix, Fig. S2A), including a relative twist of the hydrophilic domain relative to the membrane domain experimentally described before (14–16, 23) (SI Appendix, Fig. S3F). We also observe pronounced conformational differences around the ND3/ND4L/ND6 subunits between the “active” and “deactive” state simulations, particularly at Phe67^ND6 and Tyr69^ND6 of ND6 (Fig. 1 C–E). The displacement rotates TM3^ND6 helix and results in the formation of a π-bulge, closely resembling the structural changes observed in previous cryoEM structures (Fig. 1E) (16) and further supporting that the model captures key features of the “deactive” state around this region. The “deactive” state model remains stable during unrestrained simulations, suggesting that the structure is a local free-energy minimum.

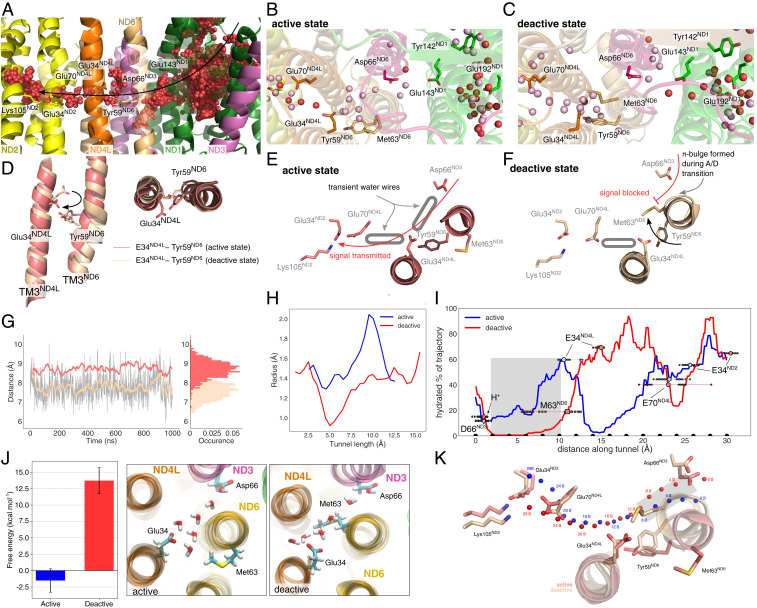
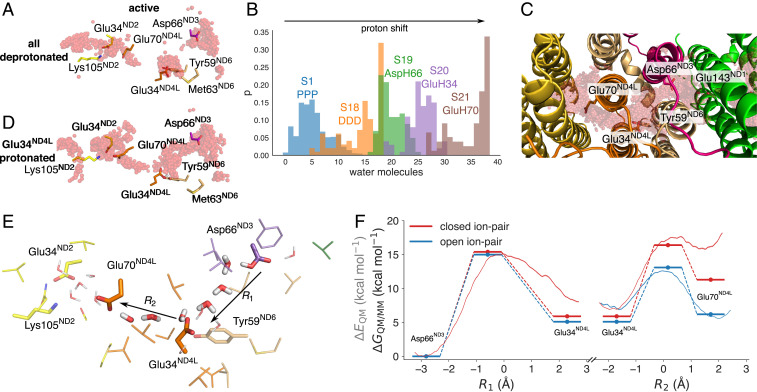
Water molecules establish S-shaped proton pathways around broken-helix elements in the three antiporter-like subunits, ND4, ND5, and ND2, in both our “active” and “deactive” state simulations (SI Appendix, Fig. S4), closely resembling the proton pathways described before (24–28). However, close to the ND1/ND3/ND4L/ND6 subunits, the conformational changes between the “active” and “deactive” states strongly alter the protonation dynamics: in the “active” state simulations, we observe a proton wire that forms on ca. 0.5-μs timescales and establishes a hydrogen-bonded connection from the negatively charged (N) side of the membrane to a network of carboxylates in ND1 (Asp199^ND1, Glu202^ND1, Glu204^ND1, Glu227^ND1, Glu192^ND1, and Glu143^ND1) (Fig. 2 A and B). This proton wire continues toward Glu34^ND4L/Tyr59^ND6 and extends further to Glu70^ND4L, located next to the Glu34^ND2/Lys105^ND2 ion-pair of ND2 (Figs. 2 A and B and 3 A and E). However, despite rather extensive hydration in ND1, we observe large (around 8- to 10-Å) gaps in the proton wire in the ND3/ND6/ND4L region between Asp66^ND3 and Glu34^ND4L and Glu34^ND4L and Glu70^ND4L/Glu34^ND2 that could prevent efficient proton transfer between the residues (Fig. 3A and SI Appendix, Fig. S5). When we protonate Asp66^ND3, mimicking a putative proton transfer from the E-channel, a water wire is established during the 100-ns simulation between Asp66^ND3 and Glu34^ND4L/Tyr59^ND6 (Fig. 3B and SI Appendix, Fig. S5B), and by further transferring the proton to Glu34^ND4L, we obtain a proton wire between Glu34^ND4L and Glu70^ND4L (Fig. 3D) that stabilizes during the 100-ns MD simulations initiated after the microsecond trajectory (SI Appendix, Fig. S6). Shifting a proton through the acidic residues in this area increases the overall hydration level during the simulations (Fig. 3B). These findings suggest that the proton transfer reaction could create its own conduction pathway through the channel from the putative second membrane-bound Q-binding region to the interface of the first ion pair Glu34^ND2/Lys105^ND2 in ND2. Proton transfer reactions and protonated water molecules themselves have also previously been suggested to create their own proton wires (29).

Fig. 2.

Hydration dynamics in the “active” and “deactive” states. (A) Ensemble average of water molecules during 1,000-ns MD simulations of the “active” state. The water molecules form an effective proton wire via the E-channel in ND1 and connect via the ND3/ND4L/ND6 region to the ND2 interface. (B and C) Snapshot of individual water molecules (in red) after the 1,000-ns MD simulations in the ND1/ND3/ND4L/ND6 region in the “active” (B) and “deactive” (C) states. Water molecules in pink are obtained from simulations with shifted protonation states (simulations S19 and S23; SI Appendix, Table S1). Refer also to SI Appendix, Fig. S6 for cluster analysis. (D) Rotation of TM3^ND4L/ND6 helices induce conformational changes around Glu34^ND4L/Tyr59^ND6 in the “active” (red) and “deactive” (brown) states. Proton wires are established from Asp66^ND3 via Glu34^ND4L to Glu70^ND4L and further to the Glu34/Lys105 ion pair of ND2 in the "active" state (E), but are blocked in the "deactive" state (F). (G) Dynamics of the Glu34^ND4L/Tyr59^ND6 during the “active” (red) and “deactive” (brown) states. (H) Tunnel radius connecting Asp66^ND3 and Glu34^ND4L in the “active” and “deactive” state simulations, predicted using CAVER tunnel analysis (Materials and Methods). (I) Hydration fraction along the tunnels connecting the acidic residues along the ND3/ND6/ND4L/ND2 gating region. The tunnel distances correspond to the beads shown in K. (J) (Left) Hydration free energy for introducing a water wire in the gating region between Asp66^ND3 and Glu34^ND4L, obtained using alchemical FEP simulations, suggesting that the formation of a water wire in the “deactive” state is disfavored by ca. 15 kcal · mol⁻¹ as compared to the “active” state. Error bars indicate a 95% CI based on three independent simulations (SI Appendix, SI Methods). (Middle/Right) Snapshots of the fully formed water wires in the “active” and “deactive” states during the FEP calculations. (K) Tunnel positions shown in panel I relative to the structure in the “active” and “deactive” states. Beads are placed 2 Å apart to highlight the channel pathway.

Fig. 3.

Proton transfer in the ND3/ND4L/ND6 deactivation gate. (A) Proton pathways from Asp66^ND3 via Glu34^ND4L to Glu70^ND4L and the Glu34^ND2/Lys105^ND2 ion pair of ND2. (B) Shifting the protonation state in the ND4L/ND6/ND3 region favors enhanced hydration and hydrogen-bonded wiring between the putative membrane-bound Q-site and the ND2 interface (see SI Appendix, Table S1). The figure shows the count of water molecules between the tunnel region extending from ND3 to ND2 (C) during the MD simulations of each state. The distributions are normalized to 1. (C) Top view of the gating region and ensemble average of water molecules in simulations S18 to S21 (SI Appendix, Table S1). (D) Shifting the proton to Glu34^ND4L enhances water-mediated contacts to Glu70^ND4L. Refer also to SI Appendix, Fig. S5 for exploration of different protonation states in the MD simulations. (E) Residues surrounding the ND3/ND4L/ND6 water chain that were included in the quantum chemical DFT and QM/MM free energy calculations. (F) Proton transfer energetics based on QM/MM free energy simulations (red/blue lines) and quantum chemical DFT models (energy level diagrams) and effect of the ND2 ion pair conformation on the proton transfer profile. Reaction coordinates obtained from the DFT models are marked with a filled circle. Statistical errors in the free energy profiles are ca. 0.12 kcal · mol⁻¹ (transparent red), and the effects of DFT-sampling on the convergence of the free energy profiles are shown in SI Appendix, Fig. S8. Benchmarking calculations suggest that the transition states and reaction energies have a few kcal · mol⁻¹ error relative to correlated ab initio calculations (SI Appendix, Table S7).

In stark contrast to the well-wired “active” state, we observe that Met63^ND6 located in the middle of the π-bulge on TM3^ND6 blocks the proton pathway between Asp66^ND3 and Glu34^ND4L in all “deactive” state simulations (Fig. 2 C and F and SI Appendix, Fig. S5 E–H). Rotation of TM3^ND4L positions Glu34^ND4L toward the Glu70^ND4L in the “active” state, whereas the residue points away from the ND2 site in the “deactive” state (Fig. 2 D and G). Analysis of the hydration frequency across the simulation trajectories suggests that the proton pathway between Asp66^ND3 and Glu34^ND4L is well hydrated in our “active” state simulations, whereas in the “deactive” state, Met63^ND6 completely blocks the formation of a water wire by closing the tunnel (Fig. 2 H and I and SI Appendix, Fig. S5 I, J, and K). This ca. 10-Å-long tunnel region comprises on average around five water molecules in the “active” state MD simulations (Fig. 2 B and J). In the “deactive” state, the gating region remains dry in all simulated protonation states, an observation that is well reproduced in our 6-μs simulation trajectories (SI Appendix, Fig. S5 E–H and J).

To further probe whether a proton wire could form on much longer timescales, inaccessible to the MD simulations, we computed hydration free energies using alchemical free energy perturbation (FEP) calculations by creating a water wire into the gating region in both the “active” and “deactive” states (Materials and Methods). No restraints were applied on the protein to allow the system to structurally relax upon introduction of the water chain in the cavity (Materials and Methods). The FEP calculations suggest that the hydration free energy is weakly exergonic in the “active” state (−2 kcal · mol⁻¹; Fig. 2J), supporting the MD results for the well-hydrated gating region. In stark contrast, the hydration free energy is strongly endergonic (+14 kcal · mol⁻¹) in the “deactive” state (Fig. 2J) and arises from repulsive van der Waals contributions, indicating steric clashes (SI Appendix, Fig. S7). Notably, Met63^ND6 remains in its inward position during the FEP calculations, leading to a partially broken water wire (Fig. 2J and SI Appendix, Fig. S7). During the FEP calculations, we observe small conformational changes, particularly in TM3^ND6 adjacent to the hydrated cavity (SI Appendix, Fig. S7F). We expect that introduction of a protonated water species in this gating region that could favor the hydration process (29) would also experience similar steric repulsion as the neutral water chain introduced here. To probe how introduction of a protonated water species could favor the hydration process, as shown in simulations of other systems (29), we performed MD simulations with an explicit H₃O⁺ species introduced in the cavity next to Asp66^ND3 or Glu34^ND4L and modeling the respective carboxylate in the deprotonated state (SI Appendix, SI Methods). During the 110-ns simulations of these charge-separated states, the cavity remains dry (SI Appendix, Fig. S5 L–O), supporting that the thermodynamic cost of hydrating this region could be high in the “deactive” state. The combined simulation results thus support that the proton pathways are likely to be blocked in the “deactive” state also on timescales comparable to the turnover of complex I.

To probe the bond formation/breaking energetics during the proton transfer reaction, we next performed hybrid density functional theory (DFT)–based QM/MM free energy simulations as well as quantum chemical DFT calculations based on the MD simulation trajectories (Materials and Methods). These QM/MM free energy simulations are expected to describe local free energy changes due to their limited sampling in comparison to computationally faster reactive force field (29–33) or semiempirical calculations (34, 35), derived by pre-parametrizations of the protein residues and reaction intermediates involved (33, 36, 37). Hybrid functionals, such as the dispersion-corrected B3LYP-D3 used here, often provide a good balance between computational accuracy and cost, with an error of a few kilocalories · mole⁻¹ based on benchmarking calculations relative to correlated ab initio calculations (SI Appendix, Table S7; refer to ref. 38 for further discussion on challenges in DFT-modeling). Here, we computed the free energies based on 320-ps DFT-based QM/MM umbrella sampling (US) simulations that yielded converged local free energy profiles, with structures selected from the microsecond MD simulations to account for dynamical effects (Materials and Methods). We expect that the explored free energies provide an accurate description of the local proton transfer energetics in the ND1/ND4L/ND3/ND6 region, although slow-relaxing degrees of freedom arising from possible large-scale dynamical effects are difficult to accurately account for with our current models. The MD simulations are here limited to a total sampling of around 15 μs, which is unlikely to capture possible slower conformational dynamics on the millisecond turnover timescale. However, part of this problem is possibly circumvented, as we have modeled several transient states along a putative pumping cycle and created simulations of the “active” and “deactive” states based on experimental data.

In the “active” state, we obtain an endergonic proton transfer reaction (ΔG∼+6 kcal · mol⁻¹) between Asp66^ND3 and Glu34^ND4L followed by a nearly isoenergetic proton transfer to Glu70^ND4L (ΔG∼−1 kcal · mol⁻¹) (Fig. 3 E and F). The overall reaction barrier is around 15 kcal · mol⁻¹, suggesting that the reaction is kinetically feasible in millisecond timescales based on transition state theory but close to the turnover timescale of complex I. The proton transfer reaction takes place in both our DFT reaction pathway optimizations and QM/MM models via a Grotthuss-type transfer process, with Zundel/hydronium intermediates (Materials and Methods and SI Appendix, Fig. S8). However, further exploration of other reactions coordinates [e.g., the center of excess charge (29–31, 34, 35) or energy difference between diabatic states (32)], often used in semiempirical or reactive force field calculations, are beyond the scope of the present work but could provide additional insight into the proton transfer dynamics on longer simulation timescales, and beyond pre- and post-proton transfer water configurations.

This endergonic reaction step for the Asp66^ND3 → Glu34^ND4L transfer could be powered by the oxidoreduction chemistry and subsequent Q dynamics that has been suggested to release part of the 800-mV (ΔG = −18.4 kcal · mol⁻¹) driving force when the quinol docks into the second membrane-bound binding site (1, 21). The reaction energetics could be further modulated by both hydration and conformational states of the channel.

In contrast to our “active” state simulations, the proton transfer reaction is blocked in the “deactive” state by the TM3^ND6 helix rotation that prevents protonic connectivity between Asp66^ND3 and Glu34^ND4L (Fig. 2 C and F and SI Appendix, Fig. S5 E–H). Due to the absence of this pathway, we are unable to probe the proton transfer free energy profiles in the “deactive” state model, as the water wire forms a prerequisite for the reaction.

We find that the proton transfer energetics in the “active” state is further modulated by the conformational state of the Glu34^ND2/Lys105^ND2 ion pair in ND2, with the ion pair opening favoring the proton transfer reactions toward the ND2 interface (Fig. 3F and SI Appendix, Fig. S8H; Materials and Methods). Protonation of Glu70^ND4L could further trigger dissociation of the Glu/Lys ion pair, push the proton laterally toward the ND2 subunit (Fig. 3E), and initiate a long-range charge transfer cascade in the membrane domain in an electrostatic-cradle motion, as suggested before (1).

Perturbation of the Deactivation Gate by Mitochondrial Disease-Related Mutations.

Bioinformatic analysis suggests that key residues along the proposed proton pathways at the ND3/ND4L/ND6-ND2 interface are conserved and involved in multiple human mitochondrial disorders (10, 11, 39, 40) (SI Appendix, Tables S5 and S6 and Fig. S9 A–C). To probe how these residues could affect the proposed proton pathways, we modeled disease-causing point mutations in silico by locally relaxing the structure by short MD simulations based on the hydrated 1-μs simulation of the “active” state (SI Appendix, Fig. S9 and Table S1). The models are likely to account for local relaxation effects around the channel, but do not capture, for example, possible large-scale conformational changes linked to the mutations.

We find that substitution of Glu34^ND4L for alanine, which has been linked to Leber’s Hereditary Optic Neuropathy (LHON) (39, 40), blocks the proton pathway between Asp66^ND3 and Tyr59^ND6/Glu34^ND4L (SI Appendix, Fig. S9E), a substitution that also experimentally strongly inhibits the activity of Escherichia coli complex I (40) (SI Appendix, Fig. S9I). Substitution of Glu34^ND4L for glutamine results in a well-hydrated cavity, but the amide headgroup prevents the residue from participating in the proton transfer reaction (SI Appendix, Fig. S9F) that could explain the drastic loss of activity of E34Q^ND4L in E. coli complex I (SI Appendix, Fig. S9 H and I) (39, 40). Similarly, the E70A^ND4L substitution lowers the complex I activity by around 20% (SI Appendix, Fig. S9I), whereas in our MD simulations of this mutant, we observe a longer water-mediated wire to Glu34^ND2 that could increase the reaction barriers (SI Appendix, Fig. S9G). Upon substitution of Glu34^ND2 for aspartate, the channel remains well hydrated, consistent with experimental activities that are comparable to that of wild-type complex I (SI Appendix, Fig. S9 D and H).

Interestingly, several point-mutations linked to LHON and other mitochondrial disorders introduce substitutions that result in hydrogen-bonded contacts with either water molecules within the proton wires and/or the putative proton donor/acceptor groups identified in the MD simulations that could perturb the proton transfer kinetics (SI Appendix, Fig. S9 B and C). Similar mutations around the D-channel in cytochrome c oxidase lead to uncoupling of the redox-driven proton pump (41).

Quinone and Loop Dynamics.

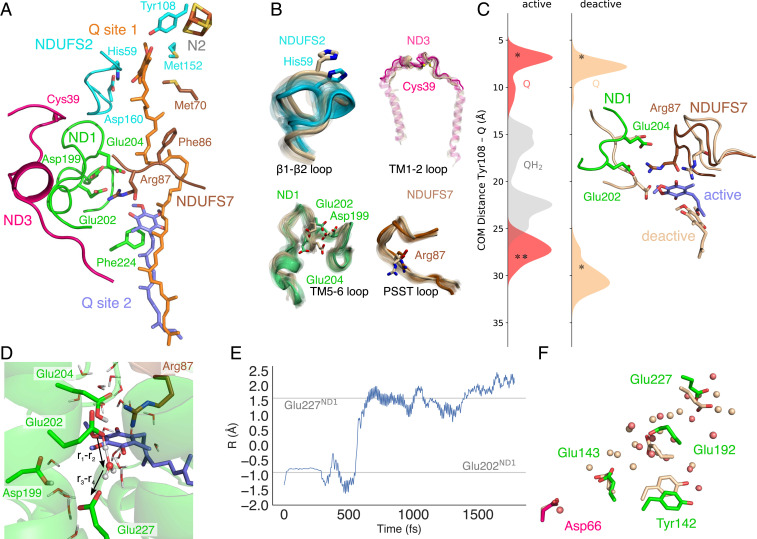
To probe the crosstalk between the proton pathways in the proposed ND3/ND4L/ND6 gating region and the quinone site, we next analyzed the dynamics of Q₁₀ modeled in its binding cavity (Fig. 4). We find that Q₁₀ can form contacts with His59^NDUFS2/Tyr108^NDUFS2 and stays bound within the 30-Å-long Q-tunnel during the MD simulations (Fig. 4 A and C and SI Appendix, Fig. S10). Q₁₀ dissociates during some of the simulations from its original position to a location ca. 5 to 10 Å from His59^NDUFS2/Tyr108^NDUFS2. Both binding modes are supported by several independent shorter MD simulations (SI Appendix, Fig. S10 C and D) that are overall consistent with results from previous studies on the simpler bacterial complex I (20, 21, 42–45). Moreover, upon loss of atomistic detail, our coarse-grained (CGMD) simulations suggest that the Q₁₀ could also stay bound on longer (10-μs) timescales (SI Appendix, Fig. S10 C and D). We note that Q₁₀ can find a stable binding pose at around 10 Å from Tyr108^NDUFS2, resembling a previously described binding site 1’ observed in computational studies (21, 42–45) (Fig. 4C), as well as in an experimentally resolved inhibitor-bound form of complex I (46). Our MD simulations suggest that both quinone and quinol can also interact with residues around a putative membrane-bound Q-site (Fig. 4 A and C), which could be important for transmitting the redox signal to the membrane domain (1, 21). In this second binding region, the Q₁₀ headgroup forms contact with Arg87^NDUFS7 and Glu204^ND1/Glu202^ND1 together with a network of other charged residues (Fig. 4C and SI Appendix, Fig. S11), but Q remains overall dynamically flexible, possibly due to its rather shallow free energy surface (21, 43–45). Glu202^ND1 and Glu204^ND1 were previously suggested to undergo conformational changes upon Q reduction (47), and the residues are observed in different conformations in various experimentally resolved structures of complex I (46, 48). These carboxylates, together with Asp199^ND1, are located on the flexible TM5-6 loop region of ND1 that contains several charged residues. This loop samples different conformational dynamics in our “active” and “deactive” simulations (Fig. 4 A–C and SI Appendix, Fig. S12) (14–16, 23): in the “active” state, part of this loop transitions into an α-helical segment around residues 209 to 216 (Fig. 4B and SI Appendix, Fig. S12B) that is stabilized by a network of serine residues (Ser209/123/125/128^ND1), whereas it remains unstructured and dynamically more flexible in the “deactive” state simulations (Fig. 4B). We note that Glu202^ND1 and Glu204^ND1 form water-wired contacts with QH₂ during the MD simulations (SI Appendix, Figs. S6, S10, and S11). Our QM/MM MD simulations (Materials and Methods) suggest that the water molecules can catalyze proton transfer from the quinol to this carboxylate cluster and result in the formation of a QH⁻ species (Fig. 4D), but the pK_a of this cluster is likely to be sensitive to the conformation of the surrounding loop regions and Arg87^NDUFS7, which also interacts with Glu202^ND1, Glu204^ND1, and Q₁₀ in the simulations (SI Appendix, Fig. S11). The carboxylate cluster is connected via water molecules to a rich network of protonatable residues within the TM5-6 loop region that could transfer the proton to Glu227^ND1 and further to Glu192^ND1 (Fig. 4 D–F). In the “active” state simulations, Glu192^ND1 forms contacts with Tyr142^ND1, but the tyrosine swings outwards in the “deactive” simulations (Fig. 4F). The Glu192^ND1/Tyr142^ND1 cluster is bridged via one to two water molecules to Glu143^ND1 that in turn forms a water wire to Asp66^ND3 next to the deactivation gate, described above (Fig. 4F).

Fig. 4.

Conformational changes, Q dynamics, and proton transfer around the substrate channel region. (A) Key regions interacting with Q₁₀ in the primary (site 1) and membrane-bound (site 2) Q-binding sites. (B) Conformational changes in loop regions during 1,000-ns MD simulations of the “active” (in subunit color) and “deactive” (in light brown) states. (C) Q₁₀ dynamics measured from the center-of-mass between the Q and Tyr108^NDUFS2 headgroups in the “active” and “deactive” states with the Q/QH₂ modeled in the first/second binding regions. Starting positions are marked with an asterisk. (D and E) Proton transfer from Glu202^ND1/QH⁻ to Glu227^ND1 during QM/MM MD simulations. The proton transfer coordinate, R = r₁−r₂+r₃−r₄, was computed as a difference between bond-forming (H•••O) and bond-breaking (O-H) distances. (F) Water molecules and conformational changes in the “active” (red/colored) and “deactive” (light brown) states leading from Glu227^ND1 to Asp66^ND3.

In addition to the TM5-6 loop of ND1, the “active” and “deactive” state simulations sample different conformational dynamics around the β1-β2 loop of NDUFS2 that comprises the Q-binding His59^NDUFS2 and a loop region in NDUFS7 that holds Arg87^NDUFS7 (the “PSST-loop”, Fig. 4B and SI Appendix, Fig. S12). Motion in the β1-β2 loop swings His59^NDUFS2 out from the binding pocket in the “deactive” state simulations that could reduce the affinity of Q for the primary binding site. These regions were also previously suggested to become more dynamic in the “deactive” state based on loss of electron density in the D-state maps in the ND1, ND3, and NDUFS2 regions (SI Appendix, Fig. S12A) (16, 23), and the PSST-loop has also been linked to Q-binding (49). The conformational changes around the TM5-6 loop of ND1, the PSST-loop of NDUFS7, and the helices embracing the Q cavity could account for the partial dissociation of the Q₁₀ from its membrane-bound site that we observe in our “deactive” state simulations but not in the “active” state (Fig. 4C). We also note some enhanced conformational dynamics in the TM1-2 loop of ND3 that contains a solvent exposed Cys-residue (Fig. 4B), a region previously shown to be relevant for coupling between the Q-oxidoreduction function and proton pumping activity (50). However, it is unlikely that our microsecond simulations exhaustively sample the rich dynamics of these loop regions.

These local conformational changes around the Q tunnel are accompanied by motion in some supernumerary subunits, in particular NDUFA10 and NDUFA5 that sample different conformational dynamics in our “active” and “deactive” state simulations, further supporting their possible functional role in the A/D transition (16, 18). In our MD simulations, this shift leads to a rearrangement of a network of ion pairs at the subunit interface that could stabilize the respective states in specific conformations (SI Appendix, Fig. S2 B–D).

Discussion

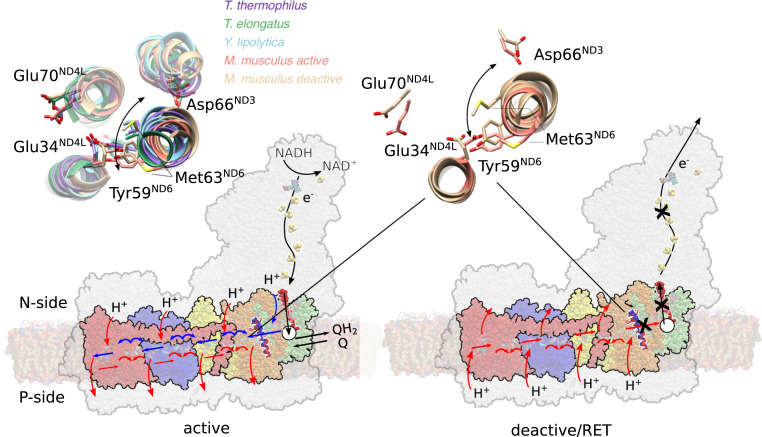
We have shown here by combination of multiscale molecular simulations with cryoEM data how structural changes between “active” and “deactive” states of the mammalian complex I could lead to a functional decoupling of the redox domain from the proton-pumping modules. We observe a molecular gate that is established by conformational changes at the ND3/ND4L/ND6 interface that regulate proton transfer toward the ND4L/ND2 interface and vice versa under RET conditions (Fig. 5). The protonation-driven hydration dynamics could be driven by the electric field created by the proton itself that, in turn, interacts with the dipole field of the water wire to minimize the overall energetic cost (51). Similar field-induced gating effects could also be employed in other energy-transducing proteins (1, 52, 53). We further suggest that protonation of the ND2 interface triggers long-range proton pumping by sequential ion pair opening, proton transfer reactions, and changes in the hydration state of the proton channels (Fig. 5) (1, 24–27).

Fig. 5.

Deactivation and proton pumping in the mammalian complex I. (Left) Quinone reduction triggers conformational and electrostatic changes around ND1 (in green), charging up the proton pump. Upon quinol binding to the membrane bound site (white circle), a proton is pushed from the second Q binding region along the ND3/ND4L/ND6 channel to the ND4L/ND2 interface (orange). The proton transfer can propagate only when the deactivation gate at TM3^ND6 is in an open state. Protonation changes at the ND4L/ND2 interface trigger (blue arrows) consecutive opening of ion pairs, protonation, and hydration changes in ND2 (yellow), ND4 (blue), and ND5 (red). Upon propagation of the signal in a backward wave to the ND2 interface (red arrows), the loaded protons are released to the P-side, and QH₂ is released to the membrane. (Right) Upon RET conditions, rotation of the TM3^ND6 (helix in red/blue) blocks the proton transfer signal to propagate between ND2 and the second quinone-binding site (cross) that decouples the pmf-driven quinone oxidoreduction. (Inset) Conformational changes around TM3^ND6 in the “active” state (PDB ID: 6TZQ)/“deactive” state model (Right) and comparison of the region in various experimental structures (Left), some of which lack the A/D transition.

We found here that the membrane-bound Q-binding site within ND1 (19, 21, 42–45, 54) is coupled with protonatable residues in the ND3/ND4L/ND6 region. The protonation cascade could be initiated by the formation of a QH⁻ species that remains locked at the membrane-bound Q-site (e.g., until a protonation backwave restores and releases the QH₂) (1). Interestingly, several residues involved in the proposed deactivation gate are linked to human mitochondrial disorders, further supporting the functional relevance of the region (11, 39, 40).

We expect that the membrane-bound Q-site and its linked protonation reactions are unable to equilibrate when the deactivation gate is in a closed state, which could in turn inhibit redox turnover during the complex I deactivation and RET conditions. Conformational changes around the Q channel and its surrounding TM helices and loop regions could further block the substrate entry to complex I and modulate the substrate affinity. In addition to the changes in the proton pumping and local Q-binding region explored here, it is important to note that complex I deactivation is likely to have also more global effects (e.g., by affecting the equilibrium redox states of the cofactors in the peripheral arm and the association of NADH with the protein) (12, 13, 23).

The bacterial complex I lacks a prevalent A/D transition (12, 13, 55); although the functional residues providing wiring between ND1 (Nqo8/NuoH in Thermus thermophilus/E. coli; SI Appendix, Table S8) and ND2 (Nqo14/NuoN in Thermus thermophilus/E. coli) are highly conserved (SI Appendix, Table S5), Met63^ND6, which is involved in blocking the proton wire at the ND4L/ND6 interface, is replaced by bulky nonpolar residues in the bacterial isoforms that could also serve a similar gating function. Based on these observations, we suggest that the homologous ND4L/ND6 interface undergoes similar but perhaps a more subtle conformational change also in the bacterial complex I, to enable proton transfer toward the ND2 (Nqo14/NuoN) interface (Fig. 5, Inset, SI Appendix, Fig. S13). Moreover, NDUFA5 (NUFM/B13), which was found to undergo conformational changes between our “active” and “deactive” simulations, is not present in Yarrowia lipolytica complex I (18, 46) and could result in smaller differences between the two states, as also suggested by recent cryoEM structures (17, 28, 54).

Our combined findings indicate that at least some conformational changes linked to the “deactive” state in the mammalian complex I could be involved in the native catalytic cycle of all canonical members of the complex I superfamily, some of which lack the A/D transition (Fig. 5 and SI Appendix, Fig. S13) (17). We suggest that the proposed deactivation gate at the ND3/ND4L/ND6 interface modulates proton pumping but has further evolved by fine-tuned modular adaptation in the mammalian complex I to enable enzyme regulation and protect against ROS formation under rapidly changing respiratory chain conditions.

Materials and Methods

Classical MD Simulations.

The 3.0-Å piericidin-bound active state cryoEM structure of mouse complex I (PDB ID:6ZTQ) was embedded in a lipid membrane comprising a 2:2:1 mixture of 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine (POPC), 1-palmitoyl-2-oleoyl-sn-glycero-3-phospho-ethanolamine (POPE), and 1,3-bis(sn-3′-phosphatidyl)-sn-glycerol (cardiolipin). Ubiquinone or ubiquinol was modeled in the first or second binding site based on starting positions extracted from earlier studies (21). For simulations S1 through S15 (SI Appendix, Table S1), the N2 iron–sulfur center was modeled in a reduced state, whereas all other iron–sulfur clusters were modeled in their oxidized states. In simulations S16/S17, the N2 center was also modeled in the oxidized state. The quinone was modeled in both the oxidized (Q) and reduced (QH₂) states and flavin mononucleotide (FMN) in its oxidized form. Initial protonation states of titratable groups were determined based on Poisson–Boltzmann continuum electrostatic calculations coupled to Monte Carlo sampling (SI Appendix, Table S2) using the adaptive Poisson–Boltzmann solver (56) in combination with Karlsberg+ (57, 58). Atoms were described by point charges, embedded in a dielectric continuum with ε = 4 employed to model the protein surroundings. Bulk water was modeled with ε = 80, with a solvent probe radius of 1.4 Å and ionic strength of 100 mM potassium chloride. Complex I was divided into three overlapping parts (SI Appendix, Fig. S1B), which were titrated independently. The MD simulations were performed by considering multiple different protonation states along the observed proton pathways in the ND1/ND4DL/ND6/ND3 region (SI Appendix, Table S2). To this end, we sequentially moved the proton along the observed proton wire in this region in addition to simulations in which key E-channel residues (Glu34^ND4L, Glu70^ND4L, and Asp66^ND3) were modeled in both their fully deprotonated and protonated states (SI Appendix, Table S1). Arg87^NDUFS7 was modeled in its γ-hydroxylated form and Arg85^NDUFS2 as symmetric dimethylarginine. The model was solvated with TIP3P water molecules, and 632 Na⁺ and 497 Cl⁻ ions were added to neutralize the system to achieve a 150 mM NaCl concentration. The full system comprises ca. 991,000 atoms. Atomistic MD simulations were carried our using the CHARMM36 force field (59) in combination with DFT-derived parameters for the cofactors (20, 26, 27). The deactive state model was prepared using the same procedure based on the cryoEM density of the deactive state map by MDFF (22) with the cryoEM density map of the “deactive” state (Electron Microscopy Data Bank, EMDB: 4356) (see section Atomic Model of the "Deactive" State). The MD simulations were propagated in an NPT ensemble at T = 310 K using the Langevin thermostat at P = 1 atm pressure with Nosé–Hoover–Langevin piston pressure control for 1 µs with a 2-fs integration timestep. Long-range electrostatics were treated using the Particle Mesh Ewald method with a grid size of 1 Å and by computing the long-range contributions in reciprocal space for pair-distances above 12 Å. The Lennard–Jones cutoff was set to 12 Å using Nanoscale Molecular Dynamics' (NAMD) built-in switching function starting at 10 Å, and rigid bonds were modeled using the ShakeH algorithm. Classical MD simulations were performed in different states and in duplicates, leading to a total MD simulation time ca. 15 μs. All MD simulations were carried out with NAMD version 2.12 (60). Visual Molecular Dynamics (61) and PyMol v. 2.4.1 (62) were used for analysis and visualization, and further clustering analysis of the hydration dynamics was performed using WATCLUST (63). Hydration content (Fig. 2I and SI Appendix, Fig. S5 I, J, and K) was also determined based on MD hydration levels along tunnel coordinates identified using CAVER (64). Tunnels corresponding to productive pathways were extracted based on snapshots extracted every 1 ns of “active” and “deactive” MD simulations using Caver version 3.0 (64) and a probe radius set to 0.9 Å. The gathered tunnel coordinates were evaluated for their individual hydration in a 2 Å sphere over the MD trajectory and visualized with a surface proportional to the average hydration over the MD trajectory. Hydration frequencies (Fig. 2I and SI Appendix, Fig. S6) were computed by identifying connections between the head groups of functional residues using CAVER3.0 and a probe radius of 0.9 Å. The “hydrated-% of trajectory” was obtained by counting the fraction of water molecules within 2 Å from each point along the tunnel coordinate during the simulation trajectory. Refer to SI Appendix, Table S1 for summary of classical MD simulations.

Atomic Model of the “Deactive” State.

A “deactive” state model of the mouse complex I was built based on “active” state mouse complex I (PDB ID:6ZTQ) model (19) that was targeted to the complete cryoEM density map of the “deactive” state (EMDB: 4356) (16) using the MDFF (22) approach to construct an intact simulation model. The MDFF approach converts the cryoEM density map (ϕ) into an external restraining potential according to the following:

$$V\left(r\right)={\displaystyle \sum }_i{w}_i\varphi \left(r_i\right)$$

and

$$\varphi \left(r\right)=\{\begin{array}{c}\xi \hspace{0.17em}\left[1-\frac{\varphi \left(r\right)-{\varphi }_{\text{thr}}}{{\varphi }_{\text{max}}-{\varphi }_{\text{thr}}}\right]\\ \\ \zeta \hspace{0.17em}for\hspace{0.17em}\varphi \left(r\right)<{\varphi }_{\text{thr}}\end{array}\hspace{0.17em}\text{for}\hspace{0.17em}\varphi \left(r\right)\ge {\varphi }_{\text{thr}},$$

where ϕ (r) is the cryoEM density map at position r, ϕ_thr is the threshold density used for flattening the solvent beyond the solvent peak (here ϕ_thr = 0), and w_i and ζ are scaling factors that tune the strength of the cryoEM map (here, w_i is an atom-specific scaling factor set to the atomic mass and ζ = 0.3). Harmonic restraints were placed on the protein secondary structure elements during the MDFF simulations. Restraints for ND6 included the first helix turn-up to residue 65 to account for unresolved density (SI Appendix, Table S3). The active state model was targeted into the “deactive” state by MDFF minimization followed by 5 ns of MDFF dynamics in implicit solvent (22). The model was characterized by computing cross-correlation of computed and experimental cryoEM densities and RMSD differences to experimentally refined models (SI Appendix, Fig. S2 A and B). The obtained deactive state model was studied in subsequent unrestrained MD simulation using the same setup as for the active state (SI Appendix, Table S1).

FEP Calculations.

The hydration free energy of the gating region was estimated using alchemical FEP calculations using a complex I model comprising 120,000 atoms constructed from the MD simulations of the “active” and “deactive” states. Briefly, a chain comprising five water molecules was created between Asp66^ND3 and Glu34^ND4L in 20 λ-steps during 220-ns MD simulations. The free energy was computed according to the following:

$$\mathrm{\Delta }{G}_{A\to B}=-k_{B}T\hspace{0.17em}\text{ln}\langle \text{exp}\left[-\frac{E_B-\hspace{0.17em}{E}_A}{k_{B}T}\right]\hspace{0.17em}\rangle ,$$

where $\mathrm{\Delta }{G}_{A\to B}$ is the free energy difference between states A and B, $k_B$ is the Boltzmann constant, T is the temperature, E_B − E_A is the energy differences state A and B, and < > is the ensemble average for the simulation propagated in state A. Free energies based on forward and backward sampling were obtained via Bennet's acceptance ratio. The hydration free energy in Fig. 2J is reported relative to removal of five water molecules from the bulk solvent. Refer to SI Appendix for detailed methods description of the FEP calculations and SI Appendix, Fig. S7 for decomposition and convergence of the FEP calculations.

Exploration of the Quinone Dynamics.

To further probe the quinone/quinol dynamics we performed additional classical MD simulations as well as CGMD based on a model constructed from the complete mouse complex I, comprising chains A, B, C, D (residues 34 to 430), H, I, J, K, P, a, b, e, r, W, X (residues 1 to 150), and Z. This ∼396,000-atom model was embedded in a POPC membrane, solvated with TIP3P water molecules, and 100 mM NaCl. The Q/QH₂ near Tyr108^NDUFS2 was modeled based on the cryoEM model (simulations S62 and S63), or docked in (simulations S64 to S77) based on the local binding minima identified in simulations of T. thermophilus complex I (21). After minimization, the system was heated up to T = 310 K with harmonic restraints (2 kcal · mol⁻¹ · Å^-2) on the entire protein structure and cofactors (0.5 ns). In a second step, restraints were applied only to the backbone atoms (1 ns), followed by release of restraints. Simulations were performed with the same simulations parameters as applied for the full-sized model, using NAMD 2.9/2.13 (60). 10 × 10 µs CGMD simulations (simulations S78 to S87) were further performed with Q docked to different locations in the substrate tunnel using the MARTINI 2.2 force field (65), by employing a 20-fs timestep, a Parrinello–Rahman barostat with τ_p = 12.0 ps, and a compressibility of χ = 3.0 × 10⁻⁴ bar⁻¹. CGMD simulation were performed at T = 310 K with a thermostat coupling constant of τ_t = 1.0 ps. Nonbonded interactions were treated using a cutoff distance of 11 Å and ε = 15. All CGMD simulations were performed using Gromacs 2016.3 (66). Refer to SI Appendix, Table S1 for a list of performed simulations.

QM/MM and DFT Calculations.

QM/MM MD simulations were performed to explore the Q binding near the membrane-bound binding site (site 2) as well as for the proton transfer in the ND3/ND4L/ND6 region. For probing the dynamics in Q site 2, a QM/MM model including the quinol and nearest residues and water molecules with n = 208 QM atoms was used (SI Appendix, Table S4). The QM region was treated at the B3LYP-D3/def2-SVP level (67–69) using a 1-fs integration timestep at T = 310 K. The remaining MM system was modeled at the CHARMM36 level in combination with in-house DFT-derived parameters for the cofactors (20, 26, 27). Link atoms were introduced at the Cα-Cβ position, with exception of arginine residues, in which the link atom was placed at Cβ-Cγ position, whereas Q₁₀ was cut at the C₉-C₁₁ bond and saturated with a link atom. The total QM/MM system was trimmed to include around 19,527 atoms. Refer to SI Appendix, Fig. S1 and Table S4 for further details.

QM/MM free energy calculations and DFT cluster models of the proton transfer at the ND4L/ND3/ND6/ND2 interface were built based on MD snapshots of the “active” state (simulation S21 after 1,000 ns), with protonic connectivity from Asp66^ND3 to Glu34^ND4L/Tyr59^ND6 and from Glu34^ND4L to Glu70^ND4L. QM/MM US simulations were performed by splitting the proton transfer reaction into two steps with 90 and 139 QM atoms, respectively (SI Appendix, Table S4). The QM region was coupled to the MM region (modeled at the CHARMM36 level), by link atoms that were introduced at the Cα-Cβ positions. The QM/MM/US simulations comprised 25 and 19 windows for the first and second pT step, respectively. Each US window was sampled for 5 ps at T = 310 K using a restraint of 100 kcal · mol⁻¹ · Å^-2 on the proton transfer reaction coordinate, R₁ = [−3 Å, +3 Å] and R₂ = [−2.5 Å, +2.5 Å], for the first and second part with the Glu34/Lys105^ND2 model in the closed and open states. The free energy profiles were calculated using the weighted histogram analysis method. Refer to SI Appendix, Fig. S8 for the definition of R₁ and R₂ and convergence of the free energies. The same proton transfer reactions were also studied using DFT cluster models but with larger QM regions comprising 190 to 250 QM atoms (SI Appendix, Table S4). Protein residues were cut at the Cα-Cβ position and saturated with hydrogen atoms. Cβ positions and some carbon atoms of aliphatic residues surrounding the proton transfer pathway were kept fixed during geometry optimizations. Geometry optimizations were performed at the B3LYP-D3/def2-SVP level of theory (67–69), using an implicit polarizable medium with ε = 4. Reaction pathways of the proton transfer reactions in the DFT models were optimized using minimum energy pathway optimization approach (70) that resembles the zero-temperature string method (SI Appendix, SI Methods). Similar Grotthuss-type transfer reactions are predicted in both the QM/MM models using a geometric reaction coordinate and the DFT models employing reaction pathway optimization, suggesting that the choice of the reaction coordinate is not sensitive to the predicted transfer process (SI Appendix, Fig. S8). The energetics of the proton transfer processes were calculated at B3LYP-D3/def2-TZVP/ε = 4 level by combining the two optimized DFT models of the first (Asp66^ND3 to Glu34^ND4L) and second (Glu34^ND4L to Glu70^ND4L) proton transfer reactions, with a combined model size of ca. 380 atoms (Fig. 3E). The DFT energetics was benchmarked against correlated ab initio theory model calculations, suggesting that the reaction barriers at the B3LYP-D3 level are underestimated by a few kilocalories · mole⁻¹ (SI Appendix, Table S7), whereas the limited free energy sampling is likely to have an opposite effect. All QM/MM or DFT calculations were performed using the CHARMM/TURBOMOLE interface (71) CHARMM version 38 (72), and/or TURBOMOLE version 7.2 to 7.5 (73), and ORCA version 4.2 (74).

Data Availability

All study data are included in the article and/or SI Appendix.