Computing the Riemannian curvature of image patch and single-cell RNA sequencing data manifolds using extrinsic differential geometry

Significance

High-dimensional datasets are becoming increasingly prevalent in many scientific fields. A universal theme connecting these high-dimensional datasets is the ansatz that data points are constrained to lie on nonlinear low-dimensional manifolds, whose structure is dictated by the natural laws governing the data. While tools have been developed for estimating global properties of these data manifolds, estimating the Riemannian curvature, a local property, has not been considered. Computing curvature of data manifolds offers both detailed criteria with which to evaluate models of these complex data (e.g., a Klein bottle model of image patches) and a way to explore detailed geometric features that cannot simply be visualized by the naked eye (e.g., in single-cell RNA-sequencing data).

Abstract

Most high-dimensional datasets are thought to be inherently low-dimensional—that is, data points are constrained to lie on a low-dimensional manifold embedded in a high-dimensional ambient space. Here, we study the viability of two approaches from differential geometry to estimate the Riemannian curvature of these low-dimensional manifolds. The intrinsic approach relates curvature to the Laplace–Beltrami operator using the heat-trace expansion and is agnostic to how a manifold is embedded in a high-dimensional space. The extrinsic approach relates the ambient coordinates of a manifold’s embedding to its curvature using the Second Fundamental Form and the Gauss–Codazzi equation. We found that the intrinsic approach fails to accurately estimate the curvature of even a two-dimensional constant-curvature manifold, whereas the extrinsic approach was able to handle more complex toy models, even when confounded by practical constraints like small sample sizes and measurement noise. To test the applicability of the extrinsic approach to real-world data, we computed the curvature of a well-studied manifold of image patches and recapitulated its topological classification as a Klein bottle. Lastly, we applied the extrinsic approach to study single-cell transcriptomic sequencing (scRNAseq) datasets of blood, gastrulation, and brain cells to quantify the Riemannian curvature of scRNAseq manifolds.

High-dimensional biological datasets have become prevalent in recent decades because of new technologies, such as high-throughput single-cell transcriptomic sequencing (scRNAseq) (1–3), mass cytometry (4, 5), and multiplex imaging (6, 7). Interpretation and visualization of such high-dimensional datasets have been challenging, however, prompting the development of tools for nonlinear projection of data points onto two or three dimensions (8). These tools, such as IsoMAP (9), t-SNE (10), and UMAP (11), appeal to the ansatz that data points in a high-dimensional ambient space are constrained to lie on a low-dimensional manifold. Unfortunately, determining the geometry of a low-dimensional manifold from these visualizations is difficult, since many geometric properties are lost after projecting onto two or three dimensions. For example, the cartographic projections used in an atlas to flatten Earth’s curved surface tear apart continuous neighborhoods and nonuniformly stretch distances.

Fortunately, topology and differential geometry provide a wealth of concepts to characterize a manifold’s shape directly without confounding projections. In particular, homology (12, 13) categorizes a manifold according to the number of holes it contains and the dimensionality of each hole (whereas, for example, the hole in a hollow sphere does not survive projection onto a two-dimensional plane). Similarly, the metric tensor defined at each point $p$ on a manifold, $g_{ij}\left(p\right)=⟨v_i,v_j⟩$ for a local basis $\left\{v\right\}$, determines the lengths of vectors tangent to the manifold at $p$ and the angles between them (14). The metric tensor may either be directly specified for a manifold or implicitly specified according to the metric tensor of the ambient space (which, in the case of ${\mathbb{R}}^n$, is often given by the Euclidean metric, $g_{ij}\left(p\right)={\delta }_{i,j}$). By using the metric, shortest-distance paths between pairs of points on a manifold, known as geodesics (9), can be determined without any distortion from a projection (whereas, for example, most atlases exaggerate distances at the poles). Likewise, the metric can be used to determine the curvature (15), a local manifold property that quantifies the extent to which a manifold deviates from the tangent plane at each point $p$. Projecting a manifold onto a plane for visualization destroys this property by definition. Recent methods have emerged for estimating homology (16, 17), metrics (14), and geodesics (18) from noisy, sampled data, with accompanying statistical guarantees (18–20). These methods have been applied to analyze images (21, 22) and biological datasets (23, 24). However, estimating curvature has received less attention, although it is fundamental to quantifying geometry.

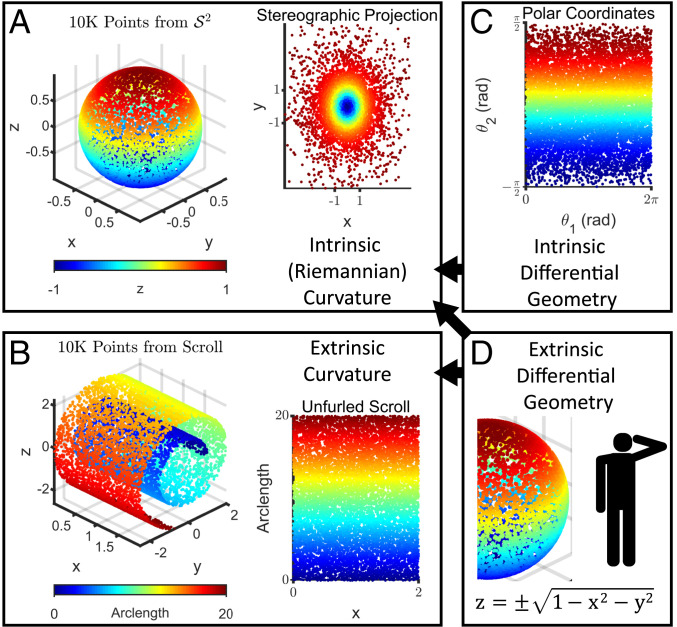
Curvature arises from two sources. On the one hand, a manifold itself can be curved, resulting in Riemannian or intrinsic curvature. A sphere has intrinsic curvature because it cannot be flattened so that all geodesics on its surface correspond to straight lines on a Euclidean plane (Fig. 1A). On the other hand, the embedding of a manifold in an ambient space can give rise to extrinsic curvature, a property that is not inherent to the manifold itself. For example, a scroll has extrinsic curvature because it is formed by rolling a piece of parchment, but the parchment itself is not inherently curved (Fig. 1B). It is important to note that both types of curvature scale inversely with the global length scale ($L$) associated with a manifold. It is for this reason that a marble ($L\approx 1$ cm) is visibly round, but the Earth ($L\approx \mathrm{10,000}$ km) is still mistaken by some to be flat. Since intrinsic curvature is an inherent property of a manifold, while extrinsic curvature is incidental to an embedding, we will restrict our attention to the former.

Fig. 1.

Riemannian curvature is an intrinsic property of a manifold, while extrinsic curvature depends on the embedding. (A, Left) $N=10^4$ points uniformly sampled from the two-dimensional hollow unit sphere, ${\mathcal{S}}^2$, embedded in the three-dimensional ambient space ${\mathbb{R}}^3$, colored according to the z coordinate. ${\mathcal{S}}^2$ has Riemannian or intrinsic curvature because there is no projection onto two-dimensional Euclidean space that preserves geodesic (shortest-path) distances. (A, Right) For example, a stereographic projection using the point $p=\left(\mathrm{0,0,1}\right)$ and the plane $z=0$ introduces distortions since the geodesic distance between any pair of points in the lower hemisphere is (nonuniformly) larger than the Euclidean distance in this projection. (B, Left) $N=10^4$ points uniformly sampled from a scroll, which is also a two-dimensional manifold embedded in ${\mathbb{R}}^3$. The scroll has extrinsic curvature because it curls away from the tangent plane at any point. (B, Right) However, it does not have intrinsic curvature, because it can be projected onto two-dimensional Euclidean space in a way that preserves geodesic distances, by unfurling. (C) Intrinsic differential geometry treats manifolds as self-contained objects that can be described by using only intrinsic coordinates, which do not depend on any embedding or ambient space. One possible set of intrinsic coordinates for ${\mathcal{S}}^2$ are polar coordinates, where ${\theta }_1$ and ${\theta }_2$ are the azimuthal and elevation angles, respectively. While this representation superficially resembles the unfurled scroll in B, distances in this plane are non-Euclidean, since the non-Euclidean induced metric is required to preserve the interpretation of distances with respect to ${\mathbb{R}}^3$. Any line segment along ${\theta }_2=\pm \frac{\pi }{2}$ has zero length, for example. (D) Extrinsic differential geometry defines manifolds in the coordinate system of the ambient space, which requires a privileged vantage point off the manifold itself. Both intrinsic and extrinsic differential geometry can be used to compute intrinsic curvature, whereas only extrinsic differential geometry can be used to compute extrinsic curvature (as indicated by the black arrows).

A precise description of intrinsic curvature is provided by the Riemannian curvature tensor, $R_{lkij}\left(p\right)$. For a given basis $\left\{v\right\}$, this tensor quantifies how much a vector initially pointing in direction $v_k$ is displaced in direction $v_l$ after parallel transport around an infinitesimal parallelogram defined by directions $v_i$ and $v_j$. If the manifold has no intrinsic curvature, this displacement is zero. Conversely, when a vector is moved by parallel transport around a closed loop on a manifold with intrinsic curvature, its initial and final orientations may differ, a phenomenon known as $\mathit{\text{holonomy}}$. For example, if a vector is moved around the closed loop bounding an octant of a sphere, it will rotate by $\frac{\pi }{2}$ after one cycle. The simplest intrinsic curvature descriptor is scalar curvature, $S\left(p\right)$, which is formed by contracting $R_{lkij}\left(p\right)$ to a scalar quantity, as its name suggests. When $S\left(p\right)$ is greater (less) than zero, the sum of the angles of a triangle formed by connecting three points near $p$ by geodesics is greater (less) than $\pi$. Likewise, when $S\left(p\right)$ is greater (less) than zero, a small ball centered at $p$ has a smaller (larger) volume than a ball of the same radius in Euclidean space. We furnish toy examples in the section Curvature Can Be Computed Accurately by Using the Second Fundamental Form to provide stronger intuition for this quantity.

In theory, intrinsic curvature can be equivalently computed by using tools from either one of the two branches of differential geometry. Intrinsic differential geometry makes no recourse to an external vantage point off a manifold, just as the polygonal characters in Edwin Abbot’s classic Flatland (25) were confined to traversing in ${\mathbb{R}}^2$ and found the notion of ${\mathbb{R}}^3$ unfathomable. In this branch, a manifold is therefore represented in intrinsic coordinates, which are agnostic to any ambient space or embedding. A hollow sphere represented in polar coordinates and k-nearest-neighbor (kNN) graph representations of a dataset, for instance, are in this spirit (Fig. 1C). Conversely, in extrinsic differential geometry, a manifold is treated as a surface embedded in an ambient space and is represented in ambient coordinates (Fig. 1D). The surface of an organ is parameterized this way, for example, in a surgical robot suturing an incision.

In this work, we explore two approaches for estimating intrinsic curvature based on these twin views, keeping in mind practical limitations of real-world datasets, which may consist of a relatively small number of noisy measurements. The first approach uses the Laplace–Beltrami operator, which is theoretically appealing as an intrinsic quantity that is embedding-invariant and whose application to geometric data analysis is well studied (14, 26–29). It has been used for dimensionality reduction, clustering, and classification of high-dimensional point cloud data (26, 30) and for quantifying geometric features of two-dimensional surface meshes (31, 32), including scalar curvature (27). However, for the task of computing curvature for point clouds, we found that the Laplace–Beltrami operator could not be estimated to sufficient accuracy from small sample sizes ($N=10^4$), suggesting that curvature estimation is especially demanding for point cloud data. Meanwhile, the second approach uses the Second Fundamental Form and the Gauss–Codazzi equation (15), identities that rely on information from the ambient space. We find that this extrinsic approach is not only more robust to small sample sizes and noise, but permits computation of the full Riemannian curvature tensor, though we focus on the scalar curvature for simplicity. Using these insights, we developed a software package to compute the scalar curvature (and associated uncertainty) at each sampled point on a manifold and applied this tool to investigate the curvature of image and scRNAseq datasets.

Results

Estimators of the Laplace–Beltrami Operator Yield Inaccurate Scalar Curvatures.

Intrinsic differential geometry treats a $d$-dimensional manifold, $M$, as a self-contained object and is agnostic to how $M$ may be represented in ambient coordinates due to any particular embedding (Fig. 1C). Conceptually, this is accomplished by only considering $M$ as a collection of local, overlapping neighborhoods. The geometry of these neighborhoods is encoded by using tools such as the Laplace–Beltrami operator, ${\mathrm{\Delta }}_M$, which captures diffusion dynamics across neighborhoods at a time scale $t$ (see, for example, ref. 33 for a more detailed discussion). For most practical applications, we do not have direct access to $M$, but instead to a finite number ($N$) of points sampled from $M$. For these cases, estimators of ${\mathrm{\Delta }}_M$ are used instead. These estimators are well-studied (14, 26–29), and the convergence rates of some have been characterized (34).

The scalar curvature averaged across $M$ has a well-known connection to ${\mathrm{\Delta }}_M$ via the heat-trace expansion (27, 35), which relates the eigenvalues, ${\lambda }_k$, of ${\mathrm{\Delta }}_M$ to the geometry of $M$:

$$Z\left(t\right)\equiv \sum _{k=1}^{\infty }{e}^{-{\lambda }_{k}t}={\left(4\pi t\right)}^{-\frac{d}{2}}\left[\sum _{i=0}^n{c}_i{t}^{\frac{i}{2}}+o\left(t^{\frac{n+1}{2}}\right)\right],{\lambda }_k\le {\lambda }_{k+1}.$$ [1]

The first few coefficients, $c_i$, are given by (27):

$$\begin{array}{cc}\hfill c_0& ={\int }_M\hspace{0.17em}dM,\hfill \\ \hfill c_1& =-\frac{\sqrt{\pi }}{2}{\int }_{\partial M}\hspace{0.17em}d\left(\partial M\right),\hfill \\ \hfill c_2& =\frac{1}{6}{\int }_{M}S\hspace{0.17em}dM-\frac{1}{6}{\int }_{\partial M}J\hspace{0.17em}d\left(\partial M\right),\hfill \end{array}$$ [2]

where $\partial M$ is the boundary of the manifold and $J$ is the mean curvature on $\partial M$. Recall that $S$ is the point-wise scalar curvature. By inspection, $c_0$ is the volume, $c_1$ is proportional to the area, and $c_2$ is directly related to the average scalar curvature.

We reasoned that if the average scalar curvature cannot be accurately computed for a manifold with constant scalar curvature using these relations, then computing the point-wise scalar curvature for more complex manifolds is intractable. To investigate this, we considered the two-dimensional hollow unit sphere, ${\mathcal{S}}^2$, for which the true scalar curvature is $S\left(p\right)=2\forall p\in M$, and uniformly sampled $N=10^4$ points to mirror the typical size of current scRNAseq datasets (Fig. 1A; SI Appendix, Supporting Methods, section D.1.1).

Since common estimators of ${\mathrm{\Delta }}_M$ only yield as many eigenvalues as data points ($N$), we cannot compute the infinite set of eigenvalues needed in Eq. 1. Therefore, we introduced a truncated series with $m$ eigenvalues, $z_m\left(x\right)$, where we have substituted $x=\sqrt{t}$ and divided through by the prefactor in the right-hand side of Eq. 1 to isolate for $c_i$, following the approach in (27):

$$\begin{array}{c}\hfill z_m\left(x\right)={\left(4\pi \right)}^{\frac{d}{2}}{x}^d\sum _{k=1}^m{e}^{-{\lambda }_k{x}^2}.\end{array}$$ [3]

The scalar curvature can then be approximated by fitting the truncated series, $z_m\left(x\right)$, to a second-order polynomial, $p_2\left(x\right)$, over intervals of small $x$:

$$\begin{array}{cc}\hfill z_m\left(x\right)& \approx p_2\left(x\right),\text{where}\hfill \\ \hfill p_2\left(x\right)& =c_0+c_{1}x+c_2{x}^2.\hfill \end{array}$$ [4]

We estimated ${\mathrm{\Delta }}_M$ using the $N$ sampled points (SI Appendix, Supporting Methods, section B.6), substituted the eigenvalues of the estimate into Eq. 3, and numerically fit $z_m\left(x\right)$ to $p_2\left(x\right)$ (SI Appendix, Fig. S1 A–G and Supporting Methods, section B.1). We obtained the scalar curvature by inspecting the resulting $c_2$ coefficient and compared the result to the true value of two. We found that the scalar curvature was always overestimated ($S>3$), regardless of $m$, the number of eigenvalues used in the truncated series (SI Appendix, Supporting Methods, section B.3), or the choice of estimator for ${\mathrm{\Delta }}_M$ (SI Appendix, Supporting Methods, section B.6). We identified the poor convergence of the estimated eigenvalues of ${\mathrm{\Delta }}_M$ as the source of error (SI Appendix, Supporting Methods, section B.4) and found that at least $N\approx 10^7$ points are required to reduce the error to $\pm 0.5$, so that $S\approx 2.5$ (SI Appendix, Fig. S1H). This is several orders of magnitude greater than what is typically feasible in current scRNAseq experiments. Noise and nonuniform sampling would confound the issue further. Most importantly, we would eventually like to compute local values of $S\left(p\right)\forall p\in M$, but this approach failed to correctly recover even average scalar curvature, which one might have expected to be feasible. To find an alternative approach, we next considered tools from extrinsic differential geometry.

Curvature Can Be Computed Accurately by Using the Second Fundamental Form.

In extrinsic differential geometry, a manifold is described in the coordinates of the ambient space in which it is embedded, usually ${\mathbb{R}}^n$ (Fig. 1D). Since the shape of the sphere in Fig. 1A is visually unambiguous to the eye (thanks to its extrinsic view from a vantage point off the manifold), we reasoned that an extrinsic approach would be more fruitful.

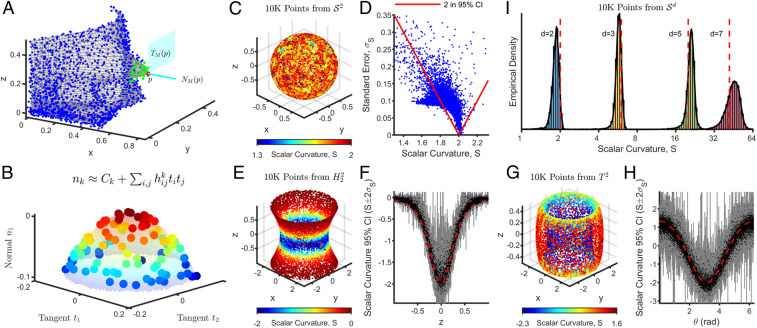
A $d$-dimensional manifold, $M$, embedded in ${\mathbb{R}}^n$ can be described at each point $p$ in terms of a $d$-dimensional tangent space, $T_M\left(p\right)$, and an ($n-d$)-dimensional normal space, $N_M\left(p\right)$, as shown in Fig. 2A. Given orthonormal bases for $T_M\left(p\right)$ and $N_M\left(p\right)$, points in the neighborhood of $p$ can be expressed as $Y=\left[t_1,\dots ,t_d,n_1,\dots ,n_{n-d}\right]$, where $t_i$ is $Y$’s coordinate along the $i$th basis vector of $T_M\left(p\right)$ and $n_k$ is $Y$’s coordinate along the $k$th basis vector of $N_M\left(p\right)$. The $n_k$s can then be locally approximated as functions of the $t_i$s; i.e., $n_k\approx f_k\left(t_1,\dots ,t_d\right)$, as shown in Fig. 2B.

Fig. 2.

Scalar curvature is accurately estimated by using the Second Fundamental Form and the Gauss–Codazzi equation. (A) A hypothetical manifold (shown in gray) from which data points are sampled (shown as colored dots). The manifold at any given point $p$ (shown in red) can be decomposed into a tangent space $T_M\left(p\right)$ (the cyan plane) and a normal space $N_M\left(p\right)$ (the cyan line). Points in the neighborhood around $p$ (shown in green) can be expressed in terms of orthonormal bases for $T_M\left(p\right)$ and $N_M\left(p\right)$ (see B). (B) The set of points in the neighborhood of $p$ (shown as green dots in A) are represented here in local tangent $\left(t_1,t_2\right)$ and normal $\left(n_1\right)$ coordinates, corresponding to orthonormal bases for $T_M\left(p\right)$ and $N_M\left(p\right)$, respectively. Coloring corresponds to magnitude in the normal direction. The normal coordinates $\left(n_1\right)$ can be locally approximated as a quadratic function (the translucent surface) of the tangent coordinates $\left(t_1,t_2\right)$, according to the Second Fundamental Form, $h_{ij}^k$. (C) Scalar curvatures computed by using the extrinsic approach for $N=10^4$ points uniformly sampled from the two-dimensional hollow unit sphere, ${\mathcal{S}}^2$. The true value is two at all points on the manifold (SI Appendix, Supporting Methods, section D.1.1). (D) Scalar curvatures ($S$) computed in C are plotted against their associated SEs (${\sigma }_S$). Points enclosed by the red lines have a 95% CI, computed as $S\pm 2{\sigma }_S$, containing the true value of two. (E) As in C, but for $N=10^4$ points uniformly sampled from a one-sheet hyperboloid, $H_2^2$, which is also a two-dimensional manifold. Due to the radial symmetry of the manifold, scalar curvature only varies only along the $z$ direction (SI Appendix, Supporting Methods, section D.1.2). (F) Scalar curvatures (black) computed in E with their associated 95% CIs (shown in gray) plotted as a function of the z coordinates of the data points. The true value is shown as a dashed red line. (G) As in C, but for $N=10^4$ points uniformly sampled from a two-dimensional ring torus, $T^2$. $T^2$ is constructed by revolving a circle parameterized by $\theta$, oriented perpendicular to the $xy$ plane, through an angle $\varphi$ around the $z$ axis. The scalar curvature only depends on the value of $\theta$ (SI Appendix, Supporting Methods, section D.1.3). (H) Scalar curvatures computed in G with their associated 95% CIs plotted as a function of the $\theta$ values of the data points. Colors are as in F. (I) Distribution of computed scalar curvatures for $N=10^4$ points uniformly sampled from the $d$-dimensional unit hypersphere, ${\mathcal{S}}^d$, for $d=\mathrm{2,3,5,7}$. As with ${\mathcal{S}}^2$, these manifolds are isotropic and have constant scalar curvature. The true values are shown as dashed red lines (SI Appendix, Supporting Methods, section D.1.1).

The Riemannian curvature of $M$ is related to the quadratic terms in the Taylor expansion of each $f_k$ with respect to the $t_i$s. Specifically, the Second Fundamental Form of $M$, $h_{ij}^k$, gives the second-order coefficient relating each $f_k$ to the quadratic term $t_i{t}_j$ (36):

$$h_{ij}^k\left(p\right)={\left.\frac{{\partial }^2{f}_k}{\partial t_i\partial t_j}\right|}_p.$$ [5]

The Riemannian curvature tensor is related to the Second Fundamental Form according to the Gauss–Codazzi equation (15):

$$R_{ijkl}=\left(h_{jk}^{\alpha }{h}_{il}^{\beta }-h_{ji}^{\beta }{h}_{kl}^{\alpha }\right)g_{\alpha \beta },$$ [6]

where $g_{\alpha \beta }$ is the metric of the ambient space, which we take to be the usual Euclidean metric ${\delta }_{\alpha ,\beta }$ going forward. The scalar curvature can be obtained by contracting the Riemannian curvature tensor:

$$S=\sum _{i,j}{R}_{ijij}.$$ [7]

This suggests a conceptually simple procedure to estimate the scalar curvature of a data manifold at each point $p$: 1) Estimate $T_M\left(p\right)$ and $N_M\left(p\right)$; 2) determine $h_{ij}^k\left(p\right)$ in local coordinates; and 3) compute $S\left(p\right)$ using Eqs. 6 and 7. We developed a computational tool that provides an implementation of this procedure. Briefly, given a set of data points $\left\{X\right\}\in {\mathbb{R}}^n$ and manifold dimension $d$, a neighborhood around each point $p$ is selected to be the $n$-dimensional ball centered on $p$ of radius $r$ encompassing $N_p\left(r\right)$ points (SI Appendix, Supporting Methods, section C.2). For each point $p$, Principal Component Analysis (PCA) (37) is performed on the $N_p\left(r\right)$ points in its neighborhood, and the first $d$ (last $n-d$) principal components (PCs) accounting for the most (least) variance are taken as an orthonormal basis for $T_M\left(p\right)$ ($N_M\left(p\right)$). The normal coordinates, $n_k$, of the $N_p\left(r\right)$ points in each neighborhood are fit by regression to a quadratic model in terms of the tangent coordinates, $t_i$, to obtain $h_{ij}^k\left(p\right)$ with associated uncertainties (Fig. 2B; SI Appendix, Supporting Methods, section C.1).

The choice of $r\left(p\right)$ is an important one since it sets the length scale at which curvature is computed for point $p$ (SI Appendix, Supporting Methods, section C.5). Our tool allows interrogation of curvature at any length scale of interest by allowing the user to manually set $r\left(p\right)$, a feature we use to inspect real-world datasets later in the paper. However, since the local geometry of the manifold may be nontrivial and unknown a priori, we also provide the ability to set $r\left(p\right)$ according to statistical, rather than geometric, principles. Specifically, our tool algorithmically chooses $r$ at each $p$ so that the uncertainty in $h_{ij}^k\left(p\right)$ from regression is less than a user-specified global parameter, ${\sigma }_h$ (SI Appendix, Supporting Methods, section C.2). Since a larger number of points reduces the uncertainty in regression, a smaller ${\sigma }_h$ requires a larger $r\left(p\right)\forall p\in M$. This strategy of setting ${\sigma }_h$ therefore allows neighborhood sizes to dynamically vary over the manifold based on the local density of the data, which means that the algorithm can gracefully handle nonuniform sampling of the manifold. The choice of ${\sigma }_h$ will depend on the global length scale, $L$, of the data points (SI Appendix, Supporting Methods, section C.5), the average density of sampled points, and, of course, the desired uncertainty in the estimates of $h_{ij}^k$. These uncertainties are, in turn, used to compute an SE, ${\sigma }_S$, accompanying the scalar curvature estimate at each point, using typical error propagation formulas (SI Appendix, Supporting Methods, section C.4). We specify ${\sigma }_h$ instead of ${\sigma }_S$ as the global parameter for choosing neighborhood sizes, since the latter depends nonlinearly on the values of $h_{ij}^k\left(p\right)$, which makes determining $r\left(p\right)$ more difficult.

Our algorithm also computes a goodness-of-fit (GOF) P value at each $p$ by comparing residuals from regression against a Gaussian distribution to quantify how well the normal coordinates are fit by a quadratic function (SI Appendix, Supporting Methods, section C.3). This P value can be tested at significance level $\alpha$ to declare a fit to be poor when the residuals are significantly non-Gaussian. The P value can be disregarded if the neighborhood size is manually specified to be larger than a length scale for which a quadratic fit is appropriate. However, when ${\sigma }_h$ is specified instead, a uniform distribution of these P values over $M$ indicates that the desired uncertainty results in neighborhoods that are well approximated using quadratic regression. We adopted this heuristic when choosing ${\sigma }_h$ for the datasets studied in this paper (SI Appendix, Supporting Methods, sections D.3, E.7 and F.6). The software is available at https://gitlab.com/hormozlab/ManifoldCurvature.

We first applied our algorithm to compute scalar curvatures for the same $N=10^4$ points uniformly sampled from ${\mathcal{S}}^2$ for which the intrinsic approach failed (Fig. 2C; SI Appendix, Supporting Methods, section D.1.1). The algorithm yielded scalar curvature estimates at each point with mean error $-0.17$ (computed by averaging the difference between the point-wise scalar curvature estimates and the ground-truth value of two across all points) using neighborhoods that only contained $N_p\left(r\right)\approx 10^2$ points. This is already superior to the intrinsic approach, which failed to compute even average scalar accurate to $\pm 1$ for the same sample size. The nonzero value of the mean error indicates that our estimator is biased. The values of $h_{ij}^k$ are not biased because they are obtained by using regression. Even so, the components of the Riemannian curvature tensor, $R_{ijkl}$, may still be biased because they are nonlinear functions of $h_{ij}^k$. Note that for ${\mathcal{S}}^2$, this bias is the same across all data points (because of the isotropic nature of the manifold) and therefore results in a systematic underestimation of scalar curvature (Fig. 2C; SI Appendix, Supporting Methods, section C.4). We also computed 95% CIs for our estimates as $S\pm 2{\sigma }_S$, and, despite the mean error, 73% of points still reported a 95% CI containing the true value of two (Fig. 2D).

We next tested our algorithm on a two-dimensional manifold with negative scalar curvature, by uniformly sampling $N=10^4$ points from the one-sheet hyperboloid, $H_2^2$ (Fig. 2E; SI Appendix, Supporting Methods, section D.1.2). Here, $71\%$ of points reported a 95% CI containing the true scalar curvature (Fig. 2F). Lastly, we considered the two-dimensional ring torus, $T^2$ (Fig. 2G; SI Appendix, Supporting Methods, section D.1.3). As a manifold with regions of positive, zero, and negative scalar curvature, $T^2$ is a useful toy model for understanding more complex two-dimensional manifolds and gaining intuition for higher-dimensional manifolds. In two dimensions, regions of a manifold with positive scalar curvature ($\theta =\mathrm{0,2}\pi$ in Fig. 2H) are dome-shaped, regions with zero scalar curvature ($\theta =\frac{\pi }{2},\frac{3\pi }{2}$ in Fig. 2H) are planar, and regions with negative scalar curvature ($\theta =\pi$ in Fig. 2H) are saddle-shaped. We applied our tool to $N=10^4$ points uniformly sampled from $T^2$ and found that $88\%$ of points reported a 95% CI containing the true scalar curvature (Fig. 2H).

To test the applicability of our algorithm to higher-dimensional manifolds, we uniformly sampled $N=10^4$ points from unit hyperspheres, ${\mathcal{S}}^d$, and found that 90%, 84%, and 78% of points reported a 95% CI containing the true scalar curvature for $d=$ 3, 5, and 7, respectively (Fig. 2I; SI Appendix, Supporting Methods, section D.1.1). The number of terms, $h_{ij}^k$, in the Second Fundamental Form grows as $d^2$. For larger $d$, a greater number of data points and, hence, larger neighborhoods are needed for regression, but these are no longer well approximated by quadratic fits according to our GOF measure. More generally, higher-dimensional manifolds require a higher density of data to estimate scalar curvatures accurately.

We additionally characterized how our algorithm performed when data points were nonuniformly sampled (SI Appendix, Fig. S2A and Supporting Methods, section D.2.1) or convoluted by observational noise (SI Appendix, Fig. S2B and Supporting Methods, section D.2.2), when the dimension of the ambient space was large (SI Appendix, Fig. S2C and Supporting Methods, section D.2.3), and when the specified manifold dimension differed from the ground truth (SI Appendix, Fig. S2D and Supporting Methods, section D.2.4). We found that the algorithm is robust to nonuniform sampling, large ambient dimension, and small observational noise and provides signatures indicating when the manifold dimension may be misspecified. However, when the noise scale is large, the resulting manifold is no longer trivially related to the noise-free manifold, consistent with existing literature (38–41), so that scalar curvature cannot be accurately computed. Lastly, we note that since the full Riemannian curvature tensor is computed as an intermediate step in our algorithm, more intricate geometric features in the data can also be analyzed by using our tool, though we defer such investigation to future studies.

Taken together, these examples demonstrate the utility of the algorithm in recovering curvature with specified uncertainties for manifolds with positive and/or negative scalar curvature. Next, we tested our algorithm on real-world data.

Curvature of Image Patch Manifold Is Consistent with a Noisy Klein Bottle.

Pixel intensity values in images of natural scenes are not independently or uniformly distributed. Understanding the statistics of such images is important for designing compression algorithms (42) and for addressing challenges in the field of computer vision, such as segmentation (43). Lee et al. (44) analyzed the van Hateren dataset (45) consisting of grayscale images of natural scenes and discovered that the 3- × 3-pixel patches whose pixels have high contrast (i.e., the differences between the intensity values of adjacent pixels in a patch are large) are not uniformly distributed in ${\mathbb{R}}^9$, but are instead concentrated on a low-dimensional manifold. This is because high-contrast regions in a natural scene usually correspond to the edges of objects in the scene. High-contrast image patches consequently tend to contain gradients and not simply random speckle. Subsequent work using topological data analysis revealed that after appropriate normalization (which takes image patches from ${\mathbb{R}}^9$ to ${\mathcal{S}}^7\in {\mathbb{R}}^8$, so that the global length scale is $L=1$; SI Appendix, Supporting Methods, section E.2), dense regions of high-contrast image patches have the same homology as a two-dimensional manifold called a Klein bottle (21).

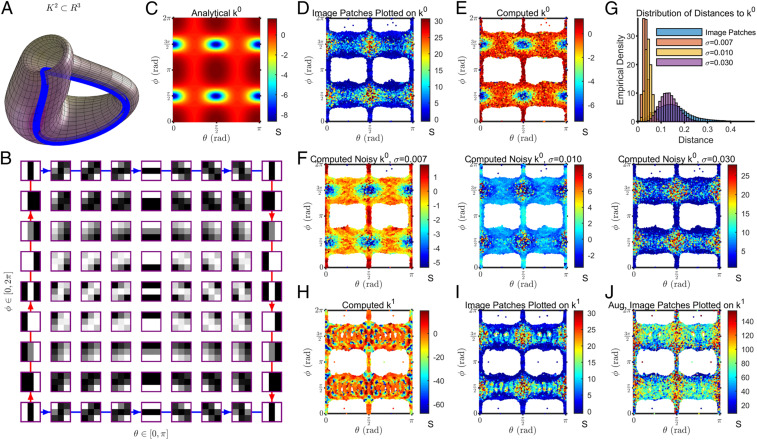
A Klein bottle, $K^2$, is a canonical manifold typically introduced in the context of orientability, where it is often visualized in ${\mathbb{R}}^3$ (as shown in Fig. 3A) to highlight that it is nonorientable. From a topological perspective, $K^2$ is a manifold parameterized by $\theta ,\varphi \in \left[\mathrm{0,2}\pi \right]$, as shown in Fig. 3B, in which vertical edges are defined to be $\theta =0$ and $\theta =\pi$, and horizontal edges are defined to be $\varphi =0$ and $\varphi =2\pi$. To make a closed surface, the vertical (horizontal) edges are glued together according to the red (blue) arrows in Fig. 3B. $K^2$ is therefore $2\pi$-periodic in $\varphi$, since a point corresponding to $\theta$ on the bottom horizontal edge ($\varphi =0$) is the same as the point corresponding to $\theta$ on the top horizontal edge ($\varphi =2\pi$). Similarly, a point corresponding to $\varphi$ on the left vertical edge ($\theta =0$) is the same as the point corresponding to $2\pi -\varphi$ on the right vertical edge ($\theta =\pi$). In short, points on $K^2$ obey the similarity relation $\left(\theta ,\varphi \right)\sim \left(\theta +\pi ,2\pi -\varphi \right)$. $K^2$ captures the dominant features in high-contrast image patches because $\theta$ can be treated as a parameter controlling rotation and $\varphi$ as a parameter controlling the relative contribution of linear vs. quadratic gradients (Fig. 3B).

Fig. 3.

Scalar curvature computed for image patches is consistent with that of a Klein bottle with added isotropic Gaussian noise. (A) The Klein bottle, $K^2$, is a two-dimensional manifold shown here in ${\mathbb{R}}^3$. (B) $k^0$ is an analytical embedding given by Carlsson et al. (21) relating parameter values $\theta ,\varphi \in \left[\mathrm{0,2}\pi \right]$ to 3- × 3-pixel patches of grayscale images (SI Appendix, Supporting Methods, section E.3, Eq. 24). $\theta$ controls the rotation of stripes in the image patches and $\varphi$ determines the relative contribution of linear vs. quadratic gradients. Importantly, as shown in the figure, this embedding has boundary conditions consistent with the topology of a Klein bottle (depicted by the blue/red arrows). In particular, the embedding produces image patches that obey the similarity relation $\left(\theta ,\varphi \right)\sim \left(\theta +\pi ,2\pi -\varphi \right)$. Adapted by permission from ref. 21: Springer Nature, International Journal of Computer Vision, copyright 2007. (C) The analytical scalar curvature of $k^0$ (derived as described in SI Appendix, Supporting Methods, section A). (D) Scalar curvatures computed for $N\approx 4.2\times 10^5$ high-contrast 3- × 3-pixel patches sampled from the grayscale images in the van Hateren dataset (45) are plotted here as a function of $\left({\theta }_0,{\varphi }_0\right)$, the parameter values of the closest point on $k^0$ associated with each image patch (SI Appendix, Supporting Methods, sections E.2 and E.4). (E) Scalar curvatures computed for the set of $N\approx 4.2\times 10^5$ closest points on $k^0$ associated with the image patches. Note the close correspondence with C, indicating that our algorithm correctly recapitulates the analytical scalar curvature. (F) As in E, but after adding isotropic Gaussian noise in ${\mathbb{R}}^9$ to the set of closest points on $k^0$ (SI Appendix, Supporting Methods, section E.6). Left to right corresponds to increasing levels of noise, $\sigma =0.007,0.01,0.03$. (G) The distribution of Euclidean distances in ${\mathbb{R}}^8$ between each image patch and its closest point on $k^0$ is shown in blue. The distribution of distances to $k^0$ after adding Gaussian noise to these closest points on $k^0$ is also shown. (H) $k^1$ is the analytical embedding from $\theta ,\varphi \in \left[\mathrm{0,2}\pi \right]$ to ${\mathbb{R}}^9$ that minimizes the sum of Euclidean distances from the image patches to the closest point on the embedding (SI Appendix, Supporting Methods, section E.5). Each of the $N\approx 4.2\times 10^5$ image patches was associated to its closest point on $k^1$, given by parameter values $\left({\theta }_1,{\varphi }_1\right)$ (SI Appendix, Supporting Methods, section E.4). Scalar curvatures computed on this set of $N\approx 4.2\times 10^5$ points on $k^1$ are shown. (I) The same scalar curvatures computed for the image patches and visualized on $\left({\theta }_0,{\varphi }_0\right)$ coordinates in D are shown here plotted on $\left({\theta }_1,{\varphi }_1\right)$ coordinates. (J) Scalar curvatures computed for a densely sampled manifold consisting of the full set of $N\approx 1.3\times 10^8$ high-contrast 3- × 3-pixel image patches in the van Hateren image dataset (SI Appendix, Supporting Methods, section E.2), visualized on $\left({\theta }_1,{\varphi }_1\right)$ coordinates.

An embedding of $K^2$ into ${\mathbb{R}}^9$ with an analytical form, $k^0$, was proposed by Carlsson et al. (21) to model image patches (SI Appendix, Supporting Methods, section E.3, Eq. 24). This embedding takes points from $\left(\theta ,\varphi \right)$ into image patches in ${\mathbb{R}}^9$, as shown in Fig. 3B. For example, $\theta =0$ ($\theta =\frac{\pi }{2}$) corresponds to patches with vertical (horizontal) stripes and $\varphi =\frac{\pi }{2},\frac{3\pi }{2}$ ($\varphi =0,\pi$) corresponds to patches with linear (quadratic) gradients. As $\theta$ increases, stripes in the image patches are rotated clockwise. As $\varphi$ increases, image patches oscillate between having quadratic and linear gradients. Importantly, the image patches constructed by this embedding obey the same similarity relation $\left(\theta ,\varphi \right)\sim \left(\theta +\pi ,2\pi -\varphi \right)$ topologically required of a Klein bottle. Whereas Carlsson et al. (21) studied the global topology of image patches using this embedding, here, we study their local geometry instead.

First, we analytically calculated the scalar curvature of $k^0$ as a function of $\left(\theta ,\varphi \right)$, as shown in Fig. 3C (SI Appendix, Supporting Methods, section A). Next, we used our algorithm to compute the scalar curvature on a data manifold of $N\approx 4.2\times 10^5$ high-contrast 3- × 3-pixel image patches randomly sampled from the same van Hateren dataset used to propose $k^0$ (SI Appendix, Supporting Methods, section E.2). We picked ${\sigma }_h$ so that the distribution of GOF P values was flat and fixed this value for all subsequent simulations (SI Appendix, Supporting Methods, section E.7). To visualize the results, we associated each image patch to its closest point on $k^0$ (SI Appendix, Supporting Methods, section E.4) and plotted the scalar curvatures on the resulting $\left({\theta }_0,{\varphi }_0\right)$ coordinates (Fig. 3D). Most image patches map to $\varphi =\frac{\pi }{2},\frac{3\pi }{2}$ or $\theta =0,\frac{\pi }{2}$ because linear gradients (of any orientation) and quadratic gradients that are vertically or horizontally oriented are the dominant features in the data, as reported (21, 44).

The scalar curvatures computed for the image patches did not match the analytical scalar curvature of $k^0$ (cf. Fig. 3 C and D). To identify the cause of this discrepancy, we first validated our algorithm by computing scalar curvatures on the set of $N\approx 4.2\times 10^5\hspace{0.17em}\left({\theta }_0,{\varphi }_0\right)$ points on $k^0$ associated with the image patches (Fig. 3E); we found close agreement with the analytical calculation (75% of points reported a 95% CI containing the true scalar curvature). Next, observing that the neighborhood sizes used for computing the scalar curvature of image patches were larger than those used for computing the scalar curvature of the associated $\left({\theta }_0,{\varphi }_0\right)$ points (cf. SI Appendix, Fig. S3 A and B), we recomputed the scalar curvatures of these $\left({\theta }_0,{\varphi }_0\right)$ points, but now with the same neighborhood sizes used for the image patches. The results agreed with the analytical calculation, but still did not match the scalar curvatures computed for the image patches (SI Appendix, Fig. S3C).

Having ruled out these two possibilities, we hypothesized that the discrepancy was caused by fluctuations in the positions of the image patches with respect to the $\left({\theta }_0,{\varphi }_0\right)$ points on the $k^0$ manifold (real image patches are noisy, and the Klein bottle embedding is only an idealization). We found that adding isotropic Gaussian noise of increasing magnitude in ${\mathbb{R}}^9$ to the set of $\left({\theta }_0,{\varphi }_0\right)$ points on $k^0$ indeed resulted in scalar curvatures that resembled the data (Fig. 3F; SI Appendix, Supporting Methods, section E.6). The best agreement between the scalar curvatures of the image patches and the noisy $\left({\theta }_0,{\varphi }_0\right)$ points was achieved when the magnitude of noise was $\sigma =0.03$. Notably, in this case, the median Euclidean distance of the noisy $\left({\theta }_0,{\varphi }_0\right)$ points to $k^0$ was 0.132, which is comparable to 0.148, the median Euclidean distance of the image patches to $k^0$ (Fig. 3G). Furthermore, the neighborhood sizes chosen by our algorithm when $\sigma =0.03$ (SI Appendix, Fig. S3A) matched those chosen for the image patches (SI Appendix, Fig. S3B).

To find an embedding of the Klein bottle that might better explain the scalar curvature of the image patches without needing to add noise, we incorporated higher-order terms to $k^0$ (SI Appendix, Supporting Methods, section E.3). The coefficients for the higher-order terms were determined by fitting the data, resulting in a new embedding, which we refer to as $k^1$ (SI Appendix, Supporting Methods, section E.5). The median Euclidean distance of the image patches to $k^1$ was 0.115 vs. 0.148 to $k^0$. As was done for $k^0$, we associated each image patch to its closest point $\left({\theta }_1,{\varphi }_1\right)$ on $k^1$ and used our algorithm to compute the scalar curvature of these $\left({\theta }_1,{\varphi }_1\right)$ points (Fig. 3H). Despite the reduction in the median Euclidean distance of images patches to the embedding, the scalar curvature of $k^1$ was even less similar to that of the image patches (visualized in Fig. 3I on these new $\left({\theta }_1,{\varphi }_1\right)$ coordinates for $k^1$) than was the scalar curvature of $k^0$; the range of scalar curvature values for $k^1$ was much larger than for either the image patches or $k^0$, and the scalar curvature fluctuates on smaller length scales.

Lastly, we reasoned that there might be fine-scale scalar curvature fluctuations in the image patches that are masked by the larger neighborhood sizes used to compute scalar curvature for the image patches (SI Appendix, Fig. S3B) relative to $k^1$ (SI Appendix, Fig. S3D). To decrease the neighborhood sizes chosen by the algorithm for the same ${\sigma }_h$, we augmented the image patch dataset using the full set of $N\approx 1.3\times 10^8$ high-contrast 3- × 3-pixel image patches from the van Hateren dataset (SI Appendix, Supporting Methods, section E.2). This resulted in neighborhood sizes comparable to those determined for $k^1$ (cf. SI Appendix, Fig. S3 D and E), but failed to recapitulate the fine-scale scalar curvature fluctuations observed in $k^1$ (Fig. 3J). As a sanity check, we confirmed that the scalar curvature of the augmented image patch dataset matched that of the original image patch dataset, when computed using the same neighborhood sizes as the latter (SI Appendix, Fig. S3F). Therefore, including higher-order terms in the embedding does not yield scalar curvatures that better agree with the data. Taken together, our analysis of curvature suggests that the image patch dataset can be best modeled by adding noise to the simplest embedding, $k^0$.

Having applied our algorithm on real-world manifold-valued data that are well modeled by an analytical embedding, we next turned our attention to scRNAseq datasets, which are generally regarded as low-dimensional manifolds and have no known analytical form.

scRNAseq Datasets Have Nontrivial Intrinsic Curvature.

In scRNAseq datasets, each data point corresponds to a cell and each coordinate to the abundance of a different gene. Here, we consider the data manifold after basic preprocessing and linear dimensionality reduction using PCA (SI Appendix, Supporting Methods, section F.1). Since many common analyses in the field, such as clustering, visualization, and inference of cell-differentiation trajectories, are performed in this reduced space, it is natural to compute curvature in this space as well. We set the ambient dimension, $n$, to be the number of PCs needed to explain 80% of the variance. The manifold dimension, $d$, for scRNAseq datasets is not well defined and needs to be chosen heuristically. As a simple heuristic, we specified $d$ as the number of PCs needed to explain 80% of the variance in the ambient space; i.e., 64% of the original variance (we show later that our computations are relatively insensitive to the choice of $d$).

We considered three datasets. The first consists of $N\approx 10^4$ peripheral blood mononuclear cells (PBMCs) collected from a healthy human donor (46). The second is a gastrulation dataset containing $N\approx 1.2\times 10^5$ cells pooled from nine embryonic mice sacked at 6-h intervals from embryonic day (E)6.5 to E8.5 (47). The final dataset is a benchmark in the field consisting of $N\approx 1.3\times 10^6$ brain cells pooled from two embryonic mice sacked at E18 (48). Refer to SI Appendix, Figs. S4A, S5A, and S6A for cell-type annotations for the three datasets.

The PBMC dataset is characteristic of the sample size of current scRNAseq data. The other two are larger than most scRNAseq datasets, and we included these to verify if geometric features seen in the first dataset can be reproduced for more densely sampled manifolds. For the PBMC, gastrulation, and brain datasets, the ambient (manifold) dimensions were determined to be 8, 11, and 9 (3, 3, and 5), respectively, according to the aforementioned heuristic (SI Appendix, Supporting Methods, section F.6). For all three datasets, the global length scale happened to be $L\approx 20$ (SI Appendix, Supporting Methods, section C.5). As before, we picked ${\sigma }_h$ for each dataset according to the distribution of GOF P values (SI Appendix, Figs. S4B, S5B, and S6B and Supporting Methods, section F.6).

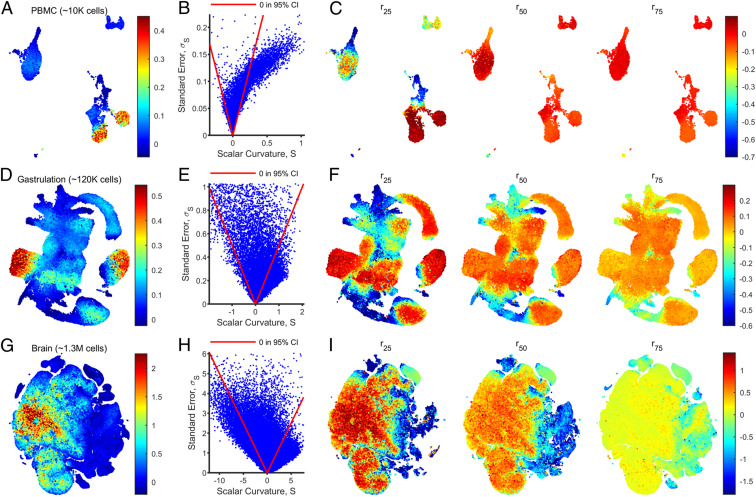
We visualized the computed scalar curvatures on standard plots employed in the field (UMAP and t-SNE; shown in Fig. 4 A, D, and G) and observed nontrivial scalar curvature for all three datasets. We found statistically significant correlations between the scalar curvature reported by each point and its kNN for $k\le 250$ (${\rho }_{Pearson}=0.58,0.18\text{and}0.38$ for the PBMC, gastrulation, and brain datasets, respectively, at $k=250$, P < 10⁻⁶; SI Appendix, Figs. S4C, S5C, and S6C), indicating that our algorithm yields scalar curvatures that vary continuously over the data manifolds. By plotting scalar curvatures against their SEs, ${\sigma }_S$, we verified that regions with nonzero scalar curvature are statistically significant (Fig. 4 B, E, and H). As a consistency check, we confirmed that the percentage of points with 95% CIs containing the scalar curvatures reported by their respective kNNs 1) decayed with increasing $k$ for $k\le 250$; and 2) was significantly larger than expected by chance (67%, 72%, and 61% for the PBMC, gastrulation, and brain datasets, respectively, at $k=250$, P < 0.001; SI Appendix, Figs. S4D, S5D, and S6D and Supporting Methods, section F.3.1).

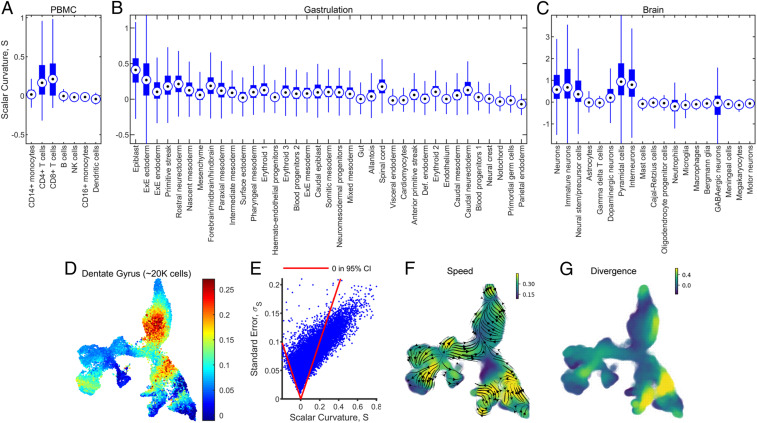
Fig. 4.

scRNAseq datasets have localized regions of nonzero scalar curvature. (A) Scalar curvatures were computed for a scRNAseq dataset with $N\approx 10^4$ PBMCs collected from a healthy human donor. The ambient ($n$) and manifold ($d$) dimensions were specified to be eight and three, respectively, and variable neighborhood sizes were chosen by setting ${\sigma }_h$ (SI Appendix, Supporting Methods, section F.6). The scalar curvatures are shown here overlaid onto UMAP coordinates, after smoothing the values over $k=250$ nearest neighbors in the ambient space. (B) Scatter plot of (unsmoothed) scalar curvatures, $S$, and associated SEs, ${\sigma }_S$, for each data point in the PBMC dataset. Points enclosed by the red lines reported a 95% CI ($S\pm 2{\sigma }_S$) including zero. (C) As in A, but with scalar curvatures computed by using a fixed neighborhood size, $r$, for all data points. The value of $r$ was set to be the 25th, 50th, and 75th percentile values (left to right) of the neighborhood sizes used in A (SI Appendix, Fig. S4E). Points for which a neighborhood of size $r$ does not include enough neighbors for regression are not shown. (D–F) As in A–C for a mouse gastrulation dataset with $N\approx 1.2\times 10^5$, $d=3$, and $n=11$. (G–I) As in A–C for a mouse brain dataset with $N\approx 1.3\times 10^6$, $d=5$, and $n=9$, plotted on t-SNE coordinates.

To rule out the possibility that localization of nonzero scalar curvature in certain regions of the UMAP/t-SNE plots is an artifact caused by other properties of the data that are also localized, we considered several factors. First, we plotted the GOF P value at each point on UMAP/t-SNE coordinates and noted that poor GOFs were not localized on the data manifolds, let alone to regions of nonzero scalar curvature (SI Appendix, Figs. S4B, S5B, and S6B). Therefore, the computed scalar curvatures are not due to poor fits.

Next, we plotted the neighborhood size, $r\left(p\right)$, used for fitting and observed that in some regions, nonzero scalar curvatures seemed to correspond to small $r$ (SI Appendix, Figs. S4E, S5E, and S6E). Since ${\sigma }_h$ is fixed, these regions necessarily have a larger number of neighbors $N_p\left(r\right)$ and are, hence, more dense (SI Appendix, Fig. S4F, S5F, and S6F). To rule out the possibility that the nonzero scalar curvatures were an artifact of smaller neighborhood size, we recomputed the scalar curvature at three fixed neighborhood sizes (Fig. 4 C, F, and I), corresponding to the 25th, 50th, and 75th percentile values of $r\left(p\right)$, which arose from setting ${\sigma }_h$ (SI Appendix, Figs. S4E, S5E, and S6E). In general, the scalar curvatures decreased in magnitude when neighborhood sizes increased. However, regions that had statistically significant nonzero scalar curvatures (zero falls outside of the 95% CI) using variable neighborhood sizes also had nonzero scalar curvatures for all three fixed neighborhood sizes. Additionally, statistically significant nonzero scalar curvature also emerged on other parts of the manifolds when using small fixed neighborhood sizes. These regions are therefore curved at small length scales, but do not have a sufficient density of points to resolve curvature to the desired uncertainty ${\sigma }_h$ (SI Appendix, Supporting Methods, section C.5). This is analogous to the image patch dataset for which we could resolve scalar curvatures of larger magnitude at a smaller length scale when the dataset was augmented with enough points to attain smaller neighborhood sizes for a fixed ${\sigma }_h$.

We also checked how computed scalar curvatures changed with density in a toy model with zero scalar curvature. Importantly, we did not observe the artifactual appearance of statistically significant nonzero scalar curvature, for either variable neighborhood sizes chosen by the algorithm to achieve ${\sigma }_h$ or for fixed neighborhood sizes (SI Appendix, Fig. S2A and Supporting Methods, section D.2.1). Taken together, although higher density allows us to resolve statistically significant nonzero scalar curvatures in scRNAseq data, these computed scalar curvatures are not an artifact of the smaller neighborhood sizes used in regions with higher density.

To ensure that the computed scalar curvatures were not sensitively dependent on the heuristically chosen manifold dimension, $d$, we also recomputed scalar curvatures for $d-1$ and $d+1$ and observed similar qualitative results (SI Appendix, Figs. S4G, S5G, and S6G). Lastly, we verified that the computed scalar curvatures were not correlated with the number of transcripts in each cell (SI Appendix, Figs. S4H, S5H, and S6H).

To confirm the robustness of our results to sampling, we randomly discarded $f\%$ of points in the ambient space determined for each dataset and recomputed scalar curvatures using the same values of $n$, $d$, and $r\left(p\right)$ used for the original dataset. We found that a statistically significant percentage of downsampled points (82% for the PBMC dataset with $f=75$, 78% for the gastrulation dataset with $f=75$, and 76% for the brain dataset with $f=50$; P < 0.001) had a 95% CI containing the scalar curvature reported by the same point for the original dataset (SI Appendix, Figs. S4I, S5I, and S6I and Supporting Methods, section F.3.2). This suggests that if the datasets were more highly sampled, and scalar curvatures were recomputed by using the same neighborhood sizes, they would be reliably contained within the currently reported 95% CIs. Unlike the two other datasets, the brain dataset could not be downsampled to $f=75$ while still having at least 75% of points report 95% CIs containing the originally reported scalar curvatures, despite having the most points. This might be because the brain dataset has a larger manifold dimension according to our heuristic and, therefore, requires a greater number of terms, $h_{ij}^k$, to be estimated in the Second Fundamental Form.

For the PBMC dataset, we additionally downsampled the single-cell count matrix by discarding $f\%$ of transcripts at random and preprocessing the same way. We recomputed scalar curvatures for this downsampled dataset with the same $n$, $d$, and $r\left(p\right)$ values used for the original dataset. Here, too, we found that when $f=50$ ($f=75$), 70% (65%) of the downsampled points had a 95% CI containing the originally reported scalar curvature (P < 0.001; SI Appendix, Fig. S4J and Supporting Methods, section F.3.3). Therefore, the computed scalar curvature is robust to changes in capture efficiency and sequencing depth. Taken together, our computational analysis reveals nontrivial intrinsic geometry in scRNAseq data.

Finally, we explored whether the computed scalar curvatures could be directly related to biological features. First, building on our observation that regions of nonzero scalar curvature are spatially localized, we considered the distribution of scalar curvatures for each cell type (Fig. 5 A–C). We found that for the PBMC dataset, there was a statistically significant difference in the mean scalar curvature between CD14⁺ monocytes and CD4⁺ T cells (false discovery rate [FDR] = 0.05; SI Appendix, Fig. S8A and Supporting Methods, section F.3.4). Likewise, for the gastrulation dataset, there were statistically significant differences in the average scalar curvature of the epiblast relative to the mesenchyme, surface ectoderm, and hemato-endothelial progenitors (SI Appendix, Fig. S8B). For the brain dataset, which had more data points by one to two orders of magnitude, we had enough statistical power to detect significant differences between 74 of the 171 pairs of cell populations, e.g., pyramidal cells and almost all other cell types (SI Appendix, Fig. S8C).

Fig. 5.

Scalar curvature is correlated with cell type and RNA velocity vector field speed and divergence. (A) Boxplot of the distribution of scalar curvatures for each annotated cell type in the PBMC dataset. The median is marked by the bullseye and the interquartile range by the thick blue bar. The whiskers extend up to 1.5 times the interquartile range in each direction. (B) As in A, but for the gastrulation dataset. (C) As in A, but for the brain dataset. (D and E) As in Fig. 4 A and B for a mouse dentate gyrus dataset with $N\approx 2\times 10^4$, $d=2$, and $n=6$. (F) Flow lines (shown as black arrows) and speed (colors) of the inferred RNA velocity vector field (SI Appendix, Supporting Methods, section F.5). (G) Divergence of the inferred RNA velocity vector field (SI Appendix, Supporting Methods, section F.5).

Next, in the PBMC dataset, we explored whether the expression levels of particular genes were correlated with the scalar curvature. We fit the scalar curvature to a linear regression model of gene expression and found nine significant genes (FDR = 0.05; SI Appendix, Supporting Methods, section F.4). These included genes with known differential expression between immune cell types [MNDA (49), LILRA2 (50), BHLHE41 (51), ACKR4 (52), ACOT7 (53), CYTOR (54), and ST8SIA6 (55)].

Lastly, we investigated whether scalar curvature was related to transcriptional dynamics, by repeating our analysis on a dataset of $N\approx 2\times 10^4$ cells from the dentate gyrus of mice (Fig. 5 D and E and SI Appendix, Fig. S7), for which counts of spliced vs. unspliced transcripts in each gene of a cell was available (56). La Manno et al. (57) showed that this information can be used to reconstruct an RNA velocity vector for each cell, from which its transcriptional trajectory can be inferred over short time scales. We reconstructed the RNA velocity vector field over all cells (Fig. 5F; SI Appendix, Supporting Methods, section F.5) using the dynamo software package (58) and found that the scalar curvature for this dataset was anticorrelated with both the speed (${\rho }_{Pearson}=-0.23$, P < 10⁻⁶; Fig. 5F) and divergence of the vector field (${\rho }_{Pearson}=-0.26$, P < 10⁻⁶; Fig. 5G). Additionally, we found that five genes were significantly correlated with the scalar curvature (FDR = 0.05; SI Appendix, Supporting Methods, section F.4), including genes with known differential expression between cell types in the brain or regions of the dentate gyrus [ID2 (59), S100A10 (60), PRMT1 (61), and CRMP1 (62)]. This preliminary exploration suggests that manifold curvature and transcriptional dynamics are closely connected.

Discussion

In this study, we explored two approaches to computing the curvature of data manifolds using tools from twin branches of differential geometry. An intrinsic approach relying on estimating the Laplace–Beltrami operator’s eigenvalues from point cloud data was determined to be infeasible for sample sizes of $N\approx 10^4$ typical of current scRNAseq datasets, since curvature is sensitive to higher-order eigenvalues of the operator. Although methods such as MAGIC (63) and diffusion pseudotime (64) apply analogs of the Laplace–Beltrami operator to smooth scRNAseq data and infer cell-differentiation trajectories, respectively, using information intrinsic to the manifold, our results suggest that the embedding of the manifold in the ambient space provides valuable information necessary for estimating the intrinsic curvature. This observation is perhaps implicit in recent tools for estimating the Laplace–Beltrami operator, which first use moving local least squares to approximate a surface, thereby incorporating information from the ambient space (29).

Certainly, we found that an extrinsic approach in which the embedding is retained and curvature is determined by local quadratic fitting of data points in ambient coordinates is feasible given the sample size and degree of noise in real-world datasets. To obtain the scalar curvature of data manifolds, our algorithm first computes the full Riemannian curvature tensor. For other applications, this tensor can be used to compute other geometric quantities, such as Ricci curvature, or may itself be of interest. More generally, we focused on intrinsic curvature because we were interested in geometric properties of the manifolds independent of their embeddings. However, the Second Fundamental Form used in our approach to compute the intrinsic curvature can be used to obtain all of the information about the extrinsic curvature as well. Indeed, $h_{ij}^k\left(p\right)$ exactly quantifies the extent to which the manifold deviates in the $k$th normal direction from the $ij$-tangent plane at point $p$.

A key limitation of our algorithm is that the manifold dimension must be specified by the user. We also assumed that the manifold dimension is the same at every point in a dataset. Extending the algorithm to determine the manifold dimension from the data itself, potentially in a position-dependent manner, may prove useful. In addition, there is no inherently correct length scale over which curvature should be computed for a data manifold. Our algorithm chooses a length scale that varies from one part of the data manifold to another, according to the density of points, and is tuned to achieve a user-specified level of uncertainty in the computed curvature. For some applications, it might be more sensible to fix a desired length scale for computing the curvature.

As a demonstration of our algorithm, we computed the scalar curvature of image patches and found that it was consistent with that of a Klein bottle. This observation further validates the claim by Carlsson et al. (21), who showed that image patches have the topology of a Klein bottle. Unlike the Klein bottle parameterization of image patches, however, no definitive analytical form has been established for scRNAseq datasets. Recent work has suggested the use of hyperbolic geometry to model branching cell-differentiation trajectories (65, 66), and specific manifolds have been proposed to model reaction networks (67), which may be applicable to scRNAseq data. These proposed manifolds can be validated or improved by using knowledge of the intrinsic geometry of scRNAseq datasets. Finally, incorporating information about curvature may provide a more principled approach for developing dimensionality reduction and visualization tools. For example, recent work has developed variants of t-SNE and UMAP that additionally preserve local volumes in the embedding (68). Since scalar curvature directly affects volumes, angles, and other geometric quantities, the work presented here could aid such efforts.

Materials and Methods

SI Appendix, Supporting Methods, section A describes how to compute the scalar curvature of, and sample from, theoretical manifolds. Details of the intrinsic approach to curvature estimation are provided in SI Appendix, Supporting Methods, section B. Refer to SI Appendix, Supporting Methods, section C for a detailed exposition of the extrinsic approach to curvature estimation used in our algorithm. SI Appendix, Supporting Methods, section D describes the performance of our algorithm when challenged by real-world confounders in the data. Additional details pertaining to the toy models in Fig. 2, image patch/Klein bottle data in Fig. 3, and scRNAseq datasets in Figs. 4 and 5 can be found in SI Appendix, Supporting Methods, sections D–F, respectively.

Data and Code Availability

The van Hateren IML dataset (45) is available at http://bethgelab.org/datasets/vanhateren/ and was loaded according to the instructions there. The PBMC dataset (46) is available at https://support.10xgenomics.com/single-cell-gene-expression/datasets/4.0.0/Parent_NGSC3_DI_PBMC. The gastrulation dataset (47) can be retrieved by using instructions found at https://github.com/MarioniLab/EmbryoTimecourse2018. The brain dataset (48) is available at https://support.10xgenomics.com/single-cell-gene-expression/datasets/1.3.0/1M_neurons. A Python notebook with the dentate gyrus dataset (57) can be retrieved at https://github.com/velocyto-team/velocyto-notebooks/blob/master/python/DentateGyrus.ipynb. The software package described here to compute scalar curvature is available at https://gitlab.com/hormozlab/ManifoldCurvature. All code and instructions to reproduce the numerics and figures in this study can be found at https://gitlab.com/hormozlab/PNAS_2021_Curvature.