Applying a Random Projection Algorithm to Optimize Machine Learning Model for Breast Lesion Classification

Abstract

Machine learning is widely used in developing computer-aided diagnosis (CAD) schemes of medical images. However, CAD usually computes large number of image features from the targeted regions, which creates a challenge of how to identify a small and optimal feature vector to build robust machine learning models. In this study, we investigate feasibility of applying a random projection algorithm (RPA) to build an optimal feature vector from the initially CAD-generated large feature pool and improve performance of machine learning model. We assemble a retrospective dataset involving 1,487 cases of mammograms in which 644 cases have confirmed malignant mass lesions and 843 have benign lesions. A CAD scheme is first applied to segment mass regions and initially compute 181 features. Then, support vector machine (SVM) models embedded with several feature dimensionality reduction methods are built to predict likelihood of lesions being malignant. All SVM models are trained and tested using a leave-one-case-out cross-validation method. SVM generates a likelihood score of each segmented mass region depicting on one-view mammogram. By fusion of two scores of the same mass depicting on two-view mammograms, a case-based likelihood score is also evaluated. Comparing with the principle component analyses, nonnegative matrix factorization, and Chi-squared methods, SVM embedded with the RPA yielded a significantly higher case-based lesion classification performance with the area under ROC curve of 0.84±0.01 (p<0.02). The study demonstrates that the random project algorithm is a promising method to generate optimal feature vectors to help improve performance of machine learning models of medical images.

I. Introduction

Developing computer-aided detection and diagnosis (CAD) schemes of medical images have been attracting broad research interest in order to detect suspicious diseased regions, classify between malignant and benign lesions, quantify disease severity, and predict disease prognosis or monitor treatment efficacy. Some CAD schemes have been used as “a second reader” or quantitative image marker assessment tools in clinical practice to assist clinicians (i.e., radiologists) aiming to improve image reading accuracy and reduce the inter-reader variability [1]. Despite of extensive research effort and progress made in the CAD field, researchers still face many challenges in developing CAD schemes for clinical applications [2]. For example, in developing CAD schemes, machine learning plays a critical role, which use image features to train classification models to predict the likelihood of the analyzed regions depicting or patterns representing diseases. However, due to the great heterogeneity of disease patterns and the limited size of image datasets, how to identify a small and optimal image feature vector to build the highly performed and robust machine learning models remains a difficult task.

In current CAD schemes, after image preprocessing to reduce image noise, detecting and segmenting suspicious regions of interest (ROIs), CAD schemes can compute many image features from the entire image region or the segmented ROIs. Recently, two methods have attracted broad research interest to compute image features. One uses a deep transfer learning model as an automated feature extractor (i.e., extracting 4,096 features in a fully connected layer (FC6 or FC7) of an AlexNet). The disadvantage of this approach is requiring very big training and validation image datasets, which are often not available in medical image fields. Another approach uses radiomics concept and method to compute and generate an initial feature pool. Although Radiomics typically computes smaller number of features than deep learning based feature extractors, it may still compute many features (i.e., >1,000 image features, which mostly represent texture patterns of the segmented ROIs in variety of scanning directions as reported in previous studies [3, 4]). However, due to the limited size of the training datasets, such large number of image features can often drive to overfit machine learning models and reduce model robustness. Thus, it is important to build an optimal feature vector from the initially large feature pool in which the generated features should not be redundant or highly correlated [5]. Then, machine learning models can be better trained to achieve the enhanced performance and robustness. In general, if the feature dimensionality reduction happens with choosing the most effective image features from the initial feature pool, it is known as feature selection (i.e., using sequential forward floating selection (SFFS) [6]). On the other hand, if the dimensionality reduction comes from reanalyzing the initial set of features to produce a new set of orthogonal features, it is known as feature regeneration (i.e., principal component analysis (PCA) and its modified algorithms [7]). Comparing between these two methods, feature regeneration method has advantages to more effectively eliminate or reduce redundancy or correlation in the final optimal image feature vector. However, most of medical image data or features have very complicated or heterogeneous distribution patterns, which may not meet the precondition that all feature variables are linear to optimally apply PCA-type feature regeneration methods.

In order to better address this challenge and more reliably regenerate image feature vector for developing CAD schemes of medical images, we investigate and test another feature regeneration method namely, a random projection algorithm (RPA), which is an efficient way to map features into a space with a lower-dimensional subspace, while preserving the distances between points under better contrast. This mapping process is done with a random projection matrix. In the lower space since the distance is preserved, it will be much easier and reliably to classify between two feature classes. Because of its advantages and high performance, RPA has been tested and implemented in a wide range of engineering applications including handwrite recognition [8], face recognition and detection [9], visual object tracking and recognition [10, 11], and car detection [12].

Thus, motivated by the success of applying RPA to the complex and nonlinear feature data used in many engineering application domains, we hypothesize that RPA also has advantages when applying to medical images with the heterogeneous feature distributions. To test our hypothesis, we conduct this study to investigate feasibility and potential advantages of applying RPA to build optimal feature vector and train machine learning model implemented in a new computer-aided diagnosis (CAD) scheme to classify between malignant and benign breast lesions depicting on digital mammograms. The details of the assembled image dataset, the experimental methods of feature regeneration using RPA and a support vector machine (SVM) model optimization, data analysis and performance evaluation results are presented in the following sections.

II. Materials and Methods

A. Image Dataset

A fully anonymized dataset of full-field digital mammography (FFDM) images acquired from 1,487 patients are retrospectively assembled and used in this study. All cases were randomly selected by an institutional review board (IRB) certified research coordinator from the cancer repository and picture archive and communication system (PACS). All selected cases have suspicious soft-tissue mass type lesions previously detected by the radiologists on the mammograms. Based on lesion biopsy results, 644 cases depict malignant lesions and 843 cases had benign lesions. These patients have an age range from 35 to 80 years old. Table I summarizes and compares case distribution information of patients’ age and mammographic density rated by radiologists using breast imaging reporting and data system (BIRADS) guidelines. As shown in the table, patients in benign group are moderately younger than the patients in the malignant group. However, there is not a significant difference of mammographic density between the two groups of patients (p = 0.576).

TABLE I.

Case number and percentage distribution of patients age and mammographic density rated by radiologists using BIRADS guidelines.

	Subgroup	Malignant Cases	Benign Cases
Density BIRADS	1	25 (3.9%)	58 (6.9%)
	2	186 (28.8%)	262 (31.1%)
	3	401 (62.3%)	502 (59.5%)
p-value = 0.576	4	32 (5.0%)	21 (2.5%)
Age of Patients (years old)	A < 40	11 (3.4%)	71 (8.4%)
	40 ≤ A < 50	109(19.2%)	158(18.7%)
	50 ≤ A < 60	167(25.6%)	285(33.8%)
	60 ≤ A < 70	180(24.4%)	192(22.8%)
	70 ≤ A	177(27.4%)	137(16.3%)

All FFDM images were acquired using one type of digital mammography machines (Selenia Dimensions made by the Hologic Company), which have a fixed pixel size of 70μm in order to detect microcalcifications. Since in this study, we only focus on classification of soft tissue mass type lesions, all images are thus subsampled using a pixel averaging method with a 5 × 5 pixel frame, so that the pixel size of the subsampled images increases to 0.35mm. This subsample method has been used and reported in many of our previous CAD studies (i.e., [13, 14]). Additionally, in this dataset, the majority of cases have two craniocaudal (CC) and mediolateral oblique (MLO) view mammograms of either left or right breast in which the suspicious lesions are detected by the radiologists, while small fraction of cases just have one CC or MLO image in which the lesions were detected. Overall, 1,197 images depicting malignant lesions and 1,302 images depicting benign lesions are available in this image dataset. All lesion centers are visually marked by the radiologists using a custom-designed interactive graphic user interface (GUI) tool. The marked lesion centers are recorded and used as “ground-truth” to evaluate CAD performance [13].

B. Initial Image Feature Pool with a High Dimensionality

In developing CAD schemes to classify between malignant and benign breast lesions, many different approaches have been investigated and applied to compute image features including those computed from the segmented lesions [15], the fixed regions of interest (ROIs) [16] and the entire breast area [14]. Each approach has advantages and disadvantages. However, their classification performance may be quite comparable with an appropriate training and optimization process. Thus, since this study focus on investigating the feasibility and potential advantages of a new feature dimensionality reduction method of RPA, we will use a simple approach to compute the initial image features from both the fixed ROI and the segmented lesion regions.

Since classification between malignant and benign lesions is a difficult task, which depends on optimal fusion of many image features related to tissue density heterogeneity, speculation of lesion boundary, as well as variation of surrounding tissues. Previous studies have demonstrated that statistics and texture features can be used to model these valuable image features including intensity, energy, uniformity, entropy, and statistical moments, etc. Thus, like most CAD schemes using the ROIs with a fixed size as classification targets (including the schemes using deep learning approaches [17]), this CAD scheme also focuses on using the statistics and texture-based image features computed from the defined ROIs and the segmented lesion regions. For this purpose, following methods are used to compute image features that are included in the initial feature pool.

First, from a ROI of an input image, gray level difference method (GLDM) is used to compute the occurrence of the absolute difference between pairs of gray levels divided in a particularly defined distance in several directions. It is a practical way for modeling analytical texture features. The output of this function is four different probability distributions. For an image I(m, n), we consider displacement in different directions like δ(d_x, d_y), then $\widehat{I}(m,n)=\mid I(m,n)-I(m+d_x,n+d_y)\mid$ estimates the absolute difference between gray levels, where d_x, d_y are integer values. Now it is possible to determine an estimated probability density function for $\widehat{I}(m,n)$ like f(.∣δ) in which $f(i\mid \delta )=P(\widehat{I}(m,n)=i)$. It means for an image with L gray levels, the probability density function is L-dimensional. The components in each index of the function show the probability of $\widehat{I}(m,n)$ with the same value of the index. In the proposed method implemented in this CAD study, we consider d_x = d_y = 11 which is calculated heuristically [18]. The probability functions are computed in four directions (φ = 0, π/4, π/2, 3π/4), which signifies that four probability functions are computed to provide the absolute differences in four primary directions that each of which is used for feature extraction.

Second, a gray-level co-occurrence matrix (GLCM) estimates the second-order joint conditional probability density function. The GLCM carries information about the locations of pixels having similar gray level values, as well as the distance and angular spatial correlation over an image sub-region. To establish the occurrence probability of pixels with the gray level of i,j over an image along a given distance of d and a specific orientation of φ, we have P(i, j, d, φ). In this way, the output matrix has a dimension of the gray levels (L) of the image [19]. Like GLDM, we compute four co-occurrence matrices in four cardinal directions (φ = 0, π/4, π/2, 3π/4). GLCM is rotation invariant. We combine the results of different angles in a summation mode to obtain the following probability density function for feature extraction, which is also normalized to reduce image dependence.

$$\begin{gathered} P(i,j)=\sum _{\phi =0,\pi ∕4,\pi ∕2,3\pi ∕4}P(i,j,d=2,\phi ) \\ P(i,j)=\frac{P(i,j)}{{\sum }_i{\sum }_{j}P(i,j)};i,j=1,2,3,\dots ,L \end{gathered}$$ (1)

Third, a gray level run length matrix (GLRLM) is another popular way to extract textural features. In each local area depicting suspicious breast lesion, a set of pixel values are searched within a predefined interval of the gray levels in several directions. They are defined as gray level runs. GLRM calculates the length of gray-level runs. The length of the run is the number of pixels within the run. In the ROI, spatial variation of the pixel values for benign and malignant lesions may be different, and gray level run is a proper way to delineate this variation. The output of a GLRM is a matrix with elements that express the number of runs in a particular gray level interval with a distinct length. Depending on the orientation of the run, different matrices can be formed [20]. We in this study consider four different directions (φ = 0, π/4, π/2, 3π/4) for GLRM calculations. Then, just like GLCM, GLRM is also rotation invariant. Thus, the output matrices of different angles in a summation mode are merged to generate one matrix.

Fourth, in addition to the computing texture features from the ROI of the original image in the spatial domain, we also explore and conduct multiresolution analysis, which is a reliable way to make it possible to perform zooming concept through a wide range of sub-bands in more details [21]. Hence, textural features extracted from the multiresolution sub-bands manifest the difference in texture more clearly. Specifically, a wavelet transform is performed to extract image texture features. Wavelet decomposes an image into the sub-bands made with high-pass and low-pass filters in horizontal and vertical directions followed by a down-sampling process. While down-sampling is suitable for noise cancelation and data compression, high-pass filters are beneficial to focus on edge, variations, and the deviation, which can show and quantify texture difference between benign and malignant lesions. For this purpose, we apply 2D Daubechies (Db4) wavelet on each ROI to get approximate and detailed coefficients. From the computed wavelet maps, a wide range of texture features is extracted from principal components of this domain.

Moreover, analyzing geometry and boundary of the breast lesions and the neighboring area is another way to distinguish benign and malignant lesions. In general, benign lesions are typically round, smooth, convex shaped, with well-circumscribed boundary, while malignant lesions tend to be much blurry, irregular, rough, with non-convex shapes [22]. Hence, we also extract and compute a group of features that represent geometry and shape of lesion boundary contour. Then, we add all computed features as described above to create the initial pool of image features.

C. Applying Random Projection Algorithm (RPA) to Generate Optimal Feature Vector

Before using RPA to generate an optimal feature vector from the initial image feature pool, we first normalize each feature to make its value distribution between [0, 1] to reduce case-based dependency and weight all features equally. Thus, for each case, we have a feature vector of size d, which is valuable to determine that case based on the extracted features as a point in a d dimensional space. For two points like X = (x₁, … , x_d) and Y = (y₁, … y_d), the distance in d dimensional spaces define as:

$$\mid X-Y\mid =\sqrt{\sum _{j=1}^d(x_j-y_j{)}^2}$$ (2)

In addition, it is also possible to define the volume V of a sphere in a d dimensional space as a function of its radius (r) and the dimension of the space as (3). This equation is proved in [23].

$$V(d)=\frac{r^d{\pi }^{\frac{d}{2}}}{\frac{1}{2}d\Gamma (\frac{d}{2})}$$ (3)

The matrix of features is normalized between [0, 1]. It means a sphere with r = 1 can encompass all the data. An interesting fact about a unit-radius sphere is that as equation (4) shows, as the dimension increase, the volume goes to zero. Since ${\pi }^{\frac{d}{2}}$ is an exponential of $\frac{d}{2}$, while growing rate of $\Gamma (\frac{d}{2})$ is a factorial of $\frac{d}{2}$. At the same time, the maximum possible distance between two points stays at 2.

$$\underset{d\to \infty }{\text{lim}}\left(\frac{{\pi }^{\frac{d}{2}}}{\frac{d}{2}\Gamma \left(\frac{d}{2}\right)}\right)\cong 0$$ (4)

Moreover, based on the heavy-tailed distribution theorem, for a case like X = (x₁, … , x_d) in the space of features, suppose with an acceptable approximation features are independent, or nearly perpendicular variables as mapped to different axes, with E(x_i) = p_i, ${\sum }_{i=1}^d{p}_i=\mu$ and E∣(x_i − p_i)^k∣ ≤ p_i for k = 2,3, … , ⌊t²/6μ⌋, then, the previous study [24] has proven that:

$$prob(\mid \sum _{i=1}^d{x}_i-\mu \mid \ge t)\le Max\left(3e^{\frac{-t^2}{12\mu }},4\times 2^{\frac{-t}{e}}\right)$$ (5)

We can perceive that the farther the value of t increases, the smaller the chance of having a point out of that distance, which means that X would be concentrated around the mean value. Overall, based on equations (4), and (5) with an acceptable approximation, all data are encompassed in a sphere of size one, and they are concentrated around their mean value. As a result, if the dimensionality is high, the volume of the sphere is close to zero. Hence, the contrast between the cases is not enough for a proper classification.

Above analysis also indicates the more features included in the initial feature vector, the higher the dimension of the space is, and the more data is concentrated around the center, which makes it more difficult to have enough contrast between the features. A powerful technique to reduce the dimensionality while approximately preserves the distance between the points, which implies approximate preservation of the highest amount of information, is the key point that we are looking for. If we adopt a typical feature selection method and randomly select a k-dimensional sup-space of the initial feature vector, it is possible to prove that all the projected distances in the new space are within a determined scale-factor of the initial d-dimensional space [25]. Hence, although some redundant features are removed, the final accuracy may not increase, since contrast between the points may still be not enough to present a robust model.

To address this issue, we take advantage of Johnson-Lindenstrauss Lemma to optimize the feature space. Based on the idea of this lemma, for any 0 < ε < 1, and any number of cases as N, which are like the points in d-dimensional space (${\mathbb{R}}^d$), if we assume k as a positive integer, it can be computed as:

$$k\ge 4\frac{\text{ln}N}{(\frac{{ϵ}^2}{2}-\frac{{ϵ}^3}{3})}$$ (6)

Then, for any set V of N points in ${\mathbb{R}}^d$, for all u,v ∈ V, it is possible to prove that there is a map, or random projection function like $f:{\mathbb{R}}^d\to {\mathbb{R}}^k$, which preserves the distance in the following approximation [26], which is known as Restricted Isometry Property(RIP):

$$\begin{gathered} (1-ϵ)\mid u-v{\mid }^2\le \mid f(u)-f(v){\mid }^2 \\ \le (1+ϵ)\mid u-v{\mid }^2 \end{gathered}$$ (7)

Another arrangement of this formula is like:

$$\frac{\mid f(u)-f(v){\mid }^2}{(1+ϵ)}\le \mid u-v{\mid }^2\le \frac{\mid f(u)-f(v){\mid }^2}{(1-ϵ)}$$ (8)

As these formulas show the distance between the set of points in the lower-dimension space is approximately close to the distance in high-dimensional space. This Lemma states that it is possible to project a set of points from a high-dimensional space into a lower dimensional space, while the distances between the points are nearly preserved.

It implies that if we project the initial group of features into a space with a lower-dimensional subspace using the random projection method, the distances between points are preserved under better contrast. This may help better classify between two feature classes representing benign and malignant lesions with low risk of overfitting.

It should be noted that for an input matrix of features like $\mathrm{X}\in {\mathbb{R}}^{n\times d}$, n and d represent the number of training samples and features, respectively. Unlike the principal component analysis (PCA) that assumes relationship among feature variables are linear and intends to generate new orthogonal features, RPA aims to preserve distance of the points (training samples) while reducing the space dimensionality. Thus, using RPA will create a subspace $\tilde{\mathrm{X}}=\text{XR}$ in which R satisfies the RIP condition, and $R\in {\mathbb{R}}^{d\times k}$, $\tilde{\mathrm{X}}\in {\mathbb{R}}^{n\times k}$. Since the subspace's geometry is preserved, previous studies [27,28] proved that a SVM based machine learning classifier could better preserve the characteristics of the image dataset to build the optimal hyperplane and thus reduce the generalization error. In other words, if an SVM classifier makes the resulting margin ${\gamma }^{\ast }={}^1∕_{\Vert w^{\ast }{\Vert }^2}$ for its optimal hyperplane (w*) after solving the optimization problem on the initial feature space of X, and on the subspace of $\tilde{\mathrm{X}}$, it makes the resulting margin ${\tilde{\gamma }}^{\ast }={}^1∕_{\Vert {\tilde{w}}^{\ast }{\Vert }^2}$ for the respective optimized hyperplane $({\tilde{w}}^{\ast })$. Another study [29] also proved that hinge loss (for margin ${\tilde{\gamma }}^{\ast }$) of the classifier trained on the subspace data ($\tilde{\mathrm{X}}$) was less than that (γ*) of the classifier trained on the original data (X). Strictly speaking, the trained classifier's error rate on the optimized subspace generated using RPA is lower than that of the classifier trained on the original space. It indicates that training a machine learning classifier using an optimal subspace under RIP condition can build a more accurate and robust model for the classification purpose

In this study, we investigate and demonstrate whether using RPA can yield better result as comparable to other popular feature dimensionality reduction approaches (i.e., PCA).

D. Experiment of Feature Combination and Dimensionality Reduction

First, the proposed CAD scheme applies an image preprocessing step to the whole images in the dataset to read them one by one, and based on the lesion centers pre-marked by the radiologists to extract a squared ROI area in which the centers of the lesion and ROI overlap. In order to identify the optimal size of the ROIs, a heuristic method is applied to select and analyze ROI size. Basically, the different ROI sizes (i.e., in the range from 128×128 to 180×180 pixels) are examined and compared. From the experiments, we observe that the ROIs with size of 150×150 pixels generate the best classification results applying to this large and diverse dataset, which reveals that this is the most efficient size to cover all mass lesions included in our diverse dataset, which corresponds to use the ROI of 52.5 × 52.5mm². Figure 1 shows examples of 4 ROIs depicting two malignant lesions and two benign lesions. After ROI determination, all the images in the dataset are saved in Portable Network Graphics (PNG) format with 16 bits in the lossless mode for the feature extraction phase.

Fig. 1.

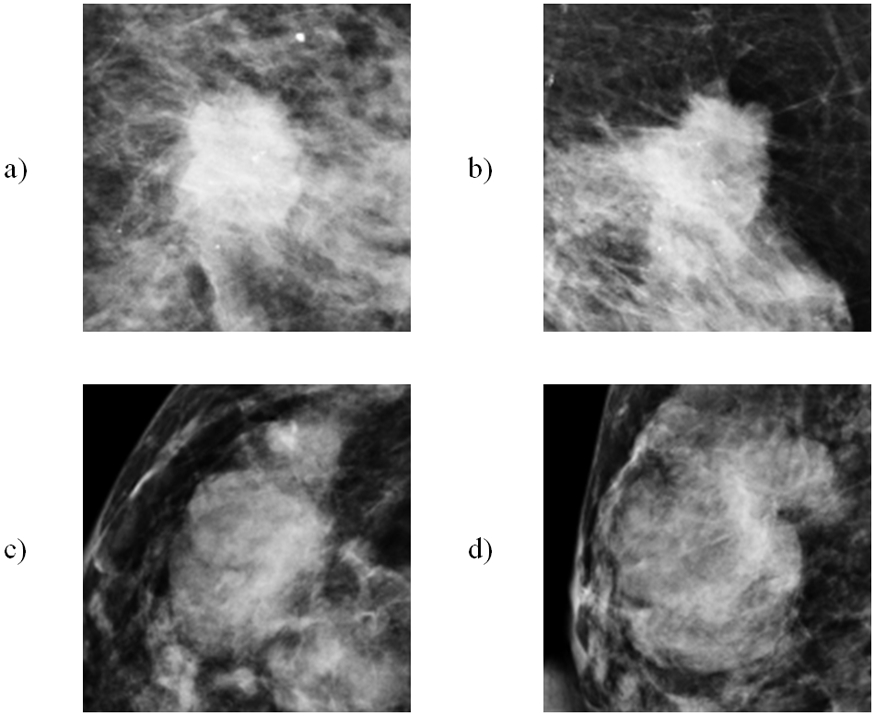
Example of 4 extracted ROIs with the detected suspicious soft-tissue masses (lesions) in ROI center. a,b) 2 ROIs involving malignant lesions and c,d) 2 ROIs involving benign lesions.

Next, the CAD scheme is applied to segment lesion from the background. For this process, CAD applies an unsharp masking method in which a low-pass filter with a window-size of 30 is first applied to filter the whole ROI. Next, CAD computes the absolute pixel value difference between the original ROI and the filtered ROI to produce a new image map that highlights the lesion and other regions (or blobs) with locally higher and heterogeneous tissue density. Then, CAD applies morphological filters (i.e., opening and closing) to delete the small and isolated blobs (with the pixel members less than 50), and repair boundary contour of the lesion and other remaining blobs with higher tissue density. Since in this study, the user clicks the lesion center and the ROI is extracted around this clicked point, the blob located in the center of ROI represents the segmented lesion. Figure 2 shows an example of applying this algorithm to locate and segment suspicious lesion from the surrounding tissue background.

Fig. 2.

Example to illustrate lesion segmentation, which include a) the original ROI, b) absolute difference of ROI from low-pass filtered version, c) combination of (a) and (b) which gives the suspicious regions better contrast to the background, d) output of morphological filtering, e) blob with the largest size is selected (a binary version of the lesion), and f) finally segmented lesion area. It is output of mapping (e) to (a).

After image segmentation, CAD scheme computes several sets of the relevant image features. The first group of features are the pixel value (or density) related statistics features as summarized in Table II. These 20 statistics features are repeatedly computed from three types of images namely, 1) the entire ROI of the original images (as shown in Figure 2(a)), 2) the segmented lesion region (as shown in Figure 2(f)), and 3) all highly dense and heterogeneous tissue blobs (as shown in Figure. 2(d)). Thus, this group of features includes 60 statistics features.

TABLE II.

List of the computed Features on ROI Area

Feature category	Feature Description
Density related features	1.Mean, 2. variance, 3. skewness, 4. kurtosis, 5. entropy, 6. correlation, 7. energy, 8. root mean square level, 9. uniformity, 10. max, 11. min, 12. median, 13. range, 14. mean absolute deviation, 15. Contrast, 16. homogeneity, 17. smoothness, 18. inverse difference movement, 19. suspicious regions volume, 20. standard deviation.

The second group of features is computed from the GLRLM matrix of the ROI area. For this purpose, 16 different quantization levels are considered to calculate all probability functions in four different directions from the histograms. After combining the probability functions, on rotation invariance version of them, the following group of features is computed. Features are short-run emphasis, long-run emphasis, gray level non-uniformity, run percentage, run-length non-uniformity, low gray level run emphasis, and high gray level run emphasis. Hence, this group of features includes seven GLRM-based features.

The third group of features includes GLDM based features computed from the entire ROI. Specifically, we select a distance value of 11 pixels for the inter-sample distance calculation. CAD computes four different probability density functions (PDFs) based on the image histogram calculation in different directions. The PDF (p) with (μ) as the mean of the population, standard deviation, root mean square level, and the first four statistical moments (n = 1, 2, 3, 4) with the following equation are calculated as features.

$${\widehat{m}}_n=\sum _{i=1}^N{p}_i(x_i-\mu {)}^n$$ (9)

It is an unbiased estimate of n^th moment possible to calculate by:

$$m_n=\underset{-\infty }{\overset{\infty }{\int }}p(x)x^{n}dx$$ (10)

As shown in equation 10, p(x) is weighted by xⁿ. Hence, any change in the p(x) is polynomially reinforced in the statistical moments. Thus, any difference in the four PDFs computed from malignant lesions is likely to be polynomially reinforced in the statistical moments of the computed coefficients. Six features from each of four GLDM based PDFs make this feature group, which has total 24 features.

The fourth group of features computes GLCM based texture feature. Based on the method proposed in the previous study [30], our CAD scheme generates a matrix of 44 textural features computed from GLCM matrix based on all GLCM based equations proposed in [19]. In this way any properties of the GLCM matrix proper for the classification purpose is granted. Hence, this group contains 44 features computed from the entire ROI.

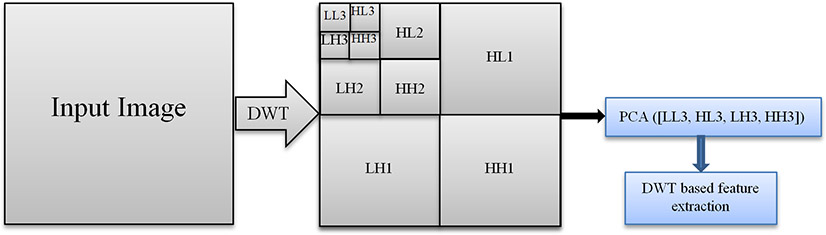
The fifth group of features includes wavelet-based features. The Daubechies wavelet decomposition is accomplished on the original ROI (i.e., Figure 2(a)). Figure 3 shows a block diagram of the wavelet-based feature extraction procedure. The last four sub-bands of wavelet transform are used to build a matrix of four sub-bands in which principal components of this matrix are driven for feature extraction and computation. The computed features are listed in Table III. We also repeat the same process to compute wavelet-based feature from the segmented lesion (i.e., Figure 2(f)). As a result, this feature group includes 26 wavelet-based image features.

Fig 3.

Wavelet based feature extraction. Wavelet decomposition is applied three times to make the images compress as possible. Then PCA is adopted as another way of data compression.

TABLE III.

List of Wavelet-based Features

Feature category	Feature Description
Wavelet-based features	1. Contrast, 2. Correlation, 3. Energy, 4. Homogeneity, 5. Mean, 6. Standard deviation, 7. Entropy, 8. Root mean square level, 9. Variance, 10. Smoothness, 11. Kurtosis, 12. Skewness, 13. IDM

Last, to address the differences between morphological and structural characteristics of benign and malignant lesions, another group of geometrical based features is derived and computed from the segmented lesion region. For this purpose, a binary version of the lesion, like what we showed in Figure 2 (e), is first segmented from the ROI area. Then, all the properties listed in Table IV are calculated from the segmented lesion region in the image using the equations reported in [31].

TABLE IV.

List of Geometrical Features

Feature category	Feature Description
Geometrical based features	1. Area, 2. Major Axis Length, 3. Minor Axis Length, 4. Eccentricity, 5. Orientation, 6. Convex Area, 7. Circularity, 8. Filled Area, 9. Euler Number, 10. Equivalent Diameter, 11. Solidity, 12. Extent, 13. Perimeter, 14. Perimeter Old,15. Max Feret Diameter,16. Max Feret Angle,18. Min Feret Diameter,19. Min Feret Angle, 20. Roundness Ratio

By combining all features computed in above 6 groups, CAD scheme creates an initial pool of 181 image features. Then, RPA is applied to reduce feature dimensionality and generate an optimal feature vector. For this purpose, we utilize sparse random matrix as the projection function to achieve the criteria as defined in equation (7). Sparse random matrix is a memory efficient and fast computing way of projecting data, which guarantees the embedding quality of this idea. To do so, if we define s = 1/density, in which density defines ratio of non-zero components in the RPA, the components of the matrix as random matrix elements (RME) are:

$$RME=\{\begin{array}{cc}-\sqrt{\frac{s}{n_{components}}},\hfill & {}^1∕_{2s}\hfill \\ 0,withprobability\hfill & 1-{}^1∕_s\hfill \\ \sqrt{\frac{s}{n_{components}}},\hfill & {}^1∕_{2s}\hfill \end{array}\phantom{\}}$$ (11)

In this process, we select n_components, which is the size of the projected subspace. As recommended in [32], we consider number of non-zero elements to the minimum density, which is: ${}^1∕_{\sqrt{n\_features}}$.

E. Development and Evaluation of Machine Learning Model

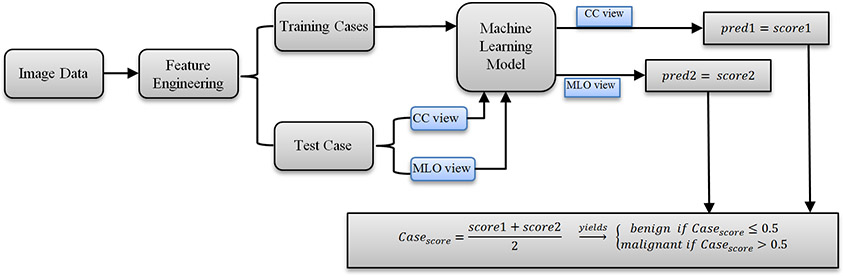
After processing images and computing image features from all 1,197 ROIs depicting malignant lesions and 1,302 ROIs depicting benign lesions, we build machine learning model to classify between malignant and benign lesions by taking following steps or measures. Figure 4 shows a block diagram of the machine learning model along with the training and testing process. First, although many machine learning models (i.e., artificial neural networks, K-nearest neighborhood network, Bayesian belief network, support vector machine) have been investigated and used to develop CAD schemes, based on our previous research experience [14], we adopt the support vector machine (SVM) to train a multi-feature fusion based machine leaning model to predict the likelihood of lesions being malignancy in this study. Under a grid search and hyperparameter analyses, linear kernel implemented in SVM model can achieve a low computational cost and high robustness in prediction results as well.

Fig 4.

Illustration of the overall classification flow of the CAD scheme developed and tested in this study.

Second, we apply the RPA to reduce the dimensionality of image feature space and map to the most efficient feature vector as input features of the SVM model. To demonstrate the potential advantages of using RPA in developing machine learning models, we build and compare 5 SVM models, which using all 181 image features included in the initial feature pool, and embedding 4 other feature dimensionality reduction methods including (1) random projection algorithm (RPA), (2) principle component analyses (PCA), (3) nonnegative matrix factorization (NMF), and (4) Chi-squared (Chi2).

Third, to increase size and diversity of training cases, as well as reduce the potential bias in case partitions, we use a leave-one-case-out (LOCO) based cross-validation method to train SVM model and evaluate its performance. All feature dimensionality reduction methods discussed in the second step are also embedded in this LOCO iteration process to train the SVM. This can diminish the potential bias in the process of feature dimensionality reduction and machine learning model training as demonstrated in our previous study [33]. When the RPA is embedded in the LOCO based model training process, it helps generate a feature vector independent of the test case. Thus, the test case is unknown to both RPA and SVM model training process. In this way, in each LOCO iteration cycle, the trained SVM model is tested on a truly independent test case by generating an unbiased classification score for the test case. As a result, all SVM-generated classification scores are independent of the training data. In addition, other fold cross-validation methods (i.e., N = 3, 5, 10) are also tested and compared with LOCO method in the study.

Fourth, since majority of lesions detected in two ROIs from CC and MLO view mammograms, in the LOCO process, two ROIs representing the same lesion will be grouped together to be used for either training or validation to avoid potential bias. After training, ROIs in one remaining case will be used to test the machine learning model that generates a classification score to indicate the likelihood of each testing ROI depicting a malignant lesion. The score ranges from 0 to 1. The higher score indicates a higher risk of being malignant. In addition to the classification score of each ROI, a case-based likelihood score is also generated by fusion of two scores of two ROIs representing the same lesion depicting on CC and MLO view mammograms.

Fifth, a receiver operating characteristic (ROC) method is applied in the data analysis. Area under ROC curve (AUC) is computed from the ROC curve and utilized as an evaluation index to evaluate and compare performance of each SVM model to classify between the malignant and benign lesions. Then, we also apply an operating threshold of T = 0.5 on the SVM-generated classification scores to classify or divide all testing cases into two classes of malignant and benign cases. By comparing to the available ground-truth, a confusion matrix for the classification results is determined for each SVM. From the confusion matrix, we compute classification accuracy, sensitivity, specificity, and odds ratio (OR) of each SVM model based on both lesion region and case. In the region-based performance evaluation, all lesion region are considered independent, while in the case-based performance evaluation, the average classification score of two matched lesion regions (if the lesions are detected and marked by radiologists in both CC and MLO view) is computed and used. In this study, all pre-processing and feature extraction steps to make the matrix of features are conducted using MATLAB R2019a package.

III. RESULTS

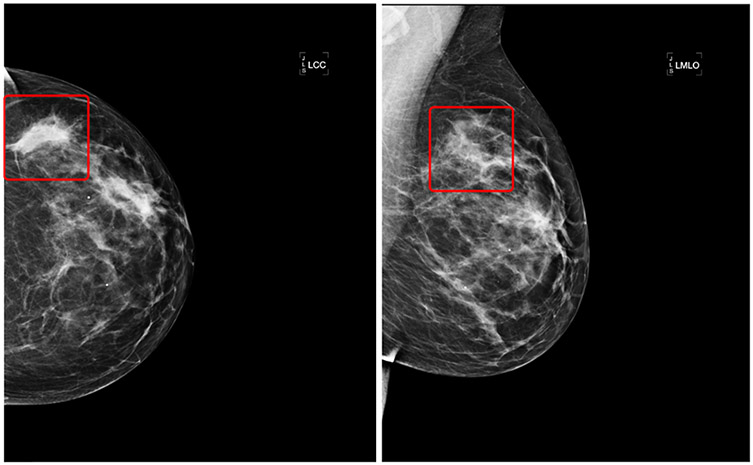
Figure 5 shows a malignant case as an example in which the lesion center is annotated by radiologists in both CC and MLO view mammograms. Based on the marked center, we plot two square areas on two images in which image features are computed by the CAD scheme. Using the whole feature vector of 181 image features, the SVM-model generates the following classification scores to predict the likelihood of two lesion regions on two view images being malignant, which are S_CCview = 0.685, and S_MLOview = 0.291. The case-based classification score is S_Case = 0.488. When using the feature vectors generated by the RPA, the SVM-model generates two new classification scores of these two lesion regions, which are S_CCview = 0.817, and S_MLOview = 0.375. Thus, the case-based classification score is S_Case = 0.596. As a result, using the SVM model trained using all 181 image features misclassifies this malignant lesion into benign when an operating threshold (T = 0.5) is applied, while the SVM model trained using the embedded RPA increases the classification scores for both lesion regions depicting on CC and MLO view images. As a result, it is correctly classified as malignant with the case-based classification score greater than the operating threshold.

Fig 5.

A malignant case annotated by radiologists in both CC and MLO views. The annotated mass is squared in each view.

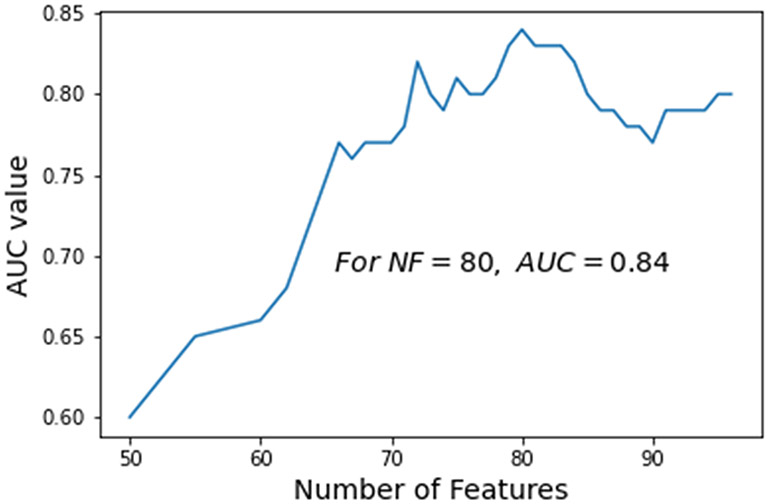
Table V summarizes the performance of using the original features computed in 6 categories to classify between the malignant and benign lesions. As shown in this table, using the group of statistical features yields the highest classification accuracy among 6 categories of features. Figure 6 shows a curve indicating the variation trend of the AUC values of the SVM models trained and tested using different number of features (ranging from 50 to 100) generated by the proposed RPA. The trend result indicates that using a reduced feature dimensionality with 80 features, the SVM yields the highest AUC value of 0.84.

TABLE V.

Accuracy of the SVM models for case-based classification based on six different categories of the original features.

Feature category	Number of features	Accuracy (%)
Statistical features	60	66
GLRLM	7	59
GLDM	24	56
GLCM	44	61
Wavelet based	26	60
Geometrical based	20	63

Fig. 6.

A trend of the case-based classification AUC values generated by the SVM models trained using different number of features (NF) generated by the RPA.

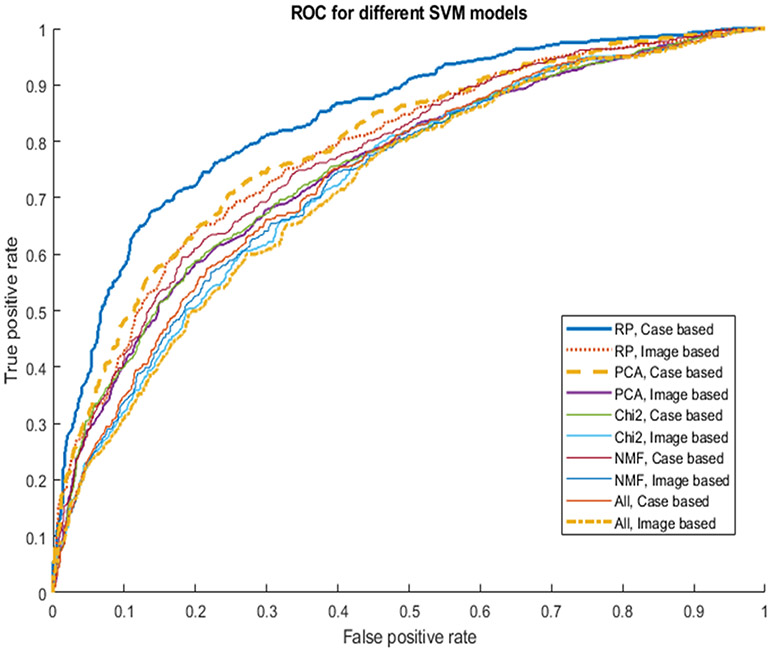
Table VI shows and compares the average number of the input features used to train 5 SVM models with and without embedding different feature dimensionality reduction methods, lesion region-based and case-based classification performance of AUC values. When embedding a feature dimensionality reduction algorithm, the size of feature vectors in different LOCO-based SVM model training and validation cycle may vary. Table VI shows that average number of features are reduced from original 181 features to 100 or less. When using RPA, the average number of features is 80. From both Table VI and Figure 7, which show and compare the corresponding AUC values and ROC curves, we observe that a SVM model trained using an embedded RPA feature dimensionality reduction method produces the statistically significantly higher or improved classification performance including a case-based AUC value of 0.84±0.01 as comparing to all other SVM model (p < 0.05) including the SVM trained using the initial feature pool of 181 features and other SVM models embedded with other three feature dimensionality reduction methods namely, principle component analyses (PCA), nonnegative matrix factorization (NMF) and Chi-squared (Chi2) in the classification model training process. In addition, the data in Table VI and ROC curves in Figure 7 also indicate that the case-based lesion classification yields higher performance than the region-based classification performance, which indicates that using and combining image features computed from two-view mammograms has advantages.

TABLE VI.

Summary of average number of image features used in 5 different SVM models and classification performance (AUC) based on both region and case-based lesion classification. p value compares results of each model to the last one (RPA) as the optimal one.

Feature sub-groups	Number of features	AUC	p value
Original features, region based	181	0.72	0.004
Original features, case based	181	0.74	0.005
NMF, region based	100	0.73	0.005
NMF, case based	100	0.77	0.023
Chi2, region based	76	0.73	0.005
Chi2, case based	76	0.75	0.015
PCA, region based	83	0.75	0.011
PCA, case based	83	0.79	0.041
RPA, region based	80	0.78	0.035
RPA, case based	80	0.84	---

Fig. 7.

Comparison of 10 ROC curves generated using 5 SVM models and 2 scoring (region and case-based) methods to classify between malignant and benign lesion regions or cases.

Table VII presents 5 confusion matrices of lesion case-based classification using 5 SVM-models after applying the operating threshold (T = 0.5). Based on this table, several lesion classification performance indices like sensitivity, specificity, and odds ratio are measured and shown in Table VIII. This table also shows that the SVM model trained based on the feature vector generated by the RPA yields the highest classification accuracy comparing to the other 4 SVM models trained using feature vectors generated either based on other three feature dimensionality reduction methods or the original feature pool of 181 features.

TABLE VII.

Five Confusion matrices of case-based lesion classification using 5 different SVM models to classify between benign and malignant cases.

Feature Group	Predicted	Actual Positive	Actual Negative
Original features	Positive	399	212
	Negative	245	631
NMF	Positive	406	173
	Negative	238	670
Chi2	Positive	405	194
	Negative	239	649
PCA	Positive	436	197
	Negative	208	646
RPA	Positive	452	177
	Negative	192	666

TABLE VIII.

Summary of the lesion case-based classification accuracy, sensitivity, specificity, and odd ratio of using 5 SVMs trained using different groups of optimized features.

Feature sub- group	Accuracy (%)	Sensitivity (%)	Specificity (%)	Odds Ratio
Original features	69.3	62.0	75.0	4.85
NMF	72.4	63.1	79.5	6.61
Chi2	70.9	63.0	77.1	5.67
PCA	72.8	68.0	76.6	6.87
RPA	75.2	70.2	79.0	8.86

Table IX shows and compares the classification results using four different cross-validation methods (N = 3, 5, 10 and LOCO). The results show two trends of performance decrease and standard deviation increase (in both AUC and accuracy) as the number of folds decreases from the maximum folds (LOCO) to the smallest folds (N = 3). This indicates that using LOCO yields not only the highest performance, but also probably highest robustness due to the smallest standard deviation.

TABLE IX.

Summary of the case-based lesion classification for the Proposed method (RPA) under different cross validation (CV) techniques.

CV	AUC	Accuracy
LOCO	0.84±0.04	75.2±4
10-fold	0.83±0.05	74.0±4
5-fold	0.82±0.07	73.1±5
3-fold	0.80±0.10	70.8±9

Additionally, to assess the reduction of feature redundancy after applying RPA, we create a feature correlation matrix, corr(i,j) with the number of M features. Then, we compute a mean absolute value of the correlation matrix:

$$meanofcorrelation=\frac{1}{M\times M}\sum _{i,j=1}^M\mid corr(i,j)\mid$$ (12)

Two mean values of correlation computed from two correlation matrices generated using the feature space (or pools) before and after applying RPA are 0.49 and 0.31, respectively, which indicates that feature correlation coefficients after using RPA is reduced. Thus, using RPA can reduces not only dimensionality of feature space, but also redundancy of the feature space.

Last, the computational processing tasks of applying RPA to generate optimal features and train the SVM model are performed using a Dell computer (Processor: Intel(R) Xeon CPU E5-1603 v3, 2.8 GHz, and 16 GB RAM) and Python-based software package. For cross validation process we use Sklearn-model library. For example, in the 10-fold cross validation, the average computation time to complete one cross-validation iteration is approximately 38.12 seconds.

IV. Discussion

Mammography is a popular imaging modality used in breast cancer screening and early cancer detection. However, due to the heterogeneity of breast lesions and dense fibro-glandular tissue, it is difficult for radiologists to accurately predict or determine the likelihood of the detected suspicious lesions being malignant. As a result, mammography screening generates high false-positive recall rates and majority of biopsies are approved to be benign [34]. Thus, to help increase specificity of breast lesion classification and reduce the unnecessary biopsies, developing CAD schemes to assist radiologists more accurately and consistently classifying between malignant and benign breast lesions remains an active research topic [35]. In this study, we develop and assess a new CAD scheme of mammograms to predict the likelihood of the detected suspicious breast lesions being malignant. This study has following unique characteristics as comparing to other previous CAD studies reported in the literature.

First, previous CAD schemes of mammograms computed image features from either the segmented lesion regions or the regions with a fixed size (i.e., squared ROIs to cover lesions with varying sizes). Both approaches have advantages and disadvantages. Due to the difficulty to accurately segment subtle lesions with fuzzy boundary, the image features computed from the automatically segmented lesions may not be accurate or reproducible, which reduces the accuracy of the computed image features to represent actual lesion regions. When using the fixed ROIs (including most deep learning based CAD schemes [17, 36]), although it can avoid the potential error in lesion segmentation, it may lose and reduce the weight of the image features that are more relevant to the lesions due to the potential heavy influence of irregular fibro-glandular tissue distribution surrounding the lesions with varying sizes. In this study, we tested a new approach that combines image features computed from both a fixed ROI and the segmented lesion region. In addition, comparing to the most of previous CAD studies as surveyed in the previous study, which used several hundreds of malignant and benign lesion regions [37], we assemble a much larger image dataset with 1,847 cases or 2,499 lesion region (including 1,197 malignant lesion regions and 1,302 benign lesion regions). Despite using a much larger image dataset, this new CAD scheme yields a higher classification performance (AUC = 0.84±0.01) as comparing to AUC of 0.78 to 0.82 reported in our previous CAD studies that using much smaller image dataset (<500 malignant and benign ROIs or images) [17, 38]. Thus, although it may be difficult to directly compare performance of CAD schemes tested using different image datasets as surveyed in [37], we believe that our new approach to combine image features computed from both a fixed ROI and the segmented lesion region has advantages to partially compensate the potential lesion segmentation error and misrepresentation of the lesions related image features, and enable to achieve an improved or very comparable classification performance.

Second, since identifying a small, but effective and non-redundant image feature vector plays an important role in CAD development to train machine learning classifiers or models, many feature selection or dimensionality reduction methods have been investigated and applied in previous studies. Although these methods can exclude many redundant and low-performed or irrelevant features in the initial pool of features, the challenge of how to build a small feature vector with orthogonal feature components to represent the complex and non-linear image feature space remains. For the first time, we in this study introduce the RPA to the medical imaging informatics field to develop CAD scheme. RPA is a technique that maximally preserves the distance between the sub-set of points in the lower-dimension space. As explained in the Introduction section, in the lower space under preserving the distance between points, classification is much more robust with low risk of overfitting. This is not only approved by the simulation or application results reported in previous studies, it is also confirmed by this study. The results in Table VI show that by using the optimal feature vectors generated by RPA, the SVM model yields significantly higher classification performance in comparison with other SVM models trained using either all initial features or other feature vectors generated by other three popular feature selection and dimensionality reduction methods. Using the RPA boosts the AUC value from 0.72 to 0.78 in comparison with the original feature vector in the lesion region-based analysis, and from 0.74 to 0.84 in the lesion case-base evaluation, which also enhances the classification accuracy from 69.3% to 75.2%, and approximately doubling the odds ratio from 4.85 to 8.86 (Table VIII). Thus, the study results confirm that RPA is a promising technique applicable to generate optimal feature vectors for training machine learning models used in CAD of medical images.

Third, since the heterogeneity of breast lesions and surround fibro-glandular tissues distributed in 3D volumetric space, the segmented lesion shape and computed image features often vary significantly in two projection images (CC and MLO view), we investigate and evaluate CAD performance based on single lesion regions and the combined lesion cases if two images of CC and MLO views were available and the lesions are detectable on two view images. TABLE VI shows and compares lesion region-based and case-based classification performance of 5 SVM models. The result data clearly indicates that instead of just selecting one lesion region for likelihood prediction, it would be much more accurate when the scheme processes and examines two lesion regions depicting on both CC and MLO view images. For example, when using the SVM trained with the feature vectors generated by the RPA, the lesion case-based classification performance increases 7.7% in AUC value from 0.78 to 0.84 as comparing to the region-based performance evaluation.

Last, although the study has tested a new CAD development method using a RPA to generate optimal feature vector and yielded encouraging results to classify between the malignant and benign breast lesions, we realize that the reported study results are made on a laboratory-based retrospective image data analysis process with several limitations. First, although the dataset used in this study is relatively large and diverse, whether this dataset can sufficiently represent real clinical environment or breast cancer population is unknown or not tested. All FFDM images were acquired using one type of digital mammography machines. Due to the difference of the image characteristics (i.e., contrast-to-noise ratio) between FFDM machines made by different vendors, the CAD scheme developed in this study may not be directly and optimally applicable to mammograms produced by other types of FFDM machines. However, we believe that the concept demonstrated in this study is valid. Thus, the similar CAD schemes can be easily retrained or fine-tuned using a new set of digital mammograms acquired using other different types of FFDM machines of interest. Second, in this retrospective study, the image dataset has a higher ratio between the malignant and benign lesions, which is different from the false-positive recall rates in the clinical practices. Thus, the reported AUC values may also be different from the real clinical practice, which needs to be further tested in future prospective clinical studies. Third, in the initial pool of features, we only extracted a limited number of 181 statistics, textural and geometrical features, which are much less than the number of features computed based on recently developed radiomics concept and technology [3, 4]. Thus, more texture features can be explored in future studies to increase diversity of the initial feature pool, which may also increase the chance of selecting or generating more optimal features. Additionally, many deep transfer learning models have been recently tested as feature extractors in medical imaging field, which produce much larger number of features than the radiomics approaches. Thus, whether using RPA can also help significantly reduce dimensionality of these feature extractors to more effectively and robustly train or build the final classification layer of the deep leaning models should be investigated in future studies.

V. Conclusions

In summary, due to the difference between human vision and computer vision, it is often difficult to accurately identify a small set of optimal and non-redundant features computed by the CAD schemes of medical images. In this study, we investigate feasibility of applying a new approach based on the random projection algorithm (RPA) to generate the optimal feature vectors for training machine learning models implemented in the CAD schemes of mammograms to classify between malignant and benign breast lesions. Study results indicate that applying this RPA approach creates a more compact feature space that can reduce feature correlation or redundancy. By comparing with other three popular feature dimensionality reduction methods, the study results also demonstrate that using RPA enables to generate an optimal feature vector to build a machine learning model, which yields significantly higher classification performance. In addition, since building an optimal feature vector is an important precondition of building optimal machine learning models, the new method demonstrated in this study is not only limited to CAD schemes of mammograms, it can also be adopted and used by researchers to develop and optimize CAD schemes of other types of medical images to detect and diagnose different types of cancers or diseases in the future