Abstract
The main objective of the study was to develop a low-cost, non-invasive diagnostic model for the early prediction of T2DM risk and validation of this model on patients. The model was designed based on the machine learning classification technique using non-linear Heart rate variability (HRV) features. The electrocardiogram of the healthy subjects (n = 35) and T2DM subjects (n = 100) were recorded in the supine position for 15 min, and HRV features were extracted. The significant non-linear HRV features were identified through statistical analysis. It was found that Poincare plot features (SD1 and SD2) can differentiate the T2DM subject data from healthy subject data. Several machine learning classifiers, such as Linear Discriminant Analysis (LDA), Quadratic Discriminant Analysis, Naïve Bayes, and Gaussian Process Classifier (GPC), have classified the data based on the cross-validation approach. A GP classifier was implemented using three kernels, namely radial basis, linear, and polynomial kernel, considering the ability to handle the non-linear data. The classifier performance was evaluated and compared using performance metrics such as accuracy(AC), sensitivity(SN), specificity(SP), precision(PR), F1 score, and area under the receiver operating characteristic curve(AUC). Initially, all non-linear HRV features were selected for classification, but the specificity of the model was the limitation. Thus, only two Poincare plot features were used to design the diagnostic model. Our diagnostic model shows the performance using GPC based linear kernel as AC of 92.59%, SN of 96.07%, SP of 81.81%, PR of 94.23%, F1 score of 0.95, and AUC of 0.89, which are more extensive compared to other classification models. Further, the diagnostic model was deployed on the hardware module. Its performance on unknown/test data was validated on 65 subjects (healthy n = 15 and T2DM n = 50). Considering the desirable performance of the diagnostic model, it can be used as an initial screening test tool for a healthcare practitioner to predict T2DM risk.
Keywords: Type 2 diabetes mellitus, Diagnostic model, Heart rate variability, Electrocardiogram, Poincare plot, Detrended fluctuation analysis, Gaussian process classifier
Introduction
Heart rate variability (HRV) is a basic, non-invasive procedure that measures the interval oscillations between successive heartbeats (RR intervals) that are associated with the autonomous nervous system (ANS) influence [1]. Several pathological conditions such as acute myocardial infarction, hypertension, coronary artery disease, type 1, and type 2 diabetes altered the ANS. Alterations in autonomic activity may be attributed to autonomic neuropathy in people with T2DM [2]. The T2DM subjects have high chances of cardiac autonomic neuropathy (CAN) development, which induces abnormalities in heart rate regulation and cardiovascular dysfunction [3]. In T2DM, CAN has been reported as a significant complication strongly linked with cardiac ischemia, cardiovascular diseases, and mortality [4–7]. HRV has been evaluated as an ECG-derived RR sampling interval for detailed information about cardiovascular disease. It assesses the relationship between the sympathetic and parasympathetic activity of the ANS [7].
In the T2DM condition, linear HRV analysis has shown a considerable reduction in parasympathetic activity that indicates a lack of autonomic cardiac regulation [8]. It has been suggested that the cardiac signal is non-linear time series, so a non-linear analysis is needed to determine minor variations in the signals [9]. The non-linear analysis was also favored with its robustness and indicated better results than the time and frequency domain analysis. The autonomic variations begin at the early stages of T2DM; hence the reduced HRV features have been prominent markers for early diabetes prediction [10]. The individual with T2DM has become a coronary disorder because coronary artery disease is probably following diabetes development. Thus HRV analysis is an important consideration to analyze the progression or risk of T2DM to avoid further cardiac complications [11].
The author Ahsan et al. demonstrated the use of non-linear HRV features like SD1, SD2, and Sample entropy (SampEN) for detecting Cardiac Autonomic Neuropathy (CAN) presence in patients using heart rate complexity analysis. The results of this investigation show that SampEN of non-linear HRV was used to differentiate between mild CAN and severe CAN [12]. Author Roy et al. effectively used Poincare plot features and detrended fluctuation analysis (DFA) component to study differences in HRV patterns of control and diabetes subjects [8].
In this study, non-linear HRV features predict the T2DM risk using the machine learning technique. The Gaussian process (GPC) based classification model adapts the Laplace approximation method, and it was implemented using a cross-validation technique with three kernels. Further, the GPC model, which shows the highest classification accuracy with the respective kernel, was used for all experimentation. The key contributions of the study are as follows-
Gaussian Process-based kernel was proposed as a low-cost, non-invasive diagnostic model to predict the T2DM risk using non-linear HRV features.
The proposed model was designed based on the real diagnostic non-linear HRV features data.
The present model considerably required only two non-linear HRV features. Moreover, it attained a 92.59% peak accuracy after ten trials of tenfold cross-validation.
Highly accurate, concise, and interpretable classification results were obtained using the diagnostic model under a physician's observation.
Following are the novelties of the proposed work-
A portable, non-invasive, machine learning-based hardware module of the diagnostic model was developed for real-time automated classification of healthy and T2DM risk subjects.
Clinically acquired 15 healthy subjects and 50 T2DM subjects data were validated using a diagnostic model, and results are presented.
This paper is organized as follows: Sect. 2 explains the proposed system, including demographic information of subjects, feature extraction and pre-processing, LDA, QDA, NB, and GPC model with kernel optimization. The results are discussed in Sect. 3. Section 4 is concerned about the design implementation. Section 5 represents the discussion and performance comparison in detail. The limitation and future directions of the proposed model are discussed in Sect. 6. Finally, Sect. 7 concludes the work with concluding remarks.
Material and methods
Design of proposed system
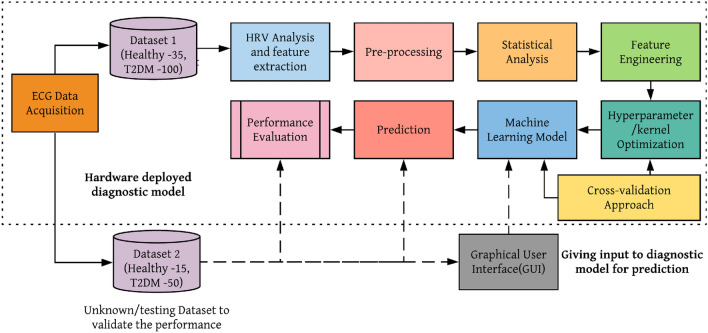
The proposed block diagram of the system is shown in Fig. 1. The first step in the proposed system is to acquire the ECG signal from a patient using a standard ECG acquisition tool. From the acquired ECG signal, HRV features have been extracted. The normalization of extracted features can be done in pre-processing step. Further, the statistical significance between the non-linear HRV features of healthy and T2DM subjects was studied using a statistical test. The most significant features were selected in the feature engineering step. Afterward, the hyperparameters of the machine learning models were optimized to get optimal results before training the model. The inner fivefold Grid search cross-validation approach was used to select the hyperparameters. The kernel is the main hyperparameter of the machine learning algorithm employed in this analysis. So before training the machine learning model, kernel optimization was performed using the k-fold cross-validation strategy. Finally, the optimized machine learning model is used for prediction. Its performance was evaluated using performance metrics. The unknown/test data will be given as input to the optimized model to predict T2DM risk.
Fig. 1.
Proposed block diagram
Workflow of proposed methodology
Subjects and ECG recording
The ECG signals were acquired from 135 subjects (35 healthy subjects and 100 T2DM subjects) between 20 to 70 years age of both genders in a relaxed supine position for 15 min. The last 5-min segment was used for HRV analysis [13]. The ECG was recorded using the Chronovisor HRV DX system, and time series RR interval signals were analyzed in Chronovisor HRV software 1.1.487. A standard lead II procedure was used for ECG recording at a sampling frequency of 1000 Hz (Fig. 2). All the subjects were instructed about the aim, objective, procedure of the study, and their informed consent was obtained. The study received approval from the Institutional Ethical Committee (IEC) of Smt. Kashibai Navale Medical College and General Hospital, Pune, India (SKNMC&GH). The subjects were selected from the OPD of SKNMC&GH by following the protocol of the American Diabetes Association [14]. The present study followed the guidelines given by the Taskforce of the European Society for Cardiology and the North American Society of Pacing and Electrophysiology [15].
Fig. 2.
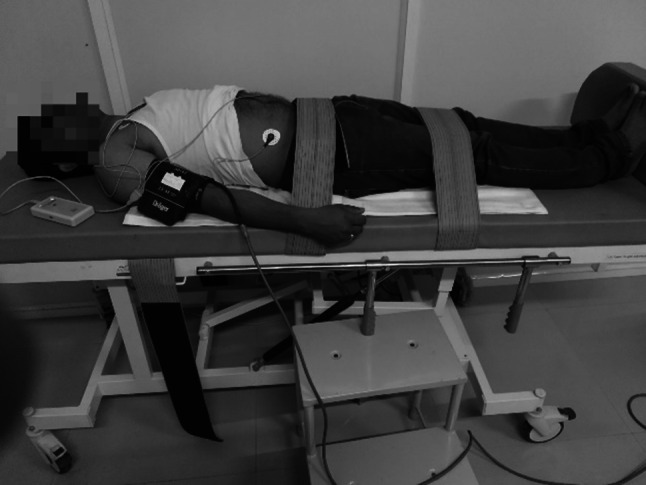
ECG recording
The subjects free from any other type of illness were considered as healthy, and their pathological test was also performed for confirmation. ECG of such healthy subjects was recorded. In regards to the T2DM subjects, the ECG data was recorded when the patient is full-blown suffered from diabetes after concerning the pathological reports of blood glucose level. The sample size of 135 subjects was used as training data.
The ECG of another 65 subjects (15 healthy subjects and 50 T2DM subjects) between 20 to 70 years age of both genders were recorded, and their HRV features extracted. This data is used as unknown/test data to validate the diagnostic model. This data is not included for training the diagnostic model.
Non-linear HRV features extraction
The feature extraction process is one of the essential steps in biomedical signal analysis and interpretation. Filtered ECG signals were used to calculate the RR intervals, and a tachogram was calibrated to extract the information of non-linear HRV features. The non-linear HRV features that have been studied include Poincare plot (PP), Detrended fluctuation analysis (DFA), Approximate entropy (AppEN), and Sample entropy (SampEN).
The Poincare plot is a geometric technique used to quantify and visualize the time series data points [1, 16]. It is a recurrence plot used to quantify the self-similarity process in a time-series signal. In the RR tachogram context, the Poincare plot is the graph between each RR interval influenced by the previous RR interval. It is a plot between RR(i) versus RR(i+1) where RR(i) is the present time interval between two adjacent R peaks, and RR(i+1) is the time interval between the successive two adjacent R peaks [17]. The Poincare plot gives three features: (1) Standard deviation of short term beat to beat variability or short term variability (SD1), (2) Standard deviation of long term beat to beat variability or long term variability (SD2), and (3) Ratio of SD1 and SD2 or standard deviation ratio (SDR).
DFA is a stochastic autoregressive process that determines the self-similarity in the signal. It quantifies the correlation properties of the RR time-series signal. The root mean square fluctuation of the RR time series signals was measured on the log–log scale [18]. The RR time-series signals autocorrelation properties are described by the scaling exponent alpha (α). In this study, short-term scaling exponent DFA- α1 and long-term scaling exponent DFA- α2 were calculated. DFA- α1 and DFA- α2 ratio is referred to as an alpha ratio that is used as a validation feature. Both DFA-α1 and DFA-α2 is a good indicator of the pathological condition. The lower value of these features indicates abnormalities.
Approximate entropy and sample entropy quantify complexity and lack of regularity in the RR time-series signal. It has been used to characterize the irregularity in physiological signals [19]. The probability of conditional similarity between the specified data sample of a given length and the next collection of the same length samples is determined. It represents the probability of data samples, similar to the data samples [20]. In healthy subjects, AppEN and SampEN are higher and decreased in pathological conditions [1].
Significance of non-linear features
The non-linear method has proven to be more helpful in analyzing quasi-periodic, non-stationary, and non-linear signals [21, 22]. As HRV is itself nonlinear in nature. Thus, the non-linear method can extract minute information from signals that could not be possible with linear techniques like the time domain and frequency domain. Hence we have used the non-linear method to extract the features in the HRV signals.
Data pre-processing
The extracted features cannot always be used directly for analysis. The first and significant step to be done in any data analysis is data pre-processing. The data includes the following attributes/features: SD1, SD2, SDR, DFA- α1, DFA- α2, Alpha ratio, AppEN, SampEN, and outcomes (Healthy-0, T2DM-1). The pre-processing steps involve the outlier rejection and data normalization.
Outlier rejection
The outlier can be rejected using the standard deviation method and interquartile range method. The first criterion to find outlier is that the data that falls outside of the third standard deviation is considered an outlier. The mathematical representation is as follows-
Let be the feature vector of dimensional space
Another criterion to identify the outlier is the interquartile range (IQR). The data that falls below the first quartile range, outside of 1.5 times of IQR and above the third quartile range, is depicted as an outlier and can be removed using manual processes.
Data normalization
Data normalization is a pre-processing procedure used to rescale the values of attributes/features to fit specific ranges. It converts all values to a standard range scale with a mean of zero and a standard deviation of one. Various data normalization techniques can be employed to perform data normalization, such as standard deviation, decimal scaling, and min–max normalization techniques [23]. In this study, we have used the min–max normalization technique for rescaling the HRV features. The data normalization is done as follows,
where and are the upper and lower limit values of the feature vector , respectively.
Statistical analysis
In order to know the significant differences between the non-linear HRV features of healthy and diabetic subjects, a non-parametric Mann–Whitney test at #p < 0.05 was conducted. Data is presented in the form of mean ± standard deviation (Mean ± SD) (Table 2). Epi Info open-source statistical tool was used for statistical analysis.
Table 2.
Analysis of non-linear HRV features
| HRV features | Healthy subject (n = 35) | T2DM subject (n = 100) | p-Value |
|---|---|---|---|
| SD1 | 38.22 ± 19.34 | 24.83 ± 13.40 | 0.0001# |
| SD2 | 87.63 ± 34.06 | 44.97 ± 16.72 | 0.0001# |
| SDR | 0.43 ± 0.14 | 0.56 ± 0.19 | 0.0002# |
| DFA-α1 | 0.92 ± 0.20 | 0.85 ± 0.22 | 0.2543 |
| DFA-α2 | 0.92 ± 0.23 | 0.90 ± 0.18 | 0.4130 |
| Alpha ratio | 1.07 ± 0.42 | 0.97 ± 0.32 | 0.2804 |
| AppEN | 1.12 ± 0.15 | 1.16 ± 0.19 | 0.1976 |
| SampEN | 1.40 ± 0.30 | 1.43 ± 0.32 | 0.6549 |
Feature engineering
Feature engineering is the process of selecting the appropriate features that require to get an accurate prediction. The dataset includes multiple features, and sometimes it may affect the model performance due to overfitting. So important features are selected in the feature engineering step. In this study, the important non-linear HRV features were selected through the individual features performance.
Machine learning classification model
The proposed system uses a supervised machine learning classification technique that takes input as non-linear HRV features and detects the patients belong to the healthy or T2DM risk category. Following are the machine learning classification algorithm used in this study.
Linear discriminant analysis (LDA)
LDA is mainly used as a dimensionality reduction technique in the pre-processing step for classification and machine learning applications [24]. The aim is to project data to a lower-dimensional space with good class separability to avoid overfitting due to dimensionality. Ronald Aylmer Fisher formulated LDA in 1936 that has a practical use as a classifier [25]. Initially, LDA was described for a two-class problem, and later it was generalized as a multiclass linear discriminant analysis by C R Rao in 1948 [26]. Principal component analysis (PCA) and LDA are two classification techniques for data classification and dimensionality reduction. PCA finds the most accurate data representation in lower-dimensional space. It projects data in the direction of maximum variance. However, the direction of maximum variance may not be helpful for classification. LDA projects a line that inherently preserves a direction that is useful for data classification. The main idea of LDA is to find a projection to a line so that the samples from different classes are well separated. LDA is a supervised algorithm and computes a linear discriminant direction representing the axis that will maximize the separation between the multiple classes. LDA is superior to PCA for a multiclass classification task. The steps to implement the LDA algorithm are as follows-
The first step to implement LDA is to calculate the separability between different classes, the distance between the means of different classes called between-class variance, or class matrixes.
| 1 |
where represents the between-class variance of the class, is the sample size of the class, is the mean of the class, and is the total mean.
The second step is to calculate the distance between each class mean and samples called within-class variance or within the class matrix.
| 2 |
where represents the within-class variance of the class, is scatter matrix of every class, represents the sample of the class.
The third step is to construct a lower-dimensional space projection that maximizes the between-class variance and minimizes the within-class variance. After calculating the between-class variance () and within-class variance (), the transformation matrix () of the LDA algorithm that is called Fisher’s criterion is given in Eq. (4). In order to train the model, the cost function or loss function is defined as-
| 3 |
| 4 |
Quadratic discriminant analysis (QDA)
QDA is formulated by Smith in 1947 [27]. QDA is similar and extension to LDA, where it is assumed that each variable of the dataset is normally distributed. However, there is no such assumption in QDA that the covariance of each variable is similar. The final quadratic discriminant equation is written as-
| 5 |
where is the values of vectors, is the transpose values of a mean of group, the inverse of the sample covariance matrix is . The classification rule of QDA is similar to LDA.
Naive Bayes (NB)
Naïve Bayes is a statistical classifier formulated based on the Bayes theorem, assuming that each class features are independent of any other features in that class [28]. It calculates the frequency of class label’s various features and then the probability of class labels. The class labels having the highest probability value (that class) are predicted. Bayes theorem and kernel density estimation are used to classify data in NB classifier, and it is estimated as
| 6 |
where is the prior probability estimation of class , is kernel density for predictable density, is the predicted estimated probability of .
Gaussian process classification (GPC)
Consider a data point from a domain with the associated class label . For a test point , to predict the class membership likelihood using function . This functional value is transformed into the function of the unit interval, such that class membership probability can be written as . The probability of class must be normalized , that is When the sigmoid function meets the condition of point symmetry, , then the probability function can be written as [29]. We used sigmoid function as-
| 7 |
Consider be the training set from a known distribution. Let be testing set from an unknown distribution. We defined training inputs , testing inputs , training target , testing target . For the training point and testing point, the covariance matrix is is the covariance matrix, is the covariance matrix, and is the covariance matrix. The class labels follow Bernoulli distribution for the function ; the probability function can be written as:
| 8 |
A GPC is a stochastic model specified by a mean function of and a positive definite covariance function . The random variable is associated with such that for a given set of input , the joint distribution is Gaussian distribution with vector . Moreover, the covariance matrix is a set of Gaussian distribution called the Gaussian process. The mean function and covariance functions depend on parameter called hyperparameter. Therefore the elements of are .
By using the Bayes rule, one can use the expression for the posterior probability distribution over the value of
| 9 |
where is the marginal probability with the hyperparameter . The joint probability density function of and for training and testing function for the inputs is
| 10 |
the training set of variables is marginalized to make predictions as -
| 11 |
the posterior product and the conditional prior product is obtained as
| 12 |
Finally, the likelihood of predictive class membership by averaging the variables for the test set
| 13 |
Equation (13) is analytically intractable for certain sigmoid functions, although it is only a one-dimensional integral in the binary case, so simple numerical techniques are usually adequate. In this case, we need to use either analytical integral approximations or Laplace-based approximation [30]. The Laplace approximation for this study was used.
The graphical model for binary Gaussian process classification is shown in Fig. 3, where circles denote unknown quantities, squares correspond to the model variables. The horizontal line means latent variables that are explicitly related. The corresponding latent variable , the observed label is conditionally independent of all other nodes. Labels and latent function values are connected by the sigmoid probability because they are taken from the same GPC, all latent function values are entirely connected. The labels are binary, while the prediction is a likelihood and may therefore have values from the entire 0–1 interval.
Fig. 3.
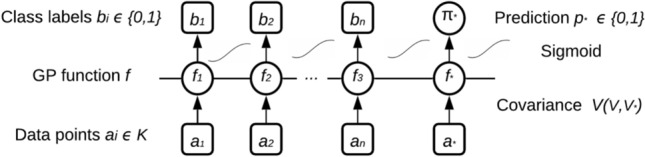
Binary Gaussian process classification (GPC) graphical model
Laplace approximation for GPC
A Gaussian approximation by doing a second-order Taylor extension of around the maximum of the posterior was obtained as -
| 14 |
where , and is the Hessian of the posterior negative log at that point.
Posterior likelihood function
The log probability of an unnormalized posterior distribution using the Bayes rule is as follows-
| 15 |
Differentiating this Eq. (15) w.r.t , the hessian of the negative is
Predictions
Under the Laplace approximation, the posterior predictive mean for can be written as
| 16 |
Compare this with the mean given by [31] as
where is the posterior mean of given , and .
The variance of under the Gaussian approximation was computed. This comprises of two terms:
| 17 |
Knowing the mean and variance of and Gaussian distribution can help to make predictions. It can be determined as follows-
| 18 |
Kernel optimization
In this study, three kernels were implemented: radial basis function (RBF), linear and polynomial kernels. The kernels for GPC were selected based on the classification accuracy using ten trials. The kernel that estimates the highest accuracy was considered to be the best GPC kernel. The k-fold cross-validation strategy with cross-fold k = 5 and k = 10 has been used to select the GPC kernel among the RBF, linear and polynomial.
Performance evaluation metrics
The performance of the diagnostic model can be measured using different performance metrics such as classification accuracy (AC), sensitivity (SE), specificity (SP), precision (PR), F1 score, and area under the receiver-operating characteristic curve(AUC). These performance metrics were obtained using the confusion matrix variable, true positive (TP), false positive (FP), true negative (TN), and false-negative (FN).
True Positive(TP): Diabetic patient is predicted as diabetic
False Positive(FP): Non-diabetic is predicted as diabetic
True Negative(TN): Non-diabetic is predicted as non-diabetic
False Negative(FN): Diabetic patient is predicted as non-diabetic
The performance metrics and their formulae are listed in Table 1.
Table 1.
Performance evaluation metrics
| Performance metrics | Description |
|---|---|
| AC | (TP + TN)/(TP + FP + TN + FN) |
| SE | (TP)/(TP + FN) |
| SP | (TN)/(TN + FP) |
| PR | (TP)/(TP) + (FP) |
| F1 Score | 2TP/(2TP + FP + FN) |
| AUC | The area under the ROC curve |
Results
Non-linear HRV features analysis using statistical test
The short-term ECG signal of 5 min segments was used to extract the non-linear HRV features from the RR tachogram of healthy and T2DM subjects. The calculated HRV features from the RR tachogram suggested reduced HRV in T2DM subjects compared to healthy subjects. The increase in sympathetic regulation with weakened parasympathetic regulation is clearly shown using non-linear HRV features. Poincare features SD1, SD2, and SDR were statistically significant in T2DM subjects. Further, the scaling exponent (α) is low in the case of T2DM subjects. The higher values of approximate and sample entropy in T2DM subjects indicate reduced beat to beat variability. These non-linear HRV features were used as input to machine learning classifiers to classify T2DM subjects from healthy subjects (Table 2).
Limitation of statistical test and importance of machine learning technique
HRV features are non-linear and have a lot of intra and inter variability (variance). It is difficult to find a precise cut-off range of HRV features for healthy and T2DM subjects by linear statistics. Therefore machine learning technique was incorporated into our analysis. The machine learning algorithm helps to understand the exact/hidden non-linear pattern in the healthy and T2DM risk groups. These patterns are independent of age, gender, BMI, and blood glucose variations in healthy and T2DM subjects.
Results of Gaussian process kernel optimization
This study has used radial basis function, linear, and polynomial kernels for the Gaussian process model. It is important to select the kernel first as the same kernel can be used further to improve classifier performance. A two k-fold cross-validation approach (k = 5, k = 10) was used to choose the best kernel for the GPC model. The kernel was selected based on the classification accuracy of classifiers. Kernel selection based on two different cross-validations is given in Table 3.
Table 3.
Kernel selection based on two different cross-validation
| K | Kernel | ||
|---|---|---|---|
| RBF | Linear | Polynomial | |
| 5 | 78.52% | 77.78% | 71.85% |
| 10 | 81.48% | 85.19% | 82.22% |
The best accuracy of GPC was obtained using the linear kernel with k = 10 cross-fold compared to other kernels. Therefore, Gaussian process-based linear kernel was used for all the experimentation.
Results of comparisons between classifiers for fivefold and tenfold cross-validation
The performance of four machine learning classifiers based on eight non-linear HRV features was compared using performance metrics. It is shown in Table 4.
Table 4.
Comparisons between classifiers
| K | Models | Performance metrics | |||||
|---|---|---|---|---|---|---|---|
| AC | SE | SP | PR | F1 score | AUC | ||
| 5 | LDA | 69.63% | 89% | 14.29% | 74.79% | 0.81 | 0.52 |
| QDA | 77.78% | 93% | 34.29% | 80.17% | 0.86 | 0.64 | |
| NB | 74.81% | 88% | 37.14% | 80.00% | 0.84 | 0.63 | |
| GPC-RBF | 78.52% | 92% | 40.00% | 81.42% | 0.86 | 0.66 | |
| GPC-linear | 77.78% | 92% | 37.14% | 80.70% | 0.86 | 0.65 | |
| GPC-polynomial | 71.85% | 92% | 14.29% | 75.41% | 0.83 | 0.53 | |
| 10 | LDA | 77.78% | 90% | 42.86% | 81.82% | 0.86 | 0.66 |
| QDA | 82.22% | 93% | 51.43% | 84.55% | 0.89 | 0.72 | |
| NB | 77.04% | 89% | 42.86% | 81.65% | 0.85 | 0.66 | |
| GPC-RBF | 81.48% | 92% | 51.43% | 84.40% | 0.88 | 0.72 | |
| GPC-linear | 85.19% | 92% | 65.71% | 88.46% | 0.90 | 0.79 | |
| GPC-polynomial | 82.22% | 92% | 54.29% | 85.19% | 0.88 | 0.73 | |
It was found that using k = 5 cross-fold validation, the maximum accuracy of the GPC classifier with the RBF kernel was 78.52%. The GPC model with a linear kernel using k = 10 cross-validation protocol provides the highest accuracy 85.19%, which is relatively better than existing classifiers. Further, GPC based linear kernel with k = 10 has given SE of 92%, SP of 65.71%, PR of 88.46%, F1 score of 0.90, and AUC of 0.79, which are also higher than other classifiers. Another meaningful pictorial way to compare the performance of classifiers is the receiver operating characteristic curve [32]. It is a plot of ‘1-specificity’ versus ‘sensitivity.’ Area under the ROC curve indicates an individual classifier performance. The AUC near 1 indicates the best classification performance, whereas near to 0.5 shows the worst classification performance. AUC for the GPC model with a linear kernel is 0.79, which is the highest among the other classifiers. The ROC curve of four classifiers using k fold cross-validation is given in Figs. 4 and 5.
Fig. 4.
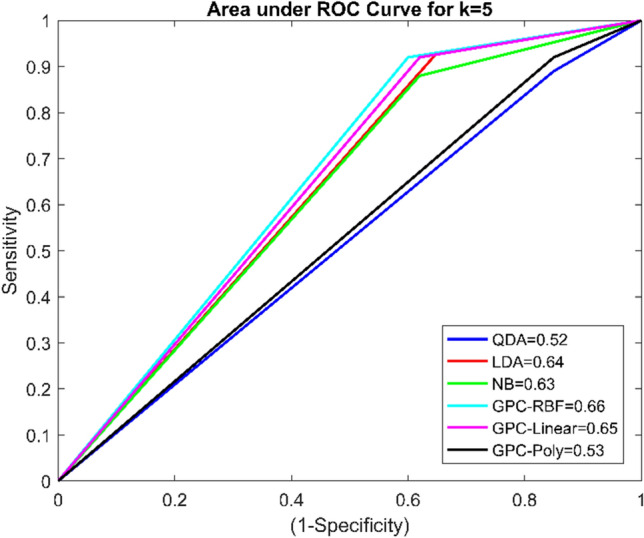
ROC curve for classifiers using k = fivefold cross-validation
Fig. 5.
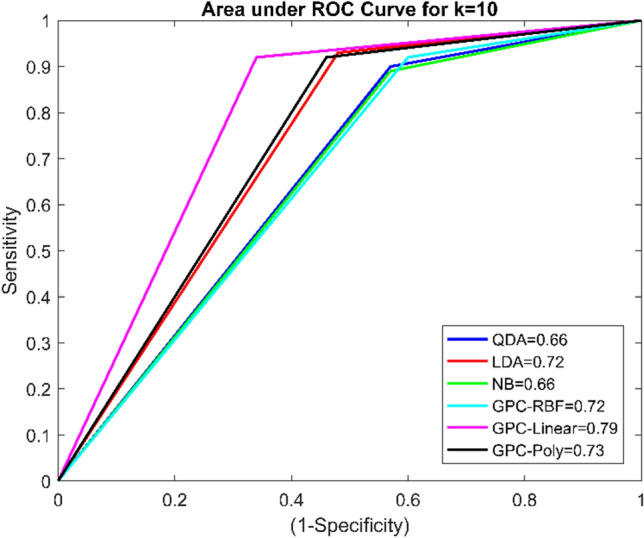
ROC curve for classifiers using k = tenfold cross-validation
The results presented in Table 4 indicate the GPC model using a linear kernel is suitable for detecting T2DM subject data from the healthy subject data. However, one of the main difficulty is the specificity of the model. The specificity of the GPC-linear kernel model was 65.71%, which is not suitable for practical application. Whenever a machine learning model is developed, it must have AC, SE, and SP values above 80%, which represents the predictive ability of the model on new data or test data. In this analysis, the specificity of the classification model was less, so this model cannot be served the actual intent. Less specificity may lead to false-positive outcomes. Thus, the individual feature performance and combined feature performance of non-linear HRV features were observed using GPC linear kernel model (Tables 5 and 6).
Table 5.
Performance using individual features
| HRV features | Performance metrics | |||||
|---|---|---|---|---|---|---|
| AC | SE | SP | PR | F1 score | AUC | |
| SD1 | 79.25% | 94% | 37.14% | 81.03% | 0.87 | 0.51 |
| SD2 | 80.74% | 92% | 48.57% | 83.63% | 0.87 | 0.70 |
| SDR | 74.07% | 100% | 0 | 74.07% | 0.85 | 0.50 |
| DFA-α1 | ||||||
| DFA-α2 | ||||||
| Alpha ratio | ||||||
| AppEN | ||||||
| SampEN | ||||||
Table 6.
Features with individual accuracy of > 75% were combined
| HRV features | Performance metrics | |||||
|---|---|---|---|---|---|---|
| AC | SE | SP | PR | F1 score | AUC | |
| SD1 + SD2 | 92.59% | 96.07% | 81.81% | 94.23% | 0.95 | 0.89 |
The best classification accuracy was observed with individual SD1 and SD2 features using the GPC-linear kernel model. Almost all non-linear HRV features individually perform the same except SD1 and SD2 (Table 5). The specificity and AUC of the model were very low while observing the individual feature performance (Table 5). Therefore, the features with individual accuracy greater than 75% were combined. The highest classification accuracy of 92.59%, sensitivity of 96.07%, specificity of 81.81%, precision of 94.23%, F1 score of 0.95, and AUC of 0.89 was achieved with the combination of SD1 and SD2(Table 6). ROC curve using SD1 and SD2 features is shown in Fig. 6. The highest accuracy of GPC using the linear kernel model was observed by combining SD1 and SD2 (Table 6). Thus, this model is used as the diagnostic model to detect T2DM risk.
Fig. 6.
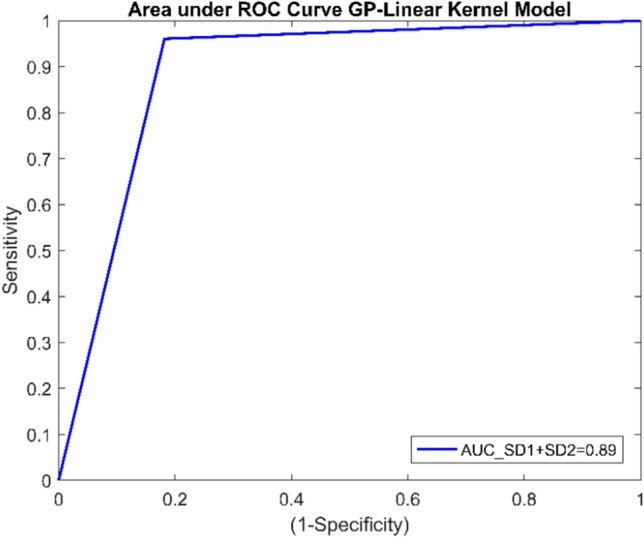
ROC curve for classifier using SD1 and SD2 feature
Design implementation for user
The four machine learning algorithms, such as LDA, QDA, NB, and GPC, were used to develop a diagnostic model using a python data manipulation tool. The results indicate that the GPC-linear kernel algorithm shows an optimum performance using the two non-linear HRV features i.e., SD1 and SD2. Thus GPC linear kernel algorithm can be used as a diagnostic model to detect T2DM risk. In the proposed work, a portable, non-invasive machine learning-based hardware setup was developed. It includes an ECG acquisition tool, Arduino UNO module, and raspberry pi with LCD screen. The ECG is acquired at the sampling frequency of 1000 Hz. Arduino is used for sketching the real-time ECG signal. The training model of the GPC linear kernel algorithm was deployed in a raspberry pi module along with the non-linear HRV feature extraction algorithm. It receives the real-time ECG signal and performs feature extraction and classification. A rich graphical user interface (GUI) was designed with backend programming of the GPC linear kernel algorithm. The proposed system facilitates two options: (1) The user can acquire real-time ECG, and the proposed system will automatically extract the HRV features with the predictive outcome. (2) The user can extract the non-linear HRV features separately or manually from the ECG signal and enter the values of HRV features through GUI to get the predictive outcome. The GUI has functionalities of accepting user input, processing results, and predicting the outcomes. The developed GUI was designed on a python platform that takes inputs as SD1 and SD2 HRV features. It processes the SD1, SD2 values and predicts the outcomes as healthy or T2DM risk. The design implementation of the proposed system and GUI are shown in Figs. 7 and 8.
Fig. 7.

Hardware module implementation
Fig. 8.
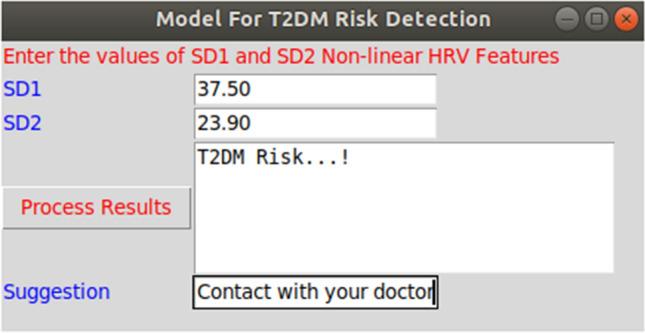
Graphical user interface for users
Time complexity analysis
The time complexity analysis is another significant metric for assessing machine learning model performance. It indicates how much time the model needs to analyze the results. The primary goal of any study is to maximize accuracy while reducing time complexity. The time complexity of a machine learning algorithm denotes how quickly or slowly it can run on input features during training and prediction. It is associated with the number of input features used while training the machine learning algorithm [33]. The number of features used in our study is SD1 and SD2 only, so time complexity was not much impacted on the proposed model. The time-complexity analysis of the proposed GPC linear kernel model and other machine learning models on two non-linear HRV features(SD1 + SD2) is illustrated in Table 7. The time complexity of machine learning models depends upon the computational configuration.
Table 7.
Comparison of the proposed model with other models in term of time complexity
| Model | HRV features | Time complexity (10 cross-fold validation) | |
|---|---|---|---|
| Training time (s) | Prediction time (s) | ||
| LDA | SD1 + SD2 | 0.0008 | 0.0003 |
| QDA | 0.0008 | 0.0003 | |
| NB | 0.0007 | 0.0004 | |
| GPC-linear kernel | 0.0013 | 0.0004 | |
Validation of the diagnostic model on patients
The proposed system was validated at Smt. Kashibai Navale Medical College and General Hospital, Pune, India. The non-linear HRV features of fifteen healthy subjects and fifty subjects with a history of T2DM were used for the model validation. The final model was developed by combining two non-linear HRV features only (SD1 and SD2). Thus, for validation of the model, the same features were used. The HRV features of sixty-five subjects (Healthy-15 and T2DM-50) were given as input to the machine learning models. The obtained results are shown in Table 8.
Table 8.
Results of sixty-five subjects obtained using the proposed and other models
| Model | TN | FP | FN | TP | Total | Performance metrics | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| AC | SE | SP | PR | F1 score | AUC | ||||||
| LDA | 8 | 7 | 15 | 35 | 65 | 66.15% | 70.00% | 53.33% | 83.33% | 0.76 | 0.61 |
| QDA | 9 | 6 | 12 | 38 | 65 | 72.31% | 76.00% | 60.00% | 86.36% | 0.80 | 0.68 |
| NB | 8 | 7 | 13 | 37 | 65 | 69.23% | 74.00% | 53.33% | 84.09% | 0.78 | 0.61 |
| GPC-linear kernel | 11 | 4 | 3 | 47 | 65 | 89.23% | 94% | 73.33% | 92.15% | 0.93 | 0.80 |
The value of TN, FP, FN, and TP was manually calculated, and their performance metrics were obtained. Further, we can improve the specificity by increasing the sample size of healthy subjects.
The proposed GPC-linear kernel model correctly classified 47 T2DM and 11 healthy subjects from 50 T2DM and 15 healthy subjects, respectively, yielding the best performance among all the machine learning models. The proposed GPC-linear kernel model outperforms other machine learning models on new data, as evidenced by classification accuracy and other performance metrics, demonstrating model reliability. Further, the reliability of the model was validated using a statistical test. The proposed model and other models were compared using the repeated ANOVA method to see if they were statistically different. The null and alternative hypothesis was established to evaluate the difference between models. The null hypothesis states that there is no statistical difference between the models, while the alternative hypothesis states that there is a difference [34]. The criteria for accepting or rejecting a hypothesis was based on 0.05 significance level. Null hypothesis is rejected if the statistical p-value is less than the level of significance. The rejection of null hypothesis signifies that the models are statistically different. We performed an ANOVA test on the results and got a p-value of 0.000005, which suggest to reject the null hypothesis and indicating that the proposed GPC linear kernel model is statistically distinct from other models.
Discussion
This work has been designed to predict the risk of T2DM. The non-linear HRV features were used to predict the risk of diabetes using the Gaussian process classification model. Initially, all HRV features have been applied to machine learning classifiers, but individual and combined feature performances were studied to improve the performance of the classifier. The highest accuracy of 92.59% with an acceptable range of sensitivity, specificity with combined SD1 and SD2 HRV features was obtained using the GPC-linear model.
Reduced HRV was observed in the T2DM condition, indicating low complexity and less regularity in RR interval [1, 8, 10, 11]. A few studies have observed diabetic autonomic neuropathy (DAN), which slowly damages the nerves and smallest blood vessel in diabetes patients. Further, DAN has suggested the diagnostic risk marker for cardiovascular abnormalities [3, 12]. Poincare features such as SD1 and SD2 have already been used in diagnosing and prognosis of T2DM diseases. The lower value of these features indicates ANS imbalance [1, 17].
A decrease in the value of DFA α1 and α2 indicates reduced parasympathetic activity. The value of α2 is higher than α1, suggests higher sympathetic activity in diabetic subjects [1]. All non-linear HRV features have been reduced except entropies in diabetes conditions. An increase in the value of entropy features reflects a short beat to beat variability in diabetes conditions [19, 20]. The reduced HRV features are used to predict the T2DM risk at the early stages to start a medical intervention. The present study demonstrated a maximum accuracy of 92.59% with the proposed Gaussian process-based linear kernel model using a group of Poincare features.
The author Acharya and co-workers [35] revealed 86% accuracy, the sensitivity of 87.50%, and 84.60% specificity, respectively, using Adaboost with a least square method with six non-linear HRV features. Another paper from author Acharya and co-workers [36] has demonstrated 90% accuracy, a sensitivity of 92.52%, and a specificity of 88.72% using perceptron Adaboost with nine non-linear HRV features. A summary from the literature review for diabetes prediction using non-linear HRV features is listed in Table 9.
Table 9.
Comparison with existing studies of diabetes prediction using non-linear HRV features
| References | Sample size | Non-linear HRV features | Number of features | Methods | AC (%) | SE (%) | SP (%) | Model validation on the number of patients |
|---|---|---|---|---|---|---|---|---|
| Acharya et al. [35] |
Control-15 Diabetes-15 |
Poincare features, Correlation dimension, recurrence plot features | 5 | Adaboost with Least Squares | 86 | 87.50 | 84.60 | – |
| Acharya et al. [36] |
Control-15 Diabetes-15 |
AppEN, Recurrence plot, Lyapunov exponent, DFA | 9 | Perceptron Adaboost | 90 | 92.52 | 88.72 | – |
| In this work |
Control-35 Diabetes-100 |
SD1 + SD2 | 2 | GPC-Linear kernel | 92.59 | 96.07 | 81.81 |
Total-65 (Control-15, Diabetes-50) |
Many researchers have used time, and frequency domain HRV features to predict diabetes risk and formulated results with good accuracy using a different machine learning technique [37–39]. In the literature, it was noted that researchers had designed a diabetes predictive model with good accuracy, sensitivity, and specificity. However, the developed model was not used or validated on patients in the hospital. In this work, our designed model was validated on patients in the hospital, and the results are desirable.
Importance of proposed diagnostic model for early detection of T2DM
In this kind of study, no study has implemented the machine learning-based hardware module that predicts the risk of T2DM. The developed module is a low-cost, compact, portable, and non-invasive system that detects T2DM risk early on based on the HRV features. HRV is a non-invasive tool that gives an early indication of disease. However, in most of the cases, we found that HRV is reduced in diabetic subjects. This reduced HRV is an early indication of T2DM disease. As HRV features have inherent non-linearity, there are less chances to have the same values of any HRV features in healthy and diabetes groups.
Even if the same values of HRV features present in the healthy and diabetes group, we have used an approach of employing a machine-learning algorithm. It explores the other non-linear features of HRV, which is difficult to study using linear statistics.
Address about the population/class imbalance
The study was based on real and authentic HRV data that are directly extracted from patients. The sample size of healthy and T2DM subjects is imbalance. We tried to balance the dataset using the synthetic minority oversampling technique (SMOTE) [40]. The model designed with such technique when tested on unknown/test data, the more false positive and false negative results were observed. Thus, it was decided to use only real data to design the diagnostic model and validate it.
Limitation and future directions
On this kind of study, whatever literature we have referred to, none of the studies have validated their proposed model on the patients. But it was our first attempt to validate it on patients. We are still working to improve the sample size of healthy subjects. However, it is difficult to know an individual is healthy unless they go through a pathological test. So it is challenging to increase the population size of healthy subjects in less time constraints because one has to go through all the pathological examinations. Less population size of healthy subjects can be the limitation of the study, and we will overcome it in the future. In the future, the diagnostic model would be interfaced with the patient health monitoring system.
Conclusion
The current work proposed a low-cost, non-invasive diagnostic model for predicting T2DM risk based on the GPC-linear kernel model using two non-linear HRV features (SD1 and SD2). The diagnostic model showed an accuracy of 92.59%, sensitivity of 96.07%, specificity of 81.81%, precision of 94.23%, F1 score of 0.95 with an AUC of 0.89. Based on these performance metrics, it can be concluded that a GPC-based linear kernel is a better classifier for segregating the subjects associated with T2DM risk from the healthy subjects. Furthermore, the diagnostic model was deployed on a hardware module, and its performance was validated on 65 patients. Therefore, the use of our model for early T2DM risk indication is highly recommended to healthcare professionals.
Funding
No funding to declare.
Declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Ethical approval
The study was approved by the Institutional Ethics Committee of Smt. Kashibai Navale Medical College and General Hospital Pune India.
Footnotes
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Acharya UR, Joseph KP, Kannathal N, Lim CM, Suri JS. Heart rate variability: a review. Med Biol Eng Compu. 2006;44(12):1031–1051. doi: 10.1007/s11517-006-0119-0. [DOI] [PubMed] [Google Scholar]
- 2.Williams SM, Eleftheriadou A, Alam U, Cuthbertson DJ, Wilding JP. Cardiac autonomic neuropathy in obesity, the metabolic syndrome, and prediabetes: a narrative review. Diabetes Therapy. 2019;1:1–27. doi: 10.1007/s13300-019-00693-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Spallone V. Update on the impact, diagnosis, and management of cardiovascular autonomic neuropathy in diabetes: what is defined, what is new, and what is unmet. Diabetes Metab J. 2019;43(1):3–30. doi: 10.4093/dmj.2018.0259. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Sardu C, De Lucia C, Wallner M, Santulli G. Diabetes mellitus and its cardiovascular complications: new insights into an old disease. 2019;1:1–2. [DOI] [PMC free article] [PubMed]
- 5.Rydén L, Grant PJ, Anker SD, Berne C, Cosentino F, Danchin N, Deaton C, Escaned J, Hammes HP, Huikuri H. ESC Guidelines on diabetes, pre-diabetes, and cardiovascular diseases developed in collaboration with the EASD: the Task Force on diabetes, pre-diabetes, and cardiovascular diseases of the European Society of Cardiology (ESC) and developed in collaboration with the European Association for the Study of Diabetes (EASD) Eur Heart J. 2013;34(39):3035–3087. doi: 10.1093/eurheartj/eht108. [DOI] [PubMed] [Google Scholar]
- 6.Dunlay SM, Givertz MM, Aguilar D, Allen LA, Chan M, Desai AS, Deswal A, Dickson VV, Kosiborod MN, Lekavich CL, McCoy RG. Type 2 Diabetes Mellitus and Heart Failure: A Scientific Statement from the American Heart Association and the Heart Failure Society of America: This statement does not represent an update of the 2017 ACC/AHA/HFSA heart failure guideline update. Circulation. 2019;140(7):e294–324. doi: 10.1161/CIR.0000000000000691. [DOI] [PubMed] [Google Scholar]
- 7.Prasad VC, Savery DM, Prasad VR. Cardiac autonomic dysfunction and ECG abnormalities in patients with type 2 diabetes mellitus-a comparative cross-sectional study. Natl J Physiol Pharm Pharmacol. 2016;6(3):178–181. doi: 10.5455/njppp.2016.6.27122015107. [DOI] [Google Scholar]
- 8.Roy B, Ghatak S. Non-linear methods to assess changes in heart rate variability in type 2 diabetic patients. Arq Bras Cardiol. 2013;101(4):317–327. doi: 10.5935/abc.20130181. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.De Souza AC, Cisternas JR, De Abreu LC, Roque AL, Monteiro CB, Adami F, Vanderlei LC, Sousa FH, Ferreira LL, Valenti VE. Fractal correlation property of heart rate variability in response to the postural change maneuver in healthy women. Int Arch Med. 2014;7(1):25–30. doi: 10.1186/1755-7682-7-25. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Yeh RG, Chen GY, Shieh JS, Kuo CD. Parameter investigation of detrended fluctuation analysis for short-term human heart rate variability. J Med Biol Eng. 2010;30(5):277–282. doi: 10.5405/jmbe.30.5.02. [DOI] [Google Scholar]
- 11.Shukla RS, Aggarwal Y. Nonlinear heart rate variability-based analysis and prediction of performance status in pulmonary metastases patients. Biomed Eng Appl Basis Commun. 2018;30(06):1850043–1850048. doi: 10.4015/S1016237218500436. [DOI] [Google Scholar]
- 12.Khandoker AH, Jelinek HF, Palaniswami M. Identifying diabetic patients with cardiac autonomic neuropathy by heart rate complexity analysis. Biomed Eng Online. 2009;8(1):3. doi: 10.1186/1475-925X-8-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Nunan D, Sandercock GR, Brodie DA. A quantitative systematic review of normal values for short-term heart rate variability in healthy adults. Pacing Clin Electrophysiol. 2010;33(11):1407–1417. doi: 10.1111/j.1540-8159.2010.02841.x. [DOI] [PubMed] [Google Scholar]
- 14.American Diabetes Association. 2. Classification and diagnosis of diabetes. Diabetes Care. 2015; 38(Supplement 1):8–16.
- 15.Electrophysiology TF. Heart rate variability: standards of measurement, physiological interpretation, and clinical use. Circulation. 1996;93(5):1043–1065. doi: 10.1161/01.CIR.93.5.1043. [DOI] [PubMed] [Google Scholar]
- 16.Faust O, Acharya UR, Molinari F, Chattopadhyay S, Tamura T. Linear and non-linear analysis of cardiac health in diabetic subjects. Biomed Signal Process Control. 2012;7(3):295–302. doi: 10.1016/j.bspc.2011.06.002. [DOI] [Google Scholar]
- 17.Brennan M, Palaniswami M, Kamen P. Do existing measures of Poincare plot geometry reflect non-linear features of heart rate variability? IEEE Trans Biomed Eng. 2001;48(11):1342–1347. doi: 10.1109/10.959330. [DOI] [PubMed] [Google Scholar]
- 18.Peng CK, Havlin S, Hausdorff JM, Mietus JE, Stanley HE, Goldberger AL. Fractal mechanisms and heart rate dynamics: long-range correlations and their breakdown with disease. J Electrocardiol. 1995;28:59–65. doi: 10.1016/S0022-0736(95)80017-4. [DOI] [PubMed] [Google Scholar]
- 19.Fusheng Y, Bo H, Qingyu T. Approximate entropy and its application in biosignal analysis. Non-linear Biomed Signal Process Dyn Anal Model. 2001;2:72–91. [Google Scholar]
- 20.Richman JS, Moorman JR. Physiological time-series analysis using approximate entropy and sample entropy. Am J Physiol Heart Circ Physiol. 2000;278(6):2039–2049. doi: 10.1152/ajpheart.2000.278.6.H2039. [DOI] [PubMed] [Google Scholar]
- 21.Xie L, Li Z, Zhou Y, He Y, Zhu J. Computational diagnostic techniques for electrocardiogram signal analysis. Sensors. 2020;20(21):6318. doi: 10.3390/s20216318. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Gupta V, Mittal M. Efficient R-peak detection in electrocardiogram signal based on features extracted using Hilbert transform and Burg method. J Inst Eng India Ser B. 2020;101:1–2. doi: 10.1007/s40031-020-00425-0. [DOI] [Google Scholar]
- 23.Patro S, Sahu KK. Normalization: A preprocessing stage. arXiv preprint http://arxiv.org/abs/1503.06462. 2015.
- 24.Jain AK, Duin RP, Mao J. Statistical pattern recognition: A review. IEEE Trans Pattern Anal Mach Intell. 2000;22(1):4–37. doi: 10.1109/34.824819. [DOI] [Google Scholar]
- 25.Fisher RA. The use of multiple measurements in taxonomic problems. Ann Eugen. 1936;7(2):179–188. doi: 10.1111/j.1469-1809.1936.tb02137.x. [DOI] [Google Scholar]
- 26.Tharwat A, Gaber T, Ibrahim A, Hassanien AE. Linear discriminant analysis: A detailed tutorial. AI Commun. 2017;30(2):169–190. doi: 10.3233/AIC-170729. [DOI] [Google Scholar]
- 27.Smith CA. Some examples of discrimination. Ann Eugen. 1946;13(1):272–282. doi: 10.1111/j.1469-1809.1946.tb02368.x. [DOI] [PubMed] [Google Scholar]
- 28.Pérez A, Larrañaga P, Inza I. Bayesian classifiers based on kernel density estimation: Flexible classifiers. Int J Approximate Reasoning. 2009;50(2):341–362. doi: 10.1016/j.ijar.2008.08.008. [DOI] [Google Scholar]
- 29.Rasmussen CE, Williams CK. Gaussian processes for machine learning. 2006; 38:715–719.
- 30.Nickisch H, Rasmussen CE. Approximations for binary Gaussian process classification. J Mach Learn Res. 2008;9:2035–2078. [Google Scholar]
- 31.Opper M, Winther O. Gaussian processes for classification: Mean-field algorithms. Neural Comput. 2000;12(11):2655–2684. doi: 10.1162/089976600300014881. [DOI] [PubMed] [Google Scholar]
- 32.Hajian-Tilaki K. Receiver operating characteristic (ROC) curve analysis for medical diagnostic test evaluation. Caspian J Intern Med. 2013;4(2):627–635. [PMC free article] [PubMed] [Google Scholar]
- 33.Burlutskiy N, Petridis M, Fish A, Chernov A, Ali N. An investigation on online versus batch learning in predicting user behaviour. In: International Conference on Innovative Techniques and Applications of Artificial Intelligence. 2016;135–49.
- 34.Demšar J. Statistical comparisons of classifiers over multiple data sets. J Mach Learn Res. 2006;7:1–30. [Google Scholar]
- 35.Acharya UR, Faust O, Sree SV, Ghista DN, Dua S, Joseph P, Ahamed VT, Janarthanan N, Tamura T. An integrated diabetic index using heart rate variability signal features for diagnosis of diabetes. Comput Methods Biomech Biomed Eng. 2013;16(2):222–234. doi: 10.1080/10255842.2011.616945. [DOI] [PubMed] [Google Scholar]
- 36.Acharya UR, Faust O, Kadri NA, Suri JS, Yu W. Automated identification of normal and diabetes heart rate signals using non-linear measures. Comput Biol Med. 2013;43(10):1523–1529. doi: 10.1016/j.compbiomed.2013.05.024. [DOI] [PubMed] [Google Scholar]
- 37.Benichou T, Pereira B, Mermillod M, Tauveron I, Pfabigan D, Maqdasy S, Dutheil F. Heart rate variability in type 2 diabetes mellitus: A systematic review and meta-analysis. PLoS ONE. 2018;13(4):1–19. doi: 10.1371/journal.pone.0195166. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Kumari VA, Chitra R. Classification of diabetes disease using support vector machine. Int J Eng Res Appl. 2013;3(2):1797–1801. [Google Scholar]
- 39.Osman AH, Aljahdali HM. Diabetes disease diagnosis method based on feature extraction using K-SVM. Int J Adv Comput Sci Appl. 2017;8(1):236–244. [Google Scholar]
- 40.Chawla NV, Bowyer KW, Hall LO, Kegelmeyer WP. SMOTE: synthetic minority over-sampling technique. J Artif Intell Res. 2002;16:321–357. doi: 10.1613/jair.953. [DOI] [Google Scholar]