Synthetic CT generation from weakly paired MR images using cycle-consistent GAN for MR-guided radiotherapy

Abstract

Although MR-guided radiotherapy (MRgRT) is advancing rapidly, generating accurate synthetic CT (sCT) from MRI is still challenging. Previous approaches using deep neural networks require large dataset of precisely co-registered CT and MRI pairs that are difficult to obtain due to respiration and peristalsis. Here, we propose a method to generate sCT based on deep learning training with weakly paired CT and MR images acquired from an MRgRT system using a cycle-consistent GAN (CycleGAN) framework that allows the unpaired image-to-image translation in abdomen and thorax. Data from 90 cancer patients who underwent MRgRT were retrospectively used. CT images of the patients were aligned to the corresponding MR images using deformable registration, and the deformed CT (dCT) and MRI pairs were used for network training and testing. The 2.5D CycleGAN was constructed to generate sCT from the MRI input. To improve the sCT generation performance, a perceptual loss that explores the discrepancy between high-dimensional representations of images extracted from a well-trained classifier was incorporated into the CycleGAN. The CycleGAN with perceptual loss outperformed the U-net in terms of errors and similarities between sCT and dCT, and dose estimation for treatment planning of thorax, and abdomen. The sCT generated using CycleGAN produced virtually identical dose distribution maps and dose-volume histograms compared to dCT. CycleGAN with perceptual loss outperformed U-net in sCT generation when trained with weakly paired dCT-MRI for MRgRT. The proposed method will be useful to increase the treatment accuracy of MR-only or MR-guided adaptive radiotherapy.

Supplementary Information

The online version contains supplementary material available at 10.1007/s13534-021-00195-8.

Introduction

In radiation therapy, radiation should be delivered accurately to the planning target volume (PTV) to eliminate cancer while simultaneously delivering minimal radiation to unwanted areas to prevent side effects. Therefore, accurate delineation of target and normal tissues is essential, and computed tomography (CT) is primarily used for target localization and organ contouring in radiotherapy planning.

Magnetic resonance imaging (MRI) is increasingly used for radiotherapy planning because of its superior soft-tissue contrast compared to CT, which facilitates tumor and organ-at-risk (OAR) delineation. However, dose estimation based solely on MR images is challenging because MR images do not provide direct information on electron density. Therefore, additional CT scans of patients are acquired and co-registered with MRI for the MR-guided radiotherapy (MRgRT) systems, including MR-Linac, which causes unnecessary radiation exposure and extra cost to patients. Dose estimation error due to spatial misregistration and temporal changes in anatomy between MRI and CT is another drawback of the co-registered CT-based approach [1].

Recently, considerable research interest has been directed toward the direct conversion of MRI into synthetic CT (sCT) based on deep learning (DL) approaches to overcome the drawbacks of co-registered CT. Previous studies using the DL method for MRI-to-CT translation employed supervised learning models that are easy to train but generally produce blurry output images [2–8]. The most commonly used neural network for MRI-to-CT translation is the U-net architecture, an encoder–decoder network with skip connections trained in a discriminative manner [9]. In contrast, the incorporation of generative models usually provides more realistic output images than discriminative models. One of the approaches to generative modeling is the generative adversarial network (GAN) in which generator and discriminator networks are trained simultaneously through min–max optimization [10]. In several recent studies on sCT generation from MR images, GANs that utilize adversarial feedback from a discriminator network have shown superior performance than the corresponding U-nets [11–14]. However, previous approaches using GANs were based on paired image-to-image translation, requiring a large dataset of precisely co-registered CT and MRI pairs that are difficult to obtain due to respiration and peristalsis in thorax and abdomen. In addition, there are a limited number of studies on generating MR-based sCT for MRgRT systems [15, 16]. The datasets used in previous studies are also limited to the head, neck, pelvis, and liver.

Therefore, in this study, we propose a method to generate sCT based on DL training from weakly paired CT and MR images acquired from the MRgRT system using a cycle-consistent GAN (CycleGAN) framework that allows unpaired image-to-image translation [17–20]. The proposed CycleGAN method has been applied to the head and neck or the pelvis area, but as far as we know it has not been applied to the abdomen and thorax [18, 21]. To improve the sCT generation performance, a perceptual loss that explores the discrepancy between high-dimensional representations of images extracted from a discriminator was incorporated into the CycleGAN. In addition, the weakly paired dataset included CT and MR images of the pelvis, thorax, and abdomen to prevent the overfitting of networks from being specialized in a specific area. The sCT generation performance of CycleGAN was compared with U-net, and the dose estimation accuracy was evaluated using the treatment planning system (TPS) of the MRgRT system.

Methods and materials

Data acquisition and preprocessing

Data from 90 cancer patients who underwent MRgRT were retrospectively used. The retrospective use of the scan data and waiver of consent were approved by the Institutional Review Board of our institute. The patient data were divided into three groups according to the treatment region: pelvis (n = 30), thorax (n = 30), and abdomen (n = 30). Detailed patient characteristics are provided in Supplementary Table 1.

CT simulation scans of all patients were acquired using the Brilliance Big Bore CT scanner (Philips, Cleveland, OH). Fifteen minutes after the CT scan, MR images were acquired using a 0.35 T MRI scanner combined with the radiation therapy unit of the MRIdian MRgRT system (ViewRay, Oakwood, OH). The MRI scans were performed in the same patient setup as the CT simulations using true fast imaging with steady-state precession (TrueFISP; TRUFI) sequence. Thereafter, the CT images were co-registered with the corresponding MR images using a deformable registration algorithm, provided by ViewRay TPS. The deformed CT (dCT) images were resampled to have the same dimensions as the MRI images (320 × 320 × 144). A dataset with mismatched body and organ boundaries on the co-registered CT and MRI were not included in the data of the 90 patients. The low-frequency intensity and non-uniformity present in MRI were corrected using the N4 bias field correction algorithm [22].

Of the 90 MR–dCT image pairs, 80% (72 pairs) were used for network training and the remaining 20% (18 pairs) were used for testing and validation. To avoid 3D discontinuities in sCT, 2.5D data consisting of three adjacent slices were provided to the network. The intensity of the images was normalized using the 95% percentile value of the intensity peak of each image to enable effective network training.

Network architecture

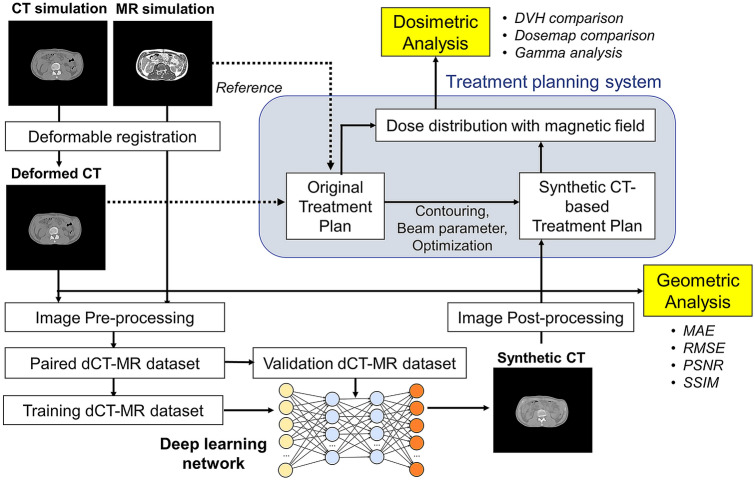
As mentioned previously, two different deep learning networks, U-net and CycleGAN, were used for sCT generation. Figure 1 shows the procedures for image processing/analysis and network training/testing, and Supplementary Fig. 1 shows the detailed structure of the deep learning networks. For U-net, the standard network architecture used in Noise2Noise paper [23] was modified. The input and output of the U-net are MRI and sCT, respectively, and the ground truth is dCT. The network consisted of 17 convolutional layers containing a convolution and a leaky rectified linear unit (ReLU) activation function, as shown in Supplementary Fig. 1.b. The filter numbers for these layers were 64, 64, 128, 256, 512, 1024, and 1024 in the encoder for down-sampling, and 1024, 1024, 512, 512, 256, 256, 128, 128, 64, and 64 in the decoder for up-sampling. The weights and biases in the layers were trained by minimizing L1 loss, the mean absolute error (MAE) between the sCT and dCT. The network was trained for 200 epochs using an adaptive stochastic gradient descent optimizer (Adam) with a learning rate of 0.0001.

Fig. 1.

Image analysis procedures

The CycleGAN consisted of two generators (G₁ and G₂) and two discriminators (D₁ and D₂), as shown in Supplementary Fig. 1.a. The U-net described above was used as the generator. The discriminators consisted of five residual neural network (ResNet) blocks [24] followed by global average pooling layer (Supplementary Fig. 1.b). The generators produce synthetic images, and discriminators determine whether the synthetic images are real or fake by minimizing the following loss functions:

$$L_{\mathit{GAN}}\left(G_1,G_2,D_1,D_2\right)=L_{\mathit{GAN}}^{\mathit{CT}}\left(G_1,D_1\right)+L_{\mathit{GAN}}^{\mathit{MR}}\left(G_2,D_2\right)$$

$$L_{\mathit{cyc}}\left(G_1,G_2\right)=L_{\mathit{cyc}}^{\mathit{CT}}\left(G_1\right)+L_{\mathit{cyc}}^{\mathit{MR}}\left(G_2\right)$$

$$L_{\mathit{id}}\left(G_1,G_2\right)=L_{\mathit{id}}^{\mathit{CT}}\left(G_1\right)+L_{\mathit{id}}^{\mathit{MR}}\left(G_2\right)$$

$$L_{\mathit{cycGAN}}=L_{\mathit{GAN}}+100\times L_{\mathit{cyc}}+10\times L_{\mathit{id}},$$

where L_GAN is the GAN loss that generates a real-like desired image, L_cyc is the cyclic loss enforcing that the output of the generator is similar to the input, and L_id is the identical loss that stabilizes the training.

Deformable registration is nearly accurate for bones, but it is not perfect for non-rigid structures areas. Therefore, we have complemented fidelity loss between the generator output and the dCT with perceptual loss in the discriminator’s view. Perception loss is used to minimize high-level differences, such as content and style discrepancies between the generated and input images. The sum of L2 norm of the features in ResNet blocks 1, 2, and 3 of the discriminators was calculated as the perceptual loss, and spectral normalization was applied to each layer to stabilize the discriminator training [25]. Accordingly, the perceptual loss and total loss can be described as follows:

$$L_{\mathit{percep}}=\sum _n\sum _{i=1}^3{\varphi }_i^{D_1}\left(\mathit{MR}\right)-{\varphi }_i^{D_1}{\left(G_1\left(\mathit{CT}\right)\right)}^2+{\varphi }_i^{D_2}\left(\mathit{CT}\right)-{\varphi }_i^{D_2}{\left(G_2\left(\mathit{MR}\right)\right)}^2$$

$$L_{\mathit{final}}=L_{\mathit{cycGAN}}+100\times L_{\mathit{percep}},$$

where n is the batch size and ${\varphi }_i^{·}$ is the i-th ResNet block used to calculate the perceptual loss, which was extracted from each discriminator.

The number of the batch size and learning rate of the generator were 1 and 0.0001, respectively. We used the two time-scale update rule to assign different learning rates to generators and discriminators [26]. The learning rate of the discriminators was four times higher than that of the generators. The Adam optimization algorithm (β₁ = 0.5 and β₂ = 0.99) was used to minimize the above losses. All models were implemented using TensorFlow and trained on an NVIDIA Geforce GTX 1080Ti with 11 GB of memory.

Image analysis and treatment planning

As previously mentioned, 18 of 90 MR–dCT image pairs were randomly selected as the test set. To assess the accuracy of the image translation for the test set, the MAE, root mean square error (RMSE), peak signal-to-noise ratio (PSNR), and structural similarity (SSIM) between the sCT generated from the pre-processed MRI using the deep neural networks and the dCT were calculated as follows:

$$MAE=\frac{1}{N}\sum _{i=1}^N\left|sC{T}_i-dC{T}_i\right|$$

$$RMSE=\sqrt{\frac{1}{N}\sum _{i=1}^N{(sC{T}_i-dCT)}^2}$$

$$PSNR=10·{log}_{10}\left(\frac{MA{X}^2}{\mathit{MSE}}\right)$$

$$SSIM=\frac{(2{\mu }_x{\mu }_y+c_1)(2{\sigma }_{\mathit{xy}}+c_2)}{({\mu }_x^2+{\mu }_y^2+c_1)({\sigma }_x^2+{\sigma }_y^2+c_2)},$$

where i is a voxel within the body, N is the total number of voxels, and MAX is the maximum voxel value of the reference image.

We also analyzed the dosimetric accuracy of the use of sCT images based on the MRIdian treatment planning system used for the Co-60 ViewRay system. The dose distribution was recalculated by replacing dCT with sCT images under the same beam parameters as the original dCT treatment plan. The Monte Carlo simulation with magnetic-field correction was performed to calculate the dose distribution with a calculation grid size of 3 mm. The prescription dose to the PTV was not the same for all patients. To evaluate the dose distribution under the same condition, the dose distribution map was scaled to correspond to the prescription dose of 70 Gy for the pelvis, 38.5 Gy for the thorax, and 50 Gy for the abdomen. To compare the dose distributions estimated using the sCT and dCT, several dose-volume histogram (DVH) parameters, such as minimum (D_min), maximum (D_max), and mean (D_mean) absorbed doses for the PTV and OARs, were calculated. For the PTV area, D_98%, D_2%, and V_100% were also calculated to assess the homogeneity and conformity of the dose distribution. Spatial dose distributions were also compared using 3D gamma analysis under 2%/2 mm and 3%/3 mm (dose discrepancy/distance agreement) criteria with 10, 50, and 90% thresholds.

All statistical analyses were performed using SPSS software. Wilcoxon signed-rank tests were used to compare the performance of the U-net and the proposed CycleGAN models. P values less than 0.05 were considered statistically significant.

Results

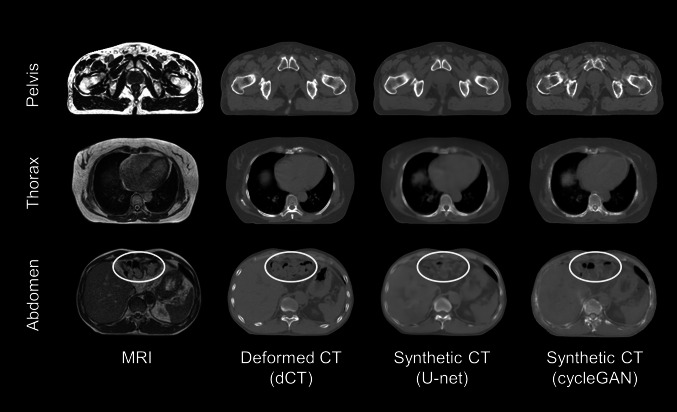
Figure 2 shows the representative case of the generated sCT slices exhibited with the corresponding MR and dCT slices in the pelvis, thorax, and abdomen. The sCT generated using CycleGAN (sCT_CyGAN) showed sharper boundaries than the sCT generated using the U-net (sCT_U-net). In addition, sCT showed better similarity to dCT in dense structures such as the pelvic bones and spine. The location and size of air pockets shown in the abdomen images are more accurate in sCT than in dCT (yellow ellipses).

Fig. 2.

Transverse slices of MRI, dCT, sCT_U-net, and sCT_cGAN in representative cases

The MAE, RMSE, PSNR, and SSIM between the dCT and sCT images calculated from the test set data are summarized in Table 1. In general, sCT_CyGAN showed smaller errors (MAE and RMSE) and higher similarities (PSNR, SSIM) relative to dCT than sCT_U-net. The error and similarity differences between CycleGAN and U-net were considerably large in the thorax and abdomen.

Table 1.

Errors (MAE and RMSE) and similarities (PSNR, SSIM) relative between sCT and dCT in the test group

	Pelvis (n = 6)	Thorax (n = 6)	Abdomen (n = 6)	Total (n = 18)
U-net
MAE	56.3 ± 9.3	134 ± 27.8	150 ± 55.4	114 ± 54.7
RMSE	104 ± 7.0	168 ± 27.3	172 ± 22.9	148 ± 33.9
PSNR	27.9 ± 0.6	23.0 ± 1.7	22.9 ± 3.1	24.6 ± 3.1
SSIM	0.87 ± 0.04	0.89 ± 0.01	0.91 ± 0.01	0.89 ± 0.03
CycleGAN
MAE	55.3 ± 5.5	63.7 ± 3.8	58.8 ± 4.4	59.2 ± 5.8
RMSE	118 ± 9.3	119 ± 8.4	113 ± 9.3	117 ± 9.4
PSNR	26.8 ± 0.7	25.9 ± 0.5	26.3 ± 0.7	26.3 ± 0.7
SSIM	0.89 ± 0.05	0.90 ± 0.02	0.91 ± 0.01	0.90 ± 0.03

MAE Mean absolute error, RMSE Root mean square error, PSNR Peak signal-to-noise ratio, SSIM Structural similarity

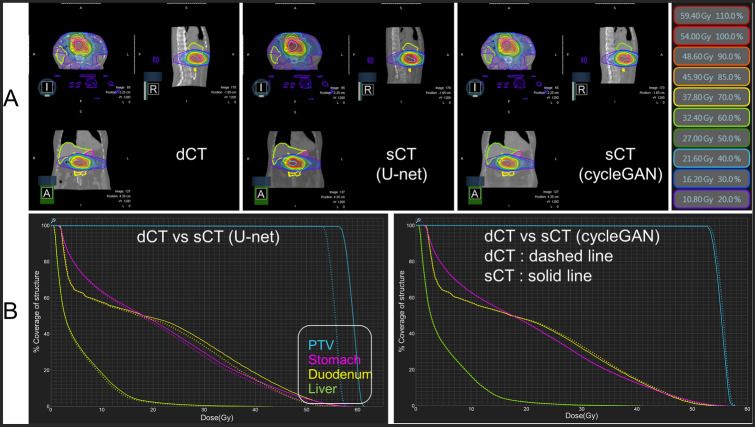
Figure 3 and Table 2 show the superiority of sCT_CyGAN over sCT_U-net in dose estimation for treatment planning. The treatment dose distribution and DVHs for the PTV and OARs generated using dCT and sCTs for a representative abdomen case are shown in Fig. 3. In this case, dCT and sCTs yield very similar isodose curves, as shown in Fig. 3a. The left column of Fig. 3b shows the significant DVH difference between dCT and sCT_U-net, which is largest in the PTV. On the other hand, dCT and sCT_CyGAN produce virtually identical DVHs, as shown in the right column of Fig. 3b. DVH parameters for the PTV and OARs in each region are summarized in Table 2.

Fig. 3.

Dosimetric comparison between dCT and sCTs in the abdomen. a Dose distribution and isodose curves. Each color contour shows the isodose line (see right legends). b Left: Comparison of dose volume histogram for PTV and OARs (stomach, duodenum, and liver) between dCT and sCT using U-net Right: Comparison of dose volume histogram for PTV and OARs between dCT and sCT using cycleGAN. Dashed line indicates the result of dCT and the solid line shows the result of sCT methods

Table 2.

Comparison of dose-Volume histogram (DVH) parameters between dCT and sCTs

	Pelvis			Thorax			Abdomen
	dCT	sCTU-net	sCTcGAN	dCT	sCTU-net	sCTcGAN	dCT	sCTU-net	sCTcGAN
PTV
Dmean	73.9 ± 0.7	75.6 ± 0.6*	74.0 ± 0.7	40.1 ± 0.6	40.8 ± 0.8	40.2 ± 0.6	50.5 ± 2.1	54.1 ± 3.0**	50.3 ± 1.5
Dmin	63.8 ± 2.1	66.3 ± 3.6	63.9 ± 2.3	35.3 ± 1.7	35.0 ± 2.0	35.2 ± 1.7	45.2 ± 2.2	48.7 ± 3.2	45.1 ± 2.5
Dmax	78.7 ± 1.3	80.3 ± 1.3*	78.8 ± 1.5	42.5 ± 1.4	43.5 ± 1.7**	42.6 ± 0.9	54.1 ± 1.2	57.5 ± 3.4**	53.3 ± 0.9
D98%	68.6 ± 1.0	69.9 ± 1.3	68.6 ± 1.0	37.7 ± 0.9	37.8 ± 0.9	37.7 ± 1.0	49.3 ± 0.2	49.7 ± 3.4	48.8 ± 0.2*
D2%	76.9 ± 1.1	78.5 ± 1.0*	77.1 ± 1.0	41.9 ± 1.3	42.8 ± 1.6	41.9 ± 1.4	53.5 ± 0.6	56.4 ± 3.1	53.1 ± 0.6
V100%	77.5 ± 18.8	79.2 ± 19.0	77.8 ± 19.1	89.6 ± 27.8	92.5 ± 29.2	89.6 ± 27.6	36.1 ± 13.0	32.0 ± 12.4	34.2 ± 12.1
OAR	Bladder			Heart			Duodenum
Dmean	47.3 ± 3.7	47.9 ± 3.6	47.4 ± 3.7	3.1 ± 0.7	3.2 ± 0.8	3.0 ± 0.7	26.1 ± 8.9	27.4 ± 9.6	25.9 ± 8.9
Dmin	20.0 ± 10.5	20.1 ± 10.5	20.0 ± 10.4	0.3 ± 0.1	0.3 ± 0.1	0.3 ± 0.1	5.4 ± 5.1	5.5 ± 5.3	5.5 ± 5.2
Dmax	75.8 ± 1.6	77.0 ± 2.1	75.7 ± 1.4	19.0 ± 10.9	19.3 ± 10.9	19.0 ± 10.9	49.4 ± 4.1	52.7 ± 5.1	46.7 ± 6.5
OAR	Rectum			Left lung			Stomach
Dmean	43.2 ± 6.1	43.7 ± 6.0	43.1 ± 6.2	1.6 ± 0.3	1.7 ± 0.3	1.6 ± 0.3	15.2 ± 5.1	15.7 ± 5.3	15.2 ± 5.1
Dmin	16.6 ± 8.0	16.5 ± 8.0	16.5 ± 7.9	0.2 ± 0.03	0.2 ± 0.04	0.2 ± 0.03	2.1 ± 1.6	2.2 ± 1.7	2.1 ± 1.7
Dmax	76.1 ± 1.7	76.9 ± 2.0	75.4 ± 1.3	9.1 ± 4.9	9.3 ± 4.7	8.9 ± 4.6	45.5 ± 5.2	47.1 ± 5.7	45.1 ± 5.4
OAR	Femur head			Right lung			Liver
Dmean	25.5 ± 6.7	25.8 ± 6.8	25.5 ± 6.7	6.4 ± 1.4	6.5 ± 1.4	6.3 ± 1.4	8.3 ± 5.3	8.7 ± 5.5	8.3 ± 5.3
Dmin	10.8 ± 6.0	11.1 ± 6.1	11.0 ± 6.1	0.2 ± 0.08	0.2 ± 0.07	0.2 ± 0.07	0.7 ± 0.3	0.8 ± 0.4	0.7 ± 0.4
Dmax	44.6 ± 7.4	45.0 ± 7.9	44.5 ± 7.9	40.1 ± 1.1	40.9 ± 0.8	39.9 ± 0.9	44.5 ± 8.9	47.4 ± 10.7	43.9 ± 8.8

The Wilcoxon test was used to compare the dose volume parameters between dCT and sCT. Significant differences were considered at p < 0.05* and p < 0.1**

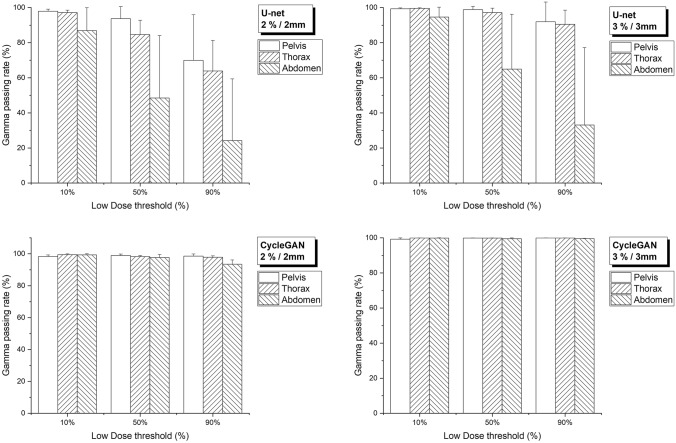
Figure 4 shows the average gamma passing rates between dCT and sCTs using 2%/2 mm and 3%/3 mm criteria at three different threshold levels. The gamma passing rate of cycleGAN exceeded 97%, except for 90% threshold in the abdomen. On the other hand, the U-net’s gamma passing rate exceeded 90% in all areas only at 3 mm/3% criteria with a 10% threshold, and was less than 90% when threshold increased or 2 mm/2% criteria was applied (see Supplementary Table 2 for detailed results).

Fig. 4.

Gamma passing rate according to two different criteria (2%/2 mm and 3%/3 mm) between dCT and sCTs

Discussion

Although MRgRT technology is advancing rapidly, generating accurate sCT from MRI is still an unsolved problem. Deep learning technology is also advancing rapidly, and image-to-image translation technology based on deep learning is being applied in various fields, including sCT generation from MRI [27–32]. However, most of the previous studies focused on generating sCT from diagnostic MRI, and in these studies, conventional TPS was used for dose calculation [3–5]. On the other hand, in our study, we generated sCT by applying deep learning models to low-field MR images used in the actual MRgRT system. The 0.35 T MRI images produced in the MRIdian MRgRT system exhibit different relaxation properties and image contrast than 1.5 T or 3 T MR images used for diagnostic purposes [33]. Furthermore, the MRIdian MRgRT system uses a TRUFI sequence that creates T2/T1 contrast that is different from the general T1 or T2 contrast [34].

Unlike most previous studies in which deep neural networks were trained using only data from a specific area, this study trained neural networks using all pelvis, thorax, and abdomen images to increase the performance and generality of the trained neural network. The main advantage of MRgRT is the application of real-time respiratory gating technology and the accurate identification of treatment targets based on the high soft-tissue contrast of MRI [35]. In this regard, it is particularly important to increase the accuracy of sCT generation in the thorax and abdomen areas that are heavily affected by respiration and inter- and intra-fraction movements [36]. However, there are limited studies that deal with the translation from MRI to CT of the thorax and abdomen because it is difficult to generate perfectly matched datasets due to changes in the shape and location of the non-rigid organs and air pockets.

U-net has shown superior performance in many image-to-image translation tasks [30, 31, 37–39]. However, this representative discriminative learning model has limited performance when trained with incomplete matched datasets, as shown in this study. To alleviate the incomplete matching problem, this study introduces CycleGAN that utilizes the flexible translation capabilities offered by the generative model structure [40]. The sCT generation performance was further improved by considering the perceptual loss that allows us to retain high-level features compared to pixel-wise loss, such as L1 or L2, which produce local smoothing [41] (Supplementary Fig. 2). Consequently, the CycleGAN using perceptual loss outperformed the U-net in terms of errors and similarities between sCT and dCT in the thorax and abdomen (Table 1). The dosimetric robustness of the proposed CycleGAN was also proven through gamma analysis (Fig. 4). In a previous study [14], conditional GAN with perceptual loss performed better than U-net in sCT generation from the MRI of patients with prostate cancer. However, the incorporation of perceptual loss in conditional GAN could not reduce MAE and improve the dose calculation accuracy, maybe because their dataset was limited to the pelvic area.

Recently, online MR-guided adaptive radiotherapy (MRgART) has been proposed to address anatomical changes in PTV and OARs during the treatment period [42]. In addition, a clinical trial called stereotactic MRI-guided on-table adaptive radiation therapy (SMART) for the pancreatic area is ongoing [43, 44]. However, changes in the air pocket position during MRgART cause significant differences in dose distribution [44]. To address this problem, in the current MRgART protocol, air pockets and body surfaces are recontoured in the dCT while referring to the MRI acquired daily, and correct electron densities are assigned to air and soft tissues, thereby increasing the time the patient is on the table. Therefore, improved sCT generation enabled by applying the proposed method will increase the accuracy of treatment planning and the convenience of patients in MRgART.

This study has some limitations, including a small number of datasets used for training and validating the network models. The accuracy of the sCT can be further improved by adding the MRI obtained daily for each fractionation and reducing the variability in MRI intensity through white stripe normalization [8, 45]. In addition, adding segmented bone regions from CT as input to networks will also improve the accuracy of sCT.

Conclusions

CycleGAN with perceptual loss outperformed U-net in sCT generation when trained with weakly paired dCT–MRI for MRgRT in abdomen and thorax. This approach will be useful to increase the treatment accuracy of MR-only radiotherapy and MRgART.

Supplementary Information

Below is the link to the electronic supplementary material.

Data availability

Research data are not available at this time.

Declarations

Conflict of interest

The authors declare that they have no conflict of interest.