Constrained maximum likelihood-based Mendelian randomization robust to both correlated and uncorrelated pleiotropic effects

Summary

With the increasing availability of large-scale GWAS summary data on various complex traits and diseases, there have been tremendous interests in applications of Mendelian randomization (MR) to investigate causal relationships between pairs of traits using SNPs as instrumental variables (IVs) based on observational data. In spite of the potential significance of such applications, the validity of their causal conclusions critically depends on some strong modeling assumptions required by MR, which may be violated due to the widespread (horizontal) pleiotropy. Although many MR methods have been proposed recently to relax the assumptions by mainly dealing with uncorrelated pleiotropy, only a few can handle correlated pleiotropy, in which some SNPs/IVs may be associated with hidden confounders, such as some heritable factors shared by both traits. Here we propose a simple and effective approach based on constrained maximum likelihood and model averaging, called cML-MA, applicable to GWAS summary data. To deal with more challenging situations with many invalid IVs with only weak pleiotropic effects, we modify and improve it with data perturbation. Extensive simulations demonstrated that the proposed methods could control the type I error rate better while achieving higher power than other competitors. Applications to 48 risk factor-disease pairs based on large-scale GWAS summary data of 3 cardio-metabolic diseases (coronary artery disease, stroke, and type 2 diabetes), asthma, and 12 risk factors confirmed its superior performance.

Introduction

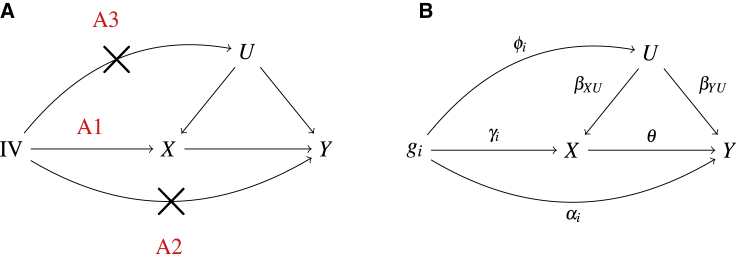
Mendelian randomization (MR) has been widely applied to assess causal relationships between pairs of complex traits (called exposures and outcomes, respectively) using genetic variants as instrumental variables (IVs) for observational data. The practice is not only motivated by fundamental scientific questions on causal relationships, but also largely facilitated by recent advances in human genetics with increasing availability of large-scale GWAS summary data on various complex traits and of the simplicity of such analyses. However, the validity of such an analysis critically depends on the IV assumptions, which are often violated due to the widespread genetic (horizontal) pleiotropy, leading to biased inference and false conclusions.^1,2 The three assumptions on a valid IV, as shown in Figure 1, are listed below:

• (A1)The IV is associated with the exposure X; i.e., ${\gamma }_i\ne 0$.
• (A2)The IV is not associated with the outcome Y conditional on the exposure X; i.e., α_i = 0.
• (A3)The IV is not associated with unmeasured confounder U; i.e., ${\phi }_i=0$.

Figure 1.

Causal model with exposure X and outcome Y

(A) Three IV assumptions.

(B) A general causal model.

Among the three, the first assumption is more straightforward to handle by using highly significant SNPs as IVs. The violation of assumption A2 introduces so-called uncorrelated pleiotropic effects, for which some MR methods, such as MR Egger regression,^3,4 have been proposed and applied. The most challenging is assumption A3, introducing so-called correlated pleiotropic effects. Under our general causal model as shown in Figure 1, the total effects of IV g_i on the outcome Y can be decomposed into two parts: that mediated through exposure X, ${\beta }_{Yi,M}=\theta \cdot \left({\gamma }_i+{\beta }_{XU}\cdot {\phi }_i\right)$, and other direct effect (not mediated through X), ${\beta }_{Yi,D}={\alpha }_i+{\beta }_{YU}\cdot {\phi }_i$. It is clear that, under the violation of assumption A3, we have ${\phi }_i\ne 0$, leading to the correlation of the mediated and direct effects ${\beta }_{Yi,M}$ and ${\beta }_{Yi,D}$, and thus the violation of the instrument strength independent of direct effect (InSIDE) assumption required by MR-Egger regression and other methods (e.g., RAPS)^5,6 that model the direct effects α_i’s as independent random effects; in turn, these methods have to impose that the pleiotropic effect of any SNP must be uncorrelated with its SNP-exposure association.

Here we propose a simple MR method based on constrained maximum likelihood and model averaging, denoted cML-MA, that is robust to the violation of both assumptions A2 and A3; i.e., it is robust to invalid IVs with uncorrelated or correlated pleiotropic effects. Table 1 compares our proposed cML-MA with some most popular and new methods that are all applicable to GWAS summary data. Our method depends only on the “plurality valid” assumption: in large samples, while (Wald) ratio estimates of the target causal effect from invalid IVs will take different values, ratio estimates from all valid IVs should approach the true causal effect and thus the valid IVs form the largest group of SNPs among all the groups giving different ratio estimates.^7,8 This assumption is weaker than the “majority valid” assumption, which states that more than 50% of the SNPs being used are valid IVs. It is noted that three new methods with this or other weak assumptions, MR-Mix, MR-ContMix, and CAUSE, impose a normal mixture model with more unknown parameters to estimate, while our proposed cML-MA does not impose such an assumption and estimates only a minimum number of necessary parameters. It is well known that mixture models are statistically difficult to estimate with small numbers of SNPs/IVs. This brings up an important point: in addition to its modeling assumptions, another key factor determining the performance of a method is how it is implemented. This point might explain why our cML-MA performed better than MR-Mix, MR-ContMix, and CAUSE as to be shown. Another example is the MR-Weighted-Mode method: although it imposes minimum modeling assumptions as cML-MA, it is difficult to estimate the mode of a distribution with small numbers of SNPs/IVs, leading to often its poor performance as shown by others^9,10 and to be confirmed later too. A similar argument in the discussion section will be made on the advantage of our method over two other related ones, MR-Lasso and MR-PRESSO: all three share the basic idea of selecting/removing invalid IVs, but due to their different implementations, they perform quite differently. As shown by previous studies,9, 10, 11 existing MR methods may not perform well with inflated type I errors and/or biased estimates, especially with a high proportion of invalid IVs among a small number of SNPs, prompting an urgent need for more robust and efficient MR methods. Here we develop an efficient algorithm, an effective model selection criterion, a model averaging approach and its variant based on data perturbation for such a purpose; our proposed cML-MA and its data perturbation-based variant are simple and easy to implement while imposing less stringent modeling assumptions, and as to be shown, perform consistently better than other methods across a wide range of scenarios.

Table 1.

Comparison of different MR methods, including whether valid IV assumption A2 or A3 can be violated

Method	A2	A3	Key assumptions	Implementation challenges/performance
cML-MA	✓	✓	plurality valid	controlling type I errors with high power
MR-Mix12	✓	✓	plurality valid; ${\hat{\beta }}_{Yi}-\theta {\hat{\beta }}_{Xi}\sim$ a mixture of normals	biased to the null, thus conservative
MR-ContMix9	✓	✓	plurality valid; ${\hat{\theta }}_i\sim \left(1-q\right)N\left(\theta ,SE{\left({\hat{\theta }}_i\right)}^2\right)+qN\left(0,{\psi }^2+SE{\left({\hat{\theta }}_i\right)}^2\right)$; NOME	difficult to pre-choose a fixed value for tuning parameter ψ
CAUSE13	✓	✓	<50% IVs have correlated pleiotropy; ${\gamma }_i{\phi }_i=0$; ${\beta }_{XU}=1$; ${\beta }_{Xi}={\gamma }_i$ or ${\phi }_i$; ${\hat{\beta }}_{Yi}\sim \left(1-q\right)N\left(\theta {\beta }_{Xi}+r_i,{\sigma }^2\right)+qN\left(\left(\theta +{\beta }_{YU}\right){\beta }_{Xi}+r_i,{\sigma }^2\right)$	difficult to estimate some parameters depending on the hidden confounder U; sensitive to assumption of ${\gamma }_i{\phi }_i=0$
MR-Lasso14	✓	✓	plurality valid;7 some condition on the exposure-association strengths of invalid IVs relative to that of valid IVs to ensure consistency;15 NOME	depending on the heterogeneity criterion for choosing the tuning parameter for the Lasso penalty
MR-Weighted-Mode16	✓	✓	plurality valid	sensitive to the difficult bandwidth selection for mode estimation
MR-Weighted-Median3	✓	✓	majority valid	robust to outliers; low powered; sometimes biased
MR-PRESSO1	✓	x	majority valid; InSIDE; Good delete-1 causal estimates	inflated type I errors; unable to completely remove invalid IVs
MR-Egger17	✓	x	InSIDE: ${\phi }_i=0$; ${\alpha }_i\sim N\left(\mu ,{\tau }^2\right)$ for a small m (but no normality needed for a large m); NOME	often biased and low powered
MR-RAPS6	✓	x	InSIDE: ${\phi }_i=0$; ${\alpha }_i\sim N\left(0,{\tau }^2\right)$ if overdispersion is specified	may be sensitive to directional pleiotropy; robust to outliers with Tukey’s loss
MR-IVW (RE)18,19	✓	x	balanced pleiotropy; NOME	sensitive to directional pleiotropy; low powered
MR-IVW (FE)18,19	x	x	all IVs are valid; NOME	efficient when all IVs are valid; sensitive to invalid IVs

The notations are defined in Figure 1 and Equation 1, and q is the (unknown) proportion of invalid IVs while ${\hat{\theta }}_i={\hat{\beta }}_{Yi}/{\hat{\beta }}_{Xi}$ and $SE\left({\hat{\theta }}_i\right)$ are the Wald ratio estimate of θ based on SNP i and its standard error, respectively. NOME refers to no measurement error assumption: the variance of any IV-exposure association estimate is negligible.²⁰

Material and methods

Overview

Suppose that we have m independent SNPs, $g_1,g_2,\cdots ,g_m$, as IVs, X is the exposure, Y is the outcome, and U is the hidden confounder. Under the true causal model as shown in Figure 1, we obtain the total effects of g_i on X and on Y as ${\beta }_{Xi}$ and ${\beta }_{Yi}$, respectively:

$$\begin{array}{l}{\beta }_{Xi}={\gamma }_i+{\beta }_{XU}\cdot {\phi }_i,\\ {\beta }_{Yi}=\theta \cdot \left({\gamma }_i+{\beta }_{XU}\cdot {\phi }_i\right)+{\alpha }_i+{\beta }_{YU}\cdot {\phi }_i=\theta \cdot {\beta }_{Xi}+r_i,\end{array}$$ (Equation 1)

where $r_i={\alpha }_i+{\beta }_{YU}\cdot {\phi }_i$ represents the direct/pleiotropic effects of IV g_i on outcome Y, not mediated by exposure X. If g_i is a valid IV, IV assumptions A2 and A3 would imply α_i = 0 and ${\phi }_i=0$, respectively, leading to r_i = 0. For an invalid IV with $r_i\ne 0$, its (Wald) ratio is biased for θ: ${\beta }_{Yi}/{\beta }_{Xi}\ne \theta$. Our goal is for unbiased inference of the causal effect θ in the possible presence of some (unknown) invalid IVs with the corresponding (unknown) $r_i\ne 0$.

From two independent GWAS summary datasets for traits X and Y, respectively, we obtain the estimated marginal effect sizes of g_i’s on X and Y (and their standard errors) as ${\hat{\beta }}_{Xi}\left({\hat{\sigma }}_{Xi}\right)$ and ${\hat{\beta }}_{Yi}\left({\hat{\sigma }}_{Yi}\right)$, $i=1,\cdots ,m$. Asymptotically (or approximately) we have ${\hat{\beta }}_{Xi}\sim N\left({\beta }_{Xi},{\hat{\sigma }}_{Xi}^2\right)$ and ${\hat{\beta }}_{Yi}\sim N\left({\beta }_{Yi},{\hat{\sigma }}_{Yi}^2\right)$ for $i=1,\cdots ,m$. With Equation 1, we have the log-likelihood function (up to a constant) as

$$L\left(\theta ,\left\{{\beta }_{Xi},r_i\right\};\left\{{\hat{\beta }}_{Xi},{\hat{\beta }}_{Yi},{\hat{\sigma }}_{Xi}^2,{\hat{\sigma }}_{Yi}^2\right\}\right)=-\frac{1}{2}\sum _{i=1}^m\left(\frac{{\left({\hat{\beta }}_{Xi}-{\beta }_{Xi}\right)}^2}{{\hat{\sigma }}_{Xi}^2}+\frac{{\left({\hat{\beta }}_{Yi}-\theta \cdot {\beta }_{Xi}-r_i\right)}^2}{{\hat{\sigma }}_{Yi}^2}\right),$$ (Equation 2)

which, for simplicity, may be written as $L\left(\theta ,\left\{{\beta }_{Xi},r_i\right\}\right)$. Throughout we use $\left\{{\beta }_{Xi},r_i\right\}=\left\{\left({\beta }_{Xi},r_i\right):i=\mathrm{1,2},\dots ,m\right\}$ to represent a set of the parameters, and similarly for $\left\{{\hat{\beta }}_{Xi},{\hat{\beta }}_{Yi},{\hat{\sigma }}_{Xi}^2,{\hat{\sigma }}_{Yi}^2\right\}$. Under the constraint that the number of the invalid IVs is K, a given integer, we can obtain the constrained maximum likelihood estimate (cMLE) $\hat{\theta }\left(K\right)$ and its standard error $\text{SE}\left(\hat{\theta }\left(K\right)\right)$. We prove that with correctly selected valid IVs, the cMLE is consistent and asymptotically normal. Accordingly, we can construct normal-based confidence intervals (CIs) or conduct significance testing for θ. In practice, since K is unknown, we propose a Bayesian information criterion (BIC) to select K consistently before drawing inference on the true causal effect θ; this is our proposed cML-BIC. For finite (especially small) sample sizes, due to model selection errors, such a procedure might have slightly inflated type I error rates as shown in the supplemental material and methods. Instead, to account for model selection uncertainty, we propose a model averaging approach,²¹ called cML-MA-BIC, or cML-MA for short. We obtain multiple estimates $\hat{\theta }\left(K\right)$, each based on a selected model with each value of 0 ≤ K < m − 1, then take their weighted average as our final estimate of the causal effect and draw inference accordingly; the weights are determined by the BIC values of the models, in which those more likely models (with lower BIC values) are given higher weights. More details are given below.

Estimation and selection consistency with the cMLE

We develop some (asymptotic) theory to support our proposed method (for fixed m as n increases). Denote $B_0=\left\{i|r_i\ne 0,i=1,\cdots ,m\right\}$ the set of truly invalid IVs, and its size $\left|B_0\right|=K_0$. Suppose that n₁ and n₂ are the sample sizes of the two GWAS summary datasets for X and Y, respectively. With Equation 2, we obtain the cMLEs by solving

$$\underset{\theta ,b_{Xi},r_i,1\le i\le m}{\text{min}}-L\left(\theta ,\left\{b_{Xi},r_i\right\};\left\{{\hat{\beta }}_{Xi},{\hat{\beta }}_{Yi},{\hat{\sigma }}_{Xi}^2,{\hat{\sigma }}_{Yi}^2\right\}\right)\text{subject}\text{to}\sum _{i=1}^{m}I\left(r_i\ne 0\right)=K.$$ (Equation 3)

Here $I(\cdot )$ is the indicator function and K is a tuning parameter representing the unknown number of invalid IVs. Denote the cMLEs from Equation 3 as $\hat{\theta }\left(K\right)$, ${\hat{b}}_{Xi}\left(K\right)$, and ${\hat{r}}_i\left(K\right)$ for $i=1,\cdots ,m$, and ${\hat{B}}_K=\left\{i|{\hat{r}}_i\left(K\right)\ne 0,i=1,\cdots ,m\right\}$ the estimated set of invalid IVs. We propose a Bayesian information criterion (BIC) based on GWAS summary data to select the best K in a candidate set $\mathcal{K}$:

$$\text{BIC}\left(K\right)=-2L\left(\hat{\theta }\left(K\right),\left\{{\hat{b}}_{Xi}\left(K\right),{\hat{r}}_i\left(K\right)\right\}\right)+\text{log}\left(n\right)\cdot K.$$ (Equation 4)

Here n could be either n₁ or n₂; we recommend using n = min(n₁, n₂). We select $\hat{K}={\text{argmin}}_{K\in \mathcal{K}}BIC\left(K\right)$, and estimate ${\hat{B}}_{\hat{K}}=\left\{i:{\hat{r}}_i\left(\hat{K}\right)\ne 0\right\}$ as the set of invalid IVs (and its complement ${\hat{B}}_{\hat{K}}^c=\left\{1,\cdots ,m\right\}-{\hat{B}}_{\hat{K}}$ as the set of valid IVs).

Now we state two assumptions used to prove the selection consistency of our proposed BIC.

Assumption 1. (Plurality valid condition.) Suppose that B₀ is the index set of the true invalid IVs with $K_0=\left|B_0\right|$. For any $B\subseteq \left\{1,\cdots ,m\right\}$ and $\left|B\right|=K_0$, if $B\ne B_0$, then the (m − K₀) ratios $\left\{r_i/{\beta }_{Xi},i\in B^c\right\}$ are not all equal.

Assumption 2. (Orders of the variances and sample sizes.) There exist positive constants $l_X,l_Y,l_n$ and $u_X,u_Y,u_n$ such that we have $l_X/n_1\le {\hat{\sigma }}_{Xi}^2\le u_X/n_1$, $l_Y/n_2\le {\hat{\sigma }}_{Yi}^2\le u_Y/n_2$, and $l_n\cdot n_2\le n_1\le u_n\cdot n_2$ for $i=1,\cdots ,m$.

Assumption 2 says that the two sample sizes n₁ and n₂ are comparable and that variance ${\hat{\sigma }}_{Xi}^2$ or ${\hat{\sigma }}_{Yi}^2$ is of order 1/n₁ or 1/n₂, which is satisfied by the usual least-squares or maximum likelihood estimates obtained from GWAS summary data. We also note that the sample sizes for the SNPs/IVs being used may vary; as long as they are comparable (in the sense as defined in assumption 2), we can take their minimum in each GWAS dataset as the corresponding sample size n₁ or n₂. With assumptions 1 and 2 we prove (in the supplemental material and methods) that our proposed BIC consistently selects invalid IVs.

Theorem 1. With assumptions 1 and 2 satisfied, if $K_0\in \mathcal{K}$, we have $P\left(\hat{K}=K_0\right)\to 1$ and $P\left({\hat{B}}_{\hat{K}}=B_0\right)\to 1$ as $n_1$, $n_2\to \infty$.

As shown in the supplemental information, it was confirmed that in the simulations the proposed BIC selected increasing proportions of the correct models as the sample size increased.

After correctly selecting (and implictly removing) invalid IVs, our proposed cMLE of θ is the same as the maximum profile likelihood estimate (MPLE) being applied to all valid IVs.⁶ Applying theorems 3.1 and 3.2 in Zhao et al.,⁶ coupled with the above selection consistency, we obtain both the estimation consistency and asymptotic normality of the cMLE $\hat{\theta }\left(\hat{K}\right)$. It is proven in the supplemental material and methods that the variance of the cMLE (based on the Fisher information matrix as shown in computation section below) and that of the MPLE are asymptotically equal. As confirmed numerically in the supplemental material and methods, our cMLE and the MPLE were essentially the same in both the simulations and real data examples.

Model selection and model averaging approaches to inference of θ

After selecting $\hat{K}$, we can use the cMLE $\hat{\theta }\left(\hat{K}\right)$ and its SE (see below for how to obtain it) to infer θ: based on the asymptotic normal distribution $\hat{\theta }\left(\hat{K}\right)\sim N\left(\theta ,S{E}^2(\hat{\theta }\left(\hat{K}\right)\right)$, we either construct a confidence interval (CI) or conduct a significance test. We call this method cML-BIC.

In spite of the selection consistency of our proposed BIC, to account for model selection uncertainties, especially with small sample sizes, we propose a model averaging (MA) approach. Following Buckland et al.,²¹ we first obtain the estimate of θ and its standard error for each candidate $K\in \mathcal{K}$, then take their weighted average as the final estimate of θ with the weights determined by the BIC values of the corresponding candidate models.

Following Buckland et al.,²¹ for a set $\mathcal{K}$ of K’s, we define the initial and standardized weights

$$w_K^0=\text{exp}\left(-BIC\left(K\right)/2\right),w_K=w_K^0/\sum _{K\in \mathcal{K}}{w}_K^0.$$

The final weighted estimate ${\hat{\theta }}_w$ and its standard error are

$${\hat{\theta }}_w=\sum _{K\in \mathcal{K}}{w}_K\cdot \hat{\theta }\left(K\right),\text{SE}\left({\hat{\theta }}_w\right)=\sum _{K\in \mathcal{K}}{w}_K\cdot \sqrt{\text{SE}{\left(\hat{\theta }\left(K\right)\right)}^2+{\left(\hat{\theta }\left(K\right)-{\hat{\theta }}_w\right)}^2}.$$ (Equation 5)

With ${\hat{\theta }}_w$ and SE$\left({\hat{\theta }}_w\right)$, based on the asymptotic normal distribution, we draw inference on θ. We call this method cML-MA-BIC. In practice, we use the set of candidate K’s, $\mathcal{K}=\left\{\mathrm{0,1},\cdots ,m-2\right\}$. K = 0 means all IVs are valid; according to assumption 1, there should be at least two valid IVs. Other choices of candidate sets of K’s could also be applied, especially when we roughly know the proportion of invalid IVs.

Instead of using BIC, we can also use the corresponding Akaike information criterion (AIC) to select K or weight its corresponding model, leading to cML-AIC and cML-MA-AIC for model selection- and model-averaging-based approaches, respectively. As shown in the supplemental material and methods, they did not perform as well as their BIC versions.

Computation

We propose a coordinate descent-like algorithm to iteratively solve Equation 3 to obtain cMLEs, $\hat{\theta }\left(K\right)$, ${\hat{b}}_{Xi}\left(K\right)$, and ${\hat{r}}_i\left(K\right)$ for $i=1,\cdots m$. We start with the initial values ${\theta }^{\left(0\right)}$ and $b_{Xi}^{\left(0\right)}$’s, then update them iteratively as below until convergence: at the $k^{th}$ iteration,

• Step 1: Given ${\theta }^{\left(k\right)},b_{Xi}^{\left(k\right)}$, update r_i. Order $\frac{{\left({\hat{\beta }}_{Yi}-{\theta }^{\left(k\right)}{b}_{Xi}^{\left(k\right)}\right)}^2}{{\hat{\sigma }}_{Yi}^2},i=1,\cdots ,m,$ decreasingly, as $\frac{{\left({\hat{\beta }}_{Y\left(1\right)}-{\theta }^{\left(k\right)}{b}_{X\left(1\right)}^{\left(k\right)}\right)}^2}{{\hat{\sigma }}_{Y\left(1\right)}^2},\frac{{\left({\hat{\beta }}_{Y\left(2\right)}-{\theta }^{\left(k\right)}{b}_{X\left(2\right)}^{\left(k\right)}\right)}^2}{{\hat{\sigma }}_{Y\left(2\right)}^2},\cdots ,\frac{{\left({\hat{\beta }}_{Y\left(m\right)}-{\theta }^{\left(k\right)}{b}_{X\left(m\right)}^{\left(k\right)}\right)}^2}{{\hat{\sigma }}_{Y\left(m\right)}^2}$. Then for $i=1,\cdots ,K$, let $r_{\left(i\right)}^{\left(k+1\right)}={\hat{\beta }}_{Y\left(i\right)}-{\theta }^{\left(k\right)}{b}_{X\left(i\right)}^{\left(k\right)}$; for $i=K+1,\cdots ,m$, let $r_{\left(i\right)}^{\left(k+1\right)}=0$.

• Step 2: Given ${\theta }^{\left(k\right)}$, $r_i^{\left(k+1\right)}$’s, update $b_{Xi}$ as

$$b_{Xi}^{\left(k+1\right)}=\frac{\frac{{\hat{\beta }}_{Xi}}{{\hat{\sigma }}_{Xi}^2}+\frac{{\theta }^{\left(k\right)}\left({\hat{\beta }}_{Yi}-r_i^{\left(k+1\right)}\right)}{{\hat{\sigma }}_{Yi}^2}}{\frac{1}{{\hat{\sigma }}_{Xi}^2}+\frac{{\left({\theta }^{\left(k\right)}\right)}^2}{{\hat{\sigma }}_{Yi}^2}}.$$ (Equation 6)

• Step 3: Given $b_{Xi}^{\left(k+1\right)}$’s, $r_i^{\left(k+1\right)}$’s, update θ as

$${\theta }^{\left(k+1\right)}=\frac{\sum _{i=1}^m\frac{\left({\hat{\beta }}_{Yi}-r_i^{\left(k+1\right)}\right)b_{Xi}^{\left(k+1\right)}}{{\hat{\sigma }}_{Yi}^2}}{\sum _{i=1}^m\frac{{\left(b_{Xi}^{\left(k+1\right)}\right)}^2}{{\hat{\sigma }}_{Yi}^2}}.$$ (Equation 7)

It is noted that at the convergence, by the expression of r_i in step 1 and that for $\hat{\theta }$ in step 3, if $r_i\ne 0$ (i.e., for an invalid IV), SNP i and its data do not contribute to estimating θ.

By default, as in all our simulations, we set ${\theta }^{\left(0\right)}$ and $b_{Xi}^{\left(0\right)}$’s all at 0. More generally, as in our main real data examples, we can also use multiple random starts; in our real data examples, in addition to the above default starting values, we tried 100 random starts, each randomly generated as ${\theta }^{\left(0\right)}\sim \text{Uniform}\left({\text{min}}_{1\le i\le m}{\hat{\beta }}_{Yi}/{\hat{\beta }}_{Xi},{\text{max}}_{1\le i\le m}{\hat{\beta }}_{Yi}/{\hat{\beta }}_{Xi}\right)$, and $b_{Xi}^{\left(0\right)}\sim N\left({\hat{\beta }}_{Xi},{\hat{\sigma }}_{Xi}^2\right)$ for 1 ≤ i ≤ m. Then we take the cMLE as the one from the initial values giving the maximum likelihood among those multiple starts. As shown in Tables S5 and S6, for our primary real data examples, among all 48 risk factor-disease pairs, only for 7 pairs the 101 starts gave slightly different results from using the default starting values; the differences in the numbers of detected invalid IVs were only 1 or 2, leading to almost the same results at the end. In our secondary real data analysis, for each of 63 null pairs we tried 10 random starts.

Next we estimate the standard error of $\hat{\theta }=\hat{\theta }\left(K\right)$ for any given K. Denote the set of the indices of K non-zero ${\hat{r}}_i$’s as ${\hat{B}}_K$, the (m − K + 1) by (m − K + 1) Fisher information matrix is

$$\mathcal{I}=\left(\begin{array}{ll}\frac{{\partial }^2\left(-l\right)}{\partial {\theta }^2}\hfill & \frac{{\partial }^2\left(-l\right)}{\partial \theta \partial \beta {\text{′}}_{XB}}\hfill \\ \frac{{\partial }^2\left(-l\right)}{\partial \theta \partial {\beta }_{XB}}\hfill & \frac{{\partial }^2\left(-l\right)}{\partial {\beta }_{XB}\partial \beta {\text{′}}_{XB}}\hfill \end{array}\right),$$ (Equation 8)

where ${\beta }_{XB}$ is a vector of elements ${\beta }_{Xi}$ with $i\in {\hat{B}}_K^c$. Plugging $\hat{\theta }$, ${\hat{b}}_{Xi}$’s into $\mathcal{I}$, we obtain the standard error of $\hat{\theta }$ as $\text{SE}\left(\hat{\theta }\right)=\sqrt{{\left({\mathcal{I}}^{-1}\right)}_{11}}$. Details are shown in the supplemental material and methods.

Data perturbation

When the sample sizes of GWAS summary data are relatively small and there are many invalid IVs with weak pleiotropic effects, the (asymptotic) selection consistency of cML-BIC as described in theorem 1 may not be achieved, leading to missing some invalid IVs and ultimately biased inference, such as inflated type I errors. To alleviate this problem, we propose using data perturbation (DP).²² For $t=1,\cdots ,T$, we generate independent perturbed samples ${\hat{\beta }}_{Xi}^{\left(t\right)}\sim N\left({\hat{\beta }}_{Xi},{\hat{\sigma }}_{Xi}^2\right)$ and ${\hat{\beta }}_{Yi}^{\left(t\right)}\sim N\left({\hat{\beta }}_{Yi},{\hat{\sigma }}_{Yi}^2\right)$ for $i=1,\cdots m$. Then similar to Equation 3, we obtain the cMLEs with perturbed data by solving

$$\underset{\theta ,b_{Xi},r_i,1\le i\le m}{\text{min}}-L\left(\theta ,\left\{b_{Xi},r_i\right\};\left\{{\hat{\beta }}_{Xi}^{\left(t\right)},{\hat{\beta }}_{Yi}^{\left(t\right)},{\hat{\sigma }}_{Xi}^2,{\hat{\sigma }}_{Yi}^2\right\}\right)\text{subject}\text{to}\sum _{i=1}^{m}I\left(r_i\ne 0\right)=K.$$ (Equation 9)

Denote the cMLEs from Equation 9 as ${\hat{\theta }}^{\left(t\right)}\left(K\right)$, ${\hat{b}}_{Xi}^{\left(t\right)}\left(K\right)$, and ${\hat{r}}_i^{\left(t\right)}\left(K\right)$ for $i=1,\cdots ,m$, we get the maximized log-likelihood as

$$L^{\left(t\right)}\left(K\right)=L\left({\hat{\theta }}^{\left(t\right)},\left\{{\hat{b}}_{Xi}^{\left(t\right)},{\hat{r}}_i^{\left(t\right)}\right\};\left\{{\hat{\beta }}_{Xi}^{\left(t\right)},{\hat{\beta }}_{Yi}^{\left(t\right)},{\hat{\sigma }}_{Xi}^2,{\hat{\sigma }}_{Yi}^2\right\}\right).$$ (Equation 10)

Averaging over T perturbed estimates, we have

$${\hat{\theta }}_{DP}\left(K\right)=\frac{\sum _{t=1}^T{\hat{\theta }}^{\left(t\right)}\left(K\right)}{T},L_{DP}\left(K\right)=\frac{\sum _{t=1}^T{L}^{\left(t\right)}\left(K\right)}{T},$$ (Equation 11)

and estimate the standard error of ${\hat{\theta }}_{DP}\left(K\right)$ as the sample standard deviation of ${\hat{\theta }}^{\left(t\right)}\left(K\right)$’s,

$$\text{SE}\left({\hat{\theta }}_{DP}\left(K\right)\right)=\sqrt{\frac{\sum _{t=1}^T{\left({\hat{\theta }}^{\left(t\right)}\left(K\right)-{\hat{\theta }}_{DP}\left(K\right)\right)}^2}{T-1}}.$$ (Equation 12)

Then, as for cML-BIC and cML-MA-BIC, with the DP estimates in Equations 11 and 12, we obtain their DP versions called cML-BIC-DP and cML-MA-BIC-DP, respectively.

Goodness-of-fit tests for the variance estimates

In general, as to be shown numerically, cML-MA-BIC-DP is more conservative for inference and thus controls the type I errors better than cML-MA-BIC, but may lose power while being computationally more demanding. To help decide which one to use for a given problem, we develop two goodness-of-fit tests, denoted GOF1 and GOF2, to check whether the (asymptotic) model-based and DP-based variance estimates converge to the same estimate; if so, then we recommend using cML-MA-BIC; otherwise, cML-MA-BIC-DP is preferred.

Suppose that cML-BIC selects a set of $\hat{K}$ invalid IVs, with the estimate $\hat{\theta }\left(\hat{K}\right)$ and its model-based variance calculated using Fisher Information matrix (Equation 8) as ${\widehat{\text{Var}}}_M\left(\hat{\theta }\left(\hat{K}\right)\right)$. If the BIC-based model selection is correct with only small model selection uncertainty, we’d expect that ${\widehat{\text{Var}}}_M\left(\hat{\theta }\left(\hat{K}\right)\right)$ would be close to the DP-based variance estimate, ${\widehat{\text{Var}}}_D\left({\hat{\theta }}_{DP}\left(\hat{K}\right)\right)$. Our proposed goodness-of-fit tests aim to test whether the two variance estimates converge to the same estimate (asymptotically).

First, based on each perturbed dataset, we obtain $V^{\left(t\right)}={\widehat{\text{Var}}}_M\left({\hat{\theta }}^{\left(t\right)}\left(\hat{K}\right)\right)$, from which we estimate the sample variance of $V^{\left(t\right)}$’s as $\widehat{\text{Var}}\left[{\text{Var}}_M\left(\hat{\theta }\left(\hat{K}\right)\right)\right]$. Second, as shown by Equation 12, ${\widehat{\text{Var}}}_D\left({\hat{\theta }}_{DP}\left(\hat{K}\right)\right)$ is the sample variance of T i.i.d. random ${\hat{\theta }}^{\left(t\right)}\left(K\right),t=1,\cdots ,T$ from some distribution $f(\cdot )$; theorem 2 in chapter 6 of Mood et al.²³ shows that its variance is

$$\text{Var}\left[{\widehat{\text{Var}}}_D\left({\hat{\theta }}_{DP}\left(\hat{K}\right)\right)\right]=\frac{1}{T}\left({\mu }_4-\frac{T-3}{T-1}{\sigma }^4\right),$$ (Equation 13)

where ${\mu }_4$ and ${\sigma }^2$ are the central fourth moment and variance of $f(\cdot )$. We use the T samples to estimate them as

$${\hat{\mu }}_4=\frac{\sum _{t=1}^T{\left({\hat{\theta }}^{\left(t\right)}\left(\hat{K}\right)-{\hat{\theta }}_{DP}\left(\hat{K}\right)\right)}^4}{T},{\hat{\sigma }}^2=\frac{\sum _{t=1}^T{\left({\hat{\theta }}^{\left(t\right)}\left(\hat{K}\right)-{\hat{\theta }}_{DP}\left(\hat{K}\right)\right)}^2}{T}.$$

Plugging them into Equation 13, we obtain

$${\widehat{\text{Var}}}_1\left[{\widehat{\text{Var}}}_D\left({\hat{\theta }}_{DP}\left(\hat{K}\right)\right)\right]=\frac{1}{T}\left({\hat{\mu }}_4-\frac{T-3}{T-1}{\hat{\sigma }}^4\right),$$ (Equation 14)

and the first GOF test statistic is

$$Z_{GOF1}=\frac{{\widehat{\text{Var}}}_D\left({\hat{\theta }}_{DP}\left(\hat{K}\right)\right)-{\widehat{\text{Var}}}_M\left(\hat{\theta }\left(\hat{K}\right)\right)}{\sqrt{{\widehat{\text{Var}}}_1\left[{\widehat{\text{Var}}}_D\left({\hat{\theta }}_{DP}\left(\hat{K}\right)\right)\right]+\widehat{\text{Var}}\left[{\widehat{\text{Var}}}_M\left(\hat{\theta }\left(\hat{K}\right)\right)\right]}}.$$ (Equation 15)

Comparing $Z_{GOF1}$ with the standard normal random variate Z, we can calculate the p value as $P\left(\left|Z\right|>\left|Z_{GOF1}\right|\right)$. This is the first goodness-of-fit test GOF1.

When T is small or only moderately large, the estimate ${\hat{\mu }}_4$ could have a large variance. Furthermore, if ${\hat{\theta }}^{\left(t\right)}\left(K\right)$’s are normally distributed, we have ${\mu }_4=3{\sigma }^4$, and the variance estimate in Equation 14 can be simplified to

$${\widehat{\text{Var}}}_2\left[{\widehat{\text{Var}}}_D\left({\hat{\theta }}_{DP}\left(\hat{K}\right)\right)\right]=\frac{2}{T-1}{\hat{\sigma }}^4.$$ (Equation 16)

Replacing ${\widehat{\text{Var}}}_1$ in Z_GOF1 with ${\widehat{\text{Var}}}_2$, we obtain a new GOF test statistic, Z_GOF2, by which and a standard normal as the null distribution, we can calculate a p value.

Other methods

We compared cML-MA with other existing two-sample MR methods, including MR-ContMix, MR-Mix, MR-CAUSE, MR-Lasso, MR-PRESSO, MR-IVW (random-effect [RE] meta-analysis), MR-Egger regression, MR-Weighted-Median, MR-Weighted-Mode, and MR-RAPS (the Robust Adjusted Profile Score) methods. We applied MR-RAPS with four different combinations of its parameters: for MR-RAPS1 and MR-RAPS2, we set the over-dispersion parameter as TRUE, and used the L₂ loss and the Tukey loss, respectively; for MR-RAPS3 and MR-RAPS4, we set the over-dispersion as FALSE and used the L₂ and the Tukey loss, respectively; we present RAPS2 to represent RAPS in the main text. We also applied the Oracle MR-IVW to only valid IVs in the simulations, called MR-IVW-Oracle.

Each method takes GWAS summary data of ${\hat{\beta }}_{Xi},{\hat{\sigma }}_{Xi},{\hat{\beta }}_{Yi},{\hat{\sigma }}_{Yi},i=1,\cdots ,m$ as input and gives an estimate of θ, say $\hat{\theta }$, along with its standard error SE$\left(\hat{\theta }\right)$.

GWAS data

Primary real data examples

We applied various methods to some large-scale GWAS summary data. Following Morrison et al.,¹³ we studied possible causal effects of 12 risk factors on 4 complex diseases: coronary artery disease (CAD [MIM: 608320]), stroke (MIM: 601367), type 2 diabetes (T2D [MIM: 125853]), and asthma (MIM: 600807) (mostly as a negative control). These 12 cardio-metabolic risk factors are triglycerides (TG), high-density lipoprotein (HDL), low-density lipoprotein (LDL), drinks per week (alcohol), ever regular smoker (smoke), body fat percentage (BF), birth weight (BW), body mass index (BMI), height (MIM: 606255), fasting glucose (FG), systolic blood pressure (SBP), and diastolic blood pressure (DBP).

For each risk factor/exposure-disease/outcome pair, we used the set of LD-independent SNPs as IVs as described in Morrison et al.¹³ (in their Table S4) and applied all methods to the GWAS summary statistics of these SNPs.

Secondary real data examples

If two traits are not genetically correlated, it is unlikely that they are causally related. As suggested by a reviewer, from LD Hub,²⁴ we collected 63 trait pairs without significant genetic correlations (i.e., p value > 0.05) as negative controls to study the type I error properties of the methods. These 63 pairs involve 13 traits in total: fasting proinsulin (FP), height, homeostasis model assessment of beta-cell function (HOMA), LDL, rheumatoid arthritis (RA [MIM: 180300]), schizophrenia (SCZ [MIM: 181510]), T2D, age at smoking (ASmk), anorexia nervosa (AN [MIM: 606788]), childhood IQ (CIQ), ever/never smoked (ESmk), former current smoker (FSmk), and infant head circumference (IHC). For each pair, we used R package TwoSampleMR to select LD-independent SNPs as IVs and extract their summary statistics following the standard procedures; sample R code is available in the supplemental material and methods. The GWAS summary data in LD Hub and TwoSampleMR are the same for 12 traits except for height. For height, LD Hub contains the GWAS data of the GIANT consortium from year 2010,²⁵ while TwoSampleMR uses the GIANT data from year 2014.²⁶ Details of the GWAS data used are in the supplemental material and methods.

Simulation set-ups

Main simulations

We compared different methods through extensive simulations. The simulation set-ups were similar to those in Burgess et al.⁹ We set the number of the SNPs/IVs m = 10, 20, or 100, and sample size n = 50,000, 100,000, or 200,000. For each SNP $i=1,\cdots ,m$, we generated ${\gamma }_i$’s from a uniform distribution on $\left(-0.2,-0.1\right)\cup \left(0.1,0.2\right)$; its MAF f_i from a uniform distribution Unif(0.1,0.3), then its genotypes SNP_ij from a bonimial Bin(2, f_i) for $j=1,\cdots ,n$. For each m, we tried different proportions q = 0%, 20%, 40%, 60% of invalid IVs: for each SNP $i=1,\cdots ,m\cdot q$, we generated its direct effect size α_i from Uniform(0.2,0.3) and set ${\phi }_i=0$ (when the InSIDE assumption was satisfied) or generated ${\phi }_i$ from Uniform(−0.1,0.1) (when InSIDE was violated). We set ${\beta }_{XU}={\beta }_{YU}=1$, generated the random errors ${\epsilon }_U$, ${\epsilon }_X$, and ${\epsilon }_Y$ independently from N(0,1). Then we generated U, X, and Y from the causal model (Equation 17):

$$U=\sum _{i=1}^m{\phi }_i\cdot g_i+{\epsilon }_U,$$ (Equation 17)

$$X=\sum _{i=1}^m{\gamma }_i\cdot g_i+{\beta }_{XU}\cdot U+{\epsilon }_X,$$

$$Y=\theta \cdot X+\sum _{i=1}^m{\alpha }_i\cdot g_i+{\beta }_{YU}\cdot U+{\epsilon }_Y.$$

We generated two independent samples, each of size n₁ = n₂ = n, and used the first sample to fit marginal linear regressions of X on SNPs, and using the second sample to fit marginal linear regressions of Y on SNPs, thus obtaining the GWAS summary statistics. We tried different $\theta =-0.1,-0.05,-0.03,-0.01,\mathrm{0,0.01},0.03,0.05,0.1$. When $\theta =0$ it was the null case; i.e., X had no causal effect on Y.

Secondary simulations

We did simulations to compare various methods with CAUSE. We generated the simulated data in the framework of CAUSE as described in the original CAUSE paper.¹³ We set the sample size n₁ = n₂ = n = 50,000 or 100,000. Denote the direct effects of SNP i on the exposure as ${\beta }_{Xi}$ and on the outcome Y as α_i. For the expected number of SNPs with non-zero associations with the exposure and the outcome (i.e., ${\beta }_{Xi}\ne 0$ and ${\alpha }_i\ne 0$), denoted by m_X and $m_{\alpha }$, we set $m_X=m_{\alpha }=m=10$ or 100. Denote the true causal effect size from the exposure to the outcome as θ. We set $\theta =0$ for the null case and $\theta =0.05$ for the non null case. In each simulation, we generated p = 100,000 independent SNPs with MAF f_i independently drawn from Uniform(0.1,0.3). In CAUSE, it is assumed that the hidden confounder U is standardized with ${\beta }_{XU}=1$; we set the effect size from U to Y at ${\beta }_{YU}=1$. We set the proportion of invalid IVs with correlated pleiotropic effects at q = 0.3. We set the heritabilities of X and Y at $h_X^2=h_Y^2=0.3$. Then we generated the standardized effect sizes ${\tilde{\beta }}_{Xi}$ and ${\tilde{\alpha }}_i$ from a mixture of bivariate normal distribution:

$$\left(\begin{array}{l}{\tilde{\beta }}_{Xi}\\ {\tilde{\alpha }}_i\end{array}\right)\sim \sum _{k=1}^4{\pi }_k\cdot N\left(\left(\begin{array}{l}0\\ 0\end{array}\right),\left(\begin{array}{ll}{\sigma }_{Xk}^2& 0\\ 0& {\sigma }_{\alpha k}^2\end{array}\right)\right).$$ (Equation 18)

Here $\pi =m/p$, and ${\pi }_1=0.2\pi ,{\pi }_2={\pi }_3=0.8\pi ,{\pi }_4=1-{\pi }_1-{\pi }_2-{\pi }_3$; ${\sigma }_{X1}^2={\sigma }_{X2}^2={\sigma }_X^2,{\sigma }_{\alpha 1}^2={\sigma }_{\alpha 3}^2={\sigma }_{\alpha }^2,{\sigma }_{X3}^2={\sigma }_{X4}^2={\sigma }_{\alpha 2}^2={\sigma }_{\alpha 4}^2=0$, and ${\sigma }_X^2=h_X^2/m_X$, ${\sigma }_{\alpha }^2=\left[h_Y^2-\left({\theta }^2+q{\eta }^2\right)h_X^2\right]/m_{\alpha }$. The non-standardized effect sizes were ${\beta }_{Xi}={\tilde{\beta }}_{Xi}/\sqrt{2f_i\left(1-f_i\right)}$, and ${\alpha }_i={\tilde{\alpha }}_i/\sqrt{2f_i\left(1-f_i\right)}$. We generated the indicator of an invalid IV, Z_i, from Bernoulli(q), and ${\beta }_{Yi}=\theta {\beta }_{Xi}+Z_j{\beta }_{YU}{\beta }_{Xi}+{\alpha }_i$. With the standard error $s_i=1/\sqrt{2n{f}_i\left(1-f_i\right)}$, the GWAS summary statistics were generated as ${\hat{\beta }}_{Xi}\sim N\left({\beta }_{Xi},s_i^2\right)$, ${\hat{\beta }}_{Yi}\sim N\left({\beta }_{Yi},s_i^2\right)$.

For each combination of $\left(m,\theta ,n\right)$ we did simulations 200 times (while the simulations in Morrison et al.¹³ were repeated only 100 times due to longer running time of CAUSE). For CAUSE, we used all p SNPs to estimate the parameters, and used its default p value threshold 0.001 to select the SNPs associated with the exposure. For other MR methods, we used the usual p value threshold 5 × 10⁻⁸ to select the exposure-associated SNPs as IVs. For comparison, we also applied the p value threshold 5 × 10⁻⁸ (instead of its default threshold 0.001) to select the SNPs for CAUSE.

Simulations with weak invalid IVs

As suggested by a reviewer, we did more simulations with many invalid IVs with weak effects (so-called “weak invalid IVs”), representing a scenario more challenging to identify invalid IVs with only weak effects. We set the number of IVs m = 50, sample size n = 20,000, and ${\gamma }_i$’s from N(0,h_x / m) for $i=1,\cdots ,50$. We had the first 60% IVs as invalid IVs with uncorrelated pleiotropic effects α_i’s from N(0,h_y / m) and correlated pleiotropic effects ${\phi }_i$’s from N(0,h_u / m) for $i=1,\cdots ,30$, and set ${\alpha }_i={\phi }_i=0$ for $i=31,\cdots 50$. Then we set ${\hat{\sigma }}_{Xi}={\hat{\sigma }}_{Yi}=1/\sqrt{n}$ and generated ${\hat{\beta }}_{Xi}\sim N\left({\gamma }_i+{\phi }_i,{\hat{\sigma }}_{Xi}^2\right)$, ${\hat{\beta }}_{Yi}\sim N\left(\theta \cdot \left({\gamma }_i+{\phi }_i\right)+{\alpha }_i+{\phi }_i,{\hat{\sigma }}_{Yi}^2\right)$, where θ was the true causal effect. We set h_x = 0.5, and tried different h_y = 0.1,0.2,0.4,0.6, different h_u = 0,0.1, and different $\theta =-0.2,-0.1,-0.05,\mathrm{0,0.05},0.1,0.2$. Here h_x, h_y, and h_u could be viewed as the heritability of the exposure, outcome, and confounder due to direct effects of the IVs. Note that for h_u = 0 there was no correlated pleiotropy, while for h_u = 0.1 there was. The smaller h_y, the weaker the direct/pleiotropic effects and thus more difficult to identify the invalid IVs.

Results

Simulations: Better type I error control and higher power of the new method than other MR methods

We compared our proposed method with ten most popular and new MR methods as shown in Table 1 through extensive simulations: MR-Mix, MR-ContMix, MR-CAUSE, MR-Lasso, MR-PRESSO, MR-Weighted-Median, MR-Weighted-Mode, MR-Egger, MR-RAPS, and MR-IVW (with a random-effect model throughout this paper). For evaluation, we also added MR-IVW-Oracle, an ideal but impractical method with all valid IVs known and being used, giving best possible performance. Since CAUSE requires full GWAS summary data (with both trait-associated and non-associated SNPs) with much longer running time, we divided the simulations into two parts. For main simulations, following Burgess et al.⁹ and Slob and Burgess,¹⁰ we only generated summary statistics for exposure-associated SNPs, and compared cML-MA with other nine methods except CAUSE. For secondary simulations, we simulated both exposure-associated and non-associated SNPs as required by CAUSE¹³ and compared cML-MA to all other 10 methods.

Main simulations: Comparison with major MR methods

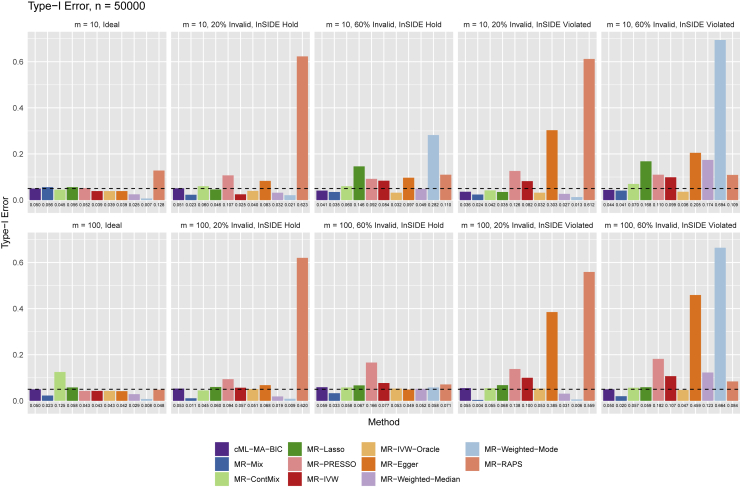
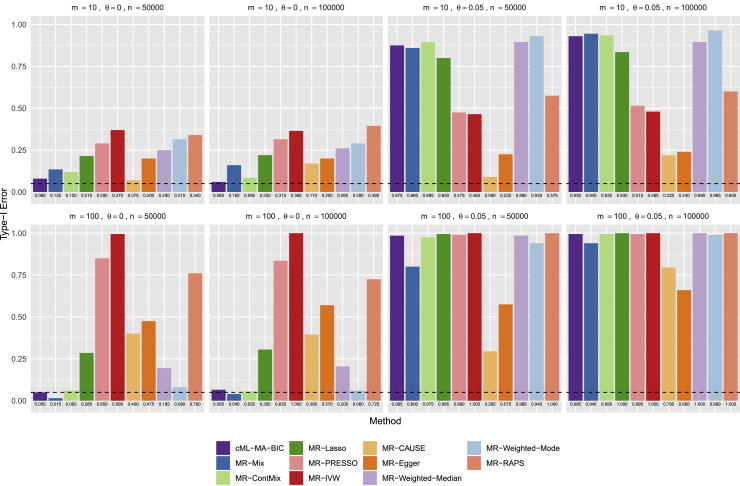
We did extensive simulations with the true causal model shown in Figure 1, including n = 50,000, 100,000, or 200,000 subjects in each GWAS dataset, using m = 10, 20, or 100 SNPs as IVs, among which 0% to 60% were invalid IVs with IV assumptions A2 or/and A3 being violated. For each setup we did 1,000 simulations to compare the proposed cML methods and other existing MR methods, and for the 10 setups shown in Figure 2, we also increased the number of simulations to 10,000 to better estimate the type I errors. For the 9 setups with 60% invalid IVs and with both IV assumptions A2 and A3 being violated, we also applied cML-BIC-DP and cML-MA-BIC-DP. We used the nominal significance level of 0.05. Here we only show some representative results while all others are available in the supplemental material and methods.

Figure 2.

Main simulations: Empirical type I error rates at the nominal level of 0.05 with sample size n = 50,000 and with m = 10 or 100 SNPs, among which 0 to 60% were invalid IVs with the InSIDE assumption either holding or violated

Figure 2 shows the empirical type I errors (at the nominal level 0.05). First, in the cases with all valid IVs, the methods generally performed well, though MR-Weighted-Mode, MR-Weighted-Median, and MR-Mix might be too conservative. On the other hand, MR-ContMix could have an inflated type I error rate, perhaps due to its inappropriately pre-selected tuning parameter value. Second, in the presence of 20% or 60% invalid IVs with IV assumption A2 violated but assumption A3 (thus the InSIDE assumption) holding, MR-PRESSO, MR-Lasso, and MR-IVW could have inflated type I error rates. It is noted that, though the InSIDE assumption held, MR-Egger could have a slightly inflated type I error rate for small m = 10 but not for large m = 100. MR-Weighted-Mode gave the most highly inflated type I error rate with the large proportion (60%) of invalid IVs and with the small number of SNPs (m = 10). Third, in the cases with both IV assumptions A2 and A3 violated, MR-IVW, MR-Egger, and MR-PRESSO all had inflated type I error rates, while MR-Weighted-Mode and MR-Weighted-Median had largely inflated type I error rates with 60% invalid IVs, and so did MR-Lasso with 60% invalid IVs and with only m = 10 SNPs. In summary, as expected, MR-IVW was problematic in the presence of invalid IVs, MR-Egger did not perform well if IV assumption A3 was violated, and MR-PRESSO often had inflated type I errors; on the other hand, in agreement with Slob and Burgess,¹⁰ MR-Lasso, MR-Weighted-Median, and MR-Weighted-Mode did not perform well with a small number of SNPs and with a high proportion of invalid IVs. We conclude that only MR-cML-BIC and MR-Mix could control the type I error rates across all the scenarios, though MR-Mix was often too conservative (with too small type I errors), especially for a large number of SNPs/IVs. The results for type I errors based on 10,000, instead of 1,000, simulations, as shown in Figure S6, were essentially the same.

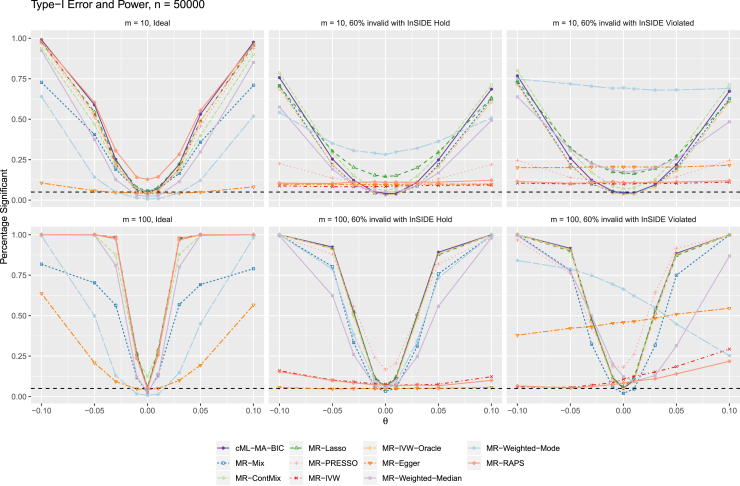
Figure 3 shows the empirical type I error (for $\theta =0$) and power (for $\theta \ne 0$) curves. It is confirmed that our proposed method cML-MA-BIC always yielded a power curve close to that of MR-IVW-Oracle, the ideal test based on using only valid IVs. In particular, cML-MA-BIC was more powerful than MR-Mix and other methods (when their type I errors were close to the nominal level).

Figure 3.

Main simulations: Empirical type I error (for $\theta =0$) and power (for $\theta \ne 0$) curves with sample size n = 50,000

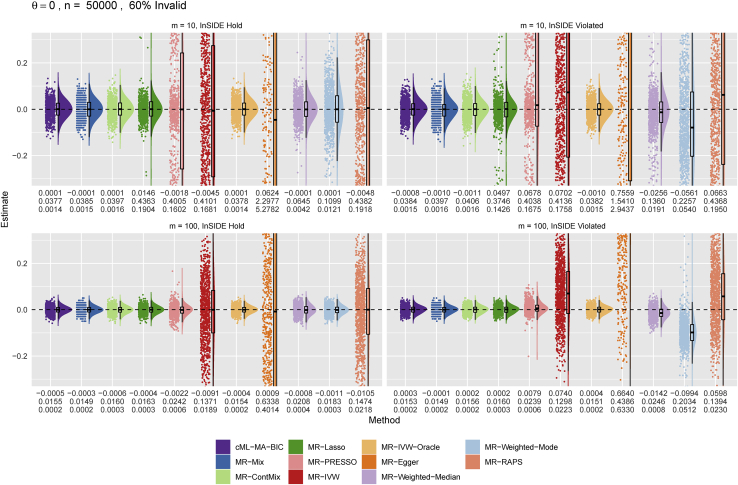
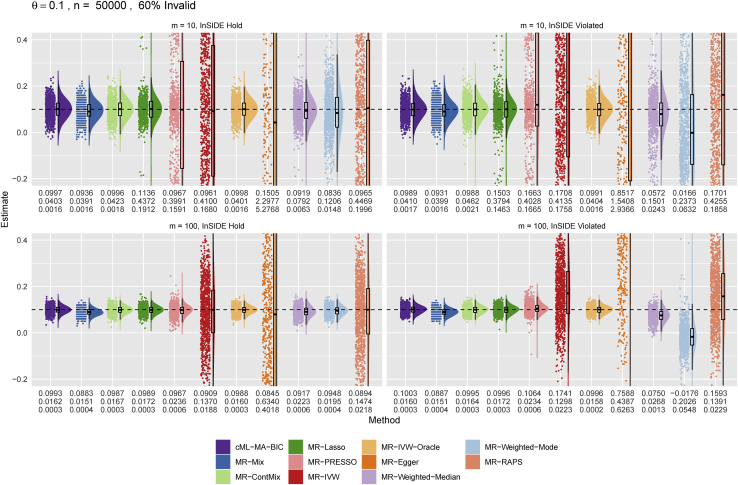
Figures 4 and 5 show the distributions of the causal estimates by each method for the true causal effect sizes $\theta =0$ and 0.1, respectively. Again it is confirmed that the distribution of the θ estimates from our proposed cML-MA-BIC was almost the same as that from the ideal MR-IVW-Oracle. In particular, cML-MA-BIC, MR-ContMix, and MR-Lasso (and MR-IVW-Oracle) always yielded (almost) unbiased estimates with smaller variances, while other methods sometimes gave biased estimates (and/or with much larger variances). In particular, as shown in Figure 5, MR-Mix was slightly biased (toward 0) for m = 100.

Figure 4.

Main simulations: Empirical distributions of the estimates of the causal effect θ by the methods with n = 50,000 and $\theta =0$

The numbers below each panel are the mean$\left(\hat{\theta }\right)$, SD$\left(\hat{\theta }\right)$, mean squared error (MSE) of $\hat{\theta }$ from top to bottom.

Figure 5.

Main simulations: Empirical distributions of the estimates of the causal effect θ by the methods with n = 50,000 and $\theta =0.1$

The numbers below each panel are the mean$\left(\hat{\theta }\right)$, SD$\left(\hat{\theta }\right)$, mean squared error (MSE) of $\hat{\theta }$ from top to bottom.

For the 9 setups with 60% invalid IVs and with both IV assumptions A2 and A3 being violated, we applied cML-BIC-DP and cML-MA-BIC-DP, with various numbers of perturbations T = 100, 200, and 500. The complete results are shown in supplemental material and methods section S5.4. cML-BIC-DP and cML-MA-BIC-DP yielded similar results to those of cML-BIC and cML-MA-BIC, respectively, in terms of both point estimation and statistical inference, and both the GOF tests performed similarly in rejecting the null hypothesis (of unequal variance estimates from the model- and DP-based approaches) with low frequencies.

In summary, overall, among all the methods, cML-MA-BIC, MR-Mix, and MR-ContMix performed best across all the scenarios; among the latter three, cML-MA-BIC was the clear winner for its higher power while better controlling the type I error rate.

Secondary simulations: Comparison with CAUSE

We did simulations in the framework of MR-CAUSE as described in Morrison et al.¹³ Figure 6 shows the empirical type I error (for $\theta =0$) and power (for $\theta =0.05$) for the methods with m = 10 or 100 exposure-associated SNPs and sample size n = 50,000 or 100,000. It is clear that our proposed method cML-MA-BIC could control type I error well with high power. In contrast, CAUSE could have largely inflated type I error rates and much lower power than cML-MA-BIC. Here the results for CAUSE were based on using its default p value threshold of 0.001 to select exposure-associated SNPs; as shown in the supplemental material and methods, using the threshold 5 × 10⁻⁸ (as for other methods shown here) did not give better results for CAUSE. The poor performance of CAUSE here is in agreement with that shown in the original CAUSE paper (Morrison et al.,¹³ Figure SN1): when it was high powered to detect SNP-exposure and SNP-outcome associations, CAUSE tended to give dramatically inflated false positive rates. In addition, compared to cML-MA-BIC, both MR-Mix and MR-ContMix had higher inflated type I error rates for small m = 10; on the other hand, MR-Mix was too conservative with too small type I error rates and lower power for m = 100 with the small sample size n = 50,000.

Figure 6.

Secondary simulations: Empirical type I error rates (for $\theta =0$) and power (for $\theta \ne 0$) with sample size n = 50,000 or 100,000, and with m = 10 or 100 exposure-associated SNPs

Simulations with weak invalid IVs

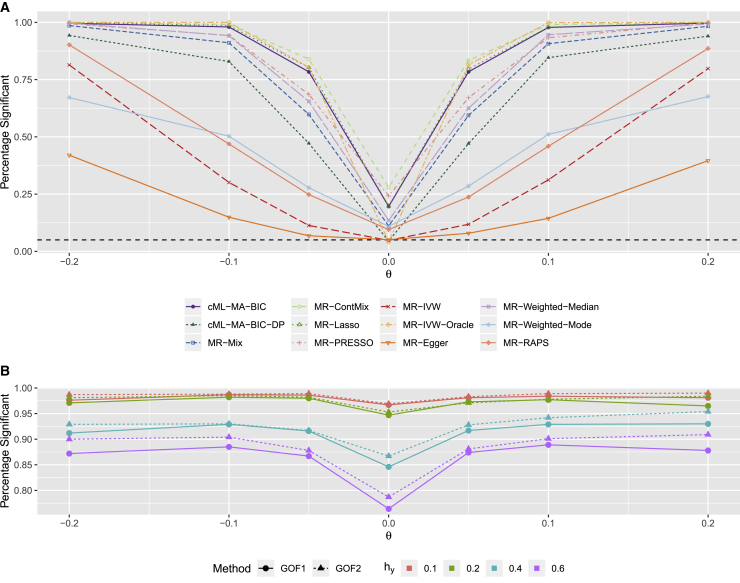
We did 1,000 simulations for each setup with a small sample size and many invalid IVs having weak direct/pleiotropic effects. Figure 7A shows some representative results for the empirical type I error (for $\theta =0$) and power (for $\theta \ne 0$) curves for h_y = 0.2 and h_u = 0 (i.e., no correlated pleiotropy); the complete results are given in the supplemental material and methods. It is clear that under this challenging situation, in addition to the ideal MR-IVW-Oracle, only three methods could control the type I error satisfactorily (while all others could not): cML-MA-BIC-DP, MR-IVW, and MR-Egger, but cML-MA-BIC-DP was much more powerful than the other two. It is noted that here the (weak) direct effects were balanced (i.e., with mean 0) and from a normal distribution, explaining the reasons for the relatively good performance by MR-IVW and MR-Egger. Nevertheless, as shown in Tables S107–S110, as the pleiotropic effect sizes (i.e., h_y) increased, the power of cML-MA-BIC-DP improved (by better identifying invalid IVs), but, perhaps surprisingly, both MR-IVW and MR-Egger became less powerful (because of the increasing error variances in their models by treating the pleiotropic effects as random).

Figure 7.

Simulation results with many invalid IVs having weak pleiotropic effects

(A) Empirical type I error (for $\theta =0$) and power (for $\theta \ne 0$) curves with h_y = 0.2 and h_u = 0.

(B) Relative frequencies of the goodness-of-fit tests rejecting the null hypothesis.

In the presence of correlated pleiotropy with h_u = 0.1, as shown in Tables S111–S114, only our proposed cML-BIC-MA-DP could satisfactorily control type I error and was well powered, while all other methods, including MR-IVW, MR-Egger, and MR-RAPS, yielded inflated type I errors and possibly low power.

Figure 7B shows the relative frequencies of the goodness-of-fit tests’ rejecting the null hypothesis that the model-based variance was equal to the DP-based variance by cML. The proposed goodness-of-fit tests could detect with high power the problem with cML-MA-BIC; the two GOF tests performed similarly, though GOF2 was slightly more powerful (presumably due to its taking advantage of the causal estimates being nearly normally distributed). In addition, as h_y decreased, it became harder to identify invalid IVs, leading to more inflated type I error rates by most methods, including cML-MA-BIC; accordingly the two GOF tests rejected the null hypothesis more frequently, demonstrating their effectiveness.

Computational time

We did simulations to compare the running times of different methods as detailed in supplemental material and methods section S8. In summary, cML-MA-BIC runs reasonably fast: its computing time was comparable to that of MR-ContMix and MR-RAPS, while being faster than MR-Mix and MR-Weighted-Mode but slower than MR-IVW, MR-Egger, and MR-Weighted-Median. As expected, using more random starting points or data perturbation would take much more time. Nevertheless, on a MacBook Pro laptop, with 10 to 100 SNPs/IVs, it took from a few seconds to less than 10 minutes with cML-MA-BIC-DP with five random starts and T = 200 data perturbations; in contrast, cML-MA-BIC with five random starts ran from 0.3 to 4 seconds.

Identifying causal risk factors of complex diseases

We compare our proposed cML with other methods to identify possible causal effects of 12 risk factors on three cardio-metabolic diseases—coronary artery disease (CAD),²⁷ stroke,²⁸ and type 2 diabetes (T2D)²⁹—plus asthma largely used as a negative control.³⁰ These 12 risk factors (and their corresponding GWASs) are LDL cholesterol, HDL cholesterol, triglycerides (TG),³¹ drinks per week (alcohol), ever regular smoker (smoke),³² body fat percentage (BF),³³ birth weight (BW),³⁴ body mass index (BMI),³⁵ height,²⁶ fasting glucose (FG),³⁶ systolic blood pressure (SBP), and diastolic blood pressure (DBP).³⁷ As used and shown in Morrison et al.,¹³ the sample sizes of these GWASs ranged from 46,186 for FG and 69,033 for T2D, to 100,716 for BF, 142,486 for asthma, 188,577 for TG, HDL, and LDL, 253,288 for height, 322,154 for BMI, then 446,696 for stroke, 547,261 for CAD, 757,601 for DBP and SBP, finally to near and above a million for alcohol and smoke, respectively. For each risk factor/exposure-disease/outcome pair, we used the set of LD-independent SNPs as IVs as described in Morrison et al.¹³ (in their Table S4) and applied all methods except CAUSE to the GWAS summary statistics of these SNPs; for CAUSE, we extracted the results from the original paper.¹³

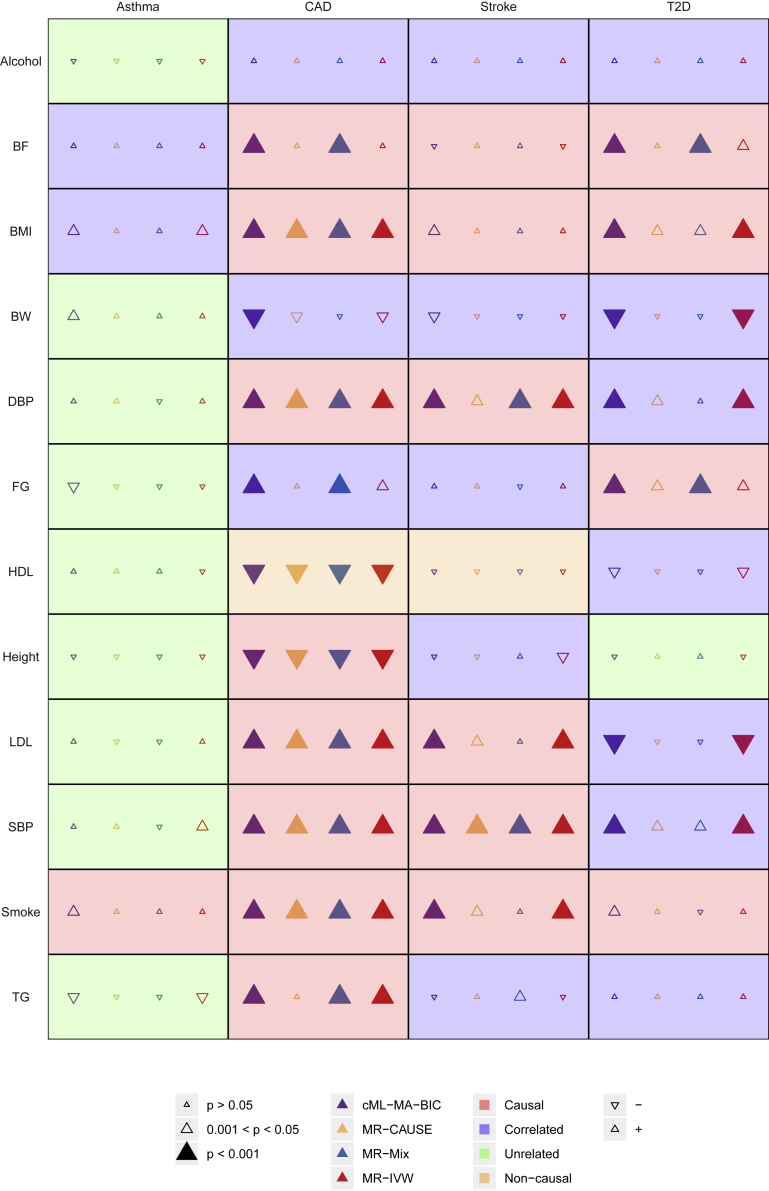
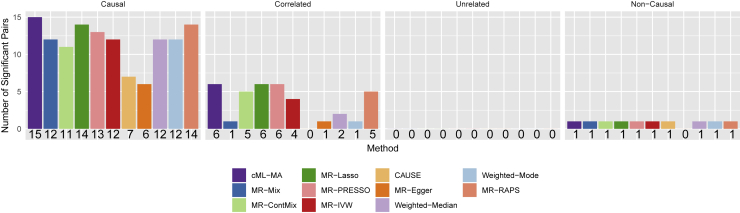
In Morrison et al.,¹³ the 48 exposure-outcome pairs were classified into 5 categories: considered causal (9 pairs), likely causal as supported by the literature (10 pairs), correlated but unknown to be causal or with conflicting evidence (17 pairs), unrelated (10 pairs), and considered non-causal (2 pairs); here we combined the first two categories into one to represent (likely) causal pairs. In Figure 8 we compare cML-MA-BIC with three representative methods: CAUSE, a new one specifically proposed to deal with correlated pleiotropy, and two MR methods, one robust and competitive (MR-Mix) and the other perhaps most popular (MR-IVW), for all of these 48 risk factor-disease pairs. Figure 9 compares the numbers of the detected pairs by these and other methods, and other detailed results (of the causal parameter estimates, SEs, and p values) for all methods are available in the supplemental material and methods. Here we discuss the results based on the Bonferroni adjusted significance level of $0.05/48\approx 0.001$. For the 19 known or likely causal risk factor-disease pairs, cML-MA-BIC, CAUSE, MR-Mix, and MR-IVW identified 15, 7, 12, and 12 significant pairs, respectively; among the 17 correlated pairs, the four methods detected 6, 0, 4, and 1 pairs, respectively; among the 10 unrelated pairs, none of the methods identified any, while for the two pairs of non-causal pairs, all four methods indicated one and the same one (i.e., HDL-CAD, which is still under debate as whether it is truly causal). In addition, although none of the methods detected causal smoke-asthma, smoke-T2D, and BMI-stroke, our method was the only one among the four methods giving marginally significant p values. It is clear that our proposed cML-MA-BIC identified the largest numbers of the known or likely causal pairs, showcasing its highest power. On the other hand, it also detected more pairs from the category of “correlated” pairs. It is possible that these pairs, such as BW-CAD, BW-T2D, and DBP/SBP-T2D, may be false positives, but at the same time, they may be truly causal as to be confirmed (or refuted) by further studies. As shown in Figure 10, only based on the data, there seems to be evidence to support these causal relationships as detected by our cML-MA-BIC and many other tests (shown in the supplemental material and methods). It is noted that CAUSE also gave marginally significant p values < 0.05 for three of these six pairs.

Figure 8.

Results of cML-MA-BIC, MR-CAUSE, MR-Mix, and MR-IVW to detect causal relationships among 48 risk factor-disease pairs

Figure 9.

The numbers of the significant risk factor-disease pairs detected by various methods at the significance cutoff of p value < 0.001

MR-RAPS refers to RAPS2 (with the Tukey loss and overdispersion).

Figure 10.

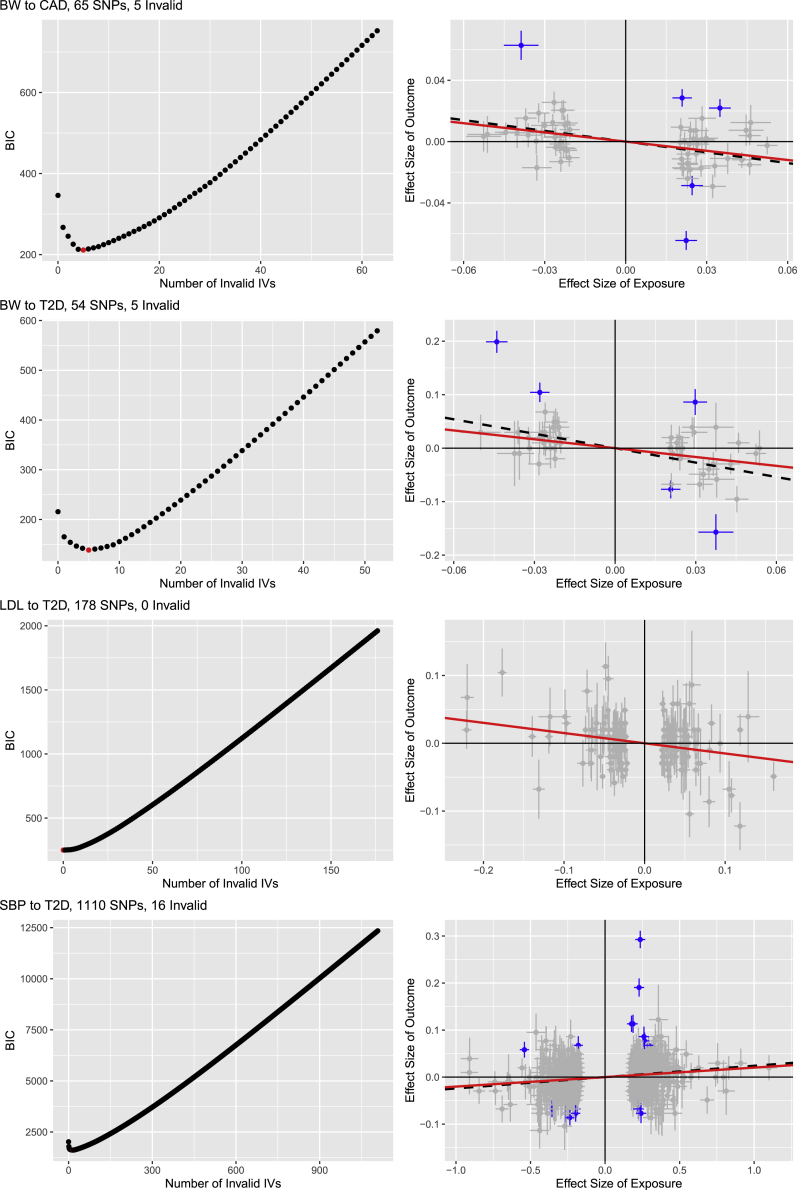
BIC and scatter plots for four pairs

For four risk factor-disease pairs, the left panels show the numbers of invalid IVs versus BIC values, while the right panels show ${\hat{\beta }}_{Xi}$ versus ${\hat{\beta }}_{Yi}$ (with their errors bars indicating ${\hat{\sigma }}_{Xi}$ and ${\hat{\sigma }}_{Yi}$). In the right panels, those for invalid IVs detected by BIC are blue, the red solid lines give the causal estimates (after removing the detected invalid IVs), and the black dashed lines are for the estimates based on all IVs.

Among the tens to about 1,000 SNPs used as IVs for the 48 risk factor-disease pairs, 0 to 96 SNPs, mostly <10, ranging from 0% to 30%, mostly <3%, were identified as invalid IVs by our method (Table S5). However, as for BW-CAD and BW-T2D in Figure 10, although only five (out of 65 and 54) SNPs were identified as invalid IVs based on the BIC-selected best models, the models containing up to K = 20 SNPs as invalid IVs were estimated to be better (with lower BIC values) than the model treating all SNPs as valid IVs (i.e., K = 0). In general there were fewer invalid IVs for asthma, stroke, and T2D, but more for CAD. It can be seen that the influence of invalid IVs is somewhat complex; the difference between the two causal estimates with and without invalid IVs may or may not simply depend on the presence or the number of invalid IVs, but more on the configuration of invalid IVs relative to that of valid ones. For example, with the same number of invalid IVs detected for the BW-CAD and BW-T2D pairs, the causal estimates with and without the detected invalid IVs were almost the same for the former pair, but more different for the latter (Figure 10).

We then applied cML-MA-BIC-DP with T = 200 perturbations and 10 additional random starts in each perturbation. Compared to those of cML-MA-BIC, the results remained the same for 46 pairs in terms of statistical significance, but changed from being significant to marginally significant for only two pairs: one known or likely causal pair, BF-CAD; and one correlated pair, BW-T2D.

In summary, it is encouraging that most methods detected similar numbers of significant pairs, though MR-Egger and CAUSE detected much fewer as shown in Figure 9. In addition, there were some notable differences in specific pairs detected across the methods. For example, while our methods detected the causal pairs BF-T2D and FG-T2D, MR-IVW missed both and MR-RAPS missed BF-T2D. We conclude that our proposed methods performed competitively.

Secondary real data analysis

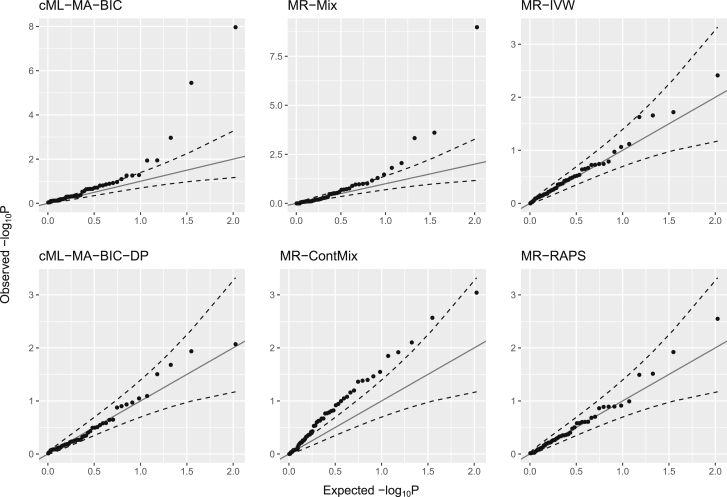
We compared the type I errors of the cML methods and other existing MR methods with 63 pairs of traits that were not genetically correlated (with their p values greater than 0.05). For 10 of 63 pairs with HOMA as the exposure, TwoSampleMR gave only 2 LD-independent SNPs as IVs, which was too small to apply MR-ContMix, MR-Lasso, MR-Egger, MR-Weighted-Median, MR-Weighted-Mode, and MR-PRESSO; although cML methods are applicable to only two IVs, they would require K = 0, i.e., no invalid IVs. Hence we applied all methods to the other 53 pairs (without HOMA as the exposure). Figure 11 shows the Q-Q plots of cML-MA-BIC, cML-MA-BIC-DP, MR-Mix, MR-ContMix, MR-IVW, and MR-RAPS for these 53 pairs; Figure S5 shows the results for all methods. While the methods based on selection of invalid IVs, i.e., cML-MA-BIC, MR-Mix, and MR-ContMix, all seemed to have inflated type I errors, the proposed cML-MA-BIC-DP with T = 200 perturbations and 10 additional random starts in each perturbation, along with MR-IVW and MR-RAPS, appeared to perform well in satisfactorily controlling the type I errors. The complete results are in the supplemental material and methods.

Figure 11.

Q-Q plots for 53 (likely) null trait-pairs in the secondary real data examples

Discussion

We have proposed several methods based on constrained maximum likelihood (cML) to consistently identify invalid IVs with either or both of correlated and uncorrelated pleiotropic effects, thus leading to consistent estimation and inference of the causal effect between an exposure and an outcome. For finite samples, the (asymptotic) selection consistency may not be achieved. To account for model selection uncertainty, we first propose a model-averaging approach, cML-MA-BIC, which performs better, especially in better controlling the type I error rate, than the selection-based version, cML-BIC. In addition, in more challenging situations with many invalid IVs with only weak pleiotropic effects, both model selection and model averaging may not perform well by failing to fully account for model selection uncertainty; accordingly, we propose a version based on data perturbation, cML-MA-BIC-DP, which could control the type I error rate satisfactorily across all simulated and real data examples. However, cML-MA-BIC-DP is computationally more demanding and may be conservative with some loss of power as compared to cML-MA-BIC. To help a user determine which one is preferred, we propose two GOF tests for the null hypothesis that the two approaches give the equivalent variance estimates (and thus inferential results); if the null hypothesis is not rejected, one can simply apply cML-MA-BIC; otherwise, cML-MA-BIC-DP is preferred. All the proposed methods are applicable to GWAS summary data.

Three new competitors to our methods include CAUSE,¹³ MR-Mix,¹² and MR-ContMix.⁹ As shown in our simulations and in agreement with the original study,¹³ CAUSE may have dramatically inflated type I error rates, presumably due to its complex modeling and estimation of the parameters related to hidden/unobserved confounding. Furthermore, CAUSE imposes an assumption of ${\gamma }_i{\phi }_i=0$ (i.e., that an IV can only have a direct effect on either the exposure or the hidden confounder, but not on both simultaneously), though it is yet unknown and debatable whether this assumption is reasonable for real data. It seems advantageous that our proposed methods simply estimate only a small number of necessary parameters (without such an assumption). Both MR-Mix and MR-ContMix are based on multivariate normal mixture models on various effect sizes across the genome, which not only impose stronger modeling assumptions, but also are computationally more demanding. In our experiments, overall, MR-Mix performed only second to our proposed methods with mostly controlled type I error rates and high power, though it might still have either largely inflated or too conservative type I errors while giving biased estimates (e.g., Figures 6 and 5). On the other hand, it is challenging to pre-select a fixed tuning parameter in MR-ContMix, which may negatively influence its performance in some situations as shown in our simulations. At the same time, it is confirmed that two most popular methods, MR-IVW and MR-Egger, do not perform well with dramatically inflated type I error rates and low power in the presence of correlated pleiotropy. Most importantly, we conclude that our proposed cML-MA-BIC (or cML-MA-BIC-DP) was the overall winner based on our extensive numerical studies.

MR-PRESSO and MR-Lasso are two existing methods looking most similar to our proposed methods. For our cML estimates, if an SNP has an estimated total direct effect ${\hat{r}}_i\ne 0$, then it is an invalid IV and does not contribute to estimating the causal effect θ (as shown in the material and methods section); otherwise it is a valid IV and contributes to estimating θ. Hence, our methods work by selecting and (implicitly) removing invalid IVs, in which sense they are related to MR-PRESSO and MR-Lasso (and an improved variant of MR-PRESSO³⁸). However, there are some important differences. First, we propose a BIC for consistent model selection (and weighting) while MR-PRESSO uses resampling-based significance testing and MR-Lasso is based on a heuristic heterogeneity criterion. We have a rigorous theory to support our proposed method. Second, both MR-PRESSO and MR-Lasso draw inference on the causal effect θ based on a single selected model; due to selection bias, they often have inflated type I error rates and in general biased estimates of θ. In contrast, by accounting for model selection uncertainties through model averaging, our method cML-MA-BIC performs much better as shown in simulations. Third, since MR-PRESSO selects invalid IVs one by one while ours and MR-Lasso select multiple ones simultaneously, MR-PRESSO may miss some invalid IVs (e.g., as well known in statistics that two invalid IVs/outliers may not appear so if checked one by one). In addition, MR-PRESSO fails to properly account for the variability of the delete-1 (IV) estimates of the causal effect while assuming that the delete-1 estimates are all accurate, which may be false, leading to both false positives and false negatives in selecting invalid IVs. On the other hand, MR-Lasso depends on a specified candidate set of the tuning parameter values for the Lasso penalty, which may be difficult to specify a priori. There is also lack of theoretical justification for its heterogeneity-based model selection criterion. Furthermore, in general, as most penalized methods, MR-Lasso yields biased estimates due to the shrinkage effects of the Lasso penalty. Finally, MR-LASSO, as MR-IVW and MR-Egger, imposes the NOME (no measurement errors) assumption by ignoring the variability in estimating each IV-exposure association. Presumably due to these reasons, our proposed methods performed much better than the other two methods in our numerical examples.

Our proposed cML-MA-BIC not only performs extremely well in our numerical examples, but also is quite simple and intuitive with strong theoretical support. In fact, it may be surprising that such a method has not appeared in the MR literature. We note that our methods are based on classic statistical theory (for “large n, small m,” i.e., asymptotics for a large sample size and a fixed/small number of parameters), which is suitable for typical GWASs (with n in tens to hundreds of thousands, while m is no more than a few hundreds). It might be of interest to extend our methods to a high-dimensional “large n, large m” scenario with even a much larger number of IVs: instead of using the full likelihood, we can use the profile likelihood⁶ as shown in the supplemental material and methods; we will also need to adopt or develop some new model selection criteria for high-dimensional data.39, 40, 41 There are other limitations of our proposed methods. First, we propose a fast algorithm to select valid (or equivalently, invalid) IVs to obtain cML estimates. Since it is a combinatorial and non-convex variable selection problem, the proposed algorithm cannot guarantee finding a global solution. Nevertheless, in our simulations it yielded good results with only one starting value (by setting all parameters at 0). A simple strategy is to use multiple random starting values as used in the real data examples, for which little difference was found. In the future other more sophisticated algorithms^42,43 may be adapted and applied. Second, we assume that the two GWAS (summary) data for the exposure and outcome are independent. As in CAUSE, we may estimate and model possible correlations between the two GWAS datasets due to overlapping subjects, and then modify the log-likelihood accordingly. More generally, it is critical to adjust for possible sample structure, including population stratification and subject relatedness, present in some GWAS data.^44,45 Our methods, cML-MA-BIC and especially cML-MA-BIC-DP, appeared to work in some preliminary simulaions (not shown) with population stratification as the hidden confounding factor U. Third, as in typical MR applications, we used the same GWAS sample to select significant SNPs as IVs (to meet IV assumption A1) before using the same data for inference. It is known that this double-use of the data could lead to biased inference due to selection bias. Alternatively, we may use an independent GWAS sample to select SNPs to avoid selection bias as in the three-sample MR design,⁴⁶ or account for selection explicitly.^44,47 Fourth, we considered only independent SNPs as IVs; extending to using correlated SNPs as IVs may be useful in other applications, e.g., transcriptome-wide association studies,48, 49, 50, 51, 52, 53, 54 which equally face the analysis challenges with pleiotropic SNPs and thus invalid IVs.⁵⁵ These are interesting topics for future investigation.

Declaration of interests

The authors declare no competing interests.

Published: July 1, 2021

Data and code availability

This study used the GWAS summary datasets that are all publicly available as indicated in their corresponding references. The proposed methods are implemented in R package MRcML, which is publicly available to download on GitHub at https://github.com/xue-hr/MRcML. All other MR methods used for comparison are in publicly available R packages with links given in the web resources section.

Web resources

• CAUSE, https://github.com/jean997/cause

• LD Hub, http://ldsc.broadinstitute.org/lookup

• MR-ContMix, https://cran.r-project.org/web/packages/MendelianRandomization

• MR-IVW, MR-Egger, MR-Weighted-Median, MR-Weighted-Mode, MR-RAPS, https://github.com/MRCIEU/TwoSampleMR

• MR-Lasso, https://onlinelibrary.wiley.com/doi/full/10.1002/gepi.22295

• MR-Mix, https://github.com/gqi/MRMix

• MR-PRESSO, https://github.com/rondolab/MR-PRESSO

• OMIM, https://www.omim.org/

• Software/R package for MR-cML, https://github.com/xue-hr/MRcML