Protodomains: Symmetry-Related Supersecondary Structures in Proteins and Self-Complementarity

Abstract

We will consider in this chapter supersecondary structures (SSS) as a set of secondary structure elements (SSEs) found in protein domains. Some SSS arrangements/topologies have been consistently observed within known tertiary structural domains. We use them in the context of repeating supersecondary structures that self-assemble in a symmetric arrangement to form a domain. We call them protodomains (or protofolds). Protodomains are some of the most interesting and insightful SSSs. Within a given 3D protein domain/fold, recognizing such sets may give insights into a possible evolutionary process of duplication, fusion, and coevolution of these protodomains, pointing to possible original protogenes. On protein folding itself, pseudosymmetric domains may point to a “directed” assembly of pseudosymmetric protodomains, directed by the only fact that they are tethered together in a protein chain. On function, tertiary functional sites often occur at protodomain interfaces, as they often occur at domain-domain interfaces in quaternary arrangements.

First, we will briefly review some lessons learned from a previously published census of pseudosymmetry in protein domains (Myers-Turnbull, D. et al., J Mol Biol. 426:2255–2268, 2014) to introduce protodomains/protofolds. We will observe that the most abundant and diversified folds, or superfolds, in the currently known protein structure universe are indeed pseudosymmetric. Then, we will learn by example and select a few domain representatives of important pseudosymmetric folds and chief among them the immunoglobulin (Ig) fold and go over a pseudosymmetry supersecondary structure (protodomain) analysis in tertiary and quaternary structures. We will point to currently available software tools to help in identifying pseudosymmetry, delineating protodomains, and see how the study of pseudosymmetry and the underlying supersecondary structures can enrich a structural analysis. This should potentially help in protein engineering, especially in the development of biologics and immunoengineering.

1. Introduction

1.1. Structural Protein Domains

Protein domains have been used by nature as building blocks in larger chains and protein complexes. Biologists have used them to build chimeric proteins, following one of nature’s paths in fusing domains together assuming a function for each domain. Such is the case of immunotoxins where an antibody-based domain is fused to a bacterial toxin, the first one for binding to a tumor cell surface antigen target and the second one for cell killing [2]. More recently CAR T-cell therapies have made use of CARs (chimeric antigen receptors) that go beyond in the “engineering” of new proteins by fusing domains in a single chain. In the case of CARs, in addition to fused immunoglobulin (Ig) domains (scFv), entirely new domains are composed of subdomains extracted from various T-cell surface proteins (CD28 and/or CD8 and CD3z) in order to retain desired functional properties [3].

Nature has used a protodomain fusion mechanism in a distant evolutionary past, or so it seems, when one observes pseudosymmetric domains. Hence, we can gain insights in domain creation from an analysis of tertiary pseudosymmetry. Many domains have been structurally characterized, so we can not only look at domain creation but domain evolution in terms of the constituting parts. The immunoglobulin fold [4, 5] is at the heart of a very large number of cell surface proteins of the immune systems [6, 7], beyond immunoglobulins themselves. We will review its tertiary symmetry as well as one level of quaternary structure symmetry in the case of CD8, as a revealing example. Also, as we seek to move to lighter therapeutic proteins, from Fabs to Fvs to single Ig domains as antigen binding domains, Ig domain-level pseudosymmetry properties may be able to guide some immunoengineering efforts.

1.2. Domain-Level Pseudosymmetry and Structural Protodomains

1.2.1. Systematic Census of Tertiary Pseudosymmetry

Structural pseudosymmetry in protein domains has been observed very early on, even within the very first protein structures solved, for example, ferredoxin, myohemerythrin, serine and aspartyl proteases, immunoglobulins, the TIM barrels (triose-phosphate isomerase), or the Rossmann fold [8–15]. It is interesting to note that some of these domains that were characterized early turned out to be some of the most diversified and prototypic domains: in the SCOP classification [16, 17], they are noted d.58, a.24, b.47, b.49, b.1, c.1, and c.2, respectively.

Structural pseudosymmetry corroborated observations a decade earlier of possible ancestral gene duplications within today’s genes [12–15] and established a basis for interpreting sequence duplication with pseudosymmetry, hence conceptually defining what we now call “protodomains.” We recently performed a systematic census of tertiary pseudosymmetry in the currently known universe of protein domains in the PDB database. We found that a significant number of protein domains (folds) exhibit pseudosymmetry. We can decompose such domains into protodomains (protofolds), i.e., supersecondary structures related by symmetry.

We shall mention here the top five protein fold classes in that study where, on average, 20% of the folds exhibit internal pseudosymmetry (see Table 1 hereafter and Table S2 in [1]). In these classes the most diversified folds, i.e., those with the highest number of functional superfamilies, were all pseudosymmetric: a.24 (four-helix bundle/myohemerythrin), b.1 (immunoglobulin), c.1 (TIM), and d.58 (ferredoxin) in the SCOP classification [16, 17]. In that classification, membrane proteins (Class F) are grouped together yet two-thirds are alpha-helical folds vs. approximately one-third of all beta-sheet folds, with 24% overall exhibiting symmetry. We chose to highlight the 7-transmembrane protein fold (GPCRs) with a different criterion. It is a single fold and family with a conserved signaling function for an astounding ligand diversity. We can call superfolds these highly resilient folds associated with a large number of superfamilies and highly diversified functions.

Table 1.

Pseudosymmetry for major structural classes and for the most diversified folds

Fold class	# Folds in class	# SFs in class	% SFs with symmetry	Superfolds: most diversified fold in class	# SFs in fold	% SFs with symmetrya
A	284	507	19%	a.24	28	57%
B	174	354	25%	b.1	28	39%
C	147	244	17%	c.1	33	36%
D	376	551	14%	d.58	59	58%
F	57	109	24%	f.13 (GPCRs)	1b	N/A
	1038	1765	20%

Fold classes according to SCOP 1.75 (A, all alpha; B, all beta; C, alpha+beta; D, alpha-beta mixed; F, membrane proteins). Total number of folds and superfamilies (SFs) in class, with percentage of SFs deemed symmetrical. “Superfolds”, i.e. folds with the highest number of superfamilies in class, as a measure of their diversification. For each of them the percentage of superfamilies exhibiting pseudosymmetry (these results were obtained computationally using a threshold of 30%, i.e. a minimum of 30% of superfamilies associated with a given fold were found pseudosymmetric (see Ref. 1,Table S2). In that study 1831 superfamilies representing 157,432 domains were used, including Class E, not shown)

^aRepresentatives of superfamilies were used. Pseudosymmetry was detected for a number of them for each fold. With a score of 30% or more the fold is “called” as symmetric. Experience shows that other folds are symmetric but were undetected with the parameters used. An example would be the Hfq/Sm fold and others sharing an SH3 topology (b.34/b.38), which fall under that 30% threshold

^bWe added GPCRs, classified as one fold, one superfamily in SCOP. Technically it could be classified as A: all alfa. It represents a special case of a highly diversified structural domain within a single superfamily with over 800 different GPCRs just in humans and a staggering 2300 hundred in elephants, diversifying ligand binding for a conserved signaling function within cells

Pseudo symmetry is a geometrical property. It does however establish a link to folding, evolution, and biological function. The knowledge of protodomains and symmetry operators defines a pseudosymmetric domain entirely, apart from a variable linker region, most often short, chaining protodomains within a domain. While protein domains are well defined and have been extensively classified through a number of taxonomies (SCOP, CATH, ECOD) [16–19], the underlying protodomains, in the case of pseudosymmetric domains, have not. Hence the first task is to delineate them and analyze them in terms of similarities and differences, through structure-based sequence alignments.

1.3. Symmetry and Self-Association

1.3.1. Quaternary Symmetry and Self-Assembly

Symmetry in quaternary structures has been extensively studied [20–23]. Among the 3D macromolecular structural complexes in the Protein Data Bank (PDB), symmetry is pervasive [20–23]. The PDB (www.rcsb.org) stores all publicly available structures. As of today, it contains 140,000 structures of macromolecular complexes, with 51% of oligomers: 50,600 (38%) of homomers and 18,000 (13%) of heteromers. In terms of quaternary symmetry, ca. 53,000 structures represent symmetric complexes, with close to 42,000 (78%) presenting a cyclic symmetry and 10,000 (19%) presenting a dihedral symmetry. While quaternary cyclic symmetry is observed up to the 39th order (C39), as in the Vault ribonucleoprotein particle (PDBid: 4HL8), the C2 symmetry represents the vast majority of symmetric structures with ca. 32,000 representatives, of which ca. 31,000 are homodimers.

While these numbers correspond to structures obtained to date on all macromolecular complexes, and are not necessarily fully representative of all (fluctuating) protein complexes in vivo, they nevertheless indicate a natural principle of self-assembly of macromolecules [24]. It is natural to view quaternary symmetry or pseudosymmetry as a result of oligomerization of homomers or heteromers, demonstrating the propensity of protein domains to self-assemble.

1.3.2. Tertiary PseudoSymmetry and Self-Assembly of Supersecondary Structures

Most known oligomeric protein structures are symmetric or pseudosymmetric and can be classified using closed symmetry groups. The same is true from pseudosymmetric domains, where at least 20% of known protein domains are pseudosymmetric (see Table 1). This reflects a seemingly similar self-association process of protodomains. Of course, protodomains are chained together, and they have little choice but to assemble, yet they favor a pseudosymmetric arrangement, a pseudosymmetric fold. The vast majority of pseudosymmetric tertiary domains exhibits C2 symmetry, as in known quaternary structures. Higher-order symmetries are also observed in tertiary as in quaternary structures. Pseudosymmetry order up to 30 can be found in, for example, Toll-like receptor 8 (PDBid: 4R0A) with 29 repeats and room for an extra one, where each consecutive repeat/protodomain is related by a rotation operation of 12 degrees around a common central axis. Dihedral symmetry is also observed in tertiary as in quaternary structures.

Quaternary symmetry is a geometrical property and results from monomeric proteins self-assembling at the domain level. The same is true from pseudosymmetry domains in terms of the protodomains they are composed of. Analogously, one can also regard pseudosymmetric domains as pseudoquaternary structures and see a continuum in complexity buildup from subdomain to supra-domain organizations, from protodomain to domain assemblies. This parallel also points to a possible ancestral world where protodomains may have oligomerized spontaneously. At the gene level, it is accepted as a duplication-fusion model to lead to pseudosymmetric protein domains [25–27]. A good example of such a possible duplication-fusion event can be seen in comparing semisweet vs. sweet protein domains (Fig. 7). Of course, in today’s genomes and gene organization, it is not straightforward to reconcile protodomains and possible original protogenes. Yet it can be rewarding to analyze pseudosymmetry as a structural property, regardless of genomic organization.

Fig. 7.

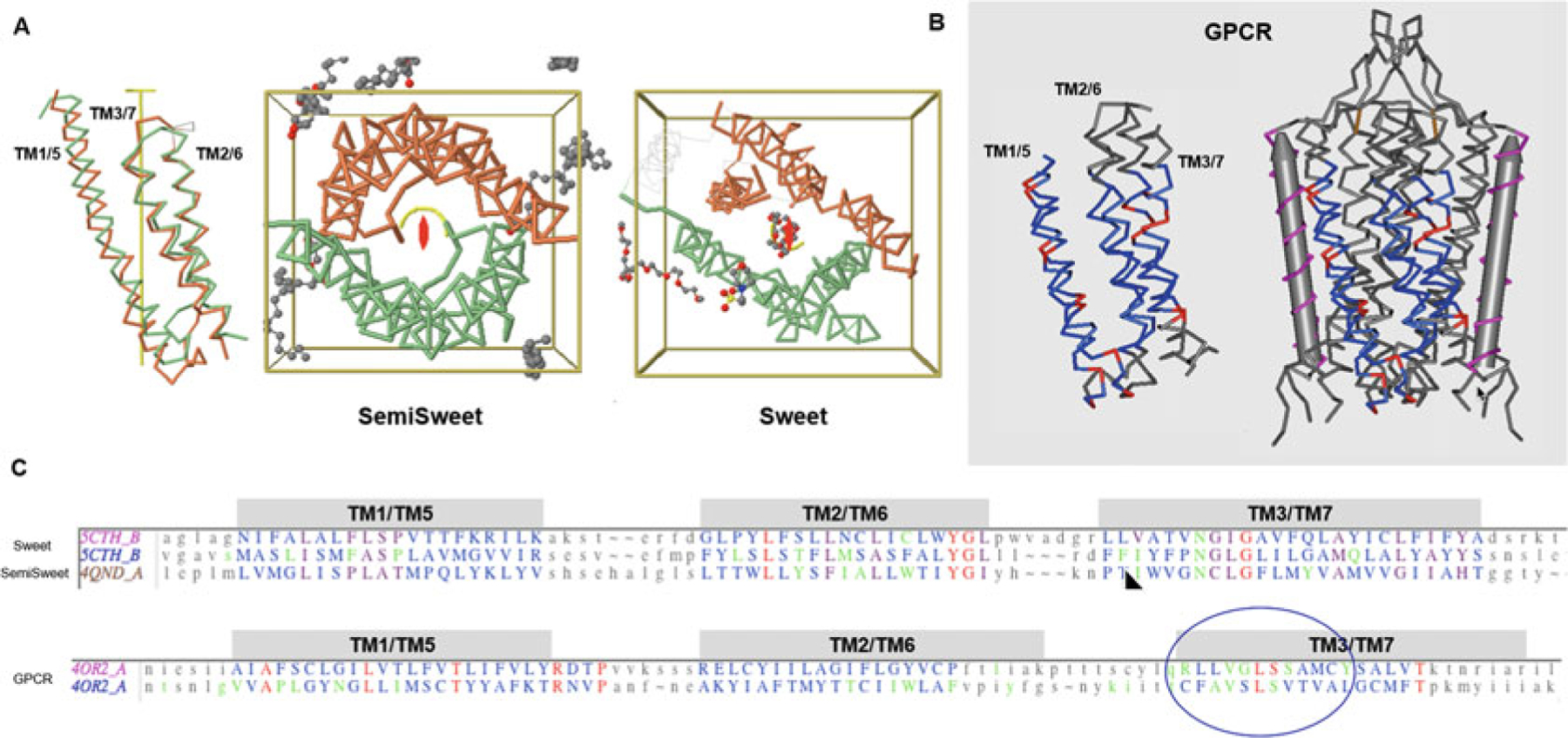
7-Transmembrane helical (7-TMH) proteins. Sweets and GPCRs. (a) Sweet protodomains (3-TMH) aligned, bacterial SemiSweet (3TMH) dimer, and 7-TMH Sweet Protein. The linker between the two Sweet protodomains forms an additional transmembrane helix (TM4). While formed with three consecutive helices in sequence, a protodomain exhibits a 1–3–2 structural arrangement in 3D that is duplicated to form a symmetric pseudosymmetric domain equivalent to a Bacterial SemiSweet symmetric dimer (less TM4). The two protodomains match each other with a RMSD of 1.36 (Sweet protein structure 5CTH) after optimization (automatic detection alignment was 2.91A). A bacterial SemiSweet 3-TMH “domain” aligns with Sweet protodomains with an RMSD of 1.98A (SemiSweet structures 3QND/3QNC). The 7-TMH and 3-TMH dimer align very well not only at the protodomain level but at the dimer vs. pseudo-dimer level. Here displayed with the symmetry axis perpendicular to the plane. The ligand lies on the axis of symmetry. (b) 7-TMH Class C GPCR (structure 4OR2—metabotropic glutamate receptors (mGlus) bound to an allosteric modulator) protodomain optimum alignment with an RMSD of 3.32A through interactive alignment software Cn3D. GPCRs can also be considered with a two-protodomain arrangements. The two protodomains exhibit a distinct 1–2–3 organization in 3D. Here we display the alignment of the whole 7-TMH protein onto itself; the symmetry match can be observed with a solid gray cylinder for the TM4 “linker.” Unlike Sweet, symmetry detection programs do not detect pseudosymmetry systematically but can, in a few cases, using stringent criteria. Interactive alignment of 3-TMH protodomains was used as the method of choice in this case. In all known Class A structures, we have examined, but also in the two Class C structures currently available, pseudosymmetry highlights symmetry equivalent residues in TM1/5, TM2/6, and TM3/7, in a systematic way for some key residues. The structurally aligned TM3/7 helices often exhibit a pseudosymmetric sequence motif (see C and text), framing ligand-binding residues pseudosymmetrically, with ligands lying for a significant part on the axis of symmetry. (c) Associated sequence alignments with mapped ligand-binding residues (or rather residues within a 4A radius from ligand) for Sweet/SemiSweet (sugar) and for the GPCR vs. its ligand. It is important to note that for any pseudosymmetric domain, a protodomain defines a domain entirely (see text). A protodomain is usually idiosyncratic. Here the Sweet protodomain is very different in topology 1-3-2 vs. GPCRs with 1-2-3 topology, yet each defines its domain through that same duplication and pseudosymmetric arrangement

1.3.3. Self-Assembly Is a Universal Molecular Organizational Principle

Self-assembly and the resulting observed symmetry is in fact a property of all biological macromolecules. Symmetry and self-assembly is of course the main characteristic of DNA pairing; in nucleosomes DNA exhibits an exquisite global C2 symmetry, with the histones assembly exhibiting three levels of C2 symmetry (Fig. S6). Recent RNA crystal structures also show that several Riboswitches RNAs exhibit symmetry whether at the tertiary or quaternary level [28] (Fig. 9). The active site of the ribosome itself, a remnant of a proto-ribosome in the RNA world, displays pseudosymmetry [29]. Self-assembly, based on non-covalent interactions, can be seen as a principle for complexity buildup of molecular systems of any size. Mimicking biological systems, and beyond molecular chemistry based on the covalent bond, a whole new field of “supramolecular chemistry” has been aiming in the last 20 years at developing highly complex chemical systems from molecular components interacting through non-covalent intermolecular forces [30, 31].

Fig. 9.

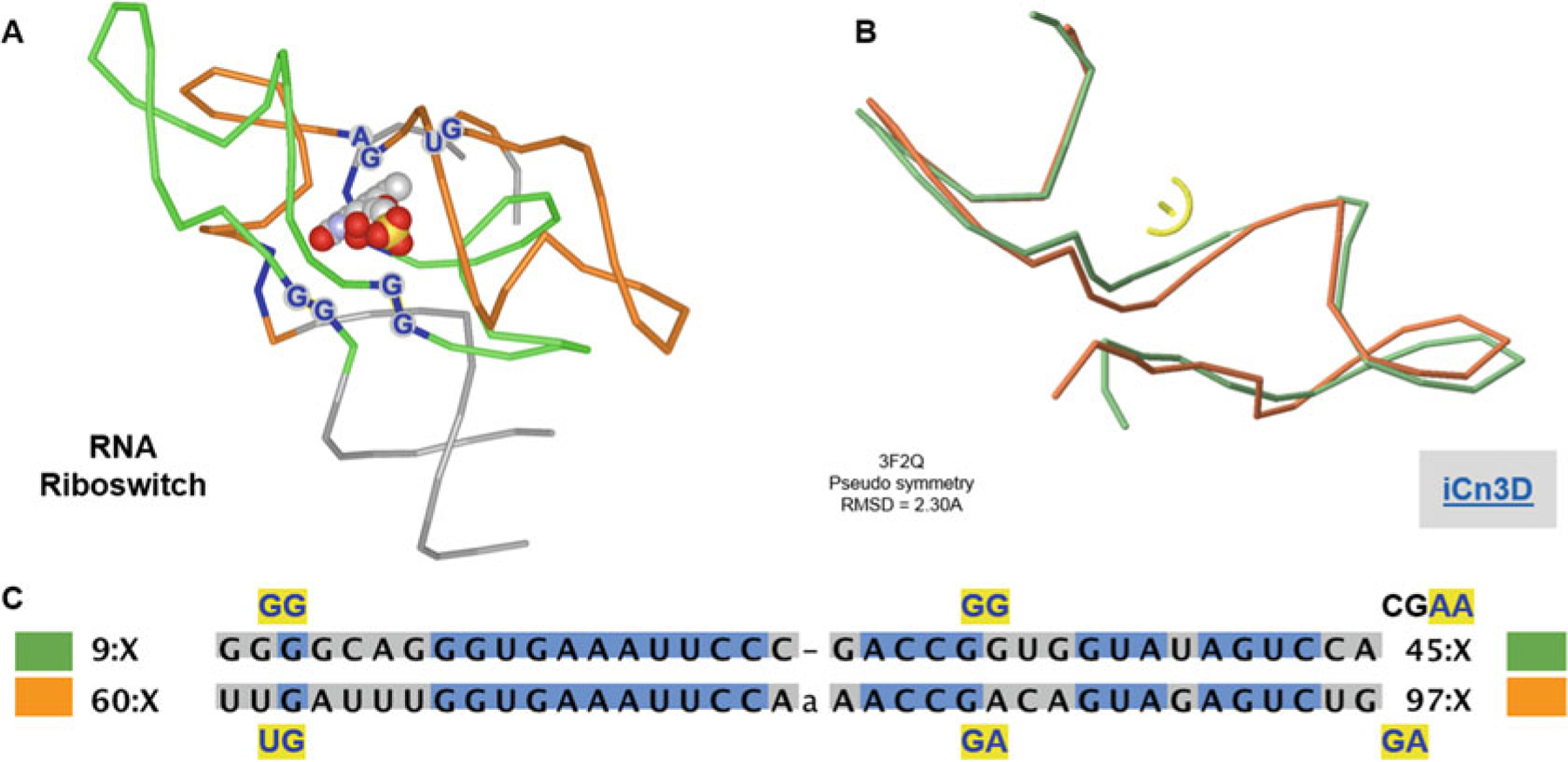
RNA protodomains in riboswitches and ligand binding. (a) Symmetric arrangements of RNA protodomains. Ligand-binding residues are highlighted dark blue. The ligand is on the axis of symmetry perpendicular to the paper plane. (b) Protodomains are structurally aligned with an RMS of 2.30 A (at the symmetry detection step, no optimization performed). (c) Structure-based protodomain sequence alignment. Ligand-binding residues are in dark blue highlighted in yellow. They match exactly in sequence position in both protodomains (GG/UG–GG/GG, and a small offset on the third binding dinucleotide AA/GA just outside of the delineated protodomains). Link to iCn3D: https://d55qc.app.goo.gl/gJee10ict11uT0Y22

1.4. Analyzing Self-Assembling Supersecondary Structures

A point group symmetry operation between two or more entities establishes a structural equivalence relation between these entities. Two residues or sets of residues related by pseudosymmetry in equivalent positions can be analyzed in terms of “internal” sequence conservation (identity, similarity or lack of), structure, and topology. If one assumes a duplication event, then this opens the door to studying the parallel evolution or coevolution of protodomains within a domain and their interfaces. In studying coevolving SSSs and drilling down coevolving SSEs and residues at equivalent positions, “internal” conservation or nonconservation of residues may be linked to either folding, coevolution of protodomain interfaces, oligomeric interfaces, or function.

Molecular interfaces can vary greatly, but as soon as we look at tertiary or quaternary symmetric arrangements, structurally homologous supersecondary structures emerge. SSSs form interfaces with symmetrically interacting SSEs. Hence protodomains have to be self-complementary where they are in contact. These contacts can vary widely from a few residues to a number of entirely self-complementary/self-interacting SSEs. They are based on nonbonded residue interactions for both alpha and for beta structures. Beta structures have, in addition, a beta strand pairing mechanism through hydrogen bonding at the backbone level, to form beta sheets. We shall see two magnificent examples in the following with the Ig fold (Figs. 1, 2, 3, 4, 5, and 6) and the Sm fold (Figs. 8 and S2). One can use symmetric and pseudosymmetric SSS decomposition at any level of complexity to analyze molecular interfaces and gain knowledge in the determinants of self-assembling systems. Pseudosymmetry and protodomain delineation of protein domains and, beyond, symmetric quaternary organization of biological units lead us to a method to analyze complexity buildup in biological systems through an architectural/organizational principle of protein structure.

Fig. 1.

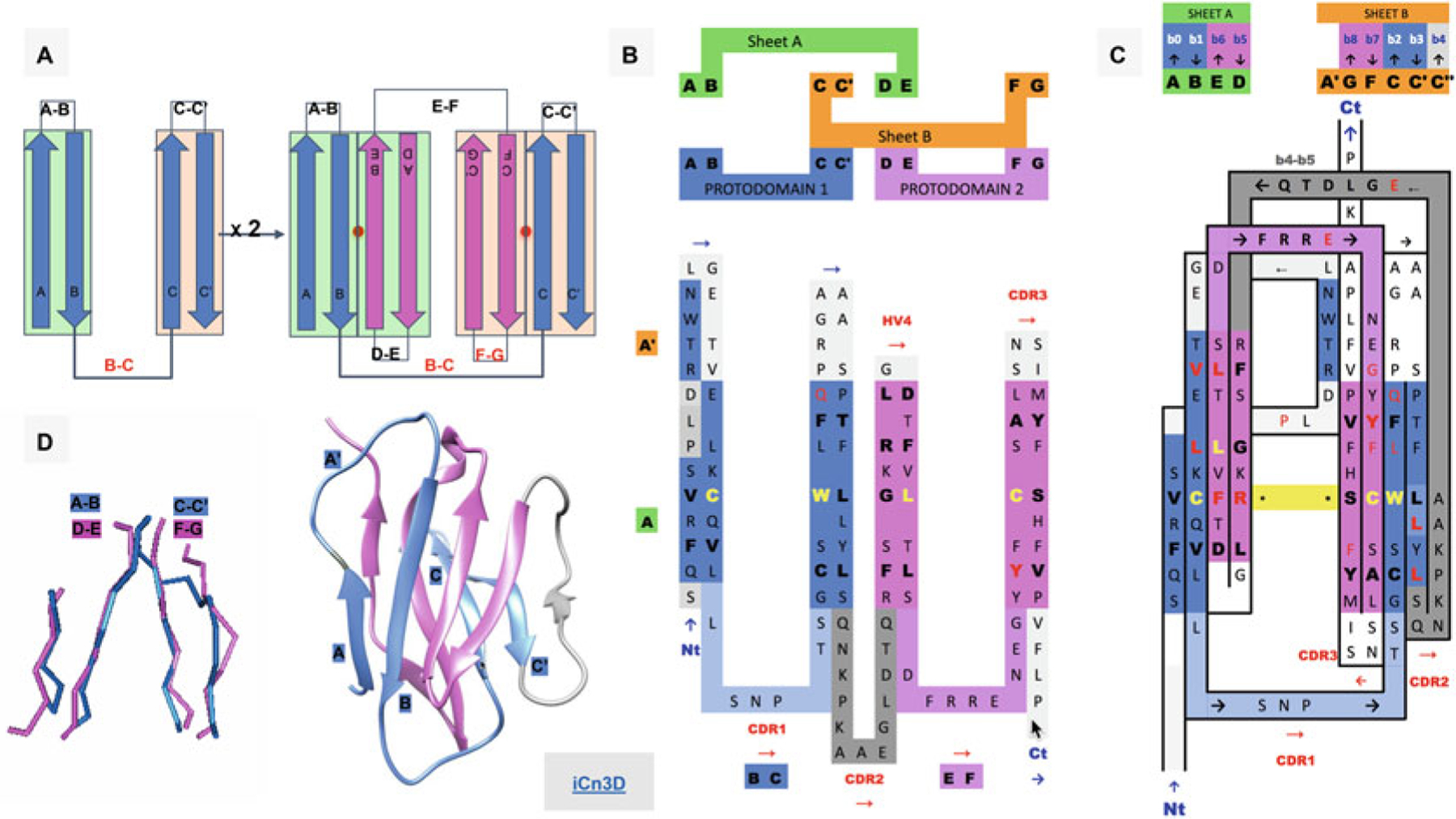
Ig Greek key protodomain topology, duplication, and symmetric arrangement of protodomains. (a) Idealized Ig protodomain motif topology bb-bb, with 2 beta hairpins connected by a Greek key linker (b, c), duplication, and schematic arrangement: A|B + C|C′ = D|E + F|G. Each hairpin theoretically forms to a plane.Each Ig type will present departures from idealized protodomains in their domain context, due to either the protodomain-protodomain linker (not shown here) or some partial structural rearrangement of strand A (see (d) and Fig. 2 for variants in IgV, VNAR, and IgC). Protodomain strands will be displayed blue and magenta for consecutive protodomains 1 and 2, respectively. Planes/Sheets A and B will be consistently shown in green and orange background color. (b) Topology/sequence of consecutive protodomains A|B − C|C′ + D|E − F|G. Interestingly, the well-known CDR1 loop in immunoglobulins appears as the Greek key linker between strands B and C, while the CDR2 is formed by linking the two protodomains (as we shall see in Fig. 2 this is where most Ig domains vary depending of the length and shape of this linker, which presents some secondary structure in the case of IgV giving rise to CDR2). (c) 2D Topology/sequence map strand arrangement of protodomains corresponding to the 3D domain C2 symmetry with the formation of symmetry equivalent B< = >E and C< = >F strand-strand protodomain interface, bringing hairpins A|B and D|E in the same sheet (Sheet A or A|B||E|D) and correlatively bringing hairpins C|C′ and F|G in the same sheet (Sheet B or G|F||C|C′) facing each other as in a sandwich. A simple 3D rotation through a common axis gives a structural correspondence of the two protodomains A|B − C|C′ and D|E − F|G, with a structural alignment (see (d)) varying usually between 1 and 2A in the most distorted cases. The well-known CCW(L) pattern highlighted in yellow is mapped at the protodomain level in symmetrically equivalent positions (see also Fig. 3d). (d) 3D protodomain alignment for a CD8a domain (1CD8) that superimpose with an RMSD of 1.98 (see Fig. 4 for corresponding sequence alignment) showing only structurally aligned residues, with ribbon picture (produced by Chimera [90]) showing strand definitions. Protodomain 1 in blue and protodomain 2 in magenta. Domain visualization with Sheet A in front in the order A|B||E|D’. Link to iCn3D https://d55qc.app.goo.gl/bmCQRj7DWcmqsmna6

Fig. 2.

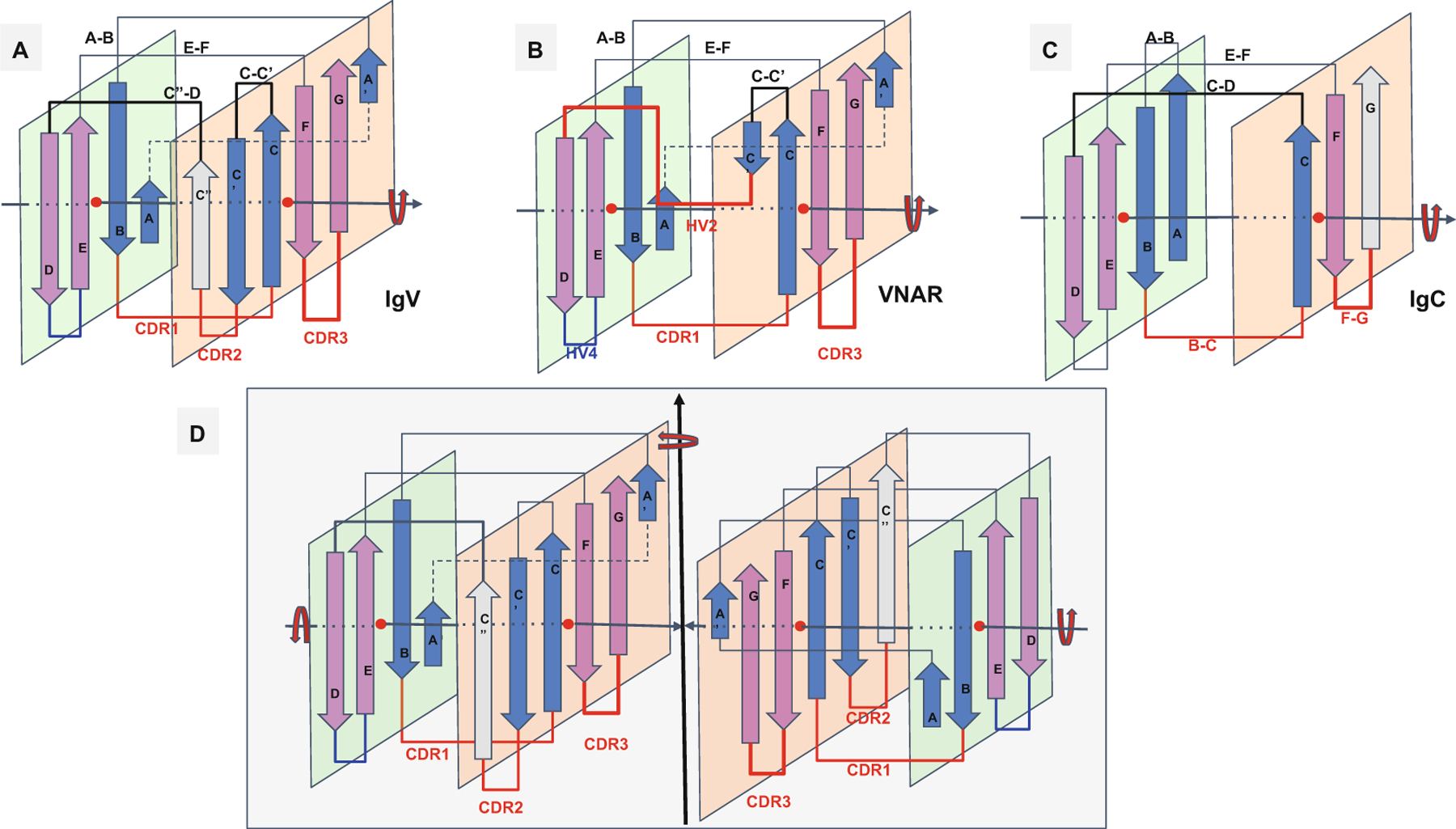
Ig domain topologies for IgV, Shark VNAR, and IgC. (a) In IgV domains, the A strand, with a flexible hinge in the middle, usually a cis-proline or a stretch of glycines, swaps the upper part of the strand from Sheet A to Sheet B in a parallel model. So-called domain swaps, which are most often SSE swaps among symmetric packing pairs of domains, are observed ubiquitously. Here we can refer to it as a protodomain (half-strand) swap by analogy. The linker between protodomains in this example of an IgV type domain forms a C′′ strand as an extension of Sheet B and the CDR2 loop between C′ and C′′, as well as a loop C′′-D bridging Sheet B back to Sheet A. (b) VNAR shows that same domain-level organization with two protodomains, yet a much smaller inter-protodomain linker, eliminating the linker’s supersecondary structure and the CDR2 loop. Instead, a short HV2 linker is observed. In the literature, C′ is usually included in the HV2 region, as it is very short. In addition, a hydrophilic set of residues on Sheet B, i.e., strands G|F||C|C′, facing out rather than hydrophobic in IgV, do not permit the formation of a symmetric dimer (as in D). This may also be due in part to the absence of an overall supersecondary structure of the linker in IgV (including C′), which may help patching an otherwise possibly semi-open eight-stranded barrel. (c) IgC. Here we consider only the IG C1-set, i.e., the antibody constant domain-like to exemplify an Ig constant domain protodomain connectivity. In this case the final domain is formed by a full four-stranded A|B||E|D Sheet A, with no half swapping of strand A, vs. a three-stranded G|F||C Sheet B, no C′ strand. Interestingly this enables C-domain-level dimerization through that four-stranded Sheet A as opposed the IgV dimer interface obtained through Sheet Bs, enabling a further helical level symmetric arrangements of chained Ig domains. When looking at an IgC protodomain alignment, only three strands are considered. (d) IgV dimer. In CD8aa, two IgV domains pack together symmetrically as homodimers through their Sheet B (G|F||C|C′) facing out form an eight-stranded semi-closed central barrel, with external strands C′ and G of two domains closing the central (quaternary) barrel symmetrically. In CD8ab, as in IgV light and heavy chain quaternary assembly, they pack pseudosymmetrically as heterodimers (see Figs. 3, 4, and S1). As the heterogeneity of domains increases, and even if a pseudosymmetry is maintained at the sheet level, packing, i.e., quaternary interface, becomes more asymmetric, and central barrels become open with an asymmetrical arrangement between “closing strands” C/G, resulting in at least one side of the central dimer barrel open. This is the case of a PD1-PDL1 pair (see Fig. 4)

Fig. 3.

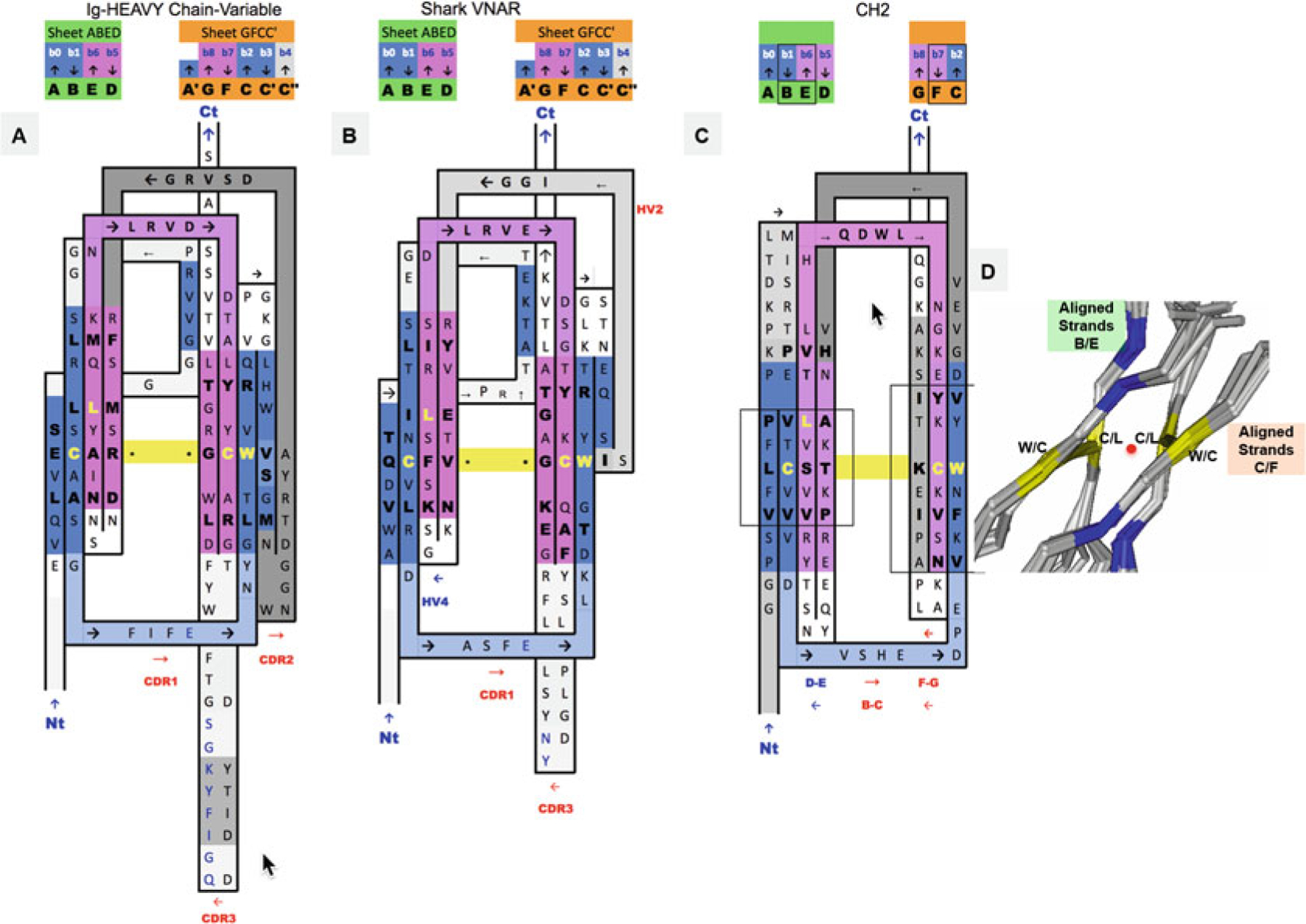
2D Sequence/topology maps of Ig domain topologies for IgV, Shark VNAR, and IgC. (a–c) Corresponding to schematic topology drawing in Fig. 2 for IgV, VNAR, and IgC, respectively: Topology/sequence map alignments based on 3D structure domain- and protodomain-level alignments of a Human Antibody Fab 5ESV (chain H, IgV domain), Shark VNAR 1VES, and an CH2 domain-isolated 3DJ9 and/or in an Fc chain context 4N0U (chain E). (d) Central strands B/E on Sheet A (A|B||E|D) and on Sheet B (G|F||C|C′). Protodomain 1 = A|B − C(C′)/Protodomain 2 = D|E − F(G). From 3D structure 2ATP (see Fig. 5) of CD8ab. The exact same pattern is observed here in IgV, VNAR, and IgC. These are four invariant residues (L can vary somewhat and be replaced by another hydrophobic residue). The cystine bridge flanked by a tryptophan is a well-known pattern that in fact exhibits pseudosymmetry with the residues in symmetry equivalent positions: C Cys (Strand B) ⇔ L Leu (Strand E) and W Trp (Strand C) ⇔ C Cys (Strand F). (d) Within a domain C/L on Sheet A central strands B/E and W/C on Sheet B central strands C/F occupy symmetry equivalent positions. The symmetry axis, perpendicular to the beta sheets A and B and the plane of the paper, is represented by a red dot. In symmetric dimers the two C2 domain axes coincide. These schematic maps are idealized showing vertical strands. The two sheets forming the central barrel are actually tilted vs. each other (relative rotation of one domain vs. the other around the common domain-dimer symmetry axis). This is true of any beta strand in any barrel

Fig. 4.

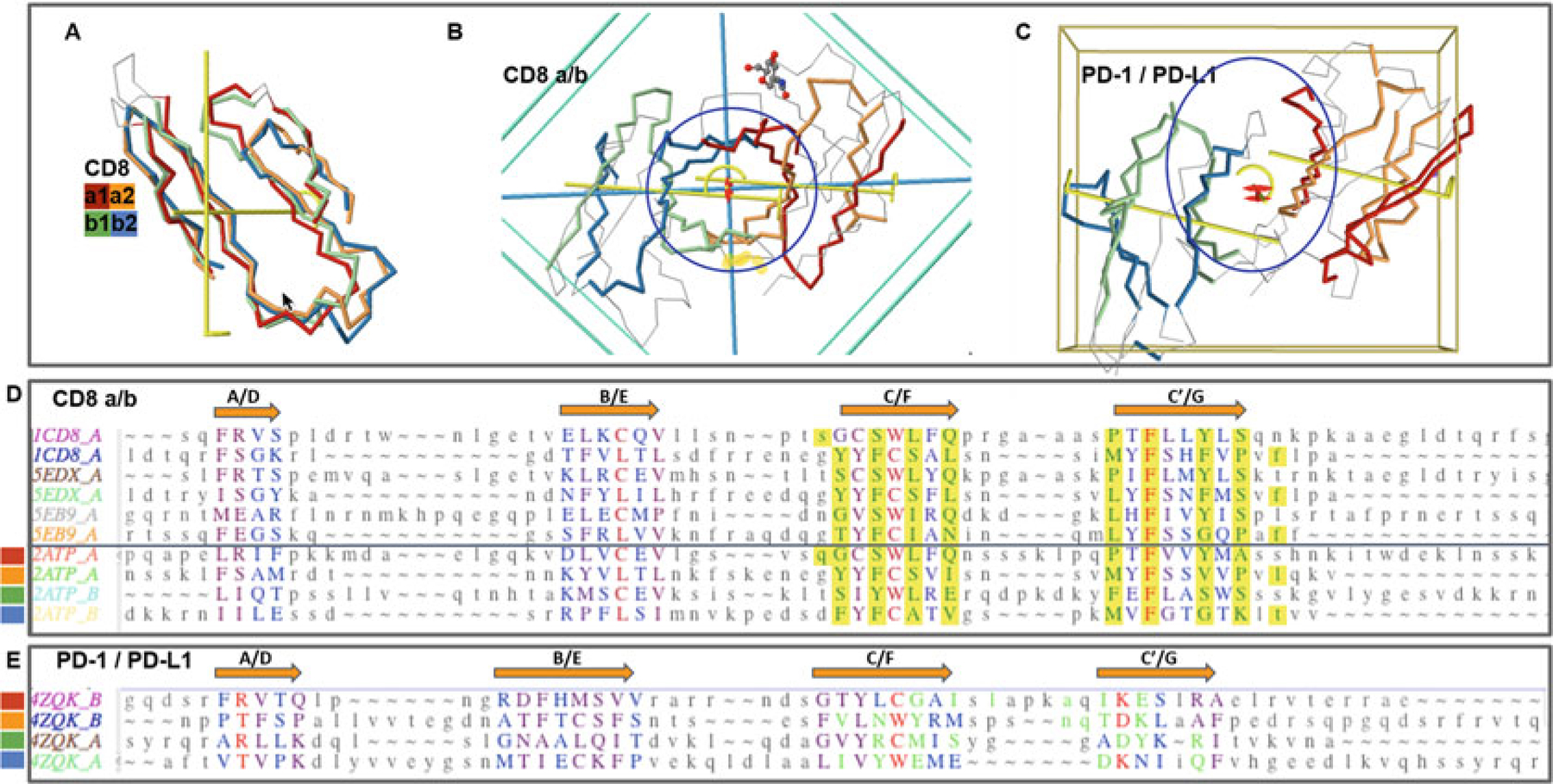
CD8ab and PD1/PDL1 heterodimers. Protodomains and quaternary symmetric arrangements. (a) CD8ab (structure of mouse CD8ab: 2ATP). Four protodomains aligned for CD8a and CD8b colored red/orange and green/blue, respectively. Automatic symmetry detection and protodomain alignment performed with CE-symm and displayed with JMol. Average RMS on protodomains as computed by CE-symm is 2.71. (b) CD8ab dimer with two orthogonal axes of symmetry: Two C2 levels of symmetry detected as overall D2 symmetry, meaning the two axes domain level and dimer level intersect in the center of symmetry, as for a CD8aa homodimer (see schematic representation in Fig. 2d). A small departure from perfect symmetry is observed between the actual domain-level yellow axes of symmetry vs. perfect orthogonality to the dimer axis, perpendicular to the plane of the paper. One can see a pseudosymmetric eight-stranded central barrel formed by the two faces of each monomer, from both sheets G|F||C|C′ facing each other (the symmetric homodimer CD8aa—structure 1CD8 is presented in Fig. S1 with an iCn3D Link). (c) PD-1/PD-L1 receptor ligand interface (structure of human PD1-PDL1: 4ZQK). Here we still have a pseudosymmetry for each domain, and for the heterodimer, the two external faces of the respective Sheet B of PD1 and PDL1 are shifted laterally relative to each other, to form the interface. We still have two C2 levels of symmetry but the domain-level axes to not cross with the dimer axis on the center of symmetry. There is still a C2 domain level of symmetry for each domain, and a dimer center and C2 axis of (pseudo) symmetry, but not a D2 symmetry. The average on automatic detection RMS is 3.38A. (d) Optimized structural alignment of protodomains of CD8a in the homodimer CD8aa (structures of CD8aa: Human 1CD8; Swine 5EDX; Chicken 5EB9) and the heterodimer CD8ab (structure of mouse CD8ab: 2ATP chains A and B, respectively). The RMSD for the optimized multiple domains/protodomains alignment for each first and second protodomain vs. the first Human CD8a protodomain are 1.61, 0.436, 1.71, 0.852, 1.57, 0.522, 1.95, 0.895, and 1.54 A, respectively. The computer-generated alignment is higher by 1–2A (this is usually the case). In this case it does a good job to match key symmetry equivalent residues, especially C/L and W/C. However accurate delineation and multiple structure alignment is only possible through interactive software Cn3D currently. Noticeable is the absolutely conserved F residue in strands C′ and G. Interface residues are contributed pseudosymmetrically as can be seen in the alignment for residues colored in green and highlighted in yellow, except for F colored red. (e) Optimized protodomain alignment of PD-1 and PD-L1 (structure 4ZQK chains B and A, respectively). In this case the automatic alignment is not as good as for CD8ab but is good enough to detect two levels of symmetry. The structural alignment optimized interactively gives a very good RMSD for the four protodomains with 1.73, 1.53, and 1.84 A, respectively, for the second PD-1 and the first and second PDL1 protodomains relative to the first PD-1 protodomain. Noticeable is a C/M match vs. a C/L match between protodomains of PD-1 vs. PD-L1. On the PD-1/PD-L1 interface, it is clearly not as symmetric as for CD8 as the barrel opens on one side vs. the other, with the relative shift of the domains external faces of Sheets B (G|F|C|C′) observed (see c vs. b)

Fig. 5.

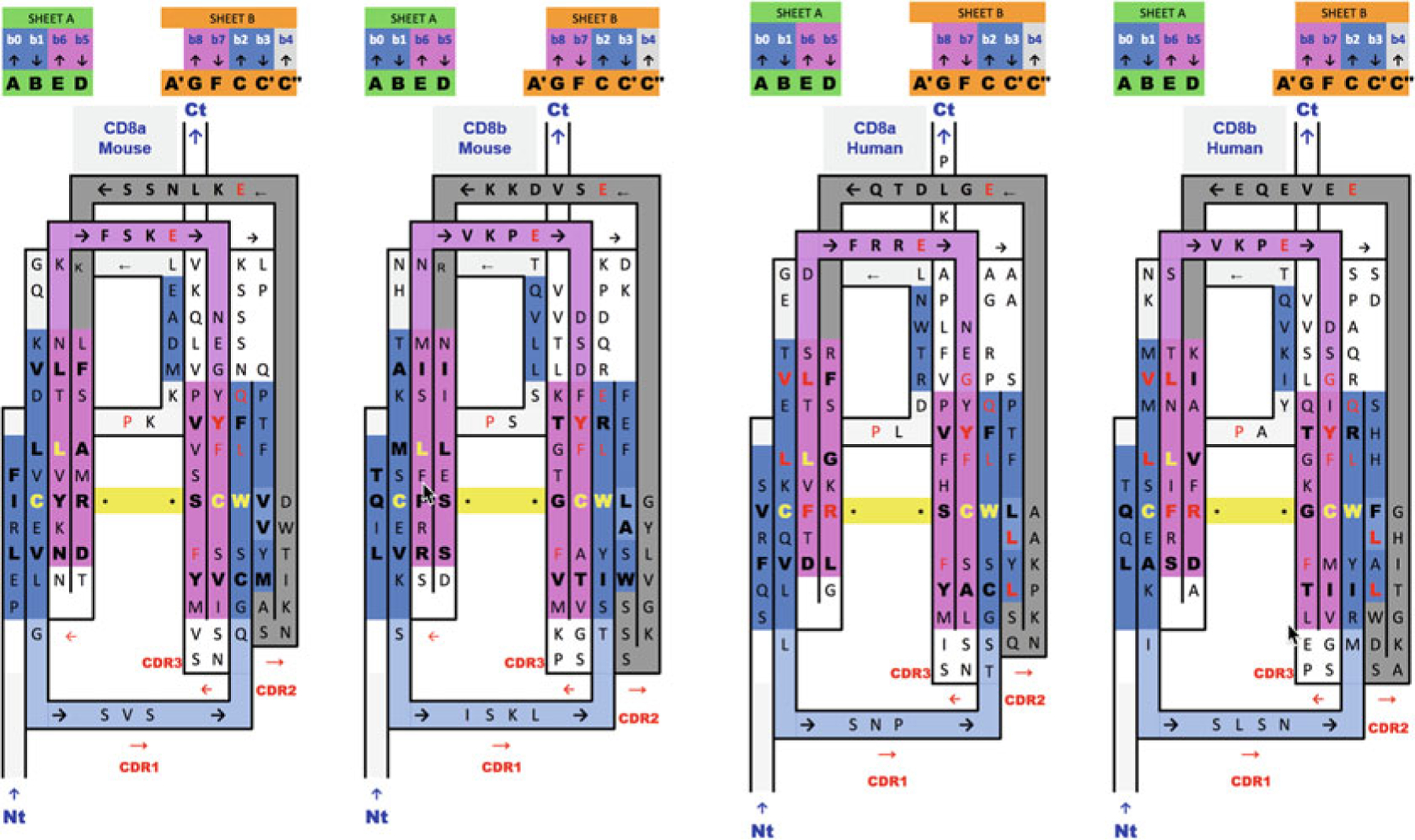
2D Sequence/topology maps and alignments of Ig domain heterodimers of human and mouse CD8ab. Sequence/topology map alignments based on 3D structure domain- and protodomain-level alignments of CD8a and CD8b in a mouse structure of CD8ab (2ATP) and a human structure of CD8a in a CD8aa homodimer context (1CD8) with a human sequence mapped onto the mouse structure. Corresponding protodomain structure-based sequence alignments are available in Fig. 4. Topology/sequence maps corresponding to schematic topology drawing in Fig. 2d

Fig. 6.

FN3 Ig domains. (a) Another Ig-fold variant, the FN3 superfamily, with the example of the cytokine-binding homology region (CHR) of the cell surface receptor gp130, the second FN3 domain proximal to the membrane surface. The inter-protodomain linker now connects C′–E through a Greek key loop bridging the two sheets, composed of A|B||E and G|F||C|C′. In this case, what would otherwise be a D strand in linking back to the C′ strand (Fig. 2), removing one strand from the other Sheet A (A|B||E(D)) rather than Sheet B (G|F||C(|C′)) as in IgC (see Figs. 2 and 3). The sequence patterns SxWS in strands C′ and G and R/QxR in strands C and F match symmetrically. (b) Structure-based protodomain sequence alignment for domain 2, followed by domain 1 and 2 together, respectively, where one can observe each domain idiosyncratic protodomain “internal conservation” sequence patterns (see text for details). In domain 2 residues S, Y, and R, SxWS are matched, while in domain 1, the pattern is totally different with residues C, D, N, and E. Only one residue S is common to three out of four protodomains, while a R vs. E in symmetrically equivalent strands C and F is observed consistently, a residue which is part of that C||F zipper (see text and Fig. S2). RMSD is 1.8A between domain 2 protodomains and 2.89A for domain 1, 2.2, and 2.5, respectively, vs. domain 2 protodomains (multiple alignment). (c) The symmetric sequence patterns matched in structure forming a cation-pi ladder W*R*W*R*W from both (W)SxWS, the so called WS motif (see text). (d) Structure alignment of the two protodomains matching Strands B-C|C′ and E-F|G that combine as (A|)B||E (Sheet A) and G|F||C|C′ on Sheet B, corresponding to the pairwise protodomain alignment of domain 2 (see sequence alignment in B) https://d55qc.app.goo.gl/DcmpiJy2CVmxtHKN2

Fig. 8.

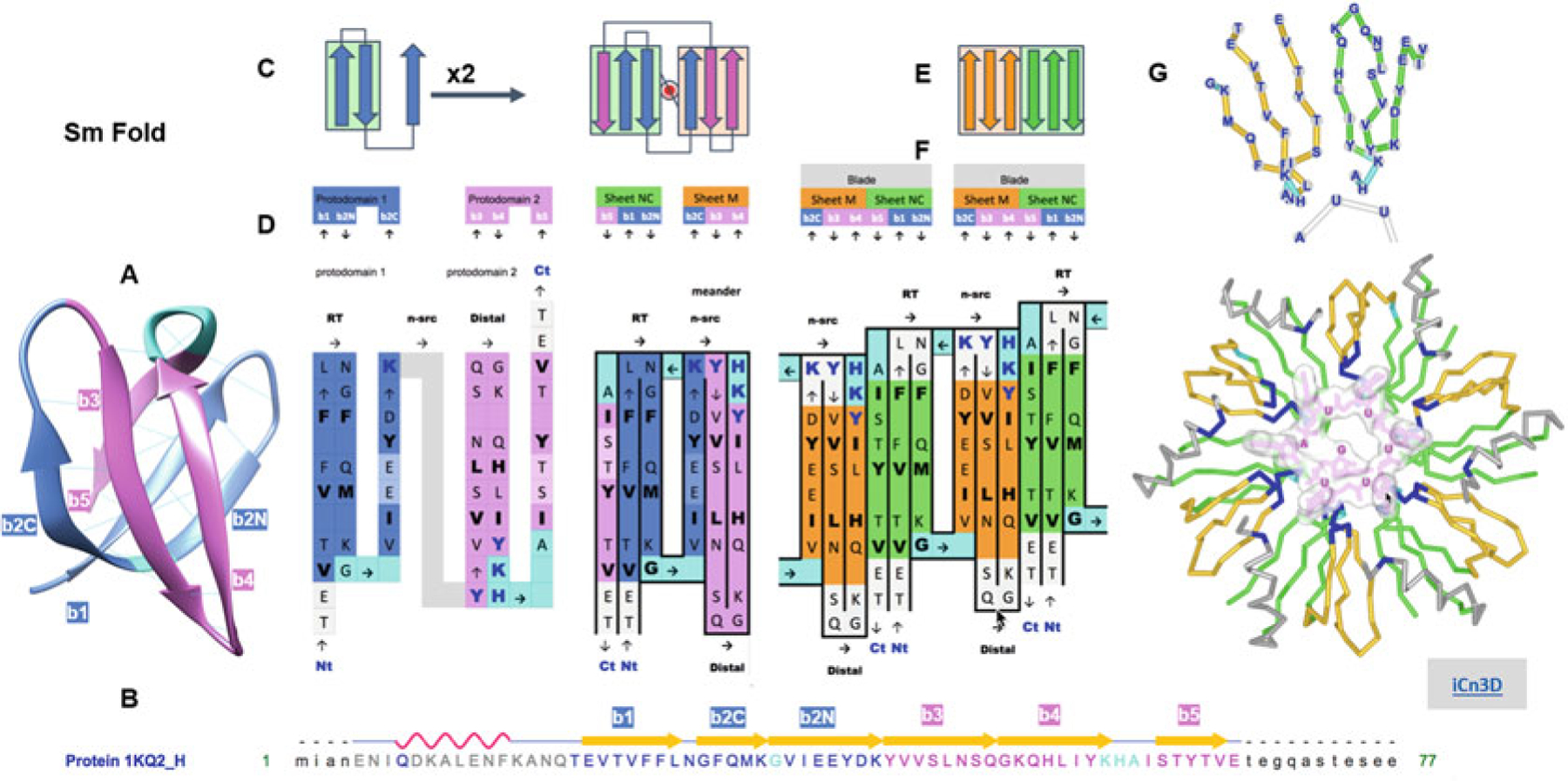
Complexity buildup through hierarchical symmetric arrangements of protodomains, domains, and oligomeric assemblies of the Sm fold (Hfq). (a) 3D structure of the bacterial Sm barrel (Hfq) (structure 1KQ2, N-terminal helix omitted for clarity). It is a small beta barrel with an SH3-like topology, usually considered as a five-stranded beta barrel (strands b1–b5). It is better represented as a six-membered barrel sandwich (splitting the long and sharply bent b2 strand in b2N and b2C at the Gly position, since b2N and b2C participate in two orthogonal sheets denoted either A and B or NC or M, as b1 and b5 N and C terminus come together in an antiparallel mode in the first sheet, vs. M a meander formed of b2C-b3-b4). Even a small barrel composed of 50 residues can exhibit C2 symmetry, bringing down to 20–25 residues the protodomain size with a bb-b topology formed by a hairpin b1|b2N-b2C. An SH3- topology, for SH3-like domains as for the Sm fold, is equivalent to short Greek key, with a simple Glycine in protodomain 1 and a 3–10 helix in protodomain 2 linking the two (orthogonal) sheets of the barrel. (b) Sequence and strand definition of an Hfq domain (1KQ2) with protodomain 1 in blue (res T20-K41) and protodomain 2 in magenta (res. Y42-E66). (c) 2D Schematic topology representation of protodomain and protodomain duplication with symmetric arrangement. (d) Sequence of two successive protodomains’ delineation and corresponding 2D topology/sequence map. Protodomain 1 in blue color, 2 in magenta. Linker residues G in protodomain 1 and YKHA (3–10 helix) in protodomain 2 are highlighted in cyan. Protodomains b1|b2N-b3 and b4|b5-b6 come together symmetrically with a b2C||b3 b5||b1 to form three-stranded Sheets A (green) and B (orange). Hydrophobic residues forming the core of the barrel are in bold black. RNA-binding residues are highlighted in dark-blue bold characters. (e) Schematic representation of the formation of a six-stranded blade from Sheet M (orange) and Sheet NC (green) of consecutive monomers. (f) “Quaternary” topology/sequence map of a dimer, with a b5||b4 quaternary interface. (g) A six-stranded blade representation in 3D labeled by sequence and the Hfq hexamer with RNA nucleotides binding at the interface between domains (RNA-binding residues highlighted in dark blue, as in (d)). All six strands can be considered calibrated with 5–6 residues (considering bulges, in the case of Sm in b2C and b5 symmetrically), so they form two calibrated three-stranded beta sheets that dock to form six-stranded blade, resulting in a six-bladed Hfq ring structure of C6 symmetry. A beautiful example of complexity buildup. Link to iCn3D: https://d55qc.app.goo.gl/pgk8GcZZNSs9KSMU6

2. Materials

For the analysis we need structural data, obtained by any structural biology method such as X-ray, NMR, or EM, and software tools to analyze them, i.e., dissect them, delineate SSEs and SSSs, and compare them in terms of sequence (1D), topology (2D), and structure (3D).

2.1. Structural Databases

2.1.1. The PDB (Protein Data Bank) and Derived Resources (NCBI Structure)

The main source of protein structure is the PDB, available through worldwide servers in the USA (PDB/RCSB), Europe (PDBe), and Japan (PDBj) [22, 32, 33]. Derived resources such as NCBI Structure (MMDB) integrate structural information with multiple databases on sequence-related information and evolutionary family classifications such as CDD [34] as well as offer structural comparisons (VAST+) across the entire PDB [35].

2.1.2. Structural Taxonomies

The two main structural classifications in use are SCOP [16, 17] and CATH [18]. More recently ECOD has been added [19]. SCOP is based on manual curation, while the others are automated. We use primarily SCOP in this work, yet the lack of automation is an issue in dealing with new structures.

2.2. Software

2.2.1. Interactive Protodomain Delineation and Symmetry Analysis

The main computational engine needed to detect structural symmetry is structural alignment software. There are numerous tools and servers to perform structural alignments automatically between protein domains. Most are not configured to enable protodomain analysis. While this was the norm in the early days, few programs today allow interactive multiple structure alignment of proteins at any level. Cn3D [36, 37] allows the retrieval of structural alignment from NCBI’s VAST+ alignment databases [35]. It allows interactive multiple structure alignment of domains, and, very importantly for our objective, one can superimpose a domain onto itself and hence delineate protodomains accurately.

2.2.2. Automatic Pseudosymmetry Detection Protodomain Delineation

Two recent programs perform symmetry analysis and enable domain-level pseudosymmetry detection: SYMD [38, 39] and CE-symm [1]. These programs will do a good job in most cases, yet they do not give exactly the same protodomain delineation. For a very accurate protodomain delineation, an interactive step using Cn3D may be the best final option, especially in complex cases (see later in Subheadings 3 and 4).

2.2.3. Structural Visualization and Analysis

iCn3D [40] is the new JavaScript viewer from NCBI available as open source (https://github.com/ncbi/icn3d). iCn3D (I-see-in-3D) allows interactive visualization but also structural analysis and comparisons of biological macromolecular assemblies and molecular interactions in a web browser using three levels of complexity 1D (sequence), 2D (topology/cartoon), and 3D (structure). Very importantly it allows scientists to exchange annotated visualizations, such as in figures hereafter (see web links on Figs. 1, 6, 8, 9, S1, S2, and S5).

Jmol [41], written in Java, is used for quaternary symmetry visualization on the RCSB web site [22] and is also used with CE-symm to visualize pseudosymmetries and multilevel symmetries combined, i.e., quaternary and tertiary. However, we should expect the use of JavaScript viewers. NGL [42] or iCn3D down the road for 3D visualization.

2.3. 2D Representations: Topology/Sequence Maps

There are a few programs that may be useful to represent graphically domain-level topologies (2D), in particular Pro-origami [43]. Such representations would benefit from using and depicting internal pseudosymmetry to identify the repeating and symmetrically organized supersecondary structures. It is not an easy task to represent 3D symmetry or pseudosymmetry in a 2D depiction for any pseudosymmetric domain with very diverse topologies. One solution is to use 2D templates, and this is what we will do, at least for the chosen beta structures used in this chapter (see Figs. 1, 3, 5, 6, and 8).

2D topological representations of protodomains and domains may also allow visualization of quaternary arrangements (see Figs. 8 and S4 for an example). Another interest of using such representations is the possibility of threading the sequence onto SSS depictions. For beta sheets one can represent lateral residue contacts due to H-bonding. Some further 3D structural information can also be mapped, by highlighting some key tertiary, quaternary, or ligand contacts, as well as any sequence conservation or mutations (see, e.g., Fig. S5). They also help visualize clustered sequence-topology patterns and allow a straightforward parallel topology/sequence alignment, where it may be easier to see patterns than in 3D, especially for non-experts. These representations could be considered to some extent 2½D. Future developments should aim at integrating such representations into existing visualization software to represent and use simultaneously 1D sequence, 2D topologies, and 3D structures [44] at any level of detail (residue, SSE, SSS/protodomain, domain, chain, multidomain assemblies). We use topological representations of SSSs to describe supersecondary structures and their pseudosymmetric arrangements. (Note that as there are four ways to represent symmetrically organized sheets on a flat surface in terms of their order, we have chosen one in Ig domains: ABED for Sheet A and GFCC’ for Sheet B; see Figs. 1, 2, and 3.)

3. Methods

3.1. Learning by Example: Selecting Structures

At this stage a structural analysis through pseudosymmetry is still more an art than a science, but with practice, we learn. Also, analytic software tools are still in their infancy and not integrated. Each step requires a tool and some tools are not automated. So, we will approach learning through practical examples.

While pseudosymmetry is found in all classes of protein structures (see Table 1), beta structures offer more examples than any other class. Beta protodomains are easier to delineate accurately than alpha or alpha-beta structures (see Notes). They offer splendid examples of complexity buildup through symmetric arrangements of supersecondary structures at both the tertiary and quaternary level. We will use examples of well-known protein domains with underrecognized (Ig) or unrecognized (Sm) tertiary pseudosymmetry despite their importance.

3.1.1. The Immunoglobulin Fold: Tertiary and Quaternary Structure Analysis

We will analyze the immunoglobulin fold (Ig fold). Although the quaternary symmetry of immunoglobulins is very well known [5], the pseudosymmetry of the Ig domain itself, which had been noticed early on even at the sequence level [13], has not been systematically analyzed or used in protein engineering to the extent possible. Also, despite the various immunoglobulin types with a different number of strands, the variable and constant domains, all exhibit pseudosymmetry. A protodomain decomposition can highlight pseudosymmetry, as well as the various loops in that context, especially Complementarity Determining Regions (CDRs) in the case of immunoglobulins. The E form shows more irregularities in matching protodomains however. We will not discuss all types, as it is beyond the scope of this chapter.

The immunoglobulin fold (SCOP b.1), beyond the immunoglobulin family itself (b.1.1), is ubiquitous. It is the most functionally diverse beta sandwich barrel fold with 28 distinct superfamilies (in SCOP 1.75). A newer taxonomies such as ECOD regroups even more superfamilies such as P53, even when classified as different folds in SCOP (b.2). From a pseudosymmetry standpoint, P53 offers a parallel to immunoglobulins, yet it is a more complex domain (Fig. S5). In the immune system, a majority of cell surface proteins are composed of Ig domains, and many such domains are involved in checkpoints: PD-1–PD-L1, for example, are not only each composed of Ig domains, they interact together as receptor ligand (see Fig. 4). The study of Ig interfaces in terms of supersecondary structures can offer valuable structural insights in the design of checkpoint blockade therapies.

Given the enormous interest in using immunoglobulins as Fabs, Fvs, or single domains to target antigens as in CARs, checkpoint blockade inhibitors, or multispecific antibodies, we’ll focus mainly on the Ig fold, as an example of both protodomain and domain-level interactions. As mentioned above, the Ig fold is shared by 28 superfamilies, of which immunoglobulins are one. The method of deconstruction and analysis of protein domains in supersecondary structures to analyze them and the families within should be useful for numerous folds and superfamily variants. We will explore, for example, the FN3 domain (SCOP b.1.2), an interesting variant of the Ig fold (Figs. 6 and S2).

3.1.2. The Sm Fold and Hierarchical Complexity Buildup Through Symmetric Arrangements

Complexity can build up through oligomerization. In beta structures not only nonbonded interactions but also beta sheet formation in either parallel or antiparallel represents a very clever self-assembly mechanism. Sm-like oligomers assemble through that mechanism, mostly as homo-hexamers in bacteria, homo-heptamers in archaea, and hetero-heptamers in eukaryotes. There are additional variants of 3-, 5-, and 8-mers [45] (the 3-mer formation is somewhat different breed, yet it still exemplifies a symmetric assembly of beta sheets). We shall briefly describe the hierarchical assembly of bacterial Sm (Hfq) hexamers (SCOP b.38; Figs. 8, S3, and S4). Many doughnut-like oligomers possess multilevel symmetries in terms of protodomains, domains, and larger quaternary structure. This is a prototypic example [46].

3.1.3. Helical Protodomains: Sweets and GPCRs

Many membrane proteins exhibit pseudosymmetry (Table 1), and two thirds of known membrane protein structures are helical. We shall briefly look at a couple of 7-transmembrane helical proteins and compare eukaryotic Sweet vs. bacterial Semisweet proteins in a pseudosymmetric tertiary arrangement vs. a quaternary dimeric arrangement, respectively. We will make a parallel with another very important structural family: GPCRs (SCOP f.13) (Fig. 7).

3.1.4. RNA Protodomains: Riboswitches

As mentioned before, proteins are not the only biological macromolecules exhibiting symmetry at either the quaternary or tertiary level. RNA riboswitches provide magnificent examples [28], and we shall look at one example of RNA protodomains [47] (see Fig. 9).

3.2. Pseudosymmetry Protodomain Analysis (PSPA) Method

The method is pretty straightforward. It involves two initial steps, symmetry detection and protodomain delineation, followed by as many analysis steps as one wishes to perform.

Symmetry detection gives the symmetry point group and a first delineation of protodomains. Both tertiary and quaternary structural symmetries can be determined at the same time.

A second step is usually required to optimize protodomain boundaries and structural alignment for an accurate protodomain delineation. A third obvious step is to analyze 1D sequence patterns resulting from the 3D structural alignment of protodomains. From there one can branch into a deeper structural analysis and understand self-complementarity of secondary structure elements. This is where a 2D sequence-topology analysis, as well as a 3D structural analysis helps, bringing together sequence conservation, symmetry, folding, and possibly function (for example, in cases where ligand binding may involve residues in symmetry-related positions in protodomains). Beyond, this may open perspectives for deeper evolutionary analyses. We will analyze a set of examples and summarize results in Figs. 1, 2, 3, 4, 5, 6, 7, 8, and 9. They should be self-explanatory, as we will present geometrical properties in simplified schematic representations and alignments. We will make use of 2D topology/sequence maps for the beta structures analyzed (Figs. 1, 2, 3, 4, 5, and 6).

3.2.1. Symmetry Detection

In many cases, recently developed computer programs allow the detection of internal pseudosymmetry in tertiary structure [1, 38]. We use the program CE-symm to that effect. A newer version of the software allows quaternary symmetry analysis of multidomain complexes at the same time (https://github.com/rcsb/symmetry), and we will see an example in Fig. 4. There are cases however where one has to revert to interactive alignment software to align a domain onto itself. We will see such a case with GPCRs (Fig. 7) and the Sm fold (Fig. 8). In all cases we optimize protodomain delineation through interactive alignments for accuracy.

3.2.2. Protodomain Delineation: Optimization Through Structural Alignment

Protodomain alignment may highlight key residues that may be internally conserved for a structural reason (folding/assembly) or for a functional reason. In most cases, the degree of overall internal conservation is low. This is a hallmark of many pseudosymmetric domains, unlike most domain/family level sequence-structure conservation, except for some clear duplication cases where protodomain homology between protodomains may be as high as 40% [48]. In such cases duplicated “protodomains” tend to have a larger size and can be considered fused domains. The low level of “internal conservation” observed however is most likely due to a long protodomain-protodomain coevolution within each and every protein domain but also at quaternary interfaces. In order to call internally conserved residues, an accurate structural alignment of the protodomain is required.

Using pseudosymmetry provides a framework for structural analysis. It allows a deconstruction of protein domains in well-defined parts that may also lead into evolutionary and/or functional analysis. The reconstruction of a domain from parts leads into a coevolutionary analysis of the parts and their interfaces and in the understanding of molecular self-assembly. This opens perspectives in developing the analysis method further in that direction. We will focus essentially on structural and topological analysis in this chapter: delineating supersecondary structures (SSS) related by symmetry and highlighting self-complementarity of interfacing SSEs, as is the case in symmetry equivalent strands (B|E) and (C|F) in immunoglobulins (Figs. 1, 2, and 3), for example.

3.2.3. Sequence Analysis: Based on Protodomain Structure Alignment

The structural alignment of protodomains naturally highlights “internally conserved” residues, i.e., identical residues at symmetrically equivalent positions. These can point to a possible original protogene duplication if the degree of conservation/sequence homology is high enough to call such a duplication. A point group symmetry operation between two or more entities establishes a structural equivalence relation between these entities. Two residues or sets of residues related by pseudosymmetry in equivalent positions can be analyzed in terms of conservation (identity, similarity or lack of) as for domains. However, “internal conservation” may or may not be as significant as in domain comparisons, as each and every domain had its own evolutionary history and each and every protodomain within had its own coevolutionary history with symmetrically related protodomains. Sometimes it may be best to talk about coincidence rather than conservation, unless a pattern appears on more than two protodomains, and/or that same pattern is observed across multiple homologous domains for their respective protodomain alignments. Nevertheless, analyzing a pattern is usually fruitful, even if the pattern belongs to that domain alone. In which case it may be functional (see Fig. 6 for the example of a FN3 domain).

Also, one may have different residues in symmetry-related positions that are conserved as residue pairs across domains of a given family or superfamily. This is the case of the symmetrically related W/C and C/L residue pairs in immunoglobulin domains (see Figs. 2 and 3). In such case we may have a coevolved pair conservation. This pattern is easy to see. There are coevolved pairs in many pseudosymmetric domains that would benefit from AI software to identify such patterns, as we are not used or trained to capture such patterns, but this is something a symmetric decomposition of domains in protodomains may help us identify. An interesting example can be found in decomposing an FN3 domain (SCOP b.1.2) for type I cytokine receptors (gp130/IL-6R, IL-2R, IL-21R, GHR, etc.) (see Figs. 6 and S2).

There are also cases where one has to shift the sequence by 1–2 residues in beta or 3–5 in alpha helical protodomains to identify matching sequence patterns, as sequence may shift on structure during domain evolution. This adds a level of difficulty in the identification of matching residues and patterns.

3.2.4. 2D Topology/Sequence Analysis

Having delineated and aligned protodomains structurally, and eventually observing some sequence patterns of internally conserved residues between them one, one can analyze the sequence relations in 2D and 3D and protodomain-protodomain interfaces specifically.

Internal residue conservation is usually highly idiosyncratic, and for two families sharing a fold or even for two different domains within a family, these may not be the same (Figs. 6 and S2). This points to a fact that each domain has its own internal protodomain coevolution history, and internally conserved residues may not be analyzed along the same line as in conservation studies across family or superfamily members. We need to depart from the usual sequence conservation patterns to some extent. It is both an evolution and a coevolution analysis. When looked in the 3D context, or simply in the 2D topological context, sequence conservation patterns and their structural or functional meaning may start to emerge.

Using 2D Topology/Sequence Maps

2D topology/sequence maps are very useful in analyzing sequence patterns in a topological context. In Fig. 1, we represent a topological representation of an Ig protodomain, itself a set of two beta hairpins (A|B)-(C|C′), connected by a Greek key linker [B-C], which duplicates as (D|E)-(F|G) connected by a Greek key linker [E-F], using the usual Ig nomenclature of strand names. The two protodomains assemble symmetrically.

Figure 2 shows variants of the immunoglobulin domain, the variable domain IgV, the constant domain IgC, and also the shark variable domain VNAR, for comparison. Following a general beta sheet H-bonding (lateral) association pattern, in antiparallel, each of the hairpins associates with its duplicate in a symmetric fashion with the symmetry-related strands (B|E) and (C|F) coming together. The IgV or other Ig domain variants have been described in great detail, yet a protodomain decomposition allows us to see Ig domain variants with a fresh look, bringing them within the same framework, varying essentially the inter-protodomain linker.

• In IgV the linker has some hypervariable sequence with some secondary structure: it forms a CDR2 loop from the C′ strand to an additional C′′ strand and a [C′′-D] loop to bridge back with the Sheet A (A|B||E|D).

• In shark immunoglobulins (IgNAR) [49–51], the variable domain VNAR has a shorter hypervariable region linker [C′-D], named HV2 between a smaller C′ strand bridging Sheet B (G|F||C|C′) back to Sheet A (A|B||E|D), no CDR2, no C′′.

• In IgC, what would otherwise be the C′ strand serves directly as a connector between the two sheets, as if the duplication did not evolve any linker. Figure 3 compares topology/sequence maps for IgV, VNAR, and IgC.

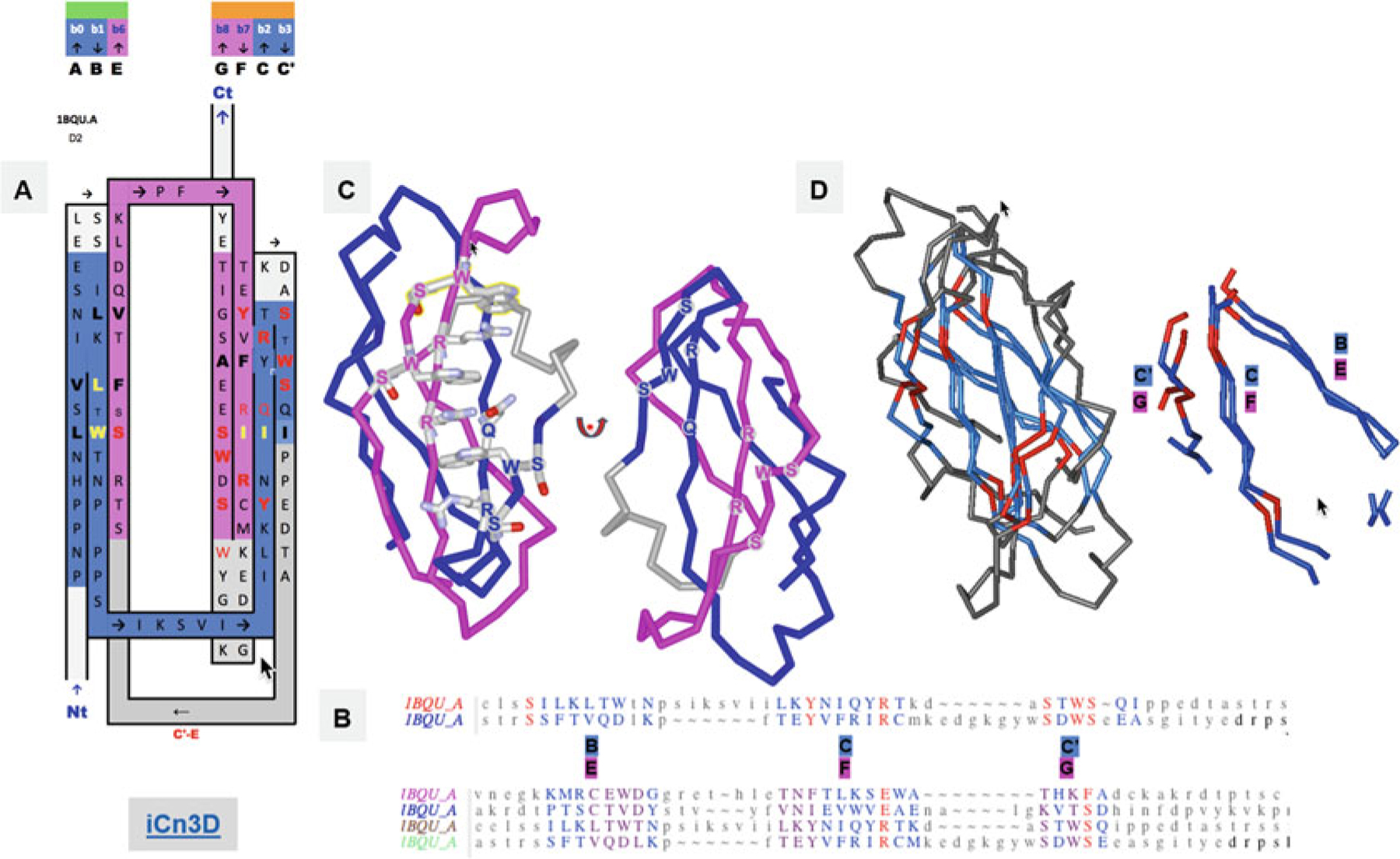
• FN3 is another variant of the Ig fold (SCOP b.1.2). In a similar way to the IgC domain, a strand, this time D on Sheet A as opposed to C′ in Sheet B, is removed to serve as a linker. The linker now connects C′–E through a Greek key loop bridging the two sheets. Sheet A is composed of (A|B||E) and Sheet B is composed of (G|F||C|C′). We use the cytokine-binding homology region (CHR) of the cell surface receptor gp130 (interleukin 6 receptor) as an example (Fig. 6) and the homologous growth hormone receptor (GHR) (Fig. S2).

Sheets A and B are consistently shown in figures with a green and orange background color, respectively, while we use blue and magenta for consecutive protodomains, respectively. In protodomain analysis the emphasis is put on sheets facing in, i.e., facing each other to form a domain core, i.e., a protodomain interface; hence we represent the in-facing (domain core) residues in bold. Naturally those in between, not in bold, are facing out (on the strand edging the barrel, especially C′′ in/out may not be relevant). Residues facing out in Sheet B (G|F||C|C′) form the quaternary interface between IgV domains (Figs. 2, 3, and 4). That interface is in itself a central barrel in homodimers, as well as in heterodimers such as CD8ab (Fig. 4). In IgC quaternary interfaces (not shown) are formed by the external faces of Sheets A (A|B||E|D) (Figs. 2 and 3).

Beyond 1D sequence patterns, in aligning topology/sequence maps, we can find 2D sequence patterns, as residues cluster in beta sheets. The well-known CCW conserved pattern (a disulfide bridge flanked by a Trp) is easy to spot, to which one could add a hydrophobic fourth residue, in most cases L, as highlighted through the symmetry operation (see Fig. 3d). In the case of Immunoglobulin domains another interesting pattern in Sheet G|F||C(|C′) is, a transversal 2D “T-Y-R motif” Threonine, tYrosine, aRginine. In CD8a, only the Tyrosine (two residues upstream from the Cys residue in strand F, is absolutely conserved, in CD8b however the full motif is there (see Figs. 1, 3 and 5). These 2D depictions give us a general topology/sequence map of the domains. A number for each residue, such as Kabat or IMGT reference numbering, can be used to pinpoint side residue lateral contacts in beta sheets [52–54].

3.2.5. 2D/3D Protodomain Interface Analysis

Once protodomains are delineated and their topologies mapped, one should look at how symmetry-related SSEs pack together to form an interface. Are symmetrically equivalent SSEs interacting directly? How, in particular, are the protodomain interfaces formed in terms of their individual SSEs? This will bring insightful information on self-assembly and domain formation itself. In terms of interactions between SSEs, are they backbone vs. side-chain packing level? The former of course is for beta or mixed alpha-beta structures. A backbone level assembly of SSSEs through hydrogen bonding is a hallmark of beta strands interactions in forming hairpins and sheets, while nonbonded (side chains) interactions is a general mechanism common to both beta strands and alpha helical SSSEs. We will see both types of examples in important beta folds: Ig (Figs. 1, 2, 3, 4, 5, and 6), Sm (Fig. 7), and alpha folds GPCRs (Fig. 8). Beta folds provide both packing mechanisms; this may be one reason why beta structure architectures exhibit a higher level of pseudosymmetry overall than other classes (Table 1). Inter-protodomain interfaces together with inter-domain quaternary interfaces may allow an interesting decoding of biological units’ complexity buildup (see examples in Figs. 4 and 8).

3.2.6. 3D Structure-Function Analysis

Local Sequence Pattern Matching from Structural Protodomain Alignment

Sequence patterns obtained from protodomain alignments are idiosyncratic. One should look where “internally conserved” residues are located in 3D, in a domain (facing in) or at a quaternary interface (facing out). A structural alignment between protodomains creates a correspondence, a mapping, and an equivalence in 3D positions. It may have some significance from a folding, assembly, or functional point of view. It may also be a coincidence in a unique evolutionary process of a domain.

Let’s take the example of the gp130 cytokine-binding homology region (CHR), a type I cytokine receptor, composed of two FN3 domains (structure PDBid: 1BQU). The 3D structural alignment of protodomains (Fig. 6) shows an internal conservation in the second FN3 domain, proximal to the membrane, where C|C′ and F|G hairpins are self-complementing each other symmetrically. A “conserved” pattern emerges. The structure exhibits not one but two (W)SxSW patterns in the external strands C′ and G, placed symmetrically. We observe that these aromatic residues are part of an extended cation-π ladder W-R-W-R-W-R, where the arginine residues R are positioned symmetrically in the central strands C and F. The structure-based sequence alignment (Figs. 6 and S2) shows a longer conservation pattern with QyR in strand C< = > RxR in strand F at the domain family level as well as at the protodomain level for each domain. These symmetric patterns across the entire Sheet B (GFCC′) can be seen in the 2D topology/sequence maps (Figs. 6 and S2). One can now analyze the structural self-complementarity that may be linked to folding and function, most likely a combination of both. The sequence alignment of strands C and F highlights what we could call an antiparallel hydrophilic beta zipper, with hydrophilic/charged residues matching (in orange in figures).

The WSxWS motif, also called the WS motif, is well-known and has been actively investigated, but it is still enigmatic. In the case of the IL-21 receptor, it has been linked to sugar binding [55, 56]. It is conserved in the family in protodomain 2. The symmetry-related pattern SxWS in protodomain 1 however is not as conserved. W is conserved in IL-2R, but not in IL-21R. The central zipper however, with the QyR-RxR pattern, seems more conserved. If we now look at a more distantly related protein, the growth hormone receptor (GHR), the central strands C|F form an extended hydrophilic zipper conserving the pattern as QyK-RxK (Fig. S2). The WS motif is now replaced by YGEFS [56, 57], while in the symmetrically related motif WK-MM in protodomain 2 conserves W. The aromatic residues Y,F and W from strands G and C, respectively, intercalate to form an extended cation-pi ladder with the central R and K residues. In GHR, Y and F are structurally equivalent to the two W in protodomain 2 of CHR (see Fig. S2).

We have here an example where protodomain sequence conservation patterns vs. family/superfamily patterns can help identify some structural and functional residues, and coevolutive pairs, without overinterpreting what internal conservation patterns may mean.

Ligand Binding

Many membrane proteins exhibit pseudosymmetry (Table 1). This has been reviewed extensively [58, 59]. Two thirds of known membrane protein structures are helical. 7-transmembrane helical proteins give examples of alpha folds exhibiting pseudosymmetry. In the case of 7-TMH eukaryotic Sweet proteins, we can compare protodomains to 3-TMH bacterial SemiSweet monomers directly, and the 7-TMH whole domain to the SemiSweet (2×3TMH) dimer, in structure and in ligand-binding function (Fig. 7). This pseudosymmetric tertiary arrangement matching a quaternary dimeric arrangement points to a possible duplication-fusion at the origin of the pseudosymmetric 7-TMH [60, 61].

We will make a parallel with another very important structural family: GPCRs (SCOP f.13). Although Rhodopsin pseudosymmetry has been detected anecdotally in the literature [62], no current symmetry detection program [1, 38] can detect GPCR pseudosymmetry systematically. While we now have over 100 GPCR structures in the PDB database, pseudosymmetry is detected for a handful of GPCRs using symmetry detection software that often requires stringent matching criteria for protodomain delineation (see Notes). Rhodopsin, a GPCR Class A, or Metabotropic Glutamate Receptor 1, a GPCR Class C for which structures are available (PDBids: 1F88; 4OR2, respectively) [63–66], are cases where one can detect a pseudosymmetry with a stringent criterion. Otherwise, only careful manual structural alignments can lead to a solid pseudosymmetry analysis. A protodomain alignment of a Class C GPCR is presented in Fig. 7.

In Sweet, one can observe the ligand lying on the axis of symmetry. One can observe some residues in symmetrically equivalent positions binding the ligand (Fig. 7) in TM3/TM7, N in the internally conserved NG(L/I)G pattern, and the structurally aligned TM3 of the semisweet protein, with a matching pattern NCLG. In GPCR Class A we find multiple instances of such patterns in TM3/TM7. The pattern is always idiosyncratic, and this is consistent with ligand-binding specificity. (Note that the topology of Sweet and GPCR protodomains is different. TM3 is in a different position, with a 132 topology in Sweet vs. 123 in GPCRs. See Fig. 7) The ligand has usually a fragment lying on the axis of symmetry with TM3/TM7 anchor residues offering a pseudosymmetric structural arrangement, but also an intriguing sequence pattern, always different across different GPCRs. In the chosen example, in Class C, while there is an offset between the ligand and the axis of symmetry, the binding region of TM3/7 offers a sequence pattern VxLS with surrounding residues providing binding. The same is true in Retinal, for example, with a matching FFA(K/T) pattern between TM3 and TM7 preceding the anchor Lysine residue to Retinal. We have performed systematic multiple alignments on known GPCR structures, and one can find recurrent patterns of matching residue pairs and ligand-binding positions around in structurally matching TM3/TM7 in each structure independently [67].

3.2.7. Multilevel Symmetries: Complexity Buildup and “Quaternary Topologies”

Inter-protodomain interfaces together with inter-domain quaternary interfaces may allow an interesting decoding of functional biological units’ complexity buildup. In Fig. 4, we can see how domain-level symmetry and dimer symmetry can produce a pseudo-D2 overall symmetry, reflected in the eight-stranded central beta barrel composed of 4 hairpins (2* G|F||C|C′) (see Figs. 2 and 4).

Another example of higher symmetry buildup with a domain level and a quaternary structure symmetry can be found in the Sm fold. In Fig. 8 we represent Hfq, the bacterial Sm hexamer. The Sm barrel is a small beta barrel (SBB) of SH3-like topology, usually considered as a five-stranded beta barrel, but it is better represented as a six-membered barrel sandwich with a highly bent central strand (that we split in two) that bridges two orthogonal sheets of the barrel. Even a small barrel composed of ca. 50 residues can exhibit C2 symmetry, bringing down to 20–25 residues the protodomain size with a b|b-b topology formed by a hairpin and a third strand connected with either a simple glycine or a 3–10 helix (the protodomain alignment is available in Fig. S3). Both result in bridging the two beta sheets of the small barrel sandwich, in a similar way that Greek key loops bridge the sheets of an Ig barrel.

A three-stranded Sheet B of a monomer can then dock laterally with a three-stranded Sheet A of another monomer to form a six-stranded antiparallel sheet (blade) and so on in building a six-bladed doughnut-shaped ring hexamer. Sm-like oligomers assemble through their b4–b5 strands as homo-hexamers in bacteria, homo-heptamers in archaea, and hetero-heptamers in eukaryotes. We can use 2D topology/sequence maps to represent a domain but also the formation of a larger hexamer (Figs. 8 and S4).

3.2.8. RNA Protodomains

Finally, proteins are not the only biological macromolecules to exhibit pseudosymmetry or as a matter of fact secondary structure. We mentioned the proto-ribosome but also riboswitches that offer splendid examples of pseudosymmetry. This has been reviewed elsewhere [28]. In Fig. 9 we show a riboswitch “protodomain” decomposition [47], which also presents a symmetric ligand-binding pattern.

The symmetry detection was performed directly with CE-symm [1] (https://github.com/rcsb/symmetry), as it can operate on proteins, RNA, and DNA.

4. Notes

4.1. Pseudosymmetry Is Found by a Computer Program, Yet Protodomains Exact Delineation and Alignment Need Some Refinement

The two programs that detect pseudosymmetries [1, 38, 39] offer examples where one can find a symmetry with one and not the other. Hence users tend to use both to identify symmetry and protodomains. The latter will vary slightly when symmetry is found by both. This is common. Computer programs use different algorithms, and scientists tend to use a consensus approach by using more than one program for asserting a result or making sure nothing may be missed [68, 69]. However, although programs have become better to delineate protodomains, there are (many) cases when pseudosymmetry is found but needs refinement in structure alignment, and depending on the goal of such alignment, one may also introduce some shifts in sequence (by 1–2 amino acids eventually in a SSE). Programs may be used with various parameters, but by experience, if one is trying to get at the most accurate structural alignment, manual alignment has no substitute. It is a well-known phenomenon of pattern recognition from a human eye. Even if a structural alignment gets a very good match, if one is interested in sequence conservation among protodomains, this can be optimized starting from a structure-based protodomain delineation, and sometimes a shift by one or two residues could reveal an internally conserved sequence pattern in helical systems (in helical systems, a structural alignment can be shifted up to 4–5 residues without significant change in RMSD. This corresponds to a helix turn shift along a helix axis. Patterns such as in Fig. 7 for GPCRs are an example). Whether that pattern is meaningful or not will necessitate deeper analysis.

4.2. Pseudosymmetry Is Not Identified by a Computer Program

Naturally, even if 20% of domains may possess pseudosymmetry, and even if this number may be conservative, as it was determined using one representative per superfamily, the majority of individual protein domains do not exhibit pseudosymmetry. Hence if one does not identify symmetry, there are chances it is a correct assessment by the program. It can however be frustrating to miss pseudosymmetry if it is not detected. The problem with non-detection of symmetry may be linked to different factors, when symmetry should be identified: programs use numerical cutoffs on all sorts for internal parameters. On the other hand, and it is often the case, structure quality varies, as well offer some conformational variability. If symmetry is not detected on one structure, it may be detected on a homologous one for a given set of default parameters. So, one may use alternative structures. Also, some parameters can be adjusted from default values, and sometimes this can be an iterative process, depending on the candidate structure analyzed. A very useful parameter to adjust in CE-symm, for example, is the maximum RMSD between symmetry-related protodomains (-maxrmsd), which can be made stringent (ca. 2A RMS for beta folds and 3–3.5A in alpha, but these can be varied by increments to seek a significant alignment). This will lead to protodomain delineation that may be shorter in aligned length but with more accurate structural alignments. In some cases, this can give as good results as manual alignments.

4.3. Checking a Pseudosymmetry Interactive Alignment

If residues are aligned, their symmetry-transformed images must be aligned. Even if dual alignments of protodomain 1 on 2 (i and j in general) and vice versa simultaneously cannot be performed by a program such as Cn3D during interactive alignment, one can check this reciprocal match visually during an interactive alignment with a simple equivalence rule (see Fig. S3 in the example of the Sm fold):

• If Res. i (domain) ⇔ Res. j (domain copy) then Res. j (domain) ⇔ Res. i (domain copy)

4.4. Helical Protein Structural Alignment and 7TM GPCR Fold (f.13)

Membrane proteins are classified as a separate class within SCOP (Class F) regardless of their secondary structure makeup. They show a higher pseudosymmetry rate than other structural classes of globular proteins, apart from all beta structures (Class B). This has been widely reviewed [58]. Although Rhodopsin pseudosymmetry has been detected anecdotally in the literature [62], no current symmetry detection program [1, 38] can detect GPCR pseudosymmetry systematically. While we now have over 100 GPCR structures in the PDB database, pseudosymmetry is detected for a handful of GPCRs by the CE-symm software that often require stringent matching criteria for protodomains (see above). Rhodopsin, a Class A GPCR, or the Metabotropic Glutamate Receptor 1, a Class C GPCRs, for which structures are available, are cases where one can find a pseudosymmetry with a stringent criterion. We use interactive structural alignment (Cn3D) to lead to accurate alignments (Fig. 7). It is frequent in helical protein structural alignments to match structures within a 3.5–4A RMSD, even when sequence matching is indicative of homology. Most of our reliable protodomain alignments for helical structures will lie between 2.0 and 4.0A RMS, with the majority in the 2.5–3.5A RMSD between protodomains made of helical SSSs. This would also be the case in alpha-beta structures, while pure beta will tend to show lower RMS deviations between well-delineated protodomains, i.e., in the 1–3A range. This is mostly due to the relative translational movements of helices along their helix axes for corresponding helical SSEs, while beta structure matches do not have this degree of freedom. In helical systems nonbonded interactions are responsible for SSSs formation, while in beta structures, strands and inter-strands’ H-bond networks forming sheets lead to a higher structural conservation of SSSs.

4.5. Pseudosymmetry Is Detected But May or May Not Be Relevant

It also happens, when we do not expect pseudosymmetry, that the program identifies one or more symmetry operations we did not expect. This happens in detecting multiple levels of symmetry; sometimes one finds more symmetries than expected. This can be quite useful if it points to a local symmetry. It may also be irrelevant depending on the objective of symmetry detection. These higher than expected symmetries are interesting in a sense that they are purely geometric and can help understand an overall architecture better. They may also be useful for protein engineering, as opposed to, for example, identifying evolutionarily related duplication-fusion events. There are also local symmetries that may be of interest if they can be related to a function. The concept of local symmetry is ubiquitous in chemistry [70], even on small substructural groups such as −CH2 or −CH3 motifs (with C2v and C3v local symmetries). Without going down to that level for proteins, one can find pseudosymmetric arrangements at the supersecondary structure level as in, for example, the interaction between 2 hairpins in a larger, overall asymmetric protein; it may be interesting then to look at it from a point of view of local symmetry and departure from symmetry.

4.6. “Translational Symmetry”: Structural Repeats Related by Arbitrary Rotation-Translation

In looking for symmetry-related protodomains, one may miss structural repeats whose arrangement is related by an arbitrary rotation-translation. Tandem repeats are one example. It occurs extremely frequently, for example, in DNA-binding proteins. While this is a clear pattern for tandem domain duplication, it may be hidden if structural elements are small SSSs that repeat without symmetry. This is also called a “translational” symmetry.

4.7. SSE Swapping

Numerous structures with cyclic symmetry of order n, where n > 2, show a tendency to form “closed” structures, where the nth repeat interfaces with the first one in the same way as any other pair of consecutive repeats, but without a linker however. In these cases, one often observes one or more SSEs swapping between the terminal repeats/protodomains. It is quite common in beta structures to observe strand swapping. This is the case, for example, in propellers. This is also observed in alpha structures. For a review on domain swapping, see [71].

4.8. The Question Is: Are Well-Defined Protodomains Shared Among Different Folds?

Structurally conserved fragments across domains have been widely observed, some forming well-defined SSSs, and they have been puzzling to a number of scientists. Some authors have been trying to even identify a set of such fragments as forming the base for a structural “vocabulary” of ancient peptides at the origin of the formation of current domains [72]. They believed that “assembly from non-identical fragments may have been one of the primary forces in the evolution of domains” but, to their surprise, “did not find even one domain that contained two or more different fragments from their set of fragments.” They found “instead that fragments either form folds by repetition or in single copy, decorated by heterologous structural elements, “finding the reasons for the lack of fragment combinations unclear.”

In fact, this is consistent with our findings on protodomains. Repetitive SSSs are highly idiosyncratic in forming domains when combining symmetrically to form domains. In other words, protodomain SSSs represent a signature of a pseudosymmetric domain/fold and may not be found in any other domain/fold. This is an interesting observation, as it points to self-association as a driving force in the formation of pseudosymmetric domains. In other words, self-association seems to be a cause of the observed symmetric organization of pseudosymmetric domains. We did not yet assess this observation exhaustively on the whole protein universe, nor can we be sure the lack of “hits” across domains in the PDB is not due to technical limitations of our current tools. We plan to perform such systematic studies in the future. In most cases where we searched for a protodomain across domains in the PDB, we did not find any other domain (“hit”) other than the pseudosymmetric domains formed out of the protodomain or homologs, except a handful of cases. More cases naturally must exist, yet the proportion vs. pseudosymmetric protodomain assemblies should be small but certainly highly instructive on evolution [73].

4.9. Tools of the Trade

All along we have been using structure alignment to delineate protodomains. It gives us a tool to compare sequences that may have an interest by themselves in terms of evolution of domains in the classical sense. Yet much more important are the protodomain-protodomain interactions, the interfaces they form, and from where they coevolved to form a specific domain with a specific function (or more) using a universal self-associating principle of supersecondary structures. The current method is in its infancy both in terms of tools and applications. Current alignment tools using structure/sequence are limited in looking at one dimension of the problem: structure/sequence similarity. We need a tool to study the self-complementarity of these SSSs and their constituting SSEs in parallel or in antiparallel, for strands and helices at a minimum. Hence, we need to develop complementary alignment tools, where we can match sequence and assembly of these sequences as we match complementary structural elements. This, naturally, can and should extend to any quaternary arrangement. Pseudosymmetric domain arrangements are simply, in that regard, pseudoquaternary structures.

Pseudosymmetry gives correspondences (pseudo-equivalence) at all levels: between SSSs, between SSEs, and down to the residue level, as we have seen in examples. It should find applications in the study of protein folding and structure-function relationships and certainly in the study of coevolution of protein domains and their quaternary arrangements at various levels of complexity. It is also reasonable to think that applications may be found at the local symmetry level. In fact, we already use local symmetry in the very definition of secondary structures, alpha helices and beta strands, which are periodic in nature. Symmetry at the supersecondary structure level is a natural step up in complexity that still reveals periodicity. After all, symmetry is an overarching principle in all Sciences at all scales [74]. It should in fact be seen as surprising that we do not make a wider use of symmetry in proteins.

4.10. Structures Used in This Work

• CD8: 1CD8 [75], 2ATP [76], 5EDX/5 EB9 [77].

• PD-1/PD-L1: 4ZQK [78].

• IgV: 5ESV [79].

• VNAR: 1VES [50].

• IgC: 3DJ9 [80], 4N0U [81].

• FN3: 1BQU [82], 3HHR [83], 2ERJ [84], 3TGX [56].

• Sweet/SemiSweet: 5CTH [85], 4QNC/4QND [86].

• GPCR: 4OR2 [65], 1F88 [63].

• Sm/Hfq: 1KQ2 [87].

• Riboswitch: 3F2Q [47].

• P53: 1TUP [88].

• Nucleosome: 3C1B [89].