Significance
This paper explores the unusual fracture behavior of vitrimers, a transient polymer network whose rupture displays various regimes including flow, crack propagation and arrest, controlled by loading rates. The existence of these regimes was not previously reported in the literature and cannot be explained by current fracture theories. This study therefore extends the fracture criterion to a time-dependent version and relates crack velocity in a vitrimer to the force-dependent kinetics of the bond exchange reaction. This framework not only successfully describes experimental results over a large range of loading conditions but also pinpoints the distinct roles of network kinetics and external loading on the deformation history of a pre-existing defect.
Keywords: vitrimer, bond exchange reaction, viscoelasticity, nonsteady fracture, crack-driving force
Abstract
We have discovered a peculiar form of fracture that occurs in polymer network formed by covalent adaptable bonds. Due to the dynamic feature of the bonds, fracture of this network is rate dependent, and the crack propagates in a highly nonsteady manner. These phenomena cannot be explained by the existing fracture theories, most of which are based on steady-state assumption. To explain these peculiar characteristics, we first revisit the fundamental difference between the transient network and the covalent network in which we highlighted the transient feature of the cracks. We extend the current fracture criterion for crack initiation to a time-evolution scheme that allows one to track the nonsteady propagation of a crack. Through a combined experimental modeling effort, we show that fracture in transient networks is governed by two parameters: the Weissenberg number that defines the history path of crack-driving force and an extension parameter that tells how far a crack can grow. We further use our understanding to explain the peculiar experimental observation. To further leverage on this understanding, we show that one can “program” a specimen’s crack extension dynamics by tuning the loading history.
Understanding the conditions that lead to fracture in polymeric materials is an important problem of both industrial and fundamental interests. A common agreement is that fracture of polymer originates from successive chain scission resulting from the application of an excessive stress on the network (1). This consideration leads to the early work of Griffith that predicts the onset of crack propagation based on the competition between two quantities: the crack tip–driving force that provides the fuel for fracture and the intrinsic fracture toughness , which represents the material’s resistance to fracture (2). To propagate a crack, the former needs to reach or exceed the latter. This criterion further leads to deformation-based measurements such as the critical crack opening distance (COD) (3), critical stretch (4), or network damage models based on the chains’ stretch limit (5–7). These models have so far been instrumental in predicting the fracture of covalent polymer networks that are both elastic (2, 8–10) and viscoelastic (11–17). However, materials formed by weaker bonds [(e.g., covalent adaptable bonds (18), ionic interaction (19, 20), or entanglements (21–23)] exhibit a much richer fracture behavior that does not only depend on deformation but also greatly depends on the rate of loading (21, 22, 24). Due to their inherent weakness, these bonds are prone to spontaneous dissociation and reassociation over time under the effects of thermal fluctuations. This leads to a wide spectrum of rate-dependent mechanical response wherein the networks behave like viscous fluid at slow loading rates (relative to the rate of bond exchange), while they exhibit elastic solid-like behavior at fast loading (21). This coupling between deformation and network relaxation makes the prediction of fracture challenging, since the mechanical response becomes both time and rate dependent. In addition, the physical picture of chain scission at its stretch limit is no longer valid as a chain may dissociate in any conformation. This raises questions about the molecular origin of fracture and on its macroscopic manifestation and particularly, the conditions for its nucleation and its speed of propagation. Although some initial efforts were taken to understand the role of loading rate on fracture (22, 25) in transient networks, a systematic study of the physical rules behind crack characteristics, initiation, and propagation is still not established.
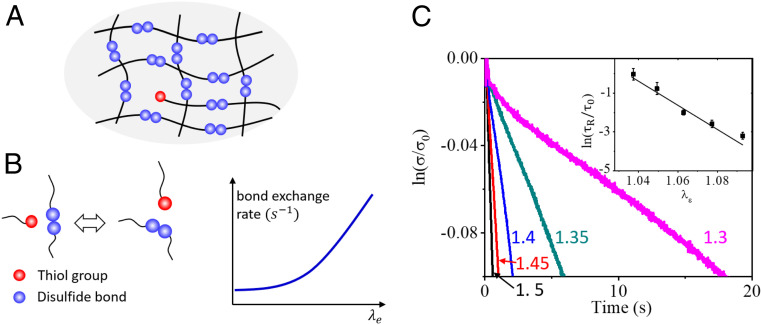
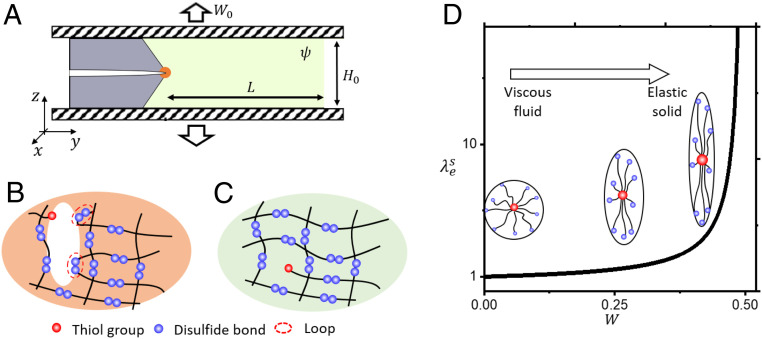
To address these questions, we have carried out fracture experiments on a vitrimer network formed by disulfide bonds. In the presence of a catalyst, the bond exchange reaction (Fig. 1B) can be triggered by thermal fluctuations at room temperature (26). A full characterization of this network has been performed in our previous study (27). In this paper, we are specifically interested in the stress relaxation experiment, as it unveils the rate of bond exchange reaction (i.e., the bond dynamics). For this, we conducted a series of stress relaxation experiments at different stretch levels, in which the inverse of characteristic relaxation time is interpreted as the average rate of bond exchange at the applied deformation (28). After calibration, we found that bond dissociation is well described by the relation , where is the spontaneous rate, and is a sensitivity parameter, as shown by the relaxation results in Fig. 1C and the fitting of relaxation time in its Inset. This exponential dependency agrees with Eyring’s model (29, 30) based on the transition state theory. To characterize the response of this vitrimer in fracture, we then devised a pure-shear fracture experiment, where a precut sample of width and height (), which contains a precut of length , was stretched vertically at constant nominal strain rate (Fig. 2A). In what follows, this variable is normalized by the bond dynamics rate so that the ratio (denoted as the nominal Weissenberg number) describes the competition between network deformation and reconfiguration.
Fig. 1.
(A) Schematic of the transient network, where (B) bond exchange reaction can spontaneously occur at rate (C) Stress relaxation experiment at different strain with uniaxial tensile loading at large deformation ().
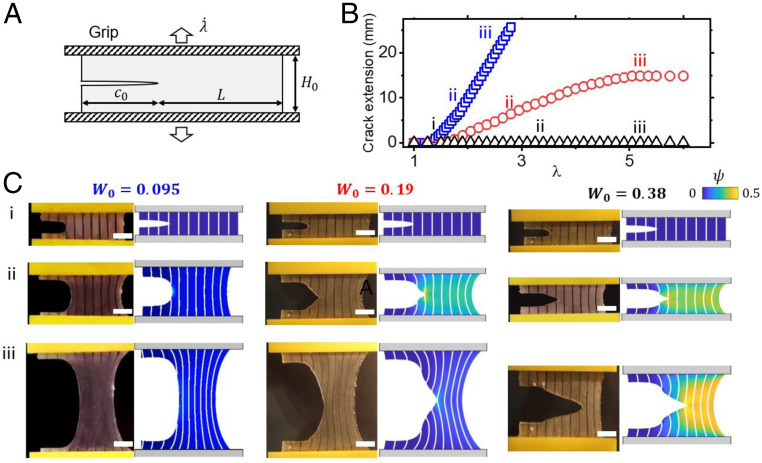
Fig. 2.
(A) A schematic of fracture of the specimen. The crack tip–driving force measures the elastic energy infused to the crack tip. (B) Measurement of crack extension during the deformation history. (C). Experimental and finite element simulation snapshots of crack profile under different loading rates. (Scale bar, 10 mm.)
Our measurements of crack extension (Fig. 2 B and C) reveal three distinct characteristic regimes depending on the magnitude of . For a small loading rate (), the induced cut opens continuously and eventually becomes a curved edge. Over the course of the experiment, no observable fracture is recorded. For an intermediate rate (), a peculiar phenomenon occurs where a sharp crack first nucleates from the tip of the cut and quickly propagates with a characteristic trumpet-shaped profile (Fig. 2C). However, the propagation stops at a finite time, after which the crack “dies” and gives rise to a blunted edge. We note that this phenomenon is not observed in covalently crosslinked networks, since a propagating crack usually travels continuously at constant velocity through the specimen (31) under monotonic loading. Finally, for fast loading (), we similarly observe an initial blunting of the cut, quickly followed by crack nucleation. In this case, this newborn crack accelerates and fully ruptures the specimen. We used image processing techniques and measured the crack extension as a function of stretch (Fig. 2B), where we see that crack propagation is highly unsteady with varying velocity. The above observations cannot be explained by the current fracture theories for the following reasons. First, the onset of fracture highly depends on loading rate in addition to the level of deformation, therefore, a criterion derived from the elastic theory such as the COD or the critical stretch cannot be used. Second, the life of a propagation crack varies between loading conditions, where it may accelerate, decelerate, or even stop under monotonic loading.
To understand these observations, we have recently developed a theoretical framework that allows one to evaluate the energetic fracture criterion and calculate crack velocity based on the stress field and bond dynamics (32). Combining this approach with finite element simulations (details provided in SI Appendix, Supplemental Information S2), we were able to simulate the nonsteady state fracture behavior of the vitrimer and qualitatively match the experimental crack profiles in Fig. 2C. Predominantly, our simulations suggest that crack initiation and propagation are associated with the increase of strain energy density stored in the network, which itself is a function of nominal Weissenberg number and loading history. In addition, the speed of the crack depends on both the magnitude of and the sensitivity of bond dynamics upon deformation. In summary, our simulation work has allowed us to identify three kinetic rates that collectively govern fracture in transient networks: the rate of loading, the rate of bond dynamics, and the rate of crack propagation. The way by which these rates compete during fracture is however unclear. This work’s objective is thus to combine theoretical analysis with experiment and extract the physical mechanisms behind these peculiar phenomena.
Fracture Controlled by Nonequilibrium Processes
Recalling from the work of Griffith (2), the criterion for crack propagation relies on the competition between the crack tip–driving force and material’s fracture resistance . As shown by Rivlin and Thomas (8), depends on both the stored elastic energy density in the specimen and its geometry. The former determines the energy stored in the system, while the latter dictates the amount of energy fed to the crack tip. As shown by our previous serial work (32–35) on the transient network theory (TNT), is directly related to the elastic distortion of the network. However, since the network constantly reconfigures, its distortion is usually different from the specimen deformation. To quantify the network distortion, the TNT introduced the so-called chain conformation tensor that measures the mean squared elastic deformation of chains in the network. At the stress-free state, is equal to the identity tensor , indicating an undeformed state. Over the deformation history, the TNT allows us to track the chain conformation and the stored elastic energy via their evolutions that read and . The tensor is the velocity gradient related to the Hencky or true strain rate (36), and is the shear modulus of the network. In both equations, the terms associated with describe the effect of external load, while the terms associated with are related to network reconfiguration. In what follows, we will explore the fracture criterion based on these two equations.
Crack Initiation and Arrest.
In a pure-shear extension experiment, the specimen only deforms along and directions (Fig. 3A). Therefore, the chain conformation tensor simplifies to a diagonal form expressed in the coordinate system with , where is the mean chain stretch along direction. During deformation, the evolution of and the stored elastic energy density become (derivation provided in SI Appendix, Supplemental Information S1):
| [1a] |
| [1b] |
where is the true Weissenberg number. At the initial state, this quantity is equal to the nominal Weissenberg number . We note that Eq. 1 can describe a wide spectrum of network response ranging from elastic solid to viscous fluid–like behavior. At extremely fast loading (), Eq. 1 becomes and , which are the evolution laws for Neo-Hookean elastic solid (36). At the other extreme (), Eq. 1 degenerates to , showing that the chains remain unstretched regardless of macroscopic deformation, similar to the behavior of Newtonian fluid. In addition, our previous studies (32, 37) show that when is held constant during deformation, the chains evolve toward a steady-state stretch . As shown by Fig. 3D, increases monotonically with , characterizing a more elastic solid-like behavior. When , the steady-state stretch diverges, implying that rate of elastic deformation is predominant over bond dynamics. We note here that our experiments (Fig. 2) were conducted at constant , which is equivalent to a monotonically decreasing true Weissenberg number with stretch given by . As a result, the specimen response becomes more fluid-like during deformation, and therefore fracture becomes less favorable. To relate the specimen’s energy state to fracture, we first note that the crack tip–driving force is defined as the energy consumed by unit area of crack extension as . The term is the energy consumed by crack propagation, which can be calculated from the conservation of energy:
| [2] |
where is the work done by external forces, is the change in elastic energy, and is the energy loss by viscous dissipations. Physically, represents the system’s dissipative energy, either by bond dynamics or crack propagation. For fluid-like materials, becomes the dominant term for dissipation and therefore fracture is unfavorable. Contrarily, for elastic network, and fracture becomes the only dissipative mechanism. In our previous work, Eq. 2 was numerically evaluated by computing , , and from the finite element solution of the stress field (32). In this work, to analytically investigate the problem, we assume that the effect of crack tip singularity and the associated network damage is restricted within a damage zone at the tip that is much smaller than the specimen size and crack size (Fig. 3 A–C). This assumption is supported by our previous study on tearing, where the result indicated that the damage zone is at submillimeter size across a wide range of crack speed ( changes from 0.01 to 10 mm/s) (28). Under this assumption, we could then apply a binary simplification to the stress field (i.e., the specimen is split into a uniformly loaded and a fully unloaded region) as shown in Fig. 3A. Under such simplifications, a first order approximation of the crack tip–driving force can be obtained as the following (derivation provided in SI Appendix, Supplemental Information S3):
| [3] |
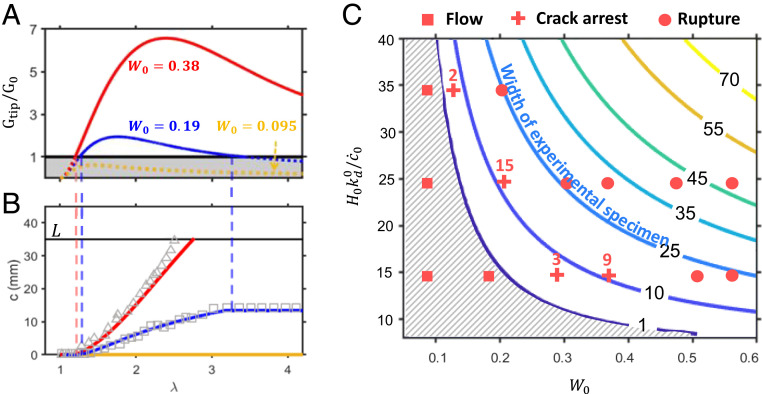
This expression takes a similar form as that its counterpart for elastic materials (8) with two major differences. First, due to bond dynamics, the strain energy is rate and history dependent, as shown by Eq. 1. Second, there is a factor due to the mismatch between chain stretch and the applied deformation. For elastic networks, and Eq. 2 degenerates to its form for elastic solids (38). To further simplify our analysis, we assume a constant bond dynamic in the specimen due to the relatively small chain stretch under small strain rate, except for the damage zone. Using Eqs. 1 and 3, Fig. 4A plots the change of over the loading history for the three strain rates used in experiment. By comparing its value with the intrinsic fracture toughness (obtained as by fitting with experiment on crack initiation), we split Fig. 4A into two regimes, the flow regime () shown in gray background and crack propagation regime () with white background. For a slow loading rate (), the curve remains in the flow regime, and no fracture occurs. At faster loading, we see a nonmonotonic behavior where the specimen first enters the crack propagation regime but eventually drops toward the flow regime as it becomes increasingly fluid-like. This yields the peculiar crack arrest behavior, where the crack only propagates within a range of deformation. According to Eq. 3, this “propagation window” solely depends on the experimental control of the specimen height and the nominal Weissenberg number . Therefore, one way to regulate the fracture of the specimen is to control the propagation window via these two parameters.
Fig. 3.
(A) A schematic of fracture of the specimen. (B and C) Schematics of network configuration at the damage zone and in the bulk, respectively. (D) Under constant true Weissenberg number loading, the mean chain stretch increases monotonically with . (Insets) The graphical visualization of chain stretch along vertical direction.
Fig. 4.
(A) relation for different loading rates conducted in experiment. (B) Comparison between model prediction (lines) and experimental measurement (scattered symbols) on the evolution of crack length over loading history. (C) A contour map with unit of mm that relates experimental conditions to the three characteristic fracture phenomena (flow, crack arrest, and rupture). Scatter points are experimental results for flow (square), crack arrest (cross), and rupture (circle).
Load-Dependent Crack Velocity.
We note that the above analysis on crack arrest was carried out by assuming an infinitely large specimen (i.e., the crack never propagates through the sample). Since the experiments were conducted on a finite-size specimen, the crack may travel through the specimen before it is arrested. To capture the effect of the specimen’s finite size, we thus introduce another nondimensional parameter, the extension parameter , where is a characteristic crack length derived from the Trumpet model by De Gennes (11, 16). This length describes the size of a region around the crack tip within which the network behaves like an elastic solid due to the amplified strain rate. A large () indicates a rapid crack propagation such that network reconfiguration becomes negligible. In this scenario, phenomena observed in elastic fracture can be seen in transient networks, including a parabolic crack profile and steady crack velocity, as shown in the fracture experiment of complex fluid filaments (21, 22, 39) during extension. Contrarily, a small () indicates that network reconfiguration occurs at the same time scale as crack propagation, which leads to more complicated trumpet-shaped crack profile and nonsteady crack propagation. In our experiment, the maximum value of is calculated from experiment as , implying that the elastic fracture theory cannot be used to describe crack propagation. To address this, we need to look closely at the crack tip region and understand the local processes. A physical picture of this process can be shown by Fig. 3B and explained as follows. When energy is infused to the crack tip, it leads to an amplification of chain stretch in the tip neighborhood and an increase in rate of bond dynamics. This facilitates the formation of elastic ineffective chains (such as loops shown in Fig. 3B), as chain reassociation occurs more likely at the stress-free configuration than at a stretched state. This further facilitates the formation of cavities or microcracks within the fracture process zone during propagation. Based on this physical picture, our previous work (28) showed that the crack velocity ()—crack tip–driving force () obeyed the following relationship:
| [4] |
where is a characteristic chain velocity that depends on chain length , bond dynamics , and its sensitivity . The parameter is a characteristic crack-driving force that increases with the size of damage zone. In this work, is set as the fitting parameter since the damage zone size cannot be accurately measured. Physically, Eq. 4 suggests that as energy is fed to the crack tip, bonds cannot sustain the stretch and dissociate more frequently, leading to a more rapid network damage and crack propagation. This understanding also shines light on the physical meaning of When less energy flows to the crack tip (), chain deformation is relatively slow, and bond dynamics become the dominant process. In this scenario, the network around the crack tip is more likely to reconfigure and relax its stress rather than damage continuously, in which case the crack does not propagate. Under this physical picture, the fracture energy of a dynamic network is interpreted as an energetic threshold above which network damage dominates network reconfiguration. This interpretation is different from the case of permanent networks, where is usually associated to the chains’ stretch limit (40). In this work, we were able to predict crack propagation by setting for all cases. The specimen size independence of confirms that the damage zone size is small compared to the specimen. From Eq. 4, we can gain some insight on the effect of the damage zone size where for a larger damage zone (i.e., larger ), more energy is needed to maintain the crack velocity. As discussed in the literature (41–43), the size of damage zone (i.e., the magnitude of ) can be tuned by modifying the microscopic properties of the network, such as varying the bond connectivity, having a higher polydispersity, or increasing the bond sensitivity. To control crack velocity, one may also tune the characteristic parameter , which changes linearly with bond sensitivity, chain length, and natural bond dissociation rate. To sum up, over the deformation history, one can track the mechanical state of the specimen via Eq. 1. Using this information, one can determine the evolution of the crack based on Eqs. 3 and 4.
Nonsteady State Fracture of Vitrimer.
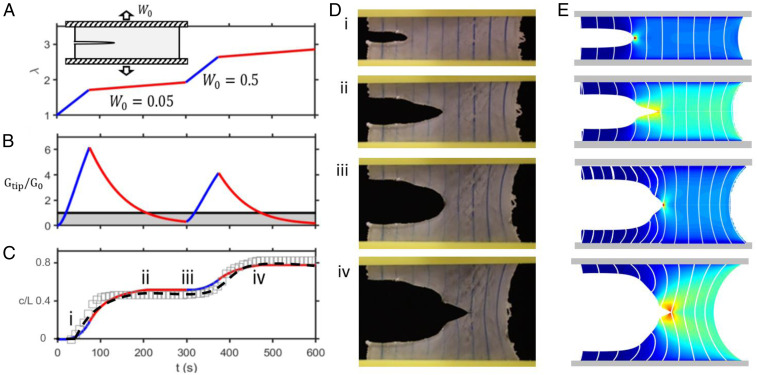
To check whether this model is consistent with experimental observations, we used Eqs. 1, 3, and 4 to predict the stability and the velocity of a crack subjected to our experimental conditions. By matching predictions with experiment measurements on crack extension history (Fig. 4 A and B), we found that our model accurately captured the nonsteady extension of the crack by using the fitting parameter . We however noticed that the model tended to underpredict the crack velocity when as it approaches the right boundary of the specimen (this was especially apparent for the case ). We used finite element simulations (SI Appendix, Fig. S5) and found the discrepancy to be caused by boundary effect when the crack interacted with the free edge, producing complicated stress patterns that are not captured by the analytical model. To inform the experimental design, we then theoretically explore the crack arrest length under different conditions. Since modifying the molecular properties is out of the scope of this work, we keep the extension parameter constant and tune the crack tip–driving force by varying the loading rate (the normalized Weissenberg number ) and the specimen’s normalized height . By performing large numbers (∼2,000 simulations) of virtual experiments using Eqs. 1, 3 and 4, we summarize our result in a contour map of (units in mm) shown in Fig. 4C. We see that increasing both the specimen height and loading rate favors crack propagation, as shown by the increase of . To verify this prediction, we performed additional fracture tests and overlayed contour plots with scatter points representing the experimental results with squares (flow), crosses (crack arrest), and circles (rupture). We note that rupture occurs when the crack arrest length is greater than the specimen width. When the cracks were arrested, we experimentally measured their final length as represented by the numbers on top of the crosses in Fig. 4C. We see that the model accurately captures each regime as well as provides reasonable predictions on the crack arrest length. Furthermore, while the results of Fig. 4C are generated under relatively simple loading conditions (constant ), one may ask if this quantitative understanding can be used to mitigate or even control fracture using more complicated loading processes. For instance, can we tune the loading history such that the material preserves its mechanical integrity during most of its life? To illustrate this, we designed a pure-shear experiment with the loading alternating between fast () and slow stretch rates () (Fig. 5A). Our model shows that this oscillatory loading leads to sharp spike and decrease of over time (Fig. 5B), leading to multiple crack propagation events. Although a crack initiates and propagates rapidly during the fast-loading stage, it decelerates immediately once the loading rate changes and is eventually arrested. Over the course of two cycles, our model shows that the specimen maintains its integrity, although the majority of its deformation is applied during the fast-loading stage. We then performed experiment under the same condition and found that the measurement on crack extension agrees very well with the semianalytical model (Fig. 5C). In addition to crack extension, the change of crack profile also distinguishes the flow and elastic solid response of the specimen. At fast loading, the crack tip advances in a relatively sharp parabolic shape (Fig. 5 C, i and ii), after which it becomes a curved edge after arrest (Fig. 5 C, iii). Notably, during the second loading stage, fracture occurs by the nucleation of a new crack at the curved edge (Fig. 5 C, iv) instead of propagating the arrested one. This phenomenon illustrates well the transient nature of cracks in transient network. When a crack is arrested, its life comes to an end as the singular stress fields around its tip gradually relax in time. While the detailed profile and its evolution over time cannot be captured by the analytical model, finite element simulation under the same conditions clearly show the “death” of a crack as the energy level decreases, as well as the “birth” of the secondary crack during the second fast loading (Fig. 5E). Notably, Fig. 5C shows that finite element (dashed line) agrees very well with both the semianalytical model and experiment on the crack propagation. This again verifies the applicability of the semianalytical model even for complicated loading history. From a practical viewpoint, this example illustrates a strategy on fracture control of materials made of transient networks. For instance, in 3D printing applications, this example provides ideas toward a technique to “program” the fracture of ink during extrusion to achieve very thin filaments. A relevant idea on varying printing resolution by rate control was proposed by Yuk and Zhao (44). We foresee the capacity of “fracture on demand” will further enrich the design space. In addition, the combined crack propagation and flow may be related to observations in other experimental studies. For instance, in the probe tack experiments of soft adhesives, a microdefect on the interface may first grows horizontally (fracture) into a microscopic crack, after which it grows vertically (blunting) and leads to cavitation. This crack arrest phenomenon was discussed as an early stage of cavitation failure in adhesives (45, 46).
Fig. 5.
(A) Schematic of experimental geometry and loading history, where the specimen is stretched by two alternating rates. (B) The path of the specimen during loading, we see that the path enters and leaves crack propagation regime repeatedly. (C) The crack length as a function of deformation . The red and blue line is analytical model prediction, scatter square is experimental measurement, and black dash line is finite element analysis prediction. (D and E) Snapshots of experiments (D) and FEM simulation (E) taken at four time frames in experiment.
Concluding Remarks
We have identified a peculiar form of fracture that occurs in polymer networks formed by transient crosslinks in which a propagating crack evolves in a highly nonsteady manner. As a result, the specimen can continue to deform without catastrophic rupture at low loading rate. We found that this phenomenon originates from the nonequilibrium nature of the network that constantly reconfigures and dissipates energy. To understand the physical laws behind this process, we combined the rate-dependent crack tip–driving force and the local network damage near the crack tip and found that, for a given geometry, this problem was governed by two nondimensional numbers: the nominal Weissenberg number that controls the onset of crack propagation and arrest and the propagation parameter , which provides information about how far a crack can extend during propagation. Between these two parameters, the former can be controlled by varying experimental condition (loading rate and specimen height), while the latter can be tuned by the molecular structure of the polymer. We further showed how one may control the life of cracks by simply varying the loading condition.
In summary, this work enriches the field of quasi-brittle fracture by introducing a way of analyzing the fracture in nonequilibrium systems. Based on our previous computational framework (32), this paper introduces a semianalytical scheme that tracks the status and dynamics of a crack over the loading history. This semianalytical scheme explicitly describes how the interplay between network deformation and reconfiguration modulates the crack dynamics over the deformation history. By combining with experimental work, we validated the sensitivity of bond dynamics to deformation and showed that the model predicts nonequilibrium fracture with good accuracy, even under a complicated loading history. This opens the door to the prediction and control of nonsteady fracture of transient networks that are crucial in engineering applications and scientific research. For instance, some of the example problems explored in this paper can be related to the combined fracture and cavitation of adhesives (45, 47), the blunting–advancing of cracks in physical crosslinked polymers (48) and the fracture–flow transition of transient fluids made of associated polymers (22). Application wise, this model can be used to provide control guidance on the material extrusion in additive manufacturing (44), polymer coating (49), and rheological regulating (50). One important future effort is to extend the current model to cohesive fracture (i.e., when a crack propagates in the bulk) to adhesive fracture on material interface. This may not only open the door to a variety of adhesive application problems but also provide physical insights to understand the velocity-dependent crack-driving force measured in these applications (11, 51, 52). Furthermore, as a first attempt, this model employs coarse-grained approximations on both the macroscopic stress field and the crack tip damage profile. Therefore, the applicability of this model remains in small to moderate deformation with a small damage zone compared to specimen size. For ductile fracture (i.e., damage zone is comparable to specimen size), more complicated damage mechanisms become nonnegligible (including cavitation and fibrillation), and discrete modeling approaches will be an important asset to understand these highly dynamic and stochastic processes.
Materials and Methods
Materials.
EPS25 (epoxy equivalent = 777 g/equiv) was kindly provided by Akzo Nobel Chemicals; pentaerythritol tetrakis(3-mercaptopropionate) (PETMP, Sigma Aldrich), and 4-(dimethylamino)pyridine (DMAP, Sigma Aldrich) were used as received.
EPS25 Vitrimer Synthesis.
The synthesis of vitrimer followed methodology of our previous works (27). We added 5 mmol PETMP into 10 mmol EPS25 and stirred the mixture until homogeneous. Then, we added 1 wt% of DMAP as catalyst into the mixture. We stirred the mixture for 10 min and degassed under vacuum. After that, we poured the mixture into a glass mold and heated at 60 °C for 2 h. Finally, we obtained the vitrimer.
Fracture Test of Vitrimers.
We first cut the samples to a rectangular shape with the dimensions 50 × 5 × 2 mm, 50 × 10 × 2 mm, or 50 × 15 × 2 mm. We introduced a precrack into the samples with the length of 15 mm by using a sharp blazer. We glued the samples onto two rigid acrylate plates which were then clamped by the tensile grips of the tensile machine (Instron 5965 with a 10-N load cell). We set the nominal strain rate to be constant. The stress–stretch curve of samples were recorded. We also recorded the videos of fracture process by using a digital camera (Cannon EOS 80D).
Finite Element Simulation of Fracture Experiment.
The finite element simulation of fracture used a customized program written in Matlab developed in our previous studies (32, 53). This program uses the coupled Eulerian–Lagrange description of kinematics and the TNT for material constitutive model. All simulations were performed via an explicit time incremental scheme. For details on the problem setup, readers are referred to ref. 32.
Supplementary Material
Acknowledgments
We thank Akzo Nobel Chemicals for providing the EPS25 resin. F.J.V. gratefully acknowledges the support of the NSF under Award No. 1761918. S.C. acknowledges the support of the Office of Naval Research with the Grant No. N00014-17-1-2056.
Footnotes
The authors declare no competing interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at https://www.pnas.org/lookup/suppl/doi:10.1073/pnas.2105974118/-/DCSupplemental.
Data Availability
All study data are included in the article and/or supporting information.
References
- 1.Long R., Hui C.-Y., Gong J. P., Bouchbinder E., The fracture of highly deformable soft materials: A tale of two length scales. Annu. Rev. Condens. Matter Phys. 12, 71–94 (2021). [Google Scholar]
- 2.Griffith A. A., Taylor G. I., VI. The phenomena of rupture and flow in solids. Philos. Trans. R. Soc. Lond. Ser. Contain. Pap. Math. Phys. Character 221, 163–198 (1921). [Google Scholar]
- 3.Long R., Hui C.-Y., Crack tip fields in soft elastic solids subjected to large quasi-static deformation—A review. Extreme Mech. Lett. 4, 131–155 (2015). [Google Scholar]
- 4.Zehnder A. T., Lecture notes on fracture mechanics. Cornell Univ. 20, 22 (2007). [Google Scholar]
- 5.Mao Y., Talamini B., Anand L., Rupture of polymers by chain scission. Extreme Mech. Lett. 13, 17–24 (2017). [Google Scholar]
- 6.Talamini B., Mao Y., Anand L., Progressive damage and rupture in polymers. J. Mech. Phys. Solids 111, 434–457 (2018). [Google Scholar]
- 7.Volokh K. Y., Characteristic length of damage localization in rubber. Int. J. Fract. 168, 113–116 (2011). [Google Scholar]
- 8.Rivlin R. S., Thomas A. G., “Rupture of rubber. I. Characteristic fnergy for tearing” in Collected Papers of R.S. Rivlin: Volume I and II, G. I. Barenblatt, D. D. Josep, Eds. J of Polymer Sci. (1953).
- 9.Wang X., Hong W., Delayed fracture in gels. Soft Matter 8, 8171–8178 (2012). [Google Scholar]
- 10.Glassmaker N. J., Hui C. Y., Yamaguchi T., Creton C., Detachment of stretched viscoelastic fibrils. Eur Phys J E Soft Matter 25, 253–266 (2008). [DOI] [PubMed] [Google Scholar]
- 11.Saulnier F., Ondarçuhu T., Aradian A., Raphaël E., Adhesion between a viscoelastic material and a solid surface. Macromolecules 37, 1067–1075 (2004). [Google Scholar]
- 12.Williams J. G., Energy release rates for the peeling of flexible membranes and the analysis of blister tests. Int. J. Fract. 87, 265–288 (1997). [Google Scholar]
- 13.Knauss W. G., A review of fracture in viscoelastic materials. Int. J. Fract. 196, 99–146 (2015). [Google Scholar]
- 14.Schapery R. A., A theory of crack initiation and growth in viscoelastic media. Int. J. Fract. 11, 141–159 (1975). [Google Scholar]
- 15.Schapery R. A., Correspondence principles and a generalized J integral for large deformation and fracture analysis of viscoelastic media. Int. J. Fract. 25, 195–223 (1984). [Google Scholar]
- 16.de Gennes P. G., Soft adhesives. Langmuir 12, 4497–4500 (1996). [Google Scholar]
- 17.Nguyen T. D., Govindjee S., Numerical study of geometric constraint and cohesive parameters in steady-state viscoelastic crack growth. Int. J. Fract. 141, 255–268 (2006). [Google Scholar]
- 18.Bowman C. N., Kloxin C. J., Covalent adaptable networks: Reversible bond structures incorporated in polymer networks. Angew. Chem. Int. Ed. Engl. 51, 4272–4274 (2012). [DOI] [PubMed] [Google Scholar]
- 19.Walter J., Sehrt J., Vrabec J., Hasse H., Molecular dynamics and experimental study of conformation change of poly(N-isopropylacrylamide) hydrogels in mixtures of water and methanol. J. Phys. Chem. B 116, 5251–5259 (2012). [DOI] [PubMed] [Google Scholar]
- 20.Liu M., Guo J., Hui C.-Y., Zehnder A., Crack tip stress based kinetic fracture model of a PVA dual-crosslink hydrogel. Extreme Mech. Lett. 29, 100457 (2019). [Google Scholar]
- 21.Ligoure C., Mora S., Fractures in complex fluids: The case of transient networks. Rheol. Acta 52, 91–114 (2013). [Google Scholar]
- 22.Shabbir A., et al., Brittle fracture in associative polymers: The case of ionomer melts. Soft Matter 12, 7606–7612 (2016). [DOI] [PubMed] [Google Scholar]
- 23.Huang Q., Alvarez N. J., Shabbir A., Hassager O., Multiple cracks propagate simultaneously in polymer liquids in tension. Phys. Rev. Lett. 117, 087801 (2016). [DOI] [PubMed] [Google Scholar]
- 24.Wang Y., Wang S.-Q., Rupture in rapid uniaxial extension of linear entangled melts. Rheol. Acta 49, 1179–1185 (2010). [Google Scholar]
- 25.Huang Q., Exploring the mechanism of fracture for entangled polymer liquids in extensional flow. Phys. Fluids 31, 083105 (2019). [Google Scholar]
- 26.Pei Z., Yang Y., Chen Q., Wei Y., Ji Y., Regional shape control of strategically assembled multishape memory vitrimers. Adv. Mater. 28, 156–160 (2016). [DOI] [PubMed] [Google Scholar]
- 27.Song Z., Wang Z., Cai S., Mechanics of vitrimer with hybrid networks. Mech. Mater. 153, 103687 (2021). [Google Scholar]
- 28.Song Z., Shen T., Vernerey F. J., Cai S., Force-dependent bond dissociation explains the rate-dependent fracture of vitrimers. Soft Matter, 10.1039/d1sm00518a (2021). [DOI] [PubMed] [Google Scholar]
- 29.Krausz A. S., The theory of non-steady state fracture propagation rate. Int. J. Fract. 12, 239–242 (1976). [Google Scholar]
- 30.Hansen A. C., Baker-Jarvis J., A rate dependent kinetic theory of fracture for polymers. Int. J. Fract. 44, 221–231 (1990). [Google Scholar]
- 31.Qi Y., Zou Z., Xiao J., Long R., Mapping the nonlinear crack tip deformation field in soft elastomer with a particle tracking method. J. Mech. Phys. Solids 125, 326–346 (2019). [Google Scholar]
- 32.Shen T., Vernerey F. J., Rate-dependent fracture of transient networks. J. Mech. Phys. Solids 143, 104028 (2020). [Google Scholar]
- 33.Vernerey F. J., Long R., Brighenti R., A statistically-based continuum theory for polymers with transient networks. J. Mech. Phys. Solids 107, 1–20 (2017). [Google Scholar]
- 34.Lalitha Sridhar S., Vernerey F. J., The chain distribution tensor: linking nonlinear rheology and chain anisotropy in transient polymers. Polymers (Basel) 10, 848 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Vernerey F. J., Transient response of nonlinear polymer networks: A kinetic theory. J. Mech. Phys. Solids 115, 230–247 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Holzapfel G. A., Nonlinear Solid Mechanics (Wiley, Chichester, 2000), vol. 24. [Google Scholar]
- 37.Vernerey F. J., Shen T., Sridhar S. L., Wagner R. J., How do fire ants control the rheology of their aggregations? A statistical mechanics approach. J. R. Soc. Interface 15, 20180642 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Shen T., Vernerey F., Rate-dependent fracture in transient networks. J. Mech. Phys. Solids 143, 104028 (2020). [Google Scholar]
- 39.Tabuteau H., Mora S., Ciccotti M., Hui C.-Y., Ligoure C., Propagation of a brittle fracture in a viscoelastic fluid. Soft Matter 7, 9474–9483 (2011). [Google Scholar]
- 40.Lake G. J., Thomas A. G., The strength of highly elastic materials. Proc. R. Soc. Lond. A Math. Phys. Sci. 300, 108–119 (1967). [Google Scholar]
- 41.Guo J., Zehnder A. T., Creton C., Hui C.-Y., Time dependent fracture of soft materials: linear versus nonlinear viscoelasticity. Soft Matter 16, 6163–6179 (2020). [DOI] [PubMed] [Google Scholar]
- 42.Kothari K., Hu Y., Gupta S., Elbanna A., Mechanical response of two-dimensional polymer networks: Role of topology, rate dependence, and damage accumulation. J. Appl. Mech. 85, 031008 (2018). [Google Scholar]
- 43.Matsuda T., Kawakami R., Nakajima T., Gong J. P., Crack tip field of a double-network gel: Visualization of covalent bond scission through mechanoradical polymerization. Macromolecules 53, 8787–8795 (2020). [Google Scholar]
- 44.Yuk H., Zhao X., A new 3D printing strategy by harnessing deformation, instability, and fracture of viscoelastic inks. Adv. Mater. 30, 1704028 (2018). [DOI] [PubMed] [Google Scholar]
- 45.Yamaguchi T., Creton C., Doi M., Simple model on debonding of soft adhesives. Soft Matter 14, 6206–6213 (2018). [DOI] [PubMed] [Google Scholar]
- 46.Deplace F., et al., Fine tuning the adhesive properties of a soft nanostructured adhesive with rheological measurements. J. Adhes. 85, 18–54 (2009). [Google Scholar]
- 47.Creton C., Ciccotti M., Fracture and adhesion of soft materials: A review. Rep. Prog. Phys. 79, 046601 (2016). [DOI] [PubMed] [Google Scholar]
- 48.Luo F., et al., Crack blunting and advancing behaviors of tough and self-healing polyampholyte hydrogel. Macromolecules 47, 6037–6046 (2014). [Google Scholar]
- 49.Kim B.-S., Mooney D. J., Engineering smooth muscle tissue with a predefined structure. J. Biomed. Mater. Res. 41, 322–332 (1998). [DOI] [PubMed] [Google Scholar]
- 50.Kim J., et al., Applications of telechelic polymers as compatibilizers and stabilizers in polymer blends and inorganic/organic nanohybrids. Polymer (Guildf.) 45, 3527–3533 (2004). [Google Scholar]
- 51.Barquins M., Ciccotti M., On the kinetics of peeling of an adhesive tape under a constant imposed load. Int. J. Adhes. Adhes. 17, 65–68 (1997). [Google Scholar]
- 52.Ciavarella M., McMeeking R., Crack propagation at the interface between viscoelastic and elastic materials. arXiv:2012.09011v1 (16 December 2020).
- 53.Shen T., Long R., Vernerey F., Computational modeling of the large deformation and flow of viscoelastic polymers. Comput. Mech. 63, 725–745 (2018). [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All study data are included in the article and/or supporting information.