Abstract
It is important to study the genetics of complex traits in diverse populations. Here, we introduce covariate-adjusted linkage disequilibrium (LD) score regression (cov-LDSC), a method to estimate SNP-heritability (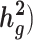 and its enrichment in homogenous and admixed populations with summary statistics and in-sample LD estimates. In-sample LD can be estimated from a subset of the genome-wide association studies samples, allowing our method to be applied efficiently to very large cohorts. In simulations, we show that unadjusted LDSC underestimates
and its enrichment in homogenous and admixed populations with summary statistics and in-sample LD estimates. In-sample LD can be estimated from a subset of the genome-wide association studies samples, allowing our method to be applied efficiently to very large cohorts. In simulations, we show that unadjusted LDSC underestimates 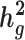 by 10–60% in admixed populations; in contrast, cov-LDSC is robustly accurate. We apply cov-LDSC to genotyping data from 8124 individuals, mostly of admixed ancestry, from the Slim Initiative in Genomic Medicine for the Americas study, and to approximately 161 000 Latino-ancestry individuals, 47 000 African American-ancestry individuals and 135 000 European-ancestry individuals, as classified by 23andMe. We estimate
by 10–60% in admixed populations; in contrast, cov-LDSC is robustly accurate. We apply cov-LDSC to genotyping data from 8124 individuals, mostly of admixed ancestry, from the Slim Initiative in Genomic Medicine for the Americas study, and to approximately 161 000 Latino-ancestry individuals, 47 000 African American-ancestry individuals and 135 000 European-ancestry individuals, as classified by 23andMe. We estimate 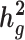 and detect heritability enrichment in three quantitative and five dichotomous phenotypes, making this, to our knowledge, the most comprehensive heritability-based analysis of admixed individuals to date. Most traits have high concordance of
and detect heritability enrichment in three quantitative and five dichotomous phenotypes, making this, to our knowledge, the most comprehensive heritability-based analysis of admixed individuals to date. Most traits have high concordance of 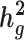 and consistent tissue-specific heritability enrichment among different populations. However, for age at menarche, we observe population-specific heritability estimates of
and consistent tissue-specific heritability enrichment among different populations. However, for age at menarche, we observe population-specific heritability estimates of 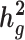 . We observe consistent patterns of tissue-specific heritability enrichment across populations; for example, in the limbic system for BMI, the per-standardized-annotation effect size
. We observe consistent patterns of tissue-specific heritability enrichment across populations; for example, in the limbic system for BMI, the per-standardized-annotation effect size 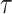 * is 0.16 ± 0.04, 0.28 ± 0.11 and 0.18 ± 0.03 in the Latino-, African American- and European-ancestry populations, respectively. Our approach is a powerful way to analyze genetic data for complex traits from admixed populations.
* is 0.16 ± 0.04, 0.28 ± 0.11 and 0.18 ± 0.03 in the Latino-, African American- and European-ancestry populations, respectively. Our approach is a powerful way to analyze genetic data for complex traits from admixed populations.
Introduction
It is important for human geneticists to study how genetic variants that influence phenotypic variability act in different populations worldwide (1,2). However, to date, most genome-wide association studies (GWAS) have been conducted in populations of European ancestry (3). Non-European ancestry populations, particularly those with largely admixed ancestry such as African American and Latino populations, have been underrepresented in genetic studies. Many statistical methods to analyze genetic data assume homogeneous ancestry, for example by assuming negligible long-range linkage disequilibrium. In order to ensure that the benefits of GWAS are shared beyond individuals of homogeneous ancestry, statistical methods for admixed populations are needed (4).
Among methods to analyze polygenic complex traits in populations of homogeneous ancestry, summary statistics-based methods such as linkage disequilibrium score regression (5,6) (LDSC) and its extensions (7–9) have become particularly popular due to their computational efficiency, relative ease of application and their applicability without raw genotyping data (10). These methods can be used to estimate the proportion of phenotypic variance explained by genotyped variants (SNP-heritability) (7,11,12), distinguish polygenicity from confounding (5), establish relationships between complex phenotypes (7) and model genome-wide polygenic signals to identify key cell types and regulatory mechanisms of human diseases (6,9).
Summary statistics-based methods for polygenic analysis frequently rely on linkage disequilibrium (LD) calculations. For LD score regression, the LD information needed is the LD score for each SNP, defined to be the sum of its pairwise correlations (r2) with all other SNPs. For many populations with homogeneous ancestry, there is a reference panel of individuals with close-enough matching ancestry that can be used to approximate the in-sample LD. For studies with heterogeneous or admixed ancestry, however, even when reference panels are available, they may not be representative of the precise populations used in the genetic study. For example, Latino populations in different regions worldwide may share the same ancestral continental populations, but with dramatic differences in subcontinental ancestry, admixture proportions and timing of the admixture event (13). A generic reference panel cannot easily capture these differences and hence cannot produce accurate LD scores that can be widely used for all Latino populations. Moreover, the structure of LD in heterogeneous and admixed populations is complex and includes longer range correlations that are absent or negligible in homogeneous populations. Thus, while LD scores computed from a matching reference panel reflect the appropriate matching LD for summary statistics computed in many populations of homogeneous ancestry, it has not been clear what the appropriate matching LD is for summary statistics computed in a heterogenous or admixed population, and so LDSC has only been recommended to be applied in populations of homogeneous ancestry.
Here, we evaluate the heritability estimates using LDSC in admixed populations and observe systematic underestimation. We then introduce covariate-adjusted LD score regression (cov-LDSC) to estimate heritability and partitioned heritability in admixed populations. We apply our approach to 8124 participants from the SIGMA study (14) and to 161 894 participants classified by 23andMe (15) as having Latino genetic ancestry, 46 844 classified as having African American genetic ancestry and 134 999 classified as having European genetic ancestry. We analyze three quantitative phenotypes (body mass index (BMI), height and age at menarche), and five dichotomous phenotypes (type 2 diabetes – T2D (available in the SIGMA cohort only), left handedness, morning person, motion sickness and nearsightedness).
One powerful component of LDSC is that it can be used to test whether a particular genome annotation—for example, sets of genes that are specifically expressed within a candidate tissue or cell type—capture more heritability than expected by chance (9,16). We demonstrate that cov-LDSC can be applied in the same way to identify trait-relevant tissue and cell types in admixed and homogenous populations with well-calibrated type I error. We examine height, BMI and morning person since these traits had sufficient statistical power for cell-type enrichment analyses in the 23andMe cohort. We observe a high level of consistency among enriched tissue types, highlighting that the underlying biological processes are shared among studied populations. This heritability enrichment analysis of hundreds of genome annotations in cohorts of over 100 000 individuals would have been challenging with existing genotype-based methods (17–19).
Results
Overview of methods
In this work, we extended the LDSC-based methods to heterogeneous and admixed populations by introducing cov-LDSC. We first showed through derivations that the appropriate matching LD for summary statistics computed in a heterogeneous or admixed population is in-sample LD computed on genotypes that have been adjusted for the same covariates (e.g. principal components) included in the summary statistics (Supplementary Material, Appendix A). In cov-LDSC, we computed these covariate-adjusted LD scores and then used LDSC to estimate heritability and its enrichment (see Materials and Methods). We showed that, unlike LDSC, cov-LDSC produces accurate estimates of heritability with summary statistics from admixed populations (see Materials and Methods, Fig. 1). Furthermore, heritability can be partitioned to identify key gene sets that have disproportionately high heritability. While access to the genotype data of the GWAS samples is required to compute the covariate-adjusted LD scores, LD can be estimated on a random subset of the individuals, preserving the computational efficiency of LDSC and allowing for its application to very large studies. Individual cohorts can also release the in-sample covariate-adjusted LD scores as well as the summary statistics to avoid privacy concerns associated with genotype-level information to facilitate future studies.
Figure 1 .
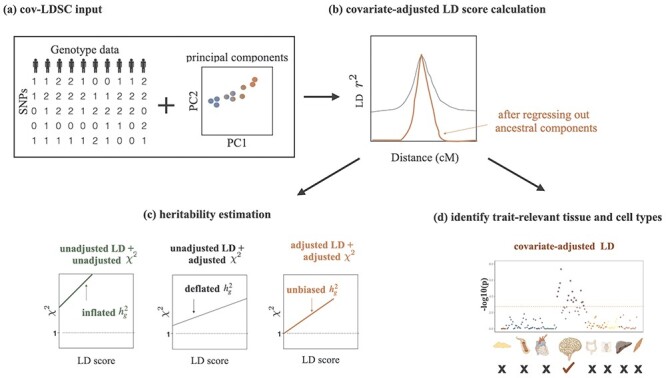
Overview of the covariate-adjusted LD score regression. (a) As input, cov-LDSC takes raw genotypes of collected GWAS samples and their global principal components. (b) cov-LDSC regresses out the ancestral components based on global principal components from the LD score calculation and corrects for long-range admixture LD. Black and red lines indicate estimates before and after covariate adjustments, respectively. (c) Adjusted heritability estimation based on GWAS association statistics (measured by χ2) and covariate-adjusted LD scores. (d) Estimation of heritability enrichment in tissue-specific gene sets.
Robustness of LD score estimation
To demonstrate the effect of admixture on the stability of LD score estimates, we first calculated LD scores with genomic window sizes ranging from 0 to 50 cM in both European (EUR, N = 503) and admixed American (AMR, N = 347) populations from the 1000 Genomes Project (20). As window size increases, we expect the mean LD score to plateau because LD should be negligible for large enough distance. If the mean LD score does not plateau, but continues to rise with increasing window size, then one of two possibilities may apply: first, the window is too small to capture all of the LD; second, the LD scores are capturing long-range pairwise SNP correlations arising from admixture. If this increase is non-linear then there is non-negligible distance-dependent LD, violating LDSC assumptions. Examining unadjusted LD scores, we observed that in the EUR population (5), the mean LD score estimates plateaued at windows beyond 1 cM in size, as previously reported. However, in the AMR population the mean LD score estimates continued to increase concavely with increasing window size. In contrast, when we applied cov-LDSC with 10 PCs to calculate covariate-adjusted LD scores, we observed that LD score estimates plateaued for both EUR and AMR at a 1 and 20 cM window size, respectively (<1% increase per cM, Supplementary Material, Table S1). This suggested that cov-LDSC was able to correct the long-range LD due to admixture and yielded stable estimates of LD scores (see Materials and Methods, Supplementary Material, Fig. S1), and also that cov-LDSC was applicable in homogeneous populations (Supplementary Material, Table S1). The larger window size for the AMR population was needed due to residual LD caused by recent admixture. We next tested the sensitivity of the LD score estimates with regard to the number of PCs included in the cov-LDSC. We observed that in the AMR panel, LD score estimates were unaffected by adding PCs and by increasing window sizes above 20 cM (Supplementary Material, Fig. S2). In practice, we recommend using a 20-cM genomic window and including 10 PCs when estimating LD scores.
Simulation with simulated genotypes
To assess whether cov-LDSC produces less biased estimates of 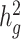 , we simulated genotypes from two admixed populations, based on published demographic models for African American and Latino populations (21,22) (see Methods). We simulated genotypes of 10 000 unrelated diploid admixed individuals for ~400 000 common SNPs on chromosome 2 in a coalescent framework using msprime (23) (see Methods). First, we tested LDSC and cov-LDSC with different admixture proportions between two ancestral populations, and a quantitative phenotype with a
, we simulated genotypes from two admixed populations, based on published demographic models for African American and Latino populations (21,22) (see Methods). We simulated genotypes of 10 000 unrelated diploid admixed individuals for ~400 000 common SNPs on chromosome 2 in a coalescent framework using msprime (23) (see Methods). First, we tested LDSC and cov-LDSC with different admixture proportions between two ancestral populations, and a quantitative phenotype with a 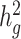 of 0.4 using an additive model (see Methods). We observed that as the proportion of admixture increased,
of 0.4 using an additive model (see Methods). We observed that as the proportion of admixture increased, 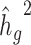 for LDSC increasingly underestimated true
for LDSC increasingly underestimated true 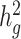 by as much as 18.6%. In marked contrast, cov-LDSC produced consistently less biased estimates regardless of admixture proportion for both the simulated Latino (Supplementary Material, Fig. S3a) and African American (Supplementary Material, Fig. S4) populations. Since we saw consistent results in the two simulated admixed populations, we performed the subsequent simulations in the simulated Latino population only.
by as much as 18.6%. In marked contrast, cov-LDSC produced consistently less biased estimates regardless of admixture proportion for both the simulated Latino (Supplementary Material, Fig. S3a) and African American (Supplementary Material, Fig. S4) populations. Since we saw consistent results in the two simulated admixed populations, we performed the subsequent simulations in the simulated Latino population only.
Second, we varied the percentage of causal variants from 0.01 to 50% in a polygenic quantitative trait with 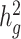 = 0.4 in a population with a fixed admixture proportion of 50%. LDSC again consistently underestimated
= 0.4 in a population with a fixed admixture proportion of 50%. LDSC again consistently underestimated 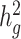 by 12–18.6%. In contrast, cov-LDSC yielded less biased estimates regardless of the percentage of causal variants (Supplementary Material, Fig. S3b).
by 12–18.6%. In contrast, cov-LDSC yielded less biased estimates regardless of the percentage of causal variants (Supplementary Material, Fig. S3b).
Third, we assessed the robustness of LDSC and cov-LDSC for different assumed total 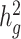 (0.05, 0.1, 0.2, 0.3, 0.4 and 0.5). At each
(0.05, 0.1, 0.2, 0.3, 0.4 and 0.5). At each 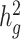 value, LDSC underestimated by 11.5–19.6%. For cov-LDSC, we observed that the standard error increased with
value, LDSC underestimated by 11.5–19.6%. For cov-LDSC, we observed that the standard error increased with 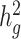 , but point estimates remained less biased (Supplementary Material, Fig. S3c).
, but point estimates remained less biased (Supplementary Material, Fig. S3c).
Fourth, we included an environmental stratification component aligned with the first PC of the genotype data (see Methods), and concluded that cov-LDSC was also robust to confounding (Supplementary Material, Fig. S3d).
Finally, to assess the performance of cov-LDSC in polygenic binary phenotypes, we simulated genotype data for a binary trait with a prevalence of 0.1 assuming a liability threshold model (see Methods). Compared with quantitative traits, cov-LDSC provided slightly more biased results for binary phenotypes. Regardless, we showed that cov-LDSC consistently provided less biased estimates compared with LDSC in the same four simulation scenarios (Supplementary Material, Fig. S5).
Simulation results with real genotypes
We next examined the performance of both unadjusted LDSC and cov-LDSC on real genotypes of individuals from admixed populations. We used genotype data from the SIGMA cohort, a T2D study conducted in Mexico (14). Using ADMIXTURE (24) and populations from the 1000 Genomes Project (20) as reference panels, we observed that each individual in the SIGMA cohort had different admixture proportions (Supplementary Material, Fig. S6), with a distribution of inferred ancestry proportions similar to the 1000 Genomes AMR population. As in the AMR panel, we observed that using a 20-cM window, LD score estimates plateaued in the SIGMA cohort (Supplementary Material, Fig. S7, Table S2), and were unaffected by different numbers of PCs (Supplementary Material, Fig. S8). When we simulated phenotypes using a non-infinitesimal, additive model with 1% of all SNPs to be causal and 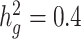 , we observed that cov-LDSC
, we observed that cov-LDSC 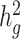 estimates produced less biased estimates using a 20-cM window with 10 PCs (Supplementary Material, Fig. S9). We subsequently used a 20-cM window and 10 PCs in all simulations.
estimates produced less biased estimates using a 20-cM window with 10 PCs (Supplementary Material, Fig. S9). We subsequently used a 20-cM window and 10 PCs in all simulations.
We observed that cov-LDSC yielded less biased 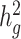 estimates in simulated traits where we varied the number of causal variants and total heritability compared with the original LDSC (Fig. 2a and b). In contrast, LDSC underestimated heritability by as much as 62.5%. To examine the performance of cov-LDSC in the presence of environmental confounding factors, we simulated an environmental stratification component aligned with the first PC of the genotype data, representing European versus Native American ancestry. In this simulation scenario, cov-LDSC still provided less biased
estimates in simulated traits where we varied the number of causal variants and total heritability compared with the original LDSC (Fig. 2a and b). In contrast, LDSC underestimated heritability by as much as 62.5%. To examine the performance of cov-LDSC in the presence of environmental confounding factors, we simulated an environmental stratification component aligned with the first PC of the genotype data, representing European versus Native American ancestry. In this simulation scenario, cov-LDSC still provided less biased 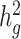 estimates (Fig. 2c). Intercepts of all the simulation scenarios were less than the genomic control (GC) inflation factor, suggesting that polygenicity accounts for a majority of the increase in the mean
estimates (Fig. 2c). Intercepts of all the simulation scenarios were less than the genomic control (GC) inflation factor, suggesting that polygenicity accounts for a majority of the increase in the mean 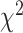 statistic compared with potential confounding biases (Supplementary Material, Fig. S10a–c, Table S3).
statistic compared with potential confounding biases (Supplementary Material, Fig. S10a–c, Table S3).
Figure 2 .
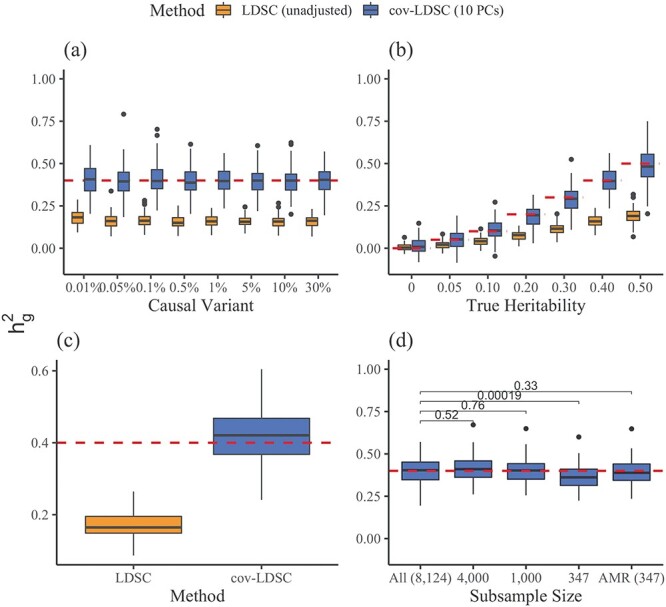
Estimates of heritability ( ) under different simulation scenarios using the SIGMA cohort. LDSC (orange) underestimated
) under different simulation scenarios using the SIGMA cohort. LDSC (orange) underestimated  and cov-LDSC (blue) yielded robust
and cov-LDSC (blue) yielded robust 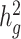 estimates under all settings. Each boxplot represents the mean LD score estimate from 100 simulated phenotypes using the genotypes of 8214 unrelated individuals from the SIGMA cohort. We used a window size of 20 cM in both LDSC and cov-LDSC, and 10 PCs were included in cov-LDSC in all scenarios. A true polygenic quantitative trait with
estimates under all settings. Each boxplot represents the mean LD score estimate from 100 simulated phenotypes using the genotypes of 8214 unrelated individuals from the SIGMA cohort. We used a window size of 20 cM in both LDSC and cov-LDSC, and 10 PCs were included in cov-LDSC in all scenarios. A true polygenic quantitative trait with 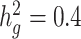 is assumed for scenarios (a), (c) and (d) and 1% causal variants are assumed for scenarios (b)–(d). (a)
is assumed for scenarios (a), (c) and (d) and 1% causal variants are assumed for scenarios (b)–(d). (a) 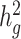 estimation with varying proportions of causal variants (
estimation with varying proportions of causal variants ( ). (b)
). (b) 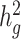 estimation with varying heritabilities (0, 0.05, 0.1, 0.2, 0.3, 0.4 and 0.5). (c)
estimation with varying heritabilities (0, 0.05, 0.1, 0.2, 0.3, 0.4 and 0.5). (c) 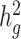 estimation when an environmental stratification component aligned with the first PC of the genotype data was included in the phenotype simulation. (d)
estimation when an environmental stratification component aligned with the first PC of the genotype data was included in the phenotype simulation. (d) 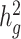 estimation when using a subset of the cohort to obtain LD score estimates and using out-of-sample LD score estimates obtained from admixed American individuals included in the 1000 Genomes Project.
estimation when using a subset of the cohort to obtain LD score estimates and using out-of-sample LD score estimates obtained from admixed American individuals included in the 1000 Genomes Project.
Thus far, we have used cov-LDSC by calculating LD scores on the same set of samples that were used for association studies (in-sample LD scores). In practical applications, computing LD scores on the whole data set can be computationally expensive and difficult to obtain, so we investigated computing LD scores on a subset of samples. To investigate the minimum number of samples required to obtain accurate in-sample LD scores, we computed LD scores on subsamples of 100, 500, 1000 and 5000 individuals from a GWAS of 10 000 simulated genotypes (Supplementary Material, Fig. S11). We repeated these analyses in simulated phenotypes in the SIGMA cohort. We subsampled the SIGMA cohort, and obtained unbiased estimates when using as few as 1000 samples (Fig. 2d). We therefore recommend computing in-sample LD scores on a randomly chosen subset of at least 1000 individuals from a GWAS in our approach.
Assessing power and bias in tissue type specific analysis
Following Finucane et al. (9), we extended cov-LDSC so that we can assess enrichment in and around sets of genes that are specifically expressed in tissue and cell-types (cov-LDSC-SEG). To test whether cov-LDSC can produce robust results with properly controlled type I error, we calculated the in-sample LD scores using LDSC and cov-LDSC, respectively, using a 20-cM window and 10 PCs in cov-LDSC for all 53 baseline and limbic system annotations in the SIGMA cohort. We used PLINK2 (25) for association test and performed tissue type specific enrichment analysis using both LDSC and cov-LDSC for limbic system conditioning on all 53 baseline annotations. We reported the number of significant tests out of 1000 simulations in each scenario. We observed no inflation in false-positive rate (FPR) at 0.05 for both LDSC and cov-LDSC under null (i.e. no enrichment). The greatest gains in power were observed in cases where there was modest enrichment (< 2×). We showed that cov-LDSC-SEG was better powered to detect tissue type specific signals compared with LDSC-SEG (Supplementary Material, Fig. S12).
Heritability estimation in the SIGMA and 23andMe cohorts
We next used cov-LDSC to estimate 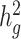 of height, BMI and T2D phenotypes, measured within the SIGMA cohort (see Methods, Table 1). We estimated
of height, BMI and T2D phenotypes, measured within the SIGMA cohort (see Methods, Table 1). We estimated 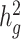 of height, BMI and T2D to be 0.38 ± 0.08, 0.25 ± 0.06 and 0.26 ± 0.07, respectively. These results were similar to reported values from UK Biobank (26,27) and other studies (17,28) of European populations. Although estimates differed in different studies (see Methods), we noted that without cov-LDSC, we would have obtained severely deflated estimates (Table 1). To confirm that our reported heritability estimates were robust under different model assumptions, we applied an alternative approach based on restricted maximum likelihood estimation (REML) in the linear mixed model framework implemented in GCTA (17). To avoid biases introduced from calculating genetic relatedness matrices (GRMs) in admixed individuals, we obtained a GRM based on an admixture-aware relatedness estimation method REAP (29) (see Methods). GCTA-based results were similar to reported
of height, BMI and T2D to be 0.38 ± 0.08, 0.25 ± 0.06 and 0.26 ± 0.07, respectively. These results were similar to reported values from UK Biobank (26,27) and other studies (17,28) of European populations. Although estimates differed in different studies (see Methods), we noted that without cov-LDSC, we would have obtained severely deflated estimates (Table 1). To confirm that our reported heritability estimates were robust under different model assumptions, we applied an alternative approach based on restricted maximum likelihood estimation (REML) in the linear mixed model framework implemented in GCTA (17). To avoid biases introduced from calculating genetic relatedness matrices (GRMs) in admixed individuals, we obtained a GRM based on an admixture-aware relatedness estimation method REAP (29) (see Methods). GCTA-based results were similar to reported 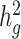 estimates from cov-LDSC, indicating our method was able to provide reliable
estimates from cov-LDSC, indicating our method was able to provide reliable 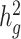 estimates in admixed populations (Table 1). We noted, however, that the GCTA-based results would be computationally expensive to obtain on the much larger datasets, for example the 23andMe cohort described below.
estimates in admixed populations (Table 1). We noted, however, that the GCTA-based results would be computationally expensive to obtain on the much larger datasets, for example the 23andMe cohort described below.
Table 1.
Heritability estimates of height, BMI and T2D using different estimation methods. Reported values are estimates of 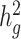 (with standard deviations in brackets) from LDSC using a 20 cM window, cov-LDSC using a 20 cM window and 10 PCs, and GCTA using REAP to obtain the genetic relationship matrix with adjustment by 10 PCs. The final column provides reported
(with standard deviations in brackets) from LDSC using a 20 cM window, cov-LDSC using a 20 cM window and 10 PCs, and GCTA using REAP to obtain the genetic relationship matrix with adjustment by 10 PCs. The final column provides reported 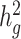 estimates in European populations from various studies (11,24,25)
estimates in European populations from various studies (11,24,25)
We next applied both LDSC and cov-LDSC to a dataset from 23andMe which included 161 894 participants classified by their local ancestry analysis (15) as having Latino genetic ancestry, 46 844 classified as having African American genetic ancestry, and 134 999 classified as having European genetic ancestry. We analyzed three quantitative and four dichotomous phenotypes (see ***Methods, Supplementary Material, Table S4). In this setting, we noted that if new samples were recruited or different individuals were included in different traits of interests, one would need to re-compute the GRM for each trait when using genotype-based methods such as GCTA (17) or BOLT-REML (19). Whereas for cov-LDSC we do not require complete sample overlap between LD reference panel and summary statistics generation. We used a 20-cM window and 10 PCs in LD score calculations for all three populations (Supplementary Material, Fig. S13, Table S5). LDSC and cov-LDSC produced similar heritability estimates in the European ancestry population, whereas in the admixed populations, LDSC consistently provided low estimates of 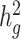 (Supplementary Material, Table S6). For each phenotype, we estimated
(Supplementary Material, Table S6). For each phenotype, we estimated 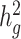 using the same population-specific in-sample LD scores. Intercepts of all the traits were substantially less than the genomic control inflation factor (
using the same population-specific in-sample LD scores. Intercepts of all the traits were substantially less than the genomic control inflation factor (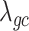 ), suggesting that polygenicity accounts for a majority of the increase in the mean
), suggesting that polygenicity accounts for a majority of the increase in the mean 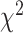 statistics (Supplementary Material, Table S7). To test for heterogeneity of the reported
statistics (Supplementary Material, Table S7). To test for heterogeneity of the reported 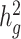 among the three populations, we performed both pairwise t-test between each pair of populations, and the Q statistic for all three populations (Fig. 3, Supplementary Material, Table S8). Among seven tested traits, only age at menarche showed statistically significant differences between different ancestry populations (two-sample t-test P = 7.1 × 10−3 between Latino and European populations, Phet = 0.01). It has been long established that there is population variation in the timing of menarche (30–32). Early menarche might influence the genetic basis of other medically relevant traits since early age at menarche is associated with a variety of chronic diseases such as childhood obesity, coronary heart disease and breast cancer (33,34). These results highlighted the importance of including diverse populations in genetic studies in order to enhance our understanding of complex traits that show differences in their genetic heritability.
among the three populations, we performed both pairwise t-test between each pair of populations, and the Q statistic for all three populations (Fig. 3, Supplementary Material, Table S8). Among seven tested traits, only age at menarche showed statistically significant differences between different ancestry populations (two-sample t-test P = 7.1 × 10−3 between Latino and European populations, Phet = 0.01). It has been long established that there is population variation in the timing of menarche (30–32). Early menarche might influence the genetic basis of other medically relevant traits since early age at menarche is associated with a variety of chronic diseases such as childhood obesity, coronary heart disease and breast cancer (33,34). These results highlighted the importance of including diverse populations in genetic studies in order to enhance our understanding of complex traits that show differences in their genetic heritability.
Figure 3 .
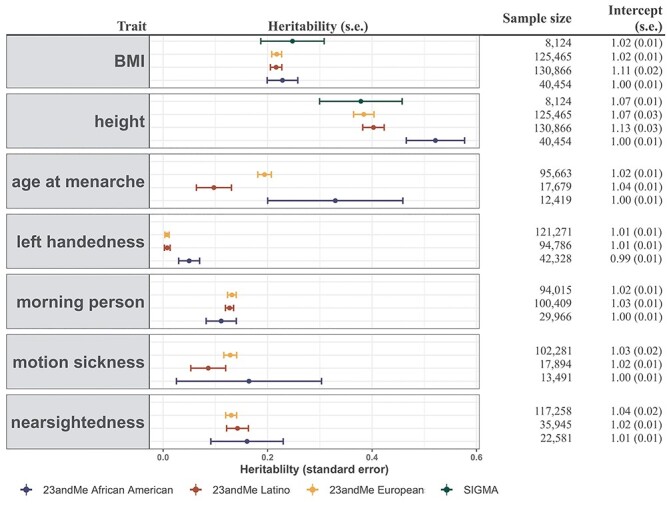
Estimates of heritability (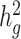 ) of three quantitative and four dichotomous traits in two admixed populations in the 23andMe research cohort. For seven selected non-disease phenotypes (BMI, height, age at menarche, left handedness, morning person, motion sickness and nearsightedness) in the 23andMe cohort, we reported their estimated genetic heritability and intercepts (and their standard errors) using the baseline model. LD scores were calculated using 134 999 individuals with European ancestry, 161 894 with Latino ancestry, and 46 844 individuals with African American ancestry from the 23andMe cohort, respectively. For each trait, we reported the sample size in obtained summary statistics used in cov-LDSC. For BMI and height, we also reported the
) of three quantitative and four dichotomous traits in two admixed populations in the 23andMe research cohort. For seven selected non-disease phenotypes (BMI, height, age at menarche, left handedness, morning person, motion sickness and nearsightedness) in the 23andMe cohort, we reported their estimated genetic heritability and intercepts (and their standard errors) using the baseline model. LD scores were calculated using 134 999 individuals with European ancestry, 161 894 with Latino ancestry, and 46 844 individuals with African American ancestry from the 23andMe cohort, respectively. For each trait, we reported the sample size in obtained summary statistics used in cov-LDSC. For BMI and height, we also reported the 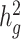 estimates from the SIGMA cohort.
estimates from the SIGMA cohort.
Tissue type specific analysis in the 23andMe cohort
We applied stratified cov-LDSC to sets of specifically expressed genes (9) (SEG) to identify trait-relevant tissue and cell types in traits included in the 23andMe cohort in the European-, Latino-, and African American-ancestry populations. We only tested height, BMI and morning person, which were the three traits that had heritability z-scores larger than seven (6) in at least two populations (Supplementary Material, Table S9). We also performed inverse-variance weighting meta-analysis across the three populations (Supplementary Material, Table S10).
Across different populations, BMI showed consistent enrichment in central nervous system gene sets. In the European ancestry population, most of the enrichments recapitulated the results from a previous analysis using UK Biobank (9,26). We found similar but fewer enrichments in the Latino- and African American-ancestry populations, most likely due to smaller sample sizes. The most significantly enriched tissue types for BMI in all three populations were limbic system (τ*EUR = 0.18, τ*LAT = 0.16, τ*AA = 0.28, τ*meta = 0.18, Phet = 0.63), entorhinal cortex (τ*EUR = 0.18, τ*LAT = 0.15, τ*AA = 0.24, τ*meta = 0.17, Phet = 0.80) and cerebral cortex (τ*EUR = 0.16, τ*LAT = 0.14, τ*AA = 0.15, τ*meta = 0.15, Phet = 0.98); none of the three effects were significantly different across populations, suggesting key tissue types for BMI are shared among different ancestry populations. When we compared the enrichment for all of the tissues between population pairs, we observed that they have significant non-zero concordance correlation coefficient (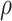 EUR-LAT = 0.78 (95% CI: 0.72–0.83),
EUR-LAT = 0.78 (95% CI: 0.72–0.83), 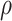 EUR-AA = 0.32 (95% CI: 0.21–0.42)) (Fig. 4a–e, Supplementary Material, Table S11). The sizes of these three brain structures have been shown to be correlated with BMI using magnetic resonance imaging data (35). The midbrain and the limbic system are highly involved in the food rewarding signals through dopamine releasing pathway (36). Furthermore, the hypothalamus in the limbic system releases hormones that regulate appetite, energy homeostasis and metabolisms, like leptin, insulin and ghrelin (36,37).
EUR-AA = 0.32 (95% CI: 0.21–0.42)) (Fig. 4a–e, Supplementary Material, Table S11). The sizes of these three brain structures have been shown to be correlated with BMI using magnetic resonance imaging data (35). The midbrain and the limbic system are highly involved in the food rewarding signals through dopamine releasing pathway (36). Furthermore, the hypothalamus in the limbic system releases hormones that regulate appetite, energy homeostasis and metabolisms, like leptin, insulin and ghrelin (36,37).
Figure 4 .
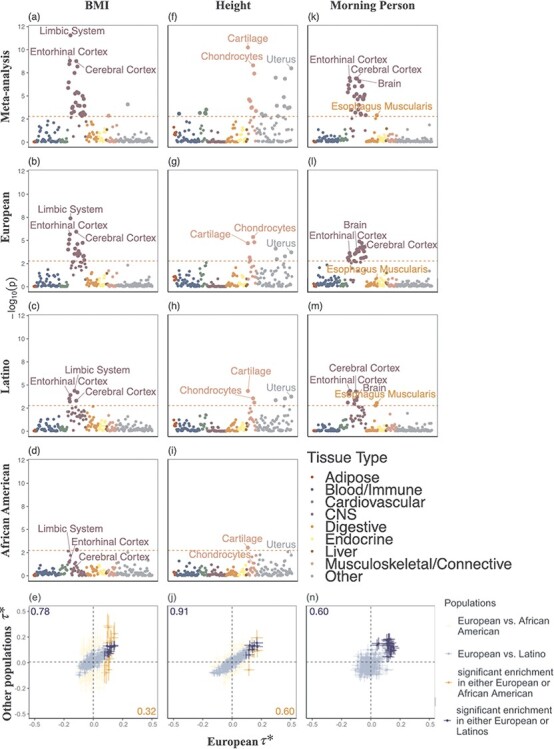
Results of multiple-tissue analysis for height, BMI and morning person. Each point represents a tissue type from either the GTEx data set or the Franke lab data set as defined in Finucane et al. (9). From top to bottom, (a–d) show multiple-tissue analysis for BMI in the cross-population meta-analysis and in European-, Latino- and African American-ancestry, respectively. (e) shows the scatter plot of the estimated per-standardized-annotation effect size τ*, which represents the proportional change of averaged per-SNP heritability for one standard deviation increase in value of the annotation of each cell type, conditional on other 53 non-cell type specific baseline annotations, in the three populations for all tested tissue types (see Methods). The x-axis shows the τ* in European population and the y-axis shows either τ* in Latino (blue) or in African American (orange) population. We reported the slope and P-value when we regress Latino (blue) and African American (orange) population τ* on European population τ* for all tissue types. Error bars indicate standard errors of τ*. Similarly, the results are shown in (f)–(j) for height and (k)–(n) for morning person. The significance threshold in plots (a)-(d), (f-i) and (k-m) is defined by the FDR < 5% cutoff, −log10(P) = 2.75. Numerical results are reported in Supplementary Material, Table S10.
For height, we also identified previously reported enrichments in the gene sets derived from musculoskeletal and connective tissues (9). In the meta-analysis, the three most significant enrichments were cartilage (τ*EUR = 0.21, τ*LAT = 0.19, τ*AA = 0.24, τ*meta = 0.20, Phet = 0.84), chondrocytes (τ*EUR = 0.21, τ*LAT = 0.15, τ*AA = 0.11, τ*meta = 0.17, Phet = 0.40) and uterus (τ*EUR = 0.17, τ*LAT = 0.15, τ*AA = 0.16, τ*meta = 0.16, Phet = 0.93). A heterogeneity test revealed no difference across three populations (I2 < 70% and Phet > 0.05), suggesting again that the key tissue types for height are shared among different ancestry populations. The concordance correlation coefficients were  EUR-LAT = 0.91 (95% CI: 0.89–0.93) between European- and Latino-ancestry populations;
EUR-LAT = 0.91 (95% CI: 0.89–0.93) between European- and Latino-ancestry populations;  EUR-LAT = 0.60 (95% CI: 0.50–0.68) between European- and African American ancestry populations (Fig. 4f–j, Supplementary Material, Table S11). The importance of these tissues and their roles in height have been addressed in the previous pathway analysis, expression quantitative trait loci (eQTLs) and epigenetic profiling (38,39). Previous studies have shown that the longitudinal growth of bones is partly controlled by the number and proliferation rate of chondrocytes on the growth plate, which is a disk of cartilages (40).
EUR-LAT = 0.60 (95% CI: 0.50–0.68) between European- and African American ancestry populations (Fig. 4f–j, Supplementary Material, Table S11). The importance of these tissues and their roles in height have been addressed in the previous pathway analysis, expression quantitative trait loci (eQTLs) and epigenetic profiling (38,39). Previous studies have shown that the longitudinal growth of bones is partly controlled by the number and proliferation rate of chondrocytes on the growth plate, which is a disk of cartilages (40).
For the morning person phenotype, we found enrichments in many brain tissues in the European ancestry population, concordant with a previous study (41). Entorhinal cortex (τ*EUR = 0.16, τ*LAT = 0.22, τ*meta = 0.18, Phet = 0.40), cerebral cortex (τ*EUR = 0.15, τ*LAT = 0.22, τ*meta = 0.18, Phet = 0.34), and brain (τ*EUR = 0.17, τ*LAT = 0.19, τ*meta = 0.18, Phet = 0.82) were enriched in both the Latino- and European-ancestry populations. Evidence showed that circadian rhythm was controlled by the suprachiasmatic nucleus, the master clock in our brain, and also the circadian oscillator that resides in neurons of the cerebral cortex (42–44). We also found unique enrichments of esophagus muscularis and the esophagus gastroesophageal junction in the Latino populations, but the heterogeneity test showed that the difference is not significant (I2 = 49% and 50%; Phet = 0.16 and 0.16, for esophagus gastroesophageal junction and muscularis, respectively). We observed that the concordance correlation coefficient across gene sets was  EUR-LAT = 0.63 (95% CI: 0.51–0.68) between the Latino- and European-ancestry populations (Fig. 4k–n, Supplementary Material, Table S11). Compared with the original LDSC-SEG, cov-LDSC-SEG appeared to have increased statistical power in detecting tissue type specific enrichment in the African American- and Latino-ancestry population (Supplementary Material, Figs S12–S16).
EUR-LAT = 0.63 (95% CI: 0.51–0.68) between the Latino- and European-ancestry populations (Fig. 4k–n, Supplementary Material, Table S11). Compared with the original LDSC-SEG, cov-LDSC-SEG appeared to have increased statistical power in detecting tissue type specific enrichment in the African American- and Latino-ancestry population (Supplementary Material, Figs S12–S16).
Discussion
As we expand genetic studies to explore admixed populations around the world, extending statistical genetics methods to make inferences within admixed populations is crucial. This is particularly true for methods based on summary statistics, which are dependent on the use of LD scores that we showed to be problematic in admixed populations. In this study, we confirmed that LDSC, originally designed for populations of homogeneous ancestry, should not be applied to admixed populations. We introduced cov-LDSC, which regresses out global PCs on individual genotypes during the LD score calculation, and showed it can yield less biased LD scores and estimates of heritability and its enrichments, including trait-relevant cell and tissue type enrichments, in homogenous and admixed populations.
We applied cov-LDSC to approximately 344 000 individuals classified by 23andMe as having European, African American, and Latin American ancestry, and we observed mostly consistent results across the three populations. For age at menarche, though, we observed evidence of heritability differences across different populations. Differences in environmental exposures and allele frequencies can both contribute to the observed differences in genetic heritability across populations. These differences highlight the importance of studying diverse populations.
We next extended cov-LDSC to partition heritability by different cell type- and tissue-specific annotations to investigate trait-relevant tissue and cell types. We detected a broad range of enrichments that recapitulate known biology in height, BMI and morning person. Our results demonstrated that although there are some cases of nominal heterogeneity across ancestry populations among tested tissue-types, most of the tissue-specific enrichments are consistent among the populations studied here. This is consistent with the previous findings that show strong correspondence in functional and cell type enrichment between European and East Asian ancestry populations (45,46). Seeing the same tissue-type for a single trait emerge in multiple populations can give us more confidence that this tissue may account for polygenic heritability. Larger sample sizes are needed to increase the power of our current analyses and to enhance our understanding of how genetic variants that are responsible for heritable phenotypic variability are similar and different among ancestry populations.
Although our work provides a novel, efficient approach to estimate genetic heritability and to identify trait-relevant cell and tissue types using summary statistics in admixed populations, it has a few limitations.
First, covariates included in the summary statistics should match the covariates included in the covariate-adjusted LD score calculations (Supplementary Material, Appendix A). To demonstrate this, we simulated the phenotypes using real genotypes included in the SIGMA cohort. We performed cov-LDSC to measure total heritability and its enrichment with a varied number of PCs included in summary statistics and in LD score calculation. As the differences between the number of PCs included in the summary statistics and LD score calculation increase, we observed an increase in bias of the total heritability estimation (Supplementary Material, Fig. S17) and a loss in power when detecting tissue-specific enrichment (Supplementary Material, Fig. S18).
Second, 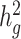 estimates and their enrichment in admixed populations are more sensitive to potentially unmatched LD reference panels. Unmatched reference panels are likely to produce biased estimates and under-powered enrichment analysis (47,48) (Supplementary Material, Table S12, Figs S19–S21). We examined the performance of using an out-of-sample reference panel in admixed populations (Supplementary Material, Appendix B) and caution that when using 1000 Genomes Project (20) or any out-of-sample reference panels for a specific admixed cohort, users should ensure that the demographic histories are shared between the reference and the study cohort (Supplementary Material, Figs S22 and S23). Large sequencing projects such as TOPMed (49) that include large numbers (N > 1000) of admixed samples can potentially serve as out-of-sample LD reference panels, although further investigations are needed to study their properties. We therefore advise to compute in-sample LD scores from the full or a random subset of data (N > 1000) used to generate the admixed GWAS summary statistics when possible. We have released open-source software implementing our approach based on all genome annotations derived previously (URLs). We strongly encourage cohorts to release their summary statistics and in-sample covariate-adjusted LD scores at the same time to facilitate future studies.
estimates and their enrichment in admixed populations are more sensitive to potentially unmatched LD reference panels. Unmatched reference panels are likely to produce biased estimates and under-powered enrichment analysis (47,48) (Supplementary Material, Table S12, Figs S19–S21). We examined the performance of using an out-of-sample reference panel in admixed populations (Supplementary Material, Appendix B) and caution that when using 1000 Genomes Project (20) or any out-of-sample reference panels for a specific admixed cohort, users should ensure that the demographic histories are shared between the reference and the study cohort (Supplementary Material, Figs S22 and S23). Large sequencing projects such as TOPMed (49) that include large numbers (N > 1000) of admixed samples can potentially serve as out-of-sample LD reference panels, although further investigations are needed to study their properties. We therefore advise to compute in-sample LD scores from the full or a random subset of data (N > 1000) used to generate the admixed GWAS summary statistics when possible. We have released open-source software implementing our approach based on all genome annotations derived previously (URLs). We strongly encourage cohorts to release their summary statistics and in-sample covariate-adjusted LD scores at the same time to facilitate future studies.
Third, in our work, we chose to report the genetic heritability tagged by common (minor allele frequency – MAF ≥ 5%) HapMap3 variants, including tagged causal effects of both common and low-frequency variants (see Methods). We noted this quantity is different from the heritability casually explained by all common SNPs excluding tagged causal effects of low-frequency variants as reported in the original LDSC (5,50)). Recent studies have shown that heritability estimates can be sensitive to the choice of the LD- and frequency-dependent heritability model (12,16,50–52). However, as mentioned above, we do not currently have data necessary to estimate MAF-stratified heritability due to the lack of a sequencing reference panel. Regardless, our approach provides a good foundation for addressing the question of how to incorporate ancestry-dependent frequencies in the LD-dependent annotations, and to understand frequency-dependent heritability architecture in the future (Methods).
Fourth, as a generalized form of LDSC, cov-LDSC shares some of the same limitations and properties as LDSC. For example, when a trait is less polygenic (proportion of causal variants is <0.01%), cov-LDSC may yield biased 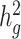 estimates (Supplementary Material, Fig. S3b). Moreover, recent work has shown that LDSC can provide biased estimates in the presence of extreme ascertainment for dichotomous phenotypes (53). Adapting cov-LDSC into case–control studies under strong binary effects remains a potential avenue for future work.
estimates (Supplementary Material, Fig. S3b). Moreover, recent work has shown that LDSC can provide biased estimates in the presence of extreme ascertainment for dichotomous phenotypes (53). Adapting cov-LDSC into case–control studies under strong binary effects remains a potential avenue for future work.
Fifth, summary statistics derived from linear mixed models cannot currently be used for cov-LDSC analysis (Supplementary Material, Fig. S24). This is due to the fact that, just as the LD needs to be adjusted for the same covariates included in the summary statistics (Supplementary Material, Appendix A), it also needs to be corrected appropriately for the random effect. We leave efficient computation of random effect-adjusted LD scores to future work.
Despite these limitations, in comparison with other methods, such as those based on REML (17,19) with an admixture-aware GRM (29), for estimating 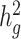 in heterogeneous or admixed populations, cov-LDSC has a number of attractive properties. First, covariate-adjusted in-sample LD scores can be obtained with a subset of samples, enabling analysis of much larger cohorts than was previously possible (Supplementary Material, Fig. S25). Second, LD scores only need to be calculated once per cohort; this is particularly useful in large cohorts such as 23andMe and UK Biobank (26), where multiple phenotypes have been collected per individual and per-trait heritability and its enrichment can be estimated based on the same LD scores. Third, as a generalized form of LDSC, it is robust to population stratification and cryptic relatedness in both homogenous and admixed populations (Supplementary Material, Fig. S26). Fourth, similar to the original LDSC methods, cov-LDSC can be extended to perform analyses such as estimating genetic correlations (Supplementary Material, Fig. S27), partitioning
in heterogeneous or admixed populations, cov-LDSC has a number of attractive properties. First, covariate-adjusted in-sample LD scores can be obtained with a subset of samples, enabling analysis of much larger cohorts than was previously possible (Supplementary Material, Fig. S25). Second, LD scores only need to be calculated once per cohort; this is particularly useful in large cohorts such as 23andMe and UK Biobank (26), where multiple phenotypes have been collected per individual and per-trait heritability and its enrichment can be estimated based on the same LD scores. Third, as a generalized form of LDSC, it is robust to population stratification and cryptic relatedness in both homogenous and admixed populations (Supplementary Material, Fig. S26). Fourth, similar to the original LDSC methods, cov-LDSC can be extended to perform analyses such as estimating genetic correlations (Supplementary Material, Fig. S27), partitioning 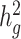 by functional annotations, identifying disease-relevant tissue and cell types and multi-trait analysis (6,9,54,55).
by functional annotations, identifying disease-relevant tissue and cell types and multi-trait analysis (6,9,54,55).
Finally, we would like to note that ‘African American’ and ‘Latino’ are both terms with many definitions and, while self-identified African American and Latino individuals often have admixed ancestry, neither group can be defined in purely genetic terms. Here, we have analyzed sets of individuals that were classified by 23andMe as having African American or Latino ancestry based on local ancestry inference, but because these groups were defined based on genetics, they may not have perfect agreement with the more common definitions of ‘African American’ and ‘Latino.’ Moreover, there is a great deal of genetic diversity within self-identified African American and Latino populations; analysis of sub-populations within these broad populations is a direction for future work.
As the number of admixed and other diverse GWAS and biobank data become readily available (1, 49, 56), our approach provides a powerful way to study admixed populations.
Materials and Methods
Mathematical framework of cov-LDSC
Details of the mathematical derivation of cov-LDSC are presented in Supplementary Material, Appendix A. Briefly, in the standard polygenic model on which LDSC is based, 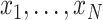 are the length-
are the length- 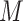 genotype vectors for the
genotype vectors for the 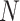 individuals, where
individuals, where 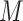 is the number of SNPs. We model the phenotypes
is the number of SNPs. We model the phenotypes 
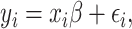 where
where 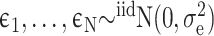 and
and 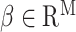 is a vector of per-normalized-genotype effect sizes, which we model as random with mean zero. In standard LDSC, the variance of
is a vector of per-normalized-genotype effect sizes, which we model as random with mean zero. In standard LDSC, the variance of 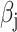 , var(
, var(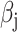 ), is the per-SNP heritability of SNP
), is the per-SNP heritability of SNP 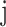 , that is, the total SNP-heritability
, that is, the total SNP-heritability 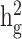 divided by the total number of SNPs
divided by the total number of SNPs 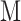 (
(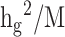 ). In stratified LD score regression the variance of
). In stratified LD score regression the variance of 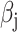 depends on a set of genome annotations.
depends on a set of genome annotations.
Let 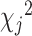 denote the chi-square statistic for the jth SNP, approximately equal to
denote the chi-square statistic for the jth SNP, approximately equal to 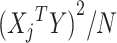 , where
, where 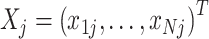 and
and 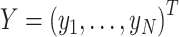 . The main equation on which LDSC is based is:
. The main equation on which LDSC is based is:
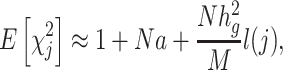 |
(1) |
where 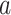 is a constant that reflects population structure and other sources of confounding, and the LD score,
is a constant that reflects population structure and other sources of confounding, and the LD score, 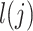 , is:
, is: 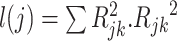 is the correlation between SNPs
is the correlation between SNPs 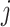 and
and 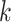 in the underlying population. A new derivation for this equation is given in Supplementary Material, Appendix A. We estimate the total SNP-heritability
in the underlying population. A new derivation for this equation is given in Supplementary Material, Appendix A. We estimate the total SNP-heritability 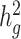 via weighted regression of
via weighted regression of 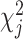 on our estimates of
on our estimates of 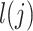 , evaluating significance with a block jackknife across SNPs (6).
, evaluating significance with a block jackknife across SNPs (6).
In the absence of covariates, the LD scores can be estimated from an external reference panel such as 1000 Genomes, as long as the correlation structure in the reference panel matches the correlation structure of the sample. In most homogeneous populations, we can also assume that the true underlying correlation is negligible outside of a 1-cM window.
In the presence of covariates, we let 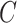 denote the N × K matrix of covariates, each column centered to mean zero, and let
denote the N × K matrix of covariates, each column centered to mean zero, and let 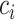 be the
be the 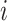 th row of
th row of 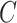 . Equation (1) can then be replaced with
. Equation (1) can then be replaced with 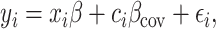 where
where 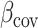 is a vector of effect sizes of covariates. We can project the covariates out of this equation by multiplying by P = I – C (CT C)–1CT on the left to get
is a vector of effect sizes of covariates. We can project the covariates out of this equation by multiplying by P = I – C (CT C)–1CT on the left to get
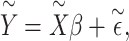 |
(2) |
where 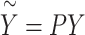 ,
, 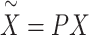 and
and 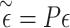 (if the covariates are genotype principal components, then
(if the covariates are genotype principal components, then 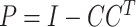 ). Under this model, an equation identical to Equation (2) can be derived, but where both summary statistics and LD are adjusted for the same covariates (Supplementary Material, Appendix A).
). Under this model, an equation identical to Equation (2) can be derived, but where both summary statistics and LD are adjusted for the same covariates (Supplementary Material, Appendix A).
If 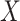 is a homogeneous population, then the covariate-adjusted LD will be similar to the non-covariate-adjusted LD and well-approximated by a reference panel. However, if
is a homogeneous population, then the covariate-adjusted LD will be similar to the non-covariate-adjusted LD and well-approximated by a reference panel. However, if 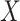 is the genotype matrix from an admixed or heterogeneous population and the covariates include PCs, then the covariate-adjusted LD is no longer well-approximated by either non-covariate-adjusted LD or by a reference panel. Thus, in cov-LDSC, we compute LD scores directly from the covariate-adjusted in-sample genotypes or a random subsample thereof. We call them the covariate-adjusted LD scores.
is the genotype matrix from an admixed or heterogeneous population and the covariates include PCs, then the covariate-adjusted LD is no longer well-approximated by either non-covariate-adjusted LD or by a reference panel. Thus, in cov-LDSC, we compute LD scores directly from the covariate-adjusted in-sample genotypes or a random subsample thereof. We call them the covariate-adjusted LD scores.
Using genotype data to compute LD scores means that the model being fit is based on the joint effects of a sparser set of SNPs, e.g. the genotyped SNPs, than when sequence data are used to compute LD scores. For estimating total SNP-heritability, this means that cov-LDSC estimates the same estimand as GCTA (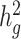 ) and not the usual estimand of LDSC (
) and not the usual estimand of LDSC (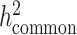 ; see below). For partitioned heritability, the density of reference panel SNPs can be important because the joint effect of a SNP in an annotation can include the tagged effect of an untyped SNP that is not in the annotation, deflating estimates of enrichment. Thus, we recommend using cov-LDSC only on annotations made of large contiguous regions, such as gene sets. Moreover, we urge caution when interpreting quantitative estimates of heritability enrichment. Here, we look at the significance of the conditional enrichment (i.e. regression coefficient) of gene sets for our tissue-specific analysis (see below).
; see below). For partitioned heritability, the density of reference panel SNPs can be important because the joint effect of a SNP in an annotation can include the tagged effect of an untyped SNP that is not in the annotation, deflating estimates of enrichment. Thus, we recommend using cov-LDSC only on annotations made of large contiguous regions, such as gene sets. Moreover, we urge caution when interpreting quantitative estimates of heritability enrichment. Here, we look at the significance of the conditional enrichment (i.e. regression coefficient) of gene sets for our tissue-specific analysis (see below).
Window size and number of PCs in LD score calculations
In addition to computing LD from the covariate-adjusted genotypes, we also investigate the appropriate window size for estimating LD scores. To do this, we examine the effect of varying the genomic window size for both simulated and real data sets. We determine that LD score estimates were robust to the choice of window size if the increase in the mean LD score estimates was less than 1% per cM beyond a given window. Using this criterion, we use window sizes of 5 and 20 cM for the simulated and real genotypes, respectively (Supplementary Material, Tables S13, S2 and S5). We also calculate the squared correlations between LD score estimates using the chosen window size and other LD score estimates with window sizes larger than the chosen window. The Pearson’s squared correlations were greater than 0.99 in all cases (Supplementary Material, Tables S14–S16) indicating the LD score estimates were robust at the chosen window sizes.
Similarly, to determine the number of PCs needed to be included in the GWAS association tests and cov-LDSC calculations, we examine the effect of varying the genomic window size using different numbers of PCs. The number of PCs that needed to be included for covariate adjustment depended on the population structure for different datasets.
Genotype simulations
We evaluate the performance of LDSC and cov-LDSC with simulated phenotypes and both simulated and real genotypes. For the simulated genotypes, we used msprime version 0.6.1 (23) to simulate population structure with mutation rate 2 × 10−8 and recombination maps from the HapMap Project (57). We adapt the demographic model from Mexican migration history (21) for Latino population and the out of Africa model (22) for African American population using parameters that were previously inferred from the 1000 Genomes Project (20). We assume the admixture event happened ~500 years and 200 years ago for Latino and African American populations, respectively. We set different admixture proportions to reflect different admixed populations. In each population, we simulate 10 000 individuals after removing second degree related samples (kinship > 0.125) using KING (58).
Slim Initiative in Genomic Medicine for the Americas Type 2 Diabetes cohort
We analyzed 8214 samples that are genotyped with the Illumina HumanOmni2.5 array. We further filter the genotyped data to be MAF ≥ 5%. Prior to the PC analysis, we pruned all SNPs in LD (r2 > 0.2) and removed all the SNPs in the high LD regions (such as the MHC region) because these can overly influence the principal components model (59). After QC, a total of 8214 individuals and 943 244 SNPs remain. We estimate the in-sample LD score with a 20-cM window and 10 PCs in all scenarios.
We use these genotypes for simulations. We also analyze three phenotypes from the SIGMA cohort: height, BMI and T2D. For T2D, we assume a reported prevalence in Mexico of 0.144 (14). For each phenotype, we include age, sex, and the first 10 PCs as fixed effects in the association analyses.
Phenotype simulations
We simulate phenotypes with two different polygenic genetic architectures, given by GCTA (17) and the baseline model (6), respectively. In the GCTA model, all variants are equally likely to be causal independent of their functional or MAF structure, and the standardized causal effect size variance is constant, i.e. 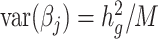 . In contrast, the baseline model incorporates functionally dependent architectures. Briefly, it includes 53 overlapping genome-wide functional annotations (e.g. coding, conserved, regulatory). It models
. In contrast, the baseline model incorporates functionally dependent architectures. Briefly, it includes 53 overlapping genome-wide functional annotations (e.g. coding, conserved, regulatory). It models 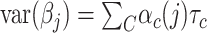 , where
, where 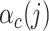 is the value of annotation
is the value of annotation 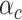 at variant
at variant 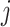 and
and  represents the per-variant contribution, of one unit of the annotation
represents the per-variant contribution, of one unit of the annotation 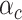 , to heritability. We generate all causal variants among common observed variants with MAF ≥ 5% (~40 000 SNPs in simulated genotypes and 943 244 SNPs in the SIGMA cohort). To represent environmental stratification, similar to previously described (5), we add 0.2× standardized first principal component to the standardized phenotypes.
, to heritability. We generate all causal variants among common observed variants with MAF ≥ 5% (~40 000 SNPs in simulated genotypes and 943 244 SNPs in the SIGMA cohort). To represent environmental stratification, similar to previously described (5), we add 0.2× standardized first principal component to the standardized phenotypes.
We simulate both quantitative and case–control traits with both GCTA and baseline model genetic architectures, using both simulated and real genotypes, varying the number of causal variants, the true heritability and environmental stratification. For case–control simulations, we adopt a liability threshold model with disease prevalence 0.1. We simulated 50 000 admixed individuals and simulated continuous liability scores. We extracted individuals with top 10% liability as cases and randomly selected 5000 individuals from the rest as control samples for each simulation scenario.
To obtain summary statistics for the simulated traits, we apply single-variant linear models for quantitative traits and logistic models for binary trait both with 10 PCs as covariates in association analyses using PLINK2 (25).
23andMe cohort
All participants were drawn from the customer base of 23andMe, Inc., a direct to consumer genetics company. Participants provided informed consent and participated in the research online, under a protocol approved by the external AAHRPP-accredited IRB, Ethical & Independent Review Services (www.eandireview.com). Samples from 23andMe are then chosen from consented individuals who were genotyped successfully on an Illumina Infinium Global Screening Array (~640 000 SNPs) supplemented with ~50 000 SNPs of custom content. We restrict participants to those who have European, African American or Latino ancestry determined through an analysis of local ancestry (15).
To compute LD scores in each ancestry population, we use both genotyped and imputed SNPs. We filter genotyped variants with a genotype call rate  90% non-zero self-chain score, strong evidence of Hardy Weinberg disequilibrium (P > 10−20 to accommodate large sample sizes included for detecting deviations), and failing a parent-offspring transmission test. For imputed variants, we use a reference panel that combined the May 2015 release of the 1000 Genomes Phase 3 haplotypes with the UK10K imputation reference panel (60). Imputed dosages are rounded to the nearest integer (0, 1, 2) for downstream analysis. We filter variants with imputation r2
90% non-zero self-chain score, strong evidence of Hardy Weinberg disequilibrium (P > 10−20 to accommodate large sample sizes included for detecting deviations), and failing a parent-offspring transmission test. For imputed variants, we use a reference panel that combined the May 2015 release of the 1000 Genomes Phase 3 haplotypes with the UK10K imputation reference panel (60). Imputed dosages are rounded to the nearest integer (0, 1, 2) for downstream analysis. We filter variants with imputation r2  0.9. We also filter genotyped and imputed variants for batch effects (if an F-test from an ANOVA of the SNP dosages against a factor dividing genotyping date into 20 roughly equal-sized buckets has a P-value less than 10−50) and sex-dependent effects (if the r-squared of the SNP is greater than 0.01 after fitting a linear regression against the gender). To minimize rounding inaccuracies, we prioritize genotyped SNPs over imputed SNPs in the merged SNP set. We restrict the merged SNP set to HapMap3 variants with MAF ≥ 5%. We measure LD scores in a subset of African American (N = 61 021) and Latino individuals (N = 9990) on chromosome 2 with different window sizes from 1 to 50 cM (Supplementary Material, Table S5) and squared correlation between different window sizes (Supplementary Material, Table S16). We compute all LD scores with a 20 cM window.
0.9. We also filter genotyped and imputed variants for batch effects (if an F-test from an ANOVA of the SNP dosages against a factor dividing genotyping date into 20 roughly equal-sized buckets has a P-value less than 10−50) and sex-dependent effects (if the r-squared of the SNP is greater than 0.01 after fitting a linear regression against the gender). To minimize rounding inaccuracies, we prioritize genotyped SNPs over imputed SNPs in the merged SNP set. We restrict the merged SNP set to HapMap3 variants with MAF ≥ 5%. We measure LD scores in a subset of African American (N = 61 021) and Latino individuals (N = 9990) on chromosome 2 with different window sizes from 1 to 50 cM (Supplementary Material, Table S5) and squared correlation between different window sizes (Supplementary Material, Table S16). We compute all LD scores with a 20 cM window.
In genome-wide association analyses, for each ancestry population, we choose a maximal set of unrelated individuals for each analysis using a segmental identity-by-descent (IBD) estimation algorithm (61). We define individuals to be related if they share more than 700 cM IBD.
We perform association tests using linear regression model for quantitative traits and logistic regression model for binary traits assuming additive allelic effects. We include covariates for age, sex and the top 10 PCs to account for residual population structure in height, BMI, morning person, motion sickness, left handedness and nearsightedness. For age at menarche, we studied only female subjects and included age and top 10 PCs as covariates. We list details of phenotypes and genotypes in Supplementary Material, Table S4.
Heritability estimation
We calculate in-sample LD scores using both a non-stratified LD score model (5) and the baseline model (6) for each studied ancestry population. In simulated phenotypes generated with the GCTA model, we use non-stratified LDSC to estimate heritability. In simulated phenotypes generated using the baseline model, we use LDSC-baseline to estimate heritability. We use the 53 non-frequency dependent annotations included in the baseline model to estimate 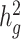 in the 23andMe research database and the SIGMA cohort real phenotypes. We recognize that recent studies have shown that genetic heritability can be sensitive to the choice of LD-dependent heritability model (8,12,16). However, understanding the LD- and MAF-dependence of complex trait genetic architecture is an important but complex endeavor potentially requiring both modeling of local ancestry as well as large sequenced reference panels that are currently unavailable. We thus leave this complexity for future work.
in the 23andMe research database and the SIGMA cohort real phenotypes. We recognize that recent studies have shown that genetic heritability can be sensitive to the choice of LD-dependent heritability model (8,12,16). However, understanding the LD- and MAF-dependence of complex trait genetic architecture is an important but complex endeavor potentially requiring both modeling of local ancestry as well as large sequenced reference panels that are currently unavailable. We thus leave this complexity for future work.
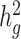 versus
versus 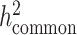
The quantity (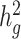 ) we reported in the main analysis is defined as heritability tagged by HapMap3 variants with MAF ≥ 5%, including tagged causal effects of both low-frequency and common variants. This quantity is different from
) we reported in the main analysis is defined as heritability tagged by HapMap3 variants with MAF ≥ 5%, including tagged causal effects of both low-frequency and common variants. This quantity is different from 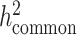 , the heritability casually explained by all common SNPs excluding tagged causal effects of low-frequency variants, reported in the original LDSC (5). In European and other homogeneous populations, it is possible to estimate
, the heritability casually explained by all common SNPs excluding tagged causal effects of low-frequency variants, reported in the original LDSC (5). In European and other homogeneous populations, it is possible to estimate 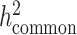 , since reference panels, such as 1000 Genomes Project (20), are available which include >99% of the SNPs with frequency > 1%. However, in-sample sequence data are usually not available for an admixed GWAS cohort, and so cov-LDSC can only include genotyped SNPs in the reference panel, and thus can only estimate the heritability tagged by a given set of genotyped SNPs. In order to compare the same quantity across cohorts, we use common HapMap3 SNPs (57) (MAF ≥ 5%) for in-sample LD reference panel calculation, since most of them should be well imputed for a genome-wide genotyping array. To quantify the difference between
, since reference panels, such as 1000 Genomes Project (20), are available which include >99% of the SNPs with frequency > 1%. However, in-sample sequence data are usually not available for an admixed GWAS cohort, and so cov-LDSC can only include genotyped SNPs in the reference panel, and thus can only estimate the heritability tagged by a given set of genotyped SNPs. In order to compare the same quantity across cohorts, we use common HapMap3 SNPs (57) (MAF ≥ 5%) for in-sample LD reference panel calculation, since most of them should be well imputed for a genome-wide genotyping array. To quantify the difference between 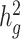 and
and 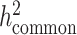 , we pre-phase the genotype data in the SIGMA cohort using SHAPEIT2 (62). We use IMPUTE2 (63) to impute genotypes at untyped genetic variants using the 1000 Genomes Project Phase 3 dataset as a reference panel. We merge genotyped SNPs and all well imputed (INFO > 0.99) SNPs (>6.9 million) in the SIGMA cohort as a reference panel and reported
, we pre-phase the genotype data in the SIGMA cohort using SHAPEIT2 (62). We use IMPUTE2 (63) to impute genotypes at untyped genetic variants using the 1000 Genomes Project Phase 3 dataset as a reference panel. We merge genotyped SNPs and all well imputed (INFO > 0.99) SNPs (>6.9 million) in the SIGMA cohort as a reference panel and reported 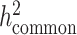 , to approximate what the estimate of
, to approximate what the estimate of  would have been with a sequenced reference panel (Supplementary Material, Table S17).
would have been with a sequenced reference panel (Supplementary Material, Table S17).
Tissue type specific analyses
We generate the 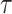 for 53 baseline annotations with 40% of annotations with non-zero
for 53 baseline annotations with 40% of annotations with non-zero  and 60% of annotations with zero
and 60% of annotations with zero 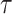 . We annotate the genes with the same set of tissue specific expressed genes identified previously (9) using the genotype–tissue expression (GTEx) project (64) and a public dataset made available by the Franke lab (65,66). We then generate different regression coefficients
. We annotate the genes with the same set of tissue specific expressed genes identified previously (9) using the genotype–tissue expression (GTEx) project (64) and a public dataset made available by the Franke lab (65,66). We then generate different regression coefficients 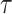 for the limbic system in gene sets with different enrichment. We scale all the
for the limbic system in gene sets with different enrichment. We scale all the 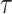 to make the total
to make the total 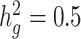 . For each variant
. For each variant 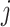 , the variance of
, the variance of 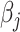 is the sum of the of all the categories that the variant is in (
is the sum of the of all the categories that the variant is in (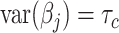 ). We randomly draw
). We randomly draw 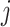 from a normal distribution with mean zero and variance
from a normal distribution with mean zero and variance 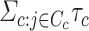 to simulate the phenotypes. We run 1000 simulations for each enrichment set (ranging from no (1×) enrichment to 2.5× enrichment). For the real traits included in the 23andMe cohort, we calculate within-sample stratified cov-LD scores with a 20-cM window and 10 PCs for each of these
to simulate the phenotypes. We run 1000 simulations for each enrichment set (ranging from no (1×) enrichment to 2.5× enrichment). For the real traits included in the 23andMe cohort, we calculate within-sample stratified cov-LD scores with a 20-cM window and 10 PCs for each of these  gene sets and 53 baseline annotations for each ancestry population. We obtain regression coefficients
gene sets and 53 baseline annotations for each ancestry population. We obtain regression coefficients 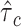 from the model and normalize them as
from the model and normalize them as
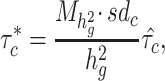 |
(3) |
where 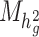 is the number of SNPs used to calculate
is the number of SNPs used to calculate 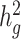 and
and 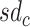 is the standard deviation (sd) of annotation
is the standard deviation (sd) of annotation 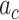 . We interpret
. We interpret 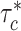 as the proportional change of averaged per-SNP heritability by one sd increase in value of the annotation of each cell type, conditional on other 53 non-cell type specific baseline annotations. We calculate a one-tailed P-value for each coefficient where the null hypothesis is that the coefficient is non-positive. All the significant enrichments are reported with false discovery rate < 5% (−log10(P) > 2.75). We perform fixed-effect inverse variance weighting meta-analysis using
as the proportional change of averaged per-SNP heritability by one sd increase in value of the annotation of each cell type, conditional on other 53 non-cell type specific baseline annotations. We calculate a one-tailed P-value for each coefficient where the null hypothesis is that the coefficient is non-positive. All the significant enrichments are reported with false discovery rate < 5% (−log10(P) > 2.75). We perform fixed-effect inverse variance weighting meta-analysis using 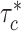 and normalized standard error across populations.
and normalized standard error across populations.
URLs
cov-LDSC software and tutorials, https://github.com/immunogenomics/cov-ldsc;
msprime, https://pypi.python.org/pypi/msprime;
GCTA, http://cnsgenomics.com/software/gcta/;
BOLT-LMM, v2.3.4, https://data.broadinstitute.org/alkesgroup/BOLT-LMM/;
LDSC, https://github.com/bulik/ldsc/;
PLINK2, https://www.cog-genomics.org/plink2;
REAP v1.2, http://faculty.washington.edu/tathornt/software/REAP/download.html;
ADMIXTURE v1.3.0, http://www.genetics.ucla.edu/software/admixture/download.html;
Author Contributions
Y.L., X.L, H.K.F and S.R. conceived and supervised the study. Y.L. and X.L. analyzed data. X.W. and A.A. contributed and analyzed the 23andMe data. S.G., B.M.N. and A.L.P. gave critical feedback on LDSC and statistical models. J.M.M. and J.C.F. contributed to the SIGMA study. All authors contributed to the writing of this manuscript.
Members of the 23andMe Research Team: Michelle Agee, Babak Alipanahi, Robert K. Bell, Katarzyna Bryc, Sarah L. Elson, Pierre Fontanillas, Nicholas A. Furlotte, Barry Hicks, David A. Hinds, Karen E. Huber, Ethan M. Jewett, Yunxuan Jiang, Aaron Kleinman, Keng-Han Lin, Nadia K. Litterman, Matthew H. McIntyre, Kimberly F. McManus, Joanna L. Mountain, Elizabeth S. Noblin, Carrie A.M. Northover, Steven J. Pitts, G. David Poznik, J. Fah Sathirapongsasuti, Janie F. Shelton, Suyash Shringarpure, Chao Tian, Joyce Y. Tung, Vladimir Vacic, and Catherine H. Wilson.
Supplementary Material
Acknowledgements
We thank the research participants of the SIGMA and 23andMe cohort for their contribution to this study.
Conflict of Interest statement. X.W., A.A. and members of the 23andMe Research Team are employees of 23andMe, Inc., and hold stock or stock options in 23andMe.
Contributor Information
Yang Luo, Center for Data Sciences, Brigham and Women’s Hospital, Harvard Medical School, Boston, MA, USA; Division of Rheumatology, Immunology, and Immunity, Brigham and Women’s Hospital, Harvard Medical School, Boston, MA, USA; Division of Genetics, Brigham and Women’s Hospital, Harvard Medical School, Boston, MA, USA; Department of Biomedical Informatics, Harvard Medical School, Boston, MA, USA; Broad Institute of MIT and Harvard, Cambridge, MA, USA.
Xinyi Li, Center for Data Sciences, Brigham and Women’s Hospital, Harvard Medical School, Boston, MA, USA; Division of Rheumatology, Immunology, and Immunity, Brigham and Women’s Hospital, Harvard Medical School, Boston, MA, USA; Division of Genetics, Brigham and Women’s Hospital, Harvard Medical School, Boston, MA, USA; Department of Biomedical Informatics, Harvard Medical School, Boston, MA, USA; Broad Institute of MIT and Harvard, Cambridge, MA, USA.
Xin Wang, 23andMe, Inc., Mountain View, California, USA.
Steven Gazal, Broad Institute of MIT and Harvard, Cambridge, MA, USA; Department of Epidemiology, Harvard T.H. Chan School of Public Health, Boston, MA, USA.
Josep Maria Mercader, Division of Genetics, Brigham and Women’s Hospital, Harvard Medical School, Boston, MA, USA; Diabetes Unit and Center for Genomic Medicine, Massachusetts General Hospital, Boston, MA, USA; Department of Medicine, Harvard Medical School, Boston, Massachusetts, USA.
23 and Me Research Team, 23 and Me, Inc., Mountain View, CA, USA.
Benjamin M Neale, Broad Institute of MIT and Harvard, Cambridge, MA, USA; Analytic and Translational Genetics Unit, Massachusetts General Hospital and Harvard Medical School, Boston, MA, USA.
Jose C Florez, Broad Institute of MIT and Harvard, Cambridge, MA, USA; Diabetes Unit and Center for Genomic Medicine, Massachusetts General Hospital, Boston, MA, USA; Department of Medicine, Harvard Medical School, Boston, Massachusetts, USA.
Adam Auton, 23andMe, Inc., Mountain View, California, USA.
Alkes L Price, Broad Institute of MIT and Harvard, Cambridge, MA, USA; Department of Epidemiology, Harvard T.H. Chan School of Public Health, Boston, MA, USA; Department of Biostatistics, Harvard T.H. Chan School of Public Health, Boston, MA, USA.
Hilary K Finucane, Broad Institute of MIT and Harvard, Cambridge, MA, USA; Department of Medicine, Harvard Medical School, Boston, Massachusetts, USA; Analytic and Translational Genetics Unit, Massachusetts General Hospital and Harvard Medical School, Boston, MA, USA.
Soumya Raychaudhuri, Center for Data Sciences, Brigham and Women’s Hospital, Harvard Medical School, Boston, MA, USA; Division of Rheumatology, Immunology, and Immunity, Brigham and Women’s Hospital, Harvard Medical School, Boston, MA, USA; Division of Genetics, Brigham and Women’s Hospital, Harvard Medical School, Boston, MA, USA; Department of Biomedical Informatics, Harvard Medical School, Boston, MA, USA; Broad Institute of MIT and Harvard, Cambridge, MA, USA; Arthritis Research UK Centre for Genetics and Genomics, Manchester Academic Health Science Centre, University of Manchester, Manchester, UK.
Funding
The study was supported by the National Institutes of Health (NIH) TB Research Unit Network (Grant U19 AI111224-01). The content is solely the responsibility of the authors and does not necessarily represent the official views of the NIH.
A.L.P. receives funding from National Institutes of Health (Grant R37 MH107649).
J.M.M. is supported by American Diabetes Association Innovative and Clinical Translational Award 1-19-ICTS-068.
References
- 1. Sirugo, G., Williams, S.M. and Tishkoff, S.A. (2019) The missing diversity in human genetic studies. Cell, 177, 26–31. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Martin, A.R., Kanai, M., Kamatani, Y., Okada, Y., Neale, B.M. and Daly, M.J. (2019) Clinical use of current polygenic risk scores may exacerbate health disparities. Nat. Genet., 51, 584–591. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Popejoy, A. B. and Fullerton, S. M. (2016) Genomics is failing on diversity. http://www.nature.com/news/genomics-is-failing-on-diversity-1.20759 (accessed 8 April 2021). [DOI] [PMC free article] [PubMed]
- 4. Seldin, M.F., Pasaniuc, B. and Price, A.L. (2011) New approaches to disease mapping in admixed populations. Nat. Rev. Genet., 12, 523–528. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Bulik-Sullivan, B.K., Loh, P.-R., Finucane, H.K., Ripke, S., Yang, J., Schizophrenia Working Group of the Psychiatric Genomics Consortium, Patterson, N., Daly, M.J., Price, A.L. and Neale, B.M. (2015) LD Score regression distinguishes confounding from polygenicity in genome-wide association studies. Nat. Genet., 47, 291–295. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Finucane, H.K., Bulik-Sullivan, B., Gusev, A., Trynka, G., Reshef, Y., Loh, P.-R., Anttila, V., Xu, H., Zang, C., Farh, K. et al. (2015) Partitioning heritability by functional annotation using genome-wide association summary statistics. Nat. Genet., 47, 1228–1235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Bulik-Sullivan, B., Finucane, H.K., Anttila, V., Gusev, A., Day, F.R., Loh, P.-R., ReproGen Consortium, Psychiatric Genomics Consortium, Genetic Consortium for Anorexia Nervosa of the Wellcome Trust Case Control Consortium 3, Duncan, L. et al. (2015) An atlas of genetic correlations across human diseases and traits. Nat. Genet., 47, 1236–1241. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Gazal, S., Finucane, H.K., Furlotte, N.A., Loh, P.-R., Palamara, P.F., Liu, X., Schoech, A., Bulik-Sullivan, B., Neale, B.M., Gusev, A. et al. (2017) Linkage disequilibrium-dependent architecture of human complex traits shows action of negative selection. Nat. Genet., 49, 1421–1427. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Finucane, H. K., Reshef, Y. A., Anttila, V., Slowikowski, K., Gusev, A., Byrnes, A., Gazal, S., Loh, P.-R., Lareau, C., Shoresh, N. et al. (2018) Heritability enrichment of specifically expressed genes identifies disease-relevant tissues and cell types. Nat. Genet., 50, 621–629. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Pasaniuc, B. and Price, A.L. (2017) Dissecting the genetics of complex traits using summary association statistics. Nat. Rev. Genet., 18, 117–127. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Yang, J., Benyamin, B., McEvoy, B.P., Gordon, S., Henders, A.K., Nyholt, D.R., Madden, P.A., Heath, A.C., Martin, N.G., Montgomery, G.W. et al. (2010) Common SNPs explain a large proportion of the heritability for human height. Nat. Genet., 42, 565–569. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Speed, D., Cai, N., UCLEB Consortium, Johnson, M.R., Nejentsev, S. and Balding, D.J. (2017) Reevaluation of SNP heritability in complex human traits. Nat. Genet., 49, 986–992. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Homburger, J.R., Moreno-Estrada, A., Gignoux, C.R., Nelson, D., Sanchez, E., Ortiz-Tello, P., Pons-Estel, B.A., Acevedo-Vasquez, E., Miranda, P., Langefeld, C.D. et al. (2015) Genomic insights into the ancestry and demographic history of South America. PLoS Genet., 11, e1005602. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. SIGMA Type 2 Diabetes Consortium, Williams, A. L., Jacobs, S. B. R., Moreno-Macías, H., Huerta-Chagoya, A., Churchhouse, C., Márquez-Luna, C., García-Ortíz, H., Gómez-Vázquez, M. J., Burtt, N. P. et al. (2014) Sequence variants in SLC16A11 are a common risk factor for type 2 diabetes in Mexico. Nature, 506, 97–101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Durand, E.Y., Do, C.B., Mountain, J.L. and Michael Macpherson, J. (2014, 2014) Ancestry composition: a novel, efficient pipeline for ancestry deconvolution. bioRxiv, 010512. 10.1101/010512 [DOI] [Google Scholar]
- 16. Gazal, S., Marquez-Luna, C., Finucane, H.K. and Price, A.L. (2019) Reconciling S-LDSC and LDAK functional enrichment estimates. Nat. Genet., 51, 1202–1204. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Yang, J., Lee, S.H., Goddard, M.E. and Visscher, P.M. (2011) GCTA: a tool for genome-wide complex trait analysis. Am. J. Hum. Genet., 88, 76–82. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Zaitlen, N., Pasaniuc, B., Sankararaman, S., Bhatia, G., Zhang, J., Gusev, A., Young, T., Tandon, A., Pollack, S., Vilhjálmsson, B.J. et al. (2014) Leveraging population admixture to characterize the heritability of complex traits. Nat. Genet., 46, 1356–1362. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Loh, P.-R., Tucker, G., Bulik-Sullivan, B.K., Vilhjálmsson, B.J., Finucane, H.K., Salem, R.M., Chasman, D.I., Ridker, P.M., Neale, B.M., Berger, B. et al. (2015) Efficient Bayesian mixed-model analysis increases association power in large cohorts. Nat. Genet., 47, 284–290. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. 1000 Genomes Project Consortium, Auton, A., Brooks, L. D., Durbin, R. M., Garrison, E. P., Kang, H. M., Korbel, J. O., Marchini, J. L., McCarthy, S., McVean, G. A. et al. (2015) A global reference for human genetic variation. Nature, 526, 68–74. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Gutenkunst, R.N., Hernandez, R.D., Williamson, S.H. and Bustamante, C.D. (2009) Inferring the joint demographic history of multiple populations from multidimensional SNP frequency data. PLoS Genet., 5, e1000695. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Gravel, S., Henn, B.M., Gutenkunst, R.N., Indap, A.R., Marth, G.T., Clark, A.G., Yu, F., Gibbs, R.A, 1000 Genomes Project and Bustamante, C. D (2011) Demographic history and rare allele sharing among human populations. Proc. Natl. Acad. Sci. U. S. A., 108, 11983–11988. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. Kelleher, J., Etheridge, A.M. and McVean, G. (2016) Efficient coalescent simulation and genealogical analysis for large sample sizes. PLoS Comput. Biol., 12, e1004842. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Alexander, D.H., Novembre, J. and Lange, K. (2009) Fast model-based estimation of ancestry in unrelated individuals. Genome Res., 19, 1655–1664. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25. Chang, C.C., Chow, C.C., Tellier, L.C., Vattikuti, S., Purcell, S.M. and Lee, J.J. (2015) Second-generation PLINK: rising to the challenge of larger and richer datasets. Gigascience, 4, 7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. Sudlow, C., Gallacher, J., Allen, N., Beral, V., Burton, P., Danesh, J., Downey, P., Elliott, P., Green, J., Landray, M. et al. (2015) UK biobank: an open access resource for identifying the causes of a wide range of complex diseases of middle and old age. PLoS Med., 12, e1001779. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27. Ge, T., Chen, C.-Y., Neale, B.M., Sabuncu, M.R. and Smoller, J.W. (2017) Phenome-wide heritability analysis of the UK Biobank. PLoS Genet., 13, e1006711. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Xue, A., Wu, Y., Zhu, Z., Zhang, F., Kemper, K.E., Zheng, Z., Yengo, L., Lloyd-Jones, L.R., Sidorenko, J., Wu, Y. et al. (2018) Genome-wide association analyses identify 143 risk variants and putative regulatory mechanisms for type 2 diabetes. Nat. Commun., 9, 2941. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Thornton, T., Tang, H., Hoffmann, T.J., Ochs-Balcom, H.M., Caan, B.J. and Risch, N. (2012) Estimating Kinship in Admixed Populations. Am. J. Hum. Genet., 91, 122–138. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. Demerath, E.W., Liu, C.-T., Franceschini, N., Chen, G., Palmer, J.R., Smith, E.N., Chen, C.T.L., Ambrosone, C.B., Arnold, A.M., Bandera, E.V. et al. (2013) Genome-wide association study of age at menarche in African-American women. Hum. Mol. Genet., 22, 3329–3346. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31. Fernández-Rhodes, L., Malinowski, J.R., Wang, Y., Tao, R., Pankratz, N., Jeff, J.M., Yoneyama, S., Carty, C.L., Setiawan, V.W., Le Marchand, L. et al. (2018) The genetic underpinnings of variation in ages at menarche and natural menopause among women from the multi-ethnic Population Architecture using Genomics and Epidemiology (PAGE) study: a trans-ethnic meta-analysis. PLoS One, 13, e0200486. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32. Horikoshi, M., Day, F.R., Akiyama, M., Hirata, M., Kamatani, Y., Matsuda, K., Ishigaki, K., Kanai, M., Wright, H., Toro, C.A. et al. (2018) Elucidating the genetic architecture of reproductive ageing in the Japanese population. Nat. Commun., 9, 1977. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Canoy, D., Beral, V., Balkwill, A., Wright, F.L., Kroll, M.E., Reeves, G.K., Green, J., Cairns, B.J. and Collaborators*, M.W.S. (2015) Age at menarche and risks of coronary heart and other vascular diseases in a large UK cohort. Circulation, 131, 237–244. [DOI] [PubMed] [Google Scholar]
- 34. Bodicoat, D.H., Schoemaker, M.J., Jones, M.E., McFadden, E., Griffin, J., Ashworth, A. and Swerdlow, A.J. (2014) Timing of pubertal stages and breast cancer risk: the breakthrough generations study. Breast Cancer Res., 16, R18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35. Taki, Y., Kinomura, S., Sato, K., Inoue, K., Goto, R., Okada, K., Uchida, S., Kawashima, R. and Fukuda, H. (2008) Relationship between body mass index and gray matter volume in 1,428 healthy individuals. Obesity, 16, 119–124. [DOI] [PubMed] [Google Scholar]
- 36. Berthoud, H.-R., Münzberg, H. and Morrison, C.D. (2017) Blaming the brain for obesity: integration of hedonic and homeostatic mechanisms. Gastroenterology, 152, 1728–1738. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37. Clemmensen, C., Müller, T.D., Woods, S.C., Berthoud, H.-R., Seeley, R.J. and Tschöp, M.H. (2017) Gut-brain cross-talk in metabolic control. Cell, 168, 758–774. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38. Wood, A. R., Esko, T., Yang, J., Vedantam, S., Pers, T. H., Gustafsson, S., Chu, A. Y., Estrada, K., Luan, J. ‘an, Kutalik, Z. et al. (2014) Defining the role of common variation in the genomic and biological architecture of adult human height. Nat. Genet., 46, 1173–1186. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39. Guo, M., Liu, Z., Willen, J., Shaw, C.P., Richard, D., Jagoda, E., Doxey, A.C., Hirschhorn, J. and Capellini, T.D. (2017) Epigenetic profiling of growth plate chondrocytes sheds insight into regulatory genetic variation influencing height. elife, 6: e29329. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40. Villemure, I. and Stokes, I.A.F. (2009) Growth plate mechanics and mechanobiology. A survey of present understanding. J. Biomech., 42, 1793–1803. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41. Jones, S.E., Lane, J.M., Wood, A.R., van Hees, V.T., Tyrrell, J., Beaumont, R.N., Jeffries, A.R., Dashti, H.S., Hillsdon, M., Ruth, K.S. et al. (2019) Genome-wide association analyses of chronotype in 697,828 individuals provides insights into circadian rhythms. Nat. Commun., 10, 343. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42. Potter, G.D.M., Skene, D.J., Arendt, J., Cade, J.E., Grant, P.J. and Hardie, L.J. (2016) Circadian rhythm and sleep disruption: causes, metabolic consequences, and countermeasures. Endocr. Rev., 37, 584–608. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43. Gnocchi, D. and Bruscalupi, G. (2017) Circadian rhythms and hormonal homeostasis: pathophysiological implications. Biology, 6, 10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44. Bering, T., Carstensen, M.B., Wörtwein, G., Weikop, P. and Rath, M.F. (2018) The circadian oscillator of the cerebral cortex: molecular, biochemical and behavioral effects of deleting theArntlClock gene in cortical neurons. Cereb. Cortex, 28, 644–657. [DOI] [PubMed] [Google Scholar]
- 45. Kichaev, G. and Pasaniuc, B. (2015) Leveraging functional-annotation data in trans-ethnic fine-mapping studies. Am. J. Hum. Genet., 97, 260–271. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46. Kanai, M., Akiyama, M., Takahashi, A., Matoba, N., Momozawa, Y., Ikeda, M., Iwata, N., Ikegawa, S., Hirata, M., Matsuda, K. et al. (2018) Genetic analysis of quantitative traits in the Japanese population links cell types to complex human diseases. Nat. Genet., 50, 390–400. [DOI] [PubMed] [Google Scholar]
- 47. Yang, J., Bakshi, A., Zhu, Z., Hemani, G., Vinkhuyzen, A. A. E., Nolte, I. M., van Vliet-Ostaptchouk, J. V., Snieder, H., Lifelines Cohort Study, Esko, T. et al. (2015) Genome-wide genetic homogeneity between sexes and populations for human height and body mass index. Hum. Mol. Genet., 24, 7445–7449. [DOI] [PubMed] [Google Scholar]
- 48. Yang, J., Zeng, J., Goddard, M.E., Wray, N.R. and Visscher, P.M. (2017) Concepts, estimation and interpretation of SNP-based heritability. Nat. Genet., 49, 1304–1310. [DOI] [PubMed] [Google Scholar]
- 49. Taliun, D., Harris, D. N., Kessler, M. D., Carlson, J., Szpiech, Z. A., Torres, R., Taliun, S. A. G., Corvelo, A., Gogarten, S. M., Kang, H. M. et al. (2021) Sequencing of 53,831 diverse genomes from the NHLBI TOPMed Program. Nature, 590, 290–299. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50. Evans, L. M., Tahmasbi, R., Vrieze, S. I., Abecasis, G. R., Das, S., Gazal, S., Bjelland, D. W., de Candia, T. R., Haplotype Reference Consortium, Goddard, M. E. et al. (2018) Comparison of methods that use whole genome data to estimate the heritability and genetic architecture of complex traits. Nat. Genet., 50, 737–745. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51. Gazal, S., Finucane, H.K., Furlotte, N.A. and Loh, P.R. (2017) Linkage disequilibrium-dependent architecture of human complex traits shows action of negative selection. Nature. 49, 1421–1427. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52. Speed, D. and Balding, D.J. (2019) SumHer better estimates the SNP heritability of complex traits from summary statistics. Nat. Genet., 51, 277–284. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53. Weissbrod, O., Flint, J. and Rosset, S. (2018) Estimating SNP-based heritability and genetic correlation in case-control studies directly and with summary statistics. Am. J. Hum. Genet., 103, 89–99. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54. Gusev, A., Lee, S.H., Trynka, G., Finucane, H., Vilhjálmsson, B.J., Xu, H., Zang, C., Ripke, S., Bulik-Sullivan, B., Stahl, E. et al. (2014) Partitioning heritability of regulatory and cell-type-specific variants across 11 common diseases. Am. J. Hum. Genet., 95, 535–552. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55. Turley, P., Walters, R. K., Maghzian, O., Okbay, A., Lee, J. J., Fontana, M. A., Nguyen-Viet, T. A., Wedow, R., Zacher, M., Furlotte, N. A. et al. (2018) Multi-trait analysis of genome-wide association summary statistics using MTAG. Nat. Genet. 50, 229–237. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56. Wojcik, G.L., Graff, M., Nishimura, K.K., Tao, R., Haessler, J., Gignoux, C.R., Highland, H.M., Patel, Y.M., Sorokin, E.P., Avery, C.L. et al. (2019) Genetic analyses of diverse populations improves discovery for complex traits. Nature, 570, 514–518. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57. Consortium, T. I. H. and The International HapMap Consortium (2007) A second generation human haplotype map of over 3.1 million SNPs. A second generation human haplotype map of over 3.1 million SNPs. Nature, 449, 851–861. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58. Manichaikul, A., Mychaleckyj, J.C., Rich, S.S., Daly, K., Sale, M. and Chen, W.-M. (2010) Robust relationship inference in genome-wide association studies. Bioinformatics, 26, 2867–2873. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59. Price, A. L., Weale, M. E., Patterson, N., Myers, S. R., Need, A. C., Shianna, K. V., Ge, D., Rotter, J. I., Torres, E., Taylor, K. D. et al. (2008) Long-range LD can confound genome scans in admixed populations. Long-range LD can confound genome scans in admixed populations. Am. J. Hum. Genet. (2008), 83, 132–135; author reply 135–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60. UK10K Consortium, Walter, K., Min, J. L., Huang, J., Crooks, L., Memari, Y., McCarthy, S., Perry, J. R. B., Xu, C., Futema, M. et al. (2015) The UK10K project identifies rare variants in health and disease. Nature, 526, 82–90. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61. Henn, B.M., Hon, L., Macpherson, J.M., Eriksson, N., Saxonov, S., Pe’er, I. and Mountain, J.L. (2012) Cryptic distant relatives are common in both isolated and cosmopolitan genetic samples. PLoS One, 7, e34267. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62. O’Connell, J., Gurdasani, D., Delaneau, O., Pirastu, N., Ulivi, S., Cocca, M., Traglia, M., Huang, J., Huffman, J.E., Rudan, I. et al. (2014) A general approach for haplotype phasing across the full spectrum of relatedness. PLoS Genet., 10, e1004234. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63. Howie, B., Fuchsberger, C., Stephens, M., Marchini, J. and Abecasis, G.R. (2012) Fast and accurate genotype imputation in genome-wide association studies through pre-phasing. Nat. Genet., 44, 955–959. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64. The GTEx Consortium (2015) The Genotype-tissue expression (GTEx) pilot analysis: multitissue gene regulation in humans. Science, 348, 648–660. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65. Pers, T.H., Karjalainen, J.M., Chan, Y., Westra, H.-J., Wood, A.R., Yang, J., Lui, J.C., Vedantam, S., Gustafsson, S., Esko, T. et al. (2015) Biological interpretation of genome-wide association studies using predicted gene functions. Nat. Commun., 6, 5890. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66. Fehrmann, R.S.N., Karjalainen, J.M., Krajewska, M., Westra, H.-J., Maloney, D., Simeonov, A., Pers, T.H., Hirschhorn, J.N., Jansen, R.C., Schultes, E.A. et al. (2015) Gene expression analysis identifies global gene dosage sensitivity in cancer. Nat. Genet., 47, 115–125. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


