Embryonic Tissues as Active Foams

Abstract

The physical state of embryonic tissues emerges from non-equilibrium, collective interactions among constituent cells. Cellular jamming, rigidity transitions and characteristics of glassy dynamics have all been observed in multicellular systems, but it is unclear how cells control these emergent tissue states and transitions, including tissue fluidization. Combining computational and experimental methods, here we show that tissue fluidization in posterior zebrafish tissues is controlled by the stochastic dynamics of tensions at cell-cell contacts. We develop a computational framework that connects cell behavior to embryonic tissue dynamics, accounting for the presence of extracellular spaces, complex cell shapes and cortical tension dynamics. We predict that tissues are maximally rigid at the structural transition between confluent and non-confluent states, with actively-generated tension fluctuations controlling stress relaxation and tissue fluidization. By directly measuring strain and stress relaxation, as well as the dynamics of cell rearrangements, in elongating posterior zebrafish tissues, we show that tension fluctuations drive active cell rearrangements that fluidize the tissue. These results highlight a key role of non-equilibrium tension dynamics in developmental processes.

Many essential processes in multicellular organisms, from organ formation to tissue homeostasis, require a tight control of the tissue physical state ^{1, 2}. While tissue mechanics and structure at supracellular scales emerge from the collective physical interactions among the constituent cells, their control occurs at cell and subcellular levels. Bridging these scales is essential to understand the physical nature of active multicellular systems and to identify the processes that cells use to control the physical state of embryonic tissues.

In vitro experiments of cell monolayers on synthetic substrates have revealed characteristics of glassy dynamics ^{3, 4} and rigidity transitions ^5–7, which are thought to be linked to biological function and multiple pathologies. In contrast, suspended epithelial monolayers are largely solid-like in vitro ⁸ and show evidence of fracture in vivo ⁹. Experiments with embryonic tissues have shown characteristics of glassy dynamics in cell movements ¹⁰, viscous behavior at long timescales ¹¹ and also structural signatures reminiscent of jamming transitions ¹², with cell divisions, cell shape and/or changes in cell adhesion suspected to play a role in the control of these emergent behaviors ^{5, 11, 13, 14}. Recent in vivo experiments in developing zebrafish embryos showed the existence of a rigidity transition underlying the formation of the vertebrate body axis, revealing a functional role of rigidity transitions in embryonic development ¹⁵ (Fig. 1a). Both the presence of adhesion-dependent spaces between cells (Fig. 1b–d) and the dynamics of cell-cell contacts (Fig. 1e,f) were shown to influence the physical state of the tissue ¹⁵. However, the relative roles of cell adhesion and cell-cell contact dynamics in the control of posterior tissue fluidization are still unclear. Generally, little is known about how different cell behaviors control rigidity transitions and tissue fluidization in embryonic tissues, and whether all these observed emergent phenomena share a common physical origin.

Figure 1: Characteristics of multicellular systems and simulation framework.

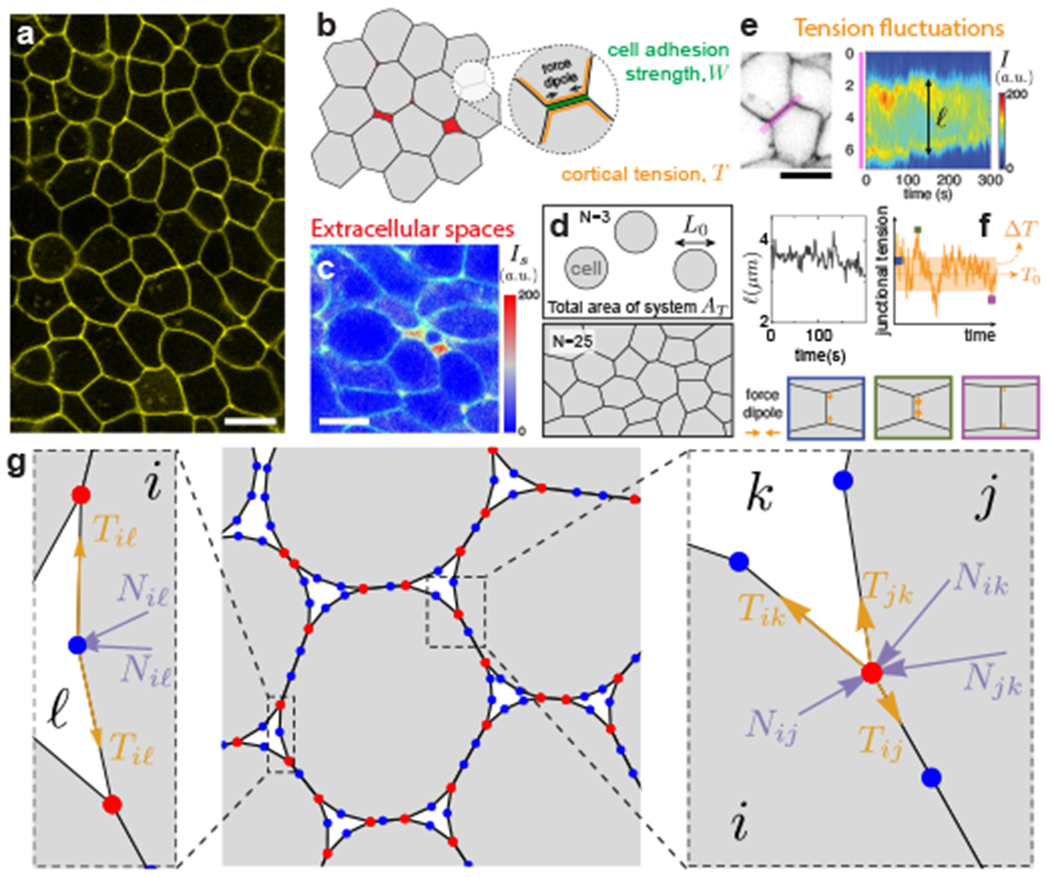
a, Confocal section of embryonic tissue in a zebrafish embryo (membranes labeled; yellow). b, Schematics of cortical tension and adhesion at cell-cell contacts in a multicellular system with spaces (red) between cells (gray). c, Confocal section through zebrafish embryonic tissues showing the intensity (I_s) of fluorescent reporter protein secreted extracellularly as well as cell membranes (green), indicating the presence of extracellular spaces (red range). d, Schematics defining the cell size L₀, cell number N and simulation box area A_T, which specify cell density. e, Kymograph of membrane signal intensity (I) along a tissue region (pink; left panel) containing a cell-cell contact, showing contact length ℓ fluctuations (bottom). f, Simulated tension fluctuations causing cell-cell contact length fluctuations. Increasing (decreasing) tension shortens (lengthens) cell-cell junctions (bottom). g, Schematics of the dynamic vertex model formulation. Triple vertices (physical vertices; red) and non-physical intermediate vertices (blue) are shown.

The physical behavior of multicellular systems has been studied theoretically using various approaches. Vertex models ^16–21 and Cellular Potts models ^{22, 23} account for cell geometry and use equilibrium formulations to describe the physical state of the system. These descriptions predict a density-independent rigidity transition in confluent systems that depends on the balance between actomyosin-generated cortical tension T₀ and cell adhesion W (treated as passive, effective tensions), with the resulting cell shape being the control parameter for solid/fluid states ¹⁷. Since cell shape plays a central role in models of confluent systems, the ability to accurately describe complex cell shapes, beyond polygonal shapes, may be important to understand the physical state of the system, as recently suggested ^{24, 25}. Non-vertex models of deformable particles have instead focused on configurations in non-confluent equilibrium systems, both in the presence ^{26, 27} and absence of cell adhesion ^{24, 28}. In contrast, self-propelled particle and Voronoi models that focus on cell movements on synthetic substrates account for the dynamics of the system and predict rigidity transitions that depend on cell density and self-propulsion ^{29, 30}. All these descriptions capture some important aspects of the problem, but each neglects a subset of key cell behaviors and/or restricts the allowed configurations. No current theoretical description accounts for all observed relevant cell behaviors in a common framework, hindering our understanding of how cells control the emergent physical state of the tissue.

Dynamic Vertex Model with Extracellular Spaces

To study the dynamics of embryonic tissues and their physical state, we generalize 2D vertex models by accounting for (i) extracellular spaces (Fig. 1b,c,g; Methods), (ii) the stochastic dynamics of active cortical tensions (Fig. 1e,f) and (iii) complex cell shapes (Fig. 1a,g; Methods). Unlike previous vertex models, we do not assume the existence of a preferred cell perimeter, as experimental evidence for this constraint is lacking. Instead, since cells actively control adhesion, cortical tension and osmotic pressure ^{1, 2}, we derive a physical description reminiscent of foams but with active tension dynamics. Tissue dynamics and structure, as well as cell movements and their shapes, are all determined by the dynamics of vertices (Fig. 1g), which follow from force balance, namely

$${\eta }_R\frac{d{\overrightarrow{R}}_{\alpha }}{dt}=\sum _{i,j\in F(\alpha )}\left({\overrightarrow{T}}_{ij}\mathrm{\Theta }(T_{ij})+{\overrightarrow{N}}_{ij}\right),$$ (1)

where ${\overrightarrow{R}}_{\alpha }$ is the position of the vertex α, η_R is a friction coefficient characterizing the dissipation associated with moving a vertex, ${\overrightarrow{T}}_{\mathit{ij}}$ is the effective tension at the contact between cell i and j (with F(α) representing the set of all cells sharing vertex α) and ${\overrightarrow{N}}_{\mathit{ij}}$ are the normal forces acting on vertex α. Θ(·) represents the Heaviside step function and prevents unrealistic negative tensions ^{15, 31}. Normal forces arise from osmotic pressure differences in adjacent cells and are given by N_ij = (ΔP_i − ΔP_j) L_ij/2 (Methods), where L_ij and ΔP_i (ΔP_j) are, respectively, the contour length of the contact between cells i and j and the osmotic pressure difference across cell i (j).

To capture the observed fluctuating nature and finite persistence of tension dynamics ¹⁵, T_ij, we describe them as an Ornstein-Uhlenbeck process, with a tension that fluctuates around a fixed point $T_{\mathit{ij}}^0$ and has a persistence time τ_T ^32,33, specifically

$${\tau }_T\frac{d{T}_{ij}}{dt}=-(T_{ij}-T_{ij}^0)+\mathrm{\Delta }T\xi ,$$ (2)

where ΔT is the amplitude of tension fluctuations and ξ is Gaussian white noise (Fig. 1f; Methods). The fixed point effective tensions depend on both the average cortical tension, T₀, and average strength of cell-cell adhesion, W, which, like ΔT, are different at cell-cell contacts and free cell boundaries (Fig. 1b; Methods).

Scaling all quantities, we obtain the relevant dimensionless parameters (Table 1; Methods). Since P₀L₀/T₀ and τ_T/τ_R can be estimated from existing experimental data (Methods), we focus on the parameter space spanned by ΔT/T₀, W/T₀ and ρ.

Table 1:

Definition of the relevant dimensionless parameters in the problem.

Dimensionless Parameters	Description
ΔT/T0	Magnitude of tension fluctuations (Fig. 1e,f).
W/T0	Relative strength of cell-cell adhesion W and average cortical tension T0 (Fig. 1b).
$\rho \equiv N{L}_0^2∕A_T$	Normalized system density (with AT and N being the total area of the system and the number of cells, respectively; Fig. 1d).
P0L0/T0	Relative magnitude of normal to tensional forces.
τT/τR	Ratio of persistence time of tension fluctuations and characteristic timescale τR ≡ ηT L0/T0 of dissipation at vertices.

Structural Transitions and Mechanics of Equilibrium Systems

We first explore how the states and mechanics of the system change if spaces between cells are allowed. In the absence of tension fluctuations (ΔT/T₀ = 0), the amount of extracellular spaces in equilibrium configurations is determined by force balance and varies with both the cell density ρ and the relative cell adhesion strength W/T₀ (Fig. 2a). Increasing cell density results in larger cellular volume fraction ϕ (Fig. 2b) and cell contact number z (Fig. 2c), with the system eventually becoming confluent at an adhesion-dependent critical density, ρ_c(W/T₀). For any fixed cell density, the system undergoes a non-confluent to confluent transition as W/T₀ is increased, since higher adhesion promotes stronger cell-cell contacts (Fig. 2a,b). These results extend previous studies for purely repulsive deformable particles ²⁸ to arbitrary adhesion levels.

Figure 2: Equilibrium configurations and structural transitions.

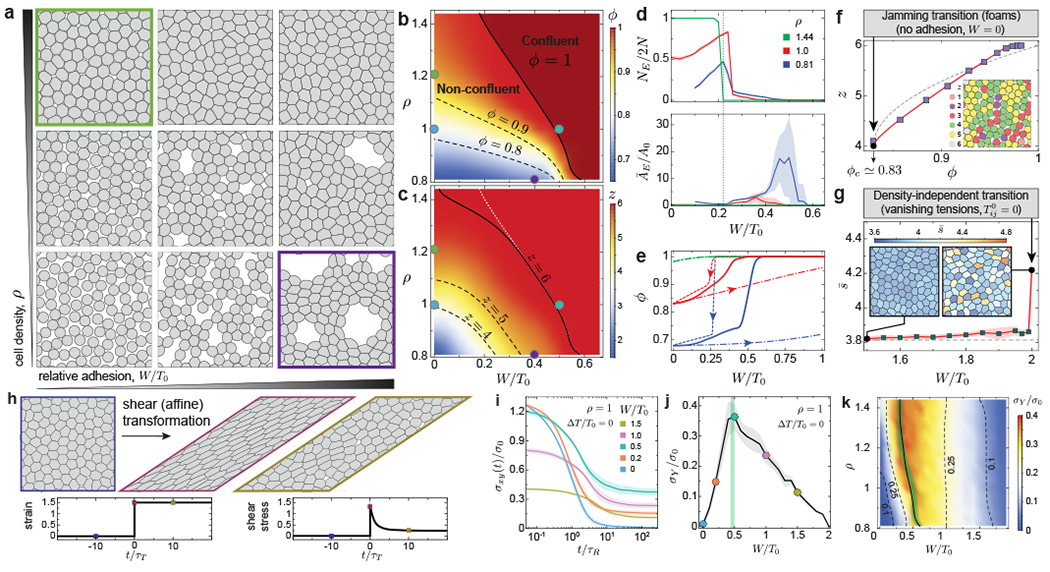
a-c, Representative equilibrium configurations (a), volume fraction ϕ (b) and mean number of neighbors z (c) for varying values of relative adhesion W/T₀ and cell density ρ. d, number N_E (top) and average area Ā_E (bottom) of extracellular spaces for varying relative cell adhesion and different cell densities, showing a sharp structural transition at W/T₀ ≈ 0.23 (gray line) leading to the opening of large extracellular spaces. e, Lowering (dashed line) and increasing (dash-dotted line) relative adhesion quasi-statically shows bistable states and strong hysteresis in equilibrium configurations. Equilibrium quenched states are also shown (solid line). f, Average neighbor number (cell contacts) z as the system volume fraction changes at vanishing cell adhesion, showing the existence of a jamming transition at ϕ_c ≃ 0.83 (configuration shown in inset). Power law fits z – z_c = z₀(ϕ − ϕ_c)^1/2 + z₁(ϕ − ϕ_c) with non-zero z₀ and z₁ (red line) and with z₁ = 0 (gray line) are shown. g, Average shape factor for varying relative adhesion showing a sharp increase at W/T₀ = 2 (vanishing tensions), leading to anisotropic cell shapes (inset), recapitulating density-independent transitions. h, Schematics of a simple shear deformation imposing a large strain step (ϵ_xy = 1.5), with associated temporal evolution of both strain and shear stress. i, Temporal relaxation of shear stress σ_xy (normalized to ${\sigma }_0\equiv \sqrt{\rho }{T}_0∕L_0$) after the imposed strain step for varying adhesion levels. j-k, Dependence of the yield stress σ_Y on the relative adhesion strength (j) and on both cell density and relative adhesion (k), showing a maximum at the structural transition between confluent and non-confluent states (green line). Error bands = SD. N= 20 (b,c,d,f,g) and N=10 (e,i,j,k) independent simulations for each parameter set.

Changes in relative cell adhesion not only affect the volume fraction but also the structural characteristics of extracellular spaces. Equilibrium configurations sharply transition from a large number of small extracellular spaces to a few large extracellular spaces at W/T₀ ≈ 0.23 (Fig. 2a,d), as small triangular extracellular spaces can only be stabilized below this value (Supplementary Section 1). Concomitant to the presence of large extracellular holes, which are reminiscent of epithelial fracture in vivo ⁹, the spontaneous clustering of cells strongly resembles flocculation in sticky emulsions ^{34, 35} (Fig. 2a). Moreover, the system displays bistability between two possible equilibrium configurations for W/T₀ ≥ 0.23, namely a confluent state with stretched cells and a non-confluent state with sparse and large extracellular holes (Fig. 2e), with strong hysteresis in equilibrium configurations if adhesion or cortical tension are varied in a quasi-static manner (Fig. 2e and Supplementary movie 1; Methods). Some of the predicted system configurations (Fig. 2a) are analogous to those previously obtained for equilibrium systems with open boundaries ²⁷, but the bistability and hysteresis of configurations reported here can only be observed in closed systems that more closely resemble epithelial tissues.

In the limit of vanishing cell adhesion, the system should behave as foams/emulsions, which display a jamming transition at a critical value ϕ_c. The isostatic condition (z = 4 in 2D) sets the critical volume fraction ϕ_c ≈ 0.83 of the system³⁶ (Fig. 2f). Both this ϕ_c value and the power-law dependence of z (Fig. 2f), are in agreement with recent equilibrium simulations of deformable particles ²⁸, indicating that our description accurately describes the foam limit. In the confluent limit, previous works reported density-independent rigidity transitions, which are controlled by the cell shape factor s ($s=P∕\sqrt{A}$, with P and A being the cell perimeter and the area, respectively). The system switches from a solid to a fluid state at approximately s_c ≃ 3.81, with cells transiting from isotropic to anisotropic shapes ^{17, 37, 38}. The fluid state in these descriptions is characterized by vanishing effective tensions ($T_{\mathit{ij}}^0=0$), allowing neighbor exchanges at no energetic cost ¹⁹. Setting W/T₀ = 2 in our framework leads to vanishing effective tensions and a sharp increase in average shape factor due to the emergence of anisotropic cell shape (Fig. 2g), recapitulating density-independent transitions.

To directly assess the physical state of the system, we monitor shear stress relaxation after imposing an affine deformation (Fig. 2h; Methods). The initial stress jump is largest with no adhesion and vanishes when effective tensions vanish (Fig. 2i; Supplementary Figure S5). Subsequently, shear stress relaxes with a characteristic timescale τ_R towards a constant value at long timescales, namely the yield stress σ_Y ³⁹, which depends non-monotonically on cell adhesion (Fig. 2j; Supplementary movie 2). For low relative adhesion W/T₀, the system is non-confluent and the yield stress increases with increasing adhesion as extracellular spaces close down. In contrast, for adhesion values leading to confluence, increasing W/T₀ leads to a decreasing yield stress due to lower effective tensions. Vanishing yield stress indicates a fluid tissue state, which occurs only for W/T₀ = 0 and W/T₀ = 2 and corresponds to the jamming transition (Fig. 2f) and the density-independent rigidity transition (Fig. 2g), respectively, with the tissue being solid for all other values in the 0 < W/T₀ < 2 range. These results show that equilibrium systems are maximally rigid at the structural transition between confluent and non-confluent states (Fig. 2j,k), with increasing adhesion rendering the system more rigid in non-confluent systems and doing the opposite in confluent states.

Dynamics of Active Multicellular Systems

Unlike equilibrium systems, tension dynamics at cell-cell contacts can drive cell movements, neighbor exchanges and cell shape changes (Supplementary movies 3–4). At timescales longer than all characteristic timescales (t ⪢ τ_T > τ_R), cell movements are caged for small ΔT/T₀, as indicated by the saturation of the Mean Squared Displacement (MSD) and bounded cell trajectories (Fig. 3a,b; Methods). For increasing magnitudes of tension fluctuations, cell uncaging starts to occur and the asymptotic behavior of the MSD for t ⪢ τ_T becomes a power law (MSD ~ t^α), with an exponent α that increases with activity (Fig. 3a inset). This evidences sub-diffusive (α < 1) cell movements for intermediate activities, and diffusive (α = 1) behavior for large enough tension fluctuations (Fig. 3a,b).

Figure 3: Tissue dynamics with finite tension fluctuations.

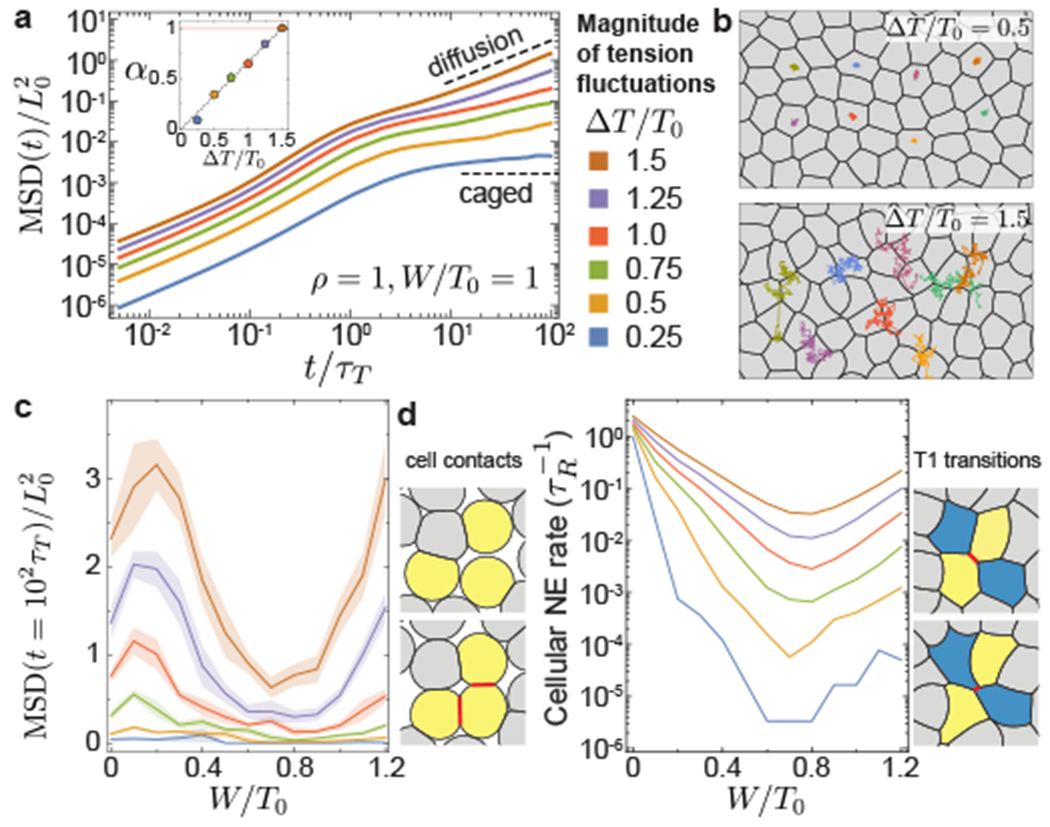
a, MSD for varying magnitudes of tension fluctuations ΔT/T₀, showing sub-diffusive (0 < α < 1) and diffusive (α = 1) behaviors as tension fluctuation increase (inset). b, Snapshots of dynamic configurations with examples of cell trajectories over t/τ_T = 10². c, MSD at long timescales (t = 10²τ_T ⪢ τ_T > τ_R), showing non-monotonous behavior for varying relative adhesion strength and minimal values at the structural transition. d, Cellular neighbor exchange (NE) rate for varying relative adhesion. Distinct types of neighbor exchange events: gain/loss of cell contacts (left) and T1 transitions (right). Error bands = SD. 10 independent simulations for each set of parameters.

Comparing MSD values at long timescales (t = 10²τ_T ⪢ τ_T > τ_R) shows that increasing tension fluctuations always leads to higher cell movements, regardless of cell adhesion strength, as recently reported for confluent systems ³³. However, for a fixed level of activity, MSD values vary non-monotonically as adhesion increases, displaying very reduced cell movements at the transition between non-confluent to confluent states (Fig. 3c). Similar to the MSD, the NE rate displays analogous non-monotonic behavior, with minimal NE events at the structural transition. Close to confluence for high adhesion levels, the neighbor exchange (NE) rate is dominated by T1 transitions and related to the MSD by MSD $(t={10}^2{\tau }_T)~k_{\mathrm{NE}}^{3∕4}$ (Extended Figure 1), with the timescale for T1 transitions, 1/k_NE, diverging as the activity vanishes, a signature of glassy dynamics. In contrast, at low adhesion levels leading to non-confluent states, loss and formation of new cell contacts dominate NE events (Fig. 3d) and the MSD and NE behaviors differ close to jamming. The non-monotonic behavior of both MSD and NE events, with minimal values at the transition between non-confluent to confluent states, suggests that the non-equilibrium system is also maximally solid-like at the structural transition.

Physical State of Active Multicellular Systems

To study the rigidity of active systems, we apply a shear strain step and monitor stress relaxation, as described above (Fig. 2h). The presence of finite tension fluctuations qualitatively changes stress relaxation at long timescales compared to equilibrium systems, displaying a slow stress decay rather than plateauing to a yield stress (Fig. 4a; Supplementary movie 5). This long timescale stress relaxation is driven by actively-induced T1 transitions (Fig. 4b), and can be accurately described by a stretched-exponential function (Fig. 4a inset), as previously done to explain the dynamics of systems with a large number of intrinsic timescales ^{40, 41}. The stress relaxation timescale, τ_SR, at which shear stress reaches the level of active shear stress in the unperturbed system (Fig. 4a inset; Supplementary Figure S2), varies by over five orders of magnitude as the magnitude of tension fluctuations or relative adhesion change slightly (Fig. 4d). While larger activity values reduce τ_SR monotonically, increasing the relative adhesion strength leads to non-monotonic changes in τ_SR, which rapidly increases in non-confluent states and displays the opposite behavior in confluent states. The largest stress relaxation timescale occurs at the structural transition between non-confluent to confluent states, indicating that tissues are minimally fluid at long timescales close to this structural transition (Fig. 4d), consistent with the predicted low cell movements and NE rates close to the transition (Fig. 3c,d).

Figure 4: Stress relaxation and structure in active multicellular systems.

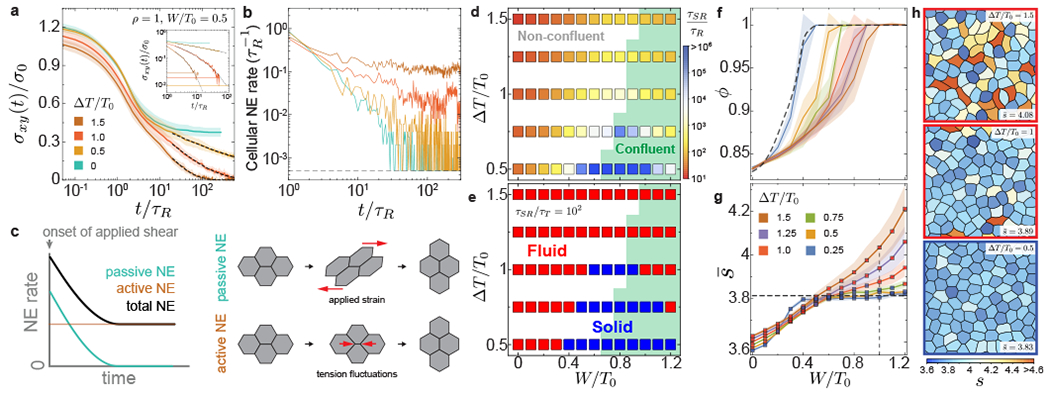
a-b, Stress relaxation (a) and temporal changes in cellular NE rate (b) after the imposed strain step for varying magnitudes of tension fluctuations. The long timescale stress relaxation follows stretched exponentials (black dashed lines) and eventually reaches the average value σ_A of active shear stress fluctuations (horizontal lines in inset). The cellular NE rate quickly decays to zero in the absence of activity (t ~ τ_R), but remains finite in the presence of activity. c, Sketch showing the dynamics NE induced by the externally applied shear strain (passive) and by tension fluctuations in cells (active). Active NE enables further stress relaxation and tissue fluidization after the initial passively induced NE. d, Stress relaxation timescale τ_SR for varying magnitude of tension fluctuations and relative adhesion, showing a sharp increase as the structural transition between non-confluent and confluent (green background) states. e, Phase diagram showing the transition between fluid and solid tissue states for different activity values and relative adhesion strength. Solid states surround the structural transition and are found both in confluent and non-confluent configurations for low enough activity. f-h, Dependence of the system volume fraction ϕ (f) and average shape factor $\stackrel{‒}{s}$ (g; with red/blue squares indicating fluid/solid states, respectively) on relative adhesion for different magnitudes of tension fluctuations. Representative snapshots of dynamic configurations for fixed relative adhesion (W/T₀ = 1; vertical dashed line in g) and increasing tension fluctuations are shown (h), with red/blue contours indicating fluid/solid states, respectively. Error bands = SD. 10 independent simulations for each set of parameters.

In contrast to previous equilibrium vertex models, our results show that a given tissue can behave as a fluid or a solid depending on the time necessary to form embryonic structures. If the characteristic timescale τ_d of developmental processes is larger (smaller) than the stress relaxation timescale τ_SR, namely τ_d/τ_SR ⪢ 1 (τ_d/τ_SR « 1), the tissue behaves as a fluid (solid). Using typical developmental timescales (τ_d ~ 1-2 hours; τ_d/τ_T ~ 10²), we obtain the tissue phase diagram (Fig. 4e). Over a critical value of tension fluctuations, the tissue is always fluid regardless of cell adhesion levels. Below that critical activity value, the tissue is fluid at both low and high adhesion levels, but solid in between, in the region of the phase diagram surrounding the structural transition between non-confluent to confluent states. This non-monotonic behavior mirrors the behavior of NE and cell movements, but care must be taken in inferring the physical state of the system solely from cellular movements (Extended Figure 2). While cell density and cell shape are the control parameters associated with jamming transitions and density-independent transitions, respectively, our results show that tension fluctuations control a distinct rigidity transition in both confluent and non-confluent states, as suggested recently for confluent states ³³.

To relate the mechanics of the system to its structure in the presence of tension dynamics, we study the configurations of the system. Tension fluctuations generally promote transitions from confluent to non-confluent states by opening up extracellular spaces at weak regions (Fig. 4f), implying that larger adhesion values are required to reach confluent states for increasing ΔT/T₀. This effect becomes negligible for large cell densities (ρ > 1) and volume fraction is then solely determined by cell density ρ and relative cell adhesion W/T₀ (Supplementary Figure S3). While cell shapes are only moderately affected by tension fluctuations in non-confluent regimes, with low shape factors associated with rounder cells, increasing tension fluctuations in confluent regimes leads to substantially larger shape factors (Fig. 4g,h). In contrast to density-independent transitions, where large shape factors (above approximately 3.81) result from vanishing junctional tensions in fluid states¹⁷, the large shape factors reported here are due to spatiotemporal tension fluctuations (Fig. 4h), with cell-cell contacts maintaining finite tensions (Supplementary Figure S4; Supplementary movie 6), as observed experimentally ^{31, 42}. In particular, we find the presence of both fluid and solid tissue states for adhesion values in the range 0 < W/T₀ < 2 that would correspond solely to solid states in previous equilibrium descriptions. These results indicate that the tissue fluid or solid state cannot be inferred from static measurements of cell shape factor only, as the tissue physical state and its structure depend strongly on the magnitude of tension fluctuations (Fig. 4g,h).

Fluidization of embryonic tissues

Our theoretical results indicate that in the presence of active tension fluctuations, active NE events control stress relaxation at long timescales both in confluent and non-confluent tissues. To experimentally address the role of tension fluctuations in stress relaxation and tissue fluidization, we employed magnetically-responsive oil droplets to directly measure strain and stress relaxation in posterior tissues of developing zebrafish embryos (Fig. 5a), as these tissues have been previously shown to be in a fluid-like state ¹⁵. After injecting a single droplet in the mesodermal progenitor zone (MPZ), we induced large droplet deformations of multiple cell diameters by applying a controlled magnetic field for a 15 min period ^{15, 43} (Fig. 5b,c; Methods). We subsequently monitored the droplet relaxation for one hour after removing the magnetic field and measured the decay of stress in the tissue (Fig. 5d; Methods). We observed an initial fast decay (~ 30s) followed by a very slow relaxation at long timescales that displays the stretched exponential behavior predicted theoretically for a fluctuation-induced stress relaxation (Fig. 4a). This slow relaxation was previously interpreted as a yield stress due to limitations in the measurement timescales ¹⁵, a well-known limitation in mechanical measurements of complex materials ³⁹. The present long timescale measurements reveal a very slow stress relaxation and indicate that posterior tissues completely fluidize on timescales of approximately 1h, enabling nearly complete remodeling of posterior tissues during axis elongation, as this occurs at rates of approximately 45 μm/h ^{44, 45}.

Figure 5: Stress relaxation and tissue fluidization in posterior tissues during body axis elongation.

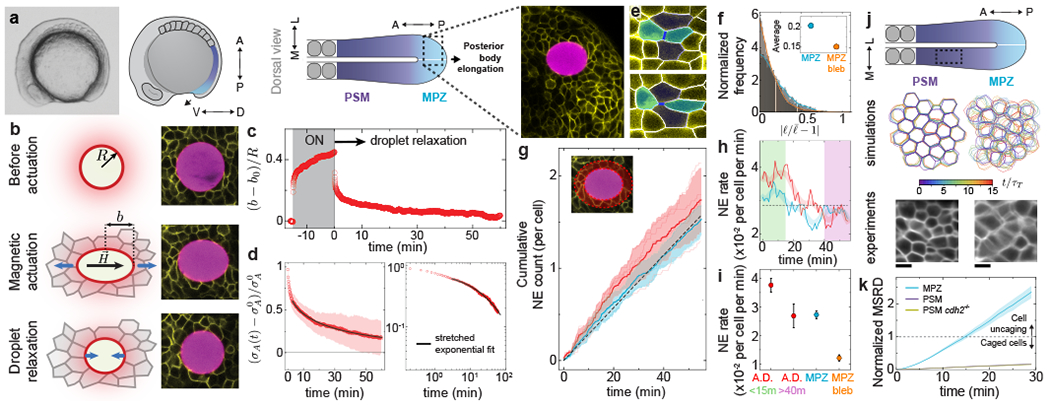
a, Lateral view of a zebrafish embryo and sketches showing lateral and dorsal views of posterior tissues, indicating the fluid-like MPZ and solid-like PSM. A confocal section showing a portion of the MPZ (cell membranes, yellow) with a magnetic droplet (magenta) is highlighted. b, Schematic sketches and confocal snapshots of magnetic droplet actuation in the MPZ tissue. c, Time evolution of the strain, (b – b₀)/R, before, during and after magnetic actuation. d, Relaxation of anisotropic stress σ_A(t) after magnetic actuation in both linear and log-linear scales, with ${\sigma }_A^0={\sigma }_A(t=0)$. The fit (black line) corresponds to a stretched-exponential function. e, Example of NE events. f, Normalized frequency of amplitude of junctional length fluctuations for the MPZ, both in the absence and presence of blebbistatin (average amplitudes in inset). g, Cumulative NE events in the MPZ (away from the droplet, cyan) and in the close neighborhood of the droplet (around droplet, red). h, Temporal evolution of NE rate in the MPZ (cyan) and also in the region around droplet (red). i, Average NE rates in the region around droplet (A.D., both during initial droplet relaxation (green) and at its final stages (pink)) and in the MPZ, both in the absence (cyan) and presence (orange) of blebbistatin. j, Experimentally measured and simulated dynamics of cell shapes in both MPZ and PSM, showing faster dynamics in the MPZ and largely static cell boundaries in the PSM. Experimental data is an average intensity projection of a confocal section timelapse. k, MSRD shows uncaging behavior for the MPZ but caged for the PSM of both wild type and cdh2^−/− embryos. Error Band=SD (d,g), SEM (i,k). N=10 (d), N=298 from 4 embryos (g,h,i; A.D), N=396 from 3 embryos (g,h,i; MPZ). Data in f, MPZ bleb in i and MRSD for MPZ and PSM in wild type embryos in k were reanalyzed from Ref. ¹⁵.

To address the role of active NE (T1 transitions) in tissue fluidization (Fig. 4c), we quantified the characteristics of NE events (Fig. 5e) during droplet relaxation in the MPZ, as cells in this region display considerable cell-cell contact fluctuations (Fig. 5f; Methods). Measurement of cumulative NE events in the MPZ (away from the droplet) shows a linear increase over time (Fig. 5g; Methods), indicating an approximately constant NE rate in the MPZ with characteristic timescales of tens of minutes (Fig. 5h,i). Inhibiting myosin II activity with blebbistatin causes a reduction in the magnitude of cell-cell contact fluctuations (Fig. 5f; methods) and a decrease of nearly 50% in the NE rate (Fig. 5i), indicating that the measured NE events in the MPZ are actively-induced by actomyosin-generated tension fluctuations. While NE events in the tissue directly adjacent to the droplet display the same NE rate as the rest of the MPZ in the final stages of droplet relaxation (40-55 min; Fig. 5g–i), the NE rate close to the droplet is higher than the rest of the MPZ during the beginning of droplet relaxation (0-15 min; Fig. 5g–i). This observed initial excess of NE events close to the droplet indicates the presence of passive NE events caused by the capillary stresses imposed by the droplet on the tissue during its relaxation, as predicted theoretically (Fig. 4c). The measured low and constant rate of active NE events in the MPZ is consistent with the measured stretched-exponential behavior of the stress relaxation at long timescales (tens of minutes), and indicates that tissue fluidization is largely caused by active NE events arising from tension fluctuations at cell-cell contacts.

To characterize the relative roles of tension fluctuations and cell-cell adhesion in rigidity transitions, we used N-cadherin (cdh2^−/−) mutants lacking N-cadherin mediated cell-cell adhesion ⁴⁶ (Methods). While the MPZ tissue in wild type embryos is fluidized by active NE events (Fig. 5d–i) and displays cellular movements and mean squared relative displacements (MSRD) compatible with cell uncaging (Fig. 5j,k), the presomitic mesoderm (PSM) has been shown to be in a solid-like state ¹⁵, with cells caged by their neighbors (MRSD « 1 at 30 min; Fig. 5j,k). Our measurements indicate that cell movements in the PSM of N-cadherin (cdh2^−/−) mutants, a tissue that has been shown to be characterized by reduced cell volume fraction and lower yield stress but similar cell-cell contact fluctuations as wild type embryos ¹⁵, display the same MSRD behavior as wild type embryos (Fig. 5k). These results indicate that lowering cell-cell adhesion while maintaining low cell-cell contact fluctuations does not allow cells to uncage themselves to remodel the tissue.

Altogether, both our computational and experimental results indicate that actomyosin-generated tension fluctuations actively drive structural rearrangements that cause stress relaxation in the tissue, thereby controlling tissue fluidization and enabling tissue remodeling.

Methods

Pressure and volume relation.

The (osmotic) pressure P of a cell has been experimentally shown to vary with its volume according to P = K/V ⁴⁷, meaning that changes in the osmotic pressure difference between the inside (P) and outside (P₀) of the cell lead to changes in the cell volume V, with K characterizing the cell compressibility (we assumed for simplicity that cells are never compressed close to their dry mass limit). In our 2D description, the cell area A plays the role of the volume, so that P = K/A, with the characteristic cell size L₀ (or preferred area $A_0=L_0^2$) being set by this relation, namely $L_0\equiv \sqrt{K∕P_0}$. However, while we use the experimentally measured relation between osmotic pressure and cell volume ⁴⁷ (area in 2D), the specific P-V (or P-A) functional form does not change our results qualitatively as long as the cell volume decreases with increasing applied osmotic pressure, namely P − P₀ = −Γ(A − A₀) (with Γ being a coefficient characterizing the cell’s compressibility), and the deviations from the preferred cell area in 2D (A₀) are mild.

Fixed point tension and tension dynamics.

The fixed point tension, $T_{\mathit{ij}}^0$, corresponds to an average effective tension at cell-cell contacts and has contributions from the average actomyosin-generated cortical tension T₀ in each cell and the average cell-cell adhesion strength W, so that $T_{\mathit{ij}}^0=2T_0-W$ (Fig. 1b). At free cell boundaries (cell boundaries contacting the extracellular space), the average effective tension is just the average cortical tension of the cell, namely $T_{\mathit{ij}}^0=T_0$. Here we assume the average tension T₀ not to change with the cell perimeter, as no current experimental observations suggest that dependence. In situations where the cell shape becomes very anisotropic or contorted enough to have very large perimeters, a dependence of the average effective tension on the perimeter could potentially arise from limitations in plasma membrane availability.

The stochastic dynamics of tensions depends on the magnitude of tension fluctuations, which is ΔT at cell-cell contacts and ΔT/2 at free cell boundaries (cell boundaries contacting the extracellular space).

Parameter estimation.

Since the relaxation timescale τ_R has been measured to be much smaller than the persistence timescale of tension variations (τ_R ≲ 20s ^{42, 43}; τ_T ≃ 90s ¹⁵) we set the ratio to τ_T/τ_R = 10. While the values of osmotic pressure are unknown in vivo, they are expected to be larger than cortical stresses ⁴⁷, so that P₀L₀/T₀ ⪢ 1. Consequently, we fix P₀L₀/T₀ = 10 for all simulations. This ensures relatively mild cell size variations, as observed experimentally ¹⁵. Fixing these parameters reduces the parameter space to the normalized amplitude of tension fluctuations ΔT/T₀, the ratio W/T₀ of average adhesion strength and average cortical tension, and the ratio $N{L}_0^2∕A_T$ of the cell’s total preferred area and the total available area.

Numerical integration.

The dimensionless version of the governing equations (Eqs. 1–2) was integrated numerically using Euler-Maruyama method with a time step, Δt. We used Δt = 0.005 τ_R for all simulations to have a time resolution much smaller than the smallest characteristic timescale in the system, τ_R.

Initial configuration generation protocol.

A polygonal tiling of confluent states is first generated by random Poisson Voronoi tessellation in a square periodic box of total area A_T. Prior to the introduction of extracellular spaces, the initial confluent configuration is first annealed to a local equilibrium state to prevent sudden adjustment of cell shape with extracellular spaces. Extracellular spaces are introduced by replacing each vertex in the confluent configurations with a small triangular extracellular space ’cell’ centered around the original vertex position, and with the 3 new vertices located on the each of the original edges and of 1% their original length. Small tension fluctuations (ΔT/T₀ = 0.5) are applied for a duration τ_T. The resulting configuration is used as an initial configuration for simulations of both equilibrium configurations and dynamics.

As for any model of multicellular systems, some of the observed configurations depend on the initialization protocol. Regular hexagonal packings can be obtained by choosing regularly arranged initial cellular configurations. However, since most embryonic tissues typically show topologically disordered configurations, we used random Poisson Voronoi tessellation as an initial configuration.

Equilibrium configurations and quasi-static changes.

Equilibrium states were obtained by quenching the system from an initial state with tension fluctuations (ΔT/T₀ = 0.5) to an equilibrium state (ΔT/T₀ = 0) for each parameter set. While we observe small changes in the resulting configurations if the magnitude of the initial tension fluctuations is varied in the annealing protocol, our results, including the existence of the structural transition, remain qualitatively unchanged. Quasistatic changes of the relative adhesion at equilibrium where performed by first quenching the system to equilibrium at a given parameter value, and then performing a small change in the parameter (W/T₀) and letting the system relax. Specifically, the system was initialized at a large value of the relative adhesion strength that ensured a confluent state (W/T₀ = 1) and then quenched to a local equilibrium state. The relative adhesion strength was then progressively reduced to W/T₀ = 0 by small changes (ΔW/T₀ = −0.02). Similarly, the other branch was found by initializing the system at zero adhesion strength (W/T₀ = 0) and progressively increasing it to W/T₀ = 1 by small increments (ΔW/T₀ = 0.02). After each adhesion adjustment, the system is relaxed to local equilibrium states.

Introducing spaces between cells.

Extracellular spaces are first introduced to initial configurations of confluent states as cells with different properties. Each vertex is replaced by a small triangular extracellular space centered around the original vertex position, and with the 3 new vertices located on the each of the original edges and of 1% their original length. These extracellular spaces then behave like ’cells’ with different properties (see Methods above) and their size and geometrical features are determined by force balance at the vertices, as is the case for cells too. When two extracellular space ’cells’ become neighbors, they are merged. This implementation allows non-confluent states in vertex models and is different from previous descriptions of non-confluent states, which used center particles ^{26, 27} or deformable particles models ²⁸.

Intermediate non-physical vertices.

Intermediate vertices are introduced for both cell-cell contacts and free cell boundaries to allow for more realistic cell shapes. With intermediate vertices, individual edges consist of linear segments joined together to form a piecewise linear edge. The desired segment length is introduced as a parameter and the number of intermediate vertices for each edge is equal to the closest lower integer given by the ratio of instantaneous edge length to the segment length criterion. When the edge length increases (decreases), an intermediate vertex can be added (deleted) following the criterion just described. As the number of intermediate vertices changes, intermediate vertex positions are reassigned uniformly along the edge. If the longest segment is longer than twice the shortest segment in a given edge, intermediate vertex positions are also reassigned uniformly along the piecewise linear line. This implementation of intermediate vertices is similar to the one used for confluent equilibrium systems ²⁵.

While we considered all vertices to have the same drag coefficient, physical and non-physical vertices may, in general, be characterized by different drag coefficients. This approximation is not due to technical reasons, as the simulation framework presented here can simulate different drag coefficients at different vertices different drag coefficients. Previous works have shown that the measured stress relaxation timescales for movement of vertices is much smaller (~1-20s ^{42, 43}) than the persistence timescale of active tension fluctuations, which is approximately 100s ¹⁵. Since we are interested in the behavior of the system at long timescales (longer than the persistence timescale of active tension fluctuations (t ⪢ τ_T)) and the timescales associated to viscous relaxation at vertices are much smaller than the persistence timescale of active stresses (τ_T ⪢ τ_R), we neglected the differences in drag coefficient at the different vertices, as they are irrelevant in this limit.

Treatment of topological transitions.

T1 transitions occurs in our description when a given edge length is shorter than a critical length ℓ_c = 0.01 × 2πL₀. When a T1 transition leads to the formation of a new vertex between 3 cells, we introduce a small triangular extracellular space ’cell’ and let it evolve in time, as described above. Free cell boundaries (a boundary of a cell and the extracellular space) occasionally intersect each other due to the system dynamics. This event corresponds to the formation of a new contact between two cells. Therefore, when an intersection between any two free boundary edges is detected, a new cell-cell contact is introduced, splitting the extracellular space in two.

While not simulated here, cell divisions and cell death, which would also introduce topological transitions, are straightforward to simulate in this framework. Since these events would also induce cell rearrangements, they are also likely to enable tissue fluidization, as previously suggested ^{5, 11, 13, 14}.

Cell trajectories and mean squared displacement (MSD).

To obtain the Mean Squared Displacement (MSD) we first computed the cell centers (centroid of polygon), ${\overrightarrow{r}}_{C,i}$, for each time point, t, based on vertex positions. Then, the cell trajectories were obtained by monitoring the changes of cell centers. Using the cell trajectories ${\overrightarrow{r}}_{C,i}(t)$, we obtained the MSD according to

$$\mathit{MSD}(t)=\frac{1}{N}\sum _i{({\overrightarrow{r}}_{C,i}(t_0+t)-{\overrightarrow{r}}_{C,i}(t))}^2.$$ (3)

MSD values were averaged over all cells and also all initial time points t₀ for any given set of model parameters.

Application of a step strain.

Since tissue fluidization in biological tissues is associated with their non-linear mechanical response ¹⁵, we impose large strains ϵ_xy of 150%. The large step strain was applied by deforming the simulation box from a square to a parallelogram of the target shear strain, namely 150%. An affine deformation is applied to all vertex positions when imposing the step strain. Lees-Edwards periodic boundary conditions were imposed throughout the simulation to avoid mismatch of cell geometry across system boundaries.

Stress calculation.

The non-dimensional stress tensor can be computed from the transient tissue geometry with knowledge of junctional tensions and cell pressures ^{48, 49} (lowercase indicates normalized quantities), namely

$${\sigma }_{\mathit{mn}}=\rho \left[-\sum _{i:\text{cell}}\Delta p_i{a}_i{\delta }_{\mathit{mn}}+\sum _{\mathit{ij}:\text{edge}}{t}_{\mathit{ij}}\frac{l_{\mathit{ij},m}{l}_{\mathit{ij},n}}{\mid {\overrightarrow{l}}_{\mathit{ij}}\mid }\right],$$ (4)

where Δp_i ≡ p_i − p₀, m, n are indices indicating the spatial direction (m = x, y and n = x, y), aⁱ is the dimensionless cell area and ${\overrightarrow{l}}_{\mathit{ij}}$ is the vector form of the edge length between cells i and j. The shear stress term can be written as

$${\sigma }_{\mathit{xy}}=\rho \left[\sum _{\mathit{ij}:\text{edge}}{t}_{\mathit{ij}}\frac{l_{\mathit{ij},x}{l}_{\mathit{ij},y}}{\mid {\overrightarrow{l}}_{\mathit{ij}}\mid }\right].$$ (5)

Active shear stress.

Due to tension fluctuations, the macroscopic shear stress shows fluctuations around zero. To quantify the magnitude of these active shear stress fluctuations, the shear stress values are monitored over a time interval of 10³ τ_R and their standard deviation is computed for each parameter set (no macroscopic imposed strain). The level of active shear stress corresponds to the computed standard deviation of shear stress, and increases approximately linearly with the magnitude of tension fluctuations for a given relative cell adhesion strength (Supplementary Section 2).

Zebrafish husbandry, lines and experimental manipulations.

Zebrafish (Danio rerio) were maintained under standard conditions⁵⁰. The cdh2^tm101 mutant line ⁴⁶ was used to disrupt adhesions between cells, otherwise phenotypically wild-type lines were used. Animal husbandry and experiments were done according to protocols approved by the Institutional Animal Care and Use Committee (IACUC) at the University of California Santa Barbara. Transgenic lines Tg(hsp70:secP-mCherry)^p151 and Tg(h2afva:eGFP)^kca6 were used to visualize extracellular spaces and nuclei, respectively. Both Tg(bact2:mem-neonGreen-neonGreen)^hm40 and Tg(actb2:memCherry2)^hm29 transgenic lines were used to visualize cell membranes in different experiments. In some cases, membranes were labelled by injection with 80-100 pg membrane-GFP mRNA at 1-2 cell stage.

Imaging.

In all cases, 8-10 somite stage zebrafish embryos were mounted in 1% low-melting point agarose in a glass bottom petri dish (MatTek Corporation) for a dorsal view of the tailbud and imaged at 25°C using a 40x water immersion objective (LD C-Apochromat 1.1 W, Carl Zeiss) on an inverted Zeiss Laser Scanning Confocal (LSM 710, Carl Zeiss Inc.).

For kymograph of cell-cell contacts, confocal timelapse data of MPZ and PSM regions in Tg(h2afva:eGFP)^kca6 x Tg(actb2:memCherry2)^hm29 double transgenic embryos were acquired (2 second time intervals for 30 minutes). The intensity profile of a single junction was tracked over 300 seconds and measured over a 5-pixel width segment line to minimize the error induced by the estimation of the junction location.

Images of extracellular spaces were obtained using an outcross of Tg(hsp70:secP-mCherry)^p151 and Tg(bact2:mem-neonGreen-neonGreen)^hm40, to label the extracellular spaces and cell membranes, respectively. To trigger the expression of mCherry in the extracellular space, a 1 hour heat shock in a water bath at 39°C was performed when the embryos were at 75% epiboly stage. Confocal sections through PSM and MPZ tissues were subsequently acquired.

Imaging of ferrofluid droplets was done as previously reported ^{15, 43}. Briefly, images of a droplet previously inserted in the MPZ region of the embryo were taken every 5 seconds. Ferrofluid droplets were fluorescently labelled using a custom-synthesized fluorous cyanine dye FCy5 dissolved in the fluorocarbon-based ferrofluid oil at a final concentration of 25 μM ⁵².

Tracking of cell movements in the PSM of N-cadherin mutants.

Both mutant (cdh2^−/−) and sibling (cdh2^+/+;+/−) embryos were injected with 80-100 pg each of H2B-mRFP mRNA and membrane-GFP mRNA at 1-2 cell stage to label nuclei and membranes, respectively. Confocal stacks through the PSM were acquired with a z-step size of 1 μm and time interval of 1 minute for 30 mins, and processed using Imaris (Bitplane). Data were smoothed using a 1-pixel gaussian filter, to correct for photobleaching over time the normalize timepoints function was used, then attenuation correction was applied to correct for z-attenuation. After processing, data were cropped to the tissue of interest, then nuclei were detected using the spots function, and tracked using the Brownian motion algorithm. Nuclei positions were output for further analyses. The Mean Squared Relative Displacement (MSRD) is calculated from the cell trajectories and normalized using the cell diameter d. The normalized MSRD is MSRD/d^{2 15}.

Generation and injection of ferrofluid droplets.

Ferrofluid droplets were prepared as previously described ^{15, 43}. Briefly, DFF1 ferrofluid (Ferrotec) was diluted in filtered 3M Novec 7300 fluorocarbon oil. To prevent non-specific adhesion between cells and droplets, a fluorinated Krytox-PEG(600) surfactant (008-fluorosurfactant, RAN Biotechnologies ⁵³) was diluted in the ferrofluid at a 2.5% (w/w) concentration. The ferrofluid was calibrated before each experiment as previously described ⁴³, so that the applied magnetic stresses are known. Once prepared and calibrated, the ferrofluid was injected in the MPZ tissue of phenotypically wild-type zebrafish embryos at the 4-6 somite stage to form droplets of 30 – 40μm diameter, as previously described ^{15, 43}. Imaging of droplets started at least 1.5 hours after the injection to let the tissue fully recover from it.

Magnetic actuation of ferrofluid microdroplets.

Actuation of ferrofluid droplets was performed following the previously described protocol ⁴³. Briefly, ferrofluid droplets were actuated by a uniform and constant magnetic field ⁴³ applied along the direction of smaller droplet deformation, as given by the smallest semi-axis of elliptical deformation before the magnetic field was applied. The droplet shape was monitored before (15 min) and during magnetic actuation (15 min), as well as during droplet relaxation (1 hour).

Measurements of strain and stress relaxation.

Upon application of a uniform, constant magnetic field ferrofluid droplets acquire an ellipsoidal shape, elongated along the direction of the applied magnetic field and symmetrical about it ^{43, 54}. The observed confocal section through the middle of the droplet was fitted to an ellipse of short and long semi-axes a and b, respectively, as previously described ⁴³. The droplet strain, (b − b₀)/R, is defined as the ratio of its elongation along the direction of applied magnetic field, namely (b − b₀) (with b₀ being the value of b just before magnetic actuation), and the droplet radius R, and can be monitored over time by measuring the change in the droplet long semi-axis b(t). The stresses at supracellular (tissue) scales associated with a particular droplet deformation were obtained from the elliptical droplet deformation, as previously described ¹⁵, namely σ_A = 2γ (H_b − H_a), where γ is the droplet interfacial tension and H_b and H_a are the mean curvatures of the droplet ellipsoidal shape at the intersection of the principal axis with the fitted ellipsoid. Since the droplet shape is that of a prolate spheroid, H_b and H_a read H_b = b/a² and H_a = 1/2a + a/(2b²). By monitoring the changes in droplet shape over time, we obtained the time evolution of both the mean curvatures, namely H_b(t) and H_a(t). The droplet interfacial tension γ was measured in each experiment in situ and in vivo, as previously described ^{15, 43}. Using the measured value of the interfacial tension for each droplet and the time evolution of the mean curvatures H_b(t) and H_a(t), we obtained the time evolution of the stresses during relaxation using σ_A(t) = 2γ (H_b(t) − H_a(t)).

Neighbor Exchange Analysis

One hour long confocal timelapses of the MPZ region of membrane-labeled embryos containing a previously inserted droplet were acquired at 1 frame every 5 seconds. A region of the MPZ away from the droplet and a region adjacent to the droplet were cropped and the time at which T1 transitions occurred in each region was recorded. T1 transitions were detected manually by inspecting cell configurations between frames. To improve accuracy of the analysis, smaller sections of each region containing approximately 10 to 15 cells were further cropped and analyzed separately. The cumulative NE were obtained by adding up the NE events occurring over time in each region. The NE rate was obtained by taking the derivative of the cumulative NE function.

Extended Data

Extended Data Fig. 1. Power law relation between NE rate and MSD at long timescales.

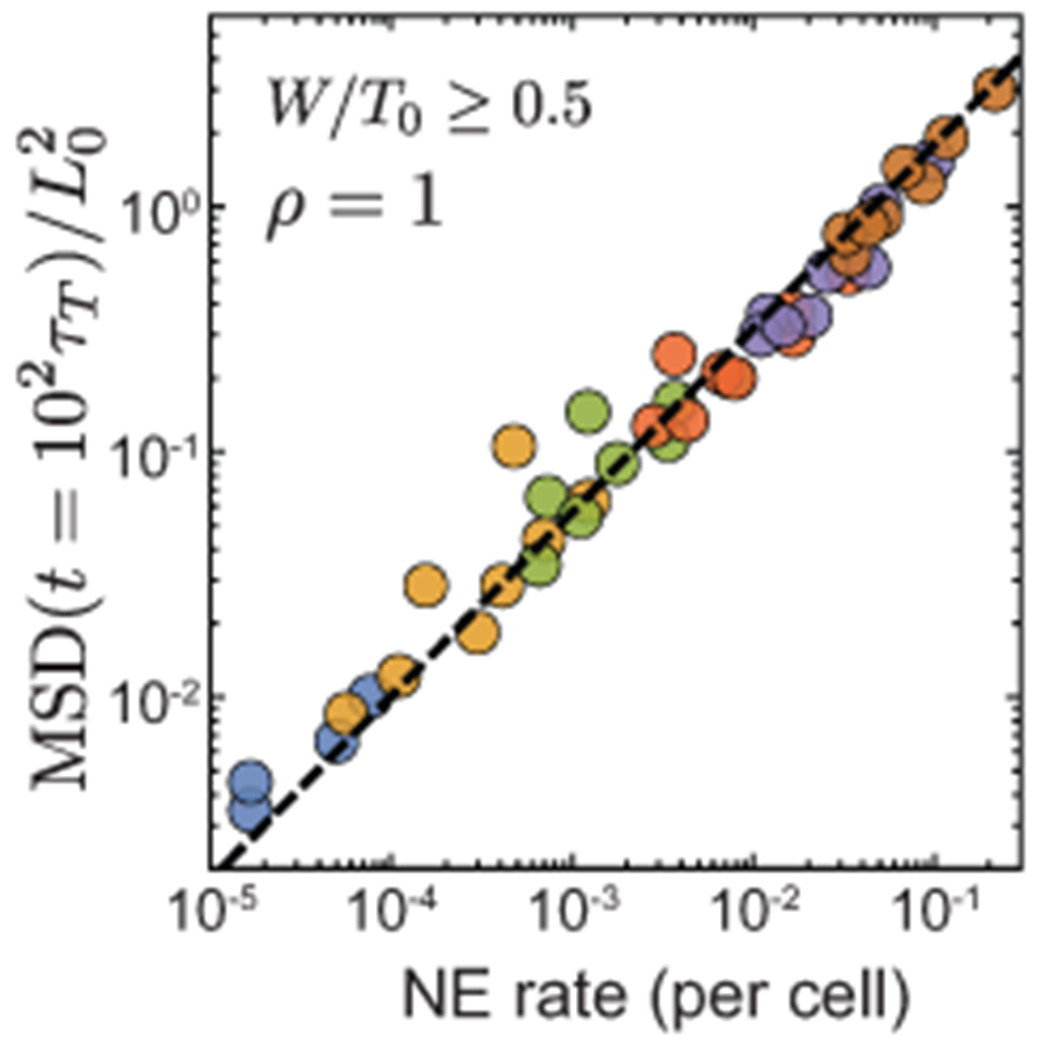
Power law relation between long time MSD values and NE rate when the systems are close to confluence for high adhesion levels. NE rate and longtime MSD show a power law relation with an exponent of 0.75.

Extended Data Fig. 2. Comparison of solid/fluid phase diagrams obtained from stress relaxation and from cell movements.

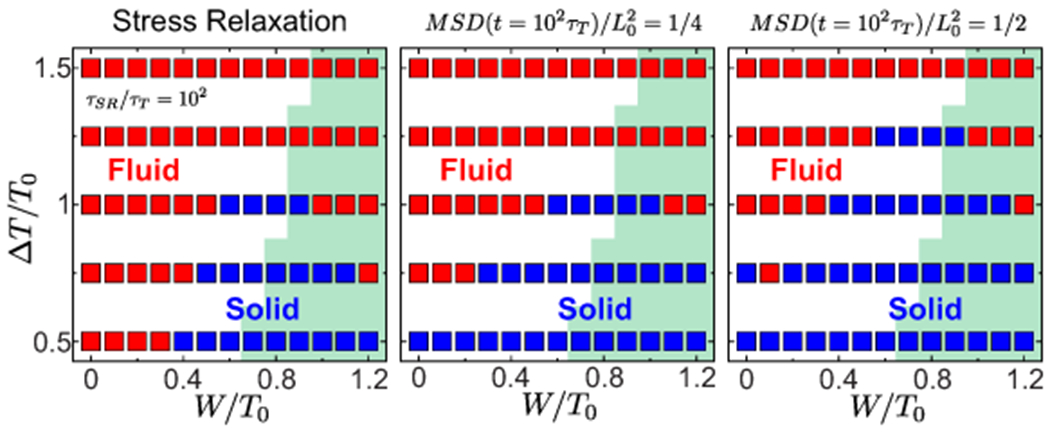
Solid/fluid phase diagrams determined by mechanical measurement of stress relaxation (left) and cell movements, MSD=1/2 (middle) and MSD=1/4 (right). Green region indicates confluent states.