Causal role for the primate superior colliculus in the computation of evidence for perceptual decisions

Abstract

Trained monkeys performed a two-choice perceptual decision-making task in which they reported the perceived orientation of a dynamic Glass pattern, before and after unilateral, reversible, inactivation of a brainstem area involved in preparing eye movements, the superior colliculus (SC). Surprisingly, we found that unilateral SC inactivation produced significant decision biases and changes in reaction times consistent with a causal role for the primate SC in perceptual decision-making. Fitting signal detection theory and sequential sampling models to the data revealed that SC inactivation produced a decrease in the relative evidence for contralateral decisions, as if adding a constant offset to a time-varying evidence signal for the ipsilateral choice. The results provide causal evidence for an embodied cognition model of perceptual decision-making and provide compelling evidence that the SC of primates, a brainstem structure, plays a causal role in how evidence is computed for decisions, a process usually attributed to the forebrain.

INTRODUCTION

Our ability to translate what we see into perceptual reports and choices of action may arise from the gradual accumulation of perceptual evidence in sensorimotor regions of the forebrain^1,2. In monkeys, forebrain regions implicated in cognitive processing leading to perceptual decisions include the lateral intraparietal³ (LIP) and dorsolateral prefrontal⁴ (dlPFC) areas of cerebral cortex as well as the subcortical, striatum^5–7. A key observation linking these forebrain areas to the computations for perceptual decisions is that the spiking activity of neurons in these areas gradually ramps up over time, as decisions evolve. Moreover, electrical stimulation in area LIP⁸ and the striatum of monkeys⁹, alters decision-making in ways predicted by popular mathematical models of decision-making.

Ramping activity of neurons is not unique to the forebrain. The brainstem superior colliculus (SC) also exhibits ramping activity when monkeys and rodents perform decision-making tasks^10–13. The field, however, generally assumes that the ramping activity of SC neurons results from cerebral cortical inputs to the SC and therefore, is unrelated to decision-making per se. Therefore, it is possible that the ramping activity in the SC simply reflects the sensory and motor aspects of preparing the eye movement used to report the decision. Here, we tested the hypothesis that the SC of monkeys plays a causal role in perceptual decision-making, independently of its role in visual and motor processes for eye movements. We performed reversible GABA-agonist (muscimol) inactivation of the SC unilaterally in two monkeys while they performed a perceptual decision task as well as a simple saccade selection task. Importantly, the selection task did not contain perceptual ambiguity, as did the decision task, so we could assess alterations in decisions or in sensory and motor processes produced by SC inactivation separately, by comparing performance in both tasks. We modeled the data using signal detection theory (SDT) methods and sequential sampling model variants (drift-diffusion; HDDM, DDM and urgency gating; UGM) and all yielded similar results. Based on our results, we conclude that reversible inactivation of the SC produces significant decision biases and changes in reaction times consistent with a causal role for the primate SC in perceptual decision-making, independently of visual or motor biases. Inhibiting the SC of monkeys unilaterally changes decision-making behavior of monkeys in a way that is consistent with a shift in the time-varying evidence accumulation away from decisions into the inactivated field. A biologically plausible computational model of the decision changes indicates that the SC regulates the gain of how evidence is computed for perceptual decision-making.

RESULTS

Trained monkeys (Macaca mulatta) performed a two choice perceptual decision-making task in which they viewed a dynamic Glass pattern stimulus^14,15 and reported the perceived orientation of the stimulus by making saccades to a target located in either the left or right hemifield, before and after reversible, unilateral inactivation of the SC with muscimol (Fig. 1). Monkeys reported their decisions in two sets of experiments: one with the cue to report the choice occurring with a delay after the appearance of the Glass pattern (Fig. 1a; Delay task) and a second with no delay, allowing monkeys to report their decisions immediately (Fig. 1b; RT task). The latter version, known as a reaction time (RT) task, allowed us to fit dynamic decision-making models to the behavioral data to determine what decision-making processes changed, if any, after unilateral muscimol inactivation of the SC.

Fig. 1. Decision and selection tasks before and after unilateral SC inactivation.

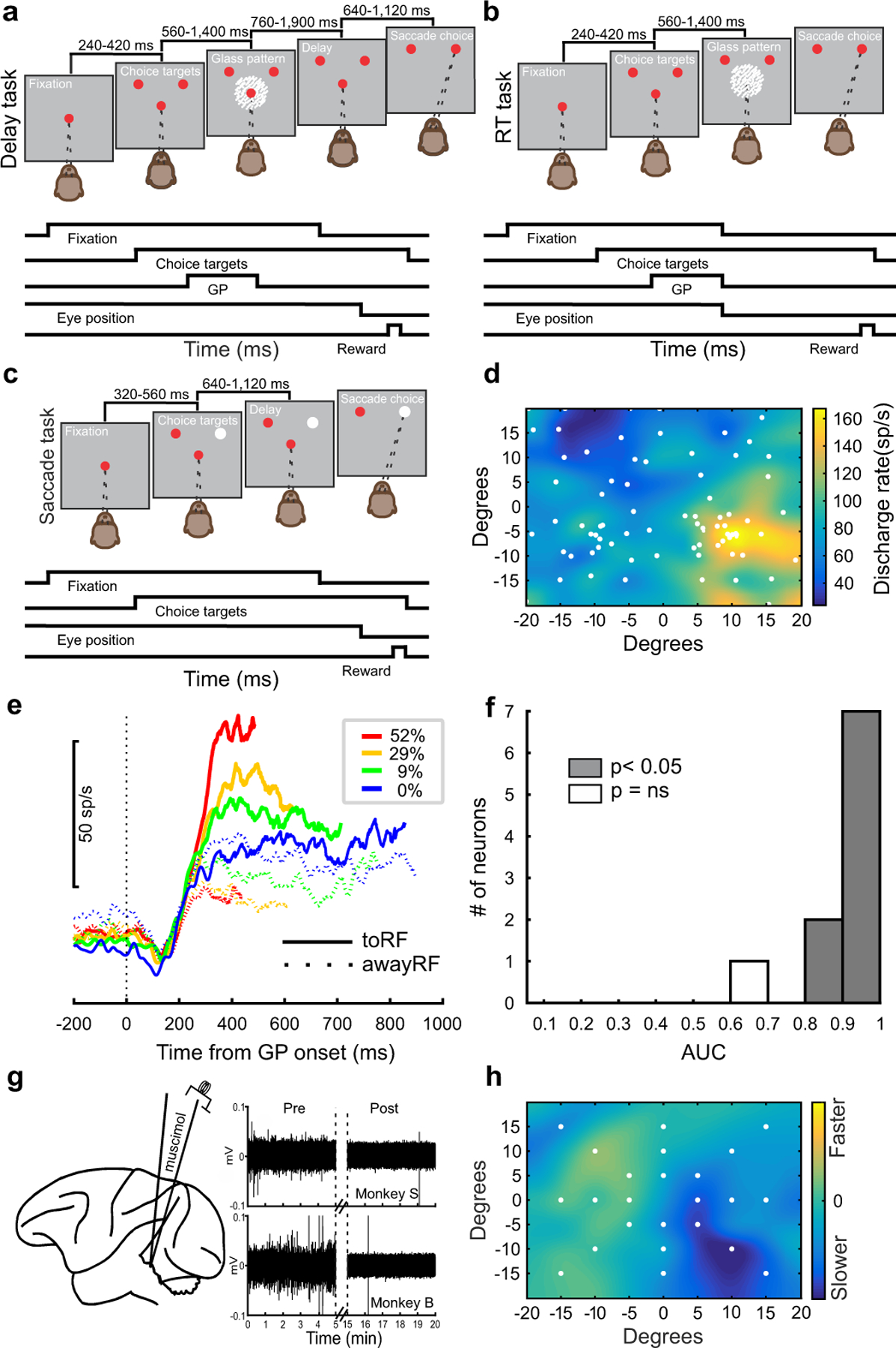
a The sequence of grey boxes depicting the visual display and the temporal sequence of the events appears as running line displays below the spatial display (Delay task). b Same as in a for the reaction time version of the task (RT Task). c Schematic display of the saccade selection task. The timings of the tasks appear above the schematic illustrations. d The pre-muscimol discharge rate of an SC neuronal recording measured 50 ms before and 50 ms after the onset of a saccade, is plotted as a heat map using linear interpolation between the target positions (white circles). Warmer colors indicate higher discharge rates (sp/s). The position 0 horizontal and 0 vertical in degrees marks the position of the centrally-located fixation spot. e Averaged spike density function (σ = 10 ms) for ten SC neurons aligned to Glass pattern stimulus onset, conditioned on coherence (color) and choice (solid or dashed lines) excluding activity 20 ms before saccade onset. f Number of neurons plotted against the area under the receiver operating characteristic curve (AUC) for the ten neurons in the 0% coherence condition calculated from the epoch of 100 ms to 20 ms before saccade onset (Methods). AUC values with p < 0.05 (shaded grey) significantly differ from 0.5 (two-tailed bootstrap test). g Schematic of the experimental arrangement showing a lateral view of the rhesus monkey brain and an injectrode targeting the SC. The traces to the right show the raw voltage traces against time in min before and after muscimol injections in two monkeys (monkey S; top and monkey B; bottom). The 10 min injection time is marked by the vertical dashed lines. h Post-muscimol saccadic velocity minus pre-muscimol saccadic velocity divided by pre-muscimol saccadic velocity multiplied by 100, is plotted for the target positions indicated by the white circles. Cooler colors indicate slower saccadic velocities post-muscimol. The plots shown in d and h show one injection in monkey S. See Extended Data Fig. 1 for more examples. The location of the response field (RF) as in d, determined the positions of the choice targets in the decision and selection tasks.

Monkeys also performed a saccade selection task in which two possible choice targets appeared at the same two locations as in the decision task. One target was red and the other white, and the monkeys made saccades to the white target, which alternated between the left and right positions randomly on each trial (Fig. 1c). We imposed delays in the selection task similar to those used in the delayed version of the Glass pattern decision task so we could compare muscimol effects on eye movement biases in a task with similar timing but without perceptual ambiguity. The selection task required the same attention to the peripheral location and the same motor preparation as in the decision task but did not contain perceptual ambiguity nor did it require the transformation of an orientation decision to a motor action located elsewhere. Performing the selection task before and after unilateral inactivation of the SC allowed us to assess the influence of unilateral muscimol in the SC on motor preparation and saccade bias.

Fig. 1d shows a heat map of neuronal discharge recorded from an SC neuron before a muscimol injection. Warmer colors show a typical SC neuronal response field (RF) measured while a monkey made visually-guided saccades to the locations shown by the white circles. We positioned the choice targets for the decision and selection tasks at the RF center (to inactivated field (toIF)) and in the opposite hemifield (awayIF). Previous work using a random dot motion direction decision task and a brightness discrimination task shows that SC neuronal activity correlates with the strength of sensory evidence for decisions^10–12,16. Furthermore, recent work reveals that second order statistics of single trial spiking activity in the SC reflects a process of accumulation in the random dot motion direction discrimination task¹⁷. Here, we confirmed that SC neuronal activity also correlated with evidence strength in our novel Glass pattern task (Fig. 1e). In a third monkey, we recorded from a small sample of SC neurons (n=10) during performance of the RT version of the Glass pattern orientation decision task. Fig. 1e shows that SC neuronal activity scales with sensory evidence strength such that high neuronal activity correlates with strong sensory evidence and weaker neuronal activity correlates with weaker sensory evidence. Moreover, we observed large differences in neuronal activity for decisions made toward and away from the RF when monkeys based their decisions on strong evidence, compared to when monkeys based their decisions on weak evidence (cf., Fig. 1e red solid and dashed lines and blue solid and dashed lines). Confirming that SC neuronal activity recorded in the Glass pattern decision task correlates with the monkey’s decisions, we calculated the area under the receiver operating characteristic curve (AUC) for the 0% coherence trials using signal detection theory (SDT) methods^18,19. Fig. 1f shows that all SC neurons had AUC values exceeding 0.60. Taken together, the electrophysiological results from the Glass pattern decision task are consistent with the literature that places the SC in the network of brain areas that participate in the computation of evidence for perceptual decisions¹.

Confirming the efficacy of the inactivation experiments, unilateral injections of muscimol into the SC reliably reduced or silenced the spontaneous activity of SC neurons within 10–15 minutes of the injection (Fig. 1g). Monkeys also performed visually-guided saccades to predefined targets before and after inactivation, allowing us to map changes in saccadic velocity and providing an independent, behavioral measure of the efficacy of the muscimol injection^20–22 (Fig. 1h). Supplementary Table 1 shows details of the injections made in two monkeys and Extended Data Fig. 1 shows examples of velocity maps from the injection experiments with estimates of the extent of muscimol spread.

SC inactivation biases perceptual decision-making

Unilateral muscimol injections (n=23) into the SC produced reliable ipsilateral (awayIF) decision biases in both monkeys for all 23 injections in both the delay and RT tasks (Fig. 2a). Unilateral saline injections into the SC (n=6) produced little discernible effect on decision-making performance (Fig. 2b). Parameter estimation from logistic fits (Extended Data Fig. 2) to the performance data for muscimol injections revealed a statistically significant lateral, rightward shift in α, the decision bias parameter (Fig. 2c, pre α = −0.29, post α = 10.21, t(22) = 9.81, p = 1.725 × 10⁻⁹, 95% CI = [8.33, 13.74]). In some experiments, the perceptual sensitivity parameter β, decreased with muscimol, but on average, the decrease in β failed to reach significance with Bonferonni correction (Fig. 2d, pre β = 0.12, post β = 0.10, t(22) = −2.23, p = 0.037, 95% CI = [−0.02, 0]). Saline injections affected neither parameter (Fig. 2e,f; pre α = 0.13, post α = 0.07, w(5) = 7, p = 0.563; pre β = 0.12, post β = 0.11, t(5) = 1.71, p = 0.148, 95% CI = [−0.02, 0.06]). We also compared the change in α before and after muscimol to the change in α before and after saline, and found a significant difference (bootstrap hypothesis testing, post - pre mean α muscimol = 11.04, post - pre mean α saline = −0.73, t(27) = 5.21, p = 3.0 × 10⁻⁵). Likewise, we found significant differences for these comparisons of the β parameter (post - pre mean β muscimol = −0.01, post - pre mean β saline = 0.02, t(27) = −2.78, p = 0.01). Calculating signal detection theory (SDT) quantities, criterion (c) and sensitivity (d’) also revealed statistically significant changes in c and not d’ (Extended Data Fig. 3).

Fig. 2. Unilateral Inactivation of the SC biases perceptual decision making.

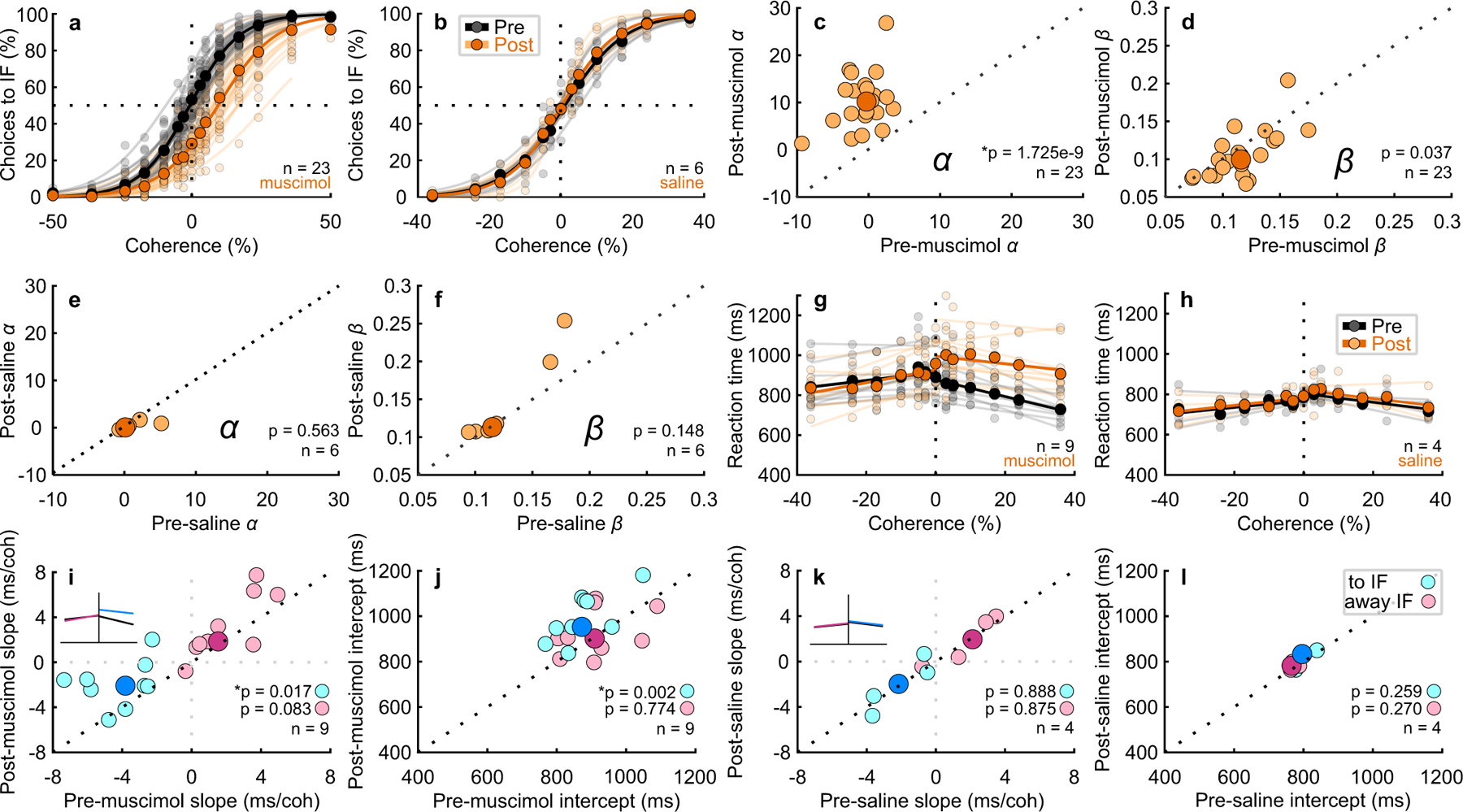
a Decisions to the inactivated field (toIF) plotted against Glass pattern coherence, where positive coherences are toIF evidence and negative coherences are awayIF evidence, for 23 experiments performed in two monkeys before (black circles and lines) and after (orange circles and lines) unilateral injection of muscimol into the SC; n=11 injections in monkey B and n=12 injections in monkey S for both delay and RT tasks. The horizontal dashed lines show 50% chance performance. Vertical dashed lines show 0% coherence. Each lighter shade line shows the two parameter logistic fit to the data for individual experiments and the darker shade lines show the two parameter logistic fit pooled across 23 experiments (see Extended Data Fig. 2 for comparisons of two, three and four parameter logistic fits). Extended Data Fig. 4 shows the results of the 24-hour recovery for muscimol and saline and Supplementary Table 2 shows the associated statistics. b Same as in a for the Glass pattern task performance before (black) and after (orange) saline injections, n=2 injections in monkey B and n=4 injections in monkey S. Note that there are no 50% coherence for saline experiments (Methods). c–f Post-muscimol and post-saline parameters of the logistic fits are plotted against the same parameters measured pre-muscimol and pre-saline from the fits shown in a and b. The darker symbols show the medians whereas the lighter symbols show the parameters from individual experiments. Note that the text reports the confidence intervals relative to the means. * indicates significance with a critical α value of 0.025 Bonferroni corrected. g For the same experiments and data shown in a that were performed with the RT version of the decision task (n=9 injections), mean RT is plotted against coherence pre-muscimol (black circles and lines) and post-muscimol (orange circles and lines) for all correct trials. The lines show linear fits to the data points (Supplementary Note). h The same as in g for the saline injections (n=4 injections). i The slopes of the post-muscimol linear fits to the RT data are plotted against the pre-muscimol slopes for toIF decisions (cyan circles) and awayIF decisions (magenta circles). The inset shows which changes in slope correspond to the changes seen in the chronometric function. The black dotted line shows unity. The dark circles show medians. j Same as in i for the intercept parameter. k–l The same as in i-j for the saline experiments.

Of the 23 muscimol injections, nine were performed during the RT version of the task (seven in monkey S and two in monkey B). On average, mean RT increased for toIF decisions and did not change for awayIF decisions post-muscimol (Fig. 2g; mean RT pre toIF = 808.71 ms, mean RT post toIF = 971.77 ms, t(53) = 12.86, p = 6.24 × 10⁻¹⁸, 95% CI = [133.82, 192.30]; mean RT pre awayIF = 887.31 ms, mean RT post awayIF = 871.41 ms, t(53) = −1.11, p = 0.27, 95% CI = [−48.98, 17.17]). However, mean RTs showed a negative correlation with coherence for toIF decisions before the injection and the slopes of the chronometric functions flattened after injections (Fig. 2g, Fig. 2i cyan circles, pre = −3.83 ms/coherence, post = −2.09 ms/coherence, t(8)= 3.00, p = 0.02, 95% CI = [0.19, 4.42]). We found no significant changes in slopes for awayIF decisions (Fig. 2g, Fig. 2i magenta circles, pre = 1.55 ms/coherence, post = 1.84 ms/coherence, t(8) = 1.98, p = 0.08, 95% CI = [−0.44, 2.70]). Significant changes occurred in the intercept parameter for toIF decisions, but not for awayIF decisions (Fig. 2j cyan circles, pre toIF = 873.085 ms, post toIF = 952.62 ms, t(8) = 4.64, p = 0.002, 95% CI = [48.12, 188.25]; magenta circles, pre awayIF = 909.725 ms, post awayIF = 901.225 ms, t(8) = 0.30, p = 0.77, 95% CI = [−94.56, 117.39]). The significant changes in slope of the chronometric functions for toIF decisions indicate a unilateral, coherence-dependent change in mean RT. That the lower coherence trials show less of a change in RT than the higher coherence trials, indicates that the change in RT is not solely a result of motor impairment, but suggests instead, that SC inactivation alters decision-making processes. The four saline injections changed neither the slope nor the intercept of the chronometric functions (Fig. 2h; Fig. 2k cyan circles, pre slope toIF = −2.14 ms/coherence and post slope toIF = −1.99 ms/coherence, t(3) = 0.15, p = 0.89, 95% CI = [−2.17, 2.33]; magenta circles, pre slope awayIF = 2.11 ms/coherence and post slope awayIF = 1.94 ms/coherence, w(3) = 6, p = 0.88; Fig. 2l cyan circles, pre intercept toIF = 796.70 ms and post intercept toIF = 832.71 ms, t(3) = 1.38, p = 0.26, 95% CI = [−33.92, 67.66]; magenta circles, pre intercept awayIF = 765.92 ms and post intercept awayIF = 781.98 ms, t(3) = 1.35, p = 0.27, 95% CI = [−25.65, 50.13]). See Extended Data Fig.4 and Supplementary Table 2 for recovery results.

Based on the results described above and shown in Fig. 2, we propose that the SC plays a causal role in perceptual decision-making beyond its known role in visual and motor processes. Below we describe the results of experiments designed to rule out interpretations based on motor and attentional processes. Then, we present the results from a modeling exercise designed to determine which aspects of decision-making unilateral inactivation of the monkey SC affects.

SC inactivation alters decision and not selection accuracy

Fig. 3a shows decision accuracy collapsed across coherences for toIF (cyan) and awayIF (magenta) sides for monkey S (triangles) and monkey B (circles) before and after unilateral SC inactivation experiments (n=23). For trials with evidence favoring toIF decisions, accuracy dropped from 83% to 64% for monkey B (t(10) = −5.60, p = 2.28 × 10⁻⁴, 95% CI = [−0.26, −0.11]) and 79% to 59% for monkey S (w(11) = 0, p = 0.002). For trials with evidence favoring awayIF decisions, accuracy increased from 79% to 90% for both monkey B (w(10) = 66, p = 0.003), and monkey S (t(11) = 7.967, p = 7.00 × 10⁻⁶, 95% CI = [0.07, 0.14]). Unilateral SC inactivation, however, impairs visual and attentional processing and saccade generation^20,21,23. Therefore, one possibility is that the biased decision-making stems from an impairment in visual or attentional processing of the choice target location or generating the movement and not decision-making processes per se. We think, however, that these interpretations are unlikely, as on average, unilateral muscimol injection did not affect the slope of the psychometric function, which is associated with perceptual sensitivity, and both monkeys reported toIF decisions in the high coherence conditions indicating that they could see the choice targets and make those saccades. The change in performance in the decision task suggests instead that SC inactivation impairs the balance of evidence for a decision rather than visual or attentional processing or the ability to report the decision. In the case of high coherence trials, the relative levels of activity between the each SC remains greater for toIF decisions after muscimol compared to the lower coherence trials^19,22,24. Nevertheless, we tested the attention and motor impairment hypotheses directly.

Fig. 3. Decision but not selection accuracy is altered after SC inactivation.

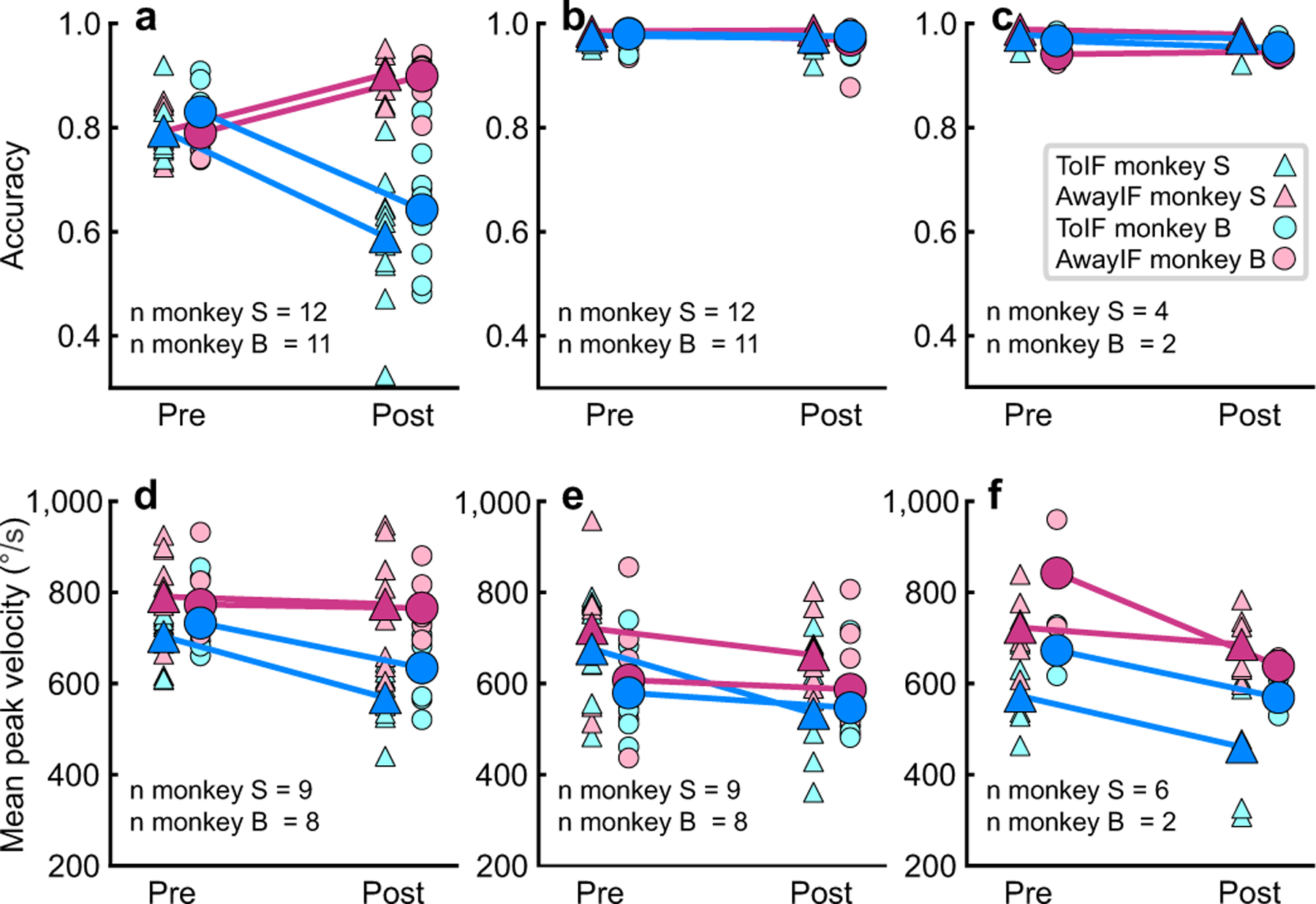
a Proportion correct (accuracy) in the delay and RT versions of the decision task is plotted for toIF trials (cyan) and awayIF trials (magenta) for 23 muscimol experiments in two monkeys, collapsed over coherence, before and after inactivation. Dark filled symbols show the mean accuracy from all experiments and less saturated colors show the accuracies of individual experiments. b Accuracy in the saccade selection task for the same experiments and monkeys. c Same as in b for the six saline injections in the two monkeys. d Mean peak saccadic velocity for the decision task before and after muscimol for toIF and awayIF decisions for 17 injections in two monkeys. Six datasets were excluded due to technical issues with the eye tracker that impacted measurement of eye speed but not assessment of choice or RT. e Same as in d for the saccade selection task. f Same as in d and e for the visually-guided saccade task used to measure saccadic velocity. There are fewer points in this plot because there were fewer saccades in this task that had the same vector target and saccade as in the decision and selection tasks. Note we also did not perform statistics with these data because of the fewer points. The data are useful for visual comparison. All statistics for accuracy and saccadic velocity appear in Supplementary Table 3.

To rule out an interpretation based on attentional or motor bias or impairment, monkeys performed a selection task in which they prepared and made saccades to the same two target locations as in the decision task with similar timing, but without perceptual ambiguity or the need for the transformation of an orientation direction decision to a saccade (Fig. 1c). Performance accuracy in the selection task did not change significantly after muscimol injection for either monkey for all 23 injections (Fig. 3b). Both monkey S and monkey B’s accuracy for toIF decisions changed from 99% to 98% after muscimol (monkey S, w(11) = 28, p = 0.656; monkey B, w(10) = 5, p = 0.249). Unilateral saline injections also produced statistically indistinguishable changes in accuracy in the selection task for toIF decisions (Fig. 3c; monkey B, 97% to 95%, w(10) = 1, p = 0.655; monkey S, 99% to 98%, w(11) = 0, p = 0.317).

Since the decision task is more difficult than the selection task, it is possible that monkeys opt to make the unaffected, awayIF saccade in the decision task more often than in the selection task. If true, we reasoned that we would see no bias in the decision task at the easiest toIF coherence trials, such as 36% and 50%, since the accuracy in these trials was near 100% pre-muscimol indicating that there would be no need to opt for an easier saccade. Yet, we still observed a pronounced change in accuracy post-muscimol even for the 36% coherence trials, a finding that is better explained by a change in aspects of decision-making, rather than a motor preference under uncertainty. Also, assuming the monkeys opted for easier awayIF saccades, we reasoned that toIF saccades in the decision task should be harder to make and would therefore be slower, than saccades in the selection task, given that slower saccades indicate reduced vigor²⁵. Interestingly, in some cases, the velocity of toIF saccades in the decision task was higher than the velocity of saccades in the selection task after muscimol, despite matched metrics (cf., post cyan symbols in Fig. 3d and e). The mean peak toIF saccadic velocity post-muscimol was 563.54°/s for monkey S and 634.58°/s for monkey B in the decision task. In the selection task, the mean peak toIF saccadic velocity post-muscimol was 529.00°/s for monkey S and 546.78°/s for monkey B. The decision task had significantly higher saccadic velocities than those in the selection task in six out of eight muscimol injections in monkey B, and four out of nine for monkey S (Supplementary Table 3). Fig. 3f shows a subset of the data in which monkeys made visually-guided saccades in the task used to map changes in saccade velocities. Simple, visually-guided toIF saccades also tended to be slower than those measured in the decision task, although we did not perform statistics as the data from the simple saccade task were fewer. The higher saccadic velocities in the decision task compared to the selection task, the profound change in accuracy in the decision task, and the lack of change in accuracy in the selection task, together support the embodied cognition model of decision-making^26,27. The results show that a sensorimotor region of the primate brainstem involved in generating action, plays a causal role in a cognitive function - decision-making - independent of its role in action generation. The results also show that decision biases in the Glass pattern task do not stem from simple motor or visual attentional biases.

SC inactivation alters the computation of evidence for decisions

We next wished to determine what aspects of perceptual decision-making, if any, unilateral inactivation of the SC affected. A popular model of perceptual decision-making proposes that sensory evidence for or against a particular decision accumulates over time until a bound crossing, at which time, a decision is made. An example of a sequential sampling model is the drift-diffusion model (DDM)^28,29. In the DDM framework, model parameters instantiate particular aspects of decision-making processes as well as non-decision processes such as the time required for visual processing and the generation and execution of the action used to report the decision. Some of the model parameters in the DDM have analogous components in SDT. In the SDT framework (Fig. 4a), there are two distributions, one representing the signal and the second representing noise or, choice 1 and choice 2 and in our experiment, this would be toIF and awayIF. In the DDM framework, one can think of these two distributions as the internal, sensory representations for the two decisions that provide input to the accumulator(s). In the DDM framework, the difference of evidence for or against a decision is computed to determine the net evidence (also referred to as momentary evidence^8,30). The evidence is then integrated over time until a bound is reached. In SDT, an internal response is compared to a criterion and evidence is stationary whereas in the DDM evidence is time-varying. The distance between the two distributions in SDT reflects perceptual sensitivity and is measured as d’ (Fig. 4a). Changes in d’ will appear as changes in the slope of the psychometric function. In the DDM, an analogous term is the proportionality factor between coherence and drift rate³¹ (k; Fig. 4b; Supplementary Note). Changes in the proportionality factor change perceptual sensitivity (assuming fixed noise) and appear as changes in the slope of the psychometric function. Note that symmetric changes in the bound can also change sensitivity.

Fig. 4. Comparison of aspects of signal detection theory (SDT) and the drift-diffusion model (DDM).

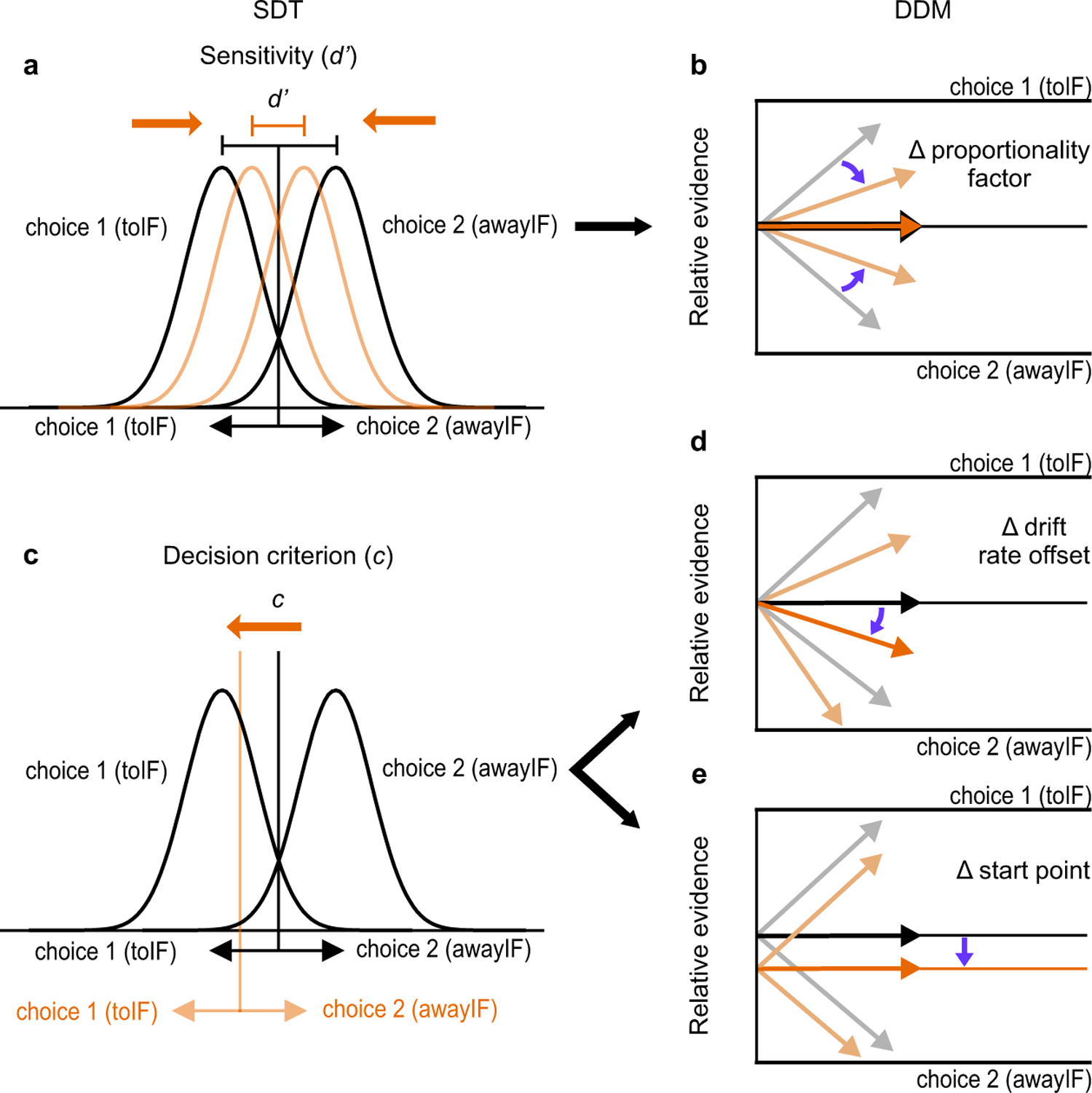
a. Changes in sensitivity (d’) results when the mean distance between the two distributions decreases (cf., black and orange distributions). b. In the DDM framework, this is analogous to a change in the proportionality factor between coherence and drift rate (assuming fixed noise; cf., black and orange arrows). Blue arrows show the change in proportionality factor with no change in mean indicated by the dark orange and black arrows. Note that symmetric changes in the bound in the DDM framework can also affect d’ (not shown). c. Changes in decision criterion (c) in SDT result in changes in the probability of making one or another decision (cf., black and orange vertical line). In the DDM framework, decision biases are implemented by either a change in the d. drift rate offset, or e. a change in the starting point of evidence accumulation or both. Blue arrows show changes in drift rate offset in d or starting point in e. See Extended Data Fig. 5 for a further comparison using DDM simulations. Although we assumed that drift rates would change across coherence based on a simple linear function of coherence conditions for the simulations, note that our fitting of HDDMs, DDMs, and UGMs, are agnostic to the relationship of drift rates to coherence conditions and were found by directly fitting the data for each coherence condition.

The decision criterion in the SDT framework is defined as the willingness to decide on one or the other choice (toIF or awayIF) and is reflected by the parameter c - or the position of the criterion (Fig. 4c black and orange vertical lines). In the DDM framework, there is no single parameter that reflects the decision criterion. Rather, the combined action of the drift rate offset (Fig. 4d), defined as the mean drift rate across all coherences and decision directions (a.k.a. the distance from the drift criterion³² or the drift bias³³), and the start point of evidence accumulation (Fig. 4e), are two ways to implement a decision criterion. Changes in the decision criterion in SDT, and the drift rate offset and the starting point of evidence accumulation in the DDM framework, all result in lateral shifts of the psychometric function. In our previous work using a detection task and sensorimotor priming³⁴, we found that a simple difference in sensory evidence for the presence or absence of a stimulus (we referred to this difference as the decision variable), could not explain SC neuronal activity, changes in behavior or changes in behavior resulting from electrical stimulation of SC neurons. Rather, a model based on a normalized difference of evidence (effectively, a measure of the distance from the SDT criterion) best explained the data. In that experiment, however, we could not determine whether criterion position changes resulted from changes in the drift rate offset (which would affect the computation of time-varying evidence in the DDM framework), or from changes in the starting point of evidence accumulation. The experiments reported here together with the application of the DDM framework, allow us to determine the role of the SC in decision-making with greater precision. Fig. 4 shows the relationships between these variables in the two general model cases. Extended Data Fig. 5 provides further explanation using model simulations.

To illustrate predicted changes in decisions and mean RTs that may occur with alterations in different aspects of decision-making, we first simulated multiple DDM variants with only specific parameters varying (Fig. 5, Extended Data Fig. 5, Supplementary Note). Based on visual comparisons of model predictions and observed data, we can rule out three possibilities to explain the effect of unilateral SC inactivation. First, the data from both monkeys are inconsistent with a decrease in the proportionality factor between coherence and the drift rate, as the slope of the psychometric function showed little to no change with SC inactivation (cf., simulation in Fig. 5a–d, simulation in Extended Data Fig. 5a–d and actual data Fig. 5q–x, shaded). Second, a symmetric increase in the toIF and awayIF boundaries is also unlikely to explain the effect of muscimol since the predicted slight changes in sensitivity and the lack of a shift in the psychometric function do not match the observed results (cf., simulation in Extended Data Fig. 5q–t and actual data in Fig. 5q–x, shaded). Third, we can rule out a model based only on non-decision time, as this predicts no change in the psychometric function and joint changes in the mean RT, neither of which occurred in the post-muscimol data (cf., simulation in Extended Data Fig. 5u–x and actual data Fig. 5q–x, shaded). The simulations with a change in drift rate offset (Fig. 5m–p and Extended Data Fig. 5m–p), proportional start point change (Fig. 5e–h and Extended Data Fig. 5e–h), and an increase in the toIF boundary (Fig. 5i–l and Extended Data Fig. 5i–l), are the only parameter changes by themselves that can explain the shift in the psychometric functions that we observed in the data after muscimol (Fig. 5r,v, shaded). However, a proportional start point change alone cannot explain the observed increases in mean error toIF RTs and predicts a large decrease in mean correct RTs for awayIF decisions, which we did not observe (cf., simulations in Fig. 5g,h and Extended Data Fig. 5g,h and actual data in Fig. 5s,t,w,x, shaded). An increase in the toIF boundary may explain the changes observed in the mean correct RTs (cf., simulations in Fig. 5k,l, and Extended Data Fig. 5k,l and actual data in Fig. 5s,t,w,x, shaded), but fails to explain the magnitude of the lateral shift in the psychometric function observed in the post-muscimol data (cf., simulations in Fig. 5j, Extended Data Fig. 5j and actual data in Fig. 5r,v, shaded). Therefore, simulations show qualitatively that a change in the drift rate offset favoring awayIF decisions explains most of the observed post-muscimol data in both monkeys.

Fig. 5. Unilateral SC inactivation alters the drift rate offset.

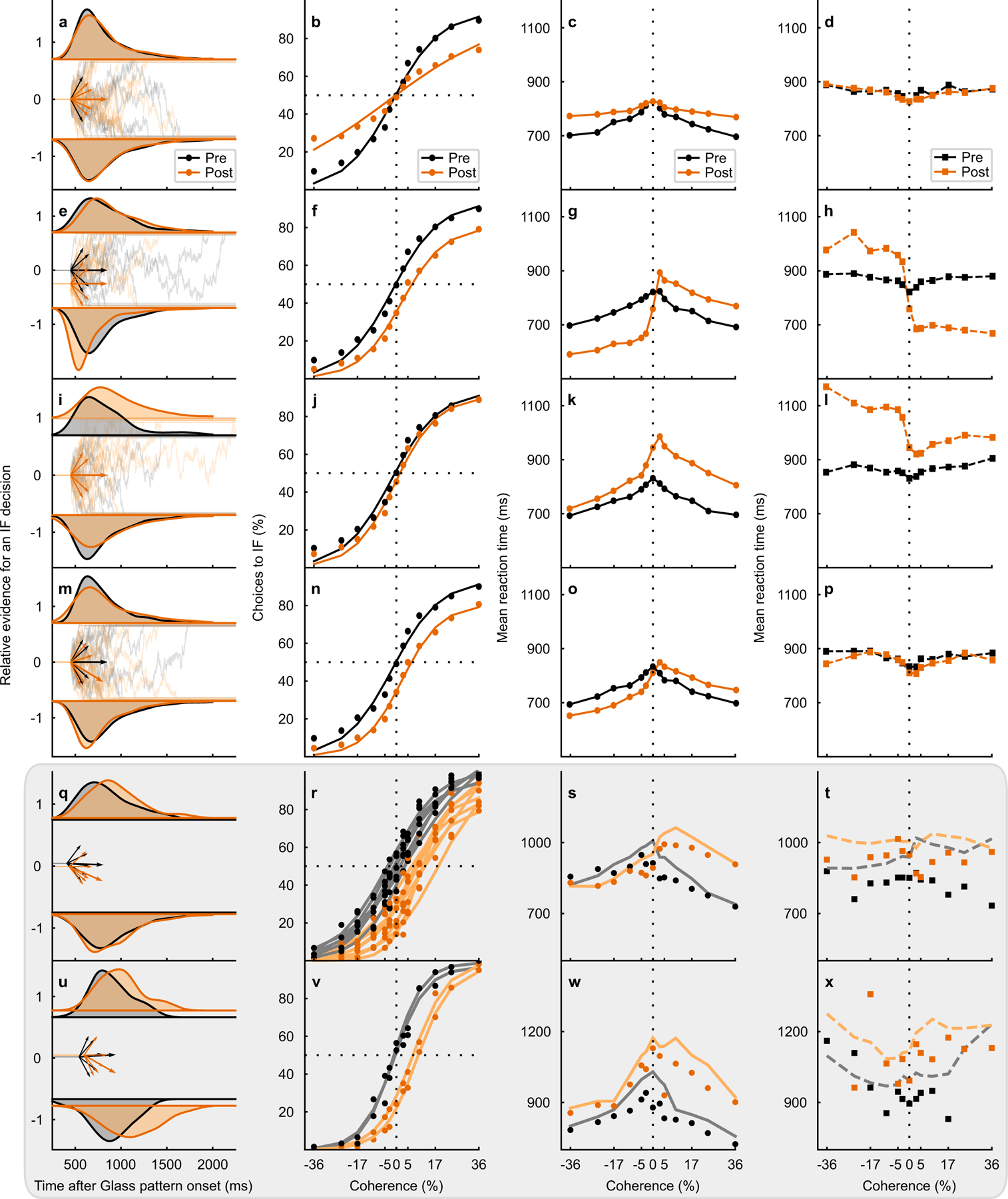
a RT distributions (black = pre- and orange = post-muscimol, top = toIF RTs, and bottom = awayIF RTs) from the 0% coherence condition (density approximated through kernel smoothing) predicted by a DDM simulation with only a decrease in proportionality factor between coherence and drift rate. The relative evidence for toIF decisions is plotted over time from Glass pattern onset and the short arrows show drift rates for toIF decisions (positive) and awayIF decisions (negative) pre- and post-muscimol, for the 0%, 10%, and 36% coherence conditions. The longer arrow shows the drift rate offset. b The psychometric function, plotted as a proportion of toIF decisions over coherences, predicted by the model simulation with a decrease in proportionality factor between coherence and drift rate. c Mean RT predictions for correct trials for each coherence condition for the DDM variant with a decrease in proportionality factor between coherence and drift rate. d Same as in c but for error trials. e–h Same as in a-d but for the DDM variant with only a change in proportional starting point of the evidence accumulation away from the IF. i–l Same as in a-d but for the DDM variant with an increase in the upper boundary but no absolute start point change. m–p Same as in a-d but for the DDM with only a decrease in the drift rate offset parameter, implemented by shifting all the drift rates by the same amount away from the IF. q RT distributions from the 0% coherence condition of the actual data from monkey S, along with the fitted HDDM parameters of the drift rates and the drift rate offset below. r Psychometric function of the RT task sessions (n=7 sessions) in monkey S. The circles show the data and the lines show the HDDM fits to the data. The change in the drift rate offset is evident as a rightward lateral shift in the psychometric function post-muscimol (orange). s The mean RT for correct trials (circles) for all RT task data from monkey S are plotted against coherence along with their HDDM fits (lines). t Same as in s but for mean RT for error trials (squares) and their HDDM fits (lines). u–x Same as in q-t for monkey B showing all RT task data (n=2 sessions) and the HDDM fits. Note that the first four rows show simulations and the last two rows with gray shading show the data from the two monkeys. See Extended Data Fig. 5 for additional simulations and explanation.

The above comparisons are qualitative. Therefore, to determine quantitatively whether and which decision-making process or processes are affected by unilateral SC inactivation, we next fitted hierarchical and non-hierarchical drift-diffusion model variants (HDDM and DDM) and urgency-gating model variants^35,36 (UGM) to the performance and RT data (seven injections in monkey S and two injections in monkey B; Methods and Supplementary Note). Parameter estimation of pre- and post-muscimol data indicated that multiple parameters changed after muscimol (Extended Data Fig. 6). However, the only consistent parameter change in the two monkeys across experimental sessions that explained the lateral, rightward shift in psychometric functions was the drift rate offset favoring awayIF decisions (Fig. 5q,u arrows, Extended Data Fig. 6). The drift rate offset differed from zero after muscimol for both monkeys (HDDM, monkey S, Bayes factor (BF) = 3.19 × 10⁶; monkey B BF = 17.87) but not before muscimol (monkey S BF =0.08; monkey B BF = 0.14). The posterior probability of a change in the drift rate offset favoring the awayIF, was 99.7% in monkey S (posterior medians pre = −0.06, post = −0.64) and 99.0% in monkey B (posterior medians pre = 0.09, post = −0.85). Monkey S showed a high probability of a small start point change away from the IF (95.1% posterior probability of a proportional start point change away from the IF and posterior medians pre = 0.54, post = 0.49, the latter value being indistinguishable from 0.5; BF⁻¹ = 11.51). Monkey B in contrast, showed a 70.6% posterior probability of a small proportional start point change toward the IF (posterior medians pre = 0.52, post = 0.55, BF⁻¹ = 2.82). These opposite starting point changes in the two monkeys, although small, may reflect different strategic responses to the muscimol inactivation. The posterior probability of a non-decision time increase was 94.5% in monkey S (posterior medians pre = 408 ms, post = 433 ms) and 97.0% in monkey B (posterior medians pre = 543 ms, post = 597 ms). The posterior probability of a symmetric boundary increase was 78.9% in monkey S (posterior medians pre = 1.5, post = 1.6) and 95.2% in monkey B (posterior medians pre = 1.3, post = 1.5). We found little evidence for a change in the proportion of lapse trials, trials in which decisions are determined randomly, for either monkey (a positive change in lapse proportion was 72.5% in monkey S with posterior medians pre = 0.32 and post = 0.38 and 54.0% in monkey B with posterior medians pre = 0.45 and post = 0.46). The non-hierarchical DDM fits also showed the same patterns of parameter changes indicating that the results are robust to modeling methods (Extended Data Fig. 6k,l). Overall, the drift rate offset was the only parameter that changed significantly (> 95% posterior probability) after SC inactivation in both monkeys. Likely (> 94.5%) non-decision and somewhat likely (> 78.9%) symmetric boundary increases were observed in both monkeys, but neither parameter explains the lateral, rightward shift in psychometric functions we observed in the post-muscimol data. Although we observed start point and single boundary changes, both failed to explain the lateral shift in the psychometric functions and the changes in RT distributions.

The above analysis provides a quantitative assessment of which DDM parameters changed with unilateral muscimol injection in the SC. We found that the drift rate offset was the parameter that changed significantly across both monkeys and all experiments most consistently. We next tested directly which parameter change best explained the effect of SC inactivation on decision-making by fitting HDDM variants with the following parameters free to vary while keeping all others fixed to the observed data: drift rate offset (HDDM-Δ), proportional start point (HDDM-w), non-decision time (HDDM-τ), and proportional start point along with bound (HDDM-a,w, to test the fitting of either single or symmetric bound changes; Supplementary Note). An HDDM fitted with the drift rate offset allowed to change explained the shift in psychometric function almost as well as the HDDM fitted with all parameters free to vary (HDDM-Δ explained 97.6% of the variance of the psychometric function and the full HDDM explained 98.3% for monkey S; the HDDM-Δ explained 98.3% of the variance and the full HDDM explained 99.3% for monkey B) and fit the shifts in psychometric function better than all other model variants (Extended Data Fig. 7, Supplementary Table 4). Thus, the best explanation for the influence of muscimol in the SC unilaterally on decision-making is that inhibiting the SC acts as if adding an evidence independent offset to the drift rate (or momentary evidence), biasing decisions away from the IF.

We also fitted an urgency-gating model (UGM) to the data for both monkeys to assess whether our findings were robust to different decision-making model assumptions and to determine whether a change in an urgency signal might also explain the effect of SC inactivation (Supplementary Note). Our goal was not to assess whether a UGM fit the data better than a DDM, but rather, to determine whether muscimol affected similar parameters using a different sequential sampling model as reflected by the UGM. By fitting the UGM, we could test whether muscimol effects could be explained by a change in urgency, rather than the drift rate offset as indicated above. Note that the drift rate offset impacts the computation of evidence leading to a decision, whereas the urgency signal does not. Fig. 5q,u and Extended Data Fig. 7 also show that the pre-muscimol RT distributions of monkey B had a more symmetric shape, relative to monkey S, which the UGM predicts. Although evidence for the best fitting model type was mixed across monkeys (Supplementary Table 4), only a decrease in the drift rate offset and the urgency slope parameter decrease were consistent in both monkeys (Extended Data Fig. 6k–l). However, allowing the drift rates to vary from pre- to post-muscimol, and therefore allowing drift rate offset to change (Supplementary Note), explained more of the in-sample variance in the psychometric function of both monkeys (UGM-δ explained 87.8% for monkey S and 83.1% for monkey B, Supplementary Table 4) than UGMs with urgency slope allowed to vary, a parameter that also influences response proportion and RT (UGM-m explained 20.0% for monkey S and 26.2% for monkey B, Supplementary Table 4). Taken together, in both the DDM and the UGM, a change in the drift rate offset best explains the effect of unilateral SC inactivation on perceptual decision-making. This finding indicates that inactivation of the SC alters the computation of perceptual evidence, rather than altering an urgency signal that affects decisions after evidence is computed.

As described above, we used a traditional, one-dimensional DDM and variants as well as a UGM and variants, to determine which parameter change best explained the results of muscimol inactivation of the SC on perceptual decision-making. Our goal was not to perform model comparisons, but rather to determine which aspect of decision-making was most affected by muscimol inactivation of the SC. That both the DDM and the UGM converged on the same parameter - the drift rate offset - for both monkeys across all experiments, provides compelling evidence that the SC plays a causal role in the computation of evidence for perceptual decisions. The data indicate that the SC plays a causal role in the cognitive processing required for perceptual decisions; however, they do not provide us with biological mechanistic insight into how the SC may play a role. Some evidence suggests that the SC participates in the process of evidence accumulation and contains two accumulators, one in each SC³⁷, similar to LIP^38,39. Although where in the brain evidence accumulation occurs is unknown, it is likely to occur in multiple areas¹. A biologically plausible mechanism by which inhibiting the SC can affect the computation of evidence for a decision, and the drift rate offset may be implemented, is by assuming two independent accumulators in which inactivation of the SC reduces the gain in one. To test the two independent accumulator with gain model, we fitted the full HDDM with the same parameters but with drift rates constrained to a linear comparison of two accumulators (Supplementary Note). In the two dimensional model, the gain of the toIF accumulator decreases with unilateral SC inactivation and the gain of the awayIF accumulator remains unchanged. The BF of G_(toIF) not equal to one was estimated to be very large (>10³⁰⁷) with a posterior median of G_(toIF) = 0.6217, consistent with a post-muscimol gain decrease on the toIF accumulator. We found no evidence for gain decreases in any other experimental conditions; recovery, pre-saline, post-saline, BF of G_(toIF) not equal to one ranged between 0.0114 to 0.2232 and the posterior medians of G_(toIF) ranged from 0.9307 to 1.0832. These results point toward a biologically plausible mechanism by which unilateral inhibition of SC activity affects the computation of evidence for perceptual decisions. Inhibiting SC activity alters the gain of evidence accumulation in one of two competing accumulators. Note, however, that comparing the R² predictions for the in-sample and out-of-sample data for the 2D model for both monkeys revealed that the 2D model fit the data well but not as well than the full 1D HDDM (Supplementary Table 4). Thus, whether the 1D or the 2D model better explains SC activity and its relationship to decision-making performance in two choice discrimination tasks remains an important open question.

DISCUSSION

We provide compelling physiological, reversible inactivation and modeling evidence that unilateral inactivation of the primate SC alters perceptual decision-making, not by changing sensory or motor processing but rather, by shifting the balance of time-varying evidence accumulation away from the IF. Shifting the balance of time-varying evidence accumulation away from the IF produces a change in the decision criterion in the SDT framework and is consistent with results in rodents and our previous results in monkeys^13,34. Specifically, in our previous work using SDT revealed a relationship between SC activity and the position of a decision-criterion. We could not, however, determine whether criterion position changes resulted from changes in the drift rate offset (which would affect the computation of time-varying evidence in the DDM framework), or from changes in the starting point of evidence accumulation. The experiments reported here together with the application of the DDM framework, allowed us to determine that the SC acts on decision-making as though adding a constant to the time varying evidence accumulation.

Current conceptions of perceptual decision-making fall into two main categories; one in which sensory evidence is evaluated, categorized and then forwarded to motor areas to guide choices of action⁴⁰, and a second, in which brain areas involved in getting ready to act are the same areas that accumulate evidence over time to form a decision; referred to as embodied cognition^26,27,41,42. Our results support an embodied cognition model of perceptual decision-making. The SC is well-known for its role in saccade preparation and generation^43,44, and we show here that toIF saccades remain relatively intact with SC inactivation^20,22, in spite of significant alterations in decision-making about the orientation of a Glass pattern.

Our results suggest exciting new possibilities for how perceptual decisions are formed and converted to choices of action in the brain. In primates, including humans, and in rodents, perceptual decisions are thought to arise from evidence accumulation in forebrain areas such as area LIP (PPC) and dlPFC (FOF) and striatum. Our results indicate that the SC, a brainstem region downstream of these areas and presumably processes, plays a causal role in the computation of perceptual evidence for decisions. Recent evidence from experiments inactivating the forebrain accumulators, LIP (PPC) and dlPFC (FOF), calls into question the causal role of these areas in evidence accumulation^40,45,46 and further suggests that FOF in rodents and FEF in monkeys participate in decision-making after evidence has been accumulated^47–49. Our results show that the SC participates in decision-making by adding an evidence independent constant to the momentary evidence, surprisingly similar to what was observed with stimulation of cortical area MT in the dot motion task⁵⁰. Our results also share some similarities with those reported for stimulation of cortical area LIP and striatum^8,51. Although we cannot yet say with certainty that the SC is performing evidence accumulation in our orientation direction decision task, we can confidently say that the SC is controlling either the sensory input to the accumulator or the accumulator itself. Based on previous work in monkeys and our modeling work reported here, it is possible that each SC contains an independent accumulator³⁷ and inactivation of one SC shifts the balance of evidence toward the other accumulation process and decision. Therefore, we propose that the SC is critical for the computations of perceptual evidence and transformation of a decision to a choice of action. These computations may occur in the SC or the SC may also impact the computation of evidence for decisions occurring elsewhere in the brain, including the cerebral cortex and striatum⁶, perhaps through feedback circuits via thalamic nuclei from the SC⁴⁴. This exciting possibility awaits further investigation.

METHODS

Surgery

We implanted three adult male rhesus monkeys (Macaca mulatta), weighing between 9–11 Kg (monkey S 15yo and monkey B 11yo and monkey J 11yo) with eye loops for measuring eye position⁵², a post for stabilizing the head and a recording chamber⁵³ for accessing the superior colliculus (SC). Devices were placed using MRI-guided surgical software (Brainsight, v.2.4.7, Rogue Research, Montreal, CA) and stereotaxic coordinates (0ML, −3AP, angled 38⁰ posteriorly). All surgical procedures were performed under general anesthesia using aseptic procedures and all surgical and experimental procedures were approved by the UCLA Chancellor’s animal research committee and complied with and generally exceeded standards set by the Public Health Service policy on the humane care and use of laboratory animals as well as the American Primate Veterinarian Guidelines.

Behavior and electrophysiology

We used a real-time experimental control and visual stimulus generation system, REX and VEX, developed and distributed by the Laboratory of Sensorimotor Research National Eye Institute (Bethesda, MD) to create the behavioral paradigms⁵⁴. We used the magnetic induction technique⁵⁵ (Riverbend instruments, Birmingham, AL) and the EyeLink 1000 eye tracker system (SR Research Ontario, CA) to measure voltage signals proportional to horizontal and vertical components of eye position (monocular mode; 2kHz). Eye position signals were low-pass filtered (8 pole Bessel −3dB, 180 Hz; Bak Electronics; Umatilla, FL) and digitized at 16-bit resolution and sampled and saved to disk at 30 kHz using Blackrock Microsystems NSP hardware system controlled by the Cerebus software suite (Blackrock Microsystems, Salt Lake, UT). We used an automated procedure to define the onset of saccadic eye movements using eye velocity (20°/s) and acceleration criteria (5000°/s²). The adequacy of the algorithm was verified and adjusted as necessary on a trial-by-trial basis by the experimenter. We omitted < 10% of trials from one monkey because of saccadic festination (i.e., small saccades toward the target).

Two trained monkeys (monkey B and monkey S) performed three behavioral tasks: 1) a visually-guided saccade task to map response fields (RF) before muscimol injections as well as obtain changes in saccade velocity after muscimol, 2) a selection task to measure saccadic motor preparation and bias before and after muscimol injection, and 3) a task for assessment of perceptual decision-making performance before and after muscimol. We varied the ordering of the tasks for some experiments before and after injection to ensure approximately similar muscimol efficacy for each task. A third monkey (monkey J) performed the decision task for recording of SC neuronal activity shown in Fig. 1e. We collected 500–1000 trials in the decision task, and 300 trials each in the selection and visually-guided saccade tasks before muscimol injection to ensure an adequate amount of pre-injection data. We started collecting data at least 10 minutes post-injection for each experiment for consistency. Pre- and post-muscimol data were collected on the same day and recovery data were collected ~24 hours after muscimol injection. Recovery data appear in Extended Data Figs. 2 and 4 and the associated statistics in Supplementary Table 2.

Response field (RF) mapping

We used a visually-guided saccade task to map RFs of SC sites. A red fixation spot appeared (14.32 cd/m² for monkey B and 22.37 cd/m² for monkey S) and monkeys maintained fixation at this location for a random time of 500–1000 ms with an accuracy of 3.5° square determined by an electronic window. Next, a white spot (48.27 cd/m² for monkey B and 109.76 cd/m² for monkey S) appeared in the periphery. Monkeys remained fixating centrally for a random time of 800–1200 ms until the fixation spot disappeared, cueing the monkeys to look at the spot in the periphery. If monkeys looked at the peripherally-located spot within a 4.5° square determined by an electronic window, they received a sip of water or preferred juice for reward. Incorrect saccades were not rewarded. The saccade target was positioned manually and pseudorandomly throughout the visual field (Fig. 1d).

While monkeys performed the visually-guided saccade task, we recorded single and multiple neurons in the intermediate layers of the SC using custom injectrodes that allowed for neuronal recording and injection of compounds simultaneously (Fig. 1g). Injectrodes were inserted through a guide tube positioned by a grid system⁵³ and were moved in depth by an electronic microdrive system controlled by a graphical user interface on a PC running Windows (Nan Instruments, Israel). Action potential waveforms were bandpass filtered (250 Hz to 5 kHz; 6 pole Butterworth) and amplified by a differential amplifier and then sampled, digitized and saved to disk at 30 kHz with 16 bit resolution using the Blackrock NSP hardware system controlled by the Cerebus software suite for offline sorting as necessary (Blackrock Microsystems, Salt Lake, UT). When possible, neurons were isolated online using time and amplitude windowing criteria and the times of action potentials were saved to disk similarly. Response fields (RF) of SC neurons (either single neurons, if well-isolated, or multiple neurons, if not) were mapped during the experiment using customized MATLAB scripts (MathWorks Natick, MA) that plotted the average discharge rate from 50 ms before to 50 ms after the saccade onset for each target position (Fig. 1d). We considered the center of the RF to be the location at which a saccade was associated with maximal discharge (audibly, visually and quantitatively). Only locations with RF eccentricities greater than 11.5⁰ were included to ensure as little overlap of the RF with the center of the visual field as possible.

A variant of this task allowed us to measure peak saccadic velocity before and after muscimol injections. This task had randomized delay times taken from a truncated exponential distribution (fixation time mean 400 ms, range 320–560 ms; delay-time mean 800 ms, range 640–1120 ms) and fixed target positions (Fig. 1h).

Selection task

The second task was a visually-guided, delayed-saccade task in which two isoluminant targets (14.65 cd/m² for monkey B or 21.38 cd/m² for monkey S) appeared in the periphery. One target was located at the center of the RF and the other was located in the opposite hemifield (Fig. 1c). One target was red and the other was white. The position of the red and white targets switched randomly on each trial. After the fixation point (48.62 cd/m² for monkey B or 106.86 cd/m² for monkey S) appeared, monkeys remained fixating on this spot for a mean delay time of 400 ms (320–560 ms, truncated exponential) until the targets appeared. A second mean delay of 800 ms (640–1120 ms, truncated exponential) occurred and then the fixation spot disappeared, cueing the monkey to look at the white target. If the monkey looked at the white target with an accuracy of 5.5° determined by an electronic window, it received a sip of preferred juice or water for reward. For 12 of the 23 muscimol experiments and two of six saline experiments we used fixation delays of 100 ms and a mean delay-period of 350 ms (200–500 ms, truncated exponential). For the latter data, we analyzed only those trials with a 400 ms or greater delay-period. This task required the same attentional allocation to the target location as well as the same motor preparation as the decision task, however, it did not vary in perceptual ambiguity, nor did it require the transformation of the Glass pattern orientation to the saccade location as did the decision task, allowing us to assess impairments in visual selection, motor preparation and biases in saccades to the left or right hemifields before and after the muscimol injection.

Glass pattern decision-making task

To assess perceptual decision-making performance before and after muscimol injections, monkeys performed a one interval, two-choice, perceptual decision-making task in which they reported the orientation of a dynamic Glass pattern (decision task)^14,15. Monkeys reported their decisions by making saccades to a target located in the left or right hemifield corresponding to the orientation of the perceived Glass pattern. The orientation of the Glass Pattern was fixed to 45⁰ for rightward decisions and 135⁰ for leftward decisions, regardless of the RF location, dissociating the specific stimulus orientation from the choice location. We parameterized the difficulty of the decision by varying the coherence of the Glass pattern among two sets of coherences: 0%, 5%, 10%, 17%, 24%, 36%, 50% performed by monkey S for 3 muscimol experiments on the delay decision task, and 0%, 3%, 5%, 10%, 17%, 24%, 36% performed by both monkeys for all other experiments, including both muscimol and saline and delay and RT task versions. Monkeys received water or preferred juice reward for correct trials and on the 0% coherence trials, they received reward on half of the trials randomly. Once monkeys were well-trained and after performing the first three muscimol experiments on a fixed ratio (FR) 1 reward schedule (rewarded on every correct trial), monkeys performed the task on a variable ratio (VR) schedule such that on average, but with some variation, every third or fifth correct trial received reward to encourage consistent performance (VR3 or VR5)⁵⁶.

Trained monkeys performed the decision task in a delayed version and a reaction time (RT) version. In the delayed version, a fixation spot appeared (2.93 cd/m² for monkey B and 9.62 cd/m² for monkey S) at the center of the display. After a mean 300 ms delay (240–420 ms, truncated exponential), two isoluminant choice targets appeared (3.06 cd/m² for monkey B or 6.36 cd/m² for monkey S). After another mean delay of 700 ms, (560–1400 ms, truncated exponential), the Glass pattern cue appeared at the location of the fixation point and remained illuminated for 950 ms (760–1900 ms, truncated exponential). After the Glass pattern cue disappeared, there was a delay-period with mean of 800 ms (640–1120ms, truncated exponential). The removal of the fixation point cued the monkeys to report their decision by looking at one of the two choice targets. Monkeys remained fixating at the correct choice target for a mean of 350 ms (280–490 ms, truncated exponential), before receiving fluid reward. Monkeys performed a variant of the delayed task with a shorter delay period (50–100 ms) for 12 muscimol experiments and two saline experiments (Fig. 1a).

The RT version of the decision task was identical to the delay version except that, in the RT task, the Glass pattern appearance and the removal of the fixation spot occurred simultaneously and the monkeys reported their decisions at any time (Fig. 1b). To discourage fast guessing, we implemented a fixed time to reward (900 ms monkey B, 1000 ms monkey S) and a RT-dependent inter-trial interval⁵⁷. The results of muscimol injections on choice behavior were similar in both the delay and RT versions of the task, so the data are collapsed unless otherwise indicated. Modeling of RTs and choice behavior is based on data only from the RT task for each monkey separately.

Statistics and Reproducibility

We analyzed all the data using customized scripts developed in MATLAB 2016b (MathWorks Natick, MA), Python 3 (3.7.6), R (v.3.4.0), and IBM SPSS Statistics 25. To assess for significant differences between the α, β, RT mean collapsed across coherences and injections, RT slope, and RT intercept parameters of pre- and post-injection, and pre-injection and recovery, we performed the following tests: paired two-tailed t-tests (if both session data sets were normally distributed) using Lilliefors or Shapiro-Wilk test); Wilcoxon Signed rank test if any of the data from the sessions was non-normally distributed. We applied Bonferroni corrections (two comparisons, α = 0.05/2 = 0.025) where appropriate. The pre- vs post-injection comparisons appear in the main text and the pre-injection vs recovery comparisons appear in Supplementary Table 2. The same tests were performed for the analysis of accuracy data from the decision and the selection tasks for toIF and awayIF with the Bonferroni corrections for four pairwise comparisons tests (Supplementary Table 3), significance cut-off value α is 0.05/4 = 0.0125. We performed a bootstrapped test using the t-statistic with 100,000 simulations to compare pre- and post-injection differences of α and β parameters between muscimol and saline injections⁵⁸. To analyze the post-muscimol peak saccadic velocity for toIF saccades between the decision task and the selection task, we performed unpaired t-tests (for normal data, two-tailed) or Wilcoxon Rank Sum (if non-normally distributed) with Bonferroni correction of α = 0.05/9 = 0.0056 for the tests for monkey S, since nine t-tests were performed on data from each injection, and α = 0.05/8 = 0.0063 for the tests for monkey B, since eight t-tests were performed on data from each injection, with a total of 17 muscimol injections between the two monkeys (Supplementary Table 3). Six injections were excluded due to technical issues with the eye tracker that impacted measurement of eye speed but not assessment of choice or RT.

Modeling and simulations

We fitted signal detection theory (SDT), drift-diffusion (DDM) and urgency-gating models (UGM) to the behavioral data to understand how decision-making was impacted by unilateral inactivation of the SC^28,35,59. SDT is a static model of decision-making and makes predictions only about choice performance, whereas the DDM and UGM are dynamic models that make predictions about both choice performance and RTs. Parameters of decision-making models are thought to be instantiated by aspects of neuronal activity and many have been verified in human behavioral experiments^60,61. We performed simulations, model fitting and model comparisons using customized scripts developed in MATLAB 2016b (MathWorks Natick, MA), Python 3 (3.7.6), JAGS⁶² (4.3.0), and R (v.3.4.0). We also used the published libraries Palamedes⁶³, pyjags (https://github.com/michaelnowotny/pyjags; 1.2.2), the Wiener module for JAGS⁶⁴, and ChaRTr⁶⁵. For equations, simulations, parameter estimation, and model comparison results, see Supplementary Note, Extended Data Fig. 5–7, and Supplementary Table 4.

Parameter estimates in SDT

We fitted a two parameter logistic function using the Palamedes toolbox to the choice performance data for each monkey for all experiments using the equation:

$$p\left(\mathit{\text{IF}}\right)=1/\left(1+\mathit{\text{exp}}\left(-\beta \left(k-\alpha \right)\right)\right)$$ (1)

where p(IF) denotes the proportion of choices to the inactivated field (IF) for each coherence condition (k). α and β are free parameters determined using maximum likelihood methods and provide measures of decision bias and sensitivity of the psychometric function respectively^63,66,67. Fig. 2 and Extended Data Fig. 4 show the two parameter model fits and results. Extended Data Fig. 2 shows comparisons between the two, three and four parameter model fits. Because there were no differences in the quality of the fits for the three models, we opted to use the simpler fewer parameter model for the analysis. For three of the muscimol injections, we used 50%, 36%, 24%, 17%, 10%, 5%, and 0% coherence conditions for the fits. For the other 20 muscimol sessions and 6 saline injection sessions, we used 36%, 24%, 17%, 10%, 5%, 3%, and 0% coherence conditions. We also calculated d’ and c, using SDT equations as described in⁵⁹ and Supplementary Note (S1–2), and these results appear in Extended Data Fig. 3.

We calculated the choice probabilities for each of the ten SC neurons for 0% coherence trials (Fig. 1f) by computing the area under the receiver operating characteristic (ROC) curve with SDT methods^18,19. Briefly, we created ROC curves by calculating the probability that the spike count for an epoch 100 ms to 20 ms before saccade onset, for away and to RF decisions, exceed a criterion in each measurement epoch on a trial-by-trial basis. The criterion was incremented from the minimum to the maximum spike count in the epoch in step sizes of (maximum - minimum spike count) / number of counts for toRF and awayRF. Next, we calculated the area under the ROC curve (AUC) for each neuron for 0% coherence trials. We performed a two-tailed bootstrap test to determine if the AUC values differed from 0.5.

Parameter estimates in drift-diffusion models (DDMs)

We fitted a hierarchical DDM (HDDM) and a non-hierarchical DDM (DDM) that describe RT and choice distributions. Non-decision time (τ) is the sum of visual and motor processing. The decision boundary (a) determines the amount of evidence needed to make a decision. The starting point of evidence accumulation (w) was fit as a proportion of the boundary parameter and describes the initial bias in evidence accumulation before a trial begins, where w = 0.5 indicates the start point is the middle between the upper (toIF) and lower (awayIF) bound, w > 0.5 indicates the start point is closer to the upper (toIF) bound, the w < 0.5 indicates the start point is closer to the lower (awayIF) bound. The drift rate (δ) is the average evidence accumulation rate during a trial and is driven by the strength of the evidence extracted from the Glass pattern stimulus. The drift rate offset³¹, also known as distance from the drift criterion³² or the drift bias³³, is a parameter we defined as the mean of all the drift rates across both toIF and awayIF directions and all coherences. This parameter was explicitly fit in the HDDM, but in the non-hierarchical DDM, the drift rate offset was calculated from the drift rate parameter estimates and the change in drift rate offsets was determined by comparing pre- and post- muscimol drift rate offsets. The lapse rate (λ), was fitted and defined as the percentage of trials in which choices were determined randomly. The lapse rate was only fit in the HDDM.

We used both hierarchical Bayesian methods (HDDM with k = 13 coherence conditions) and quantile maximum products estimation (QMPE; DDM with k = 11) to estimate parameters. Both estimation methods yielded similar parameters (Extended Data Fig. 6). Hierarchical Bayesian methods were applied to fit the HDDM to the data from the RT task from both monkeys: seven muscimol and four saline injections from monkey S and two muscimol injections from monkey B. We used JAGS to draw samples from posterior distributions using Markov Chain Monte Carlo (MCMC) samplers⁶². Hierarchical mean parameters per monkey and experimental condition (pre-, post-, and recovery for muscimol and saline) were assumed to better fit the data from each experimental session (Supplementary Note equations S9–15 and Supplementary Table 4), with different prior distributions of these hierarchical mean parameters having no impact on the parameter results (Supplementary Note and Supplementary Table 5). We also fitted HDDM with only the drift rate offset, proportional start point, non-decision time, or proportional start point with the bound, varying across conditions (Supplementary Note equations S16–44, Supplementary Fig.1). Parameter estimates for full hierarchical models appear in Extended Data Fig. 6a–j.

To calculate the probability of change in drift rate offset and other parameters, we estimated the posterior distributions using kernel density estimation and then summed the density from the lowest negative sample to zero. We also calculated Bayes Factors (BF) using the Savage-Dickey density ratio. BF describes the relative evidence of the drift rate offset (Δ) not equal to zero. The BF for the drift rate offset was the ratio of the prior density at Δ = 0 over the posterior density at Δ = 0. We also calculated a BF⁻¹ for whether the proportional start point was the same as 50% of the relative evidence units required to make a decision (the boundary was also a free parameter). The BF⁻¹ for hierarchical initial bias was calculated as the ratio of the posterior density at w = 0.5 over the prior density at w = 0.5. In the model HDDM-G (Supplementary Note) the BF for a gain change on one accumulator resulting from inactivation of one SC, not equal to one was calculated as the ratio of the prior density at G_(toIF) = 1 over the posterior density at G_(toIF) = 1. A BF over three is considered positive evidence for an effect (i.e., the effect is three times more likely under the alternative hypothesis than the null hypothesis) or no effect (i.e., no effect is three times more likely under the null hypothesis than the alternative) whereas, over 20 is strong evidence. Note that BFs were dependent upon the prior distributions we chose, whereas prior distributions had little effect on the posterior distributions themselves and thus the probability calculations (Supplementary Note and Supplementary Table 5). For this reason, although the posterior distributions and probability calculations will not change significantly for reasonable prior distribution choices, we caution against over-interpreting BFs, which will change when alternative priors are chosen.

Parameter estimates in urgency-gating model (UGM)

UGMs are another class of decision-making model in which the sensory evidence is low-pass filtered to prioritize more recent evidence and then multiplied by a linearly growing urgency signal^35,36. We used QMPE (k = 11) to estimate UGM parameters from the data from the RT task from both monkeys; seven muscimol injections from monkey S and two muscimol injections from monkey B (Supplementary Note). See Supplementary Fig. 2 for parameter recovery results. We fitted the UGM to pre- and post-muscimol data separately and pooled across all injections to discover which parameters changed. We found little difference between the parameter estimates for pooled versus individual fits (Supplementary Fig. 3). As in the HDDM and non-hierarchical DDM, we defined the drift rate offset as the mean drift rate across both toIF and awayIF directions and all coherences. As in the non-hierarchical DDM, we did not explicitly estimate the drift rate offset parameter from model fits, but instead calculated it from the fitted estimates of the drift rate for each coherence and direction. We also fitted UGMs with an urgency slope parameter or drift rate parameters free to vary in post-muscimol data while keeping other parameters fixed to their parameter estimates from the pre-muscimol data (Supplementary Note). The UGMs with the individual drift rates per coherence and direction free to vary allowed us to assess whether changes in the drift rate offset best explained the effects of muscimol. Parameter estimates for all models appear in Extended Data Fig. 6.

Model comparisons

We generated posterior predictive samples for hierarchical drift-diffusion models (HDDMs) and predicted choice and RT distributions from non-hierarchical DDM and UGM parameter estimates using QMPE with in-sample and out-of-sample datasets generated from an 80% / 20% random data split in each experimental session. We used predicted choice and RT distributions, as well as Akaike and Bayesian Information Criteria (AIC/BIC) where applicable, to find models that best described the effect of unilateral inactivation of the SC. Percentage variance of RT and choice statistics explained by prediction are given as derived from R²_pred (Supplementary Note). In-sample and out-of-sample prediction results appear in Supplementary Table 4.

Extended Data

Extended Data Fig. 1. Estimates of muscimol spread in the SC.

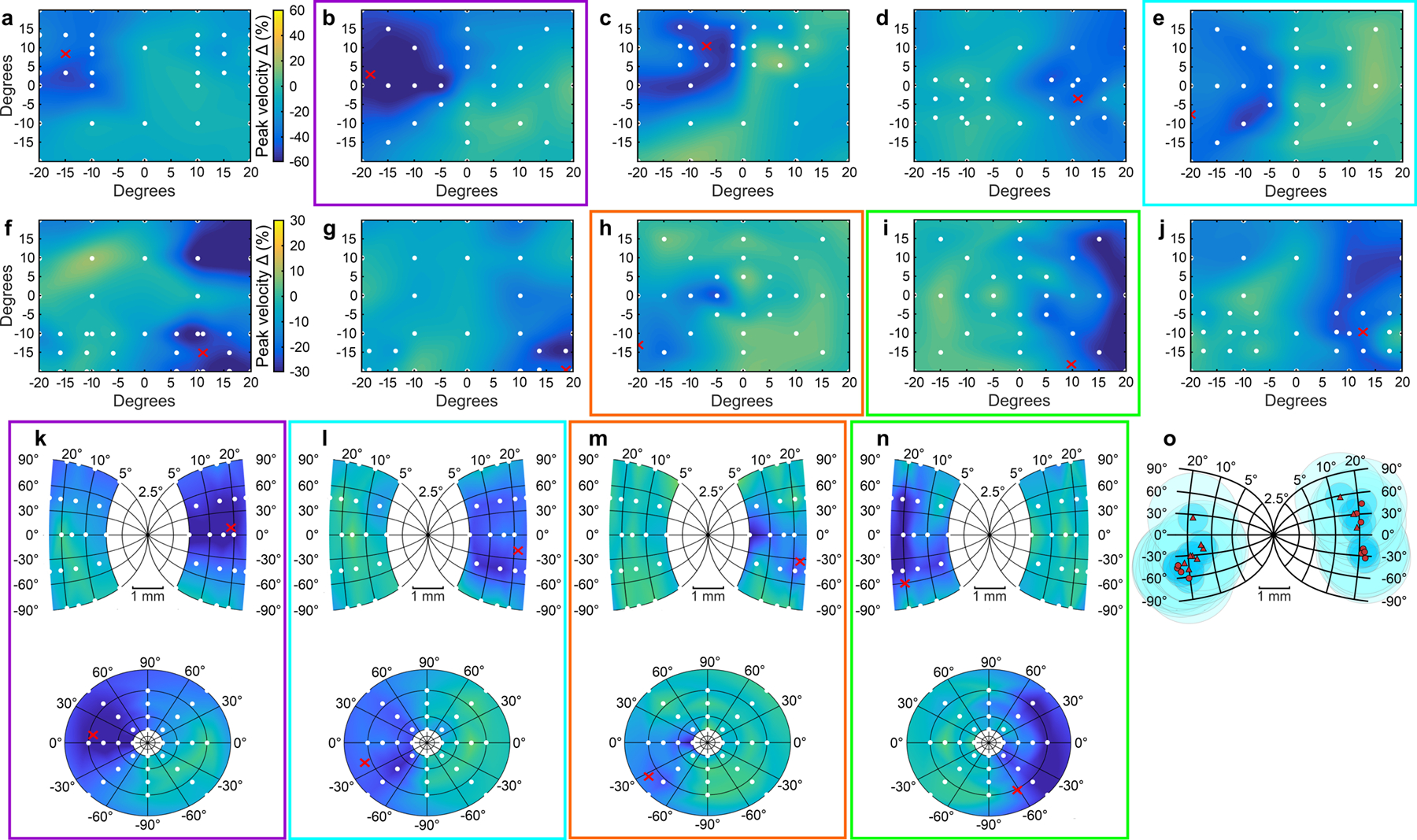
(Associated with Fig. 1 main text) a–j The reduction in peak velocity from pre- to post-muscimol for 10 muscimol injections (four from monkey B, six from monkey S), one to two hours post injection. The percent change in peak velocity after muscimol injection (post-muscimol saccade velocity minus pre-muscimol saccade velocity divided by pre-muscimol saccade velocity multiplied by 100), is plotted for the target positions indicated by the white circles and linearly interpolated on the visual field in Cartesian coordinates. Cooler colors indicate slower saccadic velocities post-muscimol. a–e shows five injections with more concentrated effects of muscimol (color bar scaled from −60% to 60%), whereas f–j shows five injections with smaller but more diffuse effects of muscimol (color bar scaled from −30% to 30%), showing the range in the efficacy of our muscimol injections based on changes in saccade velocity at least one hour post injection. Red Xs show the site of injection based on the RF determined electrophysiologically (Supplementary Table 1). The peak velocity maps highlighted by the colored boxes in a–j had a uniform and homogenous sampling of positions in the visual field that allowed us to calculate the estimated spread across the SC map as shown in k–n (Quaia, C., Aizawa, H., Optican, L.M. & Wurtz, R.H. Reversible inactivation of monkey superior colliculus: II. Maps of saccadic deficits. Journal of Neurophysiology 79, 2097–2110 (1998).). k–n show the same percent change in peak velocity after muscimol injections plotted on the SC map (top) and the visual field in polar coordinates (bottom) for the injections in the corresponding colored boxes in a–j. o shows the locations of muscimol injections and spread estimates plotted onto the SC map. Red circles show injection locations for monkey B and red triangles show injections from monkey S. Each injection’s estimated muscimol spread is represented by two concentric circles. The darker shaded circles show 0.5 mm radius and the lighter shaded circles shows 1.5 mm radius from the center of the injection site based on estimates from (Allen, T.A., et al. Imaging the spread of reversible brain inactivations using fluorescent muscimol. Journal of Neuroscience Methods 171, 30–38 (2008).). There were three injections in which muscimol may have spread into the pretectal region and thus also the foveal region of the rostral SC, as evidenced by the occurrence of ocular nystagmus about an hour after the injection. In these cases, we aborted the experiment and omitted the data from analyses upon appearance of nystagmus. One example appears in b and k (maps highlighted by purple boxes). The Glass pattern decision and selection task data before the occurrence of nystagmus are included in the analysis in the main text. The effect on the psychometric function from this example was the largest that we observed (Fig. 2a, rightmost transparent orange psychometric function).

Extended Data Fig. 2. AIC and BIC scores for the two, three and four parameter logistic function fits.

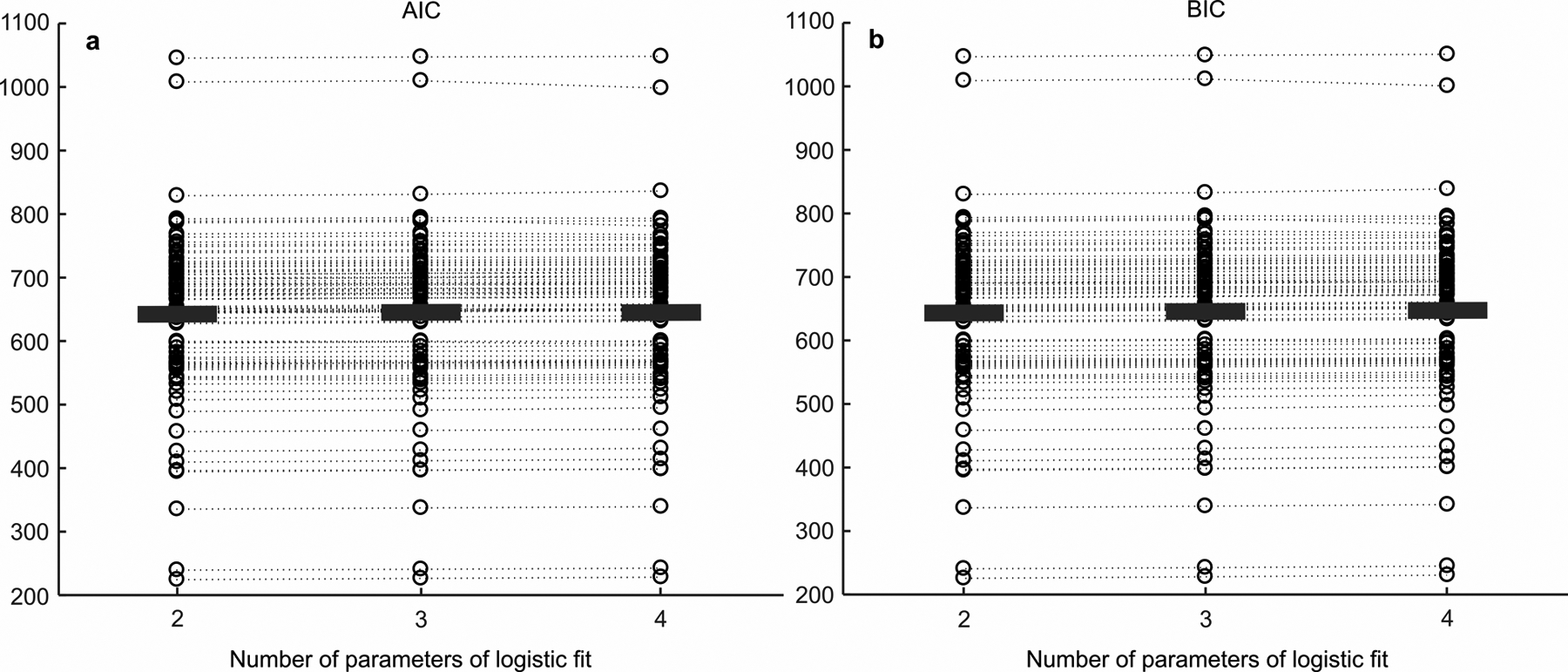
(Associated with Fig. 2 of the main text) a AIC scores for each pre- and post-injection and recovery sessions for all muscimol and saline injections (n=87 sessions) for two, three, and four parameter logistic fits to the performance data. The circles show the AIC score of the logistic fit to each individual session from the n=87 total sessions (pre-, post- and recovery * 29 injections), and the black, horizontal bars show the mean AIC score. The dotted lines connect the same data sessions that were fit across the two, three, and four parameter fits to see if there were any changes in AIC score between the fits with different number of parameters. The two parameter logistic model has two parameters: α (decision bias) and β (sensitivity) following the equation p(IF) = 1/(1+exp(−β(k-α))) (Eq 1 in Methods), which was used to fit the psychometric functions in Fig. 2 and Extended Data Fig. 4. The three parameter logistic model includes: α, β, and ʎ (lapse rate or the difference between perfect performance and the top and bottom asymptotes) following the equation p(IF) = ʎ + (1–2ʎ)/(1+exp(−β(k-α))). The four parameter logistic model includes: α, β and ʎ (lapse rate or the difference in perfect performance and asymptotic performance for toIF decisions) and γ (lapse rate or the difference in perfect performance and asymptotic performance for awayIF decisions) following the equation p(IF) = γ + (1-γ-λ)/(1+exp(−β(k-α))). When looking at the AIC scores for the two, three, and four parameter fits (lower AIC scores indicate a better fit given model complexity), we see that the data are explained equally well or better with the models without lapse rates, with mean scores of 638.80 for the two parameter fit, 640.51 for the three parameter fit, and 641.47 for the four parameter fit. Therefore, we selected the simpler, two parameter model to fit the performance data. b Same as in a for the BIC scores, with mean of 639.93 for the two parameter fit, 642.20 for the three parameter fit, and 643.73 for the four parameter fit. The lack of difference in the quality of the fits with or without the lapse rate parameters is consistent with the parameter estimation results of lapse rates in the hierarchical DDM (Extended Data Fig. 6i,j).

Extended Data Fig. 3. Decision criterion but not sensitivity, is impacted by unilateral SC inactivation during one-interval, two-choice perceptual decision-making.

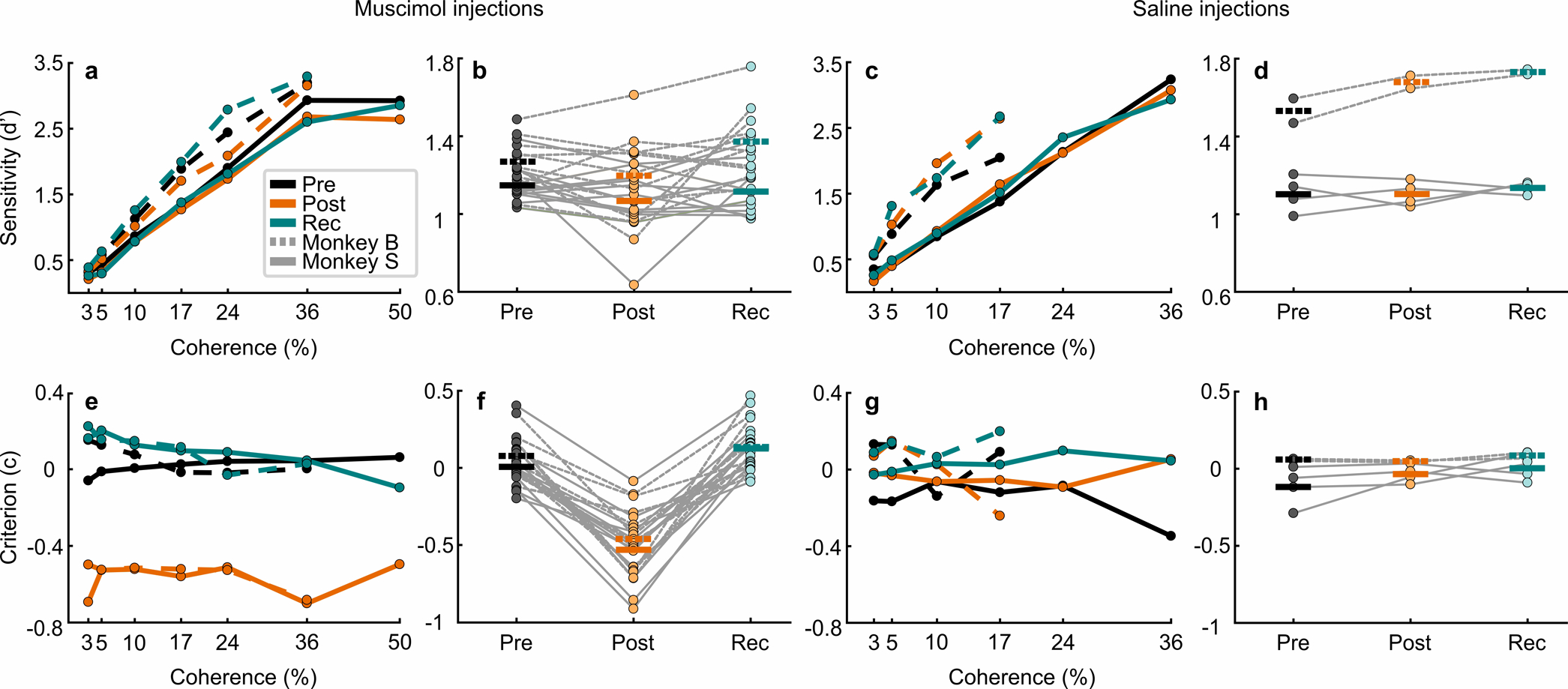
(Associated with Fig. 2 main text) a Sensitivity, as measured by d’ is plotted against coherence for all experiments from both monkeys pre-muscimol (black circles and lines), post-muscimol (orange circles and lines) and 24 hour recovery (green circles and lines). Dashed lines show data from monkey B and solid lines show data from monkey S. Note that for monkey S, there is an additional 50% coherence condition (Methods). Qualitatively, monkey B showed a higher sensitivity for the same Glass pattern coherences than monkey S. b d’ collapsed over coherence and plotted for pre-muscimol (grey circles), post-muscimol (orange circles) and recovery (green circles) for all experiments from both monkeys. Dashed lines show data from monkey B (n=11 injections) and solid lines show data from monkey S (n=12 injections). The horizontal lines indicate the mean d’ across sessions. On average there were no significant changes in d’ with muscimol in either monkey (monkey S, t(11) = −1.54, p = 0.152, 95% CI = [−0.23, 0.07]; monkey B, t(10) = −1.51, p = 0.161, 95% CI = [−0.21, 0.07]). c–d Same as in a and b for the saline injections. Because we only had two saline injections in monkey B, we collapsed the data across monkeys (n=6 injections) for statistical analysis, but the data are shown separated by monkey. We found no significant differences in d’ with saline (t(5) = 1.20, p = 0.283, 95% CI = [−0.1, 0.19]). Note that there are no d’ or criterion (c) values for monkey B for the 24% and 36% coherences due to a lack of errors for the awayIF post-muscimol 24% and 36% coherence trials. e Criterion (c) plotted against coherence for pre-muscimol (black), post-muscimol (orange), and recovery (green) for all experiments from both monkeys. Dashed lines are from monkey B and solid lines are from monkey S. This plot is shown for symmetry with the d’ plot although criterion changes across coherences are not particularly meaningful as monkeys are not expected to change their criterion across coherences as the coherences were randomized from trial to trial and there was no way for the monkeys to know which coherence was impending. f Criterion collapsed over coherence plotted for pre-muscimol, post-muscimol and recovery for all experiments (n=12 injections for monkey S, n=11 injections for monkey B). For both monkeys, c changed significantly with muscimol (monkey S, t(11) = −9.34, p = 1.46 × 10 ⁻⁶, 95% CI = [−0.7, −0.38], monkey B, t(10) = −7.48, p = 2.10 × 10 ⁻⁵, 95% CI = [−0.75, −0.33]). g–h Same as in e-f for the saline experiments from both monkeys (n=6 injections). We found no significant differences in c with saline injections (w(5) = 18, p = 0.156). Consistent with the psychometric function results shown in Fig. 2, unilateral inactivation of SC with muscimol produced changes in decision bias and not perceptual sensitivity.

Extended Data Fig. 4. Decision-making behavior 24 hours after muscimol.

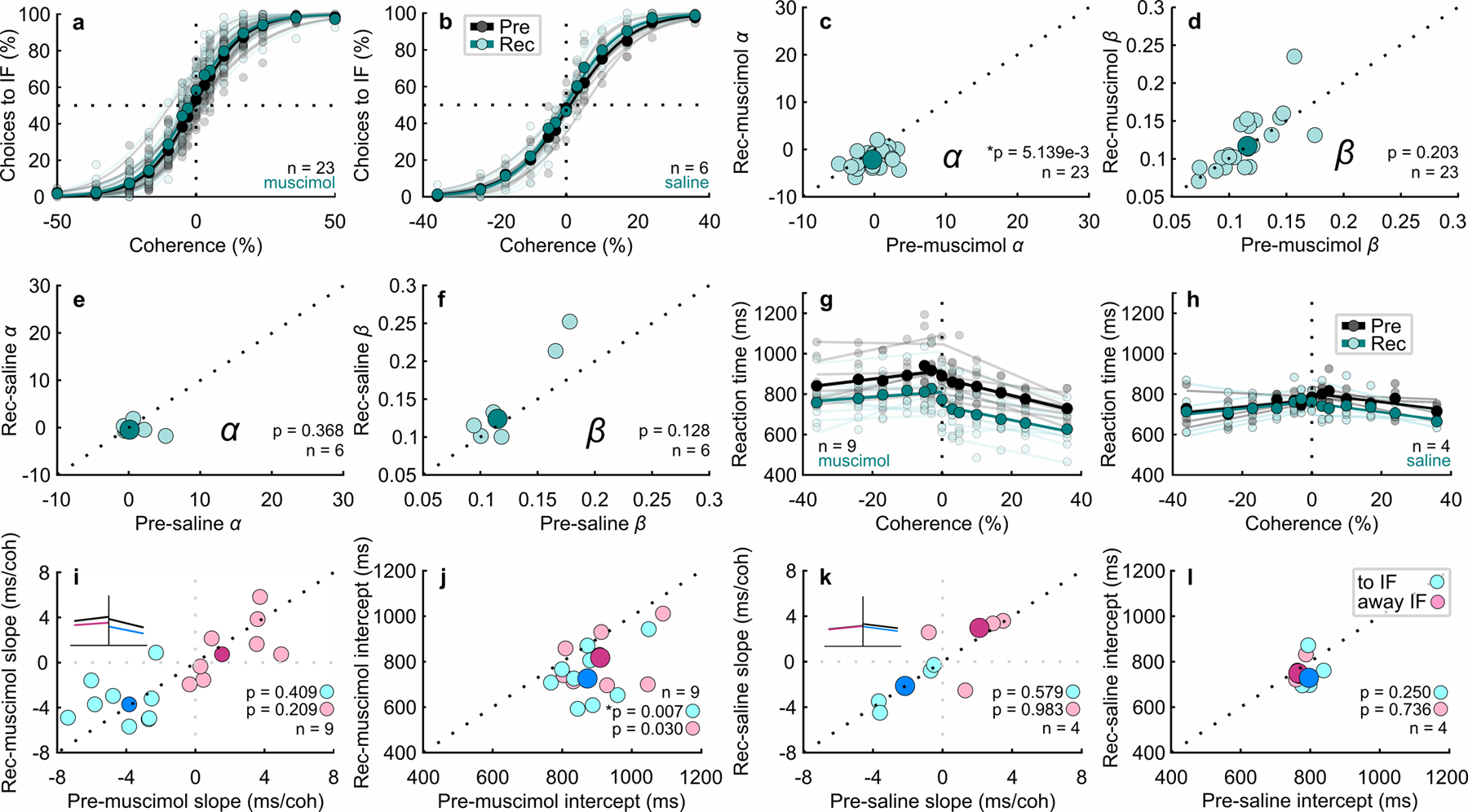
(Associated with Fig. 2 of the main text) a Proportion of choices to the inactivated field (toIF) is plotted as a function of Glass pattern coherence. Black circles show pre-muscimol performance data and green circles show 24-hour recovery performance data. The black and green lines show the two parameter logistic fits to the performance data. n=23 injections. b Same as in a for the pre-saline (black circles and lines) and the 24-hour recovery from saline (green circles and lines). n=6 injections. c α parameters from the logistic fits for the recovery data (rec-muscimol) plotted against α parameters from the fits for the pre-muscimol data. On average, the α parameter shifted leftward during the recovery period compared to the pre-muscimol control (w(22) = 230, p = 0.005). Note that this was opposite to the direction of the shift that occurred post-muscimol as seen in the main Fig. 2a, as if the monkeys over-compensated for the effect of muscimol during recovery. d β parameters from the logistic fits for the recovery data plotted against the β parameters from the fits from the pre-muscimol data. On average, there were no significant differences in the β parameter (t(22) = −1.31, p = 0.20, 95% CI = [−0.02, 6.0 × 10⁻³]). e–f Same as in c and d for the saline experiments. g Reaction time (RT) plotted against coherence for the pre-muscimol data (black circles) and recovery data (green circles) from the RT version of the decision task (n=9 injections). The lines show linear fits to the RT data. The RT was shorter for the recovery data compared to the pre-muscimol data for all coherences. Similar to the results of the α parameter comparisons, the RT finding suggests a compensatory response to the muscimol injections 24 hours earlier. h Same as in g for the saline experiments. i The slope parameter from the linear fits to the RT data for the recovery data plotted against the pre-muscimol data. Cyan circles show the parameter of the linear fits of the RT data for toIF decisions (positive coherences) and magenta circles show the RT data for awayIF decisions (negative coherences). There were no significant differences on average (RT slope awayIF, t(8) = 1.37, p = 0.21, 95% CI = [−0.87, 2.59]; RT slope toIF, t(8) = −0.87, p = 0.41, 95% CI = [−3.10, 1.61]). j same as in i for the intercept parameter. There were significant changes in the intercept on average for the toIF side (RT intercept, t(8) = 3.61, p = 0.007, 95% CI = [32.55, 240.50]) but not the awayIF side (RT intercept, t(8) =2.63, p = 0.03 n.s. Bonferroni correction, 95% CI = [−4.89, 216.53]). k–l Same as in i and j for the saline experiments. There were no significant differences in slope or intercept for these experiments (RT slope awayIF, t(3) = −0.02, p = 0.98, 95% CI = [−6.26, 6.19]; RT slope toIF, t(3) = 0.62, p = 0.58, 95% CI = [−0.88, 1.19]; RT intercept awayIF, t(3) = 0.37, p = 0.74, 95% CI = [−71.20, 85.05]; RT intercept toIF, w(3) = 9, p = 0.25). Note that four saline experiments were performed in the RT task and the other two were performed using the delayed version of the task so only four observations appear in this plot. Note that the darker shaded symbols show the median values and the 95% confidence intervals are from the means.

Extended Data Fig. 5. DDM model simulations for changes in model parameters.

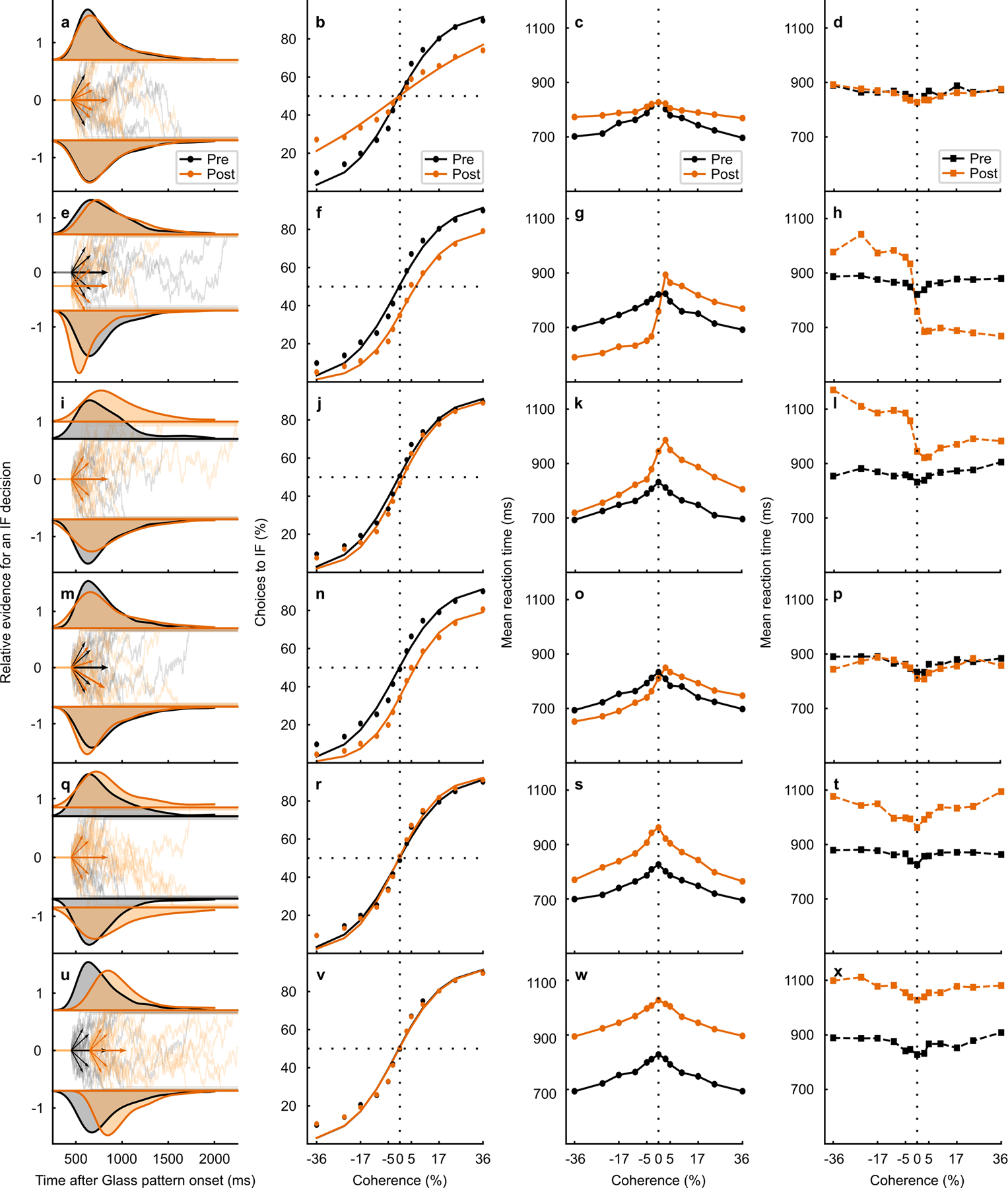
(Associated with Fig. 4 and 5 of the main text). Panels a-p are the same as those shown in Fig. 5 of the main text. a RT distribution from the 0% coherence condition (density approximated through kernel smoothing) predicted by a DDM simulation with only decrease in proportionality factor between coherence and drift rate post-muscimol (orange). Pre-muscimol shown in black. Below the RT distributions, the relative evidence for toIF decisions is plotted over time since the Glass pattern onset and the short arrows show drift rates for toIF decisions (positive) and awayIF decisions (negative) pre- and post-muscimol, for the 0%, 10%, and 36% coherence conditions. The longer arrows show the mean drift rate across both toIF and awayIF directions and all coherences, termed drift rate offset²⁸ b The psychometric function, plotted as a proportion of toIF choices over coherences, predicted by the DDM variant simulation with a decrease in proportionality factor between coherence and drift rate which changes the slope (without a shift) of the psychometric function. A change in the slope of the psychometric function was not observed in the data (Fig. 5r, v, shaded), making the decrease in proportionality factor between coherence and drift rate an unlikely explanation for the observed data. c Mean RT predictions for correct trials for each coherence condition for the DDM simulation with a decrease in proportionality factor between coherence and drift rate, for pre- (black) and post-muscimol (orange). d Same as in c but for error trials. e–h Same as in a-d but for the DDM variant simulation with only a change in proportional start-point of the evidence accumulation path away from the IF (often interpreted as an initial bias away from the IF). A decrease in proportional start point away from the IF predicts a shift in the psychometric function as observed in the real data (Fig. 5r,v, shaded), making a change in the proportional start point a possibility in explaining the decision bias we observed in the post-muscimol data. However, a start point change away from the IF also predicts a decrease in error toIF RTs which we did not observe in the data (Fig. 5t,x, shaded). i–l Same as in a-d but for the DDM variant with an increase in the upper boundary but no absolute start point change (start point proportionally decreased away from the IF). This parameter change also predicts a lateral shift in the psychometric function away from IF decisions as we observed in the data (Fig. 5r,v, shaded). However, this parameter change cannot explain the magnitude of the psychometric function shift we observed (Fig. 5r,v, shaded) with similar changes in simulated and observed mean RTs (Fig. 5s,t,w,x, shaded). m–p Same as in a-d but for the DDM variant with a change in drift rate offset favoring awayIF decisions. The psychometric function predictions of the model simulation with a change in the drift rate offset predict a lateral shift in the psychometric function that is observed in the data (Fig. 5r,v, shaded). The increases in correct mean RT for toIF decisions are predicted and shown for both monkeys (Fig. 5s,w, shaded). Overall, a change in drift rate offset is most likely to explain the data we obtained after muscimol inactivation of the SC. q–t Same as in a-d but for the DDM model variant that describes RT distributions and performance with only an increase in the symmetric boundaries. This parameter change predicts only slight steepening of the slope of the psychometric function and no changes in the shift of the psychometric function as observed in the data (Fig. 5r,v, shaded), making the symmetric boundary change an unlikely possibility for explaining the effects of SC inactivation. u–x Same as in a-d but for the DDM variant that describes RT distributions and performance with only an increase in non-decision time. Non-decision time changes do not explain any changes in performance and thus cannot explain a shift in the psychometric function observed in the data from both monkeys (Fig. 5r,v, shaded), making a change in non-decision time unlikely to explain the effects of SC inactivation on decision-making.

Extended Data Fig. 6. Parameter estimates for HDDM, DDM, and UGM.

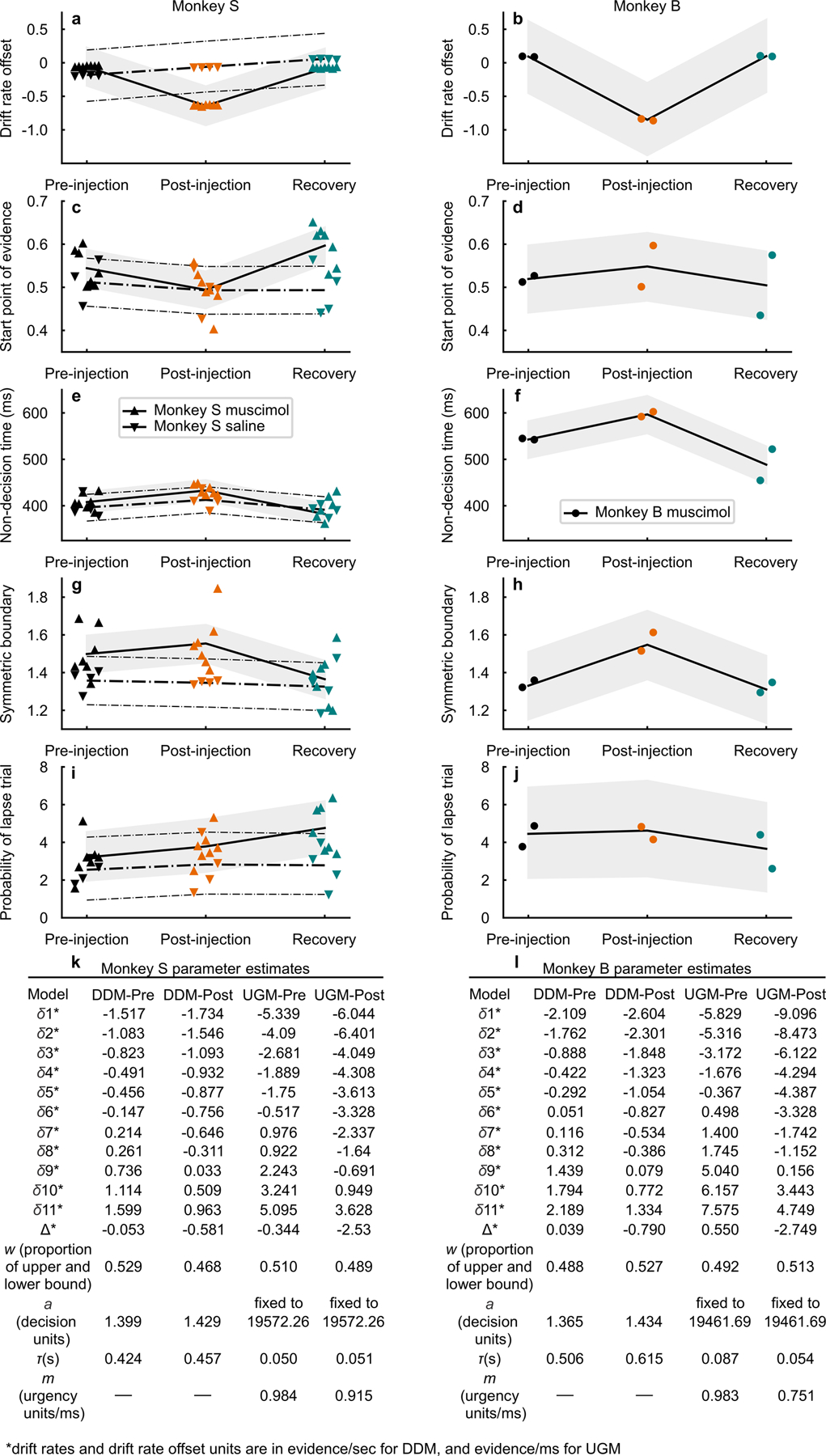
(Associated with Fig. 5 of the main text). a–j Estimates from the full HDDM of hierarchical parameters (μ) for each monkey (solid lines in the muscimol experimental condition; dotted lines for monkey S in the saline experimental condition, we did not collect data from the RT task for monkey B in the saline condition). 95% credible intervals with 2.5th and 97.5th quantile boundaries of hierarchical parameters provided by shading for the muscimol condition and smaller dot-dashed lines for the saline condition. Also shown are individual session parameter estimates for monkey S’s muscimol data (upward-pointing triangles), monkey B’s muscimol data (circles), and monkey S’s saline data (downward-pointing triangles). Estimates were obtained from the median posterior distributions of each parameter. a Estimates of the HDDM session-level drift rate offset (Δ) and hierarchical drift rate offset (μ_Δ) for monkey S (pre BF = 0.08, post BF = 3.19 × 10⁶, 99.7% probability of decrease pre to post). b Same as in a but for monkey B (pre Bayes factor BF = 0.14, post BF = 17.87, 99.0% probability of decrease pre to post). c Estimates of the HDDM session-level start point (w) and hierarchical start point (μ_w) for monkey S (post BF⁻¹ = 11.51, 95.1% probability of a proportional start point bias away from the IF from pre to post). d Same as in c but for monkey B (post BF⁻¹ = 2.82, 70.6% probability of a proportional start point bias towards the IF from pre to post). e Estimates of the session-level non-decision time (τ) and hierarchical non-decision time (μ_τ) for monkey S (94.5% probability of an increase from pre to post). f Same as in e for monkey B (97.0% probability of increase pre to post). g Estimates of the session-level symmetric boundary (a) and hierarchical symmetric boundary (μ_a) for monkey S (78.9% probability of an increase from pre to post). h Same as in g but for monkey B (95.2% probability of increase pre to post). i Estimates of the session-level lapse proportion (λ) and hierarchical lapse proportion (μ_λ) for monkey S (72.5% probability of increase from pre to post). j Same as in i but for monkey B (54.0% probability of increase pre to post). k–l The parameter estimates obtained from fitting the DDM and the UGM to the pre- and post-muscimol data for monkey S (panel k) and monkey B (panel l). The first row describes the model that was fit (DDM or UGM) and which data session (pre or post) was used to fit the model. The next 11 rows represent the drift rate parameter estimates (δ_K) in evidence units/sec for the DDM or evidence units/ms for the UGM, for the k = 11 conditions (−24%, −17%, −10%, −3%, −5%, 0%, 5%, 3%, 10%, 17%, 24% coherences). The next row shows the drift rate offset (Δ). This parameter was not explicitly fit in the non-hierarchical DDM and UGM, but rather calculated as the mean of the all the drift rates across all coherences for toIF and awayIF directions that were estimated from fits. The drift rate offset decreased from pre- to post-muscimol for both DDM and UGM and for both monkeys (difference in monkey S, 0.53 evidence units/sec decrease for DDM, 2.19 evidence units/ms decrease for UGM; monkey B, 0.83 evidence units/sec decrease for DDM, 3.30 evidence units/ms decrease for UGM). The next row shows the proportional start point parameter w, defined as the proportion of the distance between the upper and lower bound. For monkey S, the start point parameter had slightly decreased from pre- to post-muscimol in both the DDM (0.06 decrease) and UGM (0.02 decrease), indicating the start point moved closer to the awayIF decision bound, and for monkey B, the start point parameter slightly increased in the DDM (0.04 increase) and UGM (0.02 increase), indicating the start point moved closer to the toIF decision bound. The next row shows the bound height parameter a, defined as the distance between the upper and lower bounds. For both monkeys, but more prominent in monkey B, the bound parameter had slightly increased from pre to post in the DDM (monkey S, pre to post increase of 0.03 decision units; monkey B, pre- to post-muscimol increase of 0.07 decision units), whereas the bound was fixed in the UGM (Supplementary Note). The row after shows the non-decision time τ, in seconds, where we see a slight increase in the DDM (0.03 sec increase) and UGM (0.001 sec increase) for monkey S and a greater increase in the DDM for monkey B (0.11 sec increase), but not for the UGM (0.03 sec decrease). The last row shows the urgency slope estimates for the UGM, m, decreasing slightly with muscimol for monkey S (0.07 urgency units/ms), and decreasing more for monkey B (0.23 urgency units/ms).

Extended Data Fig. 7. Model predictions versus data for RT distributions and psychometric functions.

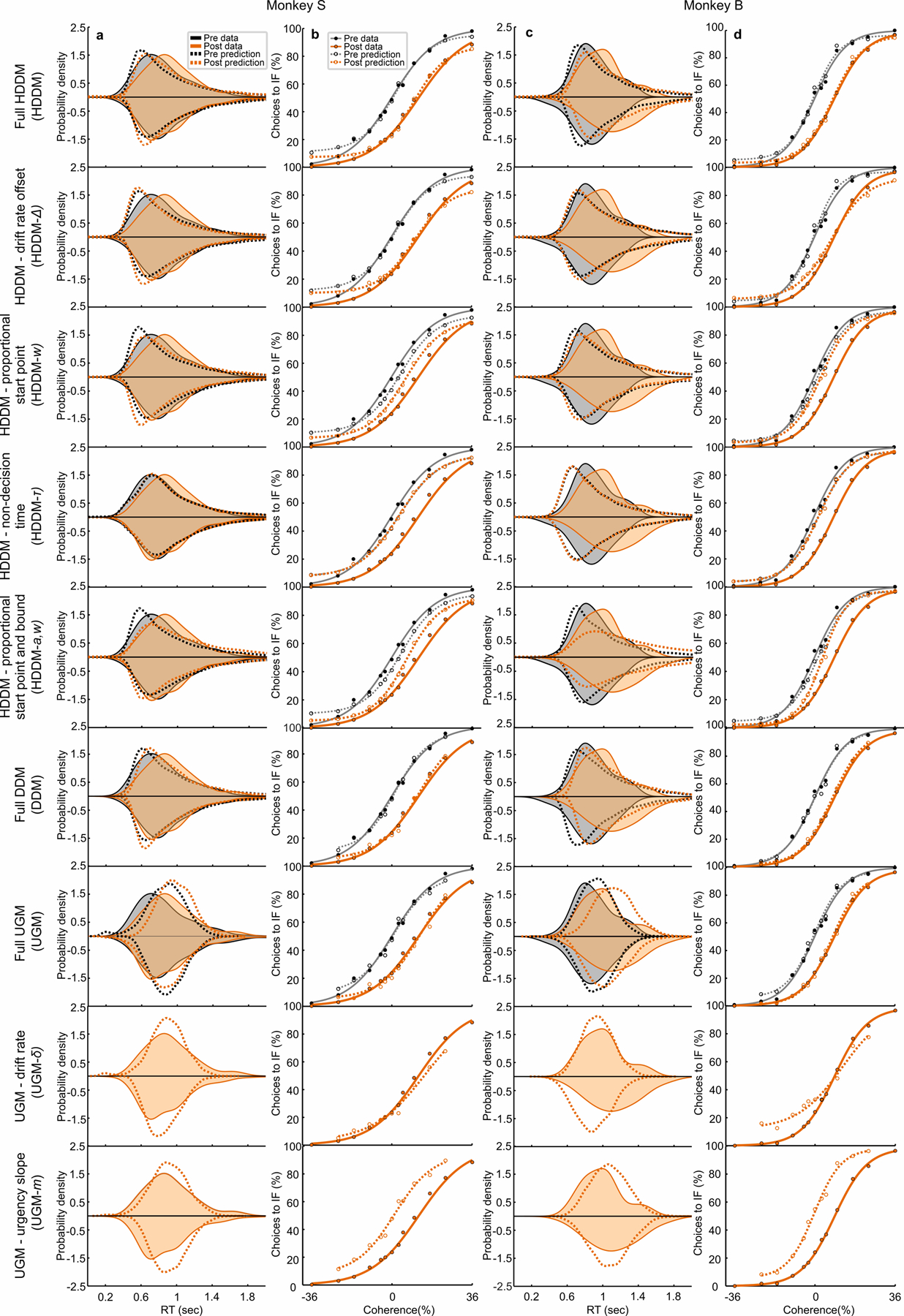
(Associated with Fig. 5 of the main text). Column a shows the predicted RT distributions (0% coherence, density approximated through kernel smoothing) from the DDM, HDDM and UGM model variants (dashed lines) together with the actual data (solid lines), pre-muscimol (black) and post-muscimol (orange), for monkey S. We observed a rightward skew of the RT distribution, consistent with a fixed bound model of decision-making and captured by the DDM rather than the UGM as was also indicated by the R²_pred, AIC, and BIC goodness of fit values (Supplementary Table 4). Column b shows the same as in a but for psychometric functions (performance data, four parameter logistic model using equation shown in Extended Data Fig. 2). Column c shows the same as in a for monkey B’s data and model fits. The RT distributions from monkey B were more normally distributed compared to the skewed RT distributions of monkey S, suggesting that the UGM rather than the DDM would explain monkey B’s data, consistent with the goodness of fit values (Supplementary Table 4). Column d shows the same as in c but for psychometric function (performance data). Each row indicates the results of each model’s prediction compared to data for both monkey S and monkey B. The models from top to bottom are the full HDDM, HDDM with a free-to-vary drift rate offset (HDDM-Δ), HDDM with a free-to-vary proportional start point (HDDM-w), HDDM with free-to-vary non-decision time (HDDM-τ), HDDM with both a proportional start point and bound free to vary (HDDM-a,w), the non-hierarchical DDM, the full UGM, the UGM with free-to-vary drift rates (UGM-δ), and UGM with a free-to-vary urgency slope (UGM-m). Note that only the post-muscimol data are shown for the UGM with a single free parameter since we only fit the post data with those models where we let only one parameter free to vary while the rest of the parameters were fixed to pre-muscimol parameter estimates (Supplementary Note). Also for the DDM and UGM fits, note that there are only 11 conditions (−24 to 24 % coherence) for the psychometric functions because only 11 conditions were fitted (Supplementary Note). For the HDDM, out of all the variants (first five rows), the full HDDM predictions visually match the data for both performance and RT. The prediction of the HDDM-Δ captures the decision bias from the data almost equally well for both monkeys. The prediction for the HDDM-w and HDDM-a,w also predicts a decision bias, but is insufficient to explain the magnitude of the shift in decision bias that we observed in the data. The HDDM-τ fails to capture any decision bias (RT and performance predictions for pre and post are overlapping). The predictions of the simple DDM also capture the 0% RT distribution well, more so for monkey S than for monkey B, and also capture the choice data well. The opposite is true for the full UGM predictions, where the RT predictions capture monkey B’s data more than monkey S (see goodness of fit values in Supplementary Table 4), but also captures performance data well for both monkeys. The UGM-δ captures the shift in decision bias from the post-muscimol data from both monkeys, consistent with the findings from the HDDM, whereas the UGM-m fails to capture the decision bias in the post data.