Harmonic optical tomography of nonlinear structures

Abstract

Second-harmonic generation microscopy is a valuable label-free modality for imaging non-centrosymmetric structures and has important biomedical applications from live-cell imaging to cancer diagnosis. Conventional second-harmonic generation microscopy measures intensity signals that originate from tightly focused laser beams, preventing researchers from solving the scattering inverse problem for second-order nonlinear materials. Here, we present harmonic optical tomography (HOT) as a novel modality for imaging microscopic, nonlinear and inhomogeneous objects. The HOT principle of operation relies on inter-ferometrically measuring the complex harmonic field and using a scattering inverse model to reconstruct the three-dimensional distribution of harmonophores. HOT enables strong axial sectioning via the momentum conservation of spatially and temporally broadband fields. We illustrate the HOT operation with experiments and reconstructions on a beta-barium borate crystal and various biological specimens. Although our results involve second-order nonlinear materials, we show that this approach applies to any coherent nonlinear process.

Second-harmonic generation microscopy (SHGM) has emerged as a powerful technique for intrinsic contrast optical imaging of cells and tissues^1–4. As the nonlinear susceptibility χ⁽²⁾ is non-zero only for materials that lack inversion symmetry⁵, the second-harmonic field can report on molecules organized in filaments with high specificity. SHGM signals in biological tissues are dominated by specific types of collagen fibres^6–10, myosin in muscle fibres^11–13 and polarized microtubules¹⁴. The ability to selectively image collagen in the tissue extracellular matrix has been exploited for studying tumor microenvironments^15,16 as a marker for characterizing cancer aggressiveness^17–19. The list of diseases that can be characterized using SHGM continues to grow at a rapid pace^20–22.

Conventional laser-scanning SHGM relies on the intrinsic optical sectioning capability that is afforded by using tightly focused, short laser pulses. This restricts the SHG scattering to a small volume at the focus of the incident light pulse²³. The SHGM image depends on the spatial variation in the intensity and phase of the fundamental beam, as well as on the spatial distribution of harmonophores and phase matching^24–26. Phase matching of the coherent SHG scattering process thus often obscures the quantitative interpretation of the images. Traditional imaging requires scanning of the focused fundamental beam followed by single-point detection²⁷. It has recently been shown that three-dimensional (3D) images can be obtained by sample rotation followed by multiview registration and reconstruction²⁸. By contrast, mixing the signal with a strong reference field provides interferometric access to both the amplitude and phase of the SHG signal^29–34. Early publications demonstrated that a direct measurement of a complex SHG field eliminates the image artefacts due to phase mismatch^35,36. Using this approach, holographic SHGM has been demonstrated on biological structures; however, to our knowledge, a solution to the SHG scattering inverse problem has not been reported so far. In other words, the 3D images presented in the literature represent distributions of the SHG field, which depends on both χ⁽²⁾ and local phase matching, not of the nonlinear susceptibility itself.

In this Article we present harmonic optical tomography (HOT) as a novel modality for measuring three-dimensional nonlinear structures. By solving the nonlinear and inhomogeneous wave equation, we developed a new theoretical description of SHG scattering and derived an analytic solution for the inverse problem. By collecting data through a holographic experimental system with spatially and temporally broadband fields, HOT offers wide frequency support for tomographic imaging. The transparent 3D nonlinear structures are visualized through computed solutions of the inverse problem. We demonstrated the method with experiments on microscopic defects that are embedded in a beta-barium borate (BBO) crystal and various tissues. The theoretical results highlight the importance of phase matching and the 3D reconstructions demonstrate the substantial sectioning improvement over conventional SHGM.

Results

HOT experimental system.

The HOT system (Fig. 1a) measures the complex SHG field by using off-axis holography (see section 6.2 in ref.³⁷ for an overview of off-axis operation). The laser pulses used for illumination are generated with a mode-locked Yb:fibre laser that is followed by a parabolic fibre amplifier. The collimated laser beam is passed through a SHG crystal to generate a reference field for interference, after which the fundamental field (with a central wavelength of 1,060 nm) is separated into sample and reference fields by a dichroic beam splitter. The fundamental beam is directed towards the specimen through an aspheric 0.5 numerical aperture (NA) condenser lens while the harmonic reference beam travels along a separate path. The reference field interferes with the sample SHG light and the interferogram intensity is captured by a scientifc complementary metal–oxide–semiconductor camera. The fundamental field is defocused so that a wide-field illumination of the specimen is possible. The SHG signal generated in the sample by the defocused illumination field is imaged to the camera with a 4f imaging system using a ×100/0.9 NA objective lens. The fundamental field is suppressed by using an optical filter placed near the pupil plane of the objective. After passing through a non-polarizing beam splitter, the sample and reference beams are recombined at the image plane through a tube lens, with a slight offset in the propagation angle to permit off-axis holography. The high numerical aperture objective and broad angular illumination provide high axial sectioning capability.

Fig. 1 |. A schematic of HOT and the procedure of complex field retrieval.

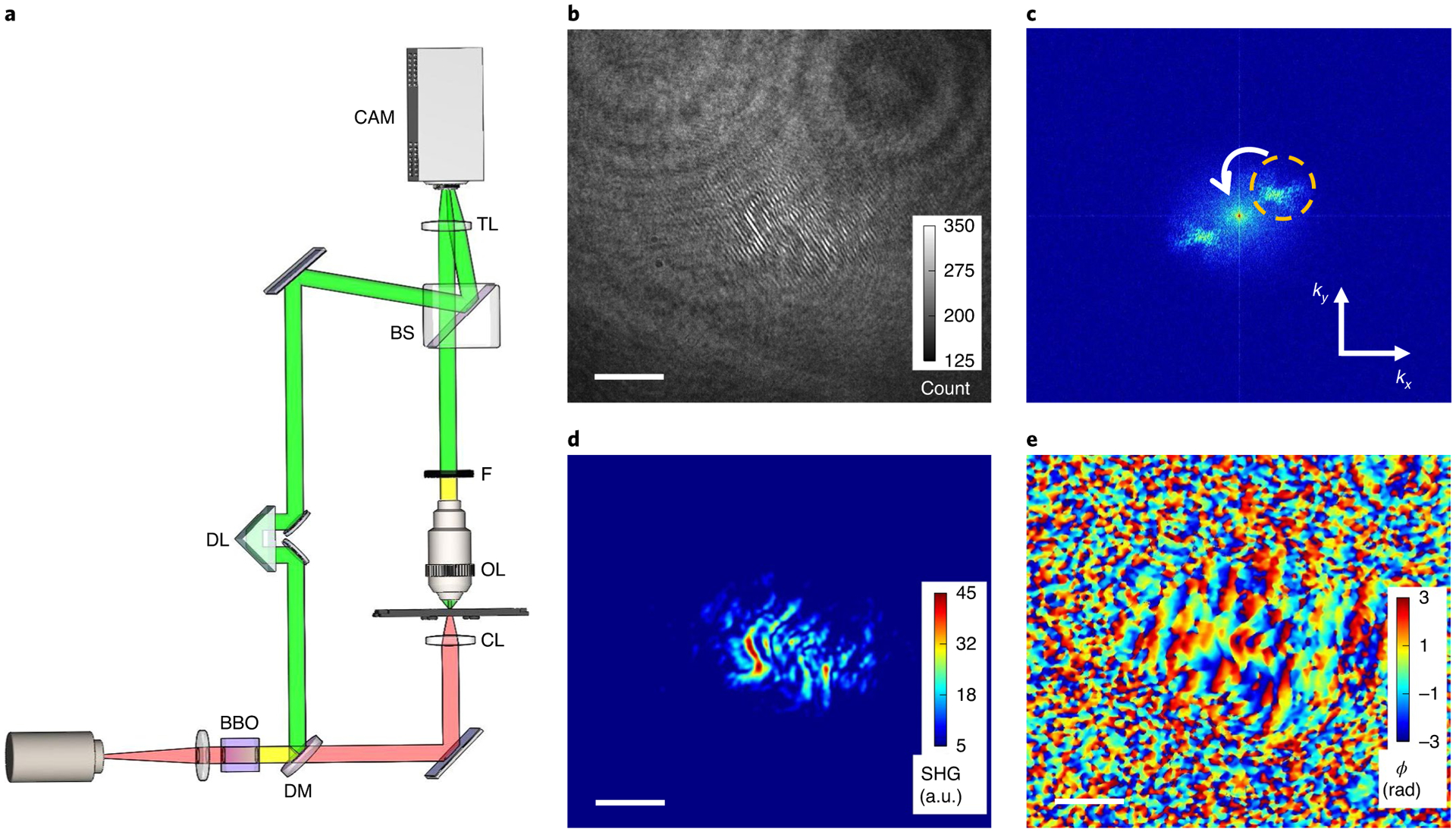
a, The HOT optical set-up; the system records the complex SHG field by using off-axis holography. BBO, a beta-barium borate crystal; DM, dichroic mirror; DL, delay line; CL, condenser lens; OL, objective lens; F, filter; BS, non-polarized beam splitter; TL, tube lens; CAM, camera. A detailed description of the system design is provided in the Methods. b, A representative hologram recorded by HOT. The sample is a tissue slice of a rabbit lymph node measured in focus. c, The spatial power spectrum of the image in b. One of the sidebands (indicated by the circular dashed line) is isolated and shifted to the origin of the frequency domain. d, The amplitude of the SHG field, extracted from the inverse Fourier transform of c. e, The phase of the SHG field. Scale bars, 10 μm.

An optical delay is integrated into the path of the reference, such that the two interfering pulses arrive at the camera plane within a small fraction of the coherent time of the SHG fields. The relative dispersion between the two arms was carefully minimized to ensure high-visibility fringes in the recorded interferograms.

The amplitude and phase of the SHG signal are extracted from the holograms through a numerical processing algorithm (see Supplementary Section 3 and ref.³⁸), as shown in Fig. 1b–e. Specifically, the real-valued hologram (Fig. 1b) is Fourier transformed and one of the sidebands is isolated and shifted to the origin of the frequency domain (Fig. 1c) while the remaining signal is filtered out. Performing an inverse Fourier transform on the isolated sideband yields a complex SHG signal field that is incident on the camera, and whose amplitude and phase can be extracted separately, as shown in Fig. 1d,e. This processing is repeated for the sequence of depth-resolved holograms, which are collected by scanning the axial position of the specimen mounted on a motorized stage.

HOT reconstruction model.

We derived a physical model for the second-harmonic field scattering—under the undepleted pump and the first-order Born approximations—to reconstruct the 3D nonlinear structure. Consider the optical field (U) that is propagating inside of a static, nonlinear, inhomogeneous medium according to the inhomogeneous Helmholtz equation (see Fig. 2 and Supplementary Section 1).

$${\nabla }^{2}U\left(r,\omega \right)+n^2\left(r,\omega \right)\frac{{\omega }^2}{c^2}U\left(r,\omega \right)=-\frac{{\omega }^2}{c^2}{\chi }^{\left(2\right)}\left(r\right)\left[U\left(r,\omega \right){ⓥ}_{\omega }U\left(r,\omega \right)\right]$$ (1)

Fig. 2 |. The second-harmonic scattering.

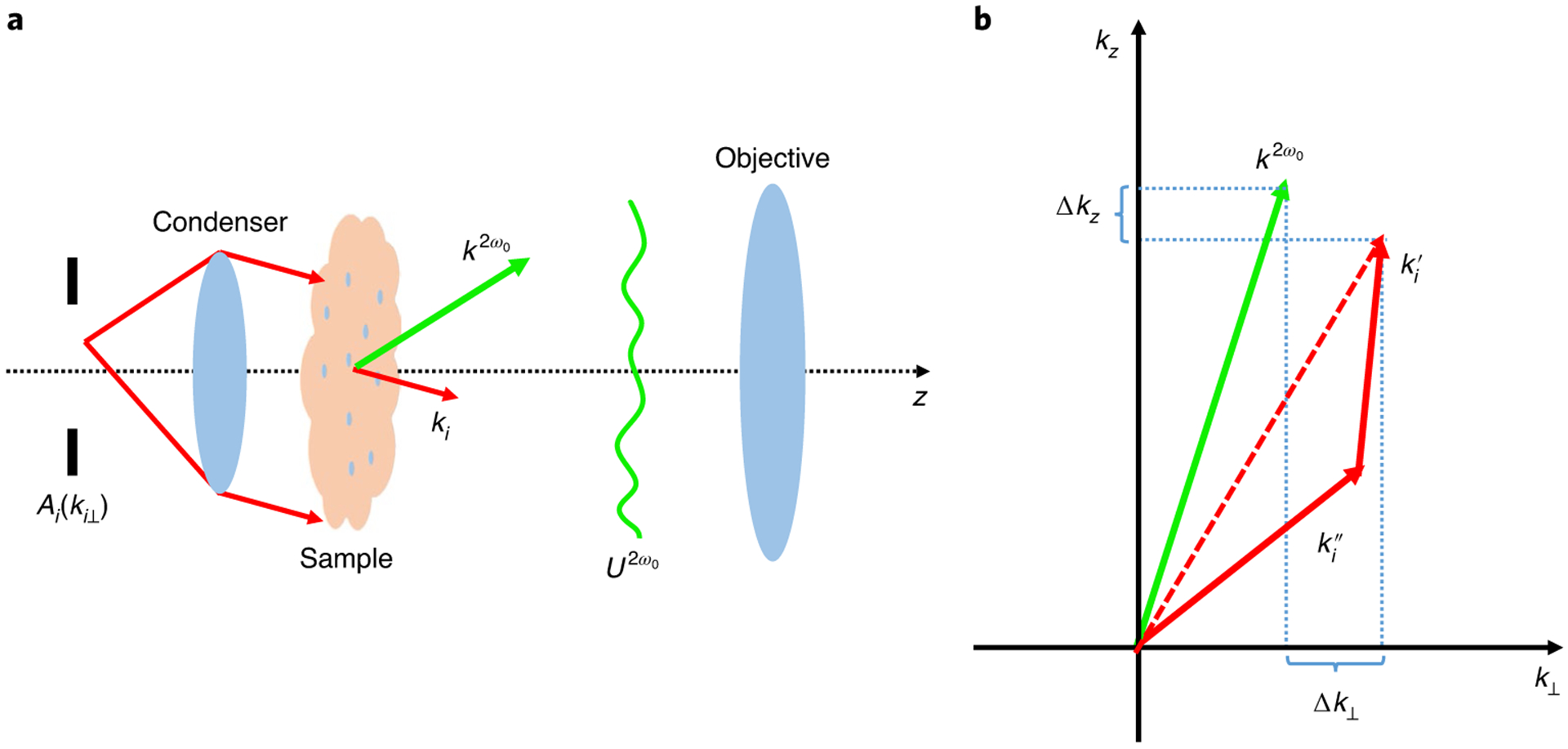
a, A collection of plane waves that are incident on a nonlinear inhomogeneous object generate SHG light. Under the first-order Born approximation, the spatially dependent SHG field is produced following interaction with the object and only those frequency components within the objective NA are able to propagate. b, An illustration of the non-collinear phase-matching condition. Two fundamental photons generate one second-harmonic photon and the object spatial frequency structure is recorded by fulfilling the condition that is imposed by momentum conservation (phase matching). The efficiency of this process is related to the difference of the wavevectors in transverse and axial directions.

In equation (1), n(r,ω) is the refractive index at frequency ω, ⓥ is the convolution operation and c is the speed of light in vacuum. Note that U is the total field, which comprises the incident, harmonic and linearly scattered fields, and the nonlinearly scattered field. Both n and χ⁽²⁾ depend on the spatial coordinate, r; that is, they are spatially inhomogeneous. Here we assume that χ⁽²⁾ is non-dispersive and that the thickness (L) of the object is below the transport mean free path. By considering one arbitrary plane wave of wavevector k_i that emerges from the condenser aperture, we can write the illumination field U_i as

$$U_i^{{\omega }_0}\left(k\right)=A_i\left(k_{i\perp }\right)\delta \left(k-k_i\right),$$ (2)

where ω₀ is the fundamental frequency, A_i is the two-dimensional (2D) condenser aperture and k_i⊥ is the transverse wavevector of the illumination plane wave (see Fig. 2a and Supplementary Section 1).

Under the first-order Born approximation (see Supplementary Section 1) the SHG field solution takes the form

$$U_{\text{SHG}}^{2{\omega }_0}\left(k_{\perp },z\right)=\frac{{\beta }_2^2}{2{\gamma }_2}{e}^{i{\gamma }_{2}z}{A}_o\left(k_{\perp }\right)A_i\left(k_{i\perp }^{\prime }\right)A_i\left(k_{i\perp }^{″}\right)\times {\chi }^{\left(2\right)}\left(k_{\perp }-k_{i\perp }^{\prime }-k_{i\perp }^{″},{\gamma }_2-{\gamma }_1^{\prime }-{\gamma }_1^{″}\right).$$ (3)

Equation (3) shows that, for a particular pair of incident fundamental transverse k-vectors ($k_{i\perp }^{\prime }$ and $k_{i\perp }^{″}$), a scattered SHG field is produced with transverse spatial frequency, k_⊥, where β₂ is the wavenumber of the second-harmonic field in vacuum (β₂ = 2ω₀/c); γ₂ is the longitudinal wavenumber $\left({\gamma }_2=\sqrt{{\overline{n}}_2^2{\beta }_2^2-{\left|k_{\perp }\right|}^2}\right)$, ${\overline{n}}_2$ the spatially averaged refractive index at the second-harmonic frequency ${\overline{n}}_2=\sqrt{{\langle n^2\left(r,2{\omega }_0\right)\rangle }_r}$; and A_o is the objective pupil function; z is the coordinate in the axial direction, and i is the imaginary unit. Note that this expression is obtained from the wave equation without the paraxial approximation.

Equation (3) clearly reveals the phase matching condition in the spatially inhomogeneous object (see details in Supplementary Section 1). As illustrated in Fig. 2b, two fundamental waves—propagating in the ($k_{i\perp }^{\prime }$, ${\gamma }_1^{\prime }$) and ($k_{i\perp }^{″}$, ${\gamma }_1^{″}$) directions—produce a second-harmonic wave that travels in the (k_⊥,γ₂) direction. The efficiency of this process is related to matching between the wavevectors of the fundamental and harmonic light, or momentum conservation. For example, if there is perfect wavevector matching along the z-axis (that is, ${\gamma }_2={\gamma }_1^{\prime }+{\gamma }_1^{″}$) then the SHG signal is summed up over the entire L of the object, as the central ordinate theorem (see chapter 4 in ref.³⁹) indicates that ${\chi }^{\left(2\right)}\left(k_z=0\right)=\underset{0}{\overset{L}{\int }}{\chi }^{\left(2\right)}\left(z\right)dz$. Note that the objective captures the SHG transverse frequencies within its pupil function, A_o(k_⊥).

Following the calculation in Supplementary Section 2, we derived a relationship between the measured SHG field, $U_{\text{SHG}}^{2{\omega }_0}\left(k_{\perp },k_z\right)$, and the nonlinear susceptibility,

$$U_{\text{SHG}}^{2{\omega }_0}\left(k_{\perp },k_z\right)=H\left(k_{\perp },k_z\right){\chi }^{(2)}\left(k_{\perp },k_z\right),$$ (4a)

$$H\left(k_{\perp },k_z\right)=\int {\beta }_2^{2}W\left({\omega }_0\right)P\left(k_{\perp },k_z\right)\otimes \left[U_i\left(k_{\perp },k_z\right)ⓥU_i\left(k_{\perp },k_z\right)\right]d{\omega }_0.$$ (4b)

In equations (4a,4b), H(k_⊥,k_z) is the effective transfer function of the system; W(ω₀) is the cross spectral density of the reference and specimen scattered SHG fields; P(k_⊥,k_z) is the 3D pupil function $\left(P\left(k_{\perp },k_z\right)=\frac{1}{2{\gamma }_2}{A}_o\left(k_{\perp }\right)\delta \left(k_z-{\gamma }_2\right)\right)$ and ⊗ represents the correlation operation.

Due to the broad angular spectrum of the illumination and the high NA objective, we collect a large range of scattered SHG spatial frequencies, which in turn yields high transverse and axial resolution of the HOT reconstruction. Figure 3 shows H as a function of condenser NA (NA_c). Note that for a narrow angular spectrum of the illumination light, the axial spectral frequency is also very narrow resulting in low optical sectioning. The v-shaped appearance incorporates the effects of the illumination and collection apertures, as well as temporal bandwidth. The thin distribution in k_z at the origin indicates that sectioning is weak at low transverse wavevectors, k_⊥, and becomes much stronger at high k_⊥ values. At a fixed value of k_⊥, NA_c is the dominant factor for achieving strong sectioning. The axial resolution improves significantly by increasing NA_c, at a faster rate than in the linear case^40–42. This is because the nonlinear process results in a convolution of the condenser pupil function, U_i(k)ⓥU_i(k), which gives twice the transverse wavevector spread due to non-collinear SHG scattering. For the condition in the current set-up (shown in Fig. 3c), we calculated the reciprocal of the transfer function bandwidth, which yields the lateral resolution to be 0.2 μm (at k_z = 0), and an axial resolution of 1.2 μm (at k_⊥ = 0).

Fig. 3 |. The normalized transfer function under different NA_c values.

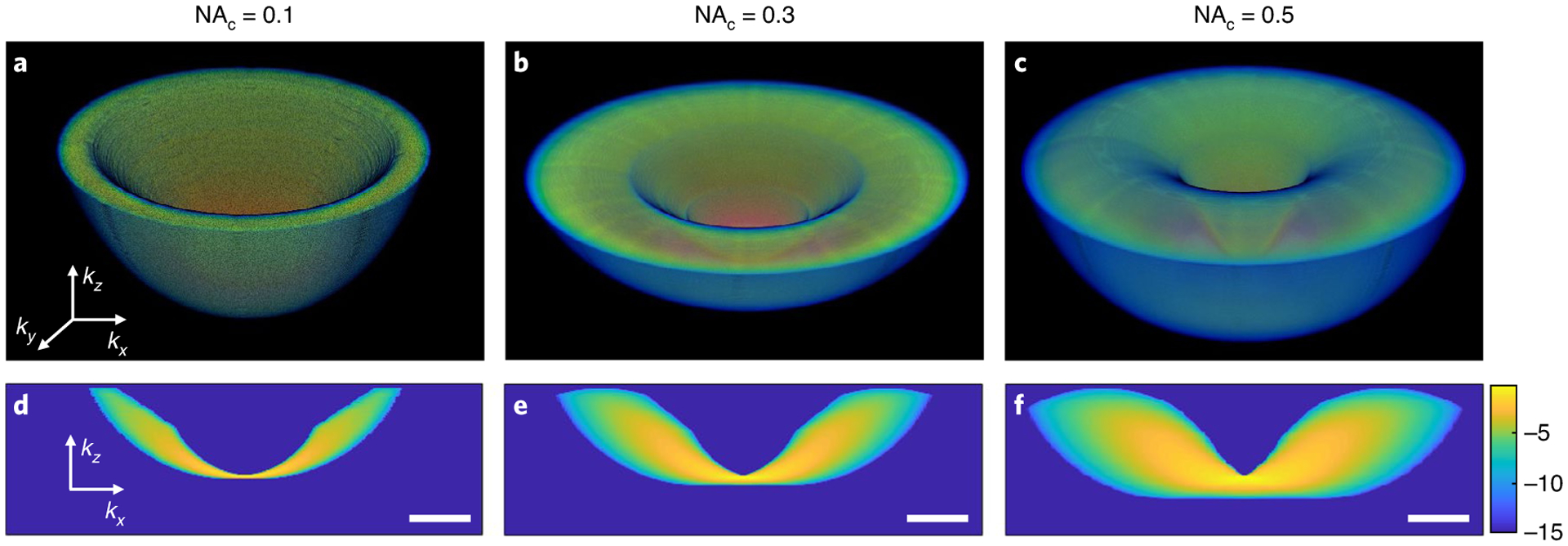
a–c, 3D views of the transfer function with NA_c = 0.1 (a), 0.3 (b) and 0.5 (c). d–f, The corresponding cross-sectional views of the transfer function with the same condenser NA values from a–c, respectively. All values are presented on a logarithmic scale in arbitrary units. Scale bars, 10 rad μm⁻¹.

Tomographic reconstruction of an inhomogeneous nonlinear crystal.

Figure 4 illustrates the depth-resolved acquired data and the corresponding tomographic reconstruction. We imaged a BBO crystal to test the performance of the reconstruction (see Methods for the imaging procedure). The crystal has defects and enclosures that form compact and roughly spherical features of various sizes; for comparison, wide-field SHG images were also recorded at each depth position by blocking the reference beam. Figure 4a shows the transverse SHG images at three axial positions: at the focal plane, and 7 μm above and below the focal plane. As indicated by arrows, out-of-focus artefacts are present in the wide-field SHG measurements. These artefacts are especially prevalent 7 μm below the focal plane. By contrast, the HOT reconstruction (Fig. 4b,c) removes these artefacts while preserving the features of the crystal. A video of the 3D rendering can be found in Supplementary Video 1. In essence, the tomographic reconstruction uses the physical model in equation (4a,4b) to numerically reverse the out-of-focus propagation.

Fig. 4 |. HOT of an inhomogeneous nonlinear crystal.

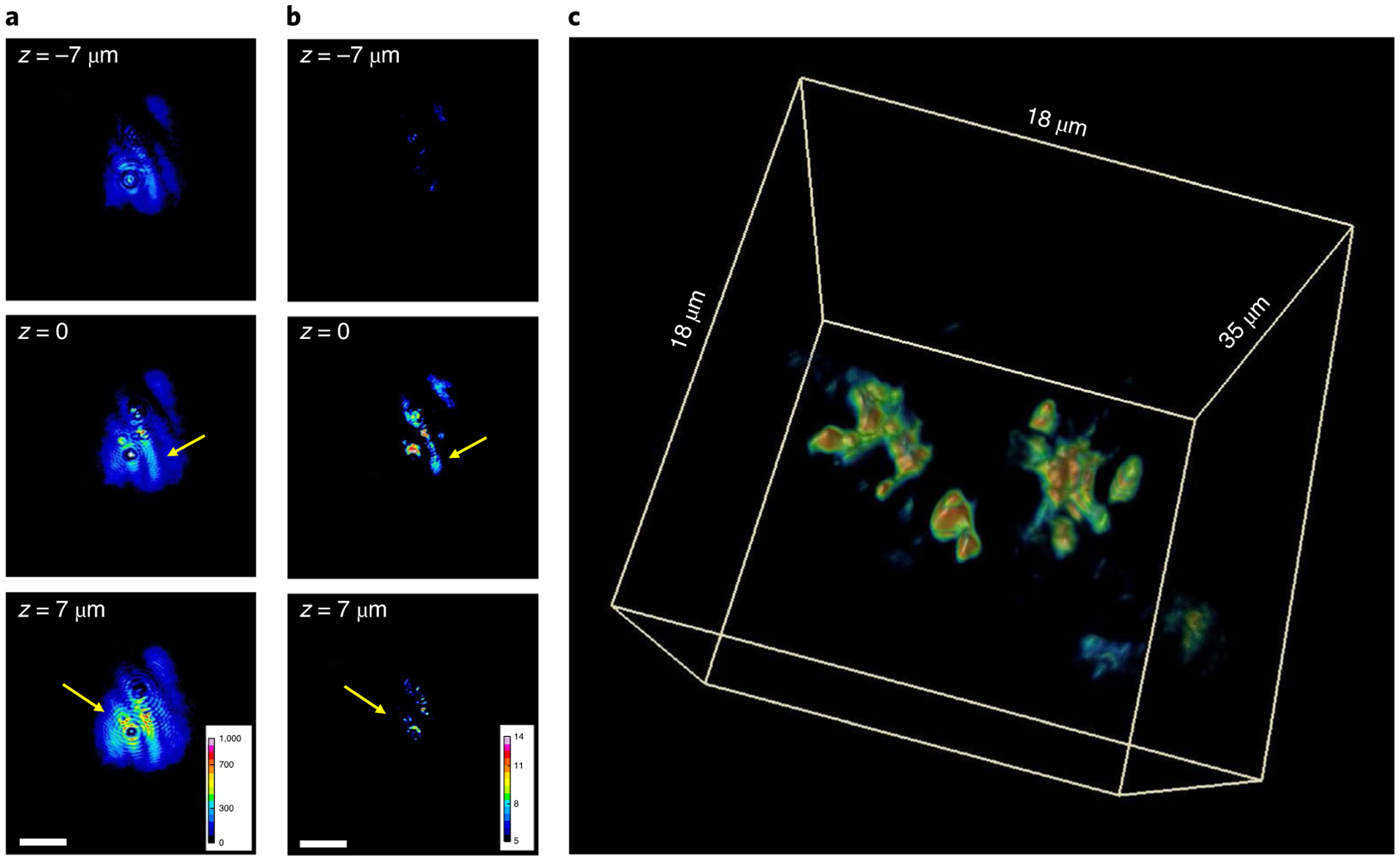
a, Three transverse SHG intensity images of a BBO crystal, measured at the focal plane (z = 0) and 7 μm above and below the focal plane. b, HOT reconstruction results of the same z-slice in a. Colour bars in a and b are in arbitrary units. c, A 3D view of the HOT reconstruction. A rotating rendering of this reconstruction can be viewed in Supplementary Video 1. Scale bars, 10 μm.

Tomographic imaging of muscle tissue.

We measured specimens of murine skeletal muscle—in which the SHG signal is mainly due to myosin—to illustrate the applicability of HOT to tissue imaging. For this sample, our system produces an imaging speed of ~4 fps, and the volumetric imaging time is approximately 2.26 min (limited by the mechanical scanning stage). Figure 5 shows the results obtained from a 27 × 27 × 12 μm³ piece of fixed muscle slice that is imaged by wide-field SHG and HOT. Although the tissue structure is vaguely visible in the wide-field SHG image (Fig. 5a), the SHG signal is dominated by the out-of-focus light. On the other hand, the HOT reconstruction (Fig. 5b) reveals the structure of the myosin filaments in the tissue without corruption from out-of-focus SHG light. The average spacing between the bands is measured to be 1.3 μm, which agrees with previous results^43,44. At the plane of interest, the signal-to-noise ratio of the reconstructed image is evaluated to be 15.8. A video of 3D rendering is included in Supplementary Video 2. These results underline the fundamental difference between a direct and inverse problem. Direct imaging, whether with linear or harmonic fields, yields the distribution of light, which contains information about the object, obscured by out-of-focus contributions. On the other hand, combining these data with a theoretical model that accounts for the physics of the propagation yields the structure of the object itself, free of artefacts.

Fig. 5 |. HOT of murine skeletal muscle slice.

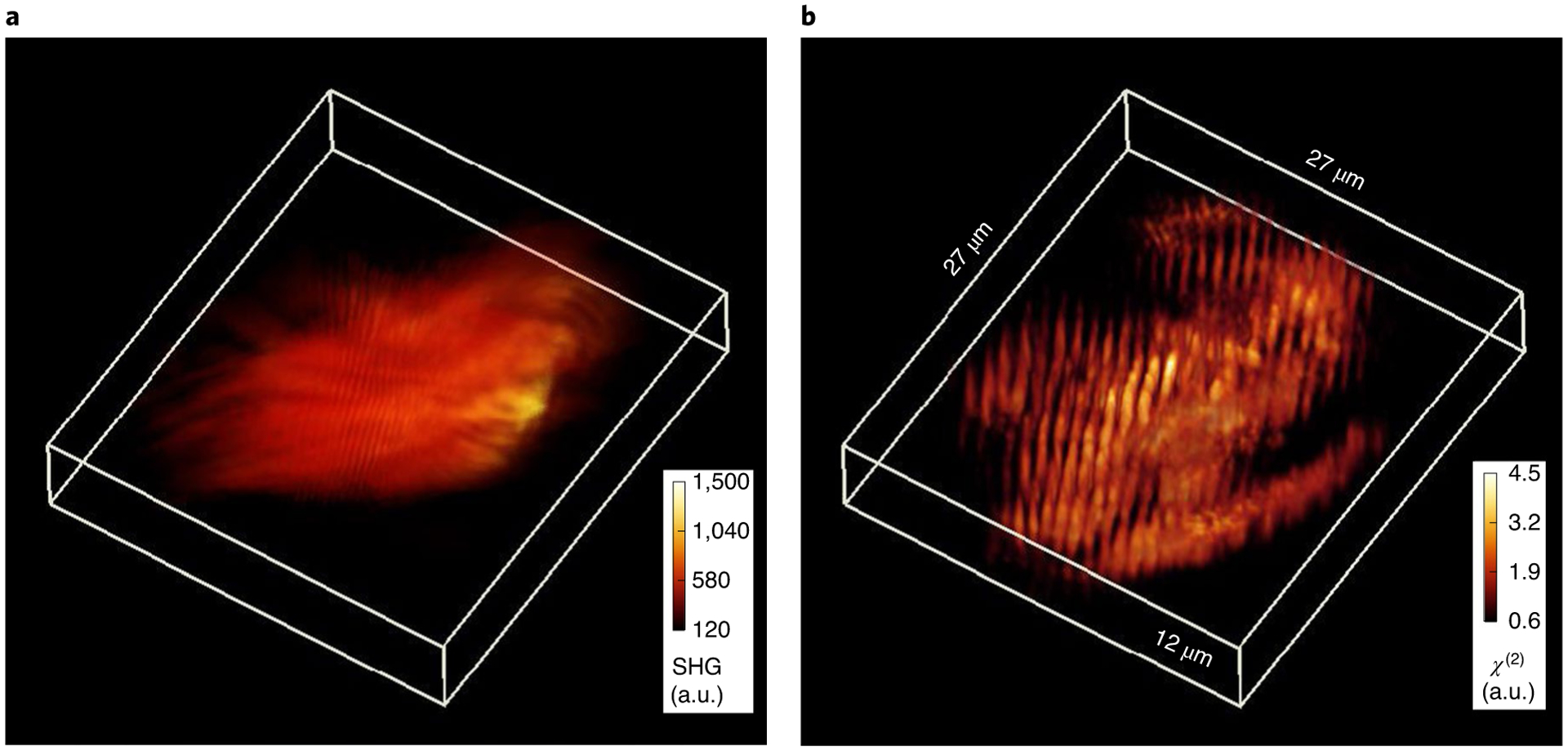
a, A 3D view of the wide-field SHG intensity measurement of a murine muscle slice. b, A 3D view of the sample tissue block from a after HOT reconstruction. A rotating rendering is included in Supplementary Video 2.

Summary

We demonstrated HOT as a novel label-free modality to achieve tomography of nonlinear, inhomogeneous objects. By solving the wave equation under the first-order perturbation, undepleted pump and Born approximations, we obtained a linear relation between the second-order susceptibility and the complex SHG field. This result allows the reconstruction of the three-dimensional nonlinear response by solving the scattering inverse problem. HOT utilizes a defocused broadband illumination field combined with a high NA objective lens to extract a broad range of spatial frequencies from the sample. The Mach–Zehnder interferometric geometry yields information about both the amplitude and phase of the SHG signal, which is necessary for solving the inverse problem. We demonstrated the performance of HOT with measurements on inhomogeneous nonlinear crystals and biological specimens. The results of our reconstruction show a significant enhancement in sectioning capability when compared with standard SHG imaging.

HOT can be applied to materials with dispersive χ⁽²⁾, that is, where the Kleinman’s symmetry breaks down (see, for example, section 1.5.5 in ref.⁵). A common such sample is collagen imaged at 800–900 nm. In this case, the best approach would be to use a narrow-band excitation laser, which will minimize χ⁽²⁾ dispersion, at the expense of reduced sectioning and increased image speckle, whereas the HOT reconstruction will remain the same.

Although laser-scanning SHGM generates images with a high signal-to-noise ratio, HOT produces tomograms without phase-matching artefacts. Moreover, our full-field approach yields volumetric images with high throughput. If the tissue specimen used in this research were measured by laser-scanning SHGM at the same sampling rate and voxel resolution for a minimum dwell time of 5 μs per voxel, this volume would require 1.6 h, which is ~42 times slower than HOT. The current set-up employs a coherent laser source. As all of the spatial frequency components are in phase after going through a high-NA condenser lens, the light is focused down, forming a small area on the sample plane. We used a defocused excitation beam to generate a bigger field of view, and the axial phase dependence of the defocused illumination beam admits the ability for broad spatial frequency support in the coherent SHG image transfer function, due to the effect of non-collinear SHG scattering that is enabled by the nonlinear object response. In principle, the field of view can be enlarged further, at the expense of using larger irradiance. Supplementary Fig. 1 presents a few HOT tomograms with degraded sectioning results; these specimens were measured with a 0.15 NA condenser.

The field of quantitative phase imaging (QPI)³⁷, in which the complex field information is measured quantitatively, has received significant interest due to its broad range of potential biomedical applications⁴⁵. QPI can produce the necessary data for tomographic reconstruction, provided that these data are recorded in 3D; that is, they represent a sequence of 2D images as function of the illumination depth, angle or wavelength. Thus, by using QPI data, label-free tomographic methods that are based on linear scattering have received increased scientific interest^46,47 and they have recently been extended to strongly scattering specimens^48,49. We anticipate that the work presented here will establish the basis for a complementary type of investigation, in which the non-centrosymmetric contributions of the specimen are imaged tomographically with high specificity. Such information obtained from collagen fibres has been correlated with patient survival^50–52. In principle, HOT can be combined with a linear diffraction tomography system, such that the two types of data can be obtained simultaneously, complementing each other.

As a final thought, we would like to mention that the main procedure for our theoretical derivation and reconstruction can be generalized to higher-order nonlinearity, as long as the interaction is coherent. As an example, we show the tomography result of χ⁽³⁾ in Supplementary Section 5.

Methods

HOT optical set-up.

We constructed a HOT microscope to measure complex SHG fields (Fig. 1). The system uses a home-built mode-locked Yb:fibre laser⁵³ to generate a pulse train at 66.7 MHz, which is spectrally filtered and then fibre-amplified⁵⁴ under self-similar conditions⁵⁵. The amplified pulse spectrum spans 96 nm full-width at half-maximum, centered at 1,060 nm, with a roughly parabolic shape. After compression with a grating pair, the system delivers 35 fs pulses with 70 nJ energy. In practice, only a few nanojoules of pulse energy are required for data acquisition in the microscope; for example, to collect the SHG HOT image of murine skeletal muscle shown in Fig. 5, the average power of the NIR pulses at the input of the microscope (before generating a reference SHG pulse) was approximately 350 mW.

A 0.5 mm thick BBO frequency doubling crystal is placed at the output of the laser source to produce reference SHG pulses. The beam exiting the doubling crystal is directed to a long pass dichroic beam splitter (ThorLabs, DMLP650) to separate the remaining NIR beam (~140 mW) from the reference beam.

The fundamental beam transmitted through the dichroic beam splitter is directed through a polarizing beam splitter and a λ/2 waveplate (ThorLabs, AHWP05M-980) to provide linearly polarized light at a user-defined angle. The fundamental beam is then passed through an aspheric condenser lens with 0.5 NA (Newport, 5724-C-H) to focus the pulse train onto the specimen. The condenser is defocused to increase the spot size on the sample, thereby increasing the field of view while maintaining the diversity of spatial frequencies provided by the 0.5 NA lens. The SHG signal generated in the specimen is imaged at the camera in a 4f configuration with a ×100/0.9 NA air immersion objective lens (Mitutoyo M Plan Apo HR) and a 200 mm focal length tube lens (ThorLabs LB1945-A-ML). A shortpass filter (Semrock, Brightline Multiphoton 720/SP) is placed between the objective lens and the tube lens (in the infinity space) to block residual fundamental light. Images are collected with a scientific complementary metal–oxide–semiconductor camera (Andor Neo 5.5). The field of view at the specimen is approximately 60 × 53 μm².

The reference beam is passed through a 4f telescope to image the surface of a kinematic mirror to the camera sensor. This allows the tilt angle of the reference pulse train relative to the signal pulse train to be adjusted with little to no translation of the beam on the camera, thereby permitting adjustment of the fringe density in the interferometric SHG images without losing spatial overlap on the camera sensor. The second lens of the telescope used for the reference pulse train is the same tube lens used by the signal pulse train, while the first lens is a 75 mm focal length achromatic lens (ThorLabs AC254-075-A-ML).

A non-polarizing beam splitter (Newport 05BC17MB.2) is placed in the infinity space of the microscope to combine the SHG signal from the specimen with the reference SHG pulses. The non-polarizing beam slitter is placed between the two lenses used for image relay, and after the shortpass filter mentioned above. A wire-grid polarizer (VersaLight) is placed at the output of the non-polarizing beam splitter to pass light from both the signal and reference pulses that is polarized in the same direction, ensuring interference on the camera. An interference filter (Chroma ET535/70m) is placed after the polarizer. In total, there are four optics placed in the infinity space: the short pass filter, the non-polarizing beam splitter, the wire-grid polarizer, and the interference filter.

HOT data were collected by recording interferograms while the sample was scanned axially with a motorized stage (Applied Scientific Instruments, LS50A). Wide-field SHG images were collected for comparison by blocking the reference pulse train and scanning the specimen axially. For both the HOT and wide-field SHG measurements, the axial scanning step size was 0.2 μm. During the measurement, the holograms displayed observable fringes with stable fringe visibility between 0.5 and 0.6 across all frames.

Tomogram reconstruction.

The 3D HOT reconstruction was performed in MATLAB. At the start of this procedure, the complex SHG field was retrieved from the 2D holograms at each depth position such that a 3D SHG field stack was obtained. This approach is based on the principles of off-axis holography³⁸ and is described in detail in Supplementary Section 3. Given the a priori information about our optical system (that is, the illumination bandwidth, the numerical apertures of the condenser and objective, and the voxel size), a normalized 3D transfer function (H(k_⊥,k_z)) was digitally generated using equation (4b). The condenser and objective apertures were modelled as 2D uniform disk functions. After the construction of the effective transfer function, a HOT tomogram can be reconstructed through a Tikhonov-regularized deconvolution

$${\chi }^{(2)}\left(k_{\perp },k_z\right)=\frac{H\left(k_{\perp },k_z\right)}{H^2\left(k_{\perp },k_z\right)+\epsilon }{U}_{\text{SHG}}^{2{\omega }_0}\left(k_{\perp },k_z\right),$$ (5)

where $U_{\text{SHG}}^{2{\omega }_0}\left(k_{\perp },k_z\right)$ is the 3D Fourier transform of the SHG field and the regularization factor (ε) was set as 8 × 10⁻⁴ to suppress noise, mainly caused by the linear scattering of the SHG field. The reconstructed nonlinear susceptibility was eventually obtained by performing a 3D inverse Fourier transform of the deconvolved susceptibility spatial frequency spectrum. In addition, a spatial high-pass filter (k_⊥ > 0.4 rad μm^–1, or an effective NA of ~0.02 for the transverse spatial frequency cutoff) was applied to remove homogeneous features and a 3D Gaussian filter (σ = 0.1, kernel size = 3 pixels) was used to further reduce background noise. With an Intel Core i9–9900K CPU and 64 GB RAM, the deconvolution process was completed in 5.7 s. The 3D rendering is conducted in Amira or Volume Viewer (an ImageJ plugin) with customized settings. Due to low-amplitude SHG signal in the background, we only display the amplitude of the reconstruction.