Abstract
COVID-19 is a respiratory disease that, as of July 15th, 2021, has infected more than 187 million people worldwide and is responsible for more than 4 million deaths. An accurate diagnosis of COVID-19 is essential for the treatment and control of the disease. The use of computed tomography (CT) has shown to be promising for evaluating patients suspected of COVID-19 infection. The analysis of a CT examination is complex, and requires attention from a specialist. This paper presents a methodology for detecting COVID-19 from CT images. We first propose a convolutional neural network architecture to extract features from CT images, and then optimize the hyperparameters of the network using a tree Parzen estimator to choose the best parameters. Following this, we apply a selection of features using a genetic algorithm. Finally, classification is performed using four classifiers with different approaches. The proposed methodology achieved an accuracy of 0.997, a kappa index of 0.995, an AUROC of 0.997, and an AUPRC of 0.997 on the SARS-CoV-2 CT-Scan dataset, and an accuracy of 0.987, a kappa index of 0.975, an AUROC of 0.989, and an AUPRC of 0.987 on the COVID-CT dataset, using our CNN after optimization of the hyperparameters, the selection of features and the multi-layer perceptron classifier. Compared with pretrained CNNs and related state-of-the-art works, the results achieved by the proposed methodology were superior. Our results show that the proposed method can assist specialists in screening and can aid in diagnosing patients with suspected COVID-19.
Keywords: COVID-19, Classification, Deep learning, Parameter optimization, Genetic algorithm
1. Introduction
COVID-19 is a disease caused by Severe Acute Respiratory Syndrome 2 (SARSCoV-2) [1]. As of July 15th, 2021, COVID-19 has infected around 187 million people worldwide, and has been responsible for about 4 million deaths [2]. Early diagnosis of COVID-19 is important for the treatment and control of the disease. Real-time polymerase chain reaction (RT-PCR) or imaging exams such as chest X-ray and computerized chest tomography (CT) examination have been shown to be feasible alternatives for the first diagnosis of COVID-19 [3]. Studies have reported that X-ray and CT scans show changes before the onset of COVID-19 symptoms for some patients [[4], [5], [6]]. In particular, chest CT exams have given fast and efficient results, and show typical radiographic characteristics for patients infected with COVID-19 [[7], [8], [9], [10]].
However, due to the rapid increases in the number of patients with COVID-19, overloading of the capacity of public health services may result in a shortage of doctors and radiologists to analyze CT images. In this context, computer-aided diagnostic (CAD) systems can offer an alternative to assist the specialist in medical diagnosis. These systems use computational techniques for image processing and analysis, thus providing a second opinion to the doctor, and are especially important in cases where diagnosis is challenging for the human eye [[11], [12], [13]].
Recently, deep learning methods have shown promise in the development of CAD systems [14,15]. Convolutional neural networks (CNNs), which are deep learning techniques, can automatically interpret CT images and predict whether a patient is positive for COVID-19. Although CNN architectures perform very well in image classification, the development of a CAD system using a CNN requires large datasets and high processing power in order to give good results.
In this work, we propose the use of a relatively simple CNN architecture for image characterization that requires low processing power. We then use a genetic algorithm to select the set of features that best represents the images, and classification is performed using four classifiers with different approaches that are commonly used in CAD systems. Finally, we evaluate our method on two public image databases. We believe that this work contributes to the fields of medicine and computing in the following respects:
-
1.
In the field of medicine, we propose an efficient, low-cost method that can be applied in real clinical environments to aid in the diagnosis and screening of patients with COVID-19;
-
2.In the field of computing, and specifically in the context of methods for COVID-19:
-
●We propose a relatively simple and robust CNN architecture;
-
●We use efficient techniques to optimize the hyperparameters of the architecture; and,
-
●We construct a genetic algorithm (GA) to select the best attributes to classify CT scans into COVID-19 and Non-COVID-19 images.
-
●
The paper is organized as follows: in Section 2, related work is discussed; in Section 3, we present the proposed methodology; the results are presented and discussed in Sections 4, 5, respectively; and in Section 6, we present the conclusions and suggest future work.
2. Background and related work
COVID-19 is a respiratory disease, the first case of which was detected in Wuhan (in the Hubei province of China) and described as a case of pneumonia [2]. Later, the virus was named Severe Acute Respiratory Syndrome Coronavirus 2 (SARS-CoV-2), and the disease caused by this virus was called COVID-19. On March 11th, 2020, the World Health Organization (WHO) declared COVID-19 a pandemic [16]. COVID-19 can be transmitted from person to person, and this poses the main challenge in terms of controlling its transmission and obtaining an early, quick, and accurate diagnosis [17]. Chest X-Ray and CT scans have been the two main types of images used for the classification and diagnosis of this disease [4,18]. Since the focus of this work is on the use of CT images for the diagnosis of COVID-19, this section reviews the existing literature on the diagnosis of COVID-19 using CT images.
The use of deep learning techniques for the detection of COVID-19 has recently become a trending topic, and has attracted a lot of attention. Chaudhary and Pachori [17] used subband images (SBIs) to train several pre-trained CNN models using a transfer learning approach. Various classifiers were used to differentiate COVID-19 from other viral and bacterial types of pneumonia and healthy individuals. Their methodology achieved an accuracy of 650.976, a precision of 0.970, a sensitivity of 0.970, a specificity of 0.965, an F-score of 0.970, and an AUC of 0.980. Wang et al. [19] proposed the use of a redesigned COVID-Net architecture for the diagnosis of COVID-19. Their methodology obtained an accuracy, F-score, recall, precision, and AUC of 0.908, 0.908, 0.858, 0.957, and 0.962, respectively, for the SARS-CoV-2 CT scan dataset, and an accuracy, F-score, recall, precision, and AUC of 0.786, 0.788, 0.797, 0.780 and 0.853, respectively, on the COVID-CT dataset.
Kaur et al. [20] proposed a system based on deep features extracted from the MobileNetv2 architecture and a parameter-free BAT (PF-BAT)-optimized fuzzy K-nearest neighbor (PF–FKNN) classifier. Their methodology obtained an accuracy of 0.993, a precision of 0.992, a recall of 0.996, an F-score of 0.994, and an AUC of 0.995. Sen et al. [21] proposed a CNN architecture to extract the characteristics of the images, and then carried out feature selection in two stages. In the first stage, they applied a guided feature selection methodology that employed two filter methods, mutual information (MI) and Relief-F, for the initial screening of the characteristics obtained from the CNN model. In the second stage, the dragonfly algorithm (DA) was used to select the most relevant characteristics. Their methodology achieved an accuracy of 0.983 on the SARSCoV-2 CT scan dataset and 0.900 on the COVID-CT dataset.
Carvalho et al. [22] used a LeNet-5 architecture to extract the features from CT images, and the classification was carried out by XGBoost. This methodology obtained an accuracy of 0.950, a recall of 0.950, a precision of 0.949, an F-score of 0.950, an AUC of 0.950, and a kappa index of 0.900. The same authors [14] developed a pre-processing step for images using histogram equalization and CLAHE, and used a basic CNN to extract the features from the CT scans. Classification was then performed using several classifiers. The results showed an accuracy of 0.978, a recall of 0.977, a precision of 0.979, an F-score of 0.978, an AUC of 0.977, and a kappa index of 0.957.
Gifani et al. [23] proposed the use of 15 pre-trained CNN architectures. To improve the performance of their approach, they developed a method that selected a set of architectures based on voting by the majority of the best combination of results. This approach obtained an accuracy of 0.850, a recall of 0.854, and a precision of 0.857. He et al. [24] proposed a method called Self-Trans that combined contrasting self-supervised learning with transference learning to pre-train networks. This scheme obtained an F-score of 0.850 and an AUC of 0.940 for the diagnosis of COVID-19.
Chen et al. [10] adopted a prototype network for the diagnosis of COVID-19 that was pre-trained using a momentum contrasting learning method [25]. They obtained values for the accuracy, precision, recall, and AUC of 0.870, 0.885, 0.874, and 0.932, respectively. Jaiswal et al. [26] used learning transfer with a pre-trained DeseNet201 network on the ImageNet [27] dataset to diagnose COVID-19, achieving an accuracy of 0.962, a precision of 0.962, a recall of 0.962, an F-score of 0.962, and a specificity of 0.962. Hou et al. [28] proposed the use of a CNN architecture with peripheral recognition enhanced with contrasting representation for the diagnosis of COVID-19. This scheme achieved values for the accuracy, sensitivity, specificity, and AUC of 0.981, 0.977, 0.984, and 0.992, respectively. Loey et al. [29] used classical data augmentation techniques in conjunction with a conditional generative adversarial network (CGAN) based on a deep transfer learning model to diagnose COVID-19, obtaining an accuracy of 0.829, a sensitivity of 0.776, and a specificity of 0.876.
The medical imaging data sets used in the studies described above were SARS-CoV-2 CT-Scan [17,20,26], COVID-CT [10,14,[22], [23], [24],28,29], SARS-CoV-2 CT-Scan and COVID-CT [19,21]. These sets of images are too small to train very deep CNN architectures, and lead to overfitting. To alleviate this problem, some authors have used pre-trained CNN architectures on the ImageNet dataset [17,23,26] and others have used data augmentation [29]. Some attempts have been made to explore the potential of contrasting learning [10,19,24]. In addition, CNNs have been used to extract convolutional features [14,[20], [21], [22]], and have yielded very promising results.
From the discussion above on prior research in this area, it is clear that many researchers have been striving to develop automatic diagnostic methods for COVID-19. Although these approaches have made significant contributions to the diagnosis of COVID-19, it can be seen that methodologies based on deep CNNs are slow, and that some of the methods have relatively low precision in terms of the diagnosis of COVID-19. In our work, we explore the use of a simple CNN architecture to extract the convolutional features. We also apply an additional step to optimize the CNN hyperparameters using the tree Parzen estimator (TPE) and the selection of characteristics using a GA. In particular, we have approached this as an auxiliary learning task that can effectively improve the performance of the COVID-19 rating of normal people.
3. Methodology
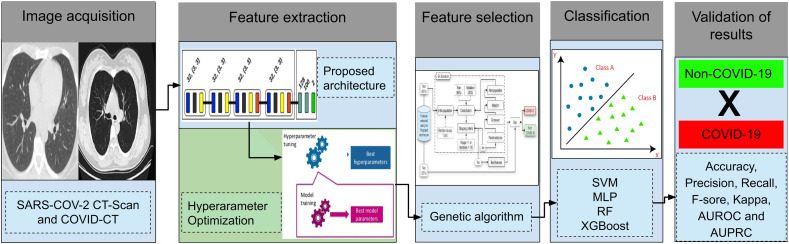
To enable a clearer understanding of the proposed methodology, Fig. 1 illustrates the five steps followed in our approach, as follows: (i) image acquisition; (ii) feature extraction, which is divided into two parts: (a) using the proposed CNN architecture; and (b) using the optimization of hyperparameters; (iii) feature selection using GA; (iv) the classification of images, using four classifiers with different approaches; and (v) the validation of results.
Fig. 1.
Proposed methodology.
3.1. Image acquisition
To evaluate and validate the proposed method, we used two public CT image datasets, SARS-CoV-2 CT-Scan [30] and COVID-CT [31].
-
●
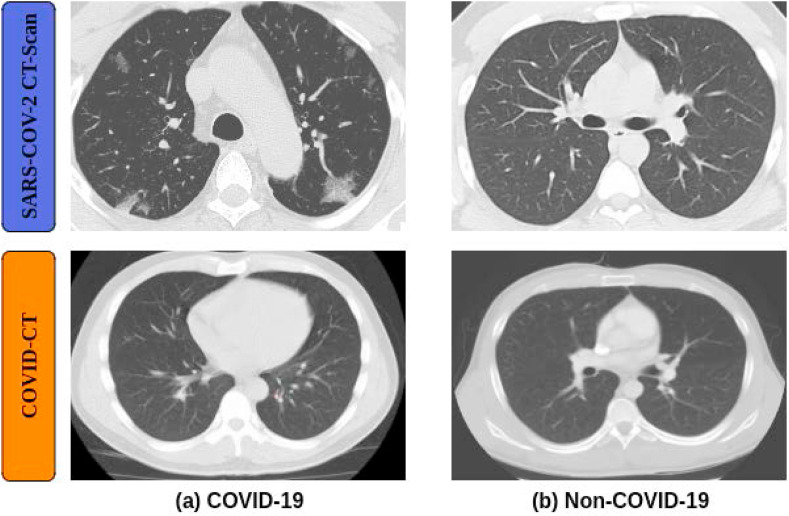
SARS-COV-2 CT-Scan [30] is a publicly available set of 2D CT images. It contains 2,482 CT images, 1,252 of which are positive CT scans for SARS-CoV-2 infection (COVID-19), and 1,230 are CT scans of patients that were not infected with SARS-CoV-2 (Non-COVID-19). The sizes of the images vary from 119 × 104 to 416 × 512. Fig. 2 shows examples of images from this dataset.
-
●
COVID-CT [31] is a publicly available set of 2D CT images for the binary classification of COVID-19. The set consists of 708 CT images, of which 312 show COVID-19 cases and 396 Non-COVID-19 cases. The resolution of these images ranges from 102 × 137 to 1853 × 1485. Fig. 2 shows examples of images from this dataset.
Fig. 2.
Example images from two different datasets, for (a) COVID-19 and (b) Non-COVID-19 patients.
Although CT images are normally in DICOM format, the images in the two databases used here are in PNG format. At the pre-processing stage, we resized the images to 224 × 224 in the axial plane, which was the input size for the proposed CNN architecture, and the images were then normalized to between 0 and 1, to provide better stability for the CNN model [17].
3.2. Feature extraction
In this section, we introduce the procedures used to build the proposed architecture and carry out hyperparameter optimization, with the aim of achieving better performance.
3.2.1. Proposed architecture
Several CNN architectures are already established in the literature that were designed to handle numerous different classes [32]. However, these architectures were designed to be robust when trained on large datasets, and when trained on smaller datasets, they tend towards overfitting. Since the image datasets contained 3,190 images, we decided to create a CNN architecture from scratch in order to achieve high accuracy, to avoid overfitting of the CNN architecture and to create a less complex architecture that required less hardware.
CNN is a neural network that implements several distinct layers, the main ones being convolutional, pooling, and fully connected layers [14,22]. The convolutional layer has the function of extracting attributes from the input data, composed of several filters followed by a non-linear activation function. The pooling layer is responsible for reducing the dimensionality of the resulting volume after the convolutional layers, helping to make the representation invariant to small translations at the entrance. Finally, the fully connected layer is responsible for propagating the signal through point-to-point multiplication and an activation function.
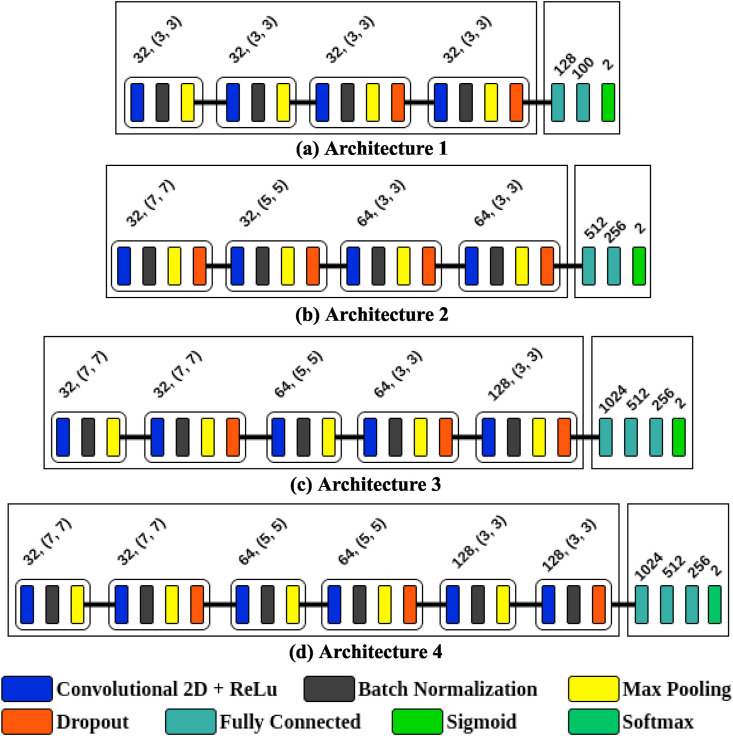
Initially, four CNN architectures were implemented. Fig. 3 shows the convolutional layers that were used to extract features and the fully connected layers with the final activation function used for classification. The architectures shown in Fig. 3(a) and (b) have four convolutional layers in the backbone, where as those in Fig. 3(c) and (d) have five and six convolutional layers, respectively, in the backbone. In addition to the standard layers of a CNN, batch normalization, regularization, and dropout operations were applied to reduce overfitting. A rectified linear unit (ReLu) was used as an activation function and a maximum function for pooling operations. To calculate the probability of data belonging to a particular class after the fully connected layers, the architectures presented in Fig. 3(a), (b), and (c) use a sigmoid function, while in the architecture presented in Fig. 3(d), this is changed to a softmax function.
Fig. 3.
The four proposed CNN architectures. Architectures (a) and (b) have four convolutional layers in the backbone, whereas architectures (c) and (d) have five and six convolutional layers, respectively.
To choose the best architecture from these four schemes, we randomly split the features into training (80%) and test (20%) sets. It is important to note that the same image sets defined for training and testing were used in all the experiments, meaning that the image set used for testing was not known to the model. The set of training images was divided into two further sets of 90%, which was used to train the architectures, and 10% as a validation set. After training each epoch, the validation set was used to evaluate each architecture. The ultimate goal was to achieve an architecture that achieved higher accuracy while avoiding overfitting. The architecture most likely to yield these results would be the one with the smallest oscillations in the accuracy.
After evaluating the four proposed architectures (Fig. 3), we found that the best results were yielded by Architecture 1. We believe this was due to the properties of the images, since they had a resolution of only 8 bits per pixel and varying dimensions. When converted to network input standards, they provided the best properties.
In addition, our network has low complexity, as it contains only a few layers and consequently requires low processing power.
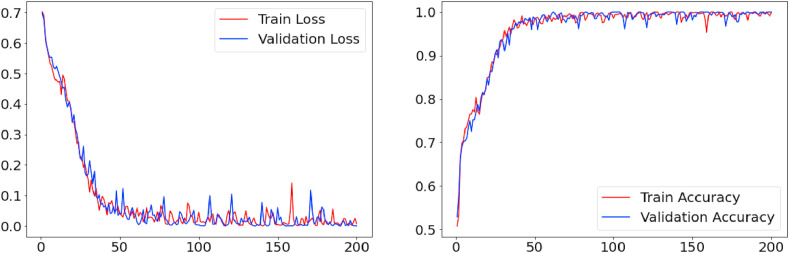
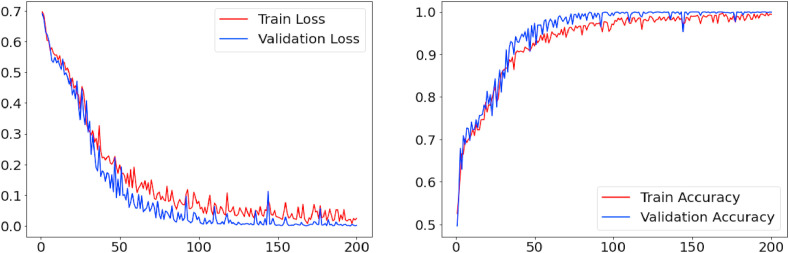
Fig. 4 presents the learning curve for the best alternative (Architecture 1) over 200 training epochs. We can observe that as the number of training epochs increases, the accuracy tends to improve and the loss tends to decrease. For 200 epochs, the proposed architecture shows a stable learning curve, with a training accuracy of 0.985 and a loss of 0.014, a validation accuracy of 0.988, and a validation loss of 0.008. Architecture 1 is composed of an input layer, four convolutional layers with 32 filters and a 3 × 3 kernel, four pooling layers with step 2; a batch normalization layer in each convolutional block, a 30% dropout layer in the third convolutional block and a 20% dropout layer in the fourth convolutional block, and two fully connected layers, the first of which has 128 neurons and the second 100 neurons, where the latter is used to extract the features of each image.
Fig. 4.
Model evaluation for the proposed CNN architecture (architecture 1).
3.2.2. Hyperarameter optimization
CNN architectures are sensitive to the choice of specific hyperparameters for a given problem [33]. In this work, a hyperparameter optimization step was applied to estimate the CNN parameters for the problem in an automated and efficient way. We used the TPE [34] as an evolution mechanism and to select the parameters. When optimizing a hyperparameter x, TPE creates two hierarchical processes, l(x) and g(x), for all target variables in the generative models. Process modeling occurs when the objective function is defined in the range specified by y*, as shown in Equation (1).
| (1) |
The processes l(x) and g(x) are adjusted using Parzen's univariate estimators [34]. Based on these two distributions, closed terms can be optimized according to the expected improvement (EI) [34]. In this work, an EI acquisition function was used [35]. The search space for the CNN hyperparameters used at the optimization stage is presented in Table 1 .
Table 1.
Search space for the proposed CNN hyperparameters.
| Parameters | Value Range |
|---|---|
| Learning rate | [0.1, 0.01, 0.001] |
| Decay rate | [0, 1] |
| First fully connected layer | [50, 200] |
| Second fully connected layer | [50, 200] |
| First Dropout | [0.1, 0.5] |
| Second Dropout | [0.1, 0.5] |
Within the search space shown in Table 1, the CNN was trained for 200 epochs for each hyperparameter configuration, which was established in Hyperopt. The hyperparameters selected for the proposed CNN architecture are shown in Table 2 , and the learning curve for the selected hyperparameters is shown in Fig. 5.
Table 2.
Selected hyperparameters.
| Parameters | Value |
|---|---|
| Learning rate | 0.01 |
| Decay rate | 0.7 |
| First Fully Connected Layer | 72 |
| Second Fully Connected Layer | 120 |
| First Dropout | 0.33 |
| Second Dropout | 0.27 |
Fig. 5.
Learning curves for the CNN architecture with the selected hyperparameters.
Over 200 training epochs, the architecture yielded a training accuracy of 0.998, a training loss of 0.008, a validation accuracy of 0.999, and a validation loss of 0.001. For the evaluation data without parameter optimization (Fig. 4), we can see an improvement in the model's performance evaluation parameters.
As shown in Table 2, the network was changed as follows: the third and fourth block dropout layers were set to values of 33% (previously 30%) and 27% (previously 20%), respectively; the first fully connected layer contained 72 neurons (previously 128), and the second contained 120 neurons (previously 100). As we used the last fully connected layer to extract the features, this architectural configuration allowed us to extract a set of 120 features for each CT image.
Second Bergstra et al. [34], optimization methods based on Bayesian models build a probability model of the objective function to propose smarter choices for the next set of hyperparameters to be evaluated. Based on this, we use TPE, an algorithm that uses Bayesian reasoning, to build the substitute model and select the next hyperparameters using EI. TPE recommends the best candidate hyperparameters for evaluation, thereby improving the objective function score much faster than with a random or grid search, requiring fewer overall objective function evaluations, and giving a shorter execution time to find the best hyperparameters. In addition, TPE is more efficient at finding the best hyperparameters for a machine learning model than a random or gridded search [36].
3.2.3. Platforms and hardware used
The CNN architectures were implemented using Tensorflow [37] and Keras [38] in a Python environment. The experiments were run in the Google Colab [39] environment, which offers 12.72 GB of RAM and 358.27 GB of hard disk space at each runtime of 12 h, after which the runtime is reset and the user must establish a new connection. The final model used to extract the features (Architecture 1) was achieved by training the network with the following parameters: 200 epochs, the Adam training algorithm [40], a decay rate of 0.9, a batch size of 32, and a learning rate of 10−3.
3.3. Feature selection
CNN models tend to extract and select only the most representative features of the input image. However, the number of features extracted by the CNNs is not always essential, since the number of features is directly related to the architecture used, especially when few images are available for training. The deeper the network, the more features it will extract. Based on this, we consider the possibility that the features extracted by the CNN are not the most significant. Furthermore, working with a reduced set of features can offer benefits in several respects, such as lower processing times and a reduction in the number of correlated, irrelevant, or noisy variables.
To address this issue, we use a GA [41] to select the set with the best features extracted with the proposed architecture. We chose to use a GA because the evolutionary process on which it is based can provide features that represent the best solution for a particular dataset, and consequently give better results. The GA used in our method is detailed below. The aim is to find the best set of features to classify CT images as COVID-19 and Non-COVID-19.
-
●
Features are first extracted for each input image using the proposed model;
-
●
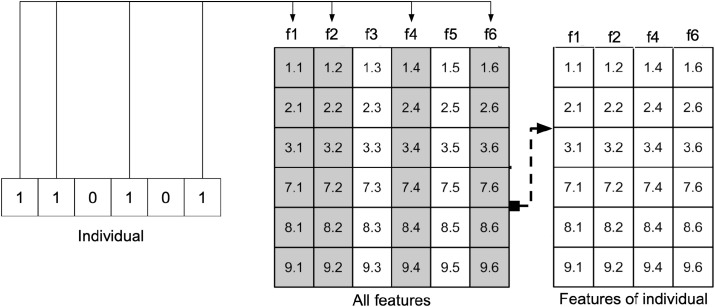
The initial population is then created with n individuals (in our tests, n = 50). Each individual is represented by values of zero or one, indicating the absence or presence of a given attribute in the individual. Individual values are initialized randomly. The size of each individual corresponds to the total number of extracted features. Fig. 6 shows an example of one individual.
-
●
Classification is performed using a multi-layer perceptron (MLP) with all the default parameters [42]. To assess the aptitude of each individual in a given generation, we calculate the fitness based on the kappa index [43]; in other words, the individual with the best fitness will always be the one with the highest kappa index value. The fitness calculation is shown in Equation (2). This metric is calculated based on a confusion matrix made up of the number of true positives (TP), false positives (FP), true negatives (TN), and false negatives (FN).
| (2) |
where,
| (3) |
and
| (4) |
-
●
To select the pairs of parents who will mate to generate two new children, the roulette method [44] is used to select individuals with the highest aptitude. A one-point crossover [45] technique is used, in which one crossover point is chosen at random for each pair of parents to be mated. The first offspring generated from this cross is made up of the genes to the right of the first parent's crossover point and to the left of the second parent's crossover point, and vice versa for the second child. Equation (5) is used to calculate the crossing:
| (5) |
where x is the vector of child elements; i denotes the index of the corresponding position between parents and children; t represents the size of the parent; γ denotes a randomly chosen one-point crossover less than t; and P1 and P2 represent the element vectors for the parents.
-
●
A bitwise mutation [44] was used, which is the most common mutation operator in binary encodings. This approach considers each gene separately, allowing each bit to be subjected to a small probability of being inverted. The new population is created using a concept known as elitism, in which some of the best individuals of the past generation are taken to generate the best children. The proportion chosen was 20% elitism and 80% new children born. The mutation rate used in our method was 5%. The evolutionary cycle was repeated until the stopping criterion was reached.
Fig. 6.
Example of the creation of an individual.
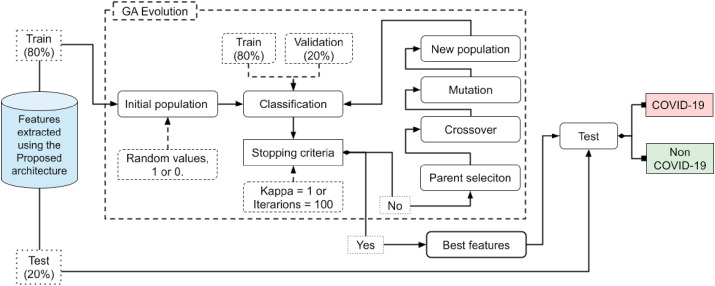
Fig. 7 presents a summary of the steps applied by the GA in our method. It can be seen that after the stopping criterion is reached, following the selection criteria applied in the GA, the best feature set is found. The number of features selected by the GA is independent, and can vary depending on the data analyzed (Table 6). When the set of best features has been selected, the final classification is then made. It is not necessary to retrain the network, since the task of the GA is only to select the most representative set of features for the data sample, and this set will then be passed as input to the classifiers.
Fig. 7.
Flowchart of the genetic algorithm used for feature selection.
Table 6.
Number of features selected by GA for each architecture.
| Dataset | Description |
Extracted features |
Selected features |
|---|---|---|---|
| Without hyperparameter optimization | 100 | 47 | |
| SARS-COV-2 CT-Scan |
With hyperparameter optimization | 120 | 53 |
| Without hyperparameter optimization | 100 | 68 | |
| COVID-CT | With hyperparameter optimization | 120 | 76 |
3.4. Classification
Classification is a process of categorization based on the knowledge acquired in a dataset that contains observations for which the category is known. In this case, classification consisted of categorizing the CT images as COVID-19 and Non-COVID-19 cases using several classifiers: a random forest approach [46], a multi-layer perceptron (MLP) [42] and a support vector machine (SVM) [47] (available in the sci-kitlearn library), and an eXtreme Gradient Boosting (XGBoost) algorithm [48]. Table 3 presents a summary of the parameters used for each classifier; in each case, the default parameters were used.
Table 3.
Summary of parameters used in each classifier.
| Classifier | Parameters |
|---|---|
| Random forest | bag size percent = 100, batch size = 100, number of execution slots = 1, max depth = 0 (unlimited), number of randomly chosen attributes = 0, number of iterations to be performed = 100, minimum number of instances per leaf = 1.0, minimum variance for split = 0.001, random number seed to be used = 1 |
| MLP | learningrate = 0.3, momentum = 0.2, number of epochs used for training = 500, validation set size = 0 (the network will by training for the specified number of epochs), seed = 0, validation threshold = 20, hidden layers = ((number of attributes + classes)/2) |
| SVM | C = 1.0, kernel = radial basis function (RBF), degree = 3, gamma = scale, shrinking = true, probability = false, tol = 0.001, cache size = 200, max iter = −1, random state = none |
| XGBoost | max depth = 7, learning rate = 0.1, ite = 1000, gama = 0, max delta step = 1, objective = “multi:softmax” |
3.5. Validation of results
We validated the results based on four commonly used statistical evaluation metrics in the literature: the accuracy (A), recall (R), precision (P), and F-score (F), as shown in Equations (6), (7), (8), (9), respectively. These metrics are calculated based on a confusion matrix containing the number of true positives (TP), false positives, (FP), true negatives (TN) and false negatives (FN).
| (6) |
| (7) |
| (8) |
| (9) |
The kappa index (K) measures the agreement between the results from the proposed methodology and the ground truth labels assigned by pathologists [43]. The area under the receiver operating characteristic (AUROC) curve measures how well the classifier can distinguish between the classes based on the true positive rate versus the false positive rate [49]. The area under the precision-recall curve (AUPRC) measures the number of true positives divided by the sum of the true positives and false positives [50]. The closer to one the value of these validation metrics, the more effectively the classifier can distinguish between COVID-19 and Non-COVID-19 images.
4. Experiments and results
To demonstrate the efficiency of the proposed methodology, we performed experiments on the test set containing 20% of the images (Section 3.2.1). The features were first extracted with the proposed CNN architecture, and classification was then carried out using the algorithms described in Section 3.4. Table 4 presents the results.
Table 4.
Results of the proposed CNN without hyperparameter optimization.
| Classifier | A | R | P | F | K | AUROC | AUPRC |
|---|---|---|---|---|---|---|---|
| SARS-COV-2 CT-Scan Dataset | |||||||
| Random forest | 0.979 | 0.980 | 0.979 | 0.979 | 0.959 | 0.910 | 0.913 |
| MLP | 0.981 | 0.981 | 0.982 | 0.981 | 0.963 | 0.935 | 0.944 |
| SVM | 0.979 | 0.979 | 0.980 | 0.979 | 0,959 | 0.908 | 0.911 |
| XGBoost | 0.985 | 0.985 | 0.985 | 0.985 | 0.971 | 0.937 | 0.958 |
| COVID-CT Dataset | |||||||
| Random forest | 0.917 | 0.916 | 0.912 | 0.914 | 0.829 | 0.906 | 0.904 |
| MLP | 0.905 | 0.902 | 0.910 | 0.904 | 0.810 | 0.899 | 0.879 |
| SVM | 0.905 | 0.906 | 0.907 | 0.904 | 0.809 | 0.900 | 0.889 |
| XGBoost | 0.917 | 0.917 | 0.917 | 0.917 | 0.835 | 0.908 | 0.905 |
Values in bold indicate the best results found for all classifiers.
As shown in Table 4, the results obtained by the classifiers in the two datasets were satisfactory for the categorization of CT scans into COVID-19 and Non-COVID-19 images. XGBoost performed best on both datasets, because as it gives good results for large feature sets. Overall, the results showed that the proposed CNN could extract robust features, allowing the classifiers to achieve promising performance in terms of the categorization of CT images, since all of the classifiers yielded comparable results.
CNNs are sensitive to the choice of specific hyperparameters for a problem. To address this issue, we applied a step in which the best hyperparameters for the proposed architecture were determined (as described in Section 3.2.2). When the proposed CNN architecture hyperparameters had been optimized, the features were extracted from the CT images. The results from the optimized network are presented in Table 5 .
Table 5.
Results from the proposed CNN with hyperparameter optimization.
| Classifier | A | R | P | F | K | AUROC | AUPRC |
|---|---|---|---|---|---|---|---|
| SARS-COV-2 CT-Scan Dataset | |||||||
| Random forest | 0.989 | 0.989 | 0.989 | 0.989 | 0.979 | 0.950 | 0.962 |
| MLP | 0.993 | 0.994 | 0.994 | 0.993 | 0.988 | 0.974 | 0.970 |
| SVM | 0.989 | 0.990 | 0.990 | 0.989 | 0.980 | 0.946 | 0.951 |
| XGBoost | 0.990 | 0.990 | 0.991 | 0.990 | 0.981 | 0.966 | 0.962 |
| COVID-CT Dataset | |||||||
| Random forest | 0.930 | 0.932 | 0.932 | 0.930 | 0.860 | 0.928 | 0.917 |
| MLP | 0.953 | 0.948 | 0.948 | 0.948 | 0.897 | 0.932 | 0.926 |
| SVM | 0.930 | 0.932 | 0.932 | 0.927 | 0.855 | 0.927 | 0.915 |
| XGBoost | 0.929 | 0.936 | 0.929 | 0.929 | 0.858 | 0.930 | 0.919 |
Values in bold indicate the best results for all classifiers.
From the results in Table 5, we observed that the optimization of CNNs hyperparameters provided more representative features for categorizing CT images into COVID-19 and Non-COVID-19 cases. The MLP classifier obtained the best results on both datasets. Furthermore, when we compare the results in Table 4 with those obtained after hyperparameter optimization, we notice that all of the classifiers achieved better results in the second case. If we consider the kappa index as the most important metric, the classifiers are shown to be able to categorize CT images very efficiently. These results demonstrate the effectiveness of optimizing the proposed CNN hyperparameters, as this gives features that allow for better discrimination between COVID-19 and Non-COVID-19 images.
The set of features extracted from the images must be representative in order to enable a useful classification, and must be sufficient to avoid causing errors in the classification step. In view of this, another important aspect of the proposed method is the selection of the most important features via a GA. Table 6 presents a summary of the experiments performed with feature selection.
We used a GA to carry out feature selection (Section 3.3) in the proposed architecture, both with and without hyperparameter optimization. We present the results for both architectures here to demonstrate that our feature selection method with a GA is efficient. As shown in Table 6, the GA selects different numbers of features for each experiment; this is as expected, since a specific solution will be found for each dataset. After feature selection, we carried out data classification again, using only the MLP classifier, since this was the algorithm that yielded the best results in our experiments (Table 5). Table 7 presents the results obtained with the feature selection by GA.
Table 7 shows that feature selection using GA performed best in terms of categorizing CT scans into COVID-19 and Non-COVID-19 images. A comparison of the kappa index obtained with the MLP classifier for the SARS-COV-2 CT-Scan dataset in Table 4 (without hyperparameter optimization) with those obtained in Table 7 shows that the selection of features yielded an improvement of 0.024, while on the COVID-CT dataset, the MLP obtained an improvement of 0.141 in the kappa index. When the values of the kappa index for the features obtained with the proposed architecture are compared with the results of hyperparameter optimization (Table 5), we see that feature selection (Table 7) gave an improvement in the kappa index of 0.007 on the SARS-COV-2 CT-Scan dataset and 0.078 on the COVID-CT dataset. We can therefore conclude that even with a smaller feature set, it is still possible to improve on the results obtained in all of our experiments with the proposed architectures.
Table 7.
Results using feature selection with a GA and the MLP classifier.
| Architecture | A | R | P | F | K | AUROC | AUPRC |
|---|---|---|---|---|---|---|---|
| SARS-COV-2 CT-Scan Dataset | |||||||
| Without optimization | 0.993 | 0.993 | 0.994 | 0.993 | 0.987 | 0.993 | 0.993 |
| With optimization | 0.997 | 0.997 | 0.998 | 0.997 | 0.995 | 0.997 | 0.997 |
| COVID-CT Dataset | |||||||
| Without optimization | 0.975 | 0.975 | 0.975 | 0.975 | 0.951 | 0.975 | 0.975 |
| With optimization | 0.987 | 0.989 | 0.986 | 0.987 | 0.975 | 0.989 | 0.987 |
Values in bold indicate the best results found, for all experiments.
Finally, to further evaluate the proposed method, we performed a new experiment in which we considered all images in the SARS-CoV-2 CT-Scan dataset (2,482 images) as a training set, and applied the final prediction model to the COVID-CT dataset (708 images). In this experiment, we applied the proposed architecture with hyperparameter optimization, with the best features selected by the AG that for this experiment were selected 64, using the MLP classifier. The results were encouraging: in this experiment, our method achieved an accuracy of 0.901, a recall of 0.901, a precision of 0.899, an F-score of 0.9, a kappa of 0.8, an AUROC of 0.901, and an AUPRC of 0.9. These values demonstrate the efficiency of the proposed method, since the test set was unknown to the constructed model.
4.1. Comparison with related techniques and works
In this section, we report the results of further experiments with the same datasets. We first compare the results achieved by the proposed model with those of other CNN models. We then carry out quantitative comparisons with existing works from the literature (Section 2), in order to provide a fair comparison and to allow our method to be reproduced in future work.
4.1.1. Classification using pre-trained CNNs
To test the robustness of our method, we performed tests with five different CNN architectures that are widely used for image problems, namely VGG16 and VGG19 [51], Xception [52], ResNet50 [53] and Inception-v4 [54]. Table 8 presents the results achieved by these models. We used only the MLP classifier for these experiments, as our best results were achieved with this algorithm.
Table 8.
Results using features extracted with pre-trained CNNs and an MLP classifier.
| Dataset | A | R | P | F | K | AUROC | AUPRC |
|---|---|---|---|---|---|---|---|
| VGG16 | |||||||
| SARS-COV-2 CT-Scan |
0.959 | 0.959 | 0.959 | 0.959 | 0.919 | 0,959 | 0,959 |
| COVID-CT | 0.877 | 0.876 | 0.874 | 0.875 | 0.750 | 0.876 | 0.874 |
| VGG19 | |||||||
| SARS-COV-2 CT-Scan |
0.965 | 0.965 | 0.966 | 0.966 | 0.932 | 0.966 | 0.965 |
| COVID-CT | 0.863 | 0.862 | 0.863 | 0.862 | 0.725 | 0.862 | 0.861 |
| Xception | |||||||
| SARS-COV-2 CT-Scan |
0.957 | 0.957 | 0.957 | 0.957 | 0.915 | 0.957 | 0.957 |
| COVID-CT | 0.870 | 0.870 | 0.871 | 0.870 | 0.741 | 0.870 | 0.870 |
| ResNet50 | |||||||
| SARS-COV-2 CT-Scan |
0.975 | 0.976 | 0.975 | 0.975 | 0.952 | 0.975 | 0.975 |
| COVID-CT | 0.823 | 0.820 | 0.822 | 0.821 | 0.642 | 0.820 | 0.821 |
| Inception-v4 | |||||||
| SARS-COV-2 CT-Scan |
0.949 | 0.950 | 0.950 | 0.949 | 0.900 | 0.950 | 0.949 |
| COVID-CT | 0.836 | 0.833 | 0.839 | 0.835 | 0.670 | 0.833 | 0.833 |
Values in bold indicate the best results for each architecture.
The results in Table 8 show that our method achieved promising performance. Our scheme achieved the highest accuracy on both datasets, meaning that it can be used to categorize CT images into COVID-19 and Non-COVID-19 cases more effectively than alternative methods. It should also be noted that the number of features extracted per image with the proposed CNN architecture was much lower than with the pre-trained CNN architectures. Furthermore, our architecture contained only a few layers, and this proved to be more efficient for the problem at hand. Finally, although pre-trained network methods are widely used for various data classification problems, the results are not always satisfactory for certain problems, and in view of this, several proposals for improvements have been presented. Without undermining the architectures presented in Table 8, we propose steps for optimizing architectures, hyperparameters and selecting the best features with the aim of achieving more efficient results for this particular problem.
4.1.2. Comparison with related works
Ensuring a fair comparison of results is very complex, since many factors can influence the reliability of comparison, such as the databases and techniques used. We summarize the results obtained from the proposed method with those of the approaches described in Section 2, in order to achieve an illustrative quantitative comparison. Table 9 presents the results obtained using alternative state-of-the-art schemes for the diagnosis of COVID-19 from CT images.
Table 9.
Comparison of results obtained with the proposed methodology and those of related works.
| Work | Dataset | A | P | F |
|---|---|---|---|---|
| He et al. [24] | COVID-CT | 0.850 | ||
| Chen et al. [10] | 0.870 | 0.885 | ||
| Carvalho et al. [22] | 0.950 | 0.949 | 0.950 | |
| Carvalho et al. [14] | 0.978 | 0.979 | 0.978 | |
| Gifani et al. [23] | 0.850 | 0.857 | ||
| Hou et al. [28] | 0.981 | |||
| Loey et al. [29] | 0.829 | |||
| Chaudhary and Pachori [17] | SARS-CoV-2 CT-Scan | 0.976 | 0.970 | 0.970 |
| Jaiswal et al. [26] | 0.962 | 0.962 | 0.962 | |
| Kaur et al. [20] | 0.993 | 0.992 | 0.994 | |
| Wang et al. [19] | SARS-CoV-2 CT-Scan | 0.908 | 0.957 | 0.908 |
| COVID-CT | 0.786 | 0.780 | 0.788 | |
| Sen et al. [21] | SARS-CoV-2 CT-Scan | 0.983 | 0.982 | 0.980 |
| COVID-CT | 0.900 | 0.935 | 0.885 | |
| Our work | SARS-CoV-2 CT-Scan | 0.997 | 0.998 | 0.997 |
| COVID-CT | 0.987 | 0.986 | 0.987 |
It can be seen from Table 9 that the proposed methodology achieved very promising results. On the SARS-CoV-2 CT-Scan dataset, the values for the accuracy of each scheme were as follows: Chaudhary and Pachori [17] obtained 0.993; Sen et al. [21] obtained 0.983; Wang et al. [19] obtained 0.908; Jia et al. [4] obtained 0.993; and Jaiswal et al. [26] obtained 0.962. On the COVID-CT dataset, the accuracy values were as follows: Sen et al. [21] obtained 0.900; Carvalho et al. [22], Carvalho et al. [14] and Gifani et al. [23] obtained 0.950, 0.978 and 0.850, respectively; Wang et al. [19] obtained 0.786; Chen et al. [10], Hou et al. [28] and Loey et al. [29] obtained 0.870, 0.981 and 0.829, respectively, and Kaur et al. [20] obtained 0.993. On the SARS-CoV-2 CT-Scan dataset, our approach obtained an accuracy of 0.997, which was better than the other reported works. On COVID-CT, our algorithm obtained an accuracy of 0.987, which again was higher than the other related works. To further evaluate the effectiveness of the proposed method, we performed an experiment using the SARS-CoV-2 CT-Scan dataset for training and COVID-CT for testing, which yielded an accuracy of 0.901. These results demonstrate the superiority of the proposed methodology.
5. Discussion
The proposed method used trainable features obtained with a CNN architecture to diagnose COVID-19 from CT images. Based on the results presented here, we can identify some advantages of our approach and other aspects that need to be investigated further.
5.1. Advances
-
1.
Optimization of the hyperparameters of the CNN produced better features, which improved the final results;
-
2.
The GA yielded an improvement in the results, in addition to achieving a significant reduction in the dimensionality in the feature files, and consequently making the classification process more agile;
-
3.
Our architecture is robust, efficient, and has low complexity, meaning that it requires less processing power than other traditional models;
-
4.
After the model had been constructed, the time required for characterization and classification of the test set was only 0.035 h with the MLP classifier;
-
5.
The proposed architecture provided robust features for the classification of CT scans into COVID-19 and Non-COVID-19 cases, and could be used as a diagnostic or screening aid for COVID-19.
5.2. Limitations
-
1
Since our method involves several optimizations (such as the choice of architecture, optimization of hyperparameters, and use of a GA to select the best features), it requires a relatively long time to construct the final model. On average, it took about: (i) 1.5 h to select the best architecture; (ii) 22.2 h for the hyperparameter optimization step; and (iii) 4 h for the selection of the best features;
-
2.
The proposed methodology was developed based on a dataset of 2D CT images, and would require modifications for application to 3D CT examinations.
6. Conclusion
The COVID-19 pandemic has plagued the world and has caused significant losses and difficulties at a global level. Furthermore, a great deal of concern has arisen due to the emergence of new variants. Thus, in this paper, we have proposed a method that is capable of diagnosing COVID-19 from CT images, using two public image datasets. Our method consists of a CNN architecture with hyperparameter optimization for feature extraction. A GA is employed to select important features. Classification is then performed using four algorithms with different approaches. Our methodology gave promising results, achieving a final accuracy of 98% on the two image databases used. We have also shown that a GA can provide a relatively small feature set and gives good results in terms of the metrics used. Our methodology was able to avoid the problem of overfitting, which is common for small databases, and outperformed pre-trained architectures and other state-of-the-art approaches. Our method can therefore be used as part of a computer-aided diagnostic system, and can serve as a second opinion for a specialist in diagnosing patients with COVID-19.
In future work, we intend to use other datasets of images to make our model more robust and generic; to apply other techniques, such as information gain, for feature selection; and to adapt our method for use directly with the volumes generated by CT exams.
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgment
The proposed method was supported by the following institutions: FAPEPI - www.fapepi.pi.gov.br (5492.UNI253.59248.15052018); CAPES - www.capes.gov.br and the CNPq - www.cnpq.br (435244/2018-3).
Biographies
Edson Damasceno Carvalho: master's degree student in Electrical Engineering from the Federal University of Piauí (UFPI). Graduated in Bachelor of Information Systems from the Federal University of Piauí (UFPI).
Flávio Henrique Duarte de Araújo: received a Ph.D. in Teleinformatics Engineering from the Federal University of Ceará, Brazil, in 2018. He is currently a professor at the Federal University of Piauí (UFPI).
Romuere Rodrigues Voloso e Silva: received a Ph.D. in Teleinformatics Engineering from the Federal University of Ceará, Brazil, in 2018. He is currently a professor at the Federal University of Piauí (UFPI).
Ricardo de Andrade Lira Rabelo: is a professor at the Federal University of Piauí (UFPI). He received the B.Sc. degree in computer science from the UFPI, Brazil, in 2005, and the Ph.D. degree in power systems from the University of Sao Paulo (USP), Brazil, in 2010. His research interests include smart grid, Internet of Things, intelligent systems, and power quality.
Antonio Oseas de Carvalho Filho: received a Ph.D. in Electrical Engineering at Federal University of Maranhão - Brazil in 2016. Currently, he is a professor at the Federal University of Piaui (UFPI). His research interests include medical image processing, machine learning and deep learning.
Footnotes
Supplementary data to this article can be found online at https://doi.org/10.1016/j.compbiomed.2021.104744.
Appendix A. Supplementary data
The following are the Supplementary data to this article:
References
- 1.A. E. Gorbalenya, S. C. Baker, R. S. Baric, R. J. de Groot, C. Drosten, A. A. Gulyaeva, B. L. Haagmans, C. Lauber, A. M. Leontovich, B. W. Neuman, D. Penzar, S. Perlman, L. L. Poon, D. Samborskiy, I. A. Sidorov, I. Sola, J. Ziebuhr, Severe acute respiratory syndrome-related coronavirus: the species and its viruses – a statement of the Coronavirus Study Group, bioRxiv doi:10.1101/2020.02.07.937862.
- 2.Organization W.H. Coronavirus disease (COVID-19) pandemic. 2021. https://www.who.int/emergencies/diseases/novel-coronavirus-2019 URL.
- 3.Bernheim A., Mei X., Huang M., Yang Y., Fayad Z.A., Zhang N., Diao K., Lin B., Zhu X., Li K., Li S., Shan H., Jacobi A., Chung M. Chest CT findings in coronavirus disease-19 (COVID-19): relationship to duration of infection. Radiology. 2020:200463. doi: 10.1148/radiol.2020200463. pMID: 32077789. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Jia G., Lam H.-K., Xu Y. Classification of COVID-19 chest X-Ray and CT images using a type of dynamic CNN modification method. Comput. Biol. Med. 2021;134:104425. doi: 10.1016/j.compbiomed.2021.104425. https://www.sciencedirect.com/science/article/pii/S0010482521002195 ISSN 0010-4825. URL. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Ozturk T., Talo M., Yildirim E.A., Baloglu U.B., Yildirim O., Rajendra Acharya U. Automated detection of COVID-19 cases using deep neural networks with X-ray images. Comput. Biol. Med. 2020;121:103792. doi: 10.1016/j.compbiomed.2020.103792. https://www.sciencedirect.com/science/article/pii/S0010482520301621 ISSN 0010-4825. URL. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Ucar F., Korkmaz D. COVIDiagnosis-Net: deep Bayes-SqueezeNet based diagnosis of the coronavirus disease 2019 (COVID-19) from X-ray images. Med. Hypotheses. 2020;140:109761. doi: 10.1016/j.mehy.2020.109761. https://www.sciencedirect.com/science/article/pii/S0306987720307702 ISSN 0306-9877. URL. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Bernheim A., Mei X., Huang M., Yang Y., Fayad Z.A., Zhang N., Diao K., Lin B., Zhu X., Li K., et al. Chest CT findings in coronavirus disease-19 (COVID-19): relationship to duration of infection. Radiology. 2020:200463. doi: 10.1148/radiol.2020200463. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Li Y., Xia L. Coronavirus disease 2019 (COVID-19): role of chest CT in diagnosis and management. Am. J. Roentgenol. 2020;214(6):1280–1286. doi: 10.2214/AJR.20.22954. [DOI] [PubMed] [Google Scholar]
- 9.Salehi S., Abedi A., Balakrishnan S., Gholamrezanezhad A. Coronavirus disease 2019 (COVID-19): a systematic review of imaging findings in 919 patients. Am. J. Roentgenol. 2020;215(1):87–93. doi: 10.2214/AJR.20.23034. [DOI] [PubMed] [Google Scholar]
- 10.Chen X., Yao L., Zhou T., Dong J., Zhang Y. Momentum contrastive learning for few-shot COVID-19 diagnosis from chest CT images. Pattern Recogn. 2021;113 doi: 10.1016/j.patcog.2021.107826. https://www.sciencedirect.com/science/article/pii/S0031320321000133 107826, ISSN 0031-3203. URL. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Carvalho E.D., Filho A.O., Silva R.R., Araújo F.H., Diniz J.O., Silva A.C., Paiva A.C., Gattass M. Breast cancer diagnosis from histopathological images using textural features and CBIR. Artif. Intell. Med. 2020;105:101845. doi: 10.1016/j.artmed.2020.101845. ISSN 0933-3657. [DOI] [PubMed] [Google Scholar]
- 12.de Carvalho Junior] A.S.V., Carvalho E.D., [de Carvalho Filho] A.O., [de Sousa] A.D., Silva] A.C. M. Gattass, Automatic methods for diagnosis of glaucoma using texture descriptors based on phylogenetic diversity. Comput. Electr. Eng. 2018;71:102–114. doi: 10.1016/j.compeleceng.2018.07.028. ISSN 0045-7906. [DOI] [Google Scholar]
- 13.Carvalho E.D., [de Carvalho Filho] A.O., [de Sousa] A.D., Silva A.C., Gattass M. Method of differentiation of benign and malignant masses in digital mammograms using texture analysis based on phylogenetic diversity. Comput. Electr. Eng. 2018;67:210–222. doi: 10.1016/j.compeleceng.2018.03.038. ISSN 0045-7906. [DOI] [Google Scholar]
- 14.Carvalho E.D., Carvalho E.D., de Carvalho Filho A.O., de Sousa A.D., de Andrade Lira Rabúlo R. IEEE 20th International Conference on Bioinformatics and Bioengineering. BIBE); 2020. COVID-19 diagnosis in CT images using CNN to extract features and multiple classifiers; pp. 425–431. 10.1109/BIBE50027.2020.00075, 2020. [Google Scholar]
- 15.Alshazly H., Linse C., Barth E., Martinetz T. 2020. Explainable COVID-19 Detection Using Chest CT Scans and Deep Learning. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.W. updates on COVID-19, Coronavirus disease (COVID-19) 2021. https://www.who.int/emergencies/diseases/novel-coronavirus-2019/eve nts-as-they-happen/q-a-detail/coronavirus-disease-covid-19 URL.
- 17.Chaudhary P.K., Pachori R.B. FBSED based automatic diagnosis of COVID-19 using X-ray and CT images. Comput. Biol. Med. 2021;134:104454. doi: 10.1016/j.compbiomed.2021.104454. https://www.sciencedirect.com/science/article/pii/S0010482521002481 ISSN 0010-4825. URL. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Elpeltagy M., Sallam H. 2021. Automatic Prediction of COVID- 19 from Chest Images Using Modified ResNet50, Multimedia Tools and Applications; pp. 1–13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Wang Z., Liu Q., Dou Q. Contrastive cross-site learning with redesigned net for COVID-19 CT classification. IEEE J. Biomed. Health Info. 2020;24(10):2806–2813. doi: 10.1109/JBHI.2020.3023246. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Kaur T., Gandhi T.K., Panigrahi B.K. Automated diagnosis of COVID-19 using deep features and parameter free BAT optimization. IEEE J. Transl. Eng. Health Med. 2021:1. doi: 10.1109/JTEHM.2021.3077142. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.S. Sen, S. Saha, S. Chatterjee, S. Mirjalili, R. Sarkar, A bi-stage feature selection approach for COVID-19 prediction using chest CT images, Appl. Intell. doi:10.1007/s10489-021-02292-8. [DOI] [PMC free article] [PubMed]
- 22.Carvalho E.D., Carvalho E.D., de Carvalho Filho A.O., de Araújo F.H.D., Andrade Lira Rabêlo R.d. IEEE Symposium on Computers and Communications. ISCC); 2020. Diagnosis of COVID-19 in CT image using CNN and XGBoost; pp. 1–6. 10.1109/ISCC50000.2020.9219726, 2020. [Google Scholar]
- 23.Gifani P., Shalbaf A., Vafaeezadeh M., et al. Automated detection of COVID-19 using ensemble of transfer learning with deep convolutional neural network based on CT scans. Int. J. Comput. Assisted Radiol. Surg. 2021;16(1):115–123. doi: 10.1007/s11548-020-02286-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.X. He, X. Yang, S. Zhang, J. Zhao, Y. Zhang, E. Xing, P. Xie, Sample-Efficient Deep Learning for COVID-19 Diagnosis Based on CT Scans, medrxiv .
- 25.Fang Z., Ren J., Marshall S., Zhao H., Wang S., Li X. Topological optimization of the DenseNet with pretrained-weights inheritance and genetic channel selection. Pattern Recogn. 2021;109:107608. doi: 10.1016/j.patcog.2020.107608. https://www.sciencedirect.com/science/article/pii/S0031320320304118 ISSN 0031-3203. URL. [DOI] [Google Scholar]
- 26.Jaiswal A., Gianchandani N., Singh D., Kumar V., Kaur M. Classification of the COVID-19 infected patients using DenseNet201 based deep transfer learning. J. Biomol. Struct. Dyn. 2020:1–8. doi: 10.1080/07391102.2020.1788642. 10.1080/07391102.2020.1788642, URL. pMID: 32619398. [DOI] [PubMed] [Google Scholar]
- 27.Krizhevsky A., Sutskever I., Hinton G.E. ImageNet classification with deep convolutional neural networks. Commun. ACM. 2017;60(6):84–90. doi: 10.1145/3065386. ISSN 0001-0782, doi:10.1145/3065386, URL. [DOI] [Google Scholar]
- 28.Hou J., Xu J., Jiang L., Du S., Feng R., Zhang Y., Shan F., Xue X. Periphery-aware COVID-19 diagnosis with contrastive representation enhancement. Pattern Recogn. 2021;118:108005. doi: 10.1016/j.patcog.2021.108005. https://www.sciencedirect.com/science/article/pii/S0031320321001928 ISSN 0031-3203. URL. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Loey M., Manogaran G., Khalifa N.E.M. 2020. A Deep Transfer Learning Model with Classical Data Augmentation and Cgan to Detect Covid-19 from Chest Ct Radiography Digital Images; pp. 1–13. Neural Computing and Applications. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.E. Soares, P. Angelov, S. Biaso, M. Higa Froes, D. Kanda Abe, SARS-CoV-2 CT-scan dataset: a large dataset of real patients CT scans for SARS-CoV-2 identification, medRxiv doi:10.1101/2020.04.24.20078584.
- 31.Zhao J., He X., Yang X., Zhang Y., Zhang S., Xie P. 2020. COVID-CT-dataset: a CT scan dataset about COVID-19. [Google Scholar]
- 32.Canziani A., Paszke A., Culurciello E. 2016. An Analysis of Deep Neural Network Models for Practical Applications. [Google Scholar]
- 33.Souquet L., Shvai N., Llanza A., Nakib A. CEC); 2020. Hyperparameters optimization for neural network training using Fractal Decomposition-based Algorithm; pp. 1–6. IEEE Congress on Evolutionary Computation. 2020. [DOI] [Google Scholar]
- 34.J. Bergstra, R. Bardenet, Y. Bengio, B. Kégl, Algorithms for hyper-parameter optimization, Adv. Neural Inf. Process. Syst. 24.
- 35.Jones D., Schonlau M., Welch W. Efficient global optimization of expensive black-box functions. J. Global Optim. 1998;13:455–492. doi: 10.1023/A:1008306431147. [DOI] [Google Scholar]
- 36.Bergstra J., Yamins D., Cox D.D. Proceedings of the 30th International Conference on International Conference on Machine Learning. vol. 28. 2013. Making a science of model search: hyperparameter optimization in hundreds of dimensions for vision architectures; p. ICML’13. JMLR.org, I–115–I–123. [Google Scholar]
- 37.M. Abadi, A. Agarwal, P. Barham, E. Brevdo, Z. Chen, C. Citro, G. S. Corrado, A. Davis, J. Dean, M. Devin, et al., Tensorflow: large-scale machine learning on heterogeneous distributed systems, Software available from tensorflow. org 39 (9).
- 38.Chollet F., et al. 2015. Keras.https://keras.io [Google Scholar]
- 39.Bisong E. Springer; 2019. Building Machine Learning and Deep Learning Models on Google Cloud Platform. [DOI] [Google Scholar]
- 40.Kingma D.P., Ba J. A Method for Stochastic Optimization; Adam: 2017. [Google Scholar]
- 41.Yang J., Honavar V. Feature subset selection using a genetic algorithm. IEEE Intell. Syst. Their Appl. 1998;13(2):44–49. doi: 10.1109/5254.671091. [DOI] [Google Scholar]
- 42.Russell S., Norvig P. third ed. Prentice Hall Press; Upper Saddle River, NJ, USA: 2009. Artificial intelligence: a modern approach. 0136042597, 9780136042594. [Google Scholar]
- 43.Landis J.R., Koch G.G. The measurement of observer agreement for categorical data. Biometrics. 1977;33(1):159–174. http://www.jstor.org/stable/2529310 ISSN 0006341X, 15410420, URL. [PubMed] [Google Scholar]
- 44.Eiben A.E., Smith J.E., et al. vol. 53. Springer; 2003. (Introduction to Evolutionary Computing). [Google Scholar]
- 45.A. H. Wright, Genetic algorithms for real parameter optimization, in: Foundations of Genetic Algorithms, vol. vol. 1, Elsevier, 205–218, 1991.
- 46.Breiman L. Random forests. Mach. Learn. 2001;45(1):5–32. ISSN 1573-0565. [Google Scholar]
- 47.V. Vapnik, The support vector method of function estimation, in: Nonlinear modeling, Springer, 55–85, 1998.
- 48.Chen T., Guestrin C. Association for Computing Machinery; New York, NY, USA: 2016. XGBoost: a scalable tree boosting system; pp. 785–794. Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, KDD ’16. [DOI] [Google Scholar]
- 49.Hanley J.A., McNeil B.J. The meaning and use of the area under a receiver operating characteristic (ROC) curve. Radiology. 1982;143(1):29–36. doi: 10.1148/radiology.143.1.7063747. pMID: 7063747. [DOI] [PubMed] [Google Scholar]
- 50.Keilwagen J., Grosse I., Grau J. Area under precision-recall curves for weighted and unweighted data. PloS One. 2014;9(3):1–13. doi: 10.1371/journal.pone.0092209. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Simonyan K., Zisserman A. 2015. Very Deep Convolutional Networks for Large-Scale Image Recognition. [Google Scholar]
- 52.Chollet F. 2017. Xception: Deep Learning with Depthwise Separable Convolutions. [Google Scholar]
- 53.He K., Zhang X., Ren S., Sun J. IEEE Conference on Computer Vision and Pattern Recognition. CVPR); 2016. Deep residual learning for image recognition; pp. 770–778. 2016. [Google Scholar]
- 54.Szegedy C., Ioffe S., Vanhoucke V., Alemi A. 2016. Inception-v4, Inception-ResNet and the Impact of Residual Connections on Learning. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.