Significance
Molecular simulations of proteins are often interpreted using Markov state models (MSMs), in which each protein configuration is assigned to a global state. As we explore larger and more complex biological systems, the size of this global state space will face a combinatorial explosion, rendering it impossible to gather sufficient sampling data. In this work, we introduce an approach to decompose a system of interest into separable subsystems. We show that MSMs built for each subsystem can be later coupled to reproduce the behaviors of the global system. To aid in the choice of decomposition we also describe a score to quantify its goodness. This decomposition strategy has the promise to enable robust modeling of complex biomolecular systems.
Keywords: Markov state models, independent processes, molecular dynamics, ion channels, optimal partition
Abstract
To advance the mission of in silico cell biology, modeling the interactions of large and complex biological systems becomes increasingly relevant. The combination of molecular dynamics (MD) simulations and Markov state models (MSMs) has enabled the construction of simplified models of molecular kinetics on long timescales. Despite its success, this approach is inherently limited by the size of the molecular system. With increasing size of macromolecular complexes, the number of independent or weakly coupled subsystems increases, and the number of global system states increases exponentially, making the sampling of all distinct global states unfeasible. In this work, we present a technique called independent Markov decomposition (IMD) that leverages weak coupling between subsystems to compute a global kinetic model without requiring the sampling of all combinatorial states of subsystems. We give a theoretical basis for IMD and propose an approach for finding and validating such a decomposition. Using empirical few-state MSMs of ion channel models that are well established in electrophysiology, we demonstrate that IMD models can reproduce experimental conductance measurements with a major reduction in sampling compared with a standard MSM approach. We further show how to find the optimal partition of all-atom protein simulations into weakly coupled subunits.
The dynamics of proteins and their functions are of key importance for biology. Molecular dynamics (MD) simulations are a popular method for interrogating the motions of proteins in various environments. A well-known limitation of MD is the timescale mismatch between simulations and real life. Despite advances in computer hardware and algorithms, extreme timescale simulations remain orders of magnitude shorter than many relevant protein processes. Since one requires sufficient numbers of observations to obtain statistical confidence, various strategies have been developed to address this. One approach, building Markov state models (MSM), enables the construction of simple models of long-timescale molecular kinetics from many short off-equilibrium MD simulations (1–6)—see refs. 7 and 8 for thorough reviews. MSMs have successfully been built to obtain compact and yet accurate representations of the kinetics of full proteins (9–16), protein–ligand systems (17–22), and even protein–protein systems (23).
Although MSMs have significantly helped to reduce the MD sampling problem, the fundamental problem that arises from modeling increasingly large biomolecular systems remains. As protein complexes become larger, the number of uncoupled or weakly coupled subsystems increases. If each of these subsystems contains two or more substates, the number of global system states increases exponentially (24). Therefore, any model treating the whole system by a global state poses requirements on the MD sampling that are fundamentally unscalable. This poses an inevitable problem as evolution tends to lead to increased biological complexity, including the optimization of processes through the formation of protein complexes and puncta (25–28).
In practice, many current models based on MD simulation of large biomolecular systems take the pragmatic approach of ignoring most of the system’s dynamics. For example, if one is interested in how an ion channel conducts ions across a membrane, it may be sufficient to prepare the system in a state of interest and collect sufficient statistics of ion passages and perhaps local conformational changes of the selectivity filter residues, rather than trying to sample global conformational rearrangements of the protein complex on much longer timescales. However, our field has a collective interest in developing whole-cell and systems modeling for in silico medicine, which will necessitate the eventual understanding of these large systems in a way that characterizes how all their components interact, undergo transitions, and can be influenced by, e.g., drug molecules, phosphorylation, and/or glycosylation states.
To this end, Olsson and Noé (24) have recently proposed dynamic graphical models that attempt to decompose protein systems in a way similar to Ising or Potts models—subsystems with states or “spins” that are coupled to one another. Dibak et al. (29) and del Razo et al. (30) have developed a coupling of MSMs with reaction–diffusion dynamics to establish an infrastructure in which MSMs can be integrated into whole-cell models. Here we ask a more fundamental question, the answer of which is important to all these integrative approaches: Given a large biomolecular system, how should we decompose it into subsystems, such that these subsystems can be described by independent or weakly coupled MSMs?
Fragmenting proteins at the modeling stage is compatible with prior experience as macromolecules are often subdivided into structural or functional subunits (31). There is also evidence that proteins are decomposable into “quasi-independent groups of [spatially adjacent] amino acids” coined “protein sectors” (ref. 32, p. 774). Furthermore, experimental studies on drug binding or protein functional characterization often use isolated domains or monomers with great success (33).
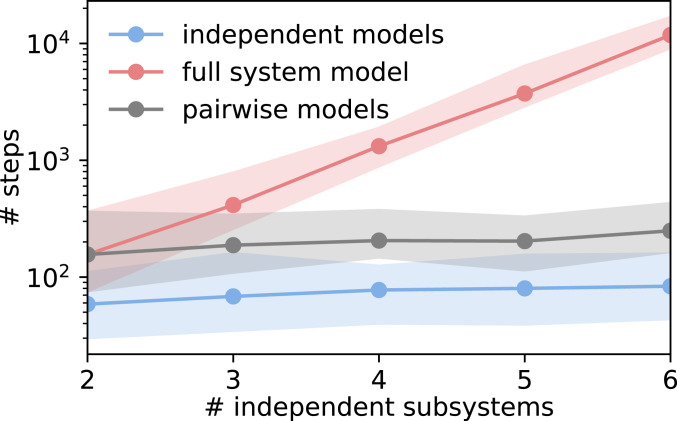
Estimating an MSM on the decomposed protein can significantly reduce the total sampling necessary. From concepts in statistical physics, given a polymer of length where each subunit exists in one of states, the total conformational space is expressed as (Fig. 1). Modeling subsystems of a constant size effectively restricts the number of states that need to be sampled reversibly to a constant. Therefore, exponentially less sampling is required for modeling smaller subsystems compared to a global model (15, 24).
Fig. 1.
Scaling behavior of a toy system consisting of independent subsystems with three states each (SI Appendix, Toy Models). The number of steps required to reversibly sample all transitions is shown for proposed independent models (blue line), the full-system model (red line), and pairwise models that are needed for computing the dependency score (gray line). Shadowed areas indicate 95% confidence intervals.
In this paper, we develop a mathematical framework of decomposing MSMs into local subsystem MSMs, termed independent Markov decomposition (IMD) (Independent Markov Decomposition), and propose a measure of decomposition quality, the dependency score (An MSM Score of Independence). In the following, we refer to IMD as the process of identifying subsystem MSMs and to an IMD model as a model that describes a system as a set of independent, local Markovian subunits.
We speculate that the IMD strategy can forge a connection to other uses of MSMs such as those employed by the neuronal and cardiac modeling communities. There, phenomenological MSMs parameterized from electrophysiology data are used to predict the behavior of action potentials (34–39). In Modeling a Tetrameric Ion Channel Using IMD we describe how a decomposed MSM can be connected to a phenomenological MSM. This connection between fields brings us closer to our goals of understanding these large systems and their behaviors, advancing in silico medicine. We further showcase how the dependency score can be used to find an optimal partition of a system that does not come with clearly defined independent subunits (Optimal Independent Markov Partitions for Tetrameric Ion Channels). We validate our approach with a toy model, showing that the decomposition approximation is high quality and that the proposed validation score works even with limited data (SI Appendix, Toy Models). Finally, we demonstrate its applicability to an all-atom MD dataset of the Synaptotagmin-C2A domain (Optimal Independent Markov Partitions for All-Atom Simulations of Synaptotagmin-C2A) and derive the graph structure of interresidue dependencies.
Independent Markov Decomposition
We first describe IMD for discrete-state MSMs before generalizing it to time series with continuous descriptors.
Markov State Models.
An MSM consists of a discretization of molecular state space into a disjoint set of states and a Markov chain transition matrix modeling a memoryless jump process between these states. We can express whether we are in the th state or not by using indicator functions:
| [1] |
The vector is thus a “one-hot” (or binary) encoding that maps the continuous state to the MSM discretization. For this or any other choice of features we can compute the instantaneous and time-lagged correlation matrices and , respectively. For a fixed-state discretization, the transition matrix that has maximum likelihood and also maximizes the variational approach of conformation dynamics (VAC) (40) is
| [2] |
Let denote the probability distribution of being in any of the states at time ; for example, denotes that the system starts in state 0 at time 0. This vector can be evolved in time using the transition matrix, until it converges to the equilibrium distribution :
| [3] |
An important concept for optimizing the parameters or hyperparameters of MSMs and other Markovian kinetic models is the variational approach for Markov processes (VAMP) (41). VAMP finds that a Markovian model that best approximates the high-dimensional continuous dynamics maximizes the VAMP- score,
| [4] |
where we can use either for the trace norm or for the Frobenius norm. If we run molecular dynamics at equilibrium conditions, we can employ correlation matrix estimators that provide and symmetric (detailed balance). In this special case, VAMP becomes the VAC mentioned above, and the variational score simply becomes . In other words, the optimal MSM is the one that maximizes the trace or the Frobenius norm of the transition matrix, which is equivalent to maximizing its eigenvalues. Since the eigenvalues equal the normalized time autocorrelation of the slowest processes (1, 42), the VAC tries to find the Markovian model that best resolves the slowest processes of the molecular process under investigation (40, 43). For a fixed state space discretization, optimizing the VAC results in the MSM estimator (2). If we also want to search over different state space discretizations, we can use VAC or VAMP as a score in a hyperparameter optimization problem (44) or optimize the VAMP score while representing with deep neural networks, leading us to VAMPnets (45).
Independent Markov Decomposition.
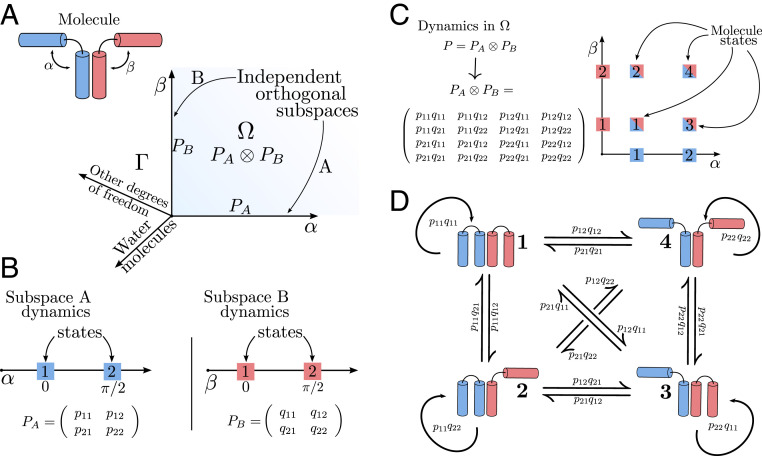
Now we move beyond the common concept of modeling the dynamics of the entire molecular system by a single MSM and instead try to decompose the system into almost independent MSMs. Let us start with the simple example shown in Fig. 2A, where a molecule consists of two domains, and , that are each described by a two-state MSM describing whether the domain is “closed” () or “open” (). We assume that the kinetics of both domains are statistically independent; i.e., each domain switches states independent of the states of the other one—we simultaneously have and (Fig. 2B). As the MSMs and are statistically independent, the probability distribution of the entire system follows Eq. 3 with
| [5] |
where is the Kronecker product (46) (SI Appendix, Markov Operators). The vector now contains the probabilities of being in the four combinatorial states ( and open, open and closed, closed and open, and closed), and is the transition matrix between these combinatorial states whose transition probabilities are simply products of the individual transition events in subsystems and (Fig. 2 C and D). The power of this approach is apparent when comparing Fig. 2 B and C: If the dynamics in and are independent or almost independent, we can estimate the 16 transition probabilities that parameterize the whole system using only the eight elements of the transition matrices of the subspaces. This advantage increases exponentially in larger systems: If we have (almost) independent domains with states each, distinguishing all states would require us to sample and estimate an exponential number of order of transitions, whereas a decomposition into independent MSMs reduces this to a polynomial number of transitions that can be scaled to large systems. From another point of view, IMD is more efficient because it obtains a greater number of “effective” transition counts for the global model by applying the Kronecker product (SI Appendix, Effective Counts and Sampling). The above example trivially generalizes to systems with . We note that it is customary to dismiss variables of the full state space (Fig. 2A) that are assumed to average quickly, e.g., solvent degrees of freedom. Thus, the modeled space in practice encompasses only the variables of interest, e.g., internal coordinates of a protein system.
Fig. 2.
Operator decomposition and discretization on a test molecule. (A) A test molecule is decomposed into two subsystems (blue and red). The two angles and span subspaces and corresponding to the two subsystems, respectively. The space is composed of all system degrees of freedom. The space is the Cartesian product of and and its dynamics are described by Perron–Frobenius operators and , respectively. The dynamics in are given as the tensor product . (B) The molecule has metastable states at and ; the subspaces and can be discretized into MSMs with transition probability matrices and . The quantities and are the transition probabilities from state to of subspaces and , respectively. (C) The discretized dynamics in are given by the tensor product , yielding the four states of the full molecule. (D) Illustration of the four possible states of the molecule and the transitions between them.
An MSM Score of Independence.
In practice, subdomains of biomolecules or biomolecular complexes will not be exactly independent. Moreover, the identification of a domain decomposition into almost independent subdomains is a nontrivial task. To enable algorithmic determination of almost independent subdomains, we develop an independence score that quantifies decomposition validity. To this end we come back to the variational approach, Eq. 4. Conveniently, matrix norms follow simple rules when applied to a Kronecker product (SI Appendix, VAMP Score Decomposition of Independent Systems). In practice, we will apply the trace and Frobenius norms that correspond to the VAMP-1 and VAMP-2 scores of the Koopman operator. The VAMP-2 score has successfully been used in many practical applications (16, 45, 47, 48). If our molecular system consists of independent subdomains such that its global MSM is a Kronecker product of subspace MSMs as described above, its VAMP score is the simple product of VAMP scores (SI Appendix, VAMP Score Decomposition of Independent Systems):
| [6] |
Here, denotes the VAMP- score of the transition operator. It could be the trace norm (VAMP-1) or Frobenius norm (VAMP-2) of the associated transition matrix. In practical applications, the VAMP- score could be rank reduced, i.e., restricted to the highest singular values. Note that Eq. 6 is a necessary but not a sufficient condition for Markov independence. Significant deviations from equality in Eq. 6 indicate that the assumption of independence is invalid. However, if separate MSMs can probe the same molecular features, it is possible to satisfy Eq. 6 even though the subsystem MSMs are not statistically independent. Eq. 6 must therefore always be used in conjunction with appropriate constraints. Here, we choose between different ways to assign independent molecular features to different MSMs and check which of these assignments best satisfies Eq. 6. In practice, we want to estimate an IMD model because often we cannot compute the global MSM due to limited sampling (Fig. 1), and we consequently do not know . Therefore, we choose to check the equality of Eq. 6 only on pairs of subsystems ; i.e., . We then search over possible partitions of the molecular system into subsystems by evaluating the graph of pairwise dependencies :
| [7] |
In practice, computing involves a new estimate of the transition probability matrix in the joint space of two systems. We show that our measure scales well with respect to limited sampling (also compare SI Appendix, Toy Models).
The product in Eqs. 6 and 7 is purely a result of the chosen basis set of MSMs (Eq. 1 and SI Appendix, VAMP Score Decomposition of Independent Systems). In practical situations, it is desirable to find a decomposition directly based on molecular features such as distances or contacts instead of performing an MSM discretization and estimation for each subsystem. When considering more general features , there are two main changes to discrete-state MSMs: 1) Observables are propagated by a different operator, called a Koopman operator (49, 50), and 2) the joint space of observables is most easily described by “stacking” observable feature vectors rather than by defining an MSM discretization on the combinatorial space. For example, if and are the one-dimensional time series of features of two systems and , the joint space would be spanned by . The transfer operator describing the independent dynamics in joint space is thus a block matrix of its constituting independent suboperators (also called a direct sum; see SI Appendix, Markov Operators for details). This also means that independent subsystem features are not correlated. We note that stacking in the MSM formulation would produce probability vectors not normalized to 1 and yield invalid (i.e., not irreducible) MSM transition matrices in the joint space. The trace and Frobenius norm of the Koopman operator thus decompose as sums such that the dependency score reads
| [8] |
where , the Koopman operator, takes the place of the transition matrix . See SI Appendix, VAMP Score Decomposition of Independent Systems for the derivation. We note that even though discussing MSM artifacts is out of the scope of this work, it is unclear how possible discretization errors might propagate to the MSM-based dependency (Eq. 7). However, such artifacts are entirely ruled out when working in observable space (Eq. 8).
Results
Modeling a Tetrameric Ion Channel Using IMD.
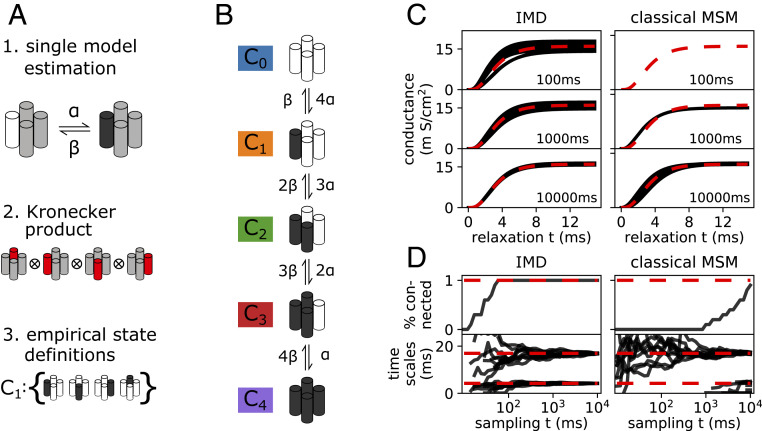
In cardiac electrophysiology, Markov models have been used to model phenomenological data from ion channels (37–39). Ion channels are transmembrane proteins that respond to physiological stimuli and selectively control the flow of ions in excitable cells. Upon a change in membrane potential, voltage-gated ion channels undergo conformational changes that modulate ionic conductance. The symphony of ion channels collectively facilitates the propagation of electrical signals in excitable tissues, such as the heart and brain, and they are important drug targets (51, 52). The plethora of experimental measurements of ion channel properties sets the stage for computational simulations to provide molecular details and mechanistic insights (53). Although it is possible to fit a phenomenological MSM using data from electrophysiological experiments, atomistic modeling remains out of reach due to the long timescales of channel opening. This is because single-gate activation events are rare, and many ion channels have multiple gates that need to activate concurrently. Reversible sampling will further be hampered by a combinatorial number of pathways that lead to a fully open channel. We propose that for cases of noncooperative gates, IMD can help solve this problem, which we demonstrate in the following series of numerical experiments. We consider a voltage-gated tetrameric potassium ion channel with four identical subunits, each with a voltage sensor. To construct an IMD model, we exploit the independence of individual subunits or gates and partition accordingly (Fig. 3 A, 1). This produces four matrices that describe individual gate opening and closing. As derived above, the Kronecker product of subsystem transition matrices yields a transition matrix of the full ion channel (Fig. 3 A, 2). The 16 states enumerate all possible combinations of open and closed gates of the full ion channel, a state space referred to as in the following. We note that this decomposition is possible only between noncooperative domains.
Fig. 3.
Reconstructing the Hodgkin–Huxley model from a simple discrete model. (A) Pipeline of steps required to assemble a full channel model from a single subunit model that describes opening and closing of a single subunit in the vicinity of the others (A, 1). The Kronecker product between all four subunit models assembles a model that still distinguishes between all combinatorial states (A, 2). Empirical state definitions account for channel symmetries (A, 3). Black denotes an open, white a closed, and gray an undefined subunit. (B) Graphical depiction of full channel model in empirical state space. Note the symmetry of the channel, i.e., that at this stage only the number of open subsystems is known. (C) Relaxation from a closed state into the native state at 63 mV. We show conductance predicted by the IMD model (Left column) and the classic MSM (Right column), using different amounts of sampling. Note that the classic approach yields only results in the high-sampling regime where all empirical states are connected. Results are compared to the original Hodgkin–Huxley model (red dashed line). (D) Sampling time necessary to estimate a decomposed MSM (Left column) compared to a classic full-system MSM (Right column) for 10 realizations of the Markov chain. We show the percentage of fully connected models in our ensemble of realizations (Top row) and the first and fourth implied timescales computed from it (Bottom row). Note that for the classic MSM, extreme amounts of sampling are necessary to even estimate all system-inherent implied timescales.
We construct a mapping to assign the 16 states of the transition matrix to those of a phenomenological MSM. Our reference empirical model is the one developed in ref. 54 for this channel (Fig. 3B). In ref. 54, channel symmetry is used to define the full-system states accordingly:
Mapping of the transition matrix into the space of these empirical states can be obtained by converting the empirical state definitions into crisp membership vectors , with each element indicating which empirical configuration a full-system configuration belongs to. For example, the membership vector describing any state with one open gate would be ; i.e., these states are associated to macroconfiguration . The full membership matrix is constructed by stacking . Subsequently, the transition matrix is coarse grained following (55, 56) with the diagonal matrix of the stationary distribution in full space and in empirical space .
Choosing rates and from the original work by Hodgkin and Huxley (34) at a voltage of 63 mV, we produce a simple discrete model. Using this model, we can generate sample trajectories from which to construct MSMs in accordance with Computational Experiments. We estimate a model for the full system from these data by applying the aforementioned pipeline. Using this derived full-system model, experimental observables from electrophysiology experiments can be assessed by relaxation of the Markov chain from a nonequilibrium distribution (e.g., a closed configuration) into the equilibrium at this particular voltage (57, 58). We start from a configuration of fully closed states and further assume that the channel conducts ions only if it is open; i.e., our observable is nonzero only for the open state. This experiment is the computational analog to a voltage jump experiment from resting to +63 mV in voltage clamp mode. Shown in Fig. 3C, the modeled conductance of the channel over time is reported. The predicted conductance time series is compared with the numerically integrated ordinary differential equation for the potassium ion channel derived by Hodgkin and Huxley (34). We find that the IMD model can accurately reproduce the full channel dynamics. IMD models were built by separately fitting four single-gate trajectories (i.e., a full-system trajectory split into its subsystems) and assembled using the aforementioned steps. For comparison, traditional MSMs were fitted to sample trajectories computed from the full-system transition matrix in its empirical state definition. We note that we compare the sampling necessary for IMD models to the empirical 5-state formulation (which does not resolve all 16 combinatorial states). In this way, we can rule out that the described sampling advantages of IMD are an artifact of exploited channel symmetry. The reduction in the amount of sampling needed due to the use of IMD can be quantified in terms of the length of simulation required to form a fully connected transition matrix. In Fig. 3D we present the percentage of connected IMD models estimated on an ensemble of 10 realizations of the Markov chain and compare the result to a classic MSM. Note that even though a necessary condition for MSM estimation, connectivity is not a quality criterion—we discuss approximation quality below. Connectivity is computed as a function of simulated time (in milliseconds); i.e., it shows how probable a modeler can estimate a connected Markov model, IMD or classic, from a fixed amount of sampling. We note that the classic MSM approach can estimate all system-inherent implied timescales only when all empirical states are reversibly sampled, i.e., only for very large amounts of data. In terms of model approximation quality, the higher computational efficiency of IMD is evident from the much faster convergence of implied timescales as a function of simulation length (Fig. 3D; also note root-mean-square error between estimated and ground-truth eigenvalue spectra in SI Appendix, Fig. S4). We find a reduction in sampling by three orders of magnitude, from tens of seconds to tens of milliseconds (Fig. 3D). For example, ionic conductance is reasonably approximated with 100 ms of sampling and the IMD approach (Fig. 3C).
Here, we have presented an example where each gate operates independently. In practice, the gating behaviors of most ion channels are not completely independent, but are instead coupled. In this case, the decomposition yields an approximate model of the real dynamics; see SI Appendix, Weakly Coupled Systems for a discussion. The theoretical limit is posed by the assumption of stationarity that underlies MSM estimation. It is violated if external influences are strong and on similar timescales to those of the processes to be modeled. External influences that are much faster than the local dynamics are incorporated as an average over Markov states, similar to water molecules in regular MSMs. As demonstrated in SI Appendix, Fig. S1, modeling of weakly coupled systems is possible in a robust fashion.
Optimal Independent Markov Partitions for Tetrameric Ion Channels.
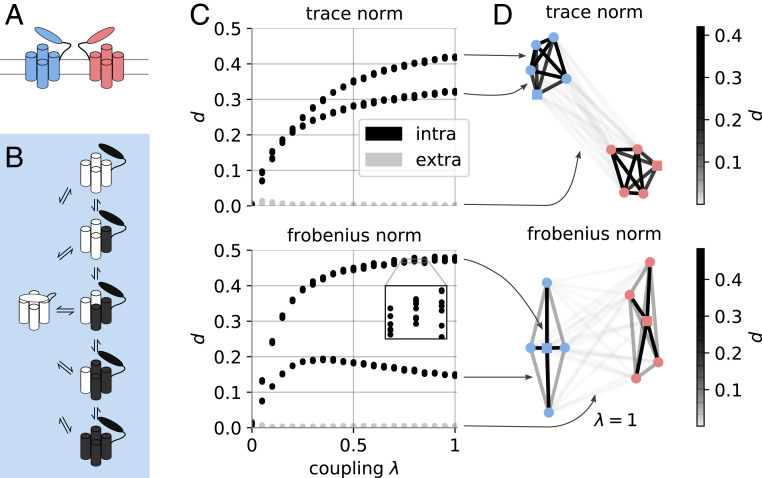
For our previous example, we prescribed a convenient partitioning scheme for the ion channel system. In contrast, in real-world situations a complex system may involve multiple independent subsystems but the coupling graph is unknown a priori. For instance, it might not be clear how to find independent protein segments of an unknown protein. A method is necessary to aid in the discovery of viable partitions that produce independent subsystems. In this section we demonstrate how the dependency defined in An MSM Score of Independence can be used as a score to bisect clusters of coupled subsystems from weakly coupled ones. The idea is to compute all possible pairwise dependencies between all subsystems and to use them as edge weights in a graph. If they exist, (almost) independent clusters of strongly coupled subsystems will be revealed by analyzing this graph. Once identified, these clusters might be modeled with single-subsystem transition matrices within the IMD framework. For the purposes of demonstration, we zoom out from a single-channel protein to a membrane patch (Fig. 4A). In our setup, this patch contains a dimer of channels that we model to be coupled by a weak, cooperative coupling. Individual channels are modeled using the same parameters as in the above ion channel model but contain the additional element of an external deactivation switch (Fig. 4B). In a cellular environment, such a switch could, for example, be an inhibitory ligand that binds and unbinds at a certain rate. It is modeled as a Markov process with probability 0.01 to change its state. The deactivation switch alters the conformational dynamics of each gate such that the probability to close or to stay closed is 95%. Thus, by construction, it is not possible to decompose a channel MSM into single-gate MSMs because each gate is now coupled to the deactivation switch. Further, the strength of the intrachannel coupling can be controlled by a linear mixture parameter . The dynamics described above correspond to , strong coupling. The coupling can be entirely deactivated by setting . See SI Appendix, Dimer Model for implementation details.
Fig. 4.
Visualization of channel dimer. (A) Two channels located in a membrane. Each channel consists of four gates (akin to a Hodgkin–Huxley model, depicted by cylinders) and one desensitization switch (depicted as an additional oval domain). (B) States and possible transitions of individual channels (simplified, short-lived switch-deactivated open states are omitted). As both channels have the same dynamics, only one is shown as an example. (C) Dependency score as a function of coupling strength as defined by the linear mixture parameter . Color code: Gray denotes scores between two molecules, and black denotes intrachannel pairs. (D) Graph of pairwise dependencies between all channel subunits for . Edges are color coded according to dependency scores between two systems. Nodes belonging to a single channel are color coded accordingly, and square nodes represent deactivation switches.
We generate discrete time series data from a transition matrix that models a dimer with these properties (SI Appendix, Dimer Model and Computational Experiments). From the data, the dependency is computed for all possible pairs of subsystems. This involves the estimation of transition matrices for two isolated subsystems and comparing them with the transition matrix estimated in the joint space using Eq. 7. For example, one such pair could be the deactivation switch of one channel and a gate of the other channel. A natural representation of these pairwise norms between subsystems is a graph. It is formed by nodes (subsystems) and dependency-weighted edges; no assumption about its structure is made (e.g., that it is a fully connected graph). For the numerical experiment described in this section, our analysis yields the graph shown in Fig. 4D. The graph is visualized by positioning the subsystems or graph nodes with the Fruchterman–Reingold algorithm (59, 60), which is sensitive to the edge weights. This means that subsystems with high dependency are grouped together. This helps us to visually identify clusters of coupled subsystems. Groups of subsystems that are far apart in this representation are coupled relatively weakly. We find that dependencies between subsystems of the same channel are significantly larger than zero while interchannel interactions yield dependencies close to zero (Fig. 4D). Further, reducing the coupling strength within a channel does not alter our qualitative results (Fig. 4C). The observed bifurcation of dependencies is due to the two types of coupling in the system (gate–gate vs. gate–deactivation switch) and is a feature of the dimer model system. In summary, our results show that we can learn the connectivity of a network of subsystems from discrete, simulated time series data. In particular, the dependency score provides an approach to find an optimal partition of a system with multiple types of coupling.
Optimal Independent Markov Partitions for All-Atom Simulations of Synaptotagmin-C2A.
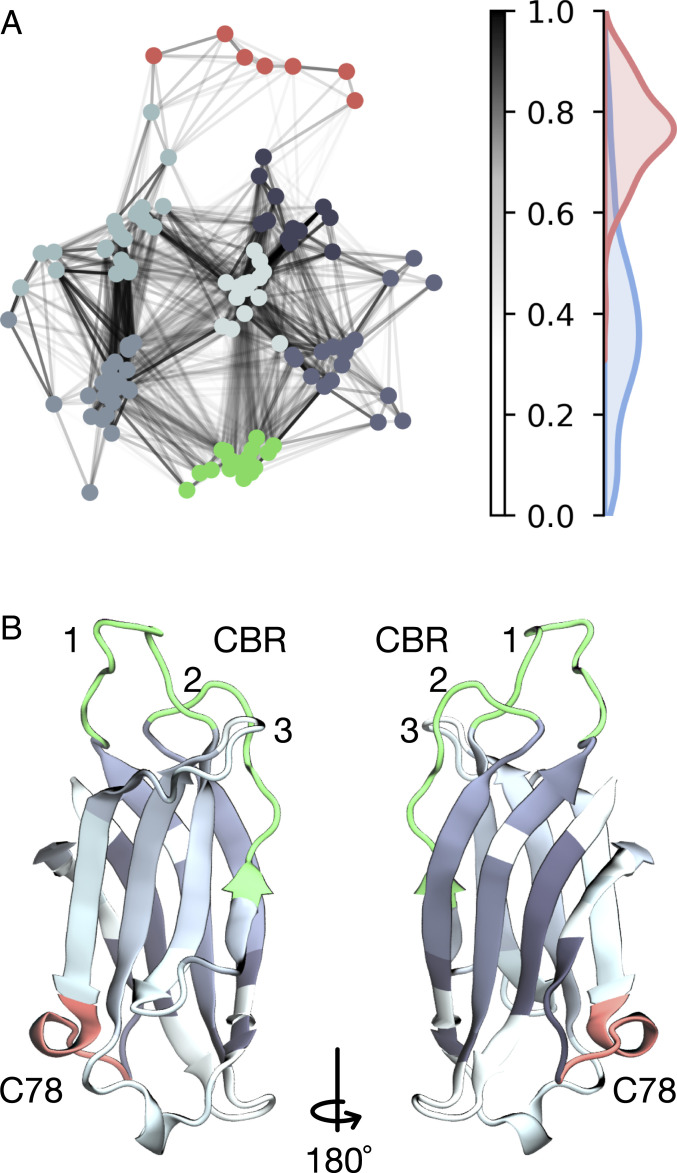
To showcase the applicability of the dependency score, we apply our method to a 180- molecular dynamics dataset of the C2A domain of Synaptotagmin-1 (Syt). Syt is a crucial player in the neurotransmitter release machinery (61). In our previous study we have found that single loops of its C2A domain can be described independently of each other using a hand-crafted partition (15). Here, we attempt to find an optimal partition by using the dependency score at the residue resolution (Application to MD Dataset). Instead of working with MSM transition probabilities, we directly work in protein feature space to omit discretization artifacts. We find that indeed, Syt-C2A can be partitioned into defined subunits, or conformational switches, using a VAMP-2–based dependency score (Fig. 5). The dependency network spanned by Syt-C2A residues expresses defined subsystem clusters. Within each subsystem cluster, residues are embedded with high normalized dependency scores whereas between different subsystem clusters, these links are weaker (Fig. 5A). The boundary between what is considered a high and a low normalized dependency tends to be ; we, however, note that this value might be system specific. The discovered partition contains the conformational switches defined in our last study (15): In particular, the C78 switch (Fig. 5B, red) emerges as an independent cluster in the Fruchterman–Reingold projection, confirming our previous results. However, even though conformational switches in the calcium-binding region (CBR), CBR-1 and -2 together (Fig. 5B, green), are connected to the other protein residues by a low dependency, describing these loops independently is an approximation that is only partially backed by this current study. Similar results are obtained when using a VAMP-1–based dependency (SI Appendix, Fig. S2).
Fig. 5.
Dependency network between residues of Syt-1 C2A depicted using a standard graph layout (Fruchterman–Reingold algorithm). (A) VAMP-2 normalized dependency network. Edge weights are indicated by color bar. Nodes are colored according to an unsupervised classification by the -means algorithm (). Dependency histograms depict coupling strength of residues within a subsystem cluster (red) and between different subsystem clusters (blue). (B) Visualization of protein structure with color-coded segments from our VAMP-2 analysis (colors correspond to classification in A). VAMP-1 yields similar results (not shown here; see SI Appendix, Fig. S2).
Discussion
Over the past several decades, MSM methodology has matured into a valuable tool for MD data analysis (1, 3, 4, 7, 8, 13, 20–23, 42). For practitioners, modeling MD data with MSMs remains a nontrivial task, especially as researchers turn their focus toward the study of progressively larger biomolecular complexes. Larger systems generally come with an increasing number of (metastable) states that demand vast amounts of sampling time and hamper attempts to rigorously model protein dynamics. In these scenarios, the classic MSM method reaches a point where the combinatorial explosion of states becomes a critical bottleneck. It is a fundamental problem that is inherent to any method that seeks to describe the global protein state (24). One possible solution is to appreciate the notion of independent protein segments (32) and to split large systems into smaller, more manageable subsystems. In this spirit, we have proposed independent Markov decomposition. For practitioners, this means that, for example, an ion channel is modeled as a set of individual gates as opposed to a single protein. This approach approximates the system as a set of independent subsystems and is naturally agnostic to global system size. In this paper we have shown how the conceptual idea of IMD relates to the underlying transfer operator formulation, what sampling advantages can be expected, and how to use the proposed dependency score to find an optimal partition of an unknown system. Using the tetrameric potassium ion channel as a model system, we show that we can estimate a fully converged model with approximately three orders of magnitude less sampling when compared to a classic MSM. IMD therefore has the potential to leverage sampling efforts for large biological systems into a regime that is achievable with state-of-the-art simulation techniques and computer hardware. This effect is due to data being used more efficiently while small compromises are made by a mean-field–like approximation. For systems with potentially weak couplings, the validity of the approximation can be checked with our dependency score a posteriori. We further posit that due to the tremendous sampling advantages, the estimation errors introduced by weak couplings are likely to be smaller than the sampling error for classic global-state MSMs. Our results suggest that IMD improves the assessment of sampling convergence for large systems. As real-world MD datasets are usually very high dimensional, in practice, it is a nontrivial task to assess whether the sampling is converged. Often, researchers can only speculate by using semiempirical tests, i.e., matching of high-level experimental observables to model predictions. IMD offers a more rigorous way to tackle this problem. For example, when modeling a single protein loop, it is much easier to see whether the process is sampled reversibly, a question that can be difficult to answer with a classic MSM on global states.
Furthermore, we have proposed a dependency score that quantifies the coupling between two subsystems. As there is no general rule for how to define protein subsystems, the dependency score serves as an objective function to judge IMD model approximation quality and to find an optimal partition of unknown systems. In a numerical test system of a switched dimer model with weak cooperative coupling, the dependency score has robustly bisected clusters of strongly coupled subsystems from weakly coupled ones. It thus enabled IMD model estimation without knowing the dependency graph structure a priori. To optimally partition a system in practical applications, a sufficiently large biomolecular system could be first partitioned into minimal subsystems such as residue side chains. Scoring the dependency between these subsystems can reveal the structure of the dependency graph and thus give rise to a definition of (almost) independent protein segments. We note that IMD is designed for systems with time-constant, independent subunits; i.e., it is most probably not suitable for few-residue peptides or protein folding [for a counterexample using Chignolin (62), cf. SI Appendix, Fig. S3 ]. We have shown that for the C2A domain of Synaptotagmin-1, the dependency score can be used to identify clusters of subsystems that are linked relatively weakly between each other. These subsystems are similar to the conformational switches identified and independently modeled in ref. 15. We, however, note that the current, prototypical implementation of assigning residues to subsystems is subject to stochasticity. For future work, in particular for larger biomolecular complexes, it will be desirable to incorporate experimental knowledge about size and properties of “protein sectors” (32). An aspect excluded in this conceptual study is the discretization of MD data, a step that can be crucial in practical MSM applications (4, 63). We note that subsystem MSMs have smaller dimensionality and therefore discretization errors are smaller compared to those in the higher-dimensional full system. This implies that IMD models may reduce discretization artifacts compared to classic MSMs. However, further work should consider the implications of the discretization error as it is unclear how it propagates to joint space probability estimates and dependency score. Furthermore, the lag time has twofold implications on IMD: First, when estimating local, independent subunit MSMs, the choice of lag time must be verified for each independent MSM as for classic MSMs (e.g., by an implied timescales test). This might yield different lag times for different subunits, which is justified when working with independent models alone. However, if a global (or pairwise) model is desired, all constituting local models must strictly have the same lag time such that a global (or pairwise) operator is defined. This, second, is the reason why the dependency score can be applied only for a single global lag time. In practice, choosing a lag time for dependency network estimation might therefore be done as common practice with, e.g., time-lagged independent component analysis analyses (63), i.e., starting with a lag time that most likely yields converged estimates. This choice should be validated by ensuring subsystem implied timescales convergence.
In this work, we propose that one way to keep pace with our interest in modeling large biological systems is by using a decomposition technique. For large systems, IMD models are more data efficient and might be easier to apply than classic global-state MSMs. We believe that interrogating local features, e.g., ligand-binding pockets, instead of global system states can be more informative and give better predictions at reduced computational cost. Because this approach comes with all of the established methods and software of the MD MSM community, we anticipate that IMD will have a broad application basis for in silico cell biology.
Materials and Methods
Computational Experiments.
Gate opening and closing rates of the toy potassium ion channel were obtained from the Hodgkin–Huxley model. Under voltage clamp conditions and neglecting the sodium and leak currents, we are left with the potassium ion channel contribution. The current is given as
where is the current, is the conductance, is the maximal conductance, and and are the total transmembrane potential and potassium ion reversal potential, respectively. Here is a dimensionless quantity corresponding to channel activation. The time dependence of is described using the following ordinary differential equation (ODE),
where and are the kinetic rates () of activation and deactivation, respectively. In the original Hodgkin–Huxley model (34), the voltage sensitivity of the ion channel is modeled by the voltage dependence of the rates and ,
The term is the joint probability that the four independent subunits of the tetrameric potassium ion channel are concomitantly open. Thus and are the kinetic rates for an individual subunit to open and close, respectively. This set of ODEs was integrated using the odeint function provided by scipy (64) to serve as the ground truth for later comparison with IMD model and MSM results. We apply our framework to discrete time series data with known full-system dynamics. For each system that we are using, details and generator matrix are given in SI Appendix, Toy Models and Dimer Model. Generally, a transition matrix describing a (full) test system (possibly including couplings) is chosen, akin to in Eq. 5. Time series are generated using the Markov chain sampler implemented in pyEMMA/msmtools (65). Subsequently, full-system states are mapped to individual subsystem states, yielding subsystem trajectories that are parallel in time. Estimation of subsystem transition matrices [ in Eq. 5] is followed by assembly of a full-system transition matrix. The latter is utilized to extract full-system observables such as implied timescales.
Application to MD Dataset.
The protocol that was used to obtain MD simulation data and featurization of Syt-C2A is described in detail in ref. 15. In particular, as in the cited study, we use heavy atom coordinates of the superposed protein. We are aware that this could potentially yield spurious correlations; however, 1) no better descriptor of the slow dynamics could be found and 2) we want to ensure compatibility to our previous study. Each residue is encoded as a vector of flattened coordinates and the dependency is computed on each pair of residues. The pairwise features are the stacked vectors . Note that when directly working on coordinate features, unlike in the MSM examples, the dependency decomposes as a sum, not as a product (SI Appendix, VAMP Score Decomposition of Independent Systems). Furthermore, the dependency is normalized to untangle the amount of kinetic variance from actual dependency; i.e.,
| [9] |
with being the VAMP- score of residue . Note that in the case of high dependency scores, the two observable features might be proxies of the same process; however, one of them could encode an additional one. Dividing by the ensures we are normalizing only to the processes contained in both subsystem vectors. To not obfuscate the histogram analysis conducted for the dependency score network with weak links in otherwise strongly coupled clusters, we have taken into account only the strongest link connecting each residue. We thus extract the maximal normalized dependency score that connects a given residue to all other residues within a subsystem cluster (intrasubsystem) or to all residues of a different subsystem cluster (intersubsystem), respectively. The VAMP- scores for Syt-C2A are computed with PyEMMA (65) at a lag time of 50 ns. The lag time was chosen based on implied timescales convergence reported in ref. 15.
Supplementary Material
Acknowledgments
T.H. thanks Moritz Hoffmann and Andreas Mardt (FU Berlin) for fruitful discussions. We acknowledge funding from Deutsche Forschungsgemeinschaft (SFB/TRR 186, Project A12; SFB1114, Project A04), the Berlin Mathematics Research Center MATH+ (AA1-6), the Bundesministerium für Bildung und Forschung, and the European Commission (CoG 772230 “ScaleCell”). M.J.d.R. acknowledges support by the Dutch Institute for Emergent Phenomena at the University of Amsterdam. B.C.T. and R.E.A. acknowledge support from the National Biomedical Computation Resource via NIH Grant P41-GM103426. C.T.L. acknowledges support from a Hartwell Foundation postdoctoral fellowship. R.E.A. acknowledges funding from NIH R01 GM132826.
Footnotes
The authors declare no competing interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at https://www.pnas.org/lookup/suppl/doi:10.1073/pnas.2105230118/-/DCSupplemental.
Data Availability
The code that implements our discrete models, generates the data, and reproduces the presented results can be found in our GitHub repository (https://github.com/markovmodel/decomposed_msms) (66). The molecular dynamics dataset of Synaptotagmin C2A is available upon request. Some study data are available upon request.
References
- 1.Swope W. C., Pitera J. W., Suits F., Describing protein folding kinetics by molecular dynamics simulations. 1. Theory. J. Phys. Chem. B 108, 6571–6581 (2004). [Google Scholar]
- 2.Singhal N., Snow C. D., Pande V. S., Using path sampling to build better Markovian state models: Predicting the folding rate and mechanism of a tryptophan zipper beta hairpin. J. Chem. Phys. 121, 415–425 (2004). [DOI] [PubMed] [Google Scholar]
- 3.Noé F., Schütte C., Vanden-Eijnden E., Reich L., Weikl T. R., Constructing the equilibrium ensemble of folding pathways from short off-equilibrium simulations. Proc. Natl. Acad. Sci. U.S.A. 106, 19011–19016 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Prinz J. H., et al. , Markov models of molecular kinetics: Generation and validation. J. Chem. Phys. 134, 174105 (2011). [DOI] [PubMed] [Google Scholar]
- 5.Chodera J. D., Singhal N., Pande V. S., Dill K. A., Swope W. C., Automatic discovery of metastable states for the construction of Markov models of macromolecular conformational dynamics. J. Chem. Phys. 126, 155101 (2007). [DOI] [PubMed] [Google Scholar]
- 6.Noé F., Horenko I., Schütte C., Smith J. C., Hierarchical analysis of conformational dynamics in biomolecules: Transition networks of metastable states. J. Chem. Phys. 126, 155102 (2007). [DOI] [PubMed] [Google Scholar]
- 7.Chodera J. D., Noé F., Markov state models of biomolecular conformational dynamics. Curr. Opin. Struct. Biol. 25, 135–144 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Husic B. E., Pande V. S., Markov state models: From an art to a science. J. Am. Chem. Soc. 140, 2386–2396 (2018). [DOI] [PubMed] [Google Scholar]
- 9.Voelz V. A., et al. , Slow unfolded-state structuring in Acyl-CoA binding protein folding revealed by simulation and experiment. J. Am. Chem. Soc. 134, 12565–12577 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Qiao Q., Bowman G. R., Huang X., Dynamics of an intrinsically disordered protein reveal metastable conformations that potentially seed aggregation. J. Am. Chem. Soc. 135, 16092–16101 (2013). [DOI] [PubMed] [Google Scholar]
- 11.Shukla D., Meng Y., Roux B., Pande V. S., Activation pathway of Src kinase reveals intermediate states as targets for drug design. Nat. Commun. 5, 3397 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Sultan M. M., Kiss G., Pande V. S., Towards simple kinetic models of functional dynamics for a kinase subfamily. Nat. Chem. 10, 903–909 (2018). [DOI] [PubMed] [Google Scholar]
- 13.Hanson S. M., et al. , What makes a kinase promiscuous for inhibitors?. Cell Chem. Biol. 26, 390–399.e5 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Paul F., Meng Y., Roux B., Identification of druggable kinase target conformations using Markov model metastable states analysis of apo-Abl. J. Chem. Theor. Comput. 16, 1896–1912 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Hempel T., Plattner N., Noé F., Coupling of conformational switches in calcium sensor unraveled with local Markov models and transfer entropy. J. Chem. Theor. Comput. 16, 2584–2593 (2020). [DOI] [PubMed] [Google Scholar]
- 16.Löhr T., Kohlhoff K., Heller G. T., Camilloni C., Vendruscolo M., A kinetic ensemble of the Alzheimer’s A peptide. Nat. Comput. Sci. 1, 71–78 (2021). [DOI] [PubMed] [Google Scholar]
- 17.Silva D. A., Bowman G. R., Sosa-Peinado A., Huang X., A role for both conformational selection and induced fit in ligand binding by the LAO protein. PLoS Comput. Biol. 7, e1002054 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Kohlhoff K. J., et al. , Cloud-based simulations on Google Exacycle reveal ligand modulation of GPCR activation pathways. Nat. Chem. 6, 15–21 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Tiwary P., Limongelli V., Salvalaglio M., Parrinello M., Kinetics of protein–ligand unbinding: Predicting pathways, rates, and rate-limiting steps. Proc. Natl. Acad. Sci. U.S.A. 112, E386–E391 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Plattner N., Noé F., Protein conformational plasticity and complex ligand-binding kinetics explored by atomistic simulations and Markov models. Nat. Commun. 6, 7653 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Paul F., et al. , Protein-peptide association kinetics beyond the seconds timescale from atomistic simulations. Nat. Commun. 8, 1095 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Taylor B. C., Lee C. T., Amaro R. E., Structural basis for ligand modulation of the CCR2 conformational landscape. Proc. Natl. Acad. Sci. U.S.A. 116, 8131–8136 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Plattner N., Doerr S., Fabritiis G. D., Noé F., Complete protein–protein association kinetics in atomic detail revealed by molecular dynamics simulations and Markov modelling. Nat. Chem. 9, 1005–1011 (2017). [DOI] [PubMed] [Google Scholar]
- 24.Olsson S., Noé F., Dynamic graphical models of molecular kinetics. Proc. Natl. Acad. Sci. U.S.A. 116, 15001–15006 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Adami C., Ofria C., Collier T. C., Evolution of biological complexity. Proc. Natl. Acad. Sci. U.S.A. 97, 4463–4468 (2000). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.McShea D. W., Brandon R. N., Biology’s First Law: The Tendency for Diversity and Complexity to Increase in Evolutionary Systems (University of Chicago Press, Chicago, IL, 2010). [Google Scholar]
- 27.Wolf Y. I., Katsnelson M. I., Koonin E. V., Physical foundations of biological complexity. Proc. Natl. Acad. Sci. U.S.A. 115, E8678–E8687 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Marsh J. A., Teichmann S. A., Structure, dynamics, assembly, and evolution of protein complexes. Annu. Rev. Biochem. 84, 551–575 (2015). [DOI] [PubMed] [Google Scholar]
- 29.Dibak M., del Razo M. J., De Sancho D., Schütte C., Noé F., MSM/RD: Coupling Markov state models of molecular kinetics with reaction-diffusion simulations. J. Chem. Phys. 148, 214107 (2018). [DOI] [PubMed] [Google Scholar]
- 30.M. J. del Razo, M. Dibak, C. Schütte, F. Noé, Multiscale molecular kinetics by coupling Markov state models and reaction-diffusion dynamics. arXiv [Preprint] (2021). https://arxiv.org/abs/2103.06889 (Accessed 20 July 2021).
- 31.Ponting C. P., Russell R. R., The natural history of protein domains. Annu. Rev. Biophys. Biomol. Struct. 31, 45–71 (2002). [DOI] [PubMed] [Google Scholar]
- 32.Halabi N., Rivoire O., Leibler S., Ranganathan R., Protein sectors: Evolutionary units of three-dimensional structure. Cell 138, 774–786 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Tong Y., Hughes D., Placanica L., Buck M., When monomers are preferred: A strategy for the identification and disruption of weakly oligomerized proteins. Structure 13, 7–15 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Hodgkin A. L., Huxley A. F., A quantitative description of membrane current and its application to conduction and excitation in nerve. J. Physiol. 117, 500–544 (1952). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Noble D., Cardiac action and pacemaker potentials based on the Hodgkin-Huxley equations. Nature 188, 495–497 (1960). [DOI] [PubMed] [Google Scholar]
- 36.Clancy C. E., Rudy Y., Linking a genetic defect to its cellular phenotype in a cardiac arrhythmia. Nature 400, 566–569 (1999). [DOI] [PubMed] [Google Scholar]
- 37.Fink M., Noble D., Markov models for ion channels: Versatility versus identifiability and speed. Philos. Trans. Math. Phys. Eng. Sci. 367, 2161–2179 (2009). [DOI] [PubMed] [Google Scholar]
- 38.Sigg D., Modeling ion channels: Past, present, and future. J. Gen. Physiol. 144, 7–26 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Moreno J. D., Lewis T. J., Clancy C. E., Parameterization for in-silico modeling of ion channel interactions with drugs. PloS One 11, e0150761 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Noé F., Nüske F., A variational approach to modeling slow processes in stochastic dynamical systems. Multiscale Model. Simul. 11, 635–655 (2013). [Google Scholar]
- 41.Wu H., Noé F., Variational approach for learning Markov processes from time series data. J. Nonlinear Sci. 30, 23–66 (2019). [Google Scholar]
- 42.Schütte C., Fischer A., Huisinga W., Deuflhard P., A direct approach to conformational dynamics based on Hybrid Monte Carlo. J. Comput. Phys. 151, 146–168 (1999). [Google Scholar]
- 43.Nüske F., Keller B. G., Pérez-Hernández G., Mey A. S. J. S., Noé F., Variational approach to molecular kinetics. J. Chem. Theor. Comput. 10, 1739–1752 (2014). [DOI] [PubMed] [Google Scholar]
- 44.McGibbon R. T., Pande V. S., Variational cross-validation of slow dynamical modes in molecular kinetics. J. Chem. Phys. 142, 124105 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Mardt A., Pasquali L., Wu H., Noé F., VAMPnets for deep learning of molecular kinetics. Nat. Commun. 9, 5 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Satake I., “Linear algebra” inPure and Applied Mathematics, Taft E. J., Hewitt E., Eds. (Dekker, New York, NY, 1975), pp. 231–243. [Google Scholar]
- 47.Mardt A., Pasquali L., Noé F., Wu H., “Deep learning Markov and Koopman models with physical constraints” in Proceedings of the First Mathematical and Scientific Machine Learning Conference, Proceedings of Machine Learning Research, Lu J, Ward R, Eds. (PMLR, Princeton University, Princeton, NJ, 2020), vol. 107, pp. 451–475. [Google Scholar]
- 48.Xie T., France-Lanord A., Wang Y., Shao-Horn Y., Grossman J. C., Graph dynamical networks for unsupervised learning of atomic scale dynamics in materials. Nat. Commun. 10, 2667 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Mezić I., Analysis of fluid flows via spectral properties of the Koopman operator. Annu. Rev. Fluid Mech. 45, 357–378 (2013). [Google Scholar]
- 50.Wu H., et al. , Variational Koopman models: Slow collective variables and molecular kinetics from short off-equilibrium simulations. J. Chem. Phys. 146, 154104 (2017). [DOI] [PubMed] [Google Scholar]
- 51.Clare J. J., Targeting voltage-gated sodium channels for pain therapy. Expert Opin. Invest. Drugs 19, 45–62 (2010). [DOI] [PubMed] [Google Scholar]
- 52.Ashcroft F., Ion Channels and Disease: Channelopathies (Academic Press, 2000). [Google Scholar]
- 53.Flood E., Boiteux C., Lev B., Vorobyov I., Allen T. W., Atomistic simulations of membrane ion channel conduction, gating, and modulation. Chem. Rev. 119, 7737–7832 (2019). [DOI] [PubMed] [Google Scholar]
- 54.Rudy Y., Silva J. R., Computational biology in the study of cardiac ion channels and cell electrophysiology. Q. Rev. Biophys. 39, 57–116 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Deuflhard P., Huisinga W., Fischer A., Schütte C., Identification of almost invariant aggregates in reversible nearly uncoupled Markov chains. Lin. Algebra Appl. 315, 39–59 (2000). [Google Scholar]
- 56.Röblitz S., Weber M., Fuzzy spectral clustering by PCCA+: Application to Markov state models and data classification. Adv. Data Anal. Classif. 7, 147–179 (2013). [Google Scholar]
- 57.Noé F., et al. , Dynamical fingerprints for probing individual relaxation processes in biomolecular dynamics with simulations and kinetic experiments. Proc. Natl. Acad. Sci. U.S.A. 108, 4822–4827 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Buchete N. V., Hummer G., Coarse master equations for peptide folding dynamics. J. Phys. Chem. B 112, 6057–6069 (2008). [DOI] [PubMed] [Google Scholar]
- 59.Hagberg A. A., Schult D. A., Swart P. J., “Exploring network structure, dynamics, and function using NetworkX” in Proceedings of the 7th Python in Science Conference, Varoquaux G., Vaught T., Millman J., Eds. (SciPy, Austin, TX, 2008), pp. 11–15. [Google Scholar]
- 60.Fruchterman T. M. J., Reingold E. M., Graph drawing by force-directed placement. Software Pract. Ex. 21, 1129–1164 (1991). [Google Scholar]
- 61.Südhof T. C., Neurotransmitter release: The last millisecond in the life of a synaptic vesicle. Neuron 80, 675–690 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Lindorff-Larsen K., Piana S., Dror R. O., Shaw D. E., How fast-folding proteins fold. Science 334, 517–520 (2011). [DOI] [PubMed] [Google Scholar]
- 63.Wehmeyer C., et al. , Introduction to Markov state modeling with the PyEMMA software [Article v1.0]. LiveCoMS 1, 5965 (2018). [Google Scholar]
- 64.Virtanen P., et al. , SciPy 1.0: Fundamental algorithms for scientific computing in python. Nat. Methods 17, 261–272 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Scherer M. K., et al. , PyEMMA 2: A software package for estimation, validation, and analysis of Markov models. J. Chem. Theor. Comput. 11, 5525–5542 (2015). [DOI] [PubMed] [Google Scholar]
- 66.Hempel T., et al. , Independent Markov decomposition. Zenodo. 10.5281/ZENODO.5091726. Deposited 27 May 2021. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The code that implements our discrete models, generates the data, and reproduces the presented results can be found in our GitHub repository (https://github.com/markovmodel/decomposed_msms) (66). The molecular dynamics dataset of Synaptotagmin C2A is available upon request. Some study data are available upon request.