Iterative single-cell multi-omic integration using online learning

Abstract

Integrating large single-cell gene expression, chromatin accessibility and DNA methylation datasets requires general and scalable computational approaches. Here we describe online integrative nonnegative matrix factorization (iNMF), an algorithm for integrating large, diverse, and continually arriving single-cell datasets. Our approach scales to arbitrarily large numbers of cells using fixed memory, iteratively incorporates new datasets as they are generated, and allows many users to simultaneously analyze a single copy of a large dataset by streaming it over the internet. Iterative data addition can also be used to map new data to a reference dataset. Comparisons with previous methods indicate that the improvements in efficiency do not sacrifice dataset alignment and cluster preservation performance. We demonstrate the effectiveness of online iNMF by integrating more than a million cells on a standard laptop, integrating large single-cell RNA-seq and spatial transcriptomic datasets, and iteratively constructing a single-cell multi-omic atlas of the mouse motor cortex.

Editorial summary:

A new algorithm enables scalable and iterative integration of single-cell datasets.

Introduction

Cell types have long been qualitatively characterized by a combination of features such as morphology, presence or absence of cell surface proteins, and broad function¹. Recently, high-throughput single-cell sequencing technologies have enabled researchers to profile multiple molecular modalities, including gene expression, chromatin accessibility and DNA methylation². Integrating diverse single-cell datasets offers tremendous opportunities for unbiased, comprehensive, quantitative definition of discrete cell types and continuous cell states.

Several recent single-cell data integration approaches have been developed, including Seurat v3 and Harmony^2–4, but these approaches are not designed to integrate multiple modalities or do not scale to massive datasets. Furthermore, none of these existing methods can incorporate new data without recalculating from scratch.

We address these limitations by developing online iNMF, an algorithm that allows scalable and iterative integration of single-cell datasets generated by different omics technologies. We extend the nonnegative matrix factorization approach at the heart of our recently published LIGER method⁵ to develop an online learning algorithm (Fig. 1a). LIGER infers a set of latent factors (“metagenes”) that represent the same biological signals in each dataset while also retaining the ways in which these signals differ across datasets; these shared and dataset-specific factors are then jointly used to identify cell types and states while also identifying and retaining cell-type-specific differences in the metagene features that define cell identities. In the present study, we combine LIGER with techniques for “online learning”⁶, in which calculations are performed iteratively and incrementally as new datasets become available. Note that online learning is a technical term that does not refer to the internet—an online learning algorithm is not necessarily a web tool, although internet applications with continually arriving data often benefit from such approaches. Online iNMF enables scalable and efficient data integration with fixed memory usage, as well as incorporating new data without recalculating from scratch.

Figure 1. Overview of the online iNMF algorithm.

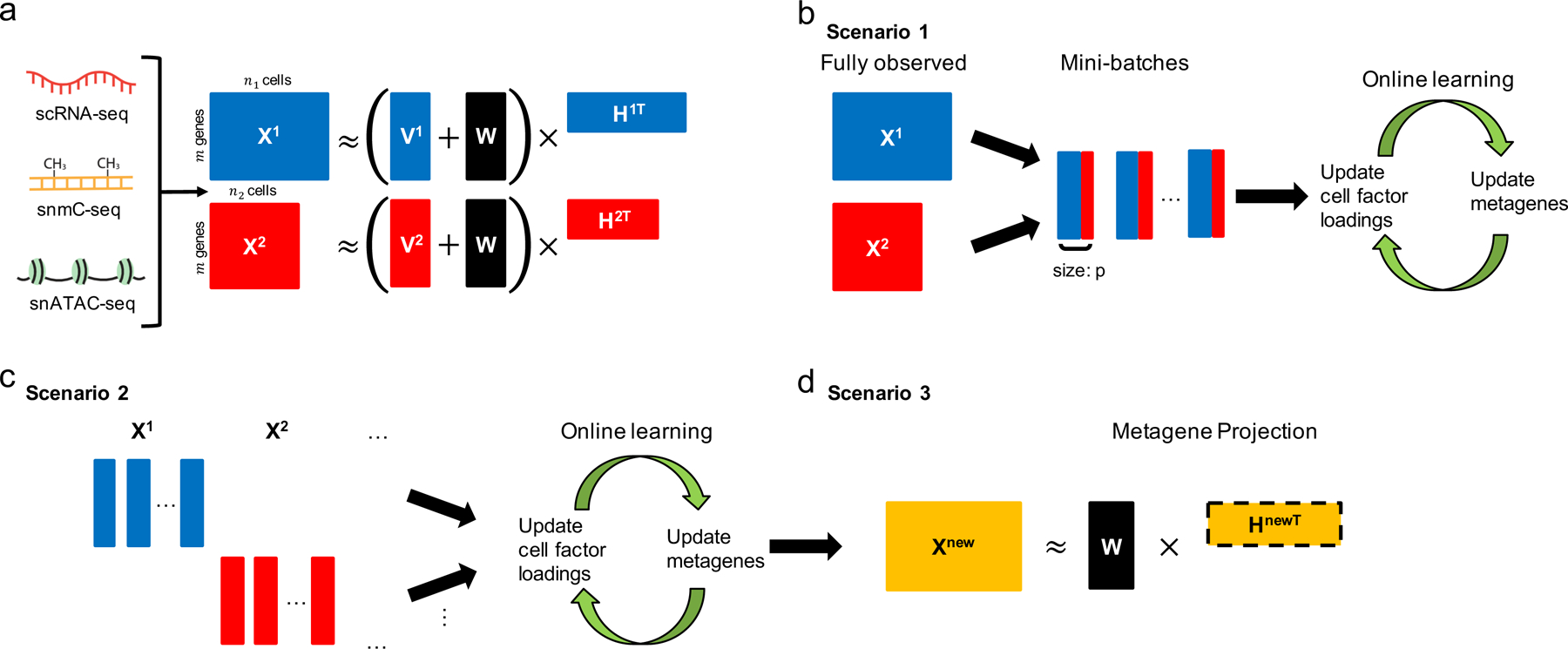
a, Schematic of integrative nonnegative matrix factorization (iNMF): the input single-cell datasets are jointly decomposed into shared $\left(W\right)$ and dataset-specific $\left(V^i\right)$ metagenes and corresponding “metagene expression levels” or cell factor loadings $\left(H^i\right)$. These metagenes and cell factor loadings provide a quantitative definition of cell identity and how it varies across biological settings. b-d, Three different scenarios in which online learning can be used for single-cell data integration. (b) Scenario 1: the single-cell datasets are large but fully observed. Online iNMF processes the data in random mini-batches, enabling memory usage and/or disk storage independent of dataset size. Each cell may be used multiple times in different epochs of training to update the metagenes. (c) Scenario 2: the datasets arrive sequentially, and online iNMF processes the datasets as they arrive, using each cell to update the metagenes exactly once. (d) Scenario 3: online iNMF is performed as in scenario 1 or scenario 2 to learn $W$ and $V^i$. Then cell factor loadings for the newly arriving dataset are calculated using the shared metagenes $\left(W\right)$ learned from previously processed datasets. The new dataset is not used to update the metagenes.

Results

An Online Learning Algorithm for Iterative Single-Cell Multi-Omic Integration

We developed an algorithm for online iNMF inspired by the online nonnegative matrix factorization approach of Mairal et al.⁶. Online iNMF provides two significant advantages: (1) integration of large single-cell multi-omic datasets by cycling through the data multiple times in small mini-batches and (2) integration of continually arriving datasets, where the entire dataset is not available at any point during training.

We envision using online iNMF to integrate single-cell datasets in three different scenarios. In scenario 1, where the datasets are large and fully observed, the algorithm accesses mini-batches from all datasets at the same time and repeatedly updates the metagenes $\left(W,V^i\right)$ and cell factor loadings $\left(H^i\right)$. Each cell can be revisited throughout multiple epochs of training (Fig. 1b). A key advantage of scenario 1 (compared to batch iNMF) is that only a single mini-batch needs to be in memory at a time. Scenario 1 even allows processing of large datasets without downloading them to disk, by streaming them over the internet. In scenario 2, the input datasets arrive sequentially, and the online algorithm uses each cell exactly once to update the metagenes, without revisiting data already seen (Fig. 1c). The key advantage of scenario 2 is that the factorization is efficiently refined as new data arrive, without requiring expensive recalculation each time. A third scenario allows us to project new data into the latent space already learned, without using the new data to update the metagenes. In scenario 3, we first use online iNMF to learn metagenes as in scenario 1 or scenario 2. Then, we use the shared metagenes $\left(W\right)$ to calculate cell factor loadings for a new dataset, without using the new data to update the metagenes. Scenario 3 efficiently incorporates new data without changing the existing integration results, allowing users to query their data against a curated reference (Fig. 1d).

Online iNMF Converges Efficiently Without Loss of Accuracy Compared to Batch iNMF

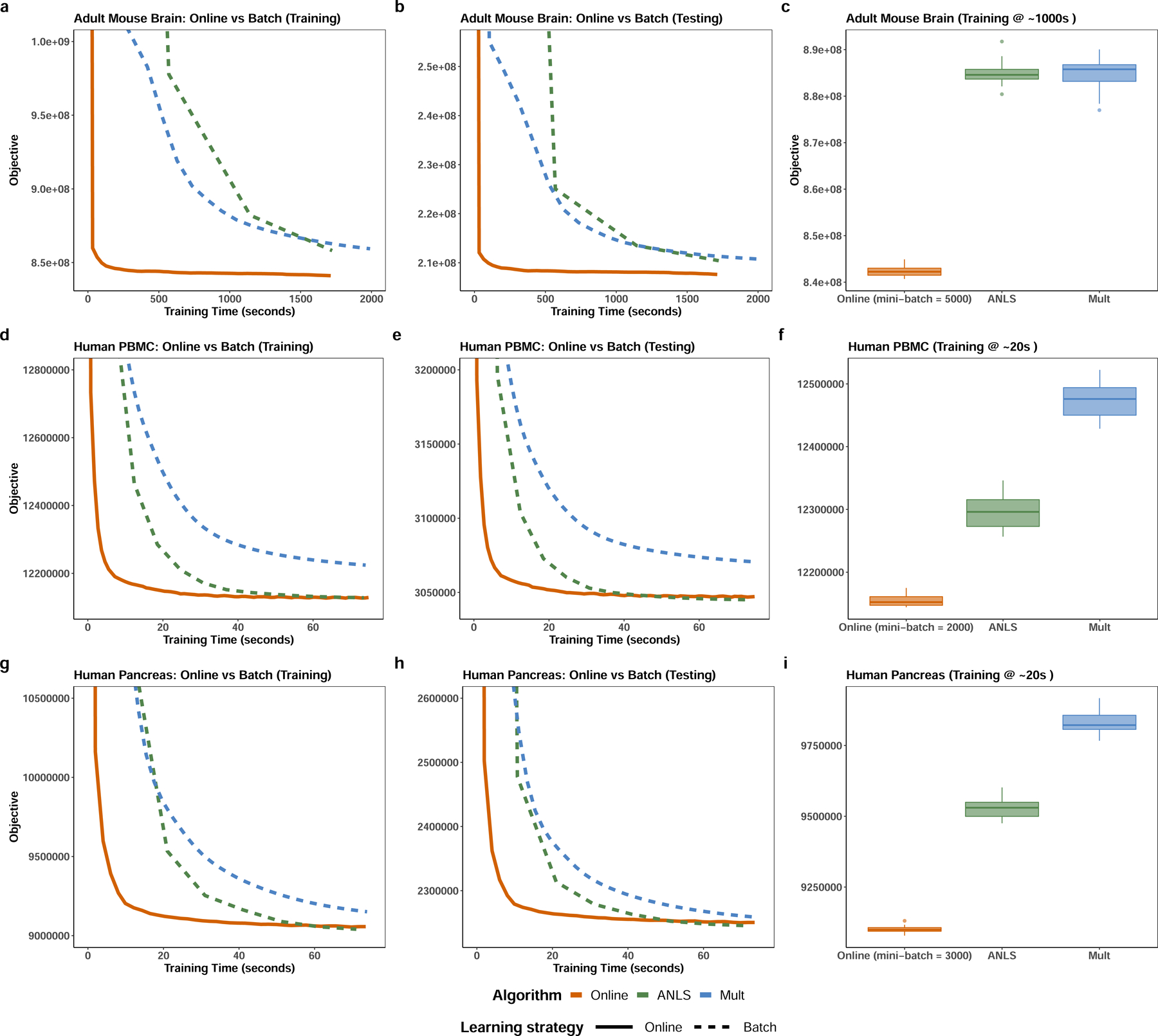
In our first experiment, we evaluated the convergence performance of the online iNMF algorithm on the adult mouse cortex dataset⁷, which comprises 156,167 cells from the frontal cortex and 99,186 cells from the posterior cortex. The online iNMF algorithm converges much faster than previous batch iNMF algorithms on both the training set and a held-out test set (Fig. 2a–b), converging to a significantly lower training iNMF objective in a fixed amount of time (Fig. 2c). Online iNMF also shows superior performance on several other datasets from different biological contexts (Extended Data Fig. 1). Furthermore, the convergence behavior of the online algorithm on both training and test sets is relatively insensitive to the mini-batch size (Fig. 2d–e).

Figure 2. Online iNMF converges much faster than previously published batch algorithms.

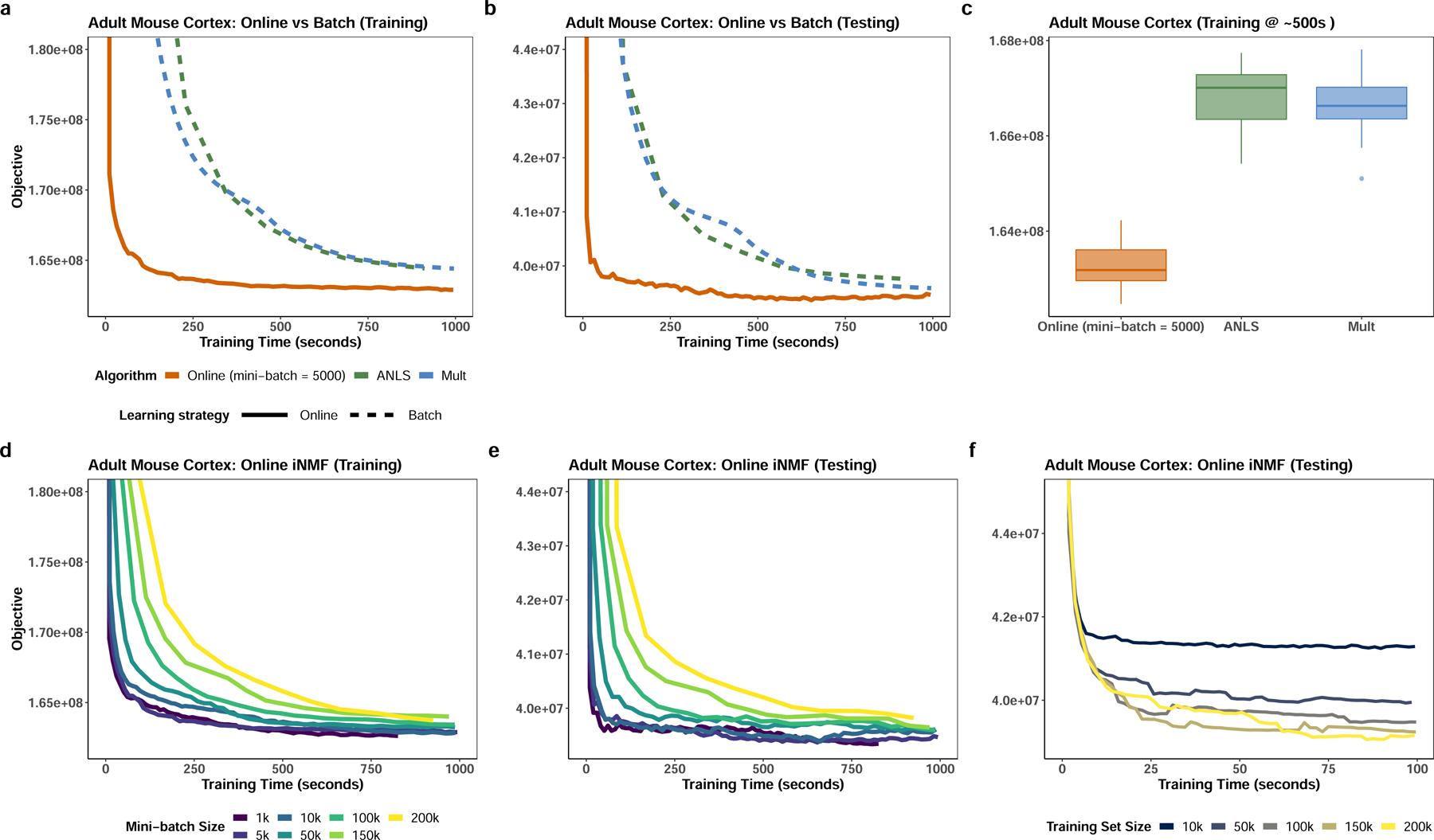
a,b, The online iNMF algorithm converges much more rapidly to a similar or better objective function value compared to the previously published batch methods--alternating nonnegative least squares (ANLS) and multiplicative updates (Mult)—on both training and testing sets. c, Box plots comparing the objective function values achieved by applying online and batch iNMF algorithms on the mouse cortex data $\left(n=255,353\right)$ after a fixed amount of training time. Center line shows the median; box limits, upper and lower quartiles; whiskers, 1.5x interquartile range; and points are outliers. d-e, The convergence behavior of online iNMF is nearly identical for mini-batch sizes from 1,000 to 10,000. f, The online iNMF algorithm becomes increasingly efficient (in terms of decrease in objective function value per unit time) as dataset size increases. The time required for the algorithm to converge does not significantly increase with growing dataset size once the dataset size exceeds 50,000 cells.

Moreover, for a fixed test set, the runtime needed to reach convergence remains nearly constant once the total number of cells exceeds some minimum threshold (around 50,000, in this case). (Fig. 2f). This behavior likely occurs because, for a cell population of fixed complexity (for example, a tissue containing 12 cell types), only some fixed number of observations is required to effectively learn the metagenes. Thus, using the entire dataset to update the shared and data-specific metagenes at each iteration becomes increasingly inefficient as the dataset size exceeds the minimum threshold size needed to learn the metagenes. Conversely, the relative efficiency of online iNMF compared to batch methods increases with dataset size.

Next we investigated whether online iNMF yields similar dataset alignment and cluster preservation to our previously published alternating nonnegative least squares (ANLS) algorithm. (We refer to the ANLS algorithm as batch iNMF in subsequent discussions, to distinguish it from online iNMF.) We applied both online iNMF and batch iNMF to three scRNA-seq data collections, then visualized the factor loadings using UMAP plots (Extended Data Fig. 2). The online iNMF algorithm yields visualizations that are qualitatively very similar to batch iNMF, suggesting nearly identical dataset alignment and accurate preservation of the original cluster structure for all three data collections.

Online iNMF Yields State-of-the-Art Single-Cell Data Integration Results Using Significantly Less Time and Memory

We next benchmarked online iNMF (scenario 1) against batch iNMF⁵ and two state-of-the-art single-cell data integration methods, Seurat v3² and Harmony⁴. We selected these methods for comparison because a recent paper benchmarked 14 single-cell data integration methods and found that Harmony, Seurat, and LIGER consistently achieved the best dataset alignment and cluster preservation on a range of datasets⁸.

To benchmark time and memory usage, we generated five datasets of increasing sizes (ranging from 10,000 to 255,353 cells in total) sampled from the same adult mouse frontal and posterior cortex data. Then we utilized them to compare the runtime and peak memory usage of online iNMF (mini-batch size = 5,000) and the other methods (Fig. 3a).

Figure 3. Benchmark of online iNMF, batch iNMF, Harmony, and Seurat.

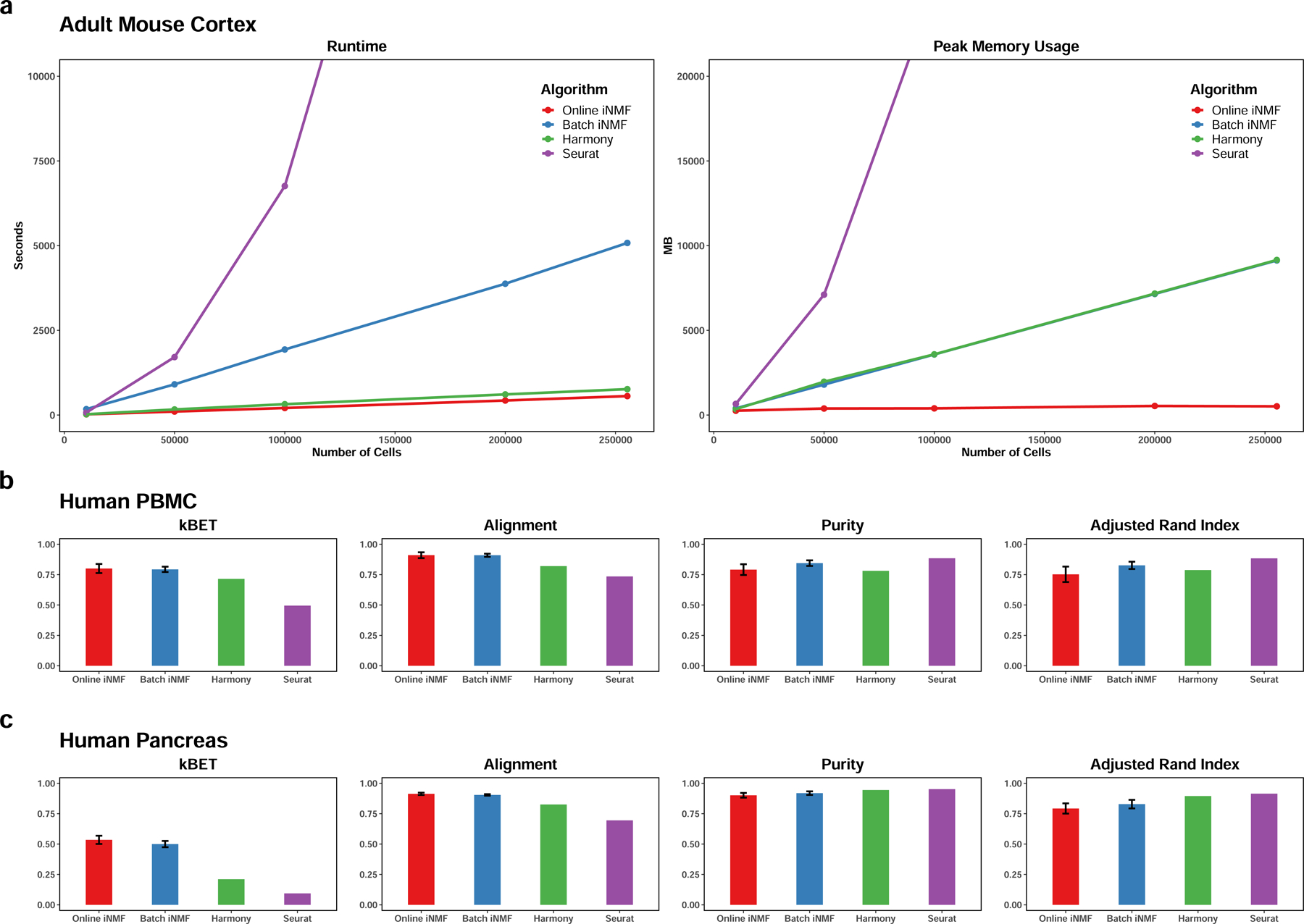
The data are sampled from the adult mouse cortex ($n=10,000, 50,000, 100,000, 200,000, 255,353\text{ cells}$, 2 individual datasets), human PBMC ($n=13,999\hspace{0.17em}\text{cells}$, 2 individual datasets) and human pancreas ($n=14,890\hspace{0.17em}\text{cells}$, 8 individual datasets). a, The runtime and peak memory usage required for online iNMF, batch iNMF, Harmony and Seurat to integrate the frontal and posterior cortex datasets. b,c, Quantitative assessment of data integration and low-dimensional embedding carried out by four methods on the human PBMC and human pancreas datasets. Higher values are better for all 4 metrics. Error bars indicate standard deviation across 100 random initializations. The results from iNMF approaches (100 initializations each) are presented as $\text{mean}\hspace{0.17em}\text{values}\pm \text{standard deviation}$, while Harmony and Seurat were only run once.

As expected, the runtime required for online iNMF does not increase significantly as the dataset size grows, and the amount of memory needed for storing each minibatch is independent of the total number of cells. Online iNMF is also the fastest method overall, with Harmony the second fastest. Notably, the gap between Harmony and online iNMF widens as the dataset size increases; on a dataset of 1.3 million cells from the mouse embryo, online iNMF finishes dimension reduction in 25 minutes using 1.9 GB of RAM on a laptop, whereas Harmony requires 98 minutes and 109 GB of RAM on a large-memory server. Seurat and batch iNMF are significantly slower than online iNMF and Harmony on the mouse cortex data, and the runtime of Seurat increases the most rapidly of any method.

Furthermore, the online iNMF algorithm uses far less memory than any other approach, with memory usage primarily determined by mini-batch size, which is independent of the number of cells. Updating the factors with a mini-batch size of 5,000 and $K=40$ factors requires less than 500MB. In contrast, the memory requirements of batch iNMF, Harmony, and Seurat grow quickly with dataset size.

Next, we quantified the dataset alignment and cluster preservation performance for online iNMF and the other methods (Fig. 3b–c). Following the benchmarking strategy used by Tran et al., we assessed both the alignment performance (measured using two metrics) and cluster preservation performance (measured using two metrics). Our results show that online iNMF performs as well as or better than the state-of-the-art methods. The online and batch iNMF algorithms align the PBMC⁹ and pancreas^10–14 datasets equally well, beating Harmony and Seurat. Furthermore, the online algorithm achieves scores close to batch iNMF on both data collections, confirming that the gain in computational efficiency does not come at the cost of accuracy in data embedding. The difference between iNMF and the other methods is especially pronounced when comparing the values of kBET. We suspect that this difference occurs because our approach includes quantile normalization, which is stronger than the alignment strategies used by Harmony or Seurat. Consistent with our results, the benchmark of Tran et al. also included the pancreas dataset and found that LIGER (batch iNMF) gave substantially higher kBET values than competing methods⁸. The online and batch iNMF algorithms produce comparable clustering results to the other approaches, although Harmony and Seurat give slightly higher cluster purity and adjusted rand index. This may be because the cluster labels we used for comparison are not real ground truth, but derived from PCA followed by clustering, which is more similar to the approaches used by Harmony and Seurat.

We also compared the performance of online iNMF, Seurat, Harmony and BBKNN when integrating two datasets of different modalities (Extended Data Fig. 3). Harmony and BBKNN showed inferior alignment, possibly because these approaches were not originally designed for multi-modal integration, unlike LIGER and Seurat. In contrast, both LIGER and Seurat produced UMAP visualizations indicating successful alignment of snRNA-seq and snATAC-seq data. Furthermore, the kBET and alignment metrics indicate that LIGER (alignment score = 0.714, kBET = 0.574) better integrates that datasets than either Seurat (alignment score = 0.481, kBET = 0.231) or Harmony (alignment score = 0.113, kBET = 0.041).

Online iNMF Rapidly Factorizes Large Datasets Using Fixed Memory

To demonstrate the scalability of our approach, we used online iNMF (scenario 1) to analyze the scRNA-seq data of Saunders et al., which contains 691,962 cells sampled from nine regions (stored in nine individual datasets) spanning the entire mouse brain. Using online iNMF, we factorized all of the datasets in 24 minutes on a MacBook Pro using about 1 GB of RAM. We note that the published analysis by Saunders et al. did not analyze all nine tissues simultaneously due to computational limitations, and that performing this analysis using our previous batch algorithm would have taken approximately 3.8 hours and 25 GB of RAM.

Cells within each class are well grouped together, and the distribution of neurons varies widely across regions, indicating neuronal subtypes specialized to different parts of the brain (Fig. 4a). For example, neurogenic cells are identified predominantly in the hippocampus and striatum, consistent with reports of hippocampal and striatal neurogenesis in adult mammals^7,15,16.

Figure 4. Joint analysis of nine regions of the adult mouse brain $\left(n=\text{691,962}\hspace{0.17em}\text{cells}\right)$ using online iNMF.

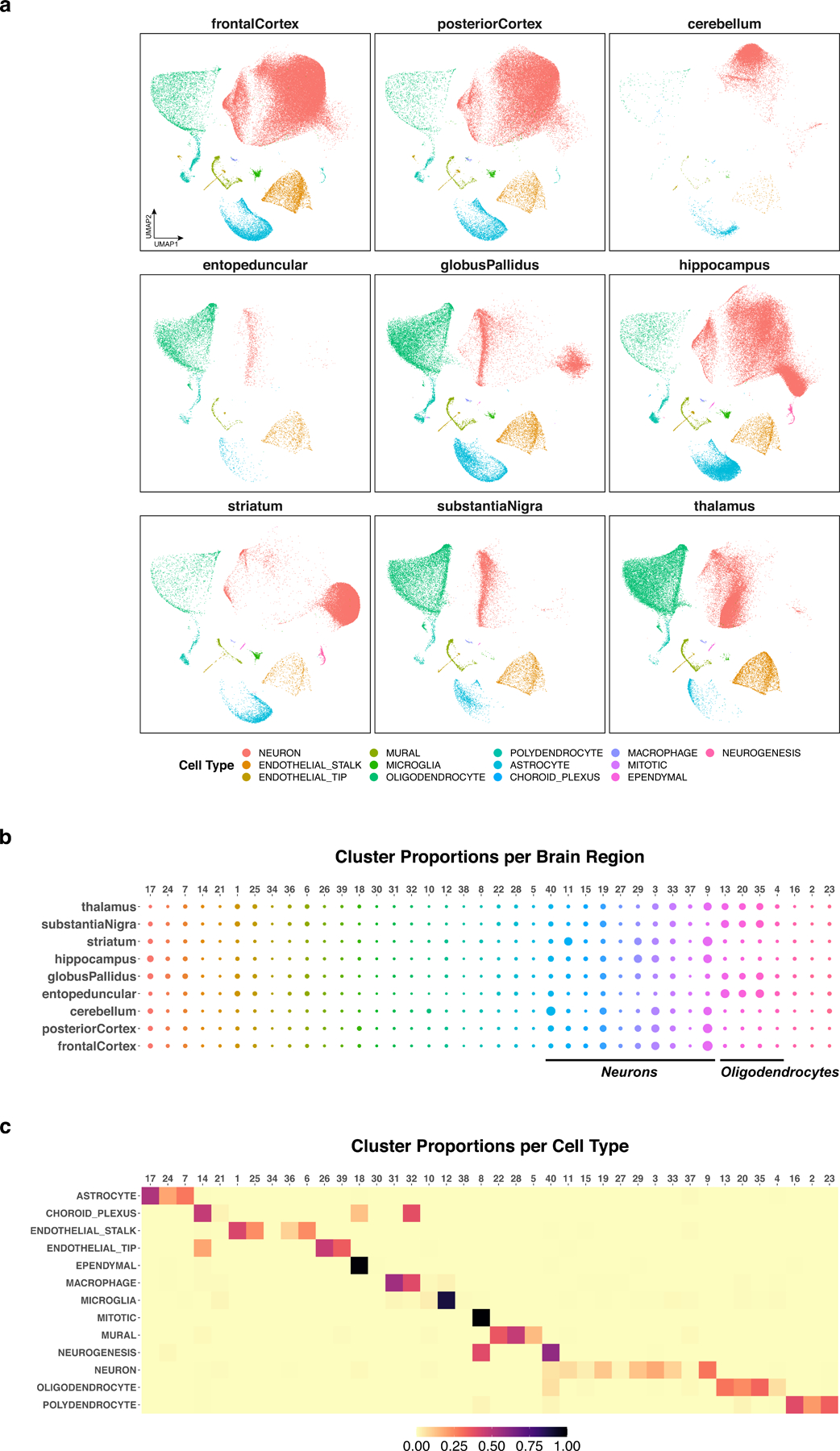
a, UMAP visualization of the iNMF factors learned for each brain region, colored by published cell class. b, Dot plot showing the proportion of each of 40 clusters inferred from iNMF in each brain region. c, Proportion of cells from each cluster in every cell type. The cells in each cluster mostly correspond to a single cell type.

We used the factorization to group the cells into 40 clusters by assigning each cell to the factor on which it has the largest loading. We then examined differences in the regional proportions of each cell cluster. Neurons and oligodendrocytes show the most regional variation in composition, consistent with previous analyses¹⁷. The total proportion of oligodendrocytes varies by region, but individual subtypes of oligodendrocytes are not region-specific, as expected. In contrast, individual subtypes of neurons are highly region-specific, reflecting diverse regional specializations in neuronal function (Fig. 4b). We also investigated the biological properties of these cell factor loadings. Reassuringly, our cluster assignments largely represent subtypes within the broad cell classes and do not span class boundaries. As expected, neurons show by far the most diversity with eight subclusters. In contrast, ependymal cells, macrophages, microglia, and mitotic cells each correspond to only a single cluster (Fig. 4c).

To further demonstrate the scalability of online iNMF, we analyzed the mouse organogenesis cell atlas (MOCA) recently published by Cao et al.¹⁸. After filtering, MOCA contains 1,363,063 cells from embryos between 9.5 to 13.5 days of gestation. We performed online iNMF on this dataset in 25 min using about 1.9 GB of RAM on a MacBook Pro. By comparison, we were not able to run Harmony on a laptop because of its high memory usage; running Harmony on a large-memory server required 98 minutes and 109 GB of RAM. Note that online iNMF’s memory usage is higher for MOCA than for the mouse brain dataset primarily because of the higher value of $K$ and a larger number of variable genes, not because of the number of cells. UMAP visualization shows that the cells from all five gestational ages are well aligned (Fig. S1a), and the structure of 10 different developmental trajectories as defined by Cao et al. is also accurately preserved (Fig. S1b).

Because online iNMF processes only one mini-batch at a time, our approach allows processing datasets by streaming them over the internet instead of from disk. To demonstrate this capability, we created an HDF5 file containing the mouse cortex datasets (255,353 cells), saved the file on a remote server, then read mini-batches directly over the internet. Processing the cortex dataset in this fashion took about 18 minutes, compared to around 6 minutes using local disk reads. This capability provides the unique advantage that many users can simultaneously analyze a single copy of a large cell atlas, without requiring each user to download and store the entire data collection.

Online iNMF Efficiently Integrates Large Single-Cell RNA and Spatial Transcriptomic Datasets

We next used online iNMF to integrate single-cell RNA-seq and spatial transcriptomic datasets (Slide-seq and MERFISH). These spatial transcriptomic protocols provide spatial coordinates, but each has tradeoffs compared to scRNA-seq: Slide-seq may capture multiple cells on each barcoded bead and provides sparse transcriptome-wide measurements^19,20, and MERFISH measures only selected genes²¹. Integration with scRNA-seq data mitigates these limitations by incorporating deeper, transcriptome-wide data. Both spatial technologies can measure millions of cells, necessitating scalable methods for integration.

We used online iNMF in scenario 3 to project Slide-seq data from mouse hippocampus (59,858 beads) onto a large single-cell RNA-seq dataset (193,155 cells)^19,22. Each Slide-seq bead may contain transcripts from more than one cell; thus, identifying $H^i$ using $W$ serves as a “deconvolution” operation in this case¹⁹. The original Slide-seq paper performed a similar analysis using conventional nonnegative matrix factorization of single-cell RNA-seq data¹⁹. Consistent with the published analysis, we found that most Slide-seq beads contained a single dominant cell type, though a small number contained two cell types or no clear cell types (Fig. 5b). Overall, the proportions of cell types were consistent across technologies, except that the scRNA-seq data contained fewer non-neurons, because the cells were experimentally enriched for neurons (Fig. 5a). The spatial distributions of our annotated cell types reflect the known organization of the hippocampus, with Ammon’s horn, dentate gyrus, white matter, part of the ventricles, and adjacent deep cortical layers clearly visible (Fig. 5c). Thus, this integration reveals the spatial distributions of the clusters from the scRNA-seq data (Fig. 5d).

Figure 5. Online iNMF integrates large single-cell RNA-seq and spatial transcriptomic datasets.

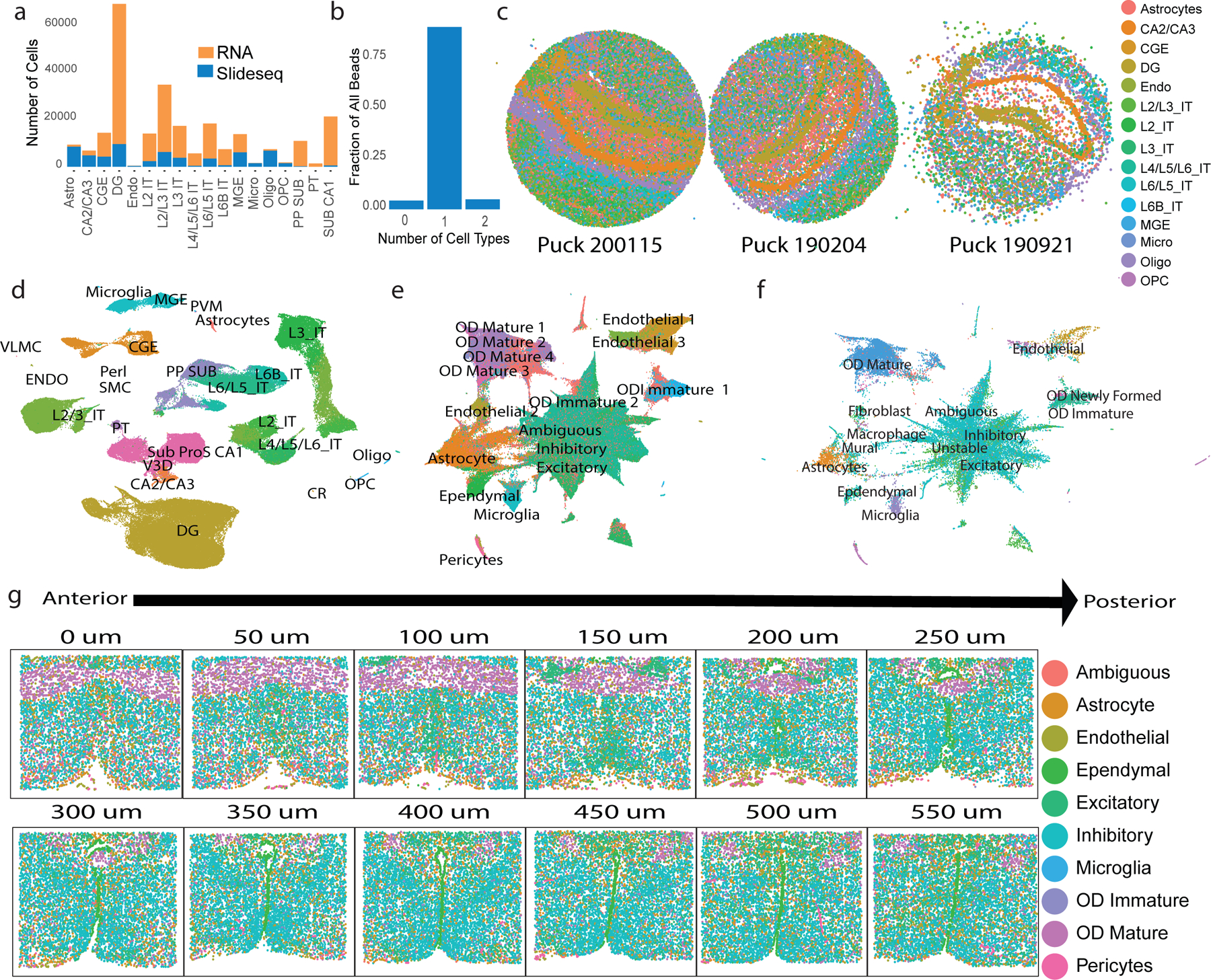
a, The number of cells per cell type in scRNA-seq $\left(n=193,155 cells\right)$ and Slide-seq $\left(n=59,858\hspace{0.17em}\text{beads}\right)$ datasets from mouse hippocampus. b, Number of cell types assigned to each bead in the Slide-seq analysis. c, Slide-seq beads colored by labels derived from projection onto scRNA-seq data using online iNMF (scenario 3). The coordinates of each bead reflect its spatial position within the tissue. d, UMAP plot of cell factor loadings (online iNMF, scenario 1) for scRNA-seq data from mouse hippocampus. e, UMAP plot of MERFISH cells from mouse hypothalamus $\left(n=1,026,840\hspace{0.17em}\text{cells}\right)$, colored by published cluster assignments. The UMAP coordinates are derived from online iNMF (scenario 3) integration of MERFISH and scRNA-seq data. f, UMAP plot of scRNA-seq cells from mouse hypothalamus $\left(n=31,250\hspace{0.17em}\text{cells}\right)$, colored by published cluster assignments. The UMAP coordinates are derived from online iNMF (scenario 3) integration of MERFISH and scRNA-seq. g, MERFISH slices, ordered from anterior to posterior, colored by labels derived from the online iNMF integration. The coordinates of each cell reflect its spatial position within the tissue.

We also used online iNMF (scenario 1 and 3) to integrate MERFISH (1,026,840 cells) and scRNA-seq (31,250 cells) data from the preoptic region of mouse hypothalamus²³. Scenario 1 and scenario 3 gave very similar results (Fig. S2). This integration analysis revealed the correspondence between scRNA-seq and MERFISH clusters (Fig. 5e–f), which had been analyzed only separately in the original publication. The spatial distributions of our joint clusters accord well with the known structure of the hypothalamus (Fig. 5g).

Online iNMF Enables Iterative Refinement of Single-Cell Multi-Omic Atlas from Mouse Motor Cortex

One of the most appealing properties of our online learning algorithm is the ability to incorporate new data points as they arrive. This capability is especially useful for large, distributed collaborative efforts to construct comprehensive cell atlases^24–26. Such cell atlas projects involve multiple research groups asynchronously generating experimental data with constantly evolving protocols, making the ultimate cell type definition a moving target.

To demonstrate the utility of online iNMF for iteratively refining cell type definitions, we used data generated by the BRAIN Initiative Cell Census Network (BICCN)²⁷. During a pilot phase starting in 2018, the BICCN generated single-cell datasets from a single region of mouse brain (primary motor cortex, MOp) spanning 4 modalities (single-cell RNA-seq, single-nucleus RNA-seq, single-nucleus ATAC-seq, single-nucleus methylcytosine-seq) and totaling 786,605 cells.

Following scenario 2 (Fig. 1c), we used online iNMF to incorporate the MOp datasets in chronological order, refining the factorization with each additional dataset (Fig. 6). Our approach successfully incorporated each new single-cell or single-nucleus RNA-seq dataset without revisiting previously processed cells, using each cell exactly once during the optimization process (Fig. 6a). UMAP visualizations indicate that the structure of the datasets is iteratively refined with each successive dataset that is added. We jointly identified 15 cell types from the transcriptomic and epigenomic datasets (Fig. 6d). Alignment and kBET metrics also indicate that the datasets are well aligned (Alignment score = 0.786, kBET = 0.324). To put these numbers in context, Seurat achieved scores of 0.481 and 0.231 on a simpler integration analysis of one scRNA-seq and one snATAC-seq dataset (Extended Data Fig. 3).

Figure 6. Iterative refinement of cell identity using multiple single-cell modalities from the mouse primary motor cortex.

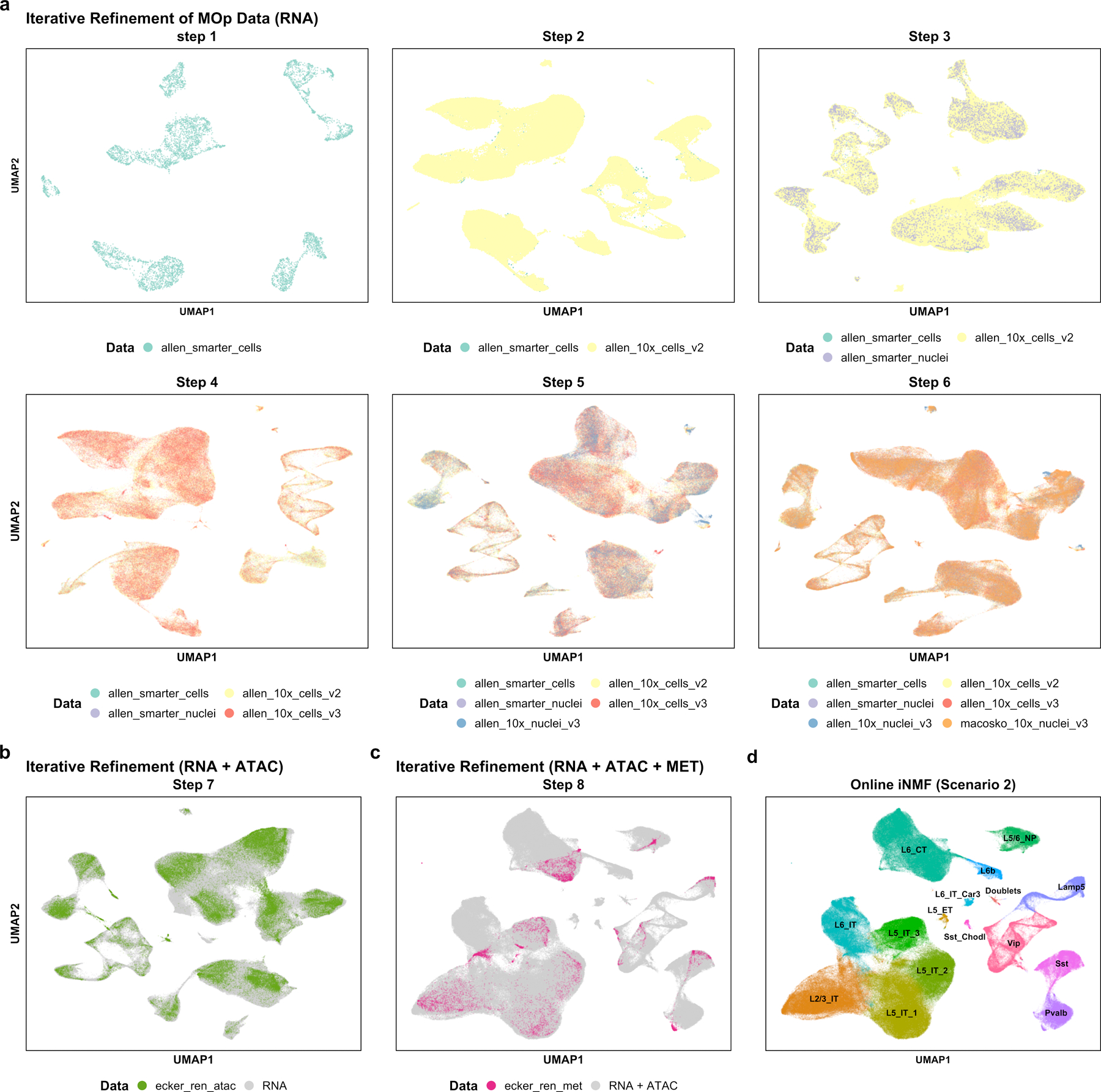
We integrated four scRNA-seq datasets, two snRNA-seq datasets, one snATAC-seq dataset and one snmC-seq dataset $\left(n=408,885\hspace{0.17em}\text{neurons}\right)$. a, Sequential integration of six scRNA-seq datasets (scenario 2). Each panel shows a UMAP plot using cell factors obtained after adding an additional dataset. b, UMAP plot of cell factors obtained by adding snATAC-seq to the latent space learned from six RNA datasets in a (scenario 2). c, UMAP plot of cell factors obtained by adding DNA methylation data (snmC-seq, abbreviated “MET”) to the latent space learned from the seven datasets shown in b (scenario 2). d, Clusters obtained using the cell factor loadings of all eight aligned datasets. The clusters were named using marker genes from Tasic et al²⁸.

The results from performing this single-cell multi-omic integration are very similar whether the integration is performed iteratively (scenario 2), using all of the data at once (scenario 1), or by projecting the epigenomic data onto the transcriptomic data (scenario 3; Extended Data Fig. 4). We also confirmed that scenario 2 is robust to the order of dataset arrival. To do this, we inspected the effect of random initializations and orderings of the input datasets on the iterative multi-omic integration (scenario 2). We integrated all eight datasets in their original order using 10 different initializations as well as five different orderings where each of the other sc/snRNA- seq datasets served as the first input. With our annotations as the reference, different orderings result in comparable variation in final cluster assignments compared to the variation from random initialization (average ARI = 0.759 from random input orders vs. 0.744 from random initializations).

Discussion

By reading mini-batches from disk, online iNMF not only converges faster than batch approaches, but also decouples memory usage from dataset size. The efficiency gains of online iNMF will be even greater as the scale of single-cell datasets increases.

We envision online iNMF enabling iterative single-cell data integration in three different scenarios. In scenario 1, when all single-cell datasets are currently available, the online iNMF algorithm rapidly factorizes the single-cell data into metagenes and cell factor loadings using multiple epochs of training. In scenario 2, the online algorithm iteratively incorporates single-cell datasets as they arrive sequentially. We anticipate that scenario 2 will prove useful as researchers continually incorporate newly sequenced cells to build comprehensive cell atlases. Scenario 3 holds great promise for rapidly querying datasets against a large, curated reference atlas.

We anticipate that online iNMF will become increasingly useful for integrating single-cell multi-omic datasets of growing scale from projects such as the BRAIN Initiative, Human Body Map, and Human Cell Atlas.

Online Methods

About Online iNMF

Utility of Online iNMF

In this study, we extend the online NMF approach of Mairal et al.⁶ to make it suitable for iNMF. Online iNMF provides two significant advantages: (1) integration of large multi-modal datasets by cycling through the data multiple times in small mini-batches and (2) integration of continually arriving datasets, where the entire dataset is not available at any point during training (Fig. 1).

We envision using online iNMF to integrate single-cell datasets in three different scenarios (Fig. 1). We note that our online iNMF approach is distinct from stochastic gradient descent (SGD), a general optimization technique that can be used for a range of objective functions. Instead of employing SGD, we have derived an online learning algorithm specifically tailored to the iNMF objective function. Our approach has two key advantages compared to SGD: (1) SGD requires choosing a data-dependent schedule of learning rates that vary over the whole learning process, while our approach does not involve a learning rate parameter at all and (2) we use optimization techniques that leverage the unique structure of the iNMF optimization problem, allowing theoretical convergence guarantees and fast empirical convergence. Mairal et al. explain this distinction in more detail⁶.

Derivation of iNMF Updates

iNMF takes $N$ single-cell multi-omic datasets $X^1,\dots ,X^N$ as input. After normalization, gene selection ($m$ variable genes selected) and scaling, we have the preprocessed input data $X^i\in {ℝ}_{+}^{m\times n_i}\left(i=1,\dots ,N\right)$. The goal is to find the shared and dataset-specific factors (metagenes) $W\in {ℝ}_{+}^{m\times K},V^i\in {ℝ}_{+}^{m\times K}$ and $H^i\in {ℝ}_{+}^{n_i\times K}\left(i=1,\dots ,N\right)$ that minimize the following empirical cost of the iNMF problem, given parameters $K$ and λ.

$$\underset{\begin{array}{l}W,V^i,H^i\ge \text{0}\\ i=1,\dots ,N\end{array}}{\min }\sum _{i=1}^N\left({\Vert X^i-\left(W+V^i\right)H^{i\top }\Vert }_F^2+\lambda {\Vert V^i{H}^{i\top }\Vert }_F^2\right)$$

For given $W$ and $V^i$, we update $H^i$ by numerically solving a nonnegative least squares problem:

$$H^i=\underset{H\ge \text{0}}{\arg \min }{\Vert \left(\begin{array}{c}W+V^i\\ \sqrt{\lambda }{V}^i\end{array}\right)H^{\top }-\left(\begin{array}{c}{X}^i\\ {\text{0}}^{m\times n_i}\end{array}\right)\Vert }_F^2$$

We derived hierarchical alternating least squares (HALS) updates to calculate $W$ and $V^i$, holding the other two matrix blocks fixed:

$$W_{\cdot j}^{*}={\left[W_{\cdot j}+\frac{{\sum }_i{\left(X^i{H}^i\right)}_{\cdot j}-\left(W+V^i\right){\left(H^{i\top }{H}^i\right)}_{\cdot j}}{{\sum }_i{\left(H^{i\top }{H}^i\right)}_{jj}}\right]}_{+}$$

$$V_{\cdot j}^{i*}={\left[V_{\cdot j}^i+\frac{{\left(X^i{H}^i\right)}_{\cdot j}-\left(W+\left(1+\lambda \right)V^i\right){\left(H^{i\top }{H}^i\right)}_{\cdot j}}{\left(1+\lambda \right){\left(H^{i\top }{H}^i\right)}_{jj}}\right]}_{+}$$

See Supplementary Note for detailed derivation of HALS updates.

Optimizing a Surrogate Function for iNMF

We developed an online learning algorithm for integrative nonnegative matrix factorization by adapting a previously published strategy for online dictionary learning⁶. The key innovation that makes it possible to perform online learning is to optimize a “surrogate function” that asymptotically converges to the same solution as the empirical iNMF cost. In the NMF problem with a sparsity penalty (e.g. L1 regularization), we want to find the nonnegative factors $W\in {ℝ}_{+}^{m\times K}$, $H\in {ℝ}_{+}^{n\times K}$ that optimally reconstruct the input $X\in {ℝ}_{+}^{m\times n}$ ($n$ data points) by minimizing the following empirical cost function:

$$f_n\left(W\right)=\frac{1}{n}\sum _{s=1}^n\ell \left({\mathit{x}}_s,W\right)$$

$$\ell \left({\mathit{x}}_s,W\right)=\underset{\mathit{h}\ge \text{0}}{\min }\sum _{s=1}^n\left({\Vert {\mathit{x}}_s-W{\mathit{h}}_s^{\top }\Vert }_2^2+\lambda {\Vert {\mathit{h}}_s^T\Vert }_1\right)$$

where ${\mathit{x}}_s$ is the $s\text{th}$ data point and $h$ represents a row of $H$. The goal is to minimize the expected cost:

$$f\left(W\right)={\mathbb{E}}_x\left[\ell \left(\mathit{x},W\right)\right]=\underset{n\to \infty }{\lim }{f}_n\left(W\right)$$

Assuming we randomly sample a data point ${\mathit{x}}^{\left(t\right)}$ at the $t\text{th}$ iteration, the original Mairal paper proved that the following surrogate function ${\widehat{f}}_T\left(W\right)$ converges almost surely to $f_T\left(W\right)$ (and to a local minimum) as $T\to \infty$:

$${\widehat{f}}_t\left(W\right)=\frac{1}{T}\sum _{t=1}^T\left({\Vert x^{\left(t\right)}-W{\mathit{h}}^{\left(t\right)\top }\Vert }_2^2+\lambda {\Vert {\mathit{h}}^{\left(t\right)\top }\Vert }_1\right)$$

where ${\mathit{x}}^{\left(t\right)}$, $W$, ${\mathit{h}}^{\left(t\right)}$ are nonnegative and $T$ is the total number of iterations. Mairal et al. derived an online learning algorithm that performs NMF by updating $\mathit{h}$ and $W$ in an alternating fashion. They first solve for ${\mathit{h}}^{\left(t\right)}$ using $W^{\left(t-1\right)}$ from the previous iteration and then obtain $W^{\left(t\right)}$ that minimizes the surrogate function. Intuitively, this strategy allows online learning because it expresses a formula for incorporating a new observation ${\mathit{x}}^{\left(t\right)}$ given the factorization result $W$ and $\mathit{h}$ for previously seen data points. Thus, we can iterate over the data points one-by-one or in small mini-batches.

In the proposed online iNMF algorithm, we process the data in mini-batches, which improves convergence speed. Assuming we have data matrices $X\in {ℝ}_{+}^{m\times n_i}\left(i=1,\dots ,N\right)$ and mini-batch $X_M^{\left(t\right)}$ of size $p$, where $X_M^{\left(t\right)}$ comprises data points $X_M^{i\left(t\right)}$ sampled from $X^i$, the empirical cost of iNMF is given by:

$$\underset{\begin{array}{c}W,V^i,H^i\ge \text{0}\\ i=1,\dots ,N\end{array}}{\min }\frac{1}{{\sum }_i^N{n}_i}\sum _{i=1}^N\left({\Vert X^i-\left(W+V^i\right)H^{i\top }\Vert }_F^2+\lambda {\Vert V^i{H}^{i\top }\Vert }_F^2\right)$$

The corresponding surrogate function after the $T\text{th}$ iteration is:

$${\widehat{f}}_t\left(W,V^i,\dots ,V^N\right)=\frac{1}{T\times p}\sum _{t=1}^T\sum _{i=1}^N\left({\Vert X_M^{i\left(t\right)}-\left(W+V^i\right)H_M^{i\left(t\right)\top }\Vert }_F^2+\lambda {\Vert V^i{H}_M^{i\left(t\right)\top }\Vert }_F^2\right)$$

where subscript $M$ indicates a sampled mini-batch.

For a new mini-batch $X_M^{\left(t\right)}$, we first compute the corresponding cell factor loadings $H_M^{i\left(t\right)}$ for all input data using the shared $\left(W^{\left(t-1\right)}\right)$ and dataset-specific $\left(V^{i\left(t-1\right)}\right)$ factors from the last iteration. The authors of the original online learning paper employed the least angle regression algorithm (LARS) in their study. Here we use the ANLS update instead because it is highly efficient, designed specifically for NMF (rather than dictionary learning in general) and addresses the subproblem by running the solver exactly once within a single iteration of the online iNMF algorithm. We also tried using a HALS update for $H_M^{i\left(t\right)}$, but found that convergence was slower (Fig. S3). Upon acquiring $H_M^{i\left(t\right)}$, we utilize the HALS method to update the shared $W^{\left(t\right)}$ and $V^{i\left(t\right)}$, which is analogous to the updates used by Mairal et al.⁶ but derived specifically for iNMF. Because the updates for $W$ and $V^i$ depend on all of the previously seen data points and their cell factor loadings, a naive implementation would require storing all of the data and cell factor loadings in memory. However, the HALS updates depend on $X^i$ and $H^i$ only through the matrix products $H^{i\top }{H}^i$ and $X^i{H}^i$ (see Supplementary Note for details). These matrix products have only $K^2$ and $mK$ elements respectively, allowing efficient storage, and can be computed incrementally with the incorporation of each newly sampled mini-batch $X_M^{i\left(t\right)}$ of size $p_i$:

$$A^{i\left(t\right)}\leftarrow A^{i\left(t-1\right)}+\frac{1}{p_i}{H}_M^{i\left(t\right)\top }{H}_M^{i\left(t\right)}$$

$$B^{i\left(t\right)}\leftarrow B^{i\left(t-1\right)}+\frac{1}{p_i}{X}_M^{i\left(t\right)}{H}_M^{i\left(t\right)}$$

Note that, analogous to the mini-batch extension of the original online dictionary learning algorithm, we divide by $p_i$ to average the inner products across all data points within each mini-batch.

Implementation of Online iNMF

Algorithm 1 summarizes our implementation of online iNMF. We use our previous Rcpp implementation of the block principal pivoting algorithm⁵ to calculate the ANLS updates for $H_M^{i\left(t\right)}$. We implement the HALS updates for $W$ and $V^i$ using native R, since the updates require only matrix operations, which are highly optimized in R. Because the online algorithm does not require all of the data on each iteration (only a fixed-size mini-batch), we use the hdf5r package to load each mini-batch from disk on the fly. By creating HDF5 files with chunk size no larger than the mini-batch size, we achieve a time- and memory-efficient implementation that never loads more than a single mini-batch of the data from disk at once. In fact, we can go a step further and analyze datasets that are not stored on the same physical hard drive as the machine performing iNMF. We show that it is possible to analyze data by streaming over the internet without downloading the entire dataset onto the disk.

$$\overline{\underset{\_}{\begin{array}{l}\mathbf{\text{Algorithm}} \mathbf{\text{1}}\hspace{0.17em}\text{Online Learning for Integrative Nonnegative Matrix Factorization}\\ \overline{\begin{array}{l}\mathbf{\text{Require}}:X^i\in {ℝ}_{+}^{m\times n_i}, i=1,\mathrm{...}, N\\ 1:\hspace{0.17em}\hspace{1em}\text{Initialize}\hspace{0.17em}{A}^{i\left(0\right)}\in {\mathbf{\text{0}}}^{K\times K},\hspace{0.17em}{B}^{i\left(0\right)}\in {\mathbf{\text{0}}}^{K\times K},\hspace{0.17em}i=1,\dots ,N\\ 2:\hspace{0.17em}\hspace{1em}\text{Initialize}\hspace{0.17em}{W}^{\left(0\right)}\hspace{0.17em}\text{with random samples from a uniform distribution over}\hspace{0.17em}\left[0,2\right]\end{array}}\\ 3:\hspace{0.17em}\hspace{1em}\text{Initialize}\hspace{0.17em}{V}^{i\left(0\right)}\hspace{0.17em}\text{with random samples from}\hspace{0.17em}{X}^i,i=1,\dots ,N\\ 4:\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em} \mathbf{\text{for}}\hspace{0.17em}t=1\hspace{0.17em}\text{to}\hspace{0.17em}T\hspace{0.17em}\mathbf{\text{do}}\\ 5:\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em} \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em} \hspace{0.17em}\mathbf{\text{for}}\hspace{0.17em}i=1\hspace{0.17em}\text{to}\hspace{0.17em}N\hspace{0.17em}\mathbf{\text{do}}\\ 6:\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em} \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em} \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{Sample}\hspace{0.17em}\text{a}\hspace{0.17em}\text{mini-batch}\hspace{0.17em}{X}_M^{i\left(t\right)}\hspace{0.17em}\text{of}\hspace{0.17em}\text{size}\hspace{0.17em}{p}_i\hspace{0.17em}\text{from}\hspace{0.17em}{X}^i,i=1,\dots ,N\\ 7:\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em} \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em} \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{Compute}\hspace{0.17em}{H}_M^{i\left(t\right)}\hspace{0.17em}\text{using}\hspace{0.17em}\text{ANLS},\hspace{0.17em}i=1,\dots ,N\\ 8:\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em} \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em} \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em} \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em} \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em} \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{H}_M^{i\left(t\right)}=\underset{H\ge \mathbf{\text{0}}}{\arg \min }{\Vert \left(\begin{array}{c}{W}^{\left(t-1\right)}+V^{i\left(t-1\right)}\\ \sqrt{\lambda }{V}^{i\left(t-1\right)}\end{array}\right)H^{\top }-\left(\begin{array}{c}{X}_M^{i\left(t\right)}\\ {\mathbf{\text{0}}}^{n\times p_i}\end{array}\right)\Vert }_F^2\\ 9:\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em} \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em} \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{Update}\hspace{0.17em}{A}^{i\left(t\right)}\hspace{0.17em}\text{and}\hspace{0.17em}{B}^{i\left(t\right)}\hspace{0.17em}\left(\text{remove old information older than }2\text{ epochs}\right)\\ 10:\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em} \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em} \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em} \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em} \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em} \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em} \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em} \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em} \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em} \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em} \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em} \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{A}^{i\left(t\right)}\leftarrow {\beta }^{\left(t\right)}{A}^{i\left(t-1\right)}+\frac{1}{p_i}{H}_M^{i\left(t\right)\top }{H}_M^{i\left(t\right)}\\ 11:\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em} \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em} \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em} \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em} \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em} \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em} \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em} \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em} \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em} \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em} \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em} \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{B}^{i\left(t\right)}\leftarrow {\beta }^{\left(t\right)}{B}^{i\left(t-1\right)}+\frac{1}{p_i}{X}_M^{i\left(t\right)\top }{H}_M^{i\left(t\right)}\\ 12:\hspace{0.17em}\hspace{1em}\mathbf{\text{end}}\hspace{0.17em}\mathbf{\text{for}}\\ 13:\hspace{0.17em}\hspace{1em}\text{Initialize}\hspace{0.17em}{W}^{\left(t\right)}=W^{\left(t-1\right)}\\ 14:\hspace{0.17em}\hspace{1em}\mathbf{\text{for}}\hspace{0.17em}j=1\hspace{0.17em}\text{to}\hspace{0.17em}K\hspace{0.17em}\mathbf{\text{do}}\\ 15:\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em} \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em} \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em} \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em} \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em} \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em} \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em} \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em} \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{W}_{\cdot j}^{\left(t\right)}={\left[W_{\cdot j}^{\left(t\right)}+\frac{{\sum }_i{B}_{\cdot j}^{i\left(t\right)}-\left(W^{\left(t\right)}+V^{i\left(t-1\right)}\right)A_{\cdot j}^{i\left(t\right)}}{{\sum }_i{A}_{jj}^{i\left(t\right)}}\right]}_{+}\\ 16:\hspace{0.17em}\hspace{1em}\mathbf{\text{end}}\hspace{0.17em}\mathbf{\text{for}}\\ 17:\hspace{0.17em}\hspace{1em}\text{Initialize}\hspace{0.17em}{V}^{i\left(t\right)}=V^{i\left(t-1\right)}\\ 18:\hspace{0.17em}\hspace{1em}\mathbf{\text{for}}\hspace{0.17em}j=1\hspace{0.17em}\text{to}\hspace{0.17em}K\hspace{0.17em}\mathbf{\text{do}}\\ 19:\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em} \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em} \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em} \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em} \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em} \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em} \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em} \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em} \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em} \hspace{0.17em}\hspace{0.17em}{V}_{\cdot j}^{i\left(t\right)}={\left[V_{\cdot j}^{i\left(t\right)}+\frac{B_{\cdot j}^{i\left(t\right)}-\left(W^{\left(t\right)}+\left(1+\lambda \right)V^{i\left(t\right)}\right)A_{\cdot j}^{i\left(t\right)}}{\left(1+\lambda \right)A_{jj}^{i\left(t\right)}}\right]}_{+}\\ 20:\hspace{0.17em}\hspace{1em}\mathbf{\text{end}}\hspace{0.17em}\mathbf{\text{for}}\\ 21:\mathbf{\text{end}}\hspace{0.17em}\mathbf{\text{for}}\\ 22:\text{Compute}\hspace{0.17em}{H}^{i\left(T\right)}\hspace{0.17em}\text{using}\hspace{0.17em}\text{ANLS},\hspace{0.17em}i=1,\dots ,N\\ 23:\mathbf{\text{return}}\hspace{0.17em}{W}^{\left(T\right)},V^{i\left(T\right)}\hspace{0.17em}\text{and}\hspace{0.17em}{H}^{i\left(T\right)},\hspace{0.17em}i=1,\dots ,N\end{array}}}$$

For scenario 1, in which the mini-batch size $p$ specifies the total number of cells to be processed per iteration across all datasets, we sample $p^i$ cells from each dataset $i$, proportional to its full dataset size $\left(p_i=p\times n_i/{\sum }_i^N{n}_i\right)$. Thus, each mini-batch in scenario 1 contains a representative sample of cells from all datasets. For scenario 2, in which only one dataset is available at a time, we sample the entire mini-batch from the current dataset. We also employ three heuristics that were used in the original online NMF paper: (1) we initialize the dataset-specific metagenes using $K$ cells randomly sampled from the corresponding input data; (2) we downscale $A^{i\left(t-1\right)}$ and $B^{i\left(t-1\right)}$ when obtaining $A^{i\left(t\right)}$ and $B^{i\left(t\right)}$ using $H_M^{i\left(t\right)}$; and (3) we remove information older than two epochs from matrices $A^{i\left(t\right)}$ and $B^{i\left(t\right)}$ (only once at the start of a new epoch, exclusive to scenario 1 in practice). The intuition behind the second and third heuristics is as follows. By design, $A^{i\left(t\right)}$ and $B^{i\left(t\right)}$ carry all the $H_M^{i\left(t\right)\top }{H}_M^{i\left(t\right)}$ and $X_M^{i\left(t\right)}{H}_M^{i\left(t\right)}$ values respectively from $t$ iterations. Each time when the same data points are revisited (assuming $t$ iterations comprise multiple epochs), the accuracy of resulting cell factor loadings is improved because the metagene factors get refined during the implementation of the algorithm. Consequently, the variability in the quality of cell factor loadings is carried over to $A^{i\left(t\right)}$ and $B^{i\left(t\right)}$ by summing up matrix products shown above. Therefore, by downscaling $A^{i\left(t-1\right)}$ and $B^{i\left(t-1\right)}$(old information), the weight of the latest $H_M^{i\left(t\right)\top }{H}_M^{i\left(t\right)}$ and $X_M^{i\left(t\right)}{H}_M^{i\left(t\right)}$ increases. Mairal et al. observed faster convergence of online learning on small datasets by removing the matrix product involving the less-refined cell factor loadings and thus they adopted this heuristic in their online learning implementation. An example of applying heuristic (2) and (3) for $A^{i\left(t\right)}$ is shown in algorithm 2 (the same strategy applies to $B^{i\left(t\right)}$).

$$\overline{\underset{\_}{\begin{array}{l}\mathbf{\text{Algorithm}} \mathbf{\text{2}}\hspace{0.17em}\text{Example of Heuristics }\left(2\right)\text{ and }\left(3\right)\\ \overline{\begin{array}{l}\hspace{0.17em}1:\hspace{1em}\hspace{0.17em}\mathbf{\text{if}}\hspace{0.17em}{3}^{rd}\hspace{0.17em}\text{epoch}\hspace{0.17em}\text{starts}\hspace{0.17em}\text{at}\hspace{0.17em}{t}^{th}\hspace{0.17em}\text{iteration}\hspace{0.17em}\left(t\ge 3\right)\hspace{0.17em}\mathbf{\text{then}}\\ 2:\hspace{1em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{A}^{i\left(t-1\right)}\leftarrow A^{i\left(t-1\right)}-A^{i\left(t-2\right)}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}⊳\text{Remove}\hspace{0.17em}\text{old}\hspace{0.17em}\text{information}\end{array}}\\ 3:\hspace{1em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\beta }^{\left(t\right)}=\frac{t-2}{t-1}\\ 4:\hspace{1em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{A}^{i\left(t\right)}\leftarrow {\beta }^{\left(t\right)}{A}^{i\left(t-1\right)}+\frac{1}{p_i}{H}_M^{i\left(t\right)\top }{H}_M^{i\left(t\right)}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}⊳\text{Downscale old }\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{1em}\hspace{0.17em}\text{information}\\ 5:\hspace{1em}\hspace{0.17em}\mathbf{\text{end}}\hspace{0.17em}\mathbf{\text{if}}\end{array}}}$$

Additionally, we implemented dataset preprocessing—including library size normalization, variable gene selection, and gene scaling—using fixed-size mini-batches, so that preprocessing requires only a prespecified amount of memory.

Data Loading Methods and Overhead

To investigate whether loading data from disk causes significant overhead, we ran online iNMF (scenario 1) with 1,111 variable genes on the mouse cortex datasets stored either on disk or in memory. Then we implemented both approaches with different choices of mini-batch size $\left(n=1,000, 5,000, 10,000, 50,000\right)$ for 50 iterations, while keeping the other parameters the same $\left(K=40,\hspace{0.17em}\lambda =5\right)$. The average runtime for 50 iterations for each setting is reported in the barplot. The standard deviation is displayed as error bars (Fig. S4).

Quantile Normalization and Joint Clustering

We also implemented a much more efficient strategy for quantile normalization (See Algorithm 3) than our previously published approach⁵. We found that, rather than performing time- and memory-intensive shared factor neighborhood clustering to identify joint clusters, we can perform the following steps: (1) assign each cell to the factor on which has the highest loading, giving a number of joint clusters equal to the number of metagene factors $K$. Note that one can center the cell factor loadings at first if the distribution of cell factor loadings from a given dataset significantly differs from the others (e.g. due to different data modalities); (2) for each input dataset, efficiently find approximate within-dataset nearest neighbors using the RANN package (k-nearest neighbors $k=20$ and $ϵ=0.9$ by default) and then correct these maximum factor assignments by taking a majority vote among within-dataset nearest neighbors; and (3) perform quantile normalization on the refined joint clusters as before⁵. By default, we choose the dataset with the largest number of cell samples as the reference dataset. Then, for cells from each of the joint clusters, we normalize the quantiles of the factor loadings for each metagene factor in the other datasets to match the quantiles of the factor loadings for the same metagene in the reference dataset. This strategy performs just as well as shared factor neighborhood clustering, but uses significantly less time and memory. Unless otherwise specified, we implemented quantile normalization with $k=20$ (default) for $k$-nearest neighbors in analyses of both real and simulated datasets (note that $k$ is denoted as $Q$ in algorithm 3).

$$\overline{\underset{\_}{\begin{array}{l}\mathbf{\text{Algorithm}} \mathbf{\text{3}}\hspace{0.17em}\text{Quantile Normalization}\\ \overline{\begin{array}{l}\mathbf{\text{Require}}:H^i\in {ℝ}_{+}^{n_i\times K},i=1,\dots ,N\\ 1:\hspace{1em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathbf{\text{for}}\hspace{0.17em}i=1\hspace{0.17em}\text{to}\hspace{0.17em}N\hspace{0.17em}\mathbf{\text{do}}\\ 2:\hspace{1em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{1em}\hspace{0.17em}\mathbf{\text{for}}\hspace{0.17em}j=1\hspace{0.17em}\text{to}\hspace{0.17em}K\hspace{0.17em}\mathbf{\text{do}}\\ 3:\hspace{1em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{1em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{1em}\hspace{0.17em}\text{Scale}\hspace{0.17em}{H}_{\cdot j}^i\hspace{0.17em}\left(centering is optional\right)\hspace{0.17em}\hspace{1em}\hspace{0.17em}\hspace{1em}\hspace{0.17em}\hspace{1em}\hspace{0.17em}\hspace{1em}\hspace{0.17em}\hspace{1em}⊳\text{Cell}\left(\text{from}\hspace{0.17em}{X}^i\right)\hspace{0.17em}\text{loadings}\hspace{0.17em}\text{on}\hspace{0.17em}{j}^{th}\hspace{0.17em}\text{metagene factor}\end{array}}\\ 4:\hspace{1em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{1em}\hspace{0.17em}\mathbf{\text{end}}\hspace{0.17em}\mathbf{\text{for}}\\ 5:\hspace{1em}\hspace{0.17em}\hspace{0.17em} \mathbf{\text{end}}\hspace{0.17em}\mathbf{\text{for}}\\ 6:\hspace{1em}\hspace{0.17em}\hspace{0.17em} \text{Set}\hspace{0.17em}{X}^R\hspace{0.17em}\text{as}\hspace{0.17em}\text{reference dataset}\hspace{0.17em}\left(R=\arg {\max }_i{n}_i\right)\\ 7:\hspace{1em}\hspace{0.17em}\hspace{0.17em} \mathbf{\text{for}}\hspace{0.17em}i=1\hspace{0.17em}\text{to}\hspace{0.17em}N\hspace{0.17em}\mathbf{\text{do}}\\ 8:\hspace{1em}\hspace{0.17em}\hspace{0.17em} \hspace{1em}\hspace{0.17em} \mathbf{\text{for}}\hspace{0.17em}s=1\hspace{0.17em}\text{to}\hspace{0.17em}{n}_i\hspace{0.17em}\mathbf{\text{do}}\\ 9:\hspace{1em}\hspace{0.17em}\hspace{0.17em} \hspace{1em}\hspace{0.17em} \hspace{1em}\hspace{0.17em}{c}_s^i=\arg {\max }_j{H}_{sj}^i\\ 10:\hspace{1em}\hspace{0.17em}\hspace{0.17em} \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em} \mathbf{\text{end}}\hspace{0.17em}\mathbf{\text{for}}\\ 11:\hspace{1em}\hspace{0.17em}\mathbf{\text{end}}\hspace{0.17em}\mathbf{\text{for}}\\ 12:\hspace{1em} \mathbf{\text{for}}\hspace{0.17em}i=1\hspace{0.17em}\text{to}\hspace{0.17em}N\hspace{0.17em}\mathbf{\text{do}}\hspace{0.17em}\hspace{1em}\hspace{0.17em}\hspace{1em}\hspace{0.17em}\hspace{1em}\hspace{0.17em}\hspace{1em}\hspace{0.17em}\hspace{1em}\hspace{0.17em}\hspace{1em}\hspace{0.17em}\hspace{1em}\hspace{0.17em}\hspace{1em}\hspace{0.17em}\hspace{1em}\hspace{0.17em}\hspace{1em}\hspace{0.17em}\hspace{1em}\hspace{0.17em}\hspace{1em}\hspace{0.17em}\hspace{1em}\hspace{0.17em}\hspace{1em}\hspace{0.17em}\hspace{1em}\hspace{0.17em}\hspace{1em}\hspace{0.17em}\hspace{1em}\hspace{0.17em}\hspace{1em}\hspace{0.17em}\hspace{1em}\hspace{0.17em}\hspace{0.17em}⊳\text{Cluster re-assignment of}\hspace{0.17em}{\mathit{x}}_s^i\\ 13:\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathbf{\text{for}}\hspace{0.17em}s=1\hspace{0.17em}\text{to}\hspace{0.17em}{n}_i\hspace{0.17em}\mathbf{\text{do}}\\ 14:\hspace{1em}\hspace{0.17em}\hspace{1em}\hspace{0.17em}\hspace{1em}\hspace{0.17em}\text{Identify}\hspace{0.17em}Q\hspace{0.17em}\text{nearest}\hspace{0.17em}\text{neighbors of}\hspace{0.17em}{\mathit{x}}_s^i\\ 15:\hspace{1em}\hspace{0.17em}\hspace{1em}\hspace{0.17em}\hspace{1em}\hspace{0.17em}\text{Obtain}\hspace{0.17em}{c}_{s\left(q\right)}^i,q=1,\dots ,N\\ 16:\hspace{1em}\hspace{0.17em}\hspace{1em}\hspace{0.17em}\hspace{1em}\hspace{0.17em}{c}_s^{i\ast }=\arg {\max }_j{\sum }_{q=1}^Q\mathbb{I}\left[c_{s\left(q\right)}^i=j\right]\\ 17:\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathbf{\text{end}}\hspace{0.17em}\mathbf{\text{for}}\\ 18:\hspace{1em}\hspace{0.17em}\mathbf{\text{end}}\hspace{0.17em}\mathbf{\text{for}}\\ 19:\hspace{1em}\hspace{0.17em}\mathbf{\text{for}}\hspace{0.17em}j=1\hspace{0.17em}\text{to}\hspace{0.17em}K\hspace{0.17em}\mathbf{\text{do}}\\ 20:\hspace{1em}\hspace{0.17em}\hspace{1em}\hspace{0.17em}\mathbf{\text{for}}\hspace{0.17em}i=1\hspace{0.17em}\text{to}\hspace{0.17em}N\left(i\ne R\right)\hspace{0.17em}\mathbf{\text{do}}\\ 21:\hspace{1em}\hspace{0.17em}\hspace{1em}\hspace{0.17em}\hspace{1em}\hspace{0.17em}\mathbf{\text{for}}\hspace{0.17em}k=1\hspace{0.17em}\text{to}\hspace{0.17em}K\hspace{0.17em}\mathbf{\text{do}}\\ 22:\hspace{1em}\hspace{0.17em}\hspace{1em}\hspace{0.17em}\hspace{1em}\hspace{0.17em}\hspace{1em}\hspace{0.17em}\text{Obtain}\hspace{0.17em}{H}_{j,k}^R\hspace{0.17em}⊳\text{Cell}\hspace{0.17em}\left(\text{from}\hspace{0.17em}{X}^R\right)\hspace{0.17em}\text{loadings}\hspace{0.17em}\text{in}\hspace{0.17em}\text{cluster}\hspace{0.17em}j\hspace{0.17em}\text{on}\hspace{0.17em}{k}^{th}\hspace{0.17em}\text{metagene factor}\\ 23:\hspace{1em}\hspace{0.17em}\hspace{1em}\hspace{0.17em}\hspace{1em}\hspace{0.17em}\hspace{1em}\hspace{0.17em}\text{Obtain}\hspace{0.17em}{H}_{j,k}^i\hspace{0.17em}⊳\text{Cell}\hspace{0.17em}\left(\text{from}\hspace{0.17em}{X}^i\right)\hspace{0.17em}\text{loadings}\hspace{0.17em}\text{in}\hspace{0.17em}\text{cluster}\hspace{0.17em}j\hspace{0.17em}\text{on}\hspace{0.17em}{k}^{th}\hspace{0.17em}\text{metagene factor}\\ 24:\hspace{1em}\hspace{0.17em}\hspace{1em}\hspace{0.17em}\hspace{1em}\hspace{0.17em}\hspace{1em} \text{Match the quantiles of}\hspace{0.17em}{H}_{j,k}^R\hspace{0.17em}\text{and}\hspace{0.17em}{H}_{j,k}^i\\ 25:\hspace{1em}\hspace{0.17em}\hspace{1em}\hspace{0.17em}\hspace{1em}\hspace{0.17em}\mathbf{\text{end}}\hspace{0.17em}\mathbf{\text{for}}\\ 26:\hspace{1em}\hspace{0.17em}\hspace{1em}\hspace{0.17em}\mathbf{\text{end}}\hspace{0.17em}\mathbf{\text{for}}\\ 27:\hspace{1em}\hspace{0.17em}\mathbf{\text{end}}\hspace{0.17em}\mathbf{\text{for}}\\ 28:\hspace{1em}\hspace{0.17em}\text{return}\hspace{0.17em}\text{normalized}\hspace{0.17em}{H}^i,\hspace{0.17em}i=1,\dots ,N\end{array}}}$$

After performing quantile normalization, one can perform a second clustering step (e.g., Louvain community detection) using the normalized cell factor loadings $H^i$ (or unnormalized $H^i$ if the data are aligned well even without quantile normalization).

Quantitative Metrics for Evaluating Alignment and Clustering

Alignment score, devised by Butler et al.²⁹, measures the uniformity of mixing among samples from different datasets $\left(N\ge 2\right)$ in the aligned latent space. High score (close to 1) implies the datasets share underlying cell types and are well integrated, while low score (close to 0) indicates the datasets do not share cognate populations and the samples are not aligned. In the manuscript, we report the alignment score calculated from the cell factor loading matrices $H$ (dimension = number of metagenes $K$). We also employ the k-nearest neighbor batch-effect test (kBET)³⁰ to assess the data integration results on $H$. kBET first creates a $k$-nearest neighbor graph (we used $k=20$ for all analyses in the paper), and then randomly samples 1,000 cells to examine the batch label distribution in the cell’s neighbourhood against the global batch label distribution, using a ${\chi }^2$-test (100 repeats) under the null hypothesis that input data batches are mixed well. If the datasets are well integrated, the local batch label distribution will be similar to the global batch label distribution and the statistical tests will not reject the null hypothesis, resulting in a low rejection rate for 1,000 tested data points in each repeat. In our analyses, we took the median of the rejection rates from all repeats and subtracted it from 1 to report the overall acceptance rate. High acceptance rate indicates well-mixed datasets. To quantify clustering performance, we used the purity metric and the adjusted Rand index (ARI)³¹. Purity assesses the resulting clusters with respect to a reference clustering. To calculate purity, one can assign each cluster to the dominant class in the cluster and count the number of correctly assigned samples in it. Then the purity is calculated by taking the sum over all clusters and dividing by the total number of samples. ARI is another popular method to compare clustering results. It counts pairs of samples where two clustering results agree or disagree. ARI was built upon the Rand index (RI)³², and fixes the issues in practice suffered by RI such as narrow range and non-constant baseline. ARI lies between 0 (no match) and 1 (perfect match).

Integrative Analyses on Real Data

Study of Convergence Behavior of Online iNMF

To investigate the convergence behavior of online iNMF (scenario 1), we utilized several strategies and datasets. The first experiment was conducted on the adult mouse frontal $\left(n=156,167\right)$ and posterior cortex $\left(n=99,186\right)$ datasets, generated by Saunders et al.⁷. We split both into training (80%) and testing sets (20%). Three methods were used for comparison: online iNMF (mini-batch size = 5,000 cells), ANLS (batch iNMF) and multiplicative updates (Mult). With 1,111 genes jointly selected from the input datasets, we tracked the training and testing objectives calculated based on the resulting factors (Fig. 2a,b). In order to evaluate the testing objective, we calculated cell factor loadings for cells in the testing set using the metagene factors obtained from the training set. As the online iNMF algorithm aims to minimize the expected cost, we expect the online iNMF to converge more rapidly than batch methods on the testing set, which can be viewed as a surrogate of the expected cost. Mairal et al. took a similar approach to evaluate their online NMF algorithm. In the second experiment, we monitored the iNMF objective on the training set after 500 seconds and repeated 20 times with random initializations, in order to further demonstrate the efficiency of the algorithms (Fig. 2c). For the third part of this study, we focused on the effect of the mini-batch size. We applied online iNMF on the same training and testing cortex datasets, but with mini-batches of increasing size $\left(n=1,000, 5,000, 10,000, 50,000, 100,000, 150,000, 200,000\right)$. Similarly, we tracked the training and testing objectives until the algorithm converged (Fig. 2d,e). Lastly, we implemented online iNMF on multiple subsets of different sizes sampled from the training set (Fig. 2f). At multiple time points throughout the training process, we used the learned metagenes to solve for the cell factor loadings on the testing set, and calculated the testing objective. We set the key parameters $K=40$ and $\lambda =5$ for all analyses discussed above.

We also carried out three additional analyses on different datasets to support our conclusions, where we looked at the trajectories of training/testing objectives as well as the minimization of the training objective within a given amount of time (Extended Data Fig. 1). The datasets and key parameters are listed as follows. 1) adult mouse brain (DropViz), 9 datasets (each corresponds to a brain region), $n=691,962$, $K=40$, $\lambda =5$, mini-batch size = 5,000; 2) human PBMC (SeuratData package), $n=13,999,\hspace{0.17em}2000$ variable genes (selected through Seurat pipeline), $K=20$, $\lambda =5$, mini-batch size = 2,000; 3) human pancreas (SeuratData package), $n=14,892,\hspace{0.17em}2000$ variable genes (selected through Seurat pipeline), $K=40$, $\lambda =5$, mini-batch size = 3,000.

Benchmark of Runtime and Peak Memory Usage

The benchmark study was carried out on the adult mouse frontal $\left(n=156,167\right)$ and posterior cortex $\left(n=99,186\right)$ datasets from the DropViz data collection⁷ (Fig. 3a). We created four pairs of subsets of increasing sizes by sampling from each of the full datasets. Within each pair, the subset from the frontal cortex and the one from the posterior cortex held the same ratio as their full datasets (61.2 : 38.8). This resulted in five pairs of inputs $\left(n=10,000, 50,000, 100,000, 200,000, 255,353\right)$ for online iNMF (scenario 1), batch iNMF, Harmony and Seurat v3. To ensure fair comparison, we preprocessed the data as suggested by each method. The preprocessing steps suggested by each method differ slightly as follows: (1) online iNMF and batch iNMF normalize the gene expression measurements for each cell and then scale the gene expression data without centering to zero mean, because iNMF expects nonnegative inputs. (2) Seurat log-transforms the normalized gene expression matrices. (3) Harmony log-transforms the normalized gene expression and scales each gene to unit variance, and centers to zero mean (Note that we ran Harmony using the SeuratWrappers package.).For fair comparison, we used the same set of 1,111 variable genes for all approaches, the same number of dimensions of the latent space $K=40$ and the same penalty parameter $\lambda =5$ for iNMF-based approaches. We ran online iNMF for 5 epochs, the default setting. We also ran batch iNMF, Seurat and Harmony. During the benchmark, we measured runtime (using the tictoc package) and peak memory usage (peakRAM package) for factorization and alignment (quantile normalization included for online/batch iNMF). We did not include data preprocessing (normalization and scaling) in runtime and memory benchmarks.

Analysis of Human PBMC and Pancreas

We analyzed the human PBMC $\left(n=13,999\hspace{0.17em}\text{cells}\right)$ and human pancreas $\left(n=14,890\right)$ datasets in several experimental settings. The human PBMC dataset consists of two batches, control $\left(n=6,548\right)$ and stimulated cells $\left(n=7,451\right)$. The human pancreas dataset comprises eight batches $\left(n=638, 1,937, 1,004, 2,285, 1,724, 3,605, 1,303, 2,394\right)$ across five different technologies (SMARTSeq2, Fluidigm C1, CelSeq, CelSeq2, inDrops). In the first experiment (Extended Data Fig. 1b–c), we used these datasets to study the convergence behavior of the algorithms (discussed above). In the second experiment (Extended Data Fig. 2), we performed online iNMF (scenario 1) on the PBMC with 1,778 variable genes ($K=20$, $\lambda =5$, mini-batch size = 2,000, epochs = 5), and on the pancreatic islets with 2,051 variable genes ($K=40$, $\lambda =5$, mini-batch size = 3,000, epochs = 5), followed by quantile normalization. We ran batch iNMF with the same variable genes, $K$, and $\lambda$ until convergence. For the third experiment (Fig. 3b–c), we used the human PBMC and pancreas to benchmark online iNMF (scenario 1), along with batch iNMF, Harmony and Seurat, with respect to alignment and clustering performance. We used the top 2,000 highly variable genes selected by Seurat for all algorithms. For online and batch iNMF, the analytical pipelines and the key parameters stayed the same as in the previous experiment. To account for the effect of random initialization, the iNMF-based analyses were repeated 100 times. For Harmony and Seurat, we ran the analyses once, with the number of dimensions for the latent space set to 20 and 40 respectively (matching the iNMF $K$). We also ran additional analyses on human PBMC to inspect the data reconstruction ability of online iNMF, as well as the effect of $\lambda$ on resulting data integration using online iNMF (see Supplementary Note for details).

Analysis of Adult Mouse Brain

The adult mouse brain dataset (DropViz) comprises nine individual scRNA-seq datasets, each generated from a specific brain region. The brain regions assayed include frontal cortex $\left(n=156,167\right)$, posterior cortex $\left(n=99,186\right)$, cerebellum $\left(n=26,139\right)$, entopeduncular $\left(n=19,214\right)$, globus pallidus $\left(n=66,318\right)$, hippocampus $\left(n=113,507\right)$, striatum $\left(n=77,454\right)$, substantia nigra $\left(n=44,416\right)$ and thalamus $\left(n=89,561\right)$, totaling 691,962 cells. We picked 1,111 variable genes and integrated the frontal and posterior cortex datasets using online iNMF (scenario 1) and batch iNMF. Then we obtained the UMAP coordinates from the quantile normalized cell factor loadings and colored the cells by datasets and published cell type labels. Although all 255,353 cells from the cortex were used for factorization, 117,985 of them were annotated by Saunders et al. and shown in the plot (Extended Data Fig. 2). Moreover, we integrated the data across all nine brain regions (Fig. 4). We identified 1,914 genes that are highly variable in at least one of the regions. Using these genes, we performed 3 epochs of online iNMF (scenario 1) with mini-batch size of 5,000, $K=40$ and $\lambda =5$. In this analysis, we found that quantile normalization was not necessary for these dataset--iNMF alone was sufficient for integration.

Analysis of Spatial Transcriptomic Data

In the Slide-seq analysis, we filtered the scRNA-seq data for low quality cells--labeled in the original annotation file--for a total of 193,155 cells. We combined Pucks 190921, 191204, and 200115 from the Slide-seq data for a total of 59,858 beads. We selected 16,655 variable genes. We ran scenario 1 with $K=30$ for 5 epochs, $\lambda =5$ on the scRNA-seq data, then projected the Slide-seq data following scenario 3. After factorization, we performed quantile normalization and Louvain clustering. We then colored the Slide-seq beads with the new labels generated based on the marker genes. Because each Slide-seq bead may contain more than one cell, we used the cell factor loadings to estimate the proportion of each cell type on each bead. To do this, we annotated each iNMF factor to assign it to a cell type, as described in the original Slide-seq paper.The loading value of each metagene factor then indicates the cell proportions of the corresponding cell types on each bead. We excluded the beads with no clear cell type, and for those with two cell types contributing more than 35% to the factor loadings, we colored the beads by the one with the higher loading. In the second analysis, we used the MERFISH dataset $\left(n=1,026,840\hspace{0.17em}\text{cells}\right)$ and scRNA-seq $\left(n=31,250\right)$ in scenario 1 and scenario 3. We used the 134 genes measured in the MERFISH dataset. We used $K=30$ and $\lambda =5$. Scenario 1 was run for 5 epochs, and the slides plotted for Fig. 5g are from animal 1.

Analysis of Mouse Primary Motor Cortex

The mouse primary motor cortex (MOp) datasets were generated by the BRAIN Initiative Cell Census Network (BICCN). The eight datasets span four modalities (single-cell RNA-seq, single-nucleus RNA-seq, single-nucleus ATAC-seq, single-nucleus methylcytosine-seq) and include 786,605 cells. For most of the analyses on MOp, we only used the neurons, 408,885 in total, except for the analyses involving oligodendrocytes. These datasets are (in the chronological order they were generated) allen_smarter_cells $\left(n=6,244\hspace{0.17em}\text{neurons}\right)$, allen_10x_cells_v2 $\left(n=121,440\hspace{0.17em}\text{neurons}\right)$, allen_smarter_nuclei $\left(n=5,911\hspace{0.17em}\text{neurons}\right)$, allen_10x_cells_v3 $\left(n=69,727\hspace{0.17em}\text{neurons}\right)$, allen_10x_nuclei_v3 $\left(n=39,706\hspace{0.17em}\text{neurons}\right)$, macosko_10x_nuclei_v3 $\left(n=101,647\hspace{0.17em}\text{neurons}\right)$, ecker_ren_atac $\left(n=54,844\hspace{0.17em}\text{neurons}\right)$, ecker_ren_met $\left(n=9,366\hspace{0.17em}\text{neurons}\right)$. The RNA and ATAC datasets were preprocessed following the standard LIGER pipeline. We selected variable genes using the genes shared across all datasets. We preprocessed methylation data as described in the original LIGER paper⁵. Briefly, we inverted the direction of gene-body mCH methylation (which is anticorrelated with gene expression) by taking the difference between the maximum of the matrix and each matrix element. The resulting gene-level methylation features are positively correlated with gene expression. Methylation data does not require library size normalization because its values are already ratios (the number of methylated nucleotides divided by the number of detected nucleotides). For iterative multi-omic integration using online iNMF (scenario 2), we performed a single epoch of training (each cell participates in exactly one mini-batch). When adding a new dataset $i$ $\left(1\le i\le N\right)$, we incorporated a new dataset-specific metagene $V^i$ and randomly initialized it. We did not use the data previously seen to refine the metagenes after the initial single epoch per dataset. Then we re-computed the cell factor loadings for all datasets $\left(H^1,\dots ,H^N\right)$ using the latest metagenes and quantile normalized them. For integration of the entire MOp dataset $\left(N=8\right)$ in scenario 2 (Fig. 6), we identified 4,783 variable genes from the first input (i.e. allen_smarter_cells) and used a fixed mini-batch size of 5,000 cells, $K=30$, $\lambda =1$. For integrating all MOp datasets in scenario 1 (Extended Data Fig. 4a), we applied the same parameter setting except for $\lambda =5$. Moreover, we attempted another strategy, where we integrated the first six sc/snRNA-seq datasets sequentially in scenario 2 and then projected both epigenomic datasets (snATAC-seq and snmC-seq) into the learned latent space, followed by quantile normalization and Louvain clustering (Extended Data Fig. 4c). In order to benchmark the cross-modality data integration performance across algorithms (Extended Data Fig. 3), we randomly sampled 5,000 cells from the snRNA-seq dataset (macosko_10x_nuclei_v3) and 5,000 cells from the snATAC-seq dataset (ecker_ren_atac). We implemented data integration using online iNMF (scenario 1, 3,717 variable genes, $K=30$, $\lambda =5$) as well as Seurat v3, Harmony and BBKNN with the same set of genes and dimension = 30 for dimension reduction process. Unlike the other methods, BBKNN only outputs a graph, on which alignment score and kBET cannot be calculated. Therefore, in the main text we only reported these metrics for online iNMF, Seurat v3 and Harmony, which produce the latent coordinates. In addition, we tried calculating the alignment metrics on the UMAP coordinates. In this setting, online iNMF is still the best (alignment score = 0.816, kBET = 0.651), followed by Seurat v3 (alignment score = 0.747, kBET = 0.544), BBKNN (alignment score = 0.409, kBET = 0.218) and Harmony (alignment score = 0.139, kBET = 0.092). For other supplementary analyses, we retained or held out the cell types of interest and carried out online iNMF in scenario 1, 2, and 3 as introduced in the supplementary notes (Fig. S5, S6, S7). More specifically, for the analyses in scenario 2 reported in Fig. S5a, we used 2,011 and 1,997 variable genes respectively. Similarly, for the analyses reported in Fig. S5b, we selected 2,019 variable genes for both. The other key parameters are $K=30$, $\lambda =1$, and $k=200$ for quantile normalization. For the results displayed in Fig. S6a, we used the same 2,111 variable genes and set $K=30$ for all approaches, while using $\lambda =1$ for online iNMF (scenario 2) and $\lambda =5$ for online iNMF (scenario 1) as well as batch iNMF. Upon completion of the factorization, we performed quantile normalization with $k=2,000$. In order to generate Fig. S6b, we integrated two sc/snRNA-seq datasets with 2,045 genes, $K=30$, $\lambda =5$ in scenario 1, and then projected the snATAC-seq dataset into the learned latent space. We quantile normalized the cell factor loadings with $k=1,000$. For the analysis shown in Fig. S7, we used 2,210 variable genes, $K=30$, $\lambda =5$ for the part done in scenario 1. After the last dataset was incorporated in scenario 3, we ran quantile normalization with $k=200$. As shown in Fig. S8, we factorized snATAC-seq and snmC-seq data both alone and jointly with an snRNA-seq dataset using online iNMF in scenario 1 (2,008 variable genes, $K=30$, $\lambda =5$). Then we run quantile normalization and Louvain clustering following standard procedure.

Analysis of Mouse Organogenesis Cell Atlas

The mouse organogenesis cell atlas (MOCA) consists of 1,363,063 cells from embryos between 9.5 to 13.5 days of gestation (e9.5, e10.5, e11.5, e12.5, e13.5). We first selected 2,557 variable genes and then integrated the five MOCA datasets in scenario 1 with the following setting: mini-batch size = 5,000 cells, $K=50$, $\lambda =5$, epochs = 1. As the alignment was quite good without quantile normalization, the 3D UMAP coordinates were obtained from the unnormalized cell factor loadings. Lastly, we visualized the cells, colored by datasets (gestational age) and published developmental trajectory labels using the rgl package (Fig. S1). We employed Harmony for this analysis with the same set of variable genes and dimensionality of the latent space (PCA). As with all the other benchmark studies of the runtime and peak memory usage, we did not include the steps for data normalization, gene selection and gene expression scaling.

Integrative Analyses on Simulated Data

Generating Simulated scRNA-seq Data

We employed the R package Splatter³³ to simulate scRNA-seq datasets. Each dataset has 50,000 cells and 10,000 genes, separated into 6 batches and 8 cross-batch cell types (clusters). We adopted the settings from the recently reported benchmark study⁸ while adjusting the proportion of each batch and cluster according to our needs. We determined the dataset compositions following one of these three strategies: 1) randomly sample the cluster proportions from the Dirichlet distribution for each simulation while keeping the batch sizes (also generated by Dirichlet distribution) in each simulation the same (Fig. S9, S10); 2) randomly sample the batch sizes from the Dirichlet distribution for each simulation while keeping the cluster proportions (also generated by Dirichlet distribution) in each simulation the same (Fig. S9); 3) use the same cell type and batch proportions to isolate the effect of differences in cell cluster membership across partially overlapping datasets (Fig. S10, S11, S12).

Analysis of Simulated Data with Unbalanced Cell Clusters and Dataset Sizes

We generated the datasets for this analysis following the first and second data generation strategies described in the “Generating simulated scRNA-seq data” section, corresponding to the analysis of unbalanced cell clusters and datasets sizes respectively. To quantitatively measure the level of imbalance in each analysis, we computed the Shannon entropy (H) of both the cluster proportions (H_cluster) and batch sizes (H_batch) using the equation below, where P is a vector of n probabilities that add up to 1:

$$H\left(P\right)=-\sum _{i=1}^n{p}_i\hspace{0.17em}lo{g}_2\left(p_i\right),\hspace{0.17em}where$$

Where $P=\left\{p_1,\dots ,p_n\right\}$, $0<p_i<1$, ${\sum }_{i=1}^n{p}_i=1$. We then measured the performance of online iNMF in scenario 1 and 2 (Table S1, 1st row). We also computed the Spearman correlation between the evaluation metrics (Alignment, Purity, ARI, and kBET) and the entropy of cluster proportions and batch sizes (Fig. S9e).

Analysis of Simulated Data with Missing Cell Clusters

We generated the datasets used in this analysis following the third data generation strategy described above. In this case, the cluster proportions and batch sizes were exactly the same for all 10 simulations, to isolate the effect of variable batch compositions. We then excluded 1–5 cell types from the first 5 batches to mimic the situations when the newly arriving data (Batch 6) share a varying number of common cell types with the reference data (Fig. S11a). We applied online iNMF in scenario 1 and 2 (Table S1, 2nd row) and visualized the evaluation metrics against the number of held-out cell types in line plots (Fig. S11e). To test the performance of online iNMF (scenario 3), we ran the pipeline again while treating the first 5 batches with missing cell types as the “reference data” and the last batch as the “projected data” (Table S1, third row). We plotted the results from the two evaluation metrics for online iNMF on all cells, cells in the missing cell types, and cells in the shared cell types, along with the number of held-out cell types (Fig. S12).

Analysis of Simulated Data with No Cell Types Shared Across All Datasets

We generated the datasets used in this analysis following the first data generation strategy described in previous section. Within each simulation, we excluded one different cluster in 5 batches and excluded the other three remaining clusters in the sixth batch to ensure that the intersection of cell types across all batches is the empty set (Fig. S10a). To measure the performance of online iNMF (scenario 1 and 2), we ran a number of regular LIGER analyses using mostly default parameters (Table S1, 4th row) and drew the boxplots using each evaluation metric calculated from 50 runs (Fig. S10e).

Analysis of Simulated Data with Varying Number of Factors $\left(K\right)$

The datasets used in this analysis were generated following the third data generation strategy described in the “Generating simulated scRNA-seq data” section, without any further subsetting or filtering. To measure the performance of online iNMF (scenario 1 and 2) across a range of $K$ values, we ran a number of analyses (Table S1, last row), and drew the line plots to show the relationship between each of the four evaluation metrics and values of $K$ ranging from 10 to 40 (Fig. S13).

Reporting Summary

Further information on research design is available in the Nature Research Reporting Summary linked to this article.

Extended Data

Extended Data Fig. 1. Convergence behavior for online iNMF and batch iNMF algorithms on scRNA-seq data from the adult mouse brain, human PBMC and human pancreas.

The online iNMF algorithm exhibits faster convergence and better objective minimization after a fixed amount of training time. The advantage of the online algorithm in convergence speed is more apparent for larger datasets. a-c, Adult mouse brain ($n=691,962\hspace{0.17em}\text{cells}$, 9 individual datasets). d-f, Human PBMCS ($n=13,999\hspace{0.17em}\text{cells}$, 2 individual datasets). g-i, Human pancreas ($n=14,890\hspace{0.17em}\text{cells}$, 8 individual datasets). Center lines of box plots show the median; box limits, upper and lower quartiles; whiskers, 1.5x interquartile range; and points are outliers.

Extended Data Fig. 2. Online and batch iNMF yield highly similar UMAP visualizations.

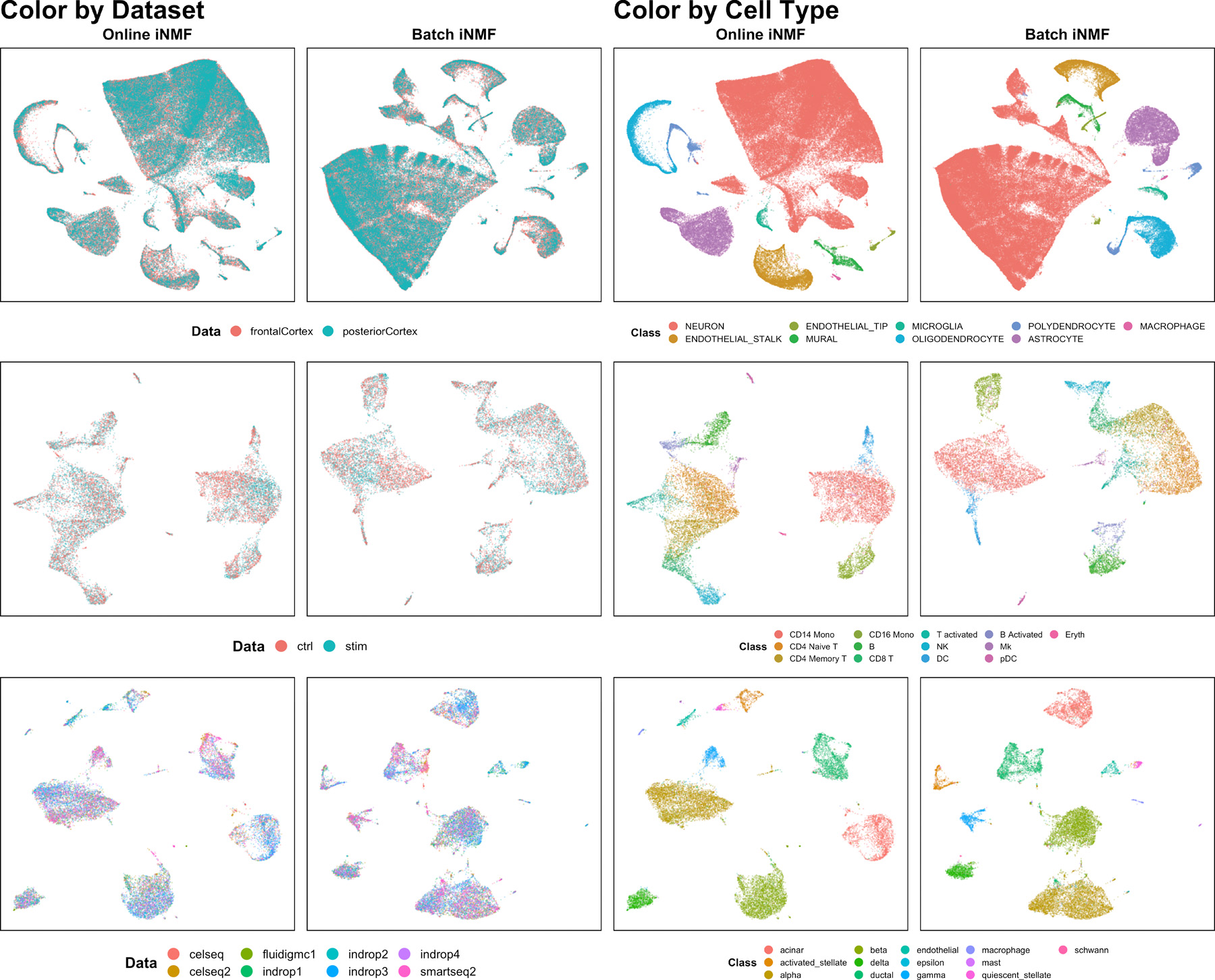
We performed online iNMF and batch iNMF on data from mouse cortex $\left(n=255,353\hspace{0.17em}\text{cells}\right)$, human PBMC $\left(n=13,999\hspace{0.17em}\text{cells}\right)$, and human pancreas $\left(n=14,890\hspace{0.17em}\text{cells}\right)$. Online iNMF and batch iNMF produce very similar visualizations, suggesting that the approaches give very similar dataset alignment and cluster preservation. We subsequently confirmed this qualitative observation using quantitative metrics.

Extended Data Fig. 3. Benchmarking integration across data modalities (RNA+ATAC).

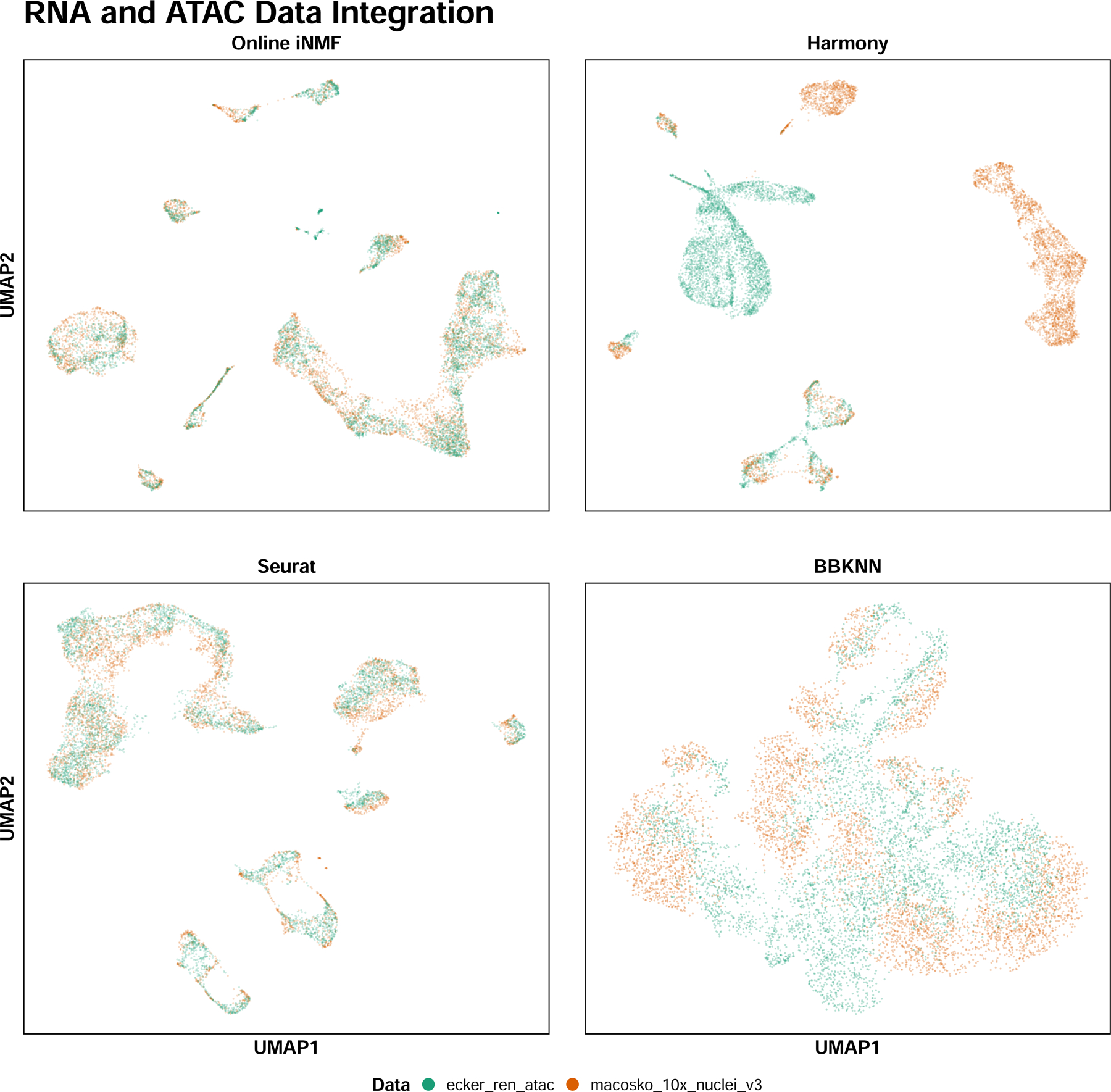
5,000 cells from the snRNA-seq dataset and 5,000 cells from the snATAC-seq dataset from MOP data collection were integrated using four different methods. The cells are exhibited in 2-dimensional UMAP space and colored by dataset.

Extended Data Fig. 4. Performing online iNMF in three scenarios produces similar results.

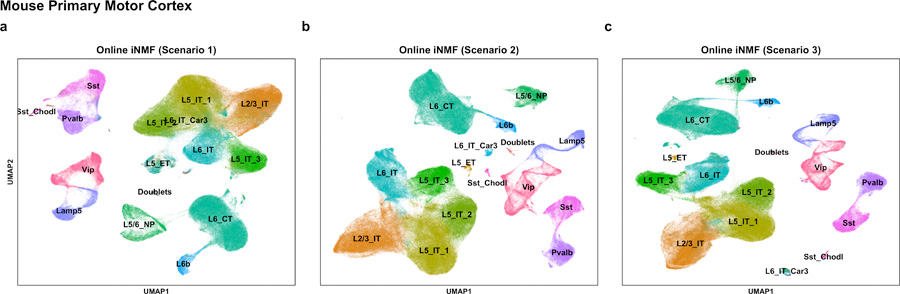
These analyses were carried out separately to integrate 8 MOp datasets (scRNA-seq, snRNA-seq, snATAC-seq and snmC-seq, $n=408,885$) using online iNMF in scenario 1 (a), scenario 2 (b), and scenario 3 (c). The results are visualized in UMAP coordinates and the cells are colored by the cell type annotations from Fig. 6.

Data availability

• Human PBMC from Kang et al.⁹ (GSE96583) distributed by SeuratData

• Human pancreatic islet cells from Grün et al. ¹⁰(GSE81076), Muraro et al.¹¹ (GSE85241), Lawlor et al.¹² (GSE86469), Baron et al.¹³ (GSE84133), and Segerstolpe et al.¹⁴ (E-MTAB-5061) distributed by SeuratData

• Adult mouse brain cells from Saunders et al.⁷ (http://dropviz.org/)

• Mouse organogenesis cell atlas from Cao et al.¹⁸ (https://oncoscape.v3.sttrcancer.org/atlas.gs.washington.edu.mouse.rna/downloads)

• Mouse hippocampus cells from Rodriques et al.¹⁹ (https://singlecell.broadinstitute.org/single_cell/study/SCP354/slide-seq-study#study-download)

• Mouse hippocampus cells from Yao et al.²² (http://data.nemoarchive.org/biccn/grant/zeng/zeng/transcriptome/scell/10X/processed/YaoHippo2020/)

• Mouse hypothalamic preoptic region data from Moffitt et al.²³ (https://datadryad.org/stash/dataset/doi:10.5061/dryad.8t8s248 and GSE113576)

• Mouse primary motor cortex cells from Yao et al.²⁷ (https://assets.nemoarchive.org/dat-ch1nqb7)