Mendelian randomization and pleiotropy analysis

Abstract

Background:

Mendelian randomization (MR) analysis has become popular in inferring and estimating the causality of an exposure on an outcome due to the success of genome wide association studies. Many statistical approaches have been developed and each of these methods require specific assumptions.

Results:

In this article, we review the pros and cons of these methods. We use an example of high-density lipoprotein cholesterol on coronary artery disease to illuminate the challenges in Mendelian randomization investigation.

Conclusion:

The current available MR approaches allow us to study causality among risk factors and outcomes. However, novel approaches are desirable for overcoming multiple source confounding of risk factors and an outcome in MR analysis.

Author summary:

Mendelian randomization analysis is a popular approach to studying the causality of exposures on an outcome, and it shares similarities with randomized controlled trials. Since MR is based on observational data, it requires assumptions that are difficult to validate. We review the current developed MR approaches and the challenges in performing MR analysis and interpreting the results.

INTRODUCTION

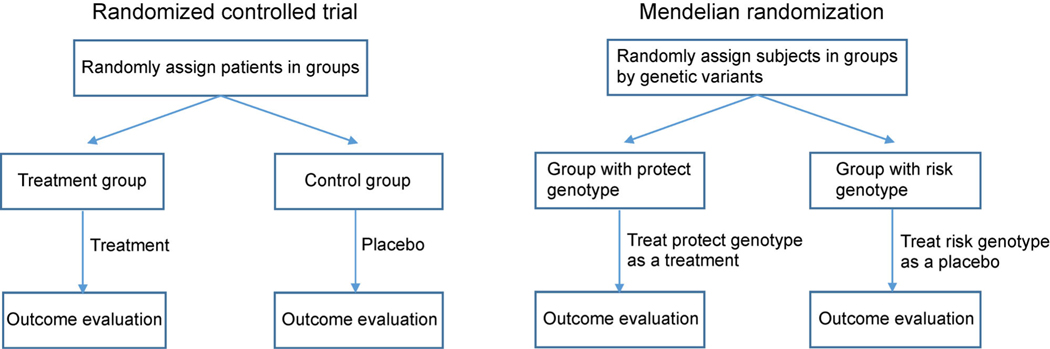
Randomized controlled trials (RCTs) are considered as the gold standard to establish a causal relationship between an exposure and an outcome in epidemiology studies. Many associations observed in epidemiological studies have failed to be replicated in RCTs, such as fiber and colon cancer [1], vitamin E, cardiovascular disease and lung cancer [2,3], and vitamin C and cardiovascular disease [4]. The failed replications in RCTs can be potentially attributed to confounding, reverse causation, and various biases [5,6]. Thus, RCTs are the primary tool to establish a causation between a risk factor and an outcome, but they come with a high cost. To circumvent the high cost in RCTs, Mendelian randomization (MR) has become a widely used epidemiological approach to infer causality of an exposure to a disease outcome [7–9]. This is benefitted from the rapid identifications of genetic variants associated with complex traits in large genome wide associations (GWAS) [10]. Intuitively, MR shares a similarity with RCTs (Fig. 1). In RCTs, the enrolled patients are randomly assigned to a treatment or a control group to eliminate potential confounding associated with both the treatment and the outcome. Therefore, causal effect can be estimated in an unbiased fashion. In contrast, MR assigns subjects based on their carried alleles, which are inherited from their parents. Since the alleles are transmitted from parents to offspring randomly, individuals are therefore divided into different groups randomly based on their genotypes. If the allele is associated with an exposure and the exposure causally affects the disease, we will observe different disease frequencies among different genotype groups. Otherwise, such an association will not be present if the exposure does not contribute to the disease. Furthermore, this association is independent of environment confounding because the allele predisposes to environment [8]. This idea was originally proposed by Katan [9] who focused on testing for the association of a genotype and an outcome rather than estimating the effect of an exposure to an outcome. Hence, the data on exposure in Katan’s approach is not required given that the association between the genotype and the exposure has been established. Recent development of MR focus on the causal effect estimation by using the genetic markers as “instrumental variables (IVs)” [8,11]. With that many large GWASs having already collected genomic data, the MR approach is an appealing method to estimate the causal effect between an exposure and an outcome with much less cost than RCTs.

Figure 1. Comparison between RCT and MR designs.

Early MR approach is based on having one genetic marker as an IV. To be a valid IV, the genetic marker must satisfy the following three IV conditions [8]: (IV1) the genetic marker is reliably associated with the exposure, (IV2) the genetic marker is associated with the outcome only through the exposure, and (IV3) the genetic marker is independent of unobserved confounders that affect the exposure and outcome after conditioning on observed confounders. The IV2 condition is also referred to as the exclusion restriction, and both IV2 and IV3 are difficult to be fully examined in reality [12]. VanderWeele et al. [12] listed multiple exclusion restriction violations in MR analysis when a single genetic marker is used for IV. The potential violations include: pleiotropic genetic instrument variable; measurement error; time-dependent exposure; reverse causation; sample selection bias; linkage disequilibrium between the genetic marker and a causal variant; and population structure. All the above violations will create a pathway from the genetic marker to the outcome that does not go through the exposure, therefore, bringing bias into the causal estimation. An IV with pleiotropic effect is a major concern in a MR analysis. In the past decade, GWASs have been successful in identifying genetic variants associated with complex traits (https://www.genome.gov/gwastudies/). A recent study showed that 90% of the identified variants are associated with multiple traits [13], a term that is characterized as cross phenotype association [14]. This also suggests pleiotropic variants are widely spread across traits. Such pleiotropic variants can be detected by analyzing multiple traits together [15], but the method itself does not indicate which variant is a pleiotropic variant. Thus, methods of using multiple genetic variants for IVs in MR analysis have been rapidly developed [16], and because the impact of some of the violations is alleviated when multiple IVs are applied.

In this review, I will discuss MR approaches using multiple genetic variants as IVs with summary statistics. I will also discuss the pros and cons for these methods (Table 1).

Table 1.

Summary of MR methods

Methods	Conditions	Strengths	Weakness	Software Web address
IVW	Valid IVs or Balanced pleiotropy	Most efficient, Computationally fast	Large bias with invalid IVs	1
MR-Egger	InSIDE	Less requirement for IVs, Computationally fast	Less efficient, Sensitive to outliers	1
Weighted median	>50% valid IVs	Robust to outliers, Computationally fast	Sensitive to selecting IVs	1
MBE	ZEMPA*	Robust to outliers, Computationally fast	Less efficient, Depending on bandwidth parameter	1
MR-Robust	Robust to outliers	Efficient with valid IVs	Inflated FPR with invalid IVs	2
MR-Lasso	Robust to outliers	Efficient with valid IVs	Inflated FPR with invalid IVs	2
MRMix	ZEMPA*	Robust to outliers	Inflated FPR for some cases, Computationally slow	3
MR-PRESSO	>50% valid IVs	Detect pleiotropy variants	Inflated FPR with invalid IVs, Requires simulations/Computational intense	4
iMRP	>50% valid IVs	Identify pleiotropy variants, computationally fast	Inflated FPR with invalid IVs	5

^*ZEMPA: the zero modal pleiotropy assumption

^1. https://cran.r-project.org/web/packages/MendelianRandomization/index.html

^2. http://cran.r-project.org/package=robustbase

^3.https://github.com/gqi/MRMix)

^4. https://github.com/rondolab/MR-PRESSO

^5.Available from the author

STATISTICAL METHODS FOR MR APPROACHES USING SUMMARY STATISTICS

IVW and MR-Egger

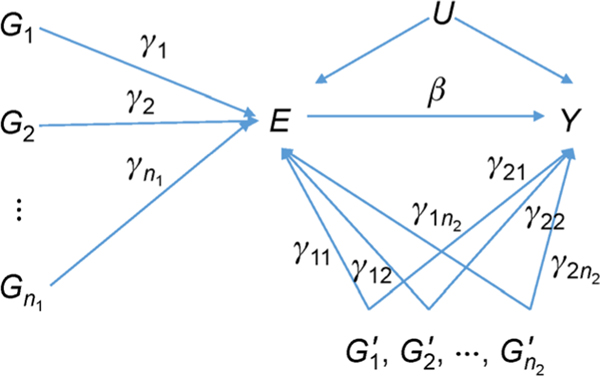
When individual level data is available, an MR analysis can be performed by using the standard two-stage least squares (TSLS) [17]. The same idea can be extended to the data where only summary statistics are available. We denote E and Y as the exposure and the outcome described in Fig. 2, respectively. The goal of MR is to establish the causal relationship from the exposure E to the outcome Y using independent genetic variants as the IVs. We assume that the association of an IV and the exposure has already been reliably established in GWAS. Because the genetic variants associated with the exposure are possibly associated with the outcome through different paths (Fig. 2), we use the following general models:

$$E=\sum _{i=1}^{n_1}{\gamma }_i{G}_i+\sum _{i=1}^{n_2}{\gamma }_{1i}{G}_i^{\prime }+U+{\epsilon }_1,$$ (1)

$$Y=\beta E+\sum _{i=1}^{n_2}{\gamma }_{2i}{G}_i^{\prime }+U+{\epsilon }_2,$$ (2)

where γ_i is the direct contribution of the variant G_i to the exposure E, γ_1i and γ_2i are the direct contributions of variant $G_i^{\prime }$ to traits E and Y, β is the causal effect of E to trait Y, U represents confounding factors, and ε₁ and ε₂ are error terms, respectively. We use G_i and $G_i^{\prime }$ to separately represent two kinds of genetic IVs, that the contribution of G_i (i = 1,...,n₁) to the outcome Y is mediated through the exposure E, and $G_i^{\prime }$ has a pleiotropic effect for the exposure and the outcome in independent paths (γ_1i ≠ 0 and γ_2i ≠ 0). In literature G_i and $G_i^{\prime }$ are often referred to as a vertical and a horizontal pleiotropy (Fig. 2). In the case of horizontal pleiotropy, there is a direct path from its genetic variant G to the outcome Y besides through the exposure E, which causes a biased causal effect estimate in an MR analysis.

Figure 2. A causal path diagram for multiple instrumental variables.

Let ${\widehat{\gamma }}_i$ and ${\widehat{\gamma }}_{1i}$ be the estimated effect sizes of variants G_i and $G_i^{\prime }$ on the exposure E from the GWAS, respectively. Correspondingly, let ${\widehat{\mathrm{\text{Γ}}}}_i$ and ${\widehat{\mathrm{\text{Γ}}}}_{1i}$ be the estimated effect sizes of variants G_i and $G_i^{\prime }$ on the outcome Y, respectively. From the Eqs. (1) and (2), we observe that $E\left({\widehat{\mathrm{\text{Γ}}}}_{1i}\right)=\beta E\left({\widehat{\gamma }}_i\right)$ for G_i, and $E\left({\widehat{\mathrm{\text{Γ}}}}_{1i}\right)=\beta E\left({\widehat{\gamma }}_{1i}\right)+{\gamma }_{2i}$ for the variant $G_i^{\prime }$.

In general, we can estimate the causal effect and its variance from the exposure to the outcome without differentiating G_i and $G_i^{\prime }$ by the following equation [18]

$$\begin{gathered} {\widehat{\beta }}_i=\frac{{\widehat{\mathrm{\text{Γ}}}}_i}{{\widehat{\gamma }}_i}, \\ \mathrm{var}\left({\widehat{\beta }}_i\right)=\frac{\mathrm{var}\left({\widehat{\mathrm{\text{Γ}}}}_i\right)}{{\widehat{\gamma }}_i^2}+\frac{{\widehat{\mathrm{\text{Γ}}}}_i^2}{{\widehat{\gamma }}_i^4}\mathrm{var}\left({\widehat{\gamma }}_i\right)-2\frac{{\widehat{\mathrm{\text{Γ}}}}_i^2}{{\widehat{\gamma }}_i^3}\mathrm{cov}\left({\widehat{\mathrm{\text{Γ}}}}_i,{\widehat{y}}_i\right). \end{gathered}$$ (3)

It is apparent that the causal estimate ${\widehat{\beta }}_i$ is unbiased based on G_i but biased based on $G_i^{\prime }$. The bias for $G_i^{\prime }$ is induced by the nonzero effect γ_2i, or horizontal pleiotropy. Because ${\widehat{\beta }}_i$ is inversely proportional to ${\widehat{\gamma }}_i$, smaller effect size of IV leads to a larger bias of the causal effect estimation. The MR analysis based on a single IV has a poor statistical power and potentially a large bias because

$${\widehat{\beta }}_{IVW}=\frac{\sum _{i=1}^{n_1}{\widehat{\gamma }}_i^2{\widehat{\beta }}_i/\mathrm{var}\left({\widehat{\mathrm{\text{Γ}}}}_i\right)+\sum _{i=1}^{n_2}{\widehat{\gamma }}_{1i}^2{\widehat{\beta }}_i/\mathrm{var}\left({\widehat{\mathrm{\text{Γ}}}}_i\right)+\sum _{i=1}^{n_2}{\widehat{\gamma }}_{1i}^2{\widehat{\beta }}_{1i}/\mathrm{var}\left({\widehat{\mathrm{\text{Γ}}}}_{1i}\right)}{\sum _{i=1}^{n_1}{\widehat{\gamma }}_i^2/\mathrm{var}\left({\widehat{\mathrm{\text{Γ}}}}_i\right)+\sum _{i=1}^{n_2}{\widehat{\gamma }}_{1i}^2/\mathrm{var}\left({\widehat{\mathrm{\text{Γ}}}}_{1i}\right)}.$$ (4)

This ${\widehat{\beta }}_{IVW}$ is referred to as an inverse-variance weighted (IVW) estimate, which is calculated by assuming all the genetic variants are in linkage equilibrium. The IVW estimate can be calculated from summary statistics, an advantage over TSLS that requires individual-level data.

$$\text{Bias of}{\widehat{\beta }}_{IVW}=\frac{\sum _{i=1}^{n_2}{\widehat{\gamma }}_{1i}^2{\widehat{\gamma }}_{2i}/\mathrm{var}\left({\widehat{\mathrm{\text{Γ}}}}_{1i}\right)}{\sum _{i=1}^{n_1}{\widehat{\gamma }}_{1i}^2/\mathrm{var}\left({\widehat{\mathrm{\text{Γ}}}}_i\right)+\sum _{i=1}^{n_2}{\widehat{\gamma }}_{1i}^2/\mathrm{var}\left({\widehat{\mathrm{\text{Γ}}}}_{1i}\right)},$$

which comes from the average effect of the pleiotropic variants. If the pleiotropic effects happen to cancel out, the bias term tends to zero. When the pleiotropic effect γ_2i on the outcome is independent of the effect γ_1i on the exposure, or cov (γ_2i,γ_1i) = 0, the bias can approximate to 0. This condition is referred to as the InSIDE (Instrument Strength Independent of Direct Effect) assumption and can be viewed as a weaker version of the exclusion restriction assumption [22]. Asymptotically, the InSIDE assumption will guarantee the bias tends to zero. In reality, the InSIDE assumption can be difficult to satisfy. To solve this problem, Bowden et al. [22] adopted the idea of Egger’s test, which assesses small study bias in meta-analysis in epidemiology studies, into the MR analysis. They named this method as MR-Egger regression [23].

Without specifically distinguishing G_i and $G_i^{\prime }$, we consider a linear regression of the ${\widehat{\mathrm{\text{Γ}}}}_i$ coefficients on ${\widehat{\gamma }}_i$ coefficients for a set of IVs,

$${\widehat{\mathrm{\text{Γ}}}}_i={\beta }_0+\beta {\widehat{\gamma }}_i+{\epsilon }_i,i=1,2,\dots ,n,$$ (5)

where ${\widehat{\mathrm{\text{Γ}}}}_i$ and ${\widehat{\gamma }}_i$ represent the regression coefficients of the i^th IV for the outcome and the exposure, respectively. The error term ε_i follows a normal distribution: ${\epsilon }_i\sim N\left(0,\mathrm{var}\left({\widehat{\mathrm{\text{Γ}}}}_i\right)\right)$. When regression model (5) constrains the intercept β₀ = 0, the regression coefficient estimate of β corresponds to the IVW estimate. Alternatively, when regression model (5) includes the intercept term β₀, the regression coefficient estimate of β corresponds to the MR-Egger estimate. Testing β₀ = 0 also assesses the presence of pleiotropic variants. The ${\widehat{\beta }}_0$ itself is interpreted of the small variance explained by the IV. Therefore, using multiple IVs has been popular. Multiple IVs may partially mitigate the bias because it is possible to cancel the bias effect due to the nonzero effects of γ_2i [8]. For multiple genetic variants, the causal effect of the exposure on the outcome is estimated by a weighted meta-analysis approach [19–21] given by as an estimate of the average pleiotropic effects [22]. When the InSIDE assumption is satisfied with balanced pleiotropy, referring to γ_2i in Eq. (2) taking positive and negative values randomly, both IVW and MR-Egger approaches have unbiased causal estimate. In the presence of directional pleiotropy, the MR-Egger estimate is still consistent as long as the InSIDE assumption is satisfied, but IVW is not [22]. However, the MR-Egger estimator has a larger standard error than the IVW estimator. Intuitively, this is not surprising because an additional parameter is required for MR-egger, and the pleiotropic IVs will increase the uncertainty in the regression analysis. When sample sizes of GWAS are relatively small, MR-Egger estimator could be even worse [24].

Weighted median and mode-based estimate

An extension of the IVW is the weighted median estimator [25], which is less biased than IVW but more powerful than MR-Egger. The weighted median estimator takes the media of the ${\widehat{\beta }}_i$ of individual genetic variants in Eq. (3), either using equal weights or the inverse of the variance of the ratio estimates by $\frac{{\widehat{\gamma }}_i^2}{\mathrm{var}\left({\widehat{\mathrm{\text{Γ}}}}_i\right)}$. The weighted median estimator has a consistent causal estimator when less than 50% instrumental variables are invalid. Because the weighted median estimate is calculated by a single IV (median) when the number of IVs is odd and an average of two IVs when the number of IVs is even, more than 50% valid IVs is a necessary condition. Unlike IVW, the weighted median estimator is robust to outliers which depart from the true causal line.

Another extension is the weighted mode-based estimate (MBE) [26]. Let ${\widehat{\beta }}_i$ be the causal effect estimate in Eq. (3). The standard weights for the MBE is:

$$w_t=\mathrm{var}{\left({\widehat{\beta }}_i\right)}^{-1}/\sum _{j=1}^n\mathrm{var}{\left({\widehat{\beta }}_j\right)}^{-1}.$$

A simple MBE has $w_1=w_2=\cdots =w_n=1$. We define the normal kernel density function as

$$f(x)=\frac{1}{b\sqrt{2\pi }}\sum _{j=1}^n{w}_j\exp \left[-\frac{1}{2}{\left(\frac{x-{\widehat{\beta }}_i}{b}\right)}^2\right],$$

where b is the smoothing bandwidth parameter. The MBE causal effect estimate is ${\widehat{\beta }}_M=\underset{x}{\max }f(x)$. The magnitude of parameter b reflects a bias-variance trade-off. A larger b leads to a higher precision but also a larger bias. The bandwidth parameter is chosen according to the modified Silverman’s bandwidth rule [27,28]. The MBE relies on the assumption named the zero modal pleiotropy assumption (ZEMPA), that is, across all IVs, the most frequent value of γ_2i in Eq. (2) is 0. The MBE is less biased and has lower type I error than the above mentioned methods under the null. The MBE is also less powerful in detecting causal effect than the IVW and weighted median methods, but it is more powerful than MR-Egger regression.

MR-Robust and MR-Lasso

In ordinary linear regression, one outlier can have a large impact to the regression coefficient estimate. Robust regression methods [29] have been recently applied to perform MR analysis. The current MR-Robust regression estimate by Rees et al. [30] is based on the MM-estimation approach by Koller and Stahel [31], which keeps asymptotic efficiency of the M-estimator and provides robustness against outliers. Lasso regression has been widely applied in high dimensional data by shrinking regression coefficients toward zero through a penalty term [32]. Recently, Lasso regression has been applied to MR analysis when individual level data is available [33,34]. Rees et al. [30] extended the Lasso regression to summary level data by modeling the pleiotropic effects γ_2i in Eq. (2). MR-Lasso considers minimizing the following objective function by including a separate intercept coefficient for each genetic variant in the MR-Egger regression but with a Lasso-penalty term:

$$\sum _{i=1}^n\mathrm{var}{\left({\widehat{\mathrm{\text{Γ}}}}_i\right)}^{-1}{\left({\widehat{\mathrm{\text{Γ}}}}_i-{\beta }_{0i}-\beta {\widehat{\gamma }}_{0i}\right)}^2+\lambda \sum _{i=1}^n\left|{\beta }_{0i}\right|.$$ (6)

If β_0i shrinks to 0 in Eq. (6), the genetic variant is considered as a valid IV. These genetic variants with a zero β_0i are carried forward to perform the IVW analysis to estimate the causal effect β. The MR-Lasso shares some similarity with MR-PRESSO [18], which we will introduce later. When number of invalid IVs increases, both MR-Robust and MR-Lasso have inflated false positive rate and increased the bias of a causal effect estimate.

Mixture model MRmix

With substantial differences, Qi and Chatterjee developed a parametric mixture model (MRmix) by assuming bivariate effect-size distribution of the IVs across pairs of traits [35]. MRmix is an estimating equation approach that requires the residuals, ${\widehat{\mathrm{\text{Γ}}}}_i-\beta {\widehat{\gamma }}_i$, to follow a normal mixture model. The normal mixture model seems plausible when the genetic instruments include mediation variants, horizontal pleiotropic variants, as well as the genetic variants contributing to reverse causality. In order to achieve an unbiased causal estimate, MRmix requires the ZEMPA assumption, which is also required by MBE approach. When the sample size is large, MRmix usually shows a better trade-off between bias and variance than the approaches mentioned before, even more than when 50% IVs are invalid [35]. Similar to MR-Egger, MRmix did not performed well when the number of IVs is small.

MR-PRESSO

The MR-Lasso searches for potential outliers that may present pleiotropic effects [30]. Similarly, MR-PRESSO first identifies horizontal pleiotropic variants and then performs IVW to estimate the causal effect by removing the pleiotropic variants [18]. MR-PRESSO comprises of three steps: 1) testing whether horizontal pleiotropic variants are present through a global test; 2) performing an outlier test to detect pleiotropic variants; 3) comparing the causal estimates before and after removal of pleiotropic variants through a distortion test. The global test is based on a leave-one out approach which consists of 4 steps: 1) for each variant i, IVW regression is performed to obtain the causal effect ${\widehat{\beta }}_{-i}$ after excluding the variant i; 2) the residual square is calculated by) $RS{S}_{\text{obs}}(i)=({\widehat{\mathrm{\text{Γ}}}}_i-{{\widehat{\beta }}_{-i}{\widehat{\gamma }}_i)}^2$ and the global observed RSS is calculated by $RS{S}_{\text{obs}}=\sum _{i=1}^{n}RS{S}_{\text{obs}}(i)$; 3) The expected distribution of RSS under null hypothesis (no pleiotropic variants) is simulated by randomly drawing ${\widehat{\gamma }}_i^{\text{random}}$ from a Gaussian distribution $N\left({\widehat{\gamma }}_i,\mathrm{var}\left({\widehat{\gamma }}_i\right)\right)$ and ${\widehat{\mathrm{\text{Γ}}}}_i^{\text{random}}$ from a Gaussian distribution $N\left({\widehat{\beta }}_{-i}{\widehat{\gamma }}_i,\mathrm{var}\left({\widehat{\mathrm{\text{Γ}}}}_i\right)\right)$, respectively. The expected RSS is $RS{S}_{\text{exp}}=\sum _{i=1}^n\left(RS{S}_{\text{exp}}(i)\right)=\sum _{i=1}^n{\left({\widehat{\mathrm{\text{Γ}}}}_i^{\text{random}}-{\widehat{\beta }}_{-i}{\widehat{\gamma }}_i^{\text{random}}\right)}^2$; 4) An empirical p-value is computed by taking the proportion of expected RSS greater than the observed RSS among K simulations in the third step. For the variant i, the p-value of the outlier test is calculated by taking the proportion of the expected RSS_exp(i) greater than the observed RSS_obs(i) among K simulations. Since MR-PRESSO estimates the causal effect after removing potential pleiotropic variants, it is less biased than IVW. However, MR-PRESSO is also biased when the InSIDE assumption fails. In addition, MR-PRESSO is computationally intensive because a large number of simulations are necessary, especially when the number of IVs is increasing.

Iterative Mendelian randomization and pleiotropy (IMRP)

It is easy to observe that $E\left({\widehat{\mathrm{\text{Γ}}}}_i\right)=\beta E\left({\widehat{\gamma }}_i\right)$ for the mediation variant G_i, and $E\left({\widehat{\mathrm{\text{Γ}}}}_{1i}\right)=\beta E\left({\widehat{\gamma }}_{1i}\right)+{\gamma }_{2i}$ for the pleiotropic variant $G_i^{\prime }$. Note that the effect size of a pleiotropic variant to the outcome has an additional term γ_2i besides the effect through the exposure. If we know the true β, we can test mediation against horizontal pleiotropy by testing the null hypothesis Γ = βγ using a test statistic

$$T_{\text{Pleio}}=\frac{\widehat{\mathrm{\text{Γ}}}-\beta \widehat{\gamma }}{\sqrt{\mathrm{var}(\widehat{\mathrm{\text{Γ}}}-\beta \widehat{\gamma })}},$$

where $\widehat{\mathrm{\text{Γ}}}$ and $\widehat{\gamma }$ are the estimated effect sizes of a variant on E and Y, respectively. The statistic T_pleio asymptotically follows a standard normal distribution N(0,1) when mediation is true. Under the alternative hypothesis that a variant has a pleiotropic effect, T_Pleio departs from the mean of 0. The problem of this test is that the causal effect β is unknown. However, this problem can be solved through an iterative approach by combining the pleiotropy test and the MR analysis, which is named as iterative Mendelian randomization and pleiotropy (IMRP) [24]:

1. Performing MR-Egger analysis using all IVs to obtain the initial causal estimate of β, named as ${\widehat{\beta }}_0$.

2. For all the IVs, performing pleiotropy test T_pleio by substituting β with ${\widehat{\beta }}_{k-1}$ at the k^th iteration to determine which variant g_i has a horizontal pleiotropic effect at a predefined significance level α.

3. Performing IVW analysis to obtain ${\widehat{\beta }}_k$ after removing the variants found to be significant in pleiotropy test at step 2;

4. Repeating the above steps 2 and 3 until there is no change in detected pleiotropic variants.

At step 2 above, the pleiotropy test statistic for a genetic variant is modified as

$$T_{\text{Pleio}}=\frac{\widehat{\mathrm{\text{Γ}}}-\beta \widehat{\gamma }}{\sqrt{\mathrm{var}(\widehat{\mathrm{\text{Γ}}}-\widehat{\beta }\widehat{\gamma })}},$$

where the denominator variance is approximated by

$$\begin{array}{c}\mathrm{var}(\widehat{\mathrm{\text{Γ}}}-\widehat{\beta }\widehat{\gamma })\approx \mathrm{var}(\widehat{\mathrm{\text{Γ}}})+{\widehat{\beta }}^2\mathrm{var}(\widehat{\gamma })+{\widehat{\gamma }}^2\mathrm{var}(\widehat{\beta })\\ -2\widehat{\beta }\rho \sqrt{\mathrm{var}(\widehat{\mathrm{\text{Γ}}})\mathrm{var}(\widehat{\gamma })},\end{array}$$

where ρ is the correlation coefficient of the exposure E and the outcome Y, which can be estimated using GWAS summary statistics [15,36] or LD score regression [37]. Similarly to MR-PRESSO, the global test: $S{S}_{GT}^2=\sum _{i=1}^n{T}_{\text{pleio},i}^2$, which approximately follows a chisquare distribution with n degrees of freedom for n independent IVs, is used to test for the presence of horizontal pleiotropic variants. A genetic variant with a T_pleio test p-value less than 0.05/n, is considered as a variant having a horizontal pleiotropic effect. Thus IMRP can perform both MR analysis and test horizontal pleiotropy simultaneously.

MR analysis often assumes that the IVs are in linkage equilibrium. At a single locus, multiple variants may contribute to exposure and the outcome in different ways, as illustrated in Fig. 3. Let $\widehat{\mathrm{\text{Γ}}}$ and $\widehat{\gamma }$ vectors representing the estimated effect sizes of outcome and exposure from GWAS of M variants, respectively. Let $\widehat{\mathrm{\text{Γ}}}=({\widehat{\mathrm{\text{Γ}}}}_1,{\widehat{\mathrm{\text{Γ}}}}_2,\dots {\widehat{\mathrm{\text{Γ}}}}_M)$ and $\widehat{\gamma }=\left({\widehat{\gamma }}_1,{\widehat{\gamma }}_2,\dots ,{\widehat{\gamma }}_M\right)$. The test statistics T_pleio can be extended to M variants by $S_{\text{pleio}}={(\widehat{\mathrm{\text{Γ}}}-\widehat{\beta }\widehat{\gamma })}^{\mathrm{\text{T}}}\sum ^{-1}(\widehat{\mathrm{\text{Γ}}}-\widehat{\beta }\widehat{\gamma })$, where $\sum$ is an M × M variance–covariance matrix [24]. If working on the standardized E, Y, and genotype values, S_pleio can be simplified to

$$S_{\text{pleio}}=\frac{N_1{N}_2}{N_1+{\widehat{\beta }}^2{N}_2-2\rho \widehat{\beta }\sqrt{N_1{N}_2}}{(\widehat{\mathrm{\text{Γ}}}-\widehat{\beta }\widehat{\gamma })}^{\text{T}}{R}^{-1}(\widehat{\mathrm{\text{Γ}}}-\widehat{\beta }\widehat{\gamma }),$$

where R is the linkage disequilibrium (LD) matrix among the M variants. Under the null hypothesis of mediation, S_pleio follows a chi-square distribution with M degrees of freedom.

Figure 3. The relationships of genetic variants, exposure and outcome.

(A) Mediation: the causal variant lies on the causal path to Y. (B) Horizontal pleiotropy: the causal variant affects both E and Y. (C) Colocalization: two different causal variants at one locus affect E and Y. The red star represents the causal variant and S represents genetic markers.

A significant difference between IMRP and MR-PRESSO is that IMRP removes horizontal pleiotropic variants step by step and re-estimates the causal effect accordingly, while MR-PRESSO removes horizontal pleiotropic variants in one step. Since the causal effect estimate is sensitive to outliers, an iterative method is less biased and can advantageously detect pleiotropic variants [24]. Because usually less than 10 iterations are sufficient, iMRP is more computationally efficient than other methods, such as MR-PRESSO, MRmix, MBE, MR-Lasso or MR-Robust. iMRP shares the same computational efficiency as IVW but is almost unbiased even if half of IVs are invalid [24]. iMRP can be easily extended to include multiple variants on a locus, whether they are in LD or not, thereby testing for pleiotropy and colocalization.

APPLICATIONS

In this review, it is not our intention to list all methods and software for performing MR analysis. Rather, we introduced the basic concept and strategy for performing MR analysis. In practice, inferring causality is extremely challenging because of many unmeasured confounders, reverse causality, and weak instrument bias. Burgess et al. recently published guidelines for performing MR in practice [38]. Multiple analytical steps have been suggested and these steps are categorized into: motivation and scope, data sources, choice of genetic variants, variant harmonization, primary analysis, supplementary and sensitivity analyses, data presentation, and interpretation [38]. These guidelines are useful for correctly inferring causality and unbiasedly estimating the causal effect of an exposure to an outcome, given more and more practices of MR analyses have been performed in this post genome wide association era. For example, it is clearly different to infer potential causality versus to estimate the causal effect, with the former focusing on hypothesis test and the latter focusing on the size of the causal effect. In the original MR analysis by Katan [9], testing for association of a genetic variant and an outcome will be sufficient to infer the causality, as long as the genetic variant is a valid IV. Such analysis does not require genotype data for the exposure, but statistical power for testing the association between the variant and the outcome is critical. In comparison, the intervention effect of an exposure to an outcome can be estimated from MR analysis, which is usually achieved by a randomized clinical trial. In this case, it will be important to know how well the genetic variant can proxy the true causal variant, whether the genetic variant has heterogeneous effects on exposure to outcome, for example due to gene-gene interactions, and whether the associations with exposure and outcome are obtained from the same population [38,39]. Mendelian randomization can be performed in either one sample with individual level data for both exposure and outcome or two samples with summary statistics for the exposure and the outcome in separate datasets. Although one sample with individual level data allows for flexible modeling and the exposure and outcome to be measured from the same individuals, the sample size is often small, leading to low statistical power. In comparison, two samples with summary statistics can often reach large sample sizes, but its dangers include potential different populations for the exposure and outcome, and different demographic information, which will make interpretation difficulty and invalidate causal inferences [40,41]. In GWAS meta-analysis, allele flips can cause loss of statistical power when meta-analyzing multiple datasets [42,43]. The same problem can occur in a two sample MR analysis when variant harmonization is a necessary step. In general, multiple analysis methods should be performed because these methods are valid under different assumptions, which have been reviewed before. As suggested by the guidelines [38], both IVW based methods and robust methods should be applied with additional sensitivity analysis. The iMRP method [24] can assess colocalization, which will help to identify more plausible genetic IVs for MR analysis. In addition, the interpretation of findings from MR analysis should always be cautious because of multiple untestable assumptions, as is illuminated in the guidelines [38,44].

Perhaps, which genetic variants should be included in a MR analysis might be the most important decision [38]. In MR analysis, only mediation genetic variants can satisfy the three IV conditions as valid instrumental variables [45]. In fact, there is a debate about whether MR can reliably identify causality between two traits given the widespread of pleiotropy or colocalization [46,47]. The variants with pleiotropic effects violate the IV2 condition for valid IVs. Detecting horizontal pleiotropy is challenging, as demonstrated that the recent HOPS approach has an inflated type I error [48], which may reduce the power of MR analysis compared with IMRP and MR-PRESSO.

AN MR ANALYSIS OF THE CAUSALITY OF HIGH-DENSITY LIPOPROTEIN CHOLESTEROL (HDL-C) ON CORONARY ARTERY DISEASE (CAD)

Many large-scale population studies have reported an inverse relationship between HDL-C and CAD [49,50]. A well cited MR analysis using 15 genetic variants as IVs suggested that there is no causal relationship between HDL-C and myocardial infarction [51], which was consistent with the evidence from a clinical trial study [52]. However, the MR study using more genetic variants by Holmes et al. [53] suggested uncertainty in a causal role for HDL-C on CVD risk. We downloaded the GWAS summary statistics of Global Lipids Genetics Consortium (cholesterol traits) (http://csg.sph.umich.edu/abecasis/public/lipids2013/) and CARDIoGRAMplusC4D Consortium (coronary artery disease) (http://www.cardiogramplusc4d.org/data-downloads/). We obtained 143 genome wide significant independent variants (p-value < 5 × 10⁻⁸) associated with HDL-C after pruning (r2 < 0.1) using the software Plink [54] on a 500 kb window size. We performed the MR analysis by assuming the path diagram in Fig. 4A, representing no confounders. Table 2 presents the causal estimates and p-values for the different MR methods, including IVW, MR-Egger, median, MBE, MRmix, MR_PRESSO and IMRP. In general, IVW, simple median, and MR_PRESSO had the largest protected causal effect estimates followed by IMRP and weighted median. MRmix and MBE had the smallest protected causal estimates. Interestingly, MR-Egger had a positive causal estimate, but it was not significant. We also observed that MR-Egger and MRmix had the largest standard errors, which suggested these approaches may lose statistical power. IVW, simple median, MR_PRESSO and IMRP also suggested significant causal effect of HDL-C on CAD, but the rest of the methods did not. The IMRP analysis also identified 10 pleiotropic variants for HDL-C and CAD.

Figure 4. The two path diagrams for HDL-C and CAD.

(A) There is no separate path through TG. (B) There is a separate path through TG.

Table 2.

Causal effect estimates of HDL on CAD using 143 IVs by different MR methods

Method	Casual estimate	Standard error	95% CI	p-value
IVW	−0.163	0.046	(−0.252, −0.073)	3.95 × 10−4
MR-Egger	0.06	0.084	(−0.103, 0.224)	0.47
Simple median	−0.241	0.054	(−0.348, −0.135)	8.08 × 10−4
Weighted median	−0.062	0.046	(−0.152, 0.028)	0.174
MBE	−0.023	0.055	(−0.130, 0.084)	0.668
MRmix	−0.04	0.086	(−0.209, 0.129)	0.642
MR_PRESSO	−0.187	0.037	(−0.260, −0.115)	1.4 × 10−6
IMRP	−0.075	0.027	(−0.128, −0.022)	5.19 × 10−3
IMRP*	−0.062	0.031	(−0.123, −0.001)	0.043

^*IMRP analysis after dropping 60 pleiotropy variants.

It is known that HDL-C and triglycerides (TG) are correlated. The correlation between the summary statistics of HDL-C and TC was −0.235. It is then possible that a genetic instrumental variable (G) has a pleiotropic effect on HDL-C and TG, therefore, conditional on HDL-C, G can still affect CAD by the mediation of TG (Fig. 4B). The mediation of TG also led to a loss of statistical power to detect pleiotropic variants for HDL-C and CAD. Thus, we performed IMRP for HDL-C and TG to identify pleiotropic variants for these two correlated traits. We were able to identify 60 pleiotropic variants among the 143 IVs. After dropping these 60 variants, the OR of HDL-C on CAD estimated by IMRP was reduced to 0.94 (p = 0.043), suggesting that the initial significant causal effect of HDL-C on CAD was biased because of the correlated trait TG. This example also suggests the importance to examine the traits correlated with both the exposure and outcome.

FUTURE RESEARCH

We reviewed statistical approaches for performing a Mendelian Randomization analysis using summary statistics from genome wide associations. The application of HDL-C on CAD clearly suggested that there is no uniformly best approach. There is always a trade-off between bias and efficiency. Among the methods, MR-PRESSO and IMRP are able to both perform the MR analysis and detect pleiotropic variants, and IMRP is computationally 3 order faster than MR-PRESSO and is less biased [24]. MBE and MRmix are less biased, but they also lose statistical power. Although MR is easy to conduct due to increased availability of genome data, the challenges remain. First, one challenge is the identification of valid IVs, i.e., the genetic variants have no horizontal pleiotropic between exposure and outcome. Because of the modest contribution of a genetic variant to a trait, statistical power in detecting pleiotropy can be low and requires a large sample size. New statistical approaches will be welcomed for detecting horizontal pleiotropy. Second, most of the current MR approaches assess the causal effect of one exposure on one outcome. Traits are often correlated with shared genetic contributions [55]. The correlated traits can easily lead to confounding in MR analysis, which can create multiple independent paths from a genetic IV to an outcome without pathing through the exposure, as we observed in the MR analysis of HDL-C and CAD. Multivariate MR with multiple exposures and one outcome was less developed and the current multivariate MR is unable to deal with unknown pleiotropy [56], but has advantages to solve the problems of multiple correlated exposures. Third, a single genetic variant has little prediction power. To improve the power, polygenic risk score (PRS) has been used for predicting disease and inferring putative causal relationships among traits [57]. However its false positive rate is also inflated when inferring causality [58]. A PRS has less concern caused by weak instruments. Further methodological development is necessary to unbiasedly estimate and correctly interpret the causal effect estimation through a PRS. Fourth, large GWAS also demonstrated gene-environment/life style interactions contributing to phenotype variation, and these summary statistics are available [59,60]. It will be beneficial to develop MR approaches that can be applied to summary statistics from GWAS of gene-environment interaction studies, which can potentially provide better causal effect estimations. Lastly, current large GWASs have mainly been conducted in European ancestry populations. The sample sizes in other ancestry populations are much less, resulting less identifications of genetic variants. Utilizing the GWAS information from European ancestry populations to perform MR analysis in other ancestry populations needs innovative statistical approaches. In conclusion, current genomic advances provide an unprecedented opportunity to study casual relationships among risk factors and diseases via MR analysis, and the results will lay a foundation for future, well designed randomized control trials.