Biomolecular QM/MM Simulations: What are some of the “Burning Issues”?

Abstract

QM/MM simulations have become an indispensable tool in many chemical and biochemical investigations. Considering the tremendous degree of success, including the recognition by a 2013 Nobel Prize in Chemistry, are there still “burning challenges” in QM/MM methods, especially for biomolecular systems? In this short Perspective, we discuss several issues that we believe greatly impact the robustness and quantitative applicability of QM/MM simulations to many, if not all, biomolecules. We highlight these issues with observations and relevant advances from recent studies in our group and others in the field. Despite such limited scope, we hope the discussions are of general interest and will stimulate additional developments that help push the field forward in meaningful directions.

Graphical Abstract

1. Introduction

Following many years of development and calibration, hybrid quantum mechanical/molecular mechanical (QM/MM) methods^1–4 have become an essential tool^5–8 in chemical and biochemical research. Applications of QM/MM simulations to enzymes include not only dissection of reaction mechanisms, elucidation of various factors that contribute to catalysis, but also design of enzyme inhibitors, analysis and improvement of designed enzymes as well as understanding evolutionary relations between enzymes.^9–16 Indeed, a search using the keyword “QM/MM” or “ONIOM”¹⁷ in the Web of Science points to >800 articles published in 2019–2020 alone. Numerous molecular simulation packages such as CHARMM, AMBER, NAMD, OpenMM and Gromacs all have QM/MM functionalities, some with build-in QM modules, while others providing interfaces with popular QM packages such as Gaussian, Q-Chem, Turbomole, Psi4 and ORCA; similarly, many quantum chemistry packages such as Gaussian, ORCA, C2PK and DFTB+ offer coupling with external MM models; there are also platforms that focus entirely on QM/MM calculations, such as the celebrated Chemshell environment¹⁸ pioneered by Sherwood and the late Walter Thiel,¹⁹ who has made numerous important contributions to the field in terms of both method developments and systematic analyses of factors that impact the accuracy of QM/MM simulations.

In light of such tremendous success, including the recognition by the 2013 Nobel Prize in Chemistry, one is tempted to ask: are there still “burning issues” for QM/MM methods, especially for biomolecular systems? If so, are the corresponding challenges fundamental in nature, or should they be better thought as establishing the best practice and enabling most efficient execution for realistic applications? The answers to such questions are clearly highly subjective, and in this short Perspective article, we discuss our views based on the recent research interest and developments in the group. Despite such limited scope, we hope the discussions are of general interest and will stimulate additional developments that help push the field forward in meaningful directions.

Before turning to these discussions, it is worth noting that application of QM/MM methods to solid/liquid interfaces,^20,21 for example in the important context of electrochemistry²² and heterogeneous catalysis,²³ has been much more limited compared to biomolecular studies. This is perhaps due mainly to the less obvious scheme to divide the solid into QM and MM regions without considerable perturbation to the electronic structure of the solid, especially for metallic systems (e.g., the electrode). Therefore, efforts have focused primarily on pure QM based embedding approaches, such as those pioneered by Carter and co-workers based on orbital-free DFT,²⁴ which have been successfully applied to many materials problems. Nevertheless, these pure QM based embedding approaches remain computationally expensive for solid/liquid interfaces, for which an adequate sampling of the interfacial solvent and ions (i.e., the electric double layer²⁵) is expected to be essential. Therefore, further development, implementation and calibration of robust QM/MM methods for solid/liquid interfaces, especially under the condition of constant potential,^26,27 ought to be considered an important area of research. Similar to the studies of reactions in solution, QM/MM simulations with explicit solvent²⁸ and advanced implicit solvent models^29,30 are expected to be complementary to each other for the mechanistic analysis of electrochemical reactions.

2. Several “Burning Issues”

In the following, we discuss several “burning issues” that we believe greatly impact the robustness and quantitative applicability of QM/MM simulations to many, if not all, biomolecules. We group these issues into several general topics related to QM/MM simulations, and we highlight them with observations and relevant advances from recent studies in our group and others in the field.

2.1. Potential Function: QM and MM Selections

The choices for QM/MM partitioning and the relevant QM and MM methods are largely system-dependent. Nevertheless, given a considerable number of recent studies and sometimes passionate debates^31–40 regarding these choices, it is worth discussing several issues explicitly.

2.1.1. The value of semi-empirical and machine learning potentials

Since adequate sampling is important to biomolecular applications, the need of an efficient QM potential is compelling, especially when the proper QM region contains at least hundreds of atoms. Along this line, approximate QM approaches such as semi-empirical QM methods^41,42 and the empirical valence bond (EVB) method⁴³ remain particularly attractive in many applications. They need to be carefully calibrated to generate meaningful results; once calibrated (e.g., using spline fits to high-level reference reactions⁴⁴), they are uniquely powerful for the analysis of systems and/or experimental observables that demand extensive sampling. For example, as discussed further below, DFTB3/MM simulations enable the sampling of multi-dimensional free energy surfaces, which are required to analyze complex reaction pathways and to characterize the coupling between different processes (e.g., mechanochemical coupling). On the other hand, EVB based simulations have been instrumental to the computation of experimental observables that require extensive sampling to achieve the necessary numerical precision, such as activation entropy⁴⁵ and linear free energy relations,⁴⁶ which are difficult to compute otherwise. These examples include >150 ns of DFTB3/MM simulations⁴⁷ and thousands of independent EVB free energy profile simulations,⁴⁸ which are indeed very difficult, if not currently impossible, to reach with ab initio QM/MM simulations, despite impressive progress in computational algorithm as well as hardware.^49,50

Motivated by these considerations, a “burning issue” is to improve the accuracy and applicability of semi-empirical QM methods; work along this line has been reviewed fairly recently⁵¹ and will not be repeated here. A notable advance since then is the development of the extended tight binding model of Grimme et al. (xTB),⁵² which has been parameterized for the entire periodic table. While the model was developed mainly for capturing structures and vibrational frequencies, it gives encouraging results also for energetics, especially for non-covalent interactions.⁵³ In Fig.1a, we compare the performance of several popular semi-empirical methods for computing the second virial coefficients of small molecules of different levels of polarity; in Fig.1b, we compare the two-body and three-body interactions of water molecules by DFTB3 and xTB using the dataset of Paesani and co-workers.⁵⁴ Evidently, despite the minimal basis nature of these methods, the performance is quite respectable even for three-body interactions of water, and these tight binding methods outperforms several NDDO methods, even those including empirical corrections for hydrogen-bonding interactions (see Supporting Information). On the other hand, there is clearly room for improvements, which would also require analysis in the condensed phase environment,⁵⁵ such as the computation of solvation free energy and binding affinity.

Figure 1:

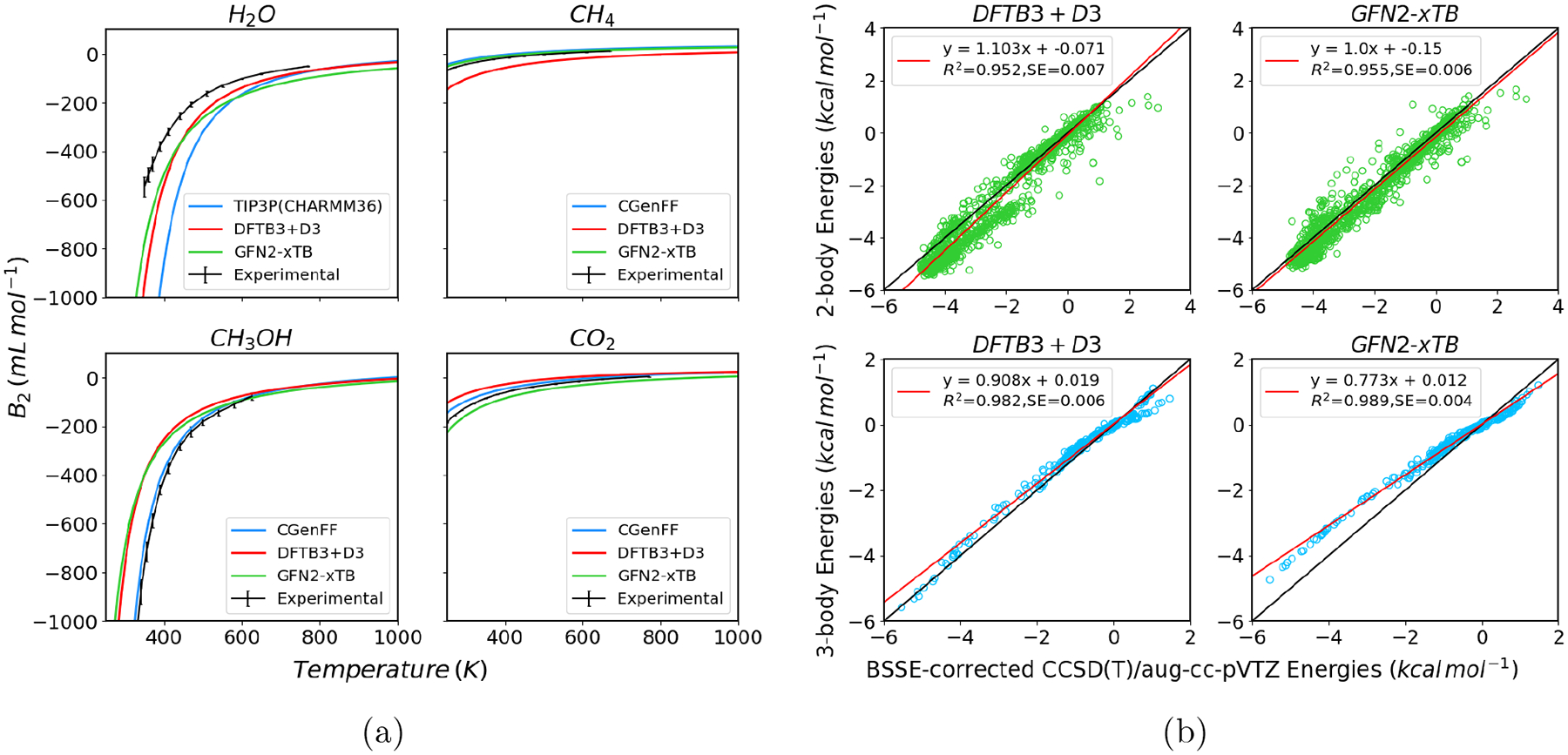
Non-covalent interaction with two density functional tight binding methods. (a) Second virial coefficients (B₂) for several small molecules, in comparison with CHARMM-CGenFF⁵⁶ and experimental results; (b) 2,3-body interactions of water in comparison with the BSSE corrected CCSD(T)/aug-cc-pVTZ database of Paesani and co-workers.⁵⁴ For additional results, see Supporting Information.

A major remaining challenge for the semi-empirical QM methods (and ab initio QM methods) is the treatment of transition metal ions, which are common in enzymes. The highly localized nature of the d and f electrons requires a reliable treatment of electron correlation, both dynamic and static. For structural properties, both DFTB3 and xTB appear to be able to provide adequate equilibrium parameters,^51,53 although the energy landscape has not been thoroughly analyzed. Analysis of the electronic structure using Natural Bonding Orbital analysis^57,58 found that DFTB3 provides physically sound descriptions for different bonding scenarios, including those exhibiting pseudo Jahn-Teller effects (see Fig.2a as an example). The degree of ligand to metal charge transfer and ionic character of certain bonds are overestimated, likely reflecting the minimal basis nature of DFTB3, and certain orbital interactions, such as geminal interactions, were observed to be grossly overestimated by DFTB3 for several transition metal compounds. Energetics are generally less satisfying, especially when considering different spin states, since interactions among d/f electrons are treated in an averaged fashion in the current tight-binding models. One possible improvement is to treat the d/f electrons separately, along the line of the DFT+U model in materials science⁵⁹ or the ligand-field model in the inorganic chemistry literature.^60,61 In a recent explorative study,⁶² together with collaborators we have implemented a preliminary version of the DFTB3+U model,

$$E^{\mathit{\text{DFBT}}3+U}=E^{\mathit{\text{DFTB}}3}+\sum _{\alpha ,\beta ,{\alpha }^{\prime },{\beta }^{\prime }\in d/f}\left[P_{\alpha \beta }^U{P}_{{\alpha }^{\prime }{\beta }^{\prime }}^U\langle \alpha {\alpha }^{\prime }\Vert \beta {\beta }^{\prime }\rangle -P_{\alpha \beta }^I{P}_{{\alpha }^{\prime }{\beta }^{\prime }}^I\langle \alpha {\beta }^{\prime }\mid {\beta }^{\prime }\alpha \rangle \right],$$ (1)

in which P^U(P^I) are the spin unpolarized (polarized) density matrix elements involving the d/f electrons and the usual two-electron integrals are parameterized in terms of the Slater integrals or the Racah parameters.⁶⁰ It was found⁶² that the additional U contribution indeed improved the splitting between the low-spin and high-spin states in a series of Ni(II) and Ni(III) compounds as well as the populations of the 3d orbitals.⁶³ Further self-consistent tuning of the electronic parameters in the model will be informative regarding the degree of transferability and expected accuracy for the +U model, and whether a multi-determinant formulation of the DFTB3 model (e.g., in the framework of ensemble⁶⁴ or multi-state⁶⁵ DFT) is warranted.

Figure 2:

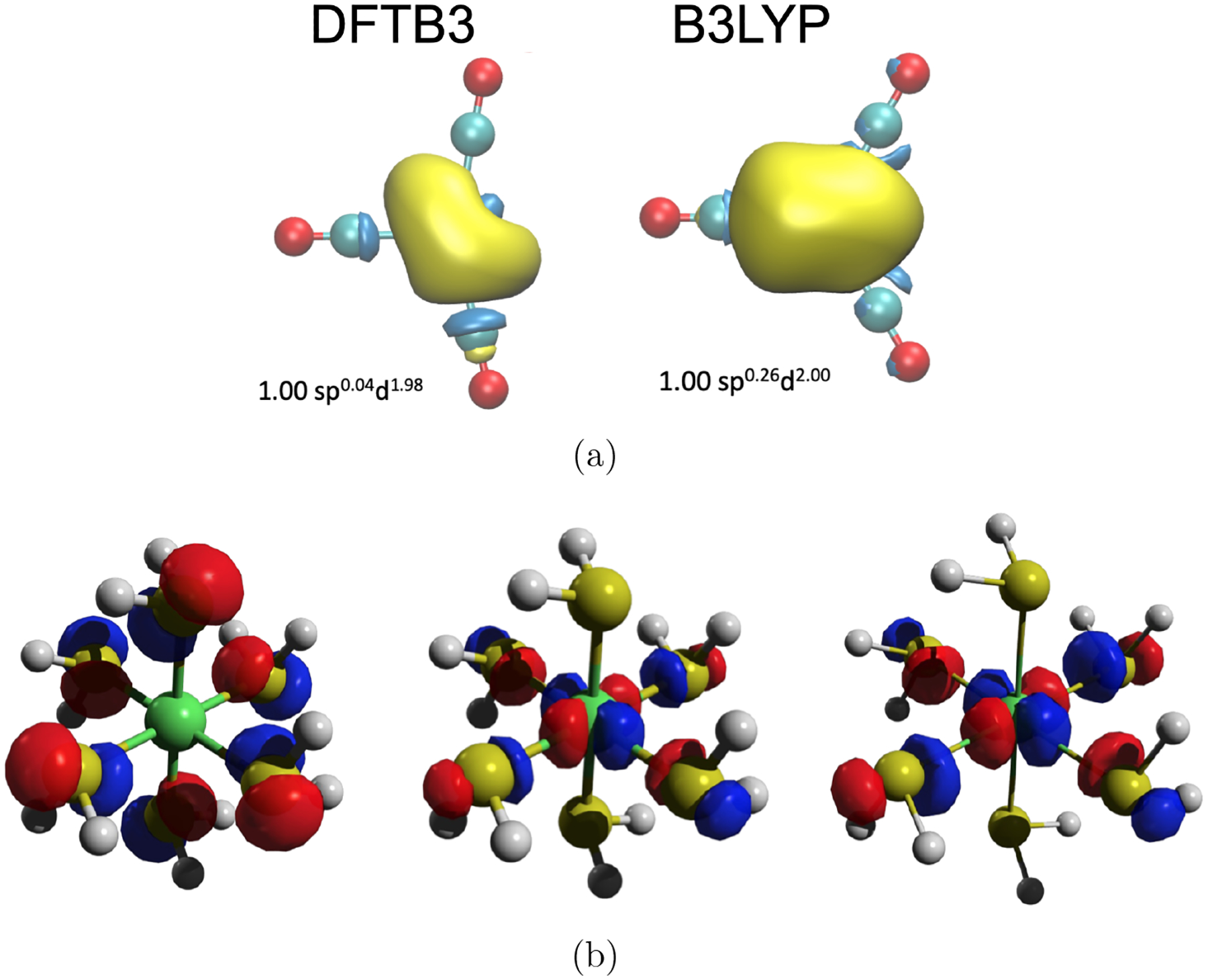
Description of Ni compounds with DFTB3. (a) Comparison of the nickel lone valence hybrid in [Ni(CO)₃]²⁺ with DFTB3/3OB and B3LYP based Natural Bonding Orbital analyses;^57,58 DFTB3 and B3LYP favor D_3h and C_2v symmetry, respectively. (b) Examples of frontier orbital comparisons between DFTB3, DFTB3+U and PBE calculations for high-spin [Ni(H₂S)₆]²⁺. Including the +U correction in DFTB3/3OB⁶² improves various properties such as d orbital populations, nature of frontier orbitals, ligand field splitting and energy difference between low/high-spin states.

Another promising direction for improving approximate (tight-binding and DFT) methods is to employ machine learning (ML) techniques,⁶⁶ which have seen explosive progress in recent years for developing potential energy functions,⁶⁷ predicting molecular/materials properties⁶⁸ as well as enhancing conformational sampling.⁶⁹ Specific for metal ions, for example, ML approaches have been used to analyze spin state properties⁷⁰ as well as diagnostics for static electron correlations.⁷¹ ML models have also been used to improve the accuracy of mean-field models such as tight-binding and Hartree-Fock, with features ranging from simply atomic coordinates to Fock matrix elements.^72,73 For realistic condensed phase QM/MM applications, the judicious combination of a physical reference QM level and ML is required to ensure the optimal balance of accuracy, robustness and transferability. Further developments along this line, so as to enable stable, energy-conserving MD simulations,^74,75 will be exciting and transformative in terms of the type of problems that QM/MM simulations are able to tackle.

2.1.2. Going beyond popular additive MM models

Most QM/MM applications to biomolecules use popular fixed-charge MM force fields. The general success of these applications suggests that this combination is adequate for many problems, an observation also made in several comparisons of QM/MM results using both fixed-charge and polarizable force fields.⁷⁶ Nevertheless, the need to include explicit electronic polarization for certain problems has also been well documented, such as for the prediction of absorption spectra,^77,78 reduction potential⁷⁹ and pK_a values;⁸⁰ i.e., for situations where there is a very large change in the electrostatic properties (e.g., either the net charge or dipole moment) of the QM region. While more ad hoc models such as charge scaling⁸⁰ or atomic polarizability models⁸¹ were used in earlier studies, more systematic efforts that integrate QM with well calibrated polarizable force fields such as AMOEBA, Effective Fragment Potential and MB-pol have been reported.^79,82–84

A systematic comparison between QM/MM simulations with different MM models will be informative for better identifying problems for which an explicit treatment of electronic polarization makes a qualitative difference; for example, it was suggested that to properly capture the electric field in enzyme active site for the purpose of guiding design, including electronic polarization is essential.⁸⁵ Along this line, we highlight that a meaningful comparison will require extensive sampling. In part, this is because electrostatic interactions between groups in a biomolecule are screened quite effectively;^86,87 this is especially the case for many enzyme active sites, which are buried but not far from the protein/solvent interface. To properly capture the screening effect, it is important to consider reorientation of the protein and solvent dipoles during a chemical reaction (this contrasts to the situation of ultrafast spectroscopy,^78,83 for which electronic dielectric response of the environment tends to be particularly important due to the limited degree of dipolar reorientation during the short time scale); without adequate sampling of such dipolar reorientations, the effect of distant groups can be overestimated. A somewhat extreme illustration is that contributions from distant charged residues to the pK_a of a titratable group are significantly overestimated (>10 kcal/mol) when analyzed in a perturbative fashion,^88,89 i.e., by computing the change of QM/MM interaction energies without re-sampling the MD trajectory after the MM partial charges on a charged residue are turned off. For a similar reason, without adequate sampling, the effect of altering the description (MM vs. QM) of distal residues can be exaggerated, thus the issue of sampling is also highly pertinent to the discussion of QM region size in QM/MM simulations.^31–39

The sampling challenge is particularly significant for the prediction of properties that involve a net change of total charge, such as reduction potential and pK_a values, since the corresponding “charging” process is likely coupled with non-trivial changes in the protein structure and local hydration levels.^90,91 Along this line, recent studies suggested that the lack of explicit electronic polarization leads to errors more than 1 eV for the reduction potential of flavins in proteins;⁷⁹ this important observation is somewhat surprising as fixed-charge force field models have been quite successful at capturing relative reduction potential and pK_a values based on alchemical free energy simulations,^92–94 provided that adequate sampling is done; one possible explanation is that the average polarization effect is empirically included in the fixed-charge force fields. Therefore, thorough comparison of different QM/MM models for both absolute and relative free energies with sufficient sampling is of great value. To enable such comparisons, advanced sampling techniques, including grand canonical Monte Carlo approaches for efficiently sampling local hydration level, are expected to be essential; subtle technical issues such as the effect of net charge change in Ewald summation, which are well understood,⁹⁵ should be considered when comparing results from different set ups, as many ab initio QM/MM simulations, especially those employ advanced MM models, still do not use periodic boundary condition while many semi-empirical QM/MM simulations do.^96,97

Another deviation from standard QM/MM setups is to employ coarse-grained (CG) models for at least part of the MM environment,^98–100 which was motivated by applications that involve slow processes such as large-scale structural transitions of the biomolecule¹⁰¹ or protein design. Considering that QM/MM interaction terms are crucial to the accuracy of QM/MM simulations in general, it is challenging to construct reliable QM/CG models that are transferable among distinct conformational states, although solid progress have been reported.⁹⁸

2.2. Local Sampling: Multi-dimensional and Multi-level free energy simulations

For effective sampling, depending on the nature of the bottleneck, different strategies are required. Thus we separately discuss several “burning issues” related to local sampling and remote (allosteric) effects in this and subsequent subsections, respectively. We focus on issues most relevant to biomolecular QM/MM applications, since excellent reviews are available on the general topic of enhanced sampling for biomolecules.^102,103

2.2.1. Multi-dimensional free energy simulations: competitive pathways and causal relations among different processes

One could argue that to capture the key features of the chemical step(s) in most enzymes, standard QM/MM free energy simulations (e.g., umbrella sampling and metadynamics) using one or two collective variables (CVs) are likely adequate. For more complex transformations that explicitly involve multiple catalytic groups, such as ATP hydrolysis in molecular motors, finite temperature string methods¹⁰⁴ that parameterize the minimum free energy path with a large number of CVs can be very effective.^105,106 A direction of major interest is to develop the finite temperature analog of automated and exhaustive reaction path searches^107,108 on potential energy surfaces such that catalytic mechanism analysis for multi-step reactions in enzymes can be done in an automated fashion without prior bias by human intuition.

On the other hand, some problems require alternative approaches. For example, one hall-mark that distinguishes biomolecules from artificial catalysts is that the chemical activities in the former are often tightly coupled to other processes. As a result, chemical reactions can be used in biology to drive other events such as conformational transitions or pumping ions across the cell membrane, forming the basis of energy and signal transductions in cells.¹⁰⁹ As the other side of the coin, the level of chemical activity in biomolecules can be significantly perturbed by processes that occur either proximal or distal to the active site, giving rise to a multitude of regulatory mechanisms of enzyme catalysis. Therefore, understanding the physical principles that govern the coupling between the chemical step and other events, such as penetration of water molecules into the active site,^110–112 recruitment of transient metal ions,^113,114 or conformational rearrangements near and afar,^115–119 is of great fundamental and practical importance.

For such problems, the most revealing approach that can clearly elucidate the causality among different processes is to conduct multi-dimensional free energy simulations. This is computationally demanding and therefore particularly requires a balance between computational accuracy and efficiency; semi-empirical QM/MM methods, perhaps augmented with ML corrections, are uniquely appropriate in this context. Even with inexpensive QM/MM methods, it is essential to ensure optimal efficiency in building up the free energy surface and allocating computational resources for the sampling of the relevant CV space; the selection of the appropriate set of CVs is not unique to QM/MM simulations and has been discussed extensively in the literature.^69,103

Along this line, ML approaches can again offer simple and effective solutions. For example, Zhang et al.¹²¹ developed a reinforcement learning approach in which a neural network ensemble is used to learn the multi-dimensional free energy surface. The approach takes advantage of the numerical flexibility of neural networks to parameterize high-dimensional functions; in addition, the use of an ensemble of neural networks makes it straightforward to identify regions of the CV space that have been undersampled, so that computational resources are automatically re-allocated accordingly. The approach can be straightforwardly applied to QM/MM simulations (Fig. 3) to analyze competition of multiple reaction pathways as well as coupling between the chemical step and other local processes, such as metal ion trafficking. In the current form, the approach does not actively enhance the sampling of degrees of freedom not included in the CV space, which again is not a unique challenge to QM/MM simulations.

Figure 3:

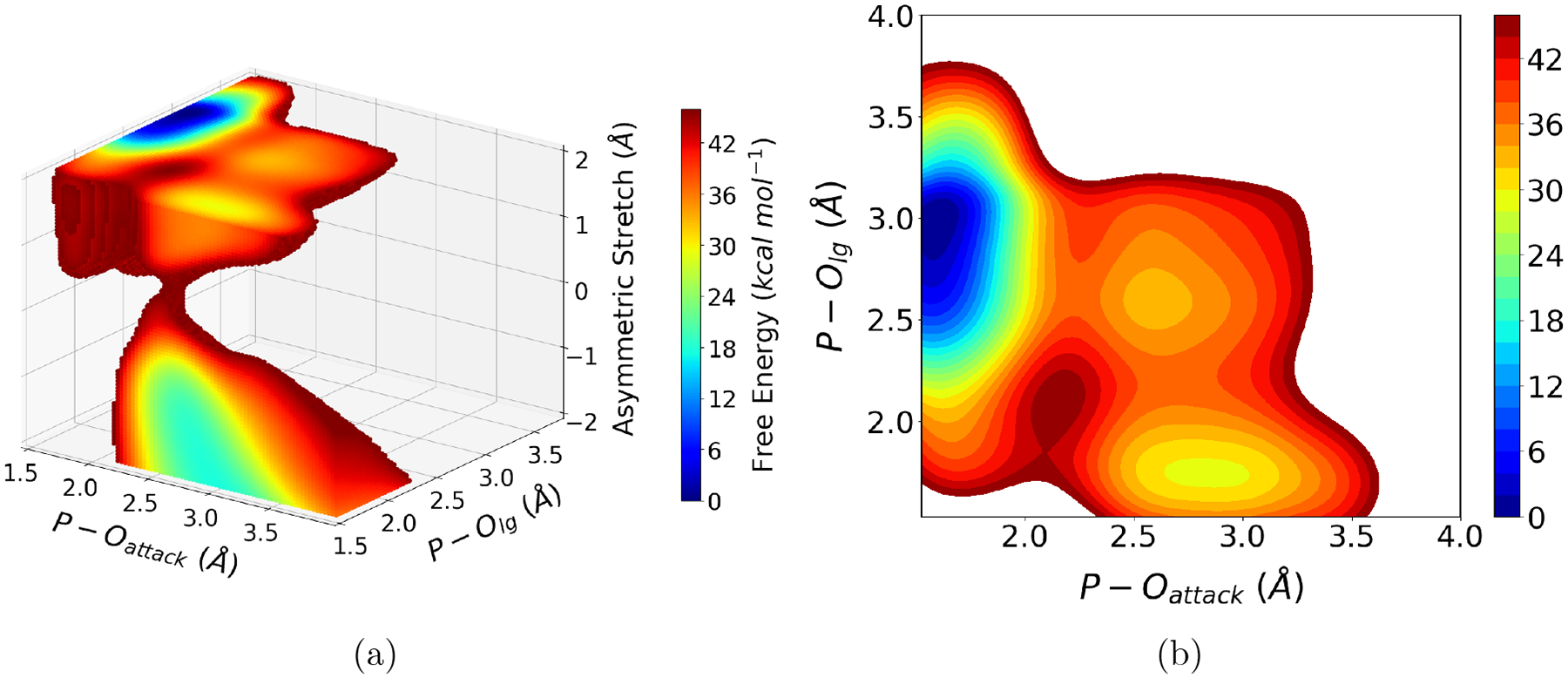
Results from an automated reinforcement learning driven free energy simulation of methyl phosphate hydrolysis in solution. The three coordinates are the nucleophilic attack P-O distance, the leaving group P-O distance and the antisymmetric O-H-O stretch that describes the proton transfer from the nucleophile (water) to the phosphate oxygen. (a) The three-dimensional PMF converges after 42 iterations of automated restrained MD-reinforcement learning cycles; the results indicate that with the current DFTB3/MM model, the solvent-assisted pathway¹²⁰ is not the dominant mechanism. (b) The two-dimensional PMF cut after the proton transfer is complete indicates a dissociative pathway that involves a loosely bound metaphosphate species. Further refinement of the QM/MM energetics will provide insights into this prototypical phosphoryl transfer reaction at an unprecedented level of detail.

2.2.2. Multi-level free energy simulations: bridging the distributions at different levels of theory

In quantum chemistry, it is routine to combine different levels of theory to focus on structure and energetics, respectively.¹²² It is therefore natural to pursue “multi-level” free energy simulations^123,124 in which an inexpensive QM/MM potential is used to explore the conformational space and a more accurate QM/MM potential is used to improve the energetics. The fundamental challenge for condensed phase simulations at a finite temperature is that the configurations with high Boltzmann weights may differ significantly at different levels of theory, thus merely re-weighting of samples collected from a low-level simulation with high-level energies¹²⁵ is unlikely to lead to proper convergence,¹²⁶ especially when the QM region is large (for example, 100–250 atoms, as in many semi-empirical QM/MM simulations¹²⁷).

As discussed extensively in the literature, the success of “multi-level” free energy simulations depends critically on the overlap of the configurational distributions; specifically in the framework of free energy perturbation upon changing potential energy, one useful metric is the overlap in the energy gap (i.e., ΔU^LH(X) = U^H(X) − U^L(X)) distribution at the two levels (L, H) of theory (ρ_L(ΔU^LH) vs. ρ_H(ΔU^LH)), as reflected by the well-established identity,¹²⁸

$$e^{-\beta \Delta U^{LH}}{\rho }_L\left(\Delta U^{LH}\right)=e^{-\beta \Delta A^{LH}}{\rho }_H\left(\Delta U^{LH}\right),$$ (2)

in which ΔA^LH is the free energy difference between the two levels of theory; more quantitative criteria for the degree of overlap have been proposed in the literature,^129–131 many of which are based on the work of Kofke and co-workers for free energy perturbation in general.¹³² Therefore, the key challenge is to establish protocols that ensure adequate overlap during the L to H transformation while maintaining computational efficiency, i.e., to minimize the amount of computations at the H level.

One natural approach is to improve the L level towards the H level, by either system-specific reparameterization of L,¹³³ learning the difference between L and H on the fly via ML,⁷² or switching from L to H via many short, non-equilibrium simulations¹³⁴ in which L and H potentials are mixed explicitly. Alternatively, one can systematically identify the degrees of freedom that lead to poor energy gap overlaps at L/H levels, and treat these “problematic” degrees of freedom separately. Several studies of systems that included relatively small QM regions suggested that the bonded, stiff degrees of freedom tend to be problematic,^{131,135–137} as even small structural differences between L and H can have significant energetic consequences and thus leading to a poor overlap in energy gap distributions. Different approaches have been developed accordingly, which involve either refitting these degrees of freedom via, for example, force-matching,^131,138 or ignoring them so as to focus on interaction energies between the QM and MM degrees of freedom.^139,140

In the “staged transformation” approach explored by us recently,¹⁴¹ these problematic degrees of freedom are subject to constraints or restraints, such that the conversion from L to H models is done through a thermodynamic route that ensures favorable distribution overlaps along the way. The free energy components associated with different steps are mostly evaluated explicitly, thus the final result can be compared to the rigorous free energy difference between the two levels of theory with limited and well-defined approximations. Importantly, the additional free energy component calculations involve simulations at the low level of theory and therefore do not incur high computational costs. The approach has been illustrated with solution systems with encouraging results, although further tests and improvements are required for treating more complex systems.

For systems that involve larger QM regions, however, it is not clear at all that only bonded degrees of freedom are problematic, as small errors associated with non-bonded degree of freedom can accumulate quickly, leading to poor energy gap overlaps. Therefore, additional developments are sorely needed to automatically identify the “problematic” degrees of freedom and mitigate their impact on the computed free energies. Along this line, we note that broadening (as opposed to narrowing, as commonly done in previous work) the distribution at the L level and/or introducing intermediate distributions that bridge the L/H distributions with generalized ensemble based sampling^102,142 or generative ML methods¹⁴³ are interesting alternative directions to pursue.

2.3. Remote Effects: Allostery, Enzyme Evolution and Design

As alluded to above, one fascinating aspect about biomolecules is the existence of coupling, or co-operativity, among distant sites. Although the mechanism of allostery in biomolecules has been studied for decades,^144–149 it remains difficult to precisely predict residues that dictate the long-range co-operativity; this incomplete level of understanding limits our ability to engineer allostery into biomolecules, although sporadic successful examples have been reported in the literature.^149–151 Specifically in the context of enzyme catalysis, it has been well documented that remote mutations may have a significant impact on catalysis,¹¹⁸ leading to hypotheses and debates about the roles of enzyme motions in catalysis. In directed evolution studies of designed enzymes, it is often observed that improvement of catalytic proficiency or expansion of substrate scope involves residues not in the active site.^{118,152–154} In enzyme evolution studies,¹⁵⁵ fitness landscape of several enzymes has been shown to be determined by residues distributed throughout the enzyme structure,¹⁵⁴ again highlighting the holistic nature of protein function.

In some cases, the roles of remote residues can be intuitively understood at a structural level;¹¹⁹ i.e., through a domino or Goldberg machine fashion, remote mutation(s) perturb the dominant conformation of active site residues^156,157 and therefore the chemical activity therein, including both catalytic proficiency and substrate scope. The challenge for any computational analysis is thus to capture such “population shifts” due to distal mutations. Several compelling examples have been reported recently using enhanced sampling techniques, such as path-variable based metadynamics simulations¹⁰³ for variants of Tryptophan synthase subunit B (TrpB);¹⁵⁸ the simulations showed that the populations of several conformational states of TrpB were modulated by distal mutations, providing a molecular level rational for the emergence of these mutation in directed evolution studies^159,160 that engineered TrpB into a standalone enzyme in the absence of the neighboring α subunit.

However, in other cases, the effects of distal changes appear more indirect. For example, in our recent analysis of ATP hydrolysis of myosin,¹⁰⁶ we studied two models for the motor domain that have almost identical conformations for residues in the nucleotide binding site but differ in distal regions and hydration of the critical R238-E459 salt bridge (Fig. 5a). String based DFTB3/MM free energy simulations found that activation free energy and exergonicity in the two models differ by as much as 9 kcal/mol, highlighting that the average ground state configurations of catalytic residues are not the only determinant. Indeed, the distal residues can instead modify the fluctuations of active site residues and water molecules, and thus the reorganization energy or entropic contributions to the activation free energy.⁴⁵ In a different context, elegant EVB analysis of Aqvist and co-workers have clearly shown that flexibility of surface protein residues plays a major role in modulating the enthalpic and entropic components of activation free energy,¹⁶¹ leading to different temperature adaptations for mesophilic and psychrophilic enzymes.⁴⁸

Figure 5:

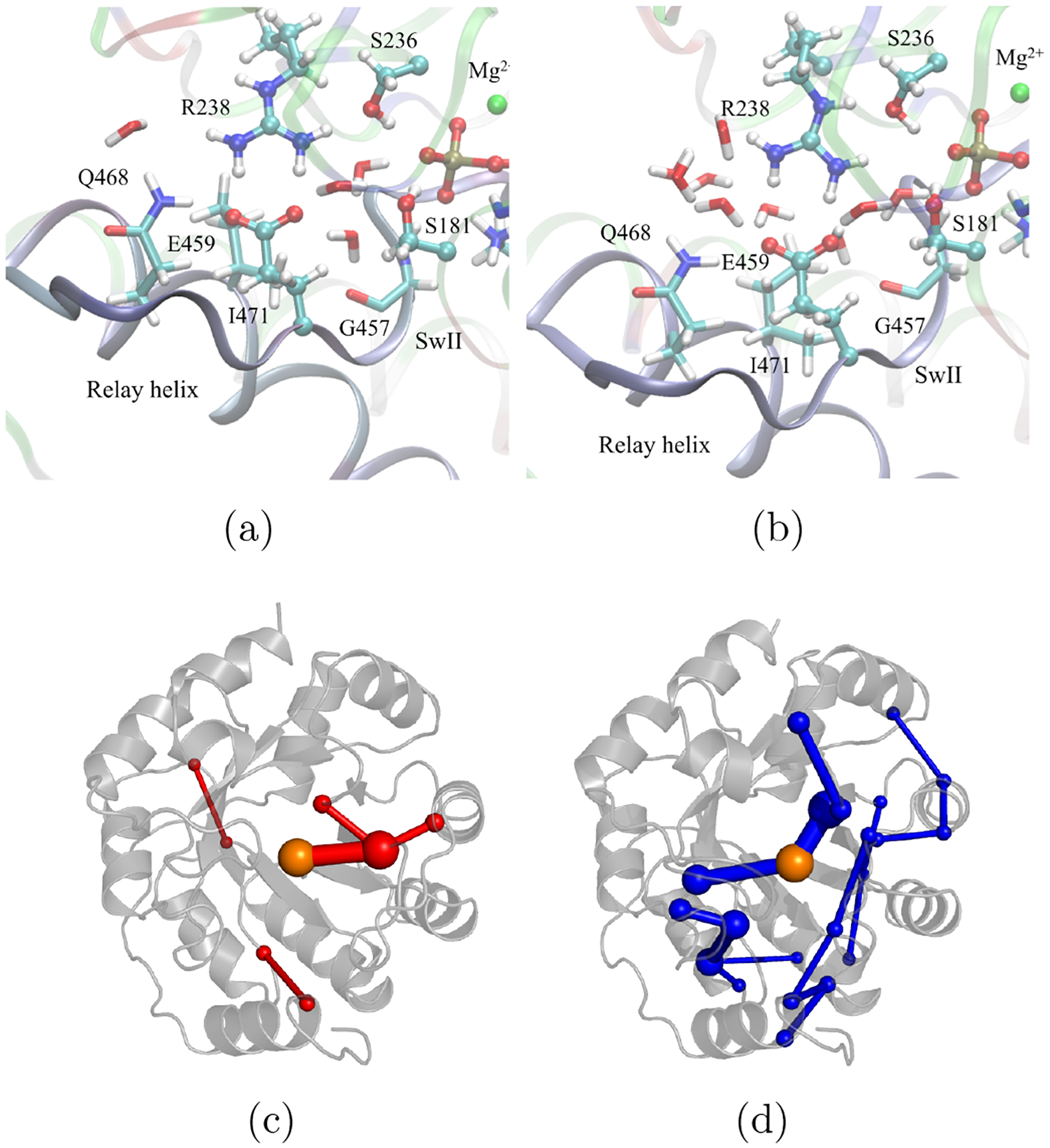
Examples of distal contributions to enzyme catalysis from computational analyses. (a-b) ATP hydrolysis in two models of the myosin motor domain may differ by ~9 kcal/mol in activation free energy although the nucleotide binding site residues have almost comparable average configurations;¹⁰⁶ (c-d) A de novo designed enzyme for Kemp elimination and its more efficient variant following directed evolution feature rather different collective motions;¹⁷³ the latter also features a negative activation heat capacity.¹⁷⁴ Panels c-d have been provided by Drs. A. Bunzel and A. Mulholland.

The temperature dependence of enzymes has led to many fascinating discussions regarding the mechanisms that govern enzyme stability and catalysis.^48,162–165 A particularly intriguing phenomenon noted in recent literature concerns non-linearity in the Arrhenius plot at high temperatures,^165–167 for which quantum mechanical tunneling of nuclei^11,168,169 is unlikely the cause. Two different models have been proposed to explain the non-linear Arrhenius plot: conformational redistribution^170,171 vs. activation heat capacity.^166,172 In the former model, the equilibrium between catalytically active and inactive conformations is perturbed by temperature, leading to different populations of the active conformation and therefore different apparent rate constants. In the latter case, a non-vanishing heat capacity difference between the ground and transition states ($\Delta C_p^{‡}$) makes the activation free energy temperature-dependent, leading also to deviation of the Arrhenius plot from linearity. Both thermodynamic models can be used to fit available experimental kinetic data, and for different systems, both models have been supported with microscopic analysis based on extensive molecular dynamics simulations,^{167,171–173} respectively. As discussed by Aqvist and co-workers,¹⁷¹ the two models do lead to significantly different predictions about activation enthalpy and entropy for broader temperatures, for which no experimental data are yet available. On the other hand, it has been suggested that the different proposals consistently point toward a general picture of more than one reactant state before passing the transition state.¹⁶⁵

A particularly interesting case concerns the de novo designed enzyme for catalyzing the Kemp elimination reaction.¹⁷⁴ While the designed enzyme, which has low catalytic proficiency, features a linear Arrhenius plot and therefore zero activation heat capacity, its more efficient variant following several generations of directed evolution exhibits a non-linear Arrhenius plot, which can be fitted with a negative $\Delta C_p^{‡}$. Mulholland and co-workers¹⁷³ showed that extensive (~5 μs) classical MD simulations with a MM model for the transition state indeed recapitulated a negative $\Delta C_p^{‡}$, which was estimated based on the fluctuation of the protein energy in the MD simulations. Further analysis of the trajectories found that the negative $\Delta C_p^{‡}$ in the more active enzyme variant was likely the result of a more compact active site in the transition state due to a higher population of an active site loop in its closed conformation. The more compact structure is also congruent with extensive correlated motions throughout the protein (Fig.5b). Therefore, an interesting notion from the analysis is that to further enhance catalytic proficiency of designed enzymes, one strategy might be to enhance correlated motions that implicate both active site and distal regions; this point was also made in the aforementioned study of TrpB,¹⁵⁸ in which the distal mutation sites observed in the directed evolution study were also identified with a motional network analysis for the wild type enzyme.

Evidently, the causal relation between correlated motion, negative $\Delta C_p^{‡}$ and catalytic proficiency remains to be further analyzed. Nevertheless, these recent studies further highlight the significance of better understanding collective motions of enzymes, their thermodynamic signature and factors that control the nature and functional implication of such motions. Along this line, close integration of extensive classical and QM/MM studies with recent breakthrough in continuous evolution techniques,^175–177 which makes it straightforward to evolve enzymes for many (>100) generations in independent trajectories,¹⁷⁸ is poised to lead to significant insights into new strategies that can be used to enhance the catalytic proficiency of designed enzymes.

3. Concluding Remarks

In this short perspective, we discussed a number of “burning issues” related to biomolecular QM/MM simulations. Although most of these discussions are motivated primarily by our own research interest, we believe many of the discussions are relevant to biomolecular QM/MM applications in general. Many aspects of the discussed issues are related to establishing “best practice” for realistic applications, such as choices of the QM region size, QM and MM potential functions, and methodologies that best integrate physical methods and established machine learning techniques for efficient free energy simulations. There are, nevertheless, in our opinion, fundamental conceptual issues, such as developing efficient methods for better treating transition metal ions,^179,180 pursuing generally applicable machine learning models for both short-range and long-range interactions,^67,181 identifying problems for which the explicit inclusion of electronic polarization makes a qualitative difference, and clearly dissecting and defining the roles of distal residues and specific motions in enzyme catalysis.

In terms of connections with experiments, while it remains important to compute multiple observables that characterize physical properties of biomolecules, such as kinetic isotope effects, free energy relations and various spectroscopies,¹⁸² an emerging opportunity is to integrate computations with high-throughput experiments. For the analysis of protein allostery, for example, deep mutation studies¹⁸³ have revealed a rather different picture for the distribution of “hotspot” residues that are essential to co-operativity.¹⁸⁴ Similarly, continuous evolution studies are starting to generate large datasets on mutation effects on catalytic properties.¹⁷⁸ Providing a molecular level understanding for these rich datasets and making testable predictions with multi-faceted computational analysis is a formidable yet exciting challenge. To paraphrase one of the ten big ideas from the National Science Foundation, developing novel methodologies that can truly embrace “the data revolution” is of great urgency. With further development and integration with data science/machine learning techniques, QM/MM methods will play increasingly essential roles in the mechanistic analysis and rational design of novel biomolecular functions.^119,185

Before closing, we note that exciting developments in ab initio quantum chemistry methodologies continue to take place at a pace as rapid as ever.¹⁸⁶ We also can’t resist mentioning that major strides are being made in the areas of quantum Monte Carlo¹⁸⁷ and related ML methods¹⁸⁸ as well as quantum computing,^189,190 in terms of both fundamental algorithms and hardware. While these more advanced and expensive methodologies are yet to directly impact biophysical and biochemical applications, it is clear that the list of powerful tools available to multi-scale computations will continue to expand rapidly and therefore the future is undoubtedly bright.

Figure 4:

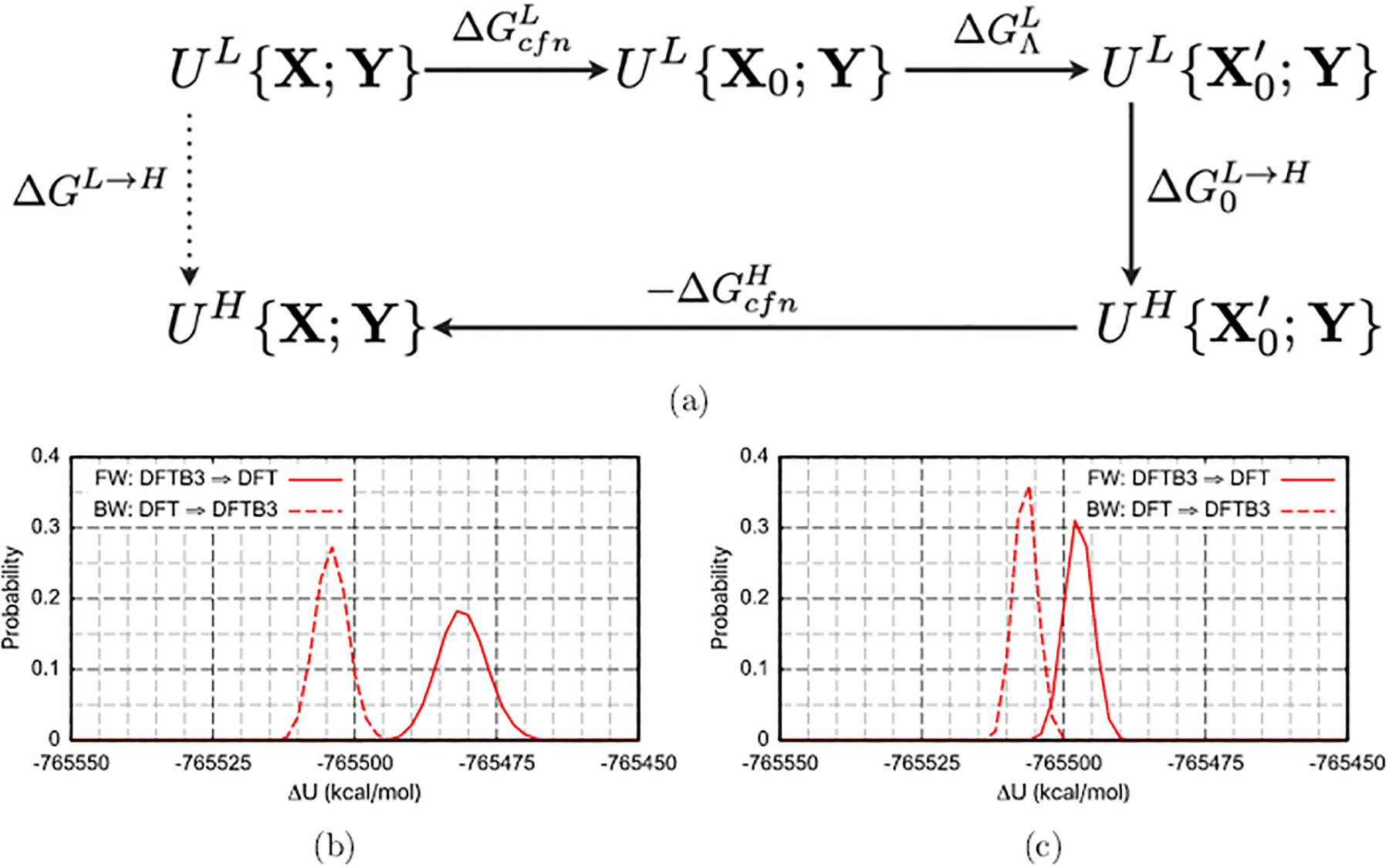
A staged transformation approach¹⁴¹ for computing the free energy difference at two levels (L/H) of theory, ΔG^L→H. (A) The staged thermodynamic path treats selected degrees of freedom (X) separately from the rest (Y); X represents the degrees of freedom that lead to a large gap in the ΔU^LH distribution. Assuming that the free energy costs for confining X to values at (or near) the free energy minima are similar at the L and H levels, ΔG^L→H is given by the sum of $\Delta G_0^{L\to H}$, which converges readily since the sampling involves only Y, and the “reorganization free energy”, $\Delta G_{\Lambda }^L$, which is the free energy cost of changing X₀ to $X_0^{\prime }$ at the low level of theory. (b-c) Illustration of the impact of bond and angle restraints on the ΔU^LH distribution for a methyl diphosphate, which is treated with either DFTB3 (L) or B3LYP (H), solvated by TIP3P water.

Biography

Qiang Cui

Qiang Cui is a professor of Chemistry at Boston University and also affiliated with Departments of Physics and Biomedical Engineering. He received B.S. in Chemical Physics from the University of Science and Technology of China in 1993, and Ph. D. in Theoretical Chemistry in 1997 from Emory University under the tutelage of Professor Keiji Morokuma. He conducted postodctoral research with Professor Martin Karplus at Harvard University and, in 2001, moved to the University of Wisconsin, Madison as an assistant professor of Chemistry. After spending almost seventeen wonderful years in Madison, he moved back to Boston in 2018. His current research interest includes quantum chemistry and statistical mechanics and their application to various chemical, biological and materials problems.

Tanmoy Pal

Tanmoy Pal recieved his B.S. in Chemistry from the Indian Institute of Science, Bengaluru in 2016. Currently he is a doctoral candidate in the Cui group at Boston University. Tanmoy’s research involves classical and QM/MM simulations of biomolecular systems. His recent interests include studies of ionic liquid-interface systems and development of machine learning based techniques to improve the accuracy and efficiency of multidimensional free energy calculations.

Luke Xie

Luke Xie is a high school senior from Newport High School, Washington. He spent the summer of 2019 in the Cui group at Boston University as a part of the RISE Internship program. He is interested in studying computer science.