Conditions for metachronal coordination in arrays of model cilia

Significance

Motile cilia can coordinate with each other to beat in the form of a metachronal wave, which can facilitate the self-propulsion of microorganisms such as Paramecium and can also be used for fluid transport such as mucus removal in trachea. How can we predict the collective behavior of arrays of many cilia coordinated by hydrodynamic interactions, and in particular, the properties of the emerging metachronal waves, from the single-cilium characteristics? We address this question using a bottom-up coarse-graining approach and present results that contribute to understanding how the dynamical self-organization of ciliary arrays can be controlled, which can have significant biological, medical, and engineering implications.

Abstract

On surfaces with many motile cilia, beats of the individual cilia coordinate to form metachronal waves. We present a theoretical framework that connects the dynamics of an individual cilium to the collective dynamics of a ciliary carpet via systematic coarse graining. We uncover the criteria that control the selection of frequency and wave vector of stable metachronal waves of the cilia and examine how they depend on the geometric and dynamical characteristics of a single cilium, as well as the geometric properties of the array. We perform agent-based numerical simulations of arrays of cilia with hydrodynamic interactions and find quantitative agreement with the predictions of the analytical framework. Our work sheds light on the question of how the collective properties of beating cilia can be determined using information about the individual units and, as such, exemplifies a bottom-up study of a rich active matter system.

Motile cilia are hair-like organelles that beat with a whip-like stroke that breaks time-reversal symmetry to create fluid flow or propel swimming microorganisms under low Reynolds number conditions (1–3). The beat is actuated by many dynein motors, which generate forces between microtubules that cause the cilium to bend in a robust cyclic manner with moderate fluctuations (4, 5). On surfaces with many cilia, the actuating organelles can coordinate with each other and collectively beat in the form of metachronal waves, where neighboring cilia beat sequentially (i.e., with a phase lag) rather than synchronously (6). The flows created from this coordinated beating are important for breaking symmetry in embryonic development (7, 8), creation of complex and dynamic flow patterns for the cerebrospinal fluid in the brain (9, 10), and providing access to nutrients (11). In microorganisms such as Paramecium and Volvox, the metachronal beating of cilia provides propulsion strategies in viscous environments (12, 13). It has been shown that depending on the parameters, beating ciliary carpets can exhibit globally ordered and turbulent flow patterns (14), which can be stable even with a moderate amount of quenched disorder (15), and that metachronal coordination optimizes the efficiency of fluid pumping (16, 17). Natural cilia have inspired various designs of artificial cilia (18–22), which may be used for pumping fluid (23, 24) and mixing (25), or fabrication of microswimmers (26).

Hydrodynamic interactions have been shown to play a key role in coordinated beating of cilia (27, 28) and mediating cell polarity control (29). To achieve synchronization between two cilia via hydrodynamic interactions, it is necessary to break the permutation symmetry between them [e.g., by exploiting the dependence of the drag coefficient on the distance from a surface (30), flexibility of the anchoring of the cilia (31), nonuniform beat patterns (32, 33), or any combination of these effects (34)]. In addition to the hydrodynamic interactions, the basal coupling between cilia can also facilitate the coordination (35–37).

How can we predict the collective behavior of arrays of many cilia coordinated by hydrodynamic interactions, and in particular, the properties of the emerging metachronal waves, from the single-cilium characteristics? Extensive numerical simulations using explicitly resolved beating filaments (16, 17, 27, 38–40) and simplified spherical rotors (13, 14, 41, 42) have demonstrated that metachronal coordination emerges from hydrodynamic interactions. However, insight into this complex many-body dynamical system at the level that has been achieved in studies of two cilia is still lacking. Here, we propose a theoretical framework for understanding the physical conditions for coordination of many independently beating cilia, which are arranged on a substrate in the form of a two-dimensional (2D) array immersed in a three-dimensional (3D) fluid. We uncover the physical conditions for the emergence of stable metachronal waves and predict the properties of the wave in terms of single-cilium geometric and dynamic characteristics.

Results

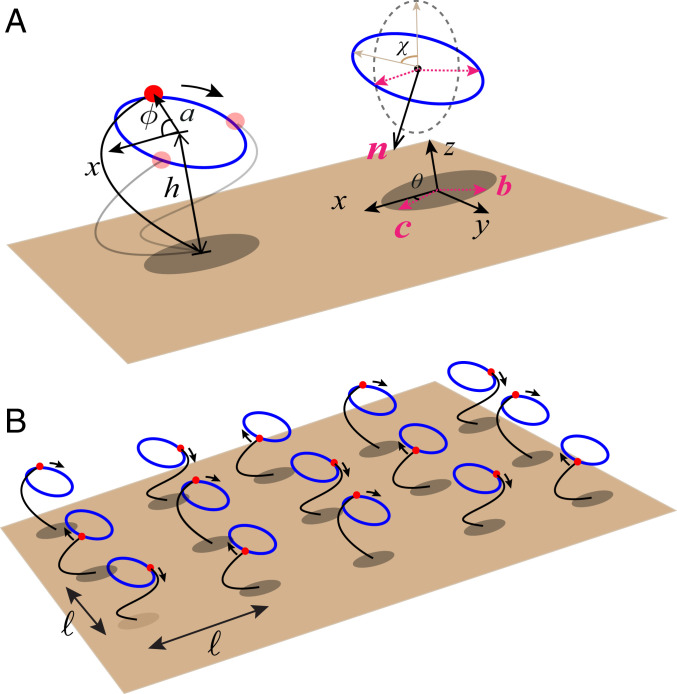
We use a simplified model of a cilium as a force monopole moving along a circular trajectory of radius $a$ above a substrate, represented by a sphere of radius $b$ driven by a force $f\left(\varphi \right)$, as shown in Fig. 1A. To theoretically study metachronal coordination, we consider such model cilia on a lattice of spacing $\ell$ in the $x$–$y$ plane as shown in Fig. 1B. We examine the role of the geometric parameters in determining the collective mode of coordination. We parametrize the orientation of the cilia by the angle $\theta$ that the plane of the circular trajectory makes with the ${\mathit{e}}_x$ direction and the tilt angle $\chi$ it makes with the ${\mathit{e}}_z$ direction. More concretely, we define the vector $\mathit{c}=\left(\cos \theta ,\sin \theta ,0\right)$ to characterize the 2D orientation of the circular orbit and $\mathit{b}=\left(-\sin \theta ,\cos \theta ,0\right)$, which is perpendicular to $\mathit{c}$, and the unit vector that is normal to circular trajectory is defined as $\mathit{n}=-\cos \chi \mathit{b}-\sin \chi {\mathit{e}}_z$ (Fig. 1A). The position of the sphere representing the force monopole along the trajectory, which we parametrize by the polar angle ${\varphi }_i$ for the ith sphere, is

$${\mathit{R}}_i={\mathit{r}}_i+h{\mathit{e}}_z+a\cos {\varphi }_i\mathit{c}+a\sin {\varphi }_i\left(-\sin \chi \mathit{b}+\cos \chi {\mathit{e}}_z\right),$$ [1]

where ${\mathit{r}}_i=\left(x_i,y_i,0\right)$ denotes the lattice coordinate (with spacing $\ell$) and $h$ denotes the distance from the center of the trajectory to the substrate. There are also simulation studies adopting noncircular trajectories of the cilia, and interested readers can refer to refs. 13, 30, 42, and 43.

Fig. 1.

(A) A simplified description of a single cilium as represented by a force monopole with a cyclic trajectory above a rigid substrate. Various geometric measures and orientation vectors are defined. (B) An array of cilia on a square lattice in the $x$–$y$ plane with the lattice constant $\ell$.

Dynamical Equations.

Each cilium is driven independently by a tangential force acting on the bead. The magnitude of the force, $f\left({\varphi }_i\right)$, depends only on the location of the bead along its trajectory, and the direction of the force is given by the tangent vector, which is defined as

$${\mathit{t}}_i\left({\varphi }_i\right)=\frac{d{\mathit{R}}_i/d{\varphi }_i}{|d{\mathit{R}}_i/d{\varphi }_i|}.$$ [2]

The friction coefficient of the bead, $\zeta \left({\varphi }_i\right)$, can, in general, depend on the location of the bead along the trajectory (e.g., due to the proximity of a substrate). Balancing the forces for a single cilium, we find that in the absence of other cilia, the velocity of the bead is ${\mathit{v}}_i={\dot{\varphi }}_{i}a\hspace{0.17em}{\mathit{t}}_i=f\left({\varphi }_i\right)/\zeta \left({\varphi }_i\right)\hspace{0.17em}{\mathit{t}}_i$. In an array of cilia, the hydrodynamic interactions between the cilia influence the beat cycle because a single cilium creates a flow that is felt by other cilia, affecting the speed at which they move around their trajectories. This leads to a system of coupled dynamical equations governing the phase variables

$$\frac{d{\varphi }_i}{dt}=\frac{f\left({\varphi }_i\right)}{\zeta \left({\varphi }_i\right)a}+\frac{1}{a}\sum _j{\mathit{t}}_i\left({\varphi }_i\right)\cdot \mathit{G}\left({\mathit{R}}_i,{\mathit{R}}_j\right)\cdot {\mathit{t}}_j\left({\varphi }_j\right)f\left({\varphi }_j\right).$$ [3]

The Green’s function $\mathit{G}\left(\mathit{R},{\mathit{R}}^{\prime }\right)$ (the Blake tensor) encodes the hydrodynamic effect felt at point $\mathit{R}$ due to a force monopole located at ${\mathit{R}}^{\prime }$ in an incompressible fluid near a substrate with a no-slip boundary condition (44).

The intrinsic angular speed of each cilium given as

$$\mathrm{\Omega }\left(\varphi \right)=f\left(\varphi \right)/\left[\zeta \left(\varphi \right)a\right]$$ [4]

can generically have phase dependence, which provides a way to connect the changing shape of a real beating cilium to our model. In our model, the phase dependence arises from the force (or stroke) pattern of the beating, which can be represented via its harmonics as

$$f\left(\varphi \right)=f_0\left[1+\sum _{n=1}{A}_n\cos n\varphi +B_n\sin n\varphi \right],$$ [5]

and the cyclic change in the friction, which we represent as

$$\zeta \left(\varphi \right)={\zeta }_0\left[1+\sum _{n=1}{C}_n\cos n\varphi +D_n\sin n\varphi \right].$$ [6]

The scale of the friction coefficient can be written as ${\zeta }_0=4\pi \eta b$, where the length scale $b$ represents the characteristic (hydrodynamic) size of a cilium. Naturally, the harmonic amplitudes are constrained to values that will correspond to strictly positive values for the force and the friction coefficient. To proceed with the analysis of Eq. 3, we introduce a coordinate transformation $\varphi \to \overline{\varphi }$, defined via the following relation:

$$\frac{d\overline{\varphi }}{d\varphi }=\frac{{\mathrm{\Omega }}_0}{\mathrm{\Omega }\left(\varphi \right)},$$ [7]

where ${\mathrm{\Omega }}_0=f_0/\left({\zeta }_{0}a\right)$ is a constant angular speed describing the dynamics of the new coordinate in the absence of hydrodynamic interactions (32). The definition can be integrated to obtain the relation between the coordinates as

$$\varphi \left(\overline{\varphi }\right)\simeq \overline{\varphi }+\sum _{n=1}\frac{1}{n}\left[\left(A_n-C_n\right)\sin n\overline{\varphi }-\left(B_n-D_n\right)\cos n\overline{\varphi }\right]$$ [8]

to the lowest order in the harmonic amplitudes.

Using the translational invariance along the substrate, we can express the Blake tensor in the 2D Fourier space $\mathit{q}=\left(q_x,q_y,0\right)\equiv q\widehat{\mathit{q}}$ (SI Appendix has the details of the derivation) and recast Eq. 3 in terms of the new coordinate. We then use a separation of timescale between the mean phase and the phase difference to simplify the dynamics (SI Appendix has some details of the calculations, and Movies S1–S12 show how a metachronal wave emerges in our simulation). By changing the notation from ${\varphi }_i\left(t\right)$ to $\varphi \left(\mathit{r},t\right)$ and averaging over the fast variables, the governing dynamical equation can be written as (SI Appendix has some details of the calculations, and Movies S1–S12 show how a metachronal wave emerges in our simulation)

$$\begin{array}{ll}\hfill & {\partial }_t\overline{\varphi }\left(\mathit{r},t\right)={\mathrm{\Omega }}_0+\frac{{\mathrm{\Omega }}_{0}hb}{16\pi }\hspace{0.17em}\sum _{{\mathit{r}}^{\prime }}\int d^2\mathit{q}\hspace{0.17em}{e}^{i\mathit{q}\cdot \left(\mathit{r}-{\mathit{r}}^{\prime }\right)}\hfill \\ \hfill & \times \left[\mathcal{M}\left(\mathit{q}\right)\cos \left(\overline{\varphi }\left(\mathit{r}\right)-\overline{\varphi }\left({\mathit{r}}^{\prime }\right)\right)+\mathcal{S}\left(\mathit{q}\right)\sin \left(\overline{\varphi }\left(\mathit{r}\right)-\overline{\varphi }\left({\mathit{r}}^{\prime }\right)\right)\right],\hfill \end{array}$$ [9]

where the $\mathit{q}$-dependent kernels are defined as

$$\mathcal{M}=g_0\left(\mathit{q}h\right)+g_1\left(\mathit{q}h\right)\left(A_2-2C_2\right)+g_2\left(\mathit{q}h\right)\left(B_2-2D_2\right),$$ [10]

$$\mathcal{S}=g_1\left(\mathit{q}h\right)\left(2B_2-D_2\right)-g_2\left(\mathit{q}h\right)\left(2A_2-C_2\right)$$ [11]

in terms of the following functions:

$$\begin{array}{lll}\hfill g_0\left(\mathit{p}\right)& =\hfill & \hfill 2p^{-1}\left[e^{-2p\left(a/h\right)}-e^{-2p}\right]\left[3-{\cos }^2\chi {\left(\widehat{\mathit{p}}\cdot \mathit{c}\right)}^2\right]\\ \hfill & +\hfill & \hfill 4\left(1-p\right)e^{-2p}\left[1-{\cos }^2\chi {\left(\widehat{\mathit{p}}\cdot \mathit{b}\right)}^2\right]\\ \hfill & -\hfill & \hfill 4\left(1+p\right)e^{-2p}{\cos }^2\chi ,\end{array}$$ [12]

$$\begin{array}{lll}\hfill g_1\left(\mathit{p}\right)& =\hfill & \hfill p^{-1}\left[e^{-2p\left(a/h\right)}-e^{-2p}\right]\left[{\left(\widehat{\mathit{p}}\cdot \mathit{b}\right)}^2-{\sin }^2\chi {\left(\widehat{\mathit{p}}\cdot \mathit{c}\right)}^2\right]\\ \hfill & +\hfill & \hfill 2\left(1-p\right)e^{-2p}\left[{\left(\widehat{\mathit{p}}\cdot \mathit{c}\right)}^2-{\sin }^2\chi {\left(\widehat{\mathit{p}}\cdot \mathit{b}\right)}^2\right]\\ \hfill & +\hfill & \hfill 2\left(1+p\right)e^{-2p}{\cos }^2\chi ,\end{array}$$ [13]

$$\begin{array}{lll}\hfill g_2\left(\mathit{p}\right)& =\hfill & \hfill 2\left\{p^{-1}\left[e^{-2p\left(a/h\right)}-e^{-2p}\right]-2\left(1-p\right)e^{-2p}\right\}\\ \hfill & \times \hfill & \hfill \sin \chi \left(\widehat{\mathit{p}}\cdot \mathit{b}\right)\left(\widehat{\mathit{p}}\cdot \mathit{c}\right).\end{array}$$ [14]

Importantly, we find that only the second harmonics in the beat pattern and the friction cycle play a key role in determining the collective behavior of the cilia at long timescales. This is essentially understood by considering interaction of two cilia moving on the same plane as follows (Materials and Methods). Cilium $\#1$ is accelerated due to the flow induced by the other ($\#2$), with a speed that is proportional to the driving force $f\left({\varphi }_2\right)$. Including geometrical factors due to the circular shape of the trajectories, the velocity shift of $\#1$ is proportional to $\sin {\varphi }_1\sin {\varphi }_2\hspace{0.17em}f\left({\varphi }_2\right)$ (SI Appendix, Fig. S1). Subtracting the velocity of $\#2$, we find that the phase difference $\mathrm{\Delta }\varphi ={\varphi }_1-{\varphi }_2$ changes as $\frac{d}{\mathrm{d}t}\mathrm{\Delta }\varphi \propto \sin {\varphi }_1\sin {\varphi }_2\left[f\left({\varphi }_2\right)-f\left({\varphi }_1\right)\right]$. Assuming that the two cilia are almost synchronized ($\mathrm{\Delta }\varphi \ll 1$), we can put ${\varphi }_1=\mathrm{\Omega }t+\frac{1}{2}\mathrm{\Delta }\varphi$ and ${\varphi }_2=\mathrm{\Omega }t-\frac{1}{2}\mathrm{\Delta }\varphi$ into the above equation and linearize it with respect to $\mathrm{\Delta }\varphi$, which yields $\frac{d}{\mathrm{d}t}\mathrm{\Delta }\varphi \propto -{\sin }^2\left(\mathrm{\Omega }t\right)f^{\prime }\left(\mathrm{\Omega }t\right)\mathrm{\Delta }\varphi$. Averaging over one cycle, we obtain $\overline{\frac{d}{\mathrm{d}t}\mathrm{\Delta }\varphi }\propto -I\mathrm{\Delta }\varphi$ with $I=\frac{1}{2\pi }{\int }_0^{2\pi }\mathrm{d}\varphi {\sin }^2\varphi \hspace{0.17em}{f}^{\prime }\left(\varphi \right)$, which means that the two cilia synchronize if $I>0$. Since the factor ${\sin }^2\varphi$ contains only second harmonics, the force $f\left(\varphi \right)$ has to contain the same harmonics to make $I$ nonvanishing. In short, the geometrical factors originating from the two trajectories are coupled with the second harmonics in the beating pattern to produce synchronizing effects.

The compact form of Eq. 9 allows us to systematically investigate the conditions under which the array of cilia can admit stable metachronal wave solutions and what determines the direction of propagation and the wavelength of the wave. As we shall see below, $\mathcal{M}\left(\mathit{q}\right)$ will determine the characteristics of the metachronal waves, and $\mathcal{S}\left(\mathit{q}\right)$ will determine their stability.

Dispersion Relation.

Let us now consider a situation where the cilia beat in coordination and generate a metachronal wave of frequency $\omega$ and wave vector $\mathit{k}$. We describe the traveling wave as $\overline{\varphi }\left(\mathit{r},t\right)=\omega t-\mathit{k}\cdot \mathit{r}+\delta {\overline{\varphi }}_{\mathit{k}}\left(\mathit{r},t\right)$, where $\delta {\overline{\varphi }}_{\mathit{k}}$ represents perturbations around the harmonic traveling wave ansatz. Evaluating Eq. 9 at the zeroth order and making use of the identity ${\sum }_{{\mathit{r}}^{\prime }}{e}^{i\mathit{q}\cdot \left(\mathit{r}-{\mathit{r}}^{\prime }\right)}={\sum }_{\mathit{G}}\frac{4{\pi }^2}{{\ell }^2}{\delta }^2\left(\mathit{q}+\mathit{G}\right)$ where $\mathit{G}$ represents the reciprocal lattice vectors, we find the dispersion relation of the metachronal waves as

$$\omega \left(\mathit{k}\right)={\mathrm{\Omega }}_0\left[1+\frac{\pi }{4}\frac{hb}{{\ell }^2}\sum _{\mathit{G}}\mathcal{M}\left(\mathit{k}+\mathit{G}\right)\right].$$ [15]

We recall, for example, that for a square lattice, we have $\mathit{G}=\frac{2\pi }{\ell }\left(m{\mathit{e}}_x+n{\mathit{e}}_y\right)$ for $m,n\in \mathbb{Z}$.

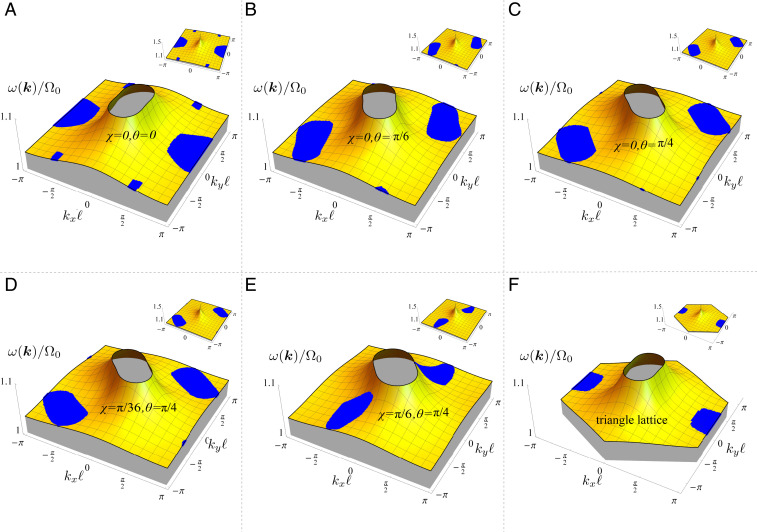
The dispersion relation is plotted in Fig. 2 for various choices of cilia orientation. Note that the resulting frequencies for all modes are somewhat larger than the single-cilium frequency ${\mathrm{\Omega }}_0$, due to a renormalization of the frequency by hydrodynamics interactions. For example, $\omega \left(\mathbf{0}\right)/{\mathrm{\Omega }}_0=1+\frac{\pi }{4}\frac{hb}{{\ell }^2}{\sum }_{\mathit{G}}\mathcal{M}\left(\mathit{G}\right)\approx 1.43$ for the parameter set corresponding to Fig. 2A, namely $\theta =0$, $\chi =0$, $h=\ell$, $a=0.2\ell$, $b=0.05\ell$, $A_2=0.5$, $B_2=0.5$, $C_2=0$, and $D_2=0$. This ratio is consistent with observations in ref. 10, where the measured beat frequency of a single cilium was found to be 15 Hz, and the beat frequency increases for increasing number of synchronized cilia and plateaus at about 22 Hz for $>20$ cilia, giving a measured value of $\omega \left(\mathbf{0}\right)/{\mathrm{\Omega }}_0\approx 1.47$. In our dispersion relation, we find higher frequencies at longer wavelengths (synchronized beating corresponds to $\mathit{k}=0$). When neighboring cilia have small phase differences, the flow created from the beats of the nearest cilia is in a direction that helps to move an individual cilium faster around its trajectory.

Fig. 2.

Dispersion relation of the metachronal waves. The (nondimensionalized) frequency $\omega \left(\mathit{k}\right)/{\mathrm{\Omega }}_0$ defined in Eq. 15 is plotted as a function of the wave vector $\left(k_x\ell ,k_y\ell \right)$ in the first Brillouin zone. A–E correspond to a ciliary array on a square lattice with the following trajectory orientation and tilt angles: (A) $\chi =0$, $\theta =0$; (B) $\chi =0$, $\theta =\pi /6$; (C) $\chi =0$, $\theta =\pi /4$; (D) $\chi =\pi /36$, $\theta =\pi /4$; and (E) $\chi =\pi /6$, $\theta =\pi /4$. (F) A triangular lattice with $\chi =0$, $\theta =0$. Other parameters for A–F are $a=0.2\ell$, $b=0.05\ell$, $h=\ell$, $A_2=0.5$, $B_2=0.5$, $C_2=0$, and $D_2=0$. Blue shaded regions denote the stable wave zones as determined by the linear stability analysis from Eq. 16. (Insets) Zoomed-out versions of dispersion relations, showing the higher frequencies obtained at longer wavelengths.

Stability Criterion.

Satisfying the dispersion relation provides a necessary condition for frequencies and wave vectors to represent metachronal waves. However, it does not guarantee that the wave is a stable solution to Eq. 9. To check the stability of a solution, we can expand Eq. 9 in terms of $\delta {\overline{\varphi }}_{\mathit{k}}$ and probe the first-order governing equation for the perturbation. In Fourier space, we find the time evolution of a perturbation with wave vector $\mathit{q}$ in a background of uniform wave with wave vector $\mathit{k}$ to satisfy the following equation:

$${\partial }_t\delta {\overline{\varphi }}_{\mathit{k}}\left(\mathit{q}\right)=-\left[\mathrm{\Gamma }\left(\mathit{q},\mathit{k}\right)-\mathrm{\Gamma }\left(\mathbf{0},\mathit{k}\right)\right]\delta {\overline{\varphi }}_{\mathit{k}}\left(\mathit{q}\right),$$ [16]

where

$$\mathrm{\Gamma }\left(\mathit{q},\mathit{k}\right)=\frac{\pi b{\mathrm{\Omega }}_0}{8{\ell }^2}\sum _{\mathit{G}}\left[\mathcal{S}\left(\mathit{q}+\mathit{k}-\mathit{G}\right)+\mathcal{S}\left(\mathit{q}-\mathit{k}-\mathit{G}\right)\right].$$ [17]

The sign of $\mathrm{\Gamma }\left(\mathit{q},\mathit{k}\right)-\mathrm{\Gamma }\left(\mathbf{0},\mathit{k}\right)$ determines whether the background wave solution with wave vector $\mathit{k}$ is stable with respect to a perturbation with wave vector $\mathit{q}$. If $\mathrm{\Gamma }\left(\mathit{q},\mathit{k}\right)-\mathrm{\Gamma }\left(\mathbf{0},\mathit{k}\right)>0$ for all values of $\mathit{q}$, then the background metachronal wave with wave vector $\mathit{k}$ is linearly stable.

In Fig. 2, the wave vectors corresponding to linearly stable solutions of Eq. 9 are shown as (blue) dots. The explicit expression for $\mathcal{S}$ allows us to make predictions about the necessary criteria for the stability of the waves. For example, when $\chi =0$, stability requires the condition $2B_2-D_2>0$ to be satisfied. In this case, one can generally observe that the stable modes propagate along the direction of the ciliary beating with wave lengths (denoted by $\lambda$) that are in the range of $2\ell \lesssim \lambda \lesssim 4\ell$. One can observe that for directions that do not coincide with the lattice axes, the domains of permissible wave vectors shrink in size and tend toward larger wave vectors (Fig. 2 A–C). Increasing the angle $\chi$, which amounts to tilting the ciliary beating orbit away from the $z$ axis, further accentuates this feature while allowing for the direction of propagation to deviate from the direction of beating, leading to the formation of dexioplectic or laeoplectic metachronism (Fig. 2 D and E).

To examine the role of the underlying lattice structure, we consider a triangular lattice, which is characterized by reciprocal lattice vectors $\mathit{G}=\frac{2\pi }{\ell }\left[\left(m{\mathit{e}}_x+\left(-m/\sqrt{3}+2n/\sqrt{3}{\mathit{e}}_y\right)\right],\left(m,n\in \mathbb{Z}\right)\right.$. The dispersion relation does not differ appreciably from that of a square lattice, as Fig. 2F shows for the case of $\theta =0$ and $\chi =0$. However, while for a square lattice the stable wave region is centered around $k_x=\pm \pi /\ell$ and $k_y=0$, for a triangular lattice it is centered around $k_x=\pm \pi /\ell$ and $k_y=0$ or $k_x=\pm \left(2-\sqrt{3}\right)\pi /\ell$ and $k_y=\pi /\ell$, which means that there will be a phase shift between the neighboring cilia along the ${\mathit{e}}_x$ direction, hence giving rise to dexioplectic or laeoplectic waves (6). This behavior can be understood by analyzing the dynamics of two cilia with the appropriate geometric arrangement (Materials and Methods and SI Appendix, Fig. S1). We thus find that tuning the orientation of the cilia trajectories and controlling the positioning of the cilia in the array provide the possibility to generate metachronal waves with desired wavelengths and directions of propagation.

We note that in our current formulation, the stability criterion is degenerate with respect to the direction of propagation (i.e., $\pm \mathit{k}$ are both either stable or unstable at the same time). The symmetry can be broken by considering near-field effects in the hydrodynamic interaction between cilia; this will be discussed in future work. Note also that while the stability analysis is performed in terms of $\overline{\varphi }$, the one-to-one correspondence in Eq. 8 guarantees that it will also describe the stability of the modes in terms of the original $\varphi$ coordinate.

Agent-Based Simulation.

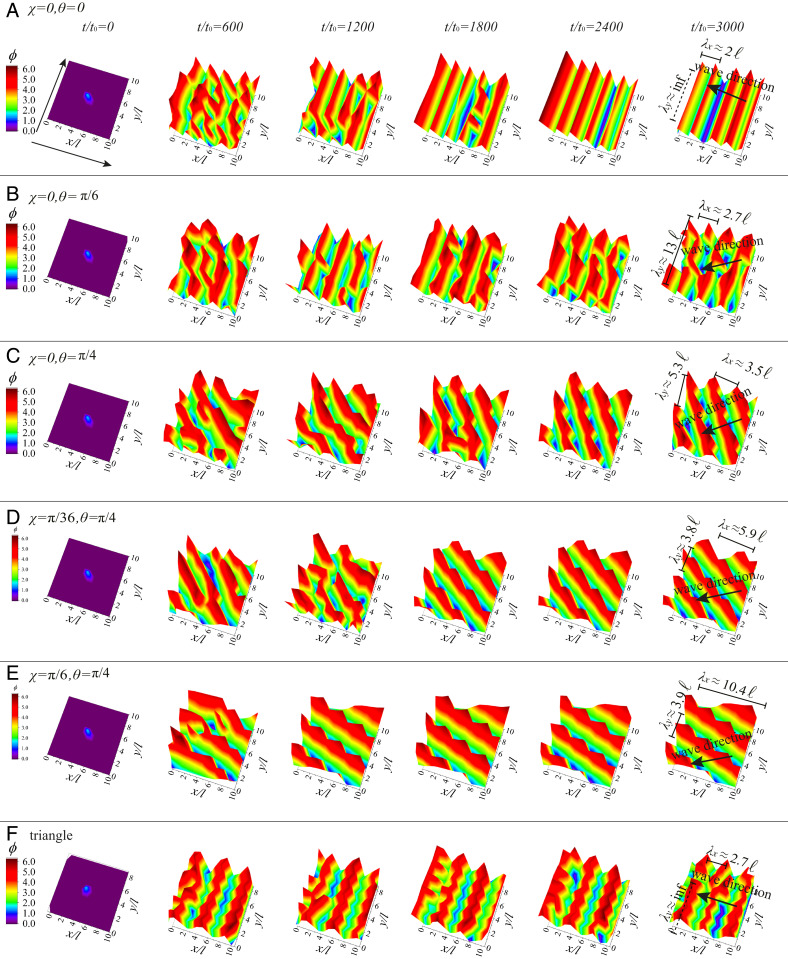
To support the validity of the above analytical description, which is analyzed within the framework of linear stability analysis, we perform numerical simulations based on the governing dynamical equations of the cilia (Eq. 3). The examples of the time evolution are presented in Fig. 3 for an $11\times 11$ cilia array, which is simulated with periodic boundary conditions. The cilia are positioned on a square lattice (Fig. 3 A–E) with different tilting angles $\theta$ and $\chi$, as well as a triangular lattice with $\theta =0$ and $\chi =0$ (Fig. 3F). The cilia are initiated with the same phase $\varphi =0$ at the start of the simulation at $t=0$, except ${\varphi }_{\mathrm{5,5}}=\pi /2$, which is taken for breaking the initial symmetry. The time interval for each simulation step is $\mathrm{d}t/t_0=10^{-3}$, with $t_0=\eta {\ell }^2/f_0$ defining a characteristic time.

Fig. 3.

Simulation snapshots showing how the phases that represent the cilia beating cycle evolve with time in an $11\times 11$ array, where the cilia rotate along the trajectory defined by the angles (A) $\chi =0$, $\theta =0$; (B) $\chi =0$, $\theta =\pi /6$; (C) $\chi =0$, $\theta =\pi /4$; (D) $\chi =\pi /36$, $\theta =\pi /4$; and (E) $\chi =\pi /6$, $\theta =\pi /4$ (Fig. 1). (F) A triangular lattice with $\chi =0$, $\theta =0$. Other parameters for A–F are $a=0.2\ell$, $b=0.05\ell$, $h=\ell$, $A_2=0.5$, $B_2=0.5$, $C_2=0$, and $D_2=0$. The characteristic timescale is $t_0=\eta {\ell }^2/f_0$. The measured wavelengths and direction of propagation are shown in the last column; in every case, the resulting wave vector lies within the range of the stable wave modes from the corresponding panels of Fig. 2.

As can be seen in Fig. 3 and Movies S1–S12 (SI Appendix has some details of the calculations, and Movies S1–S12 show how a metachronal wave emerges in our simulation), in all cases the cilia coordinate with each other and form a metachronal wave after a transient period. For example, in the case of the cilia on a square lattice with the tilting angles of the trajectory as $\theta =0$ and $\chi =0$ (as shown in Fig. 3A), the cilia beat in the form of the metachronal wave with the wave vector $k_x\simeq \pi /\ell$ and $k_y\simeq 0$. In another case, corresponding to $\theta =\pi /4$ and $\chi =0$, the cilia beat in the form of the metachronal wave with the wave vector $k_x\simeq \pi /\left(2\ell \right)$ and $k_y\simeq \pi /\left(2\ell \right)$. These simulation results agree very well with the prediction of the linear stability analysis; the values of the measured stable waves lie for all cases within the range predicted by the theoretical calculations as presented in Fig. 2.

These simulations do not use the separation of timescales that was used in the theoretical analysis. The emergence of metachronal waves is over $10^3$ beat cycles, which is long enough to verify that averaging over fast variables is a valid approximation.

Discussion

We have constructed a theoretical framework to study metachronal waves in ciliary arrays, where each cilium is driven independently with the same beat pattern and interacts with the others via hydrodynamic interactions for arbitrary geometric configurations. We calculate the dispersion relation of the system, relating the propagation frequency and the wave vector of the metachronal wave, and observe a relatively small frequency range, with higher frequencies at longer wavelengths. We have found that stable waves correspond to finite domains of wave vector, which are selected with relatively well-defined orientation of propagation that is determined by the geometric characteristics of the ciliary beating pattern and the lattice structure. Our results allow us to predict the role of the different harmonics in the moment decomposition of the beat pattern and the friction, which in turn, can be used to make predictions about control of metachronal waves using external cues, as has been demonstrated in the case of phototaxis of Chlamydomonas (45).

Although quantitative studies of the beating patterns of cilia in vivo are still lacking, a precise 3D tracking of the motion of a single cilium was recently performed using murine tracheal cilia attached onto a glass surface (46). In a 100 $\mathrm{\mu }$M adenosine triphosphate (ATP) solution, the demembranated and reactivated cilium had the beating frequency $4.9\pm 1.4$ Hz with the amplitude $3.6\pm 1.4\hspace{0.17em}\mathrm{\mu }$m. They are of the same order as those previously reported for an isolated ciliated cortex (47). The height of the cilium tip exhibited two peaks in a beating cycle, one in the recovery stroke and the other in the effective stroke. The authors of ref. 46 calculate the force profile from the time course of the tip position, which shows clear asymmetry with the peak magnitudes $0.57\pm 0.30$ pN in the effective stroke and $0.41\pm 0.20$ pN in the recovery stroke. The force and the resultant hydrodynamic flux show sawtooth-like patterns, which apparently contain higher-order harmonics (figure 3 of ref. 46). These results justify the use of a beating pattern containing second harmonics in our model. The amplitude $B_2$ of the second harmonics is estimated by the ratio between the peak magnitudes $\left(1+B_2\right)/\left(1-B_2\right)=0.57/0.41$, which gives $B_2\sim 0.16$. Note that this should be considered as the upper bound for $B_2$ as the phase shift and other harmonics are not taken into account. The waveform also depends on viscosity and ATP concentration (46). We hope that the present work triggers quantitative experimental studies on the relation between the beating pattern and collective properties of metachronal waves.

Materials and Methods

Synchronization of Two Cilia.

Consider two cilia rotating in $yz$ plane; the center of one cilium trajectory is located at ${\mathit{R}}_1=\left(\mathrm{0,0},h\right)$ with phase ${\varphi }_1$, and the other one is located at ${\mathit{R}}_2=\left(\ell \cos \mathrm{\Theta },\ell \sin \mathrm{\Theta },h\right)$ with phase ${\varphi }_2$. The dynamic equation of cilia 1 is

$${\dot{\varphi }}_1=\frac{f\left({\varphi }_1\right)}{\zeta \left({\varphi }_1\right)a}+\frac{1}{a}{\mathit{t}}_1\cdot \mathit{G}\left({\mathit{R}}_1;{\mathit{R}}_2\right)\cdot {\mathit{t}}_{2}f\left({\varphi }_2\right)$$ [18]

or alternatively,

$${\dot{\varphi }}_1=\frac{f\left({\varphi }_1\right)}{{\zeta }_{0}a}+H_{12}\frac{f\left({\varphi }_2\right)}{{\zeta }_{0}a},$$ [19]

with $H_{12}={\mathit{t}}_1\cdot \mathit{G}\left({\mathit{R}}_1;{\mathit{R}}_2\right)\cdot {\mathit{t}}_2{\zeta }_0$. After the coordinate transformation introduced in the text, $\varphi \to \overline{\varphi }$, the dynamic equation of cilia 1 can be rewritten as

$${\dot{\overline{\varphi }}}_1={\mathrm{\Omega }}_0\left[1+{\overline{H}}_{12}\left({\overline{\varphi }}_1,{\overline{\varphi }}_2\right)\frac{\overline{f}\left({\overline{\varphi }}_2\right)}{\overline{f}\left({\overline{\varphi }}_1\right)}\right],$$ [20]

where ${\overline{H}}_{12}\left({\overline{\varphi }}_1,{\overline{\varphi }}_2\right)=H_{12}\left({\varphi }_1,{\varphi }_2\right)$ and $\overline{f}\left({\overline{\varphi }}_{\mathrm{1,2}}\right)=f\left({\varphi }_{\mathrm{1,2}}\right)$. $f\left(\varphi \right)=f_0\left[1+A_2\cos 2\varphi +B_2\sin 2\varphi \right]$ is taken. Then, we can obtain

$$\begin{array}{ll}\hfill \dot{\overline{\mathrm{\Delta }}}& ={\mathrm{\Omega }}_0\left[{\overline{H}}_{12}\left({\overline{\varphi }}_1,{\overline{\varphi }}_2\right)\frac{\overline{f}\left({\overline{\varphi }}_2\right)}{\overline{f}\left({\overline{\varphi }}_1\right)}-{\overline{H}}_{21}\left({\overline{\varphi }}_2,{\overline{\varphi }}_1\right)\frac{\overline{f}\left({\overline{\varphi }}_1\right)}{\overline{f}\left({\overline{\varphi }}_2\right)}\right]\hfill \\ \hfill & ={\mathrm{\Omega }}_0{\overline{H}}_{12}\left({\overline{\varphi }}_1,{\overline{\varphi }}_2\right)\left[\frac{\overline{f}\left({\overline{\varphi }}_2\right)}{\overline{f}\left({\overline{\varphi }}_1\right)}-\frac{\overline{f}\left({\overline{\varphi }}_1\right)}{\overline{f}\left({\overline{\varphi }}_2\right)}\right],\hfill \end{array}$$ [21]

where $\overline{\mathrm{\Delta }}={\overline{\varphi }}_1-{\overline{\varphi }}_2$.

In the case of $h\ge \ell \gg a$, the Blake tensor for the cilia on a lattice coordinated as $\mathit{r}$ can be approximated as

$$G_{\alpha \beta }\simeq \frac{1}{16{\pi }^2\eta }\int d^{2}q\frac{1}{\left|\mathit{q}\right|}{e}^{i\mathit{q}\cdot \left({\mathit{r}}^{\prime }-\mathit{r}\right)}\left(2{\delta }_{\alpha \beta }-\frac{q_{\alpha }{q}_{\beta }}{|\mathit{q}{|}^2}\right),\left(\alpha ,\beta =x,y\right),$$ [22]

$$G_{\alpha z}\simeq 0,$$ [23]

$$G_{z\alpha }\simeq 0,$$ [24]

$$G_{zz}\simeq \frac{1}{16{\pi }^2\eta }\int d^{2}q\frac{1}{\left|\mathit{q}\right|}{e}^{i\mathit{q}\cdot \left({\mathit{r}}^{\prime }-\mathit{r}\right)},$$ [25]

where we ignore the difference between the projected positions ${\mathit{R}}_p$ and the lattice locations $\mathit{r}$, as well as fast decaying terms such as $\exp \left(-\left|\mathit{q}\right|h\right)$. By taking the Green’s function in Eq. 22, ${\overline{H}}_{12}\left({\overline{\varphi }}_1,{\overline{\varphi }}_2\right)$ can be approximated as ${\overline{H}}_{12}\left({\overline{\varphi }}_1,{\overline{\varphi }}_2\right)=G_{yy}\sin {\overline{\varphi }}_1\sin {\overline{\varphi }}_2+G_{zz}\cos {\overline{\varphi }}_1\cos {\overline{\varphi }}_2$. By taking $\overline{\sum }={\overline{\varphi }}_1+{\overline{\varphi }}_2$ and averaging over the fast variable $\overline{\sum }$ in terms of $⟨\dots ⟩=\frac{1}{4\pi }{\int }_0^{4\pi }\dots$, then the dynamic equation can be written as

$$\dot{\overline{\mathrm{\Delta }}}\simeq \left(G_{yy}-G_{zz}\right)B_2\sin \overline{\mathrm{\Delta }}=\frac{{\sin }^2\mathrm{\Theta }}{\ell }{B}_2\sin \overline{\mathrm{\Delta }}.$$ [26]

Here, we introduce an effective potential, which is

$$\begin{array}{ll}\hfill \mathcal{U}& =-{\int }_0^{\overline{\mathrm{\Delta }}}d{\overline{\mathrm{\Delta }}}^{\prime }\frac{{\sin }^2\mathrm{\Theta }}{\ell }{B}_2\sin {\overline{\mathrm{\Delta }}}^{\prime }\hfill \\ \hfill & =\frac{{\sin }^2\mathrm{\Theta }}{\ell }{B}_2\cos \left(\overline{\mathrm{\Delta }}-1\right)\simeq \frac{{\sin }^2\mathrm{\Theta }}{\ell }{B}_2\left(\cos \mathrm{\Delta }-1\right),\hfill \end{array}$$ [27]

where the local minimum locates at $\mathrm{\Delta }=\pi$ as the stable phase shift between the cilia. By assuming the cilia beat with a wave vector $\mathit{k}$, then the phase difference is $\mathrm{\Delta }=\mathit{k}\cdot \mathit{r}=k_x\ell \cos \mathrm{\Theta }+k_y\ell \sin \mathrm{\Theta }$, so the wave vector should follow $k_x\ell \cos \mathrm{\Theta }+k_y\ell \sin \mathrm{\Theta }=\pi$.

Data Availability

All study data are included in the article and/or supporting information.