Graphical abstract
Keywords: Machine learning, Deep learning, Genomics
Abstract
High throughput sequencing technologies have enabled the study of complex biological aspects at single nucleotide resolution, opening the big data era. The analysis of large volumes of heterogeneous “omic” data, however, requires novel and efficient computational algorithms based on the paradigm of Artificial Intelligence. In the present review, we introduce and describe the most common machine learning methodologies, and lately deep learning, applied to a variety of genomics tasks, trying to emphasize capabilities, strengths and limitations through a simple and intuitive language. We highlight the power of the machine learning approach in handling big data by means of a real life example, and underline how described methods could be relevant in all cases in which large amounts of multimodal genomic data are available.
1. Introduction
The aim of Artificial Intelligence (AI) is to simulate human intelligence in non-living agents, mimicking actions that human brains perform daily such as problem-solving and reasoning or pattern recognition and knowledge acquisition [1]. The development of AI has been largely driven by Machine Learning (ML), by which computers acquire the ability to learn and improve from experience with limited human intervention.
The most common type of ML algorithms is supervised learning, a class of AI methods that learns input-to-output mappings. It is called “supervised” learning because the output is known and the algorithm iteratively makes output predictions until an acceptable level of performance is reached. A family of ML algorithms called Neural Networks, loosely inspired by how neurons pass messages to each other in the human brain, has recently evolved into the so called Deep Learning (DL) subfield. In contrast with ML, DL methods are more flexible and can handle large amounts of data. However, since their predictions strongly depend on input training data, great care and caution should be taken in the interpretation of results, especially in the case of biological data. All ML and DL methods need to learn from input data and the majority of them require a training set, generally consisting in a random subset of the available data. After training, another data set (usually a part of the original database not used for training) is used to validate and select the best-fit ML or DL model. Sometimes a further independent test set is used for performance evaluation.
In the last fifteen years, the genomics world has been revolutionised by the advent of high throughput sequencing technologies (HTS), opening definitively the era of big data or “omic” sciences [2], [3], [4]. HTS have indeed enabled the study of complex biological aspects at single nucleotide resolution and now they are commonly applied to a variety of functional genomics problems including, for instance, the identification of genomic rearrangements and variants [5], [6], the investigation of epigenetic changes [7], or the study of transcriptional and post-transcriptional molecular dynamics [8], [9]. HTS are also recently emerging as key technologies for the discovery of biomarkers [10] and offer great promise to deliver personalized medicine [11], [12].
Nowadays, multiple “omic” applications are routinely applied to the same biological samples, raising the complex problem of integrated data analysis and interpretation [13]. In this context, ML and DL methods are indispensable to systematically analyze large volumes of heterogeneous data to better understand underlying biological processes neglected or undetectable by single “omic” approaches, and a growing number of ML and DL based computational strategies are becoming available through dedicated platforms such as TensorFlow [14] or PyTorch, [15] and/or fully equipped and documented R packages, such as Caret [16].
In the present review, we cover main ML methodologies and some principles of DL methods currently applied to genomic problems and omic data, defined here as all data generated by technologies (such as HTS) working at the genomic scale. We start from the field literature of the last decade and focus on the most used methods, providing technical descriptions as well as relevant examples and try to emphasize their capabilities, strengths and limitations. In introducing basic ML and DL principles, we have tried to use an intuitive language in order to be accessible as much as possible to researchers approaching for the first time the fascinating world of AI (drawing and simplifying concepts in [17]). Additionally, to prove the power of ML methods in handling genomic data, we provide a real life example in which we show how to predict with high accuracy age and biological sex from human gene expression experiments (generated by the RNAseq technology) taking into account a large number of deep transcriptome data available through the international Genotype-Tissue Expression (GTEx) project [19].
2. The learning problem
The primary goal of ML is to acquire skills or knowledge from experience in order to automate human tasks. As a consequence, at the heart of ML there is the learning problem in which computers learn from real data and perform useful predictions. Depending on the type of available data and on the task to perform, a variety of ML methods have been developed [20]. Nowadays, many of such methods have been applied to genomic data for solving several complex biological problems such as the prediction of specific sequence motifs for DNA or RNA binding proteins [21], of the genome methylation status [22], of the 3D organization of the chromatin [23], as well as of the pattern of post-transcriptional modifications [24] or of the most likely cell types from single cell RNAseq experiments [25]. Drawing on the field literature of the last ten years, we have collected the main ML algorithms and ranked them according to their popularity and versatility in genomic applications. In particular, we retrieved publications from the PubMed database using the query string ((“Next Generation Sequencing” OR “single cell sequencing” OR “gene expression” OR “transcriptomics”) AND (“machine learning” OR “deep learning”) AND (’human’)) AND ((“2009”[Date – Publication]: “2022”[Date – Publication])) – and organized them in a local sqlite3 database available at our Github page https://github.com/claudiologiudice/ML-DL-REVIEW) for downstream analyses. We then grouped the set of algorithms used in these publications, which include linear and non linear models for classification and regression as well as some regularization procedures, in two learning classes referred to as supervised and unsupervised, whose main characteristics are represented in Fig. 1 and summarized in Table 1, and will be discussed in the next sections.
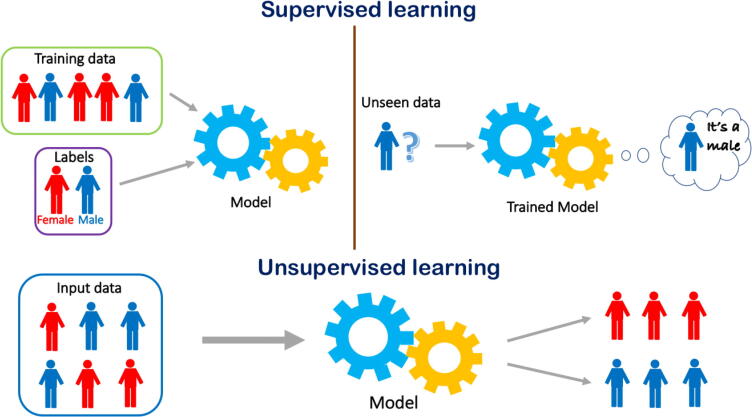
Fig. 1.
Supervised versus unsupervised learning – a pictorial representation. Supervised learning involves a training phase in which a labeled dataset is used to train the model that will subsequently be able to recognize unseen data. Unsupervised learning identifies latent factors in unmarked data and groups them based on similarity.
Table 1.
Main differences between supervised and unsupervised learning.
| Supervised learning | Unsupervised learning |
|---|---|
| Input data is labelled | Input data is unlabelled |
| There is a training phase | There is no training phase |
| Data is modelled based on training dataset | Uses properties of given data for classification |
| Divided into two types: Classification and Regression | Most popular types: Clustering and Dimensionality reduction |
| Known number of classes (for classification) | Unknown number of classes |
Since the ML field is at the intersection of Statistics, Data Science and Engineering, some terms with the same meaning could be used interchangeably. To facilitate the non-specialist reader and avoid confusion, in Table 2 we provide a list of such terms with their description and highlight in italics the terminology that will be preferentially used in this review. On our Github page, in the Supplementary Material section, we provide further mathematical details of the described ML methods for the interested reader.
Table 2.
List of alternative terminologies used in Machine Learning to represent the same concept (our preferred choice is highlighted in italics). X denotes the input, Y or G the quantitative or qualitative output, respectively.
| Synonims | Description |
|---|---|
| Quantitative or continuous variable | A variable assuming continuous values with explicit ordering |
| Qualitative, discrete, factor or categorical variable | A variable assuming discrete values with no explicit ordering |
| Observation or measurement | A realization of a statistical variable |
| Feature, predictor, attribute or independent variable j | The j-th column of the observed |
| Output, outcome, response or dependent variable | The observed Y or G |
| Output class or output label i | The i-th element of the observed |
| Data imputation | Replacing missing or inconsistent data with plausible data |
3. Supervised learning
Supervised learning is the most common and used type of ML that learns a mapping from input X to output Y for quantitative values, or output G for qualitative values. The observed values of variable X can be represented by an NxM-dimensional matrix of elements where N is the number of observations (e.g., individuals or samples) and M is the number of features (e.g., genetic factors or genomic variables); or is an N-dimensional vector of output variables assuming continuous or discrete values, respectively. When the output is quantitative (Y), i.e., corresponds to continuous measurements, the supervised learning problem is known as a regression problem (e.g., prediction of a quantitative phenotype such as age). When the outcome is qualitative (G) with no explicit ordering, the prediction problem is called classification, and the output class is specified bys a label, i.e., a digit (e.g. as in a case control study or as in cancer type or disease trait classification) or a dummy variable (“case”, “control”, or “cancer A”, “cancer B”, “cancer C”). Although here regression and classification problems have been separated into two categories, both are tasks in function approximation as both learn an input to output mapping. A third but less common variable type, defined as ordered categorical (e.g., “mild”, “medium”, “severe” as in symptom severity classification), will not be considered in this review (for further details, please refer to [17]). Also, additional material on weakly supervised learning, or ML with noisy, limited, or imprecise labels can be found in Zhou [18].
Two typical examples of input to output mappings will be presented in Section 7, where the input X will be the NxM gene expression matrix, M will be the number of genes and N the number of individuals. In the first example – biological sex classification (a classification problem) – the output G is discrete, {male, female} can have one of two values in each subject. In the second example – age regression (a regression problem) – the output Y is continuous, represents the age of individual i, and . The implemented algorithms will predict the output (biological sex or age) from the input (gene expression).
3.1. Training, validation and test set
To build an accurate and robust predictive model, the initial dataset is typically split into training, test and validation sets. The training set is the data sample employed to fit the model (i.e., to find the parameters than can best describe the full dataset) and the performance of an ML algorithm significantly depends on it. If, for instance, the size of the training set is too small, the algorithm may not have enough experience and knowledge which will lead to many prediction errors (underfitting condition). On the other hand, if the training set contains too much data, the algorithm may lose its ability to generalize on unseen data (a problem called overfitting). The validation set is the dataset used to evaluate the model fit on the training dataset and is employed to fine-tune the model hyperparameters. Finally, the test set is tipically used to provide an unbiased estimation of a final model fit on the training dataset. The test set returns the actual performance of the model and is only used once the model has been fully trained.
To better understand the general problems of over- and underfitting, it is helpful to introduce the notions of model bias and variance. The bias is the difference between the average prediction of the model and the expected value we are trying to predict. A model with high bias is making wrong assumptions about the data. For instance, see Fig. 2 on the left, where the model (Logistic Regression) is trying to find a linear boundary to separate a dataset with circular boundary. In this case, a model assuming a linear boundary will clearly lead to both high training and high testing errors. Variance, on the other hand, represents the variability of the model’s predictions and indicates how sensitive the model is to the randomness of the data in the training set. Consider for instance a model that is making hypotheses that are so general that they can possibly fit to any data. If we train this model on a given training set we will find a set of optimal parameters (optimal for that training set); if we train the same model on a second training set we will find a completely different set of optimal parameters; this model will be very sensitive to the input data, but will likely fail to perform well on unseen data. See, for instance, Fig. 2 on the right, where the algorithm (K-NN) is predicting a boundary that strongly depends on the input data (the training set represented with circles) and fails to generalize to the test set (represented with triangles) which wasn’t used for training.
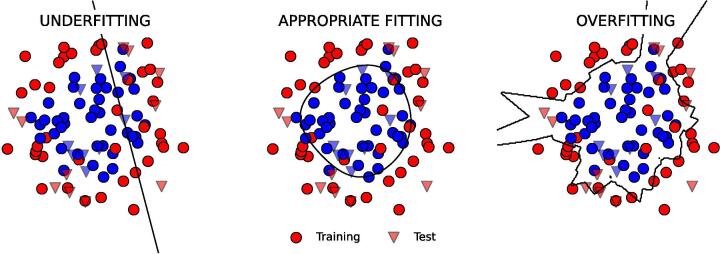
Fig. 2.
Examples of under-, appropriate and over-fitting. The input dataset consists of two classes (blue and red points) that are distributed on an inner and outer circle, respectively (with Gaussian noise) in a two dimensional feature space. Three different models are used to fit the input training set, or in other words, to find the boundary (in black) that can best separate the two classes under the model hypotheses. The training set is represented by circles, the test set by triangles. The chosen methods, Logistic Regression, Support Vector Machine with Gaussian kernel, and K-NN lead to typical over-, appropriate, and under-fitting scenarios, respectively. The code used to generate this figure is available on Github.
In supervised learning, the underfitting condition occurs when a model is unable to capture the underlying pattern of the data. Such models usually have high bias and low variance. Instead the overfitting issue occurs when a model has low bias and high variance. Fig. 2 shows in the middle an example of appropriate fitting where the used model (a Support Vector Machine with Gaussian kernel) has a good bias-variance tradeoff, as it is making an adequate assumption on the data distribution and is not too sensitive to the input data.
The performance of a predictive algorithm can be optimized via a cross-validation (CV) procedure. In the k-fold CV procedure, the training sample is divided into k mutually exclusive subsets of equal size. The algorithm is trained on subsamples and validated on the remaining subsample. This procedure is repeated for each of the k subsamples with the advantage that all observations are used for both training and validation, and each observation is used for validation exactly once. Cross-validation provides reasonable estimates of the expected error [17] and average performance is reported along with standard deviation and statistical significance.
3.2. Naive Bayes
The Naive Bayes (NB) algorithm is a classification algorithm, belonging to the class of generative models, i.e., it builds a full statistical model for both input and output. Given this model, the output can be generated from the input (using Bayes’ rule). It is called naive because it makes a simple but strong assumption that all pairs of features (columns of X) are conditionally independent given the output labels, an assumption that is generally not true. Building the model is easy and requires no complicated iterative parameter estimation. For a discrete variable it requires the construction of a frequency table for each feature against the output, then the posterior probability (a product of probabilities given the assumption of independence) is computed and the class with the highest posterior probability is returned as the predicted outcome. NB can be used to model binary, categorical unordered, continuous features, as well as to model features with unknown distribution, and to model input data it uses a Bernoulli, Multinomial, Gaussian, or a kernel density, respectively. NB classifiers have been adopted for their simplicity or as a baseline in comparison with more complex classifiers. Two of the many examples where NB is used as a baseline for comparison are [26] for classification of treatment success/failure given a set of input features (variants of hepatitis C obtained through RNAseq) cross-validated on a total of different subjects, and [27] where input features are gene expression profiles from RNAseq, output is binary drug response, and the analysis is cross-validated on individuals with cancer. For the taxonomic classification of microbiomes using metabarcoding, the RDP (Ribosomal Database Project) curators [28] have developed the RDP-classifier, a Naive Bayes classifier relying on k-mer frequencies measured on prokaryotic genera [29]. The RDP-classifier, given an input sequence of bacterial 16S rRNA, predicts an output label, the genus. The algorithm was trained on Bergey corpus, consisting of labeled sequences (the label is the genus and can have 988 different values, ) or on RDP sequences ( where 1187 is the number of genera in the NCBI taxonomy database). The classifier uses a set of M features for each input sequence, the k-mers (with ) that make up the sequence, and assigns to the sequence a genus based on the frequency of those k-mers in the labeled training set. More recently QIIME2 [30] teams have introduced a Multinomial Naive Bayes classifier to achieve taxonomic classification of metabarcoding data [31].
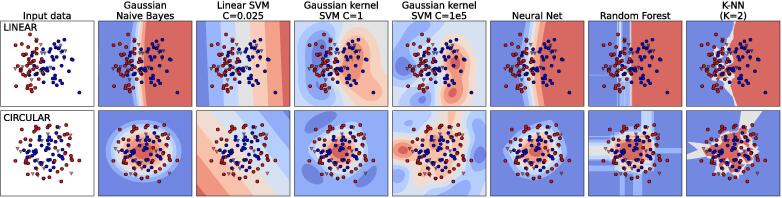
Fig. 3 illustrates the behavior of the Gaussian NB algorithm on two synthetic datasets, a linearly separable dataset (i.e., with a boundary between classes that is linear, top row in the figure) and a circularly separable dataset (i.e., with a boundary between classes that is a circle, bottom row), together with a few other classification algorithms. Despite its over-simplistic assumptions, the NB algorithm outperforms more sophisticated alternatives. Although the estimator may be biased, as it makes a priori assumptions, it has low variance, i.e. it is not sensitive to small fluctuations in the training set. Its use is typically recommended when the feature space is large (high M) and density estimations become unfeasible. In Oncofuse [32], a computational pipeline for the classification of fusion sequences with oncogenic potential, the NB algorithm has been chosen for its robustness and because it can natively handle missing data (as any generative model) which is essential when high throughput datasets from different sources need to be combined. The NB algorithm has been applied also to pharmacogenetic predictions. Boloc et al. [33], for instance, developed a NB-based predictive model of antipsychotic induced extrapyramidal symptoms using functional SNPs belonging to four genes of the mTOR pathway.
Fig. 3.
Comparison of different classifiers on a two-class (red and blue) classification problem with two features. (top) Linearly separable synthetic dataset (with noise). (bottom) Circularly separable synthetic dataset (with noise). Circles represent the training set, triangles the test set. The code used to generate this figure is available on Github (code adapted from [34]).
3.3. Linear Discriminant Analysis
Linear Discriminant Analysis (LDA) (also called Normal Discriminant Analysis) is a (two-class or multiclass) classification algorithm for continuous features. It is largely used in multiclass classification as it provides a low dimensional view of data (see 4.2). LDA is similar to the NB algorithm as both are generative models. However, LDA makes the specific assumption that observations belonging to the same class have the same Gaussian distribution and all classes share the same variance (but have a different mean).
It can be shown that the decision boundary, i.e., the surface that separates classes, estimated by LDA is flat in the space of the input features, a line in two dimensions, a hyperplane in three or more dimensions. For this reason LDA works well when data are linearly separable. Also, it can be shown that the LDA decision boundary is a function of and of the position of the class centroids, making this algorithm sensitive to outliers (see discussion in 3.5). Regularized versions of LDA, i.e., that add information in order to prevent overfitting, also exist for example with shrinkage of . The LDA algorithm has been widely applied to transcriptome profiling and miRNA biomarkers discovery. For example, in a recent study Zhang et al. [35] demonstrated the suitability of LDA for classification of cardiovascular disease patients and healthy individuals using as input high-throughput transcriptome profiling data derived from monocytes, whose infiltration into the walls of the great arteries has been recognized to play an important role in atherogenesis [36]. LDA is also used in metagenomic biomarker studies based on rRNA thanks to the LEfSe (linear discriminant analysis effect size) tool [37], to test the association of a specific taxonomic class (e.g. genus or OTU, operation taxonomic unit) with a categorical output variable (e.g. normal vs cancer samples).
3.4. Linear regression, regularization strategies and overfitting
While generative models make missing value estimation (data imputation) straightforward, as they can generate missing data drawing from the model distributions, they don’t directly try to maximize the quality of the output (e.g., to maximize the Residual Sum of Squares as we will see in (1)) on the training set. Rather they try to determine the best fit to a theoretical and sometimes inaccurate model. Discriminative models instead directly try to maximize the quality of the output on the training set. Typically, discriminative methods use an additional regularization term in the training cost function.
The most popular discriminative models are Linear Regression for a continuous output Y and Logistic Regression for a binary output G. Linear Regression minimizes the Residual Sum of Squares (RSS):
| (1) |
where is the i-th observed output, are the M input features of the i-th observation (), are the parameters of the model or regression coefficients, one for each input feature j plus an intercept for , and is the scalar product between vector and vector . In Section 7 we will show an example in which gene expression values computed in RNAseq experiments are the features (so M is the number of genes), individual samples are the observations, and the aim is to predict the age of a donor (the output ), a continuous variable.
When the number of features M is comparable to or larger than the sample size N, a penalty/regularization term can be added to the model, for having too many features in the model:
For increasing values of the parameter , the amount of penalty increases (the bias increases and the variance decreases), vice versa for decreasing values of . Depending on the functional form of B ( penalty penalty , or a linear combination of the two – to mention the most common strategies), the algorithm is called LASSO, Ridge, or Elastic Net linear regression, respectively. Ridge Regression shrinks the coefficients of a feature j towards zero, but doesn’t set any of them exactly to zero. LASSO [38] instead forces some of the coefficients to zero and can thus be seen as a variable selection method. For this reason, LASSO produces simpler and therefore more interpretable models compared to Ridge regression. Elastic Net combines properties of both regressors by both shrinking coefficients (like in Ridge regression) and setting some of them to zero (as in LASSO). Cross-validation methods can be used to identify which of these techniques performs better on a specific dataset. In Section 6 we will describe alternative variable selection procedures.
The LASSO algorithm is currently used in different genomic applications such as the study of intratumoral heterogeneity, or the selection of biomarkers and genes to name a few. Xiong et al. [39], for instance, have applied a LASSO based strategy to select an optimal subset of genes that can accurately predict cancer. Given an input NxM expression matrix from microarray data, where N is the number of subjects and M is the number of genes in the microarray, the algorithm can accurately predict if a subject has cancer (0/1 label) given expression data. Linear regression has been also applied to the analysis of single cells [40] to predict cell invasion rates using selected physical parameters as regressors (elastic modulus, maximum strain, transit time and cell size).
3.5. Logistic Regression and Softmax Regression
Despite its name, Logistic Regression (LR) (also called Binomial Regression) is not a regression algorithm i.e., a prediction model of a continuous variable), but a binary (or two-class) classification algorithm. LR is indeed a generalized linear model for the prediction of a binary output (instead of continuous variables) through the use of a link function, the logistic function which maps a real variable to the interval. As for linear regression, a regularization term can be added to the model to obtain Ridge, LASSO, and Elastic Net LR.
It can be shown that the decision boundary of LR and its multinomial version (Softmax) is flat (a hyperplane) in the space of the input features, as in LDA. However the parameters defining the hyperplane are different, as LDA makes additional assumptions on the distribution of the features. Because of those assumptions, LDA parameters have lower variance but can incur in biases when the assumptions are not valid. For example, if outliers are present, they will contribute to the estimation of the LDA covariance matrix and thus to the estimation of the optimal parameters, while in LR they will be down-weighted. Therefore LR is more robust to outliers, even though LR and LDA tend to often return similar results.
Although LR can be extended to generate non linear decision boundaries – with the use of a kernel, i.e., a mathematical functions of the input X – this typically results in a high computational cost. In contrast, a different discriminative model, namely Support Vector Machine (see next section), can be extended from its linear version with kernels at a lower computational cost.
A promising application of LR has been described by Wang et al. [41] where it has been used in combination with SVM and RF to predict autism-associated long non-coding RNAs starting from normal tissue expression patterns and sequence features. Their model was trained on a set of long non-coding RNAs labelled as non-risk/risk genes () for autism (ASD) in previous work. The algorithm learned from an NxM input matrix of expression, where each row consisted of selected sequence features and expression values of the long non-coding RNAs in healthy individuals from the BrainSpan dataset. Recently Torang et al. [42] have proposed an approach based on Elastic Net LR to identify immune cell subtypes from single cell RNAseq data, revealing cell types that were previously unannotated or misclassified. LR has been also applied to data integration problems as in Beretta et al. [43] where LR was used with decision tree learning to integrate the predictions of different eQTL mapping tools to produce more reliable results.
3.6. Support Vector Machine
A widely use ML method is the Support Vector Machine (SVM) which shares many similarities with LR. For two-class classification, SVM minimizes a loss function called Hinge Loss (HL) plus a penalty term ( penalty). The name support vector arises from the fact that many of the input observations (vectors in this context) do not play a big role in defining the SVM optimal boundary, or the hyperplane that separates observations in two classes: the few that contribute are called support vectors. The SVM algorithm proceeds iteratively. If at a specific iteration the decision boundary misclassifies some points, these points become the support vectors, and contribute to the loss proportionally to their distance from the boundary. Therefore the loss that the algorithm tries to minimize depends only on a subset of the input observations and thus optimal parameters can be efficiently estimated. Extensions of the SVM with nonlinear kernels , the most popular being the Gaussian kernel (other nonlinear kernels are rarely used), allow for nonlinear boundaries. Such kernels, can describe complicated patterns present in a real dataset by representing data in a new hyperspace.
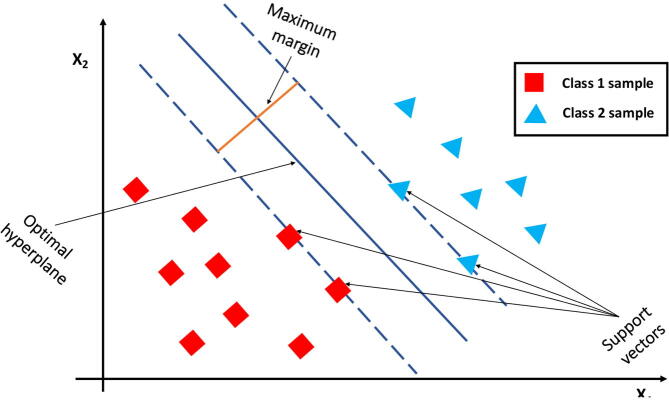
For example, in a two class classification problem with linearly separable data on a plane (Fig. 4) for example, SVM finds the optimal line that can separate the two classes while maximizing the distance from the boundary (i.e. the margin). In general SVM works well when the margin of separation between classes is clear and is computationally efficient; it is not suitable for large datasets and when the number of features exceeds the number of training data samples.
Fig. 4.
SVM optimal boundary for linearly separable data: SVM uses margins, whose distance from the decision boundary can be tuned by changing the amount of penalization. Only observations inside the margin contribute to the loss, and therefore to the definition of the optimal hyperplane.
SVM has been used in a variety of genomic applications. Hao et al. [44], for instance, used SVM to identify Hrthle cells (HC) from non-operative fine-needle aspiration biopsy (FNAB) of thyroid nodules using RNAseq data, and in particular differentially expressed nuclear and mitochondrial genes. A set of FNABs with curated cytology class labels G was used to train the algorithm ( for FNABs without HCs and otherwise) given an input NxM matrix of measured expression values of genes. Besides diagnostic classification, other genomic applications of SVM include intratumoral heterogeneity assessment [45], tissue-selective genes, gene prediction, gene selection, disease-gene association analysis, gene expression analysis, signatures recovery from gene-pathway association, disease gene prioritization, and miRNA signatures extraction (see supplementary materials for specific references). SVM is also efficiently used for integrating genomics data. De Orange et al. [46], for instance, applied SVM to predict rheumatoid arthritis disease subtypes by combining histological features and RNAseq data. Similarly, Kim et al. [47] used a modified SVM to predict cancer survival combining miRNA and mRNA expression data from different subjects.
3.7. The perceptron learning algorithm and Artificial Neural Networks
The perceptron algorithm shares some similarities with SVM. It is designed to find a decision boundary that has minimal distance from misclassified points: observations that fall inside their class boundary give null contribution to the loss, while the contribution of an observation to the loss depends on the size of the violation. Also, from the functional form of the loss (see supplementary materials), it follows that the decision boundary of the perceptron is nonlinear. A perceptron is the simplest example of a Neural Network with only one node.
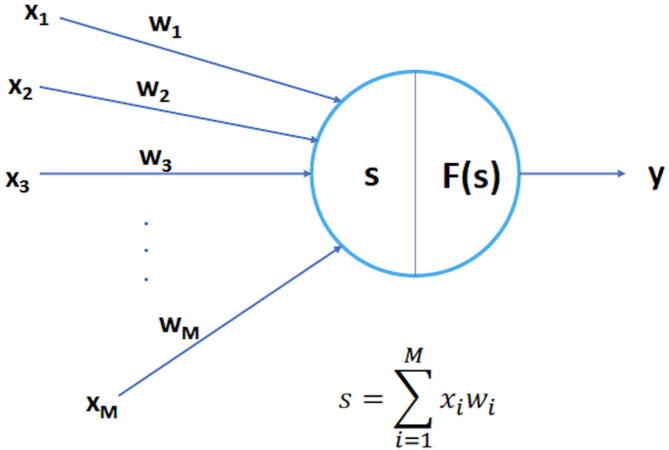
Neural Networks or Artificial Neural Networks (ANNs) are computational networks inspired by the animal brains that can learn from known examples and generalize to unknown cases. An ANN is composed by a collection of connected nodes called artificial neurons (AN). After receiving an input signal, ANs process and pass it to the connected neurons. The connections are called edges. A weight modulates the strength of the signal that is passed from input to output through the edges. These weights represent the neural synapses. Formally, each neuron has M inputs , …, , …, , and each input is assigned a weight : if the input is excitatory, otherwise it is inhibitory. The weighted sum of the inputs is passed to the output y through the activation/transfer function F:
| (2) |
A neuron may have a threshold (called Bias) such that only if the aggregate signal crosses the threshold the signal is passed to the output:
| (3) |
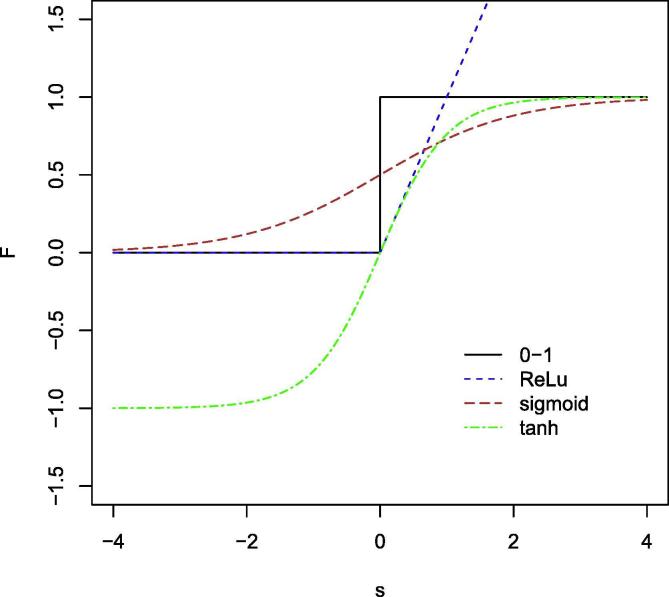
Fig. 5 shows a schematic view of an AN. The most used activation functions are the Sigmoid (or logistic function), the Hyperbolic Tangent and the ReLu (rectified linear unit). Fig. 6 shows the functional forms of different activation functions.
Fig. 5.
Schematic view of an artificial neuron: ,…, are the input nodes, y is the output node, F is the activation function.
Fig. 6.
Comparison of different activation functions. The binary step or 0–1 activation function (AF) activates the neuron when the input is greater than a threshold. While useful in binary classification tasks, it is of limited use in multiclass classification problems. The sigmoid and tanh AFs are similar in shape to the 0–1 AF but are continuosly differentiable which is essential for gradient based optimisation. The ReLU AF is computationally more efficient compared to the sigmoid and tanh function because it only activates neurons with positive input values – a subset of the nodes in the neural network (in the same way as the SVM algorithm is efficient because only support vectors contribute to the loss function). A differentiable version of the ReLU activation function exists that is smooth in 0.
Typically, neurons are aggregated into layers: input, hidden, and output layer. The number of neurons and layers are some of the parameters that need to be set to define a network architecture. When the activation function is nonlinear, a two-layer ANN can be proven to be a universal function approximator [48] (Universal Approximation Theorem). For this reason, ANNs with nonlinear activation functions can solve complex problems using only a small number of nodes; multilayer ANNs with identity activation function instead are equivalent to a single layer. Given the large number of possible architectures, ANNs are often not easy to tune. The most commonly used ANNs are feedforward networks. In these kinds of artificial networks: (i) no computation takes place in the input layer; (ii) the signal always travels forward from the input to the output; (iii) connections between the nodes do not form a cycle. The backpropagation algorithm is widely used for training feedforward neural networks. It efficiently uses the chain rule to compute the gradient of the loss function with respect to each weight one layer at a time and proceeds backwards from the last layers, thus avoiding redundant calculations of intermediate terms in the chain rule. ANN are largely used in single cell analyses for the discrimination of heterogeneous cell populations. An interesting example is offered by Arai et al. [50] in which the authors combined single cell gene expression profiles with machine learning analysis and in vivo functional studies to explore how hematopoietic stem cell (HSC) divisions rate change with ageing.
Multilayer perceptron networks (MLPs) are an example of feedforward networks, and are composed of multiple layers of fully connected nodes (each node in one layer is connected to all nodes in the next layer). Internal nodes of an MPL are perceptrons with threshold activation; the ReLu activation function is analogous to the perceptron loss function. MLP are widely used in genomic data analysis (Table 3). For instance, a MLP has been used, in combination with other machine learning models, for the systematic analysis and prediction of type IV secreted effector proteins produced by different Gram-negative bacteria during infection [49]. The algorithm was trained and cross validated on a set of proteins, with known labels, namely 390 T4SS effectors and 1112 non-effectors. The input to the algorithm was an NxM matrix of M features describing each of the N proteins, of three types: local sequence encoding (e.g., amino acid composition, represented as a 20-dimensional feature vector), global sequence encoding (e.g., position-specific scoring matrix, a Lx20 matrix where L is the length of the protein sequence), and structural descriptor encoding (e.g., predicted secondary structure, a 3x50 vector). Given the input features and the output labels the algorithm learned to classify the sequence as T4SS effectors or non-effector. (see Table 4).
Table 3.
Number of occurences of most common learning algorithms in a database of PubMed publications of the last ten years on Next Generation Sequencing, single cell sequencing, gene expression and transcriptomics. Algorithms occurring less frequently have been omitted. The PubMed query was performed on 16th January 2021. The table also reports the specific biological applications of such methods in the selected database (although it does not represent an exhaustive list in general). Explicit bibliographic references can be found on our Github page and in the Supplementary Materials together with more details on the methodology used to build the table.
| Learning algorithm | Example biological applications | #Occurrences |
|---|---|---|
| Support Vector Machine | diagnostic classification, intratumoral heterogeneity; tissue-selective genes; gene prediction; gene selection; disease-gene association; gene expression analysis; signatures from gene-pathway; disease gene prioritization; miRNA signatures | 157 |
| Random Forest | diagnostic classification, tissue-selective genes; gene prediction; co-acting gene networks; gene selection; mutation-gene-drug relations; gene expression analysis; miRNA biomarkers; drug-induced gene expression; sample-classification | 124 |
| Logistic Regression | gene prediction; gene selection; drug-induced gene expression | 38 |
| Deep Neural Network | mutation-gene-drug relations; gene expression analysis | 36 |
| LASSO | intratumoral heterogeneity; biomarkers selection; gene selection; gene expression analysis | 31 |
| Naive Bayes | gene selection; pharmacogenetic prediction | 28 |
| K-Nearest Neighbor | gene selection | 28 |
| Artificial Neural Network | gene selection; genotype-phenotype analysis; risk classification; transcriptome profiling; variant extraction | 25 |
| Autoencoder | gene prediction | 24 |
| Principal Component Analysis | single-cell analysis; gene expression | 19 |
| Linear Discriminant Analysis | transcriptome profiling; miRNA biomarkers; taxa-condition association | 14 |
| Perceptron | gene selection; gene prediction | 12 |
| K-means | candidate miRNA targets | 8 |
Table 4.
Accuracy of classification obtained through the implemented learning models. Accuracy is reported with the respective standard deviations.
| Learning models | Accuracy |
|---|---|
| Random Forest | |
| MLP | |
| Linear Model |
3.8. Boosting
The term Boosting refers to a family of predictive algorithms that converts a set (ensemble) of low-accuracy models (called weak learners or weak classifiers) into a high-accuracy model (jargon for strong learner or strong classifier). The idea behind it is to sequentially train weak learners, each trying to correct its predecessor [51]. This is done by creating a first model from the training data, and then a second model that attempts to correct errors from the first model and so on. Models are added until the training set is predicted perfectly, or within some predetermined error, or a maximum number of models are added. The most common boosting algorithm is Adaptive Boosting (AdaBoost) [52] and in its standard configuration it uses trees as the weak learners and their output is combined into a weighted sum that represents the final output of the boosted classifier. Boosting algorithms are often used to handle gene expression data or perform gene predictions in cancer studies. Maniruzzaman et al., for example, used Adaboost on colon gene expression data to identify potential high risk cancer genes, and demonstrated how this algorithm had better performance compared to other ML methods in terms of sensitivity to noisy data and outliers [53].
3.9. Random Forest
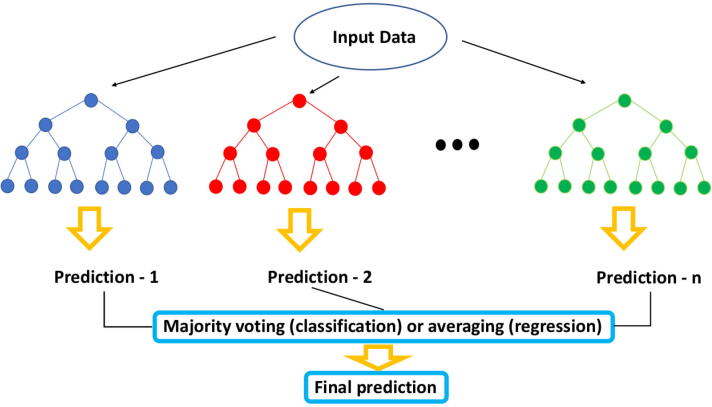
The Random Forest (RF) algorithm is an ensemble of decision trees made through bootstrapping (i.e., resampling with repetitions) of the training dataset [54]. RF trees have low mutual correlation, an important property that follows from a randomization procedure on the features in the training phase: at each node a subset of features is randomly selected. Each decision tree provides a prediction about each observation. All trees are then combined together. In a regression problem this combination is an average of the predictions from each tree. In contrast, in a classification problem, the prediction from each tree is combined into a final classification through a majority vote mechanism. Fig. 7 shows a schematization of how a Random Forest algorithm works. In general RFs have some characteristics that make them ideal in many ML problems: (i) they are easy to tune; (ii) they basically only have two parameters that need to be set: the number of trees and the number of features sampled to grow each leaf within a tree; (iii) they are not prone to overfitting; (iv) they can evaluate the importance of each input feature during the training phase; (v) because they use an out-of-bag procedure, RFs compute an unbiased estimate of the generalization error. For these reasons RF is a very popular ML algorithm in trascriptomics after SVM (see Table 3). In RF, the importance of each feature is evaluated through the mean decrease of impurity, by averaging over the whole forest of trees [54]. In classification, node impurity is measured by the Gini index, in regression through the RSS.
Fig. 7.
Random Forest architecture for classification and regression problems.
RF is used to answer a variety of genomic questions (see Table 3). Teng et al. [55], for instance, used RF and SVM to predict human tissue-specific genes using expression data and found that the RF classifier outperformed SVM. The RF algorithm is also widely used in single cell analysis for cell-type classification from individual cells gene expression profiles [56]. Asnicar et al. [57], have applied RF for prediction and classification of personal dietary habits based on microbiome data drawn from the PREDICT 1 cohorts [58].
3.10. Nearest Neighbor classifier and K-NN
A nearest neighbor (NN) classifier is based on the definition of a distance on . The algorithm assigns observations in the test set to the same class as the closest observation in the training set. Without smoothing, NN classifiers tend to overfit the data and therefore generate very complex decision boundaries. K-NN uses K nearest neighbors and classifies a new observation using the majority class in the K neighbors, thus smoothing the decision boundary and preventing overfit. The higher the value of K, the smoother the resulting decision boundary (see Fig. 2 with ; this low value of K causes overfitting). Cheng et al. have developed an accurate procedure based on an extension of the K-NN classifier to distinguish different cancer types from gene expression profiles [59].
3.11. Deep neural networks
A deep neural network (DNN) is typically a feedforward ANN with multiple layers. DNN have demonstrated superior performances than traditional ML approaches in many genomics problems including the identification of molecular biomarkers [61] and the discovery of mutation-gene-drug relationships [60]. In the latter, the authors created a database of candidate mutation-gene-PMID mappings mining PubMed abstracts and labeled each mapping as true if it was listed in the ClinVar or COSMIC database and as false otherwise, thus collecting 4440 true mutation-gene relations and 165317 false mutation-gene relations (). After additional filtering and manual curation, they trained a CNN to classify a candidate mutation-gene relation as true or false based on a set of M features. The features characterizing a mutation-gene pair were extracted using natural language processing procedures from the PubMed abstracts. With an analogous procedure they trained a classifier to learn true drug-gene relations. Recently, DNNs have been also used to infer the cell type or subgroup by analyzing thousands of highly heterogeneous scRNAseq data [62].
Convolutional Neural Networks (CNNs) are a type of DNN that break the fully-connectedness of traditional ANNs such as MLPs. While in MLPs each node in a layer is connected to all layers in the following layer which is prone to overfitting, in CNNs instead, each node in a layer receives input from only a restricted area of the previous layer called the receptive field. The CNN architecture was originally inspired by the response mechanism of a neuron in the visual cortex to a stimulus. Tipically CNNs also pool layers, i.e., reduce the dimensions of the data by combining the outputs of a group of nodes in a layer into a single node in the next layer. CNNs are widely used for instance in data integration studies, to combine information deriving from multiple datasets. Matsubara et al. [63], for example, developed a spectral-CNN to integrate protein interaction network data and gene expression profiles for lung cancer classification, and showed how CNN had superior performance compared to other ML methods such as SVM or RF.
Recurrent Neural Networks (RNNs) are also popular ANNs. They use sequential data (also time series data) and have a “memory”, i.e., in a RNN the output of a node depends on the prior element within the sequence, while in traditional ANNs inputs and outputs are assumed to be independent. RNNs have been applied in several Nanopore base-callers, such as Metrichror [64], Nanonet [65] and DeepNano [66].
3.12. Performance metrics
Many different measures of performance can be introduced for the classification problem.
First, the confusion matrix, also known as contigency table, is a table with rows containing counts of predicted labels for each class and columns containing counts of true labels. Assuming there is a total of two classes (positive and negative sets), the table contains: (i) true positives (TP or positives correctly recognized by the classifier); (ii) true negatives (TN or negatives correctly recognized by the classifier); (iii) false negatives (FN or positives recognized as negatives by the classifier); (iv) false positives (FP or negatives recognized as positives by the classifier).
The area under the receiver operating characteristic curve (AUC-ROC) is an important metric used for binary classification problems. The AUC quantifies the ability of the model to discriminate between one class or another: an AUC-ROC of 1 represents a perfect classifier, while a value of 0.5 means that the algorithm performs as well as a random guess.
Accuracy, namely the rate of correct classifications, is defined as
Sensitivity, namely the fraction of tests classified as positive among all positives, is
specificity, namely the fraction of tests classified as negatives among all negatives, is
precision or positive predictive value (PPV) is
negative predictive value (NPV) is
and F1 score, which combines precision and sensitivity by taking their harmonic mean, is:
For a regression problem the most common statistical performance indicators are the Root Mean Square Error (RMSE)
where is the observed value and is the predicted value, the Mean Absolute Error (MAE)
the Mean Absolute Percentage Error (MAPE)
and the Pearson’s correlation coefficient (defined in (4)) between the predicted values and the real/observed values.
4. Unsupervised learning
While the aim of supervised learning methods is to determine the properties of , i.e., of the output Y given the input X, in unsupervised learning there is no output variable and the aim is to characterize , i.e., to describe the associations and patterns among the set of input variables. The performance of a supervised method can be measured from the expected loss over the density . In unsupervised learning instead there is no direct measure of success.
Clustering is the most common unsupervised learning method. It can be defined as the task of partitioning a set of observations into groups in such a way that pairwise dissimilarities between observations assigned to the same group (also called cluster) are smaller than those in other groups. Identification of the groups/clusters is usually subjective and more follow-up efforts are needed to interpret the identified groups. Other unsupervised learning methods include Dimensionality Reduction algorithms and Generative Adversarial Networks.
4.1. K-means and K-medoids clustering
The K-means algorithm is one of the most popular clustering techniques and can be applied to quantitative variables as it uses Euclidian distances between observations. It is an iterative descent method that tries to minimize within-cluster variances (squared Euclidean distances). The algorithm is not guaranteed to converge to a global minimum and different initialization strategies can result in different performances. In the literature various modifications of K-means have been proposed that use non Euclidian distance measures, for example K-medoids, and that can be applied to qualitative data as well.
An example application of K-means clustering to the inference of candidate miRNA targets is provided by Al-Shaer et al. [67] where this unsupervised machine learning method is used in conjunction with statistical analyses to facilitate the discovery of signaling pathways and miRNAs that inform mechanisms underlying the fetal alcohol spectrum disorder (FASD), a condition causing neurodevelopmental disability.
4.2. Dimensionality reduction algorithms
Reducing the number of input features for a predictive model, whilst also preserving the main structure of the data, is referred to as dimensionality reduction (DR). In DR, new features are constructed from the input data that are not directly comparable to the original data.
LDA, a multiclass classification procedure, can be used to perform dimensionality reduction while preserving as much of the class discriminatory information as possible. LDA defines a simpler reduced space using class centroids. K centroids, one for each class, span at most a dimensional subspace; if M, the number of input features, is much larger than K, LDA can provide a considerable drop in dimension. LDA DR is by definition a supervised DR algorithm; nonetheless it deserved to be mentioned here for completeness and because it is widely used for DR.
Among unsupervised DR algorithms the most common method is Principal Component Analysis (PCA). PCA projects a multidimensional set of features onto a low dimensional set of features (i.e., the first few principal components) which are constructed so as to preserve as much of the variance of the original data as possible [68], [69].
Autoencoders (AE) are ANNs used typically in DR, that are trained to minimize a reconstruction error. In its simplest form an AE is an MLP with one or more hidden layers (the code) and the same number of input and output nodes. If the number of output nodes is less than the number of input nodes, then the output nodes are a compressed representation of the input nodes. AE can be used to reduce the number of input features [41] and in genomic data integration studies as in Lemsara et al. [70] in which an AE based method was employed to characterize cancer patients by integrating multiple omics data such as gene expression, miRNA profiles and DNA methylation. AEs have been also recently applied as generative models for data imputation to handle single cell data minimizing biases of dropout genes that appear at a low or moderate expression level in a cell but are zero in another cells of the same type [71].
Another popular DR algorithm is the Self Organizing Map (SOM). In its simplest form, it maps each observation x (with M features) to a cell on a 2D grid, the output layer. It does so in an unsupervised manner, mapping similar observations to neighboring cells in this 2D grid. The optimal mapping is reached with an iterative algorithm that maximizes the similarity between observations mapped to the same neighborhood. As a result, a SOM can represent a dataset with a high number of features M on a two dimensional space. A new observation can be mapped to the same cell where observations similar to have been mapped to, on the 2D grid built from N input observations.
4.3. Generative Adversarial Networks
Given a training set, a Generative Adversarial Network (GAN) is a DNN that learns to generate new data with the same distribution as the training set [72]. In a GAN, a generative network generates data from a candidate distribution, while a discriminative network evaluates them. The generative network is trained to “fool” (or increase the error rate of) the discriminative network. Training is completed when a predetermined performance threshold is reached, and the generative network has learnt to create synthetic data that the discriminator classifies as true data. GANs were originally proposed as a generative model in unsupervised learning, but they are now used in supervised, semisupervised learning, and also in reinforcement learning (see below). Recently [73] used GANs to detect biologically relevant alternate expression patterns between samples from human healthy and kidney tumor samples; further recent examples include [74], [75].
5. Reinforcement learning
Besides supervised and unsupervised methods there is a third type of ML methods called Reinforcement Learning (RL). RL is a general machine learning model where, although there is human supervision, this is limited to the definition and the perturbation of a system environment and to the definition of a system of rewards and penalties. The final purpose of RL is to push the machine to solve a problem by itself or to perform a task in an expected way. Interesting applications of RL are reported in Imani et al. and Sirin et al. [76], [77] in which a RL algorithm is designed to control gene regulatory networks using observed gene expression data.
6. Feature selection
Feature selection is a procedure that selects a subset of relevant and informative features to be used in a model. The central premise of feature selection is that the data contain some features that are either redundant or irrelevant, and that can thus be removed without incurring much loss of information [78]. Redundant and irrelevant are two distinct notions, as a relevant feature may be redundant if another relevant feature is present that is strongly correlated with it [79]. There can be several disadvantages in dealing with large feature sets such as computational burden, as the algorithm may require too many resources, or decrease in accuracy, as many ML algorithms perform poorly when the number of features is significantly higher than an optimal number or they are prone to overfitting [80]. In general feature selection methods include two different techniques: (i) feature subset selection, in which a subset of features is selected that result into better performance of the model; (ii) feature ranking, that provides a measure of the relative importance of each feature for the model.
In this work we describe three methods that differ in how they evaluate the importance of each feature in the subset: Filter, Wrapper and Embedded techniques.
6.1. Filter methods
Filter methods use a proxy measure, chosen to be fast to compute, to evaluate the usefulness of the feature set. They return a feature set which is not tuned to a specific type of predictive model and are usually less computationally intensive and robust to overfitting than the other algorithms [81]. Many filter techniques provide a feature ranking rather than an explicit best feature subset, and can also be used as a preprocessing step for wrapper methods. An example of filter method is based on Pearson’s correlation. Given two sets of observed features and this statistic measure estimates the linear correlation between features a and b and is defined as:
| (4) |
where and are the mean of a and b respectively. The coefficient r has a value between and −1, where 1 is total positive linear correlation, 0 is no linear correlation, and −1 is total negative linear correlation.
6.2. Wrapper methods
Wrapper methods use a predictive model to score each feature subset used to train a model, which is tested on a control set. These methods present some criticalities: they are computationally intensive and they tend to overfit when the number of observations is insufficient, but usually they provide the best performing feature set for the particular predictive model used. Stepwise regression/classification is a wrapper method in which the choice of predictive variables is carried out by an automatic procedure. In this procedure, at each step, a variable is considered for addition to or subtraction from the set of explanatory features by means of some specified evaluation criterion. The final goal is to achieve a balance between simplicity and fit. Stepwise procedures can have three different approaches:
-
•
Forward Selection, which starts with no variables in the model, evaluates the addition of each feature using a chosen criterion, adds the feature whose inclusion gives the most statistically significant improvement of the fit, and repeats this process until there is no statistically significant improvement;
-
•
Backward Elimination, which starts with all candidate features, evaluates the deletion of each variable using a chosen criterion, deletes the variable whose loss gives the less statistically significant deterioration of the model fit, and repeats this process until no further variables can be deleted at a prespecified significance threshold;
-
•
Bidirectional elimination (or Stepwise Selection) is a combination of the forward selection and backward elimination techniques.
A wrapper method is implemented in the Boruta package [82] on a Random Forest model (Boruta is a god of the forest in the Slavic mythology). In Boruta, RF trees are independently grown on different bagging samples of the training set. Feature importance is computed through the loss of classification accuracy caused by random permutation of the variables.
6.3. Embedded methods
Embedded methods try to combine advantages of both Filter and Wrapper methods, but unlike these they do not separate the learning process from the feature selection process [83]. LASSO, for instance, is an embedded feature selection method (embedded in the regression problem).
7. Use case: age and biological sex prediction by human RNAseq data
To prove the power of ML methods, here we report a real example in which we show how gene expression data from RNAseq experiments can be used to predict biological sex and age of unknown donor samples. Our example is based on public gene expression data from the GTEx project, an international effort whose goal is to provide a comprehensive overview of gene expression and regulation in human tissues [19]. GTEx comprises more than 9000 RNAseq experiments from 54 non-diseased tissue sites across nearly 1000 individuals. From the whole dataset, freely available at https://www.gtexportal.org/home/datasets, we downloaded a subset including gene expression values for 2219 RNAseq experiments from 30 different tissues.
Our initial dataset consisted of 56202 gene expression values (according to Gencode v19 annotations), the features of our models, calculated for each human tissue. We aimed to investigate the relationship between gene expression and metadata such as biological sex (a binary outcome) and age (a continuous outcome) by means of machine learning approaches. Since the number of input features was much higher than the number of experiments (2219), we performed feature selection to maximize prediction performances by retaining the most informative genes. First, we removed 814 features which had null standard deviation. Then, we compared the performance of three different state-of-the-art ML algorithms, namely RF, MLP, and the linear model. The RF was grown with trees and , with M being the number of features and m the number of features sampled to grow each leaf within a tree. The MLP model was designed to have two hidden layers with 50 and 10 neurons, respectively, and a sigmoid activation function. The reliability of the models was estimated by a 5-fold CV procedure repeated 100 times.
7.1. Biological sex classification
For biological sex classification we filtered out features containing redundant information using a filter based on Pearson’s correlation (defined in (4)). In particular, we excluded a feature if its correlation with another feature was greater than (correlations in the range from to 1 are generally high). Also, we removed genes belonging to the Y chromosome. After these pre-processing steps we were left with 3127 features (genes) for downstream analyses. The remaining features were further filtered through two wrapper methods, the Boruta algorithm and the Stepwise Regression procedure based on the linear model yielding a subset of 21 informative features. In Table 1 we report the classification accuracy of the three tested models obtained through a 5-fold CV procedure. Although all models displayed an accuracy higher than 90% and no significant difference among tested methodologies were detected by the Kruskal–Wallis test [84], the RF and MLP appeared to be the most effective models, predicting biological sex with an accuracy higher than 97%.
7.2. Age regression
For age regression, we performed feature selection using the Boruta algorithm in two steps, followed by Stepwise Regression. First, we divided the set of 55388 features into 28 subsets with about 1978 features () and selected important features in each subset using the Boruta algorithm (thus obtaining 28 sets of important features). Second, we applied the Boruta to the union of these features subsets, which left us with a total of 184 important features. Then we performed Stepwise Regression to obtain 99 relevant genes which we used in model construction. The performance of RF, MLP and the linear model using these features are summarized in Table 5 and show that all tested learning methods give robust age predictions with minimal differences. Nonetheless, the RF model appeared to be the most accurate, predicting the age with MAE and RMSE errors of years and years, respectively. In addition, using MAE error values, the difference between the best performing algorithm and the worst one was just years, corresponding to a relative uncertainty of about 10%, a result proving the reliability and robustness of tested ML methods.
Table 5.
Summary table of regression performance measures of the three implemented learning models. Pearson’s correlation, RMSE and MAE are reported with the respective standard deviations.
| Learning models | Correlation | RMSE (years) | MAE (years) |
|---|---|---|---|
| Random Forest | |||
| MLP | |||
| Linear Model |
More figures representing results of age and biological sex prediction are available in the supplementary materials.
8. Summary and outlook
“Omic” sciences based on HTS methodologies are revolutionising the genomics world. HTS have enabled the production of huge amounts of data and their analysis requires novel bioinformatics and computational algorithms. In this context, machine learning and deep learning methods are emerging as indispensable tools for interpreting heterogeneous HTS data in a variety of genomic applications. Here we have provided an overview of the state of the art ML and DL methods for handling genomic data. Through a real life example we have shown the power of ML in predicting biological sex and age from a large dataset of gene expression values. However, the appropriate ML method for investigating a specific genomic task depends on the characteristics of the input data as well as on the biological question. In Table 6, we provide a summary of major advantages and disadvantages of the main ML methods described in this review, hoping that they can be of help in facilitating the choice of the appropriate algorithm. We foresee that AI technologies will accelerate novel discoveries in the area of genomics and become the gold standard for biomarkers selection and precision medicine in which multimodal data are prominent.
Table 6.
Major advantages and disadvantages of main learning models described in this work.
| Learning Method | Pros | Cons |
|---|---|---|
| Naive Bayes | It is simple, does not suffer from outliers, can deal with missing data, is recommended when there are many features and density estimation becomes unfeasible. | Assumes conditional independence of input variables given the output label. |
| Linear Discriminant Analysis | Works well on linearly discriminable data. Widely used for Dimensionality Reduction. | Assumes that features belonging to the same class have the same Gaussian distribution. Can be sensitive to outliers. |
| Linear regression | Usually the method of choice for small N and/or large M problems. Can be easily regularized with straightforward procedures. | Assumes linearity between features and output variables. |
| Logistic regression and softmax regression | Widely used in classification problems for its simplicity as a generalized linear model. Can be easily regularized with straightforward procedures. More robust to outliers compared to LDA. | Works well on linear problem. Its extension to non linear problems is computationally expensive and SVM is generally preferred. |
| Support Vector Machine | Works well on linear and nonlinear (Gaussian Kernel function) problems. | Not appropriate for large datasets where the number of features exceed the number of observations. |
| Perceptron learning and ANN | Can solve complex problems. | Difficult to tune due to the large number of parameters and of possible architectures. |
| Random Forest | Easy to tune. Robust to overfitting. Can provide an estimate of the importance of each feature in the model. | Can be slow as computation time increases linearly with the number of trees (inadequate for some real-time applications). |
| Deep Neural Networks | Able to solve complex problems. | Difficult to tune due to the large number of parameters/possible architectures. |
CRediT authorship contribution statement
Alfonso Monaco: Investigation, Formal analysis, Software, Writing - original draft. Ester Pantaleo: Investigation, Formal analysis, Software, Writing - original draft. Nicola Amoroso: Validation, Software, Writing - review & editing. Antonio Lacalamita: Validation, Software, Writing - review & editing. Claudio Lo Giudice: Validation, Data curation, Writing - original draft, Writing - review & editing. Adriano Fonzino: Validation, Resources, Writing - review & editing. Bruno Fosso: Validation, Resources, Writing - review & editing. Ernesto Picardi: Conceptualization, Writing - original draft, Writing - review & editing. Sabina Tangaro: Validation, Resources, Writing - review & editing. Graziano Pesole: Supervision, Writing - review & editing, Funding acquisition. Roberto Bellotti: Supervision, Writing - review & editing.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgements
This work was supported by the Italian node of ELIXIR (ELIXIR-IIB: the Italian Infrastructure for Bioinformatics). We also thank Maria Rosa Mirizzi, Barbara De Marzo, Annarita Armenise and Laura Marra for technical assistance.
References
- 1.McCarthy J. Basic questions. What is Artificial Intelligence?http://www-formal.stanford.edu/jmc/whatisai.html.
- 2.Reuter J.A., Spacek D.V., Snyder M.P. High-throughput sequencing technologies. Mol Cell. 2015;58(4):586–597. doi: 10.1016/j.molcel.2015.05.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Horner D.S., Pavesi G., Castrignanò T., De Meo P.D., Liuni S., Sammeth M., Picardi E., Pesole G. Bioinformatics approaches for genomics and post genomics applications of next-generation sequencing. Brief Bioinf. 2010;11(2):181–197. doi: 10.1093/bib/bbp046. Epub 2009 Oct 27. [DOI] [PubMed] [Google Scholar]
- 4.Mardis E.R. Next-generation DNA sequencing methods. Annu Rev Genomics Hum Genet. 2008;9:387–402. doi: 10.1146/annurev.genom.9.081307.164359. [DOI] [PubMed] [Google Scholar]
- 5.Tattini L., D’Aurizio R., Magi A. Detection of genomic structural variants from next-generation sequencing data. Front Bioeng Biotechnol. 2015;25(3):92. doi: 10.3389/fbioe.2015.00092. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Ho S.S., Urban A.E., Mills R.E. Structural variation in the sequencing era. Nat Rev Genet. 2020;21(3):171–189. doi: 10.1038/s41576-019-0180-9. Epub 2019 Nov 15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Barros-Silva D., Marques C.J., Henrique R., Jerónimo C. Profiling DNA methylation based on next-generation sequencing approaches: new insights and clinical applications. Genes (Basel) 2018;9(9):429. doi: 10.3390/genes9090429. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Blencowe B.J., Ahmad S., Lee L.J. Current-generation high-throughput sequencing: deepening insights into mammalian transcriptomes. Genes Dev. 2009;23(12):1379–1386. doi: 10.1101/gad.1788009. [DOI] [PubMed] [Google Scholar]
- 9.Helm M., Motorin Y. Detecting RNA modifications in the epitranscriptome: predict and validate. Nat Rev Genet. 2017;18(5):275–291. doi: 10.1038/nrg.2016.169. Epub 2017 Feb 20. [DOI] [PubMed] [Google Scholar]
- 10.Kim R.Y., Xu H., Myllykangas S., Ji H. Genetic-based biomarkers and next-generation sequencing: the future of personalized care in colorectal cancer. Per Med. 2011;8(3):331–345. doi: 10.2217/pme.11.16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Cirillo D., Valencia A. Big data analytics for personalized medicine. Curr Opin Biotechnol. 2019;58:161–167. doi: 10.1016/j.copbio.2019.03.004. Epub 2019 Apr 6. [DOI] [PubMed] [Google Scholar]
- 12.Xuan J., Yu Y., Qing T., Guo L., Shi L. Next-generation sequencing in the clinic: promises and challenges. Cancer Lett. 2013;340(2):284–295. doi: 10.1016/j.canlet.2012.11.025. Epub 2012 Nov 19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Alyass A., Turcotte M., Meyre D. From big data analysis to personalized medicine for all: challenges and opportunities. BMC Med Genomics. 2015;27(8):33. doi: 10.1186/s12920-015-0108-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Abadi M, et al. TensorFlow: Large-scale machine learning on heterogeneous systems, 2015. Software available from tensorflow.org.
- 15.Paszke A, Gross S, Massa F, Lerer A, Bradbury J, Chanan G, et al. PyTorch: An Imperative Style, High-Performance Deep Learning Library. In: Advances in Neural Information Processing Systems 32 [Internet]. Curran Associates, Inc.; 2019. p. 8024–35. Available from: http://papers.neurips.cc/paper/9015-pytorch-an-imperative-style-high-performance-deep-learning-library.pdf.
- 16.Kuhn M, et al. caret: Classification and Regression Training. R package version 6.0-71. 2016.https://CRAN.R-project.org/package=caret.
- 17.Hastie T., Tibshirani R., Friedman J. Springer New York Inc.; New York, NY, USA: 2001. The Elements of Statistical Learning. [Google Scholar]
- 18.Zhou Z.-H. A brief introduction to weakly supervised learning. National Sci Rev. 2018;5(1):44–53. [Google Scholar]
- 19.GTEx Consortium. The Genotype-Tissue Expression (GTEx) project. Nat Genet. 2013 Jun;45(6):580-5. doi: 10.1038/ng.2653. [DOI] [PMC free article] [PubMed]
- 20.Libbrecht M.W., Noble W.S. Machine learning applications in genetics and genomics. Nat Rev Genet. 2015;16(6):321–332. doi: 10.1038/nrg3920. Epub 2015 May 7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Down T., Leong B., Hubbard T.J. A machine learning strategy to identify candidate binding sites in human protein-coding sequence. BMC Bioinf. 2006;26(7):419. doi: 10.1186/1471-2105-7-419. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Holder L.B., Haque M.M., Skinner M.K. Machine learning for epigenetics and future medical applications. Epigenetics. 2017;12(7):505–514. doi: 10.1080/15592294.2017.1329068. Epub 2017 May 19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Zhu G., Deng W., Hu H., Ma R., Zhang S., Yang J., Peng J., Kaplan T., Zeng J. Reconstructing spatial organizations of chromosomes through manifold learning. Nucl Acids Res. 2018;46(8) doi: 10.1093/nar/gky065. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Chen K., Wei Z., Zhang Q., Wu X., Rong R., Lu Z., Su J., de Magalhães J.P., Rigden D.J., Meng J. WHISTLE: a high-accuracy map of the human N6-methyladenosine (m6A) epitranscriptome predicted using a machine learning approach. Nucl Acids Res. 2019;47(7) doi: 10.1093/nar/gkz074. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Petegrosso R., Li Z., Kuang R. Machine learning and statistical methods for clustering single-cell RNA-sequencing data. Brief Bioinf. 2020;21(4):1209–1223. doi: 10.1093/bib/bbz063. [DOI] [PubMed] [Google Scholar]
- 26.Haga H., Sato H., Koseki A., Saito T., Okumoto K., Hoshikawa K., Katsumi T., Mizuno K., Nishina T., Ueno Y. A machine learning-based treatment prediction model using whole genome variants of hepatitis C virus. PLoS One. 2020;15(11) doi: 10.1371/journal.pone.0242028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Madani Tonekaboni S.A., Beri G., Haibe-Kains B. Pathway-based drug response prediction using similarity identification in gene expression. Front Genet. 2020;9(11):1016. doi: 10.3389/fgene.2020.01016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Cole JR, Wang Q, Fish JA, Chai B, McGarrell DM, Sun Y, Brown CT, Porras-Alfaro A, Kuske CR, Tiedje JM. Ribosomal Database Project: data and tools for high throughput rRNA analysis. Nucleic Acids Res. 2014 Jan; 42(Database issue):D633–42. doi: 10.1093/nar/gkt1244. Epub 2013 Nov 27. [DOI] [PMC free article] [PubMed]
- 29.Wang Q., Garrity G.M., Tiedje J.M., Cole J.R. Naive Bayesian classifier for rapid assignment of rRNA sequences into the new bacterial taxonomy. Appl Environ Microbiol. 2007;73(16):5261–5267. doi: 10.1128/AEM.00062-07. Epub 2007 Jun 22. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Bolyen E. Reproducible, interactive, scalable and extensible microbiome data science using QIIME 2. Nat Biotechnol. 2019;37(8):852–857. doi: 10.1038/s41587-019-0209-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Bokulich N.A., Kaehler B.D., Rideout J.R., Dillon M., Bolyen E., Knight R., Huttley G.A., Gregory Caporaso J. Optimizing taxonomic classification of marker-gene amplicon sequences with QIIME 2’s q2-feature-classifier plugin. Microbiome. 2018;6(1):90. doi: 10.1186/s40168-018-0470-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Shugay M, Ortiz de Mendíbil I, Vizmanos JL, Novo FJ. Oncofuse: a computational framework for the prediction of the oncogenic potential of gene fusions. Bioinformatics 2013 Oct 15;29(20):2539–46. doi: 10.1093/bioinformatics/btt445. Epub 2013 Aug 16. [DOI] [PubMed]
- 33.Boloc D., Gortat A., Cheng-Zhang J.Q., García-Cerro S., Rodríguez N., Parellada M., Saiz-Ruiz J., Cuesta M.J., Gassó P., Lafuente A., Bernardo M., Mas S. Improving pharmacogenetic prediction of extrapyramidal symptoms induced by antipsychotics. Transl Psychiatry. 2018;8(1):276. doi: 10.1038/s41398-018-0330-4. Erratum. In: Transl Psychiatry. 2019 May 2;9(1):145. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.https://scikit-learn.org/stable/auto_examples/classification/plot_classifier_comparison.html.
- 35.Zhang H., Bredewold E.O.W., Vreeken D., Duijs J.M.G.J., de Boer H.C., Kraaijeveld A.O., Jukema J.W., Pijls N.H., Waltenberger J., Biessen E.A.L., van der Veer E.P., van Zonneveld A.J., van Gils J.M. Prediction power on cardiovascular disease of neuroimmune guidance cues expression by peripheral blood monocytes determined by machine-learning methods. Int J Mol Sci. 2020;21(17):6364. doi: 10.3390/ijms21176364. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Moroni F., Ammirati E., Norata G.D., Magnoni M., Camici P.G. The Role of Monocytes and Macrophages in Human Atherosclerosis, Plaque Neoangiogenesis, and Atherothrombosis. Mediators Inflamm. 2019;4(2019):7434376. doi: 10.1155/2019/7434376. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Segata N., Izard J., Waldron L. Metagenomic biomarker discovery and explanation. Genome Biol. 2011;12:R60. doi: 10.1186/gb-2011-12-6-r60. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Tibshirani R. Regression shrinkage and selection via the lasso. J R Stat Soc: Ser B (Methodological) 1996;58(1):267–288. [Google Scholar]
- 39.Xiong Y., Ling Q.H., Han F., Liu Q.H. An efficient gene selection method for microarray data based on LASSO and BPSO. BMC Bioinf. 2019;20(Suppl 22):715. doi: 10.1186/s12859-019-3228-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Nyberg K.D., Bruce S.L., Nguyen A.V., Chan C.K., Gill N.K., Kim T.H., Sloan E.K., Rowat A.C. Predicting cancer cell invasion by single-cell physical phenotyping. Integr Biol (Camb) 2018;10(4):218–231. doi: 10.1039/c7ib00222j. [DOI] [PubMed] [Google Scholar]
- 41.Wang J., Wang L. Prediction and prioritization of autism-associated long non-coding RNAs using gene expression and sequence features. BMC Bioinf. 2020;21(1):505. doi: 10.1186/s12859-020-03843-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Torang A., Gupta P., Klinke D.J., 2nd An elastic-net logistic regression approach to generate classifiers and gene signatures for types of immune cells and T helper cell subsets. BMC Bioinf. 2019;20(1):433. doi: 10.1186/s12859-019-2994-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Beretta S., Castelli M., Gonçalves I., Kel I., Giansanti V., Merelli I. Improving eQTL analysis using a machine learning approach for data integration: a logistic model tree solution. J Comput Biol. 2018;25(10):1091–1105. doi: 10.1089/cmb.2017.0167. Epub 2018 Jul 27. [DOI] [PubMed] [Google Scholar]
- 44.Hao Y., Duh Q.Y., Kloos R.T. Identification of Hürthle cell cancers: solving a clinical challenge with genomic sequencing and a trio of machine learning algorithms. BMC Syst Biol. 2019;13:27. doi: 10.1186/s12918-019-0693-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Sung J.Y., Shin H.T., Sohn K.A., Shin S.Y., Park W.Y., Joung J.G. Assessment of intratumoral heterogeneity with mutations and gene expression profiles. PLoS One. 2019;14(7) doi: 10.1371/journal.pone.0219682. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Orange DE, Agius P, DiCarlo EF, Robine N, Geiger H, Szymonifka J, McNamara M, Cummings R, Andersen KM, Mirza S, Figgie M, Ivashkiv LB, Pernis AB, Jiang CS, Frank MO, Darnell RB, Lingampali N, Robinson WH, Gravallese E; Accelerating Medicines Partnership in Rheumatoid Arthritis and Lupus Network, Bykerk VP, Goodman SM, Donlin LT. Identification of Three Rheumatoid Arthritis Disease Subtypes by Machine Learning Integration of Synovial Histologic Features and RNA Sequencing Data. Arthritis Rheumatol. 2018 May; 70(5):690–701. doi: 10.1002/art.40428. Epub 2018 Apr 2. [DOI] [PMC free article] [PubMed]
- 47.Kim S., Park T., Kon M. Cancer survival classification using integrated data sets and intermediate information. Artif Intell Med. 2014;62(1):23–31. doi: 10.1016/j.artmed.2014.06.003. Epub 2014 Jun 21. [DOI] [PubMed] [Google Scholar]
- 48.Cybenko G. Approximation by superpositions of a sigmoidal function. Math Control Signals Syst. 1989;2(4):303–314. [Google Scholar]
- 49.Wang J., Yang B., An Y., Marquez-Lago T., Leier A., Wilksch J., Hong Q., Zhang Y., Hayashida M., Akutsu T., Webb G.I., Strugnell R.A., Song J., Lithgow T. Systematic analysis and prediction of type IV secreted effector proteins by machine learning approaches. Brief Bioinf. 2019;20(3):931–951. doi: 10.1093/bib/bbx164. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Arai F., Stumpf P.S., Ikushima Y.M., Hosokawa K., Roch A., Lutolf M.P., Suda T., MacArthur B.D. Machine Learning of Hematopoietic Stem Cell Divisions from Paired Daughter Cell Expression Profiles Reveals Effects of Aging on Self-Renewal. Cell Syst. 2020;11(6):640–652.e5. doi: 10.1016/j.cels.2020.11.004. Epub 2020 Dec 8. [DOI] [PubMed] [Google Scholar]
- 51.Friedman J., Hastie T., Tibshirani R. Additive logistic regression: a statistical view of boosting. Ann Stat. 2000;28 337–407:MR1790002. [Google Scholar]
- 52.Freund, Y., Schapire, R. 1996. Experiments with a new boosting algorithm. In Machine Learning: Proceedings of the Thirteenth International Conference 148-156. Morgan Kaufman, San Francisco
- 53.Maniruzzaman M., Jahanur Rahman M., Ahammed B., Abedin M.M., Suri H.S., Biswas M., El-Baz A., Bangeas P., Tsoulfas G., Suri J.S. Statistical characterization and classification of colon microarray gene expression data using multiple machine learning paradigms. Comput Methods Programs Biomed. 2019;176:173–193. doi: 10.1016/j.cmpb.2019.04.008. Epub 2019 Apr 10. [DOI] [PubMed] [Google Scholar]
- 54.Breiman L. Random forests Mach Learn. 2001;45(1):5–32. [Google Scholar]
- 55.Teng S, Yang JY, Wang L. Genome-wide prediction and analysis of human tissue-selective genes using microarray expression data. BMC Med Genomics. 2013;6 Suppl 1(Suppl 1):S10. doi: 10.1186/1755-8794-6-S1-S10. Epub 2013 Jan 23. [DOI] [PMC free article] [PubMed]
- 56.Aevermann B.D., Novotny M., Bakken T., Miller J.A., Diehl A.D., Osumi-Sutherland D., Lasken R.S., Lein E.S., Scheuermann R.H. Cell type discovery using single-cell transcriptomics: implications for ontological representation. Hum Mol Genet. 2018;27(R1):R40–R47. doi: 10.1093/hmg/ddy100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Asnicar F., Berry S.E., Valdes A.M. Microbiome connections with host metabolism and habitual diet from 1,098 deeply phenotyped individuals. Nat Med. 2021;27:321–332. doi: 10.1038/s41591-020-01183-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Berry S. et al. Personalised REsponses to DIetary Composition Trial (PREDICT): an intervention study to determine inter-individual differences in postprandial response to foods, 2020. Preprint at https://protocolexchange.researchsquare.com/article/pex-802/v1.
- 59.Cheng X., Cai H., Zhang Y., Xu B., Su W. Optimal combination of feature selection and classification via local hyperplane based learning strategy. BMC Bioinf. 2015;10(16):219. doi: 10.1186/s12859-015-0629-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Lee K., Kim B., Choi Y., Kim S., Shin W., Lee S., Park S., Kim S., Tan A.C., Kang J. Deep learning of mutation-gene-drug relations from the literature. BMC Bioinf. 2018;19(1):21. doi: 10.1186/s12859-018-2029-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Wu L., Liu X., Xu J. HetEnc: a deep learning predictive model for multi-type biological dataset. BMC Genomics. 2019;20(1):638. doi: 10.1186/s12864-019-5997-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Lin C., Jain S., Kim H., Bar-Joseph Z. Using neural networks for reducing the dimensions of single-cell RNA-Seq data. Nucl Acids Res. 2017;45(17) doi: 10.1093/nar/gkx681. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Matsubara T., Ochiai T., Hayashida M., Akutsu T., Nacher J.C. Convolutional neural network approach to lung cancer classification integrating protein interaction network and gene expression profiles. J Bioinform Comput Biol. 2019;17(3):1940007. doi: 10.1142/S0219720019400079. [DOI] [PubMed] [Google Scholar]
- 64.Metrichor. Oxford Nanopore Technologies. 2017. https://nanoporetech.com/products/metrichor.
- 65.Nanonet. Oxford Nanopore Technologies. 2017. https://github.com/nanoporetech/nanonet.
- 66.Boža V., Brejová B., Vinař T. DeepNano: deep recurrent neural networks for base calling in MinION nanopore reads. PLoS One. 2017;12(6) doi: 10.1371/journal.pone.0178751. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Al-Shaer A.E., Flentke G.R., Berres M.E., Garic A., Smith S.M. Exon level machine learning analyses elucidate novel candidate miRNA targets in an avian model of fetal alcohol spectrum disorder. PLoS Comput Biol. 2019;15(4) doi: 10.1371/journal.pcbi.1006937. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Monaco A., Amoroso N., Bellantuono L., Lella E., Lombardi A., Monda A., Tateo A. Shannon entropy approach reveals relevant genes in Alzheimer’s disease. PloS One. 2019;14(12) doi: 10.1371/journal.pone.0226190. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Monaco A., Pantaleo E., Amoroso N., Bellantuono L., Lombardi A., Tateo A. Identifying potential gene biomarkers for Parkinson’s disease through an information entropy based approach. Phys. Biol. 2020;18 doi: 10.1088/1478-3975/abc09a. [DOI] [PubMed] [Google Scholar]
- 70.Lemsara A., Ouadfel S., Fröhlich H. PathME: pathway based multi-modal sparse autoencoders for clustering of patient-level multi-omics data. BMC Bioinf. 2020;21(1):146. doi: 10.1186/s12859-020-3465-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Badsha M.B., Li R., Liu B., Li Y.I., Xian M., Banovich N.E., Fu A.Q. Imputation of single-cell gene expression with an autoencoder neural network. Quant Biol. 2020;8(1):78–94. doi: 10.1007/s40484-019-0192-7. Epub 2020 Jan 22. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Goodfellow I.J., Pouget-Abadie J., Mirza M., Xu B., Warde-Farley D., Ozair S., Courville A., Bengio Y. vol. 2. MIT Press; Cambridge, MA, USA: 2014. Generative adversarial nets; pp. 2672–2680. (Proceedings of the 27th International Conference on Neural Information Processing Systems). [Google Scholar]
- 73.Targonski C., Bender M.R., Shealy B.T., Husain B., Paseman B., Smith M.C., Feltus F.A. Cellular State Transformations Using Deep Learning for Precision Medicine Applications. Patterns (N Y). 2020;1(6) doi: 10.1016/j.patter.2020.100087. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Park J., Kim H., Kim J., Cheon M. A practical application of generative adversarial networks for RNA-seq analysis to predict the molecular progress of Alzheimer’s disease. PLoS Comput Biol. 2020;16(7) doi: 10.1371/journal.pcbi.1008099. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Mirakhorli J., Amindavar H., Mirakhorli M. A new method to predict anomaly in brain network based on graph deep learning. Rev Neurosci. 2020;31(6):681–689. doi: 10.1515/revneuro-2019-0108. [DOI] [PubMed] [Google Scholar]
- 76.Imani M, Braga-Neto UM. Control of Gene Regulatory Networks Using Bayesian Inverse Reinforcement Learning. IEEE/ACM Trans Comput Biol Bioinform. 2019 Jul-Aug;16(4):1250–1261. doi: 10.1109/TCBB.2018.2830357. Epub 2018 Apr 26. [DOI] [PubMed]
- 77.Sirin U, Polat F, Alhajj R. Batch Mode TD for Controlling Partially Observable Gene Regulatory Networks. IEEE/ACM Trans Comput Biol Bioinform. 2017 Nov-Dec;14(6):1214–1227. doi: 10.1109/TCBB.2016.2595577. Epub 2016 Jul 28. [DOI] [PubMed]
- 78.Bermingham M.L., Pong-Wong R., Spiliopoulou A., Hayward C., Rudan I., Campbell H. Application of high-dimensional feature selection: evaluation for genomic prediction in man. Scientific Rep. 2015;5:10312. doi: 10.1038/srep10312. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Guyon I., Elisseeff A. An introduction to variable and feature selection. J Mach Learn Res. 2003;3:1157–1182. [Google Scholar]
- 80.Kohavi R., John G.H. Wrappers for feature subset selection. Artif Intell. 1997;97(1–2):273–324. [Google Scholar]
- 81.Zhang Y., Li S., Wang T., Zhang Z. Divergence based feature selection for separate classes. Neurocomputing. 2013;101:32–42. [Google Scholar]
- 82.Kursa M.B., Rudnicki W.R. Feature selection with the Boruta package. J Stat Software. 2010;36(11):1–13. [Google Scholar]
- 83.Saghapour E., Kermani S., Sehhati M. A novel feature ranking method for prediction of cancer stages using proteomics data. PloS One. 2017;12(9) doi: 10.1371/journal.pone.0184203. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84.Kruskal W.H., Wallis W.A. Use of ranks in one-criterion variance analysis. J Am Stat Assoc. 1952;47:583–621. [Google Scholar]