Global and Simultaneous Hypothesis Testing for High-Dimensional Logistic Regression Models

Abstract

High-dimensional logistic regression is widely used in analyzing data with binary outcomes. In this paper, global testing and large-scale multiple testing for the regression coefficients are considered in both single- and two-regression settings. A test statistic for testing the global null hypothesis is constructed using a generalized low-dimensional projection for bias correction and its asymptotic null distribution is derived. A lower bound for the global testing is established, which shows that the proposed test is asymptotically minimax optimal over some sparsity range. For testing the individual coefficients simultaneously, multiple testing procedures are proposed and shown to control the false discovery rate (FDR) and falsely discovered variables (FDV) asymptotically. Simulation studies are carried out to examine the numerical performance of the proposed tests and their superiority over existing methods. The testing procedures are also illustrated by analyzing a data set of a metabolomics study that investigates the association between fecal metabolites and pediatric Crohn’s disease and the effects of treatment on such associations.

1. INTRODUCTION

Logistic regression models have been applied widely in genetics, finance, and business analytics. In many modern applications, the number of covariates of interest usually grows with, and sometimes far exceeds, the number of observed samples. In such high-dimensional settings, statistical problems such as estimation, hypothesis testing, and construction of confidence intervals become much more challenging than those in the classical low-dimensional settings. The increasing technical difficulties usually emerge from the non-asymptotic analysis of both statistical models and the corresponding computational algorithms.

In this paper, we consider testing for high-dimensional logistic regression model:

$$\text{log}\left(\frac{{\pi }_i}{1-{\pi }_i}\right)=X_i^{\top }\beta ,\text{ for }i=1,\dots ,n.$$ (1)

where $\beta \in {ℝ}^p$ is the vector of regression coefficients. The observations are i.i.d. samples Z_i = (y_i,X_i) for i = 1,..,n, and we assume y_i | X_i ~ Bernoulli(π_i) independently for each i = 1, …, n.

1.1. Global and Simultaneous Hypothesis Testing

It is important in high-dimensional logistic regression to determine 1) whether there are any associations between the covariates and the outcome and, if yes, 2) which covariates are associated with the outcome. The first question can be formulated as testing the global null hypothesis H₀:β = 0; and the second question can be considered as simultaneously testing the null hypotheses H_0,i:β_i = 0 for i = 1, …, p. Besides such single logistic regression problems, hypothesis testing involving two logistic regression models with regression coefficients β⁽¹⁾ and β² in ${ℝ}^p$ is also important. Specifically, one is interested in testing the global null hypothesis H₀:β⁽¹⁾ = β⁽²⁾, or identifying the differentially associated covariates through simultaneously testing the null hypotheses $H_{0,i}:{\beta }_i^{(1)}={\beta }_i^{(2)}$ for each i = 1, …, p.

Estimation for high-dimensional logistic regression has been studied extensively. van de Geer (2008) considered high-dimensional generalized linear models (GLMs) with Lipschitz loss functions, and proved a non-asymptotic oracle inequality for the empirical risk minimizer with the Lasso penalty. Meier, van de Geer, and Bühlmann (2008) studied the group Lasso for logistic regression and proposed an efficient algorithm that leads to statistically consistent estimates. Negahban et al. (2010) obtained the rate of convergence for the ${\mathcal{l}}_1$-regularized maximum likelihood estimator under GLMs using restricted strong convexity property. Bach (2010) extended tools from the convex optimization literature, namely self-concordant functions, to provide interesting extensions of theoretical results for the square loss to the logistic loss. Plan and Vershynin (2013) connected sparse logistic regression to one-bit compressed sensing and developed a unified theory for signal estimation with noisy observations.

In contrast, hypothesis testing and confidence intervals for high-dimensional logistic regression have only been recently addressed. van de Geer et al. (2014) considered constructing confidence intervals and statistical tests for single or low-dimensional components of the regression coefficients in high-dimensional GLMs. Mukherjee, Pillai, and Lin (2015) studied the detection boundary for minimax hypothesis testing in high-dimensional sparse binary regression models when the design matrix is sparse. Belloni, Chernozhukov, and Wei (2016) considered estimating and constructing the confidence regions for a regression coefficient of primary interest in GLMs. More recently, Sur, Chen, and Candès (2017) and Sur and Candès (2019) considered the likelihood ratio test for high-dimensional logistic regression under the setting that p / n → κ for some constant κ < 1 / 2, and showed that the asymptotic null distribution of the log-likelihood ratio statistic is a rescaled χ² distribution. Cai et al. (2017) proposed a global test and a multiple testing procedure for differential networks against sparse alternatives under the Markov random field model. Nevertheless, the problems of global testing and large-scale simultaneous testing for high-dimensional logistic regression models with p ≳ n remain unsolved.

In this paper, we first consider global and multiple testing for a single high-dimensional logistic regression model. The global test statistic is constructed as the maximum of squared standardized statistics for individual coefficients, which are based on a two-step standardization procedure. The first step is to correct the bias of the logistic Lasso estimator using a generalized low-dimensional projection (LDP) method, and the second step is to normalize the resulting nearly unbiased estimators by their estimated standard errors. We show that the asymptotic null distribution of the test statistic is a Gumbel distribution and that the resulting test is minimax optimal under the Gaussian design by establishing the minimax separation distance between the null space and alternative space. For large-scale multiple testing, data-driven testing procedures are proposed and shown to control the false discovery rate (FDR) and falsely discovered variables (FDV) asymptotically. The framework for testing for single logistic regression is then extended to the setting of testing two logistic regression models.

The main contributions of the present paper are threefold.

1. We propose novel procedures for both the global testing and large-scale simultaneous testing for high dimensional logistic regressions. The dimension p is allowed to be much larger than the sample size n. Specifically, we require $\text{log}p=O\left(n^{c_1}\right)$ for the global test and $p=O\left(n^{c_2}\right)$ for the multiple testing procedure, with some constant c₁, c₂ > 0. For the global alternatives characterized by the ${\mathcal{l}}_{\infty }$ norm of the regression coefficients, the global test is shown to be minimax rate optimal with the optimal separation distance of order $\sqrt{\text{log}p/n}$.

2. Following similar ideas in Ren, Zhang, and Zhou (2016) and Cai et al. (2017), our construction of the test statistics depends on a generalized version of the LDP method for bias correction. The original LDP method (Zhang and Zhang 2014) relies on the linearity between the covariates and outcome variable. For logistic regression, the generalized approach first finds a linearization of the regression function, and the weighted LDP is then applied. Besides its usefulness in logistic regression, the generalized LDP method is flexible and can be applied to other nonlinear regression problems (see Section 7 for a detailed discussion).

3. The minimax lower bound is obtained for the global hypothesis testing under the Gaussian design. The lower bound depends on the calculation of the χ²-divergence between two logistic regression models. To the best of our knowledge, this is the first lower bound result for high-dimensional logistic regression under the Gaussian design.

1.2. Other Related Work

We should note that a different but related problem, namely inference for high-dimensional linear regression, has been well studied in the literature. Zhang and Zhang (2014), van de Geer et al. (2014) and Javanmard and Montanari (2014a,b) considered confidence intervals and testing for low-dimensional parameters of the high-dimensional linear regression model and developed methods based on a two-stage debiased estimator that corrects the bias introduced at the first stage due to regularization. Cai and Guo (2017) studied minimaxity and adaptivity of confidence intervals for general linear functionals of the regression vector.

The problems of global testing and large-scale simultaneous testing for high-dimensional linear regression have been studied by Liu and Luo (2014), Ingster, Tsybakov, and Verzelen (2010) and more recently by Xia, Cai, and Cai (2018) and Javanmard and Javadi (2019). However, due to the nonlinearity and the binary outcome, the approaches used in these works cannot be directly applied to logistic regression problems. In the Markov random field setting, Ren, Zhang, and Zhou (2016) and Cai et al. (2017) constructed pivotal/test statistics based on the debiased LDP estimators for node-wise logistic regressions with binary covariates. However, the results for sparse high-dimensional logistic regression models with general continuous covariates remain unknown.

Other related problems include joint testing and false discovery rate control for high-dimensional multivariate regression (Xia, Cai, and Li 2018) and testing for high-dimensional precision matrices and Gaussian graphical models (Liu 2013; Xia, Cai, and Cai 2015), where the inverse regression approach and de-biasing were carried out in the construction of the test statistics. Such statistics were then used for testing the global null with extreme value type asymptotic null distributions or to perform multiple testing that controls the false discovery rate.

1.3. Organization of the Paper and Notations

The rest of the paper is organized as follows. In Section 2, we propose the global test and establish its optimality. Some comparisons with existing works are made in detail. In Section 3, we present the multiple testing procedures and show that they control the FDR/FDP or FDV/FWER asymptotically. The framework is extended to the two-sample setting in Section 4. In Section 5, the numerical performance of the proposed tests are evaluated through extensive simulations. In Section 6, the methods are illustrated by an analysis of a metabolomics study. Further extensions and related problems are discussed in Section 7. In Section 8, some of the main theorems are proved. The proofs of other theorems as well as technical lemmas, and some further discussions are collected in the online Supplementary Materials.

Throughout our paper, for a vector $a={\left(a_1,\dots ,a_n\right)}^{\top }\in {ℝ}^n$, we define the ${\mathcal{l}}_p$ norm $\Vert a{\Vert }_p={\left(\sum _{i=1}^n{a}_i^p\right)}^{1/p}$, and the ${\mathcal{l}}_{\infty }$ norm $\Vert a{\Vert }_{\infty }={\text{max}}_{1\le j\le n}|a_i|$. $a_{-j}\in {ℝ}^{n-1}$ stands for the subvector of a without the j the component. We denote diag(a₁, …, a_n) as the n × n diagonal matrix whose diagonal entries are a₁, …, a_n. For a matrix $A\in {ℝ}^{p\times q}$, λi (A) stands for the i-th largest singular value of A and λ_max (A) = λ₁ (A), λ_min (A) = λ_p^q (A). For a smooth function f(x) defined on $ℝ$, we denote $\dot{f}(x)=df(x)/dx$ and $\ddot{f}(x)=d^{2}f(x)/d{x}^2$. Furthermore, for sequences {a_n} and {b_n}, we write a_n = o(b_n) if $\underset{n}{\text{lim}}{a}_n/b_n=0$, and write a_n = O(b_n), a_n ≲ b_n or b_n ≳ a_n if there exists a constant C such that a_n ≤ Cb_n for all n. We write a_n ≍ b_n if a_n ≲ b_n and a_n ≳ b_n. For a set A, we denote |A| as its cardinality. Lastly, C, C₀, C₁, … are constants that may vary from place to place.

2. GLOBAL HYPOTHESIS TESTING

In this section, we consider testing the global null hypotheses

$$H_0:\beta =0\text{ vs}.H_1:\beta \ne 0,$$

under the logistic regression model with random designs. The global testing problem corresponds to the detection of any associations between the covariates and the outcome.

Our construction of the global testing procedure begins with a bias-corrected estimator built upon a regularized estimator such as the ${\mathcal{l}}_1$-regularized M-estimator. For high-dimensional logistic regression, the ${\mathcal{l}}_1$-regularized M-estimator is defined as

$$\widehat{\beta }=\underset{\beta }{\text{argmin}}\left\{\frac{1}{n}\sum _{i=1}^n\left[-y_i{\beta }^{\top }{X}_i+\text{log}\left(1+e^{{\beta }^{\top }{X}_i}\right)\right]+\lambda \Vert \beta {\Vert }_1\right\},$$ (2)

which is the minimizer of a penalized log-likelihood function. Negahban et al. (2010) showed that, when X_i are i.i.d. sub-gaussian, under some mild regularity conditions, standard high-dimensional estimation error bounds for $\widehat{\beta }$ under the ${\mathcal{l}}_1$ or ${\mathcal{l}}_2$ norm can be obtained by choosing $\lambda \asymp \sqrt{\text{log}p/n}$. Once we obtain the initial estimator $\widehat{\beta }$, our next step is to correct the bias of $\widehat{\beta }$.

For technical reasons, we split the samples so that the initial estimation step and the bias correction step are conducted on separate and independent datasets. Without loss of generality, we assume there are 2n samples, divided into two subsets ${\mathcal{D}}_1$ and ${\mathcal{D}}_2$, each with n independent samples. The initial estimator $\widehat{\beta }$ is obtained from ${\mathcal{D}}_1$. In the following, we construct a nearly unbiased estimator $\check{\beta }$ based on $\widehat{\beta }$ and the samples from ${\mathcal{D}}_2$, using the generalized LDP approach. Throughout the paper, the samples Z_i = (X_i, Y_i), i = 1, …, n, are from ${\mathcal{D}}_2$, which are independent of $\widehat{\beta }$. We would like to emphasize that the sample splitting procedure is only used to simplify our theoretical analysis, which does not make it a restriction for practical applications. Numerically, as our simulations in Section 5 show, sample splitting is in fact not needed in order for our methods perform well (see further discussions in Section 7).

2.1. Construction of the Test Statistic via Generalized Low-Dimensional Projection

Let X be the design matrix whose i-th row is X_i. We rewrite the logistic regression model defined by (1) as

$$y_i=f\left({\beta }^{\top }{X}_i\right)+{ϵ}_i$$ (3)

where f (u) = e^u / (1 + e^u) and ϵ_i is error term. To correct the bias of the initial estimator $\widehat{\beta }$, we consider the Taylor expansion of f (u_i) at ${\widehat{u}}_i$ for u_i = β^⊤ X_i and ${\widehat{u}}_i={\widehat{\beta }}^{\top }{X}_i$

$$f\left(u_i\right)=f\left({\widehat{u}}_i\right)+\dot{f}\left({\widehat{u}}_i\right)\left(u_i-{\widehat{u}}_i\right)+R{e}_i$$

where Re_i is the reminder term. Plug this into the regression model (3), we have

$$y_i-f\left({\widehat{u}}_i\right)+\dot{f}\left({\widehat{u}}_i\right)X_i^{\top }\widehat{\beta }=\dot{f}\left({\widehat{u}}_i\right)X_i^{\top }\beta +\left(R{e}_i+{ϵ}_i\right).$$ (4)

By rewriting the logistic regression model as (4), we can treat $y_i-f\left({\widehat{u}}_i\right)+\dot{f}\left({\widehat{u}}_i\right)X_i^{\top }\widehat{\beta }$ on the left hand side as the new response variable, whereas $\dot{f}\left({\widehat{u}}_i\right)X_i$ as the new covariates and Re_i + ϵ_i as the noise. Consequently, β can be considered as the regression coefficient of this approximate linear model.

The bias-corrected estimator, or, the generalized LDP estimator $\check{\beta }$ is defined as

$${\check{\beta }}_j={\widehat{\beta }}_j+\frac{\sum _{i=1}^n{v}_{ij}\left(y_i-f\left({\widehat{\beta }}^{\top }{X}_i\right)\right)}{\sum _{i=1}^n{v}_{ij}\dot{f}\left({\widehat{\beta }}^{\top }{X}_i\right)X_{ij}},j=1,\dots ,p,$$ (5)

where X_ij is the j-th component of X_i and v_j = (v_1j, v_2j, …, v_nj) is the score vector that will be determined carefully (Ren, Zhang, and Zhou 2016; Cai et al. 2017). More specifically, we define the weighted inner product 〈·,·〉_n for any $a,b\in {ℝ}^n$ as ${\langle a,b\rangle }_n=\sum _{i=1}^n\dot{f}\left({\widehat{u}}_i\right)a_i{b}_i$, and denote 〈·,·〉 as the ordinary inner product defined in Euclidean space. Combining (4) and (5), we can write

$${\check{\beta }}_j-{\beta }_j=\frac{\langle v_j,ϵ\rangle }{{\langle v_j,x_j\rangle }_n}+\frac{\langle v_j,Re\rangle }{{\langle v_j,x_j\rangle }_n}-\frac{{\langle v_j,h_{-j}\rangle }_n}{{\langle v_j,x_j\rangle }_n},$$ (6)

where $x_j\in {ℝ}^n$ denote the j-th column of X, $h_{-j}=X_{-j}\left({\widehat{\beta }}_{-j}-{\beta }_{-j}\right)$ where $X_{-j}\in {ℝ}^n\times {ℝ}^{p-1}$ is the submatrix of X without the j-th column, and Re = (Re₁, …, Re_n) with $R{e}_i=f\left(u_i\right)-f\left({\widehat{u}}_i\right)-\dot{f}\left({\widehat{u}}_i\right)\left(u_i-{\widehat{u}}_i\right)$. We will construct score vector v_j so that the first term on the right hand side of (6) is asymptotically normal, while the second and third terms, which together contribute to the bias of the generalized LDP estimator ${\widehat{\beta }}_j$, are negligible.

To determine the score vector v_j efficiently, we consider the following node-wise regression among the covariates

$$x_j=X_{-j}{\gamma }_j+{\eta }_j,j=1,\dots ,p,$$ (7)

where ${\gamma }_j=\text{arg}{\text{min}}_{\gamma \in {ℝ}^{p-1}}\mathbb{E}\left[\Vert x_j-X_{-j}\gamma {\Vert }_2^2\right]$ and η_j is the error term. Intuitively, if we set $v_j={\widehat{W}}^{-1}{\eta }_j$ for $\widehat{W}=\text{diag}\left(\dot{f}\left({\widehat{u}}_1\right),\dots ,\dot{f}\left({\widehat{u}}_n\right)\right)$, then it should follow that

$${\langle v_j,h_{-j}\rangle }_n\le \underset{k\ne j}{\text{max}}|{\langle v_j,x_k\rangle }_n|\cdot \Vert \widehat{\beta }-\beta {\Vert }_1=\underset{k\ne j}{\text{max}}|\langle {\eta }_j,x_k\rangle |\cdot \Vert \widehat{\beta }-\beta {\Vert }_1\approx 0.$$

In practice, we use the node-wise Lasso to obtain an estimate of η_j. For X from ${\mathcal{D}}_2$ and $\widehat{\beta }$ obtained from ${\mathcal{D}}_1$, the score v_j is obtained by calibrating the Lasso-generated residue ${\widehat{\eta }}_j$, i.e.

$$\begin{gathered} v_j(\lambda )={\widehat{W}}^{-1}{\widehat{\eta }}_j(\lambda ),{\widehat{\eta }}_j(\lambda )=x_j-X_{-j}{\widehat{\gamma }}_j(\lambda ), \\ {\widehat{\gamma }}_j(\lambda )=\underset{b}{\text{argmin}}\left\{\frac{\Vert x_j-X_{-j}b{\Vert }_2^2}{2n}+\lambda \Vert b{\Vert }_1\right\}. \end{gathered}$$ (8)

Clearly, v_j (λ) depends on the tuning parameter λ. Define the following quantities

$${\zeta }_j(\lambda )=\underset{k\ne j}{\text{max}}\frac{|{\langle v_j(\lambda ),x_k\rangle }_n|}{\Vert v_j(\lambda ){\Vert }_n},{\tau }_j(\lambda )=\frac{\Vert v_j(\lambda ){\Vert }_n}{|{\langle v_j(\lambda ),x_j\rangle }_n|}.$$ (9)

The tuning parameter λ can be determined through ζ_j (λ) and τ_j (λ) by the algorithm in Table 1, which is adapted from the algorithm in Zhang and Zhang (2014).

Table 1.

Computation of v_j from the Lasso (8)

Input:	An upper bound ${\zeta }_j^{*}$ for ζj with default value ${\zeta }^{*}=\sqrt{2\text{log}p}$,
	tuning parameters κ0 ∈[0,1] and κ1 ∈(0,1];
Step 1:	If ${\zeta }_j(\lambda )>{\zeta }_j^{*}$ for all λ = 0, set ${\zeta }_j^{*}=\left(1+{\kappa }_1\right)\underset{\lambda >0}{\text{inf}}{\zeta }_j(\lambda )$;
	$\lambda \leftarrow \text{max}\left\{\lambda :{\zeta }_j(\lambda )\le {\zeta }_j^{*}\right\},{\zeta }_j^{*}\leftarrow {\zeta }_j(\lambda ),{\tau }_j^{*}\leftarrow {\tau }_j(\lambda );$
Step 2:	${\lambda }_j\leftarrow \text{min}\left\{\lambda :{\tau }_j(\lambda )\le \left(1+{\kappa }_0\right){\tau }_j^{*}\right\};$
	vi ← vj(λj), τj ← τj(λj), ζj ← ζj(λj)
Input:	An upper bound ${\zeta }_j^{*}$ for ζj with default value ${\zeta }^{*}=\sqrt{2\text{log}p}$,
Output:	λj, vj, τj, ζj

Once ${\check{\beta }}_j$ and τ_j are obtained, we define the standardized statistics

$$M_j={\check{\beta }}_j/{\tau }_j,$$

for j = 1, …, p. The global test statistic is then defined as

$$M_n=\underset{1\le j\le p}{\text{max}}{M}_j^2.$$ (10)

2.2. Asymptotic Null Distribution

We now turn to the analysis of the properties of the global test statistic M_n defined in (10). For the random covariates, we consider both the Gaussian design and the bounded design. Under the Gaussian design, the covariates are generated from a multivariate Gaussian distribution with an unknown covariance matrix $\Sigma \in {ℝ}^{p\times p}$. In this case, we assume

(A1). X_i ~ N(0, Σ) independently for each i = 1, …, n.

In the case of bounded design, we assume instead

(A2). X_i for i = 1, …, n are i.i.d. random vectors satisfying $\mathbb{E}{X}_i=0$ and max_1≤i≤n ‖ X_i‖_∞ ≤ T for some constant T > 0.

Define the ${\mathcal{l}}_1$ ball

$${\mathcal{B}}_1(k)=\left\{\Omega =\left({\omega }_{ij}\right)\in {ℝ}^{p\times p}:\underset{1\le i\le p}{\text{max}}\sum _{j=1}^p\text{min}\left(|{\omega }_{ij}|\sqrt{\frac{n}{\text{log}p}},1\right)\le k\right\}.$$

In general, ${\mathcal{B}}_1(k)$ includes any matrix Ω whose rows ω_i are ${\mathcal{l}}_0$ sparse with ‖ω_i‖₀≤ k or ${\mathcal{l}}_1$ sparse with $\Vert {\omega }_i{\Vert }_1\le k\sqrt{\text{log}p/n}$ for all i = 1, …, p. The parameter space of the covariance matrix Σ and the regression vector β are defined as following.

(A3). The parameter space Θ(k) of $\theta =(\beta ,\Sigma )\in {ℝ}^p\times {ℝ}^{p\times p}$ satisfies

$$\Theta (k)=\left\{(\beta ,\Sigma ):\Vert \beta {\Vert }_0\le k,M^{-1}\le {\lambda }_{\text{min}}(\Sigma )\le {\lambda }_{\text{max}}(\Sigma )\le M,{\Sigma }^{-1}\in {\mathcal{B}}_1(k)\right\},$$

for some constant M ≥ 1. For convenience, we denote ${\Theta }_1(k)=\left\{\beta \in {ℝ}^p:\Vert \beta {\Vert }_0\le k\right\}$ and ${\Theta }_2(k)=\left\{\Sigma \in {ℝ}^{p\times p}:M^{-1}\le {\lambda }_{\text{min}}(\Sigma )\le {\lambda }_{\text{max}}(\Sigma )\le M,{\Sigma }^{-1}\in {\mathcal{B}}_1(k)\right\}$, so that Θ(k) = Θ₁(k) × Θ₂(k).

The following theorem states that the asymptotic null distribution of M_n under either the Gaussian or bounded design is a Gumbel distribution.

Theorem 1. Let M_n be the test statistic defined in (10), D be the diagonal of Σ⁻¹ and (ζ_ij) = D^−1/2Σ⁻¹D^−1/2. Suppose max_1≤i<j≤p |ζ_ij|≤ c₀ for some constant 0 < c₀ < 1, log p = O(n^r) for some 0 < r < 1/5, and

1. under the Gaussian design, we assume (A1) (A3) and$k=o\left(\sqrt{n}/{\text{log}}^{3}p\right)$; or

2. under the bounded design, we assume (A2) (A3) and$k=o\left(\sqrt{n}/{\text{log}}^{5/2}p\right)$.

Then under H₀, for any given$x\in ℝ$,

$$P_{\theta }\left(M_n-2\text{log}p+\text{loglog}p\le x\right)\to \text{exp}\left(\frac{1}{\sqrt{\pi }}\text{exp}(-x/2)\right),\text{ as }(n,p)\to \infty .$$

The condition that log p = o(n^r) for some 0 < r < 1/5 is consistent with those required for testing the global hypothesis in high-dimensional linear regression (Xia, Cai, and Cai 2018) and for testing two-sample covariance matrices (Cai, Liu, and Xia 2013). It allows the dimension p to be exponentially large comparing to the sample size n, which is much more flexible than the likelihood ratio test considered in Sur, Chen, and Candès (2017) and Sur and Candès (2019), where the dimension can only scale as p < n. Under the Gaussian design, it is required that the sparsity k is $o\left(\sqrt{n}/{\text{log}}^{3}p\right)$ whereas for the bounded design, it suffices that the sparsity k to be $o\left(\sqrt{n}/{\text{log}}^{5/2}p\right)$.

Remark 1. The analysis can be extended to testing H₀:β_G = 0 versus H₁:β_G ≠ 0 for a given index set G. Specifically, we can construct the test statistic as $M_{G,n}={\text{max}}_{i\in G}{M}_j^2$ and obtain a similar Gumbel limiting distribution by replacing p by | G |, as (n,|G|) → ∞. The sparsity condition thus should be forwarded to the set G.

Based on the limiting null distribution, the asymptotically α level test can be defined as

$${\Phi }_{\alpha }\left(M_n\right)=I\left\{M_n\ge 2\text{log}p-\text{loglog}p+q_{\alpha }\right\},$$

where q_α is the 1 − α quantile of the Gumbel distribution with the cumulative distribution function $\text{exp}\left(-\frac{1}{\sqrt{\pi }}\text{exp}(-x/2)\right)$, i.e.

$$q_{\alpha }=-\text{log}(\pi )-2\text{loglog}{(1-\alpha )}^{-1}.$$

The null hypothesis H₀ is rejected if and only if Φ_α(M_n) = 1.

2.3. Minimax Separation Distance and Optimality

In this subsection, we answer the question: “What is the essential difficulty for testing the global hypothesis in logistic regression.” To fix ideas, we begin with defining the minimax separation distance that measures such an essential difficulty for testing the global null hypothesis at a given level and type II error. In particular, we consider the alternative

$$H_1:\beta \in \left\{\beta \in {ℝ}^p:\Vert \beta {\Vert }_{\infty }\ge \rho ,\Vert \beta {\Vert }_0\le k\right\}$$

for some ρ > 0. This alternative concerns the detection of any discernible signals among the regression coefficients where the signals can be extremely sparse, which has interesting applications (see Xia, Cai, and Cai (2015)). Similar alternatives are also considered by Cai, Liu, and Xia (2013) and Cai, Liu, and Xia (2014).

By fixing a level α > 0 and a type II error probability δ > 0, we can define the δ-separation distance of a level α test procedure Φ_α for given design covariance Σ as

$$\begin{gathered} \rho \left({\Phi }_{\alpha },\delta ,\Sigma \right)=\text{inf}\{\rho >0:\underset{\beta \in {\Theta }_1(k)\Vert \beta {\Vert }_{\infty }\ge \rho }{\text{inf}}{P}_{\theta }({\Phi }_{\alpha }=1)\ge 1-\delta \} \\ =\text{inf}\left\{\rho >0:\underset{\beta \in {\Theta }_1(k)\Vert \beta {\Vert }_{\infty }\ge \rho }{\text{sup}}{P}_{\theta }({\Phi }_{\alpha }=0)\le \delta \right\}. \end{gathered}$$ (11)

The δ-separation distance ρ(Φ_α, δ,Θ(k)) over Θ(k) can thus be defined by taking the supremum over all the covariance matrices Σ ∈Θ₂(k), so that

$$\rho \left({\Phi }_{\alpha },\delta ,\Theta (k)\right)=\underset{\Sigma \in {\Theta }_2(k)}{\text{sup}}\rho \left({\Phi }_{\alpha },\delta ,\Sigma \right),$$

which corresponds to the minimal ${\mathcal{l}}_{\infty }$ distance such that the null hypothesis H₀ is well separated from the alternative H₁ by the test Φ_α. In general, δ-separation distance is an analogue of the statistical risk in estimation problems. It characterizes the performance of a specific α-level test with a guaranteed type II error δ. Consequently, we can define the (α, δ)-minimax separation distance over Θ(k) and all the α-level tests as

$${\rho }^{*}(\alpha ,\delta ,\Theta (k))=\underset{{\Phi }_{\alpha }}{\text{inf}}\rho \left({\Phi }_{\alpha },\delta ,\Theta (k)\right).$$

The definition of (α, δ)-minimax separation distance generalizes the ideas of Ingster (1993), Baraud (2002) and Verzelen (2012). The following theorem establishes the minimax lower bound of the (α, δ)-separation distance under the Gaussian design for testing the global null hypothesis over the parameter space Θ′(k) ⊂ Θ(k) defined as

$${\Theta }^{\prime }(k)=\left({\Theta }_1(k)\cap \left\{\beta \in {ℝ}^p:\Vert \beta {\Vert }_2\lesssim {\left(n^{1/4}\text{log}p\right)}^{-1}\right\}\right)\times {\Theta }_2(k).$$

Theorem 2. Assume that α + δ ≤ 1. Under the Gaussian design, if (A1) and (A3) hold, (β, Σ) ∈ Θ′(k) and $k\lesssim \text{min}\left\{p^{\gamma },\sqrt{n}/{\text{log}}^{3}p\right\}$ for some 0 < γ <1 / 2 , then the (α, δ)-minimax separation distance over Θ′(k) has the lower bound

$${\rho }^{*}\left(\alpha ,\delta ,{\Theta }^{\prime }(k)\right)\ge c\sqrt{\frac{\text{log}p}{n}}$$ (12)

for some constant c > 0.

In order to show the above lower bound is asymptotically sharp, we prove that it is actually attainable under certain circumstances, by our proposed global test Φ_α. In particular, for the bounded design, we make the following additional assumption.

(A4). It holds that P_θ(max_1≤i≤n |β^⊤X_i|≥ C) = O(p^−c) for some constant C, c > 0.

Theorem 3. Suppose that log p = O(n^r) for some 0 < r < 1. Under the alternative $H_1:\Vert \beta {\Vert }_{\infty }\ge c_2\sqrt{\text{log}p/n}$ for some c₂ > 0, and

(i) under the Gaussian design, assume that (A1) and (A3) hold, $\Vert \beta {\Vert }_2\le C(\text{loglog}p)/\sqrt{\text{log}n}$ for $C\le \text{min}\left\{\sqrt{2/{\lambda }_{\text{max}}(\Sigma )},{(2r\sqrt{2{\lambda }_{\text{max}}(\Sigma )})}^{-1}\right\}$, log p ≳ log^1+δ n for some δ > 0 and $k=o\left(\sqrt{n}/{\text{log}}^{3}p\right)$; or

(ii) under the bounded design, assume that (A2), (A3), and (A4) hold, and$k=o\left(\sqrt{n}/{\text{log}}^{5/2}p\right)$.

Then we have P_θ(Φ_α(M_n) = 1) → 1 as (n, p) → ∞.

In Theorem 3, (A4) is assumed for the bounded case and $\Vert \beta {\Vert }_2=O(\text{loglog}p/\sqrt{\text{log}n})$ is required for the Gaussian case. In particular, since log p = O(n^r) for some 0 < r < 1, the upper bound $\text{loglog}p/\sqrt{\text{log}n}$ for ‖β‖₂ can be as large as $\sqrt{\text{log}n}$. In Theorem 2, the minimax lower bound is established over (β, Σ) ∈Θ′(k), so that the same lower bound holds over a larger set

$$(\beta ,\Sigma )\in \left({\Theta }_1(k)\cap \left\{\beta \in {ℝ}^p:\Vert \beta {\Vert }_2\le \text{loglog}p/\sqrt{\text{log}n}\right\}\right)\times {\Theta }_2(k),$$ (13)

since $\text{loglog}p/\sqrt{\text{log}n}\gtrsim {\left(n^{1/4}\text{log}p\right)}^{-1}$. On the other hand, Theorem 3 (i) indicates an upper bound ${\rho }^{*}\lesssim \sqrt{\text{log}p/n}$ attained by our proposed test under the Gaussian design over the set (13). These two results imply the minimax rate ${\rho }^{*}\asymp \sqrt{\text{log}p/n}$ and the minimax optimality of our proposed test over the set (13).

2.4. Comparison with Existing Works

In this section, we make detailed comparisons and connections with some existing works concerning global hypothesis testing in the high-dimensional regression literature.

Ingster, Tsybakov, and Verzelen (2010) addressed the detection boundary for high-dimensional sparse linear regression models, and more recently Mukherjee, Pillai, and Lin (2015) studied the detection boundary for hypothesis testing in high-dimensional sparse binary regression models. However, although both works obtained the sharp detection boundary for the global testing problem H₀:β = 0, their alternative hypotheses are different from ours. Specifically, Mukherjee, Pillai, and Lin (2015) considered the alternative hypothesis $H_1:\beta \in \left\{\beta \in {ℝ}^p:\Vert \beta {\Vert }_0\ge k,\text{min}\left\{|{\beta }_j|:{\beta }_k\ne 0\right\}\ge A\right\}$, which implies that β has at least k nonzero coefficients exceeding A in absolute values. Ingster, Tsybakov, and Verzelen (2010) considered the alternative hypothesis $H_1:\beta \in \left\{\beta \in {ℝ}^p:\Vert \beta {\Vert }_0\le k,\Vert \beta {\Vert }_2\ge \rho \right\}$, which concerns k sparse β with ${\mathcal{l}}_2$ norm at least ρ. In fact, the proof of our Theorem 2 can be directly extended to such an alternative concerning the ${\mathcal{l}}_2$ norm, which amounts to obtaining a lower bound of order $\sqrt{\frac{k\text{log}p}{n}}$ for high dimensional logistic regression. However, developing a minimax optimal test for such alternative is beyond the scope of the current paper.

Additionally, in contrast to the minimax separation distance considered in this paper, the papers by Ingster, Tsybakov, and Verzelen (2010) and Mukherjee, Pillai, and Lin (2015) considered the minimax risk (or the minimax total error probability) given by

$$\underset{\Phi }{\text{inf}}\underset{\mathbf{\Sigma }\in {\Theta }_2(k)}{\text{sup}}\text{Risk}(\Phi ,\Sigma )=\underset{\Phi }{\text{inf}}\underset{\mathbf{\Sigma }\in {\Theta }_2(k)}{\text{sup}}\left\{\underset{\beta \in H_0}{\text{max}}\right\}{P}_{\theta }(\Phi =1)+\underset{\beta \in {\Theta }_1(k){\Vert \beta \Vert }_{\infty }\ge \rho }{\text{max}}{P}_{\theta }(\Phi =0)\},$$ (14)

where the infimum is taken over all tests Φ. This minimax risk can be also written as

$$\underset{\Phi }{\text{inf}}\underset{\mathbf{\Sigma }\in {\Theta }_2(k)}{\text{sup}}\text{Risk}(\Phi ,\mathbf{\Sigma })=\underset{\alpha \in (0,1)}{\text{inf}}\left\{\alpha +\underset{{\Phi }_{\alpha }}{\text{inf}}\underset{\mathbf{\Sigma }\in {\Theta }_2(k)}{\text{sup}}\underset{\beta \in {\Theta }_1(k)\Vert \beta {\Vert }_{\infty }\ge \rho }{\text{sup}}{P}_{\theta }\left({\Phi }_{\alpha }=0\right)\right\}.$$ (15)

A comparison of (11) and (15) yields the slight difference between the two criteria, as one depends on a given Type I error α and the other doesn’t.

Moreover, these two papers considered different design scenarios from ours. In Ingster, Tsybakov, and Verzelen (2010), only the isotropic Gaussian design was considered. As a result, the optimal tests proposed therein rely highly on the independence assumption. In Mukherjee, Pillai, and Lin (2015), the general binary regression was studied under fixed sparse design matrices. In particular, the minimax lower and upper bounds were only derived in the special case of design matrices with binary entries and certain sparsity structures.

In comparison with the recent works of Sur, Chen, and Candès (2017), Candès and Sur (2018) and Sur and Candès (2019), besides the aforementioned difference in the asymptotics of (p, n), these two papers only considered the random Gaussian design, whereas our work also considered random bounded design as in van de Geer et al. (2014). In addition, Sur, Chen, and Candès (2017) and Sur and Candès (2019) developed the Likelihood Ratio (LLR) Test for testing the hypothesis $H_0:{\beta }_{j_1}={\beta }_{j_2}=\dots ={\beta }_{j_k}=0$ for any finite k. Intuitively, a valid test for the global null and p / n → κ ∈(0, 1 / 2) can be adapted from the individual LLR tests using the Bonferroni procedure. However, as our simulations show (Section 5), such a test is less powerful compared to our proposed test.

Lastly, our minimax results focus on the highly sparse regime k ≲ p^γ where γ ∈(0, 1 / 2). As shown by Ingster, Tsybakov, and Verzelen (2010) and Mukherjee, Pillai, and Lin (2015), the problem under the dense regime where γ ∈(1 / 2,1) can be very different from the sparse regime. Mostly likely, the fundamental difficulty of the testing problem changes in this situation so that different methods need to be carefully developed. We leave these interesting questions for future investigations.

3. LARGE-SCALE MULTIPLE TESTING

Denote by β the true coefficient vector in the model and denote ${\mathcal{H}}_0=\left\{j:{\beta }_j=0,j=1,\cdots ,p\right\},{\mathcal{H}}_1=\left\{j:{\beta }_j\ne 0,j=1,\cdots ,p\right\}$. In order to identify the indices in ${\mathcal{H}}_1$, we consider simultaneous testing of the following null hypotheses

$$H_{0,j}:{\beta }_j=0\text{ vs}.H_{1,j}:{\beta }_j\ne 0,1\le j\le p.$$

Apart from identifying as many nonzero β_j as possible, to obtain results of practical interest, we would like to control the false discovery rate (FDR) as well as the false discovery proportion (FDP), or the number of falsely discovered variables (FDV).

3.1. Construction of Multiple Testing Procedures

Recall that in Section 2, we define the standardized statistics $M_j={\check{\beta }}_j/{\tau }_j$, for j = 1, …, p. For a given threshold level t > 0, each individual hypothesis H_0,j:β_j = 0 is rejected if |M_j|≥ t. Therefore for each t, we can define

$${\text{FDP}}_{\theta }(t)=\frac{\sum _{j\in {\mathcal{H}}_0}I\left\{|M_j|\ge t\right\}}{\text{max}\left\{\sum _{j=1}^{p}I\left\{|M_j|\ge t\right\},1\right\}},{\text{FDR}}_{\theta }(t)={\mathbb{E}}_{\theta }[\text{FDP}(t)],$$

and the expected number of falsely discovered variables ${\text{FDV}}_{\theta }(t)={\mathbb{E}}_{\theta }\left[\sum _{j\in {\mathcal{H}}_0}I\left\{|M_j|\ge t\right\}\right]$

Procedure Controlling FDR/FDP.

In order to control the FDR/FDP at a pre-specified level 0 < α < 1, we can set the threshold level as

$${\tilde{t}}_1=\text{inf}\left\{0\le t\le b_p:\frac{\sum _{j\in {\mathcal{H}}_0}I\left\{|M_j|\ge t\right\}}{\text{max}\left\{\sum _{j=1}^{p}I\left\{|M_j|\ge t\right\},1\right\}}\le \alpha \right\},$$ (16)

for some b_p to be determined later.

In general, the ideal choice ${\tilde{t}}_1$ is unknown and needs to be estimated because it depends on the knowledge of the true null ${\mathcal{H}}_0$. Let G₀(t) be the proportion of the nulls falsely rejected by the procedure among all the true nulls at the threshold level t, namely, $G_0(t)=\frac{1}{p_0}\sum _{j\in {\mathcal{H}}_0}I\left\{|M_j\rangle \ge t\right\}$, where $p_0=|{\mathcal{H}}_0|$. In practice, it is reasonable to assume that the true alternatives are sparse. If the sample size is large, we can use the tails of normal distribution G(t) = 2 − 2Φ(t) to approximate G₀(t). In fact, it will be shown that, for $b_p=\sqrt{2\text{log}p-2\text{loglog}p}$ in probability as (n, p) → ∞. To summarize, we have the following logistic multiple testing (LMT) procedure controlling the FDR and the FDP.

Procedure 1 (LMT). Let 0 < α < 1, $b_p=\sqrt{2\text{log}p-2\text{loglog}p}$ and define

$$\widehat{t}=\text{inf}\left\{0\le t\le b_p:\frac{pG(t)}{\text{max}\left\{\sum _{j=1}^{p}I\left\{|M_j|\ge t\right\},1\right\}}\le \alpha \right\}.$$ (17)

If$\widehat{t}$in (17) does not exist, then let $\widehat{t}=\sqrt{2\text{log}p}$. We reject H_0,j Whenever $|M_j|\ge \widehat{t}$.

Procedure Controlling FDV.

For large-scale inference, it is sometimes of interest to directly control the number of falsely discovered variables (FDV) instead of the less stringent FDR/FDP, especially when the sample size is small (Liu and Luo 2014). By definition, the FDV control, or equivalently, the per-family error rate control, provides an intuitive description of the Type I error (false positives) in variable selection. Moreover, controlling FDV = r for some 0 < r < 1 is related to the family-wise error rate (FWER) control, which is the probability of at least one false positive. In fact, FDV control can be achieved by a suitable modification of the FDP controlling procedure introduced above. Specifically, we propose the following FDV (or FWER) controlling logistic multiple testing (LMT_V) procedure.

Procedure 2 (LMT_V). For a given tolerable number of falsely discovered variables r < p (or a desired level of FWER 0 < r < 1), let ${\widehat{t}}_{FDV}=G^{-1}(r/p)$. H_0,j is rejected whenever $|M_j|\ge {\widehat{t}}_{FDV}$.

3.2. Theoretical Properties for Multiple Testing Procedures

In this section we show that our proposed multiple testing procedures control the theoretical FDR/FDP or FDV asymptotically. For simplicity, our theoretical results are obtained under the bounded design scenario. For FDR/FDP control, we need an additional assumption on the interplay between the dimension p and the parameter space Θ(k).

Recall that η_j = (η_j1, …, η_jn) for j = 1, …, p defined in (7). We define $F_{jk}={\mathbb{E}}_{\theta }\left[{\eta }_{ij}{\eta }_{ik}/\dot{f}\left(u_i\right)\right]$ for 1 ≤ j, k ≤ p, and ${\rho }_{jk}=F_{jk}/\sqrt{F_{ij}{F}_{kk}}$. Denote $\mathcal{B}(\delta )=\left\{(j,k):|{\rho }_{jk}|\ge \delta ,i\ne j\right\}$ and $\mathcal{A}(ϵ)=\mathcal{B}\left({(\text{log}p)}^{-2-ϵ}\right)$.

(A5). Suppose that for some ϵ > 0 and q > 0, $\sum _{(j,k)\in \mathcal{A}(ϵ):j,k\in {\mathcal{H}}_0}{p}^{\frac{2|{\rho }_{jk}|}{1+|{\rho }_{jk}|}+q}=O\left(p^2/{(\text{log}p)}^2\right)$.

The following proposition shows that M_j is asymptotically normal distributed and G₀(t) is well approximated by G(t).

Proposition 1. Under (A2) (A3) and (A4), suppose p = O(n^c) for some constant c > 0, $k=o\left(\sqrt{n}/{\text{log}}^{5/2}p\right)$, then as (n, p) → ∞,

$$\underset{j\in {\mathcal{H}}_0}{\text{sup}}\underset{0\le t\le \sqrt{2\text{log}p}}{\text{sup}}|\frac{P_{\theta }\left(|M_j|\ge t\right)}{2-2\Phi (t)}-1|\to 0.$$ (18)

If in addition we assume (A5), then

$$\underset{0\le t\le b_p}{\text{sup}}|\frac{G_0(t)}{G(t)}-1|\to 0$$ (19)

in probability, where Φ is the cumulative distribution function of the standard normal distribution and $b_p=\sqrt{2\text{log}p-2\text{loglog}p}$.

The following theorem provides the asymptotic FDR and FDP control of our procedure.

Theorem 4. Under the conditions of Proposition 1, for $\widehat{t}$ defined in our LMT procedure, we have

$$\underset{(n,p)\to \infty }{\text{lim}}\frac{{\text{FDR}}_{\theta }(\widehat{t})}{\alpha p_0/p}\le 1,\underset{(n,p)\to \infty }{\text{lim}}{P}_{\theta }\left(\frac{{\text{FDP}}_{\theta }(\widehat{t})}{\alpha p_0/p}\le 1+ϵ\right)=1$$ (20)

for any ϵ > 0.

For the FDV/FWER controlling procedure, we have the following theorem.

Theorem 5. Under (A2) (A3) and (A4), assume p = O(n^c) for some c > 0 and $k=o\left(\sqrt{n}/{\text{log}}^{5/2}p\right)$.

Let r < p be the desired level of FDV. For${\widehat{t}}_{FDV}$defined in our LMT_Vprocedure, we have$\underset{(n,p)\to \infty }{\text{lim}}\frac{{\text{FDV}}_{\theta }\left({\widehat{t}}_{FDV}\right)}{r{p}_0/p}\le 1$. In addition, if 0 < r < 1, we have $\underset{(n,p)\to \infty }{\text{lim}}\frac{{\text{FWER}}_{\theta }\left({\widehat{t}}_{FDV}\right)}{r{p}_0/p}\le 1$.

The above theoretical results are obtained under the dimensionality condition p = O(n^c), which is stronger than that of the global test. Essentially, the condition is needed to obtain the uniform convergence (18), whose form (as ratio) is stronger than the convergence in distribution in the ordinary sense (as direct difference).

4. TESTING FOR TWO LOGISTIC REGRESSION MODELS

In some applications, it is also interesting to consider hypothesis testing that involves two separate logistic regression models of the same dimension. Specifically, for $\mathcal{l}=1,2$ and $i=1,\dots ,n_{\mathcal{l}}$, where $n_1\asymp n_2,y_i^{(\mathcal{l})}=f\left({\beta }^{(\mathcal{l})\top }{X}_i^{(\mathcal{l})}\right)+{ϵ}_i^{(\mathcal{l})}$, where f (u) = e^u / (1 + e^u), and ${ϵ}_i^{(l)}$ is a binary random variable such that $y_i^{(\mathcal{l})}|X_i^{(\mathcal{l})}~\text{Bernoulli}\left(f\left({\beta }^{(\mathcal{l})\top }{X}_i^{(\mathcal{l})}\right)\right)$. The global null hypothesis H₀:β⁽¹⁾ = β⁽²⁾ implies that there is overall no difference in association between covariates and the response. If this null hypothesis is rejected, we are interested in simultaneously testing the hypotheses $H_{0,j}:{\beta }_j^{(1)}={\beta }_j^{(2)}$ for each j = 1, …, p.

To test the global null H₀:β⁽¹⁾ = β⁽²⁾ against H₁:β⁽¹⁾ ≠ β⁽²⁾, we can first obtain ${\check{\beta }}_j^{(\mathcal{l})}$ and ${\tau }_j^{(\mathcal{l})}$ for each model, and then calculate the coordinate-wise standardized statistics $T_j=\frac{{\check{\beta }}_j^{(1)}}{\sqrt{2}{\tau }_j^{(1)}}-\frac{{\check{\beta }}_j^{(2)}}{\sqrt{2}{\tau }_j^{(2)}}$, for j = 1, …, p. Define the global test statistic as $T_n={\text{max}}_{1\le j\le p}{T}_j^2$, it can be shown that the limiting null distribution is also a Gumbel distribution. The α level global test is thus defined as Φ_α(T_n) = I{T_n ≥ 2log p−loglog p + q_α}, where q_α = −log(π) − 2loglog(1 − α)⁻¹. For multiple hypotheses testing of two regression vectors $H_{0,j}:{\beta }_j^{(1)}={\beta }_j^{(2)}$, we consider the test statistics T_j defined above. The two-sample multiple testing procedure controlling FDR/FDP is given as follows.

Procedure 3. Let 0 < α < 1 and define $\widehat{t}=\text{inf}\left\{0\le t\le b_p:\frac{pG(t)}{\text{max}\left\{\sum _{j=1}^{p}I\left\{|T_j|\ge t\right\},1\right\}}\le \alpha \right\}$. If the above $\widehat{t}$ does not exist, let $\widehat{t}=\sqrt{2\text{log}p}$. We reject H_0,j whenever $|T_j|\ge \widehat{t}$.

5. SIMULATION STUDIES

In this section we examine the numerical performance of the proposed tests. Due to the space limit, for both global and multiple testing problems, we only focus on the single regression setting, and report the results on two logistic regressions in the Supplementary Materials. Throughout our numerical studies, sample splitting was not used.

5.1. Global Hypothesis Testing

In the following simulations, we consider a variety of dimensions, sample sizes, and sparsity of the models. For alternative hypotheses, the dimension of the covariates p ranges from 100, 200, 300 to 400, and the sparsity k is set as 2 or 4. The sample sizes n are determined by the ratio r = p / n that takes values of 0.2, 0.4 and 1.2. To generate the design matrix X, we consider the Gaussian design with the blockwise-correlated covariates so that Σ = Σ_B, where Σ_B is a p × p blockwise diagonal matrix including 10 equal-sized blocks, whose diagonal elements are 1’s and off-diagonal elements are set as 0.7. Under the alternative, suppose $\mathcal{S}$ is the support of the regression coefficients β and $|\mathcal{S}|=k$, we set $|{\beta }_j|=\rho 1\left\{j\in \mathcal{S}\right\}$ for j = 1, …, p and ρ = 0.75 with equal proportions of ρ and −ρ. We set κ₀ = 0 and κ₁ = 0.5.

To assess the empirical performance of our proposed test (“Proposed”), we compare our test with (i) a Bonferroni procedure applied to the p-values from univariate screening using MLE statistic (“U-S”), and (ii) to the method of Sur, Chen, and Candès (2017); Sur and Candès (2019) (“LLR”) in the setting where r = 0.2 and 0.4.

Table 2 shows the empirical type I errors of these tests at level α = 0.05 based on 1000 simulations. Figure 1 shows the corresponding empirical powers under various settings. As we expected, our proposed method outperforms the other two alternatives in all the cases (including the moderate dimensional cases where r = 0.2 and 0.4), and the power increases as n or p grows. In the rather lower dimensional setting where r = 0.2, the LLR performs almost as well as our proposed method.

Table 2.

Type I error with α = 0.05 for the proposed method (Proposed), the Bonferroni corrected univariate screening method (U-S) and the Bonferroni corrected likelihood ratio based method of Sur and Candès (2019) (LLR), for different n, p and k.

p / n	k = 2				k = 4
	p = 100	200	300	400	p = 400	600	800	1000
Proposed
0.2	0.052	0.066	0.042	0.054	0.058	0.050	0.046	0.070
0.4	0.038	0.054	0.062	0.054	0.046	0.050	0.060	0.074
1.2	0.026	0.044	0.042	0.045	0.014	0.044	0.054	0.054
U-S
0.2	0.040	0.032	0.024	0.018	0.018	0.022	0.028	0.034
0.4	0.050	0.032	0.024	0.020	0.028	0.028	0.032	0.046
1.2	0.028	0.038	0.024	0.020	0.032	0.018	0.034	0.014
LLR
0.2	0.050	0.050	0.068	0.040	0.058	0.044	0.046	0.034
0.4	0.084	0.070	0.048	0.056	0.062	0.042	0.058	0.064

Fig. 1.

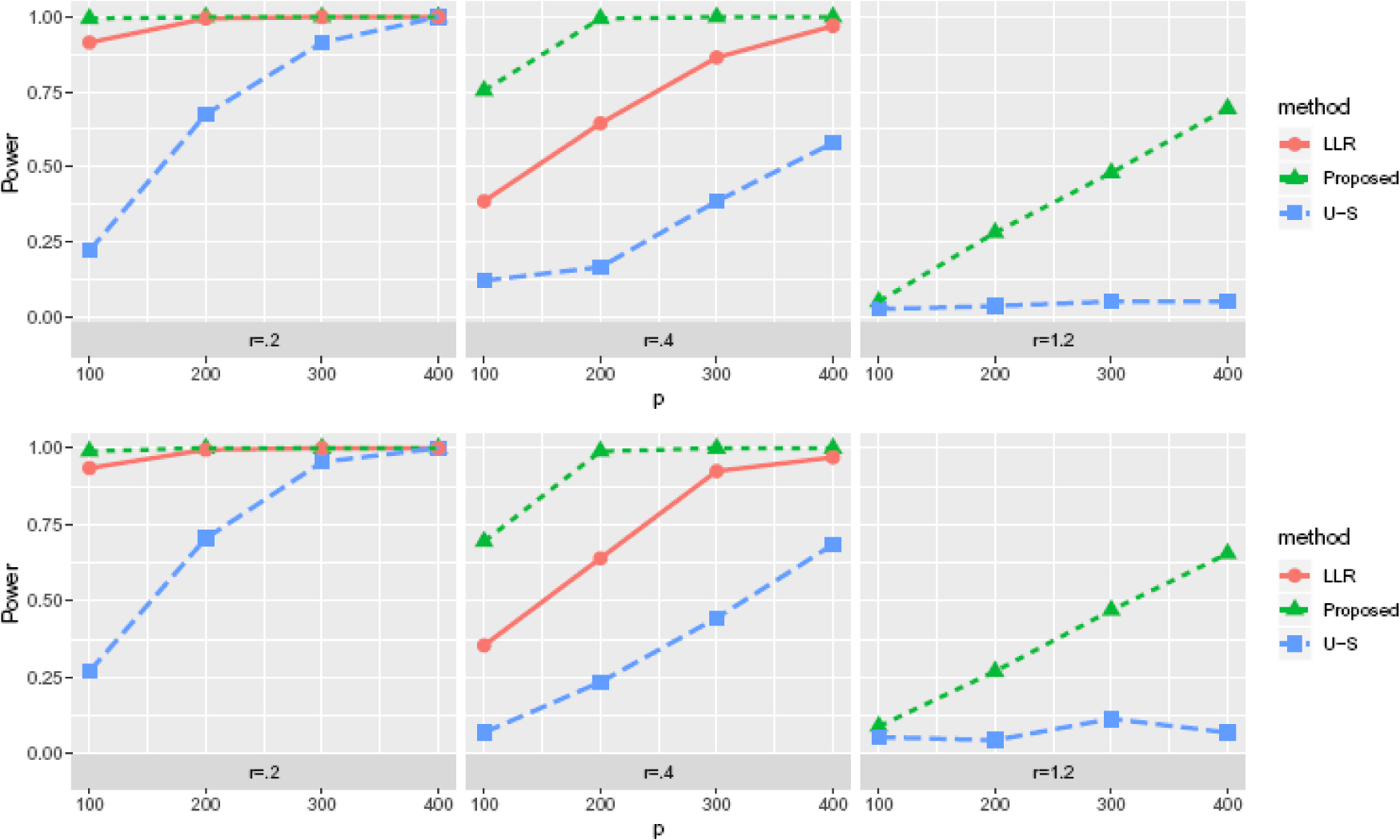
Empirical power with α = 0.05 for the proposed method (Proposed), the Bonferroni corrected univariate screening method (U-S) and the Bonferroni corrected likelihood ratio based method of Sur and Candès (2019) (LLR). Top panel: k = 2; bottom panel: k = 4.

5.2. Multiple Hypotheses Testing

FDR Control.

In this case, we set p = 800 and let n vary from 600, 800, 1000, 1200 to 1400, so that all the cases are high-dimensional in the sense that p > n / 2. The sparsity level k varies from 40, 50 to 60. For the true positives, given the support $\mathcal{S}$ such that $|\mathcal{S}|=k$, we set $|{\beta }_j|=\rho 1\left\{j\in \mathcal{S}\right\}$ for j = 1, …, p with equal proportions of ρ and −ρ. The design covariates X_i’s are generated from a $\left(|X_i^{\top }\beta |<3\right)$-truncated multivariate Gaussian distribution with covariance matrix Σ = 0.01Σ_M, where Σ_M is a p × p blockwise diagonal matrix of 10 identical unit diagonal Toeplitz matrices whose off-diagonal entries descend from 0.1 to 0 (see Supplementary Material for the explicit form). The choice of κ₀ and κ₁ are the same as the global testing. Throughout, we set the desired FDR level as α = 0.2.

We compare our proposed procedure (denoted as “LMT”) with following methods: (i) the basic LMT procedure with b_p in (17) replaced by ∞ (“LMT0”), which is equivalent to applying the BH procedure (Benjamini and Hochberg 1995) to our debiased statistics M_j, (ii) the BY procedure (Benjamini and Yekutieli 2001) using our debiased statistics M_j (“BY”), implemented using the R function p.adjust(…,method=“BY”), (iii) a BH procedure applied to the p-values from univariate screening using the MLE statistics (“U-S”), and (iv) the knockoff method of Candès et al. (2018) (“Knockoff”). Figure 2 shows boxplots of the pooled empirical FDRs (see Supplementary Material for the case-by-case FDRs) and Figure 3 shows the empirical powers of these methods based on 1000 replications. Here the power is defined as the number of correctly discovered variables divided by the number of truly associated variables. As a result, we find that LMT and LMT0 correctly control FDRs and have the greatest power among all the cases. In particular, the power of LMT and LMT0 are almost the same, which increases as the sparsity decreases, the signal magnitude ρ increases, or the sample size n increases, while LMT0 has slightly inflated FDRs. The U-S method, although correctly controls the FDRs, has poor power, which is largely due to the dependence among the covariates.

Fig. 2.

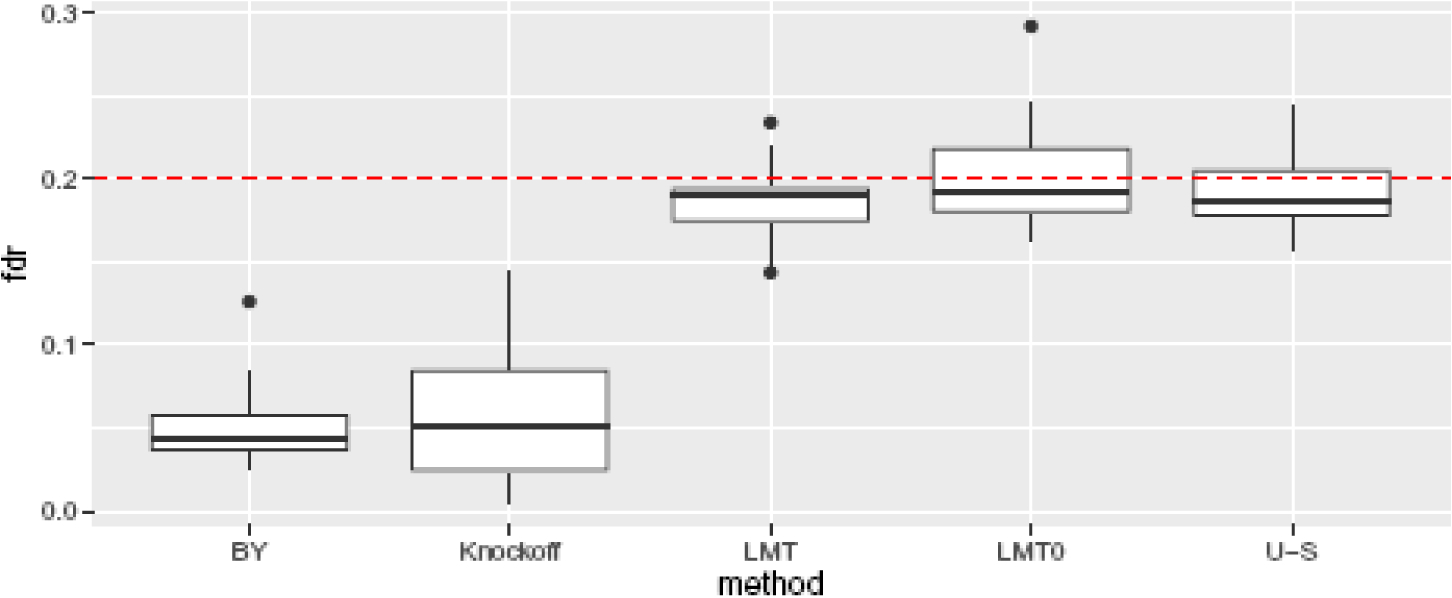
Boxplots of the empirical FDRs across all the settings for α = 0.2.

Fig. 3.

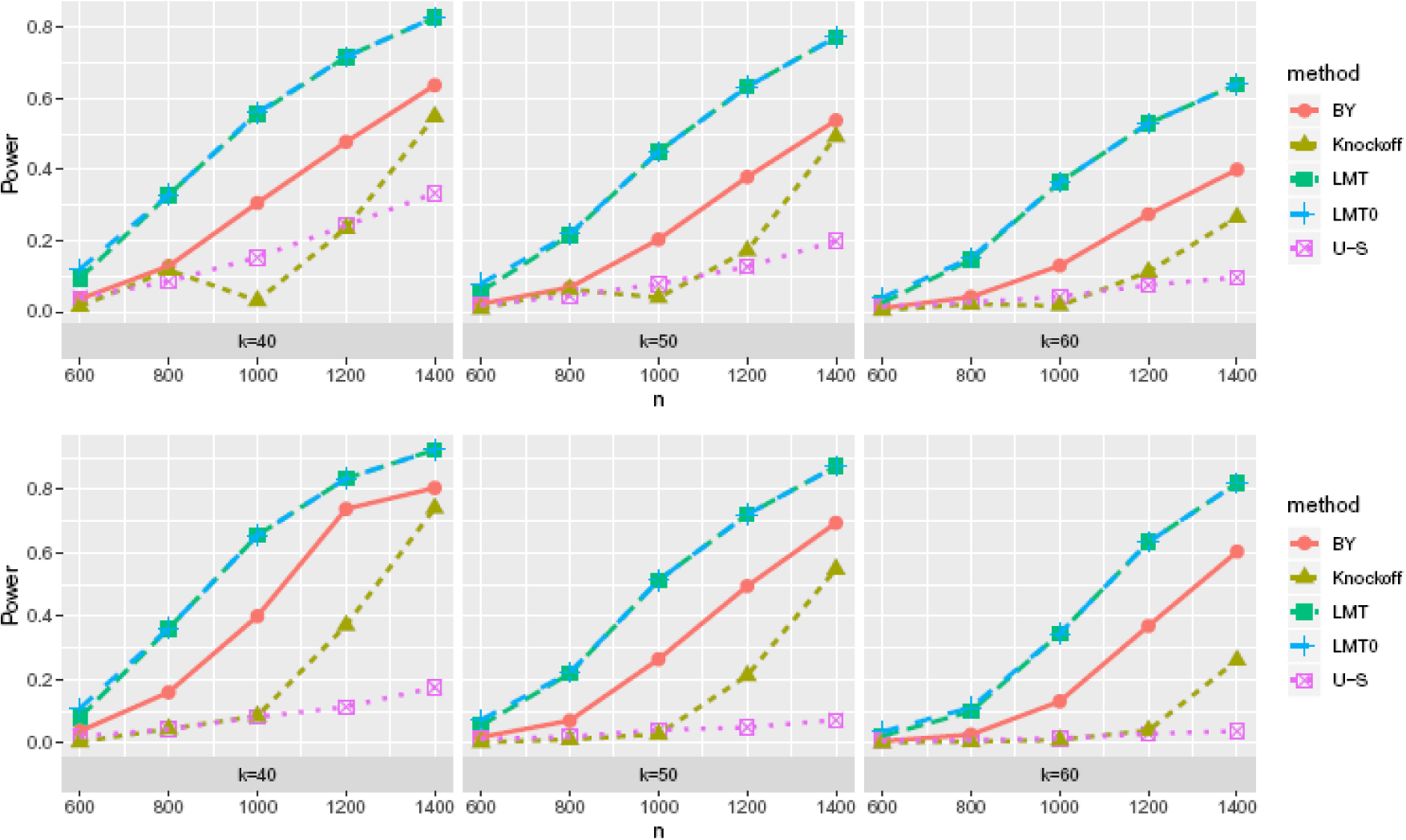
Empirical power under FDR α = 0.2 for ρ = 3 (top) and ρ = 4 (bottom).

FDV Control.

For our proposed test that controls FDV (denoted as LMT_V), by setting desired FDV level r = 10, we apply our method to various settings. Specifically, we set ρ = 3, p ∈{800,1000,1200}, set k ∈{40,50,60}, and let n vary from 400, 600, 800 to 1000. The design covariates are generated similarly as the previous part. The resulting empirical FDV and powers are summarized in Table 3. Our proposed LMT_V has the correct control of FDV in all the settings and the power increases as n grows, k decreases, or p decreases.

Table 3.

Empirical performance of LMT_V with FDV level r = 10.

ρ	p	k	Empirical FDV				Empirical Power
			n = 400	600	800	1000	400	600	800	1000
		40	4.07	5.45	6.44	7.11	0.08	0.23	0.40	0.59
	800	50	4.30	6.29	7.27	8.26	0.06	0.16	0.32	0.49
		60	4.33	6.63	7.48	8.42	0.05	0.12	0.25	0.42
		40	3.30	4.59	5.79	6.82	0.06	0.18	0.35	0.52
3	1000	50	3.49	5.42	6.43	7.03	0.05	0.13	0.26	0.43
		60	3.68	5.47	7.29	7.97	0.03	0.09	0.20	0.34
		40	2.69	4.36	5.00	5.68	0.05	0.15	0.31	0.46
	1200	50	2.97	4.22	5.73	6.43	0.03	0.11	0.21	0.36
		60	2.78	4.91	5.91	7.25	0.02	0.07	0.16	0.27

6. REAL DATA ANALYSIS

We illustrate our proposed methods by analyzing a dataset from the Pediatric Longitudinal Study of Elemental Diet and Stool Microbiome Composition (PLEASE) study, a prospective cohort study to investigate the effects of inflammation, antibiotics, and diet as environmental stressors on the gut microbiome in pediatric Crohn’s disease (Lewis et al. 2015; Lee et al. 2015; Ni et al. 2017). The study considered the association between pediatric Crohn’s disease and fecal metabolomics by collecting fecal samples of 90 pediatric patients with Crohn’s disease at baseline, 1 week, and 8 weeks after initiation of either anti-tumor necrosis factor (TNF) or enteral diet therapy, as well as those from 25 healthy control children (Lewis et al. 2015). In details, an untargeted fecal metabolomic analysis was performed on these samples using liquid chromatography-mass spectrometry (LC-MS). Metabolites with more than 80% missing values across all samples were removed from the analysis. For each metabolite, samples with the missing values were imputed with its minimum abundance across samples. To avoid potential large outliers, for each sample, the metabolite abundances were further normalized by dividing 90% cumulative sum of the abundances of all metabolites. The normalized abundances were then log transformed and used in all analyses. The metabololomics annotation was obtained from Human Metabolome Database (Lee et al. 2015). In total, for each sample, abundances of 335 known metabolites were obtained and used in our analysis.

6.1. Association Between Metabolites and Crohn’s Disease Before and After Treatment

We first test the overall association between 335 characterized metabolites and Crohn’s disease by fitting a logistic regression using the data of 25 healthy controls and 90 Crohn’s disease patients at the baseline. We obtain a global test statistic of 433.88 with a p-value < 0.001, indicating a strong association between Crohn’s disease and fecal metabolites. At the FDR < 5%, our multiple testing procedure selects four metabolites, including C14:0.sphingomyelin, C24:1.Ceramide.(d18:1) and 3-methyladipate/pimelate (see Table 4). Recent studies have demonstrated that sphingolipid metabolites, particularly ceramide and sphingosine-1-phosphate, are signaling molecules that regulate a diverse range of cellular processes that are important in immunity, inflammation and inflammatory disorders (Maceyka and Spiegel 2014). In fact, ceramide acts to reduce tumor necrosis factor (TNF) release (Rozenova et al. 2010) and has important roles in the control of autophagy, a process strongly implicated in the pathogenesis of Crohn’s disease (Barrett et al. 2008; Sewell et al. 2012).

Table 4.

Significant metabolites associated with Crohn’s disease (coded as 1 in logistic regression) at the baseline, one week and 8 weeks after treatment with FDR < 5%. The refitted regression coefficients show the direction of the association.

Disease Stage	HMDB ID	Synonyms	Refitted Coefficient
Baseline	00885	C16:0.cholesteryl ester	4.45
	12097	C14:0.sphingomyelin	1.74
	04953	C24:1.Ceramide.(d18:1)	4.25
	00555	3-methyladipate/pimelate	−12.82
Week 1	06726	C20:4.cholesteryl ester	2.17
	12097	C14:0.sphingomyelin	2.06
	04949	C16:0.Ceramide.(d18:1)	0.87
	00555	3-methyladipate/pimelate	−6.10
	00056	beta-alanine	2.95
	00448	adipate	−4.50
Week 8	00883	valine	1.40
	00222	C16.carnitine	0.58
	00848	C18.carnitine	0.39
	00555	3-methyladipate/pimelate	−5.95
	00056	beta-alanine	0.63

We next investigate whether treatment of Crohn’s disease alters the association between metabolites and Crohn’s disease by fitting two separate logistic regressions using the metabolites measured one week or 8 weeks after the treatment. At each time point, a significant association is detected based on our global test (p-value < 0.001). One week after the treatment, we observe six metabolites associated with Crohn’s disease, including all four identified at the baseline and two additional metabolites, beta-alanine and adipate (see Table 4). The beta-alanine and adipate associations are likely due to that beta-alanine and adipate are important ingredients of the enteral nutrition treatment of Crohn’s disease. However, it is interesting that at 8 weeks after the treatment, valine, C16.carnitine and C18.carnitine are identified to be associated with Crohn’s disease together with 3-methyladipate/pimelate and beta-alanine. It is known that carnitine plays an important role in Crohn’s disease, which might be a consequence of the underlying functional association between Crohn’s disease and mutations in the carnitine transporter genes (Peltekova et al. 2004; Fortin 2011). Deficiency of carnitine can lead to severe gut atrophy, ulceration and inflammation in animal models of carnitine deficiency (Shekhawat et al. 2013). Our results may suggest that the treatment increases carnitine, leading to reduction of inflammation.

6.2. Comparison of Metabolite Associations Between Responders and Non-Responders

To compare the metabolic association with Crohn’s disease for responders (n = 47) and non-responders (n = 34) eight weeks after treatment, we fit two logistic regression models, responder versus normal control and non-responder versus normal control. Our global test shows that there is an overall difference in regression coefficients for responders and for non-responders when compared to the normal controls (p-value < 0.001). We next apply our proposed multiple testing procedure to identify the metabolites that have different regression coefficients in these two different logistic regression models. At the FDR < 0.05, our procedure identifies 9 metabolites with different regression coefficients (see Table 5). It is interesting that all these 9 metabolites have the same signs of the refitted coefficients, while the actual magnitudes of the associations between responders and non-responders when compared to the normal controls are different. Besides C24:4.cholesteryl ester, beta-alanine, valine, C18.carnitine and 3-methyladipate/pimelate that we observe in previous analyses, metabolites 5-hydroxytryptopha, nicotinate, and succinate also have differential associations between responders and non-responders when compared to the controls.

Table 5.

Significant metabolites identified via logistic regression of responder vs normal control and non-responder vs normal control for FDR ≤ 5%.

HMDB ID	Synonyms	Refitted Coefficients
		Responder vs.	Non-Responder vs.
		Normal	Normal
06726	C20:4.cholesteryl ester	0.139	1.854
01043	Linoleic.acid	−0.686	−0.388
00472	5-hydroxytryptophan	1.000	1.034
00056	beta-alanine	0.503	2.298
00883	valine	0.628	0.530
00848	C18.carnitine	1.100	0.457
01488	nicotinate	−1.936	−4.312
00254	succinate	0.750	1.508
00555	3-methyladipate/pimelate	−1.989	−4.209

7. DISCUSSION

In this paper, for both global and multiple testing, the precision matrix Ω = Σ⁻¹ of the covariates is assumed to be sparse and unknown. Node-wise regression among the covariates is used to learn the covariance structure in constructing the debiased estimator. However, if the prior knowledge of Ω = I is available, the algorithm can be simplified greatly. Specifically, instead of incorporating the Lasso estimators as in (8), we let $v_j={\widehat{W}}^{-1}{x}_j$ and τ_j = ‖v_j‖_n/〈v_j, x_j〉 for each j = 1, …, p. The theoretical properties of the resulting global testing and multiple testing procedures still hold, while the computational efficiency is improved dramatically. However, from our theoretical analysis, even with the knowledge of Ω = I, the theoretical requirement for the model sparsity ($k=o\left(\sqrt{n}/{\text{log}}^{3}p\right)$ in the Gaussian case and $k=o\left(\sqrt{n}/{\text{log}}^{5/2}p\right)$ in the bounded case) cannot be relaxed due to the nonlinearity of the problem.

Sample splitting was used in this paper for theoretical purpose. This is different from other works on inference in high-dimensional linear/logistic regression models, including Ingster, Tsybakov, and Verzelen (2010), van de Geer et al. (2014), Mukherjee, Pillai, and Lin (2015) and Javanmard and Javadi (2019), where sample splitting is not needed. However, as we discussed throughout the paper, the assumptions and the alternatives that we considered are different from those previous papers. In the case of high-dimensional logistic regression model, a sample splitting procedure seems unavoidable under the current framework of our technical analysis without making additional strong structural assumptions such as the sparse inverse Hessian matrices used in van de Geer et al. (2014) or the weakly correlated design matrices used in Mukherjee, Pillai, and Lin (2015). Our simulations showed that the sample splitting is actually not needed in order for our proposed methods to perform well. It is of interest to develop technical tools that can eliminate sample splitting in inference for high dimensional logistic regression models.

As mentioned in the introduction, the logistic regression model can be viewed as a special case of the single index model y = f (β^⊤x) + ϵ where f is a known transformation function (Yang et al. 2015). Based on our analysis, it is clear that the theoretical results are not limited to the sigmoid transfer function. In fact, the proposed methods can be applied to a wide range of transformation functions satisfying the following conditions: (C1) f is continuous and for any $u\in ℝ$, 0 < f (u) < 1; (C2) for any $u_1,u_2\in ℝ$, there exists a constant L > 0 such that $|\dot{f}\left(u_1\right)-\dot{f}\left(u_2\right)|\le L|u_1-u_2|$; and (C3) for any constant C > 0, there exists δ > 0 such that for any $|u|\le C,\dot{f}(u)\ge \delta$. Examples include but are not limited to the following function classes

• Cumulative density functions: f (x) = P(X ≤ x) for some continuous random variable X supported on $ℝ$. In particular, when X ~ N(0, 1), the resulting model becomes the probit regression.

• Affine hyperbolic tangent functions: $f(x)=\frac{1}{2}\text{tanh}(ax+b)+1$ for some parameter $a,b\in ℝ$. In particular, (a, b) = (1, 0) corresponds to f (x) = e^x / (1 + e^x).

• Generalized logistic functions: f (x) = (1 + e^−x)^−α for some α > 0.

Besides the problems we considered in this paper, it is also of interest to construct confidence intervals for functionals of the regression coefficients, such as ‖β‖₁,‖β‖₂, or θ^⊤β for some given loading vector θ. In modern statistical machine learning, logistic regression is considered as an efficient classification method (Abramovich and Grinshtein 2018). In practice, a predicted label with an uncertainty assessment is usually preferred. Therefore, another important problem is the construction of predictive intervals of the conditional probability π* associated with a given predictor X*. These problems are related to the current work and are left for future investigations.

8. PROOFS OF THE MAIN THEOREMS

In this section, we prove Theorems 1, Theorem 2 and Theorem 4 in the paper. The proofs of other results, including Theorems 3 and 5, Proposition 1 and the technical lemmas, are given in our Supplementary Materials.

Proof of Theorem 1

Define $F_{ij}=\mathbb{E}\left[{\eta }_{ij}^2/\dot{f}\left(u_i\right)\right]$. Under H₀, $F_{ij}=4\mathbb{E}\left[{\eta }_{ij}^2\right]=4/{\omega }_{jj}$, and by (A3), c < F_jj < C for j = 1, …, p and some constant C ≥ c > 0. Define statistics

$${\tilde{M}}_j=\frac{\langle v_j,ϵ\rangle }{\Vert v_j{\Vert }_n},\text{ and }{\check{M}}_j=\frac{\sum _{i=1}^n{\eta }_{ij}{ϵ}_i/\dot{f}\left(u_i\right)}{\sqrt{n{F}_{jj}}},j=1,\dots ,p.$$

and ${\tilde{M}}_n={\text{max}}_j{\tilde{M}}_j^2$, ${\check{M}}_n={\text{max}}_j{\check{M}}_j^2$. The following lemma shows that ${\tilde{M}}_n$ and therefore ${\check{M}}_n$ are good approximations of M_n.

Lemma 1. Under the condition of Theorem 1, the following events

$$B_1=\left\{|{\tilde{M}}_n-{\check{M}}_n|=o(1)\right\},B_2=\left\{|{\tilde{M}}_n-M_n|=o\left(\frac{1}{\text{log}p}\right)\right\},$$

hold with probability at least 1 − O(p^−c) for some constant c > 0.

It follows that under the event B₁ ∩ B₂, let y_p = 2log p − loglog p + x and ϵ_n = o(1), we have

$$P_{\theta }\left({\check{M}}_n\le y_p-{ϵ}_n\right)\le P_{\theta }\left(M_n\le y_p\right)\le P_{\theta }\left({\check{M}}_n\le y_p+{ϵ}_n\right)$$

Therefore it suffices to prove that for any $t\in ℝ$, as (n, p) → ∞,

$$P_{\theta }\left({\check{M}}_n\le y_p\right)\to \text{exp}\left(-\frac{1}{\sqrt{\tau }}\text{exp}(-x/2)\right).$$ (21)

Now define ${\widehat{M}}_j=\frac{\sum _{i=1}^n{\widehat{Z}}_{ij}}{\sqrt{n{F}_{ij}}},j=1,\dots ,p.$ where ${\widehat{Z}}_{ij}=v_{ij}^0{ϵ}_{i}1\left\{|v_{ij}^0{ϵ}_i|\le {\tau }_n\right\}-\mathbb{E}\left[v_{ij}^0{ϵ}_{i}1\left\{|v_{ij}^0{ϵ}_i|\le {\tau }_n\right\}\right]$ for τ_n = log(p + n), $v_{ij}^0={\eta }_{ij}/\dot{f}\left(u_i\right)$ and ${\widehat{M}}_n={\text{max}}_j{\widehat{M}}_j^2$. The following lemma states that ${\widehat{M}}_n$ is close to ${\check{M}}_n$.

Lemma 2. Under the condition of Theorem 1, $|{\check{M}}_n-{\widehat{M}}_n|=o(1)$ with probability at least 1 − O(p^−c) for some constant c > 0.

By Lemma 2, it suffices to prove that for any $t\in ℝ$, as (n, p) → ∞,

$$P_{\theta }\left({\widehat{M}}_n\le y_p\right)\to \text{exp}\left(-\frac{1}{\sqrt{\pi }}\text{exp}(-x/2)\right).$$ (22)

To prove this, we need the classical Bonferroni inequality.

Lemma 3. (Bonferroni inequality) Let $B=\underset{t=1}{\overset{p}{\cup }}{B}_t$. For any integer k < p / 2, we have

$$\sum _{t=1}^{2k}{(-1)}^{t-1}{A}_t\le P(B)\le \sum _{t=1}^{2k-1}{(-1)}^{t-1}{A}_t,$$ (23)

where $A_t=\sum _{1\le i_1<\dots <i_t\le p}P\left(B_{i_1}\cap \dots \cap B_{i_t}\right)$.

By Lemma 3, for any integer 0 < q < p / 2,

$$\sum _{d=1}^{2q}{(-1)}^{d-1}\sum _{1\le j_1\le \dots \le j_d\le p}{P}_{\theta }\left(\underset{k=1}{\overset{d}{\cap }}{A}_{j_k}\right)\le P_{\theta }\left(\underset{1\le j\le p}{\text{max}}{\widehat{M}}_j^2\ge y_p\right)\le \sum _{d=1}^{2p-1}{(-1)}^{d-1}\sum _{1\le j_1<\dots <j_d\le p}{P}_{\theta }\left(\underset{k=1}{\overset{d}{\cap }}{A}_{j_k}\right),$$ (24)

where $A_{j_k}=\left\{{\widehat{M}}_{j_k}^2\ge y_p\right\}$. Now let $w_{i_j}={\widehat{Z}}_{ij}/\sqrt{F_{jj}}$ for j = 1, …, p, and $W_i={\left(w_{i,j_1},\dots ,w_{i,j_d}\right)}^{\top }$ for 1 ≤ i ≤ n. Define ‖a‖_min = min_1≤i≤d | a_i| for any vector $a\in {ℝ}^d$. Then we have

$$P_{\theta }\left(\underset{k=1}{\overset{d}{\cap }}{A}_{j_k}\right)=P((n^{-1/2}\sum _{i=1}^n{W}_i{(}_{\text{min}}\ge y_p^{1/2}).$$

Then it follows from Theorem 1.1 in Zaitsev (1987) that

$$P_{\theta }(\left(n^{-1/2}\sum _{i=1}^n{W}_i{(}_{\text{min}}\ge y_p^{1/2}\right)\le P_{\theta }\left(\Vert N_d{\Vert }_{\text{min}}\ge y_p^{1/2}-{ϵ}_n{(\text{log}p)}^{-1/2}\right)+c_1{d}^{5/2}\text{exp}\left\{-\frac{n^{1/2}{ϵ}_n}{c_2{d}^3{\tau }_n{(\text{log}p)}^{1/2}}\right\},$$ (25)

where c₁ > 0 and c₂ > 0 are constants, ϵ_n → 0 which will be specified later, and $N_d=\left(N_{m_1},\dots ,N_{m_d}\right)$ is a normal random vector with $\mathbb{E}\left(N_d\right)=0$ and cov(N_d) = cov(W₁). Here d is a fixed integer that does not depend on n, p. Because log p = o(n^1/5), we can let ϵ_n → 0 sufficiently slow, say, ${ϵ}_n=\sqrt{{\text{log}}^{5}p/n}$, so that for any large c > 0,

$$c_1{d}^{5/2}\text{exp}\left\{-\frac{n^{1/2}{ϵ}_n}{c_2{d}^3{\tau }_n{(\text{log}p)}^{1/2}}\right\}=O\left(p^{-c}\right).$$ (26)

Combining (24), (25) and (26), we have

$$P_{\theta }\left(\underset{1\le j\le p}{\text{max}}{\widehat{M}}_j^2\ge y_p\right)\le \sum _{d=1}^{2p-1}{(-1)}^{d-1}\sum _{1\le j_1<\dots <j_d\le p}{P}_{\theta }\left(\Vert N_d{\Vert }_{\text{min}}\ge y_p^{1/2}-{ϵ}_n{(\text{log}p)}^{-1/2}\right)+o(1).$$ (27)

Similarly, one can derive

$$P_{\theta }\left(\underset{1\le j\le p}{\text{max}}{\widehat{M}}_j^2\ge y_p\right)\ge \sum _{d=1}^{2p}{(-1)}^{d-1}\sum _{1\le j_1<\dots <j_d\le p}{P}_{\theta }\left(\Vert N_d{\Vert }_{\text{min}}\ge y_p^{1/2}+{ϵ}_n{(\text{log}p)}^{-1/2}\right)+o(1).$$ (28)

Now we use the following lemma from Xia, Cai, and Cai (2018).

Lemma 4. For any fixed integer d ≥ 1 and real number $t\in ℝ$,

$$\sum _{1\le j_1<\dots <j_d\le p}{P}_{\theta }\left(\Vert N_d{\Vert }_{\text{min}}\ge y_p^{1/2}\pm {ϵ}_n{(\text{log}p)}^{-1/2}\right)=\frac{1}{d!}{\left(\frac{1}{\sqrt{\pi }}\text{exp}(-t/2)\right)}^d(1+o(1)).$$

It then follows from the above lemma, (27) and (28) that

$$\underset{n,p\to \infty }{\text{limsup}}{P}_{\theta }\left(\underset{1\le j\le p}{\text{max}}{\widehat{M}}_j^2\ge y_p\right)\le \sum _{d=1}^{2p}{(-1)}^{d-1}\frac{1}{d!}{\left(\frac{1}{\sqrt{\pi }}\text{exp}(-t/2)\right)}^d,$$

$$\underset{n,p\to \infty }{\text{liminf}}{P}_{\theta }\left(\underset{1\le j\le p}{\text{max}}{\widehat{M}}_j^2\ge y_p\right)\ge \sum _{d=1}^{2p-1}{(-1)}^{d-1}\frac{1}{d!}{\left(\frac{1}{\sqrt{\pi }}\text{exp}(-t/2)\right)}^d,$$

for any positive integer p. By letting p → ∞, we obtain (22) and the proof is complete. □

Proof of Theorem 2.

The proof essentially follows from the general Le Cam’s method described in Section 7.1 of Baraud (2002). The key elements can be summarized as the following lemma that reduces the lower bound problem to calculation of the total variation distance between two posterior distributions.

Lemma 5. Let ${\mathcal{H}}_1$ be some subset in an ${\mathcal{l}}_2$ bounded Hilbert space and ρ some positive number. Let μ_ρ be some probability measure on ${\mathcal{H}}_1=\left\{\theta \in \Theta ,\Vert \theta \Vert =\rho \right\}$. Set $P_{{\mu }_{\rho }}=\int P_{\theta }d{\mu }_{\rho }(\theta )$, P₀ as the (posterior) distribution at the null, and denote by Φ_α the level-α tests, we have

$$\underset{{\Phi }_{\alpha }}{\text{inf}}\underset{\theta \in {\mathcal{H}}_1}{\text{sup}}{P}_{\theta }\left({\Phi }_{\alpha }=0\right)\ge \underset{{\Phi }_{\alpha }}{\text{inf}}{P}_{{\mu }_{\rho }}\left({\Phi }_{\alpha }=0\right)\ge 1-\alpha -TV\left(P_{{\mu }_{\rho }},P_0\right),$$

where $TV\left(P_{{\mu }_{\rho }},P_0\right)$ denotes the total variation distance between $P_{{\mu }_{\rho }}$ and P₀.

Now since by definition ρ*(Φ_α, δ, Θ(k)) ≥ ρ*(Φ_α, δ, Σ) for any Σ ∈Θ₂(k), by Lemma 5, it suffices to construct the corresponding ${\mathcal{H}}_1$ for β ∈Θ_β(k) and find a lower bound ρ₁ = ρ(η) such that

$$\forall \rho \le {\rho }_1\underset{{\Phi }_{\alpha }}{\text{inf}}{P}_{{\mu }_{\rho }}\left({\Phi }_{\alpha }=0\right)\ge 1-\alpha -\eta =\delta .$$ (29)

for fixed covariance Σ = I. In this case, an upper bound for the χ²-divergence between $P_{{\mu }_{\rho }}$ and P₀, defined as ${\chi }^2\left(P_{{\mu }_{\rho }},P_0\right)=\int \frac{{\left(d{P}_{{\mu }_{\rho }}\right)}^2}{d{P}_0}-1$, can be obtained by carefully constructing the alternative space ${\mathcal{H}}_1$. Since $TV(f,g)\le \sqrt{{\chi }^2(f,g)}$ (see p.90 of Tsybakov (2009)), it follows that $\underset{{\Phi }_{\alpha }}{\text{inf}}{P}_{{\mu }_{\rho }}\left({\Phi }_{\alpha }=0\right)\ge 1-\alpha -\sqrt{{\chi }^2\left(P_{{\mu }_{\rho }},P_0\right)}$. By choosing ρ₁ = ρ(η) such that for any ρ ≤ ρ₁, ${\chi }^2\left(P_{{\mu }_{\rho }},P_0\right)\le {\eta }^2={(1-\alpha -\delta )}^2$, we have (29) holds. In the following, we will construct the alternative space ${\mathcal{H}}_1$ and derive an upper bound of ${\chi }^2\left(P_{{\mu }_{\rho }},P_0\right)$ where P₀ corresponds to the null space ${\mathcal{H}}_0$ defined at a single point β = 0. We divide the proofs into two parts. Throughout, the design covariance matrix is chosen as Σ = I.

Step 1: Construction of ${\mathcal{H}}_1$.

Firstly, for a set M, we define $\mathcal{l}(M,n)$ as the set of all the n-element subsets of M. Let [1: p] ≡ {1, …, p}, so $\mathcal{l}([1:p],k)$ contains all the k-element subsets of [1: p]. We define the alternative parameter space ${\mathcal{H}}_1=\left\{\beta \in {ℝ}^p:{\beta }_j=\rho 1\left\{j\in I\right\}\text{ for }I\in \mathcal{l}([1:p],k)\right\}$. In other words, ${\mathcal{H}}_1$ contains all the k-sparse vectors β(I) whose nonzero components ρ are indexed by I. Apparently, for any $\beta \in {\mathcal{H}}_1$, it follows ‖β‖_∞ = ρ and ${\mathcal{H}}_1\subseteq {\Theta }_1(k)$.

Step 2: Control of ${\chi }^2\left(P_{{\pi }_{{\mathcal{H}}_1}},P_0\right)$.

Let π denote the uniform prior of the random index set I over $\mathcal{l}([1:p],k)$. This prior induces a prior distribution ${\pi }_{{\mathcal{H}}_1}$ over the parameter space ${\mathcal{H}}_1$. For $\left\{0_p\right\}={\mathcal{H}}_0$, the corresponding joint distribution of the data ${\left\{\left(X_i,y_i\right)\right\}}_{i=1}^n$ is

$$f=\prod _{i=1}^{n}p\left(X_i,y_i\right)=\frac{1}{{(2\pi )}^{np/2}}\prod _{i=1}^n\frac{1}{2}{e}^{-\Vert X_i{\Vert }_2^2/2}.$$

Similarly, the posterior distribution of the samples over the prior ${\pi }_{{\mathcal{H}}_1}$ is denoted as

$$g=\prod _{i=1}^n\underset{{\mathcal{H}}_i}{\int }p\left(X_i,y_j;\beta \right){\pi }_{{\mathcal{H}}_i}=\frac{1}{\left(\begin{array}{l}p\hfill \\ k\hfill \end{array}\right)}\sum _{\beta \in {\mathcal{H}}_1}\prod _{i=1}^{n}p\left(X_i,y_i;\beta \right).$$

As a result, we have the following lemma controlling ${\chi }^2\left(P_{{\pi }_{{\mathcal{H}}_1}},P_0\right)={\chi }^2(g,f)$.

Lemma 6. Let ${\rho }^2=\frac{1}{n}\text{log}\left(1+\frac{p}{h(\eta )k^2}\right)$ where h(η) = [log(η² + 1)]⁻¹ and η = 1 − α − δ, then we have χ²(g, f) ≤ (1 − α − δ)².

Combining Lemma 5 and Lemma 6, we know that for α, δ > 0 and α + δ < 1, if $\rho =\sqrt{\frac{1}{n}\text{log}\left(1+\frac{p}{h(\eta )k^2}\right)}$, then $\forall {\rho }^{\prime }\le \rho ,\underset{{\Phi }_{\alpha }}{\text{inf}}\underset{\beta \in \Theta (k):\Vert \beta {\Vert }_{\infty }\ge {\rho }^{\prime }}{\text{sup}}{P}_{\theta }\left({\Phi }_{\alpha }=0\right)\ge \delta$. Therefore, it follows that

$${\rho }^{*}(\alpha ,\delta ,\Theta (k))\ge {\rho }^{*}(\alpha ,\delta ,I)\gtrsim \sqrt{\frac{1}{n}\text{log}\left(1+\frac{p}{k^2}\right)}.$$ (30)

Lastly, note that for the above chosen ρ, ${\mathcal{H}}_1\subset {\Theta }_1(k)\cap \left\{\beta \in {ℝ}^p:\Vert \beta {\Vert }_2\lesssim {\left(n^{1/4}\text{log}p\right)}^{-1}\right\}$ when $k\lesssim \text{min}\left\{p^{\gamma },\sqrt{n}/{\text{log}}^{3}p\right\}$ for some 0 < γ < 1 / 2. This completes the proof. □

Proof of Theorem 4.

The proof follows similar arguments of the proof of Theorem 3.1 in Javanmard and Javadi (2019). We first consider the case when $\widehat{t}$, given by (17), does not exist. In this case, $\widehat{t}=\sqrt{2\text{log}p}$ and we consider the event ${\Omega }_0=\left\{\sum _{j\in {\mathcal{H}}_0}I\left(|M_j|\ge \sqrt{2\text{log}p}\right)\ge 1\right\}$ that there are at least one false positive. In order to show the FDR/FDP can be controlled in this case, we show that

$$P_{\theta }\left({\Omega }_0\right)\to 0,\text{ as }(n,p)\to \infty .$$ (31)

Note that for $j\in {\mathcal{H}}_0$, we have $M_j=\frac{{\check{\beta }}_j}{{\tau }_j}=\frac{\langle v_j,ϵ\rangle }{\Vert v_j{\Vert }_n}+\frac{\langle v_j,Re\rangle }{\Vert v_j{\Vert }_n}-\frac{{\langle v_j,h_{-j}\rangle }_n}{\Vert v_j{\Vert }_n}$ Then

$$P_{\theta }\left({\Omega }_0\right)\le P_{\theta }\left(\sum _{j\in {\mathcal{H}}_0}I\left(\frac{\langle v_j,ϵ\rangle }{\Vert v_j{\Vert }_n}+\frac{\langle v_j,Re\rangle }{\Vert v_j{\Vert }_n}-\frac{{\langle v_j,h_{-j}\}}_n}{\Vert v_j{\Vert }_n}\ge \sqrt{2\text{log}p}\right)\ge 1\right)+P_{\theta }\left(\sum _{j\in {\mathcal{H}}_0}I\left(\frac{\langle v_j,ϵ\rangle }{\Vert v_j{\Vert }_n}+\frac{\langle v_j,Re\rangle }{\Vert v_j{\Vert }_n}-\frac{{\langle v_j,h_{-j}\rangle }_n}{\Vert v_j{\Vert }_{\pi }}\le \sqrt{2\text{log}p}\right)\ge 1\right).$$ (32)

For any ϵ > 0, we can bound the first term by

$$\begin{gathered} P_{\theta }\left(\sum _{j\in {\mathcal{H}}_0}I\left(\frac{\langle v_j,ϵ\rangle }{{\Vert v_j\Vert }_k}+\frac{\langle v_{f}Re\rangle }{{\Vert v_j\Vert }_v}-\frac{{\langle v_j,h_{-j}\rangle }_n}{{\Vert v_j\Vert }_n}\ge \sqrt{2\text{log}p}\right)\ge 1\right) \\ =P_{\theta }\left(\sum _{j\in {\mathcal{H}}_0}I\left({\tilde{M}}_j\ge \sqrt{2\text{log}p}+\frac{{\langle v_j,h_{-j}\rangle }_n}{{\Vert v_j\Vert }_n}-\frac{\langle v_j,Re\rangle }{{\Vert v_j\Vert }_n}\right)\ge 1\right) \\ \le P_{\theta }\left(\sum _{j\in {\mathcal{H}}_0}I\left({\tilde{M}}_j\ge \sqrt{2\text{log}p}-ϵ\right)\ge 1\right)+P_{\theta }\left(\underset{j\in {\mathcal{H}}_0}{\text{max}}|\frac{{\langle v_j,h_{-j}\rangle }_n}{{\Vert v_j\Vert }_n}-\frac{\langle v_j,Re\rangle }{{\Vert v_j\Vert }_n}|\ge ϵ\right) \\ \le p\underset{j\in {\mathcal{H}}_0}{\text{max}}{P}_{\theta }\left({\tilde{M}}_j\ge \sqrt{2\text{log}p}-ϵ\right)+P_{\theta }\left(\underset{j\in {\mathcal{H}}_0}{\text{max}}|\frac{{\langle v_j,h_{-j}\rangle }_n}{{\Vert v_j\Vert }_n}-\frac{\langle v_j,Re\rangle }{{\Vert v_j\Vert }_n}|\ge ϵ\right) \end{gathered}$$

By the proof of Lemma 1, we know that $P_{\theta }\left({\text{max}}_{j\in {\mathcal{H}}_0}|\frac{{\langle v_j,h_{-j}\rangle }_n}{\Vert v_j{\Vert }_n}-\frac{\langle v_j,Re\rangle }{\Vert v_j{\Vert }_n}|\ge ϵ\right)\to 0$. In addition, for $j\in {\mathcal{H}}_0,P_{\theta }\left({\tilde{M}}_j\ge \sqrt{2\text{log}p}-ϵ\right)\le P_{\theta }\left({\check{M}}_j\ge \sqrt{2\text{log}p}-2ϵ\right)+P_{\theta }\left(|{\tilde{M}}_j-{\check{M}}_j|\ge ϵ\right)$, where ${\text{max}}_{j\in {\mathcal{H}}_0}{P}_{\theta }\left(|{\tilde{M}}_j-{\check{M}}_j|\ge ϵ\right)=O\left(p^{-c}\right)$ for some sufficiently large c > 0. Now since ${\check{M}}_j=\frac{\sum _{i=1}^n{\eta }_{ij}{ϵ}_i/\dot{f}\left(u_i\right)}{\sqrt{n{F}_{jj}}}$ where $\mathbb{E}\frac{{\eta }_{ij}{ϵ}_i/\dot{f}\left(u_i\right)}{\sqrt{F_{jj}}}=0$ and $\text{Var}\left(\frac{{\eta }_{ij}{ϵ}_i/\dot{f}\left(u_i\right)}{\sqrt{F_{jj}}}\right)=1$, by Lemma 6.1 of Liu (2013), we have $\underset{0\le t\le 4\sqrt{\text{log}p}}{\text{sup}}|\frac{P_{\theta }\left(|{\check{M}}_j|\ge t\right)}{G(t)}-1|\le C{(\text{log}p)}^{-1}$. Now let $t=\sqrt{2\text{log}p}-2ϵ$, we have $P_{\theta }\left({\check{M}}_j\ge \sqrt{2\text{log}p}-2ϵ\right)\le G(\sqrt{2\text{log}p}-2ϵ)+C\frac{G(\sqrt{2\text{log}p}-2ϵ)}{\text{log}p}$.

Hence $p{\text{max}}_{j\in {\mathcal{H}}_0}{P}_{\theta }\left({\tilde{M}}_j\ge \sqrt{2\text{log}p}-ϵ\right)\le CpG(\sqrt{2\text{log}p}-2ϵ)+O\left(p^{-c}\right)$, which goes to zero as (n, p) → ∞. By symmetry, we know that the second term in (32) also goes to 0. Therefore we have proved (31).

Now consider the case when $0\le \widehat{t}\le b_p$ holds. We have

$${\text{FDP}}_{\theta }(\widehat{t})=\frac{\sum _{j\in {\mathcal{H}}_0}I\left\{|M_j|\ge \widehat{t}\right\}}{\text{max}\left\{\sum _{j=1}^{p}I\left\{|M_j|\ge \widehat{t}\right\},1\right\}}\le \frac{p_{0}G(\widehat{t})}{\text{max}\left\{\sum _{j=1}^{p}I|M_j|\ge \widehat{t}\right\},1\}}\left(1+A_p\right),$$

where $A_p=\underset{0\le t\le b_p}{\text{sup}}|\frac{\sum _{j\in {\mathcal{H}}_0}I\left\{|M_j|\ge t\right\}}{p_{0}G(t)}-1|$ Note that by definition $\frac{p_{0}G(\widehat{t})}{\text{max}\left\{\sum _{j=1}^{p}I\left\{|M_j|\ge \widehat{t}\right\},1\right\}}\le \frac{p_0\alpha }{p}$. The proof is complete if A_p → 0 in probability, which has been shown by Proposition 1. □