Stimulus- and goal-oriented frameworks for understanding natural vision

Abstract

Our knowledge of sensory processing has advanced dramatically in the last few decades, but this understanding remains far from complete, especially for stimuli with the large dynamic range and strong temporal and spatial correlations characteristic of natural visual inputs. Here we describe some of the issues that make understanding the encoding of natural image stimuli challenging. We highlight two broad strategies for approaching this problem: a stimulus-oriented framework and a goal-oriented one. Different contexts can call for one or the other framework. Looking forward, recent advances, particularly those based in machine learning, show promise in borrowing key strengths of both frameworks and by doing so illuminating a path to a more comprehensive understanding of the encoding of natural stimuli.

Introduction

The neural circuits that process sensory inputs are shaped by the properties of the stimuli they encounter as well as the behavioral demands of the animal. Because of this, a deep understanding of sensory circuits and the computations they support requires connecting what we know about sensory systems to properties of natural stimuli. In this review, we discuss some of the progress and the challenges in describing the neural encoding of complex stimuli such as those encountered in the real world; related issues extend to many areas beyond neurophysiology. We refer to the encoding of visual scenes as a paradigmatic example, but many of the same issues arise in other sensory modalities.

Progress in studying sensory coding has traditionally relied on parameterized, artificial stimuli designed to isolate and characterize specific circuit mechanisms, such as nonlinearities in the integration of signals across space (reviewed by (Gollisch and Meister, 2010; Schwartz and Rieke, 2011)) or adaptation to changes in particular stimulus properties such as intensity, contrast, or orientation (reviewed by (Demb and Singer, 2015; Graham, 2011; Rieke and Rudd, 2009; Solomon and Kohn, 2014)). These approaches have revealed the mechanistic basis of many important circuit computations but have not led to a clear understanding of the encoding of natural stimuli.

Two issues make studying the encoding of natural stimuli challenging compared to typical artificial stimuli. First, complex stimuli, such as natural visual inputs, engage a host of interacting circuit mechanisms rather than individual mechanisms in isolation. This complexity is difficult to capture with computational models. For example, many predictive neurobiological models for stimulus-response transformations in the early visual system are based on a common architecture: linear filtering over space and time, followed by a (generally time-dependent) nonlinearity. These models do not generalize well to capture responses to inputs other than those to which they were fit (Carandini et al., 2005; Heitman et al., 2016). Natural images can highlight such failures of generalization (David and Gallant, 2005; Turner and Rieke, 2016; Turner et al., 2018). Incorporating known circuit features, or stacking multiple Linear-Nonlinear layers, can improve generalization in both retina and V1 (David and Gallant, 2005; Maheswaranathan et al., 2017; Mcintosh et al., 2016). Stacked computations are also a central element of Deep Neural Network models for modeling higher cortical areas (Yamins and DiCarlo, 2016), as described in more detail below.

A second challenge inherent in the study of natural stimulus encoding is the complex statistics of natural scenes (reviewed by (Hyvärinen, 2010; Lewicki et al., 2014; Simoncelli and Olshausen, 2001; Zhaoping, 2014)). For example, across different visual scenes and even within a single scene, image statistics (e.g. mean intensity, spatial contrast, and other, higher-order statistics) can vary widely but (fortunately) not randomly (Coen-Cagli et al., 2012; Frazor and Geisler, 2006; Karklin and Lewicki, 2005; Parra et al., 2001; Ruderman and Bialek, 1994). Within a single visual scene, different image features are often strongly correlated, which makes it difficult to relate a neural response to a particular feature of a scene (see (Sharpee et al., 2006) for a computational approach to this issue). One approach to managing this complexity is to develop generative models of natural images that enable a low dimensional representation. Parametric models exist for naturalistic textures (Portilla and Simoncelli, 2000) -- i.e. semi-regular, repeating patterns (see Figure 1) -- and recent advances in machine learning show promise in generating not only textures (Gatys et al., 2015) but non-homogeneous naturalistic images (Arjovsky et al., 2017; Karras et al., 2018); for applications of these approaches see (Freeman et al., 2013; Okazawa et al., 2015; Rust and DiCarlo, 2010).

Figure 1: Texture Synthesis based on Deep Convolutional Neural Networks.

The activations of different layers of a DNN trained for object recognition can be employed to capture statistics of textures beyond second order (Gatys et al., 2015). Texture synthesis is accomplished by numerical optimization of the pixel values of an image that matches the statistics of a reference image (Original Image enclosed in black). Statistics can be obtained from activation values at different stages of the deep DNN. Images enclosed in red are synthesized by considering only activations from the first and second pooling stages of the DNN, whereas images enclosed in blue include the third and fourth pooling stages in their statistics. In the case of the inhomogeneous images (bottom row) the texture generation tiles local features in scrambled places that will match the activation statistics that have been averaged over space.

There is a long history of studying the encoding of natural scenes in neurophysiology experiments (e.g. (Baddeley et al., 1997; Creutzfeldt and Nothdurft, 1978; Smyth et al., 2003; Stanley et al., 1999; Vickers et al., 2001; Vinje and Gallant, 2000)), and recent years have seen this interest expand (e.g., (Sharpee et al., 2006; Theunissen and Elie, 2014; Zwicker et al., 2016) and references therein). Normative (“why”) models can incorporate knowledge about the statistical structure of natural scenes or the task goals and hence add an additional perspective on top of descriptive and mechanistic models (Dayan and Abbott, 2001).

Stimulus- and goal-oriented approaches to natural stimulus encoding

We will focus on two theoretical frameworks that are often appealed to in the study of natural stimulus encoding:

1. A stimulus-oriented (or efficient coding) framework, that formalizes the idea that a major goal of sensory processing is to encode as much information as possible about a stimulus using limited resources. This framework identifies transformations of sensory input signals that reduce statistical redundancies present in the natural world. These transformations often rely on general purpose computations that care about the information available in a stimulus and are blind to the specific uses of this information. Complementary approaches based on generative modeling seek to capture the statistical dependencies of natural scenes, and by doing so reveal how they can be reduced. Stimulus-oriented approaches are closely related to unsupervised machine learning, for which learning is based only on properties of the input and does not require a specific goal such as object recognition.

2. A goal-oriented framework, which appeals to the computational or behavioral goal of the circuit or animal. Unlike stimulus-oriented approaches, goal-oriented approaches explicitly treat some features of the stimulus differently than others, and which features are encoded depends on the desired behavioral output or goal. These approaches include recent advances in Deep Convolutional Neural Networks, particularly those based on supervised, discriminative learning from large databases of images with identified and labeled objects.

These two frameworks may appear to be at odds. For instance, a model focused solely on a high-level goal like object recognition will not necessarily reduce redundancies or capture general statistical properties of the stimulus. Conversely, models focusing on reducing redundancies are not likely to explain, at least not explicitly, complex tasks such as object recognition. Historically, stimulus-oriented frameworks have largely been applied to early visual areas and goal-oriented objectives to later cortical areas. But these boundaries are beginning to blur. Indeed, in some cases the two approaches can be seen as complementary. For instance, even well-established visual computations like lateral inhibition can be seen through both lenses: as a mechanism to suppress responses to low spatial frequencies and eliminate some of the redundancies present in natural images (Atick and Redlich, 1992; Srinivasan et al., 1982), or as a way to facilitate the detection of specific features of a scene, namely edges (Marr and Hildreth, 1980). We will discuss some modern computational approaches that may facilitate the merger of these two frameworks, allowing one to inform the other and vice-versa. In particular, deep neural networks provide a promising route for exploring how stimulus- and goal-oriented constraints together shape sensory processing.

Stimulus-oriented approaches to natural vision

An influential hypothesis that undergirds much of the study of natural scene processing is the “efficient coding hypothesis,” first proposed by Barlow (Barlow, 2001, 1961) (see also (Attneave, 1954)), and influenced by Shannon’s earlier work on information theory (Shannon, 1948).

Barlow proposed that an efficient coding scheme should reduce the redundancy of natural inputs, but without loss of the information that is encoded (Barlow, 1961). Redundancy as defined by Barlow is the fraction of the total information carrying capacity of a neuron or neural population that is not used to transmit information about the stimulus. Efficient coding has been contrasted with a “sparse” neural code, where the goal is not defined as redundancy reduction, but rather to produce a sparse representation of natural inputs (Field, 1994).

Redundancy reduction predicts that a single noiseless neuron should distribute its responses uniformly (e.g., subject to a constraint on the maximal firing rate), such that each possible response occurs with equal frequency; to do otherwise would mean that the neuron is not making full use of its dynamic range. Examples of approximately uniformly-distributed sensory representations can be found in a variety of sensory systems (Bhandawat et al., 2007; Laughlin, 1981). Consideration of neural noise can substantially alter predictions of efficient coding because in that case efficiency involves both using a cell’s full response range and mitigating the effect of noise (Brinkman et al., 2016; Gjorgjieva et al., 2014; Kastner et al., 2015).

Redundancy reduction in a population of neurons (i.e., multiple channels) relies on removing statistical dependencies among their responses (Barlow, 1961). Reducing redundancy for natural stimuli is particularly challenging because natural visual inputs contain strong (nonlinear) statistical regularities across time and space (for a review, see (Simoncelli and Olshausen, 2001)). We start by describing the application of these ideas in early sensory areas (largely the retina) and then turn to efficient coding in visual cortex.

Efficient coding and second order statistics

Second-order spatial correlations in natural scenes have been a particular focus of efficient coding approaches. Such correlations, on average, obey a power law scaling: the power spectrum of spatial frequencies falls as the inverse of the square of the spatial frequency (Figure 2b) (Field, 1987). This is the result of the scale invariance of natural images -- i.e. many statistical properties are unchanged by magnifying or demagnifying an image (Ruderman and Bialek, 1994). Scale invariance has been suggested to result from the fact that objects can appear at any distance from an observer (Ruderman, 1994).

Figure 2: Efficient coding strategies rely on self-generated movement.

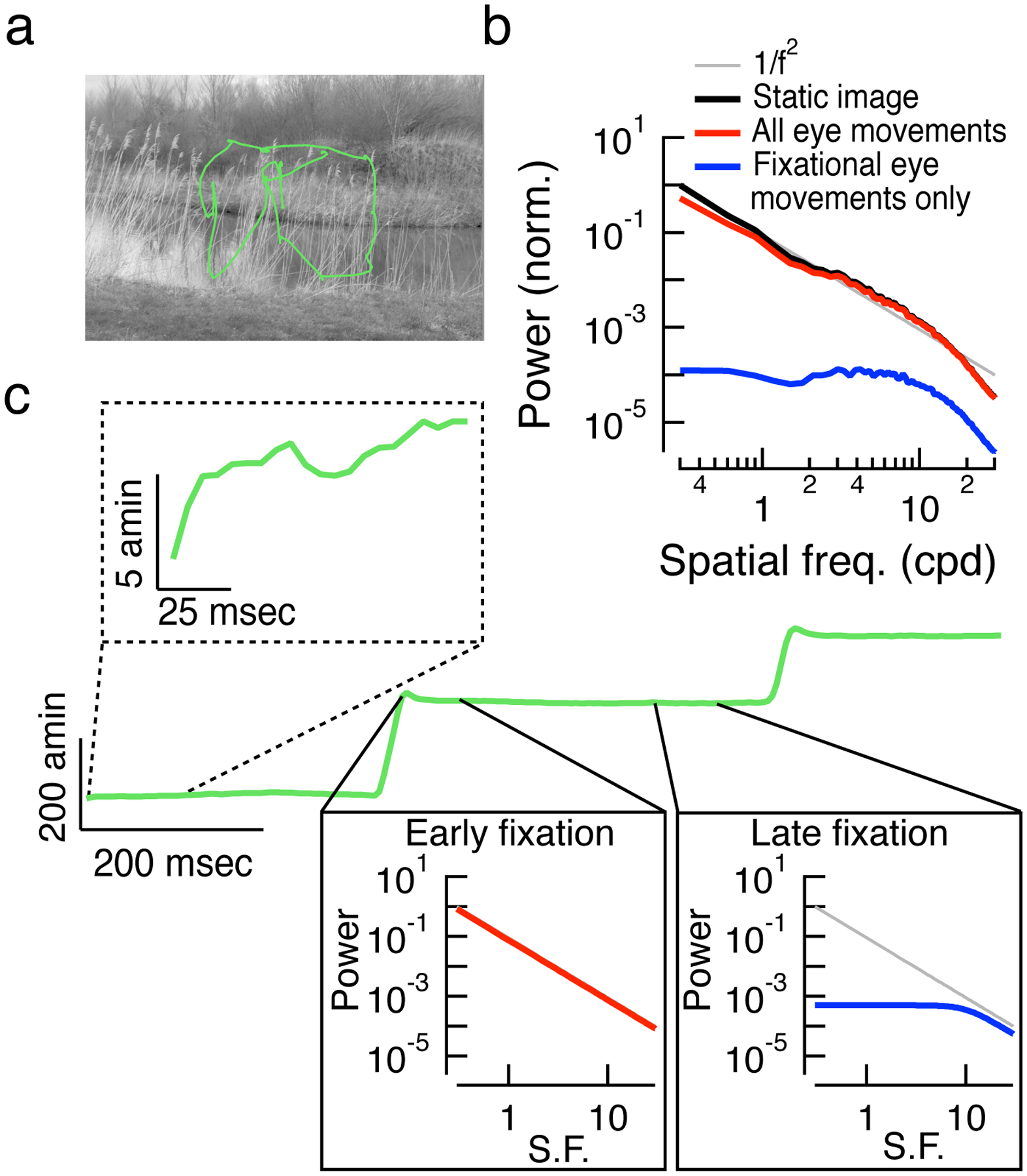
(a) A natural image and measured human eye movement trajectory from (Van Der Linde et al., 2009). An observer will explore a scene using large, ballistic changes in fixation called saccades. In the time between saccades, observers make much smaller, involuntary eye movements called fixational eye movements (for review, see (Rucci and Victor, 2015)). (b) Using these eye movement data, we can reconstruct the time-varying image on the retina into a naturalistic movie stimulus. We summed the Fourier spatial power spectra of each frame of this movie, resulting in a roughly 1/f² power law scaling, which is characteristic of static natural images (black trace). Following the analysis in (Kuang et al., 2012), we then measured spatial power spectra for the dynamic component of the natural movie. To produce these spatial power spectra, we computed the spatiotemporal power spectrum of a movie and summed over all non-zero temporal frequencies. Fixational eye movements simply shift much of the power, except that at the lowest spatial frequencies, to higher temporal frequencies. The removal of the temporal DC component of the movie thus selectively removes low spatial frequency content, and the result is a whitened spatial power spectrum (Fig. 2b, blue trace). Importantly, this result relies on fixational eye movements and not saccades. When saccades are included in the natural movie stimulus, considerable low spatial frequency content is still present at nonzero temporal frequencies, so whitening does not occur (Fig. 2b, red trace). (c) The position (in one dimension) of the eye as a function of time is shown by the green trace. Examining the eye position at a finer time scale (dashed inset) reveals smaller fixational eye movements. Boi et al. (Boi et al., 2017) suggested that during a saccade, the dynamic spatial frequency content of natural images follows the familiar 1/f² power law scaling (left inset, red trace). As the fixation proceeds, the retinal input is whitened (right inset, blue trace). Between saccades (when the image is relatively stable), any low spatial frequency content is present mostly in the temporal DC component of the input. In other words, the large-scale spatial structure isn’t changing very much within a single fixation. The whitening effect of fixational eye movements will depend on how completely (and how quickly) a visual neuron adapts to the (mostly static) low spatial frequency content imposed by each new fixation.

The prevalence of low spatial frequencies in natural images produces correlated responses in nearby cells, leading to a redundant population code. Receptive field surrounds of neurons in retina and LGN decorrelate responses of nearby neurons by suppressing responses to low spatial frequencies. This is sometimes referred to as “whitening” (Atick and Redlich, 1992; Dan et al., 1996) (but see (Franke et al., 2017; Pitkow and Meister, 2012; Vincent and Baddeley, 2003)). Whitening, however, will increase high spatial frequency noise such as that in photoreceptor signals; consideration of noise predicts that the suppressive surround should be minimal or absent when noise is high (for a review, see (Atick, 1992; Zhaoping, 2006)). Similar principles of whitening without amplifying noise have also been proposed in other domains, such as stereo coding in cortex (Li and Atick, 1994).

These applications of efficient coding in the retina do not consider the impact of self-generated movement on stimulus statistics. Eye movements are one example. Human eye movements are characterized by small fixational movements and occasional discrete and rapid saccades (Figure 2a,c). The spatial frequency spectrum of natural images, subject to fixational eye movements, is roughly flat (i.e., whitened) at low spatial frequencies (Kuang et al., 2012) (Figure 2b). Natural inputs that simulate fixational eye movements indeed appear to decorrelate responses in populations of salamander retinal ganglion cells (Segal et al., 2015). This whitening effect does not hold for large and rapid eye movements like saccades (Boi et al., 2017) (see Figure 2b). Thus, Rucci & colleagues (especially (Boi et al., 2017)) suggest that a single cell may use different decorrelation strategies throughout the course of natural stimulation: classical surround-mediated decorrelation or decorrelation via nonlinearities in spike generation (Pitkow and Meister, 2012) immediately following a saccade and eye-movement generated whitening during the later parts of the fixational periods between saccades. Understanding the effects of such self-generated motion on the encoding of natural scenes will require further experiments (e.g., manipulating the statistics of synthetic eye movements in experiments on primate retina).

Efficient coding beyond second order statistics

Much of the classical work on efficient coding considers only second-order statistics and their removal by decorrelation. There is, however, much more to natural images than their spatial frequency spectra. This is evident when viewing artificial stimuli with a “natural” distribution of energy across spatial frequencies but no other statistical constraints; such images look highly unnatural (e.g Figure 3). This raises a concern that coding algorithms focusing on decorrelation may miss essential features of what early visual neurons do.

Figure 3: Beyond-pairwise statistics contribute to complex structure in natural images.

Top row: Two grayscale natural images. Middle row: The natural images above with randomized phase spectra. Both of these images have the roughly 1/f² spatial power spectrum characteristic of natural images, yet appear quite unnatural. Bottom row: The natural images with their phase spectra swapped, such that the image on the left now has the phase spectrum of the original image on the right, and vice-versa. See (Simoncelli and Olshausen, 2001; Thomsom, 1999).

Statistical independence provides a stronger constraint on efficient coding between channels (i.e. neurons or neuron-like receptive fields) than decorrelation (for a comprehensive review, see book by (Hyvärinen et al., 2009)). Although achieving independence in general is a difficult problem, it can be simplified by considering only linear transformations followed by a point nonlinearity (i.e. a linear-nonlinear approach). Two such approaches applied to natural images (Independent Component Analysis and Sparse Coding) yield filters that qualitatively resemble the oriented and localized structure of receptive fields in primary visual cortex (Bell and Sejnowski, 1997; Olshausen and Field, 1996); for a review, see (Simoncelli and Olshausen, 2001). More recent work shows that optimizing for a form of hard sparseness in which only a limited number of neurons are active can yield a better match to the full variety of cortical receptive fields in macaque (Rehn and Sommer, 2007).

Different channels can also exhibit nonlinear statistical dependencies that cannot be fully removed by linear or linear-nonlinear approaches (see (Eichhorn et al., 2009; Golden et al., 2016; Schwartz and Simoncelli, 2001) and references therein). This has prompted work on reducing statistical dependencies via nonlinear transformations. These approaches have led to more direct comparisons between models derived from scene statistics and nonlinear neural behaviors. One focus in area V1 has been on modeling nonlinear contextual phenomena, whereby the responses of neurons to a target stimulus are influenced by stimuli that spatially surround the target, or by stimuli that have been observed in the past. Such effects can be modeled by reducing statistical dependencies between filter responses across space or time via a nonlinear computation known as divisive normalization or by other complementary approaches (Coen-Cagli et al., 2012; Karklin and Lewicki, 2009; Lochmann et al., 2012; Rao and Ballard, 1999; Schwartz and Simoncelli, 2001; Spratling, 2010; Zhu and Rozell, 2013). The statistical dependencies between filter responses can also be exploited to build models of V1 complex cells that pool together filters, resulting in invariances to translation and other properties (Hyvärinen and Hoyer, 2000; Karklin and Lewicki, 2009) (for a review see book by (Hyvärinen et al., 2009) and references therein; see also (Berkes and Wiskott, 2005; Cadieu and Olshausen, 2012)). V2 models have been derived by stacking multiple layers of linear-nonlinear transforms to achieve statistical independence, sparseness, or other related stimulus-driven goals (Coen-Cagli and Schwartz, 2013; Hosoya and Hyvarinen, 2015; Lee et al., 2008; Shan and Cottrell, 2013). One can in principle stack many layers to model higher level visual areas, but this has been rather challenging from a stimulus-based scene statistics perspective.

Generative models that capture image statistics can complement efficient coding approaches (Dayan et al., 2003; Hinton and Ghahramani, 1997). Efficient coding approaches seek to transform and manipulate inputs so as to maximize the transfer of information, which can result in statistical independence of the transformed inputs. But learning to generate the statistical dependencies prevalent in natural scenes also shows how to reduce them. To make this more concrete, consider an example in which efficient coding and generative models are complementary. Multiplicative generative models for the nonlinear dependencies in filter responses to images lead immediately to approaches to reduce such dependencies via division (Wainwright and Simoncelli, 2000). Furthermore, these approaches lead to richer models of divisive normalization, predicting that normalization in V1 neurons (e.g., to reduce statistical dependencies) is absent unless center and surround are deemed statistically homogeneous or dependent for a given image (Coen-Cagli et al., 2012) (see also (Li, 1999)). Cagli et al. (Coen-Cagli et al., 2015) used predictions about statistical dependencies in images to fit V1 neural data for large natural image patches that extend beyond the classical receptive field. This resulted in better generalization than some descriptive models of divisive normalization, demonstrating the value of incorporating understanding about statistical dependencies in images.

Goal-oriented approaches to natural vision

Efficient coding predicts that neural processing will maximize the information transmitted about a stimulus without explicitly considering behavioral demands such as the specific tasks required for survival. These behavioral considerations are central to goal-oriented approaches, which view the importance of stimulus structure and circuit mechanisms on coding through the lens of specific behavioral demands. Because many behaviorally-relevant tasks require rich stimuli, goal-oriented approaches are often used to investigate the coding of natural inputs. We first illustrate these issues from studies of the retina and insect behavior, and then turn to their application in cortex.

Retinal ganglion cells support specific behavioral goals

A common observation that supports goal-oriented approaches is high neural selectivity to specific stimulus features to the exclusion of other (equally probable) stimulus features. In an early study of retinal feature selectivity, Lettvin and colleagues interpreted retinal ganglion cell (RGC) types in explicitly ethological terms, famously going so far as to speculate that one class of ganglion cell in the frog retina may be a “bug perceiver” (Lettvin et al., 1959). But the idea that the earliest neurons in the visual system are tuned to highly specific features of the visual world was ahead of its time. Instead, the dominant view of retinal processing for several decades thereafter focused on basic processing, including lateral inhibition (via a center-surround spatial receptive field) and simple forms of luminance adaptation (Masland and Martin, 2007). In this view, the computational heavy lifting to support specific behavioral goals is done in visual areas downstream of the retina and LGN.

A great deal of evidence has now accumulated that retinal computation is more complex (for a review see (Gollisch and Meister, 2010)). A wide variety of “non-standard” RGC computations have been discovered and often explained at the circuit and synaptic level. These include: direction-selectivity, orientation selectivity (Nath and Schwartz, 2016), an omitted stimulus response (Schwartz et al., 2007), and image recurrence sensitivity (Krishnamoorthy et al., 2017). Of specific relevance here, recent work emphasizes intricate specializations of direction-selective circuits for extracting information about the direction of motion, often to the detriment of encoding other visual features (Franke et al., 2016; Zylberberg et al., 2016).

The degree to which retinal neurons are specialized to guide a particular behavior or to perform general-purpose computations predicted by efficient coding may depend on species and on location within the retina. The “complex” computations discussed above (like direction selectivity) have not been observed in primate retina, although many primate RGC types remain unexplored. Further, the fovea and peripheral retina differ dramatically in circuitry (reviewed by (Rodieck, 1998)) and in functional properties (Hecht and Verrijp, 1933; Sinha et al., 2017; Solomon et al., 2002); these differences could indicate a difference in the division of computational labor between retinal and cortical circuits across retinal eccentricity.

Differences like these - across cell types, species, or retinal eccentricity - suggest one way to reconcile stimulus- and goal-oriented frameworks in the retina. Retinal neurons that support a variety of behavioral goals or project to image-forming downstream thalamocortical circuits may show more general purpose computational features in line with efficient coding - these cells act as a common front-end for many downstream feature extractions. To transmit enough information to support a variety of downstream feature extractions, computation in these neurons resembles predictions from efficient coding. Other retinal neurons may violate predictions from efficient coding because they project to areas of the brain that underlie more specialized visually-guided behaviors -- for example, direction selective neurons (Oyster and Barlow, 1967) that project to superior colliculus or the accessory optic system to guide eye movements, or RGCs that control circadian rhythms (for review see (Hughes et al., 2016)).

Lessons from insect vision: behavioral goals shape and constrain visual processing

Goal-oriented approaches have yielded particularly satisfying explanations for complex visual processing in insects. The fly vision community has a long history of examining visual processing as it relates to behaviors like flying (Hausen and Egelhaaf, 1989). Motion processing pathways in several different insects appear tuned to each species’ particular flight behaviors (O’Carroll et al., 1996). Some visual neurons in the fly encode visual features directly relevant for flight control, such as optic flow elicited by rotations or translations around and along specific body axes (Krapp and Hengstenberg, 1996; Longden et al., 2017) (see Figure 4). These neurons act as “matched filters” for specific types of optic flow (Franz and Krapp, 2000; Kohn et al., 2018). Optic flow encoding may seem obvious in hindsight, but the local motion receptive fields of these cells would appear quite mysterious if not for the careful consideration of the impact of the fly’s own motion on visual inputs.

Figure 4: Motion sensitive neurons encode self-movement across the animal kingdom.

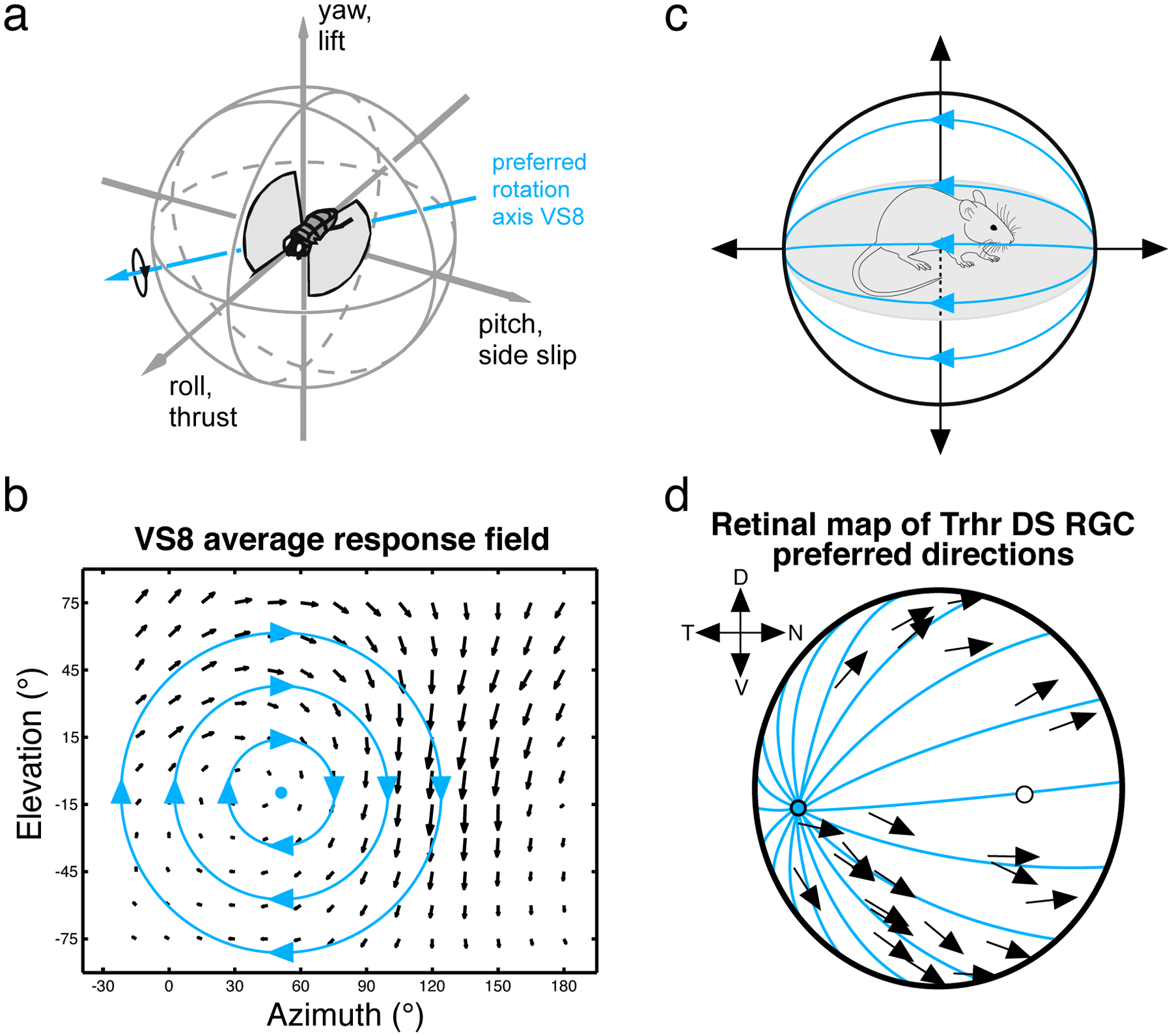
(a) Schematic showing a fly in flight. (b) Local motion receptive field of the VS8 neuron in the blowfly Calliphora. The direction of each arrow indicates the local preferred direction, and the length of each arrow indicates the cell’s motion sensitivity. This local motion receptive field corresponds to the optic flow pattern that would result from a rotation of the animal. The rotation axis around which the fly would need to turn to maximally activate this neuron is indicated in (a). Data & schematic provided by Holger Krapp. (c) Schematic showing a mouse ambulating in a forward direction. The resulting visual input is an optic flow pattern emanating from a singularity directly ahead of the animal (blue lines). (d) Direction preferences of a population of DS RGCs in mouse retina are overlaid on the retinal surface. Forward motion optic flow moves outward from a point in the retina (blue lines). The direction preferences of this cell type roughly align with the optic flow lines that result from forward motion. Other DS RGC types similarly respond to optic flow resulting from other directions of motion of the animal. Data redrawn from (Sabbah et al., 2017).

Recent work on mouse directionally-selective RGCs has similarly recast their function in terms of self-generated motion while navigating the environment (Sabbah et al., 2017) (see Figure 4). A long-standing view of directionally-selective RGCs held that they consist of four subtypes, each preferring a cardinal axis of motion (up, down, left, right, each separated by ~90 degrees) and in alignment with the axes of eye movements produced by the four rectus muscles of the eye (Oyster and Barlow, 1967). These RGCs project to the superior colliculus (Gauvain and Murphy, 2015), which further suggests that they are involved in controlling eye movements. While this distribution of preferred directions holds in the mouse central retina, in other regions of the retina the preferred axes of directionally-selective RGCs are not perpendicular and thus do not neatly align with the rectus muscles of the eye. Sabbah & colleagues mapped retinotopic differences in direction-selectivity in relation to extrapersonal visual space and motion by the animal (Figure 4). They found that directionally-selective cells are in fact better thought of as encoding the animal’s own “advance/retreat” and “rise/fall” movements than the movement of some external object.

Goal-directed Approaches in Cortex

Goal-directed approaches have also been applied to visual cortex. Geisler and colleagues have promoted the importance of understanding how particular tasks may exploit different properties of natural scenes (Burge and Jaini, 2017; Geisler et al., 2009). They have focused on the representations learned by tasks such as patch identification, foreground identification, retinal speed estimation and binocular disparity. For instance, filters learned for a foreground identification task were oriented either parallel or perpendicular to surface boundaries (Geisler et al., 2009), while filters from an image patch identification task had less discrete orientation preferences and more closely resembled V1 filters. Thus, the representations learned can depend on the visual processing goals imposed on the system.

Deep Neural Networks

Recent years have seen tremendous advances in an area of machine learning known as deep neural networks (DNNs; (Krizhevsky et al., 2012; Lecun et al., 2015)); these advances have driven progress in computer vision and a host of other fields. In deep neural networks, stimuli such as natural images are represented and processed hierarchically, loosely matched to the hierarchical structure of the brain. These networks come in many different flavors, including those that are trained in an unsupervised manner -- i.e. training in which the network learns to identify and encode statistical structure in the inputs without a specific goal. Here we focus on supervised discriminative networks, which learn to perform specific tasks using labeled training data sets. DNNs have many potential applications; we emphasize their potential to help understand and make predictions about the neural processing of natural images, particularly how the nervous system could achieve invariant object recognition (e.g. to pose, background clutter, and other within class variations).

Architecture and neural circuitry

Deep neural networks consist of a series of connected layers, each of which implements a set of basic computations (Figure 5). The computations in a single layer include linear filtering (convolution), rectification, pooling, and sometimes local response normalization. DNNs can be considered as a hierarchical extension of the linear-nonlinear models often used to empirically describe visual responses. The dimensionality (number of elements) is reduced between successive layers; as a result, effective receptive fields become larger as one progresses along the hierarchy. Thus, individual layers implement computations like those found in descriptive models of neural circuits, and the hierarchical arrangement of layers resembles the organization of visual (and other sensory) pathways.

Figure 5: Deep neural networks reflect some, but not all, architectural and computational motifs found in neural circuits.

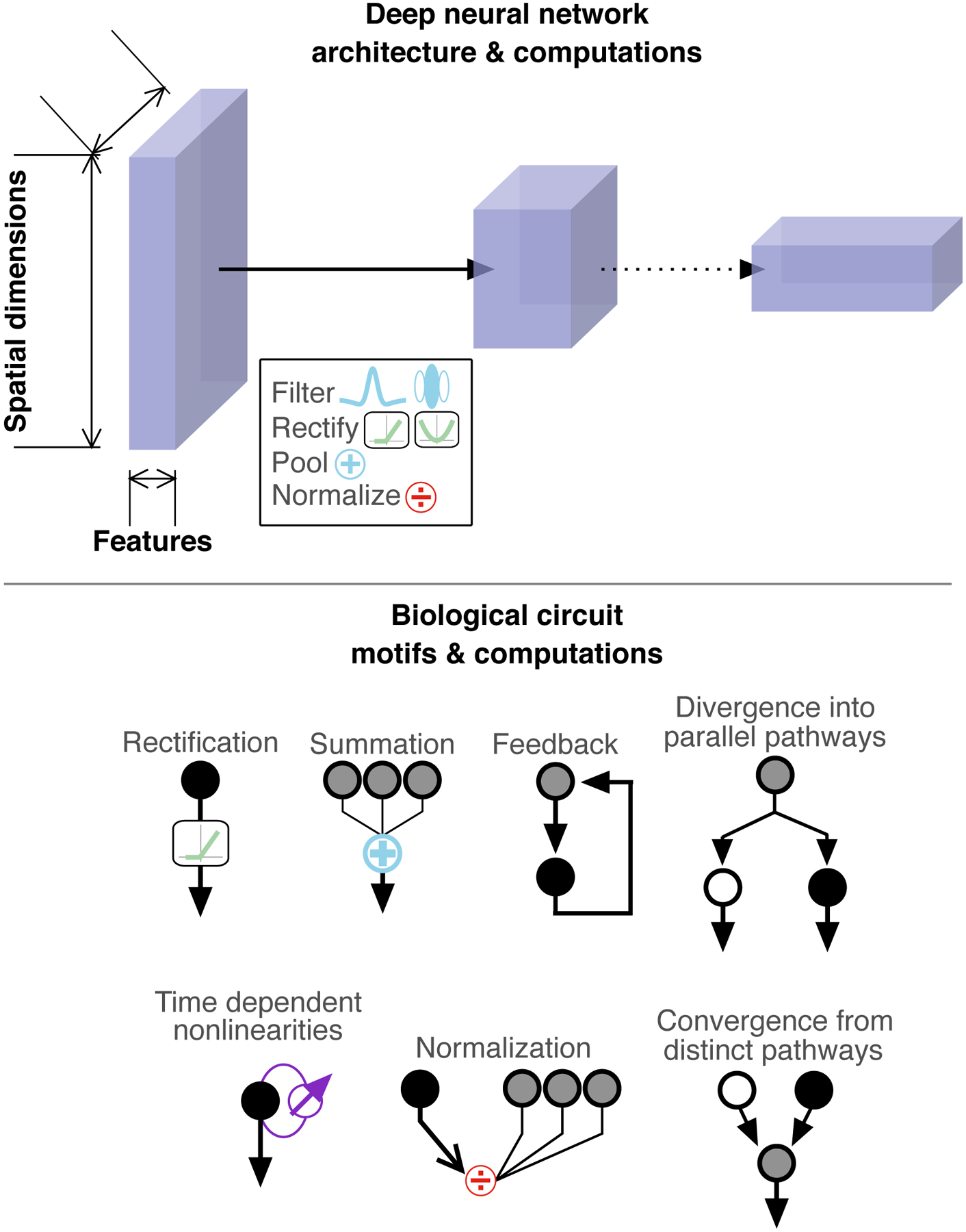
Top: Deep neural networks are composed of multiple, connected layers. Several basic computations are performed within each layer. Bottom: examples of common circuit motifs and computations observed in neural circuits. Some of these examples are well-represented by many DNNs (e.g. pooling / filtering), others can be included in DNNs but their precise nature & location are not necessarily well reflected (e.g. rectification or normalization), and still others are excluded from most DNNs (e.g. time-dependent nonlinearities).

The parameters governing DNN behavior are not determined by specific low-level computational principles (e.g. reducing statistical dependencies as in efficient coding), but instead emerge by learning to minimize the difference between the DNN output and a desired response corresponding to the DNN goal. For example, DNNs are often trained to categorize a large collection of images into discrete classes based on objects they contain (boats, cars, faces, chairs, etc.). DNNs can also be used in a descriptive (and therefore not goal-oriented) manner by fitting them directly to neural data, rather than training them on a high-level task. One such model, when fit to retinal ganglion cell responses to natural movies, reproduced several of the “complex” retinal computations discussed above. The model did not reproduce these behaviors when fit to white noise stimulation (Maheswaranathan et al., 2018). While neural networks have been around for decades, recent years have seen dramatic improvements in performance due to increases in computer speed and the availability of large data sets (e.g. images with labeled objects) that together make it possible to efficiently train networks with many layers.

Learning from successes and failures of DNNs

DNNs trained on object classification show an intriguing ability to predict the responses of cortical neurons to natural images (for recent reviews, see (Kriegeskorte, 2015; Yamins and DiCarlo, 2016); for other recent work, see (Cadena et al., 2017; Cichy et al., 2016; Pospisil et al., 2016)). This approach has been applied with particular success to processing in the ventral visual pathway, which culminates in neurons in inferotemporal (IT) cortex. Many IT neurons exhibit high feature selectivity -- responding to specific objects and (famously) faces (Young and Yamane, 1992).

The flow of signals from the retina to IT is characterized by the loss of a veridical representation of the retinal image: receptive fields become progressively larger and more complex, invariances to properties like object size and position emerge, and the appropriate space to specify inputs (e.g. inputs that produce similar responses of a given neuron) becomes increasingly difficult to identify. These transformations are challenging to learn using stimulus-based models. DNNs, however, have been more successful. Interrogation of the architecture of DNNs trained on object classification suggests that invariances may arise from the pooling stages of the networks (Fukushima, 1980; Riesenhuber and Poggio, 1999). DNNs show an ability to generalize in two important ways: (1) they are able to classify images of objects not in the original training set, including adjusting their representation of inputs for different tasks through transfer learning (Razavian et al., 2014); and, (2) they capture several aspects of neural responses even though neural data is not used in training. But DNNs are, of course, imperfect. For example, current DNN models fail to capture some aspects of human perception such as insensitivity to perturbations to an image (Szegedy et al., 2013; Ullman et al., 2016). One suggestion is that current DNN architectures operating in rather linear regimes lead to this behavior (Goodfellow et al., 2014), and that more biologically realistic saturating nonlinearities may improve performance (Nayebi and Ganguli, 2017) (although see (Brendel and Bethge, 2017)). DNNs capture some but not all aspects of responses of neurons in mid-cortical layers (Pospisil et al., 2016). In addition, interpreting DNNs can be difficult. Unlike more principled efficient coding approaches in which the form of the computation itself (e.g., divisive normalization or gain control) can be motivated by the computational goal, it is often not clear what feature of the DNN leads to a given level of performance.

Any insights that DNNs trained on high-level tasks like classification provide about how the visual system computes comes from identifying, through learning, key statistical structure in the inputs that is important for performing the specific task used in training. Motivation for such an approach comes from convergent evolution of computations like motion detection in insect and vertebrate visual systems (see above). Given that DNNs are only loosely modeled after visual circuits, a realistic expectation is that they identify the computational capabilities and limitations of specific architectures rather than provide a literal model of how the visual system works. If statistical structure of the inputs, rather than specific hardware constraints, dominates which computational strategies are effective for a given task, we might expect DNNs and neural systems to converge on similar computational algorithms even if the implementations of these algorithms differ due to differences in hardware.

Future directions

Understanding neural computation and coding in the context of naturalistic visual stimuli is a difficult problem. But the wealth of neurophysiological data about the visual system and the emergence of new computational tools for building and fitting models put us in a good position to make progress. Below we highlight a few emerging directions that we believe will help advance understanding. Many of these approaches merge techniques and ideas from the stimulus- and goal-oriented frameworks discussed above.

Identify key circuit mechanisms and integrate into models

A complete understanding of natural visual encoding entails building models that can accurately predict neural responses to natural scenes. We believe that a major reason for the shortcomings of current models is that they lack key architectural and computational features present in biological circuits, and that these features substantially shape neural responses. Certain model abstractions (for example, linearity of the receptive field) may be appropriate under some stimulus conditions but not others. At the same time, simply building models using realistic components is not likely to explain complex computations such as object recognition. Merging DNN techniques with more realistic biological circuitry offers one path forward.

DNNs components and connectivity are typically chosen largely based on the computational efficiency of learning using current optimization tools (e.g. gradient descent). This can lead to architectures that lack key components of neural circuits. Identifying and incorporating biologically-inspired computational motifs will help identify which motifs are important for specific computations -- e.g. computations at different stages of the visual hierarchy. This in turn could lead to direct predictions about the mechanisms operating in the relevant neural circuits.

One indication of the potential benefits of such an approach comes from comparing physiologically-based models of early visual areas (linear-nonlinear models with two forms of local normalization) and layers of the VGG network (which lack normalization): physiological models captured human sensitivity to image perturbations considerably better than DNNs (Berardino et al., 2017). A challenge is our current inability to identify which biological mechanisms are essential for specific computations and which can be abstracted as in linear-nonlinear models. Progress will also require probing the interactions between coactive mechanisms that are likely engaged strongly for complex stimuli such as natural images. A partial list of computational features prominent in neural circuits but under-represented in DNNs includes more sophisticated forms of normalization by stimulus context (for recent work in this direction, see (Giraldo and Schwartz, 2017; Han and Vasconcelos, 2014; Ren et al., 2017)), recurrent connections and adaptation (Mcintosh et al., 2016; Spoerer et al., 2017), and architectures for pooling across neurons (see recent work with descriptive models: (Eickenberg et al., 2012; Pagan et al., 2016; Rowekamp and Sharpee, 2017; Sharpee et al., 2013; Vintch et al., 2015)).

Combine the merits of stimulus- and goal-oriented approaches

DNNs are designed to perform well on the discriminative recognition task at the top level of the network, but this constraint does not uniquely specify the architecture of the other layers. On the other hand, stimulus-oriented approaches provide a principled approach to capture more detailed computations and nonlinearities in early stages of visual processing, including retina and primary visual cortex. But it is not clear if such approaches could capture computations in later stages of the cortical hierarchy.

An important future task is therefore finding better ways to reconcile and integrate the merits of both approaches. For instance, most of the early stages of processing that take place before primary visual cortex are neglected in current DNNs (an exception is (Mcintosh et al., 2016)). Incorporating these early stages into networks could become a merger point between goal-directed objectives shaping the top levels of the network and stimulus-driven constraints shaping the initial stages of the architecture. Another direction is to incorporate computational motifs derived from stimulus-driven normative approaches (such as the normalization discussed above) into DNNs.

New theoretical and practical approaches that balance stimulus- and goal-oriented approaches provide promising directions. For instance, an approach known as the information bottleneck formalizes the idea of capturing relevant information rather than all information (for recent application to deep learning, see (Shwartz-Ziv and Tishby, 2017)). Another recent approach unifies several definitions of efficient coding and considers the impact of incorporating only stimuli that are predictive about the future on coding (Chalk et al., 2018). Other recent work connects generative (stimulus-oriented) and discriminative (goal-oriented) components in a single model through a shared representation (Kuleshov and Ermon, 2017). This combination has been exploited in ‘semi-supervised’ machine learning, which makes use of scarce labeled data along with unlabeled data, and therefore is a hybrid between supervised and unsupervised approaches. However, this combined stimulus and goal-oriented representation has not been applied to neuroscience and understanding natural vision. Recent theoretical work has also expanded the notion of efficient coding by recasting it as a specific case of Bayesian inference (Park and Pillow, 2017). By using a broader definition of optimality, Bayesian efficient coding allows one to evaluate the efficiency of neural representations in terms of encoding goals beyond simple information maximization.

There is also a need for progress with stimulus-oriented unsupervised learning approaches that exploit the power of DNNs without specialization for a specific goal. Unsupervised learning is considered by many the “holy grail” of learning (for recent examples, see (Ballé et al., 2016) which incorporates multiple levels of divisive normalization; and (Hirayama et al., 2017) which incorporates pooling). It is still unclear whether deep network architectures with unsupervised learning can predict responses of neurons to natural scenes or capture the invariances that characterize higher visual processing.

Train DNNs using multiple, behaviorally-inspired tasks

A DNN trained to perform a particular task can recapitulate some aspects of sensory circuits; for example, the middle layers of an image classification DNN resemble in some respects neurons in intermediate stages of the ventral stream (reviewed by (Yamins and DiCarlo, 2016); (Pospisil et al., 2016)). Presumably these correspondences arise from similarities in both network architecture and task. A real sensory system, however, supports a wide array of tasks or behavioral goals simultaneously. The result is that, especially in early sensory areas, neurons have to process sensory input in a way that supports multiple parallel feature extractions or behavioral goals. Neurons that make up this common biological front end (e.g. photoreceptors or some types of retinal ganglion cells) may therefore align their encoding strategies with efficient coding to support a wide variety of downstream goals. Downstream circuits performing more specialized computations, on the other hand, may not behave according to classical efficient coding principles. This agrees with our intuition that efficient coding somehow applies more neatly to peripheral sensory systems. Formalizing this intuition requires grappling with several difficult questions: Are there general rules that govern when a stimulus- or goal-oriented perspective is more appropriate? At what point does a sensory pathway stop simply efficiently packaging information and start “doing” something with that information?

Multi-task DNNs offer one approach for exploring how shared circuitry could support multiple tasks (Scholte et al., 2017). Indeed, such networks trained for speech and music classification naturally divide into separate pathways, and the level at which that split occurs can affect the performance of the network on these two tasks (Kell et al., 2018). An interesting question is whether constraining networks by multiple mid-level tasks (as in (Chengxu Zhuang, 2018)) can provide a more general-purpose representation resembling that predicted by efficient encoding. A major impediment to developing multi-task DNNs is the limited availability of datasets that could be used to train such networks (e.g. ImageNet, which consists of a collection of labeled objects, is the dominant dataset used for vision-related applications).