Predicting and characterizing a cancer dependency map of tumors with deep learning

A novel deep learning method links in vitro CRISPR screens to the context of cancer genomics and translates to individual tumors.

Abstract

Genome-wide loss-of-function screens have revealed genes essential for cancer cell proliferation, called cancer dependencies. It remains challenging to link cancer dependencies to the molecular compositions of cancer cells or to unscreened cell lines and further to tumors. Here, we present DeepDEP, a deep learning model that predicts cancer dependencies using integrative genomic profiles. It uses a unique unsupervised pretraining that captures unlabeled tumor genomic representations to improve the learning of cancer dependencies. We demonstrated DeepDEP’s improvement over conventional machine learning methods and validated the performance with three independent datasets. By systematic model interpretations, we extended the current dependency maps with functional characterizations of dependencies and a proof-of-concept in silico assay of synthetic essentiality. We applied DeepDEP to pan-cancer tumor genomics and built the first pan-cancer synthetic dependency map of 8000 tumors with clinical relevance. In summary, DeepDEP is a novel tool for investigating cancer dependency with rapidly growing genomic resources.

INTRODUCTION

The development of novel cancer therapies requires knowledge of specific biological pathways to target individual tumors and eradicate cancer cells. Toward this goal, the landscape of genetic vulnerabilities of cancer, or the cancer dependency map, is being systematically profiled. Using RNA interference (RNAi) loss-of-function screens, Marcotte et al. (1), Project Achilles (2), and Project DRIVE (3) completed several high-throughput screenings of hundreds of cancer cell lines (CCLs). Recently, the Cancer Dependency Map (DepMap) projects of the Broad Institute (4–6) and Wellcome Sanger Institute (7) performed genome-wide CRISPR-Cas9 knockout screens in extensive collections of CCLs. Because the CRISPR technology is less susceptible to off-target effects (8), these efforts produce the two largest catalogs of gene dependencies with high concordance (9). However, since different genomic mechanisms dictate the process of tumorigenesis and genetic vulnerability, relationships between cancer genomes and cancer dependency are nonlinear (2, 10). The nonlinearity makes it challenging to predict and investigate these relationships and translate the findings of CCL screens to tumors.

Deep learning (DL) is a class of machine learning (ML) methods that uses multilayered neural networks to extract high-order features. DL is increasingly being used in genomics research for cancer survival (11, 12) and cancer classification (13–15). DL methods have also been applied to pharmacogenomics for predicting drug sensitivity and synergy (16, 17). Predicting gene dependencies using CCLs’ genomics, although distinct in the goal, shares a similar computational formulation as the prediction of drug sensitivity. Early research endeavors have demonstrated the capacity of sophisticated ML methods in predicting drug sensitivity using CCLs’ genomics (Fig. 1A) (18). However, the sample size of CCLs could be limited to materialize the power of DL models. Furthermore, a model trained using merely CCL data may not fully capture tumor-specific contexts such as tumor heterogeneity and its microenvironment (19, 20). A recent study used the “few-shot learning” technique of DL to translate high-throughput drug screens of CCLs to individual tumors with small samples (21). Such a method requires supervised pretraining on labeled samples from in vitro screens and then model fine-tuning with in vivo screening samples. However, this strategy is not applicable for CRISPR screening with a standard in vitro protocol.

Fig. 1. Architecture of DeepDEP.

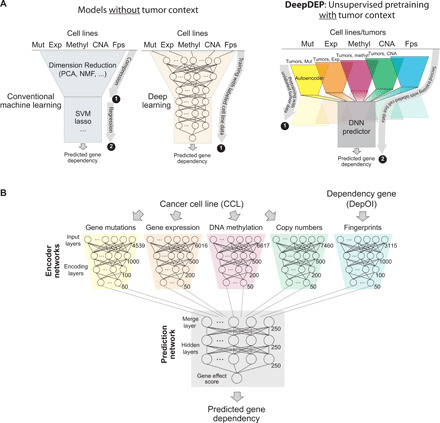
(A) Study designs of conventional methods and the proposed model with an unsupervised pretraining scheme. Conventional ML methods (left) were designed on the basis of merely labeled data of CCLs on related topics, such as prediction of drug sensitivity. An analog DL model can be implemented using a similar scheme (middle). The proposed DeepDEP model (right) has an unsupervised pretraining design that captures unlabeled tumor genomic representations and is further trained with gene dependency data of CCLs (labeled data). Mut, mutation; Exp, expression; methyl, DNA methylation; Fps, functional fingerprint of gene dependencies; DNN, deep neural network. (B) Architecture of DeepDEP. DeepDEP is designed to predict the gene effect score of a dependency of interest (DepOI) for a cancer sample (CCL or tumor). It is composed of encoders for each type of genomic data of a sample and fingerprint of a DepOI; the former was transferred from an unsupervised pretraining of autoencoders using tumors of TCGA. The complete model was trained and tested using CCL data of Broad DepMap.

Here, we proposed a DL model, namely, DeepDEP, to predict the gene dependency profile of an unscreened CCL or impracticable-to-screen tumors. Our model is established with an emerging “unsupervised pretraining” design of transfer learning (22) that has lately revolutionized the field of natural language processing but yet adapted to genomic applications. As illustrated in Fig. 1A, the unsupervised pretraining design allows our model to be (i) pretrained using thousands of “unlabeled” tumor samples (i.e., with genomics data but no screening results) to capture genomic representations of tumors and then (ii) fine-tuned on relatively limited “labeled” CCL samples (with both genomics and screens) to optimize the prediction of gene dependencies. The present study addresses an unmet demand for a comprehensive investigation of genetic dependencies with respect to the genomic context. In this study, we hypothesized that a DL model learns the nonlinear interactions between molecular contexts (input genomics) and cell vulnerabilities (dependencies) and thus makes accurate predictions. Combining multiomics of CCLs, novel functional fingerprints of genes, and their corresponding dependency data, DeepDEP enables analyses that are otherwise challenging. In this study, we demonstrated three major advances. By systematically interpreting DL model behaviors, we (i) identified expression signatures that predicted and characterized gene dependencies and (ii) constructed a proof-of-concept in silico assay for synthetic essentiality (SE) at a single CCL level. We further applied the model to tumor genomics data of The Cancer Genome Atlas (TCGA) and established the first pan-cancer tumor dependency map with clinical relevance in treatment effectiveness and prognosis. We expect the model’s capability to be enhanced along with the rapid growth of the DepMap and multiomics resources.

RESULTS

Model design

Gene dependency or essentiality is defined as the degree to which a gene is essential for cell proliferation and survival. In particular, gene dependency is highly genetic context dependent in cancer cells (2, 3, 23). Here, we present DeepDEP to predict gene dependency based on the representations learned from high-dimensional genomic profiles of both tumor and cell line samples. DeepDEP embeds a transfer-learning design with unsupervised pretraining using the unlabeled tumor samples to learn data representations, followed by parameters fine-tuning on labeled CCL samples to capture the relationship between genomics and gene dependencies (Fig. 1A). The model is composed of (i) dimension-reducing encoder neural networks for a diverse array of molecular data including DNA mutation, gene expression, DNA methylation, and copy number alteration (CNA); (ii) an encoder network for abstracting functional fingerprints of a gene dependency of interest (DepOI); and (iii) a prediction network to convert the learned features into a dependency score (Fig. 1B and fig. S1). An autoencoder, a dimension-reducing DL model widely used in high-dimensional genomic data, was first trained for each type of genomic data using 8238 TCGA tumors with hyperparameter optimization (tables S1 to S4). Structure and parameters of the encoder subnetwork of the constructed autoencoders were transferred to four corresponding encoders of DeepDEP. The entire network was further trained using CRISPR-Cas9 dependency profiles of 278 CCLs with four types of genomic data (Broad DepMap 2018Q2 version; table S5) to produce a feature space of gene dependency. Here, the functional fingerprint of a DepOI was implemented by a 3115-dimension binary “fingerprint vector,” which denotes the involvement of the DepOI (1, involved; 0, not involved) in 3115 molecular signatures associated with chemical and genetic perturbations (CGPs) curated by the Molecular Signature Database (MSigDB) (24).

The original dependency scores were gene effect scores (5) estimated and corrected by CERES (4) with a mode near zero (Fig. 2A). The scores were calculated with stringent quality controls on single-guide RNAs (sgRNAs), screen replicates, and CCLs (table S6) (4, 5). A more negative value denotes a stronger dependency and, therefore, stronger essentiality. We selected 1298 candidate DepOIs with implications in cancers, due either to their highly selective dependencies (with an SD of >0.2 in the dependency scores across 278 CCLs) or to being part of the COSMIC Cancer Gene Census (table S7). On average, each DepOI was involved in 33.2 molecular signatures (number of 1s in the fingerprint vector) (Fig. 2B). Together, 360,844 (278 CCLs × 1298 DepOIs) labeled samples were available. We randomly partitioned CCLs into training/validation (90%) and testing (10%) sets, where eight-ninth of the samples in the former set were randomly selected for training and one-ninth for validation (Fig. 2C). No significant bias was observed between the training and testing sets in terms of tissue type, cell culture type, culture medium, or quality of CRISPR screen (table S6).

Fig. 2. Performance and validation of DeepDEP.

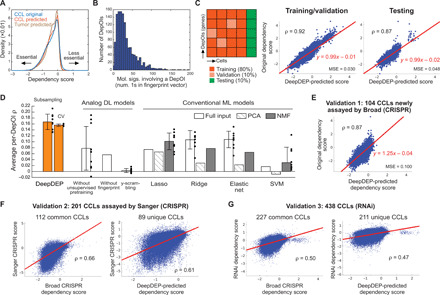
(A) Distributions of original dependency scores of CCLs and predicted scores of CCLs and tumors. (B) Nonzero elements in functional fingerprint vectors (membership of 3115 molecular signatures) of 1298 DepOIs. (C) Model performance of DeepDEP. (D) Performance comparisons with other DL and ML methods. Average per-DepOI ρ across 1298 DepOIs are summarized by means (bars) and SD (error bars) of 10 independent subsampling trainings (dots), or three rounds of 10-fold cross-validations (CV). The results were contrasted to identically structured DL models trained merely on CCLs without unsupervised pretraining on tumors, trained by individual DepOIs without the fingerprints to learn from other DepOIs, or with scrambled dependency scores (“y-scrambling”), and linear and nonlinear conventional ML methods with full or dimension-reduced inputs of genomic data and gene fingerprints. For each ML method, a model was trained using the same training/testing partition as used in the final reported DeepDEP model. Using the type of input data [full, principal component analysis (PCA), or nonnegative matrix factorization (NMF)] yielding the best performance for each ML method, we further trained and tested 10 models with the training/testing subsamples as used for DeepDEP (the first bar). Support vector machine (SVM) with nonlinear Gaussian and radial basis function (RBF) kernels did not converge and are not included here. A data point of SVM with NMF inputs at −0.07 and the SD of the model without the fingerprints at 0.23 are not shown since they are beyond the range of the vertical axis. Results of two subsets of highly variable DepOIs are shown in fig. S2. (E to G) Analysis of three independent validation datasets. Scores predicted by DeepDEP were compared to dependency scores in (E) newly assayed CCLs by Broad DepMap using a refined computational pipeline, (F) the Sanger DepMap using a different CRISPR library and computational algorithm, and (G) RNAi-based screens.

Model performance and comparisons to other methods

The prediction on the testing set was highly accurate (Pearson correlation coefficient ρ = 0.87 across 28 testing CCLs × 1298 DepOIs) (Fig. 2C). The performance was robust to the experimental uncertainty associated with the replicates of the CRISPR screen (see Supplementary Text). We evaluated the model by the correlation (per-DepOI ρ) between predicted and original dependency scores of each DepOI among testing CCLs, a metric commonly used to measure the prediction performance of genetic and chemical screening data (10, 18). Overall, our model achieved an average per-DepOI ρ of 0.18 across all 1298 DepOIs (Fig. 2D and fig. S2), much higher than expected by random chance using the y-scrambling method (0.003 ± 0.007). To further assess the performance on the DepOIs that cannot be simply predicted by the mean value across CCLs (25), we focused on two subsets of highly variable DepOIs: 61 DepOIs with SD in dependency scores of >0.3 (table S7) and 506 “high-variance” DepOIs with top 3% most variable scores as defined by the Broad DepMap. These DepOIs are more likely cancer-relevant genes for their selective essentialities, such as the top variable dependency of TP53 (SD, 0.61). Our model achieved stronger average per-DepOI ρ of 0.34 and 0.28 among the 61 and 506 DepOIs, respectively (fig. S2). A strong ρ of 0.62 was achieved for TP53 (fig. S2).

We compared the model performance to variations of DeepDEP and conventional ML methods. Notably, DeepDEP achieved a marked improvement in performance and stability over an identically configured DL model without unsupervised pretraining (i.e., trained on CCLs alone; average per-DepOI ρ across all DepOIs, 0.08 ± 0.07; Fig. 2D). The data suggested that the unsupervised representations of genomic data learned from large-sample tumors are beneficial to the prediction of relatively limited cell line screens. The DeepDEP model outperformed 100 identically configured models, each of which was trained and tested using only one DepOI (average per-DepOI ρ = 0.06 ± 0.23), demonstrating the benefit of the fingerprint in capturing functional similarities shared among DepOIs. We further compared DeepDEP to six linear and nonlinear ML methods with a total of 18 settings (see Materials and Methods). Since a transfer learning strategy is not part of standard ML implementation, the ML models were trained using CCLs alone to benchmark the optimal performance that a prediction machine can achieve in merely labeled CCL data. These models used full genomic data and gene fingerprints as inputs or dimension-reduced inputs obtained by principal component analysis (PCA) or nonnegative matrix factorization (NMF). Support vector machines (SVMs) with nonlinear Gaussian or radial basis function (RBF) kernels failed to converge on any set of input data. Compared to DeepDEP, all ML methods resulted in significantly lower per-DepOI correlation coefficients across 10 rounds of subsampling (average per-DepOI ρ = 0.03 to 0.11; paired one-tailed t test, P < 9.5 × 10⁻⁴; Fig. 2D). Model evaluations on the two sets of highly variable DepOIs demonstrated even more evident improvements by DeepDEP over other ML algorithms (fig. S2).

Model validations

To address the concern of model overfitting, we validated the model performance by subsampling (average per-DepOI ρ = 0.17 ± 0.03; Fig. 2D) and 10-fold cross-validations (0.16 ± 0.004; table S8). The performance remained even with the leave-cluster-out cross-validation by training and testing the model with distinct clusters of CCLs formed in the expression data (see Supplementary Text and table S9). Our data also indicated a moderate dependency of model performance on the diversity of training samples, given the underlying difference between hematopoietic and solid tumor lineages in the original dependency profile (fig. S3). Overall, the model evaluations demonstrate the performance of DeepDEP, a critical assessment before we attempted to predict tumor dependency.

We used three independent datasets to validate the model (table S5). For 104 CCLs newly assayed in the 2018Q3 to 2020Q2 period by the Broad DepMap, DeepDEP-predicted scores were in line with the actual dependency scores (Pearson ρ = 0.87 across 104 CCLs × all DepOIs) (Fig. 2E), although the scores were generated using an updated computational pipeline (see Materials and Methods) (5). On a per-DepOI basis, DeepDEP achieved average per-DepOI ρ of 0.21, 0.16, and 0.10 among the two sets of highly variable DepOIs and all DepOIs, respectively. The other two datasets were collected from (i) a CRISPR-Cas9 screens conducted by the Sanger Institute using a different CRISPR library (7) and (ii) RNAi-based genome-wide dependency screens (25). Despite the distinct screening mechanisms and/or computational algorithms used to process these screening data, we confirmed a general agreement between the Broad and the other two screens among the common CCLs (112 and 227 CCLs; ρ = 0.66 and 0.50; Fig. 2, F and G) as observed in a recent study (9). For CCLs unique to the validation sets, our predicted dependencies recapitulated their real screening results (89 and 211 CCLs; ρ = 0.61 and 0.47). Average per-DepOI ρ were 0.24, 0.17, and 0.10 among the two sets of highly variable DepOIs and all DepOIs, respectively, in the CCLs unique to the Sanger screen and 0.22, 0.14, and 0.10 in the CCLs unique to the RNAi screen.

Assessment of gene fingerprints in DeepDEP

DeepDEP includes unique functional fingerprints of DepOIs to facilitate model learning of functional similarities (pathway/signature involvement) shared among DepOIs. The CGP signatures were selected as fingerprint features because they encode molecular responses of cells to perturbations. Substituting the CGP fingerprints by 5247 gene ontology (GO) terms or 1175 canonical pathways of MSigDB reduced the performance of DeepDEP (12.4 and 20.2% drops in average per-DepOI ρ, respectively; fig. S4). The drops were largely attributable to the lower information content and higher dependence between features of these fingerprints (fig. S4).

Model interpretation by characterizing gene dependencies using gene expression profiles

To enable applications to samples with only one or part of the genomic assays, we built several simplified models, e.g., Mut-DeepDEP for mutation data alone and Mut/Exp-DeepDEP for paired mutation and expression data. Most of the simplified models, such as Mut/Exp-DeepDEP and the expression-alone model (Exp-DeepDEP), achieved comparable performance to DeepDEP, while CNA- and mutation-alone models yielded weaker performance (fig. S5). Details of the simplified models can be found in Supplementary Text.

We interpreted Exp-DeepDEP to understand the information learned by a single-omic model or, more specifically, the associations captured by our model between dependency and expression profiles. The hyperparameter optimization during initial training on the TCGA data resulted in 50 neurons for the bottleneck (encoder output) layer (table S2). However, only two neurons carried nonzero values after the final training using the CCL dependency data. The training process of Exp-DeepDEP was repeated for 10 times with consistent results (average, 2.1 nonzero neurons; range, 1 to 3). This is likely due to the limited diversity and sample size of CCLs (n = 222 for training) and intercorrelation of gene expression levels (see Discussion). To decipher the effects of these bottleneck layer neurons, we artificially intervened the two neurons and examined the changes in predicted dependency scores (illustrated in Fig. 3A; see Materials and Methods). We decoded the expression signatures of the two neurons by reconstructing the gene expression profiles of 6016 genes through the decoder network from each of two neurons (Fig. 3B and table S10) and analyzed the functional relevance by Gene Set Enrichment Analysis (GSEA). Signature 1 was positively associated with pathways related to cell proliferation, such as DNA repair, E2F targets, and G2M checkpoint [all false discovery rate (FDR), ~0; Fig. 3, C and D]. Signature 2 encoded a broader range of processes involved in tumorigenesis and tumor microenvironment, including P53 signaling, epithelial-mesenchymal transition (EMT), and hypoxia (all FDR, ~0).

Fig. 3. Characterization of gene dependencies using Exp-DeepDEP.

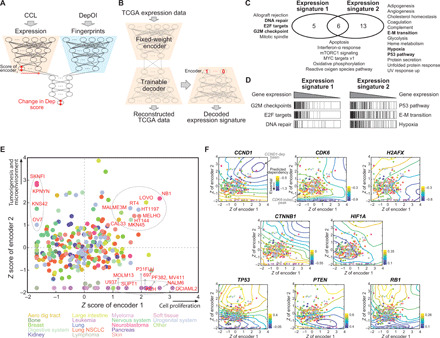
(A) Architecture of Exp-DeepDEP and its usage in characterizing gene dependencies. We examined encoded expression nodes for the relevance of gene dependencies. (B) Networks for decoding the encoded expression nodes. We retrained a decoder network to reverse the encoder of Exp-DeepDEP [as shown in (A)] using TCGA samples. A vector with 1 at the node of interest and 0 otherwise was fed into the decoder to reconstruct a decoded gene expression signature. (C) GSEA analyses of expression signatures decoded from two encoder nodes. Hallmark gene sets with significant positive enrichments (FDR, <0.001) in each expression signature are listed. E-M transition, epithelial-mesenchymal transition. UV, ultraviolet. (D) Enrichment plots of selected gene sets [bold in (C)]. (E) CCLs by z-transformed scores of the two encoder nodes. Samples with high scores specifically in one node (≥1 in one node but minimum in the other) or both nodes (≥1 in both nodes) are denoted by dashed circles. (F) Essentiality maps of selected genes. An essentiality map was generated using contours of the dependency scores generated by intervening the two encoders for each gene dependency. Dark blue (or yellow) indicates an area where knocking out a gene has strong (weak) inhibitory effects. Dots (CCLs) and axes are identical to (E).

We mapped 278 CCLs through the encoder network that converted the expression profile of each CCL into two signature scores at the bottleneck layer. We found that 20 of 24 leukemia, lymphoma, and myeloma CCLs exhibited the lowest activities in signature 2 but high variations in signature 1 (Fig. 3E), reaffirming the fundamental difference in the dependency profile compared to solid cancer cells (fig. S3). Otherwise, CCLs of different tissue origins appeared indistinguishable. We designed a simplified linear regression model to evaluate the predictive power of the signature scores. The two signatures predicted 459 (35.4%) and 321 (24.7%) DepOIs, respectively, with Bonferroni-adjusted P < 0.05 (fig. S6 and table S11). We further assessed the impact of potential cofactors related to cell culture and screen quality by fitting the dependency of each DepOI with the expression signatures and other variables (see Materials and Methods). The expression signatures were the major factors that predicted 389 DepOIs (fig. S6 and table S11). However, dependencies known to be closely associated with their own expression levels, such as ESR1, ERBB2, and SOX10, could be predicted by self-gene expression only.

Gene essentiality depends on the genomic context of a CCL (2, 3, 23). We predicted gene dependencies by combining different signature scores and visualized the results using contour plots (Fig. 3F) or the “essentiality map” for a DepOI. The constructed maps revealed distinct characteristics for each gene. Genes associated with the cell cycle (CCND1 and CDK6), DNA repair (H2AFX), and EMT tended to be more essential with higher signature 1. In addition, the essentiality of a hypoxia marker, HIF1A, was high in cells with moderate signature 2 but low signature 1. Among tumor suppressors, such as TP53, PTEN, and RB1, we identified peaks of positive dependency scores (denoting cellular growth when the gene is knocked out) in cells where signature 2 was enhanced. Further investigations into genes sharing common functions revealed an intrafunction concordance [such as oxidative phosphorylation (OXPHOS)] or rather diversity (G2M checkpoint, MYC targets, and the P53 pathway) in essentiality maps (figs. S7 to S10). Together, these maps provide a novel view of genes’ function—their potential to act as essential genes in different contexts.

Model interpretation by investigating SE using Mut-DeepDEP

The mutation-alone model (Mut-DeepDEP) with binary mutation input is a simple model with a prediction error comparable to the full-DeepDEP model yet subpar average per-DepOI ρ (see Supplementary Text and fig. S5). To interpret what our model learned given binary input data, we used Mut-DeepDEP to predict the change in a gene dependency associated with a synthetically induced or removed gene mutation in a CCL, or SE between a mutation and a gene knockout (26). For simplicity, we perturbed one mutation at a time; changing from 0 to 1 represents switching endogenous wild-type to mutated or from 1 to 0 vice versa (Fig. 4A). For each mutation-DepOI pair in a CCL, an SE score was calculated by comparing the predicted dependency of a DepOI with versus without a mutation (mutation status, 1 versus 0). Thus, a more negative SE score indicates stronger essentiality in a CCL carrying an endogenous or synthetic mutation. In general, SE scores were modest (5th to 95th percentiles, −0.0055 to 0.0054; Fig. 4B) and appeared to be independent of cell lineages (Fig. 4C). Only aerodigestive tract, breast, kidney, non–small cell lung cancer (NSCLC), nervous system, skin, and urogenital system exhibited significantly stronger intralineage similarities in SE scores than between lineage (with Bonferroni-adjusted one-tailed t test, P < 0.05; Fig. 4C and fig. S11), implying that SE may be a genomic context-specific, rather than lineage-specific, phenomenon in many cancer cells.

Fig. 4. Investigation of SE by Mut-DeepDEP.

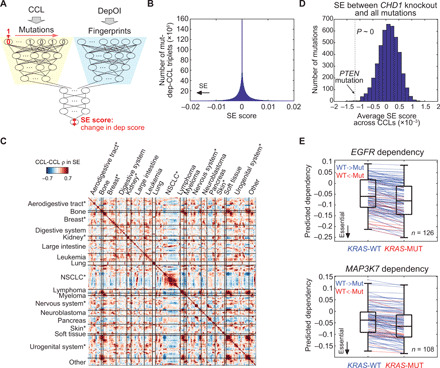
(A) Architecture of Mut-DeepDEP and its usage in investigating SE. For each CCL, we perturbed the status of one gene mutation at a time [from endogenous wild-type (0) to mutated (1), or vice versa] and observed how much it altered individual gene dependency score (SE scores). (B) Histogram of SE scores across all mutation-DepOI pairs and CCLs (n = 4539 mutations × 1298 DepOIs × 278 CCLs). An SE score is calculated as the change in predicted dependency score of a DepOI in a CCL carrying a gene mutation compared to the same CCL without the mutation. A more negative SE score is indicative of stronger SE. (C) CCL-CCL similarities in SE scores. Pearson correlation coefficients were calculated between two CCLs across all mutation-DepOI pairs and represented in a heatmap. Asterisks denote lineages with significantly stronger intralineage correlations than interlineage ones (with Bonferroni-adjusted one-tailed t test, P < 0.05; see fig. S11 for summary of correlation coefficients per lineage). (D) Histogram of average SE scores across CCLs between CHD1 knockout and 1298 gene mutations. Dashed line and arrow indicate the average SE score of a well-known SE pair, PTEN/CHD1. Statistical significance was assessed by comparing all scores against the one of PTEN by a one-sample one-tailed t test. (E) SE interactions of KRAS mutations with EGFR and MAP3K7 knockouts. Blue (and red) line segments denote CCLs converted from endogenous wild-type to mutated KRAS (and vice versa). MUT, mutated; WT, wild type.

We examined two of the best-known SE pairs, PTEN mutation/CHD1 depletion (27) and BRCA1/PARP1 (28); the latter is more synergistic and also categorized as synthetic lethality. We note that in the original dependency data, CHD1 essentiality was not significantly stronger in 43 CCLs harboring PTEN mutations compared to the other 235 CCLs (one-tailed t test, P = 0.46), and neither was BRCA1/PARP1 (P = 0.10; 20 mutated CCLs versus others), indicating that the complexity of genomics may overcome SE effects. Since CHD1 and PARP1 were not part of the 1298 DepOIs, we predicted their dependency scores using Mut-DeepDEP without additional training. SE scores of PTEN/CHD1 were significantly lower than zero among CCLs (one-sample one-tailed t test, P = 0.018). The average SE score of PTEN/CHD1 across CCLs was significantly more negative than those between CHD1 and any other 4538 gene mutations (P ~ 0 and ranked among the top 12 of all mutations; Fig. 4D), although the magnitude of the SE scores was subtle. Similar results were observed for BRCA1/PARP1 (P = 1.3 × 10⁻⁶ and 5.7 × 10⁻²¹⁹ for comparisons against zero and other mutations, respectively). The two examples demonstrated the feasibility of using Mut-DeepDEP to study SE, while the model may become more sensitive with mutation data harboring more functional/complex information beyond binary states (see Discussion).

We further explored the capability of our model to investigate SE in a CCL-specific manner. As a demonstrating example, we investigated SE genes associated with mutations in KRAS, one of the hardest-to-target oncogenic variants (26, 29). In our prediction, mutated KRAS was associated with stronger dependencies on 12 genes (with top ranking negative SE scores in at least 100 CCLs; see Materials and Methods). The genes included key players in the KRAS signaling pathways, such as EGFR and MAP3K7 (table S12). EGFR is an upstream regulator of the RAS pathway. Our data revealed that EGFR was an SE interactor with KRAS in 126 CCLs (Fig. 4E). Among them, 18 CCLs (or 108 CCLs) with endogenous KRAS mutations (or wild-type) were synthetically converted to wild-type (or mutated). On average, a CCL exhibited a 78.5% increase in EGFR dependency when the KRAS mutation was synthetically added. Our analysis also indicated MAP3K7, a member of the mitogen-activated protein kinase family involved in the downstream signaling of KRAS, as another promising SE interactor of KRAS in 108 CCLs (Fig. 4E). Future studies are warranted to further investigate these SE interactions as potential targets for KRAS mutations (see Discussion).

Prediction of tumor dependencies

The DeepDEP model is embedded with the tumor genomic context through the unsupervised pretraining of the autoencoders using the TCGA data. To confirm the effectiveness of this scheme, we carried out a proof-of-concept prediction of gene expression by training a DeepDEP-like model with an identical transfer-learning scheme. The satisfactory performance (ρ = 0.50 ± 0.20) and meaningful model behaviors of well-predicted genes (see Supplementary Text and fig. S12) supported our transfer-learning scheme. Thus, we applied DeepDEP with full genomic input to the TCGA data to predict the dependency profiles of the 1298 DepOIs in 8238 tumors (table S13). To our knowledge, this study is first to report a pan-cancer dependency map in tumors. The predicted dependency scores followed similar distributions as the original and predicted dependency scores of CCLs (Fig. 2A). In general, correlation in the overall dependency profile between a tumor and a CCL was similar to that between two CCLs (Fig. 5A). Variations of most dependencies across tumors were modest (average SD, 0.087; fig. S13 and table S14). Among the top selective genes were two cell cycle regulators, CCND1 and CDK6, that have inhibitors approved for cancer treatment and novel gene dependencies that worth further studies, such as SCAP and YRDC.

Fig. 5. A predicted pan-cancer dependency map of tumors.

(A) Distributions of pairwise CCL-CCL and CCL-tumor correlation coefficients in predicted dependency scores across 1298 DepOIs. (B) t-distributed stochastic neighbor embedding (t-SNE) plots of the predicted dependency map and baseline gene expression and methylation data of CCLs and tumors. (C) Heatmap of the predicted tumor dependency map and associations with genomics and cancer types. Hierarchical clustering of tumors by the predicted dependencies revealed groups of samples with distinct genomic patterns (e.g., groups 1 to 3). Abbreviations of cancer types are according to TCGA and are detailed in Supplementary Text. (D) Summary of dependencies driven by individual genomics. Inset: the definition of a mutation-driven dependency (M-Dep) event. Definitions of expression-driven dependency (E-Dep), methylation-driven dependency (Me-Dep), and CNA-driven dependency (C-Dep) are identical. Left: Genomics-driven dependency events. Right: Dependencies dominated by each type of genomics-driven events. (E) Distributions of genomics-driven events across 1298 dependencies.

Associations of predicted tumor dependencies with genomics

Similar to CCLs (fig. S3), the gene dependency profile of tumors generally did not cluster by lineages (Fig. 5, B and C). This observation was in contrast to the cancer-type specificity seen in the genome-wide expression and methylation data (Fig. 5B). Dependency profiles of some tumors were associated with higher mutation burdens (e.g., group 1 in Fig. 5C), increased CNA (group 2), and expression/methylation patterns (group 3). Group 1 was composed of 593 tumors with a significantly higher mutation burden than others (average number of mutated genes per tumor, 363.0 versus 61.5; one-tailed t test P = 2.0 × 10⁻³¹⁴; fig. S14). These heavily mutated tumors were predicted to have stronger dependencies on 660 DepOIs (with one-tailed t test, P < 10⁻⁵) that predominantly perform mitochondrial functions (table S15). Our finding agreed with previous reports that mitochondrial dysfunction is closely related to the induction of DNA damage (30) and it may be targeted to enhance tumor vulnerability due to the interplay among mitochondrial metabolism, cell cycle checkpoint regulators, and mutation burden [reviewed in (31)]. Group 2 (n = 285) had significantly higher copy numbers (average CNA score per tumor, 0.52 versus 0.16; P = 4.6 × 10⁻¹³³; fig. S14). In the group of tumors, we observed enhanced essentialities on 312 genes related to miscellaneous functions, such as transcription factor activities, cell differentiation, and cell proliferation (table S15). In the predicted tumor dependency map, group 3 (n = 551) had unique expression and DNA methylation profiles compared to other tumors (Fig. 5C). Tumors of this group exhibited significantly higher correlations with another tumor within the group than with a tumor outside the group in both expression (average correlation coefficients, 0.66 versus 0.43 and P ~ 0; fig. S14) and methylation profiles (0.77 versus 0.68; P ~ 0). A total of 594 DepOIs were predicted to be more essential in group 3, which had no significant overlap with the 360 up-regulated genes in the group (two-tailed Fisher’s exact test, P = 1.0; fig. S14). However, the two sets of genes significantly overlapped in GO terms (right-tailed Fisher’s exact test, P = 9.4 × 10⁻⁵; fig. S14 and table S15). This implies that highly active cellular functions and processes (as marked by up-regulated genes in our analysis) may be targeted for cancer vulnerability.

Next, we sought to determine the effects of genomic mechanisms in codetermining gene dependencies. Through a systematic search (see Materials and Methods), we identified 1.6 million M-Dep (mutation-driven dependency), 2.1 million E-Dep (expression-driven dependency), 1.3 million Me-Dep (DNA methylation-driven dependency), and 1.7 million C-Dep (CNA-driven dependency) events (Fig. 5D). For each DepOI, we calculated the percentage of the four classes of events. Most DepOIs were dominated by E-Dep, M-Dep, and C-Dep events (48.6, 27.7, and 22.0%, respectively) (Fig. 5, D and E), echoing a recent study showing that gene expression had higher power than DNA level features in predicting cancer cell vulnerability (32). While Me-Dep accounted for 19.7% of all events (Fig. 5D), these events often cooccurred with E-Dep events (Fig. 5E). Thus, Me-Dep dominated only 1.8% of DepOIs. Given that methylation sites are mostly probed within promoter regions on microarrays, the results support our understanding that DNA methylation mediates cancer cell proliferation/dependency largely through the regulation of gene expression.

Validation of predicted tumor dependencies using clinical and preclinical data

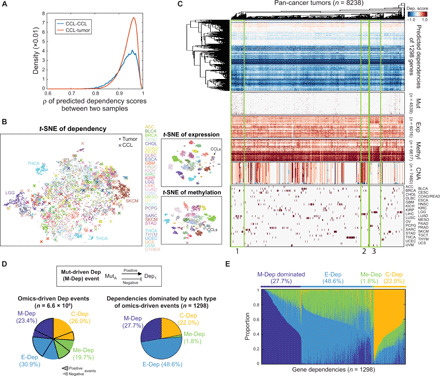
For a lack of ground truth, we validated the predicted tumor dependencies by clinical parameters and clinical/preclinical treatment responses. We first investigated breast cancer (BRCA) because of its comprehensive clinical data from TCGA. Estrogen receptor–positive (ER⁺) tumors were predicted to have stronger dependencies on ESR1 (t test, P = 2.2 × 10⁻²⁶; Fig. 6A). We also evaluated drug response data categorized as “targeted molecular therapy,” where a monoclonal antibody against human epidermal growth factor receptor 2 (HER2), trastuzumab (Herceptin, n = 10), was the only drug with an analyzable number of samples. All BRCA tumors with a complete response (CR; n = 9) to trastuzumab were more dependent on ERBB2 than the only tumor with stable disease (Fig. 6B), yet the sample size was too small to assess the statistical significance. To further validate our prediction, we collected an independent dataset from preclinical drug screening on patient-derived xenografts (PDXs) performed by the PDX Encyclopedia project (33). Since CR was not often achieved among the PDX trials, we only analyzed LLM871, an inhibitor of fibroblast growth factor receptor 2/4 (FGFR2/4), that had the largest number of CR samples in BRCA. The Exp-DeepDEP model was used to predict the dependencies of each xenograft on FGFR2 and FGFR4 by the baseline expression profiles. Three PDXs achieving CR were predicted to be significantly more dependent on FGFR2/FGFR4 than 22 PDXs with progressive diseases (PDs; Kruskal-Wallis test, P = 0.030; Fig. 6C). Another important dependency previously reported from in vitro and in vivo studies (34, 35) was WRN in cancer with high microsatellite instability (MSI). Tumors with high MSI were predicted to be significantly more dependent on WRN both across MSI-prone cancers of TCGA (t test, P < 6.4 × 10⁻¹⁴; Fig. 6D) and within individual cancer types (P < 7.3 × 10⁻³; fig. S15). Together, the predicted tumor dependencies were concordant with clinical and preclinical data, although the statistical power was limited by small sample sizes and the availability of in vivo CRISPR screens (see Discussion).

Fig. 6. Validation of clinical significance of predicted tumor dependencies by clinical data (TCGA) and preclinical drug trials (PDX Encyclopedia).

(A) Predicted ESR1 dependencies in breast tumors (BRCA) with positive and negative immunohistochemical (IHC) status of estrogen receptor (ER⁺ and ER⁻). Statistical significance is assessed by the one-tailed t test. (B) ERBB2 dependencies in BRCA with different responses to trastuzumab. SD, stable disease. (C) Validation of predicted FGFR2/FGFR4 dependencies by drug response of LLM871 in preclinical PDX models. Predicted dependency scores of FGFR2 and FGFR4 were averaged for each PDX. Statistical significance is assessed by the Kruskal-Wallis test. (D) Predicted WRN dependencies across five MSI-prone cancers of TCGA, including colon adenocarcinoma, esophageal carcinoma, rectum adenocarcinoma, stomach adenocarcinoma, and uterine corpus endometrioid carcinoma. MSI categories were experimentally determined by TCGA: MSI-high (MSI-H), MSI-low (MSI-L), and microsatellite stable (MSS). Statistical significance is assessed by the one-tailed t test. See fig. S15 for the results of individual cancer types and pan-cancer MSI scores predicted by the MANTIS algorithm.

Clinical relevance of predicted tumor dependencies in chemoresistance and survival

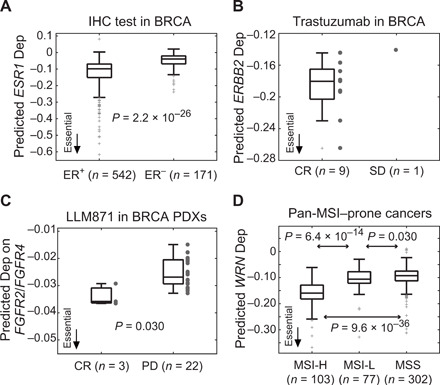
To explore the clinical relevance of the predicted tumor dependencies in nontargeted therapies, we searched for dependencies related to chemoresistance in BRCA. We compared predicted dependencies between patients who achieved a CR (n = 117) and PD (n = 6) after chemotherapy. A total of 71 genes exhibited significantly differential dependencies between these two groups (t test, P < 0.05; Fig. 7A and table S16). The vast majority of these dependencies (98.6%) was positively associated with chemoresistance, where a more negative dependency score was associated with a poorer response to chemotherapy. NDUFS5, an enzyme of the electron transport chain, was the most significant dependency (P = 2.9 × 10⁻³; Fig. 7B). The chemoresponse-related DepOIs were significantly enriched in the GO terms of mitochondrion and OXPHOS (one-tailed Fisher’s exact test, P = 9.0 × 10⁻²⁶ and 9.5 × 10⁻¹⁰; Fig. 7C), echoing the dependency of chemoresistant cells on the energy metabolism (36, 37).

Fig. 7. Clinically relevance of predicted tumor dependencies.

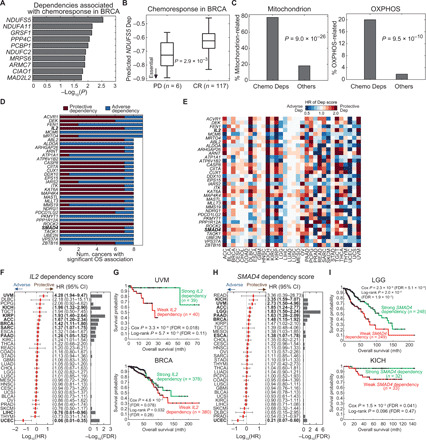
(A) Top 10 dependencies associated with chemoresponse in BRCA. Statistical significance is assessed by the t test comparing predicted tumor dependency scores of each DepOI between samples achieving CR and PD after chemotherapy. (B) NDUFS5, the most significant chemoresistance-associated dependency in BRCA. (C) Associations of chemoresistance-associated dependencies (Chemo Deps) with GO terms of mitochondrion and OXPHOS in BRCA. Significance is assessed by a one-tailed Fisher’s exact test for enrichment. (D and E) Top OS-associated gene dependencies and their hazard ratios (HR) identified by a univariate Cox proportional hazard regression model (Benjamini-Hochberg FDR, <0.2). A DepOI with a more negative dependency score, which indicates stronger dependency, associated with better (or worse) survival is termed as a protective (or adverse) dependency. Thus, a dependency score with a hazard ratio of >1 indicates a protective dependency. Full results of the univariate and multivariate Cox models are provided as table S16. (F and G) Pan-cancer significance of IL2 and Kaplan-Meier curves of uveal melanoma (UVM) and BRCA (see fig. S16 for other cancer types). Cancers with a Cox FDR of <0.2 are labeled in bold. CI, confidence interval; mth, month. (H and I) Significance of SMAD4 dependency and Kaplan-Meier curves of lower-grade glioma (LGG) and kidney chromophobe (KICH) (see fig. S17 for other cancer types).

To further establish the physiological relevance of our model, we analyzed the associations between gene dependencies and overall survival (OS) of patients with cancers from different lineages. We identified 4655 prognostic dependencies among 32 cancers (Benjamini-Hochberg FDR, <0.2; table S16). Thirty-four DepOIs were prognostic in at least eight cancers (Fig. 7, D and E). For instance, a more negative dependency score of (stronger dependency on) a tumor-suppressive gene, interleukin-2 (IL2), was associated with better OS in seven cancers and adverse OS in two cancers (Fig. 7F). IL2 is an approved treatment for melanoma and metastatic renal cell carcinoma. Our data echoed that a stronger dependency on IL2 marked better OS in uveal melanoma (UVM; FDR, 0.018; Fig. 7G), kidney chromophobe (KICH; fig. S16), and kidney papillary cell carcinoma (KIRP), although its dependency data may be prone to non–cell-autonomous effects of pooled screens (see Discussion). Another top prognostic gene, SMAD4 is also a tumor suppressor. Tumors with stronger SMAD4 dependencies had significantly better OS in seven cancers (Fig. 7, H and I, and fig. S17). To assess the interaction of the prognostic dependencies with other clinical variables, we performed a multivariate Cox analysis that included patients’ age, gender, and pathological/clinical stage. Among the nine cancer types with a large sample size (n ≥ 300), 68.6% of the prognostic dependencies (711 of 1036) remained significant with multivariate Cox P < 0.05 (table S16). Together, we demonstrate that gene dependency scores have clinical implications in both treatment responses and prognosis. Future studies aimed at validating these genes in physiologically relevant cancer models will have far-reaching clinical significance.

DISCUSSION

This study addresses significant bioinformatics challenges that have arisen from the rapid accumulation of cancer dependency maps: how to link genomic contexts to cell viability and how to systematically translate cell line assays to tumors. DeepDEP links a cell’s genomic context to its gene dependencies assayed by CRISPR-Cas9 screens and creates a model to predict tumor dependency via a transfer-learning design. Our model demonstrated the promise of bridging CCL-based screens and tumor genomics with an unsupervised pretraining design, echoing a recent success of applying another transfer learning technique, namely, the few-shot learning, to translate high-throughput drug screens to individual patients (21). We note that this few-shot learning is different from our transfer-learning strategy because it is a supervised pretraining method that requires model pretraining using labeled samples. It also needs fine-tuning of the pretrained model using labeled tumor data, which are not applicable to a standard pooled CRISPR protocol. In vivo CRISPR screen is a potential path to directly optimizing computational models to mitigate the gap between CCLs and tumors. However, such a screen remains challenging and costly and can only be carried out in few mouse models (38, 39). When systematic in vivo screens become available, the proposed model can be a stepping stone toward an accurate prediction for tumor dependencies. Furthermore, methods that align genomic profiles between CCLs and tumors (40, 41) may help to reduce the differences between tumor and CCL domains. We expect that the incorporation of these methods will improve the translational capability of DeepDEP along with the expansion of CCLs being screened by the DepMap projects.

The study of SE between a mutation and an essentiality may lead to the critical discovery of cancer-specific vulnerabilities and thus context-specific therapeutic targets (26, 27). Traditional approaches identify SE by statistically inferring mutual exclusivity between two mutations in tumors (27), comparing gene dependency profiles between CCLs in the presence or absence of a specific gene mutation, or experimentally searching for a gene inhibition effectively killing a CCL harboring a mutation. However, the wet laboratory exploration is costly, and conventional computational methods require a huge sample size to infer mutual exclusivity and overcome genomic variations in heterogeneous cancer cells (26). We demonstrated the utility of Mut-DeepDEP to study SE by mimicking a virtual switch of a gene mutation in a given CCL and observing the effect on a dependency. We observed our model’s behaviors and identified known (PTEN/CHD1 and BRCA1/PARP1) and novel SE pairs with KRAS. With the expanding genomics and screening resources, we expect to see the establishment of a curated SE database that will permit us to systematically substantiate our results. The current model only considers binary mutation status, so the mutation matrix was highly sparse (5.7% of nonzero elements). Our simplified model, as well as the perturbation of binary mutation status, may not fully represent the functional heterogeneity of gene mutations as multiple somatic alterations and mechanisms can activate/inactivate genes in cancers. For instance, VHL can be inactivated by both deletion and mutation in kidney cancers, so as EGFR amplification/mutation in glioblastoma and lung cancer, and TP53 deletion/mutation. Future studies that enrich the mutation contents and refine our model are warranted to produce candidates for wet laboratory validations and develop hypotheses for novel patient-specific therapeutic targets.

KRAS is a frequently mutated oncogene in cancer (~7% in our reanalysis of TCGA data). It has been one of the hardest gene mutations to target. Thus, targeting its SE interactors may be an effective alternative (42). Using our prediction machine, we identified frequent SE interactions of KRAS with 12 gene knockouts, including its upstream (EGFR) and downstream (MAP3K7) interactors and other less studied genes associated with ribosomal (RPL21 and RPL22) and mitochondrial function (NARS2). EGFR is part of the ERBB family. Our prediction of EGFR as a potential SE target of KRAS echoed findings from several in vivo studies. A study suggested pancreatic tumorigenesis driven by oncogenic KRAS is strongly dependent on EGFR; knockdown of EGFR expression by short hairpin RNAs (shRNAs) effectively inhibited tumorigenesis (43). Concordantly, genetically engineered mouse models of NSCLC showed that EGFR deletion impaired mutant KRAS activity and transiently reduced tumor growth, which then triggers an escape mechanism mediated by the activation of other non-EGFR ERBB family members (44). Thus, a pan-ERBB inhibitor, afatinib, effectively inhibited tumor growth of KRAS-mutated NSCLC on patient- or cell line–derived xenografts (44). We note that our data and other reports do not imply that currently approved EGFR inhibitors would be efficacious for KRAS-mutated tumors, since EGFR tyrosine kinase domain inhibitors (gefitinib and erlotinib) function via distinct inhibition mechanisms from CRISPR-Cas9 and are prone to the aforementioned resistance mechanisms. As for MAP3K7, our prediction was in line with previous studies reporting that (i) shRNA-based depletion of MAP3K7 has the most potent and selective effects among a panel of kinases in inhibiting the viability of KRAS-mutant colon CCLs (45); and (ii) pharmacologic inhibition of MAP3K7 suppresses KRAS-mutated colorectal cancer growth in vitro and in vivo (46). Our prediction also indicated the need to investigate SE interactions in a tumor context–specific manner [Fig. 4C; reviewed in (47)]. Together, comprehensive in vitro and in vivo investigations into these potential SE partners of KRAS mutations are necessary to confirm our predictions and to gain better biological and clinical insights.

Mitochondrial dysfunction is a hallmark of cancer (48). Energy metabolism is vital for cancer cells to survive the damage induced by chemotherapeutic drugs (36); therefore, targeting energy metabolism may overcome drug resistance. Our analysis of the pan-cancer dependency map revealed predominant mitochondrial functions in genes essential in chemoresistant tumors. However, activity of the OXPHOS pathway in CCLs can be modulated by the culture medium (49) and confounded by the timing that a CCL is derived relative to chemotherapy. Our data also suggested that the dependencies on certain tumor-suppressive genes (SMAD4 and IL2) and less studied genes (ACVR1 and DEK) are associated with OS in many cancers. IL2 is a key cytokine, and its receptor is expressed in many different immune cells. Endogenous expression of IL2 in tumors is related to cancer cell proliferation and histological tumor grade in different cancer lineages (50). Besides, IL2 has been approved as immunotherapy of metastatic cancers of melanoma and renal cell carcinoma. Our predicted tumor dependencies indicated a potential prognostic role of IL2 dependency in UVM, KICH, KIRP, and other cancers (Fig. 7F). We noted that more research is needed to further elucidate the mechanism of IL2 dependency in tumor prognosis and to validate the screening results of IL2 in view of a common limitation of pooled screens by non–cell-autonomous effects (51) including paracrine signaling of cytokines. SMAD4 is a well-studied tumor suppressor gene. However, in a malignant background, it may perform multifaceted functions since its tumor-suppressive functions may have already been compromised by mutations or bypassed through other oncogenic pathways. We found that tumors with stronger dependency on SMAD4 had significantly better survival in multiple cancers including BRCA, echoing a previous in vivo study demonstrating knockdown of SMAD4 in BRCA cells effectively inhibits bone metastasis (52). Overall, survival analysis of the predicted tumor dependencies revealed interesting candidate genes for future studies and demonstrated a novel strategy to identify prognostic markers.

We used the unbounded gene effect score as model output to facilitate subsequent investigations with genomic data. However, the gene effect score may be vulnerable to biases and uncertainty associated with batch effects and screen quality (5). Future studies may extend our model to predict the dependency probability (4–6) or the binary fitness score (7, 53), which indicates the likelihood of a gene knockout to have real depletion effects, by applying a softmax or sigmoid output layer to our model. Addressing the common limitation of DL models as “black boxes,” we implemented an interpretation strategy by perturbing and/or decoding the input (e.g., gene mutations) or intermediate nodes (e.g., gene signatures) to mimic typical molecular biology assays that study functional genomics by perturbing individual genes or pathways. A promising alternative of model construction/interpretation may be the visible neural network (54) that integrates the GO hierarchy into DL architecture to enable gene set level interpretation.

Project DRIVE suggested that ~1% of gene dependencies are predominantly determined by their self-expression levels (3), such as SOX10. To predict these dependencies, simple uni- or few-variate models, as well as properly regularized models such as an elastic net, are expected to achieve optimal or near-optimal performance to capture specific associations between model inputs and outputs. Expanding the range of biological contexts, computational tools such as CEN-tools (55) identify dependencies that are specific to the tissue of origin and/or individual mutation state and expression level. On the basis of the concepts of differential network biology (56) and genetic coessentiality (57), an interactive tool called FIREWORKS (58) interrogates functional relationships between gene dependencies using context-specific “coessentiality networks” and identifies multiomic signatures associated with differential gene dependencies. Since our goal is to link multiomics to the landscape of dependencies regardless of their simple or complex associations, we designed a unique architecture to allow the model to learn from genes with similar functions implemented by a functional fingerprint. Taking Exp-DeepDEP as an example, the encoder network of our model captured two gene expression signatures that predicted (as demonstrated by simple linear regressions in fig. S6) and characterized a broad panel of gene dependencies. Such a prediction machine also allows interpolating and extrapolating gene dependencies beyond the limited screened CCLs. The constructed essentiality maps create a novel way of visualizing gene dependencies, both at the level of individual genes (Fig. 3F) and the landscape of genes in the same pathway (figs. S7 to S10). The implementation of functional fingerprint is a key to the enhanced performance and efficiency of DeepDEP. Unlike the chemical fingerprints of drugs, to our knowledge, there is no fingerprinting system to describe the functions of a gene. The proposed functional fingerprint focuses on CGPs. Besides the involvement of genes in curated molecular signatures, other biochemical and functional features may be used to enrich the information captured by fingerprints. To alleviate the limitation in the sample size, we also adopted the unsupervised pretraining strategy to train our model by two steps (22). The model captured data representation of each type of genomic data using TCGA samples and was then fine-tuned toward the prediction of dependencies using CCL data. The benefits of this strategy were demonstrated in our previous study for predicting drug response (16). For expression data, pretraining suggested an optimal architecture of 6016 to 500 to 200 to 50 neurons to capture the most information out of the tumors’ expression data. However, when we incorporated the encoder into Exp-DeepDEP and retrained the model using CCLs’ dependency data (Fig. 3A), the model was exposed to only 222 unique expression profiles (80% of 278 CCLs)—not enough to support network optimization. This limitation may cause neuron degradation to prevent model overfitting, largely accounting for the abundant zeros we observed at the bottleneck layer of the Exp-DeepDEP model. We expect a further improvement of our model by incorporating training techniques, such as data augmentation and regularization, and with the expansion of the DepMap projects and other large genetic screens.

MATERIALS AND METHODS

Datasets

Dependency profiles of CCLs

The primary dataset used in this study was CRISPR-Cas9 essentiality screens of 17,634 genes in 436 CCLs from the publicly available Broad DepMap dataset (2018Q2 version; https://depmap.org/portal/). Summary statistics of the CCLs can be found in table S6. Gene effect scores estimated and corrected by CERES (4) were used as the measure of gene dependency (5). Here, we used the dependency profiles of 1298 genes (DepOIs) with high-essentiality variation among the CCLs (SD, >0.2) and those listed in the Cancer Gene Census of COSMIC (59). We included three independent validation datasets (table S5). One dataset included 348 CCLs newly assayed by Broad DepMap (2018Q3 to 2020Q2), while the present study was in progress. This validation dataset contains gene effect scores derived from a refined computational pipeline that incorporated the batch correction of CERES scores, the newer hg38 reference genome, an updated list of genes used to scale the gene effect scores, etc. The second dataset was collected from a recently published CRISPR screen conducted by the Sanger Institute using a different CRISPR library (7). Here, we used the fitness effect score that was calculated as the quantile-normalized depletion log fold change between targeting sgRNAs and plasmid library. We also downloaded data from three RNAi-based large screens [Marcotte et al. (1), Project Achilles (2), and Project DRIVE (3)] combined and harmonized by the DEMETER2 algorithm (25). The RNAi dataset contains dependency scores of 712 CCLs on 17,212 genes.

Genomic profiles of CCLs and tumors

We collected four types of genomic profiles (mutations, gene expression, methylation, and CNAs) of CCLs and tumors of TCGA. Mutation profiles were reprocessed into gene-level binary status (i.e., 1 for mutated and 0 for wild-type) from Mutation Annotation Format files downloaded from Cancer Cell Line Encyclopedia (CCLE) (1463 cells) (60) and TCGA PanCanAtlas (9093 tumors) (61) databases. Here, we considered five types of nonsynonymous mutations—missense and nonsense mutations, frameshift insertions and deletions, and splice sites. For the TCGA dataset, we only included high-confident mutations that passed the Multi-Center Mutation Calling in Multiple Cancers filter (61). Overall, we included 4539 genes mutated in at least 1% of TCGA samples. We represented gene expression levels by log₂(TPM + 1), where TPM denotes the number of transcripts per million, in 935 CCLs and 9806 TCGA tumors downloaded from the Cancer Target Discovery and Development Network (62) established by the National Cancer Institute’s Office of Cancer Genomics and the UCSC TumorMap (63), respectively. We used 6016 genes with means and SD greater than 1 in the TCGA samples. For DNA methylation, we collected data of 1028 CCLs assayed by Illumina 450K BeadChip (GSE68379) (64) and 12,039 TCGA samples with merged Illumina 27K and 450K BeadChips from the PanCanAtlas (65). We eliminated probes with low methylation (β value, <0.3) in >90% of TCGA samples, leaving 6617 probes for subsequent analysis. CNA data called from Affymetrix SNP 6.0 arrays of 1043 CCLs and 11,101 TCGA samples were downloaded from CCLE and PanCanAtlas, respectively. Here, we generated ~310,000 consecutive segments of length 10,000 bases along the chromosomes and mapped each CNA onto these segments weighted by the percentage covered by CNA. DeepDEP included 7460 informative CNA segments (zeros in <5% of samples, mean of absolute values of >0.20, and coefficient of variation of >0.20 in TCGA). In this study, mutation and expression data were gene-based, while methylation and CNA data were represented by probes and chromosomal segments, respectively.

Pairing genomic and dependency profiles

A total of 278 CCLs [covering 17 tissue types according to annotations of Genomics of Drug Sensitivity in Cancer (64)] with four genomic profiles and CRISPR-Cas9 dependency data were incorporated into DeepDEP. Among TCGA tumors, merging four genomic profiles yielded a sample size of 8238, covering 32 tumor types.

Fingerprint vector of a DepOI

To define the functional features of a DepOI, we collected molecular signatures of 3433 CGPs (3115 signatures after removing those not containing any of the 1298 DepOIs) from MSigDB v6.2 (24). Each DepOI was described by its involvement in the 3115 signatures. Mathematically, the fingerprint matrix fps∈{0,1}^D×S is written as

$$\mathbf{\text{fps}}(d,s)=\{\begin{array}{c}1,d\mathrm{\in }{\mathbf{G}}_s\\ 0,\text{otherwise}\end{array}$$ (1)

where d and s denote DepOI d and a molecular signature s, respectively, and G_s is the set of genes of signature s. Thus, a DepOI can be mathematically described by the corresponding row vector of the fps matrix, or a fingerprint vector.

Design of DeepDEP

Model overview and performance assessment

DeepDEP was designed to predict the essentiality for a gene in an unscreened CCL or tumor based on four genomic profiles of a sample and the fingerprint vector of the gene of interest (Fig. 1). An autoencoder network was constructed to learn high-order representations of each genomic data and fingerprint. Outputs of the five encoder networks were concatenated into the prediction network to yield a predicted gene effect score. The entire model was trained and tested using the data from CRISPR-Cas9 knockout screens of 1298 DepOIs in 278 CCLs (i.e., 360,844 samples). We used 80% of these samples to train the model, 10% to monitor the training process to control overfitting, and 10% to test model performance. The model was optimized with a loss function of mean squared error (MSE). After model training, we evaluated the performance by per-DepOI Pearson correlation coefficient ρ between the predicted and original scores of each DepOI in testing CCLs. Performance assessment on the most variable 61 DepOIs with an SD of >0.3 and 506 DepMap-defined high-variance DepOIs with top 3% most variable scores (https://depmap.org/portal/; version 20Q2) is provided in the Supplementary Materials.

General DL settings and computation environment

We implemented and optimized the model using the Python library Keras 1.2.2 with TensorFlow backend. For a neuron j in our fully connected neural networks, its output y_j is calculated by

$$y_j=F({\sum }_i{w}_{\mathit{i}\mathit{j}}{x}_i+b_j)$$ (2)

where x_i denotes the output of neuron i at the previous layer; w_ij and b_j are the weight and bias, respectively; and F represents the activation function. Summarization of all neurons at a layer can thus be written as

$$\mathbf{y}=F(\mathbf{\text{wx}}+\mathbf{b})$$ (3)

During training, weights and biases are adjusted to minimize a loss function. We optimized the model by an Adam optimizer (66) with a loss function of MSE. We set F as a rectified linear unit (ReLU); activation of the output layer was linear to fit the unbounded distribution of gene effect scores. All analyses were performed on a Linux server with 4× 24-core Xeon E7-8890 v4 2.20-GHz processors with 512-gigabyte random-access memory.

Encoder networks for genomic data and gene fingerprints

DeepDEP has five input encoder networks, four of which were designed for genomic data of a CCL/tumor and the other for the functional fingerprint of a DepOI (Fig. 1). For each set of genomic data, an autoencoder was pretrained using TCGA (n = 8238) to learn low-dimensional embeddings of high-dimensional inputs, which we previously showed to improve the convergence and stability of a DL model (16). We used a hyperparameter optimization method, hyperas (https://github.com/maxpumperla/hyperas), to determine the optimal number of neurons for each layer of an autoencoder as previously described (16). Hyperas is a grid-searching algorithm that searches a prefixed parameter space by a fixed number of parameter combinations using the Hyperopt optimization library (67). Here, we set the parameter space as follows: the first {1000,500,200}, second {200,100,50}, and bottleneck layers {50,20,10}. For each genomic data, 20 combinations were evaluated for 20 epochs using the TCGA data. The best-performing autoencoders were then fully trained for 100 epochs. The architectures of the four encoder subnetworks were used in the DeepDEP model; the weights and biases were used to initialize the corresponding networks in DeepDEP. The encoder for gene fingerprints adopted the architecture of that for mutations since they had similar inputs of binary data, while the former was not pretrained and randomly initialized by the He’s uniform distribution (68).

Prediction network

The prediction network was designed to learn from embedded genomic features (characterizing a CCL/tumor) and gene fingerprints (portraying the functions of a DepOI) and to predict a gene dependency score. Bottleneck layer neurons of the five encoders were concatenated and passed onto two fully connected hidden layers, followed by a single-neuron output. The number of nodes at each hidden layer was set at the total number of neurons passed from the encoder networks. The output value is a predicted gene dependency score of a DepOI in a CCL/tumor sample. The network was randomly initialized by the He’s uniform distribution.

Implementation of linear and nonlinear ML methods

The performance of DeepDEP was compared to several ML methods. We used the (i) full input data or the top 50 components of either (ii) PCA or (iii) NMF of each genomic profile and gene fingerprints (250 dimensions in total). The input data were fed into six conventional ML models: (i) linear least squares regression models with lasso (least absolute shrinkage and selection operator), (ii) ridge, or (iii) elastic net (with equal weighting on L₁ and L₂ penalties) regularizations, and (iv) SVMs with linear, (v) Gaussian, or (vi) RBF kernels to predict gene dependencies. A random forest model was not implemented because of extreme computation cost due to large input dimension. These models were trained and tested on the same 90-10 partition of CCLs used for DeepDEP. The best model of each ML method was repeated 10 times with subsampling; in each round, a set of sample partitions was used across ML methods and DeepDEP. All ML models were implemented using MATLAB built-in functions (Statistics and Machine Learning Toolbox, MathWorks Inc., MA).

Leave-cluster-out cross-validations and y-scrambling

We performed leave-cluster-out cross-validation analyses to test model performance. CCLs were divided into 10 groups by k-means clustering (k = 10) based on the squared Euclidean distance of the expression data. Each k-means analysis was repeated three times to ensure convergence with a MATLAB built-in function. For each leave-cluster-out analysis, a cluster of CCLs was used to test three independent models trained on the rest of the samples. Because of the differences in the number of CCLs among clusters, the performance of leave-cluster-out cross-validations was assessed by MSE only and summarized by means ± SD across the three models.

We also performed y-scrambling validation to verify that the achieved performance was “real” and not by random chance according to previous reports (69, 70). We randomly permuted dependency scores among all CCL-DepOI samples to generate mismatched input and output data. We used 90 and 10% of CCLs to train/validate and test a model as the reported DeepDEP model. The performance of the random model was evaluated by the per-DepOI ρ in the testing samples. The entire process was performed 100 times, and the final performance was summarized by mean and SD.

Model interpretation

Interpretation of encoded gene expression bottleneck nodes

We investigated gene expression nodes to explore the relevance of gene expression signatures in determining genetic vulnerabilities. At the output layer of the expression encoder of Exp-DeepDEP, for each node of interest, we performed a step-wise simulation to its output value from the mean of all CCLs with a step size of 0.25 SD. To understand the expression signature encoded in the node, we built an autoencoder comprising (i) the expression encoder of Exp-DeepDEP with hard-coded weights to retain the data embedding and (ii) a symmetric decoder network with fully trainable weights. The autoencoder was then trained using the TCGA data to optimally “reverse engineer” the expression signatures captured by the encoder network. After training, we fed a vector of all 0s except for 1 at the node of interest into the decoder network, and the output represents the expression signature captured by the node. Each signature was analyzed by GSEA (71) using a single-sample setting (i.e., ranked by the levels, instead of differences) for the association with hallmark gene sets of the MSigDB (24). We only considered positive enrichments with an FDR of <0.001.

Multivariate linear regression models were used to test the predictive power of the two identified signatures on the original gene effect scores with the absence or presence of other variables

$${\mathbf{\text{Eff}}}_{\mathit{d}}=\{\begin{array}{c}{\mathrm{\beta }}_1{\mathbf{\text{Sig}}}_{\mathrm{1}}+{\mathrm{\beta }}_2{\mathbf{\text{Sig}}}_{\mathrm{2}}+{\mathrm{\beta }}_3{\mathbf{\text{Sig}}}_{\mathrm{1}}\bullet {\mathbf{\text{Sig}}}_{\mathrm{2}}+\mathbf{\epsilon }\\ {\mathrm{\beta }}_1{\mathbf{\text{Sig}}}_{\mathrm{1}}+{\mathrm{\beta }}_2{\mathbf{\text{Sig}}}_{\mathrm{2}}+{\mathrm{\beta }}_3{\mathbf{\text{Sig}}}_{\mathrm{1}}\bullet {\mathbf{\text{Sig}}}_{\mathrm{2}}+{\mathrm{\beta }}_4{\mathbf{\text{Exp}}}_{\mathit{d}}+{\displaystyle {\sum }_{k=1}^7}{\mathrm{\beta }}_{v_k}{\mathbf{v}}_k+\mathbf{\epsilon }\end{array}$$ (4)

where Eff_d is a vector of original gene effect scores of the dth DepOI, Sig₁ and Sig₂ are expression signature scores, Exp_d is the expression level of the DepOI, v_k is screen or cell variable k, and β and ε are regression coefficients and error. The Sig₁∙Sig₂ term represents the interaction effect between two signatures. Here, v_k included seven variables in two categories: cell culture [adhesion (versus suspension), Dulbecco’s modified Eagle’s medium (DMEM), Eagle’s minimum essential medium (EMEM), minimum essential medium (MEM), and Roswell Park Memorial Institute medium (RPMI)], and screen quality [strictly standardized mean difference (SSMD) and Cas9 activity] as listed in table S6. All CCLs (n = 278) were used for the regression. All input and output data were z-transformed. Statistical significance of each term was assessed by t statistics against zero and corrected for multiple tests by the Bonferroni correction with a factor of 278. Bonferroni-adjusted P < 0.05 was used for significance. We defined a category of variables to be predictive of a DepOI if any of its component variables was significant.

Model interpretation by perturbing input mutation data to study SE

To comprehensively study SE, to each CCL, we perturbed the mutation status of one gene at a time (from 0 to 1 or 1 to 0), with all other genes unchanged, and fed the mutation profile into Mut-DeepDEP to predict gene dependencies. We defined an SE score as the change in the predicted dependency score of a DepOI d in a CCL c carrying a gene mutation g compared to the same CCL without the mutation

$$\mathbf{E}(d,g,c)=\text{Dep}(d,{\mathbf{M}}_c^{g^1})-\text{Dep}(d,{\mathbf{M}}_c^{g^0})$$ (5)

where Dep is the prediction function of Mut-DeepDEP given d and the binary mutation vector (length, 4539) M_c of c, and ${\mathbf{M}}_c^{g^1}$ and ${\mathbf{M}}_c^{g^0}$ represent the mutation vectors of c with a 1 (mutated) and 0 (wild type), respectively, at gene g. Here, we only considered mutation-DepOI pairs with a negative SE score, which represents a stronger essentiality in a CCL carrying a mutation than the wild type.

For the identification of SE interactors of a gene mutation (e.g., KRAS) in each CCL, we used two criteria: (i) at least 5% of change in the predicted dependency score associated with a gene mutation as compared to the baseline prediction and (ii) an SE score ranked among the top 5% of all mutation-DepOI pairs in the CCL.

Definition of dependencies driven by each genomics in TCGA

We defined an M-Dep event when a gene mutation is associated with a stronger (positive) or weaker (negative event) dependency across TCGA samples (t test with Benjamini-Hochberg FDR, <10⁻²⁰). All mutation-DepOI pairs were tested for M-Dep. Similarly were E-Dep (FDR for correlation coefficient, <10⁻⁵⁰), Me-Dep (FDR, <10⁻⁵⁰), and C-Dep (FDR, <10⁻¹⁰⁰) defined to yield similar numbers of events among the four categories. A DepOI was called to be “dominated” by M-Dep if it had more M-Dep events than any other events; E-, Me-, and C-dominant Dep were defined similarly.

Association analyses of gene dependencies with clinical data

Clinical data of TCGA were downloaded using the R/Bioconductor package TCGAbiolinks (72). For the analysis of chemoresponse, we considered only primary tumors and excluded samples with multiple records of chemotherapy that were assigned to different response groups. We collected the MSI status of pan-cancer tumors that were experimentally determined by TCGA [curated by (73)] or predicted by the MANTIS algorithm (74). For the former, we only considered the MSI-high (MSI-H), MSI-low (MSI-L), and microsatellite stable (MSS) categories that were available in five MSI-prone cancers: colon adenocarcinoma, esophageal carcinoma, rectum adenocarcinoma, stomach adenocarcinoma, and uterine corpus endometrioid carcinoma. The MANTIS algorithm examined the whole-exome sequencing data of TCGA and used mutation burden, mutation signatures, and somatic variants to predict a continuous MSI score for each tumor. A score greater than 0.4 was indicative of the MSI-H status.

Gene dependency scores of each DepOI were analyzed for the association with OS in individual cancers by a univariate Cox proportional hazards regression model. Here, dependency scores of each gene were z-transformed before being fed into the Cox model. A gene was defined as a protective dependency when tumors with more negative predicted dependency scores (indicating stronger dependency) had significantly better OS (i.e., the hazard ratio of dependency score > 1) with an FDR of <0.2 (Benjamini-Hochberg adjustment with respect to the number of DepOI-cancer pairs). Kaplan-Meier curves and log-rank tests were conducted by a median cutoff on the gene dependency scores. For the multivariate Cox analysis, we included age, gender (female/male), and tumor stage (discrete classes, 1 to 4) in addition to the dependency score. For each cancer type, the tumor stage was determined by either the pathological or clinical stage that gave a larger sample size. The multivariate analysis was performed on nine cancers that had at least 300 samples with available clinical data.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/7/34/eabh1275/DC1

View/request a protocol for this paper from Bio-protocol.