Significance
There is a lack of global observational data to monitor the application of nonpharmaceutical interventions (NPI) and evaluate the effect of NPIs for pandemic management in different territories. We find that economic activity reduction inferred from NO2 is a driver of case deceleration in most of the territories. The effect, however, is not linear but dampens over time, and further reductions are only associated with weaker deceleration. Over the winter of 2020/2021, nearly 1 million daily COVID-19 cases could have been avoided by optimizing the timing and strength of activity reduction in different regions relative to a scenario based on the real distribution.
Keywords: COVID-19, machine learning, satellite observation, air pollution, pandemic management
Abstract
The real-time monitoring of reductions of economic activity by containment measures and its effect on the transmission of the coronavirus (COVID-19) is a critical unanswered question. We inferred 5,642 weekly activity anomalies from the meteorology-adjusted differences in spaceborne tropospheric NO2 column concentrations after the 2020 COVID-19 outbreak relative to the baseline from 2016 to 2019. Two satellite observations reveal reincreasing economic activity associated with lifting control measures that comes together with accelerating COVID-19 cases before the winter of 2020/2021. Application of the near-real-time satellite NO2 observations produces a much better prediction of the deceleration of COVID-19 cases than applying the Oxford Government Response Tracker, the Public Health and Social Measures, or human mobility data as alternative predictors. A convergent cross-mapping suggests that economic activity reduction inferred from NO2 is a driver of case deceleration in most of the territories. This effect, however, is not linear, while further activity reductions were associated with weaker deceleration. Over the winter of 2020/2021, nearly 1 million daily COVID-19 cases could have been avoided by optimizing the timing and strength of activity reduction relative to a scenario based on the real distribution. Our study shows how satellite observations can provide surrogate data for activity reduction during the COVID-19 pandemic and monitor the effectiveness of containment to the pandemic before vaccines become widely available.
The outbreak of COVID-19 in the winter of 2019/2020 has spread over the globe, leading to >83 million cases and >1.8 million deaths by 1 January 2021, with resurgence possibly in 2021 and even 2022 in the Northern Hemisphere (1). Nonpharmaceutical interventions (NPIs) in general and confinements in particular are demonstrated to be effective in containing this pandemic (2–7). However, many governments chose to suppress confinement and lift mobility restrictions soon after cases decreased, with a poor understanding of the relationship between activity recovery and acceleration of COVID-19 cases under lagging effects of lifting controls (8). The probability of resurgence is 97% in China if controls were lifted 14 d after the first day with zero ascertained cases (3) and 95% in Europe if activity reopened without coordinated deconfinement strategies (4). Facial masking, social distancing, and “test–trace–isolate” strategies affect microbehavior of individuals, while their effectiveness depends on small-scale conditions and rate of adoption (9). However, the effectiveness of limiting economic activity and social interactions during COVID-19 confinement depends on larger-scale circumstances. For example, Sweden initially slowed down the epidemic spread of COVID-19 without a strict lockdown, likely due to the high share of single-person households and low population density (10), whereas India put into place strict lockdowns to cut off the path of COVID-19 transmission, given the large household sizes and high population density (11). Recent studies have suggested a potential association between air pollution and COVID-19 mortality and infectivity, but the direction of causality has not been examined (12–14).
The effects of NPIs to mitigate the spread of COVID-19 have been verified (2–7), but the relationship between activity reduction and case deceleration is yet unquantified. In epidemiological studies, the effects of NPIs are characterized by government response indicators (15), mobility networks (16), volume of travelers (17), average distance traveled by passengers (5), and flight bookings (18). However, indicators such as government responses (15) lack details in space, and the impact of imperfect compliance and voluntary actions cannot be quantified (19). Sectorial statistics leave blind spots to elucidate the coupling between activity recovery and acceleration of new cases as they do not cover the entire economy (20). Unlike bottom-up activity data, being sector-specific and not always geolocalized, spaceborne observations of atmospheric tracers can be used to track changes in industrial, mobile, residential, commercial, and agricultural activities (21–25). Nitrogen oxides are emitted from fossil-fuel combustion, biomass burning, agricultural practices, and aircrafts (26). We extended this method to 211 territories by analyzing tropospheric vertical column concentrations of nitrogen dioxide (NO2) measured by two satellites: Ozone Monitoring Instrument (OMI) (27) for 2016 to 2020 and Tropospheric Monitoring Instrument (TROPOMI) (28) for 2019 to 2020. NO2 with a short lifetime (∼1 d) in the atmosphere is temporally correlated with variations in economic activity and mobility, which is a good indicator of social interactions (25, 26, 29, 30). SI Appendix, Fig. S1 shows that NO2 is spatially correlated with purchasing-power-parity gross domestic product (GDP) across 142 countries (R = 0.73 using OMI and 0.69 using TROPOMI) and 21,556 0.5° × 0.5° pixels (R = 0.51 using OMI and 0.50 using TROPOMI).
We used the meteorology-adjusted weekly NO2 changes after the 2020 COVID-19 outbreak relative to the 2016 to 2019 baseline (ΔNO2) as a proxy of activity anomalies to predict the weekly deceleration (Eq. 6) of COVID-19 cases with a machine-learning model. NO2 data from two satellites, OMI and TROPOMI, were used. The coverage is for 211 territories, including 31 provinces in China, 51 states (including the District of Columbia) in the United States, and 129 countries. The model is evaluated by fourfold and leave-one-out cross-validation and performs better than the same model using alternatively NPI indicators (15, 31) or human mobility (32, 33) as predictors. The model predicts the trends in cases over the first 60 d after the COVID-19 outbreak in each territory and is then used to predict the evolution of cases in the winter of 2020/2021. By recognizing the regional differences in the sensitivity of new daily COVID-19 cases to activity reduction, we optimized the regional distribution of activity reduction required to maximize reduction of cases, which informs policies to improve the efficacy of global joint actions to contain COVID-19. Our approach analyzes the coupling between activity reduction and deceleration of COVID-19 cases, but neither identifies measures that induce the activity changes nor accounts for changes at the microlevel such as mask wearing and social distancing. The adoption of microbehavior such as facial masking and social distancing is a crucial factor, but the compliance (19) cannot be measured and considered in such analysis. Our method helps to overcome limitations for territories lacking statistical data.
Results
Global Activity Reductions Following the Outbreak of COVID-19.
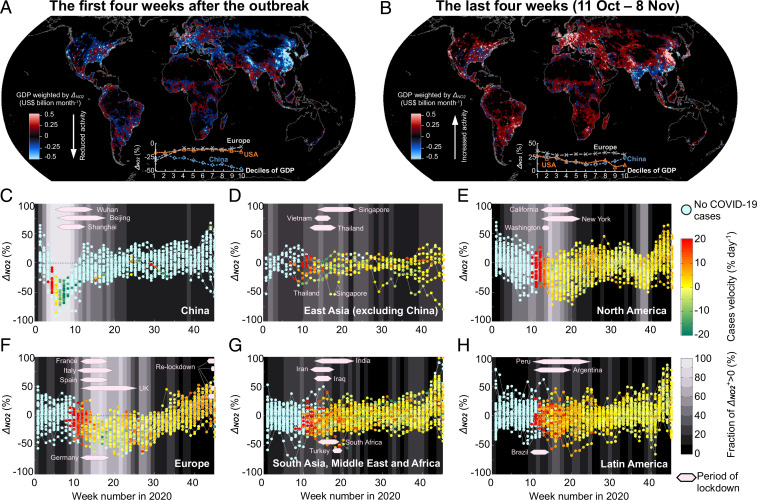
Regionally and globally, NO2 decreased after the COVID-19 outbreak (30, 34, 35). We used a fixed-effects model (36) to estimate the meteorology-adjusted differences in NO2 (ΔNO2) by week from OMI in 2020 relative to 2016 to 2019 (or 2019 for TROPOMI). In this fixed-effects model, the COVID-19 outbreak explains reductions in NO2 from 2016 to 2019 to 2020 of 6% in China, 8% in the United States, 5% in Europe, and 6% globally (SI Appendix, Fig. S2). We ultimately mapped the variations in ΔNO2 as a marker of economic activity over space and time (Fig. 1 for OMI and SI Appendix, Fig. S3 for TROPOMI).
Fig. 1.
Use of NO2 as an indicator for activity changes (ΔNO2) during the COVID-19 pandemic in 2020 relative to the same weeks in 2016 to 2019. (A and B) Spatial distribution of GDP weighted by ΔNO2 in the first 4 wk after the COVID-19 outbreak in each territory (A) or the last 4 wk in this study (B). (Insets) ΔNO2 as an average for 10 deciles of gridded GDP density in China, the United States, and Europe. (C–H) Weekly variations in ΔNO2 from 1 January to 8 November 2020 in 31 provinces in China (C), 11 East Asian countries excluding China (D), 51 states in the United States (including the District of Columbia) and Canada (E), 37 countries in Europe (F), 57 countries in southern Asia, the Middle East, and Africa (G), and 23 countries in Latin America (H). The color of the circles evolves from green to red as the weekly velocity of COVID-19 cases increases. The color of the background evolves from black to white as the fraction of territories with a negative upper bound (mean + SE) of ΔNO2 (ΔNO2+) increases. The periods of confinement in representative territories are shown as bars (SI Appendix, Table S1).
The observed NO2 in 31 provinces in China decreased by 35 to 80% in the second week after the outbreak, of which the upper bound (average + SE) became negative in all provinces (Fig. 1C). By contrast, in the United States, the upper bound of ΔNO2 in the second week after the outbreak in each territory was negative in only 20 of 51 states (including the District of Columbia). In European countries, such a decrease was observed in 14 of 37 European countries and in the rest of the world for 20 of 90 countries (Fig. 1 D–H). During the 4 wk after the COVID-19 outbreak, NO2 was reduced by 47% in China, 15% in the United States, and 7% in Europe in the 10% of pixels with the highest GDP, compared to a reduction of 20%, 18%, and 34% in the 10% of pixels with the lowest GDP, respectively (Fig. 1A). This result suggests a larger impact of confinement on activity over richer regions with a higher population in China. From 11 October to 8 November 2020 (i.e., the last day of NO2 observations in this study), ΔNO2 was, however, positive over most of territories except in India and the Indochinese Peninsula (Fig. 1B). As a sign of global reopening (8), ΔNO2 in the 10% of pixels with the highest GDP was +27% in China, +15% in the United States, and +31% in Europe from 11 October to 8 November 2020. Using NO2 measured by TROPOMI over 2019 to 2020 (rather than OMI over 2016 to 2020) produces a similar map of ΔNO2, yet with a regional difference of 10 to 35% relative to OMI (SI Appendix, Fig. S3). Meanwhile, a fixed-effects model without filtering the effects of meteorology overestimates ΔNO2 by 12 to 42% in Europe, eastern China, and India (SI Appendix, Fig. S4), because interannual weather variability (37) alone could lead to higher NO2 in 2020 relative to 2016 to 2019.
Relationships between the Observed Activity Reduction and the Weekly Deceleration of Daily COVID-19 Cases.
Along with ΔNO2, we compiled daily COVID-19 cases from local data for China and the United States and national data for 129 countries from the European Centre for Disease Prevention and Control (ECDPC). Weekly velocity (V, in percent⋅day−1) and acceleration (A, the second derivative of cases in percent⋅day−2) of daily cases (Eq. 6) are estimated by logarithmic regressions. Our calculated A is correlated with real-time effective reproduction number (38) of COVID-19 (R2 = 0.50) (SI Appendix, Fig. S5), and a transparent calculation of A circumvents the need to make assumptions (39) in the transmission rate of COVID-19. For example, studies estimating effective reproduction number assumed that the timing of transmission follows a constant distribution of serial intervals, which was proven to be biased using real-time data (39). The relationship between A and effective reproduction number needs to be interpreted with caution.
The value of V was initially high but decreased as ΔNO2 became negative since the second week after the outbreak of COVID-19 in China, the fifth week in the United States, and the sixth week in Europe (Fig. 1 C, E, and F). The value of V decreased slowly in other countries with stabilized ΔNO2 (Fig. 1 D, G, and H). For different territories, a lower ΔNO2 was associated with a lower V (R = 0.093, P < 0.001) and a lower A (R = 0.14, P < 0.001) (SI Appendix, Fig. S6), but the low correlation coefficient (R) suggests that the effectiveness of reducing activity diagnosed from NO2 to decelerate cases depends on regional socioeconomic and environmental indicators.
While uncertainty in indicators of government responses (15, 31) due to imperfect compliance (19) is difficult to quantify, uncertainties in satellite NO2 data (27, 28) are estimated in our fixed-effects model (36) (SI Appendix, Fig. S7). According to the sign of upper bound (mean + SE) in ΔNO2 (ΔNO2+) and the velocity (V+) or acceleration (A+) of COVID-19 cases, we divided 5,642 wk after the COVID-19 outbreak across 211 territories into four regimes (SI Appendix, Fig. S6). In total, 14% and 40% of data are distributed in regimes I (ΔNO2+ < 0 and A+ < 0) and III (ΔNO2+ ≥ 0 and A+ ≥ 0), where activity reduction/recovery is coupled with deceleration/acceleration of COVID-19 cases. The effect of confinement could be suppressed when it follows the lifting of one control due to lagging effects (4). If we define ΔNO2+ < 0 in a week with negative ΔNO2+ lasting for three consecutive weeks before this week, the fraction of data in regimes I/III increases from 54 to 72% (SI Appendix, Fig. S6). This suggests that the effect of activity reduction is to manifest itself under the condition that the reduction lasts for at least 3 wk. The relationship between ΔNO2+ and A+ is robust when using NO2 measured by the TROPOMI (rather than OMI) or new COVID-19 cases reported by the World Health Organization (WHO) (rather than ECDPC), where the fraction of data in regimes I/III varies from 71 to 72% (SI Appendix, Fig. S8).
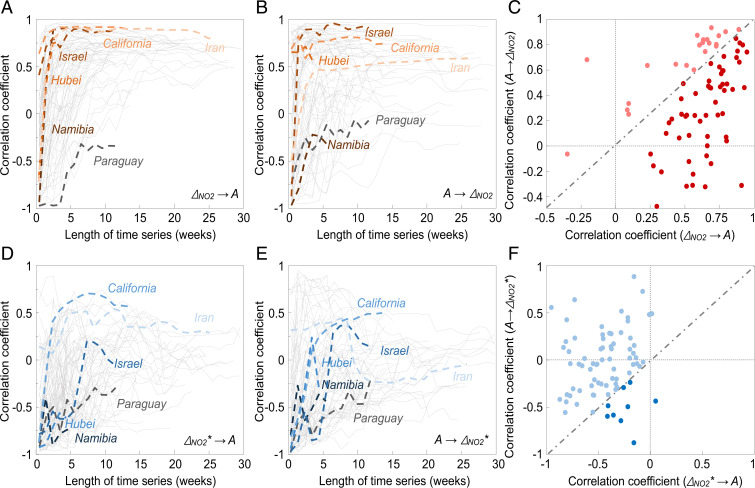
We applied a convergent cross-mapping method (40) to examine the causation between A and ΔNO2 in two steps. First, we calculated the Pearson’s correlation coefficient to evaluate the cross-mapping skill between A and ΔNO2 by a convergent cross-mapping algorithm (41). The skill in cross-mapping generally converges to a high positive level (Fig. 2 A and B). The skill mapping A from the ΔNO2 time series (correlation >0.4 for 67 of 78 territories) is better than the reverse (correlation >0.4 for 43 of 78 territories) for most of the territories, while 58 of 78 data points are below the 1:1 line (Fig. 2C). It suggests that economic activity reduction is the driver of case deceleration for most of the territories. Second, we also examined the causality between air pollution and the spread of COVID-19. Since air pollution has been suggested to exert an impact on the transmission (12–14, 42, 43) of COVID-19, we performed a sensitivity test in the cross-mapping between A and NO2 concentration without removing the effect of meteorology on NO2 (Fig. 2 D and E). The level of skill mapping A from the ΔNO2 time series (correlation >0.4 for 67 of 78 territories) is higher than that mapping A from the time series of NO2 concentration (correlation >0.4 for 6 of 78 territories) (Fig. 2F). It suggests that economic activity reduction inferred from air pollution (ΔNO2), rather than air pollution itself, is the driver of case deceleration in our study.
Fig. 2.
Detection of causality between ΔNO2 and deceleration of daily COVID-19 cases (A). ΔNO2 is derived as an indicator for activity reduction from changes in NO2 concentration by removing the impact of meteorology. (A and B) Cross-mapping of A and ΔNO2 with increasing time-series length for 78 territories with the length of data >5 wk. (C) Plot of the correlation mapping ΔNO2 from the A time series (A→ΔNO2) against the correlation mapping A from the ΔNO2 time series (ΔNO2→A) using the longest length of time series. (D–F) As in A–C, except for cross-mapping of A and NO2 concentration changes as an indicator for air pollution without removing the impact of meteorology (ΔNO2*). The code and data for this analysis are available on GitHub (https://github.com/rongwang-fudan/COVID-2019_EEC_Global).
Dependence of the Weekly Deceleration of COVID-19 Cases on Socioeconomic and Environmental Indicators.
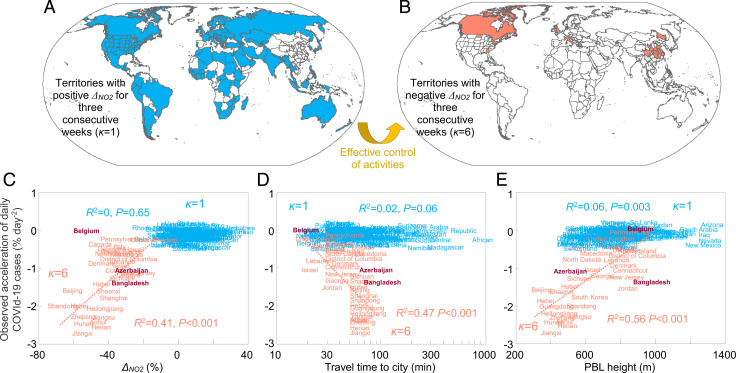
The functioning of environment, humans, and viruses is complex (1–7), making it hard to predict the deceleration of new COVID-19 cases. To represent the continuity of confinement, we defined a discrete variable (κ) for each week that takes value of 3, 2, and 1 for ΔNO2+ ≥ 0 lasting for 1, 2, and 3 wk before this week or 4, 5, and 6 for ΔNO2+ < 0 lasting for 1, 2, and 3 wk (Fig. 3 A and B). For example, A is close to zero in a branch where ΔNO2+ > 0 lasts for 3 wk (κ = 1), indicating a persistent spread of COVID-19 in the absence of control measures. The territories with negative ΔNO2+ for 3 wk are distributed over southern and northern China, western Europe, Canada, and the central and eastern United States (Fig. 3B). In a branch with ΔNO2+ < 0 lasting for 3 wk (κ = 6), longer travel time required to reach the nearest urban center (44) (R2 = 0.47), shorter delay in confinement (R2 = 0.51), lower GDP per capita (R2 = 0.42), and lower planetary-boundary-layer (PBL) height (R2 = 0.56) favor a faster deceleration of COVID-19 cases (Fig. 3 C–E and SI Appendix, Fig. S9). We expect that the observed correlation between A and environmental indicators such as PBL height and temperature to be a proxy of the impact of synoptic weather patterns on COVID-19 transmission. For instance, when the winter is chillier under a larger boundary layer height people tended to stay indoors with a greater risk of contamination (45), leading to a faster acceleration of COVID-19 cases. These relationships remain robust when using NO2 measured by the TROPOMI (rather than OMI) or COVID-19 cases reported by the WHO (rather than ECDPC) (SI Appendix, Fig. S10).
Fig. 3.
Relationship between the weekly acceleration of daily COVID-19 cases (A) and socioeconomic and environmental indicators. (A and B) Spatial distribution of territories with the upper bound (mean + SE) of ΔNO2 (ΔNO2+) being positive (blue, κ = 1) (A) or negative (red, κ = 6) (B) for 3 wk before one week in 2020. (C–E) The observed weekly acceleration of daily COVID-19 cases (A) is plotted against the estimated ΔNO2 (C), the average travel time of residents to the nearest urban center (D), and the PBL height as an indicator of air advection (E). Each indicator is averaged for weeks in a territory where the upper bound (mean + SE) of ΔNO2 (ΔNO2+) is positive (blue, κ = 1) or negative (red, κ = 6) for 3 wk before these weeks. The reported COVID-19 cases in Azerbaijan, Bangladesh, and Belgium were suspected to be biased and excluded from our analysis (Materials and Methods).
There are at least two factors that can influence the effect of ΔNO2 on A. First, it is likely that the effect of ΔNO2 on A is different for countries due to noneconomic factors. To examine this impact, we took the difference in distinguishing local vs. imported cases, social distancing, and facial masking as covariates in our model to predict A from ΔNO2. As a result, the coefficient of determination (R2) was increased by more than 0.1 for 17 of 78 territories with the length of data >10 wk (SI Appendix, Fig. S11). Second, there are variations in the effect of ΔNO2 on A between communities in large countries with spatial inhomogeneity in industry. To examine this impact, we compiled subnational data for the United States, China, Brazil, and Argentina (we did not consider other countries due to a lack of continuous subnational data of daily COVID-19 cases). It led to a higher correlation between ΔNO2 and A for 38 of 51 states in the United States, 3 of 7 provinces in China, 6 of 33 states in Brazil, and 10 of 21 states in Argentina than the correlation taking each country as a whole (SI Appendix, Fig. S12). These results indicate that the correlation between ΔNO2 and A can be improved by distinguishing local vs. imported cases, considering social distancing and facial masking and using cases at a higher spatial resolution. However, the limitation of applying our global model developed across countries to some countries/regions such as Paraguay with a poor performance in the prediction (Fig. 2A) should be noted. It is likely that there are other factors such as the indoor environments (46), religious events (13), and surveillance of the cold-chain food (47); more studies could consider these other factors to explain differences in the model performance between countries. Nevertheless, high-resolution ΔNO2 can be developed as an early warning indicator to monitor the effect of containment, even when detailed data of daily cases are unavailable.
Prediction of the Weekly Deceleration of Daily COVID-19 Cases from the Observed Activity Reduction.
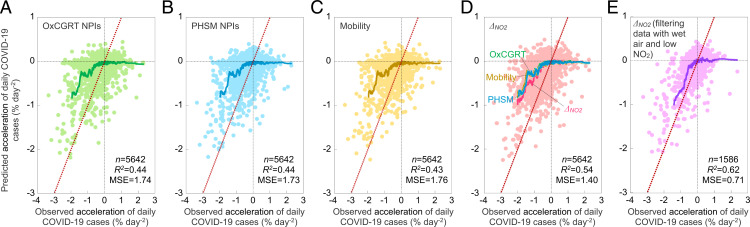
We fit a “best model” to predict A for 5,642 wk in 211 territories from ΔNO2 and 10 socioeconomic and environmental indicators by a gradient-boosting-decision-tree (GBDT) regression (48). The fitted model predicts A with a coefficient of determination (R2) of 0.54 (n = 5,642) based on weighted squared errors (49) in leave-one-out cross-validation (Fig. 4), which is higher than R2 of 0.33 using a multiple linear regression (SI Appendix, Fig. S13). R2 in our study is comparable with R2 of ∼0.4 in another machine-learning model predicting changes in COVID-19 transmission rate after implementation of the measure from NPI indicators across 79 territories (9). It should be noted that this study by Haug et al. (9), which took the rate difference as a predictand, did not explain variation in the transmission rate within a period with/without confinement.
Fig. 4.
Comparison of the predicted and observed acceleration of COVID-19 cases over 5,642 wk for 211 territories in leave-one-out cross-validation. (A–D) Weekly acceleration of daily COVID-19 cases (A) is predicted using (A) the OxCGRT NPIs, (B) PHSM NPIs, (C) human mobility, or (D) alternatively NO2 change (ΔNO2) as predictors, while other predictors including 10 socioeconomic and environmental indicators are identical. To evaluate the skill in predicting the deceleration of COVID-19 cases, the MSE is weighted by a function of (0.99)h, where h is the rank of the observed A. For example, the weighting factor decreases from 0.99 for the lowest A to 0.0000436 for h = 1,000. The coefficient of determination (R2) is defined as 1 minus the ratio of MSE to variance in the observation. Moving averages of A at an interval of 50 are shown by thick lines in different colors. (E) As in D, except for using the data filtered by precipitable water content in the air above the median and NO2 concentration below the median.
To show the advantage of using satellite NO2, we compared the prediction of A using ΔNO2 as a predictor with three benchmark models replacing ΔNO2 with the NPI indicators from the Oxford COVID-19 Government Response Tracker (OxCGRT) (15) or the WHO Public Health and Social Measures (PHSM) (31), or the Google/Baidu human mobility data (32, 33). The performance is comparable for the NPI indicators from the OxCGRT (R2 = 0.44) and PHSM (R2 = 0.44) or the global mobility data (R2 = 0.43), which are poorer than our model using ΔNO2 as the predictor (R2 = 0.54) (Fig. 4 A–D). Particularly, average squared error for A < –1.5% d−2 is reduced from 1.71 using OxCGRT NPIs, 1.70 using PHSM NPIs, and 1.81 using human mobility as the predictor to 1.21 using ΔNO2 as the predictor (SI Appendix, Fig. S14). These results suggest that satellite NO2 is more capable than either national NPI indicators or spatially explicit human mobility in predicting the effects of activity reduction on decelerating new COVID-19 cases in these territories.
While spaceborne tropospheric NO2 column concentration can be developed as an early-warning indicator for the spread of COVID-19, limitation in obtaining satellite data should be noted (27, 28). To show the impact, we compared the prediction of A from ΔNO2 and 10 socioeconomic and environmental indicators by filtering data with a threshold (SI Appendix, Fig. S15). For instance, R2 of A increases from 0.54 to 0.63 by filtering data with precipitable water content in the air above the median to reduce noises in satellite NO2 data (28) and to 0.60 by filtering data with NO2 concentration below the median to reduce the impact of nonlinear relationships between emissions and NO2 at low concentrations (50) (SI Appendix, Table S2). Applying these two thresholds together, R2 of A predicted from ΔNO2 would be 0.62 (Fig. 4E), which is still higher than 0.58 or 0.57 obtained by using either NPIs or human mobility as the predictor (SI Appendix, Fig. S15). The impact of filtering data on the prediction of A from ΔNO2 remains robust when using alternative thresholds or indicators (SI Appendix, Table S2).
Effects of Activity Reductions to Contain COVID-19 in the Winter of 2020/2021.
By predicting A from ΔNO2, we tried to answer when and where limiting activity could be more effective in containing COVID-19. For instance, we identified territories such as Hubei, New York, Turkey, New Jersey, and the Philippines with the largest number of cases in the third week after the outbreak, where reducing 50% of NO2 as an indicator for economic activity could decelerate the rate of new COVID-19 cases by >0.5%⋅d−2 (Fig. 5 A and D). The median of this sensitivity of A to ΔNO2 in 211 territories decreased from 0.74%⋅d−2 in the third week after the outbreak to 0.34%⋅d−2 on 8 November 2020 as the last day of NO2 observations in this study (Fig. 5 B and E). The percentage of GDP under high sensitivity (>1.0%⋅d−2) of A to ΔNO2 in 211 territories decreased from 35% in the third week after the outbreak to 13% on 8 November 2020 as the last day of NO2 observations in this study (Fig. 5 C and F). It indicates the sensitivity could be dampened over time, supporting the statement that it is more effective to contain the spread of COVID-19 by taking policies of confinement at an earlier stage of the pandemic (3, 21). It indicated that the chain of confinement to containment could have been broken (7) when controls were lifted in territories before new cases became zero (8).
Fig. 5.
Global effect of limiting activity in confinement to contain COVID-19. (A) Potential to decelerate the growth of cases (A) by reducing ΔNO2 from 0 to –100% as an indicator for activity reduction at the end of the third week after the COVID-19 outbreak in each territory. (B) Percentages of territories with the sensitivity of A to a reduction of ΔNO2 from 0 to –50% below a threshold at the end of the third week. (C) Distribution of the A-ΔNO2 sensitivity at the end of the third week. (D–F) As in A–C, except for showing the A-ΔNO2 sensitivity on the last day of NO2 observations (8 November 2020) in this study when vaccines had not been widely applied.
We simulated the trend in daily COVID-19 cases over 8 wk since the end of the third week after the outbreak (R2 = 0.76 between predicted global cases and the observations). At the end of this hindcast simulation, global COVID-19 cases could be reduced from 0.658 million⋅d−1 in a hypothetical scenario without limiting activity to 0.136 million⋅d−1 in the real scenario, or 0.184 million⋅d−1 in an alternative scenario with 50% activity limited in the 10% of territories with the highest sensitivity of A to ΔNO2 (SI Appendix, Fig. S16A). The effect in reducing COVID-19 cases is remarkable by reducing ΔNO2 from 0 to –10% and from –10% to –20% but becomes weaker if ΔNO2 is further reduced by the same margin in a forecast simulation over the winter of 2020/2021 (SI Appendix, Fig. S16B). The global COVID-19 cases on the last day of the forecast simulation (21 January 2021) would decrease from 1.67 million⋅d−1 to 0.976 million⋅d−1 by limiting 10% of activity, to 0.193 million⋅d−1 by limiting another 10%, and to 0.187 million⋅d−1 by limiting a further 10%.
By identifying a regional difference in the effect of ΔNO2 on A, we optimized the distribution of ΔNO2 that would maximize the reduction of global cases. Namely, a marginal increase in ΔNO2 is found for one week in a territory where the largest number of new cases is reduced (Materials and Methods). Global COVID-19 cases on 21 January 2021 (the last day of the forecast simulation) is predicted to be 0.916 million⋅d−1 if the real distribution of ΔNO2 on 8 November 2020 (the last day of NO2 observations) continues without change in policies as a baseline scenario. Under this scenario, global GDP weighted by ΔNO2 amounts to –6.5% of global GDP from the OMI NO2 (Fig. 6A) or –9.5% from the TROPOMI NO2 (SI Appendix, Fig. S17A). If we adopted the optimal distribution of ΔNO2, global daily cases on 21 January 2021 will decrease by 80% from 0.916 to 0.187 million, shifting the trend of new cases from an increase to a decline (SI Appendix, Fig. S16B). We ultimately mapped the difference between the real and optimized distributions of ΔNO2 in the winter of 2020/2021 (Fig. 6 B–D). It informs the territories where activity could be further limited to improve the efficacy of global joint actions in containing COVID-19. It is worth noting that the effectiveness of activity reduction depends on the discrete variable (κ), which represents the continuity of confinement. The effect of reducing activity could be offset by >80% due to lagging effects of lifting controls in any scenarios by holding κ = 1 (Fig. 6A). Using the TROPOMI NO2 or the WHO cases of COVID-19 as model inputs changes the number of reduced cases, but the effect of optimizing ΔNO2 remains robust (SI Appendix, Fig. S17).
Fig. 6.
Effect of optimizing the policies for activity reduction to contain COVID-19. (A) Global COVID-19 cases on 21 January 2021 as a function of global ΔNO2. We consider three scenarios using real ΔNO2 on 8 November 2020, constant ΔNO2 of 0, –10%, –20%, and –30% in all territories, and the optimized distribution of ΔNO2. The influence of unstable control measures is shown by holding κ = 1. A Monte Carlo simulation was run to propagate uncertainty in the case acceleration (A) estimated by the regression model and uncertainty in the ΔNO2 estimated by the fixed-effects model, while the uncertainty in the optimization curve is derived as the interquartile range of the predicted daily cases. (B and C) The real (B) and optimized (C) distributions of ΔNO2 under the same global average ΔNO2 weighted by GDP (6.5%). (D) The difference between B and C shows the adjustment of current policies required for case minimization.
Concluding Remarks
Measures to contain the spread of COVID-19 at the microlevel such as facial masking and social distancing are not universally applicable and difficult to globally enforce (18). Other NPIs by limiting mobility are tied to the economic activities and social interactions by closing factories, restaurants, and schools, restricting mobility of road vehicles and aircrafts, suspending infrastructure construction, interrupting agricultural practices, limiting religious celebrations, and freezing tourism (51). Quantification of the relationship between activity reduction or recovery and the deceleration or acceleration of COVID-19 cases was hindered by a delay of data availability to monitor activity anomalies for the entire economy. This complexity is manifested when comparing the effects of NPIs among different countries. We found that reductions in spaceborne tropospheric NO2 column concentration, as a proxy of economic activity, could be a significant predictor for deceleration of COVID-19 cases. This method has three important applications. First, it can be applied to identify territories where containment can effectively decelerate the increase in COVID-19 cases. This application allows us to achieve global joint actions by realizing that “policy action should become better targeted to where it is needed most and to strengthen the recovery” (52). Second, this method can be applied to evaluate the effects of large-scale activity reduction and microlevel NPIs (53, 54). This application is particularly important for territories where limiting activity is less effective for containing COVID-19 under current circumstances. At subnational levels in large countries other than China and the United States, the high-resolution data of NO2 can be used to interpret the changes in the transmission rate of COVID-19 locally (5, 11) and to optimize the activity reduction within the country during lockdown easing as we did for the globe. Third, this method can be combined with atmospheric inversion models (25) to attribute the observed changes in NO2 to specific economic sectors, since the real-time NO2 can be achieved at a high resolution from space to match the resolution (50 to 100 km) of transport models. This application will provide information on the sectors where activity could be limited before others in containing the pandemic. Our study applying global real-time satellite observations of air pollution to quantify the relationship between activity reduction and the epidemic spread of COVID-19 provides the possibility of monitoring the efficacy of limiting human social and economic activity and of containing COVID-19 and other emerging public-health risks before the vaccines are widely available.
Materials and Methods
Code and Data Availability.
Code and materials are available on the GitHub repository: https://github.com/rongwang-fudan/COVID-2019_EEC_Global.
Global Data of Satellite-Based NO2 and Meteorology.
NO2 is emitted from the combustion of fossil fuels and biomass in all industrial, mobile, residential, and commercial activities. With a short lifetime in the atmosphere, atmospheric NO2 concentrations are less sensitive to background concentrations than are other long-lived tracers (e.g., carbon dioxide), making it possible to correlate changes in NO2 to human activity in the economy (25, 26, 29, 30). We used NO2 retrieved from backscattered radiance and solar irradiance measured by the OMI onboard the US NASA Aura satellite (27) or the TROPOMI onboard the European Copernicus Sentinel-5 Precursor satellite (28). The TROPOMI instruments provide data at a finer spatial resolution than do the OMI instruments.
Daily NO2 data from the OMI product version 3.0 (OMI/Aura NO2 Cloud-126 Screened Total and Tropospheric Column L3 Global Gridded 0.25° × 0.25° Version 3), available for 2016 to 2020 are compiled from the Earth Observing System Data in the Information System Distributed Active Archive Centers (https://earthdata.nasa.gov/). The pixel-level data are binned for sky conditions (27) by removing data with a cloud fraction lower than 30%. Daily NO2 below the random noises of the retrieval product (0.45 × 1015 molecules per centimeter−2) are excluded from our analysis to reduce errors in observation at high solar-zenith angles and over snow or ice surfaces (27, 55). The daily gridded NO2 data from the TROPOMI product (Sentinel-5P offline nitrogen dioxide), available for 2019 to 2020 (http://www.tropomi.eu/data-products/nitrogen-dioxide) are compiled from the Google Earth Engine cloud platform (56) (https://developers.google.com/earth-engine/datasets/catalog), which provides global daily NO2 at a spatial resolution of 0.01° × 0.01°.
Accompanying NO2, global daily meteorological data for 2016 to 2020 are compiled from the Google Earth Engine cloud platform (https://developers.google.com/earth-engine/datasets/catalog). Relative humidity 2 m above the ground, meridional and zonal winds 10 m above the ground, columnar precipitable water content in the air, air temperature 2 m above the ground, and horizontal wind speed 10 m above the ground at a resolution of 0.25° × 0.25° are obtained from the Global Forecast System of the National Center for Environmental Prediction (https://www.ncdc.noaa.gov/data-access/model-data/model-datasets/global-forcast-system-gfs). In addition, atmospheric pressure and the height of the PBL at a resolution of 0.2° × 0.2° are produced by the Climate Forecast System of Climate Forecast System Reanalysis (https://climatedataguide.ucar.edu/climate-data/climate-forecast-system-reanalysis-cfsr).
The Fixed-Effects Model to Estimate the Impact of COVID-19 on Daily NO2 by Week.
We estimated the meteorology-adjusted changes in NO2 (ΔNO2) by week for 1 January to 8 November 2020 relative to the same weeks in previous years (2016 to 2019 for OMI or 2019 only for TROPOMI) using a fixed-effects model (36). In this statistical model, the factor of interest can be considered as a dummy variable to quantify the impact on the concentration of NO2 for days with or without the impact of COVID-19 for this study. For our study, the predictand is the concentration of weekly NO2 and the predictors are the dummy variables for COVID-19, meteorology, year, and season on each day. Because the measurements of NO2 concentration by satellites are almost identical for all weeks, they meet the criterion of applying the fixed-effects model (https://www.meta-analysis.com/downloads/Meta-analysis%20Fixed-effect%20vs%20Random-effects%20models.pdf). We noticed that this fixed-effects model had been applied to attribute changes in the observed changes in NO2 concentration to COVID-19 (34). Therefore, we applied this fixed-effects model to quantify the change in NO2 due to COVID-19 for each spatial pixel in our study. Considering nonlinear impacts of meteorology (50, 57) and linear impacts of seasonality (30) and interannual trends (35), we fit the fixed-effects model to predict the daily NO2 as
| [1] |
where i is a grid, t is a day, yt is a year, st is a season, w is a given week in 2020, and xt,w is a dummy variable (1 for week w in 2020 and 0 elsewhere). M is a matrix of meteorological conditions (surface ambient temperature, atmospheric pressure, zonal wind, meridional wind, relative humidity, horizontal wind speed, precipitable water content in the air and PBL height). We used a GBDT method (48) with 10 decision trees to find the nonlinear function (F) that returns the lowest mean squared error in the prediction of daily NO2. Based on the fitted model, we estimated the change in NO2 during the COVID-19 pandemic as an indicator of activity change in week w (ΔNO2,w) due to COVID-19 as
| [2] |
where and are the averages of the predicted daily NO2 with or without the impact of COVID-19 in week w for 2016 to 2020, respectively.
To indicate the activity change in a region of interest (I), we derived the average of ΔNO2,w weighted by the gridded purchasing-power-parity GDP in a region as
| [3] |
where gi is the predicted purchasing-power-parity GDP in grid i in 2020 exclusive of the impact of the COVID-19 outbreak (58) (available at https://www.cger.nies.go.jp/gcp/population-and-gdp.html). Across different territories, we defined the total GDP weighted by ΔNO2 (GWN), in units of billion $2015, as
| [4] |
We compared the spatial distributions of ΔNO2 using NO2 measured by OMI in Wuhan, China and Los Angeles, California to that using NO2 measured by TROPOMI at different resolutions from 0.01° × 0.01° to 2° × 2° (SI Appendix, Fig. S18). The resolution of ΔNO2 is finer using the high-resolution data measured by TROPOMI, but a higher requirement of data from TROPOMI leads to a lower coverage of grid boxes. In addition, the TROPOMI data are only available for 2019 to 2020. To demonstrate the influence exclusive of interannual trends, the estimated ΔNO2 in Wuhan varies from –70% using the OMI data for 2019 to 2020 to –90% if the same OMI data for 2016 to 2020 are used. Nevertheless, the temporal trend of ΔNO2 is similar using the two measurements from different instruments, which are both considered in this study (SI Appendix, Figs. S3, S4, S8, S10, and S17).
Global Data of Daily COVID-19 Cases.
Daily COVID-19 cases are compiled for the 211 territories globally, including 31 provinces in China, 51 states (including the District of Columbia) in the United States, and 129 countries for 1 January to 25 November 2020. These territories contribute to a total population of 6.88 billion in 2019 (90% of the global total), a total purchasing-power-parity GDP of $114.56 trillion for 2016 to 2019 (94% of the global total), and a total number of COVID-19 cases of 57.918 million for 1 January to 25 November 2020 (96% of the global total).
Daily COVID-19 cases in the 31 provinces in China are compiled by distinguishing between local and imported cases in three steps. First, local cases of COVID-19 in 30 provinces (excluding Hubei) for 1 January to 29 February 2020 are compiled from the Harvard dataset (https://dataverse.harvard.edu/dataverse/2019ncov). Second, local COVID-19 cases are obtained by subtracting the imported cases (https://datanews.caixin.com/interactive/2020/pneumonia-h5/#live-data) from the total cases (http://www.nhc.gov.cn/xcs/xxgzbd/gzbd_index.shtml) for 1 March to 11 March 2020 in the 31 provinces and for 1 January to 11 March 2020 in Hubei province. Third, local COVID-19 cases for 12 March to 25 November 2020 are compiled from the National Health Commission of China (http://www.nhc.gov.cn/xcs/xxgzbd/gzbd_index.shtml). A prison in Shandong province reported 200 COVID-19 cases on 20 February 2020 (https://baijiahao.baidu.com/s?id=1659113674465060786&wfr=spider&for=pc), which is excluded from this analysis. The number of cases is multiplied by a factor of 1/0.23 = 4.34, because of a 23% ascertainment rate of cases due to incomplete testing at the early stage of the pandemic in Hubei (3).
Daily COVID-19 cases in 51 states (including the District of Columbia) in the United States are compiled from the Johns Hopkins University Center for Systems Science and Engineering COVID-19 Dataset (https://github.com/CSSEGISandData/COVID-19/tree/master/csse_covid_19_data). In addition, daily COVID-19 cases in 27 states in the Brazil are compiled from the COVID-19-Brazil-timeseries dataset (https://github.com/elhenrico/covid19-Brazil-timeseries) and the CORONAVÍRUS BRASIL reports (https://covid.saude.gov.br/). Daily COVID-19 cases in 24 states in Argentina are compiled from the SistemasMapache dataset (https://github.com/SistemasMapache/) and the Ministerio de Salud report (https://www.argentina.gob.ar/coronavirus/informe-diario). For the remaining 129 countries, daily COVID-19 cases are compiled from the ECDPC (https://www.ecdc.europa.eu/en/publications-data). In addition, daily new cases in these countries compiled from the WHO (https://covid19.who.int/table) are used for comparison.
The time series of daily COVID-19 cases may contain breakpoints due to changes in the criteria for COVID-19 testing (59). For example, the number of daily cases in Equatorial Guinea reported by the ECDPC varies abruptly from 1,070 cases per day in a week centered on 3 July or 1,750 cases per day in a week centered on 2 August to zero in the preceding and following weeks. To reduce the impact of discrete data, we used a statistical procedure (60) to identify outliers in the time series as Nd > (M + 3σ), which is replaced with (M + 3σ), or Nd < (M – 3σ), which is replaced with (M – 3σ), where M and σ are the mean and SD of the time series, respectively.
Weekly Velocity and Acceleration of Daily COVID-19 Cases.
The transmission dynamics of COVID-19 were previously simulated using epidemiological models (1–7), where the accuracy was improved by accounting for the sensitivity of ordinary differential equations to observational data (5), reducing uncertainties in the model parameters with full dynamics (3) and improving the representation of variations in transmission rate (7). As an empirical study, we did not run such an epidemiological model but estimated the weekly velocity (V) and acceleration (A) of daily COVID-19 cases reported by the ECDPC or WHO to quantify the empirical relationship between activity reduction in COVID-19 confinement and the epidemic spread of COVID-19. To reduce the cases ascertainment bias that may vary across jurisdictions due to the surveillance and diagnostic capacity, we adopted a 7-d moving average to calculate the daily COVID-19 cases (61). However, this treatment did not exclude the biases in daily cases reported by countries with consistently low capacities in virus testing (62).
We estimated the velocity of daily cases (Vw) in week w using logarithmic regression (63) within a 3-wk moving window as
| [5] |
where Nd is the number of confirmed daily cases as a 7-d moving average. The deceleration of daily cases (Aw) in week w is estimated within a 3-wk moving window as
| [6] |
The first day of the outbreak of COVID-19 varies from territory to territory, which may be influenced by sporadic imported cases (62). To reduce the impact of sporadic cases, we defined the first week (w0) in a territory when the number of daily cases (Nw) increases continuously to 100 cases per day as
| [7] |
| [8] |
| [9] |
where w100 is the first week when daily cases (Nw) exceed 100 cases per day. We considered the first day in week w0 as the time of the outbreak of COVID-19 in this territory. The first peak of Nw (4,263 cases per day on 1 to 7 April 2020) in France reported by the ECDPC is much lower than the second peak (48,720 cases per day on 4 to 11 November 2020), so we derived w100 from the second peak.
We tried to exclude data which were potentially biased. The Philippines adopted two kinds of COVID-19 tests by June, so we used w0 for daily cases reported after June to reduce the impact of the different testing (https://www.philstar.com/headlines/2020/05/21/2015542/there-are-two-kinds-covid-19-tests-used-philippines-how-are-they-different). The ECDPC-reported daily cases fluctuated greatly in the United Arab Emirates (0, 16, 0, 14, 15, 0, and 11 cases per day on 7 to 13 March 2020, respectively), Serbia (13, 6, 17, 5, 9, 2, and 15 cases per day on 12 to 18 March 2020, respectively), and Ukraine (2, 9, 5, 7, 0, 15, and 6 cases per day on 17 to 23 March 2020, respectively), where the data from the first week are not used. In addition, because of a low capacity of COVID-19 testing in Bangladesh (64) and the 2020 Nagorno-Karabakh war between Armenia and Azerbaijan (65), data for Bangladesh and Azerbaijan were excluded. Because unconfirmed cases were mixed up with confirmed cases in Belgium (66), data for Belgium were also excluded.
Convergent Cross-Mapping Method.
We examined the causal relationships between ΔNO2 and A in three steps. First, the results of cross-mapping are sensitive to the choice of the optimal embedding dimension (E), which decides how many time lags are used to reconstruct the state space. We selected the optimal E values based on the ΔNO2 and A time series for each territory in a period with an increasing correlation for >5 wk to reduce the impact of other factors using a phase space reconstruction method (67). Second, the cross-mapping between ΔNO2 and A for each territory was performed using the convergent cross mapping algorithm package “SugiLM” in MATLAB (41). Third, the Pearson’s correlation coefficient was used to evaluate the cross-map skill between ΔNO2 and A as a proxy for describing the causal relationships between two variables (40, 68). The random noises in the time series of ΔNO2 and A were reduced according to the upward and downward trends in the correlation series. The code and data for the convergent cross-mapping analysis are available on GitHub (https://github.com/rongwang-fudan/COVID-2019_EEC_Global).
Government Response Indicators and Human Mobility Data.
We compiled the public health and social measures by week after the outbreak of COVID-19 for 211 territories from the WHO PHSM data (31). This product combines data from different data products including the ACAPS COVID-19 Government Measures (https://www.acaps.org/), the OxCGRT (15), the US Centers for Disease Control and Prevention (https://www.cdc.gov/coronavirus), the Complexity Science Hub Vienna (https://www.csh.ac.at/), the Global Public Health Intelligence Network (https://www.canada.ca/en/public-health.html), the WHO International Health Regulations (https://www.who.int/health-topics), and the Johns Hopkins University Coronavirus Resource Center (https://coronavirus.jhu.edu/). This product provides 42 coded categories of NPI, including 6 types of individual measures, 3 environmental measures, 5 surveillance and response measures, 15 social and physical distancing measures, 9 international travel measures, 2 drug-based measures, and 2 biological measures, which are considered in our study as predictors in the machine-learning model. In addition to the WHO PHSM data, we compiled the common policy responses released in 181 countries from the OxCGRT (15). In this product, the coded government response indicators include nine indicators for containment and closure policies and four indicators for economic policies, and seven indicators record information on health system policies, which were used as predictors in our machine-learning model.
We compiled global daily human mobility data by territory in two steps. First, we compiled the daily workplace movement changes as an indicator of human mobility for 128 countries except for China, which are published by the Google community (32). Second, because the Google data do not cover China, we compiled the daily human mobility data from the Baidu Qianxi Web Platform (33) for 31 provinces in China. To ensure the consistency between different mobility records in the Google and Baidu engines, we derived the ratio of human mobility after the outbreak of COVID-19 to the average mobility during the 5 wk from 3 January to 6 February 2020 as a baseline. This ratio of human mobility was adopted as a predictor in our machine-learning model.
Prediction of the Weekly Acceleration of Daily COVID-19 Cases by Machine Learning.
To model the relationship between weekly acceleration of daily COVID-19 cases (A) and 10 socioeconomic and environmental indicators, we used a GBDT regression (48), which is described in the “Statistics and Machine Learning” toolbox in MATLAB environment software (https://www.mathworks.com/help/stats/fitrensemble.html). GBDT adopts an ensemble learning algorithm that models complex and nonlinear relationships between predictors (Xi) and many response predictands (Y) by combining multiple regression trees with gradient boosting. The decision tree is a popular type of universal approximators. The universal approximation theory states that any piecewise continuous mathematical function with enough universal approximators and correctly tuned parameters can be approximated by the superposition of continuous functions of variables (69). Apart from this theoretical guarantee, GBDT has been shown to be effective in real-world applications including epidemiological studies (e.g., ref. 70).
We trained the model to fit the 5,642 observations of acceleration of COVID-19 cases by week from 1 January to 8 November 2020 across the 211 territories globally based on the weekly changes in NO2 (ΔNO2,w), together with another 10 socioeconomic and environmental indicators: relative humidity, horizontal wind speed, precipitable water content, ambient temperature, PBL height, average travel time of residents to the nearest urban center [data provided by Weiss et al. (44)], delay in confinement as the number of weeks with ΔNO2+ > 0 after the outbreak of COVID-19, purchasing-power-parity GDP per capita, the average population density of a territory, and the continuity of confinement (the variable κ, defined above). The fitted model is evaluated by fourfold cross-validation, where 25% of the samples are used as a test and the remaining samples are designated to train the model, and by leave-one-out cross validation, where one sample is used as a test and the remaining samples are designated to train the model (71).
When we applied GBDT to predict weekly acceleration of daily COVID-19 cases from ΔNO2 and 10 socioeconomic and environmental indicators we considered the impact of the maximum depth of each tree, learning rate, and the number of trees on the performance of the model using a mean squared error (MSE) metric (71). Increasing the maximum depth of each tree produces a sufficient residual current that fits well but reduces the efficiency in training each tree. Increasing the learning rate improves the effect of model training by increasing the contribution of each tree but leads to a risk of overfitting. Increasing the number of trees for each ensemble also improves the effect of model training but leads to an overload of training data and increases the noise in model training. To assess the impact of one parameter, we held the other two parameters and vary only one parameter in different experiments (SI Appendix, Fig. S19). In a fourfold cross-validation, MSE increased when we increased the number of trees under a learning rate of 1. MSE decreased before increasing when we increased the number of trees under a learning rate of 0.25, 0.5, and 1, and the curve became flatter under a higher number of trees. This produces a lowest peak of MSE under a threshold number of trees under a learning rate of 0.25, 0.5, and 1. However, the computing time increased dramatically when the learning rate increased. When the maximum depth of each tree increased from 1 to 8 and to 64, the peak of MSE decreased. To ensure an efficient learning of the model, we adopted 64 for the maximum depth of tree, 0.25 for the learning rate, and 7 for the number of trees in this study.
Hindcast and Forecast Simulations of COVID-19 Cases.
Based on weekly acceleration of daily COVID-19 cases predicted from ΔNO2 using the machine-learning model, we simulated the evolution of daily COVID-19 cases following a simplified dynamic procedure as
| [10] |
| [11] |
where d is a day, w is a week, Δt is a time step (1 d in this study), Nd is the daily cases, Vd is the velocity of daily cases, and Awd is the acceleration of daily cases predicted from ΔNO2 using machine learning. We run a hindcast simulation for 8 wk starting on the last day of the first 3 wk after the outbreak of COVID-19 in each territory and a forecast simulation for 25 November 2020, as the last day in this study, to 21 January 2020. We used the estimated real-time SE of ΔNO2 to determine ΔNO2+ and the real-time discrete variable κ in the hindcast simulations. The SE of ΔNO2 estimated for the last week (2 to 8 November 2020) in this study is used as a constant to determine ΔNO2+ and the discrete variable κ in the forecast simulations.
Optimization of the Regional Distribution of ΔNO2.
We used a stepwise method to optimize the global distribution of ΔNO2 as an indicator of changes in activity due to confinement to achieve the highest efficacy of a global joint action to contain COVID-19. The influence of reducing ΔNO2 from –20% to –30% on the number of daily COVID-19 cases on 21 January 2021 is weak (SI Appendix, Fig. S16B), so we considered ΔNO2 = –30% as an upper bound of limited activity during confinement in the winter of 2020. The effect of limiting activity on reducing daily COVID-19 cases accumulates over time by decelerating the growth of new case (A), so we reasonably considered that limiting activity is more efficient to reduce cases by reducing ΔNO2 in earlier weeks.
We considered a reduction of ΔNO2 by 10% in a week as a minimal interval when reducing ΔNO2 in our optimizing procedure. Reducing ΔNO2 from 0 to –30% in the following eight weeks leads to 24 intervals, which generates 25 scenarios of ΔNO2 for each territory. In the first scenario, ΔNO2 is 0 in all weeks. In the second to fourth scenarios, ΔNO2 is –10%, –20%, and –30%, respectively, in the first week and 0 in other weeks. In the fifth to seventh scenarios, ΔNO2 is –30% in the first week, –10%, –20%, and –30%, respectively, in the second week, and 0 in other weeks. Then, in the 23rd to 25th scenarios, ΔNO2 is –30% in the first to seventh weeks and –10%, –20%, and –30% in the eighth week, respectively.
We run the 25 scenarios for each territory to estimate the reduced number of daily cases for 21 January 2021 (ΔNk,i) in scenario k relative to the number in the 25th scenario as
| [12] |
where i is a territory, and Nk,i or N25,i is the number of daily cases for 21 January 2021 in the kth or 25th scenario, respectively, in territory i.
We chose a threshold (H) for the reduced number for 21 January 2021 (ΔNk) to find the scenario k, where ΔNk exceeds H as
| [13] |
As an advantage, this procedure ensures that the reduction in daily cases for 21 January 2021 by further reducing of ΔNO2 to –30% in this territory is <H.
We increased H continuously from 10 to 250,000 cases per day to determine k for each territory and to obtain the distribution of ΔNO2 where activity can be limited to achieve the largest reduction in daily cases for 21 January 2021.
We ultimately derived the global number of new cases on 21 January 2021 corresponding to each value of H, which is plotted as a function of total purchasing-power-parity GDP weighted by ΔNO2 (Eq. 4) for the 211 territories under the corresponding scenario (Fig. 6A).
Monte Carlo Ensemble Simulation.
We ran the Monte Carlo ensemble simulation (72) to propagate 1) uncertainty in the acceleration of case (A) predicted by the linear regression model (Eqs. 5 and 6) and 2) uncertainty in the activity reduction (ΔNO2) from NO2 concentration changes predicted by the fixed effect model (Eq. 1). These two uncertainties as the average for the study period are mapped (SI Appendix, Fig. S7). Based on the means and SDs of the predicted A and ΔNO2, we randomly generated 1,000 pairs of A and ΔNO2 from normal distributions for each week in each territory. With each pair of A and ΔNO2, we repeated the training of one machine-learning model and the optimization of the regional distribution of ΔNO2 for the forecast simulation from 9 November 2020 to 21 January 2021. Based on the Monte Carlo ensemble simulations, the interquartile range of the predicted global new COVID-19 cases on 21 January 2021 was derived as a measure of uncertainty in the estimated effect of optimization (Fig. 6A).
Supplementary Material
Acknowledgments
We thank H. J. Yu for important comments and J. H. Pan for help in compiling the epidemiological data. This work was supported by the National Natural Science Foundation of China (41877506), the Fudan’s Wangdao Undergraduate Research Opportunities Program (18107), the Chinese Thousand Youth Talents Program, the PolEASIA-ANR project (ANR-15-CE04-0005), and the Australia-China Centre for Air Quality Science and Management. J.P. and J.S. acknowledge financial support from the Catalan Government grant AGAUR-2020PANDE00117. P.C. acknowledges support from the European Space Agency Climate Change Initiative ESA-CCI RECCAP2 project (ESRIN/4000123002/18/I-NB) and the Observation-based system for monitoring and verification of greenhouse gases project (VERIFY, grant 725546).
Footnotes
The authors declare no competing interest.
This article is a PNAS Direct Submission. R.C.C. is a guest editor invited by the Editorial Board.
This article contains supporting information online at https://www.pnas.org/lookup/suppl/doi:10.1073/pnas.2109098118/-/DCSupplemental.
Data Availability
Anonymized code and materials have been deposited in GitHub (https://github.com/rongwang-fudan/COVID-2019_EEC_Global).
References
- 1.Kissler S. M., Tedijanto C., Goldstein E., Grad Y. H., Lipsitch M., Projecting the transmission dynamics of SARS-CoV-2 through the postpandemic period. Science 368, 860–868 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Flaxman S.et al.; Imperial College COVID-19 Response Team , Estimating the effects of non-pharmaceutical interventions on COVID-19 in Europe. Nature 584, 257–261 (2020). [DOI] [PubMed] [Google Scholar]
- 3.Hao X., et al., Reconstruction of the full transmission dynamics of COVID-19 in Wuhan. Nature 584, 420–424 (2020). [DOI] [PubMed] [Google Scholar]
- 4.Ruktanonchai N. W., et al., Assessing the impact of coordinated COVID-19 exit strategies across Europe. Science 369, 1465–1470 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Candido D. S.et al.; Brazil-UK Centre for Arbovirus Discovery, Diagnosis, Genomics and Epidemiology (CADDE) Genomic Network , Evolution and epidemic spread of SARS-CoV-2 in Brazil. Science 369, 1255–1260 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Ferretti L., et al., Quantifying SARS-CoV-2 transmission suggests epidemic control with digital contact tracing. Science 368, eabb6936 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Worobey M., et al., The emergence of SARS-CoV-2 in Europe and North America. Science 370, 564–570 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Rojas R., Delkic M., As states reopen, governors balance existing risks with new ones. NY Times, 17 May 2020.
- 9.Haug N., et al., Ranking the effectiveness of worldwide COVID-19 government interventions. Nat. Hum. Behav. 4, 1303–1312 (2020). [DOI] [PubMed] [Google Scholar]
- 10.Rader B., et al., Crowding and the shape of COVID-19 epidemics. Nat. Med. 26, 1829–1834 (2020). [DOI] [PubMed] [Google Scholar]
- 11.Laxminarayan R., et al., Epidemiology and transmission dynamics of COVID-19 in two Indian states. Science 370, 691–697 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Copat C., et al., The role of air pollution (PM and NO2) in COVID-19 spread and lethality: A systematic review. Environ. Res. 191, 110129 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Travaglio M., et al., Links between air pollution and COVID-19 in England. Environ. Pollut. 268 (Pt A), 115859 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Lipsitt J., et al., Spatial analysis of COVID-19 and traffic-related air pollution in Los Angeles. Environ. Int. 153, 106531 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Hale T., Webster S., Petherick A., Phillips T., Kira B., Oxford COVID-19 Government Response Tracker (Blavatnik School of Government & University of Oxford, 2020). https://www.bsg.ox.ac.uk/research/research-projects/coronavirus-government-response-tracker. Accessed 30 December 2020.
- 16.Chang S., et al., Mobility network models of COVID-19 explain inequities and inform reopening. Nature 589, 82–87 (2021). [DOI] [PubMed] [Google Scholar]
- 17.Lai S., et al., Assessing spread risk of Wuhan novel coronavirus within and beyond China, January-April 2020: A travel network-based modelling study. medRxiv [Preprint] (2020). 10.1101/2020.02.04.20020479 (Accessed 21 December 2020). [DOI]
- 18.Wu J. T., Leung K., Leung G. M., Nowcasting and forecasting the potential domestic and international spread of the 2019-nCoV outbreak originating in Wuhan, China: A modelling study. Lancet 395, 689–697 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Bargain O., Aminjonov U., Trust and compliance to public health policies in times of COVID-19. J. Public Econ. 192, 104316 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Pearce N., Lawlor D. A., Brickley E. B., Comparisons between countries are essential for the control of COVID-19. Int. J. Epidemiol. 49, 1059–1062 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Wang R., et al., Daily CO2 emission reduction indicates the control of activities to contain COVID-19 in China. Innovation (N Y) 1, 100062 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Wang R., et al., Representativeness error in the ground-level observation networks for black carbon radiation absorption. Geophys. Res. Lett. 45, 2106–2114 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Wang R., et al., Estimation of global black carbon direct radiative forcing and its uncertainty constrained by observations. J. Geophys. Res. Atmos. 121, 5948–5971 (2016). [Google Scholar]
- 24.Wang R., et al., Exposure to ambient black carbon derived from a unique inventory and high-resolution model. Proc. Natl. Acad. Sci. U.S.A. 111, 2459–2463 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Zheng B., et al., Satellite-based estimates of decline and rebound in China’s CO2 emissions during COVID-19 pandemic. Sci. Adv. 6, eabd4998 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Kaynak B., Hu Y., Martin R. V., Sioris C. E., Russell A. G., Comparison of weekly cycle of NO2 satellite retrievals and NOx emission inventories for the continental United States. J. Geophys. Res. Atmos. 114, D05302 (2009). [Google Scholar]
- 27.Krotkov N. A., et al., The version 3 OMI NO2 standard product. Atmos. Meas. Tech. 10, 3133–3149 (2017). [Google Scholar]
- 28.van Geffen J., et al., S5P TROPOMI NO2 slant column retrieval: Method, stability, uncertainties and comparisons with OMI. Atmos. Meas. Tech. 13, 1315–1335 (2020). [Google Scholar]
- 29.Russell A. R., Valin L. C., Cohen R. C., Trends in OMI NO2 observations over the United States: Effects of emission control technology and the economic recession. Atmos. Chem. Phys. 12, 12197–12209 (2012). [Google Scholar]
- 30.Goldberg D. L., et al., Disentangling the impact of the COVID-19 lockdowns on urban NO2 from natural variability. Geophys. Res. Lett. 47, e2020GL089269 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.World Health Organization , Tracking public health and social measures: A global dataset. https://www.who.int/emergencies/diseases/novel-coronavirus-2019/phsm. Accessed 28 December 2020.
- 32.Aktay A., et al., Google COVID-19 community mobility reports: Anonymization process description (version 1.0) (Google, 2020).
- 33.Hu T., et al., Building an open resources repository for COVID-19 research. DIM 4, 130–147 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Liu F., et al., Abrupt decline in tropospheric nitrogen dioxide over China after the outbreak of COVID-19. Sci. Adv. 6, eabc2992 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Bauwens M., et al., Impact of coronavirus outbreak on NO2 pollution assessed using TROPOMI and OMI observations. Geophys. Res. Lett. 47, e2020GL087978 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Hedges L. V., “Fixed effects models” in The Handbook of Research Synthesis, Cooper H., Hedges L. V., Eds. (Russell Sage Foundation, New York, 1994), pp. 285–299. [Google Scholar]
- 37.Gaubert B., et al. , Global changes in secondary atmospheric pollutants during the 2020 COVID-19 pandemic. J. Geophys. Res. Atmos. 126, e2020JD034213 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Abbott S., Hellewell J., Funk S., Estimating the time-varying reproduction number of SARS-CoV-2 using national and subnational case counts. Wellcome Open Res. 5, 112 (2020). [Google Scholar]
- 39.Ali S. T., et al., Serial interval of SARS-CoV-2 was shortened over time by nonpharmaceutical interventions. Science 369, 1106–1109 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Sugihara G., et al., Detecting causality in complex ecosystems. Science 338, 496–500 (2012). [DOI] [PubMed] [Google Scholar]
- 41.MathWorks , Use of the SugiLM function. https://www.mathworks.com/matlabcentral/fileexchange/52964-convergent-cross-mapping (MathWorks, 2020).
- 42.Liang D., et al., Urban air pollution may enhance COVID-19 case-fatality and mortality rates in the United States. Innovation (N Y) 1, 100047 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Reyes M. S. S., Medina P. M. B., Environmental pollutant exposure can exacerbate COVID-19 neurologic symptoms. Med. Hypotheses 144, 110136 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Weiss D. J., et al., A global map of travel time to cities to assess inequalities in accessibility in 2015. Nature 553, 333–336 (2018). [DOI] [PubMed] [Google Scholar]
- 45.Morawska L., Cao J., Airborne transmission of SARS-CoV-2: The world should face the reality. Environ. Int. 139, 105730 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Morawska L., et al., A paradigm shift to combat indoor respiratory infection. Science 372, 689–691 (2021). [DOI] [PubMed] [Google Scholar]
- 47.Sun C., Cheng C., Zhao T., Chen Y., Ayaz Ahmed M., Frozen food: Is it safe to eat during COVID-19 pandemic? Public Health 190, e26 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Friedman J. H., Greedy function approximation: A gradient boosting machine. Ann. Stat. 29, 1189–1232 (2001). [Google Scholar]
- 49.Willett J. B., Singer J. D., Another cautionary note about R2: Its use in weighted least-squares regression analysis. Am. Stat. 42, 236–238 (1988). [Google Scholar]
- 50.Laughner J. L., Cohen R. C., Direct observation of changing NOx lifetime in North American cities. Science 366, 723–727 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.The World Bank , COVID-19 to plunge global economy into worst recession since World War II. https://www.worldbank.org/en/news/press-release/2020/06/08/covid-19-to-plunge-global-economy-into-worst-recession-since-world-war-ii. Accessed 18 December 2020.
- 52.Organisation for Economic Co-operation and Development , Coronavirus (COVID-19): Joint actions to win the war. https://www.oecd.org/about/secretary-general/Coronavirus-COVID-19-Joint-actions-to-win-the-war.pdf. Accessed 18 December 2020.
- 53.Sun K., et al., Transmission heterogeneities, kinetics, and controllability of SARS-CoV-2. Science, 10.1126/science.abe2424 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Zhang J., et al., Changes in contact patterns shape the dynamics of the COVID-19 outbreak in China. Science 368, 1481–1486 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Ialongo I., et al., Characterization of OMI tropospheric NO2 over the Baltic Sea region. Atmos. Chem. Phys. 14, 7795–7805 (2014). [Google Scholar]
- 56.Gorelick N., et al., Google Earth Engine: Planetary-scale geospatial analysis for everyone. Remote Sens. Environ. 202, 18–27 (2017). [Google Scholar]
- 57.Wang X., Zhang R., How did air pollution change during the COVID-19 outbreak in China? Bull. Am. Meteorol. Soc. 101, E1645–E1652 (2020). [Google Scholar]
- 58.Murakami D., Yamagata Y., Estimation of gridded population and GDP scenarios with spatially explicit statistical downscaling. Sustainability 11, 2106 (2019). [Google Scholar]
- 59.Nkengasong J. N., Mankoula W., Looming threat of COVID-19 infection in Africa: Act collectively, and fast. Lancet 395, 841–842 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Feng S., Hu Q., Qian W., Quality control of daily meteorological data in China, 1951–2000: A new dataset. Int. J. Clim. 24, 853–870 (2004). [Google Scholar]
- 61.Li Q., et al., Early transmission dynamics in Wuhan, China, of novel coronavirus-infected pneumonia. N. Engl. J. Med. 382, 1199–1207 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Hasell J., et al., A cross-country database of COVID-19 testing. Sci. Data 7, 345 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Wang R., et al., Induced energy-saving efficiency improvements amplify effectiveness of climate change mitigation. Joule 3, 2103–2119 (2019). [Google Scholar]
- 64.Cousins S., Bangladesh’s COVID-19 testing criticised. Lancet 396, 591 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Kazaryan A. M.et al.; Doctors Against The War collaborators , War in the time of COVID-19: Humanitarian catastrophe in Nagorno-Karabakh and Armenia. Lancet Glob. Health 9, e243–e244 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Bustos Sierra N., et al., All-cause mortality supports the COVID-19 mortality in Belgium and comparison with major fatal events of the last century. Arch. Public Health 78, 117 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Kennel M. B., Brown R., Abarbanel H. D. I., Determining embedding dimension for phase-space reconstruction using a geometrical construction. Phys. Rev. A 45, 3403–3411 (1992). [DOI] [PubMed] [Google Scholar]
- 68.Sugihara G., May R. M., Nonlinear forecasting as a way of distinguishing chaos from measurement error in time series. Nature 344, 734–741 (1990). [DOI] [PubMed] [Google Scholar]
- 69.Kolmogorov A. N., Fomin S. V., Elements of the Theory of Functions and Functional Analysis (Graylock, Rochester, NY, 1957). [Google Scholar]
- 70.Messina J. P., et al., The current and future global distribution and population at risk of dengue. Nat. Microbiol. 4, 1508–1515 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Efron B., Gong G. A., leisurely look at the bootstrap, the jackknife, and cross-validation. Am. Stat. 37, 36–48 (1983). [Google Scholar]
- 72.Sokalr R. R., Rohlf F. J. B., The Principles and Practice of Statistics in Biological Research (W. H. Freeman, 1981). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Anonymized code and materials have been deposited in GitHub (https://github.com/rongwang-fudan/COVID-2019_EEC_Global).