A modular framework for early-phase seamless oncology trials

Abstract

Background:

As our understanding of the etiology and mechanisms of cancer becomes more sophisticated and the number otf therapeutic options increases, phase I oncology trials today have multiple primary objectives. Many such designs are now ‘seamless’, meaning that the trial estimates both the maximum tolerated dose and the efficacy at this dose level. Sponsors often proceed with further study only with this additional efficacy evidence. However, with this increasing complexity in trial design, it becomes challenging to articulate fundamental operating characteristics of these trials, such as (i) what is the probability that the design will identify an acceptable, i.e. safe and efficacious, dose level? or (ii) how many patients will be assigned to an acceptable dose level on average?

Methods:

In this manuscript, we propose a new modular framework for designing and evaluating seamless oncology trials. Each module is comprised of either a dose assignment step or a dose-response evaluation, and multiple such modules can be implemented sequentially. We develop modules from existing phase I/II designs as well as a novel module for evaluating dose-response using a Bayesian isotonic regression scheme.

Results:

We also demonstrate a freely available R package called seamlesssim to numerically estimate, by means of simulation, the operating characteristics of these modular trials.

Conclusions:

Together, this design framework and its accompanying simulator allow the clinical trialist to compare multiple different candidate designs, more rigorously assess performance, better justify sample sizes, and ultimately select a higher quality design.

1. Background

Current phase I oncology trial designs are often ‘seamless’ in nature [1], meaning both a maximum tolerated dose (MTD) and an initial efficacy estimate at this dose level are sought. Trial sponsors may be unwilling to proceed with further study without this additional efficacy evidence [2]. We recently designed such a trial for relapsed/refractory indolent lymphoma. The objective was to estimate the MTD and obtain preliminary estimates of efficacy as measured by complete response. Success for this trial reflects the seamless perspective: the primary objective is to identify a dose level that is both tolerable and efficacious. As in all such trials, a key statistical concern is the potential for uncertainty to compound across objectives. Future success in the pipeline depends upon the current trial correctly estimating both the MTD and the response rate at this estimated MTD.

Our understanding of both the etiology and mechanisms of many cancers has increased over the past decades, and the number of therapeutic options has correspondingly increased. However, one characteristic remaining relatively static is that most trial designs are still variants of the ‘3+3’ algorithm [3, 4]. This is notable given that the canonical reference for this design recommends against its use [5]. The continued use of the 3+3 instead of demonstrably superior alternatives such as the continual reassessment method [CRM, 6] highlights a persistent gap between method and practice in this area, which is widened by the multifaceted objectives of seamless oncology trials.

We argue that this gap can be bridged with an accessible framework for seamless trial design and the software for simulating such designs. To that end, this paper has two primary contributions. First, we develop a modular perspective for seamless oncology trial design, which decomposes complex designs with multiple decision points into simpler components. This atomic approach individualizes the choices required for seamless designs, thus providing a framework to evaluate the effect of each choice on overall performance. Second, we present a seamless trial design simulator to conduct this performance assessment, implemented in the R statistical environment [7–10] as a freely available package called seamlesssim [11]. Users can evaluate the impact of each design choice with respect to important operating characteristics.

Many model-based designs for recommending dose levels based upon safety and efficacy have been proposed, including the bivariate CRM [bCRM, 12], ‘EffTox’ [13], the trivariate CRM [TriCRM, 14], and others [15–26]. Some of these designs have even been implemented in trial practice, like the use of an EffTox design to assess the performance of sitravatinib and nivolumab in renal cell cancer [27] or a trial of FLAG-IDA and ponatinib in myeloid leukemia [28], or the use of the bivariate CRM in a trial on T cell co-stimulators for solid tumors [29]. However, these examples aside, the uptake of these advanced designs has been slow, and protocols often try to satisfy these dual objectives under the 3+3 framework. For example, a trial may estimate an MTD using the 3+3 and then, under the assumption that it has been correctly identified, enroll an additional ‘expansion cohort(s)’ of subjects at a fixed dose level(s) and/or in different subpopulations in order to evaluate efficacy [30–33]. An extreme example of this is the KEYNOTE-001 trial of pembrolizumab, which started as a 3+3 trial of 10 subjects across three dose levels and subsequently evolved into a multi-amendment trial enrolling a total of 1235 subjects across multiple expansion cohorts [34, 35]. As of 2016, there were at least four other phase I trials enrolling more than 1000 patients [36].

The favorable outcome of KEYNOTE-001 was unusual: a recent study found that only 3.4% of phase I oncology trials that opened between Jan 1, 2000 and Oct 31, 2015 led to eventual approval [37], which is consistent with reported success rates from an earlier study [38]. Stopping dose-escalation after a small number of subjects, as in the 3+3, risks ending at too low of a dose [31]; the subsequent expansion may stop for lack of efficacy, when a higher dose level might have been found to be efficacious. Or escalation might have occurred too quickly, and lower dose levels, in addition to being safer, are equally efficacious, which would only be revealed through a more methodical exploration of efficacy across the full range of dose levels. This piecemeal approach to seamless trial design makes difficult a formal assessment of operating characteristics and highlights the challenges of quantifying the implications of multiple sequential decision trials.

Recognizing these weaknesses, the FDA published draft guidance on designing seamless oncology trials [1, 39]. However, because the FDA does not make design recommendations, this guidance does not resolve the tension between logistical simplicity on the one hand and a rigorous quantification of uncertainty on the other. To that end, this paper outlines a modular framework that captures the decision points made in designing a seamless oncology trial and gives several possible options for each decision. Section 2 describes each module and presents our specific design choices intended to adhere to the FDA guidance. We present a freely available trial simulator, implemented in an R package called seamlesssim and an accompanying vignette, both available via GitHub [11], allowing the user to evaluate and compare many design options at once. Section 3 demonstrates this simulator with a numerical study. We show that sensible choices for each module exist, and we provide the computational tools for clinical trialists and statisticians to make this assessment.

2. Methods

2.1. Conceptual Framework

Our framework encompasses many styles of early phase, seamless-type trials. We allow for two stages, both enrolling cohorts of subjects to an assigned dose level(s) and following for toxicity or response endpoints; the second stage may be dropped if a certain response threshold is not achieved in the first stage. Each stage is subdivided into two ‘modules’, one for dosing subjects and one for assessing efficacy, for up to four modules total. Figure 1 provides a high-level schematic of our framework.

Figure 1:

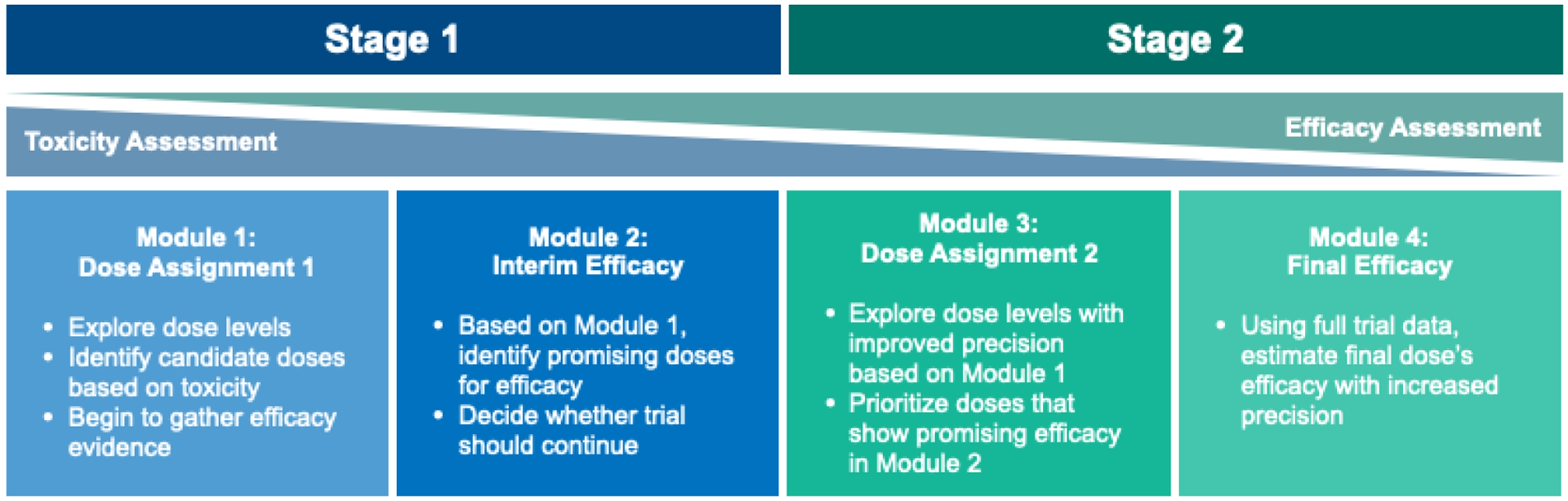
A high-level schematic of our two-stage, four-module framework for Phase I/II seamless designs. Note that toxicity and efficacy are assessed concurrently in both stages, rather than a stark divide between the two objectives, with toxicity the priority in Stage 1, while efficacy is the focus of Stage 2. Trials may choose to stop after Stage 1 if the Module 2 interim efficacy analysis is not promising.

This paper defines a ‘seamless design’ to be any valid combination of the four modules. Since each module can be selected independently of the remaining modules, with some exceptions, there are many possible designs. Some modules can be skipped altogether, and thus our schema includes both classical phase I dose-escalation designs, such as the 3+3 or the CRM, and two-stage phase II designs [40]. It also yields novel hybridizations of the two, and we elucidate the benefits and pitfalls of these hybridizations. The specific choices for each module that we have considered are summarized in Table 1. Throughout this document, we use a typewriter font family to refer to the simulator and its inputs.

Table 1:

Module options currently implemented in the seamless design trial simulator. The option names are in bold, and the names immediately below each option, which follow the ‘$’ symbol, give the inputs required for that option.

Stage 1		Stage 2
Module 1	Module 2	Module 3	Module 4
crm	bayes	crm	bayes
$n	$prob_threshold	$n	$prob_threshold
$skeleton	$prob_means	$skeleton†	$prob_means
$starting_dose	$prior_n_per	$beta_scale†	$prior_n_per
$beta_scale		$dose_cohort_size	$include_stage1_data
$dose_cohort_size		$dose_cohort_size_first_only
$dose_cohort_size_first_only		$earliest_stop
$earliest_stop
3pl3	bayes_isoreg	3pl3	bayes_isoreg
$starting_dose	$prob_threshold		$prob_threshold
	$alpha_scale		$alpha_scale
			$include_stage1_data
empiric	inverted_score	empiric	inverted_score
$n	$ci_level_onesided	$n	$ci_level_onesided
$starting_dose		$rule	$include_stage1_data
$rule		$first_patient_look
$first_patient_look		$thresh_decrease
$thresh_decrease
fixed	min_num_resp	fixed	min_num_resp
$n	$number	$n	$number
$starting_dose		$include_stage1_data
	min_pct_resp	continume_crm‡	min_pct_resp
	$percent	$n	$percent
			$include_stage1_data
	none	none	none

^†these arguments are optional if module 1 is crm. If this is the case and these arguments are not provided, the module 1 options will be used.

^‡this option can only be selected if module 1 is crm because this indicates a simple continuation of that crm

Remark 1

Our “1st stage” and “2nd stage” terminology are not synonymous with the traditional phase 1 and phase 2 terminology. Rather, the seamless framework means that phase 1 and phase 2 occur throughout both stages. As we will show, the staging protects patients by allowing to stop for futility.

The data to be collected for each subject are dose level, occurrence of dose limiting toxicity (DLT), and indicator of response. The true MTD is the dose level with true probability of DLT closest to some pre-specified threshold, usually between 0.25 and 0.35. The objective of seamless oncology trials is typically to establish that the true response probability at the true MTD exceeds some minimal efficacy boundary. Well-designed seamless trials should guard against two distinct errors: the MTD may be incorrectly estimated and/or the estimated response rate may be inefficient or biased. Either error decreases the probability of correctly estimating the efficacy at the true MTD, and moreover, the consequences of either error may be different.

Remark 2

Because our goal is simplicity, the modules currently implemented assume that the probabilities of DLT and response for each dose are mutually independent. However, additional modules that relax this assumption could be implemented.

2.2. Module 1: Dose Assignments for 1st Stage

An initial cohort of n₁ subjects is enrolled and followed for DLT and/or response, which are assumed to be binary. Subjects may be adaptively assigned to one of several dose levels based upon the observed dose-toxicity relationship in the previous subjects, or all subjects in this module may be enrolled to a fixed dose level, and the sole primary endpoint is response. Depending on the aims of the trial, a dose-modifying or fixed-dose module is possible.

We recommend the model-based CRM for module 1 [6, 10] (crm, Table 1). In this design, the first subject is assigned to a pre-specified starting dose. A statistical model is fit to estimate the DLT probabilities for each dose based upon the first subject’s data; this model is usually fit using Bayesian methods to account for sparsity in the data. The MTD is estimated after the first subject, and the next subject is assigned to the new estimated MTD. With each subsequent enrollment, the MTD is re-estimated using all previous subjects’ data.

There are usually safety constraints accompanying the CRM to avoid unsafe escalation [41]. These include never escalating more than one dose level per subject, never escalating before at least one subject has completed a full DLT window at the current dose, and stopping the trial for toxicity if no dose falls below the toxicity threshold.

We have implemented other options for module 1 in our simulator, including the 3+3 algorithm (3pl3); a de-escalation scheme that lowers the assigned dose whenever some percentage of subjects experience a DLT at the current dose level (empiric); and a fixed dose-assignment scheme (fixed). None of these alternatives explicitly estimate the MTD but instead simply assign dose levels according to a rule-based algorithm.

2.3. 1st Stage Futility Analysis (Module 2)

Due to the longer timeframe typically required to observe response, it may be infeasible to re-evaluate the dose-response curve after each subject as is done with the dose-toxicity curve. Rather, it is common to assess efficacy at a few discrete time points during the trial. Module 2 demarcates the first such time point in our framework. Module 1 ends after dose assignments have been made for n₁ subjects, and module 2 occurs when response has been measured for them.

Module 2 is a gatekeeper: if the probability of finding evidence for efficacy at the end of the trial, given the data thus far, is low, then the trial should stop. If module 1 assigned all n₁ subjects to the same dose level, then module 2 can be as simple as requiring a minimum number of responders in order to proceed (min_num_resp). In the absence of any subsequent modules, this would be the single-stage design of A’hern [42]. If dose assignments vary from subject to subject, such that the actual number of subjects at the estimated MTD is likely to be less than n₁, then it would make more sense to require a minimum proportion of responders in order to proceed (min_pct_resp). Even this may be insufficient, as simply requiring a proportion does not take into account uncertainty in observed response rates; this can be achieved by calculating a confidence interval for the probability of response at the estimated MTD, e.g. based on the inverted score test [inverted_score 43].

We also implement a Bayesian version (bayes, Table 1), which, assuming that the efficacy at the estimated MTD is a random variable, calculates the posterior probability that efficacy at the MTD exceeds some minimal response rate. The trial continues only if this posterior probability exceeds some prespecified value. It is common to assume that the distribution of the random variable is Beta, with hyperparameters a₁ > 0 and a₂ > 0, which can be linked to prior beliefs about the mean historical response probability, a₁/(a₁ + a₂), and the historical effective sample size, a₁ + a₂. This is akin to the prior elicitation approach of Mayo and Gajewski [44].

One limitation facing all of the above approaches when the dose-assignment scheme in module 1 is adaptive is that the number of subjects at the estimated MTD can be highly variable. As an extreme example, suppose that, after the n₁th subject, the dose-assignment mechanism updates the estimated MTD to a never-before-tried dose level. If no dose-response model is in place, and assuming a Bayesian perspective, then the distribution of the MTD’s efficacy will be entirely prior-driven. This is undesirable behavior if there is evidence that the response rate at the dose level just above the estimated MTD is itself quite low, the knowledge of which would actually suggest stopping for futility. A parametric dose-response model, e.g. logistic regression or a CRM-type model, could help overcome this limitation. Alternatively, one could impose a weaker assumption that the true probability of response is simply non-decreasing between dose levels. To this end, our recommendation for module 2 is a novel Bayesian variant of isotonic regression that we have developed (bayes_isoreg, Table 1), which we briefly describe in Supplement 1. In standard isotonic regression, observing a large response rate at a lower dose level would be taken as evidence that the response rates at high dose levels are also large and, conversely, observing a small response rate at a higher dose level is taken as evidence that the response rate at low dose levels is also small [45]. Standard isotonic regression may be inadequate under sparse data scenarios, and our Bayesian variant addresses this limitation.

2.4. Dose Assignments for 2nd Stage (Module 3)

Seamless trials often enroll a second cohort of n₂ subjects, either using an adaptive dose-assignment scheme or at a fixed dose level, sometimes called a ‘dose expansion cohort’ [DEC, 30]. Module 3, which delineates this next set of dose assignments, can be any of the options used in module 1, but the starting dose is now the estimated MTD from module 1. An expansion cohort starting at the estimated MTD with or without a simple de-escalation rule would be simulated using empiric or fixed, respectively (Table 1).

Because the estimated MTD is subject to uncertainty, we recommend that module 3 continue adaptive dose assignments and re-estimation of the MTD [31, 32]. Under this recommendation, an entirely new CRM could be initiated, starting at the previously estimated MTD (crm), or the CRM from module 1 could resume at the exact state it ended at in module 1 (continue_crm). Alternatively, a new 3+3 starting at the estimated MTD could be selected (3pl3). Finally, module 3 can be skipped altogether if no second stage is required (none).

2.5. Dose Recommendation (Module 4)

A final efficacy analysis is conducted at the end of the trial, either using all enrolled subjects’ data or data from just the second stage. The design choices for module 4 are the same as for module 2, and all of the same options exist (bayes, bayes_isoreg, inverted_score, min_num_resp, and min_pct_resp).

3. Results

3.1. Trial Simulator: Description

We present a numerical study of our seamless trial simulator to demonstrate how it can be used to compare the performance of heterogenous seamless trial designs. Code and instructions for recreating the simulation study, which makes use of our seamlesssim R package, are available in a separate GitHub repository [46], and the instructions are reprinted in Supplement 2. Ten data-generating scenarios were considered; the true dose-toxicity and dose-response curves are given with the results in Figures 2–4 and Figure S2 in Supplement 1. For all scenarios, the true MTD was the dose level with true probability of DLT closest to 0.25 but not exceeding 0.30, and an ‘acceptable’ dose level was defined as any dose level with true probability of DLT not exceeding 0.30 and true probability of response at least 0.20. Based on this definition, two scenarios (numbers 7 and 9) had no acceptable dose levels, and three scenarios (1, 3, and 10) had two acceptable dose levels. The remaining five had exactly one acceptable dose level.

Figure 2:

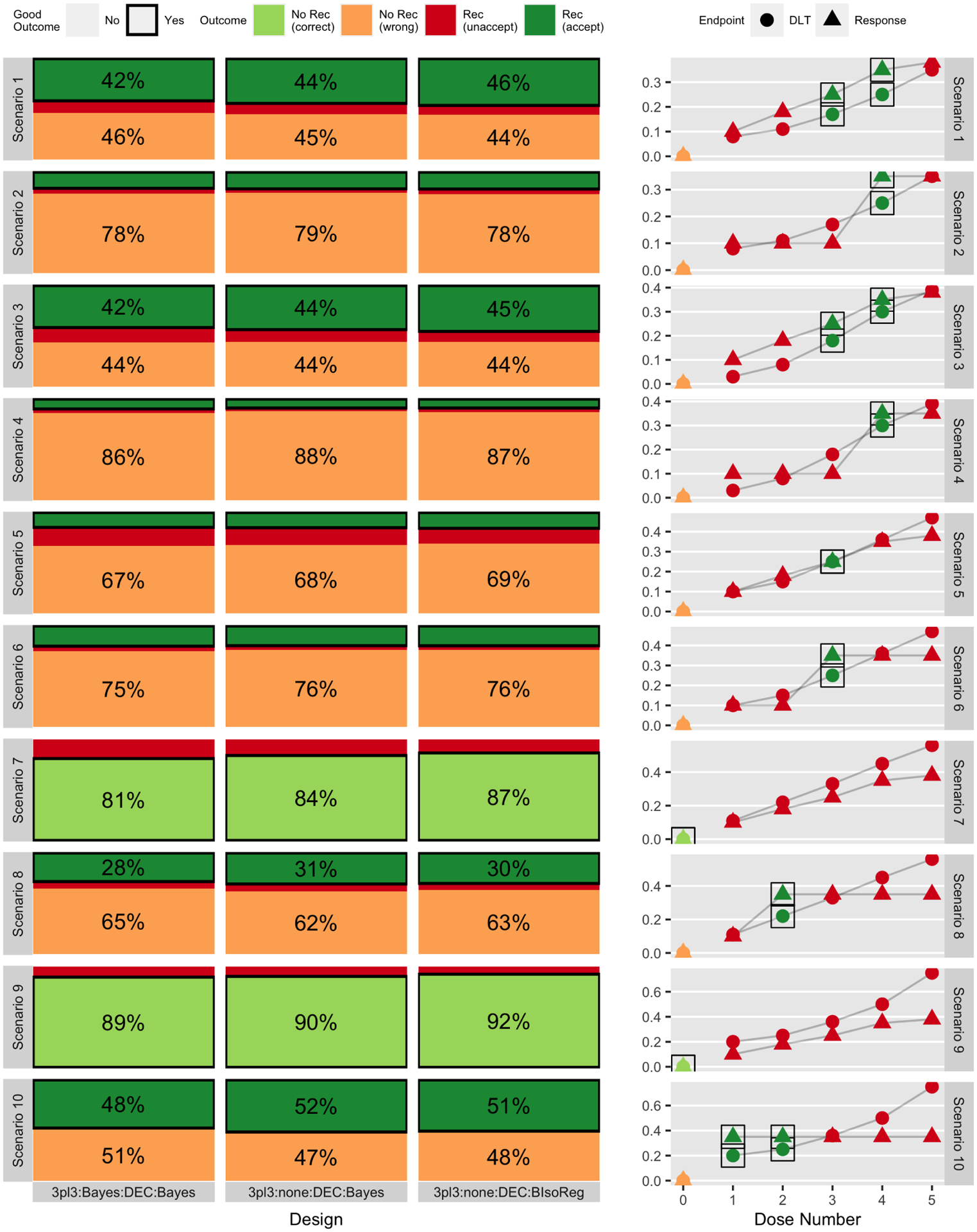
Simulation-based probability of outcomes (based on 2000 simulations) for three designs (out of six total) across ten scenarios, separated into whether or not any dose level was recommended and whether or not that outcome was acceptable or not. The right-hand column gives the true generating toxicity and efficacy curves. Each row corresponds to a different scenario, and consecutive pairs of scenarios (1&2, 3&4, etc.) are linked in that they share a common dose-toxicity curve but differ in the dose-response curve. Figure 3 gives the same results for three different designs.

Figure 4:

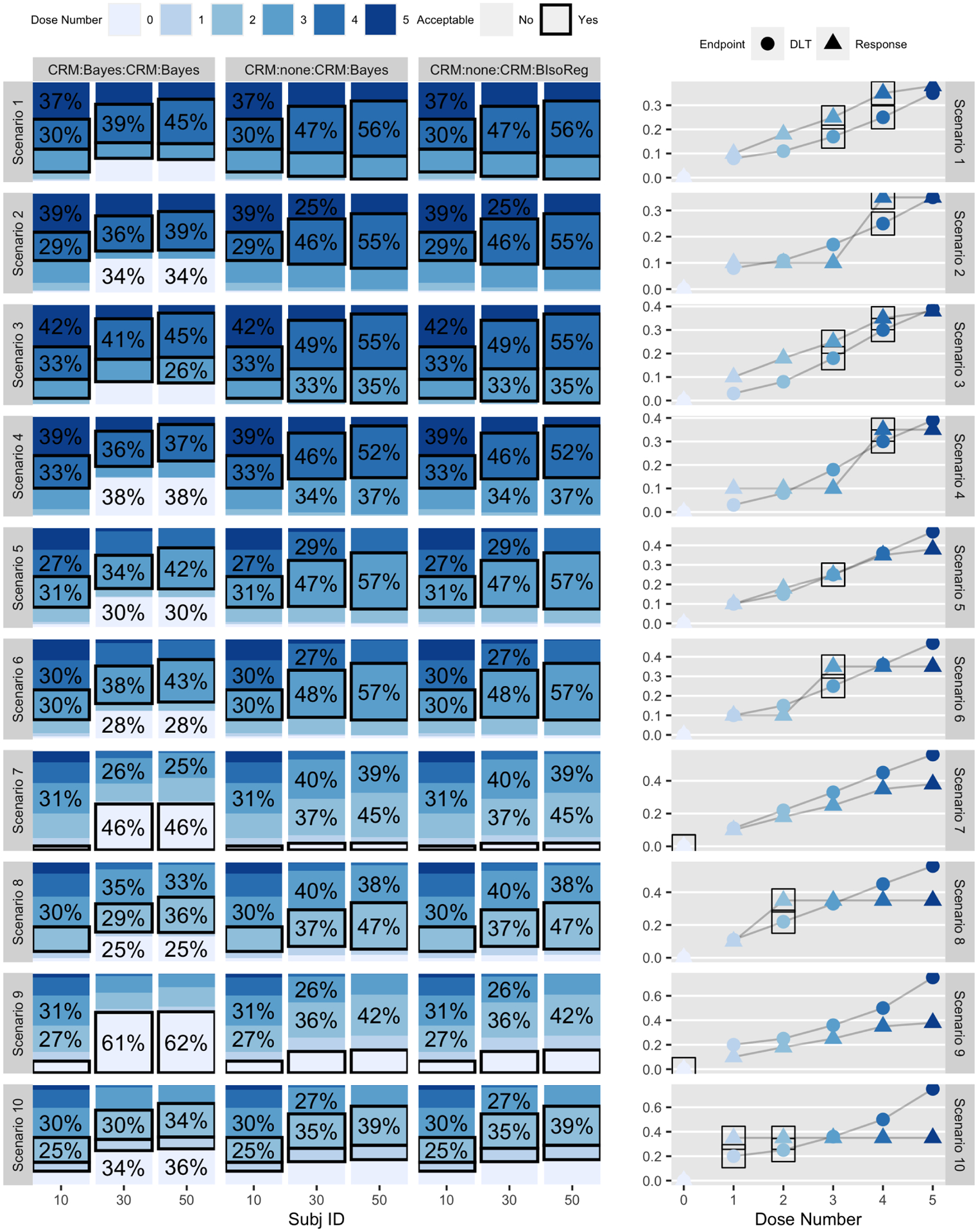
Distribution of dose assignments at subjects 10, 30, and 50 (based on 2000 simulations) for three CRM-type designs (out of six total) across ten scenarios. The right-hand column gives the true generating toxicity and efficacy curves. Each row corresponds to a different scenario, and consecutive pairs of scenarios (1&2, 3&4, etc.) are linked in that they share a common dose-toxicity curve but differ in the dose-response curve. The proportion(s) corresponding to the preferred dose level are bordered by a solid box. If a trial has stopped for futility or safety, the patient was treated as having been assigned to dose level ‘0’. Figure S2 in Supplement 1 gives the same results for the three 3+3-type designs.

We compared six designs comprising combinations of modules: two choices of dose-assignment mechanism each combined with three different efficacy analyses. All designs are described in Table 2. The first dose-assignment mechanism is a ‘3+3’ algorithm (module1 = 3pl3), which will have a maximum sample size of 6 patients per dose level, or n₁ = 30 patients, followed by a fixed DEC of size n₂ = 35 (module3 = empiric); the DEC enrolls subjects at the estimated MTD from the ‘3+3’ algorithm and only de-escalates if the observed DLT rate after the first 10 patients in the cohort exceeds 33%. The second dose-assignment mechanism is a CRM (module1 = module3 = crm) with n₁ = 25 and n₂ = 35 subjects in the first and third modules, respectively.

Table 2:

Choice of modules for six designs considered. The upper three designs will enroll up to n₁ = 30 patients (cohorts of six for each of five dose levels) in module 1 and n₂ = 35 in module 3; the lower three designs will enroll up to n₁ + n₂ = 60 subjects across both modules.

Design name	module 1	module 2	module 3	module 4	max n1 + n2
3pl3:Bayes:DEC:Bayes	3pl3	bayes	empiric	bayes	65
3pl3:none:DEC:Bayes	3pl3	none	empiric	bayes	65
3pl3:none:DEC:BIsoReg	3pl3	none	empiric	bayes_isoreg	65
CRM:Bayes:CRM:Bayes	crm	bayes	crm	bayes	60
CRM:none:CRM:Bayes	crm	none	continue_crm	bayes	60
CRM:none:CRM:BIsoReg	crm	none	continue_crm	bayes_isoreg	60

We evaluated three sets of efficacy analyses. The first utilized a Bayesian futility analysis (module2 = bayes) and a final Bayesian analysis (module4 = bayes); the second conducted only a final Bayesian analysis (module4 = bayes); and the third implemented our Bayesian isotonic regression at the end (module4 = bayes_isoreg). To compare between all six designs, the module 2 and module 4 efficacy parameters were set so that the probability of recommending the MTD in scenario 9 was about 0.10. This corresponds to a type I error (false positive) rate of 0.10, since the MTD is not acceptable in this scenario. For each of the 60 combinations of six designs and ten scenarios, we ran 2000 simulated trials.

3.2. Trial Simulator: Results

Figures 2 and 3 display the simulation-based probability of recommending any dose and whether or not that recommendation was a good one. Each figure gives a set of three designs, grouped by choice of dose-assignment mechanism. When at least one dose level is acceptable, as in scenarios 1–6, 8, and 10, there are three possible outcomes to the trial – no recommendation, recommendation of an unacceptable dose, or recommendation of an acceptable dose – and when no dose levels are acceptable, as in scenarios 7 and 9, there are two possible outcomes – no recommendation or recommendation of an unacceptable dose.

Figure 3:

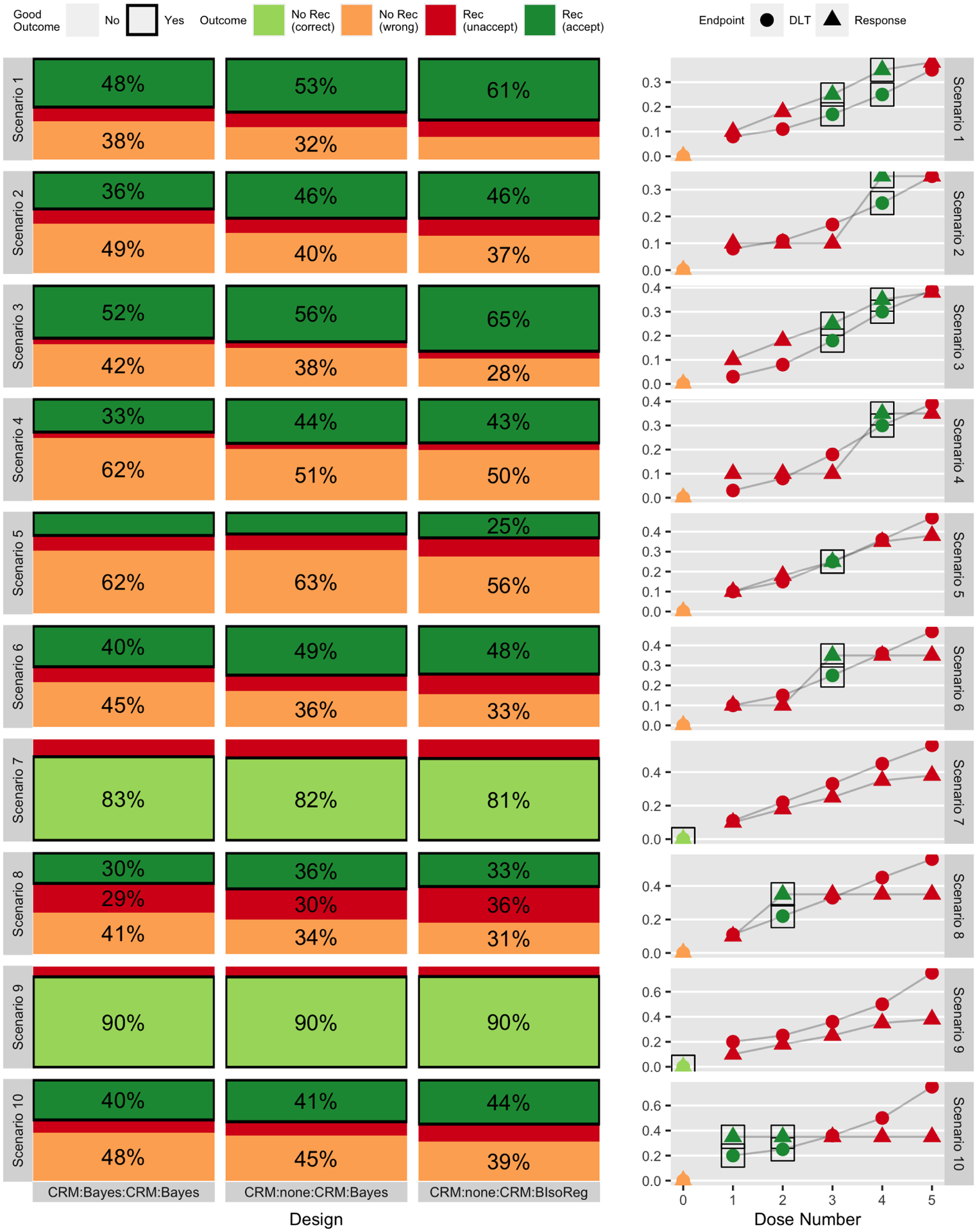
Simulation-based probability of outcomes (based on 2000 simulations) for three designs (out of six total) across ten scenarios, separated into whether or not any dose level was recommended and whether or not that outcome was acceptable or not. The right-hand column gives the true generating toxicity and efficacy curves. Each row corresponds to a different scenario, and consecutive pairs of scenarios (1&2, 3&4, etc.) are linked in that they share a common dose-toxicity curve but differ in the dose-response curve. Figure 2 gives the same results for three different designs.

From Figure 2, which contains the 3+3-type designs, whether or not there is an interim futility analysis in module 2, i.e. comparing 3pl3:Bayes:DEC:Bayes to 3pl3:none:DEC:Bayes, has relatively little impact on the probability of making a correct dose recommendation. This is not surprising, given that the DEC in module 3 is unlikely to change the estimated MTD unless extreme toxicity is observed, making this comparison analogous to that of a two-stage phase II design against a one-stage phase II design. In contrast, the use of a Bayesian isotonic regression in module 4 in place of independent beta priors on each dose level, i.e. comparing 3pl3:none:DEC:Bayes to 3pl3:none:DEC:IsoReg, generally increases the overall probability of recommending a dose level. That is, the ‘No Rec (correct)’ and ‘No Rec (wrong)’ proportions are generally larger for 3pl3:none:DEC:Bayes, and the ‘Rec (unaccept)’ and ‘Rec (accept)’ proportions are generally larger for 3pl3:none:DEC:BIsoReg. These differences range from 1–4% across all ten scenarios. This is also an expected finding, since sharing information between dose levels allows the isotonic regression to more easily recommend dose levels.

Figure 3 gives the same sets of results for the CRM-type designs, all of which have the same maximum possible sample size of n₁ + n₂ = 60 subjects. As expected, the CRM-type designs select an acceptable dose with higher probability than the 3+3-type designs. Moreover, in contrast to Figure 2, the interim efficacy analysis has a greater effect on the final outcome of the trial, as seen from comparing CRM:Bayes:CRM:Bayes to CRM:none:CRM:Bayes. This is likely because of the final 35 patients of the trial, who are only enrolled to CRM:Bayes:CRM:Bayes if the module 2 efficacy analysis is passed. Comparing CRM:none:CRM:Bayes to CRM:none:CRM:BIsoReg, the isotonic regression generally increases the recommendation probability.

Figure 4 gives the distribution of dose assignments at subjects 10, 30, and 50 for the three CRM-type-designs. Analogous results for the 3+3-type-designs are given in Figure S2 of Supplement 1. For the CRM designs, as the trial proceeds, subjects are assigned to the preferred dose level in increasing proportions. Although the 3+3 designs generally assign the 10th subject to the preferred dose with high probability, their performance degrades as the trial proceeds, meaning that the 30th and 50th subjects are often assigned to the preferred dose level with small probabilities. This is an expected result given the known deficiencies of the 3+3, but the inclusion of the interim efficacy analysis would make it difficult to quantify these probabilities in the absence of this simulator. Comparing Figure 4 to Figure S2, CRM:none:CRM:BIsoReg is uniformly preferred to 3pl3:Bayes:DEC:Bayes except for scenarios 7 and 9, in which no dose levels are acceptable in truth. Based on this, we would conclude that CRM:none:CRM:BIsoReg would be improved with a choice of module 2 = bayes_isoreg, if we were actually proposing the design for a clinical protocol.

4. Conclusion

This paper characterizes seamless oncology trial design in a modular framework, which confers several advantages. It formalizes each decision needed for a seamless-type trial, including a provision for interim futility analyses. It puts forward a concrete definition of a ‘seamless trial’, namely any logically coherent set of modules. Because this modular framework is implemented in seamlesssim[11], a freely available R package and an accompanying vignette that together form the main contribution of this paper, it is possible to quantify design decisions’ impact on operating characteristics. By providing the trial simulator, we have made it simpler for clinical trialists to quantify seamless design decisions’ impact on operating characteristics. Even very heterogeneous designs can be compared using our simulator, which reports the same operating characteristics regardless of the module configuration. These advantages address three key challenges to the statistical design of seamless trials outlined in Hobbs, et al. [33]: lack of formal design for DECs, imprecise operating characteristics, and difficulties in implementing interim safety and futility analyses. Future extensions could use the time-to-event-CRM [47] in Modules 1 and 3 as a means of handling late-onset toxicities. Another important direction would be to extend Modules 2 and 4 to estimate an optimal biological dose or minimum efficacious dose.

Although our primary goal was not to recommend a particular configuration of modules, our findings reiterate the importance of keeping the dose assignment mechanism open for the full duration of the trial and efficiently sharing information across dose levels and stages. With regard to this second point, an isotonic regression model for estimating dose-response curves, such as bayes_isoreg, is sensible. This approach could also be adapted as an option for module 1 or module 3, to estimate the dose-toxicity curve.