Abstract
Tumor doubling time can significantly affect the outcome of anticancer therapy, but it is very challenging to determine. Here, we present a statistical approach that extracts doubling times from progression-free survival (PFS) plots, which inherently contains information regarding the growth of solid tumors. Twelve cancers were investigated and multiple PFS plots were evaluated for each type. The PFS plot showing fastest tumor growth was deemed to best represent the inherent growth kinetics of the solid tumor, and selected for further analysis. The exponential tumor growth rates were extracted from each PFS plot, along with associated variabilities, which ultimately allowed for the estimation of solid tumor doubling times. The mean simulated doubling times for pancreatic cancer, melanoma, hepatocellular carcinoma (HCC), renal cell carcinoma, triple negative breast cancer, non-small cell lung cancer, hormone receptor positive (HR+) breast cancer, human epidermal growth factor receptor-2 positive (HER-2+) breast cancer, gastric cancer, glioblastoma multiforme, colorectal cancer, and prostate cancer were 5.06, 3.78, 3.06, 2.67, 2.38, 2.40, 4.31, 4.12, and 3.84 months, respectively. For all cancers, clinically reported doubling times were within the estimated ranges. For all cancers, except HCC, the growth rates were best characterized by a log-normal distribution. For HCC, the gamma distribution best described the data. The statistical approach presented here provides a qualified method for extracting tumor growth rates and doubling times from PFS plots. It also allows estimation of the distributional characteristics for tumor growth rates and doubling times in a given patient population.
Keywords: PK/PD modeling and simulation, preclinical-to-clinical translation, progression-free survival, solid tumor doubling time, tumor growth rate
INTRODUCTION
Knowledge of tumor doubling time is very important for the management of cancer. In the clinic, it has been shown that the knowledge of tumor doubling times allows for the determination of optimal follow-up times for screening the patients (e.g., hepatocellular carcinoma (HCC) (1)). Tumor doubling time has also been shown to be a good prognostic marker for the survival and disease progression of various cancers (2–4). For example, Spratt et al. have demonstrated that for the pulmonary cancers, there is a reasonable correlation between the growth rates of tumors and the observed tumor malignancy (5). In addition, tumor doubling times also allow for the selection of optimal dosing regimens and assessment of the probability of tumor growth inhibition in treated patients (6). For example, Shackney et al. (7) have noted that faster growing tumors are more likely to respond to the conventional cancer therapies. Tumor doubling times have also been proposed as a gold standard for selection between surgical procedure and therapeutic interventions. For example, Ollila et al. (8) have suggested that for patients undergoing pulmonary tumor resection, the surgical procedure is only recommended for patients with tumor doubling times ≥ 60 days. Apart from the clinical tumor management, the knowledge of tumor doubling time and associated variability is also important for successful preclinical-to-clinical translation of novel anticancer therapeutics. Using the principles of pharmacokinetics/pharmacodynamics (PK/PD) modeling and simulation (M&S), we have shown that clinical predictions of antibody-drug conjugate (ADC) efficacy are very sensitive to parameters associated with growth rates of tumors in the clinic (9). As such, accurate measurement of tumor doubling times is essential for the management of cancer.
The method for calculating tumor doubling times in the clinic was first introduced by Schwartz (10), who derived an equation for calculating tumor doubling times by assuming an exponential tumor growth. This method allowed for tumor doubling time calculations based on the observed differences in tumor diameters between two serial measurements of tumor volumes, obtained using radiologic imaging. While this approach is useful for calculating clinical doubling times of tumors, there are a few limitations of this approach. In cases where there is infinitesimal change in tumor volume between the two measurements, or there is a high degree of uncertainty in the measured volume, the calculated doubling time for a patient can be erroneous (11). In addition, the method by Schwartz (10) is also not efficient for estimating population variability in tumor growth rates. In fact, Mehrara et al. (11) have conducted Monte-Carlo simulations and showed that most reported mean tumor doubling times obtained using Schwartz’s method are likely overestimated. To overcome these drawbacks, here, we have presented an alternative method for estimating doubling times of solid tumors, and associated population variability, using progression-free survival (PFS) data.
Ever since the Food and Drug Administration (FDA) moved away from objective response rate (ORR) as the prime determinant for drug approval, PFS has been increasingly utilized by the oncologists (12). PFS is defined as the time from the treatment randomization to the objective tumor progression, and it has served as a surrogate for accelerated drug approval in the field of oncotherapeutics (13). Out of all the commonly used efficacy endpoints in the clinical trials (i.e., time to progression, event-free survival, time to next treatment, progression-free survival, objective response rate, duration of response, and overall survival), PFS is the only one that provides information regarding tumor growth. Here, we have proposed a strategy to exploit this property of PFS. We have outlined a novel statistical approach that extracts the exponential growth rates of tumors from published PFS analyses, and utilizes them to calculate mean tumor doubling times and associated population variability. Our approach has been evaluated using 12 different types of cancers: colorectal cancer (CRC), gastric cancer, glioblastoma multiforme (GBM), human epidermal growth factor receptor-2 positive (HER-2+) breast cancer, hormone receptor positive (HR+) breast cancer, triple negative (TN) breast cancer, melanoma, non-small cell lung cancer (NSCLC), pancreatic cancer, prostate cancer, renal cell carcinoma (RCC), and HCC.
METHODS
Data Selection
For each of the 12 cancer types, published PFS data from different clinical trials were collected and all patients included in these studies were receiving active treatment. PFS analyses from the trials in which the assigned therapy had no/negligible effect on the growth of the tumor were selected to determine the natural growth rate of each cancer. A total of 47 clinical trials were identified that reported appropriate PFS data for one of the 12 cancer types (see Table S1 for references), and the Kaplan-Meier plots from these trials were digitized using the software “Grab It!®.” The digitized data for a given cancer type were superimposed to allow for visual comparison of all PFS plots. The final PFS cohort for each cancer type was selected based on two criteria: (i) median PFS value had to be the smallest among the cohorts for the same cancer, and (ii) the terminal slope of progression (i.e., the time from median PFS to the final observation time point) had to be higher than other cohorts of the same cancer. The final PFS plots chosen to estimate the doubling time of each cancer type and the corresponding reference are provided in Table S1.
Extraction of Number of Patients with an Event (i.e., Disease Progression)
For each PFS analysis listed in Table S1, the number of patients with an event at each observation time point was extracted. An event was defined as progressive disease (PD), if the sum of longest diameters (SLD) increased by 20 or 25% as outlined by either the response evaluation criteria in solid tumors (RECIST) or the World Health Organization (WHO) criteria, respectively (14,15). Whether WHO or RECIST criteria were chosen to define an event depended on which criteria the authors used in the published study. One of the two approaches was then implemented to calculate the number of events at each time point. The first approach was used if the published studies provided the number of patients at risk, and determined the number of patient events by subtracting the sample sizes between observation time points. The second approach was used when the risk tables were not provided, and the number of patient events was calculated using Eq. 1, which is derived from the Kaplan-Meier estimation of the survival function.
| (1) |
above, di denotes number of deaths (events in this case), ni is the number of patients at risk, S(t)i is the Kaplan-Meier estimate for the survival function, n0 is the intent to treat (ITT) sample size, and S(t)0 is equal to one (see supplementary material for more information). When censored patients were reported, they were omitted from the number of patients calculated to have the event. Using the extracted data, Kaplan-Meier curves were re-plotted in R (version 3.3.1) (16) and compared with the published plots to verify the quality of data extraction. Of note, the second approach to calculate the number of events was employed only for glioblastoma (17) and gastric carcinoma (18). For glioblastoma, Yung et al. (17) evaluated cohort members every 2 months, therefore the number of events was also calculated every 2 months. For gastric carcinoma, information on the exact time of tumor evaluation was not reported, and it was assumed to occur every 2 months.
Calculation of Exponential Growth Rates
To obtain the tumor growth rates for each patient reported to have the event, exponential growth rate was assumed and tumor volume (TV) was defined as:
| (2) |
above, TV0 denotes the initial tumor volume, kg is the exponential growth rate, and t is the time. For simplicity, TV0 was assumed to be 1 cm3 for all the patients (note, the simulated results are independent of the initial tumor volume). An event was defined as 20 or 25% increase in tumor diameter from the baseline (as dictated by either RECIST or WHO criteria, respectively). Tumors were assumed to be spherical and the corresponding increase in tumor volume was found using the volume of a sphere. The tumor associated with a 20–25% increase in diameter (TV20–25%) was set to either a 1.728- or 1.953-fold change (see supplementary information for further details of the mathematical description and spherical assumption). Equation 2 was re-written to define kg as:
| (3) |
where tevent denotes the time at which the event (or PD) was observed (equivalent to t in Eq. 2). Using Eq. 3, growth rates were calculated at each observation time point for patients that experienced the event. Of note, the tevent value was not the time at which tumors were evaluated, as this would yield the same growth rates for all the patients with an event at that time, which is unrealistic. Instead, tevent for each patient was selected from a random uniform distribution between the previous and current observation time point. Thus, allowing the event to take place, with equal probability, on any day between last follow-up and current evaluation. This approach provides a unique growth rate for each patient that progressed over the duration of observation. The method for determining tevent between the start of the study (tevent = 0) and the first time of tumor evaluation differed from all subsequent evaluations, to prevent the random uniform distribution from selecting event times that would yield unrealistic growth rates. For example, if the time of PD was set to 0.1 days the resulting growth rate would be 1.82 day−1, implying that the patient’s tumor doubled every 9 h, which is not realistic. Therefore, the earliest possible time for the progressive of the disease was set to 10 days. This time was chosen based on the fastest mean doubling times isolated for all the cancers in this study (6).
Statistical Modeling and Simulation
All analyses were conducted in R (version 3.3.1) (16), using the following packages: “gdata,” “scales,” “fitdistrplus,” (19) and “survival” (20).
Growth Rate Evaluation
To evaluate the accuracy of the extracted growth rates, clinical trials were simulated as follows. For each patient with PD in the simulated trial (n = 1000), growth rates were sampled with replacement from the extracted distribution of kg values. As drug effect was assumed to be negligible and tumors were assumed to grow exponentially.
Equation 1 was employed to simulate changes in the patient’s TV at each of the study’s original observation time points. To identify the patient’s time of progression, simulated TVs were evaluated to determine the time corresponding to either 20 or 25% increase in the tumor diameter compared to the baseline (1 cm), depending on which tumor response criteria authors used in the published trial (RECIST vs. WHO). This process was repeated 1000 times, using different seed numbers to generate 1000 unique clinical trial simulations. The simulated trials were collated and used to construct Kaplan-Meier visual predictive check (KM-VPC) plots, which were overlaid with the original published PFS plots. This was done to evaluate if the simulated median PFS and 90% confidence interval of the KM-VPC plots were in agreement with the PFS analysis reported by the respective authors.
Selection of Growth Rate Distribution Model
Cullen and Frey graphs plot kurtosis against the square of skewness, and were utilized to help identify the true nature of distribution of the extracted growth rates. The extracted growth rates were fitted to normal, log-normal, uniform, gamma, exponential, and Weibull continuous probability distribution functions. Clinical trials comprised of 1000 patients were simulated for each of the five fitted distributions. The proportion of patients with reported PD in each simulated trial was determined from the published PFS curve. For those with PD, specific growth rates were sampled from one of the five fitted distributions and TV was tracked over time (using Eq. 1 as described above) to determine the time of PD. To determine the most suitable distribution for characterizing the underlying population variability in the extracted growth rates, the Akaike information criterion (AIC) and a series of plots (i.e., PFS, empirical and theoretical density, Q-Q, empirical and theoretical CDF, and P-P plots) were generated. To verify the predictive ability of the identified distribution for each type of cancer, KM-VPCs were generated as previously described, but kg was sampled from the best fit distribution.
Dealing with Model Misspecification
If structural misspecification was observed, kg was sampled using a random uniform distribution from a continuous distribution of the calculated growth rates (rather than sampling kg from the best fit distribution). The intervals to apply the uniform distribution were determined using the histogram representations of the calculated growth rates. For a given interval, histogram bins and densities were used to (i) identify lower/upper kg values for the uniform distribution to select from, and (ii) calculate the number of patients to assign the selected growth rates from the specified interval. This sampling approach was crucial for determining whether the model misspecification occurred because of incorrect growth rate extraction or inappropriate distributional characterization of the extracted growth rates.
Doubling Time Calculation
Growth rates were characterized using either a log-normal or gamma distribution. If growth rates were log-normally distributed, Eqs. 4 and 6 were used to calculate the distribution’s mean (E(x)lnorm), median, and variance (Var(x)lnorm).
| (4) |
| (5) |
| (6) |
above, μ and σ denote the mean and standard deviation of the log-normal distribution. For gamma distributed growth rates, Eqs. 7 and 8 were used to calculate the distribution’s mean (E(x)gamma) and variance (Var(x)gamma).
| (7) |
| (8) |
above, α and β denote the shape and rate parameters, respectively. The median value of a gamma distribution was found using the qgamma function in R to extract the 50th quantile.
Mean and variance parameters were used to obtain summary statistics including the standard deviation (SD) and coefficient of variation (CV) by applying Eqs. 9 and 10.
| (9) |
| (10) |
The solid tumor doubling times were obtained using Eq. 11.
| (11) |
RESULTS
As shown in Fig. 1, for each cancer type, multiple PFS analyses were extracted from the literature and superimposed to identify the clinical trial cohort in which the assigned treatment had little to no effect on tumor growth. Isolating these cohorts proved most difficult in the cases of GBM, RCC, prostate cancer, and HR and HER-2 positive breast cancer. In each of these cases, either the median PFS or terminal slopes of many cohorts were similar. However, using the criteria predefined for comparing median PFS values and terminal slopes, the PFS shown as dotted lines in Fig. 1 for each cancer type was selected for further analysis.
Fig. 1.
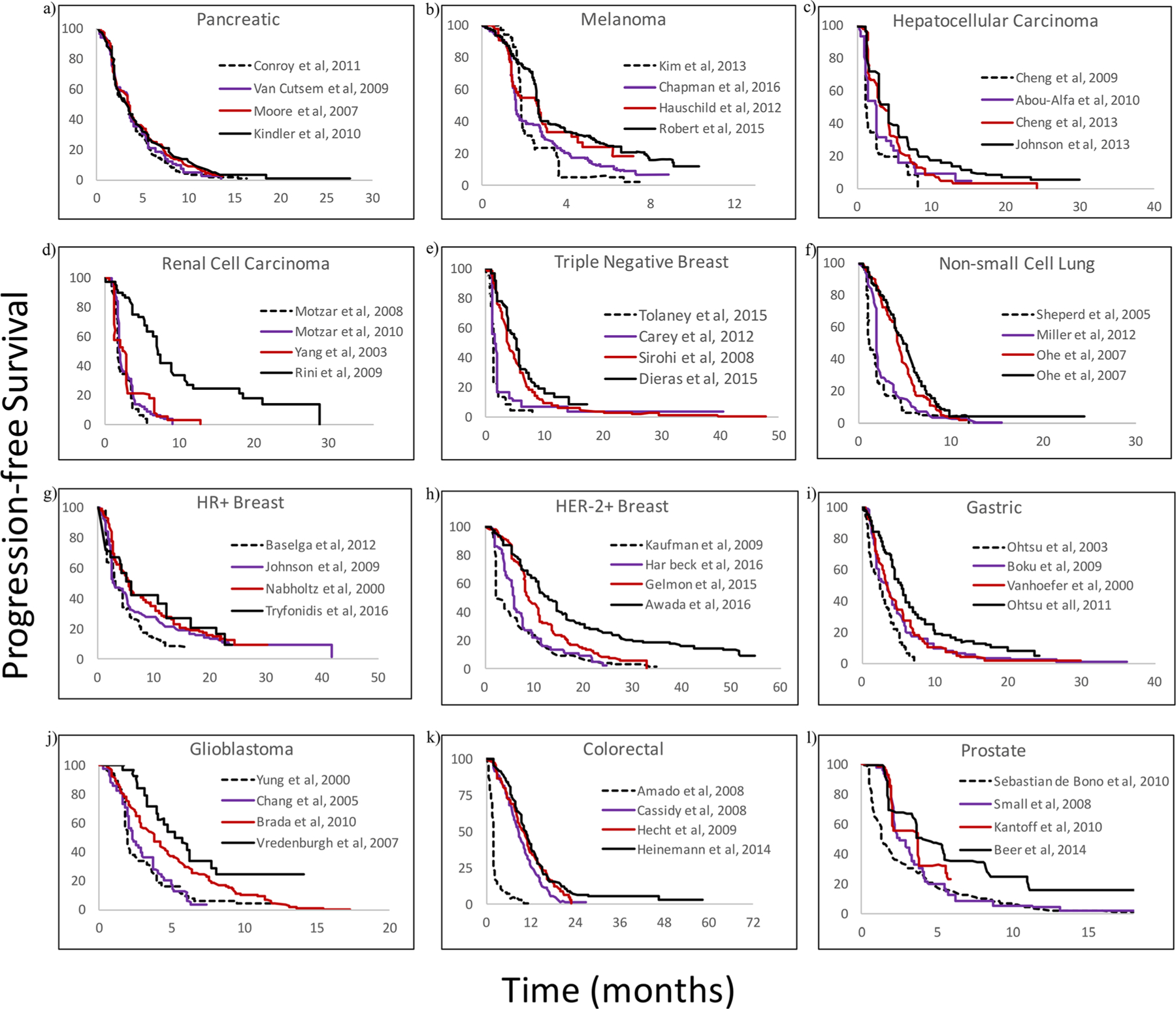
Digitized progression-free survival (PFS) curves extracted from 3 to 4 different published trials for each cancer type. Panels a to l represent pancreatic, melanoma, hepatocellular carcinoma, renal cell carcinoma, triple negative breast, non-small cell lung, hormone receptor positive breast, human epidermal growth factor receptor-2 positive breast, gastric, glioblastoma multiforme, colorectal, and prostate cancers, respectively. Publications from which PFS were obtained are listed in the panel
Calculation of Number of Patients with an Event
For each cancer type, the number of patients with an event was extracted from the selected PFS analyses (Table S1) using one of the two approaches described in the “METHODS” section. The predicted median PFS values were compared with the published estimates. The first, simpler approach performed well for all cancers, except melanoma. In the case of melanoma, the extracted median PFS value was greater by 3 months and did not match the published value of 1.8 months (21) (Fig. S2). However, when the number of patients with an event was extracted using the second approach, the results predicted a much closer median PFS value of 1.9 months. The second approach also performed well for gastric cancer and glioblastoma multiforme, for which the patient risk tables were not available.
Evaluation of Calculated Growth Rates
Figure 2 shows the KM-VPC plots generated for each cancer type (using 1000 clinical trial simulations) superimposed over the observed data. As evident from the figure, the extracted growth rates were able to adequately capture the literature reported PFS profiles. The predicted median and 90% confidence interval fell within the published 90% confidence interval for each PFS plots. More importantly, predicted medians were able to satisfactorily recapitulate the reported PFS plots, and the data points were in close agreement throughout the time course of the study.
Fig. 2.

Kaplan-Meier visual predictive check (KM-VPC) plots for the evaluation of calculated growth rates. Panels a to l represent KM-VPCs for pancreatic, melanoma, hepatocellular carcinoma, renal cell carcinoma, triple negative breast, non-small cell lung, hormone receptor positive breast, human epidermal growth factor receptor-2 positive breast, gastric, glioblastoma multiforme, colorectal, and prostate cancers, respectively. All observed data were obtained from the references listed in Table S1
Growth Rate Fitting and Evaluation
Figure 3 and Fig. S1 show our approach for assessment of statistical fitting of the PFS data. The Cullen and Frey plot shown in Fig. S1A provides information about the likely parent distributions (i.e., normal, log-normal, gamma, Weibull, or exponential) of the extracted growth rates. Whereas Fig. S1B shows how well the data fit the potential distributions. In the representative example shown in Fig. S1, the Cullen and Frey plot indicates that the data for pancreatic cancer would best fit a beta distribution (i.e., log-normal, gamma, or Weibull). This indication was supported by the plots in Fig. S1B, as when normal or uniform distributions were fitted the data deviated significantly from the reference line in QQ/PP/CDF plots. Figure 3 shows the reported and simulated PFS curves for all cancer types. If we continue with the example of pancreatic cancer, panel “a” in Fig. 3 shows that while the PFS curves visually support the assertion that the data would best fit a beta distribution, logistic regression analysis (data not shown) shows that all the distributions produced PFS curves that were not significantly different than the published PFS curve. Therefore, when multiple distributions were capable of adequately describing the distribution of extracted growth rates, the AIC value was used to determine the “best” fit. For all cancers, except HCC, the growth rates were best characterized by a log-normal distribution, as determined by QQ/PP/CDF plots (Fig. S1B) and AIC values. For HCC, the gamma distribution was found to describe the data the best (panel “c,” Fig. 3).
Fig. 3.
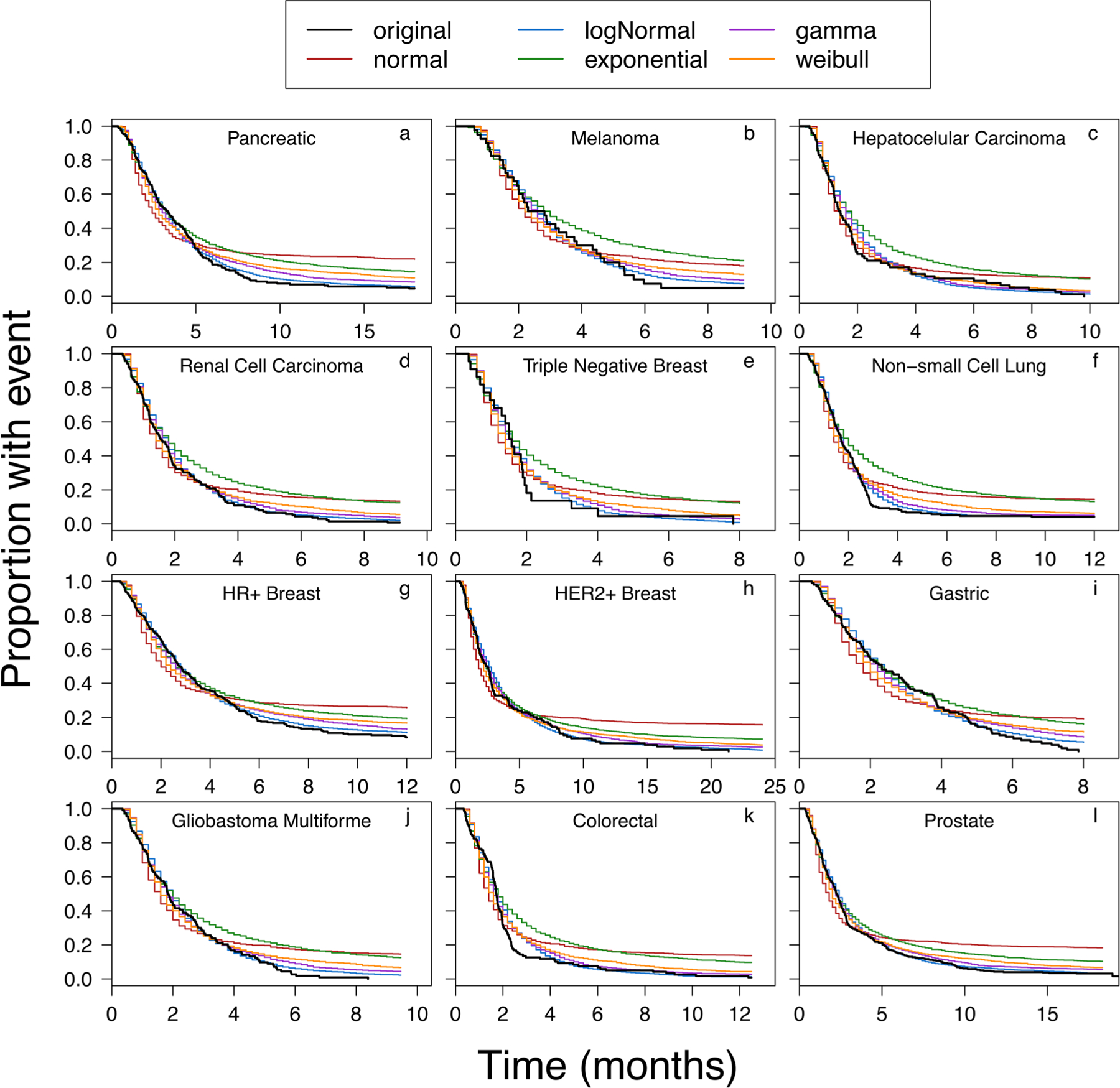
Progression-free survival (PFS) simulations using growth rates obtained from fitted distributions (normal, log-normal, gamma, Weibull, exponential) overlaid with the reported PFS plot (references listed in Table S1). Panels a to l represent PFS simulations for pancreatic, melanoma, hepatocellular carcinoma, renal cell carcinoma, triple negative breast, non-small cell lung, hormone receptor positive breast, human epidermal growth factor receptor-2 positive breast, gastric, glioblastoma multiforme, colorectal, and prostate cancers, respectively
A comparison of all the panels in Fig. 3 shows a similar trend, where the exponential distribution (green line) and normal distribution (red line) underestimate the progression, and the gamma distribution (purple line), log-normal distribution (blue line), and occasionally Weibull distribution (orange line) produce PFS plots that closely match the reported plots. While the distribution with the lowest AIC value was ultimately identified as the “best” fit, the predictive ability of the distribution was also verified using KM-VPC plots (Fig. 5). For most of the cancer types, the simulated PFS profiles were enclosed within the observed 90% confidence intervals of the reported PFS profiles. However, for HER-2+ breast cancer (panel “h,” Fig. 4) and GBM (panel “j,” Fig. 4), the simulated medians and 90% confidence intervals of the KM-VPC plot overestimated the rate of disease progression, as the predicted median and 90% confidence intervals fell below the reported values.
Fig. 5. Boxplots demonstrating distribution of simulated doubling times across the 12 cancer types. Each boxplot represents the tumor volume doubling times for 1000 samples from the best fitted distribution model that was utilized to characterize the calculated growth rates. The boxplot whiskers represent the upper/lower quartile values plus/minus 1.5 times the interquartile range. All data points outside the whiskers were considered outliers by the R software. For all cancers (except glioblastoma multiforme (GBM)), the blue transparent boxes represent the 95% confidence interval (CI) of the mean doubling time values reported in the literature (Table I.
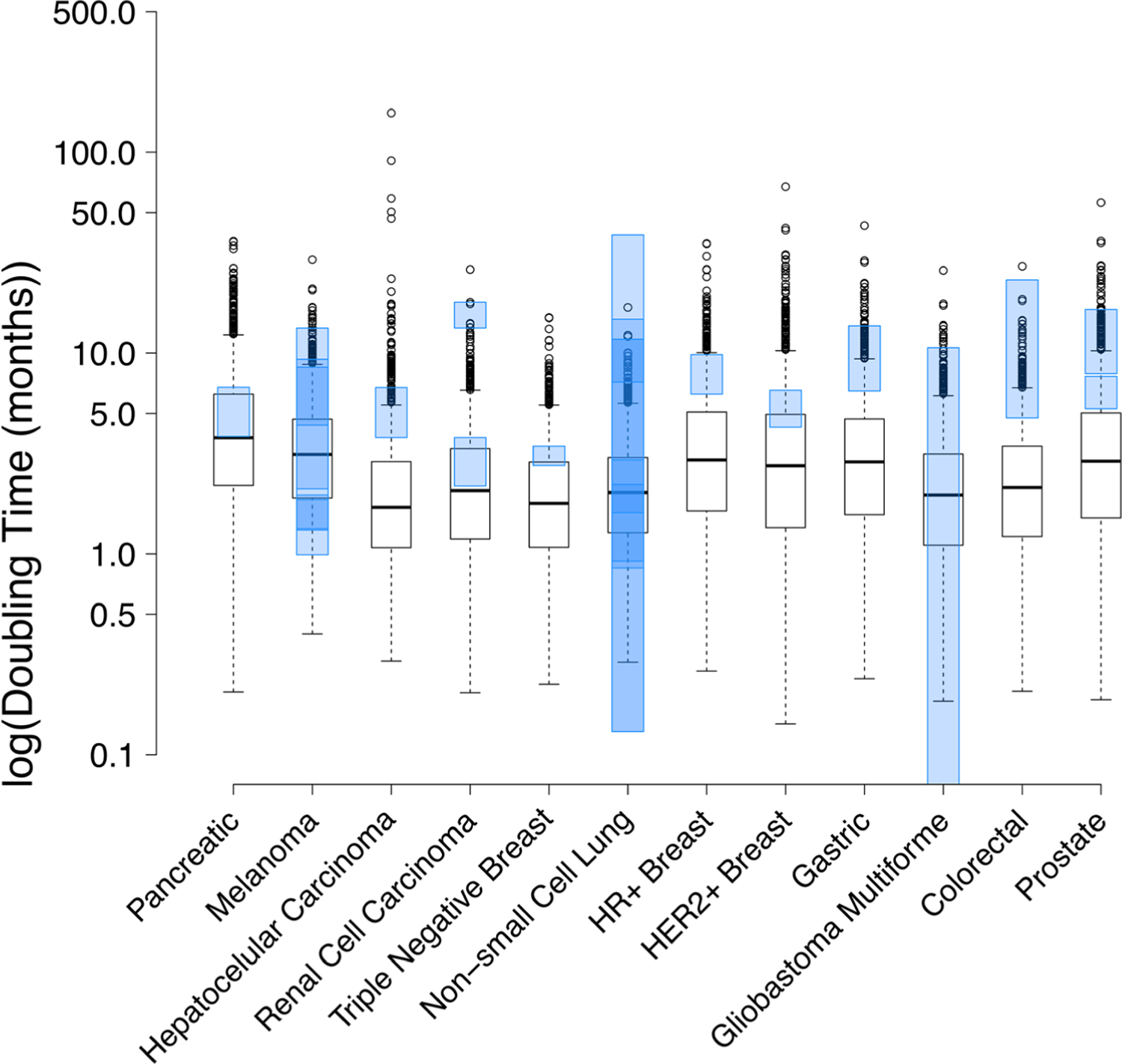
Boxplots demonstrating distribution of simulated doubling times across the 12 cancer types. Each boxplot represents the tumor volume doubling times for 1000 samples from the best fitted distribution model that was utilized to characterize the calculated growth rates. The boxplot whiskers represent the upper/lower quartile values plus/minus 1.5 times the interquartile range. All data points outside the whiskers were considered outliers by the R software. For all cancers (except glioblastoma multiforme (GBM)), the blue transparent boxes represent the 95% confidence interval (CI) of the mean doubling time values reported in the literature (Table I). The 95% CI was not reported for GBM and so the range of reported values (Table I) is shown in the blue transparent box
Fig. 4.
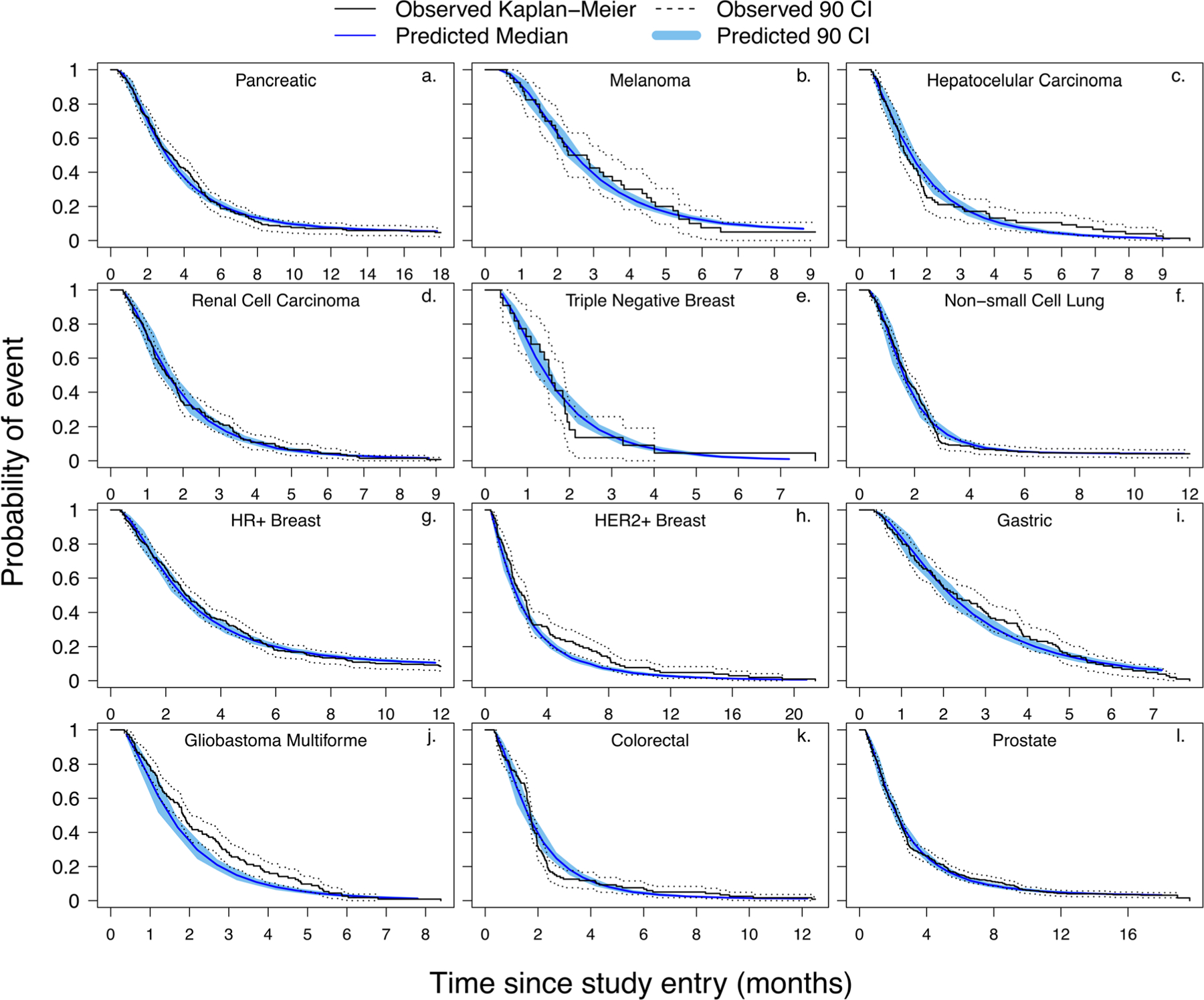
Kaplan-Meier visual predictive check (KM-VPC) plots to evaluate the predictive ability of the fitted growth rate distributions. Panels a to l represent KM-VPCs for pancreatic, melanoma, hepatocellular carcinoma, renal cell carcinoma, triple negative breast, non-small cell lung, hormone receptor positive breast, human epidermal growth factor receptor-2 positive breast, gastric, glioblastoma multiforme, colorectal, and prostate cancers, respectively. All observed plots were obtained from the references listed in Table S1
Doubling Time Evaluation
Using 1000 simulated kg values generated using the “best” fit distribution, cancer doubling times were calculated for each patient using the Eq. 11 in two ways. First, the doubling time was determined from the mean/median kg reported in Table I to get a corresponding mean/median doubling time estimate. Then, the doubling times of each individually simulated growth rate were calculated using Eq. 11 to generate a distribution of 1000 doubling times. The mean of this doubling time distribution is also reported Table I. The summary of calculated doubling times is provided in Table I and Fig. 5. It was found that the model generated doubling times were very close to the reported doubling times, with all cancer types showing some degree of overlap between the simulated and reported doubling times (Fig. 5). However, the simulations predicted a much broader range of doubling times than what was implied by the literature estimates for all cancers, except NSCLC and GBM. The boxplots in Fig. 5 indicate that the predicted variability in tumor doubling time was highest for HCC (varying by 152 months) and lowest for TN breast cancer (varying by 15 months). Note, the reported doubling time of GBM is a range (minimum, maximum) and not a 90% confidence interval, because it is not reported in the literature.
Table I.
Estimated Exponential Growth Rates and Doubling Times for Each Cancer, Along with Their Associated Summary Statistics (Mean and CV%). Distribution Models Used to Statistically Characterize Calculated Growth Rates Are Also Listed
| Cancer | Distribution | Simulated growth rate, kg (month−1) |
Simulated DBT, calculated as ln(2)/kg (months) |
Mean DBT calculated from the distribution of simulated growth rates | CV% | Reported DBT (months)a | ||
|---|---|---|---|---|---|---|---|---|
| Mean | Median | Mean | Median | |||||
| Pancreatic | Log-normal | 0.251 | 0.19 | 2.76 | 3.68 | 5.06 | 88.18 | 5.30 (3.84, 6.76) [42] |
| Melanoma | Log-normal | 0.283 | 0.23 | 2.45 | 3.01 | 3.78 | 71.25 | 4.80 (2.1–8.5)c 2.67 (1.3–13.33)c 1.64 (1.31, 1.96) [112] 6.84 (4.37, 9.31) [76] 1.43 (0.99, 1.86) [87] |
| HCC | Gamma | 0.464 | 0.39 | 1.49 | 1.77 | 3.06 | 70.10, 165.93b | 5.26 (3.78, 6.74) [103] 2.37 (1–4.9)d |
| RCC | Log-normal | 0.452 | 0.35 | 1.53 | 2.00 | 2.67 | 83.16 | 15.6 (13.34, 17.86) [18]e 2.98 (2.17, 3.79) [48]f |
| TN Breast | Log-normal | 0.482 | 0.38 | 1.44 | 1.83 | 2.38 | 78.25 | 3.43 (2.75, 3.43) [42] |
| NSCLC | Log-normal | 0.426 | 0.35 | 1.63 | 1.96 | 2.40 | 66.81 | 1.53 (0.85, 2.21) [96] 22.93 (7.18, 38.69) [192] women 7.80 (0.92, 14.68) [191] men 15.07 (11.88, 18.25) [84] 36.90 (0.13, 11.73) [36] 2.07 (1.60, 2.93) [67] |
| HR+ breast | Log-normal | 0.318 | 0.23 | 2.18 | 3.02 | 4.31 | 95.65 | 8.03 (6.25, 9.82) [69] |
| HER-2+ breast | Log-normal | 0.409 | 0.27 | 1.70 | 2.59 | 4.12 | 115.50 | 5.40 (4.27, 6.53) [37] |
| Gastric | Log-normal | 0.340 | 0.25 | 2.04 | 2.76 | 3.84 | 90.95 | 10.08 (6.48, 13.67) [63] |
| GBM | Log-normal | 0.482 | 0.37 | 1.44 | 1.89 | 2.55 | 85.09 | 1.65g 3.17 (0.05–10.63)h |
| CRC | Log-normal | 0.441 | 0.34 | 1.57 | 2.05 | 2.75 | 83.60 | 13.91 (4.75, 23.08) [82] |
| Prostate | Log-normal | 0.362 | 0.25 | 1.91 | 2.75 | 4.10 | 103.28 | 6.46 (5.28, 7.64) [66]i 12.16 (7.89, 16.43) [65] |
Results show the mean (95% confidence interval of the reported mean doubling time) (reported coefficient of variation (CV%))
CV% of simulated kg values, CV% of the simulated DBT
Median (range)
Median (interquartile range)
Primary tumor
Pulmonary metastasis
Median only
Mean (range)
Estimate based on prostate-specific antigen (PSA) doubling time and not tumor volume doubling time
CRC, colorectal cancer; GBM, glioblastoma multiforme; HCC, hepatocellular carcinoma; HER-2+, human epidermal growth factor receptor-2 positive; HR+, hormone receptor positive; TN, triple negative; NSCLC, non-small cell lung cancer; RCC, renal cell carcinoma
DISCUSSION
Here, we have sought to build a statistical framework that can extract the growth rates and doubling times of tumors from the PFS analysis of a clinical trial. As a result, we have created a repository of clinical doubling times for 12 different cancer types, and a measure of inter-individual variability associated with these doubling times. A similar approach was applied in the clinic by Okazaki et al. (1) for HCC, where the authors utilized doubling times obtained from patients that were therapy non-responsive to infer the cancer’s inherent growth rate. Similarly, Oda et al. (22) have used doubling times from RCC patients, which were clinically unresponsive to interferon therapy, to determine the cancer’s natural growth kinetics. Accordingly, with the help of predefined selection criteria outlined in the “METHODS” section, we have used PFS analyses of the most rapidly progressing clinical cohorts of a cancer to characterize the growth rate of that cancer. Precise selection of these cohorts was of utmost importance to limit the possibility of growth rate underestimation or doubling time overestimation. Once the most suitable cohorts were finalized for each cancer type (Fig. 1), a mathematical approach was employed for directly calculating tumor growth rates of solid tumors from PFS. Being cognizant of the fact that only the patients with PD provided relevant information about tumor growth in the PFS analysis, Eq. 1 was applied to calculate the number of patients that progressed at each time of tumor evaluation. After determining the number of patients with PD at each time point, Eq. 3 was used to calculate their respective tumor growth rates. Rationalizing that patients did not necessarily experience PD at the time of tumor evaluation, but in fact could have progressed at any time since the previous observation time point, a random uniform distribution was used to select a unique time of PD for each patient that fell between the previous and current time of evaluation. Figure S3 demonstrates the robustness of this approach, where instead of being lumped in accordance with time of evaluation (panel b) the growth rates were able to take on unique values for each patient (panel c), which more realistically represented the clinically observed differences in tumor growth rates between the patients. The predictive ability of the growth rates extracted using the uniform distribution approach was evaluated using KM-VPC plots (Fig. 2), which validated that simulations using the extracted growth rates were able to reproduce the clinically observed PFS curves.
We also evaluated the distributional characteristics of growth rates from each cancer type by fitting different statistical distributions. The distributional characteristics provide an ability to define the parent distribution of calculated growth rates using a few estimated parameters (e.g., location, shape, scale), which can ultimately relay crucial information about the tendency and variability of tumor growth kinetics among different patients and the heterogeneity that can occur in growth rates of tumors within a patient. Defining the parent distribution also allows for prediction of the likelihood of encountering certain growth rates or doubling times, which can be crucial for scheduling times for tumor screening and chemotherapeutic intervention (23). This information can also be used to predict the trends for metastatic onset, as it has been shown that growth rates can help estimate times of metastasis (24–27). In addition, the knowledge of doubling time distribution has been used to determine the benefit of surgical intervention in metastatic cancers like melanoma (3), which in turn can have implications on hospital budgeting. Characterizing the distribution of growth rates for each cancer type may also provide valuable insight into the relative heterogeneity in the rates of tumor growth between different cancers (11), which can ultimately help explain why early screening of some cancers (e.g., lung and breast cancer) is still not able to reduce mortality rates in patients (23).
Once the growth rates and their statistical distribution were extracted from published PFS analyses, we were able to demonstrate that the fitted growth rates were representative of the clinically observed patient growth rates (Fig. S1 and Fig. 3). Our analysis showed that for most of the cancers the growth rates were best described by a log-normal distribution, except for HCC, for which the gamma distribution was the best. For external validation of the estimated doubling times, our model predictions were compared with the literature reported values (Table I, Fig. 5). For most of the cancers, there was a close agreement between the simulated and reported doubling time values. However, with the exception of pancreatic cancer, melanoma, NSCLC, and GBM, the simulated median and interquartile range of doubling times were consistently faster than reported values, leading to underestimation of the observed doubling times. This may be due to the larger number of patients included in our simulations versus the small number of patients included in clinical trials. For example, melanoma, NSCLC, and prostate tumor doubling times were reported in multiple literature sources, and this resulted in a much wider, often overlapping, range of reported doubling times that are more reflective of the simulated variability (Fig. 5). Note, for prostate cancer, Gomez-de la Fuente et al. (28) report PSA doubling times and Watanabe (29) reports tumor volume doubling times: both were used to define an event in the reported PFS data used here for prostate cancer (30). The underestimation of doubling times may also occur because the model is informed by PFS curves that more closely reflect the “true” DBT of tumors in the absence of any efficacious treatment. Whereas the literature reported values may have been measured in the presence of efficacious drug, which would result in higher DBT estimates.
The knowledge of clinical tumor growth rates, doubling times, and associated population variability is the key for successful preclinical-to-clinical translation of anticancer drug molecules. One of the main reasons clinical trials in oncology have such a high failure rate (31,32) is because during preclinical-to-clinical translation investigators often use the same dose-response relationships they have derived from the tumor-bearing animal models to make go/no-go decisions. We advocate that clinical translation of the preclinical pharmacokinetics/pharmacodynamics (PK/PD) relationships using mechanism-based mathematical modeling-and-simulation (M&S) approaches, which use clinically relevant parameters like tumor growth rates in patients, can provide much better prediction of human dose-response relationships. In fact, using two clinically approved antibody-drug conjugates, brentuximab-vedotin (Adcetris®) and trastuzumab emtansine (Kadcyla®), we have demonstrated that this kind of PK/PD M&S approach is capable of a priori predicting the clinical efficacy and PFS of anticancer drug molecules in cancer patients (9,33). In addition, our mathematical modeling work revealed that the predictions of clinical efficacy are very sensitive to the rate of tumor growth in the clinic and inter-patient variability associated with this parameter. As such, the estimated clinical growth rates and associated population variability presented in this manuscript (Table I) can serve as a repository for future PK/PD M&S efforts towards preclinical-to-clinical translational of anticancer drugs.
While our approach for obtaining solid tumor growth rates is unprecedented and provides advantage over the older approaches, our method relies on several assumptions. For example, PD is typically characterized by either tumor growth above a predefined threshold or death. However, here, we have assumed that all patients deemed to have an event suffered from progression rather than death. This assumption is based on the fact that there is a strong correlation between death and cancer growth (3), and if a patient died the tumor progression would have been likely. It is also important to note that the method of tumor evaluation used in each study could affect the calculated growth rates. For example, a difference in the growth between primary and metastatic lesions has been observed for many cancers (34–38). However, during tumor evaluation, multiple lesions are usually measured and not just the primary lesion, so the growth rates calculated here may be a hybrid representation of both the primary and secondary neoplasms. Of note, the reported doubling time for RCC used for comparison with the estimated doubling time (Table I) was obtained from patients with the tumor at M0 stage (37). This is because the reported doubling times for primary RCC tumor are obtained predominantly from “slow type” tumors (38), and can be as high as ~ 1.76 years, which could not account for the rate of progression observed in our selected PFS (39).
Tumor growth is a complex process, often involving a combination of linear and exponential phases and is likely best described using a biphasic or Gompertzian models. However, the information extracted from published PFS curves does not provide information about a patient’s prior treatment history or tumor burden to support these complex growth models. As such, to accomplish the goals of this research, the most parsimonious model, an exponential growth, was used. This novel approach provides reasonable estimates of tumor growth rate and doubling times. In the future, patient level radiological imaging data could provide valuable additional information about the patient’s tumor burden and be used to further validate and perhaps further refine the model methodology.
CONCLUSION
We have developed a novel statistical approach for obtaining solid tumor doubling times from PFS plots, without the use of directly measured radiologic data. The presented analysis provides insights into the explicit relationships between tumor doubling time and the likely progression of disease in patients. The list of growth rates, doubling times, and population variabilities for 12 different cancer types presented here is a valuable resource for clinical oncologists interested in optimizing therapeutic intervention and drug development scientists interested in a priori predicting the clinical outcome of novel anticancer therapies.
Supplementary Material
Acknowledgments
FINANCIAL SUPPORT
This work was supported by NIH grant GM114179 and AI138195 to D.K.S., and the Centre for Protein Therapeutics at University at Buffalo.
Footnotes
Electronic supplementary material The online version of this article (https://doi.org/10.1208/s12248–019-0302–5) contains supplementary material, which is available to authorized users.
COMPLIANCE WITH ETHICAL STANDARDS
Conflict of Interest RB has served as an expert witness through Belmore Neidrauer LLP funded by Janssen Pharmaceutical. All other authors declare they have no competing interests.
REFERENCES
- 1.Okazaki N, Yoshino M, Yoshida T, Suzuki M, Moriyama N, Takayasu K, et al. Evaluation of the prognosis for small hepatocellular carcinoma based on tumor volume doubling time. A preliminary report. Cancer 1989;63:2207–10. [DOI] [PubMed] [Google Scholar]
- 2.Arai T, Kuroishi T, Saito Y, Kurita Y, Naruke T, Kaneko M. Tumor doubling time and prognosis in lung cancer patients: evaluation from chest films and clinical follow-up study. Japanese Lung Cancer Screening Research Group. Jpn J Clin Oncol 1994;24:199–204. [PubMed] [Google Scholar]
- 3.Furukawa H, Iwata R, Moriyama N. Growth rate of pancreatic adenocarcinoma: initial clinical experience. Pancreas 2001;22:366–9. [DOI] [PubMed] [Google Scholar]
- 4.Kuroishi T, Tominaga S, Morimoto T, Tashiro H, Itoh S, Watanabe H, et al. Tumor growth rate and prognosis of breast cancer mainly detected by mass screening. Jpn J Cancer Res 1990;81:454–62. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Spratt JS Jr, Spratt TL. Rates of growth of pulmonary metastases and host survival. Ann Surg 1964;159:161–71. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Stensjoen AL, Solheim O, Kvistad KA, Haberg AK, Salvesen O, Berntsen EM. Growth dynamics of untreated glioblastomas in vivo. Neuro-Oncology 2015;17:1402–11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Shackney SE, McCormack GW, Cuchural GJ Jr. Growth rate patterns of solid tumors and their relation to responsiveness to therapy: an analytical review. Ann Intern Med 1978;89:107–21. [DOI] [PubMed] [Google Scholar]
- 8.Ollila DW, Stern SL, Morton DL. Tumor doubling time: a selection factor for pulmonary resection of metastatic melanoma. J Surg Oncol 1998;69:206–11. [DOI] [PubMed] [Google Scholar]
- 9.Singh AP, Shah DK. Application of a PK-PD modeling and simulation-based strategy for clinical translation of antibody-drug conjugates: a case study with Trastuzumab Emtansine (T-DM1). AAPS J 2017;19:1054–70. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Schwartz M A biomathematical approach to clinical tumor growth. Cancer 1961;14:1272–94. [DOI] [PubMed] [Google Scholar]
- 11.Mehrara E, Forssell-Aronsson E, Ahlman H, Bernhardt P. Specific growth rate versus doubling time for quantitative characterization of tumor growth rate. Cancer Res 2007;67:3970–5. [DOI] [PubMed] [Google Scholar]
- 12.Gutman SI, Piper M, Grant MD, Basch E, Oliansky DM, Aronson N. Progression-free survival: what does it mean for psychological well-being or quality of life? Rockville, MD: Agency for Healthcare Research and Quality; 2013. http://www.effectivehealthcare.ahrq.gov/reports/final.cfm. [PubMed] [Google Scholar]
- 13.Magazines T, Savers S. Guidance for industry: clinical trial endpoints for the approval of cancer drugs and biologics. Biotechnol Law Rep 2007;26:375–86. [Google Scholar]
- 14.World Health Organization. WHO handbook for reporting results of cancer treatment Geneva: World Health Organization; 1979. http://www.who.int/iris/handle/10665/37200 [Google Scholar]
- 15.Therasse P, Arbuck SG, Eisenhauer EA, Wanders J, Kaplan RS, Rubinstein L, et al. New guidelines to evaluate the response to treatment in solid tumors. J Natl Cancer Inst 2000;92:205–16. [DOI] [PubMed] [Google Scholar]
- 16.R Core Team. R: a language and environment for statistical computing Vienna: R Foundation for Statistical Computing; 2016. https://www.R-project.org/ [Google Scholar]
- 17.Yung WK, Albright RE, Olson J, Fredericks R, Fink K, Prados MD, et al. A phase II study of temozolomide vs. procarbazine in patients with glioblastoma multiforme at first relapse. Br J Cancer 2000;83:588–93. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Ohtsu A, Shimada Y, Shirao K, Boku N, Hyodo I, Saito H, et al. Randomized phase III trial of fluorouracil alone versus fluorouracil plus cisplatin versus uracil and tegafur plus mitomycin in patients with unresectable, advanced gastric cancer: the Japan Clinical Oncology Group Study (JCOG9205). J Clin Oncol 2003;21:54–9. [DOI] [PubMed] [Google Scholar]
- 19.Dutang MLD-MC. Fitdistrplus: an R package for fitting distributions. J Stat Softw 2015;64:1–34. [Google Scholar]
- 20.Therneau TM. A package for survival analysis in S. version 2.38 2015. https://CRAN.Rproject.org/package=survival
- 21.Kim KB, Kefford R, Pavlick AC, Infante JR, Ribas A, Sosman JA, et al. Phase II study of the MEK1/MEK2 inhibitor Trametinib in patients with metastatic BRAF-mutant cutaneous melanoma previously treated with or without a BRAF inhibitor. J Clin Oncol 2013;31:482–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Oda T, Miyao N, Takahashi A, Yanase M, Masumori N, Itoh N, et al. Growth rates of primary and metastatic lesions of renal cell carcinoma. Int J Urol 2001;8:473–7. [DOI] [PubMed] [Google Scholar]
- 23.Friberg S, Mattson S. On the growth rates of human malignant tumors: implications for medical decision making. J Surg Oncol 1997;65:284–97. [DOI] [PubMed] [Google Scholar]
- 24.Eskelin S, Pyrhonen S, Summanen P, Hahka-Kemppinen M, Kivela T. Tumor doubling times in metastatic malignant melanoma of the uvea: tumor progression before and after treatment. Ophthalmology 2000;107:1443–9. [DOI] [PubMed] [Google Scholar]
- 25.Malaise EP, Chavaudra N, Charbit A, Tubiana M. Relationship between the growth rate of human metastases, survival and pathological type. Eur J Cancer 1974;10:451–9. [DOI] [PubMed] [Google Scholar]
- 26.Garland LH, Coulson W, Wollin E. The rate of growth and apparent duration of untreated primary bronchial carcinoma. Cancer 1963;16:694–707. [DOI] [PubMed] [Google Scholar]
- 27.Breur K Growth rate and radiosensitivity of human tumours. I Growth rate of human tumours. Eur J Cancer 1966;2:157–71. [DOI] [PubMed] [Google Scholar]
- 28.Gomez-de la Fuente FJ, Martinez-Rodriguez I, de Arcocha-Torres M, Quirce R, Jimenez-Bonilla J, Martinez-Amador N, et al. Contribution of (11)C-Choline PET/CT in prostate carcinoma biochemical relapse with serum PSA level below 1 ng/ml. Rev Esp Med Nucl Imagen Mol 2018;37:156–62. [DOI] [PubMed] [Google Scholar]
- 29.Watanabe H Relapse of prostate cancer from the viewpoint of total gland volume kinetics theory. Asian J Androl 2015;17:904–7discussion 7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.de Bono JS, Oudard S, Ozguroglu M, Hansen S, Machiels J-P, Kocak I, et al. Prednisone plus cabazitaxel or mitoxantrone for metastatic castration-resistant prostate cancer progressing after docetaxel treatment: a randomised open-label trial. Lancet 2010;376:1147–54. [DOI] [PubMed] [Google Scholar]
- 31.Hutchinson L, Kirk R. High drug attrition rates–where are we going wrong? Nat Rev Clin Oncol 2011;8:189–90. [DOI] [PubMed] [Google Scholar]
- 32.Begley CG, Ellis LM. Drug development: raise standards for preclinical cancer research. Nature 2012;483:531–3. [DOI] [PubMed] [Google Scholar]
- 33.Shah DK, Haddish-Berhane N, Betts A. Bench to bedside translation of antibody drug conjugates using a multiscale mechanistic PK/PD model: a case study with brentuximabvedotin. J Pharmacokinet Pharmacodyn 2012;39:643–59. [DOI] [PubMed] [Google Scholar]
- 34.Havelaar IJ, Sugarbaker PH, Vermess M, Miller DL. Rate of growth of intraabdominal metastases from colorectal cancer. Cancer 1984;54:163–71. [DOI] [PubMed] [Google Scholar]
- 35.Plesnicar S, Klanjscek G, Modic S. Actual doubling time values of pulmonary metastases from malignant melanoma. Aust N Z J Surg 1978;48:23–5. [DOI] [PubMed] [Google Scholar]
- 36.Carlson JA. Tumor doubling time of cutaneous melanoma and its metastasis. Am J Dermatopathol 2003;25:291–9. [DOI] [PubMed] [Google Scholar]
- 37.Fujimoto N, Sugita A, Terasawa Y, Kato M. Observations on the growth rate of renal cell carcinoma. Int J Urol 1995;2:71–6. [DOI] [PubMed] [Google Scholar]
- 38.Ozono S, Miyao N, Igarashi T, Marumo K, Nakazawa H, Fukuda M, et al. Tumor doubling time of renal cell carcinoma measured by CT: collaboration of Japanese Society of Renal Cancer. Jpn J Clin Oncol 2004;34:82–5. [DOI] [PubMed] [Google Scholar]
- 39.Motzer RJ, Escudier B, Oudard S, Hutson TE, Porta C, Bracarda S, et al. Efficacy of everolimus in advanced renal cell carcinoma: a double-blind, randomised, placebo-controlled phase III trial. Lancet 2008;372:449–56. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


