Genomic partitioning of inbreeding depression in humans

Summary

Across species, offspring of related individuals often exhibit significant reduction in fitness-related traits, known as inbreeding depression (ID), yet the genetic and molecular basis for ID remains elusive. Here, we develop a method to quantify enrichment of ID within specific genomic annotations and apply it to human data. We analyzed the phenomes and genomes of ∼350,000 unrelated participants of the UK Biobank and found, on average of over 11 traits, significant enrichment of ID within genomic regions with high recombination rates (>21-fold; p < 10⁻⁵), with conserved function across species (>19-fold; p < 10⁻⁴), and within regulatory elements such as DNase I hypersensitive sites (∼5-fold; p = 8.9 × 10⁻⁷). We also quantified enrichment of ID within trait-associated regions and found suggestive evidence that genomic regions contributing to additive genetic variance in the population are enriched for ID signal. We find strong correlations between functional enrichment of SNP-based heritability and that of ID (r = 0.8, standard error: 0.1). These findings provide empirical evidence that ID is most likely due to many partially recessive deleterious alleles in low linkage disequilibrium regions of the genome. Our study suggests that functional characterization of ID may further elucidate the genetic architectures and biological mechanisms underlying complex traits and diseases.

Introduction

Mating between genetically related individuals, i.e., inbreeding, has detrimental phenotypic consequences in resulting offspring.1, 2, 3, 4, 5, 6, 7, 8 This phenomenon, known as inbreeding depression (ID), has been reported for multiple human traits, such as stature, intelligence, lung function, and fertility.5, 6, 7^,9 Inbreeding results in increased homozygosity across the genome and ID can be explained by the increased homozygosity of (partially) recessive deleterious alleles, thereby exposing their detrimental effects on fitness and fitness-related traits. Detecting ID and quantifying its strength in human populations is particularly challenging because inbreeding is less common and less extreme and the effective population is larger in humans than in some other animal species.^10,11 As a consequence, sample sizes of 100,000s or more participants are required to obtain reliable estimates of ID.¹² Over recent years, the advent of large scale biobanks such as the UK Biobank (UKB) has allowed detection and quantification of ID in a wide variety of traits, including hip-to-waist ratio, heart rate, facial aging, or hemoglobin levels, which previously were not known to be associated with inbreeding.⁷

Despite a growing catalog of traits associated with inbreeding, the genetic basis of ID in humans remains elusive. Notably, genes, biological pathways, or functions involved in ID are still largely unknown. Previous studies have attempted to identify genes involved in ID by testing the association between runs of homozygosity (ROHs)¹³ and traits or diseases.¹⁴ Although the latter studies have not robustly identified such genes in humans,^15,16 the approach has been more powerful in other animal species with smaller effective population sizes, such as cattle.^17,18 In addition, studies in Drosophila19, 20, 21 have tested the association between inbreeding coefficients (F) and gene expression and have thereby identified genes implicated or affected by inbreeding. Overall, contrasting findings from human and non-human studies highlight the limited statistical power to dissect ID in humans and thus calls for larger sample sizes and new analytical methods to overcome this challenge.

Here, we develop a method to detect and quantify ID at a finer scale by breaking its effects down to genomic regions with specific annotations. An enrichment of ID within a given genomic region means that homozygosity in that region (or regions sharing the same annotation) has a disproportional effect on the mean value of a trait as compared to the effect of homozygosity at any equally sized, randomly selected genomic region. We chose genomic annotations as a higher-level unit (as opposed to lower-level units, such as genes, for example) in order to measure the functional impact on traits of homozygosity at particular types of variants. Using this method, we analyzed genetic and phenotypic data from a large sample of ∼350,000 unrelated participants of the UKB. Our method utilizes (but is not restricted to) functional annotations introduced in Finucane et al.,²² Gazal et al.,²³ and Hujoel et al.,²⁴ covering diverse properties of the human genome. We specifically quantify the degree to which variants located within these functional genomic regions contribute to ID across 11 traits. These 11 traits were selected on the basis of prior evidence of ID¹¹ and are height, hip-to-waist ratio, handgrip strength (average of left and right hand), lung function measured as the peak expiratory flow, visual acuity, auditory acuity, number of years of education, fluid intelligence score, cognitive function measured as the mean time to correctly identify matches, fertility measured as the number of offspring, and overall health measured as the number of diseases diagnosed in an individual. We use our method to quantify the enrichment of ID within trait-associated genomic regions identified through genome-wide association studies (GWASs) and finally compare functional enrichments of heritability with that of ID.

Material and methods

Quantification of the enrichment of ID via individual-level data

Model definition

Let $y$ denote a quantitative trait subject to ID. We assume an infinitesimal model where all SNPs contribute to ID. We can therefore write $y$ as

$$y=\sum _{j=1}^M{\beta }_j{F}_j+e,$$ (Equation 1)

where $F_j$ denotes an estimator of the inbreeding coefficient based on genotypes at SNP $j$ ($j=1,\dots ,M$), ${\beta }_j$ the contribution of SNP $j$ to ID, and $e$ a residual term capturing all other effects, including additive genetic and environmental effects.

Estimation of ID from inbreeding measures based on genome-wide average homozygosity (as opposed to runs of homozygosity [ROHs]) relies on the assumption that ${\beta }_j$ is random and has a constant expectation $E\left[{\beta }_j\right]=b/M$, where $b$ denotes the genome-wide ID. Other inbreeding measures, such as the excess of homozygosity measure, rely on the assumption that $E\left[{\beta }_j\right]$ is proportional to mean heterozygosity $h_j=2p_j\left(1-p_j\right)$, where $p_j$ is the minor allele frequency (MAF) at SNP $j$ in the population. We previously introduced a flexible MAF and linkage disequilibrium (LD)-stratified method to estimate ID, which we showed to yield unbiased estimation of ID even when the relationship between $E\left[{\beta }_j\right]$ and $h_j$ is misspecified.⁹ Here, we further extend this approach by allowing SNPs within different genomic annotations to have a specific contribution to ID. We propose the following model:

$$E\left[{\beta }_j\right]=\frac{b_0}{M}+\sum _{k=1}^K\left(z_{jk}\left[\frac{b_k}{m_k}\right]+(1-z_{jk})\left[\frac{b-b_k}{M-m_k}\right]\right),$$ (Equation 2)

where $b$ denotes the genome-wide ID parameter, $b_0=-\left(K-1\right)b$, $z_{jk}$. the indicator of membership of SNP $j$ to annotation $k$ ($k=1\dots K$), $b_k$ the contribution of annotation $k$ to ID, and $m_k$. ($1\le m_k\le M$)he number of SNPs in annotation $k$. We hereafter denote ${\pi }_k=m_k/M$ as the proportion of SNPs in annotation $k$. Under the null hypothesis that each SNP contributes equally to ID, each genomic annotation is expected to contribute proportionally to the number of SNPs it contains. Therefore, we can define the enrichment of ID in annotation $k$, hereter denoted ${\delta }_k$, as the ratio between the contribution of annotation $k$ to ID that is $b_k$ over the expected contribution of annotation $k$ to ID that is ${\pi }_{k}b$, i.e., ${\delta }_k=b_k/\left({\pi }_{k}b\right)$.

Combining Equation 1 and Equation 2 leads to (Appendix A)

$$y=b{F}_g+\sum _{k=1}^K\left(\frac{b_k}{{\pi }_k}-b\right)\left[\left(\frac{{\pi }_k}{1-{\pi }_k}\right)\left({\overline{F}}_k-F_g\right)\right]+e,$$ (Equation 3)

where ${\overline{F}}_k$ denotes the average inbreeding coefficient across SNPs in annotation $k$, $F_g$ denotes the average inbreeding coefficient across all $M$ SNPs, and $e$ the residual term from Equation 1.

Estimation of model parameters

Equation 3 implies that ${\tau }_k=b_k/{\pi }_k-b$can be directly estimated by performing a multivariate regression of $y$ onto $F_g$ and the $(\Delta F_k={\pi }_k\left({\overline{F}}_k-F_g\right)/\left(1-{\pi }_k\right))$ terms. Therefore, enrichment of ID in annotation $k$ can be detected with standard regression p values quantifying the statistical significance of ${\tau }_k$. We use the latter approach in all analyses.

It is important to note, as with methods for partitioning heritability,²² that certain combinations of annotations cannot be fitted jointly with Equation 3. Indeed, in some cases, overlap between annotations can induce a strong collinearity between inbreeding measures, which can make estimates unstable. For example, when the annotation is defined by chromosome number, fitting $F_g$ as well as all chromosome-specific inbreeding measures will lead to identifiability issues. In the latter case, a simple solution is to choose one class of the annotation as a reference (e.g., chromosome 1) and therefore remove it from the model.

One of the challenges of our model is to provide estimates that can be interpreted in terms of enrichment (or depletion) of ID. However, enrichment is often intuitively conceptualized on a multiplicative scale, whereas the inference in our model is done on an additive scale (linear regression). Parameters ${\tau }_k$ and ${\delta }_k=1+{\tau }_k/b$ measure the same information, but ${\tau }_k$ is on an additive scale and is directly estimated, while ${\delta }_k$ is on a multiplicative scale (the scaled used for interpretation) and derived from estimated parameters. Previous studies aiming at partitioning additive genetic variance (e.g., Finucane et al.²²) faced similar challenges and addressed them in the same way by using two scales for their model parameters. However, the parameterization chosen in our study leads to a much simpler relationship between ${\tau }_k$ and ${\delta }_k$, thereby allowing for the use of the p value of ${\delta }_k$, which is readily available from fitting the model to test the significance of ${\delta }_k$ for ${\tau }_k$.

Average ID enrichment across traits

The significance of the average ID enrichment across traits (i.e., ${\overline{\delta }}_k$) is determined by that of the average estimate of ${\tau }_k$’s across traits, hereafter denoted ${\overline{\tau }}_k$. Given that ${\overline{\tau }}_k$ is a linear combination of ordinary-least-squares (OLS) estimators, its asymptotic distribution is also Gaussian and its sampling variance defined as

$$\text{var}\left({\overline{\tau }}_k\right)=\frac{1}{T^2}\sum _{t=1}^T\sum _{t^{\text{′}}=1}^T{\rho }_{t,t^{\text{′}}}{\left[\text{var}\left({\tau }_{k,t}\right)\text{var}\left({\tau }_{k,t^{\text{′}}}\right)\right]}^{1/2},$$ (Equation 4)

where $\text{var}\left({\tau }_{k,t}\right)$ is the sampling variance of the OLS estimator of ${\tau }_k$ for trait $t$ and ${\rho }_{t,t^{\prime }}$ the correlation between OLS estimators of ${\tau }_{k,t}$ and ${\tau }_{k,t^{\prime }}$. In practice, we propose to approximate ${\rho }_{t,t^{\prime }}$ with the sample correlation between traits, which is a valid approximation given that OLS estimators are linear transformations of the phenotypes. Therefore, we test the significance of ${\overline{\tau }}_k$ by using the following test statistic, ${\overline{\tau }}_k^2/\text{var}\left({\overline{\tau }}_k\right)$, which follows a chi-square distribution with 1 degree of freedom under the null. Finally, we consistently define the average ID enrichment across traits as ${\overline{\delta }}_k=1+{\overline{\tau }}_k/\overline{b}$, where $\overline{b}$ is the average ID across traits.

ID enrichment within continuous annotations

We analyzed continuous genomic annotations defined by non-negative values (e.g., recombination rate or posterior causal probability). We scaled these annotations by the largest value observed across the genome such that each SNP is assigned a value ${\tilde{z}}_{jk}$ between 0 and 1. We then defined ${\tilde{\pi }}_k$ as the mean of the ${\tilde{z}}_{jk}$’s across the genome (which is equivalent to the proportion of annotated SNPs when genomic annotations are binary variables) and used that value as our reference to calculate enrichments of ID for continuous annotations. Note that the use of another statistic from the distribution of ${\tilde{z}}_{jk}$’s (e.g., the median) would not change statistical significance but will influence the magnitude of the estimated ID enrichment.

When reporting results for continuous annotations, we used terms such as “high” or “low” (e.g., “high recombination rates” or “low nucleotide diversity”) only to indicate the direction of the effect but not to imply that the annotation was discretized in any way.

Depletion of ID enrichment

In some cases, we observed that estimates of ${\tau }_k$ can lead to negative values of the enrichment statistic ${\delta }_k$, which are difficult to interpret. We refer to this situation as “depletion of ID signal” and report instead the estimate ${\breve{\delta }}_k=1-{\pi }_k({\delta }_k-1)/(1-{\pi }_k)$ corresponding to a transformed annotation defined by (1-$z_{jk}$) or (1-${\tilde{z}}_{jk}$).

Inbreeding measures

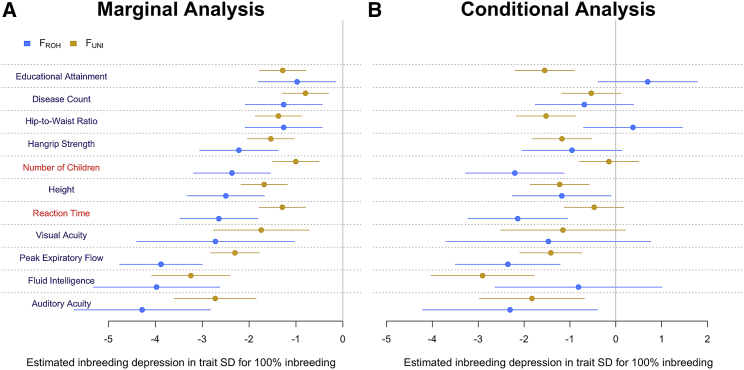
To maximize power to detect ID enrichment across a wide range of causal allele frequencies, we use two inbreeding measures in our analyses. The first is the correlation between uniting gametes^1,2 ($F_{\text{UNI}}$) and the second is the proportion, $F_{\text{ROH}}$, of SNPs contained in >1.5 Mb-long runs. Note that our definition of $F_{\text{ROH}}$ is slightly different from the widely used definition of $F_{\text{ROH}}$, which is the proportion of an individual genome that is covered by their ROHs. We chose this alternative definition because it offers more flexibility for partitioning analyses while still retaining the same amount of information (correlation > 0.99; Figure S1). $F_{\text{UNI}}$ was previously shown to be more powerful to detect ID caused by well-tagged causal variants (e.g., SNPs with a minor allele frequency [MAF] > 1%),^9,25 while $F_{\text{ROH}}$ can perform better when alleles causing ID are rarer and therefore poorly imputed via current imputation reference panels and methods.^12,26 We re-assessed the relative fraction of ID captured with either inbreeding measure and show that common and rare alleles both contribute to ID and that their relative contribution is trait specific (Figure 1).

Figure 1.

Partitioning of inbreeding depression (ID) between $F_{\text{ROH}}$ and $F_{\text{UNI}}$

Left shows marginal analyses where ID is estimated with either $F_{\text{ROH}}$ and $F_{\text{UNI}}$. Right shows estimates of ID obtained from fitting $F_{\text{ROH}}$ and $F_{\text{UNI}}$ jointly. Error bars represents 95% confidence intervals. Highlighted in red font: two traits (number of children and reaction time) for which ID is mostly captured by $F_{\text{ROH}}$. SD, standard deviation.

For ROH-based analyses, the null hypothesis is defined such that each SNP has an equal probability of being covered by identical-by-descent genomic segments, which we approximate in this study by using long ROHs. We show in the supplemental methods section that violation of this assumption because of non-uniform genomic distribution of ROHs has little impact on our results.

We used PLINK 1.9 with the –ibc command to estimate $F_{\text{UNI}}$ for each UKB participant. For continuous annotations, we used a custom C++ program (see data and code availability and web resources) that calculates weighted sums of per-SNP estimates of $F_{\text{UNI}}$ with weights proportional to the value of the annotation. For binary annotations, we calculated $F_{\text{UNI}}$ by only using SNPs assigned to those annotations. ROHs were called with the following PLINK command: –maf 0.05–homozyg–homozyg-density 50–homozyg-gap 1000–homozyg-kb 1500–homozyg-snp 50–homozyg-window-het 1–homozyg-window-missing 5–homozyg-window-snp 50. We then used 19,476,620 imputed SNPs with MAF > 0.1%, which were annotated to 187 functional categories (web resources) and defined $F_{\text{ROH}}$ as the proportion of these SNPs contained in a ROH. Similarly, annotation-specific inbreeding measures were calculated as the (weighted) proportion of SNPs assigned to a given annotation that is contained in a ROH.

SNP genotyping

We used allele counts at 44,741,804 SNPs genotyped and imputed in 487,409 participants of the UK Biobank^27,28 (UKB). Although an extensive description of our dataset was given previously,²⁹ we briefly summarize the main steps of data preparation. We identified 456,414 UKB participants of European ancestry by using projected principal components based on sequenced participants of the 1000 Genomes Projects with known ancestry.²⁹ We then restricted our analyses to a subset of these participants that contains 348,501 conventionally unrelated participants, i.e., whose estimated pairwise SNP-based genomic relationships are <0.05. Genomic relationships were estimated with 1,124,803 common (MAF ≥ 1%) HapMap3³⁰ SNPs via GCTA (v.1.9).³¹ Imputed SNPs included in our $F_{\text{UNI}}$-based analyses were selected on the basis of the following criteria: MAF > 1%, p value from the Hardy-Weinberg equilibrium test > 10⁻⁶, and imputation quality $r_{\text{INFO}}^2$ statistic > 0.3. After quality control, 9,326,198 imputed SNPs were included in our analyses. Genotyped SNPs used to call ROH were selected, as previously described,¹¹ via the following criteria: missingness rate < 1%, MAF > 5%, and Hardy-Weinberg equilibrium test p value > 0.0001. Quality control was performed with PLINK 1.9³² (v.1.90b6.13 64 bit from November 30, 2019).

Association between levels of inbreeding and phenotypes measured in the UKB

We tested the association between $F_{\text{UNI}}$ or $F_{\text{ROH}}$ and traits by using linear regression adjusted for age at recruitment (UKB field 21022-0.0), sex, assessment center (UKB field 54-0.0), genotyping chip and batch, year of birth (UKB field 34-0.0), year of birth square, and the top ten genetic principal components calculated via PLINK 2.0. For each trait, we excluded phenotypic values larger than 4 standard deviations and then pre-adjusted trait values for the covariates listed above. Residuals obtained from these pre-adjustment analyses were then inverse normally transformed and used as focal traits. UKB identifiers for our 11 focal traits are height (UKB field 50-0.0), hip-to-waist ratio (ratio of UKB field 49-0.0 over UKB field 48-0.0), handgrip strength (average of UKB fields 46-0.0 and 47-0.0), lung function measured as the peak expiratory flow (UKB field 3064-0.0), visual acuity measured on log MAR scale (average between UKB field 5201-0.0 and UKB field 5208-0.0), auditory acuity measured as the speech reception threshold (average between UKB field 20019-0.0 and UKB field 20021-0.0), number of years of education (EA), fluid intelligence score (UKB field 20016-0.0), cognitive function measured as the mean time to correctly identify picture card matches (UKB field 20023-0.0), fertility measured as the number of children (for males UKB field 2405-0.0 and for females UKB field 2734-0.0), and number of diseases diagnosed estimated as the number International Classification of Diseases, Tenth Revision (ICD10) codes reported for UKB participants (release prior to December 2020). The North West Multi-Centre Research Ethics Committee (MREC) approved the study, and all participants in the UKB study analyzed here provided written informed consent.

Genomic annotations used in individual-level analyses

We used genomic annotations previously compiled and processed by Finucane et al.,²² Gazal et al.,²³ and Hujoel et al.²⁴ The 44 genomic annotations analyzed in our study were derived from 187 annotations downloaded from the LD score regression repository (baselineLF_v2.2.UKB model; web resources).

Binary annotations include putative evolutionary old enhancers and promoters (referred to in Hujoel et al.²⁴ as ancient sequence age: × 2 annotations); flanking bivalent transcription start sites or enhancers from the Roadmap Epigenomics Project;³³ coding; intronic; promoter; 3′ UTR and 5′ UTR genomic regions from the UCSC Genome Browser³⁴ (post-processed by Gusev et al.³⁵); synonymous and non-synonymous; conserved genomic regions across mammals, primates, and vertebrates (phastCons 46-way²⁴); CTCF (annotation from Hoffman et al.³⁶); digital genomic footprint (DGF data from ENCODE³⁷ and post-processed by Gusev et al.³⁵); DNase-I hypersensitive sites (ENCODE and Roadmap Epigenomics data post-processed by Trynka et al.³⁸ and also merged with fetal DHS annotation); enhancers (merged × 2 annotations: from Andersson et al.³⁹ and Hoffman et al.³⁶); histone marks (merged H3K27ac annotations from Hnisz et al.⁴⁰ and Kundaje et al.³³ post-processed by PGC2,⁴¹ H3K4me1,³⁸ H3K4me3,³⁸ and H3K9ac³⁸); enhancers and promoters from Villar et al.;⁴² promoters of loss-of-function-intolerant genes from ExAC (annotation from Hujoel et al.²⁴); promoter flanking;³⁶ repressed genomic regions;³⁶ super enhancers;⁴⁰ transcription factor binding sites;³⁷ transcribed genomic regions;³⁶ transcription start sites;³⁶ weak enhancers;³⁶ and >4 rejected substitution from GERP++ score.⁴³

Continuous annotations include maximum posterior probability from fine-mapping of molecular QTL⁴⁴ (expression, methylation, H3K4me1, and H3K27ac), background selection statistic (McVicker B statistic),⁴⁵ predicted allele age,⁴⁶ time to most recent common ancestor,⁴⁷ nucleotide diversity within 10 kb, recombination rate (within 10 kb) based on the Oxford recombination map,⁴⁸ CpG content within 50 kb, GERP++ score (number of substitution; referred to as GERP NS), and number of species sharing a given putative enhancer.²⁴ We also analyzed LD score with 1 Mb chi-square association test-statistic with a given trait or level of heterozygosity (i.e., MAF × (1 − MAF)) as continuous annotations.

Enrichment of heritability and ID from GWAS summary statistics

Enrichment of ID in trait-associated genomic regions

We first performed a standard GWAS of each of the 11 traits included in our analyses. We tested association between SNPs and traits by using an additive model (hereafter referred to as additive GWAS) where allele counts are directly correlated with traits. We then used resulting chi-square association test statistics as a continuous annotation and estimated its corresponding ID enrichment by using the method described above.

Estimation of heritability and ID enrichment via stratified LD score regression

We quantified the enrichment of SNP-based heritability in the 44 genomic annotations described above by using stratified LD score regression²² (SLDSC). In brief, the SLDSC method, as implemented in this study, was based upon the following regression model:

$$E\left[{\chi }_j^2\right]=1+N{a}_{h^2}+N\sum _{k=1}^K{\theta }_{k,h^2}\left(\frac{{\ell }_{jk}}{M_k}\right),$$ (Equation 5)

where $a_{h^2}$ measures the level of confounding (e.g., due to uncorrected population stratification) in the GWAS, ${\chi }_j^2$ the chi-square association statistic of SNP $j$, $N$ the GWAS sample size, ${\theta }_{k,h^2}$ the effect size of annotation $k$ on trait heritability ($h^2$), ${\ell }_{jk}$ (the annotation-weighted LD score), and $M_k$ defined as

$${\ell }_{jk}=\sum _{i=1}^M{z}_{ik}{r}_{ij}^{2}and{M}_k=\sum _{l=1}^M{z}_{ik},$$ (Equation 6)

where $r_{ij}^2$ is the squared correlation of allele counts between SNP $i$ and SNP $j$.

We used publicly available annotation-weighted LD scores of 1,190,321 sequenced HapMap 3 SNPs from Finucane et al.,²² Gazal et al.,²³ and Hujoel et al.²⁴ (web resources), which were calculated against a larger set of 9,997,231 sequenced SNPs with MAF > 0.5% in a European ancestry sample from the 1000 Genomes Project. LD scores of duplicated annotations were averaged. We analyzed each annotation independently and included the standard LD score (${\ell }_{j0}=\sum _{i=1}^M{r}_{ij}^2$) and ten MAF-class-specific LD scores (i.e., LD score with SNPs within a given MAF class only) as covariates.²³ Parameters were estimated via weighted least-squares with weights proportional to $1/{\ell }_{j0}$.

Next, we re-tested the association between SNPs and traits by using a model fitting both allele counts and the indicator of heterozygosity, which estimates dominance deviation at each SNP. We refer to the latter analysis as additive-dominance GWAS. We show in Appendix B that the LD score regression methodology can be extended to estimate ID from summary statistics of an additive-dominance GWAS and further extend it below to quantify enrichment of ID in genomic annotations by using the following regression model:

$$E[-Z_{d,j}]=a_b+\sqrt{N}\sum _{k=1}^K{\theta }_{k,b}\left(\frac{{\ell }_{jk}}{M_k}\right),$$ (Equation 7)

where $Z_{d,j}$ is the Z scores of estimates of dominance deviation at SNP $j$, $a_b$ the intercept term measuring confounding effects, and ${\theta }_{k,b}$ the effect size of annotation $k$ on ID. Standard errors for ${\theta }_{k,h^2}$, ${\theta }_{k,b}$ as well as their correlation across multiple annotations were estimated with a block-jackknife (leave one block out) procedure based on 240 ∼10 Mb-long genomic segments used as blocks.

Results

The relative contribution of rare variants to ID varies across human traits

Clark et al.¹⁶ previously claimed that ID is predominantly caused by rare, recessive variants made homozygous in long ROH and not by homozygosity at variants that are in LD with common SNPs. To reach that conclusion, their study compared the magnitude of conditional estimates of ID from a bivariate linear regression model fitting $F_{\text{UNI}}$ (referred to as $F_{\text{GRM}}$ in their study) and $F_{\text{ROH}}$ jointly. Clark et al. restricted their calculation of $F_{\text{UNI}}$ to SNPs with an MAF > 5% across diverse studies in which participants were genotyped with different arrays. We show that the same analysis performed in a homogeneous and large sample like the UKB leads to a different and trait-specific conclusion regarding the contribution of rare variants to ID. As described in Clark et al., we calculated both $F_{\text{UNI}}$ and $F_{\text{ROH}}$ by using 301,412 quality-controlled genotyped SNPs (as described in Yengo et al.¹¹) with MAF > 5% and also used the same definition of ROH. For this analysis, $F_{\text{ROH}}$ was defined as in Clark et al., i.e., the cumulated length of ROH in Mb divided by 3,000.

We found that the relative fraction of ID captured by each inbreeding measure varies between traits (Figure 1). For example, the estimated effects of $F_{\text{UNI}}$ on the number of children and on the mean time to identify matches (reaction time) both became not statistically significant (p < 0.05) once conditioned on $F_{\text{ROH}}$. This observation is consistent with Clark et al.’s claims and suggests a larger relative contribution of rare variants to ID in these traits. However, we find that ID in hip-to-waist ratio as well as on fluid intelligence is mostly captured by $F_{\text{UNI}}$. Finally, for height and peak expiratory flow, the conditional effects $F_{\text{ROH}}$ and $F_{\text{UNI}}$ are of similar magnitudes, suggesting that both low frequency variants and more common partially recessive alleles are causal of ID in these traits. On average across traits, we found that the conditional effects of $F_{\text{UNI}}$ and $F_{\text{ROH}}$ were not statistically different from each another. Altogether, our results imply that alleles causing ID span a larger spectrum of the frequencies (from rare to common, e.g., >5%) and that the relative contribution of rare variants is trait specific.

Enrichment of ID within functional genomic annotations

We analyzed 44 genomic annotations (including 12 continuous annotations; material and methods), which cover ∼98% of the autosome (Figure S2). In total, our analysis involves 11 traits, 44 annotations, and 2 inbreeding measures (i.e., 11 × 44 × 2 = 968 trait-annotation-measure triplets). Therefore, statistical significance accounting for multiple testing (Bonferroni correction) was set to 0.05/968 ≈ 5.2 × 10⁻⁵. We also quantified the average ID enrichment across traits, in which case statistical significance was set to 0.05/(44 × 2) ≈ 5.7 × 10⁻⁴. Note that Bonferroni correction is most likely too conservative because the overlap between genomic annotations (Figure S3) induces a positive correlation across statistical tests. Therefore, we also report enrichments detected at a false discovery rate (FDR) threshold of 5%.

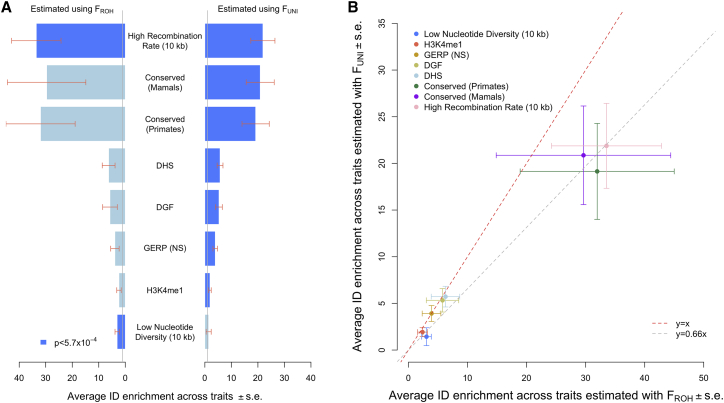
On average across traits, we detected significant enrichment of ID within 8 annotations (Figure 2; Table S1). Importantly, the largest enrichment was detected with both inbreeding measures within genomic regions with high recombination rates (${\overline{\delta }}_{F_{\text{ROH}}}$∼33.5, p = 3.2 × 10⁻⁴; and ${\overline{\delta }}_{F_{\text{UNI}}}$∼21.9, p = 1.5 × 10⁻⁶). Other significant enrichments were detected within conserved genomic regions across mammals (${\overline{\delta }}_{F_{\text{UNI}}}$∼20.9, p = 7.8 × 10⁻⁵) and primates (${\overline{\delta }}_{F_{\text{UNI}}}$∼19.1, p = 1.9 × 10⁻⁴); DNase I hypersensitive regions (DHS: ${\overline{\delta }}_{F_{\text{UNI}}}$∼5.7, p = 2.3 × 10⁻⁷); chromatin accessible regions identified through digital genomic foot printing (DGF: ${\overline{\delta }}_{F_{\text{UNI}}}$∼5.3, p = 2.1 × 10⁻⁵); regions with large GERP++ score,⁴³ which measures the strength of purifying selection at a locus (${\overline{\delta }}_{F_{\text{UNI}}}$∼3.9, p = 4.5 × 10⁻⁶); genomic regions with low nucleotide diversity (${\overline{\delta }}_{F_{\text{ROH}}}$∼3.0, p = 1.8 × 10⁻⁴); and H3K4me1 histone marks (${\overline{\delta }}_{F_{\text{UNI}}}$∼1.9, p = 4.3 × 10⁻⁵).

Figure 2.

Significant inbreeding depression (ID) enrichment within eight genomic annotations

(A and B) Estimates of ID enrichment on average across 11 traits obtained via $F_{\text{UNI}}$ and $F_{\text{ROH}}$. Statistical significance was set at p < 0.05/(44 × 2) ≈ 5.7 × 10⁻⁴. Recombination rate and nucleotide diversity were analyzed as continuous annotations. “High recombination rate” denotes that recombination rate is positively correlated with ID, and “low nucleotide diversity” denotes that nucleotide diversity is negatively correlated with ID. Data underlying this figure are reported in Table S1. DHS, DNA-se I hypersensitive sites; DGF, chromatin accessible regions from digital genomic footprint; GERP (NS), GERP++ score number of substitution; H3K4Me1, histone mark (binary annotation). Error bars represent standard errors (SEs).

Previous studies have shown that nucleotide diversity and linkage disequilibrium (LD) can influence ROH detection.^49,50 Therefore, errors in ROH calling due to these two annotations could potentially confound our results. Using data from the UKB and from an independent sample from the UK10K Project,⁵¹ we show in the supplemental methods section (Figures S4–S6) that ROH genomic density as well as errors in ROH calling cannot explain the enrichment of ID in low nucleotide diversity regions nor that in high recombination rate regions. Importantly, ID enrichment in high recombination rate regions is also detected via $F_{\text{UNI}}$, which minimizes the likelihood of this finding’s being caused by errors in ROH calling. However, we found that exclusion of the major histocompatibility complex (MHC) locus (hg19: chr6: 25,000,000–35,000,000) from our analyses has a strong impact on the significance of ${\overline{\delta }}_{F_{\text{ROH}}}$ in low nucleotide diversity regions (without MHC: ${\overline{\delta }}_{F_{\text{ROH}}}$∼2.0, p = 0.29; Table S8). Given that ROH genomic density alone cannot explain that observation, we further investigated whether population stratification of rare variants may confound our results. The latter hypothesis is justified by the fact that enrichment in low nucleotide diversity is detected with $F_{\text{ROH}}$, but not with $F_{\text{UNI}}$, which suggests a signal (or a confounding effect) coming from low frequency variants. To test this hypothesis, we used birth coordinates as proxies for geographically localized rare variants and fitted those as covariates in our analyses. To account for non-linear effects of rare variants stratification, we used a k-means clustering approach to create 100 geographical clusters from participants’ birth coordinates and fitted those as categorical covariates. Although these additional analyses were based on a slightly reduced number of participants who reported their birth location in the UK, we still found a significant enrichment of ID within low nucleotide diversity regions (adjusted for 20 PCs + 100 birth coordinates clusters and including MHC: ${\overline{\delta }}_{F_{\text{ROH}}}$∼3.3, p = 1.4 × 10⁻⁴), consistent with our main analysis. Altogether, our results show that the MHC locus disproportionately contributes to the enrichment of ID in low nucleotide diversity regions, which is not explained by higher ROH frequency at this locus nor by uncorrected population stratification.

Recognizing that the Bonferonni correction is conservative, at FDR < 5%, we detected 16 additional annotations, which include other regulatory elements (e.g., transcription factor binding sites: ${\overline{\delta }}_{F_{\text{UNI}}}$∼4.0) and conservation annotations (e.g., promoters containing evolutionary old DNA sequences: ${\overline{\delta }}_{F_{\text{UNI}}}$∼27.0) as shown in Table S1.

Next, we assessed the independence between significantly enriched annotations by fitting them jointly. On average across traits, only ID enrichment within genomic regions with low nucleotide diversity remained significant at our initial Bonferroni threshold (${\overline{\delta }}_{F_{\text{ROH}}}$∼3.1, p = 3.0 × 10⁻⁴; Table S2).

Moreover, we detected significant enrichment of ID in height within transcribed genomic regions (${\delta }_{F_{\text{ROH}}}$∼8.0, p = 4.9 × 10⁻⁵) as well as in genomic regions with a low nucleotide diversity (${\delta }_{F_{\text{ROH}}}$∼7.6, p = 4.8 × 10⁻⁹) and those with a shorter time to most recent common ancestor (TMRCA: ${\delta }_{F_{\text{ROH}}}$∼5.8, p = 7.6 × 10⁻⁶). Note that alleles with a shorter TMRCA are more likely to have arisen recently in the population. Therefore, the latter result suggests a larger contribution of recent alleles to ID, consistent with previous findings.^7,52 Importantly, these three genomic annotations were detected with $F_{\text{ROH}}$ but did not pass statistical significance when quantified via $F_{\text{UNI}}$ (p > 0.27), which suggests that rare variants within (or with large values of) these annotations could be the main drivers of our results for height. Interestingly, we also detected a significant depletion of ID signal (material and methods) for height within transcription start sites (enrichment outside TSS: ${\delta }_{F_{\text{ROH}}}$∼2.0, p = 3.2 × 10⁻⁵; Table S3). Furthermore, we detected suggestive ID enrichment at FDR < 5% for the majority of traits except for fertility and visual and auditory acuity (Table S3). Among these additional associations, we highlight the strong enrichment of ID in height and cognitive function within promoters of loss-of-function-intolerant genes from the Exome Aggregation Consortium⁵³ (>84 and p < 0.001 with both inbreeding measures; Table S3). We also highlight suggestive enrichment of ID in peak expiratory flow within DGF (${\delta }_{\text{UNI}}$∼7.2, p = 5.5 × 10⁻⁵), where ∼13% common SNPs contribute ∼90% of the genome-wide ID for that trait.

ID enrichment within GWAS-associated genomic regions

Our analyses based on $F_{\text{UNI}}$ show interesting similarities between functional enrichment of ID and that of additive genetic variance as reported previously.²² In both cases, we see a strong enrichment of ID and SNP-based heritability within genomic regions with conserved functions across species as well as within regulatory elements such as promoters, enhancers, and DHSs and a much smaller enrichment within transcriptionally repressed or transcribed regions.

To further explore these similarities, we sought to directly quantify ID enrichment within trait-associated loci identified through GWASs. Therefore, we performed GWASs of all 11 traits in our sample of ∼350,000 unrelated UKB participants (material and methods) and used chi-square association statistics of each SNP to define a new continuous annotation. Thus, we calculated 11 trait-specific inbreeding measures derived from $F_{\text{UNI}}$ such that each SNP is weighted proportionally to the strength of its association with the target trait. We then tested the ID enrichment of these 11 GWAS-derived annotations. Given that stronger association is expected at SNPs with large LD scores,⁵⁴ each analysis was also conditioned on another continuous annotation defined by the LD score of each SNP. On average across traits, we found marginally significant evidence that genomic regions with large chi-square association statistics, independently of LD, are enriched for ID signal (${\overline{\delta }}_{F_{\text{UNI}}}$∼10.6, p = 0.03; Table S4).

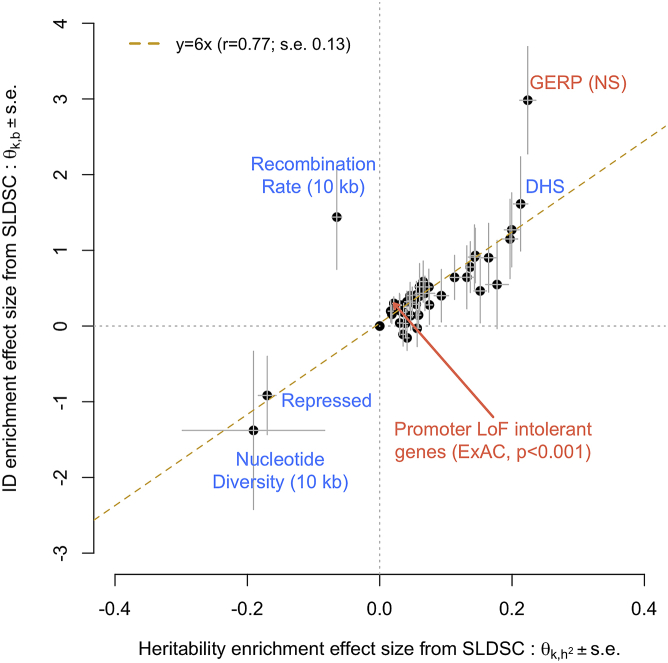
In addition, we sought to estimate the correlation between functional enrichment of heritability and that of ID across the 44 genomic annotations analyzed previously. To ensure a fair comparison, we used stratified LD score regression (SLDSC) as a unified framework to assess enrichment of SNP-based heritability and that of ID. We denote ${\theta }_{k,{\text{h}}^2}$ and ${\theta }_{k,b}$ as the SLDSC effect size of annotation $k$ on heritability and ID, respectively. We provide a theoretical justification for using LD score regression to estimate ID by highlighting its direct connection with $F_{\text{UNI}}$ (Appendix B). Consistently, the mean correlation between Z scores of ${\tau }_k$ (i.e., our individual-level data-based statistic to quantify enrichment of ID: ${\tau }_k=b({\delta }_k-1)$; material and methods) and ${\theta }_{k,b}$ is ∼0.7 (range: 0.5 up to 0.8) across traits, which shows that both enrichment measures largely capture the same information (Figure S7).

On average across traits, we find a significant positive correlation between ${\theta }_{k,{\text{h}}^2}\text{ and }{\theta }_{k,b}$of ∼0.77 with a block jack-knife standard error (b.s.e.) of ∼0.13 (Figure 3). We also detect a significant (p < 0.05/11) correlation between ${\theta }_{k,{\text{h}}^2}\text{ and }{\theta }_{k,b}$ for specific traits (Figure S8; Table S6), such as handgrip strength (r = 0.91; b.s.e. = 0.07), cognitive function (r = 0.82; b.s.e. = 0.14), and peak expiratory flow (r = 0.93; b.s.e. = 0.05). We show in the supplemental methods section and Figure S9, through theory and simulations, that a large positive correlation between enrichments of heritability and ID in fitness could be expected if the distribution of fitness effects of mutations causing ID is moderately skewed, i.e., if the proportion of mutations with large fitness effect is small. However, given that this distribution is largely unknown, our theoretical results therefore only provide a set of sufficient, but not necessary, conditions that can explain our observations. Furthermore, we performed additional simulations to show that the correlation between enrichments of ID and heritability is not due to an artifact in our methods, which would systematically induce such a correlation (supplemental methods, Figure S10).

Figure 3.

Correlation between functional enrichment of SNP-based heritability and inbreeding depression (ID) estimated from GWAS summary statistics

Enrichment statistics for heritability (x axis: ${\theta }_{k,h^2}$) and ID (y axis: ${\theta }_{k,b}$) were estimated with stratified LD score regression (SLDSC) as described in the material and methods section. Enrichments statistics were averaged over 11 traits. Each dot represents a genomic annotation, and errors bars represent standard errors (SEs) calculated with a block-jackknife procedure. Annotations highlighted in coral font show a statistically significant ID enrichment at p < 0.05/88. DHS, DNA-se I hypersensitive sites; GERP (NS), GERP++ score number of substitution; LoF, loss of function. Data underlying this figure are reported in Table S5.

Despite an overall large correlation between enrichments of heritability and ID, we find that the effect of recombination rate on ID and on heritability are in opposite directions (Figure 3). To further explore what could explain this observation, we performed extensive forward-time evolutionary simulations by using SLiM3⁵⁵ (Supplemental Methods) to quantify the effect of recombination rate on both heritability and ID enrichments. In these simulations, we considered various combinations of selection ($s$) and dominance ($h$) coefficients for mutations causing ID and additive genetic variance in fitness (material and methods). Using 1,000 simulation replicates (for each scenario), we find that recombination rate affects the enrichment of heritability and ID in a non-linear fashion that is modulated by the strength of both selection and dominance (Figures S11 and S12). More specifically, our simulations show a strong enrichment of ID in high recombination rate regions (>2 cM/Mb) only when ID is caused by partially recessive ($h=0.1$) near-neutral mutations, i.e., when $s$ is between $\sim 1/\left(2N_e\right)$ and $\sim 2/N_e,$ where $N_e$ denotes the effective population size. Under the same scenarios, heritability was either slightly enriched or even depleted in high recombination regions. However, for large selection coefficients ($s>2/N_e$) and large dominance coefficients ($h>0.3$), enrichments of heritability and ID behave consistently, and both monotonically decrease with recombination rate.

In summary, our findings imply that functional enrichments of ID and additive genetic variance in the population are most likely caused by similar mechanisms, such as variable recombination rates between genomic regions and disruption of evolutionary old regulatory elements (e.g., older than the split between marsupial and placental mammals ∼160 million years ago).⁵⁶ However, although co-localized, variants causing these two phenomena may only partially overlap, while variants causing ID may tend to be more recessive than those causing additive genetic variance.

Discussion

In this study, we introduce a method to detect and quantify the enrichment of ID within a wide range of binary and continuous genomic annotations and applied it to analyze 11 traits with prior evidence of ID. We show that ID is independently enriched within regions with high recombination rates, consistent with prior evidence in potatoes,⁵⁷ and also, to a lesser extent, within regions with a low nucleotide diversity, a marker of high functional importance of DNA sequences.^58,59 Interestingly, we find that the MHC locus contributes disproportionately to the enrichment of ID in low nucleotide diversity regions, even when analyses are adjusted for population stratification (genetic principal components + geographical birth coordinates). An enrichment of ID in low nucleotide diversity regions and in high recombination rate regions may seem counterintuitive given the negative correlation between these two annotations (r ∼ −0.2; Figure S3), which translates the fact that higher recombination rates are associated with higher nucleotide diversity. However, high recombination rates also contribute to minimize the strength of background selection⁶⁰ (i.e., purging of neutral and near-neutral alleles in LD with deleterious mutations) and selective sweeps, thereby contributing to increase diversity of slightly deleterious alleles.⁶¹ Consistent with reduced selection efficiency, recombination rate and strength of background selection annotations show a larger negative correlation (r ∼ −0.3; Figure S3). Another potential explanation for the enrichment of ID within genomic regions with high recombination rates is because frequency of deleterious de novo mutation is increased in those regions.^62,63 However, the relatively small variance in de novo mutations explained by recombination rate (R² ∼ 5%, in Kessler et al.⁶²) implies that variation in mutation rates most likely contributes a second order effect to our observations.

Using estimated coalescence times, we confirm that recent alleles contribute more to ID and also show that homozygosity in DNA sequences that are conserved across mammal and primate species contribute ∼20-fold more ID than any random equally sized portion of the genome. In humans, inbreeding between close relatives often manifests as severe Mendelian syndromes caused by homozygous loss-of-function mutations.⁸ Consistent with this observation, our study shows a large ID enrichment ($\overline{\delta }$ > 30; Table S1) within promoters of loss-of-function-intolerant genes. It is noteworthy that ID enrichment within coding regions was comparatively smaller ($\overline{\delta }$ between 1 and 7.1, p > 0.15; Table S1) and did not survive any of our corrections for multiple testing. The latter observation emphasizes that impairment of essential genes, as opposed to genes in general, is a key contributor to ID. Finally, our study shows a strong ID enrichment within multiple regulatory elements, which opens interesting avenues to quantify the effect of homozygosity on gene and protein expression in humans.

The genetic basis of ID is predicated on two hypotheses.¹ The first one, the “dominance hypothesis,” stipulates that ID is caused by directional dominance effects of partially recessive deleterious alleles. On the other hand, the “overdominance hypothesis” assumes that the genetic architecture of traits subjected to ID is such that heterozygotes express better phenotypes than both homozygotes, for example due to balancing selection. Although major progress has been made in model species,¹ disentangling these two explanations remains a challenge in natural populations. One possibility to address it could be by leveraging the distinct evolutionary consequences of these two hypotheses. The “dominance hypothesis” predicts a larger contribution to ID from loci where mutation rate is higher than average, while the “overdominance hypothesis” predicts a larger ID from loci where balancing selection is stronger.⁶⁴ Our study shows patterns of ID enrichment that are consistent with both hypotheses. However, we found a much larger magnitude of ID enrichment from annotations that are correlated with mutation rates (e.g., recombination rates^62,63 or CpG content;²³ Table S1) as compared to those correlated with strength of selection (e.g., GERP++ score or background selection; Table S1). Altogether, our results imply that both hypotheses probably contribute to explain ID in human traits, but overdominance does so to a lesser extent.

We also revisited previous claims⁷ regarding the contribution of common variants to ID. We provide new evidence that variants with an MAF > 1% substantially contribute to ID in height and educational attainment (Figure 1), while their contribution to ID in fertility remains limited. While some of the traits analyzed in this study have been shown to drive assortative mating in the population, we do not think that assortment based on polygenic traits (e.g., height) would implicitly create an enrichment of ID within any specific part of the genome, as reported here. In fact, the increased homozygosity at trait-associated loci that is induced by assortative mating is inversely proportional to the number of causal variants and therefore negligible for highly polygenic traits.^65,66 Finally, our results also contribute to illuminating the direction of causality between homozygosity and traits. Indeed, differential contribution of genomic regions to ID would not be expected if traits of parents (e.g., intelligence or socio-economic status) were causally associated with the phenotypes in their children and only incidentally associated with their relatedness, i.e., with offspring homozygosity. Note that the latter configuration has been shown to induce biases in estimates of ID, as suggested previously.⁶⁷

Our study has a number of limitations. First, we lacked statistical power to detect more trait-specific patterns of ID enrichment beyond height. Similarly, we also lacked power to estimate conditional enrichment across multiple functional annotations. Therefore, estimates of ID enrichment reported here may reflect overlap between annotations (e.g., the correlation between DHS and DGF is ∼0.5; Figure S3), including ones not observed in our study. A second limitation of our study is that estimates of ID obtained via our extension of the LD score regression method have too large standard errors to be efficiently used for partitioning analyses (Table S7; Figure S13). However, we emphasize that such methods remain valid and can still be used when sample size is sufficiently large (e.g., n ∼ 1,000,000, which is becoming more common in human studies).

A third limitation of our study is that our method assumes a linear relationship between ID and continuous annotations (Equation 2), while this relationship may be more complex in reality. For example, our forward-time evolutionary simulations showed a non-linear relationship between the recombination rate and enrichment of ID (and that of additive genetic variance), which is modulated by the distribution of selection coefficients of deleterious alleles, as well as their dominance coefficients (Figures S11 and S12). Note that such a non-linear relationship has also been reported in previous studies^23,68 that investigated the functional enrichment of trait heritability, although these studies did not emphasize that observation. As an alternative to assuming a linear relationship between continuous annotations and ID, we recommend discretizing the annotations into quantiles or testing the significance of the conditional effects of the annotation and its squared value. We show in Figure S14 that the empirical relationship between ID enrichment and recombination rate is largely monotonic, which suggests that the linear assumption made here would have a limited impact on our conclusions regarding this annotation.

In conclusion, we have proposed in this study a refined characterization of the functional effects of variants contributing to ID. Beyond conceptual parallels between estimation of ID and that of heritability established previously,⁹ our study demonstrates that functional mechanisms involved in ID are also relevant for characterizing genetic variance and genetic risk in the population. We foresee that the application of the different methods developed here to large collections of whole-genome or whole-exome sequencing data available in the near future will lead to major discoveries regarding the genetic basis of ID.

Declaration of interests

The authors declare no competing interests.

Published: July 1, 2021

Appendix A: Derivation of Equation 3

Equation 3 is derived from combining Equation 1 and Equation 2 recalled below:

$$y=\sum _{j=1}^M{\beta }_j{F}_j+e,$$ (Equation A1)

$$E\left[{\beta }_j\right]=\frac{b_0}{M}+\sum _{k=1}^K\left(z_{jk}\left[\frac{b_k}{m_k}\right]+(1-z_{jk})\left[\frac{b-b_k}{M-m_k}\right]\right).$$ (Equation A2)

Note that Equation 1 is the same as Equation A1 and that Equation 2 the same as Equation A2.

We write ${\beta }_j=E\left[{\beta }_j\right]+{\epsilon }_j$ then replace $E\left[{\beta }_j\right]$ with its expression from Equation 2. We get

$$y=\sum _{j=1}^M{\beta }_j{F}_j+e=\sum _{j=1}^{M}E\left[{\beta }_j\right]F_j+e^{\text{′}},$$ (Equation A3)

where $e^{\text{′}}=e+\sum _{j=1}^M{\epsilon }_j{F}_j$ and such as $E\left[e^{\text{′}}\right]=0$.

Besides, we can rewrite Equation 2 from the main text (methods section) as

$$E\left[{\beta }_j\right]=\frac{b(1-K)}{M}+\sum _{k=1}^K\frac{b-b_k}{M-m_k}+\sum _{k=1}^K{z}_{jk}\left[\frac{b_k}{m_k}-\frac{b-b_k}{M-m_k}\right],$$

$$E\left[{\beta }_j\right]=\frac{1}{M}\left[b(1-K)+\sum _{k=1}^K\frac{M(b-b_k)}{M-m_k}\right]+\frac{1}{m_k}\sum _{k=1}^K{z}_{jk}\left[b_k-\frac{m_k}{M-m_k}(b-b_k)\right],$$

$$E\left[{\beta }_j\right]=\frac{1}{M}\left[b(1-K)+\sum _{k=1}^K\left(\frac{b-b_k}{1-{\pi }_k}\right)\right]+\frac{1}{m_k}\sum _{k=1}^K{z}_{jk}\left[b_k-\frac{{\pi }_k}{1-{\pi }_k}(b-b_k)\right].$$

$$E\left[{\beta }_j\right]=\frac{1}{M}\left[b(1-K)+\sum _{k=1}^K\left(\frac{b-b_k}{1-{\pi }_k}\right)\right]+\frac{1}{m_k}\sum _{k=1}^K{z}_{jk}\left[\frac{b_k-{\pi }_{k}b}{1-{\pi }_k}\right].$$ (Equation A4)

where ${\pi }_k=m_k/M.$ If we denote ${\overline{F}}_k$ and $F_g$ as

$${\overline{F}}_k=\frac{1}{m_k}\sum _{k=1}^M{z}_{jk}{F}_j\mathrm{a}\mathrm{n}\mathrm{d}{F}_g=\frac{1}{M}\sum _{k=1}^K{F}_j$$

Then, combining Equation A3 and Equation A4 leads to

$$y=\left[b(1-K)+\sum _{k=1}^K\left(\frac{b-b_k}{1-{\pi }_k}\right)\right]F_g+\sum _{k=1}^K\left[\frac{b_k-{\pi }_{k}b}{1-{\pi }_k}\right]{\overline{F}}_k+e^{\text{′}},$$

$$=\left[b(1-K)+\sum _{k=1}^K\left(\frac{b-b_k}{1-{\pi }_k}\right)\right]F_g+\sum _{k=1}^K\left[\frac{b_k-{\pi }_{k}b}{1-{\pi }_k}\right]({\overline{F}}_k-F_g+F_g)+e^{\text{′}},$$

$$=\left[b\left(1-K\right)+\sum _{k=1}^K\left(\frac{b-b_k}{1-{\pi }_k}\right)+\sum _{k=1}^K\left(\frac{b_k-{\pi }_{k}b}{1-{\pi }_k}\right)\right]F_g+\sum _{k=1}^K\left(\frac{b_k}{{\pi }_k}-b\right)\left[\left(\frac{{\pi }_k}{1-{\pi }_k}\right)\left({\overline{F}}_k-F_g\right)\right]+e^{\text{′}},$$

$$=b{F}_g+\sum _{k=1}^K\left(\frac{b_k}{{\pi }_k}-b\right)\left[\left(\frac{{\pi }_k}{1-{\pi }_k}\right)\left({\overline{F}}_k-F_g\right)\right]+e^{\text{′}}.$$ (Equation A5)

QED.

Appendix B: Enrichment of ID from additive-dominance GWAS summary statistics

We assume the following model

$$y=\sum _{j=1}^M\left[\frac{x_j-2p_j}{\sqrt{2p_j(1-p_j)}}\right]{\beta }_j^{\left(a\right)}+\left[\frac{-x_j^2+\left(1+2p_j\right)x_j-2p_j^2}{2p_j(1-p_j)}\right]{\beta }_j^{\left(d\right)}+e,$$ (Equation B1)

where $x_j$ denotes the minor allele counts ($x_j=0,1,$ or 2) at SNP $j$, $p_j$ the minor allele frequency in the population, ${\beta }_j^{\left(a\right)}$ and ${\beta }_j^{\left(d\right)}$ additive and dominance effects at SNP $j,$ respectively, and $e$ a residual term. This model is the same as in Zhu et al.⁶⁹ (Equation 3) and Yengo et al. (Equations S6 and S7).⁹ Zhu et al. further assumed that $E\left[{\beta }_j^{\left(a\right)}\right]=E\left[{\beta }_j^{\left(d\right)}\right]=0$ and that $\text{var}\left[{\beta }_j^{\left(a\right)}\right]=h_a^2/M$, $\text{var}\left[{\beta }_j^{\left(d\right)}\right]=h_d^2/M,$ and $\text{var}\left[{\beta }_j^{\left(a\right)}\right]=1-h_a^2-h_d^2$. However, in order to account for ID, Equation B1 must be generalized to model the directionality of dominance effects. For that, we assume $E\left[{\beta }_j^{\left(d\right)}\right]=-b/M$, where $b$ is the genome-wide ID.

Now we denote $z_j=(x_j-2p_j)/\sqrt{2p_j(1-p_j)}$ and $F_j=\left[x_j^2-\left(1+2p_j\right)x_j-2p_j^2\right]/\left[2p_j(1-p_j)\right]$. We note that $F_j$ is exactly $F_{\text{UNI}}$ at SNP $j$. Therefore, Equation B1 can be rewritten as

$$y=\sum _{j=1}^M{z}_j{\beta }_j^{\left(a\right)}-F_j{\beta }_j^{\left(d\right)}+e=b\left(\frac{1}{M}\sum _{j=1}^M{F}_j\right)+g_a+g_d+e,$$ (Equation B2)

where $E\left[g_a\right]=E\left[g_d\right]=0$.

In an additive-dominance GWAS, the association between SNP $i$ and $y$ is tested by fitting simultaneously both additive ($a_i$) and dominance ($d_i$) effects, i.e., by fitting the following model

$$y=a_i{x}_i+d_i{H}_i+\text{ residual,}$$ (Equation B3)

where $H_i=x_i\left(2-x_i\right)$ is the indicator of heterozygosity at SNP $i$. Under the model above, we define $\hat{d}$ as the ordinary least-squares estimator of $d_i$ and SE(${\hat{d}}_i$) as its standard error. We then denote the Z score of ${\hat{d}}_i$ as $Z_{d,i}={\hat{d}}_i/\text{SE}\left({\hat{d}}_i\right)$and shows that it verifies (proof is given below)

$$E\left[-Z_{d,i}/\sqrt{N}\right]=E\left[{\hat{B}}_i\right]=b\text{ cov}\left(F_i,\frac{1}{M}\sum _{j=1}^M{F}_j\right)\approx \left(\frac{b}{M}\right){\ell }_i,$$ (Equation B4)

where ${\ell }_i$ is the LD score of SNP $i$ and $N$ is the GWAS sample size. Note that Equation B4 is analogous to the main result underlying the LD score regression methodology, which we recall below in Equation B5:

$$E\left[\left({\chi }_i^2-1\right)/N\right]\approx \left(\frac{h^2}{M}\right){\ell }_i.$$ (Equation B5)

Equation B4 and Equation B5 imply that the mean of the ${\hat{B}}_i$’s divided by the mean LD score over a given set of SNPs is in fact a measure of the “per-SNP” ID just like the mean ${\chi }^2$ (minus 1) divided by the mean LD score is a measure of the per-SNP heritability. Therefore, $E_k\left(h^2\right)$ and $E_k\left(b\right)$ quantify the relative per-SNP heritability and ID for SNPs within annotation $k$ as compared with the rest of the genome.

In principle, Equation B4 can be further extended to estimate enrichment of ID as done with the stratified LD score regression methodology. However, we found the standard errors of estimates of ID based on Equation B4 to be ~1.8-fold larger than that of estimates obtained from individual-level data (Table S7), which substantially reduces statistical power to detect enrichments. Note that estimates from LD score regression with an intercept constrained to 0 have slightly lower standard errors but also suffer large biases as shown in Table S7.

Proof of Equation B4

The proof of Equation B4 relies on two arguments. The first one is to note that under classical linear regression theory, the ordinary least-squares estimate $({\hat{a}}_i,{\hat{d}}_i)$ of $(a_i,d_i)$ in Equation B3 verifies that

$$E\left(\begin{array}{l}{\hat{a}}_i\hfill \\ {\hat{d}}_i\hfill \end{array}\right)={\left(\begin{array}{ll}\text{var}\left(x_i\right)\hfill & \text{cov}(x_i,H_i)\hfill \\ \text{cov}(x_i,H_i)\hfill & \text{var}\left(H_i\right)\hfill \end{array}\right)}^{-1}\left[\begin{array}{l}\text{cov}(x_i,y)\hfill \\ \text{cov}(H_i,y)\hfill \end{array}\right].$$

In particular for $\hat{d}$, we can write that

$$E\left[{\hat{d}}_i\right]=\frac{\text{var}\left(x_i\right)\text{cov}\left(H_i,y\right)-\text{cov}(x_i,H_i)\text{cov}(x_i,y)}{\text{var}\left(x_i\right)\text{var}\left(H_i\right)-\text{cov}{(x_i,H_i)}^2}=\text{cov}\left(\frac{\text{var}\left(x_i\right)H_i-\text{cov}(x_i,H_i)x_i}{\text{var}\left(x_i\right)\text{var}\left(H_i\right)-\text{cov}{(x_i,H_i)}^2},\text{y}\right).$$

Similarly, we derive the standard error of ${\hat{d}}_i$ (under the assumption that the phenotypic variance is equal to 1 and that each SNP explains a negligible part of the trait variance) as

$$\text{SE}\left[{\hat{d}}_i\right]\approx \frac{\text{SD}\left(y\right)}{h_i\sqrt{N}}=\frac{1}{\left[h_i\sqrt{N}\right]},$$

where $\text{SD}\left(y\right)$ denotes the standard deviation of $y$.

If we denote $p$ as the minor allele frequency, then under Hardy-Weinberg equilibrium, we can show that $\text{var}\left(x_i\right)=h_i=2p_i(1-p_i)$, $\text{var}\left(H_i\right)=h_i\left(1-h_i\right),$ and $\text{cov}\left(x_i,H_i\right)=h_i(1-2p_i)$. Using these relationships, we can further show that $\text{var}\left(x_i\right)\text{var}\left(H_i\right)-\text{cov}{\left(x_i,H_i\right)}^2=h_i^3$ and $\text{var}\left(x_i\right)H_i-\text{cov}\left(x_i,H_i\right)x_i=-h_i^2{F}_i$. Therefore,

$$E\left[{\hat{d}}_i\right]=\text{cov}\left(\frac{-F_i}{h_i},\text{y}\right)$$

or, equivalently, $E\left[-\left({\hat{d}}_i/\text{SE}\left[{\hat{d}}_i\right]\right)/\sqrt{N}\right]=E[-Z_{d,i}/\sqrt{N}]\approx \text{cov}\left(F_i,\text{y}\right).$ Now using Equation B2, we can subsequently write that

$$E\left[-\frac{Z_{d,i}}{\sqrt{N}}\right]=\text{ cov}\left[F_i,b\left(\frac{1}{M}\sum _{j=1}^M{F}_j\right)+g_a+g_d+e\right]=\frac{b}{M}\sum _{j=1}^M\text{cov}\left(F_i,F_j\right)+\text{ cov}\left(F_i,g_a+g_d+e\right).$$

Under the assumption that SNP effects are independent of genotypes and that $e$ (environment) is independent of $F_i$, we have that $\text{cov}\left(F_i,g_a+g_d+e\right)=0.$ Moreover, Yengo et al.⁹ previously showed that $\text{cov}\left(F_i,F_j\right)\approx r_{ij}^2$, where $r_{ij}^2$ is the square LD correlation between SNP $i$ and $j$. Hence,

$$E\left[-\frac{Z_{d,i}}{\sqrt{N}}\right]\approx \left(\frac{b}{M}\right)\sum _{j=1}^M{r}_{ij}^2=\left(\frac{b}{M}\right){\ell }_i.$$

Data and code availability

This study makes use of genotype and phenotype data from the UK Biobank data under project 12505. UKB data can be accessed upon request once a research project has been submitted and approved by the UKB committee. Data sources underlying all figures are provided as supplemental tables. Example R scripts from our pipeline to simulate and estimate enrichment of ID and a C++ code describing the algorithm utilized to calculate annotation-specific inbreeding measures are provided at the following URL: https://github.com/loic-yengo/Code_for_Genomic_Partitioning_of_Inbreeding_Depression.

Web resources

• Extended set of 189 functional annotations for variants with MAF>0.1% in the UK Biobank, https://storage.googleapis.com/broad-alkesgroup-public/LDSCORE/baselineLF_v2.2.UKB.tar.gz

• GCTA software, https://cnsgenomics.com/software/gcta/

• General description (README file) for all sets of functional annotations, https://alkesgroup.broadinstitute.org/LDSCORE/readme_baseline_versions

• PLINK software, https://www.cog-genomics.org/plink2/

• Set of 97 functional annotations from stratified LD score regression (baseline LD model), https://alkesgroup.broadinstitute.org/LDSCORE/baselineLD_v2.2_bedfiles.tgz