Numerical simulations for sonochemistry

Highlights

• •Theoretical model has been validated through single-bubble sonochemistry.
• •Optimum bubble temperature for production of oxidants.
• •Numerical simulations of sonochemical synthesis of nanoparticles.
• •FEM calculation of an acoustic field in a sonochemical reactor.

Abstract

Numerical simulations for sonochemistry are reviewed including single-bubble sonochemistry, influence of ultrasonic frequency and bubble size, acoustic field, and sonochemical synthesis of nanoparticles. The theoretical model of bubble dynamics including the effect of non-equilibrium chemical reactions inside a bubble has been validated from the study of single-bubble sonochemistry. By the numerical simulations, it has been clarified that there is an optimum bubble temperature for the production of oxidants inside an air bubble such as OH radicals and H₂O₂ because at higher temperature oxidants are strongly consumed inside a bubble by oxidizing nitrogen. Unsolved problems are also discussed.

1. Introduction

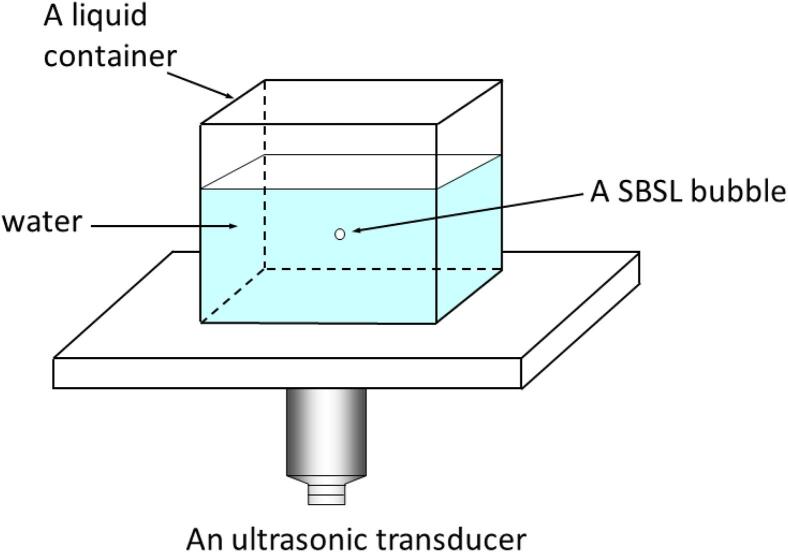
About 30 years ago when I started research in sonochemistry and sonoluminescence, reproducibility in experiments in sonochemistry was much poorer than that in recent years [1]. The turning point was the development in research on single-bubble sonoluminescence (SBSL) after the discovery by Gaitan and Crum in 1990 [2]. SBSL is a light emission phenomenon from a stably pulsating bubble trapped near the pressure antinode of a standing ultrasonic wave (Fig. 1) [2], [3], [4], [5], [6]. In 1991, Barber and Putterman [6] reported in Nature that SBSL pulse width is smaller than 100 ps. After the report, many physicists (including myself) started research on SBSL [3], [4], [5]. The considerable development in SBSL research in the following 10 years was reviewed by Brenner, Hilgenfeldt, and Lohse [4] in 2002.

Fig. 1.

An experimental apparatus for a single-bubble system [3]. Copyright (2004), with permission from Taylor & Francis.

Triggered by the research of SBSL, collaboration between chemists, physicists and ultrasonic engineers in sonochemical experiments has increased [1]. As a result, reproducibility in sonochemical experiments has been considerably improved [1], [7]. For example, pre-degassed water is used in an ultrasonic cleaning bath in which a beaker or a flask for sonochemical experiment is immersed in order to prevent the temporal variation of acoustic intensity due to degassing of water in the bath [8]. Another example is the use of impedance matching circuit to prevent the reflection of electric power from the ultrasonic transducer [9], [10].

Another development in sonochemical research triggered by the SBSL research is numerical simulations of sonochemical reactions inside a bubble [11], [12], [13], [14], [15], [16], [17], [18], [19], [20], [21], [22], [23], [24], [25], [26], [27], [28]. The first paper on numerical simulations of sonochemical reactions is probably by Kamath, Prosperetti, and Egolfopoulos [11] in 1993. There has been considerable development in numerical simulations of sonochemical reactions since then. The numerical simulations have revealed many mechanisms in sonochemistry. In the present review, various numerical simulations for sonochemistry are discussed.

2. Bubble dynamics model

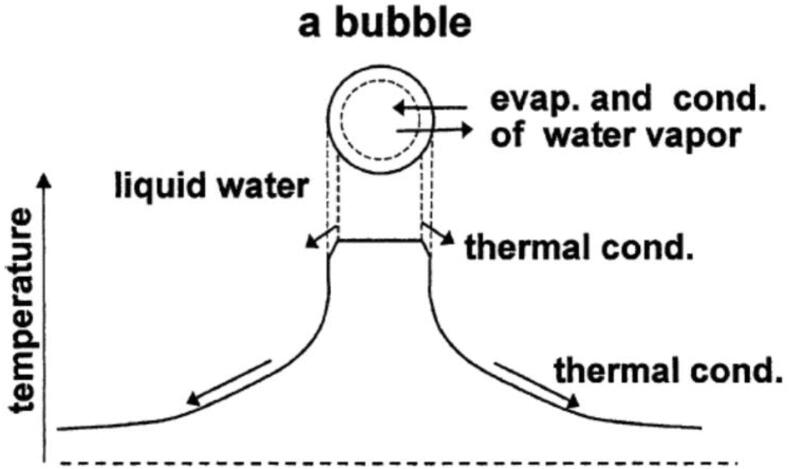
At the beginning of the SBSL research, it was believed that a spherical shock wave is formed inside a collapsing bubble [3], [4], [29], [30], [31]. When the spherical shock wave is converged at the bubble center, temperature at the bubble center increases very sharply to about 10⁶ K, which was thought to be responsible for the short pulse of SBSL light [29]. However, following researches have revealed that shock wave formation inside a collapsing bubble is unlikely because temperature near the bubble wall is lower than that near the bubble center by thermal conduction between the heated bubble interior and the surrounding liquid [3], [4], [23], [32], [33], [34], [35]. Lower temperature near the bubble wall results in smaller speed of sound near the bubble wall compared to that near the bubble center. In other words, the sound-speed increases as the distance from the bubble wall increases toward the bubble center. For the shock wave formation, pressure disturbances radiated inwardly from the bubble wall should overtake the previously radiated pressure disturbances. However, as a pressure disturbance moves with the speed of sound plus the radial fluid velocity, the pressure disturbance never overtake the previously radiated pressure disturbances because a typical bubble collapse is not so violent to overcome the adverse sound-speed gradient for the shock wave formation [35].

Actually, according to the numerical simulations of fundamental equations of fluid dynamics inside a collapsing bubble, the temperature and pressure inside a collapsing bubble are nearly spatially uniform [23]. Thus, in the theoretical model discussed in the present review, temperature is assumed to be spatially uniform inside a bubble except at the thermal boundary layer near the bubble wall (Fig. 2) [19].

Fig. 2.

The bubble dynamics model [19]. Reprinted from Ultrasonics, vol. 42, K. Yasui, T. Tuziuti, and Y. Iida, Optimum bubble temperature for the sonochemical production of oxidants, pp. 579–584, Copyright (2004), with permission from Elsevier.

In the model [10], [12], [16], [18], [21], [36], the following effects are taken into account; thermal conduction inside and outside a bubble, non-equilibrium evaporation and condensation of water vapor at the bubble wall, non-equilibrium chemical reactions inside a bubble, variation of liquid temperature at the bubble wall and corresponding changes of physical properties of the liquid such as saturated vapor pressure, surface tension, latent heat of evaporation, thermal conductivity, viscosity, etc. As the equation of bubble dynamics (temporal evolution of bubble radius), modified Keller equation is used, in which effect of liquid compressibility is taken into account to the first order [10], [36]. With regard to chemical reactions inside an air bubble, 93 chemical reactions and their backward reactions are taken into account involving N₂, O₂, H₂O, OH, H, O, HO₂, H₂O₂, O₃, N, HNO₂, HNO, HNO₃, NO, NO₂, and N₂O [18].

3. Single-bubble sonochemistry

For usual experiments of sonochemistry, direct comparison between theory and experiment is practically very difficult because there are many uncontrollable factors in the experiments such as temporal variation in number and size of bubbles as well as that of acoustic field in a sonochemical reactor, spatial movement of bubbles, etc. [10], [37], [38]. It is practically very difficult to know the exact values of number of bubbles as well as their size distribution. In 2002, Didenko and Suslick [39] experimentally reported the production rate of OH radicals from a SBSL bubble, which is called single-bubble sonochemistry. The experiment of single-bubble sonochemistry has enabled one to compare theory with experiment because the number of a bubble was fixed and the pressure amplitude of ultrasound was experimentally measured as well as the maximum bubble radius at the bubble expansion [39].

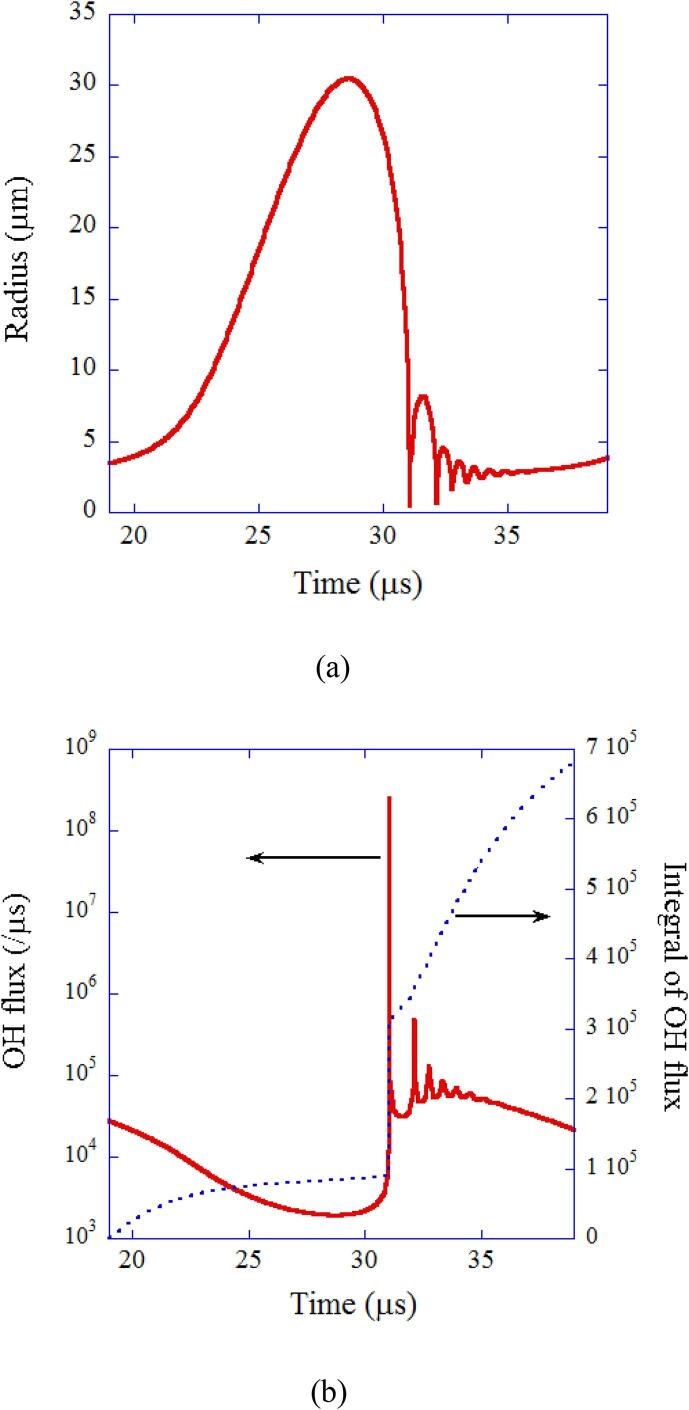
The results of numerical simulations under the condition of single-bubble sonochemistry are shown in Fig. 3, Fig. 4 [21]. During the rarefaction phase of ultrasound, a bubble expands (Fig. 3 (a)). At the compression phase of ultrasound, a bubble collapses very violently, which is called Rayleigh collapse [4], [10]. There are two reasons for the violent collapse of a bubble [10]. One is the spherical geometry of the bubble collapse. According to the continuity of liquid, speed of ingoing liquid increases as the radius from the bubble center decreases because the surface area of a spherical liquid shell decreases. The other is the inertia of the ingoing liquid toward the bubble.

Fig. 3.

The calculated results for one acoustic cycle when a SBSL bubble in a steady state in water at 3 °C is irradiated by an ultrasonic wave of 52 kHz and 1.52 bar in frequency and pressure amplitude, respectively [21]. The ambient bubble radius is 3.6 μm. (a) The bubble radius. (b) The dissolution rate of OH radicals into the liquid from the interior of the bubble (solid line) and its time integrals (dotted line). Reprinted from J. Chem. Phys., vol. 122, K. Yasui, T. Tuziuti, M. Sivakumar, and Y. Iida, Theoretical study of single-bubble sonochemistry, 224706, Copyright (2005), with the permission of AIP Publishing.

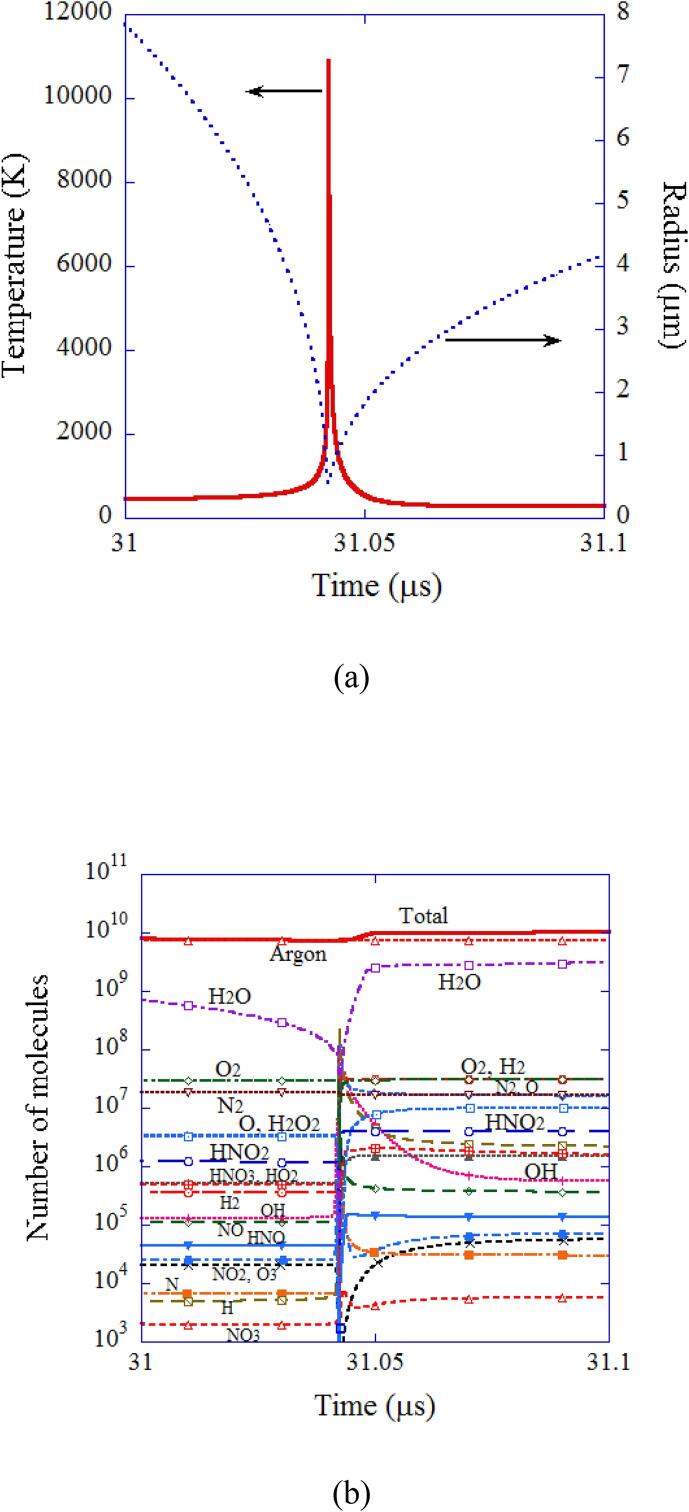
Fig. 4.

The calculated results for a SBSL bubble in a steady state at around the end of the bubble collapse only for 0.1 μs [21]. (a) The bubble radius and the temperature inside a bubble. (b) The number of molecules inside a bubble. Reprinted from J. Chem. Phys., vol. 122, K. Yasui, T. Tuziuti, M. Sivakumar, and Y. Iida, Theoretical study of single-bubble sonochemistry, 224706, Copyright (2005), with the permission of AIP Publishing.

At the end of the violent bubble collapse, temperature and pressure significantly increase due to quasi-adiabatic compression of a bubble where “quasi-“ means that appreciable amount of thermal conduction takes place between the heated interior of a bubble and the surrounding liquid [10], [12]. As a result, water vapor is dissociated inside a bubble and OH radicals are created. Here, an argon bubble is studied because nitrogen is burned inside an initial air bubble by the high bubble temperature. Then, nitrogen and oxygen are changed to water soluble species such as HNOx and NOx which gradually dissolve into water. Accordingly, only chemically inactive species argon remains inside a SBSL bubble because a SBSL bubble repeats expansion and violent collapse more than 10⁴ times per second. This is called argon rectification hypothesis which has been validated both experimentally and theoretically [4], [40].

In the present numerical simulations, the dissolution rate of chemical species such as OH radicals are also numerically calculated [21]. The result for OH radicals is shown in Fig. 3 (b) [21]. The time integral of the OH flux is also shown by dotted line in Fig. 3 (b). It is seen that the calculated amount of OH radicals dissolved into the surrounding liquid in one acoustic cycle is $6.6\times {10}^5$, which nearly agrees with the experimental result of $8.2\times {10}^5$ [21], [39]. Thus it is concluded that the theoretical model for single-bubble sonochemistry has been almost validated.

The results of numerical simulation at around the end of the bubble collapse are shown as a function of time only for 0.1 μs in Fig. 4 [21]. At the end of the violent bubble collapse, temperature sharply increases to 10900 K (Fig. 4 (a)). As a result, many molecules present inside a bubble except argon are dissociated inside the strongly heated bubble. The chemical products such as OH radicals present inside a SBSL bubble before the end of the violent collapse are produced at the previous violent collapse. When the bubble is cooled after the end of the violent collapse, many chemical species are produced inside a bubble again (Fig. 4 (b)).

4. Influence of ultrasonic frequency

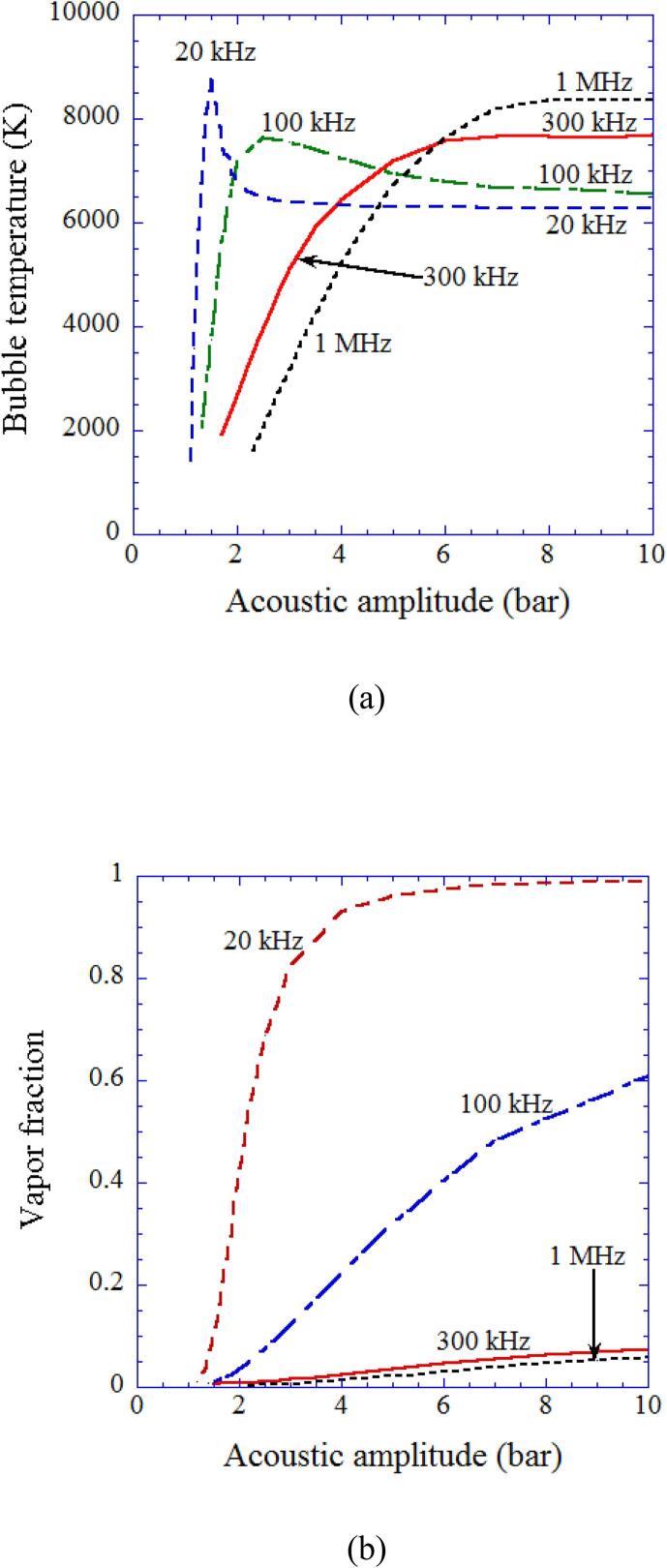
Using the theoretical model validated through the study of single-bubble sonochemistry [10], [12], [16], [18], [21], [36], influence of ultrasonic frequency on sonochemical reactions inside an air bubble is studied by numerical simulations (Fig. 5, Fig. 6, Fig. 7) [25]. For relatively low ultrasonic frequencies of 20 kHz and 100 kHz, there is a peak in bubble temperature as a function of acoustic amplitude which is the pressure amplitude of ultrasound (Fig. 5 (a)). The reason is as follows [25]. As the acoustic amplitude increases, a bubble expands more and the amount of water vapor entering a bubble by evaporation increases. As a result, the amount of water vapor trapped inside a bubble at the end of the violent collapse increases. It should be noted that condensation of water vapor at the bubble wall during the violent bubble collapse is strongly in non-equilibrium due to the high speed of the bubble collapse [41]. Thus the amount of water vapor trapped inside a bubble at the end of the bubble collapse increases as the amount of water vapor entering a bubble during bubble expansion increases. In other words, the vapor fraction, which is a mole fraction of water vapor inside an air bubble, increases as the acoustic amplitude increases (Fig. 5 (b)). Too much vapor fraction decreases the bubble temperature because water vapor has a larger molar heat than that of air and the endothermic heat of vapor dissociation cools the bubble considerably [16], [25], [42]. This is the reason for the existence of the peak in bubble temperature for 20 kHz and 100 kHz in Fig. 5 (a). For higher ultrasonic frequencies, the vapor fraction at the end of the violent collapse is very small due to shorter time for bubble expansion caused by shorter acoustic period. Thus, the bubble temperature increases as the acoustic amplitude increases although it is saturated at relatively high acoustic amplitudes [25].

Fig. 5.

The calculated result as a function of acoustic amplitude for various ultrasonic frequencies (20 kHz, 100 kHz, 300 kHz, and 1 MHz) for the first collapse of an isolated spherical air bubble [25]. The ambient bubble radii are 5 μm for 20 kHz, 3.5 μm for 100 and 300 kHz, and 1 μm for 1 MHz. (a) The temperature inside a bubble at the final stage of the bubble collapse. (b) The molar fraction of water vapor inside a bubble at the end of the bubble collapse. Reprinted from J. Chem. Phys., vol. 127, K. Yasui, T.Tuziuti, T. Kozuka, A. Towata, and Y.Iida, Relationship between the bubble temperature and main oxidant created inside an air bubble under ultrasound, 154502, Copyright (2007), with the permission of AIP Publishing.

Fig. 6.

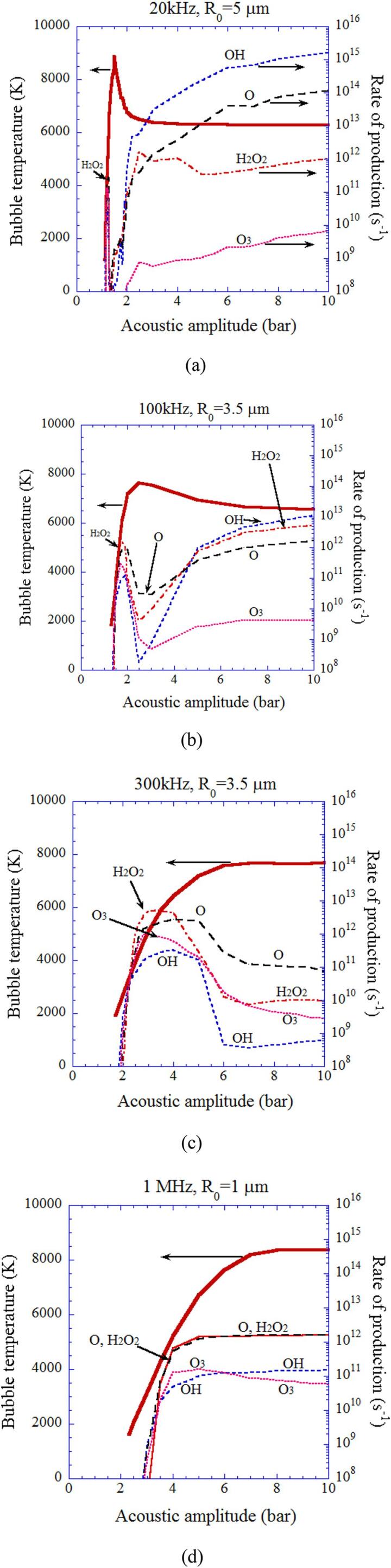
The rate of production of each oxidant inside an isolated spherical air bubble per second calculated by the first bubble collapse as a function of acoustic amplitude with the temperature inside a bubble at the end of the bubble collapse (the thick line): (a) 20 kHz and R₀ = 5 μm. (b) 100 kHz and R₀ = 3.5 μm. (c) 300 kHz and R₀ = 3.5 μm. (d) 1 MHz and R₀ = 1 μm [25]. Reprinted from J. Chem. Phys., vol. 127, K. Yasui, T. Tuziuti, T. Kozuka, A. Towata, and Y.Iida, Relationship between the bubble temperature and main oxidant created inside an air bubble under ultrasound, 154502, Copyright (2007), with the permission of AIP Publishing.

Fig. 7.

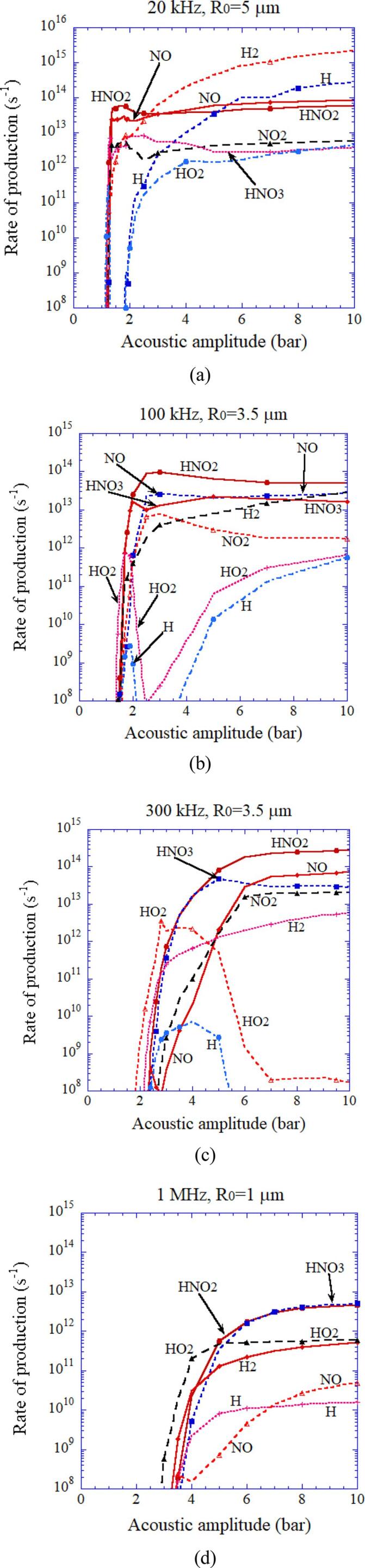
The rate of production of other main chemical species inside an isolated spherical air bubble per second calculated by the first bubble collapse as a function of acoustic amplitude [25]. (a) 20 kHz and R₀ = 5 μm. (b) 100 kHz and R₀ = 3.5 μm. (c) 300 kHz and R₀ = 3.5 μm. (d) 1 MHz and R₀ = 1 μm. Reprinted from J. Chem. Phys., vol. 127, K. Yasui, T. Tuziuti, T. Kozuka, A. Towata, and Y. Iida, Relationship between the bubble temperature and main oxidant created inside an air bubble under ultrasound, 154502, Copyright (2007), with the permission of AIP Publishing.

In Fig. 6, the rate of production of oxidants such as OH and O radicals as well as H₂O₂ and O₃ inside an air bubble in water per second calculated by the first collapse are shown with the temperature inside a bubble at the end of the violent collapse as a function of acoustic amplitude for various ultrasonic frequencies [25]. When the bubble temperature is higher than 7000 K except for the case of 1 MHz, the amount of oxidants produced inside an air bubble is relatively small because the oxidants are strongly consumed inside an air bubble by oxidizing nitrogen (N₂) [19], [25]. As a result, under the condition, large amounts of HNOx and NOx are produced inside an air bubble (Fig. 7) [25]. For the ultrasonic frequency of 1 MHz, oxidants are not so much consumed inside an air bubble even at higher temperature than 7000 K because of the much shorter duration of high temperature due to the small size of a bubble (R₀ = 1 μm, where R₀ is the ambient radius which is the bubble radius when ultrasound is absent). The typical size of a bubble at each ultrasonic frequency is determined according to the experimental data [43], [44] for active bubbles, which is probably determined by the shape instability of a bubble at each ultrasonic frequency [26], [45].

5. Influence of bubble size

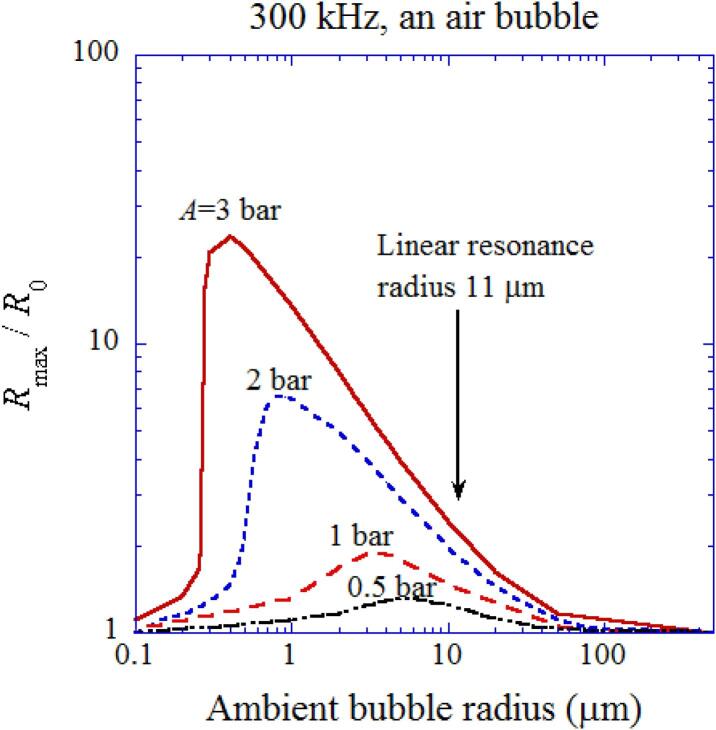
The influence of ambient bubble radius (R₀) is discussed [26]. In typical experiments of sonochemistry, the acoustic amplitude is relatively high such as more than 1 atm (=1.013 bar = 1.013 × 10⁵ Pa) [10]. Accordingly, the bubble pulsation is strongly nonlinear (non-sinusoidal) as already seen in Fig. 3 (a) [21]. At 300 kHz, the linear resonance radius of a bubble is about R₀ = 11 μm [10], [26]. However, the peak in the expansion ratio (R_max/R₀, where R_max is the maximum bubble radius at the bubble expansion) is at significantly smaller R₀ than the linear resonance radius due to the nonlinearity of the bubble pulsation (Fig. 8) [26]. As the acoustic amplitude increases, the peak of the expansion ratio shifts to smaller R₀, which is called the nonlinear resonance radius [10]. Even at acoustic amplitude as low as 0.5 bar, the nonlinear resonance radius is considerably smaller than the linear resonance radius.

Fig. 8.

The calculated expansion ratio ($R_{\mathit{max}}/R_0$) as a function of ambient bubble radius for various acoustic amplitudes at 300 kHz [26]. Both the horizontal and vertical axes are in logarithmic scale. Reprinted from J. Chem. Phys., vol. 128, K. Yasui, T. Tuziuti, J. Lee, T. Kozuka, A. Towata, and Y. Iida, The range of ambient radius for an active bubble in sonoluminescence and sonochemical reactions, 184705, Copyright (2008), with the permission of AIP Publishing.

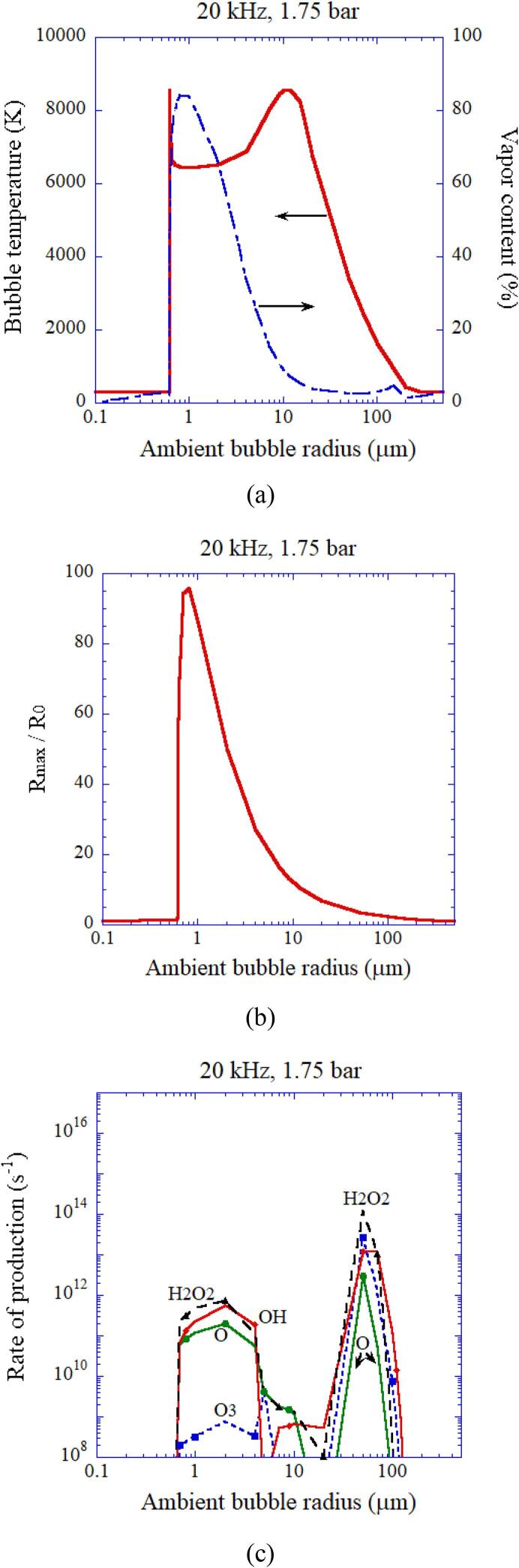
In Fig. 9, the calculated results are shown as a function of ambient radius of an air bubble at 20 kHz and 1.75 bar in ultrasonic frequency and acoustic amplitude, respectively [26]. As in the case of Fig. 5, the bubble temperature is relatively low when the vapor fraction at the end of the bubble collapse is relatively high (Fig. 9 (a)). From Fig. 9 (b), the nonlinear resonance radius is 0.8 μm, which is more than two orders of magnitude smaller than the linear resonance radius of 164 μm at 20 kHz. As in the case of Fig. 6, the rate of production of oxidants becomes relatively low when the bubble temperature is higher than 7000 K (Fig. 9 (c)). The range of ambient bubble radius for an active bubble is from the Blake threshold radius of 0.63 μm at 1.75 bar to near the linear resonance radius of 164 μm [26]. The Blake threshold is threshold for large expansion of a bubble at relatively low ultrasonic frequency [46].

Fig. 9.

The calculated result as a function of ambient bubble radius of an air bubble at 20 kHz and 1.75 bar in ultrasonic frequency and acoustic amplitude, respectively [26]. The horizontal axis is in logarithmic scale. (a) The peak temperature (solid) and the molar fraction of water vapor (dash dotted) inside a bubble at the end of the bubble collapse. (b) The expansion ratio ($R_{\mathit{max}}/R_0$). (c) The rate of production of each oxidant with the logarithmic vertical axis. Reprinted from J. Chem. Phys., vol. 128, K. Yasui, T. Tuziuti, J. Lee, T. Kozuka, A. Towata, and Y. Iida, The range of ambient radius for an active bubble in sonoluminescence and sonochemical reactions, 184705, Copyright (2008), with the permission of AIP Publishing.

6. Acoustic field

In usual experiments of sonochemistry which is a multibubble system, not only chemical reaction-rates in each bubble but also spatial distribution of number density of bubbles and acoustic amplitude are relevant to the total sonochemical activity [47], [48], [49], [50], [51], [52], [53]. In this section, numerical simulations of an acoustic field (spatial distribution of acoustic amplitude) are discussed [53].

In this section, the commercially available FEM (finite element method) software has been utilized (PAFEC-vibroacoustics, PACSYS Ltd.). In the software, the coupling of the acoustic field and the vibration of the reactor’s wall has been taken into account. For details, please see Ref. [53].

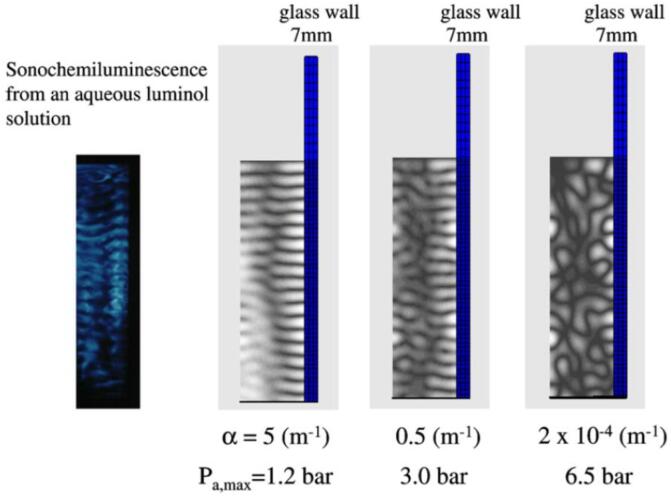
In the present FEM formulation, complex bulk modulus of the liquid is used in order to take into account the attenuation of ultrasound. In Fig. 10, the results of the FEM calculations on the spatial distribution of acoustic amplitude are shown for various attenuation coefficients of ultrasound [53]. The ultrasonic frequency is 100 kHz and the internal dimensions of the rectangular liquid container is 7 cm × 7 cm × 20 cm. The liquid (water at 20 °C) height is 13.9 cm. Only a half plane of the rectangular container is shown in Fig. 10. For comparison, the photograph of sonochemiluminescence from an aqueous solution is shown for the corresponding half plane [53], [54]. The calculated result for the attenuation coefficient of $\alpha =2\times {10}^{-4}$ (m⁻¹) corresponds to the case when no bubble exists in the liquid. In this case, the side wall of the liquid container vibrates strongly due to high acoustic amplitude. It results in the very complex spatial pattern of an acoustic field as seen in Fig. 10 because vibrating side wall radiates strong acoustic (ultrasonic) waves into the liquid [53].

Fig. 10.

The calculated spatial distribution of the acoustic amplitude for glass wall (7 mm in thickness) for various attenuation coefficients of ultrasound [53]. The photograph of sonochemiluminescence from an aqueous luminol solution has been also shown for the corresponding half plane. Reprinted from Ultrason. Sonochem., vol. 14, K. Yasui, T. Kozuka, T. Tuziuti, A. Towata, Y. Iida, J. King, and P. Macey, FEM calculation of an acoustic field in a sonochemical reactor, pp. 605–614, Copyright (2007), with permission from Elsevier.

When the attenuation coefficient is $\alpha =5$ (m⁻¹), the calculated spatial distribution of acoustic amplitude is similar to the spatial pattern of sonochemiluminescence. For the both images, horizontal stripes of pressure antinodes and nodes in the standing wave are clearly seen as well as a vertical line of a pressure node. When the attenuation coefficient is $\alpha =0.5$ (m⁻¹), some horizontal stripes of the standing-wave pattern are disconnected. Thus it is concluded that the actual attenuation coefficient of ultrasound in a bubbly liquid under ultrasound is in the range of 0.5 – 5 (m⁻¹) [53].

When the side glass wall is thin (2 mm in thickness), the side wall nearly freely vibrates under ultrasound. Thus, there is a vertical line of pressure node near the side wall in this case (Fig. 11) [53]. It should be noted that the liquid surface is always a pressure node because the liquid surface vibrates freely.

Fig. 11.

The calculated spatial distribution of the acoustic amplitude for glass wall with internal friction (2 mm in thickness) [53]. The attenuation coefficient is 5 m⁻¹. Reprinted from Ultrason. Sonochem., vol. 14, K. Yasui, T. Kozuka, T. Tuziuti, A. Towata, Y. Iida, J. King, and P. Macey, FEM calculation of an acoustic field in a sonochemical reactor, pp. 605–614, Copyright (2007), with permission from Elsevier.

7. Sonochemical synthesis of nanoparticles

Although sonochemical synthesis of nanoparticles has been intensively studied experimentally [55], [56], [57], [58], [59], [60], [61], [62], there are few numerical simulations on this topic probably because of the complex nature of the particle synthesis [63], [64], [65]. Kordylla et al. [66] performed excellent numerical simulations of sonocrystallization which is crystallization under ultrasound. In the first part of this section [63], numerical simulations of sonochemical production of BaTiO₃ nanoparticles are discussed using a model developed from the model of Kordylla et al. [66].

Dang et al. [67], [68], [69] experimentally reported sonochemical synthesis of BaTiO₃ nanoparticles. The starting materials were BaCl₂ and TiCl₄ in aqueous solution at pH14 in which Ar gas was dissolved. The aqueous solution was irradiated with ultrasound at 20 kHz using an ultrasonic horn for 20 min at 80 °C. Then BaTiO₃ nanoparticles were formed, which were spherical aggregates consisting of spherical nanocrystals of 5–10 nm in diameter. The diameter of an aggregate was 100–400 nm depending on the initial concentration of BaCl₂ and TiCl₄ [67]. Surprisingly, crystal axes of BaTiO₃ nanocrystals were aligned in an aggregate, which was confirmed by the selected area electron diffraction (SAED) pattern [68], [69]. In other words, an aggregate of BaTiO₃ nanocrystals is mesocrystal which has been intensively studied since 2005 [70], [71], [72], [73], [74], [75]. With simple mechanical stirring instead of ultrasound irradiation, BaTiO₃ particles were produced only after 8 h and they were neither mesocystals nor aggregates but larger particles with irregular shape [67], [68], [69].

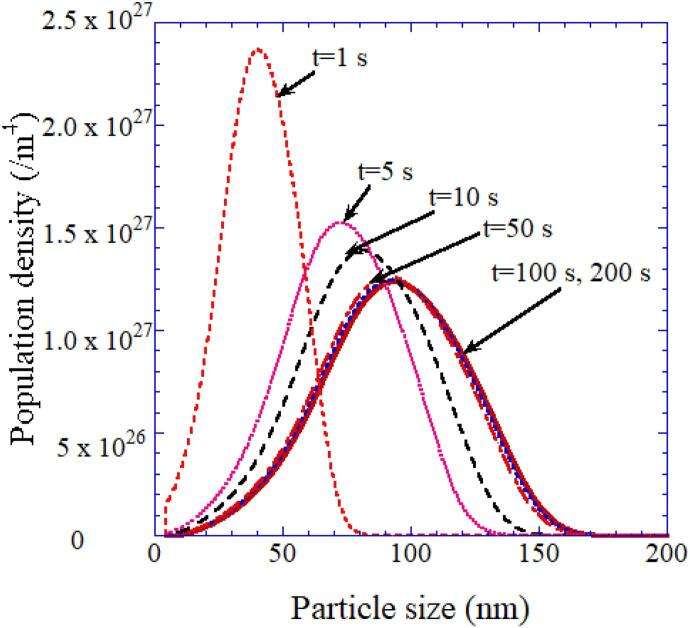
Firstly, aggregation process is numerically simulated using two different models [63]. One is the normal model used in aerosol dynamics that any particles aggregate when they collide. The other is a new model that only primary particle (a single nanocrystal) aggregates with other particles (any aggregates or a primary particle). According to the numerical simulations, the normal model results in the peak at the size of a primary particle (5–10 nm) in the size distribution of particles (aggregates) [63]. It disagrees with the experimental result of the peak at around 100 nm for the initial concentration of BaCl₂ and TiCl₄ of 0.4 mol/L [67]. On the other hand, the new model results in the peak at around 100 nm, which agrees with the experimental result (Fig. 12) [63], [67]. Thus, it is suggested that only primary particles (or possibly only small aggregates) aggregate with other particles.

Fig. 12.

The calculated results on temporal development of sonochemically synthesized BaTiO₃ particle (aggregate) size-distribution when the initial concentration of BaCl₂ and TiCl₄ is 0.4 mol/L [63]. Reprinted from Ultrason. Sonochem., vol. 18, K. Yasui, T. Tuziuti, and K. Kato, Numerical simulations of sonochemical production of BaTiO₃ nanoparticles, pp. 1211–1217, Copyright (2011), with permission from Elsevier.

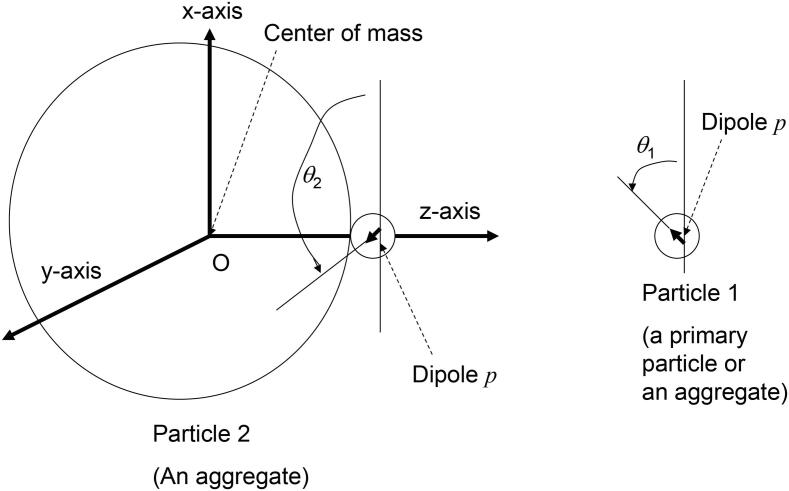
Then, what is the reason for such restriction in aggregation? Furthermore, what is the reason for the alignment of crystal axes in an aggregate? In order to study the mechanisms, numerical simulations of collisions of particles are performed using the Newton’s equation of translational motion and the equation of rotation of particles (Fig. 13) [64], [76]. For the equation of translational motion, electric dipole–dipole interaction, repulsive double layer interaction with zeta potential of −40 mV, and attractive interaction due to hydrogen bond between –OH on the surface of BaTiO₃ nanocrystals are considered [64]. The magnitude of electric dipole moment in a primary particle (a single BaTiO₃ nanocrystal) of 10 nm in diameter is assumed as 69.6 D (=2.32 × 10⁻²⁸ (C m)) from the condition of tetragonal crystal structure stabilized by adsorbate-induced charge screening [64], [77]. Without adsorbate-induced charge screening, 10 nm BaTiO₃ nanocrystals become cubic crystal structure due to the size effect caused by the increased free energy of tetragonal crystal structure by depolarization field [77]. For the equation of rotation, the following torques are considered; torque due to electric dipole–dipole interaction, van der Waals torque, torque due to friction caused by viscosity of the liquid, torque due to dynamic friction when the two particles are attached, and random torque causing the rotational Brownian motion [64].

Fig. 13.

Configuration of a collision between two particles [76]. Reprinted with permission from J. Phys. Chem. C, vol. 116, K. Yasui and K. Kato, Dipole-dipole interaction model for oriented attachment of BaTiO3 nanocrystals: a route to mesocrystal formation, pp. 319–324, Copyright (2012), American Chemical Society.

For a collision between an aggregate and a primary particle (or an aggregate), only the nearest primary particles are considered for the electric dipole–dipole interaction because the Debye length is only 0.3 nm at pH 14 in the experiment (Fig. 13) [64], [67], [68], [69], [76]. For the rotational motion, electric dipole–dipole interaction makes a pair of dipoles in antiparallel. On the other hand, van der Waals torque makes a pair of dipoles in parallel or antiparallel because van der Waals torque solely makes a pair of optical axes (due to the anisotropy in dielectric constant) aligned [78], [79].

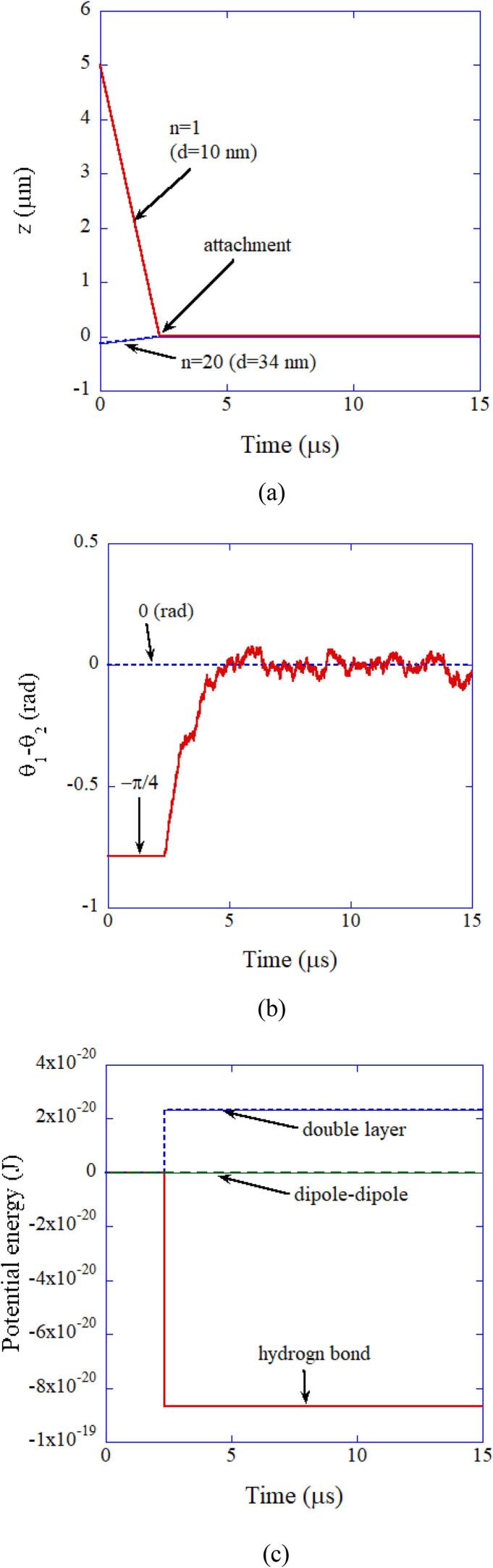
In Fig. 14, the result of numerical simulation on the collision between a primary particle (10 nm) and an aggregate (34 nm) consisting of 20 primary particles is shown [64]. The two particles are attached by attractive interaction due to hydrogen bond at time 2.3 μs. The two dipoles are aligned in parallel due to van der Waals torque. In other words, the crystal axes are aligned by van der Waals torque.

Fig. 14.

The result of the numerical simulation on the collision between a primary particle (n = 1, d = 10 nm) and an aggregate (n = 20, d = 34 nm) consisting of 20 primary particles of 10 nm in diameter in aqueous solution at pH 14 as a function of time for 15 μs [64]. (a) The position of each particle. (b) The relative angle of the two dipoles. (c) The potential energy. Reprinted from Ultrason. Sonochem., vol. 35, K. Yasui and K. Kato, Numerical simulations of sonochemical production and oriented aggregation of BaTiO₃ nanocrystals, pp. 673–680, Copyright (2017), with permission from Elsevier.

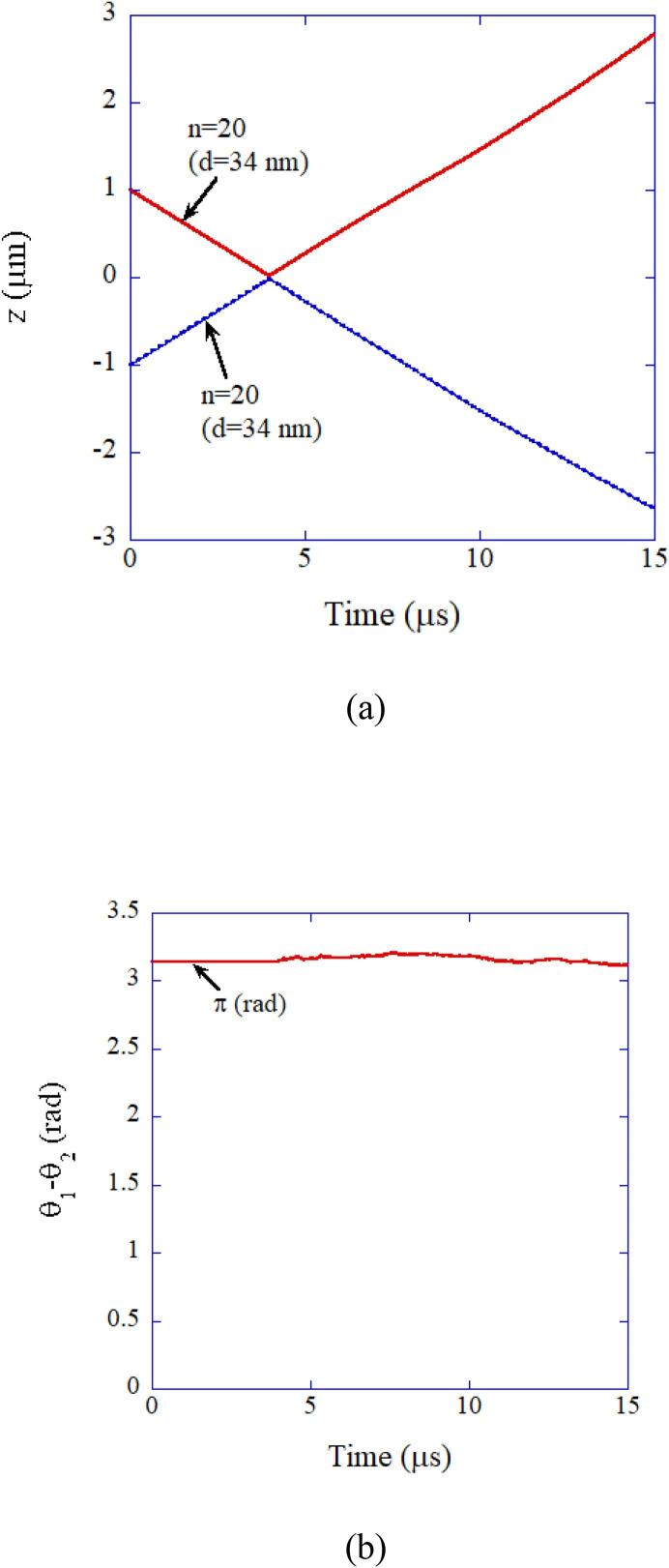
In Fig. 15, the result of numerical simulation on the collision between two aggregates (34 nm) consisting of 20 primary particles is shown [64]. The two aggregates never attach each other due to repulsive double-layer interaction. As the repulsive double-layer interaction is stronger for larger particles, larger aggregates than n = 20 never aggregate. This is the reason for the success of the new model of aggregation in Fig. 12 [63], [64].

Fig. 15.

The result of the numerical simulation on the collision between two aggregates (n = 20, d = 34 nm) consisting of primary particles of 10 nm in diameter [64]. (a) The position of each particle. (b) The relative angle of the two dipoles. Reprinted from Ultrason. Sonochem., vol. 35, K. Yasui and K. Kato, Numerical simulations of sonochemical production and oriented aggregation of BaTiO₃ nanocrystals, pp. 673–680, Copyright (2017), with permission from Elsevier.

8. Unsolved problems

In sections 3–5, chemical reactions inside a bubble are numerically simulated, and chemical reactions in the liquid phase are not simulated. One of the unsolved problems in numerical simulations for sonochemistry is the chemical reactions in the liquid phase outside a bubble [80], [81], [82], [83], [84]. The important questions are as follows. What is the lifetime of O radicals in the liquid phase [10], [37]? What is the role of O atoms in sonochemical reactions in the liquid phase?

Another unsolved problem is the effect of bubble–bubble interaction on sonochemical reaction rates [85], [86]. In a multibubble system, bubble pulsation is strongly influenced by the presence of surrounding bubbles because each bubble radiates acoustic (ultrasonic) waves into the surrounding liquid, which is called bubble–bubble interaction [85], [86], [87], [88], [89], [38], [90], [91], [92]. The important questions are as follows. What is the chemical activity of bubble clusters [93], [94], [95]? What is the role of bubble-shape instability on chemical activity [93], [96]? For numerical simulations of bubble clusters, large parameter scans are required such as bubble size distribution, bubble number density, ultrasonic frequency and pressure amplitude, etc. [97], [28]. Furthermore, chemical kinetic model has been continuously updated [98], [99], and numerical simulations for sonochemistry using updated chemical kinetic model are required. Numerical simulations with complex chemical kinetics in the presence of hydrocarbons should also be performed in future [100], [101], [102].

With regard to an acoustic field, role of Anderson localization of an acoustic (ultrasonic) wave in a bubbly liquid is to be studied [103], [104]. Some experiments on sonoluminescence (SL) have indicated that spatial localization of SL intensity occurs when there are some visibly large bubbles in the liquid [105]. On the other hand, in the absence of visibly large bubbles, the spatial distribution of SL intensity is rather uniform [105]. It suggests that Anderson localization of acoustic waves occurs when there are some visibly large bubbles in a cavitating liquid.

9. Conclusion

The bubble dynamics model including the effect of non-equilibrium chemical reactions inside a bubble has been validated through the study of single-bubble sonochemistry [21], [39]. Numerical simulations based on the model have revealed that there is an optimum bubble temperature for production of oxidants inside an air bubble because at higher temperature oxidants are strongly consumed inside an air bubble by oxidizing nitrogen [18], [19], [25], [26]. Numerical simulations of sonochemical production of nanoparticles as well as spatial distribution of acoustic amplitude in a sonochemical reactor are also discussed [53], [63], [64]. Finally, unsolved problems are described.

CRediT authorship contribution statement

Kyuichi Yasui: Conceptualization, Writing – original draft, Writing – review & editing.

Declaration of Competing Interest

The author declares that he has no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.