Gene-set integrative analysis of multi-omics data using tensor-based association test

Abstract

Motivation

Facilitated by technological advances and the decrease in costs, it is feasible to gather subject data from several omics platforms. Each platform assesses different molecular events, and the challenge lies in efficiently analyzing these data to discover novel disease genes or mechanisms. A common strategy is to regress the outcomes on all omics variables in a gene set. However, this approach suffers from problems associated with high-dimensional inference.

Results

We introduce a tensor-based framework for variable-wise inference in multi-omics analysis. By accounting for the matrix structure of an individual’s multi-omics data, the proposed tensor methods incorporate the relationship among omics effects, reduce the number of parameters, and boost the modeling efficiency. We derive the variable-specific tensor test and enhance computational efficiency of tensor modeling. Using simulations and data applications on the Cancer Cell Line Encyclopedia (CCLE), we demonstrate our method performs favorably over baseline methods and will be useful for gaining biological insights in multi-omics analysis.

Availability and implementation

R function and instruction are available from the authors’ website: https://www4.stat.ncsu.edu/~jytzeng/Software/TR.omics/TRinstruction.pdf.

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

Integrative multi-omics studies consider the molecular events at different levels, e.g. DNA variations, epigenetic marks, transcription events, metabolite profiles and clinical phenotypes. With recent technological advances, an increasing number of projects, e.g. The Cancer Genome Atlas (TCGA), International Cancer Genome Consortium (ICGC), the Encyclopedia of DNA Elements (ENCODE) and GTEx Project, have measured multiple omics features on the same samples. By incorporating complementary levels of information, integrative analyses of multi-platform data have helped to identify novel disease genes and pathways (e.g. Assié et al., 2014), enhance risk prediction (e.g. Seoane et al., 2014) and elucidate disease mechanisms (e.g. Chow et al., 2012).

One major focus of integrative multi-omics analysis has been on studying the relationships among different platforms and identifying regulatory modules or gene-sets that are associated with or predictive of clinical outcomes (e.g. Kristensen et al., 2014). In gene-set multi-platform studies, a collection of genes is examined on several platforms, each of which is designed to interrogate different aspects of the gene, e.g. methylation status, expression or copy number and the gene effects of a platform can be more accurately revealed when accounted together with other platforms. By assessing gene effects in a functional context (e.g. pathways and biological processes), gene set integrative analysis improves the detectability, reproducibility and interpretability of significant findings and facilitates the construction of follow-up biological hypotheses (Sass et al., 2013; Tyekucheva et al., 2011; Xiong et al., 2012).

Gene-set integrative approaches can be roughly classified into two types: (a) ‘meta’-based methods and (b) ‘joint-modeling’-based methods. (a) ‘Meta’-based methods first evaluate the association of single genes in a single platform, multi-genes in a single platform or multi-platforms of a single gene, and then integrate relevant summary statistics to obtain the multi-platform association of a gene set (e.g. Paczkowska et al., 2020; Xiong et al., 2012) (b) ‘joint-modeling’-based methods regress the outcome simultaneously on all omics variables from different platforms in a gene set. Such simultaneous modeling can be conducted either in a parallel fashion (which treats omics variable from different platforms equally, e.g. Tyekucheva et al., 2011); or in a hierarchical fashion (which incorporates the regulatory relationships among different platforms as prior knowledge, e.g. Wang et al., 2013; Zhu et al., 2016). Joint modeling approaches tend to outperform meta-based approaches (e.g. Huang et al., 2012; Hu and Tzeng, 2014) because they conduct simultaneous integration across genes and platforms and account for relationships among omics variables. However, joint-modeling methods encounter the challenges of high dimensional variables, which is exacerbated by the typically moderate sample size in multi-omics studies. Various strategies have been proposed to address the high-dimension issue, e.g. dimension-reduction based methods via principal component analysis (PCA; as discussed in Meng et al., 2016), and penalization regressions (as reviewed in Wu et al., 2019).

In this work, we focus on joint modeling methods and propose to use tensor regression framework (Lock, 2018; Zhou et al., 2013) to enhance model efficiency in gene-set integrative analysis. A tensor is a multi-dimensional array (e.g. a vector is an order-1 tensor and a matrix is an order-2 tensor). Because an individual’s gene-set data from multi-platforms have a P × G matrix structure, where P (or G) is the total number of platforms (or genes), the gene-set data of the n samples form an order-3 ($P\times G\times n$) data tensor. Consequently, the regression coefficients form a P × G matrix (denoted by B hereafter) and we can utilize the matrix structure of B to facilitate high-dimensional inference. Specifically, we explore the potential low rank structure of B induced by biological relationship among omics variables so as to use less degrees of freedoms to model the multi-platform variables. Compared to PCA-based methods, which only output pathway-level associations, the tensor-based methods can retain the variable-wise resolution during dimension reduction and reveal associations at gene and platform levels. Compared to penalized-based regressions (e.g. Wu et al., 2019), tensor-based modeling gains additional efficiency by accounting for the inherent structure among omics effects to reduce the number of parameters. More importantly, a tensor model can achieve dimensional reduction even if the coefficient matrix B has a non-sparse structure, such as the polygenic etiology for complex diseases, where signal sparsity can be low due to the likely involvement of many small-effect genes, rather than a few strong-effect genes.

Tensor-based modeling has been used in a variety of genomic applications and demonstrated its utility, e.g. to integrate multiple datasets and explore hidden features among genomic variables (e.g. Li et al., 2011; Ng and Taguchi, 2020; Omberg et al., 2007), to predict patient survival (e.g. Fang, 2019) and to identify genetic interactions (e.g. Wu et al., 2018). These tensor-based methods mainly focus on dimension reduction, feature extraction and outcome prediction. While there exist methods dealing with signal detection, they are either based on variable selection or designed to detect global signals. For example, Wu et al. (2018) use penalization techniques to select significant gene-gene interactions; Hung et al. (2016) consider rank-1 tensor interaction model as a screening tool; and Hung and Jou (2019) derive a global interaction test for tensor regression.

Here, we use the tensor regression framework developed by Zhou et al. (2013) to generalize the conventional regression from 2-dimension data (e.g. n × PG) to 3-dimensional data (e.g. $n\times P\times G$). Specifically, we consider the rank-R tensor decomposition of coefficient matrix and adaptively determine the optimal rank based on the data. We introduce a tensor association test to generate inferences results that can facilitate the prioritization of important omics variables and the comprehension of the relationship between omics variations and outcomes.

2 Materials and methods

2.1 Tensor regression for integrative gene-set analysis

Consider a dataset of n samples. Let y_i, $i=1,\dots n$, be the continuous clinical outcome of subject i. The multi-platform data of the n samples are stored in an order-3 tensor, $\mathcal{X}\in {\mathbb{R}}^{P\times G\times n}$, where P is the number of platforms and G is the number of genes. Let ${\mathbf{X}}_i$ be the i-th slice of $\mathcal{X}$ with respect to the third order, i.e. $\mathcal{X}(:,:,i)$; then $\mathcal{X}={\left\{{\mathbf{X}}_i\right\}}_{i=1,\dots ,n}$ and ${\mathbf{X}}_i$ is the design matrix for the i-th sample with its (p, g)-entry denoted by x_pgi, $p=1\cdots P$ and $g=1\cdots G$. Also define ${\mathit{z}}_i$ the $q\times 1$ covariate vector of sample i including the intercept. In multi-platform analysis, the effects of different platforms for a gene and the effects of different genes within a platform can be highly structured due to the regulatory connections among different levels of molecular events. Therefore, we posit the following order-2 tensor regression model to study the integrative gene-set effects of multi-platform:

$$y_i={\mathit{z}}_i^{\top }\mathit{\beta }+\langle {\mathbf{X}}_i,\mathbf{B}\rangle +{ϵ}_i \text{with} \mathbf{B}={\mathbf{B}}_1{\mathbf{B}}_2^{\top },$$ (1)

where $\mathit{\beta }$ is the parameter vector of the covariates; ϵ_i is the error term for i-th sample following a normal distribution with mean 0 and variance ${\sigma }^2$; $\mathbf{B}\in {\mathbb{R}}^{P\times G}$ is the parameter matrix for the gene-set omics variables; $\langle ·,·\rangle$ is the inner product, and $\langle {\mathbf{X}}_i,\mathbf{B}\rangle =\mathit{vec}{({\mathbf{X}}_i)}^{\top }vec(\mathbf{B})=\sum _{p=1}^P\sum _{g=1}^G{x}_{\mathit{pgi}}{B}_{pg}$ with B_pg the (p, g)-entry of B. Model (1) considers a rank-R tensor decomposition of B, i.e. $\mathbf{B}=\sum _{r=1}^R{\mathbf{B}}_1[,r]{\mathbf{B}}_2{[,r]}^{\top }={\mathbf{B}}_1{\mathbf{B}}_2^{\top }$, with ${\mathbf{B}}_1\in {\mathbb{R}}^{P\times R},\hspace{0.17em}{\mathbf{B}}_2\in {\mathbb{R}}^{G\times R},\hspace{0.17em}R\le \mathit{min}(P,G)$, and ${\mathbf{B}}_{•}[,r]$ being the rth column of Matrix ${\mathbf{B}}_{•}$. A rank-R tensor decomposition (also known as canonical polyadic or CANDECOMP/PARAFAC decomposition) factorizes a tensor into a sum of R rank-1 tensors, where a rank-1 tensor of order D is a tensor which can be expressed as the outer product of D vectors. For D = 2, the outer product of 2 vectors, a and b, is $\mathit{a}{\mathit{b}}^{\top }$. Figure 1 gives a graphical view of the rank-R decomposition of B, where B is expressed as the product of two factor matrices ${\mathbf{B}}_1$ and ${\mathbf{B}}_2$, with their columns formed by the vectors from the corresponding rank-1 components in the decomposition.

Fig. 1.

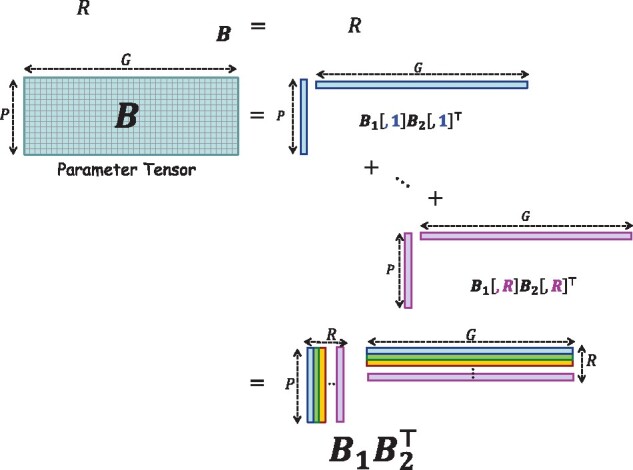
Rank-R tensor decomposition of the (order-2) parameter tensor $\mathbf{B}\in {\mathbb{R}}^{P\times G}$. In the decomposition, B is expressed as the sum of R tensors of rank 1, i.e. $\mathbf{B}=\sum _{r=1}^R{\mathbf{B}}_1[,r]{\mathbf{B}}_2{[,r]}^{\top }={\mathbf{B}}_1{\mathbf{B}}_2^{\top }$, where ${\mathbf{B}}_1\in {\mathbb{R}}^{P\times R}$ and ${\mathbf{B}}_2\in {\mathbb{R}}^{G\times R}$ are called factor matrices, with their columns formed by the vectors from the corresponding rank-1 components

Conceptually we can view that a rank-R tensor model tries to express B_pg, the effect of gene g in platform p, as certain combinations of platform effects and gene effects. To fix the idea, let ${\mathbf{B}}_1[,r]\equiv {\mathit{\alpha }}_{\mathit{r}}={\left[{\alpha }_{r1},\dots ,{\alpha }_{rP}\right]}^{\top }$ and ${\mathbf{B}}_2[,r]\equiv {\mathit{\delta }}_{\mathit{r}}={\left[{\delta }_{r1},\dots ,{\delta }_{rG}\right]}^{\top },\hspace{0.17em}1\le r\le R$. Then in a rank-1 tensor model, ${\mathbf{B}}_1={\mathit{\alpha }}_{\mathit{1}},\hspace{0.17em}{\mathbf{B}}_2={\mathit{\delta }}_{\mathit{1}}$ and $B_{pg}={\alpha }_{1p}{\delta }_{1g}$, i.e. the effect of gene g in platform p is the product of platform effect ${\alpha }_{1p}$ and gene effect ${\delta }_{1g}$. The rank-2 model considers a more complex model, i.e. ${\mathbf{B}}_1=\left[{\mathit{\alpha }}_{\mathit{1}},{\mathit{\alpha }}_{\mathit{2}}\right],\hspace{0.17em}{\mathbf{B}}_2=\left[{\mathit{\delta }}_{\mathit{1}},{\mathit{\delta }}_{\mathit{2}}\right]$ and $B_{pg}={\alpha }_{1p}{\delta }_{1g}+{\alpha }_{2p}{\delta }_{2g}$, which uses two parameters for a platform effect (i.e. ${\alpha }_{1p}$ and ${\alpha }_{2p}$) and two parameters for a gene effect (i.e. ${\delta }_{1g}$ and ${\delta }_{2g}$).

Model (1) is overparameterized and additional constraints are needed to ensure the identifiability of ${\mathbf{B}}_1$ and ${\mathbf{B}}_2$. To see this, consider an non-singular matrix $\mathbf{O}\in {\mathbb{R}}^{R\times R}$ such that $\mathbf{O}{\mathbf{O}}^{-1}=\mathbf{I}$; then given the same B, multiple decompositions are available because $\mathbf{B}={\mathbf{B}}_1{\mathbf{B}}_2^{\top }=\left\{{\mathbf{B}}_1\mathbf{O}\right\}\left\{{\mathbf{O}}^{-1}{\mathbf{B}}_2^{\top }\right\}$. To address the non-identifiability issues, we restrict ${\mathbf{B}}_1$ and ${\mathbf{B}}_2$ to take the following forms:

$${\mathbf{B}}_1=\left[\begin{array}{c}\mathbf{C}\\ {\mathbf{B}}_{12}\end{array}\right] \text{and} {\mathbf{B}}_2=\left[\begin{array}{c}{\mathbf{B}}_{21}\\ {\mathbf{B}}_{22}\end{array}\right]$$ (2)

such that ${\mathbf{B}}_1{\mathbf{B}}_2^{\top }=\mathbf{B}$, where $\mathbf{C}\in {\mathbb{R}}^{R\times R}$ is a constant matrix of rank R, ${\mathbf{B}}_{12}\in {\mathbb{R}}^{(P-R)\times R},\hspace{0.17em}{\mathbf{B}}_{21}\in {\mathbb{R}}^{R\times R}$ and ${\mathbf{B}}_{22}\in {\mathbb{R}}^{(G-R)\times R}$. We show in Supplementary Section S1 that the constrained forms in (2) assure identifiability of ${\mathbf{B}}_1$ and ${\mathbf{B}}_2$.

For the effect matrix B, when $R<\text{min}(P,G)$, the tensor regression can account for the inherent structure among omics effects and reduce the degrees of freedom (df) on modeling omics effects (referred to as omics df) from PG to $R(P+G)-R^2$, where R² df are lost because the R² constraints imposed to ensure model identifiability. When $R=\text{min}(P,G)$, Model (1) has omics df$=R(P+G)-R^2=PG$ and is a compact and structural formulation of the linear regression based on vectorized ${\mathbf{X}}_i$. We show in Supplementary Section S2 that B of rank $R=\mathit{min}(P,G)$ has its elements identical to the regression coefficients in the linear model with vectorized ${\mathbf{X}}_i$. In other words, tensor regression includes the ordinary linear model with vectorized omics covariates as a special case.

To evaluate the significance of the effect of gene g in platform p, we consider a Wald test for $H_0:B_{pg}=0$ under Model (1) with the test statistic $T_{pg}={\widehat{B}}_{pg}/\sqrt{{[\Sigma (\mathbf{C})]}_{pg}}$ where ${\widehat{B}}_{pg}$ is the tensor coefficient estimators, and $\Sigma (\mathbf{C})$ is the variance-covariance matrix of $\widehat{B}$ with ${[\Sigma (\mathbf{C})]}_{pg}$ equal to the variance of ${\widehat{B}}_{pg}$. In Supplementary Section S3, we give the specific formula of $\Sigma (\mathbf{C})$ and show that $\widehat{\mathbf{B}}$ follows a normal distribution asymptotically. Consequently, T_pg follows Normal (0,1) under the null hypothesis. We note that such variable-specific inference has also been discussed in the literature: Zhou et al. (2013) describes general results of the asymptotic property of the order-D tensor parameter estimators; Hung and Jou (2019) discusses the local test as a possible extension of their proposed global test though without further investigations. Here we complement these results by providing the details for the special case of matrix-covariate regressions (i.e. D = 2), and conducting comprehensive numerical examinations on the validity and effectiveness of the tensor testing procedure.

2.2 Estimation and implementation

We use the alternating least square (ALS) algorithm as described in Supplementary Section S4 to estimate the parameters in tensor regression. There are a few issues involved in the estimation of tensor parameters. First, Model (1) is a piece-wise convex function with respect to ${\mathbf{B}}_1$ and ${\mathbf{B}}_2$ (i.e. it is non-convex with respect to ${\mathbf{B}}_1$ and ${\mathbf{B}}_2$ together though is convex in either ${\mathbf{B}}_1$ or ${\mathbf{B}}_2$). To avoid the solutions corresponding to a local minima of the objective function instead of the global minima, we use multiple random initial values and select the solutions resulting from the minimal objective values as the final estimates.

Second, an appropriate rank has to be determined for Model (1). To identify the optimal rank R, we first fit a tensor model using the ALS algorithm for a given rank r, $r=1,\dots \mathit{min}(P,G)$, and then use information criterion to select the optimal model. We consider two information criteria, (a) Akaike information criterion (AIC), i.e. AIC$=-2\hspace{0.17em}\text{log}\hspace{0.17em}L+2k_r$, and (b) Bayesian information criteria (BIC), i.e. BIC$=-2\hspace{0.17em}\text{log}\hspace{0.17em}L+\text{log}(n)k_r$, where $-2\hspace{0.17em}\text{log}\hspace{0.17em}L=c+n\hspace{0.17em}\text{log}\{\sum _{i=1}^n{\left(y_i-{\mathit{z}}_i^{\top }\widehat{\mathit{\beta }}-⟨{\mathbf{X}}_i,{\widehat{\mathbf{B}}}_1{\widehat{\mathbf{B}}}_2^{\top }⟩\right)}^2/n\}$, $c$ is the constant in the log-likelihood function $\log L$, and k_r is the degree of freedom in the rank-r model with $k_r=q+r(P+G)-r^2$.

Third, to improve computational efficiency, we show, in Supplementary Section S3.B, that the proposed tensor inference procedure allows the constant constrain matrix C in ${\mathbf{B}}_1$ to be data-dependent. Consequently, we can (i) estimate the tensor parameters using the proposed ALS algorithm, which greatly reduces the computational cost because ${\mathbf{B}}_1$ and ${\mathbf{B}}_2$ estimates do not need to be re-scaled with respect to the constrain matrix C in each iteration, and (ii) conduct valid inference based on the tensor estimators obtained in this fashion. In variance calculation, we also bypass the need of permutation matrices by using the box products, which avoid the storage and matrix multiplication involved with permutation matrices and further save computational time.

2.3 Simulation studies

We conduct simulations to evaluate the performance of the proposed tensor regression for identifying important omics variables. For evaluation purposes, we implement 3 tensor regression (TR) models: TR evaluated at true rank (TR.true); TR evaluated at AIC-selected rank (TR.AIC); and TR evaluated at BIC-selected rank (TR.BIC). We consider two baseline methods that represent the two common strategies applied on vectorized omics variables: (i) linear regression model (LM) and (ii) penalized regression via lasso (LASSO) using BIC to select the tuning parameter.

We generate the design matrix of an individual based on the pathway, Reactome Processing of Capped Intron-Containing Pre-mRNA (M13087), as defined in MSigDB; the pathway data are obtained from the TCGA breast cancer dataset as in Hu and Tzeng (2014). Briefly, level 3 gene-summary data were obtained from copy number variation (CNV), methylation and RNA-Seq values for 530 samples and 10 371 common genes shared among the 3 platforms. The CNV values were provided in log2 format. For methylation, the beta values of all probes mapped to a gene were first computed and then converted into the mean M value (Du et al., 2010). For RNA-Seq data, the log2 reads per kilobase million (RPKM) were used as gene expression values. Within each platform, the data were then standardized to have mean 0 and standard deviation 1 across samples. Finally data from pathway M13087 were retrieved, which contains 74 genes and are used to simulate the outcome variables.

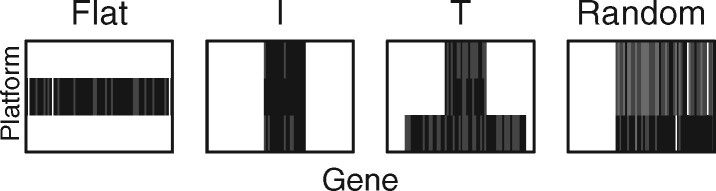
Denote the data tensor of pathway M13087 as ${\mathcal{X}}^{*}$, which has dimension (3, 74, 530), and rewrite the ith slice of ${\mathcal{X}}^{*}$ as ${\mathbf{X}}_i^{*}$. Then given ${\mathbf{X}}_i^{*}$, we simulate the outcome value y_i, $i=1,\dots ,530$, from the model $y_i={\mathit{z}}_i^{\top }\mathit{\beta }+\langle {\mathbf{X}}_i^{*},\mathbf{B}\rangle +{ϵ}_i$, where ${\mathit{z}}_i$ is a 5 × 1 covariate vector generated from N(0,1), $\mathit{\beta }={(1,1,1,1,1)}^{\top }$, the error term ϵ_i is also from N(0,1), and the non-zero entries of coefficient matrix B are generated from normal with mean d and standardized deviation $d^2/4$. We consider 4 signal patterns of B (i.e. the shape of the non-zero coefficients in B) as shown in Figure 2: i) a horizontal bar shape of B with rank 1, which is referred to as the ‘flat’ shape and represents multiple causal genes in a single platform; (ii) a rectangular shape of B with rank 1, which is referred to as the ‘I’ shape and represents a few local causal genes with effects from all platforms; (iii) a upside-down T shape of B with rank 2, which is referred to as the ‘T’ shape and represents a few master CNVs and methylations affecting the expressions of multiple genes; and (iv) a random pattern of B with rank 2, which is referred to as the ‘Random’ shape and represents a random but low-rank structure.

Fig. 2.

Signal shapes of coefficient matrix B considered in the simulation. The rectangles represent matrix B; rows represent different platforms; and columns represent different genes. Omics variables with non-zero effect coefficients are marked in black and the null variables with zero coefficients are marked in white.

For a given B shape and effect strength d, we simulated k replications to evaluate the performance of TR, LM and LASSO in selecting important omics variables. We consider d = 0.125, 0.25 or 1, and k = 200 (or 10⁵ in some sub-scenarios). We compute 3 metrics: true positive rate (TPR), false discovery rate (FDR) and the composite metric F-measure. TPR is obtained by first computing the proportion of selected omics variable among all causal variables (i.e. $B_{pg}\ne 0$) in each replication and then averaging across all replications. FDR is obtained by first computing the proportion of null variables (i.e. B_pg = 0) among all selected variables in each replication and then averaging across all replications. F-measure is obtained by first computing the harmonic mean of the TPR and (1–FDR) in each replication and then averaging across all replications. For LM and TR, a variable is selected if the P-value of a variable <0.05 unless stated otherwise; for LASSO, a variable is selected if the LASSO coefficient is not 0. We conduct all analyses using the standardized variables, i.e. each variable has mean 0 and variance 1 for better comparability among omics variables.

The data tensor of pathway M13087, ${\mathcal{X}}^{*}$, has a high degree of correlation among the omics variables: Among the 3 × 74 omics variables, there are 413 variable pairs with the absolute pairwise correlation >0.6, and 26 pairs >0.9. The median, third quartile and maximum of the variance inflation factors (VIF) of the omics variables are 5.04, 7.85 and 140.39, respectively. To examine the impact of correlated variables on the method performance, we also repeat the simulation studies using pseudo-data tensors that remove the correlation among genes. We refer to the simulations as ‘gene de-correlation’ simulations, and describe the design and results in Supplementary Section S5.

3 Results

3.1 Simulation studies

We first examine the performance of AIC and BIC in determining the model rank. Table 1 summarizes the rank of TR model determined using AIC and BIC across different B shapes and effect strength d, with 200 replications under each scenario. The results suggest that (i) BIC has higher proportions to select the true rank than AIC when the effect strength is large (e.g. d = 1). However, when the effect strengths are moderate or small, both AIC and BIC cannot always select the true rank, and BIC has lower correct proportions (e.g. in T-shape and random-shape). (ii) When an incorrect rank is selected, BIC tends to under-estimate the model rank while AIC tends to over-estimate the model rank.

Table 1.

Model rank determined using AIC and BIC for tensor regression (TR) model

	TR.AIC			TR.BIC
	Selected Rank			Selected Rank
B shape = Flat	1	2	3	1	2	3
$d=$ 0.125	0.990	0.005	0.005	1.000	0.000	0.000
$d=$ 0.25	1.000	0.000	0.000	1.000	0.000	0.000
$d=$ 1	0.995	0.000	0.005	1.000	0.000	0.000
B shape = I	1	2	3	1	2	3
$d=$ 0.125	0.640	0.360	0.000	1.000	0.000	0.000
$d=$ 0.25	0.630	0.360	0.010	0.630	0.370	0.000
$d=$ 1	0.615	0.375	0.010	0.620	0.380	0.000
B shape = T	1	2	3	1	2	3
$d=$ 0.125	0.020	0.640	0.340	1.000	0.000	0.000
$d=$ 0.25	0.000	0.605	0.395	0.600	0.400	0.000
$d=$ 1	0.000	0.850	0.150	0.000	0.910	0.090
B shape = Random	1	2	3	1	2	3
$d=$ 0.125	0.790	0.190	0.020	0.930	0.070	0.000
$d=$ 0.25	0.150	0.800	0.050	0.890	0.110	0.000
$d=$ 1	0.000	0.945	0.055	0.000	1.000	0.000

Note: The table shows the proportion of a certain rank value is selected by AIC or BIC. For a given B shape, results of true rank are shown in shaded bold; d indicates the effect strength of causal omics variables.

Supplementary Figure S1 shows the quantile-quantile (QQ) plots of the null P-values of TR test from different TR models. For a given B shape, the null P-values are obtained from those omics variables with B_pg = 0 when causal omics variables have effect strength d = 0.125, 0.25 or 1. Under TR.true, the null P-values are around the 45 degree line across different B shapes and different effect strength, confirming the validity of the tensor test. When the TR model is fitted with estimated rank (i.e. TR.AIC and TR.BIC), most of the QQ plots indicate valid null distributions; the two exceptions are the null P-values from TR.BIC under the scenario of T-shape with d = 0.125 and 0.25, where the null distributions are severely deviated from the expected Uniform (0,1). Under the T-shape scenario with d = 0.125 and 0.25, BIC tends to under-estimates the model rank and results in incorrect estimates of B_pg’s and incorrect null distributions. On the other hand, the QQ plots for TR.AIC suggest that over-estimating the rank has little impact on the null distributions. Although fitting a lower-rank model may not always lead to a deviated null distribution (e.g. ‘Random’-shape with d = 0.125 and 0.25), for robustness, we recommend to use AIC to determine model rank.

Tables 2 explores the performance of selecting causal omics variables under different B shapes and effect strength d. We focus on the comparisons of TR.AIC against other models. Compared to TR.true, TR.AIC has similar or higher F-measures, indicating a minor impact on selection performance due to unknown rank. Compared to LM, TR.AIC has higher or comparable F-measures, and the gain of TR.AIC is more obvious when the effect strength is not large (e.g. d < 1). The higher F-measures of TR.AIC tend to arise from higher TPRs while retaining comparable FDRs compared to LM. While LASSO can have higher F measures than LM in multiple scenarios, it has lower F measures than TR.AIC in almost all scenarios except one (i.e. B shape ‘Flat’ with d = 0.125). Although LASSO tends to have the highest TPRs among TR.AIC, LM and LASSO, it also has the highest FDRs, which results in lower F measures than TR.AIC. Finally, we observe that under the ‘T’ shape with d = 0.125 and 0.25, TR.BIC has unusually high FDRs compared to other TR methods, which agrees with the deviation observed in the QQ plots in Supplementary Figure S1.

Table 2.

Performance of selecting causal omics variables under different B shapes for different methods, including tensor regression evaluated at true rank (TR.true), at AIC determined rank (TR.AIC) and at BIC determined rank (TR.BIC), as well as linear regression model (LM) and LASSO on vectorized omics variables, based on 200 replications

	B shape = Flat					B shape = I					B shape = T					B shape = Random
	TR.	TR.	TR.	LM	LASSO	TR.	TR.	TR.	LM	LASSO	TR.	TR.	TR.	LM	LASSO	TR.	TR.	TR.	LM	LASSO
	true	AIC	BIC			true	AIC	BIC			true	AIC	BIC			true	AIC	BIC
$d=$ 0.125
TPR	0.371	0.370	0.371	0.274	0.683	0.695	0.698	0.695	0.214	0.664	0.736	0.744	0.981	0.669	0.832	0.626	0.849	0.892	0.396	0.796
FDR	0.044	0.047	0.044	0.257	0.275	0.222	0.146	0.222	0.331	0.429	0.127	0.094	0.442	0.076	0.317	0.043	0.032	0.027	0.053	0.184
F-measure	0.530	0.529	0.530	0.398	0.702	0.731	0.756	0.731	0.321	0.613	0.797	0.813	0.711	0.776	0.750	0.756	0.899	0.929	0.557	0.806
$d=$ 0.25
TPR	0.649	0.649	0.649	0.564	0.753	0.795	0.870	0.873	0.554	0.855	0.868	0.899	0.973	0.809	0.939	0.860	0.872	0.969	0.709	0.914
FDR	0.033	0.033	0.033	0.141	0.320	0.235	0.118	0.116	0.158	0.423	0.141	0.057	0.288	0.061	0.332	0.032	0.034	0.044	0.030	0.189
F-measure	0.773	0.773	0.773	0.679	0.714	0.779	0.875	0.877	0.666	0.688	0.863	0.919	0.807	0.869	0.780	0.911	0.915	0.962	0.819	0.860
$d=$ 1
TPR	0.954	0.954	0.954	0.932	0.965	0.815	0.914	0.914	0.895	0.957	0.967	0.979	0.980	0.971	0.990	0.961	0.960	0.961	0.936	0.967
FDR	0.036	0.037	0.036	0.093	0.412	0.238	0.107	0.106	0.103	0.475	0.081	0.055	0.053	0.055	0.350	0.025	0.026	0.025	0.025	0.231
F-measure	0.954	0.954	0.954	0.919	0.730	0.785	0.902	0.903	0.895	0.677	0.942	0.962	0.963	0.957	0.784	0.968	0.967	0.968	0.955	0.856

Note: TPR = true positive rate; FDR = false discovery rate; d indicates the effect strength of causal omics variables. For TR and LM, a variable is selected as important if P-value < 0.05. The best performed methods among TR.AIC, LM and LASSO, judged by F-measures, are shown in shaded cells.

In Supplementary Table S1, we repeat the above simulation 10⁵ times based on d = 0.25, and evaluate the selection performance of TR models using two different selection rules for TR and LM: (a) P-value < 0.05 and (b) Benjamini-Hochberg FDR (BH-FDR) < 0.05 for multiple testing. The results show that using either selection rule, TR.AIC has higher F measures than LM and LASSO in almost all B shapes, except for ‘Flat’ with Rule (b), where LASSO has the highest F measure. In Supplementary Section S5 (i.e. Supplementary Figure S2; Supplementary Tables S2A–C), we show that the results of the ‘gene de-correlation’ simulation agree with the aforementioned findings based on correlated variables.

3.2 Analysis of the CCLE dataset

3.2.1 Omics biomarkers for Vandetanib

Lung cancer is the leading cause of cancer-related death in the United States and worldwide (Siegel et al., 2019). Targeted therapy, especially drugs that target EGFR, has been shown to be a promising therapeutic method against lung cancer (e.g. Murtuza et al., 2019; Rolfo et al., 2015). Our previous study suggested that Vandetanib (ZD6474) has the strongest inhibitory effects among those drugs targeting EGFR for lung cancer treatment (Lu et al., 2013). Focusing on Vandetanib, here we analyze the multi-platform data from the cancer cell line encyclopedia (CCLE) project (Barretina et al., 2012; https://portals.broadinstitute.org/ccle/about), with an aim to identify important omics variables affecting the drug sensitivity of Vandetanib. CCLE provides a detailed genetic and pharmacologic characterization of human cancer models, which contains (i) multi-omics data of 947 human cancer cell lines encompassing 36 tumor types, e.g. DNA copy numbers, methylation and mRNA expression; as well as (ii) pharmacologic profiling of 24 compounds across ∼500 of these cell lines.

For the analysis, we focus on lung-cancer cell lines and download their CCLE data from $P=3$ platforms, i.e. copy-number values per gene, DNA methylation (promoter 1 kb upstream TSS) and RNAseq gene expression (for 1019 cell lines). We use the mean M values of a gene for methylation. For gene expression, we first perform quantile-normalization of the RPKM values across all genes and then retrieve the values of the targeted genes. We consider the gene set that consists of genes involved in the protein–protein interaction (PPI) network of EGFR (as defined in STRING, Version 11.0; https://string-db.org/). For method evaluation purposes, we also include 3 ‘null’ genes to serve as negative controls, for which we arbitrarily select 3 housekeeping genes (i.e. ACTB, GAPDH and PPIA) and reshuffle their values across individuals. After removing genes and cell lines with substantial missing values, there are n = 68 lung-cancer cell lines with omics variables from 7 PPI genes of EGFR (i.e. EGFR, EREG, HRAS, KRAS, PTPN11, STAT3 and TGFA). The outcome variable is the drug sensitivity of Vandetanib, quantified by the log-transformed activity area. Higher activity area indicates that a cell line has better sensitivity to the drug. We standardize each omics variable to mean 0 and variance 1, and conduct integrative gene-set analysis using 3 methods: TR.AIC, LM and LASSO. For TR.AIC and LM, we select a variable if P-value <0.05.

The TR model of rank 1 has the smallest AIC values among the 3 possible ranks (1, 2 and P = 3). TR.AIC (rank-1) model identifies 2 important omics variables, i.e. EGFR methylation (coefficient -0.2416; P-value 0.0022) and EGFR CNV (coefficient 0.2508; P-value 0.0061). LM does not select any variables as important, although both EGFR methylation and CNV have their P-values around 0.05 [i.e. (coefficient, P-value) = (-0.2094, 0.0584) and (0.2260, 0.0568), respectively]. LASSO identifies 11 variables as important, including the two TR.AIC-selected variables and four variables from negative control genes (see Table 3). It is not surprising to observe that LASSO selects many variables, given the performance patterns observed in the simulation studies. A rough, conservative estimate of FDR for LASSO is 4/11 = 0.36, which generally agrees with the FDR observed in the simulations. For those variables identified by both LASSO and TR.AIC, the LASSO estimates are closer to 0 compared to the estimates of TR.AIC and LM, which are not unexpected as LASSO tends to shrink the coefficients to zero. Finally, as a sensitive analysis, we also perform multi-platform gene-set analysis on the 7 PPI genes only (see Supplementary Table S3). The results are generally comparable with the 10-gene analysis. Some subtle differences include (i) in LM, EGFR methylation and EGFR CNV have their P-values < 0.05 [with (coefficient, P-value) = (-0.2671, 0.0112) and (0.2818, 0.0127), respectively)] and (ii) LASSO selects one additional variable, EREG methylation, though its coefficient is very small (i.e. 0.0035).

Table 3.

Effect estimates of omics variables on the drug sensitivity of Vandetanib in the CCLE analysis

	CNV					Methylation					mRNA Expression
	TR.AIC		LM		LASSO	TR.AIC		LM		LASSO	TR.AIC		LM		LASSO
EGFR	0.2508	(0.0061)	0.2260	(0.0568)	0.1256	−0.2416	(0.0022)	−0.2094	(0.0584)	−0.1531	0.0893	(0.2605)	0.1506	(0.1462)	0.1074
EREG	−0.0075	(0.8833)	0.0891	(0.3350)	0	0.0072	(0.8841)	0.0887	(0.3446)	0	−0.0027	(0.8855)	0.0627	(0.4830)	0
HRAS	−0.0487	(0.4195)	−0.1187	(0.2268)	−0.1115	0.0469	(0.4421)	−0.0197	(0.8258)	0	−0.0173	(0.5599)	−0.0388	(0.6989)	0
KRAS	−0.0267	(0.6003)	0.0707	(0.6149)	0	0.0257	(0.6026)	−0.0457	(0.6743)	0	−0.0095	(0.5897)	−0.1515	(0.1888)	−0.0428
PTPN11	0.0919	(0.1428)	0.0070	(0.9470)	0	−0.0886	(0.0877)	−0.0876	(0.4064)	0	0.0327	(0.3238)	0.1373	(0.2004)	0
STAT3	−0.0575	(0.3021)	−0.0703	(0.5088)	0	0.0554	(0.2685)	0.1639	(0.0977)	0.0012	−0.0205	(0.4290)	0.0275	(0.8138)	0
TGFA	0.0505	(0.4308)	0.1139	(0.2231)	0	−0.0486	(0.4135)	0.0718	(0.4111)	0	0.0180	(0.4961)	0.0260	(0.8009)	0.0355
Neg. Control 1	−0.0311	(0.5536)	0.0116	(0.8950)	0	0.0299	(0.5618)	0.0649	(0.4089)	0	−0.0111	(0.6380)	−0.0970	(0.2679)	−0.0345
Neg. Control 2	−0.0412	(0.4098)	−0.0389	(0.6686)	0	0.0397	(0.4053)	0.0374	(0.6657)	0.0053	−0.0147	(0.5112)	0.1451	(0.0958)	0.0502
Neg. Control 3	−0.0430	(0.5028)	−0.0855	(0.3094)	−0.0465	0.0414	(0.4921)	−0.0259	(0.7661)	0	−0.0153	(0.5745)	0.0014	(0.9913)	0

Note: Values in parentheses are the corresponding P-values. Shaded cells indicate ‘important’ omics variables affecting Vandetanib sensitivity. For tensor regression (TR.AIC) and linear model (LM), a variable is selected as important if P-value < 0.05. For LASSO, a variable is selected if it has non-zero coefficient.

Because the direct gene target of Vandetani is EGFR, one may expect EGFR expression to be associated with Vandetanib efficacy. Indeed, in single-platform gene-set analyses using linear model on CNV, methylation and expression separately, EGFR expression is the most significant variable associated with Vandetanib efficacy (coefficient 0.2575; P-value 0.0008), followed by EGFR CNV (coefficient 0.2335; P-value 0.0046). EGFR methylation also has its P-value <0.05 (coefficient -0.2104; P-value 0.0354) in the single-platform analysis, and becomes the most significant variable in the joint multi-platform TR analysis. The single-platform and multi-platform results suggest that the association between EGFR expression and Vandetanib efficacy might be modulated by its methylation, and the impact of methylation appears when all platforms are evaluated together. Previous studies have demonstrated that the methylation level of EGFR can regulate its downstream gene expression level of EGFR (e.g. Pan et al., 2015). Pan et al. (2015) also showed that methylation changes in the EGFR promoter region can be a predictor of the EGFR-targeted therapy. The results concurred with our findings, with the negative coefficient of EGFR methylation suggesting that an increase in methylation decreases the drug sensitivity (Zhang and Chang, 2008). In addition, Kris et al. (2003) directly manipulated the methylation level of EGFR in lung cancer cells and investigated the drug response of gefitinib, which is another EGFR-target therapy drug. Their results further suggest that blockade of DNA methylation level in EGFR may improve the anti-tumor effects of EGFR-target therapy in non-small cell lung cancer.

3.2.2 Omics biomarkers for Paclitaxel

Supplementary Section S6 presents another application that focuses on the drug sensitivity of paclitaxel, one of the most commonly used chemotherapy drug. The data consist of $P=$2 platforms (i.e. mRNA expression and protein expression), $G=$55 genes from 5 KEGG (Kyoto Encyclopedia of Genes and Genomes) pathways related to cell cycle and cell death, and n = 340 pan-cancer cell lines.

4 Conclusion and discussion

In this work, we illustrate the use of tensor regression (TR) for joint modeling of gene-set multi-omics variables and propose a tensor-based association test for identifying important omics biomarkers for continuous outcomes. With the derived normality of tensor effect estimates, it is also straightforward to compute confidence intervals of the omics effects. The rationale behind tensor modeling is based on the observation that omics variables are structurally related—genes from a biological process regulate and interact with each other, and the omics variables across platforms follow a natural flow as described in the central dogma of biology. Accounting for the fundamental relationships among omics variables across genes and platforms can more precisely model the biological effects and enhance the ability to detect true associations. TR adopts a matrix-structured formulation of the omics effects B to account for the inter-relationship among omics effects and may improve modeling efficiency: If B has a low-rank structure, TR can use fewer parameters to capture the underlying relationship between outcome and omics variables and boost detecting power. If B has full rank, TR is equivalent to the conventional linear regression model (LM) on vector-valued omics variables. Our investigation suggests that using AIC to determine the model rank would yield better performance on selecting important variables than using BIC.

Existing tensor-based tests mainly focusing on variable screening or global testing; variable screening aims to retain majority of true signals by tolerating a fair amount of false positives; global testing aims to assess the overall effect of a variable set and lacks variable-wise information. Here we explore variable-specific tensor tests that aims to have enhanced power and well-controlled false positive rates for selecting important omics biomarkers. We investigate the behavior and utility of tensor test under different effect strength and effect patterns. With a small number of platforms (i.e. $P=3)$, we observe substantial performance gain; we expect the gain can be more significant when more different types of omics data become available in real practice. To assure the validity of the variable-specific tensor test, in the proposed TR analysis, we do not always impose low-rank approximation of the parameter tensor B as typically done in global tests (e.g. Hung et al., 2016; Hung and Jou, 2019). Instead, we let the data determine the optimal rank of B among multiple possible models, including the full-rank LM. For integrative analysis, such strategy also makes tensor analysis an appealing alternative to LM (e.g. Tyekucheva et al., 2011), as tensor modeling not only includes LM as a special case, but also other low-rank models that are more parsimonious and may boost selection performance. The major price is perhaps the additional computational cost, as one needs to fit a tensor model for every possible rank r, $1\le r\le \mathit{min}(P,G)$. To reduce computational burden, we adopt a ‘speed-up’ version of ALS algorithm, which is achieved by relaxing the constrain matrix C in ${\mathbf{B}}_1$ to be data-dependent and consequently simplifies the computation in each iteration. We derive the normality, variance formula and inference procedure for the tensor estimators obtained in this fashion. We also avoid permutation matrices in our variance calculation to further save computational time.

One commonly encountered issue in joint analysis of gene-set multi-platform data is multicollinearity induced by strong correlation among different genes and platforms. Although TR does not specifically address multicollinearity, we notice that standardizing each omics variable, which was implemented to assure comparability among variables, helps to fix multicollinearity. The reason is twofold. First, TR by nature is more robust to multicollinearity than LM because TR uses a more parsimonious parameterization. Second, standardization increases the numerical stability of matrix inversions involved in TR model fitting when variables are correlated, and hence stabilizes the estimation of the TR coefficients and their standard deviations under multicollinearity. We also note that an alternative remedy for multicollinearity is to impose a ridge penalty (Hoerl and Kennard, 1970); yet doing so would invalid the ordinary significant tests of the coefficients. We are studying different methods for inference on ridge coefficients under TR framework, including those based on Cule et al. (2011), bootstrapping and debiasing.

There are also limitations with the proposed tensor tests for biomarker detection. First, because the rank of $\mathbf{B}=0$ is undefined, the gene set to be analyzed needs to include at least one outcome-associated variable. Therefore the proposed test would be more suitable for follow-up analysis of a gene set that has shown set-level of significance. Second, the parameter tensor requires omics variables of different platforms to be aligned to the same genes. Hence tensor regression modeling would suffer more severely from the impact of missing data if complete-data analysis is performed. As missing data are commonly observed in multi-platform studies due to experimental conditions and platform constraints, careful treatments of missing data with imputation-based methods may further ensure the utility of tensor-based analysis of gene-set multi-omics data. Finally, as a proof of concept, we introduce the tensor test by focusing on continuous outcomes. Although theoretically feasible, extension to binary outcomes is a more challenging task than expected in its numerical implementation, because specifying omics parameters in a structural tensor format complicates the numerical properties such as convergence and stability, as encountered in our studies of binary outcomes. We are continuing to explore algorithms to enhance numeral stability of the tensor estimates with binary outcomes.

Funding

This work was partially supported by National Institutes of Health Grants [P01CA142538 to W.L. and J.Y.T., 1UL1TR001412 to J.C.M.], and Taiwan Ministry of Science and Technology Grants [MOST-109-2118-M-006-006 to S.M.C., MOST-107-2118-M-002-004-MY3 to H.H., MOST-106-2314-B-002-134-MY2 to T.P.L., MOST-104-2314-B-002-107-MY2 to T.P.L., MOST-108-2314-B-002-103-MY2 to T.P.L.].

Conflict of Interest: none declared.