Abstract
Force-sensitive arrest peptides regulate protein biosynthesis by stalling the ribosome as they are translated. Synthesis can be resumed when the nascent arrest peptide experiences a pulling force of sufficient magnitude to break the stall. Efficient stalling is dependent on the specific identity of a large number of amino acids, including amino acids that are tens of angstroms away from the peptidyl transferase center (PTC). The mechanism of force-induced restart and the role of these essential amino acids far from the PTC is currently unknown. We use hundreds of independent molecular dynamics trajectories spanning over 120 s in combination with kinetic analysis to characterize multiple barriers along the force-induced restart pathway for the arrest peptide SecM. We find that the essential amino acids far from the PTC play a major role in controlling the transduction of applied force. In successive states along the stall-breaking pathway, the applied force propagates up the nascent chain until it reaches the C-terminus of SecM and the PTC, inducing conformational changes that allow for restart of translation. A similar mechanism of force propagation through multiple states is observed in the VemP stall-breaking pathway, but secondary structure in VemP allows for heterogeneity in the order of transitions through intermediate states. Results from both arrest peptides explain how residues that are tens of angstroms away from the catalytic center of the ribosome impact stalling efficiency by mediating the response to an applied force and shielding the amino acids responsible for maintaining the stalled state of the PTC.
Significance
As nascent proteins are synthesized by the ribosome, their interactions with the environment can create pulling forces on the nascent protein that can be transmitted to the ribosome’s catalytic center. These forces can affect the rate and outcomes of translation. We use simulations to characterize the pathway of force transduction along arrest peptides and discover how secondary structure in the nascent protein and its interactions with the ribosome exit tunnel impede force propagation. This explains how amino acids in arrest peptides that are tens of angstroms away from the ribosome’s catalytic center contribute to stalling and, more broadly, suggests how structural features in the nascent protein dictate the ribosome’s ability to functionally respond to its environment.
Introduction
Regulation of protein expression levels is an essential part of maintaining cellular homeostasis. Although this is most commonly performed at the nucleotide level by controlling rates of transcription initiation or ribosome binding, regulation at the translational level allows for immediate control of protein levels (1). One method of translation-level regulation utilizes arrest peptides, which are short amino acid sequences that induce a stall in ribosomal translation when synthesized, until an external signal breaks the stall (2). Force-sensitive arrest peptides (FSAPs) are a class of arrest peptides that allow for the restart of translation with a force-dependent rate (3). Physiologically, these peptides act as a force sensor associated with the integration of nascent proteins into the membrane or translocation across the membrane. For example, the Escherichia coli FSAP SecM is able to regulate expression of the translocase SecA because restart of SecM-stalled translation is dependent on the pulling force exerted by SecA on the nascent peptide (4). SecM has also been used as a powerful biophysical tool to measure in vivo forces arising from membrane integration (5), cotranslational folding (6,7), and charge translocation (8). The relationship between force and restart rate was quantitatively characterized through optical tweezer experiments on SecM-stalled ribosomes (3) Understanding the mechanism through which forces propagate up the nascent chain and break the stall of FSAPs will not only shed light on an essential mode of regulation in biology but also provide insights for the design of mutants that respond to forces with greater dynamic range and sensitivity, thereby enabling wider application of FSAPs as in vivo force sensors (9,10).
Considerable progress has been made in understanding the molecular mechanism behind FSAP stalling. SecM was the first FSAP identified and remains one of the best characterized. The requisite sequence in SecM for stalling has been narrowed down to a stretch of 17 amino acids, of which nine amino acids are essential for efficient stalling (11,12). Cryogenic electron microscopy (cryo-EM) structures have identified several SecM-stalled states with different ribosome conformations and transfer RNA (tRNA) occupancies (13,14). A common feature of the different stalled ribosomes is that their conformations around the peptidyl transferase center (PTC) resemble the structure of the uninduced state of the ribosome, characterized by Schmeing et al., in which the P-site tRNA is protected from nucleophilic attack (15). The importance of particular residues is made clear by the SecM-stalled structures; for example, the essential C-terminal R163 interacts with several neighboring nucleotides to distort the PTC geometry (16). However, other amino acids essential for efficient stalling, such as F150 and W155, are more than 10 Å away from the PTC and have no obvious role in altering the conformation of the ribosome. Although structural data show the essential residues far from the PTC are interacting with ribosomal proteins and RNA in the exit tunnel, there are no large-scale rearrangements in the ribosome that could lead to propagation of this signal through the ribosome (13,17, 18, 19). Instead, these residues are suggested to increase stalling by precisely arranging the conformation of C-terminal portion of the nascent chain or by controlling the degree of compaction in exit tunnel (10,20). The molecular details of how these essential C-terminal amino acids induce this arrangement have not yet been uncovered.
More recently, the structures of ribosomes stalled by VemP and MifM, two other FSAPs, have been solved (19,21). These peptides share many of the same features as SecM, including the stabilization of the uninduced state of the ribosome and the presence of many essential amino acids positioned far down the exit tunnel (15). Despite these similarities, there are also significant differences between these more recently characterized peptides and SecM, most notably the secondary structure and compaction of the nascent chain in VemP and the species specificity of MifM.
Although the available structures provide insight into how arrest peptides stall translation, the mechanism of force-dependent restart is less well understood. Experiments using optical tweezers were able to quantify the relationship between the applied force and restart rates (3), and a series of mutant arrest sequences identified amino acids critical to maintaining the stall in both the presence and absence of an applied force (10,20,22). However, these data are insufficient to reconstruct the molecular mechanism of force-induced restart. Because most experiments only report on when translation is able to restart, little is known about the conformational changes that FSAPs undergo before restart, including the number of transitions, their relative barrier heights, and whether they progress in a consecutive, random, or concerted manner. In the current work, a molecular picture of the stall-breaking processes is revealed by microsecond-timescale molecular dynamics (MD) simulations of the SecM and VemP FSAPs with an applied force on the N-terminus. Analysis of over 150 independent stall-breaking events uncovered a conserved multistep pathway in which pulling forces are unable to disrupt the conformation around the PTC until key interactions formed by the N-terminal regions of the arrest peptides are broken. We characterize the locations and height of these barriers and propose a role for the essential amino acids far from the PTC in which they control force propagation. This suggests a mutation strategy to produce FSAPs with altered force sensitivity. Comparison between the stall-breaking pathways of SecM and VemP highlights how interactions between the nascent peptide and the ribosome alter force transduction differently than intrachain interactions. Beyond FSAPs, cotranslational forces have been shown to be able to influence the rates and even outcomes of translation (23,24); thus, a better understanding of the factors that control force propagation in the exit tunnel also provides valuable insight into how ribosomes are able to sense and respond to their environment via the nascent protein.
Materials and methods
Simulation setup
Simulations of SecM were initialized from the 3.6-Å resolution Protein Data Bank structure PDB: 3JBU (13). System preparation was performed using Schrödinger Maestro. First, the covalent peptidyl-tRNA bond was manually restored. The structure was then truncated by removing amino acids with any heavy atoms 24 Å beyond the region of interested, defined as the SecM nascent chain and first three nucleotides of the P-site tRNA. This region was chosen to be sufficiently large to minimize the influence of the truncated region, as they lie beyond the cutoff distance for the nonelectrostatic interactions of the MD force field. Additionally, high-resolution structures of stalled ribosomes do not suggest large-scale conformational changes beyond the PTC (13,17, 18, 19), in contrast to earlier studies analyzing lower-resolution stalling peptide structures (25). Any amino acid or nucleotide monomers created by the truncation were removed. The SecM nascent chain was cut off at Leu149, and a SerGlySer linker was appended to the N-terminus. Hydrogens were modeled in, and N- and C-termini newly created by the truncation were capped with acetyl and N-methyl amide groups, respectively. Minimization was performed to alleviate clashes formed by the newly added capping groups. The structure was then solvated with TIP3P water and neutralized with Mg2+. Solvation filled the orthorhombic periodic simulation box, which was set to extend 10 Å beyond the truncated ribosome. The ribosome was oriented to minimize the volume of the box. To retain the structure of the ribosome despite the truncation, all nonsolvent heavy atoms 20 Å away from the region of interest were restrained with 1 kcal/mol/Å harmonic restraints. RATTLE restraints were applied to enable production time steps of 2.5 fs. The full system consists of 117,000 atoms. Initial simulation was run for 30 ns using the AMBER99SB-ILDN force field (26), the Desmond simulation package (27), and a time step of 1.5 fs. The same steps were used to prepare the VemP structure from the 2.9 Å-resolution structure PDB: 5NWY, with no truncation of the nascent chain (19). Extensive equilibration was then performed on Anton2. All Anton simulations were conducted with a time step of 2.5 fs. SecM was equilibrated for 1000 ns, and VemP was equilibrated for 500 ns. Simulations of mutant SecM were prepared starting from the SecM structure after equilibration. After mutations were introduced, each structure was re-equilibrated for 250 ns.
Force-pulling protocol
The pulling direction was determined by identifying the vector that extends from the N-terminal α-carbon of SecM or VemP and maximizes the distance between any point along the vector and the atoms of the ribosome. The optimal vector passes through the exit tunnel and maintains a distance of greater than 6 Å from any ribosomal atoms at all times.
Pulling is performed by applying a 1 kcal/mol/Å harmonic potential to the N-terminal α-carbon that constrains the distance between the α-carbon and a point 30 Å away from the α-carbon in the direction of the pulling vector. Initially, this distance is set to the equilibrium distance of 30 Å, such that there is no force applied to the α-carbon. This distance is decreased linearly with time, applying increasing force to the N-terminal α-carbon. Initial structures are drawn randomly from the last quarter of the equilibration simulations. We explore different force loading rates of 0.5, 5, and 50 pN/ns. Simulations for were run 6.5 s, 650 ns, and 78 ns, respectively. These times correspond to halting the simulation when the minimum of the harmonic potential used to apply the pulling force was 45 Å away from initial position of the SecM N-terminus. For the fastest force loading rate of 50 pN/ns, this was extended to 55 Å to ensure all conformational transitions were observed. In total, 30 independent simulations were performed at the force loading rates of 5 and 50 pN/s. Because of the longer simulations required, only five trajectories were run with a force loading rate of 0.5 pN/ns. For all simulations, frames are recorded every 1.5 ns. See Table S2 for a list of all simulations performed.
Simulations to measure the force at the C-terminus of SecM were performed as described above but with the addition of a 1 kcal/mol/Å harmonic restraint on the α-carbon of Arg163 or Gly165. The minimum of the harmonic potential was centered on the α-carbon’s position in the cryo-EM structure. In total, 25 independent trajectories were run with a loading rate of 50 pN/s and C-terminal restraint on Arg163, 10 trajectories with a loading rate of 5 pN/s and C-terminal restraint on Arg163, and 10 trajectories with a loading rate of 50 pN/s and C-terminal restraint on Gly165. Simulations of mutant SecM were performed with a force loading rate of 50 pN/ns. In all, 20 independent trajectories were generated for each mutant.
Simulations of VemP were performed analogously to SecM, albeit with a force loading rate of 35 pN/ns. Initially, 30 simulations were run until the minimum of the pulling harmonic potential was 40 Å away from the initial position of the VemP N-terminal α-carbon, corresponding to a simulation time of 80 ns. However, this was insufficient to disrupt the upper helix of VemP, and further extension would bring the N-terminus of VemP near the periodic boundary of the simulation. To overcome this, after each trajectory was pulled for 80 ns, the simulation was halted, and all amino acids of the nascent chain that were fully extended (i.e., and dihedral angles are within 30° of straight (180°) and remains so for 10 frames) were removed. Simulation was then resumed, with the distance restraint adjusted such that the applied force at the end of the previous simulation and start of the new simulation were the same. This procedure was repeated until all VemP amino acids were fully extended. No more than two rounds of truncation and restart were required to fully extend the nascent chain.
Trajectory analysis
Assigning states based on force traces
To enable identification of states over the ensemble of trajectories, force traces are compared after subtracting the linear rate of increase of force with time. Note that this rate of increase is not equivalent to the force loading rate when the spring constant of potential used to apply the pulling force is greater than the curvature of the energy landscape around a state (28), as was found to be the case in our simulations. To determine the observed rate of force increase, the beginning and end points of a linear segment are identified by finding all the local minima and maxima in a given trace. To avoid identifying spurious extrema caused by noise in the force trace, the trace is smoothed with a moving average filter and any extrema within 50 frames of another extremum are neglected, thus enforcing a minimal length for the identified linear segments (see Fig. 1 C for example results). The slope of these segments can then be calculated, revealing a singly peaked distribution with fat tails (Fig. S2, A–C). The distributions of slopes from trajectories with different pulling rates are comparable after dividing by the pulling velocities, i.e., calculating the force increase per angstrom of trap movement. The median of the combined distributions is then used as the slope to flatten each of the force traces, which are subsequently binned and fit to a mixture distribution composed of the sum of Gaussians to define the five states (Fig. S2, D–F). The assumption that a single rate of force increase is appropriate for all of the states is equivalent to assuming that the curvature of the energy landscape in each state is similar. Each frame is assigned to one of the five states based on which of the five Gaussians has the highest probability density at the force associated with that frame.
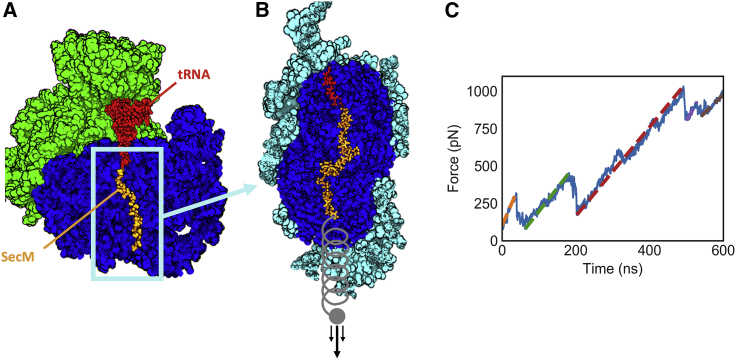
Figure 1.
Description of the simulation system and typical output. (A) cryo-EM structure of a SecM-stalled ribosome is shown (PDB: 3JBU). Only the region of the ribosome surrounding the nascent chain is included in our simulations. (B) The simulated part of the ribosome is shown, with atoms shown in cyan harmonically restrained. A ramping force is applied to the N-terminus of the nascent chain. (C) The result of a SecM pulling trajectories is shown. Several regions of linear extension can be identified (colored dashed lines), corresponding to different stable conformations of the nascent chain. Note that, for visual clarity, the structures in (A) and (B) do not show atoms that are nearer to the viewer than the nascent chain. To see this figure in color, go online.
Conformational analysis
After each frame has been assigned to a state based on the force trace, the conformational changes between states are characterized in terms of the dihedral angles. Specifically, for a given state i and amino acid a, the dihedral distance is defined by . Averages of a dihedral angle are taken over all frames belonging to a given state and are calculated as circular quantities, i.e., angles are converted to Cartesian coordinates, averaged, and then converted back to an angle.
Calculation of tension and work
To calculate the tension on the nascent chain, the forces induced by extension or contraction of the backbone covalent bonds are recorded. In particular, for each amino acid in the protein backbone, the bond distances between the amide nitrogen to α-carbon, between the α-carbon to carbonyl carbon, and between the carbonyl carbon and the subsequent amino acid’s amide nitrogen are recorded. These distances were then converted into forces based on the AMBER99SB-ILDN force field parameters (26). The forces from these three bonds are then averaged into a single quantity for each amino acid. This calculation is performed over all the frames in each state, as well as the equilibration trajectory in which no pulling force was applied. Tension on each amino acid is compared relative to the tension during equilibration and reported in Fig. 4 C and Fig. S7.
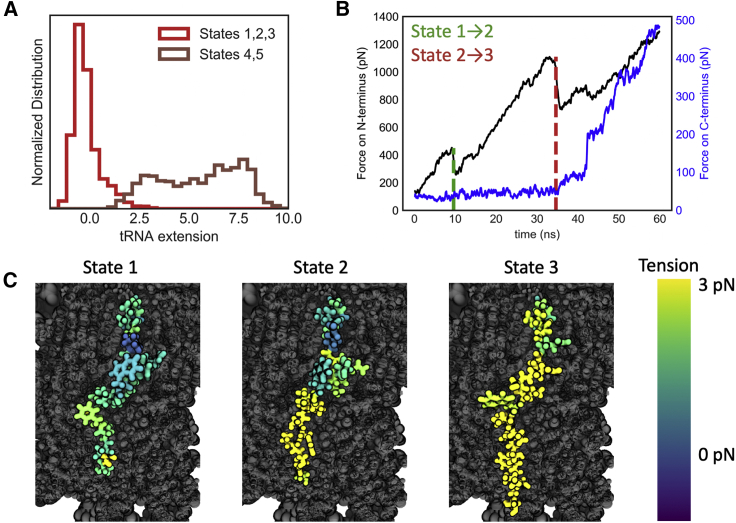
Figure 4.
Identifying which states could correspond to restart of synthesis. (A) Distributions of the extension of the 3′ hydroxyl group of the tRNA nucleotide that is bonded to the nascent chain beyond its position during equilibration are shown. Extension is measured in the direction of pulling. States 4 and 5 are unphysically extended. The data are taken from the 30 independent 5 pN/ns trajectories. (B) Simulations of SecM were run with the force on the N-terminus ramped at 50 pN/ns, as previously, but now with the C-terminal Arg163 fixed by a harmonic restraint. The pulling force is plotted in black, and the amount of force that is acting on Arg163 is plotted in blue. The force only increases above its basal level until after the transition to state 3. The transitions between states 1–2 and 2–3 were determined by the frame in which residues Ser151 and Ser157 respectively straighten. (C) Characteristic conformations of each state are shown, colored by the magnitude of the tension along the nascent chain relative to the tension in the equilibration trajectory. Tension only reaches the C-terminal amino acids once state 3 is reached. To see this figure in color, go online.
The work to reach a state is calculated as the integral of the applied force from the start of a trajectory until all the dihedral conformational changes characteristic of the given state are observed. Specifically, state 2 is reached when Ser151 is straightened; state 3 is reached when Ser157, Gln158, and Ala159 are all straightened; and state 4 is reached when Arg163 is straightened. A dihedral angle is straightened when the dihedral angle is within 30° of straight (180°) and remains so for 10 frames.
Results and discussion
Pulling-force trajectories
The force-induced restart of stalled ribosomes is a nonequilibrium biomolecular process that occurs on the timescale of seconds to minutes. Microsecond-timescale MD with an applied force on the nascent protein provides insight into these nonequilibrium effects and allows for the direct visualization of the motions and forces of the nascent chain throughout the stall-breaking pathway. Simulations are initialized using cryo-EM structures of SecM- and VemP-stalled ribosomes. SecM stalls the ribosome in many states during synthesis, and several of these states have been characterized structurally (13,14,29). Simulations of SecM were started from the structure corresponding to the earliest point in translation (PDB: 3JBU), in which Pro-tRNA has not yet bound to the ribosome (Fig. 1 A). To reduce computational cost, the ribosomes in both SecM and VemP structures are truncated beyond a 23 Å radius around the nascent chain, with an outer shell of 3 Å restrained to preserved the structure of the ribosome (Fig. 1 B; Materials and methods). With the exception of the areas near the nascent peptide and the PTC, the conformations of the 50S subunit of SecM-stalled and unstalled ribosomes are similar (13,14,30), so the dynamics of the ribosome 20 Å away from the PTC is not expected to influence the restart pathway. After truncation, the starting structures were relaxed using 1 s of equilibrium MD. During equilibration, the initial conformation of the nascent protein and ribosome around the PTC was well conserved. Small rearrangements were observed around the N-terminus of SecM (Fig. S1).
To simulate force-induced stall breaking, we apply a force on the nascent chain by placing the N-terminal α-carbon in a harmonic potential, with the minimal energy position of the harmonic potential moving out of the exit tunnel at constant velocity. This protocol mimics the commonly used force-ramping protocol in optical tweezer experiments (3,31,32). To observe stall breaking on a timescale accessible to simulation, it is necessary to pull with a faster force-ramping protocol than is done experimentally. We run simulations over two orders of magnitude in force loading rates (0.5, 5, and 50 pN/ns). These loading rates lead to rupture forces between 100 and 1000 pN and timescales from 50 ns to 5 s. Although this is faster than the presumed experimental timescale of seconds (3,29), the wide range of pulling forces applied allows us to evaluate the consistency of our trajectories with varying simulation timescale. Additionally, our simulations match experimental estimates of the free energy barrier to stalling and the effects of mutations, supporting the assumption that the pathway of stall breaking is unchanged by the accelerated timescale of our simulations. Detailed analysis of over 100 independent trajectories allows for more detailed and statistically robust analysis than previous simulations of stalling peptide restart, which consisted of two force-pulling trajectories of 10 ns each (16). The large number of long trajectories (over 120 s total) was enabled by the use of the Anton2 computer (33). Descriptions of each trajectory are provided in Table S2.
Force propagation through stall-breaking intermediates
We first consider force-pulling simulations involving the SecM sequence because SecM is the best-characterized FSAP and has seen the most use in force-measurement experiments, enabling us to validate our methodology and make readily testable predictions. The force traces indicate that several distinct conformational changes occur within a typical trajectory (Fig. 1 C). The changes are evidenced by the sharp drops in the force trace, corresponding to moments in which the nascent chain extends along the direction of the applied force. Regions of the force trace in between these drops with linearly ramping force correspond to metastable intermediate states along the stall-breaking pathway. To identify states that are consistently observed across the 5 pN/ns trajectories, the linear rate of force increase (70 pN/Å) is subtracted from each force trace (Fig. 2 A; Materials and methods). This allows for direct comparison between force traces even though the times at which conformational changes occur are stochastic (34).
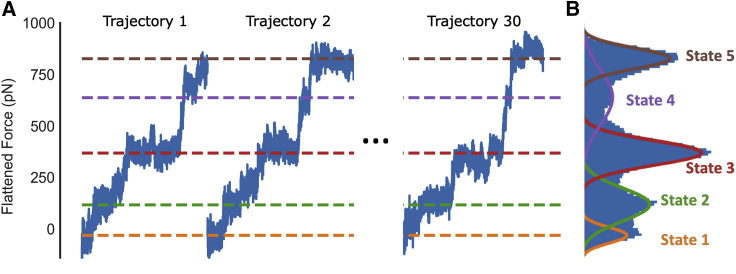
Figure 2.
Identifying states based on force traces. (A) Force traces from three representative simulations of SecM after a force ramp of 5 pN/ns has been subtracted are shown. Dashed lines indicate the peaks of the Gaussians that have been fit to the data in (B). (B) A histogram of the flattened force traces of all 30 trajectories run with a force loading rate of 5 pN/ns is shown. To see this figure in color, go online.
Combining the results of the ensemble of pulling-force trajectories reveals a distribution of applied forces with five peaks, with each peak corresponding to a conformational state that is robustly observed across the trajectories (Fig. 2 B). These data are then fit by a mixture distribution consisting of the sum five Gaussians. Each frame of the trajectories is assigned to one of the five states based on the force at that frame. Each state may contain substates that give rise to small drops in the force trace within a given state (e.g., in Fig. 1 C); however, these substates are not consistent across different trajectories. Because these substate transitions are not conserved in the stall-breaking pathway and their infrequent occurrence makes robust analysis difficult, they were not further characterized. Repeating the above analysis on simulations conducted with a faster, 50 pN/ns loading rate reveals distributions of external forces that are also well fit assuming a five-state model (Fig. S2).
With thousands of configurational samples per state, the molecular motions that govern the transitions between the observed states can be characterized. Measuring the changes in dihedral angles between consecutive states on a per-amino-acid basis (Fig. 3; Video S1) reveals that the conformational changes between states are driven by rotations of only a few adjacent amino acids per transition. For all of the amino acids that undergo changes in dihedral angle, the rotation observed involves the straightening of the dihedral angle from a bent conformation to a 0° planar conformation. This extends the nascent chain in the direction of the applied force. The set of residues that rotate in each transition progresses toward the C-terminus of nascent chain with each successive transition, from Ser151 rotating in state 1, Ser157 and Gln158 in state 2, Gly161 in state 3, and finally to Arg163 and Ala164 rotating at the C-terminus in state 4. After a state transition, there is no evidence for any of the fully extended amino acids reforming interactions with the ribosome.
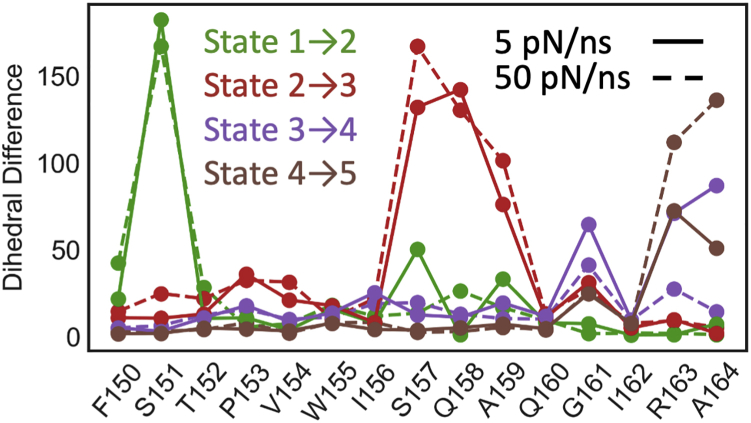
Figure 3.
Conformational changes are quantified for each amino acid in terms of the distance of the and dihedral angles between two states. The key differences between each state can be described by rotations in only a few amino acids per state. To see this figure in color, go online.
The ribosome is colored in blue, with the fully flexible region colored in dark blue and the restrained outer shell in cyan. The nascent chain is colored in orange, and the tRNA in red. Ribosomal atoms nearer to the viewer than the nascent chain are removed. As portions of the nascent chain straighten in response to the applied force, the fully straightened portions are colored in white. This region grows from the N-terminus to the C-terminus in distinct steps, corresponding to the five states characterized in Figs. 2 and 3.
The molecular descriptions of the states and the transitions between them are almost identical when simulations are performed with a 10× greater force-ramping rate (Fig. 3). The same analysis performed on trajectories run with the slower ramping rate of 0.5 pN/ns identified nearly identical conformational changes for each state transition, albeit with some overlap between the peaks that is likely due to the difficulty in assigning states with only five trajectories (Fig. S3). The rotation of the specific amino acids listed above defines a robust molecular pathway that describes the conformational changes SecM undergoes when subjected to an applied force on the N-terminus. It is important to note, however, that the amino acids undergoing dihedral rotation between states are not necessarily responsible for the free energy barrier between states. The key interactions that maintain the states will be investigated in a later section using computational mutagenesis.
Connecting peptide conformation to restart of translation
We now identify the state during force propagation that first allows the restart of translation. The five amino acids at the C-terminus of SecM are all essential to its stalling behavior, as well as being the closest to the site of new bond formation (10). It is therefore expected that only conformations in which the essential C-terminal residues have been affected by the force could allow restart of synthesis. The most dramatic movement of these amino acids occurs during the transition from states 3 to 4 when Arg163 and Ala164 straighten (Fig. 3). However, this transition is unlikely to occur under physiological conditions because it coincides with an unphysical extension of the tRNA. Characterizing the movement of the tRNA nucleotide that is covalently bonded to the nascent protein reveals that the tRNA maintains a stable position until the transition to state 4, at which point it is pulled several angstroms into the exit tunnel (Fig. 4 A). This extension is enabled by the breaking of the stacking interactions between the nucleobases in the tRNA (Fig. S4) in a manner which, to our knowledge, has not been observed in vivo. To further evaluate the possible relevance of the 3-to-4 transition, we estimated the height of the free energy barrier by fitting the observed distribution of state transition times to a probabilistic model of force-induced barrier crossing proposed by Bullerjahn et al. (Figs. S9 and S10; Table S1; (28)). This leads to an estimate for the barrier height of 120 kT (90% confidence interval (CI): 110–160 kT), which could not be crossed on biologically relevant timescale without forces far stronger than what can be exerted by SecA, estimated to be around 10 pN (35). The analyses of the conformational changes and the energetics of the state 3–4 transition both indicate that state 4 is physiologically inaccessible and therefore that restart must occur in state 3 or before.
For restart to occur, the conformation of the amino acids at the PTC must be disrupted by the applied force. This occurs only in state 3 and later (Fig. 3), suggesting that the transition from states 2 to 3 is necessary for restart of synthesis to occur. To precisely determine when the amino acids at the PTC experience pulling forces, simulations are run with a harmonic restraint on the α-carbon of the essential Arg163 (Fig. 4 B). The displacement of the restrained α-carbon reports on the force that atom experiences. Until SecM enters state 3, no significant forces are felt by Arg163, and restart of translation cannot occur. This held true across several different simulation protocols, including with two different loading rates and when the restraint was placed on Gly165 rather than Arg163 (Fig. S5). The inhibited force transmission in SecM contrasts with previously published results that measured force transmission in a nonstalling peptide and found no significant difference between the forces at the N- and C-termini (23).
To further confirm the mechanistic significance of the transition from state 2 to state 3, the tension along the backbone of the nascent chain is measured (Materials and methods). Tension in the nascent chain around the PTC only increases after state 3 is reached (Fig. 4 C). Analysis of the computed tensions as a function of position along the nascent chain leads to the same conclusions as those reached above while having the advantage of not requiring an artificial restraint and providing measurements from all SecM amino acids, instead of just the restrained atom. However, the tension fluctuates dramatically with time, and meaningful comparisons can only be made after averaging over all the frames in a state.
Both metrics of tracking the intrachain forces during a pulling trajectory indicate that overcoming the first barrier and entering the second state could not lead to a restart of translation. Only once the third state is entered does the force reach the C-terminus and enable disruption of the interactions around the PTC that hold the stall in place. Additionally, our estimate of the free energy barrier between states 2 and 3 is 27 kT (90% CI: 21–76 kT), which makes this transition the last energetically accessible step. The 4-kT (90% CI: 3–8 kT) barrier between states 1 and 2 can be overcome by thermal motion, whereas the 120-kT (90% CI: 110–160 kT) barrier between steps 3 and 4 is physiologically insurmountable, requiring the disruption of tRNA stacking. Taken together, this indicates that arrival at state 3 is both necessary and sufficient for stall breaking.
Force transduction in mutant arrest peptides
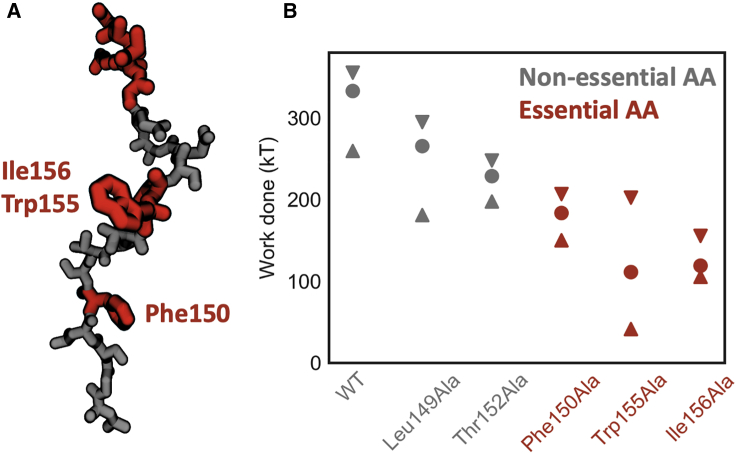
The extent to which mutations in SecM affect the response to an applied force is poorly understood. The majority of previous studies of the stalling of SecM mutants were performed in the absence of the translocation machinery that physiologically exerts the forces necessary to relieve the stall (10,11,20). These experiments identify which amino acids are essential for stalling but do not indicate which mutants alter force sensitivity. An extensive study on the force responsiveness of a series of mutants of a SecM sequence derived from Mannheimia succiniciproducens (Ms-SecM) identified a number of sequences with enhanced resistance to pulling force, and these variants have found subsequent use in characterizing biophysical processes that induce a wide range of forces (36). However, the substantial differences in sequence between Ms-SecM and the more commonly studied E. coli SecM, combined with the lack of a structure of Ms-SecM, make it difficult to rationalize the effects of the mutants in molecular terms. We thus employ MD simulations to explore how mutants alter the barriers to force propagation along the nascent chain. Several amino acids in SecM were individually mutated to alanine, equilibrated for 250 ns, and then resimulated with a force loading rate of 50 pN/ns. From these trajectories, the work required to pull the mutant into the restart-competent state 3 is calculated. Work is a convenient metric because it includes the effect of mutations on both the state 1–2 and 2–3 transitions. To focus on the effects due to force propagation rather than the conformational changes at the PTC that may occur upon mutation, mutations were made only to amino acids more than 10 Å away from the PTC. Five mutants were simulated: three were found experimentally to reduce stalling efficiency in the absence of an applied force (F150A, W155A, I156), and two were not observed to have an effect on stalling (L149A, T152A). The three mutants that required the least amount of work to restart were the same three that were found to experimentally reduce stalling efficiency (Fig. 5 B; (11)). Beyond the mutagenesis experiments, F150 and W155A were both identified in the cryo-EM study as forming specific interactions with the exit tunnel (13). Further evidence for a strong pairwise interaction between the ribosome and W155 comes from the reorientation of A751 in the 23S ribosomal RNA as the π-stacking interaction between W155 and A751 is broken (Fig. S6). Aside from this localized rearrangement, the structure of the exit tunnel is largely unchanged between states 1 and 3 (Fig. S6).
Figure 5.
Exploring the role of the essential amino acids in the restart process. (A) A snapshot of SecM with the amino acids whose identity is essential to effective stalling colored in red is shown. (B) Mean work done to reach the restart-competent state 3 is shown. The mutants colored gray are those which were experimentally found to have little effect on stalling, whereas the red mutants led to a significant reduction in stalling. Error bars indicate 95% confidence intervals on the mean. Stars indicate mutants for which the mean of the work done was significantly different from the WT work according to a t-test with unequal variances and a threshold of . To see this figure in color, go online.
The findings presented so far have broad implications for the process of force-induced restarting of stalled peptides. Firstly, it provides an explanation for why the specific identity of amino acids is essential even when they are tens of angstroms away from the PTC because the force is unable to propagate beyond these amino acids until specific interactions with the ribosomal exit tunnel are broken (Fig. 4 A). The interactions formed by these residues should also be capable of blocking or damping fluctuations on the chain, which provides a connection to mutagenesis studies that investigate stalling behavior at zero applied force (11,12,20). This mechanism also suggests that mutating these essential amino acids lower in the chain would be the most effective strategy for tuning the force response properties of SecM. Mutations of the essential residues at the C-terminus, such as Arg163, would be more likely to abrogate the stall entirely rather than change its sensitivity to an applied force. Additional variants of SecM with altered response to force would aid the use of FSAPs as in vivo force sensors because the diversity of biological processes that arrest peptides can report on is limited by the dynamic range of the reporters (22).
Alternative stall sequences
Simulations of SecM suggest a mechanism in which interactions between the nascent chain and the ribosome inhibit force propagation to the PTC and prevent restart of translation until those interactions are disrupted. To evaluate the generality of this mechanism, a second FSAP was investigated, VemP. As with SecM, force-sensitive stalling of VemP regulates the expression of protein translocation components (37). However, a recent structure of VemP stalled in the ribosome exit tunnel showed that VemP adopts a conformation in the exit tunnel highly dissimilar to SecM (Fig. 6 A; (19)). Unlike SecM, the VemP nascent chain is highly compacted with clear secondary structure: two helical regions in the upper and lower sections of the peptide. The upper helix is principally responsible for inducing the stall, with several amino acids interacting with ribosomal nucleotides in such a way as to block peptide bond formation. It has been proposed that a force applied to the nascent chain could unravel the upper helix, thereby disrupting these interactions with the ribosome and enabling the restart of translation (19). Because of the very different stalled conformation of VemP, it provides a stringent test of the generality of the mechanism uncovered for the force-induced restarting of SecM.
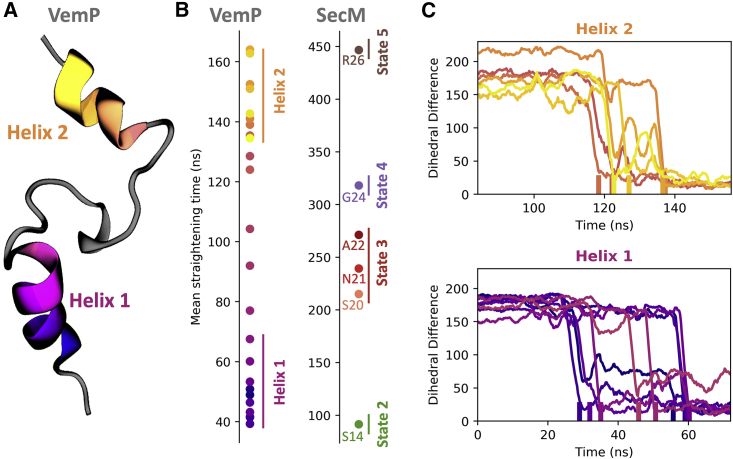
Figure 6.
Force-induced conformational changes in VemP. (A) The structure of the stalled VemP nascent chain, with the two helical regions colored, is shown. (B) The straightening time for different amino acids in VemP and SecM averaged over 30 trajectories, using a force loading rate of 35 pN/ns for VemP and 50 pN/ns for SecM, is shown. (C) A time series of the deviation of the dihedral angles in helices 1 and 2 from the fully extended conformation, taken from a representative trajectory, is shown. The amino acids within a helix do not straighten in consecutive order. To see this figure in color, go online.
Following the same protocol used to study SecM, simulations of VemP were prepared from its cryo-EM structure (PDB: 5NWY), with the ribosome cutoff and restrained beyond a 23 Å radius. Force was applied on the N-terminus along the direction of the exit tunnel with a force loading rate of 35 pN/s. Because of the high degree of compaction in VemP, if the nascent chain were fully extended from its starting configuration, the N-terminus would extend well outside the ribosome exit tunnel and require a large simulated periodic box. To reduce the total simulation volume, a pulling trajectory is divided into three parts, and the fully extended portion of the nascent chain is removed at the end of each third (Materials and methods). This relies on the assumption that the fully extended nascent chain will not inhibit the propagation of the applied force.
The N-terminal helix unravels strictly before the C-terminal helix, as measured by the average time at which the dihedral angles of each residue straighten (Fig. 6 B). This suggests that, as with SecM, interactions formed further from the PTC must be broken before force can propagate to residues nearer the PTC. Tracking tension throughout the simulations also indicates that the tension in the C-terminal helix near the PTC does not increase until the N-terminal helix is unraveled (Fig. S5).
However, the presence of secondary structure in VemP also leads to notable differences in the mechanism of restart. One such difference is that the straightening of amino acids within a helix does not necessarily occur consecutively. This can be seen both in the straightening times of the amino acids averaged over all trajectories (Fig. 6 B) and individual trajectories (Fig. 6 C). In Fig. 6, the amino acids and the markers for their transitions are colored from darker to lighter from the N-terminus to the C-terminus. If the order of straightening was strictly consecutive, the ordering of colors in Fig. 6, B and C would become monotonically lighter with time. This is evidently not the case within both helices 1 and 2. In fact, not only is the order of unraveling of different turns of a helix not consecutive, it is also not conserved across independent trajectories simulated with the same protocol (Fig. S8).
The underlying reason for the difference in ordering between SecM and VemP arises from the fact that the interactions found in SecM are between the nascent chain and the ribosome, whereas the interactions within a VemP helix are between different VemP amino acids. Interactions between the nascent chain and ribosome hold the nascent chain in place relative to the exit tunnel. Intrachain interactions in a helix still allow the helix to move as whole in response to a force, which allows force to propagate through the helix. In consequence, interactions within and downstream of a helix break are in order of their free energy barriers. For example, if there is a weak interaction between the nascent chain and the exit tunnel that is C-terminal of a helix, then that weak interaction can be broken by an applied force before the α-helix is disrupted. Conversely, if the exit-tunnel-nascent-chain interaction is stronger than the intrahelical interactions, then the α-helix will be disrupted first. The similar free energy barriers for unfolding different turns of the same helix are likely why heterogeneity is observed in the breaking order within a helix between trajectories. This difference between inter- and intrachain interactions can also explain why the middle portion of VemP, which lacks secondary structure, straightens in consecutive order.
Because of the greater cost of simulations of the longer VemP peptide, there are still several open questions regarding how its secondary structure responds to a pulling force. For instance, we were not able to investigate how the order of unraveling within a helix depends on an applied force, although we hypothesize that the heterogeneity would only increase at lower forces as thermal motion becomes more important (38). The lack of trajectories at longer timescales also prevents estimation of free energy barriers, as was done with SecM. Although challenging, this could be a particularly fruitful direction for future simulations because the barrier height determines whether nascent chain-ribosome or intrachain interactions will break first. Additionally, although it was not observed in these trajectories, steric interactions between an α-helix and a constricted region in the exit tunnel may force consecutive unraveling of the α-helix as it needs to pass through the constriction zone. Despite these open questions, simulations of VemP revealed clear similarities and differences as compared with SecM. VemP exhibits nonconsecutive breaking of interactions within a helix, whereas the interactions in SecM are disrupted consecutively from the N-terminus to the C-terminus. Importantly, both stalling peptides still require N-terminal interactions between the nascent chain and the exit tunnel to be broken before the critical conformation stalling the PTC can be disrupted.
Conclusion
The results presented here reveal a mechanism for force-induced restart of ribosomal translation in which cotranslational force propagation is governed by both interactions between the nascent chain and the ribosome and intranascent chain interactions. Simulations identified a pathway of sequential conformational changes in SecM that are required in order for a force applied at the N-terminal end of SecM to propagate to the PTC. This pathway was found to be consistent over two orders of magnitude of force-ramping rate, and mutations that were experimentally found to reduce the stalling efficacy of SecM in the absence of force also reduced the work required to progress through the various conformational changes. Analysis of the VemP restarting pathway revealed a distinct force propagation mechanism in which intrahelical interactions are broken stochastically and helix 1 was necessarily unraveled before helix 2 could be unfolded by the applied force. The results from both SecM and VemP highlight a previously underappreciated distinction between amino acids in FSAPs that induce stalling through specific interactions with the ribosome around the PTC and those that stabilize the conformation of the nascent chain and shield the residues at the PTC from external forces. We believe the latter interactions should be the principal target of mutagenesis aimed to alter the force sensitivity of FSAPs because mutations to amino acids around the PTC are likely to reduce stalling efficiency even in the absence of an applied force.
Understanding cotranslational force propagation is essential for understanding not only the restarting of FSAPs but also other cotranslational processes that are affected by pulling forces, such as translation rate or frameshifting (23,24) Comparison between the pulling-force simulations of SecM and VemP emphasizes the role of interactions between the nascent chain and the exit tunnel, which block further propagation of force up the nascent chain. This is contrasted with intrachain interactions such as in α-helices, which can move as a unit and therefore do not inhibit the propagation of force and allow breaking of interactions in nonconsecutive order. The force-induced restarting pathways of SecM and VemP both highlight the need to consider potential interactions between the nascent chain and the ribosome when estimating the cotranslational forces experienced by the ribosome (39,40). Fortunately, characterization and understanding of interactions between a nascent peptide and the exit tunnel are becoming increasingly available thanks to the rapid expansion of cryo-EM structural data. Future simulations will provide an essential connection between the study of nascent chain behavior in the exit tunnel (41, 42, 43) and the role of forces in influencing cotranslational behavior (24,40).
Author contributions
All authors contributed to the design of the research. M.H.Z. performed the simulations and processed data. All authors analyzed the results and wrote the manuscript.
Acknowledgments
Anton 2 computer time was provided by the Pittsburgh Supercomputing Center (PSC) through Grant R01GM116961 from the National Institutes of Health. The Anton 2 machine at PSC was generously made available by D. E. Shaw Research. This work was also supported by a grant from NIGMS, National Institutes of Health (R01GM125063), to T.F.M. and M.H.Z.
Editor: Thomas Perkins.
Footnotes
Supporting material can be found online at https://doi.org/10.1016/j.bpj.2021.03.041.
Supporting citations
References (44, 45, 46, 47) appear in the Supporting material
Supporting material
References
- 1.Ito K., Chiba S. In: Regulatory Nascent Polypeptides. Ito K., editor. Springer; 2014. Biological significance of nascent polypeptides that stall the ribosome; pp. 3–20. [Google Scholar]
- 2.Wilson D.N., Arenz S., Beckmann R. Translation regulation via nascent polypeptide-mediated ribosome stalling. Curr. Opin. Struct. Biol. 2016;37:123–133. doi: 10.1016/j.sbi.2016.01.008. [DOI] [PubMed] [Google Scholar]
- 3.Goldman D.H., Kaiser C.M., Bustamante C. Mechanical force releases nascent chain-mediated ribosome arrest in vitro and in vivo. Science. 2015;348:457–460. doi: 10.1126/science.1261909. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Oliver D., Norman J., Sarker S. Regulation of Escherichia coli secA by cellular protein secretion proficiency requires an intact gene X signal sequence and an active translocon. J. Bacteriol. 1998;180:5240–5242. doi: 10.1128/jb.180.19.5240-5242.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Ismail N., Hedman R., von Heijne G. A biphasic pulling force acts on transmembrane helices during translocon-mediated membrane integration. Nat. Struct. Mol. Biol. 2012;19:1018–1022. doi: 10.1038/nsmb.2376. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Chen X., Rajasekaran N., Kaiser C.M. Synthesis runs counter to directional folding of a nascent protein domain. Nat. Commun. 2020;11:5096. doi: 10.1038/s41467-020-18921-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Cymer F., Heijne G.v. Cotranslational folding of membrane proteins probed by arrest-peptide-mediated force measurements. Proc. Natl. Acad. Sci. USA. 2013;110:14640–14645. doi: 10.1073/pnas.1306787110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Ismail N., Hedman R., von Heijne G. Charge-driven dynamics of nascent-chain movement through the SecYEG translocon. Nat. Struct. Mol. Biol. 2015;22:145–149. doi: 10.1038/nsmb.2940. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Farías-Rico J.A., Goetz S.K., von Heijne G. Mutational analysis of protein folding inside the ribosome exit tunnel. FEBS Lett. 2017;591:155–163. doi: 10.1002/1873-3468.12504. [DOI] [PubMed] [Google Scholar]
- 10.Yap M.N., Bernstein H.D. The plasticity of a translation arrest motif yields insights into nascent polypeptide recognition inside the ribosome tunnel. Mol. Cell. 2009;34:201–211. doi: 10.1016/j.molcel.2009.04.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Nakatogawa H., Ito K. The ribosomal exit tunnel functions as a discriminating gate. Cell. 2002;108:629–636. doi: 10.1016/s0092-8674(02)00649-9. [DOI] [PubMed] [Google Scholar]
- 12.Yap M.N., Bernstein H.D. The translational regulatory function of SecM requires the precise timing of membrane targeting. Mol. Microbiol. 2011;81:540–553. doi: 10.1111/j.1365-2958.2011.07713.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Zhang J., Pan X., Sui S.F. Mechanisms of ribosome stalling by SecM at multiple elongation steps. eLife. 2015;4:e09684. doi: 10.7554/eLife.09684. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Bhushan S., Hoffmann T., Beckmann R. SecM-stalled ribosomes adopt an altered geometry at the peptidyl transferase center. PLoS Biol. 2011;9:e1000581. doi: 10.1371/journal.pbio.1000581. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Schmeing T.M., Huang K.S., Steitz T.A. An induced-fit mechanism to promote peptide bond formation and exclude hydrolysis of peptidyl-tRNA. Nature. 2005;438:520–524. doi: 10.1038/nature04152. [DOI] [PubMed] [Google Scholar]
- 16.Gumbart J., Schreiner E., Schulten K. Mechanisms of SecM-mediated stalling in the ribosome. Biophys. J. 2012;103:331–341. doi: 10.1016/j.bpj.2012.06.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Arenz S., Bock L.V., Wilson D.N. A combined cryo-EM and molecular dynamics approach reveals the mechanism of ErmBL-mediated translation arrest. Nat. Commun. 2016;7:12026. doi: 10.1038/ncomms12026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Seidelt B., Innis C.A., Beckmann R. Structural insight into nascent polypeptide chain-mediated translational stalling. Science. 2009;326:1412–1415. doi: 10.1126/science.1177662. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Su T., Cheng J., Beckmann R. The force-sensing peptide VemP employs extreme compaction and secondary structure formation to induce ribosomal stalling. eLife. 2017;6:e25642. doi: 10.7554/eLife.25642. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Bracken H.A., Woolhead C.A. Increased freedom of movement in the nascent chain results in dynamic changes in the structure of the SecM arrest motif. Biosci. Rep. 2019;39 doi: 10.1042/BSR20181246. BSR20181246. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Sohmen D., Chiba S., Wilson D.N. Structure of the Bacillus subtilis 70S ribosome reveals the basis for species-specific stalling. Nat. Commun. 2015;6:6941. doi: 10.1038/ncomms7941. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Cymer F., Hedman R., von Heijne G. Exploration of the arrest peptide sequence space reveals arrest-enhanced variants. J. Biol. Chem. 2015;290:10208–10215. doi: 10.1074/jbc.M115.641555. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Fritch B., Kosolapov A., O’Brien E.P. Origins of the mechanochemical coupling of peptide bond formation to protein synthesis. J. Am. Chem. Soc. 2018;140:5077–5087. doi: 10.1021/jacs.7b11044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Harrington H.R., Zimmer M.H., Schlebach J.P. Cotranslational folding stimulates programmed ribosomal frameshifting in the alphavirus structural polyprotein. J. Biol. Chem. 2020;295:6798–6808. doi: 10.1074/jbc.RA120.012706. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Mitra K., Schaffitzel C., Frank J. Elongation arrest by SecM via a cascade of ribosomal RNA rearrangements. Mol. Cell. 2006;22:533–543. doi: 10.1016/j.molcel.2006.05.003. [DOI] [PubMed] [Google Scholar]
- 26.Lindorff-Larsen K., Piana S., Shaw D.E. Improved side-chain torsion potentials for the Amber ff99SB protein force field. Proteins. 2010;78:1950–1958. doi: 10.1002/prot.22711. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Bowers K.J., Chow E., Shaw D.E. IEEE; 2006. Scalable algorithms for molecular dynamics simulations on commodity clusters; p. 43. (SC’06: Proceedings of the 2006 ACM/IEEE Conference on Supercomputing). [Google Scholar]
- 28.Bullerjahn J.T., Sturm S., Kroy K. Theory of rapid force spectroscopy. Nat. Commun. 2014;5:4463. doi: 10.1038/ncomms5463. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Tsai A., Kornberg G., Puglisi J.D. The dynamics of SecM-induced translational stalling. Cell Rep. 2014;7:1521–1533. doi: 10.1016/j.celrep.2014.04.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Polikanov Y.S., Steitz T.A., Innis C.A. A proton wire to couple aminoacyl-tRNA accommodation and peptide-bond formation on the ribosome. Nat. Struct. Mol. Biol. 2014;21:787–793. doi: 10.1038/nsmb.2871. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Elms P.J., Chodera J.D., Marqusee S. The molten globule state is unusually deformable under mechanical force. Proc. Natl. Acad. Sci. USA. 2012;109:3796–3801. doi: 10.1073/pnas.1115519109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Woodside M.T., Block S.M. Reconstructing folding energy landscapes by single-molecule force spectroscopy. Annu. Rev. Biophys. 2014;43:19–39. doi: 10.1146/annurev-biophys-051013-022754. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Shaw D.E., Grossman J.P., Young C. IEEE; 2014. Anton 2: raising the bar for performance and programmability in a special-purpose molecular dynamics supercomputer; pp. 41–53. (SC’14: Proceedings of the International Conference for High Performance Computing, Networking, Storage and Analysis). [Google Scholar]
- 34.Dudko O.K., Hummer G., Szabo A. Theory, analysis, and interpretation of single-molecule force spectroscopy experiments. Proc. Natl. Acad. Sci. USA. 2008;105:15755–15760. doi: 10.1073/pnas.0806085105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Gupta R., Toptygin D., Kaiser C.M. The SecA motor generates mechanical force during protein translocation. Nat. Commun. 2020;11:3802. doi: 10.1038/s41467-020-17561-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Nicolaus F., Metola A., Von Heijne G. Residue-by-residue analysis of cotranslational membrane protein integration in vivo. eLife. 2021;10:e64302. doi: 10.7554/eLife.64302. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Ishii E., Chiba S., Mori H. Nascent chain-monitored remodeling of the Sec machinery for salinity adaptation of marine bacteria. Proc. Natl. Acad. Sci. USA. 2015;112:E5513–E5522. doi: 10.1073/pnas.1513001112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Dudko O.K., Mathé J., Hummer G. Extracting kinetics from single-molecule force spectroscopy: nanopore unzipping of DNA hairpins. Biophys. J. 2007;92:4188–4195. doi: 10.1529/biophysj.106.102855. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Leininger S.E., Trovato F., O’Brien E.P. Domain topology, stability, and translation speed determine mechanical force generation on the ribosome. Proc. Natl. Acad. Sci. USA. 2019;116:5523–5532. doi: 10.1073/pnas.1813003116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Leininger S.E., Narayan K., O’Brien E.P. Mechanochemistry in translation. Biochemistry. 2019;58:4657–4666. doi: 10.1021/acs.biochem.9b00260. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Nilsson O.B., Hedman R., von Heijne G. Cotranslational protein folding inside the ribosome exit tunnel. Cell Rep. 2015;12:1533–1540. doi: 10.1016/j.celrep.2015.07.065. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Tian P., Steward A., Best R.B. Folding pathway of an Ig domain is conserved on and off the ribosome. Proc. Natl. Acad. Sci. USA. 2018;115:E11284–E11293. doi: 10.1073/pnas.1810523115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Kaiser C.M., Liu K. Folding up and moving on-nascent protein folding on the ribosome. J. Mol. Biol. 2018;430:4580–4591. doi: 10.1016/j.jmb.2018.06.050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Kramers H.A. Brownian motion in a field of force and the diffusion model of chemical reactions. Physica. 1940;7:284–304. [Google Scholar]
- 45.Bell G.I. Models for the specific adhesion of cells to cells. Science. 1978;200:618–627. doi: 10.1126/science.347575. [DOI] [PubMed] [Google Scholar]
- 46.Dudko O.K., Hummer G., Szabo A. Intrinsic rates and activation free energies from single-molecule pulling experiments. Phys. Rev. Lett. 2006;96:108101. doi: 10.1103/PhysRevLett.96.108101. [DOI] [PubMed] [Google Scholar]
- 47.Arya G. Models for recovering the energy landscape of conformational transitions from single-molecule pulling experiments. Mol. Simul. 2016;42:1102–1115. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
The ribosome is colored in blue, with the fully flexible region colored in dark blue and the restrained outer shell in cyan. The nascent chain is colored in orange, and the tRNA in red. Ribosomal atoms nearer to the viewer than the nascent chain are removed. As portions of the nascent chain straighten in response to the applied force, the fully straightened portions are colored in white. This region grows from the N-terminus to the C-terminus in distinct steps, corresponding to the five states characterized in Figs. 2 and 3.